EDP28 — problem solved by Terence Tao!

I imagine most people reading this will already have heard that Terence Tao has solved the Erdős discrepancy problem. He has blogged about the solution in two posts, a first that shows how to reduce the problem to the Elliott conjecture in number theory, and a second that shows (i) that an averaged form of the conjecture is sufficient and (ii) that he can prove the averaged form. Two preprints covering (i) and (ii) are here and here: the one covering (i) has been submitted to Discrete Analysis.

This post is therefore the final post of the polymath5 project. I refer you to Terry’s posts for the mathematics. I will just make a few comments about what all this says about polymath projects in general.

Recent news concerning the Erdos discrepancy problem

I’ve just learnt from a reshare by Kevin O’Bryant of a post by Andrew Sutherland on Google Plus that a paper appeared on the arXiv today with an interesting result about the Erdős discrepancy problem, which was the subject of a Polymath project hosted on this blog four years ago.

The problem is to show that if 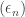is an infinite sequence of s, then for every there exist and such that has modulus at least . This result is straightforward to prove by an exhaustive search when . One thing that the Polymath project did was to discover several sequences of length 1124 such that no sum has modulus greater than 2, and despite some effort nobody managed to find a longer one. That was enough to convince me that 1124 was the correct bound.

However, the new result shows the danger of this kind of empirical evidence. The authors used state of the art SAT solvers to find a sequence of length 1160 with no sum having modulus greater than 2, and also showed that this bound is best possible. Of this second statement, they write the following: “The negative witness, that is, the DRUP unsatisfiability certificate, is probably one of longest proofs of a non-trivial mathematical result ever produced. Its gigantic size is comparable, for example, with the size of the whole Wikipedia, so one may have doubts about to which degree this can be accepted as a proof of a mathematical statement.”

I personally am relaxed about huge computer proofs like this. It is conceivable that the authors made a mistake somewhere, but that is true of conventional proofs as well. The paper is by Boris Konev and Alexei Lisitsa and appears here.

EDP27 — the modular version of Roth’s AP-discrepancy theorem

Recall from earlier posts Gil’s modular conjecture for HAPs. It states that if is large enough and is a function from to that never takes the value 0, then for every there exists a HAP such that mod . It is easy to see that this implies EDP, so it may well be very hard, or even false. However, one can hold out a little hope that, as with some strengthenings of statements, it is in fact easier, because it is in some way more symmetrical and fundamental. Given that, it makes good sense, as Gil has suggested, to try to prove modular versions of known discrepancy theorems, in the hope of developing general techniques that can then be tried out on the modular EDP conjecture.

A very obvious candidate for a discrepancy theorem that we could try to modularize is Roth’s theorem, which asserts that for any -valued function on there exists an arithmetic progression such that . That gives rise to the following problem.

Problem. Let be a prime. What is the smallest such that for every function that never takes the value 0, every can be expressed as for some arithmetic progression ?

In this post I shall collect together a few simple observations about this question.

EDP26 — three generalizations

This short post is designed as a possible way in to EDP for anyone who might be interested in participating but daunted by the idea of reading large amounts of material. One of the natural strategies for proving EDP is to try to formulate and prove stronger statements. At first that sounds paradoxical: isn’t it even harder to prove a stronger statement? But the answer to that question is often no. To give a slightly silly example, suppose you were asked to prove that for every there exists such that for every if is odd and has at least prime factors (counted with multiplicity), then mod , where is Euler’s totient function. You could make the problem easier by proving Euler’s theorem, that mod for every and every that is coprime to . You wouldn’t have as many hypotheses to use, but that’s good, since they can’t be used. Perhaps a better and more relevant example is when you generalize the class of numbers you are working with so as to allow a wider set of methods. For instance, suppose you want to prove that the largest possible product of three positive integers that add to 300 is at most . If you replace positive integers by positive reals, then you suddenly have available methods that you didn’t have before — for example, you could use compactness plus a lemma that says that if any two numbers are not equal then you can increase the product by replacing both of them by their average. (I’m not saying that’s the easiest proof — just that it’s a proof that you can’t do without first generalizing the statement.)

EDP25 — third guest post by Gil Kalai

The Polynomial Method

The polynomial method is another basic combinatorial technique that occasionally works. One way to describe the method is as a way to translate a combinatorial statement into the vanishing of a certain polynomial modulo .

A demonstration of the method

Theorem: Every graph (or hypergraph) G with n vertices and 2n+1 edges contains a nontrivial subgraph H with all vertex-degrees divisible by 3.

(This is a theorem of Noga Alon, Shmuel Friedland, and me from 1984.)

Before the proof: If we want to get a subgraph with all vertex degrees even then we need n edges (or n+1 edges for hypergraphs). This has a simple linear algebra proof which also gives an efficient algorithm.

EDP24 — an attempt to get back into the diagonal-decomposition approach

Gil has a not quite finished third post that will appear soon on this blog. Meanwhile, here are a few thoughts I’ve had recently as I tried to get my brain into EDP mode again.

The approach to the Erdős discrepancy problem that, rightly or wrongly, I found most promising when we were last working on it was to prove a certain statement about matrices that can be shown quite easily to imply a positive solution to the problem. In this post, I’m going to treat that matrix statement as the problem, and think about how one might go about trying to prove it. I’ll give the brief explanation of why it implies EDP, but not of what the possible advantages of the approach are (discussions of which can be found in some of the earlier material).

EDP23 — second guest post by Gil Kalai

The Large Deviation Heuristic: an example – triangle-free graphs

Here is a very general probabilistic-based heuristic that seems to give good predictions for questions related to EDP. I will refer to this heuristic as “LDH”. (In my polymath5 comments I referred to it as PH – probabilistic heuristic)). I am thankful to Noga Alon and to Yuval Peres for some helpful help.
Here is an example: Suppose we want to study the following extremal problem.

What is the largest number of edges in a graph on n vertices with no triangle.

If we use the probabilistic method we can ask what is the probability that a random graph in contains no triangle. As long as this probability is positive we know that a triangle-free graph with n vertices and m edges exists. (Being a little careful we can consider instead of where . Looking at random graphs gives us a perfectly correct proof of the assertion that there are triangle-free graphs with vertices and edges for every .

LDH:

1) Estimate naively the probability that a random graph in G(n,m) contains no triangle.

2) Choose m so that this estimated probability behaves like 1 over the number of graphs with n vertices and m edges.

EDP22 — first guest post by Gil Kalai

The purpose of this post is to ignite some new activity related to polymath5 about Erdős’ Discrepancy Problem. This post is thus a polymath5 research thread and comments (also unrelated to the suggestions in this post) are welcome.

The general form of a discrepancy problem

Let be a hypergraph, i.e., a collection of subsets of a ground set . The discrepancy of , denoted by is the minimum over all functions of the maximum over all of

.

We will mention one additional definition, that of hereditary discrepancy. When is a hypergraph and , the restriction of to is the hypergraph with vertex set whose edges are all sets of the form for edges of . The hereditary discrepancy of is the maximum over all of the discrepancy of restricted to .
Here is a link for a recent post discussing discrepancy and the famous Beck-Fiala theorem. The Beck-Fiala theorem assert that if every element in is included in at most sets in then . (Of course, the theorem applies also to the hereditary discrepancy.)

EDP: a possible revival

A few months ago, Gil Kalai got in touch to suggest that it was time to revisit Polymath5, the attempt to prove the Erdős discrepancy problem. I agreed, but we have both been rather busy in the interim, so it is only now that we are ready. One of the things that Gil did was write three posts, which I shall be putting up as guest posts, the first one today and the others over the next few days. I hope that people who contributed to the project the first time round will consider having another go, and that people who didn’t, but would be interested, will find that they can use the wiki that we created to record our progress to get up to speed with what is already known. Once Gil’s posts are up, I’ll probably write a post myself, and I hope that some serious work might start in early September. I always felt that when the original attempt petered out, it was just a kind of loss of energy that individual mathematicians often feel, rather than the result of hitting a brick wall. And just as having a break from a problem is often useful for individuals, I hope it will turn out to be for this polymath project. If it doesn’t, then maybe I’ll do something I meant to do much earlier, which is write up in paper form the progress that has already been made. (Of course, if I do that, then anybody is free to contribute to the writing.)

If you want to look at some of the earlier posts, they are collected together in the polymath5 category on this blog.

EDP21 — restrictions on possible proofs

The situation we are now in with EDP is roughly this. We have a statement that would imply EDP and that seems easier to prove because it is a reasonably simple existential statement (there exists a decomposition with certain properties) rather than a universal statement (every function has unbounded discrepancy on HAPs). However, the existential statement seems itself to be hard, despite one’s initial expectation that it ought to be easier. So what do we do?

One tool that we have at our disposal is duality, which is what we used to convert the problem to an existential one in the first place. Now obviously we don’t want to apply duality twice and end up with the original problem, but, perhaps surprisingly, there are ways that applying duality twice could be useful.

Here are two such ways. The first is that you prove that a certain kind of decomposition would be sufficient to prove EDP. Then you argue that if such a decomposition exists, then a more restricted kind of decomposition must also exist. Dualizing again, one ends up with a new discrepancy problem that is different from the original one (though it will imply it). The second way is this: if it is not easy to write down a decomposition that works, then one wants to narrow down the search space. And one way of doing that is to prove rigorously that certain kinds of decompositions do not exist. And an efficient way of doing that is to use duality: that is, one finds a function with low discrepancy on the class of sets that one was hoping to use for the decomposition. Since this class is restricted, solving the discrepancy problem is easier than solving EDP (but this time it doesn’t imply EDP).

We have already had an example of the first use of dualizing twice. In this post I want to give in detail an example of the second.