I’ve just learnt from a reshare by Kevin O’Bryant of a post by Andrew Sutherland on Google Plus that a paper appeared on the arXiv today with an interesting result about the Erdős discrepancy problem, which was the subject of a Polymath project hosted on this blog four years ago.
The problem is to show that if is an infinite sequence of
s, then for every
there exist
and
such that
has modulus at least
. This result is straightforward to prove by an exhaustive search when
. One thing that the Polymath project did was to discover several sequences of length 1124 such that no sum has modulus greater than 2, and despite some effort nobody managed to find a longer one. That was enough to convince me that 1124 was the correct bound.
However, the new result shows the danger of this kind of empirical evidence. The authors used state of the art SAT solvers to find a sequence of length 1160 with no sum having modulus greater than 2, and also showed that this bound is best possible. Of this second statement, they write the following: “The negative witness, that is, the DRUP unsatisfiability certificate, is probably one of longest proofs of a non-trivial mathematical result ever produced. Its gigantic size is comparable, for example, with the size of the whole Wikipedia, so one may have doubts about to which degree this can be accepted as a proof of a mathematical statement.”
I personally am relaxed about huge computer proofs like this. It is conceivable that the authors made a mistake somewhere, but that is true of conventional proofs as well. The paper is by Boris Konev and Alexei Lisitsa and appears here.
February 12, 2014 at 4:29 pm |
This is very nice! In my view a primary scientific achievement here is the ability to prove such a statement using a computer, and it is also good to know that the answer is at least 3.
February 12, 2014 at 4:39 pm |
[…] Update (February 2013): Boris Konev and Alexei Lisitsa found a sequence of length 1160 of discrepancy 2 and proved that no such sequence of length 1161 exists. A SAT Attack on the Erdos Discrepancy Conjecture The abstract reads: “We show that by encoding the problem into Boolean satisfiability and applying the state of the art SAT solvers, one can obtain a sequence of length 1160 with discrepancy 2 and a proof of the Erdos discrepancy conjecture for C=2, claiming that no sequence of length 1161 and discrepancy 2 exists. We also present our partial results for the case of C=3. See also this post. […]
February 13, 2014 at 1:37 am |
this is really way cool!!! … a gamechanger! cybersynchronicity…. was just citing some similar empirical SAT results recently on RJLs blog (who has written interesting stuff on EDP). a very big & bridge-theorem-like result that is likely to make people from both fields TCS/math really take some notice. inspires me to finally write up a blog on TCS empirical research. my big question is how they seemed to narrow down infinitary type assertions into a finite SAT proof. like the idea a lot but hope the authors will provide auxillary details/files somewhere on a web page to assist with 3rd party verification/replication/advancement efforts. will be interested to chat further with anyone with this on math.se or tcs.se ….
February 13, 2014 at 8:25 pm |
Nice.
A couple of observations about the example sequence of length 1160:
of length 1160:
The initial sequence is a maximal sequence of discrepancy 1.
is a maximal sequence of discrepancy 1. ) seems very multiplicative, at least on non-multiples of 3. In fact, the smallest
) seems very multiplicative, at least on non-multiples of 3. In fact, the smallest 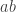 (not a multiple of 3) such that
(not a multiple of 3) such that 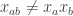 is
is  .
.
The sequence (or rather its negation, so that
February 13, 2014 at 9:58 pm
That’s interesting. I was looking forward to doing the kind of analysis on this sequence that we did on the sequences of length 1124. It would be great if someone could produce a nice visual version of it, arranged in rows of 24 with blue and green squares, as we did with the other ones. But maybe that would involve typing in a sequence of 1160 pluses and minuses, which wouldn’t be much fun.
February 13, 2014 at 10:54 pm |
[…] It finds an example of size 1160 that has value 2 and proves that that example is maximal. The polymath 5 project found an example of size 1124. The proof that 1160 is maximal required a large computer proof. For more information see this post: https://gowers.wordpress.com/2014/02/11/recent-news-concerning-the-erdos-discrepancy-problem/ […]
February 14, 2014 at 10:23 am |
Dear all, thank you for good words on our work.
I would like to just let you know that all related materials are available at
http://cgi.csc.liv.ac.uk/~konev/SAT14/
Than includes a program which generates SAT encoding of the problem for any given length and discrepancy; all mentioned in the paper and ready to use encodings; all mentioned in the paper sequences, in particular 1160 discrepancy 2 sequence – so no need to type it in.
February 14, 2014 at 11:09 am
Great — many thanks for that.
February 14, 2014 at 10:22 pm |
[…] 1. Recent news concerning the Erdos discrepancy problem | Gowers’s Weblog […]
February 14, 2014 at 11:04 pm |
oh WTG as stated your announcement & this paper was so inspiring, wrote up an entire blog in its honor on great moments in empirical/experimental math/TCS research, breakthough SAT induction idea with many refs, links, Stackexch Q/A & no less than 12 emoticons so am sure your readers will be very much impressed. oh and it has an entire research program outline at the end based on SAT induction that frankly is a revolutionary idea if you ask me. (but nobody did oh well). & would make a great polymath proj. just sayin. 😀
February 18, 2014 at 10:31 pm |
Neat. Finally an application for Levin’s Holographic proofs:
http://www.cs.bu.edu/fac/lnd/expo/holo.htm
February 19, 2014 at 11:10 am |
Here’s a graphical representation – hope you’ll forgive its being a facebook profile picture!
February 19, 2014 at 7:47 pm |
I suppose now is as good a time as any to mention my unpublished work from a few years ago working on this after Polymath 5 folded; unpublished because I didn’t think it was significant enough.
Still, I did present at a number theory seminar, so I’ve got slides at least:
Click to access erdosfinal.pdf
Probably the most interesting part is how I use a subgraph to get that a discrepancy of 1 is broken when you have positive integer triples a < b < c such that (b-a)/a, (c-a)/a and (c-b)/b are all odd integers. Since the first triplet where this is true is {9, 10, 12} that's why the break happens at 12. Page 36 has a graph of all the triples. I was able to find no relation between them and the C=2 problem. I was possibly foiled by not working with an optimal sequence; I was assuming 1124 and working with what we had from Polymath the entire time.
I also tried very hard to find an equivalent subgraph for a discrepancy of 2 but I couldn't find anything that would also be present in the integers.
February 21, 2014 at 7:44 pm |
hi all fyi there were two mainstream articles published on this breakthru in New Scientist & the Independent, one quoting Kalai & the other Budd. (& it was further way cool to scoop them 😎 )
am thinking it might just be the beginning of major innovation in this area (applying SAT solvers to very difficult math/TCS problems). again links/more info in my latest blog
February 21, 2014 at 7:46 pm |
oh, also this following question got booted from MO with -3, and another -3 on tcs.se, but its coming back from the dead in a dramatic turnaround with some key endorsements by SN/JE… connections between EDP & TCS tcs.se
February 26, 2014 at 4:56 pm |
[…] Recent news concerning the Erdos discrepancy problem on Tim Gowers’s blog […]
February 26, 2014 at 7:21 pm |
I’m as much interested in the assertion that discrepancy 3 takes us at least to 13,000. Also 1160 has highest prime factor 29. Is there any prospect of an asymptotic f(n) for discrepancy n, or any bounds on the prime numbers involved? Analysing the prime factors also gives scope for more efficient analysis. If we could identify key bottlenecks in advance (for 2, these include 1124 and 1160) it would be possible to detect sequences destined to fail much earlier, by analysing the subsequences converging on the bottlenecks. Are there bottleneck numbers for discrepancy 3?
February 27, 2014 at 7:00 am |
A simple pattern:
11 = 2^2 * 4 – 1
1160 = 3^3 * 43 – 1
So perhaps the next term will be 4^4 * (something) – 1.
February 27, 2014 at 7:02 am
Oops, I meant:
11 = 2^2 * 3 – 1
February 28, 2014 at 4:10 pm |
[…] is obvious: just consider any odd-length sub-sequence. For consider , as noted here: no sequence of length 12 has discrepancy […]
March 4, 2014 at 11:31 pm |
Already last year, we also used a SAT-based approach to attack a different combinatorial problem. In http://arxiv.org/abs/1310.6271 we resolved a 40-years-old problem by Don Knuth on optimality of certain sorting networks.
April 9, 2014 at 3:46 am |
Reblogged this on Enrique Zeleny's Blog.
May 25, 2014 at 4:00 am |
[…] attack on EDP by Konev and Lisitsa, and reaction by Gowers; also, other connections to empirical/experimental TCS (e.g. SAT automated theorem […]
May 25, 2014 at 6:22 pm |
Can’t one just prove the conjecture like this?
In an *infinite* sequence of +-1’s, you can find a subsequence which contains any combination of +-1’s you like.
Thus, for every C, it will be possible to find a subsequence which contains at least C+1 (positive) 1’s.
Q.E.D?
May 26, 2014 at 1:10 pm
The subsequence has to be of the particular form where you pick and
and  and choose the terms of the sequence in places
and choose the terms of the sequence in places  . As you say, if you were allowed to choose arbitrary subsequences, the problem would be trivial.
. As you say, if you were allowed to choose arbitrary subsequences, the problem would be trivial.
May 26, 2014 at 7:08 pm
Okay, that will be harder indeed 🙂
Do U think, given a certain C, it could ever be possible predicting the minimum value of n, i.e. the minimum length of a subsequence, to go above C? Like I could calculate that for C = 2, n must be at least 1161?
Thanks for your help.
May 26, 2014 at 7:20 pm
I think it is very unlikely indeed that an exact formula for the dependence of on
on  will ever be discovered. The best it seems reasonable to hope for is upper and lower bounds that differ by a constant factor, and even that is very ambitious.
will ever be discovered. The best it seems reasonable to hope for is upper and lower bounds that differ by a constant factor, and even that is very ambitious.
July 9, 2014 at 11:37 pm |
Inspired by this, Cynthia Kop and I have been trying a SAT attack on the completely multiplicative case of the EDP for discrepancy 3.
We have been able to generate a completely multiplicative sequence of length 18025 with discrepancy no more than 3. (In particular, of course, the regular EDP also needs a sequence of length at least 18025).
Given that the 2-discrepancy case has a 267 cutoff for the multiplicative case but 1161 for the general case this suggests that the regular EDP can go quite far with discrepancy 3!
Interestingly also, the 18025 sequence seems to heavily favour -1 on primes 1 mod 3 and 1 on primes 2 mod 3. This does seem to suggest that to construct long sequences one should at least start from a character.
July 9, 2014 at 11:42 pm
Had I thought to check http://cgi.csc.liv.ac.uk/~konev/edp/ before I posted the above comment I would have seen, however, that Konev and Lisitsa have dramatically extended their calculations and found a completely multiplicative sequence of length 127645 and discrepancy 3, which makes our 18025 look rather pitiful!
August 29, 2015 at 9:50 pm |
[…] It finds an example of size 1160 that has value 2 and proves that that example is maximal. The polymath 5 project found an example of size 1124. The proof that 1160 is maximal required a large computer proof. For more information see this post. […]
January 4, 2018 at 10:36 pm |
I’ve been waching your youtube video about this problem, and I was thinking about this problem as N inerlocking gears in 2D. maybe you can think of the C=3 problem as N interlocking gears in 3D. (yes it exist). hope you see it and reply whether it make sense…