I imagine most people reading this will already have heard that Terence Tao has solved the Erdős discrepancy problem. He has blogged about the solution in two posts, a first that shows how to reduce the problem to the Elliott conjecture in number theory, and a second that shows (i) that an averaged form of the conjecture is sufficient and (ii) that he can prove the averaged form. Two preprints covering (i) and (ii) are here and here: the one covering (i) has been submitted to Discrete Analysis.
This post is therefore the final post of the polymath5 project. I refer you to Terry’s posts for the mathematics. I will just make a few comments about what all this says about polymath projects in general.
After the success of the first polymath project, which found a purely combinatorial proof of the density Hales-Jewett theorem, there was an appetite to try something similar. However, the subsequent experience made it look as though the first project had been rather lucky, and not necessarily a good indication of what the polymath approach will typically achieve. I started polymath2, about a Banach-space problem, which never really got off the ground. Gil Kalai started polymath3, on the polynomial Hirsch conjecture, but the problem was not solved. Terence Tao started polymath4, about finding a deterministic algorithm to output a prime between and
, which did not find such an algorithm but did prove some partial results that were interesting enough to publish in an AMS journal called Mathematics of Computation. I started polymath5, with the aim of solving the Erdős discrepancy problem (after this problem was chosen by a vote from a shortlist that I drew up), and although we had some interesting ideas, we did not solve the problem. The most obviously successful polymath project was polymath8, which aimed to bring down the size of the gap in Zhang’s prime-gaps result, but it could be argued that success for that project was guaranteed in advance: it was obvious that the gap could be reduced, and the only question was how far.
Actually, that last argument is not very convincing, since a lot more came out of polymath8 than just a tightening up of the individual steps of Zhang’s argument. But I want to concentrate on polymath5. I have always felt that that project, despite not solving the problem, was a distinct success, because by the end of it I, and I was not alone, understood the problem far better and in a very different way. So when I discussed the polymath approach with people, I described its virtues as follows: a polymath discussion tends to go at lightning speed through all the preliminary stages of solving a difficult problem — trying out ideas, reformulating, asking interesting variants of the question, finding potentially useful reductions, and so on. With some problems, once you’ve done all that, the problem is softened up and you can go on and solve it. With others, the difficulties that remain are still substantial, but at least you understand far better what they are.
In the light of what has now happened, the second case seems like a very accurate description of the polymath5 project, since Terence Tao used ideas from that project in an essential way, but also recent breakthroughs in number theory by Kaisa Matomäki and Maksim Radziwiłł that led on to work by those authors and Terry himself that led on to the averaged form of the Elliott conjecture that Terry has just proved. Thus, if the proof of the Erdős discrepancy problem in some sense requires these ideas, then there was no way we could possibly have hoped to solve the problem back in 2010, when polymath5 was running, but what we did achieve was to create a sort of penumbra around the problem, which had the effect that when these remarkable results in number theory became available, the application to the Erdős discrepancy problem was significantly easier to spot, at least for Terence Tao …
I’ll remark here that the approach to the problem that excited me most when we were thinking about it was a use of duality to reduce the problem to an existential statement: you “just” have to find a function with certain properties and you are done. Unfortunately, finding such a function proved to be extremely hard. Terry’s work proves abstractly that such a function exists, but doesn’t tell us how to construct it. So I’m left feeling that perhaps I was a bit too wedded to that duality approach, though I also think that it would still be very nice if someone managed to make it work.
There are a couple of other questions that are interesting to think about. The first is whether polymath5 really did play a significant role in the discovery of the solution. Terry refers to the work of polymath5, but one of the key polymath5 steps he uses was contributed by him, so perhaps he could have just done the whole thing on his own.
At the very least I would say that polymath5 got him interested in the problem, and took him quickly through the stage I talked about above of looking at it from many different angles. Also, the Fourier reduction argument that Terry found was a sort of response to observations and speculations that had taken place in the earlier discussion, so it seems likely that in some sense polymath5 played a role in provoking Terry to have the thoughts he did. My own experience of polymath projects is that they often provoke me to have thoughts I wouldn’t have had otherwise, even if the relationship between those thoughts and what other people have written is very hard to pin down — it can be a bit like those moments where someone says A, and then you think of B, which appears to have nothing to do with A, but then you manage to reconstruct your daydreamy thought processes to see that A made you think of C, which made you think of D, which made you think of B.
Another question is what should happen to polymath projects that don’t result in a solution of the problem that they are trying to solve, but do have useful ideas. Shouldn’t there come a time when the project “closes” and the participants (and othes) are free to think about the problem individually? I feel strongly that there should, since otherwise there is a danger that a polymath project could actually delay progress on a problem by discouraging research on it. With polymath5 I tried to signal such a “closure” by writing a survey article that was partly about the work of polymath5. And Terry has now written up his work as an individual author, but been careful to say which ingredients of his proof were part of the polymath5 discussion and which were new. That seems to me to be exactly how things should work, but perhaps the lesson for the future is that the closing of a polymath project should be done more explicitly — up to now several of them have just quietly died. I had at one time intended to do rather more than what I did in the survey article, and write up, on behalf of polymath5 and published under the polymath name, a proper paper that would contain the main ideas discovered by polymath5 with full proofs. That would have been a better way of closing the project and would have led to a cleaner situation — Terry could have referred to that paper just as anyone refers to a mathematical paper. But while I regret not getting round to that, I don’t regret it too much, because I also quite like the idea that polymath5’s ideas are freely available on the internet but not in the form of a traditional journal article. (I still think that on balance it would have been better to write up the ideas though.)
Another lesson for the future is that it would be great to have some more polymath projects. We now know that Polymath5 has accelerated the solution of a famous open problem. I think we should be encouraged by this and try to do the same for several other famous open problems, but this time with the idea that as soon as the discussion stalls, the project will be declared to be finished. Gil Kalai has said on his blog that he plans to start a new project: I hope it will happen soon. And at some point when I feel slightly less busy, I would like to start one too, on another notorious problem with an elementary statement. It would be interesting to see whether a large group of people thinking together could find anything new to say about, for example, Frankl’s union-closed conjecture, or the asymptotics of Ramsey numbers, or the cap-set problem, or …
September 20, 2015 at 2:59 pm |
What is the actual lower bound on the discrepancy that TT obtains for the set system of arithmetic progressions, if the each arithmetic progression is a subset of the integers from 1 through N ?
Does he just prove that the discrepancy on this set system is greater than any constant, or from the paper, can one derive an actual function, e.g. sqrt(log N) ?
September 20, 2015 at 3:03 pm
He says in the preprint that in principle his proof gives an effective bound, but it is likely to be much weaker than .
.
September 20, 2015 at 5:01 pm |
I’m still kind of sad Polymath9 imploded early. I occasionally have tried to return to it but I have no idea how to salvage anything other than perhaps fundamentally changing the question. (I suspect the amount of prep may explain why it wasn’t popular — it required careful reading of your Borel posts.)
I have an idea for a “populist Polymath” I’d like to run sometime which is a.) a set of problems that nobody knows the answer to but b.) is perfectly understandable to amateurs and computer-based and by-hand mucking about are both likely to make progress. I’m not sure I’d call them “important” but it would be an experiment in seeing if we can get the “poly” aspect of many non-experts being able to contribute.
September 20, 2015 at 6:45 pm
I think one of the things that made EDP a success was precisely that quite a lot of people got involved with computational experiments, which were very important for building up our intuition. I think this also contributed to the success of polymath8. So I’m all in favour of problems with a computational component.
Even polymath9 wasn’t a complete failure: one of the questions I asked was answered a little while later by Pavel Pudlak. But the answer was not what I had hoped for …
September 24, 2015 at 3:22 pm
Bravo Jason. I suspect that lurking out there are numerous currently-feasible collaborative models which would greatly expand the achievability envelope of the mathematical enterprise (along a number of useful dimensions, not all of which are even on the radar, much less receiving high priority at present).
But they’re not going to announce themselves. So I hope that something like this happens, and many other variants too, increasingly often. Let a thousand flowers bloom. Let ten thousand.
September 21, 2015 at 8:25 am |
[…] in the proof. See this blog post on Tao’s blog with links to two new relevant papers, and this post by Tim […]
September 21, 2015 at 2:27 pm |
I’d like to add another perspective on the value of the Polymath projects. I’m currently a graduate student, and I’ve paid attention to the Polymath projects as I’ve grown more mathematically mature. As an inexperienced undergrad, I worked briefly on Polymath4 with my undergraduate advisor; although I contributed little to the overall discussion, I learned a lot. Perhaps more importantly, I saw how other (real) mathematicians approached and thought about this problem in real time. I both learned a bit about how research was actually done and about how the topics I was learning as an undergrad appeared “in nature,” as it were.
I have similar feelings towards Polymath5 and Polymath8, except that I was becoming more capable mathematically, I was also able to stay closer to the “edge” of the projects [not at the edge though — as you mention, they initially move at lightning speed, which is both tremendously exciting and initially a bit intimidating].
This fits broadly into your thought that the Polymath projects sometimes provoke you to think of ideas you wouldn’t normally have. They’ve certainly prompted me to think a bit more broadly about math research in general.
September 21, 2015 at 11:23 pm |
I was looking through the old Polymath5 threads and actually it is remarkable how close we were to at least reducing the problem to the Elliott conjecture, even if one would have to wait for the 2015 breakthrough of Matomaki and Radziwill to have some hope of the latter.
As early as EDP1 (Jan 19 2010), we already had the basic 3-step strategy of showing that completely multiplicative functions had unbounded discrepancy, reducing the general function case to some sort of “quasimultiplicative” case (whatever that meant), and extending the completely multiplicative case to the quasimultiplicative case. (Now we know that “random completely multiplicative” is the correct interpretation of “quasimultiplicative”.)
The Fourier-analytic reduction (giving “step 2” of the above program) came up in this Jan 27 comment of mine in EDP3 (building off of this Jan 19 comment from EDP1, and also this Jan 17 comment from the post immediately before EDP1.
In this Jan 30 comment in EDP4, I was able to rule out the case when the completely multiplicative function pretended to be a real Dirichlet character
On Feb 1 in EDP4 Tim asked the key question of whether the distribution of pairs such as was understood. Ben Green, Ernie Croot pointed to the known literature on the problem and the conventional wisdom at the time (namely, “as hard as the twin prime conjecture”). later that day, I observed that if a completely multiplicative function
was understood. Ben Green, Ernie Croot pointed to the known literature on the problem and the conventional wisdom at the time (namely, “as hard as the twin prime conjecture”). later that day, I observed that if a completely multiplicative function  had bounded discrepancy then there had to be some irregularity of distribution in a pair
had bounded discrepancy then there had to be some irregularity of distribution in a pair  . The Elliot conjecture is more or less exactly describing when such irregularity can happen, but given how hopeless these problems were at the time, it made sense to abandon this line of inquiry. It was only after the Matomaki-Radziwill breakthrough (who for instance showed for the first time that
. The Elliot conjecture is more or less exactly describing when such irregularity can happen, but given how hopeless these problems were at the time, it made sense to abandon this line of inquiry. It was only after the Matomaki-Radziwill breakthrough (who for instance showed for the first time that 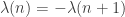 occurred for a positive density of n) that this approach became viable (and I missed it the first time round when Uwe asked me about it on my blog, I had to be asked a second time before seeing the connection).
occurred for a positive density of n) that this approach became viable (and I missed it the first time round when Uwe asked me about it on my blog, I had to be asked a second time before seeing the connection).
September 24, 2015 at 9:38 am
Apologies — it’s taken me until now to spot that this fascinating comment was lying in my moderation queue.
September 22, 2015 at 2:10 am |
[…] This resolves a problem that’s been open for more than 80 years. For more details, see this post by Timothy Gowers. Notably, Tao’s proof builds, in part, on a recent Polymath collaborative online effort. […]
September 22, 2015 at 8:39 am |
[…] part of the solution was probably solved (?) last year, Terence Tao suggest he might have come to a full solution. He has posted an article on Arxiv and the whole first piece to Discrete […]
September 22, 2015 at 1:41 pm |
[…] recent developments in analytic number theory. See this blog post from Tao’s blog and this concluding blog post from Gowers’s […]
September 22, 2015 at 8:00 pm |
There were cash prizes for solutions to a lot of Erdos’ problems. What was this one worth?
September 24, 2015 at 12:03 am
On the polymath wiki, it is mentioned that the cash prize was $500, which was relatively high in comparison to many of the other prizes.
September 23, 2015 at 1:16 am |
I think that Frankl’s conjecture is a brilliant idea for a polymath project, in the sense that it will be most interesting to hear the approaches of different mathematicians to this elementary problem.
September 23, 2015 at 9:41 am
I second that!
September 23, 2015 at 11:48 am
I’m quite tempted myself. One might argue against it on the grounds that this problem is a famous example of what Richard Lipton calls a mathematical disease. But perhaps Polymath is the cure! At any rate, even if the chances of solving the problem are small, the chances of at least saying something interesting enough to be publishable look quite a bit larger. Also, it didn’t seem as though we had much chance of solving the Erdős discrepancy problem when we started out, but that discussion turned out to be worth having.
September 23, 2015 at 9:12 pm
I apologize. My original reply was supposed to include a “On the other hand” paragraph, which was omitted by mistake.
I wanted to say that one apparent disadvantage to choosing this problem is that it is accessible to virtually anyone, in particular those without any mathematical experience. This may cloud the discussions with “noise”.
But of course, this is all pure evil, as:
1. Even if there will be a lot of commenters, I believe that most of them will have good intentions. Also there’s always the chance that some bored high school student will surprise us with a brilliant insight.
2. If one sees himself as an experimenter of polymath projects, then I think that this problem will serve nicely as an edge case to trial. (The other extreme, which is problems accessible only to one or two people, is an edge case which was rigorously tested during many mathematical eons.)
September 25, 2015 at 5:52 pm
I agree that the union closed families conjecture is a good idea for polymath. For one thing it would at least settle the question of whether Blinovsky’s approach in http://arxiv.org/abs/1507.01270 works or not.
September 25, 2015 at 9:59 pm
What have people said about it? The paper looks completely unreadable.
September 26, 2015 at 12:37 am
@Maxi Anand: Without actually trying to read this thing, I have a hunch [1] that the “approach” you’re referring to will not work.
[1] URL: https://en.wikipedia.org/wiki/Crackpot_index
September 28, 2015 at 2:51 pm
I haven’t met anyone who has taken the time to read this paper to a point where they can conclusively say “this proof can/cannot work because…”.
Blinovsky has three other papers using the same proof technique each of them claiming to solve reasonably well known combinatorics problems (one of which is published http://link.springer.com/article/10.1134%2FS0032946014040048).
Whether or not his papers are correct, their existence seems to have discouraged people from working on the relevant conjectures, which is a shame.
I guess that one positive outcome of a polymath project about Frankl’s conjecture is that it would help the combinatorics community decide on the correctness of these papers.
May 3, 2016 at 6:09 pm
If it helps … I know at least one paper by him, where I can tell you explicitly, where it does not work. Unfortunately, it is none with the smoothing technique. These I just do not understand. I really tried this for the paper that you linked.
Calling him a crackpot is not correct, because he has several correct and interesting publications (e.g. the wrong two pages paper mentioned above refers to a correct paper by the mathematician in question).
Also relevant is this question from a few days ago …
http://math.stackexchange.com/questions/1765189/vladimir-blinovskys-union-closed-sets-conjecture-proof
September 23, 2015 at 12:24 pm |
In connection with the question that you raise: “The first is whether polymath5 really did play a significant role in the discovery of the solution.” I find it intriguing that Tao in his paper on the Erdos discrepancy problem acknowledges “[..] Uwe Stroinski for suggesting a possible connection between Elliott-type results and the Erd˝os discrepancy problem.” Did this communication happen during polymath5? Was this already known to Tao or was it instrumental in him pursuing the approach via Elliott-type conjectures?
September 23, 2015 at 2:08 pm
I don’t know the answer to that question. It is conceivable that he was referring to a comment such as this one, but perhaps it was a subsequent communication.
With hindsight, at least some sort of connection seems quite natural. Tao showed during Polymath5 that the problem reduced, in a certain sense, to a question about multiplicative sequences. But for a completely multiplicative sequence the conjecture will be true if one can show that it is not too balanced in intervals. So it is natural to be interested in new number-theoretic results about correlations between neighbouring values of completely multiplicative functions and to wonder whether they might be applicable. My guess is that some thought like this (but maybe not precisely this one) went on in Terry or Uwe’s mind.
September 23, 2015 at 7:43 pm |
It seems to me that this comment was the one that triggered the aha moment in TT:
September 24, 2015 at 1:34 am |
[…] bound. Paul Erdos offered a $500 reward for solving it, back when it was originally posed. See Tim Gower’s blog for a more technical […]
September 24, 2015 at 9:40 am |
With reference to Terry’s thought processes, it turns out that he had made a long and very informative comment that (because it contained a number of links) was sitting in my moderation queue — it now appears a few comments back. Apologies for this, and do read the comment!
September 24, 2015 at 5:47 pm |
[…] briefly covered in connection with EDC here, and which became a focal point in much public PolyMath work credited liberally by […]
September 26, 2015 at 3:50 am |
Of course, doing Frankl’s Conjecture will force a lot of people to empty their pockets of whatever ideas they’ve been carrying around in the hopes of solving it independently. But I suppose that’s not grounds for ruling it out.
September 26, 2015 at 10:26 am
I can’t quite tell — is this in jest? Or do you really think someone lurking is on the verge of proving something about Frankl’s conjecture?
September 28, 2015 at 10:12 pm |
One question that arose in a conversation with Chris Cesare about EDP was what description (or “slogan” if you wish) is appropriate to describe the discrepancy phenomenon (even to non mathematicians) and maybe also one such description/slogan for the proofs. For Szemeredi theorem there are various nice description of the phenomenon (e.g., “patterns in arbitrary structures”) and a common theme of the proofs (“structure vs randomness”) which I think is very useful not only for explanation to wide public but even for expert conceptually thinking about the subject. What would you suggest for discrepancy results (and EDP in particular)? (and proofs?)
September 29, 2015 at 7:58 am
Maybe one could say something along the lines of its being impossible to find a red-blue colouring of the integers that is “perfectly balanced” in every times table. That’s not quite a slogan, but perhaps it could be worked into one.
September 29, 2015 at 8:24 am
If a slogan for the Ramsey phenomenon could be “complete disorder is impossible” maybe for the discrepancy phenomenon it is “some disorder cannot be avoided”.
September 29, 2015 at 9:07 am
I think “imbalance” is better than “disorder” there, since a constant sequence would count as complete order in a Ramsey context, so it seems a little strange to consider it as disorder in a discrepancy context. Also, random sequences tend to be quite well (though not perfectly) balanced. So I’d go for “complete balance is impossible”.
September 29, 2015 at 8:24 am
I suggested (from my non-expert perspective) that it betrays the multiplicative structure of the integers: we have maps dZ –> Z that jointly cover Z, but which aren’t disjoint enough for bonded-discrepancy sequences to be glued. The trouble is that sequences in dZ and d’Z eventually run into each other at lcm(d,d’). The analogy is with bounded functions on a countable family of intervals covering R: they may not glue to a bounded function.
September 29, 2015 at 11:41 am
Indeed “imbalance” is better. We can also say “complete fairness is impossible,” (or even “complete justice is impossible,” 🙂 ) or “The principle of unavoidable bias”
As far as the proof goes it seems that we have here a principle of bias coming from balance (or imbalance coming from balance), as the bias in EDP is coming from the balance of pairwise sign patterns.
September 29, 2015 at 1:36 pm |
As a next step, polymath could delve deep into Graph Theory and give a shot at Hadwiger’s Conjecture ( https://en.wikipedia.org/wiki/Hadwiger_conjecture_(graph_theory) )
September 30, 2015 at 1:54 pm |
[…] la seconda soluzione dei "progetti PolyMath", gli altri sono stati "abbandonati con discrezione", scrive Tim Gowers. […]
October 6, 2015 at 6:06 pm |
[…] 4. EDP28 — problem solved by Terence Tao! | Gowers’s Weblog […]
October 14, 2015 at 1:45 pm |
Who are some well-known child prodigies, and did their genius continue into adulthood?
And recently solved Erdos discrepancy problem https://gowers.wordpress.com/2015/09/20/edp28-problem-solved-by-terence-tao/
October 19, 2015 at 10:01 am |
[…] di Discrete Analysis ne dibatte, Tao ha fatto una cronologia dei suggerimenti più utili sia sul blog di Tim Gowers che sul proprio (ha scritto anche una seconda parte) dove la peer-review ha […]
October 22, 2015 at 7:12 am |
[…] discrepancy problem (EDP). A concluding post following Tao’s proof on Gowers’s blog is EDP28. You can also read about the problem and its solution on Lipton and Regan’s blog and in […]
October 22, 2015 at 2:52 pm |
I want to give thanks to our host, Tim Gowers, for organizing and motivating and for contributing so much to the EDP discussion. I had great fun participating, and for a month or so 2010 the first thing I did every day, before rolling out of bed, was check this blog to catch up on what had happened while I slept. It has been a joyous riot!
I wanted to participate in the relaunch (EDP 24 or so), but September is a busy month for academics. Late December/January is ideal for my schedule for getting completely absorbed into something.
October 23, 2015 at 4:49 pm |
[…] Aperiodical, 18 Sep 2015; Tim Gowers, “EDP28 — problem solved by Terence Tao!,” Gowers’s Weblog, 20 Sep 2015. Y por supuesto puedes leer al propio Terry Tao, “The Erdos discrepancy problem via the […]
January 20, 2016 at 5:33 am |
[…] least C. This resolves a problem that’s been open for more than 80 years. For more details, see this post by Timothy Gowers. Notably, Tao’s proof builds, in part, on a recent Polymath collaborative online effort. It was a […]
November 21, 2016 at 10:52 pm |
[…] Lo que escribió Gowers sobre Polymath5 y la resolución de Tao en: https://gowers.wordpress.com/2015/09/20/edp28-problem-solved-by-terence-tao/ […]
April 19, 2019 at 1:57 am |
“This post is therefore the final post of the polymath5 project.” Why “therefore”? What happened to the modular conjecture for HAPs? Seems a bit simplistic to just say everything is done because the initial problem has been solved.
February 26, 2020 at 10:15 am |
[…] מתמטיקה: ב – 1932, לפני יותר משמונים שנה, הגה פאול ארדש (אולי גדול המתמטיקאים של המאה ה – 20) את בעיית רצפי הפלוס-מינוס. השבוע טרנס טאו (אולי גדול המתמטיקאים של המאה ה -21 עד עכשיו) פתר אותה. […]
April 8, 2020 at 9:53 pm |
[…] have always felt that that project, despite not solving the problem, was a distinct success,” writes University of Cambridge mathematician Tim Gowers, who started the Polymath project and hopes that […]
January 29, 2021 at 9:03 am |
[…] to EDP, and a subsequent one by Kodlu who seconded Uwe’s suggestion. This is reported in EDP28, and here on my blog we celebrated the solution in this post. […]