I’ve already mentioned this on Google Plus, but my readership there is different from my readership here, so it seems a good idea to write a similar post here, to give what publicity I can to the fact that Gil Kalai has started a new Polymath project. The problem he would like solved (and I would very much like to see it solved too) is the famous delta-systems or sunflower conjecture of Erdős and Rado.
The problem, as with many problems in combinatorics, is easy to state, but fascinatingly hard to solve. It is a classic extremal problem, in that it asks how big some combinatorial object needs to be before it is guaranteed to contain a subobject of some particular kind. In this case, the object is a –uniform hypergraph, which just means a collection of sets of size
. The subobject one would like to find is a sunflower of size
, which means a collection of sets
such that we can find disjoint sets
with the
disjoint and with
for each
. I have used the letters
and
to stand for “head” and “petal” —
is the head of the sunflower and
are the petals.
How many sets of size do you need to guarantee a sunflower of size
? A simple argument gives not too bad an upper bound of
. We argue as follows. Let
be a collection of
sets, each of size
. If we can find
disjoint sets in
then we are done (with an empty head and the petals being the sets themselves). Otherwise, let
be the union of a maximal disjoint collection of sets in
, and note that
has cardinality at most
, and that every set in
has a non-empty intersection with
.
By the pigeonhole principle, we can find and a subcollection
of
containing at least
sets, such that every set
contains
.
Now remove from all the sets in
to create a collection
of sets of size
. By induction, this collection contains a sunflower of size
, and putting back the element
then gives us a sunflower in
. (The base case, when
, states that
sets are enough to guarantee a sunflower of size
.)
How about a lower bound? An easy one is obtained as follows. Let be disjoint sets of size
and let
consist of all sets that intersect each
in exactly one place. There are
such sets, and there cannot be a sunflower, since there is not enough room in each
to make it possible to have
disjoint petals.
The main question of interest is the dependence on : for fixed
, does the correct bound grow exponentially (like the lower bound just given), or more like
, or like something in between? Even when
, the first non-trivial case, the answer is not known (though there are bounds known that improve on the simple ones I’ve just given).
For more information, as well as a discussion about how a homological approach might be useful, see Gil’s post.
At the time of writing, Gil’s post has attracted 60 comments, but it is still at what one might call a warming-up stage, so if you are interested in the problem and understand what I have written above, it should still be easy to catch up with the discussion. I strongly recommend contributing — even small remarks can be very helpful for other people, sparking off ideas that they might not have had otherwise. And there’s nothing quite like thinking about a problem, writing regular bulletins of the little ideas you’ve had, and getting feedback on them from other Polymath participants. This problem has the same kind of notoriously hard feel about it that the Erdős discrepancy problem had — it would be wonderful if a Polymath collaboration could contribute to its finally getting solved.
If you have comments specific to what I’ve written above, such as to point out typos or inaccuracies, then by all means write them here, but if you have mathematical thoughts about the problem, please write them on Gil’s blog.
November 5, 2015 at 9:01 pm |
You said “disjoint sets H, P_1,\dots,P_r with the P_i disjoint”. Does H also need to be disjoint from the P_i?
November 5, 2015 at 9:10 pm
Yes it does. So an example would be the sets and
and 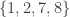 . Those form a sunflower with head
. Those form a sunflower with head  and petals
and petals 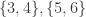 and
and 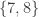 .
.
November 10, 2015 at 10:28 pm |
Even small values for k and r seem difficult to deal with! Apologies if the following is well-known but at least with k=2 one can see what is happening in terms of “playing-off” the effects of having no large sunflowers of either head size.
Suppose that the maximum size of a sunflower with no head in a family of 2-sets is r. Then the idea of the matching augmentation algorithm can be used to show that there are integers p and qi and disjoint sets Y and Xi such that:-
• r = p + Σqi
• Y has p elements
• Each Xi has 2qi +1 elements
• The given family consists only of sets with both elements in an Xi and sets with one or both elements in Y.
The maximum size of a sunflower with head of size 1 then limits the sizes of the p and qi. [Each i is supposed to be a suffix.]
November 11, 2015 at 1:54 am |
P.S. Thinking about how to write out a formal proof I realise that each Xi has a specific element which could be the same as the specific element of other Xi s – so they are almost disjoint!
December 8, 2015 at 11:15 pm |
[…] 10. Gil Kalai starts Polymath10 | Gowers’s Weblog […]