It has been in the news recently — or rather, the small corner of the news that is of particular interest to mathematicians — that Maryanthe Malliaris and Saharon Shelah recently had an unexpected breakthrough when they stumbled on a proof that two infinities were equal that had been conjectured, and widely believed, to be distinct. Or rather, since both were strictly between the cardinality of the natural numbers and the cardinality of the reals, they were widely believed to be distinct in some models of set theory where the continuum hypothesis fails.
A couple of days ago, John Baez was sufficiently irritated by a Quanta article on this development that he wrote a post on Google Plus in which he did a much better job of explaining what was going on. As a result of reading that, and following and participating in the ensuing discussion, I have got interested in the problem. In particular, as a complete non-expert, I am struck that a problem that looks purely combinatorial (though infinitary) should, according to Quanta, have a solution that involves highly non-trivial arguments in proof theory and model theory. It makes me wonder, again as a complete non-expert so probably very naively, whether there is a simpler purely combinatorial argument that the set theorists missed because they believed too strongly that the two infinities were different.
I certainly haven’t found such an argument, but I thought it might be worth at least setting out the problem, in case it appeals to anyone, and giving a few preliminary thoughts about it. I’m not expecting much from this, but if there’s a small chance that it leads to a fruitful mathematical discussion, then it’s worth doing. As I said above, I am indebted to John Baez and to several commenters on his post for being able to write much of what I write in this post, as can easily be checked if you read that discussion as well.
A few definitions and a statement of the result
The problem concerns the structure you obtain when you take the power set of the natural numbers and quotient out by the relation “has a finite symmetric difference with”. That is, we regard two sets and
as equivalent if you can turn
into
by removing finitely many elements and adding finitely many other elements.
It’s easy to check that this is an equivalence relation. We can also define a number of the usual set-theoretic operations. For example, writing for the equivalence class of
, we can set
to be
,
to be
,
to be
, etc. It is easy to check that these operations are well-defined.
What about the subset relation? That too has an obvious definition. We don’t want to say that if
, since that is not well-defined. However, we can define
to be almost contained in
if the set
is finite, and then say that
if
is almost contained in
. This is well-defined and it’s also easy to check that it is true if and only if
, which is the sort of thing we’d like to happen if our finite-fuzz set theory is to resemble normal set theory as closely as possible.
I will use a non-standard piece of terminology and refer to an equivalence class of sets as an f-set, the “f” standing for “finite” or “fuzzy” (though these fuzzy sets are not to be confused with the usual definition of fuzzy sets, which I don’t know and probably never will know). I’ll also say things like “is f-contained in” (which means the same as “is almost contained in” except that it refers to the f-sets rather than to representatives of their equivalence classes).
So far so good, but things start to get a bit less satisfactory when we consider infinite intersections and unions. How are we to define , for example?
An obvious property we would like is that the intersection should be the largest f-set that is contained in all the . However, simple examples show that there doesn’t have to be a largest f-set contained in all the
. Indeed, let
be an infinite sequence of subsets of
such that
is infinite for every
. Then
is almost contained in every
if and only if
is finite for every
. Given any such set, we can find for each
an element
of
that is not contained in
(since
is infinite but
is finite). Then the set
is also almost contained in every
, and
is properly contained in
(in the obvious sense).
OK, we don’t seem to have a satisfactory definition of infinite intersections, but we could at least hope for a satisfactory definition of “has an empty intersection”. And indeed, there is an obvious one. Given a collection of f-sets , we say that its intersection is empty if the only f-set that is f-contained in every
is
. (Note that
is the equivalence class of the empty set, which consists of all finite subsets of
.) In terms of the sets rather than their equivalence classes, this is saying that there is no infinite set that is almost contained in every
.
An important concept that appears in many places in mathematics, but particularly in set theory, is the finite-intersection property. A collection of subsets of a set
is said to have this property if
is non-empty whenever
. This definition carries over to f-sets with no problem at all, since finite f-intersections were easy to define.
Let’s ask ourselves a little question here: can we find a collection of f-sets with the finite-intersection property but with an empty intersection? That is, no finite intersection is empty, but the intersection of all the f-sets is empty.
That should be pretty easy. For sets, there are very simple examples like — finitely many of those have a non-empty intersection, but there is no set that’s contained in all of them.
Unfortunately, all those sets are the same if we turn them into f-sets. But there is an obvious way of adjusting the example: we just take sets such that
is infinite for each
and
. That ought to do the job once we turn each
into its equivalence class
.
Except that it doesn’t do the job. In fact, we’ve already observed that we can just pick a set with
and then
will be a non-empty f-intersection of the
.
However, here’s an example that does work. We’ll take all f-sets such that
has density 1. (This means that
tends
to 1 as tends to infinity.) Since the intersection of any two sets of density 1 has density 1 (a simple exercise), this collection of f-sets has the finite-intersection property. I claim that any f-set contained in all these f-sets must be
.
Indeed, let be an infinite set and
the enumeration of its elements in increasing order. We can pick a subsequence
such that
for every
, and the corresponding subset
is an infinite subset of
with density zero. Therefore,
is a set of density 1 that does not almost contain
.
The number of f-sets we took there in order to achieve an f-empty intersection was huge: the cardinality of the continuum. (That’s another easy exercise.) Did we really need that many? This innocent question leads straight to a definition that is needed in order to understand what Malliaris and Shelah did.
Definition. The cardinal p is the smallest cardinality of a collection of f-sets such that
has the finite-intersection property but also
has an empty f-intersection.
It is simple to prove that this cardinal is uncountable, but it is also known not to be as big as the cardinality of the continuum (where again this means that there are models of set theory — necessarily ones where CH fails — for which it is strictly smaller). So it is a rather nice intermediate cardinal, which partially explains its interest to set theorists.
The cardinal p is one of the two infinities that Malliaris and Shelah proved were the same. The other one is closely related. Define a tower to be a collection of f-sets that does not contain and is totally ordered by inclusion. Note that a tower
trivially satisfies the finite-intersection property: if
belong to
, then the smallest of the f-sets
is the f-intersection and it isn’t f-empty. So let’s make another definition.
Definition. The cardinal t is the smallest cardinality of a tower that has an empty f-intersection.
Since a tower has the finite-intersection property, we are asking for something strictly stronger before, so strictly harder to obtain. It follows that t is at least as large as p.
And now we have the obvious question: is the inequality strict? As I have said, it was widely believed that it was, and a big surprise when Malliaris and Shelah proved that the two infinities were in fact equal.
What does this actually say? It says that if you can find a bunch of f-sets with the finite-intersection property and an empty f-intersection, then you can find a totally ordered example
that has at most the cardinality of
.
Why is the problem hard?
I don’t have a sophisticated answer to this that would explain why it is hard to experts in set theory. I just want to think about why it might be hard to prove the statement using a naive approach.
An immediate indication that things might be difficult is that it isn’t terribly easy to give any example of a tower with an empty f-intersection, let alone one with small cardinality.
An indication of the problem we face was already present when I gave a failed attempt to construct a system of sets with the finite-intersection property and empty intersection. I took a nested sequence such that the sets
had empty intersection, but that didn’t work because I could pick an element from each
and put those together to make a non-empty f-intersection. (I’m using “f-intersection” to mean any f-set f-contained in all the given f-sets. In general, we can’t choose a largest one, so it’s far from unique. The usual terminology would be to say that if
is almost contained in every set from a collection of sets, then
is a pseudointersection of that collection. But I’m trying to express as much as possible in terms of f-sets.)
Anyone who is familiar with ordinal hierarchies will see that there is an obvious thing we could do here. We could start as above, and then when we find the annoying f-intersection we simply add it to the tower and call it . And then inside
we can find another nested decreasing sequence of sets and call those
and so on. Those will also have a non-empty f-intersection, which we could call
, and so on.
Let’s use this idea to prove that there do exist towers with empty f-intersections. I shall build a collection of non-empty f-sets by transfinite induction. If I have already built
, I let
be any non-empty f-set that is strictly f-contained in
. That tells me how to build my sets at successor ordinals. If
is a limit ordinal, then I’ll take
to be a non-empty f-intersection of all the
with
.
But how am I so sure that such an f-intersection exists? I’m not, but if it doesn’t exist, then I’m very happy, as that means that the f-sets with
form a tower with empty f-intersection.
Since all the f-sets in this tower are distinct, the process has to terminate at some point, and that implies that a tower with empty f-intersection must exist.
For a lot of ordinal constructions like this, one can show that the process terminates at the first uncountable ordinal, . To set theorists, this has extremely small cardinality — by definition, the smallest one after the cardinality of the natural numbers. In some models of set theory, there will be a dizzying array of cardinals between this and the cardinality of the continuum.
In our case it is not too hard to prove that the process doesn’t terminate before we get to the first uncountable ordinal. Indeed, if is a countable limit ordinal, then we can take an increasing sequence of ordinals
that tend to
, pick an element
from
, and define
to be
.
However, there doesn’t seem to be any obvious argument to say that the f-sets with
have an empty f-intersection, even if we make some effort to keep our sets small (for example, by defining
to consist of every other element of
). In fact, we sort of know that there won’t be such an argument, because if there were, then it would show that there was a tower whose cardinality was that of the first uncountable ordinal. That would prove that t had this cardinality, and since p is uncountable (that is easy to check) we would immediately know that p and t were equal.
So that’s already an indication that something subtle is going on that you need to be a proper set theorist to understand properly.
But do we need to understand these funny cardinalities to solve the problem? We don’t need to know what they are — just to prove that they are the same. Perhaps that can still be done in a naive way.
So here’s a very naive idea. Let’s take a set of f-sets with the finite intersection property and empty f-intersection, and let’s try to build a tower
with empty intersection using only sets from
. This would certainly be sufficient for showing that
has cardinality at most that of
, and if
has minimal cardinality it would show that p=t.
There’s almost no chance that this will work, but let’s at least see where it goes wrong, or runs into a brick wall.
At first things go swimmingly. Let . Then there must exist an f-set
that does not f-contain
, since otherwise
itself would be a non-empty f-intersection for
. But then
is a proper f-subset of
, and by the finite-intersection property it is not f-empty.
By iterating this argument, we can therefore obtain a nested sequence of f-sets in
.
The next thing we’d like to do is create . And this, unsurprisingly, is where the brick wall is. Consider, for example, the case where
consists of all sets of density 1. What if we stupidly chose
in such a way that
for every
? Then our diagonal procedure — picking an element from each set
— would yield a set of density zero. Of course, we could go for a different diagonal procedure. We would need to prove that for this particular
and any nested sequence we can always find an f-intersection that belongs to
. That’s equivalent to saying that for any sequence
of dense sets we can find a set
such that
is finite for every
and
has density 1.
That’s a fairly simple (but not trivial) exercise I think, but when I tried to write a proof straight down I failed — it’s more like a pen-and-paper job until you get the construction right. But here’s the real question I’d like to know the answer to right at this moment. It splits into two questions actually.
Question 1. Let be a collection of f-sets with the finite-intersection property and no non-empty f-intersection. Let
be a nested sequence of elements of
. Must this sequence have an f-intersection that belongs to
?
Question 2. If, as seems likely, the answer to Question 1 is no, must it at least be the case that there exists a nested sequence in with an f-intersection that also belongs to
?
If the answer to Question 2 turned out to be yes, it would naturally lead to the following further question.
Question 3. If the answer to Question 2 is yes, then how far can we go with it? For example, must contain a nested transfinite sequence of uncountable length?
Unfortunately, even a positive answer to Question 3 would not be enough for us, for reasons I’ve already given. It might be the case that we can indeed build nice big towers in , but that the arguments stop working once we reach the first uncountable ordinal. Indeed, it might well be known that there are sets
with the finite-intersection property and no non-empty f-intersection that do not contain towers that are bigger than this. If that’s the case, it would give at least one serious reason for the problem being hard. It would tell us that we can’t prove the equality by just finding a suitable tower inside
: instead, we’d need to do something more indirect, constructing a tower
and some non-obvious injection from
to
. (It would be non-obvious because it would not preserve the subset relation.)
Another way the problem might be difficult is if does contain a tower with no non-empty f-intersection, but we can’t extend an arbitrary tower in
to a tower with this property. Perhaps if we started off building our tower the wrong way, it would lead us down a path that had a dead end long before the tower was big enough, even though good paths and good towers did exist.
But these are just pure speculations on my part. I’m sure the answers to many of my questions are known. If so, I’ll be interested to hear about it, and to understand better why Malliaris and Shelah had to use big tools and a much less obvious argument than the kind of thing I was trying to do above.
September 19, 2017 at 12:16 pm |
A trivial observation : you might not be able to engineer an injection, but perhaps a subquotient.
September 19, 2017 at 1:32 pm
Just to check I understand this, is the idea you are suggesting that we could define an equivalence relation on , an order relation on the equivalence classes, and an order-preserving injection from
, an order relation on the equivalence classes, and an order-preserving injection from  to the quotient?
to the quotient?
September 19, 2017 at 8:42 pm
Correct, though one might additionally start by throwing away some elements of F, so the equivalence relation is only on a subset.
September 19, 2017 at 9:54 pm |
A further observation is that if is a non-principal ultrafilter (or more precisely, the set of equivalence classes of sets that belong to a non-principal ultrafilter
is a non-principal ultrafilter (or more precisely, the set of equivalence classes of sets that belong to a non-principal ultrafilter  ), then
), then  has cardinality equal to that of the continuum (since for each f-set, either it or its f-complement belongs to
has cardinality equal to that of the continuum (since for each f-set, either it or its f-complement belongs to  ). And given any infinite set
). And given any infinite set  , it can’t be contained in all sets in
, it can’t be contained in all sets in  , since then it would have to belong to
, since then it would have to belong to  itself, and if we were then to split it into two infinite parts, one of those parts would have to belong to
itself, and if we were then to split it into two infinite parts, one of those parts would have to belong to  and would not f-contain
and would not f-contain  . So that gives another example. Does a non-principal ultrafilter contain a tower with no non-empty f-intersection?
. So that gives another example. Does a non-principal ultrafilter contain a tower with no non-empty f-intersection?
September 20, 2017 at 5:05 am |
This seems relevant:
Click to access tesi-moranarocca.pdf
September 20, 2017 at 7:16 am
Thanks very much for that reference! It contains a four-page proof of the theorem, but that four-page proof, if written out in full, together with non-trivial results that it assumes, would expand a lot I think. It also requires a lot of advanced set-theoretic concepts. But even for the non-expert it looks like a good place to look to try to get some sort of inkling of what is going on.
September 20, 2017 at 7:45 am |
Perhaps this note by D.H. Fremlin might be relevant:
Click to access n14528.pdf
September 20, 2017 at 9:10 am
That too gives a good impression of what the argument is like, even if I understand almost none of it.
I’m still interested in the following statement, which is much stronger than the assertion that p=t.
Statement. Let be a family of f-sets with the finite intersection property and empty f-intersection. Then
be a family of f-sets with the finite intersection property and empty f-intersection. Then  contains a totally ordered subset
contains a totally ordered subset  with empty f-intersection.
with empty f-intersection.
Is that statement known to be false? Can anyone find the answer to that question in one of the two references above (or some other reference)? If it’s false, then I’ll be much more convinced of the difficulty of the problem. (That’s not to say that I’m sceptical — just that I don’t have even a rough understanding of the difficulty at the moment.)
September 20, 2017 at 10:13 am |
I think the Statement is false: you can find a family of f-sets with the finite intersection property (fip) without f-intersection so that no two distinct elements are contained in one another (so any totally ordered subfamily is a singleton which do have an f-intersection).
To do this, we take a family of f-sets which has properties (1)-(3) below and is maximal:
which has properties (1)-(3) below and is maximal: has the fip,
has the fip, (the family of complements) has the fip, and
(the family of complements) has the fip, and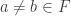 then
then  .
. too.
too.
(1)
(2)
(3) if
This is possible by Zorn’s lemma. Note that (3) holds for
If either or
or  has no f-intersection then we are done.
has no f-intersection then we are done.
Otherwise, we reach a contradiction: let be an f-intersection for
be an f-intersection for  , and
, and  be an f-intersection for
be an f-intersection for  . Take pairwise disjoint infinite sets
. Take pairwise disjoint infinite sets  and
and 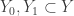 (all four are disjoint). We let
(all four are disjoint). We let  .
. (otherwise
(otherwise  is almost contained in the complement of
is almost contained in the complement of  ).
). still satisfies (1)-(3) which contradicts the maximality of
still satisfies (1)-(3) which contradicts the maximality of  . (1) holds because $X_0$ will be almost contained in any finite intersection of
. (1) holds because $X_0$ will be almost contained in any finite intersection of  . (2) holds because $Y_1$ will be almost contained in any finite intersection of
. (2) holds because $Y_1$ will be almost contained in any finite intersection of  .
. shows that
shows that  is not in any
is not in any  , and
, and  shows that
shows that  for
for  .
.
Then Z is not in
We would like to show that
Finally
September 20, 2017 at 10:53 am
Nice! It actually makes me realize that I had managed to confuse myself about something. I had been accidentally understanding “has the finite intersection property” to mean “is closed under finite intersections”, in which case obviously there must be infinite totally ordered subsets, even though that isn’t the definition I gave in the post above.
However, given a set with the finite intersection property, we can create a set
with the finite intersection property, we can create a set 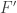 that is closed under finite intersections by simply taking all finite intersections of sets in
that is closed under finite intersections by simply taking all finite intersections of sets in  . Provided
. Provided  is infinite (as it is in the case of interest),
is infinite (as it is in the case of interest), 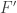 will have the same cardinality as
will have the same cardinality as  , so for the problem we are free to assume that
, so for the problem we are free to assume that 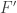 is closed under finite intersections.
is closed under finite intersections.
It feels to me as though the biggest totally ordered subset of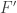 shouldn’t be that much bigger than the biggest totally ordered subset of
shouldn’t be that much bigger than the biggest totally ordered subset of  , so if
, so if  is the set you build above, I’d be surprised if
is the set you build above, I’d be surprised if 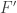 could have an uncountable totally ordered subset.
could have an uncountable totally ordered subset.
But right now I don’t see a proof. So let me ask, therefore, whether if is closed under finite f-intersections and has empty f-intersection, it must have a totally ordered subset of the same cardinality. (I expect the answer no.)
is closed under finite f-intersections and has empty f-intersection, it must have a totally ordered subset of the same cardinality. (I expect the answer no.)
September 20, 2017 at 12:24 pm
I want to think a little about the consequences of maximality for your set . So let’s think what it says if we can’t add a set
. So let’s think what it says if we can’t add a set  . I think one of the following things must go wrong.
. I think one of the following things must go wrong.
(i) is f-contained in a set that belongs to
is f-contained in a set that belongs to  .
.
(ii) f-contains a set that belongs to
f-contains a set that belongs to  .
.
(iii) There is a finite f-intersection of sets in that has empty f-intersection with
that has empty f-intersection with  .
.
(iv) There is a finite f-intersection of sets in that f-contains
that f-contains  .
.
Note that (iv) is equivalent to the assertion that there is a finite f-union of sets in that is contained in
that is contained in  . But this implies (ii), so I think we don’t have to worry about it.
. But this implies (ii), so I think we don’t have to worry about it.
Now let’s suppose I’ve found a nested sequence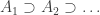 of f-sets in
of f-sets in 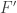 — that is, of finite f-intersections of sets in
— that is, of finite f-intersections of sets in  . This sequence has an f-intersection
. This sequence has an f-intersection  . Since
. Since  is f-contained in
is f-contained in 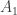 , which is a finite f-intersection of sets in
, which is a finite f-intersection of sets in  , we know that
, we know that  violates (i) and therefore cannot belong to
violates (i) and therefore cannot belong to  . But could it be a finite intersection of sets in
. But could it be a finite intersection of sets in  ?
?
The answer would be yes if we can find two disjoint subsets and
and  of
of 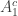 such that neither
such that neither 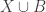 nor
nor  violates (i), (ii) or (iii).
violates (i), (ii) or (iii).
I don’t see my way through to the end here, but it seems at least possible that there may be an argument of this style to show that a countable nested sequence in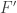 has a non-empty f-intersection that also belongs to
has a non-empty f-intersection that also belongs to 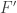 (when
(when  is the set you constructed).
is the set you constructed).
September 20, 2017 at 1:51 pm |
I am not sure about my example there, but here is a way of finding a set with the fip, without f-intersection, such that the set of finite intersections
with the fip, without f-intersection, such that the set of finite intersections 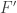 has no decreasing chains of type
has no decreasing chains of type 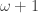 .
.
We say that is independent if for any disjoint finite subfamilies
is independent if for any disjoint finite subfamilies 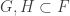 the set
the set  is infinite. This is obviously much stronger than the fip.
is infinite. This is obviously much stronger than the fip. is separable). Now there is also a trick to find an independent family with no f-intersection (see Proposition I.1 here).
is separable). Now there is also a trick to find an independent family with no f-intersection (see Proposition I.1 here).
It can be shown that there are independent families of even size continuum (this is classically done by using that the Tychonoff cube
So let be an independent family with no f-intersection; we claim that
be an independent family with no f-intersection; we claim that 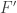 has no decreasing chains of type
has no decreasing chains of type 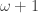 . The single observation we need is that if
. The single observation we need is that if  are finite then
are finite then  if and only if
if and only if  . Indeed, if
. Indeed, if  then
then 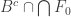 is an infinite set contained in
is an infinite set contained in  but disjoint from
but disjoint from  . Now, if
. Now, if 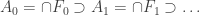 then the finite sets
then the finite sets 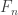 are strictly increasing and if
are strictly increasing and if 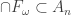 for all
for all  (for some
(for some 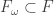 ) then
) then 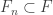 which forces
which forces 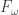 to be infinite.
to be infinite.
On a side note, the smallest independent family with no f-intersection has size too (see the above link).
too (see the above link).
September 20, 2017 at 2:51 pm
Thank you very much for these insights, which do go a long way towards explaining why the problem is hard. It seems that if one wanted an elementary proof, one would have to find an extremely non-obvious way of using to build a tower
to build a tower  .
.
September 20, 2017 at 3:03 pm
I’ve just understood the significance of your side note. I started to wonder whether one could hope to find inside
inside  at least in the case where
at least in the case where  has minimal cardinality, but what you say implies that this too is not in general possible.
has minimal cardinality, but what you say implies that this too is not in general possible.
September 20, 2017 at 5:13 pm |
Let us take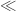 to be a total order such that
to be a total order such that ![[A]\subset_f [B]\Rightarrow [A]\ll [B]](https://s0.wp.com/latex.php?latex=%5BA%5D%5Csubset_f+%5BB%5D%5CRightarrow+%5BA%5D%5Cll+%5BB%5D&bg=ffffff&fg=333333&s=0&c=20201002) (it’s always possible with axioms weaker than Choice). We note by
(it’s always possible with axioms weaker than Choice). We note by ![]0,[X]]_{\ll}](https://s0.wp.com/latex.php?latex=%5D0%2C%5BX%5D%5D_%7B%5Cll%7D&bg=ffffff&fg=333333&s=0&c=20201002) all the minorants of
all the minorants of ![[X]](https://s0.wp.com/latex.php?latex=%5BX%5D&bg=ffffff&fg=333333&s=0&c=20201002) for the
for the 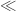 relation, and we denote by
relation, and we denote by  from
from 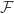 to
to  a choice function : Let’s call
a choice function : Let’s call  the image by
the image by  of
of 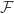 . It is a set with the same cardinality as
. It is a set with the same cardinality as 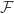 , obtained by picking a representative in each class of
, obtained by picking a representative in each class of 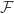 . For any
. For any 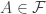 , let’s set
, let’s set ![T(A)=\bigcup C[0,[A]]_{\ll}](https://s0.wp.com/latex.php?latex=T%28A%29%3D%5Cbigcup+C%5B0%2C%5BA%5D%5D_%7B%5Cll%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Then it is obvious that
. Then it is obvious that ![T=\left\{[T(A)], A\in \mathcal F\right\}](https://s0.wp.com/latex.php?latex=T%3D%5Cleft%5C%7B%5BT%28A%29%5D%2C+A%5Cin+%5Cmathcal+F%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) has the intersection property and the same cardinality as
has the intersection property and the same cardinality as 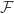 . It is also a tower, and the only thing we have to check is that no infinite set is in all the members of
. It is also a tower, and the only thing we have to check is that no infinite set is in all the members of  . Am I right? or did I misunderstand something? (because I think
. Am I right? or did I misunderstand something? (because I think  does the job, and this seems too simple…)
does the job, and this seems too simple…)
September 20, 2017 at 5:30 pm |
Oh I understand my mistake : maybe the I made is very small… But isn’t there a way to make it as big as
I made is very small… But isn’t there a way to make it as big as 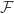 anyway? I repeat the general idea : don’t pick elements in
anyway? I repeat the general idea : don’t pick elements in 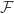 but build
but build  with unions of representatives of sets in
with unions of representatives of sets in 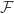 .
.
September 20, 2017 at 8:34 pm
I’ve substantially edited your comments above, so please let me know if I’ve made any mistakes. I’m intrigued by them, but I’m not sure I completely follow them yet. But let me try.
We start with a set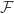 that has the finite-intersection property and no non-empty f-intersection. This has a partial order, which we extend to a total order
that has the finite-intersection property and no non-empty f-intersection. This has a partial order, which we extend to a total order 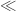 . Then for each element
. Then for each element  we let
we let ![(0,A]](https://s0.wp.com/latex.php?latex=%280%2CA%5D&bg=ffffff&fg=333333&s=0&c=20201002) denote the set of all
denote the set of all  such that
such that  . (This isn’t precisely your notation, but I think it should be OK. For me
. (This isn’t precisely your notation, but I think it should be OK. For me 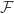 consists of f-sets — that is sets up to finite symmetric differences.)
consists of f-sets — that is sets up to finite symmetric differences.)
If I understand you, chooses for each f-set some representative set. I was going to suggest that this was unnecessary, but I now see that you are going to take infinite unions, so maybe it makes a difference after all. It means that
chooses for each f-set some representative set. I was going to suggest that this was unnecessary, but I now see that you are going to take infinite unions, so maybe it makes a difference after all. It means that  is equal to the union of all
is equal to the union of all  such that
such that  . That is, you take all f-sets that precede
. That is, you take all f-sets that precede  in the
in the 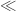 order and take the union of their representatives.
order and take the union of their representatives.
It’s clear that the sets form a tower. It’s not clear to me that if
form a tower. It’s not clear to me that if 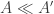 then
then  and
and 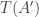 are distinct. In fact, it isn’t obvious to me that the sets couldn’t all be equal to
are distinct. In fact, it isn’t obvious to me that the sets couldn’t all be equal to 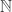 .
.
But as you suggest, the general idea might have a chance, since we have a lot of freedom to choose the total order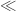 . A natural special case to look at is Daniel Soukup’s first example, where no set in
. A natural special case to look at is Daniel Soukup’s first example, where no set in 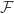 is f-contained in any other set in
is f-contained in any other set in 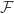 . Then all total orderings on
. Then all total orderings on  extend the initial trivial ordering, so basically we’d be looking for some ordering, and some choice of representatives, that worked.
extend the initial trivial ordering, so basically we’d be looking for some ordering, and some choice of representatives, that worked.
September 30, 2017 at 8:09 pm
Let’s call![\mathbf{R}=\left\{[A], subset \mathbb{N}\right\}](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BR%7D%3D%5Cleft%5C%7B%5BA%5D%2C+subset+%5Cmathbb%7BN%7D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) For any
For any  we define
we define  . And we will say
. And we will say 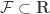 is a “good part” if we have
is a “good part” if we have  for some
for some  .
.
Let’s now consider![\mathit G=\left\{[\mathbb{N}\setminus A],[A]\in \mathit F\right\}](https://s0.wp.com/latex.php?latex=%5Cmathit+G%3D%5Cleft%5C%7B%5B%5Cmathbb%7BN%7D%5Csetminus+A%5D%2C%5BA%5D%5Cin+%5Cmathit+F%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) the set of complement of
the set of complement of 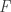 whom have the fip and no-nom-empty pseudo-interscetion(then
whom have the fip and no-nom-empty pseudo-interscetion(then  has the fup and the no-non-full pseudo-union). Then it’s easy to see that
has the fup and the no-non-full pseudo-union). Then it’s easy to see that  is closed under finite intersection, (resp finie union) if and only if
is closed under finite intersection, (resp finie union) if and only if  is closed under finite f-intersection (resp.finite f-union). Now I want to consider general intersection in
is closed under finite f-intersection (resp.finite f-union). Now I want to consider general intersection in 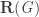 , it is not a problem because we deal with “usual sets” , the problem then could be that the sets we get are not “good parts”, but I thing the set we would get is a set of the form
, it is not a problem because we deal with “usual sets” , the problem then could be that the sets we get are not “good parts”, but I thing the set we would get is a set of the form 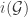 like we saw in another comment and that you commented to and noticed that
like we saw in another comment and that you commented to and noticed that 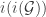 was actually empty.
was actually empty.
I would like to do the kind of thing I tried to do in the comment above, and in order to build a correct extended total order I will have to extend as well, hoping the cardinality of this extension dont get bigger then that of
as well, hoping the cardinality of this extension dont get bigger then that of 
We now say , because it is shorter, we define for any
, because it is shorter, we define for any 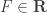 ,
, 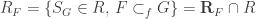 , we call it the “$F$-row” and we say that
, we call it the “$F$-row” and we say that  is the $R$-orthogonal of $F$. We will now assume that the orthogonal of each row is in
is the $R$-orthogonal of $F$. We will now assume that the orthogonal of each row is in  , you might say that it makes
, you might say that it makes  very big, but (I think…) it won’t make it bigger than $\mathit F$ (I will say later why I claim that the quotient of
very big, but (I think…) it won’t make it bigger than $\mathit F$ (I will say later why I claim that the quotient of  under the relation “having the same R-orthogonal” has actually the same cardinality then that of
under the relation “having the same R-orthogonal” has actually the same cardinality then that of 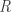 if it is closed under “orthogonality”)
if it is closed under “orthogonality”)
The thing that I’m not so sure yet, is that the total order that would extend the partial order in
that would extend the partial order in  is such that
is such that ![(0,A]_{<<}](https://s0.wp.com/latex.php?latex=%280%2CA%5D_%7B%3C%3C%7D&bg=ffffff&fg=333333&s=0&c=20201002) are good parts… It think would give us a fine tower…
are good parts… It think would give us a fine tower…
I will develop in next post the precise statement about this "orthogonality", in a more precise way. After that, we will be able to do a better examination of , but yet, it would be very heavy… (because I would like to consider an orthogonality for elements of
, but yet, it would be very heavy… (because I would like to consider an orthogonality for elements of  such as the orthogonal of the orthogonal is an involution, and it will be better for a quick understanding to define it in a general context)
such as the orthogonal of the orthogonal is an involution, and it will be better for a quick understanding to define it in a general context)
I apology if the way to present this is a bit heavy compare to the notions that I'm talking about, and I hope that my explanations are not so bad that one can't understand it easily, if it is not the case, I think it will be better if I present this "orthogonality" in a general context.
September 30, 2017 at 8:17 pm
Sorry the first line contains notation mistakes!! It should be :
Let’s call![\mathbf{R}=\left\{[A], subset \mathbb{N}\right\}](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BR%7D%3D%5Cleft%5C%7B%5BA%5D%2C+subset+%5Cmathbb%7BN%7D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) For any
For any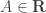 we define
we define  . And we will say
. And we will say 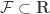 is a “good part” if we have
is a “good part” if we have  for some
for some 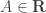
September 30, 2017 at 8:21 pm
Sorry again….![\mathbf{R}=\left\{[A], A\subset \mathbb{N}\right\}](https://s0.wp.com/latex.php?latex=%5Cmathbf%7BR%7D%3D%5Cleft%5C%7B%5BA%5D%2C++A%5Csubset+%5Cmathbb%7BN%7D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Let’s call
For any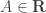 we define
we define  . And we will say
. And we will say 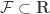 is a “good part” if we have
is a “good part” if we have  for some
for some 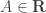
September 30, 2017 at 8:30 pm
another mistake is that $R_F$ is NOT $\mathit{R}_F\cap R$…the definition that hold is then the left member…
I’m going to write the whole comment better…maybe longer but better…I’m tired to say I’m “sorry” but I have to, once again!
September 20, 2017 at 5:39 pm |
(when I say very small I meen finite cardinal)
September 20, 2017 at 11:26 pm |
Almost certainly there are short direct proofs of the equality. But I’m not sure what is to be gained from it. The model-theoretic machinery Malliaris and Shelah developed is obviously complex and can seem too intricate for any specific problem encountered, but from what I understand it has already produced several important results. They also have a proof improving Szemeredi’s regularity lemma using model theory:
http://www.ams.org/journals/tran/2014-366-03/S0002-9947-2013-05820-5/home.html
September 21, 2017 at 9:13 am
Different mathematicians have very different instincts about this, and I don’t think one can say that one instinct is right and the other wrong. For some people, the ideal is something like what Grothendieck was famous for — developing more and more theory until previously hard-looking statements become trivial. Others feel that they understand a result much better if they have a short direct proof.
I’m in the latter camp, though I don’t take it to extremes. For example, I completely understand that in algebraic topology, if you develop the basics of homology theory and use those to prove results like the Brouwer fixed-point theorem and the Borsuk-Ulam theorem, you are saving yourself from having to repeat a lot of steps that you need to provide if you give direct proofs of all the things you can do using homology. But quite a lot of my research has been aimed at removing machinery — for example, I have been involved in finding more direct (and quantitative) proofs of results that were obtained using ergodic theory, and I think that has led to genuine gains in understanding.
Incidentally, it’s a slight oversimplification to say that Malliaris and Shelah improved Szeméredi’s regularity lemma. What they did was to improve the bounds significantly if you add a rather strong hypothesis about the graph. My instinct for this result too is to try to find a more elementary proof. The reason is that I find myself asking, “What is this model theory actually doing that makes the proof come out at the end?” And for me, the ideal answer would be something like, “Here’s a direct proof. Now the model theory wraps up these steps into a convenient form and allows one to prove similar results without laboriously writing out similar steps for each one.” Though I suppose I’d be even happier with a direct proof that was clearer and more transparent than the model-theoretic one rather than being essentially the same argument written out at greater length.
September 21, 2017 at 1:13 am |
Yes, that is exactly what I mean! Thank you for the editing operation, and for the clear and nice way to say it!
If I understand notation $\mathcal F= C(\mathit F)$ for some choice fonction $C$ where $\mathit F$ is the Daniel Soukup equivalent special case. The “worse thing” that could happen in order to use the “general idea “(of the upper post) is that, for all $(F,G)\in \mathcal F^^2$, $F\cup G\in [\mathbb N]$. And the “best case” we can have, is that there is infinitly many distinct $[F\cup G]$ . That give me an idee, to considere not only $\mathcal F’$, the finite intersection closure of $\mathcal F$, but also $\mathcal F”$ the closure of $\mathcal F’$ under general union! We have $\bigcap \mathcal F”\in [\emptyset]$, and also $\mathcal F”$ has the intersection property (any two member have an infinite intersection). The only thing that we have to be sure, is that $[\mathcal F”]=\mathit F”:=\left\{[X], \, X\in \mathcal F”\right\}$ and $\mathit F$ have the same cardinality… But if it has not, we are in the “best case” ! So we can assume that $\mathcal F”$ is the set of the open sets of a topological space. We could then try to study the compacity of $\mathbb N\in \mathcal F”$.
September 21, 2017 at 2:19 am |
Unfortunatly we cannot ask right now that $\mathcal F”$ has the same cardinality than $\mathit F”$, that is why we cannot avoid*** the $f$-set version… But I think we can assume that $\mathcal F”_0=:\left\{U\in \mathcal F”,\, [\emptyset,\mathbb N\setminus U]=\emptyset \right\}$ the set of open sets in $\mathcal F”$ that are not $\mathcal F”$-dense in $\mathbb N$ is smaller then $\mathit F$. I don’t know if it will help but, I find this “topological equivalent case” at least funny, and I hope that I’m not mistaking some where when I say that we can reduce the study to this special case, in order to proof that $|\mathit T|=|\mathit F|$
***I’m not triying to say that we shoud get rid of $f$-set formulation, but just that it would be nice if we study statement that are not “so much more easy” to say with $f$-set than without… the $f$-statement would then be an elegant translation of an equivalent usual-set statement. If we need $f$-formulation for more than elenace and nice notations, that we might give the “indication” that we are deviating from the elementary proof goal.
September 21, 2017 at 11:48 am |
I’m sorry, I’m not sure what I wrote is correct, so let’s say again the “idea” : maybe we can assume that the set of representative elements of $\mathit F$ is closed not only under finite interection, but also under general union in order to study compacity. I apologie if what I said before is not correct (I think it’s correct for finite union, but I this was alredy kind of obvious)
September 21, 2017 at 2:25 pm |
Ok I feel sorry to write with bad english so much fuzzy information, so please feel free to delete my three previous posts and this very first sentence, I am going to try to be clear and precise now :
I think the general idea of my first post probably doesn’t work. Here’s why, according to me :
Let’s have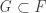 with
with ![\mathit G=([G_i])_{i\in \mathbb N}](https://s0.wp.com/latex.php?latex=%5Cmathit+G%3D%28%5BG_i%5D%29_%7Bi%5Cin+%5Cmathbb+N%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Then any sequence
. Then any sequence  would be such as
would be such as ![\left\{[S_i],\, i\in \mathbb N\right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5BS_i%5D%2C%5C%2C+i%5Cin+%5Cmathbb+N%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a finite set. If it was infinite we would be able to chose
is a finite set. If it was infinite we would be able to chose ![S'_i\in [S_i]](https://s0.wp.com/latex.php?latex=S%27_i%5Cin+%5BS_i%5D&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all 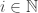 such as
such as  with
with  infinite, we would then have
infinite, we would then have 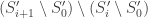 also infinite, and
also infinite, and ![\left\{[S'_i-S'_0],, \, i\in \mathbb N\right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5BS%27_i-S%27_0%5D%2C%2C+%5C%2C+i%5Cin+%5Cmathbb+N%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) would be a countable tower, and this is not possible, as you said it in the article.
would be a countable tower, and this is not possible, as you said it in the article.
So the general first idea may go nowhere, as soon as this leads to the fact that the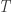 that I built in the first post is a finite set. But maybe the general following next idea can help, somehow… : it’s not an proper advance, but just a remark : I think we can build a topological space, with same
that I built in the first post is a finite set. But maybe the general following next idea can help, somehow… : it’s not an proper advance, but just a remark : I think we can build a topological space, with same  -cardinality than
-cardinality than 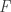
 , and
, and  have the same f-cardinality if
have the same f-cardinality if ![\left\{[A],\, A\in \mathcal A\right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5BA%5D%2C%5C%2C+A%5Cin+%5Cmathcal+A%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![\left\{[B],\, B\in \mathcal B\right\}](https://s0.wp.com/latex.php?latex=%5Cleft%5C%7B%5BB%5D%2C%5C%2C+B%5Cin+%5Cmathcal+B%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) have the same cardinality).
have the same cardinality).
(let’s say
Indeed, if is a set of representative elements of
is a set of representative elements of  , where
, where  is closed under finite intersection, then
is closed under finite intersection, then  , the general union closure of
, the general union closure of  is a topological space. Of course we cannot say (yet?) that
is a topological space. Of course we cannot say (yet?) that  and
and  have the same cardinality, but I think , that we can deduce from what I just said previously in this post, that
have the same cardinality, but I think , that we can deduce from what I just said previously in this post, that  and
and  have the same f-cardinality.( I hope this is not a irrelevant triviallity, or even some wrong statement!)
have the same f-cardinality.( I hope this is not a irrelevant triviallity, or even some wrong statement!)
September 21, 2017 at 5:12 pm |
(I forget to precise in the previous post that, $\mathit F$ has the Daniel Soukup hypothesis : no f-inclusion beetwin any two membres)
September 21, 2017 at 8:04 pm |
I think I’ve got it ! ,
,  the only increasing function from
the only increasing function from 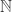 to
to  . And let’s define the convolution of
. And let’s define the convolution of  and
and 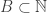 as
as  . We now build a transfinite sequence of convolutions between repesentative elements in
. We now build a transfinite sequence of convolutions between repesentative elements in 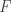 (we take
(we take 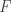 well-ordered by
well-ordered by  , and we build
, and we build 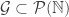 whose elements are indexed by
whose elements are indexed by 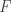 , in this way :
, in this way :  , where
, where  is the smaller element of the set of
is the smaller element of the set of  – majorant of
– majorant of  , and then
, and then ![\mathit{G}=\left\{[G],\,G\in \mathcal{G}\right\}](https://s0.wp.com/latex.php?latex=%5Cmathit%7BG%7D%3D%5Cleft%5C%7B%5BG%5D%2C%5C%2CG%5Cin+%5Cmathcal%7BG%7D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) should be our tower… )
should be our tower… )
Let’s define for any
September 21, 2017 at 9:03 pm
I like the idea of using these “convolutions”. Let me try to repeat the argument in my own words, just to make sure I understand it. I think it is incomplete, but that doesn’t mean the idea can’t work.
Given two sets and
and 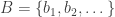 , with their elements written in increasing order, we are defining
, with their elements written in increasing order, we are defining  to be the set
to be the set  . Note that this is a subset of
. Note that this is a subset of  .
.
Now we take a collection of sets that has the finite intersection property and no pseudointersection. We well-order it somehow, and write
that has the finite intersection property and no pseudointersection. We well-order it somehow, and write  for the well-ordering. And now we want to create a tower of cardinality at most that of
for the well-ordering. And now we want to create a tower of cardinality at most that of  and argue that it too has no pseudointersection.
and argue that it too has no pseudointersection.
For each ordinal that is smaller than the order type of
that is smaller than the order type of 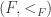 , let
, let  be the corresponding set in
be the corresponding set in  . We shall inductively define sets
. We shall inductively define sets  as follows. (They are to form the tower.)
as follows. (They are to form the tower.)
We start by setting to be
to be 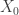 . If we have already defined
. If we have already defined  , then
, then  . (I think you meant
. (I think you meant  in your comment above, but that’s a small detail.)
in your comment above, but that’s a small detail.)
What I don’t see in your comment is a definition of when
when  is a limit ordinal. But here’s an idea. Suppose that
is a limit ordinal. But here’s an idea. Suppose that  is a limit ordinal and the collection of sets
is a limit ordinal and the collection of sets  has a pseudointersection. Then let
has a pseudointersection. Then let  be such a pseudointersection. If the collection of sets does not have a pseudointersection, then we are done.
be such a pseudointersection. If the collection of sets does not have a pseudointersection, then we are done.
The final step in this argument would need to be to prove that the tower created does not have a pseudointersection. I’m not sure I see why this has to be the case.
September 22, 2017 at 7:08 am |
Thank you for the correction and precise and very nice way to answer, it is a great luck for week reeders like me to be able to learn and understand not only exciting maths but also nice way to talk about them!
There is two reason why I thought “I’ve got it”
1) First one is that I thought that for each we have
we have  such that, by construction,
such that, by construction, 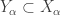 . Thus, if some
. Thus, if some ![[C]](https://s0.wp.com/latex.php?latex=%5BC%5D&bg=ffffff&fg=333333&s=0&c=20201002) is f-contained in every
is f-contained in every  , it seems to give a contradiction.
, it seems to give a contradiction. into the *-machine? I mean If the “no non empty pseudo-intersection” is not already satisfied? (please forgive the fuzzy statement here! I never did any transfinite proof, and I naîvely thought it shouldn’t be a problem.)
into the *-machine? I mean If the “no non empty pseudo-intersection” is not already satisfied? (please forgive the fuzzy statement here! I never did any transfinite proof, and I naîvely thought it shouldn’t be a problem.)
Isn’t it possible to take every member of
2) Second and (seriously wrong) reason : I translated the problem in terme of usual sets, and made the self-statement that we don’t need a (usual set) tower which is not constant by some rank, to have an empty intersection , as soon as we can remove the whole intersection from each member of the tower. .But my usual-set translation is certainly very wrong, because I could deduce from it that is …countable**!
is …countable**!
**Actually I’m not confortable with this example of “Eratosthene” tower, that seems to have the fip and the “no non empty f-intersection” property, and is clearly countable :
 , where
, where  is the
is the  -th prime number.
-th prime number.![[C_i]](https://s0.wp.com/latex.php?latex=%5BC_i%5D&bg=ffffff&fg=333333&s=0&c=20201002) anyway!
anyway!
I cannot imagine any proper f-set that is f-contained in every
So… I’m afraid that I do a very serious confusion by now… but wait a minute, I think the set of prime numbers does the job! I feel better!
September 22, 2017 at 8:15 am
I think your first reason is wrong.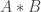 is contained in
is contained in  , but it is not necessarily contained in
, but it is not necessarily contained in  . This is important, because when we build
. This is important, because when we build  we need it to be an f-subset of
we need it to be an f-subset of  , so that we will have a tower, so I don’t see how we can use the convolution operation to ensure also that it is a subset of
, so that we will have a tower, so I don’t see how we can use the convolution operation to ensure also that it is a subset of  .
.
Also, I think limit ordinals do create problems. Suppose, for example, that you have created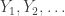 . How do you propose to create
. How do you propose to create  using the set
using the set  ?
?
Maybe there is an idea for doing this actually. At each limit ordinal you do what I suggested and take an f-intersection. And at each successor ordinal you don’t take
you don’t take  but rather you take the first
but rather you take the first  that you have not yet used. In that way it will indeed be guaranteed that every set in
that you have not yet used. In that way it will indeed be guaranteed that every set in  takes part in one of the convolutions. But the first problem remains, I think.
takes part in one of the convolutions. But the first problem remains, I think.
September 22, 2017 at 12:05 pm
I answer to the first answer because I still thing that it works. So there were two problems : the first is that $A*B$ is not included in $A$ and the second is that we have to work a little bit to take all the people in $F$ that we did not take, in a continuation of our transfinite operation : if we include in these people, the “$B$” of first problem that we didn’t take, and as second problem seems to be solved, I think we have it…
An other way to solve the first problem could be to take $G’:= B*A*B\subset A\cap B$.
Am I too optimistic?
September 22, 2017 at 12:26 pm
(I wrote “I answer to the first answer” but this sentence is useless and might be confusing, so let me explain the context of it : I was scared that what I was going to post might not follow directly the very comment that I was answering too, but would be “isolated” in te main discution, I hope this very edditing post won’t add some more confusion!
)
September 22, 2017 at 12:12 pm
I don’t think the second problem is a problem, but I do think the first one is. Your suggestion doesn’t work, because it isn’t necessarily true that is contained in
is contained in  .
.
September 22, 2017 at 1:42 pm
Oh what a ridiculous mistake!!
September 22, 2017 at 2:11 pm
Maybe we can consider a transfinite sequence of towers with “decreasing” pseudo-intersection (I put quotations mark to mean that I don’t plan to define it properly, but it could also be intersting to do it anyway, in order to solve the problem)
For example we can build for some
for some  , It seems that we are doing “nothing more” here, but maybe a similar idea would work…
, It seems that we are doing “nothing more” here, but maybe a similar idea would work…
September 22, 2017 at 10:57 am |
Here is another way that one might try to prove the result. I am thinking as I write, so this comment will probably be fairly short and end in failure.
As with jean-camille’s proof attempt, we begin by arbitrarily well-ordering . Now let us attempt to build a tower
. Now let us attempt to build a tower  inductively. However, this time, instead of trying to use sets from
inductively. However, this time, instead of trying to use sets from  , we will make the following weaker promise: that for every set in
, we will make the following weaker promise: that for every set in  there will be a set in
there will be a set in  that is f-contained in it. This will ensure that any f-intersection of
that is f-contained in it. This will ensure that any f-intersection of  is also an f-intersection of
is also an f-intersection of  , since
, since  is a tower.
is a tower.
How might this inductive construction go? Let the enumeration of the f-sets in be
be 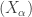 , where
, where  ranges over the ordinals belonging to the order type of the well-ordering of
ranges over the ordinals belonging to the order type of the well-ordering of  . I now want to built a tower
. I now want to built a tower  . I’ll actually make the more specific promise that
. I’ll actually make the more specific promise that  will always be f-contained in
will always be f-contained in  .
.
To start with it’s fine: we take , and so on. All these are infinite, by the finite intersection property of
, and so on. All these are infinite, by the finite intersection property of  . I don’t actually care whether they are distinct: if they aren’t, that makes my tower
. I don’t actually care whether they are distinct: if they aren’t, that makes my tower  smaller, and that’s only good for me.
smaller, and that’s only good for me.
But then we need to create . There isn’t an obvious way to do that, so what I’ll do instead is find an f-intersection
. There isn’t an obvious way to do that, so what I’ll do instead is find an f-intersection 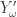 of the sets
of the sets  . (If I can’t find one, then I’m done, since it means I’ve got a countable tower with no f-intersection. Of course, that can’t exist, so this case won’t in fact arise until the tower is of size at least p.) Having found
. (If I can’t find one, then I’m done, since it means I’ve got a countable tower with no f-intersection. Of course, that can’t exist, so this case won’t in fact arise until the tower is of size at least p.) Having found 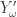 , I will let
, I will let  .
.
But it’s not clear that that works. In fact, in general there is no reason at all for it to work: I might accidentally choose an f-intersection that is disjoint from .
.
I think what I need in order to let the proof continue is something that feels hard to achieve: a set with the following two properties.
with the following two properties.
(i) is an f-intersection of the sets
is an f-intersection of the sets 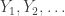 .
.
(ii) The set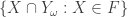 still has the finite-intersection property.
still has the finite-intersection property.
I don’t see why such a set has to exist, but it also appears to be a necessary condition for this approach to work.
September 26, 2017 at 9:19 am
A)Maybe we could make (i) and (ii) work with other hypotheses on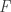
 such that
such that  has an non empty f-intersection, then the f-union of
has an non empty f-intersection, then the f-union of  can only be
can only be ![[\mathbb{N}]](https://s0.wp.com/latex.php?latex=%5B%5Cmathbb%7BN%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) (let’s call it the no-split-property).
(let’s call it the no-split-property). , where
, where  is the smallest ordinal such that
is the smallest ordinal such that  has an non empty f-intersection with
has an non empty f-intersection with 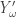 . There will be one because if there were no one
. There will be one because if there were no one ![[\mathit{Y'_{\omega}}]^c](https://s0.wp.com/latex.php?latex=%5B%5Cmathit%7BY%27_%7B%5Comega%7D%7D%5D%5Ec&bg=ffffff&fg=333333&s=0&c=20201002) would be a f-union of
would be a f-union of  .
. , where
, where  is a successor ordinal. The process has to stop when we get an empty-intersection tower. The hypothesis we made that we have instead of FIP,may be stronger,but as soon as we get the same cardinality, it’s ok.
is a successor ordinal. The process has to stop when we get an empty-intersection tower. The hypothesis we made that we have instead of FIP,may be stronger,but as soon as we get the same cardinality, it’s ok.
For example let’s ask that if we have
Then we let
We even can get rid of the finite intersection property, by doing the same operation for the
B) It has no connection with what I just said, but I wonder if we can sometime hope that a collection of f-sets has a bigger pseudo intersection. You showed that is necessary that the collection is uncountable but maybe there is some sufficient property that we could find and use, and that could be very helpful…
September 27, 2017 at 2:59 pm
Unless I’m missing something, if such a Y does not exist, then X intersection Y_1, X intersection Y_2, … is a tower with no f-intersection, and we are done (I think this will work at all limit ordinals) We’ll need each Y_alpha to have nonempty intersection with every X in F where F is closed under finite f-intersection.
September 27, 2017 at 8:44 pm
Ah yes. So let me try again. As above, we set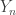 to be
to be 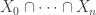 . Then, following your suggestion, we observe that the sets
. Then, following your suggestion, we observe that the sets  form a tower, and we pick our f-intersection inside that, and call it
form a tower, and we pick our f-intersection inside that, and call it  .
.
But as you also say, we’re not out of the woods, since we have to choose the f-intersection in such a way that it intersects all the sets in , or we run into trouble at the very next step.
, or we run into trouble at the very next step.
So now we have an interesting problem: given a collection of sets closed under finite intersections and a countable nested sequence of sets
of sets closed under finite intersections and a countable nested sequence of sets  from the collection, can we find an f-intersection
from the collection, can we find an f-intersection  of the sequence that intersects all the sets in
of the sequence that intersects all the sets in  ? That is, can we find an f-intersection
? That is, can we find an f-intersection  that belongs to the dual of
that belongs to the dual of  ? If
? If  is an ultrafilter, then the question becomes this: does a countable chain of sets in an ultrafilter have to have an f-intersection that also belongs to the ultrafilter?
is an ultrafilter, then the question becomes this: does a countable chain of sets in an ultrafilter have to have an f-intersection that also belongs to the ultrafilter?
Unfortunately, the answer to this is no. Consider the filter on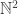 that contains a set
that contains a set  if and only if the set of
if and only if the set of  such that the set of
such that the set of  such that
such that  is cofinite is cofinite. To put that a bit more comprehensibly, I’m saying that for all but finitely many
is cofinite is cofinite. To put that a bit more comprehensibly, I’m saying that for all but finitely many  it is the case that for all but finitely many
it is the case that for all but finitely many  ,
,  . Now suppose we extend this filter to an ultrafilter on
. Now suppose we extend this filter to an ultrafilter on 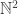 . Then the sets
. Then the sets  form a countable chain of sets in the ultrafilter, but any f-intersection
form a countable chain of sets in the ultrafilter, but any f-intersection  of these sets has to have the property that for every
of these sets has to have the property that for every  there are only finitely many
there are only finitely many  with
with  , which means that the complement of
, which means that the complement of  belongs to the filter, and hence to the ultrafilter, so
belongs to the filter, and hence to the ultrafilter, so  does not belong to the ultrafilter.
does not belong to the ultrafilter.
September 28, 2017 at 6:46 am
Let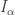 be the set of all pseudo-intersections in
be the set of all pseudo-intersections in ![[X_1,X_{\alpha}]](https://s0.wp.com/latex.php?latex=%5BX_1%2CX_%7B%5Calpha%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Maybe there is a smart way to choose
. Maybe there is a smart way to choose  such that
such that  is a good tower…
is a good tower…
September 28, 2017 at 8:04 am
A quick remark for jean-camille: if you type $latex instead of the first dollar symbol, then the TeX will compile. I should have mentioned this a long time ago. Also, the bug you experienced was because WordPress confuses the “less than” and “greater than” symbols with html. So you have to write & lt ; and & gt ; instead (but without the spaces).
September 28, 2017 at 10:52 pm
Thank you very much for for theses kind explanations! Sorry again, and thank you very much for having edited so many comments (although most didn’t deserve such a kind traitement!)
This very trivial idea to consider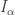 gave me many ideas in a short time, and some of them lead me to the illusion of getting the result (I didn’t actually saw where were the mistakes because I din’t have the time to examine each one yet) Let me develop one of the ideas : I think it can reduce a lot the hypothesis, and -why not – help us getting the elementary proof we look for…
gave me many ideas in a short time, and some of them lead me to the illusion of getting the result (I didn’t actually saw where were the mistakes because I din’t have the time to examine each one yet) Let me develop one of the ideas : I think it can reduce a lot the hypothesis, and -why not – help us getting the elementary proof we look for…
Let’s define![i : \mathcal{\mathcal{P}}\, \to \mathcal{\mathcal{P}},\,\,\mathcal{G}\mapsto i(\mathcal{G})\,=:\,\left\{X\subset \mathbb{N},\, [X]\subset_f [G], \forall G\in \mathcal{G}\right\}](https://s0.wp.com/latex.php?latex=i+%3A+%5Cmathcal%7B%5Cmathcal%7BP%7D%7D%5C%2C+%5Cto+%5Cmathcal%7B%5Cmathcal%7BP%7D%7D%2C%5C%2C%5C%2C%5Cmathcal%7BG%7D%5Cmapsto++i%28%5Cmathcal%7BG%7D%29%5C%2C%3D%3A%5C%2C%5Cleft%5C%7BX%5Csubset+%5Cmathbb%7BN%7D%2C%5C%2C+%5BX%5D%5Csubset_f+%5BG%5D%2C+%5Cforall+G%5Cin+%5Cmathcal%7BG%7D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) , as the “pseudo intersection set” fonction.
, as the “pseudo intersection set” fonction.
We can see that unless it is equal, and that
unless it is equal, and that  if and only if it has cardinality
if and only if it has cardinality  (the single element can then only be the usual intersection of
(the single element can then only be the usual intersection of 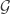 ).
).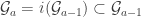 if $a$ is successor ordinal and
if $a$ is successor ordinal and  if
if  is limit ordinal. And it's easy to deduce from this that the cardinality of the super tower is at most the f-cardinality of
is limit ordinal. And it's easy to deduce from this that the cardinality of the super tower is at most the f-cardinality of 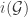 . Then what is coming write now is quite funny : we can build a f-tower with only one pseudo intersection, just by picking elements in
. Then what is coming write now is quite funny : we can build a f-tower with only one pseudo intersection, just by picking elements in  (for any ordinal
(for any ordinal  , limit or successor)
, limit or successor)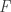 satisfying the "nnei" and the "fip", we can already assume (in order to eventually lead to a contradiction) that all the set of the form
satisfying the "nnei" and the "fip", we can already assume (in order to eventually lead to a contradiction) that all the set of the form 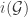 have a bigger cardinality than
have a bigger cardinality than 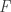 … I must have made some mistake because it sounds to good to be true…
… I must have made some mistake because it sounds to good to be true…
We can define a transfinite super-tower whose elements are
Then before saying anything about
September 28, 2017 at 11:06 pm
I edit the latex mistakes :
Let’s define![i : \mathcal{\mathcal{P}}\, \to \mathcal{\mathcal{P}},\,\,\mathcal{G}\mapsto i(\mathcal{G})\,=:\,\left\{X\subset \mathbb{N},\, [X]\subset_f [G], \forall G\in \mathcal{G}\right\}](https://s0.wp.com/latex.php?latex=i+%3A+%5Cmathcal%7B%5Cmathcal%7BP%7D%7D%5C%2C+%5Cto+%5Cmathcal%7B%5Cmathcal%7BP%7D%7D%2C%5C%2C%5C%2C%5Cmathcal%7BG%7D%5Cmapsto+i%28%5Cmathcal%7BG%7D%29%5C%2C%3D%3A%5C%2C%5Cleft%5C%7BX%5Csubset+%5Cmathbb%7BN%7D%2C%5C%2C+%5BX%5D%5Csubset_f+%5BG%5D%2C+%5Cforall+G%5Cin+%5Cmathcal%7BG%7D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) , as the “pseudo intersection set” fonction.
, as the “pseudo intersection set” fonction.
We can see that unless it is equal, and that
unless it is equal, and that  if and only if it has cardinality 1 (the single element can then only be the usual intersection of
if and only if it has cardinality 1 (the single element can then only be the usual intersection of 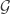 ).
). if
if  is successor ordinal and
is successor ordinal and  if
if  is limit ordinal. And it's easy to deduce from this, that the cardinality of the super tower is at most the f-cardinality of
is limit ordinal. And it's easy to deduce from this, that the cardinality of the super tower is at most the f-cardinality of 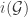 . Then what is coming write now is quite funny : we can build a f-tower with only one pseudo intersection, just by picking elements in
. Then what is coming write now is quite funny : we can build a f-tower with only one pseudo intersection, just by picking elements in 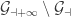 (for any ordinal
(for any ordinal  , limit or successor)
, limit or successor)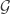 such that
such that 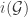 has a cardinality at most
has a cardinality at most  , then we will have finish! We can then restrict ourself to the opposite hypothesies.
, then we will have finish! We can then restrict ourself to the opposite hypothesies.
We can define a transfinite super-tower whose elements are
Then if we find ANY
September 29, 2017 at 12:30 am
A little precision (and edition of a strange notation instead of $p$)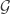 such that
such that 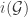 IS INFINITE AND has a cardinality at most
IS INFINITE AND has a cardinality at most  , then we will have finish!”
, then we will have finish!”
“we find ANY
Maybe that is not so surprising after all, as soon as all the $f$-subset of any f-subset in the pseudo intersection is also in the pseudo intersection…
September 29, 2017 at 10:20 am
This is another interesting idea. It isn’t clear how to use it (or at least, not clear to me after about 15 minutes of scratching my head), because I don’t see a way of controlling the number of f-intersections. The sort of thing one might try is to begin with a set with the f.i.p. and no f-intersection, and remove sets from it until the first point at which an f-intersection appears. But if that happens at a large limit ordinal, then it isn’t clear that the number of f-intersections can’t jump from zero to very very big. (I’m assuming here that the sets in
with the f.i.p. and no f-intersection, and remove sets from it until the first point at which an f-intersection appears. But if that happens at a large limit ordinal, then it isn’t clear that the number of f-intersections can’t jump from zero to very very big. (I’m assuming here that the sets in  have been well-ordered and we are removing them one by one.)
have been well-ordered and we are removing them one by one.)
At a successor ordinal things might be OK though. If has no f-intersection and we remove a single set
has no f-intersection and we remove a single set  from it, then if
from it, then if  is an f-intersection of
is an f-intersection of  , it must be not almost contained in
, it must be not almost contained in  , but almost contained in every other set in
, but almost contained in every other set in  . So
. So  is infinite.
is infinite.
Oh wait, I think I’ve noticed something that shows that the approach as you currently have it can’t work for a simple reason. The reason is that if is an f-intersection for a set-system
is an f-intersection for a set-system 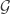 , then so is any infinite f-subset of
, then so is any infinite f-subset of  . Therefore, any non-empty
. Therefore, any non-empty 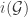 has cardinality equal to that of the continuum, and
has cardinality equal to that of the continuum, and 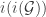 is empty.
is empty.
October 1, 2017 at 12:59 am
Yes… It make me think about new terminology and definitions that could be relevant.
Like for instance ,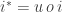 and
and 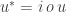 , where
, where ![u(\mathcal{G})=\bigl\{A\subset_f [\mathbb{N}],\, \forall G\in \mathcal{G},\, A\supset_f G \bigr\}](https://s0.wp.com/latex.php?latex=u%28%5Cmathcal%7BG%7D%29%3D%5Cbigl%5C%7BA%5Csubset_f+%5B%5Cmathbb%7BN%7D%5D%2C%5C%2C+%5Cforall+G%5Cin+%5Cmathcal%7BG%7D%2C%5C%2C+A%5Csupset_f+G+%5Cbigr%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) gives the set of all pseudo-union of
gives the set of all pseudo-union of 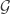 . Maybe
. Maybe  is also a good tool for next. For example we can say that when it is a set with a single element that
is also a good tool for next. For example we can say that when it is a set with a single element that 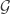 is “clean”.
is “clean”.
Note is a “good part” (of the set of all f-sets) if there exists
is a “good part” (of the set of all f-sets) if there exists  such that
such that ![i(\mathcal{G})=i(\left\{[A]\right\})](https://s0.wp.com/latex.php?latex=i%28%5Cmathcal%7BG%7D%29%3Di%28%5Cleft%5C%7B%5BA%5D%5Cright%5C%7D%29&bg=ffffff&fg=333333&s=0&c=20201002) . So maybe, by now, we can give the abbreviation
. So maybe, by now, we can give the abbreviation ![i_A=i(\left\{[A]\right\})](https://s0.wp.com/latex.php?latex=i_A%3Di%28%5Cleft%5C%7B%5BA%5D%5Cright%5C%7D%29&bg=ffffff&fg=333333&s=0&c=20201002) (and of course
(and of course ![u_A=u(\left\{[A]\right\})](https://s0.wp.com/latex.php?latex=u_A%3Du%28%5Cleft%5C%7B%5BA%5D%5Cright%5C%7D%29&bg=ffffff&fg=333333&s=0&c=20201002) ) – Then what I called
) – Then what I called  in a long previous today-post (that I’m going to write better without notation mistakes (I hope) , and in a clearest way) is now
in a long previous today-post (that I’m going to write better without notation mistakes (I hope) , and in a clearest way) is now  .
.
In another comment, I spoke about being a “good part” :
October 12, 2017 at 5:29 am
We can without lost of generality suppose that![i(\left\{X_{k},k<\alpha\right\})\ne \left\{[\emptyset]\right\}](https://s0.wp.com/latex.php?latex=i%28%5Cleft%5C%7BX_%7Bk%7D%2Ck%3C%5Calpha%5Cright%5C%7D%29%5Cne+%5Cleft%5C%7B%5B%5Cemptyset%5D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) where
where  is the smallest ordinal such that
is the smallest ordinal such that ![i(\left\{X_{k},k<\alpha\right\})\cap i(\left\{X_{\alpha}\right\})=\left\{[\emptyset]\right\}](https://s0.wp.com/latex.php?latex=i%28%5Cleft%5C%7BX_%7Bk%7D%2Ck%3C%5Calpha%5Cright%5C%7D%29%5Ccap+i%28%5Cleft%5C%7BX_%7B%5Calpha%7D%5Cright%5C%7D%29%3D%5Cleft%5C%7B%5B%5Cemptyset%5D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) .
.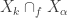 instead of
instead of 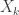 .
. , and then we have tower (with no intersection), because
, and then we have tower (with no intersection), because 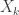 is clearly in every
is clearly in every 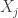 with
with 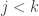 …
…
Indeed if it is not the case, we consider
It seems te me (but I don't feel so sure about it) that we can also assume that
October 12, 2017 at 7:25 pm
rectification :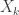 is not f_included in every
is not f_included in every 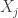 , with $j<k$ but if we pick
, with $j<k$ but if we pick  in $ latex i(\left\{X_{k},k<\beta\right\})\setminus i(\left\{X_{k},k<\beta+1\right\})$ we might have tower by considering
in $ latex i(\left\{X_{k},k<\beta\right\})\setminus i(\left\{X_{k},k<\beta+1\right\})$ we might have tower by considering  ,
,  for
for  successor ordinal, and if $k$ is a limit ordinal we take as usual
successor ordinal, and if $k$ is a limit ordinal we take as usual  in
in  .
. such that
such that  is the only increasing injection from
is the only increasing injection from 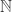 to $A$)
to $A$)
(where
I thought this tower has no intersection because![i(\left\{X_{k},k<\alpha\right\})=\left\{[\emptyset]\right\}](https://s0.wp.com/latex.php?latex=i%28%5Cleft%5C%7BX_%7Bk%7D%2Ck%3C%5Calpha%5Cright%5C%7D%29%3D%5Cleft%5C%7B%5B%5Cemptyset%5D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) , but it is not so clear… anyway I post this comment not only to correct the previous one but to give a possible idea quickly before the correct (basic) things that might be in the previous post get spoiled by its wrong end.
, but it is not so clear… anyway I post this comment not only to correct the previous one but to give a possible idea quickly before the correct (basic) things that might be in the previous post get spoiled by its wrong end.
October 24, 2017 at 10:25 pm
Let’s take a generalization of the problem and figure out few simple particular case of this generalization where it still holds. This will lead to a new formulation of the problem… considering not f-set, but tr-set, meaning classes of sets equal “up to translation”.
Let be a quasi-ordered relation on
be a quasi-ordered relation on  , such that
, such that  is thinner than
is thinner than  .
.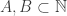 , we write
, we write  , or
, or ![[A]_o=[B]_o](https://s0.wp.com/latex.php?latex=%5BA%5D_o%3D%5BB%5D_o&bg=ffffff&fg=333333&s=0&c=20201002) if
if  and
and  . We also write for any
. We also write for any  ,
,  .
. has no
has no  -intersection if
-intersection if ![i_o(\mathcal{A})=[\emptyset]_o](https://s0.wp.com/latex.php?latex=i_o%28%5Cmathcal%7BA%7D%29%3D%5B%5Cemptyset%5D_o&bg=ffffff&fg=333333&s=0&c=20201002) that it has the $o$-intersection property (oip) if for any finite set
that it has the $o$-intersection property (oip) if for any finite set 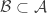 , we have
, we have  not equal to
not equal to ![0_o=:[\emptyset]_o](https://s0.wp.com/latex.php?latex=0_o%3D%3A%5B%5Cemptyset%5D_o&bg=ffffff&fg=333333&s=0&c=20201002) . We say that
. We say that  is o-saturated if it has the oip and no o-intersection. And we say that
is o-saturated if it has the oip and no o-intersection. And we say that 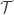 is a o-total if for any
is a o-total if for any  we have
we have  or
or  .Let's call
.Let's call 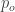 resp.
resp. 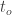 ) the smallest ordinal such that there exists a o-saturated set ( resp. o-saturated and o-total) indexed by ordinals lower than
) the smallest ordinal such that there exists a o-saturated set ( resp. o-saturated and o-total) indexed by ordinals lower than 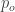 .
.
For any
We say that
We can ask our self whether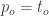 …
…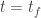 and
and  , and we hope to prove that they are equal. We can state that
, and we hope to prove that they are equal. We can state that 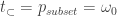 . And we can also state that the equality holds, for any
. And we can also state that the equality holds, for any  such that , any
such that , any  has the xip. Because we can use successfully the argument of the comment of the main comment.
has the xip. Because we can use successfully the argument of the comment of the main comment.
We can say that
Let's now give an example of such a quasi order. Still calling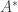 the increasing injection from $\mathbb{N}\to A$, we'll say that
the increasing injection from $\mathbb{N}\to A$, we'll say that  if there exists
if there exists  such that
such that 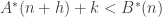 for all
for all 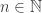 .
.
We can see that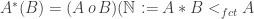 and
and 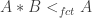 , We can
, We can
call this (***) then make two statement :
The first one is that $t_{fct}=p_{fct}$. (because (***) leads that any has the fct.ip. and we just said that the equality holds in that case)
has the fct.ip. and we just said that the equality holds in that case)
the second statement is that $t_{fct}$ is not smaller than $t=t_f$. Indeed we can then use the argument here : https://gowers.wordpress.com/2017/09/19/two-infinities-that-are-surprisingly-equal/#comment-203684 .
.
(***) assure us that the "composition tower" has no fct-intersection witch is stronger then having no f-intersection. For the same reason of strenght, we have the obvious opposite inclusion and we then have
We can also build an intermediate strongly quasi-order that we can call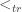 , for translation :
, for translation :  if and only if there exists
if and only if there exists  such that
such that  . We can see easily that
. We can see easily that 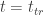 (by choosing fine representative element of a tr-tower : = total family indexed by ordinals that extend
(by choosing fine representative element of a tr-tower : = total family indexed by ordinals that extend 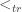 )
)
We then have :
So, the problem have a "translations 's translation" (joke with both meaning of "translation")
have a "translations 's translation" (joke with both meaning of "translation")
We have
 is compatible with "translations" (the tr-equivalence) and also the fct-equivalence.
is compatible with "translations" (the tr-equivalence) and also the fct-equivalence.
Note that this a nice thing about this equivalent condition, is that the composition
It might also be interesting to get other quasi order, by making an eventually non-empty f-intersection empty by some quotient, and consider a digressing family of such quasi order…
It could also be instructive to build quasi-order where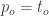 does not hold.
does not hold.
October 24, 2017 at 11:27 pm
EDIT of few LATEX in previous post (it’s better to read this one)
Let’s take a generalization of the problem and figure out when it is simple the cases that we can solve. be a quasi-ordered relation on
be a quasi-ordered relation on  , such that
, such that  is thinner than
is thinner than  .
.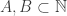 , we write
, we write  , or
, or ![[A]_o=[B]_o](https://s0.wp.com/latex.php?latex=%5BA%5D_o%3D%5BB%5D_o&bg=ffffff&fg=333333&s=0&c=20201002) if
if  and
and  . We also write for any
. We also write for any  ,
,  .
. has no o-intersection if
has no o-intersection if ![i_o(\mathcal{A})=[\emptyset]_o](https://s0.wp.com/latex.php?latex=i_o%28%5Cmathcal%7BA%7D%29%3D%5B%5Cemptyset%5D_o&bg=ffffff&fg=333333&s=0&c=20201002) that it has the o-intersection property (o-ip) if for any finite set
that it has the o-intersection property (o-ip) if for any finite set 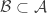 , we have
, we have  not equal to
not equal to ![0_o=:[\emptyset]_o](https://s0.wp.com/latex.php?latex=0_o%3D%3A%5B%5Cemptyset%5D_o&bg=ffffff&fg=333333&s=0&c=20201002) . We say that
. We say that  is o-saturated if it has the oip and no o-intersection. And we say that
is o-saturated if it has the oip and no o-intersection. And we say that 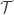 is a o-total if for any
is a o-total if for any  we have
we have  or
or  .Let's call
.Let's call 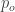 resp.
resp. 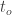 ) the smallest ordinal such that there exists a o-saturated set ( resp. o-saturated and o-total) indexed by ordinals lower than
) the smallest ordinal such that there exists a o-saturated set ( resp. o-saturated and o-total) indexed by ordinals lower than 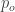 .
.
Let
For any
We say that
We can ask our self whether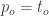 …
…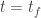 and
and  , and we hope to prove that they are equal.
, and we hope to prove that they are equal. .
. holds, for any
holds, for any  such that , any
such that , any  has the x-ip. Because we can use the argument of the main comment which is precisely : https://gowers.wordpress.com/2017/09/19/two-infinities-that-are-surprisingly-equal/#comment-203713.
has the x-ip. Because we can use the argument of the main comment which is precisely : https://gowers.wordpress.com/2017/09/19/two-infinities-that-are-surprisingly-equal/#comment-203713.
We can say that
We can also obviously notice that
We can also state that the equality
Let's then give an example of such a quasi order. Still calling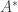 the increasing injection from
the increasing injection from  , we'll say that
, we'll say that  if there exists
if there exists  such that
such that 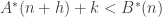 for all
for all 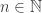 .
.
We can see that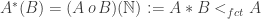 and
and 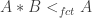 , We can
, We can
call this (***) then make two statement :
The first one is that $t_{fct}=p_{fct}$. has the fct.ip. and we just said that the equality holds in that case)
has the fct.ip. and we just said that the equality holds in that case)
(because (***) leads that any
the second statement is that $t_{fct}$ is not smaller than $t=t_f$. Indeed we can then use the argument here : https://gowers.wordpress.com/2017/09/19/two-infinities-that-are-surprisingly-equal/#comment-203534 .
.
(***) assure us that the "composition tower" has no fct-intersection witch is stronger then having no f-intersection. For the same reason of strength, we have the obvious opposite inclusion and we then have
We can also build an intermediate strongly quasi-order that we can call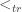 , (for "translation") :
, (for "translation") :  if and only if there exists
if and only if there exists 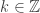 such that
such that  . We can see easily that :
. We can see easily that :
(by choosing fine representative element of a tr-tower : = total family indexed by ordinals that extend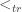 )
)
We then have :
This make the hope of picking a fct-tower (then a f-tower with the -argument) into
-argument) into  a little bit more concrete than before these obervations… because we can suppose that
a little bit more concrete than before these obervations… because we can suppose that 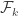 is only
is only  when
when  , and
, and  is a limit ordinal…
is a limit ordinal…
(+++) also show that
 is equivelent to
is equivelent to 
Witch is a translation of the problem in a context of classes closed "up-to translation" (like fct and tr) – note that the composition is compatible with both tr-equivalence and fct-equivalence)
composition is compatible with both tr-equivalence and fct-equivalence)
It might also be interesting to get other quasi order, by making an eventually non-empty f-intersection empty by some quotient, and consider a digressing family of such quasi order…
It could also be instructive to build , quasi-order where
, quasi-order where  .
.
October 24, 2017 at 11:35 pm
[…]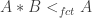 AND
AND  […]
[…]
October 24, 2017 at 11:47 pm
[…]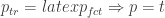 […] …not yet “equivalent”
[…] …not yet “equivalent”
October 25, 2017 at 7:06 pm
I did another wrong notation in the definition of $<_{fct}$ : I reversed the sens of an inequality!! We should read
Sorry for these notation mistakes! (I'm going to continue these attempt and ideas on mathOverflow, with the same surname, then I will post it here, when I'll be sure that it is correct and relevant!)
I hope I'll get something nice to bring and then bring kind of a compensation for all these inaccuracies, in contrast with the smart behavior and of the high quality of other interventions !
November 18, 2017 at 12:46 pm
I did few mistakes : we don’t have . But only
. But only  and also
and also  this is interesting because then, if we get
this is interesting because then, if we get  we are done.
we are done.
There is kind of an “inverse problem” by asking who are the partial orders such that .
.
I say again the definition of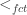 :
:
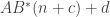 for all
for all  integer, where
integer, where 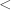 is the usual order on
is the usual order on 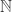 and $A^*$ is the increasing injection from
and $A^*$ is the increasing injection from 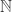 to $A=A^*(\mathbb{N})$
to $A=A^*(\mathbb{N})$
(the previous definition took $a\in \mathbb{Z}$ so there is some definition problem for the fonction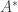 if
if  )
)
Let's also say again the two interesting fact that we have with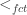
1) it is extending and compatible with
and compatible with  (where
(where  )
) and
and 
2)
So that 2) get rid of the problem we had before with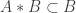 that is not true… we pay this nice fact by dealing with
that is not true… we pay this nice fact by dealing with 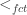 instead of
instead of 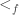 but there may be hope to get back to
but there may be hope to get back to  with new statements that are interesting independently from $p=t$.
with new statements that are interesting independently from $p=t$.
One of this statement could be the fact that $p_{fct}=p$ that I spoke about at the beginning of the post but there is another one (that might be very wrong, but we need a weaker version)
monotone no-intersection statement : is a collection of
is a collection of  families such that
families such that 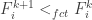 , for all
, for all  and suppose that no $F^k$ have a non-empty f-intersection, then
and suppose that no $F^k$ have a non-empty f-intersection, then  have no f-intersection as well.
have no f-intersection as well.
Suppose that
This statement, if true, would help us in the particular case of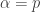 and that $F=F_0$ has the property that any ending segment has no-intersection ( $\left\{F^0_i,\, j<i<p\right\}$ has no f-intersection for all
and that $F=F_0$ has the property that any ending segment has no-intersection ( $\left\{F^0_i,\, j<i<p\right\}$ has no f-intersection for all 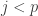 )
)
There is a construction mixing the usual argument in the main comment, the "more and more tower-like" idea in the next main comment, and the $*$ argument that failed because of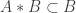 not being true :
not being true :
If is successor we say
is successor we say 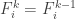 if
if  , and
, and  .if not
.if not
If is limit, we take
is limit, we take  any f-intersection of
any f-intersection of  and we say that
and we say that  if
if  , and if
, and if  we take
we take 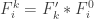 .
.
We can imagine other construction, but if the statement is true, and if we can suppose that we can assume the existence** of the particular case of a family with cardinality where the ending segment have no-intersection (I think this** is not difficult) then
where the ending segment have no-intersection (I think this** is not difficult) then 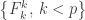 is a tower with no-intersection.
is a tower with no-intersection.
So if either monotone no-intersection statement (and **) is true either is true then we have what we want.
is true then we have what we want.
November 18, 2017 at 1:09 pm
it seems that the “greater then bug” is still there, so let’s just give the good definition of $<_{fct}$ :
 if there exists
if there exists  such that :
such that :
 for all
for all 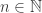
(the decreasing of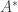 is quicker than that of
is quicker than that of 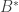 , that's why the inequality is this way, that is also why I used the "greater or equal " instead of switch the places of A and B, if the bug doesn't come in this very comment, this will show that it does'nt react to "lt" the same way tan to "gt". *)
, that's why the inequality is this way, that is also why I used the "greater or equal " instead of switch the places of A and B, if the bug doesn't come in this very comment, this will show that it does'nt react to "lt" the same way tan to "gt". *)
*by the way… is it " a > b" or " a \> b " that works ?
Well, I'm going to test it, so that you don't loose time by answering that kind of boring details :
test
 (with the barre)
(with the barre)
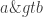 (without the barre)
(without the barre)
November 18, 2017 at 1:54 pm
The monotone-no-intersction statement is wrong anyway : if
if  and
and  if not, where
if not, where 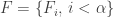 has no f-intersection.
has no f-intersection.
Take
September 22, 2017 at 12:19 pm |
Here’s another very general idea for an approach. I doubt it can be made to work, but I’ll give it anyway. We start with a set with the finite intersection property and no f-intersection. We then call this set
with the finite intersection property and no f-intersection. We then call this set  , and we try to create a transfinite sequence of sets
, and we try to create a transfinite sequence of sets 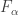 that become more and more tower-like as we continue. For example, perhaps
that become more and more tower-like as we continue. For example, perhaps  replaces two sets
replaces two sets  and
and  from
from 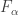 by the sets
by the sets  and
and  , or something like that. As usual, it may well be hard to say what to do when
, or something like that. As usual, it may well be hard to say what to do when  is an uncountable limit ordinal. But the hope would be that each
is an uncountable limit ordinal. But the hope would be that each 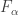 would have the same cardinality as
would have the same cardinality as  , as well as no f-intersection, that the process would have to terminate at some point, and that when it terminated we would have a tower. It would be something like an “infinite compression argument”.
, as well as no f-intersection, that the process would have to terminate at some point, and that when it terminated we would have a tower. It would be something like an “infinite compression argument”.
September 22, 2017 at 2:40 pm
To go a tiny bit further with this idea, suppose we have reached a set system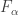 . If it is not a tower, then find inside
. If it is not a tower, then find inside 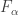 two sets
two sets 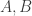 with neither f-contained in the other. Then I will indeed replace $la tex B$ by
with neither f-contained in the other. Then I will indeed replace $la tex B$ by  . If
. If  is already in
is already in  , that doesn’t matter, as we just care that the cardinality should not increase. Clearly the new set system still has the finite intersection property and it still has empty f-intersection.
, that doesn’t matter, as we just care that the cardinality should not increase. Clearly the new set system still has the finite intersection property and it still has empty f-intersection.
So the problem is, once again, what to do about limit ordinals. Suppose that is a limit ordinal and that for each
is a limit ordinal and that for each  with
with 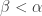 I have constructed a set system
I have constructed a set system 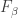 with the finite intersection property and no f-intersection. I now need to construct a limiting set system
with the finite intersection property and no f-intersection. I now need to construct a limiting set system 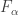 somehow. This will be fine if I can ensure that no set from
somehow. This will be fine if I can ensure that no set from  has been changed infinitely many times. But it’s not obvious that that will happen.
has been changed infinitely many times. But it’s not obvious that that will happen.
Thinking about this further, it seems to be running into the same difficulties.
September 22, 2017 at 8:55 pm |
Here is the proof and discussion about existence of tower with empty intersection that is in the main artical :
“Let’s use this idea to prove that there do exist towers with empty f-intersections. I shall build a collection of non-empty f-sets [A_\alpha] by transfinite induction. If I have already built [A_\alpha], I let [A_{\alpha+1}] be any non-empty f-set that is strictly f-contained in [A_\alpha]. That tells me how to build my sets at successor ordinals. If \alpha is a limit ordinal, then I’ll take A_\alpha to be a non-empty f-intersection of all the [A_\beta] with \beta<\alpha.
But how am I so sure that such an f-intersection exists? I’m not, but if it doesn’t exist, then I’m very happy, as that means that the f-sets [A_\beta] with \beta<\alpha form a tower with empty f-intersection.
Since all the f-sets in this tower are distinct, the process has to terminate at some point, and that implies that a tower with empty f-intersection must exist."
Instead of building one tower let's build a couple of tower, one with $f$-sets and one with representantive element. So we have built our couple $([A_{\alpha}],A_{\alpha})$ exactly the same way, but we just ask that the normal set tower is strictly increasing (it should'nt be a problem, wether $\alpha$ is a limit ordinal or not)
But if the normal set tower is strictly decreasing, the process has to stop at most when $\alpha$ is the first uncontable ordinal. I must be doing a confusion because it seems to give the result pretty easily… I steel post it, and I hope that, if it's wrong or stupid, then it's not stupid in such a way that I would feel ridiculous.
September 23, 2017 at 8:29 am
I’m not sure what you are trying to do here with the normal set tower. It’s certainly true that you can’t have an uncountable collection of subsets of the natural numbers that is well-ordered by strict inclusion. But there are two things that you can have.
(i) An uncountable collection of the subsets of the natural numbers that is well-ordered by almost inclusion.
(ii) An uncountable collection of the subsets of the natural numbers that is totally ordered by strict inclusion.
One thing I don’t see right now is whether there is a continuum-size collection that is well-ordered by almost inclusion.
September 23, 2017 at 12:44 pm
sorry for the confusion yesterday, I was thinking about this precise example futher, and trying and trying to be more general, I wrote wrong things: this next example convince me somehow that the tower we look for may look like a transfinite self-composition of a set under , i feel that this construction+the usual pattern of the proof in article give kind of something that look like it self to the way that seem to behave countable ordinal themself! But I’m far to be knowing what I’m talking about , so let’s
, i feel that this construction+the usual pattern of the proof in article give kind of something that look like it self to the way that seem to behave countable ordinal themself! But I’m far to be knowing what I’m talking about , so let’s
Let’s say it in a normal math way (at least until conclusion(s) that we can hold from it)
Let be the set of injective increasing function
be the set of injective increasing function  from
from  (so then we have
(so then we have  ).
). where the
where the  means composition of functions. We also define
means composition of functions. We also define  .
.![[\lim f(\mathbb{N})]\subset_f f^k(\mathbb N)](https://s0.wp.com/latex.php?latex=%5B%5Clim+f%28%5Cmathbb%7BN%7D%29%5D%5Csubset_f+f%5Ek%28%5Cmathbb+N%29&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all 
 a greater pseudo intersection then
a greater pseudo intersection then  , here our “
, here our “ ” is
” is  and our “
and our “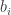 ” are
” are  )
) leads to the other fact that
leads to the other fact that 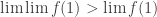
Let’s write
We can show that
(to be convinced, we can use the argument in the main page where we find
The fact that
We then build the tower the usual way, and when we have a limit ordinal we take a set of representative element function which can be written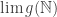 for some
for some  …
…
and then it seems to me that if we want empty f-interection, we have to use limit ordinal more than a countable many times, like we knew it, but not “much” more …
September 23, 2017 at 1:36 pm
edit : it’s not “lim F” but “lim f” (defintion of lim f)
September 23, 2017 at 4:58 pm
I)
Let me please correct the inaccuracy of what I just wrote. the condition is not sufficient to have the two property that I want
condition is not sufficient to have the two property that I want
which are![[(\lim f)(\mathbb N)]](https://s0.wp.com/latex.php?latex=%5B%28%5Clim+f%29%28%5Cmathbb+N%29%5D+&bg=ffffff&fg=333333&s=0&c=20201002) is a pseudo intersection of the
is a pseudo intersection of the !['[f^n(\mathbb{N}])_{n\in \mathbb{N}}](https://s0.wp.com/latex.php?latex=%27%5Bf%5En%28%5Cmathbb%7BN%7D%5D%29_%7Bn%5Cin+%5Cmathbb%7BN%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
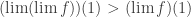 )
)
a)
b)
So at the place of we have to take something like
we have to take something like 
 that doesn’t satisfy a) and b).
that doesn’t satisfy a) and b).
It is a small detail but, if I don’t say anything, it may be confusing. Indeed, you can find $f$ increasing fonction (for exmaple
We don’t especially need to take a general $f$ and we can for example chose $f : n\mapsto 2n$ : the purpose doesn’t change. Actually, the “$f$ transfinite run” is just a particular case of a more general construction that I could have tried to) make by combining two proofs in the main page (the proof to show that a pseudo-intersection is not unique if a tower has a contable cardinal (1), and the proof that there exists a tower with no pseudo intersection (2))
I use this example with this “running fonction” because it gives an elegant self computing way to chose a representive of a non-empty pseudo intersection, but if it can show something relevant, it won’t show more than what I could have do, combining (1) and (2), by using the choice of the $b_i$ in proof (1) (istead of $f^{i}$)… and I will say later why I like this $f$-running fonction.
This is a lot of word to say nothing more than the argument I ment to use in my verywrong post of yesterday : It is the same idea but cleaned up from one stupidity (the “stupidity” was to hope to take a representant of a pseudo-intersection that in contain in the obvious way, in some reprsentant picked into the previous element of the tower)
And now that it is clean from the obviouss mistake, it can still be to optimistic to hope to combine (1) and (2) to deduce what we want.
I “feel” like the “$f$-run ” is a “run over countable ordinal” : $f$, with an instruction for ordinal that is not a limit ordinal (take $f^{\alpha+1}$, and an instruction for limit ordinal (take $lim g$, where $g$ is the fonction of the previous limit ordinal)
But I think this notion of previous limit ordinal is not aloud in general… but as soon as they are contable, we may be able to aply it, then the b) property shoud tell us that $f$ won’t take a limit cardinal instruction strictly more often than a countable many time
Then I don’t know if I cannot conclude because a) and b) are actually weak, or because I am weak myself.
II)
Anyway…
The “nice” thing that we could get from this “$f$-run” is a “fonction” that could be correlated to a precise ordinal type:
for example let’s take $f(n)=2n$, than $f^k(n)=2^k.n$, $(lim f)(n)=2^n$, $lim((lim f))(n)=2^{2n}$ etc…so here $\omega$ could correspond to $2^n$, $\omega+\omega$ could correspond to $2^{2n}$ etc.. this is a bit fuzzy, but I feel like a possible (nice?) idea to develeppe from this inspiration
It would maybe be better if we define, not $f^{n+1}=f\,o\,f^{n)$, but $f_{n+1}=f_{n}\,o\f_{n}$… in order to find a correlation between any limit ordinal and a “$\lim$-fonction”
I hope these ideas are not hidden trivialities that are made-up with some other trivialities (or if they, are, I hope that they are in a way that can leads to something nice)
September 24, 2017 at 1:47 am
EDIT : at line 9 of last comment it is not $f(n)\leq 2n$, but $f(n)\geq 2n$ that does the job.
To resume the idea of the II) : I’m looking for a $f$-tower with NPI (no pseudo-intersection). that would be a “natural copy” of countable ordinal numbers.
September 24, 2017 at 4:46 pm
A) When does there exist forall $\omega_{\mathcal{T}}$ and $\mathcal{T}=\left\{T_{\alpha},\,\alpha <\omega_{\mathcal{T}}\right\}\subset \mathcal{P}(\mathbb{N}$, such that $[[\mathcal T]]=\left\{[T],\, T\in \mathcal T\right\}$ is a tower, and such that : $T_{\alpha}*T_{\beta}=T_{\alpha+\beta}$?
(where $(A*B)^*=A^*\,o\,B^*$, where $A^*=f_A$ is the only strictly increasing fonction from $\mathbb N$ to $A$)
If the answer is yes for intersestings $<\omega_{\mathcal{T}}$ , it may be a good tool, and if the answer is not trivial and is no, it is good to know anyway…
B)Maybe we can also build a super-towers $\mathbb{T}$, whose elements are sets of f-sets, such that when you pick a f-set $[C_{\alpha}]\in \mathcal C_{\alpha}\in \mathbb{T}$, there a f-tower whose elements are [C_{\beta}]\in \mathcal C_{\beta}$ with $\beta<\alpha$
C) We could also build g-towers exactly like f-towers, where the f-topology is thiner than the f-topology. (whose closed set are finite subsets of $\mathbb{N}$) and consider all these topology such that the result still holds. (maybe we can also imagine topologyes, not on $\mathbb N$ but on any $\alpha$, countable ordinal.
October 2, 2017 at 3:11 pm
Regarding the question of possible sizes of towers: I learned from Vera Fisher today that it is possible that there is no tower of size continuum, in some models of ZFC. A reference is Dordal, Peter Lars. “Towers in![[\omega]^\omega](https://s0.wp.com/latex.php?latex=%5B%5Comega%5D%5E%5Comega&bg=ffffff&fg=333333&s=0&c=20201002) and
and 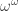 .” Annals of pure and applied logic 45.3 (1989): 247-276.
.” Annals of pure and applied logic 45.3 (1989): 247-276.
Actually, Dordal shows that for a ‘fairly closed’ set of regular cardinals and some regular
of regular cardinals and some regular  , one can force that there is a tower of order type
, one can force that there is a tower of order type  iff
iff 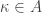 , and the continuum is
, and the continuum is  . E.g.
. E.g.  can be any finite set of regular cardinals and the continuum anything regular above
can be any finite set of regular cardinals and the continuum anything regular above  .
.
This is in quite the contrast with other families we study (e.g. almost disjoint, independent) where maximal witnesses of size continuum always exist.
December 24, 2017 at 6:45 pm
@Daniel Soukup : the question that comes to me from this precious indication is : is the maximal size of a tower, is $\latex \mu$ also the maximal size of a family
is the maximal size of a tower, is $\latex \mu$ also the maximal size of a family 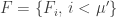 such that
such that  has no pseudo-intersection, and such that
has no pseudo-intersection, and such that  is injective. (where
is injective. (where  denote the set of all f-lower bound ("pseudo intersections") of a family
denote the set of all f-lower bound ("pseudo intersections") of a family  )
)
If
Such an necessary has the fip. Note that we can obtain such a family from any fip family without pseudo intersection
necessary has the fip. Note that we can obtain such a family from any fip family without pseudo intersection  by considering the family of the members
by considering the family of the members  of
of  that satisfy
that satisfy 
if this could be "kind of" an indication to the way to build a tower from any
this could be "kind of" an indication to the way to build a tower from any  with fip and npi.
with fip and npi.
——————————————————————————————-
For example by choosing $ latex C_i\in i_f(\left\{F_i,\, i<j\right\}$ for all and compose it with th
and compose it with th  operation that is defined here https://gowers.wordpress.com/2017/09/19/two-infinities-that-are-surprisingly-equal/#comment-203525
operation that is defined here https://gowers.wordpress.com/2017/09/19/two-infinities-that-are-surprisingly-equal/#comment-203525
The main difference is instead of composing the $F_i$ we compose the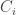 that belong to members of a decreasing family of co-filters* with empty (usual) intersection., so that we can hope in a more realistic way that the tower we get has no pseudo -intersction (npi)
that belong to members of a decreasing family of co-filters* with empty (usual) intersection., so that we can hope in a more realistic way that the tower we get has no pseudo -intersction (npi) in the paragraph "motivation" of this link on MSE : https://math.stackexchange.com/questions/2577440/decreasing-family-of-families-with-lower-bound-zero (I already wrote this in upper posts but note that $ latex A*B<_b A$ and also
in the paragraph "motivation" of this link on MSE : https://math.stackexchange.com/questions/2577440/decreasing-family-of-families-with-lower-bound-zero (I already wrote this in upper posts but note that $ latex A*B<_b A$ and also  )
)
I will develop in a MSE post some ideas I've got about the way to hope to make it work or at least exhibe a reason why it's not easy by reducing the aim to special cases to discuss : one idea could be to use the preorder that is called
(*the set of complements of is a filter for any family $X$, so I qualify
is a filter for any family $X$, so I qualify  a co-filter, but I don't know if it is the right terminology)
a co-filter, but I don't know if it is the right terminology)
December 24, 2017 at 6:52 pm
Just to correct one of the typos, just after the barre ….——————…. it is not but any ordinal (like
but any ordinal (like  )
)
September 24, 2017 at 5:22 am |
In case it is useful, here is another link to lecture notes covering the
Malliaris-Shelah proof in some detail:
https://arxiv.org/abs/1709.02408
September 24, 2017 at 4:38 pm |
[…] lots of mathematicians just expected that eventually we’d see the same thing play out here. (Tim Gowers, a former Fields Medalist himself, seems to suggest that a defeatist attitude may have held back […]
September 25, 2017 at 12:40 am |
I think some new oredered and quasi-ordered relations may be related to our goal.
For two fonctions $f,g\in\mathbb{N}^{\mathbb{N}}$ let’s say
$fk$, we have $f(n)<g(n)$.\\
($i$ is for "injection" because this quasi-ordrered relation is a partial ordered relation on injective fonctions, whom are all of the form $f_A $, where $A=f_A( \mathbb{N})$)
the first one is $f<_w g$ if and only if there exists $h\in \mathbb{Z}$ such that $f+h<_w g$.
($w$ is for "weak")
And the other one is $f<_s g$ if and only if $f<_i g+h$ where is not a constant fonction like for the $w$-order, but any fonction such that $h<_i \inf_i \left\{f,g\right\}$.
We can say $[f]_x=[g]_x$ if we have both $f<_x g$ and $g<_x f$, where $x\in \left\{i,w,s\right\}$.
And we can say for any $\mathcal A\subset \mathcal{P}(\mathbb{N})$, that his $x$-cardinal is the cardinal of $\left\{[A^*],\, A\in \mathcal A \right\}$ (where $x\in \left\{i,w,s\right\}$, and $A^*=f_A$ is the only injective fonction from $\mathbb N$ to $A$)
Then we can ask ourself what is the maximum (resp. minimum) $x$-cardinal of an $x$-tower?
Because if we can find a f-tower and a sequence of representative elements of each of its f-sets , such that they form a $x$-tower, we would be happy to be able to bound the maximal cardinal of the $x$-tower. (it feel that the "runing fonction" I talked about before is behaving this way, for any $x\in \left\{i,w,s\right\}$, if it is the case it might not be hard to proove it, but I'm scared to try because I'm not used to transfinite induction proofs)
Conversly, minimums can be also good to know, if we build a $f$-tower from a $x$-tower.
September 25, 2017 at 12:48 am |
A part of a sentence diseapered at the bigining ! Here is the entier sentence :
“For two fonctions $f,g\in\mathbb{N}^{\mathbb{N}}$ let’s say
$fk$ we have $f(n)<g(n)$."
Sorry about this!
September 25, 2017 at 12:59 am |
there is a bug,( I think I’m not responsable for it),because it’s exaclty the same cut-sentence ! let me try again with different letters :
we write $fp,\,f(n)<g(n)$
September 25, 2017 at 1:09 am |
Let’s try a last time without the dollars :
f is i-lower than g if there exists an integer k such that for all n greater than k, f(n)<g(n)
September 25, 2017 at 8:41 pm |
Most of the set-theoretic background is missing. The notion of “cardinal characteristic of the continuum” was developed in the 80s to provide a very clear organization to the proliferation of consistency results about one combinatorial property of the reals implying another such property. A dozen or so were the first ones named—most had multiple equivalent definitions, of the sort of mostly easy combinatorics that did not prove p=t—and the implications were reduced to inequalities.
(The Wikipedia article is a poor stub—it doesn’t even mention p and t!—but it at least contains a few good references. They are usually denoted with fraktur letters.)
Like special points in a triangle, there is no end of how many there are, just a limit to how many actually catch mathematical interest. A fascinating new one, the “rearrangement” number, was discovered on mathoverflow the other year, based on an elementary real analysis question.
For example, the smallest characteristic seems to be the “Martin Axiom cardinal”. That it is the smallest is why MA implies so many combinatorial results. Some of the characteristics in fact turn out to be the “Martin Axiom restricted to a subfamily of ccc posets” cardinal.
Since all the characteristics are between aleph-one and the continuum, CH implies they are all equal. Many proofs based on CH are best thought of as proofs based on x=y, for two characteristics x and y. For example, Almgren once in his life published a proof assuming CH. Decades later, someone rephrased that proof as one based on some x=y, and was able to prove that Almgren’s conclusion implied x=y. The status of x=y (independent) was well-known to set theorists, so Almgren’s question about his statement was answered.
All but the p vs t question had been resolved for one-on-one comparisons. Proper forcing was the major tool for this, but it is famously restricted to the continuum is aleph-two only. In general, getting a model with three or four characteristics distinct is very difficult, and has only recently been done. The upshot is set theorists know how to say a lot about aleph-two using forcing, but not very much about aleph-three or more.
There’s a whole world of dualities and Galois-Tukey connections and more. If you liked the Oxtoby book, you will love this stuff. And the recent model theory connection is just amazing, probably far more important than resolving p=t.
For the record, Shelah announced a model with p<t about fifteen years ago, but quickly withdrew the claim.
So the short answer why no one was expecting a proof of p=t is that dozens of other same-genre equalities had all been proven, fairly straightforwardly, and in all other cases where no equality was found, a forcing proof of the inequality, sometimes quite involved, was eventually found. The model theoretic connection, with an almost forgotten question, is just remarkable.
September 28, 2017 at 8:15 am
Thank you very much for this helpful and illuminating comment. It suggests that the probability that a simple argument was overlooked is very small (rather than merely small, which is what I had previously assumed). I still find it interesting to spend a little bit of time searching for such an argument, just to get a feel for why it is a deep question, but I will suppress any fantasies of actually finding one.
September 29, 2017 at 3:18 pm
If you assume p=aleph-one, then there exists an elementary proof that p=t, going back to Rothberger 1948. This would later imply that proper forcing can’t prove p<t, as mentioned above, so progress at the time was measured by the piecemeal incremental improvements in understanding forcing the continuum beyond aleph-two.
One breakthrough was Shelah's proof that d<a is consistent, the penultimate one-on-one comparison problem. Shelah introduced a new, fairly complicated form of forcing, which reached its conclusion "globally", instead of the usual "local" iterations. (In particular, I believe it is still open whether aleph-one=d<a=aleph-two=continuum is possible, which is what a more traditional "local" proof would show.) For awhile Shelah thought a variant of that proof gave p<t, and SPM Bulletin 5 was an extended announcement of that result.
If you want to attempt an elementary proof by contradiction, check out Shelah "A comment on p<t". He derives a ZFC consequence, the existence of "peculiar gaps". They are consistent though, but perhaps some kind of "extrapeculiar gap" is not. Either way, the complexity is daunting.
September 28, 2017 at 4:22 pm |
I’m going to build “types” for set : the idea is that the more the type is big, the more it takes steps to define it. It is related to the classic induction proofs. And I think it will be useful in a context of a collection that have the “finite union property” that has “no non full pseudo union” (like the sets of complements of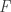 and that we would like to “no nonfully towerise” if you permit this expression.
and that we would like to “no nonfully towerise” if you permit this expression.
The general idea would be to build a tower by taking the first bricks into elements of “big types” (these elements in the union version looks like the image of integer sequences with huge increasing) , but first of all let’s define these types, in a general way, so that we can adapt definitions to what we need.
Let’s define for each a
a  -type.
-type. ,
,  is a f-decreasing injection from
is a f-decreasing injection from  to itself and
to itself and 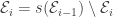 are elements of type at least
are elements of type at least  , where
, where  is a successor ordinal. Elements of type at least
is a successor ordinal. Elements of type at least  witch would be a limit ordinal , is a set that is almost contained in every member of a collection of sets of type
witch would be a limit ordinal , is a set that is almost contained in every member of a collection of sets of type  , and that is not itself of type at least
, and that is not itself of type at least 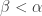 . In any case we say that the
. In any case we say that the  -type is (exactly)
-type is (exactly)  if it is at least of type
if it is at least of type  but not at least of type
but not at least of type  .
.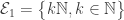 and
and  , or even
, or even 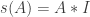 where
where  .
.
Type 1 are elements in
One can take as
I don't want to make a big comment, and, as my idea to continue is not precise yet (and maybe will never be) I stop there, and I hope the latex is fine now. I feel sorry that you had to edit it so many times the comments I made because of this "$latex" to put before every latex expression!
September 28, 2017 at 4:33 pm |
Oh the latex (almost) worked!!
Please be aware that I did’t use this infinite symbole anywhere.
there was propably a bug with the indice down the (it is not “infinite”, but “1”)
(it is not “infinite”, but “1”)
I’ve fixed the formulae that didn’t parse — it’s much quicker than doing the whole thing!
September 28, 2017 at 4:54 pm |
Let me write again the latex part for better understanding , (and turn this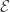 into a normal
into a normal  )
)
Let’s define for each a
a  -type.
-type. ,
,  is a f-decreasing injection from
is a f-decreasing injection from  to itself and
to itself and 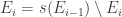 are elements of type at least
are elements of type at least  , where
, where  is a successor ordinal. Elements of type at least
is a successor ordinal. Elements of type at least  witch would be a limit ordinal , is a set that is almost contained in every member of a collection of sets of type
witch would be a limit ordinal , is a set that is almost contained in every member of a collection of sets of type  , and that is not itself of type at least $latex\beta<\alpha$. In any case we say that the
, and that is not itself of type at least $latex\beta<\alpha$. In any case we say that the  -type is (exactly)
-type is (exactly)  if it is at least of type
if it is at least of type  but not at least of type
but not at least of type 
 and
and  , or even
, or even 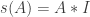 where
where 
Type 1 are elements in
One can take as
September 30, 2017 at 10:43 pm |
Hello, sorry for my bad english. Do you know if the Tukey respectively corresponding to p and t have been proved to be equal by Shelah and Malliaris? Or their techniques only prove the equality for cardinals
October 1, 2017 at 4:50 pm |
small edit of the previous note :
 is a “smart intersection part” (of the set of all f-sets) if there exists
is a “smart intersection part” (of the set of all f-sets) if there exists  such that
such that ![i(\mathcal{G})=i(\left\{[A]\right\})](https://s0.wp.com/latex.php?latex=i%28%5Cmathcal%7BG%7D%29%3Di%28%5Cleft%5C%7B%5BA%5D%5Cright%5C%7D%29&bg=ffffff&fg=333333&s=0&c=20201002) and a “good part” if there exists
and a “good part” if there exists  such that
such that ![\mathcal{G}=i(\left\{[A]\right\})](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BG%7D%3Di%28%5Cleft%5C%7B%5BA%5D%5Cright%5C%7D%29&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Let’s speak about one general result that I will call “characterization of preorder relation lemma”
If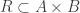 is a relation, let’s denote by
is a relation, let’s denote by 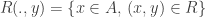 the
the  -row in
-row in  .(we denote by
.(we denote by  the
the  -row with the obvious dual definition)
-row with the obvious dual definition) -line as :
-line as :

 is a preorder
is a preorder

We also define the orthogonal of the
If $A=B$ the following assertions are equivalents :
a)
b)
c)
We can always see a set as the “lines” of a relation
as the “lines” of a relation 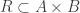 , if this relation is right (and left) separated (
, if this relation is right (and left) separated (  is injective ) and if it is closed under right and left orthogonal, then the orthogonal of the orthogonal of a line (resp. row) will be the initial line (resp. row) and you can choose an indexation of
is injective ) and if it is closed under right and left orthogonal, then the orthogonal of the orthogonal of a line (resp. row) will be the initial line (resp. row) and you can choose an indexation of  and
and  by
by  totally ordered set such that the orthogonal of the line
totally ordered set such that the orthogonal of the line  is the row
is the row 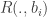 for all
for all  , and we get a natural ordered relation on
, and we get a natural ordered relation on  whom
whom  is an extended total order. If the family
is an extended total order. If the family  is not separated we can have a quotient on
is not separated we can have a quotient on  under the relation “having the same orthogonal” in order to get a order.
under the relation “having the same orthogonal” in order to get a order.
Another important fact is that, for any “line ” in our order relation
” in our order relation  , there exist a total order
, there exist a total order  that extend
that extend  such that
such that  .
. indexed by $T$, such that the coefficient
indexed by $T$, such that the coefficient  if $latex $(x,y)\in R$ and
if $latex $(x,y)\in R$ and  if not, then you will get a trigonal** matrix such that the
if not, then you will get a trigonal** matrix such that the  -line will have only
-line will have only  on the non-zero side of the diagonal. (I’m going to use this “one side line” argument later in order to fain a tower from a particular
on the non-zero side of the diagonal. (I’m going to use this “one side line” argument later in order to fain a tower from a particular  with stronger hypothesis.)
with stronger hypothesis.)
(if we take an infinite matrix
**Note that we can always obtain a total order with any separated “matrix” witch is stable under left and right orthogonality by ranging according to the increasing lexicographic order the “lines” and ranging the “rows” of the matrix that we just get according the decreasing lexicographic order… well I’m not sure this particular technique is working with any infinite set, but I think in our case we could make it work, it may be helpful later, if we try to “extend” our order, so when we will get to this step, we will examine better the possibility to have a trigonalisation this way… Of course the “trigonalisation” is always possible as soon as you can extend to a total order – it is for me a synonyme : the matrix point of view is just a tool to help for “viewing”, … although these matrix, have a “product” (in a semi-ring) so they are not just “tables of 0 and 1”, this product is realted to order relation this way : if
to a total order – it is for me a synonyme : the matrix point of view is just a tool to help for “viewing”, … although these matrix, have a “product” (in a semi-ring) so they are not just “tables of 0 and 1”, this product is realted to order relation this way : if  is any separated relation, and
is any separated relation, and 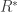 is the “complement” of it’s transposition, then the complement of
is the “complement” of it’s transposition, then the complement of  is an ordered relation…(the product is the usual product and the support fonction take any non-zero (positive!) coefficient into a “1”, and leaves the “zeros”, the complement is the matrix you get when you exchange the “0” and the “1”) This could maybe help later…
is an ordered relation…(the product is the usual product and the support fonction take any non-zero (positive!) coefficient into a “1”, and leaves the “zeros”, the complement is the matrix you get when you exchange the “0” and the “1”) This could maybe help later…
This was the first general statement but if I want to apply it to f-set I’ve got to find a trick, so I will associate to any family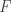 of f-sets, a family
of f-sets, a family  . This family is like a copy of
. This family is like a copy of 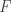 with a usual ground set, so we get rid of fuzzy sets, but we pay it by a bigger ground set.
with a usual ground set, so we get rid of fuzzy sets, but we pay it by a bigger ground set.  is also closed under left-orthogonality, but if we take a right orthogonal closure we might get some set that are not anymore “good parts”. Let’s make the statement that there exists family such that
is also closed under left-orthogonality, but if we take a right orthogonal closure we might get some set that are not anymore “good parts”. Let’s make the statement that there exists family such that  is closed under right and left orthogonal. Then we will be able to build a tower with no intersection this way : we use the “one side argument” to have infinitely many “one side” lines. (we do it by transfinite induction : let’s say we have a matrix up-trigonal relative to a partial order itself related to
is closed under right and left orthogonal. Then we will be able to build a tower with no intersection this way : we use the “one side argument” to have infinitely many “one side” lines. (we do it by transfinite induction : let’s say we have a matrix up-trigonal relative to a partial order itself related to  , then we get a “line
, then we get a “line 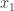 ” “one side”-meaning we extend the order such as the minorants of
” “one side”-meaning we extend the order such as the minorants of 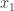 according to the partial order is also the line of minorant of
according to the partial order is also the line of minorant of 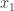 related to the extended total order, and we take
related to the extended total order, and we take  in this very minorant set… that you extend to an new total order without changing the non-minorant of
in this very minorant set… that you extend to an new total order without changing the non-minorant of 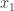 (because of trigonality), you do this for all successor ordinal extending smaller subrelations and when we get to a limit ordinal you just take the intersection of all smaller subrelation and the process has to stop when we get a finite matrix : we then have an infinite subset of “one side lines” BUT they may not have the empty intersection : indeed one may say that we “cannot ” get a non empty finite last one-side” line, because each line is infinite (even the side of continuum!!) but as soon as we wanted a separated matrix, we are dealing with a ground set that is quotient of the set of all f-sets (under the relation “having the same orthogonal) but no matter anyway, we just remove the last line of every set, and then we still have “good parts” …)
(because of trigonality), you do this for all successor ordinal extending smaller subrelations and when we get to a limit ordinal you just take the intersection of all smaller subrelation and the process has to stop when we get a finite matrix : we then have an infinite subset of “one side lines” BUT they may not have the empty intersection : indeed one may say that we “cannot ” get a non empty finite last one-side” line, because each line is infinite (even the side of continuum!!) but as soon as we wanted a separated matrix, we are dealing with a ground set that is quotient of the set of all f-sets (under the relation “having the same orthogonal) but no matter anyway, we just remove the last line of every set, and then we still have “good parts” …)
So what we proved is that the smallest tower is smaller than any such that
such that  is closed under orthogonality.
is closed under orthogonality.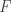 with the fip and no-intersection, a family with the above property… ? (it is possible because we know the result and because a tower has the property : this is then an intermediate result, (but maybe a trivial intermediate result that don’t make the problem easier!)
with the fip and no-intersection, a family with the above property… ? (it is possible because we know the result and because a tower has the property : this is then an intermediate result, (but maybe a trivial intermediate result that don’t make the problem easier!)
The question would then be : how to get from
Maybe we can adapt the proof for family that orthogonal closure is not to big, and such that some of the elements that we add are not necessary “good parts” (maybe take any good part in the pseudo-union set or in the pseudo-intersection set of the added element that would not be a good part… )
October 1, 2017 at 10:18 pm
line 9 : (not
(not 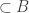
line 16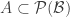 (not
(not 
October 2, 2017 at 11:22 am |
Actually the idea of the extended total order seems to work much better on down-f-set!! What I call down-f-set is a usual set of f-sets such that if![[A]](https://s0.wp.com/latex.php?latex=%5BA%5D&bg=ffffff&fg=333333&s=0&c=20201002) is one of its element, and if
is one of its element, and if ![[A']\subset_f [A]](https://s0.wp.com/latex.php?latex=%5BA%27%5D%5Csubset_f+%5BA%5D&bg=ffffff&fg=333333&s=0&c=20201002) then
then ![[A']](https://s0.wp.com/latex.php?latex=%5BA%27%5D&bg=ffffff&fg=333333&s=0&c=20201002) is also one of its element.
is also one of its element.
Let me try to develop the idea of the extended total order in this context :let be a set of downs-f-set that have the usual-set intersection property. Let
be a set of downs-f-set that have the usual-set intersection property. Let  be the support of
be the support of 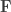 , meaning the set of all the down f sets that are include in some
, meaning the set of all the down f sets that are include in some  . It is an ordered set for usual inclusion. We then extend the usual inclusion in a total order $<<$. What is nice here is that
. It is an ordered set for usual inclusion. We then extend the usual inclusion in a total order $<<$. What is nice here is that ![[0,D]_{<<}](https://s0.wp.com/latex.php?latex=%5B0%2CD%5D_%7B%3C%3C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a down-f-set for all
is a down-f-set for all  . The set
. The set ![C=\left\{ [0,F]_{<<},\, F\in \mathbf{F}\right\}](https://s0.wp.com/latex.php?latex=C%3D%5Cleft%5C%7B+%5B0%2CF%5D_%7B%3C%3C%7D%2C%5C%2C+F%5Cin+%5Cmathbf%7BF%7D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is now a chain of usual set of f-sets, and the set
is now a chain of usual set of f-sets, and the set ![T=\left\{ [0,F]_{<<}-\bigcap C,\, F\in \mathbf{F}\right\}](https://s0.wp.com/latex.php?latex=T%3D%5Cleft%5C%7B+%5B0%2CF%5D_%7B%3C%3C%7D-%5Cbigcap+C%2C%5C%2C+F%5Cin+%5Cmathbf%7BF%7D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a chain of down-f-sets that has an empty (usual) intersection. We can pick a tower with no pseudo intersection inside.We take for
is a chain of down-f-sets that has an empty (usual) intersection. We can pick a tower with no pseudo intersection inside.We take for  our original
our original 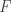 with no pseudo-intersection and the fip and it seems done…
with no pseudo-intersection and the fip and it seems done…
I don't see the mistake right now, but I'm sure I will see it just after posting!
October 2, 2017 at 10:33 pm
I think it’s wrong…because I get the same conclusion if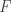 is countable, and that’s not possible…(the other statements may be wrong as well… I’m happy to have present the angle of “preorder caractérisation lemma” anyway, although it’s not working yet…)
is countable, and that’s not possible…(the other statements may be wrong as well… I’m happy to have present the angle of “preorder caractérisation lemma” anyway, although it’s not working yet…)
October 4, 2017 at 6:49 am
Oh let me try this : (the beginning is the same than the principal comment)![[A]](https://s0.wp.com/latex.php?latex=%5BA%5D&bg=ffffff&fg=333333&s=0&c=20201002) is one of its element, and if
is one of its element, and if ![[A']\subset_f [A]](https://s0.wp.com/latex.php?latex=%5BA%27%5D%5Csubset_f+%5BA%5D&bg=ffffff&fg=333333&s=0&c=20201002) then
then ![[A']](https://s0.wp.com/latex.php?latex=%5BA%27%5D&bg=ffffff&fg=333333&s=0&c=20201002) is also one of its element.Let’s call
is also one of its element.Let’s call  the set of all down-f-sets
the set of all down-f-sets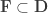 be such that
be such that 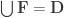 (condition 1)
(condition 1)
I call down-f-set is a usual set of f-sets such that if
let
Let’s now consider , the smallest topology such that elements of
, the smallest topology such that elements of  are closed set. As usual we extend the inclusion order in
are closed set. As usual we extend the inclusion order in  to a total order $<<$. Now we consider for all
to a total order $<<$. Now we consider for all 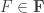 the set
the set ![G(F)=:[0,F]_{<<}\cap \mathbf{F}](https://s0.wp.com/latex.php?latex=G%28F%29%3D%3A%5B0%2CF%5D_%7B%3C%3C%7D%5Ccap+%5Cmathbf%7BF%7D&bg=ffffff&fg=333333&s=0&c=20201002) and
and  : the adherence of the union of elements in
: the adherence of the union of elements in  . Let's make the supposition that if
. Let's make the supposition that if  is a finite set, then
is a finite set, then  is not the set of all down -f-sets.(condition 2). Condition 1) tells us that
is not the set of all down -f-sets.(condition 2). Condition 1) tells us that  is an infinite inclusion ordered set such that the
is an infinite inclusion ordered set such that the  . And we also have
. And we also have  lower or equal to
lower or equal to 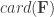 .
.
Now we are going to choose in each a f-set $choice(\mathcal{H}$ that does not belong to any
a f-set $choice(\mathcal{H}$ that does not belong to any  such that
such that  .
.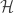 and
and 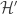 are down-f-set, we will have
are down-f-set, we will have  , and
, and ![\mathcal{T}=\left\{[\mathbb{N}]\setminus choice(\mathcal{H}),\, \mathcal{H}\in \mathbf{H}\right\}](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BT%7D%3D%5Cleft%5C%7B%5B%5Cmathbb%7BN%7D%5D%5Csetminus+choice%28%5Cmathcal%7BH%7D%29%2C%5C%2C+%5Cmathcal%7BH%7D%5Cin+%5Cmathbf%7BH%7D%5Cright%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) is a tower!
is a tower!
But as soon as
Let's get back to: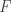 with no f-intersection and the f.i.p.
with no f-intersection and the f.i.p. , where
, where  is the set of f-sets f- included in the f-complement of
is the set of f-sets f- included in the f-complement of  , then we can conclude.
, then we can conclude.
We now remark that if we take
I'm going to turn everything into complement point of view, it will be more direct…
October 4, 2017 at 7:47 am
I made a mistake with this choice fonction, so it’s not working…but I think I can still have something (I’m quite sure that I can build a tower with no f-intersection) but It won’t be as small as I want to. Next time I’m going to try this intermediate construction…
October 29, 2017 at 3:59 pm |
A tower with no pseudo intersection (npi) satisfies two conditions,
with no pseudo intersection (npi) satisfies two conditions,
(1) has a non empty intersection for all
has a non empty intersection for all  .
.
(2) has no intersection, for all $k<c$
has no intersection, for all $k<c$
Let's say that a general family (necessarily with fip and npi) the smallest cardinality that can have such a family.
the smallest cardinality that can have such a family.
that satisfy (1) and (2) is a quasi-tower, and let's call
We obviously have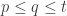 .
.
What seems to be the difficult part in order to prove that
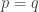 or is it
or is it  ? Are they both difficult?
? Are they both difficult?
Is it
If we have one of the two results, we can get rid of conditions that could be difficult to handle with. never the less, there is nothing to lose by having one of the two results…
November 23, 2017 at 3:12 pm |
I think I’ve got it (again)
We just have to prove a statement a bit stronger (that seems true in any lattice)
For any , and any
, and any  , let's say that
, let's say that  .
.
The "stronger statement" is then : fip-family and any
fip-family and any  such that
such that  is a tower and such that
is a tower and such that  there exists
there exists 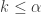 and a tower
and a tower  such that
such that  .
.
For any
We can say that " extend
extend  according to
according to  "
"
To prove this we consider minimal such that it is not true, and we say without lost of generality that
minimal such that it is not true, and we say without lost of generality that ![[0]\ne i(F^a)\ne i(F^b)](https://s0.wp.com/latex.php?latex=%5B0%5D%5Cne+i%28F%5Ea%29%5Cne+i%28F%5Eb%29+&bg=ffffff&fg=333333&s=0&c=20201002) for any
for any  . Then if
. Then if  is successor, we have
is successor, we have ![F_{\alpha-1}\ne [0]](https://s0.wp.com/latex.php?latex=F_%7B%5Calpha-1%7D%5Cne+%5B0%5D&bg=ffffff&fg=333333&s=0&c=20201002) and then
and then is minimal, we have a tower
is minimal, we have a tower  such that
such that  extend
extend  according to
according to 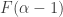 and we take
and we take  such that
such that 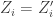 if
if  and
and  if not. And that's a contradiction.
if not. And that's a contradiction.
as
If type is limite
type is limite
we have for any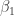 such that
such that 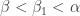 , a tower
, a tower  such that
such that 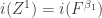 and
and  and we built like this
and we built like this 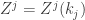 for any
for any  .
.
We have for any
for any 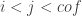 , so we can define
, so we can define  such that
such that 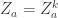 for any
for any  , it is clear that
, it is clear that  and that
and that 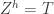 so it is a contradiction.
so it is a contradiction.  si not limite, and not successor, and it is obviously not
si not limite, and not successor, and it is obviously not  so the "stronger statement " is true.
so the "stronger statement " is true.
The result is true for all with the fip and all $T$ so it is still true if
with the fip and all $T$ so it is still true if ![i(F)=[0]](https://s0.wp.com/latex.php?latex=i%28F%29%3D%5B0%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and 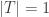 , and that seems to be what we wanted to prove.
, and that seems to be what we wanted to prove.
November 23, 2017 at 3:20 pm
Statement again (with EDIT)
For any , and any
, and any  , let's say that
, let's say that  .
.
The "stronger statement" is then : fip-family and any
fip-family and any  such that
such that  is a tower and such that
is a tower and such that  there exists
there exists  and a tower
and a tower  such that
such that  .
.
For any
AND SUCH THAT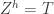
(I forget this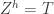 that is crucial in the proof)
that is crucial in the proof)
November 23, 2017 at 4:17 pm
…. I mean not
not 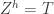 , I mixed with an older notation…
, I mixed with an older notation…
It also seems that (in the proof) we don’t need the hypothesis that if
if  (it also comes from a previous attempt that was maybe correct but a bit more uselessly complicated, anyway it doesn’t make the proof falser or truer, it’s just useless)
(it also comes from a previous attempt that was maybe correct but a bit more uselessly complicated, anyway it doesn’t make the proof falser or truer, it’s just useless)
Sorry for all these notations failure… I hope that everything is correct up to the notations/redondances edit…
November 23, 2017 at 6:42 pm
I think there is a problem anyway… when $h$ is limit and $\alpha=h+1$ … but maybe it’s possible to save something
November 30, 2017 at 5:26 pm |
regarding infinities, I’d like to complain about the recent EMS Surveys (the owner of this blog is on the editorial board there) publication:
Volume 4, Issue 2, 2017, pp. 219–320DOI: 10.4171/EMSS/4-2-3
Published online: 2017-11-13
Numerical infinities and infinitesimals: Methodology, applications, and repercussions on two Hilbert problems
Yaroslav D. Sergeyev
How this could have made it through, it totally beyond me (for it has really 0 content, and the author is well-known in a bad way…).
December 6, 2017 at 4:51 pm
This comment is not really on topic. However, rather than deleting it, let me simply say that I can’t respond straight away, but will do so when the right moment comes, which I hope will be not too long from now.
March 12, 2018 at 5:05 am
This comment, too, is off topic so feel free to delete. But I’m quite disappointed to find that it’s been over three months and there’s yet to be any public posting from you regarding the EMS Surveys matter, considering your… “avid” opining during the Elsevier controversy.
April 21, 2019 at 7:33 am |
[…] my post A theorem about infinite cardinals everybody should know; Gowers’s post Two infinities that are surprisingly equal about a recent breakthrough result by Maryanthe Malliaris and Saharon Shelah; and a recent 4-page […]
September 17, 2019 at 7:56 am |
[…] [3] Gowers blog:Two infinities that are surprisingly equal. […]
December 5, 2023 at 10:13 am |
As someone who had left the field a long time ago, I was stunned when I come across your blog post a few years back.
The first two papers I published were on the cardinals p and t, and as noted in your blog there was a firm consensus that they were different.
The question you ask about why model theory was needed to solve a purely combinatorial problem, was also the first thing I wondered at, especially since it meant the proof was not readily accessible to me.
Surprisingly, my impression from the literature is that the set theory community simply viewed this as a closed case, and instead focused on distilling the original solution to make it more accessible.
Considering the fundamental nature and importance of the problem, and the number of decades it remained unsolved (I don’t know of another comparable example since the Continuum Hypothesis) one might think that after this breakthrough, research would then be focused on gaining a deeper understanding of the reason for the equality.
This in turn stimulated me to start thinking about mathematics again, to try and understand the “reason” for this equality. The solution I eventually arrived at relies only on core set theory methods, and is published on arXiv: https://arxiv.org/abs/2212.14171
A direct proof might be expected to reveal deeper insights. Indeed, the solution answers a more difficult problem, also from Rothberger’s 1948 paper, on conditions when filter-bases can be refined to towers.