Although it was from only a couple of people, I had an enthusiastic response to a very tentative suggestion that it might be rewarding to see whether a polymath project could say anything useful about Frankl’s union-closed conjecture. A potentially worrying aspect of the idea is that the problem is extremely elementary to state, does not seem to yield to any standard techniques, and is rather notorious. But, as one of the commenters said, that is not necessarily an argument against trying it. A notable feature of the polymath experiment has been that it throws up surprises, so while I wouldn’t expect a polymath project to solve Frankl’s union-closed conjecture, I also know that I need to be rather cautious about my expectations — which in this case is an argument in favour of giving it a try.
A less serious problem is what acronym one would use for the project. For the density Hales-Jewett problem we went for DHJ, and for the Erdős discrepancy problem we used EDP. That general approach runs into difficulties with Frankl’s union-closed conjecture, so I suggest FUNC. This post, if the project were to go ahead, could be FUNC0; in general I like the idea that we would be engaged in a funky line of research.
The problem, for anyone who doesn’t know, is this. Suppose you have a family that consists of
distinct subsets of a set
. Suppose also that it is union closed, meaning that if
, then
as well. Must there be an element of
that belongs to at least
of the sets? This seems like the sort of question that ought to have an easy answer one way or the other, but it has turned out to be surprisingly difficult.
If you are potentially interested, then one good thing to do by way of preparation is look at this survey article by Henning Bruhn and Oliver Schaudt. It is very nicely written and seems to be a pretty comprehensive account of the current state of knowledge about the problem. It includes some quite interesting reformulations (interesting because you don’t just look at them and see that they are trivially equivalent to the original problem).
For the remainder of this post, I want to discuss a couple of failures. The first is a natural idea for generalizing the problem to make it easier that completely fails, at least initially, but can perhaps be rescued, and the second is a failed attempt to produce a counterexample. I’ll present these just in case one or other of them stimulates a useful idea in somebody else.
A proof idea that may not be completely hopeless
An immediate reaction of any probabilistic combinatorialist is likely to be to wonder whether in order to prove that there exists a point in at least half the sets it might be easier to show that in fact an average point belongs to half the sets.
Unfortunately, it is very easy to see that that is false: consider, for example, the three sets ,
, and
. The average (over
) of the number of sets containing a random element is
, but there are three sets.
However, this example doesn't feel like a genuine counterexample somehow, because the set system is just a dressed up version of : we replace the singleton
by the set
and that's it. So for this set system it seems more natural to consider a weighted average, or equivalently to take not the uniform distribution on
, but some other distribution that reflects more naturally the properties of the set system at hand. For example, we could give a probability 1/2 to the element 1 and
to each of the remaining 12 elements of the set. If we do that, then the average number of sets containing a random element will be the same as it is for the example
with the uniform distribution (not that the uniform distribution is obviously the most natural distribution for that example).
This suggests a very slightly more sophisticated version of the averaging-argument idea: does there exist a probability distribution on the elements of the ground set such that the expected number of sets containing a random element (drawn according to that probability distribution) is at least half the number of sets?
With this question we have in a sense the opposite problem. Instead of the answer being a trivial no, it is a trivial yes — if, that is, the union-closed conjecture holds. That’s because if the conjecture holds, then some belongs to at least half the sets, so we can assign probability 1 to that
and probability zero to all the other elements.
Of course, this still doesn’t feel like a complete demolition of the approach. It just means that for it not to be a trivial reformulation we will have to put conditions on the probability distribution. There are two ways I can imagine getting the approach to work. The first is to insist on some property that the distribution is required to have that means that its existence does not follow easily from the conjecture. That is, the idea would be to prove a stronger statement. It seems paradoxical, but as any experienced mathematician knows, it can sometimes be easier to prove a stronger statement, because there is less room for manoeuvre. In extreme cases, once a statement has been suitably strengthened, you have so little choice about what to do that the proof becomes almost trivial.
A second idea is that there might be a nice way of defining the probability distribution in terms of the set system. This would be a situation rather like the one I discussed in my previous post, on entropy and Sidorenko’s conjecture. There, the basic idea was to prove that a set had cardinality at least
by proving that there is a probability distribution on
with entropy at least
. At first, this seems like an unhelpful idea, because if
then the uniform distribution on
will trivially do the job. But it turns out that there is a different distribution for which it is easier to prove that it does the job, even though it usually has lower entropy than the uniform distribution. Perhaps with the union-closed conjecture something like this works too: obviously the best distribution is supported on the set of elements that are contained in a maximal number of sets from the set system, but perhaps one can construct a different distribution out of the set system that gives a smaller average in general but about which it is easier to prove things.
I have no doubt that thoughts of the above kind have occurred to a high percentage of people who have thought about the union-closed conjecture, and can probably be found in the literature as well, but it would be odd not to mention them in this post.
To finish this section, here is a wild guess at a distribution that does the job. Like almost all wild guesses, its chances of being correct are very close to zero, but it gives the flavour of the kind of thing one might hope for.
Given a finite set and a collection
of subsets of
, we can pick a random set
(uniformly from
) and look at the events
for each
. In general, these events are correlated.
Now let us define a matrix by
. We could now try to find a probability distribution
on
that minimizes the sum
. That is, in a certain sense we would be trying to make the events
as uncorrelated as possible on average. (There may be much better ways of measuring this — I’m just writing down the first thing that comes into my head that I can’t immediately see is stupid.)
What does this give in the case of the three sets ,
and
? We have that
if
or
or
and
. If
and
, then
, since if
, then
is one of the two sets
and
, with equal probability.
So to minimize the sum we should choose
so as to maximize the probability that
and
. If
, then this probability is
, which is maximized when
, so in fact we get the distribution mentioned earlier. In particular, for this distribution the average number of sets containing a random point is
, which is precisely half the total number of sets. (I find this slightly worrying, since for a successful proof of this kind I would expect equality to be achieved only in the case that you have disjoint sets
and you take all their unions, including the empty set. But since this definition of a probability distribution isn’t supposed to be a serious candidate for a proof of the whole conjecture, I’m not too worried about being worried.)
Just to throw in another thought, perhaps some entropy-based distribution would be good. I wondered, for example, about defining a probability distribution as follows. Given any probability distribution, we obtain weights on the sets by taking
to be the probability that a random element (chosen from the distribution) belongs to
. We can then form a probability distribution on
by taking the probabilities to be proportional to the weights. Finally, we can choose a distribution on the elements to maximize the entropy of the distribution on
.
If we try that with the example above, and if is the probability assigned to the element 1, then the three weights are
and
, so the probabilities we will assign will be
and
. The entropy of this distribution will be maximized when the two non-zero probabilities are equal, which gives us
, so in this case we will pick out the element 1. It isn’t completely obvious that that is a bad thing to do for this particular example — indeed, we will do it whenever there is an element that is contained in all the non-empty sets from
. Again, there is virtually no chance that this rather artificial construction will work, but perhaps after a lot of thought and several modifications and refinements, something like it could be got to work.
A failed attempt at a counterexample
I find the non-example I’m about to present interesting because I don’t have a good conceptual understanding of why it fails — it’s just that the numbers aren’t kind to me. But I think there is a proper understanding to be had. Can anyone give me a simple argument that no construction that is anything like what I tried can possibly work? (I haven’t even checked properly whether the known positive results about the problem ruled out my attempt before I even started.)
The idea was as follows. Let and
be parameters to be chosen later, and let
be a random set system obtained by choosing each subset of
of size
with probability
, the choices being independent. We then take as our attempted counterexample the set of all unions of sets in
.
Why might one entertain even for a second the thought that this could be a counterexample? Well, if we choose to be rather close to
, but just slightly less, then a typical pair of sets of size
have a union of size close to
, and more generally a typical union of sets of size
has size at least this. There are vastly fewer sets of size greater than
than there are of size
, so we could perhaps dare to hope that almost all the sets in the set system are the ones of size
, so the average size is close to
, which is less than
. And since the sets are spread around, the elements are likely to be contained in roughly the same number of sets each, so this gives a counterexample.
Of course, the problem here is that although a typical union is large, there are many atypical unions, so we need to get rid of them somehow — or at least the vast majority of them. This is where choosing a random subset comes in. The hope is that if we choose a fairly sparse random subset, then all the unions will be large rather than merely almost all.
However, this introduces a new problem, which is that if we have passed to a sparse random subset, then it is no longer clear that the size of that subset is bigger than the number of possible unions. So it becomes a question of balance: can we choose small enough for the unions of those sets to be typical, but still large enough for the sets of size
to dominate the set system? We’re also free to choose
of course.
I usually find when I’m in a situation like this, where I’m hoping for a miracle, that a miracle doesn’t occur, and that indeed seems to be the case here. Let me explain my back-of-envelope calculation.
I’ll write for the set of unions of sets in
. Let us now take
and give an upper bound for the expected number of sets in
of size
. So fix a set
of size
and let us give a bound for the probability that
. We know that
must contain at least two sets in
. But the number of pairs of sets of size
contained in
is at most
and each such pair has a probability
of being a pair of sets in
, so the probability that
is at most
. Therefore, the expected number of sets in
of size
is at most
.
As for the expected number of sets in , it is
, so if we want the example to work, we would very much like it to be the case that when
, we have the inequality
.
We can weaken this requirement by observing that the expected number of sets in
.
If the left-hand side is not just greater than the right-hand side, but greater by a factor of say for each
, then we should be in good shape: the average size of a set in
will be not much greater than
and we’ll be done.
If is not much bigger than
, then things look quite promising. In this case,
will be comparable in size to
, but
will be quite small — it equals
, and
is small. A crude estimate says that we’ll be OK provided that
is significantly smaller than
. And that looks OK, since
is a lot smaller than
, so we aren’t being made to choose a ridiculously small value of
.
If on the other hand is quite a lot larger than
, then
is much much smaller than
, so we’re in great shape as long as we haven’t chosen
so tiny that
is also much much smaller than
.
So what goes wrong? Well, the problem is that the first argument requires smaller and smaller values of as
gets further and further away from
, and the result seems to be that by the time the second regime takes over,
has become too small for the trivial argument to work.
Let me try to be a bit more precise about this. The point at which becomes smaller than
is of course the point at which
. For that value of
, we require
, so we need
. However, an easy calculation reveals that
,
(or observe that if you multiply both sides by , then both expressions are equal to the multinomial coefficient that counts the number of ways of writing an
-element set as
with
and
). So unfortunately we find that however we choose the value of
there is a value of
such that the number of sets in
of size
is greater than
. (I should remark that the estimate
for the number of sets in
of size
can be improved to
, but this does not make enough of a difference to rescue the argument.)
So unfortunately it turns out that the middle of the range is worse than the two ends, and indeed worse by enough to kill off the idea. However, it seemed to me to be good to make at least some attempt to find a counterexample in order to understand the problem better.
From here there are two obvious ways to go. One is to try to modify the above idea to give it a better chance of working. The other, which I have already mentioned, is to try to generalize the failure: that is, to explain why that example, and many others like it, had no hope of working. Alternatively, somebody could propose a completely different line of enquiry.
I’ll stop there. Experience with Polymath projects so far seems to suggest that, as with individual projects, it is hard to predict how long they will continue before there is a general feeling of being stuck. So I’m thinking of this as a slightly tentative suggestion, and if it provokes a sufficiently healthy conversation and interesting new (or at least new to me) ideas, then I’ll write another post and launch a project more formally. In particular, only at that point will I call it Polymath11 (or should that be Polymath12? — I don’t know whether the almost instantly successful polynomial-identities project got round to assigning itself a number). Also, for various reasons I don’t want to get properly going on a Polymath project for at least a week, though I realize I may not be in complete control of what happens in response to this post.
Just before I finish, let me remark that Polymath10, attempting to prove Erdős’s sunflower conjecture, is still continuing on Gil Kalai’s blog. What’s more, I think it is still at a stage where a newcomer could catch up with what is going on — it might take a couple of hours to find and digest a few of the more important comments. But Gil and I agree that there may well be room to have more than one Polymath project going at the same time, since a common pattern is for the group of participants to shrink down to a smallish number of “enthusiasts”, and there are enough mathematicians to form many such groups.
And a quick reminder, as maybe some people reading this will be new to the concept of Polymath projects. The aim is to try to make the problem-solving process easier in various ways. One is to have an open discussion, in the form of blog posts and comments, so that anybody can participate, and with luck a process of self-selection will take place that results in a team of enthusiastic people with a good mixture of skills and knowledge. Another is to encourage people to express ideas that may well be half-baked or even wrong, or even completely obviously wrong. (It’s surprising how often a completely obviously wrong idea can stimulate a different idea that turns out to be very useful. Naturally, expressing such an idea can be embarrassing, but it shouldn’t be, as it is an important part of what we do when we think about problems privately.) Another is to provide a mechanism where people can get very quick feedback on their ideas — this too can be extremely stimulating and speed up the process of thought considerably. If you like the problem but don’t feel like pursuing either of the approaches I’ve outlined above, that’s of course fine — your ideas are still welcome and may well be more fruitful than those ones, which are there just to get the discussion started.
January 21, 2016 at 1:48 pm |
Perhaps a suitable initial step would be to start with something a little less ambitious, for example trying to prove that any union-closed family of sets has an element that occurs in at least 1% of the member-sets.
January 21, 2016 at 4:51 pm
I agree that that seems very sensible. According to the survey article, the best that is known along those lines is that if you have sets, then some element is contained in at least
sets, then some element is contained in at least 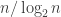 of them.
of them.
January 21, 2016 at 4:56 pm |
[…] Polymath11 (?) Tim Gowers’s proposed a polymath project on Frankl’s conjecture. If it will get off the ground we will have (with polymath10) two projects running in parallel […]
January 21, 2016 at 4:59 pm |
Cool! let’s see how it goes! I will try to take part.
January 21, 2016 at 7:13 pm |
Let me also mention that a MathOverflow question http://mathoverflow.net/questions/219638/proposals-for-polymath-projects seeks for polymath proposals. There are some very interesting proposals. I am quite curious to see some proposals in applied mathematics, and various areas of geometry, algebra, analysis and logic. Also since a polymath project was meant to be “a large collaboration in which no single person has to work all that hard,” people are more than welcome to participate simultaneously in both projects.
January 21, 2016 at 7:17 pm |
And for polymath connoisseurs, I posed a sort of Meta question regarding polymath10 that I am contemplating about. https://gilkalai.wordpress.com/2015/12/08/polymath-10-post-3-how-are-we-doing/#comment-23624
January 21, 2016 at 8:41 pm |
David, I agree that trying to prove that there is always an element that appears in at least, say, 0.0001% of the sets is a good start—and it would be a substantial improvement. My feeling is that if the conjecture is false then there should be no constant maximum frequency.
One way to prove that there’s always an element in appearing in at least 0.0001% of the sets lies in a somewhat curious link to “small” families. Let’s say we have a universe of n elements and a set family A of m sets. Let’s, moreover, assume that A is separating, that is, no element is a clone of another. Then, if there are only few sets, namely m\leq 2n then the union-closed sets conjecture holds for A (ie, there is an element that appears in at least half of the sets). This can be seen by rather elementary arguments (see Thm 23 in the survey). Now, here comes the interesting part: if you can improve the factor of 2 in that statement to say 2.0001 then you suddenly have proved that in any union-closed family there is always some element appearing in a constant fraction of the sets (Thm 24). The argument is here:
Click to access HuResult.pdf
One last remark: Jens Maßberg recently improved the factor-2 result somewhat but not to 2.00001 or any constant improvement. The paper (http://arxiv.org/abs/1508.05718) mixes known techniques in a very nice way.
January 21, 2016 at 9:36 pm |
Has anyone made it far enough in Blinovsky’s preprint http://arxiv.org/abs/1507.01270 to see if his approach is viable? Unfortunately, language issues plus very terse writing makes it hard to understand what he is doing.
January 22, 2016 at 3:47 am
I think he has several breakthroughs “pending.” Even if his proof is correct, it can be useful to find another, more standard proof.
January 21, 2016 at 10:21 pm |
I suddenly realized that I hadn’t actually stated the conjecture in the post above. I’ve done that now.
January 22, 2016 at 12:30 am |
Here are two possible strengthenings. The first is to a weighted version. Suppose that we have a positive weight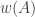 for each
for each 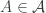 and that
and that 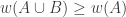 for every
for every 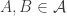 . Does it follow that there is an element
. Does it follow that there is an element  such that the sum of the weights of the sets containing
such that the sum of the weights of the sets containing  is at least half the sum of all the weights of the sets? If this strengthening isn’t obviously false, is it in fact equivalent (in some obvious way) to the original conjecture?
is at least half the sum of all the weights of the sets? If this strengthening isn’t obviously false, is it in fact equivalent (in some obvious way) to the original conjecture?
The other possibility is to the following statement: as long as there are at least elements in the union of all the sets in
elements in the union of all the sets in  , then there is a subset
, then there is a subset 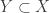 of size
of size  such that
such that  for at least
for at least  of the sets in
of the sets in  .
.
Ah, I’ve just seen that the second “strengthening” is not a strengthening, since if the original conjecture is true, then one can pick an element in at least half the sets, then another element in at least half the sets that contain the first element, and so on. But I needed to write this comment to see that.
January 22, 2016 at 4:45 am |
Years ago I remember that Jeff Kahn said that he bet he will find a counterexample to every meaningful strengthening of Frankl’s conjecture. And indeed he shot down many of those and a few I proposed, including weighted versions. I have to look in my old emails to see if this one too.
January 22, 2016 at 9:34 pm
Here’s another one: http://mathoverflow.net/questions/228119
January 22, 2016 at 9:35 am |
A small remark is that both the suggestions I made in the post for how to pick a probability distribution on that would cause an average element to belong to at least half the sets have the following nice property: if you modify the example by duplicating elements of
that would cause an average element to belong to at least half the sets have the following nice property: if you modify the example by duplicating elements of  , then the probability distribution changes appropriately.
, then the probability distribution changes appropriately.
To put that more formally, suppose you have disjoint non-empty sets
disjoint non-empty sets  , and a set system
, and a set system  that consists of subsets of
that consists of subsets of  . You can form a new set system
. You can form a new set system  by taking all sets of the form
by taking all sets of the form 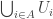 with
with 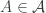 . This is a kind of “blow-up” of
. This is a kind of “blow-up” of  . If you now apply one of the two processes to
. If you now apply one of the two processes to  , then the probability that you give to
, then the probability that you give to 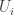 (that is, the sum of the probabilities assigned to its elements) will not depend on the choice of
(that is, the sum of the probabilities assigned to its elements) will not depend on the choice of  .
.
January 22, 2016 at 10:05 am |
In the spirit of additive combinatorics, what can be said about approximately closed under union families. That is, what if for a constant fraction of pairs of sets, their union also belongs to the family. Two natural questions are:
(1) is there a counter-example to Frankl conjecture in this case (with 1/2 possibly replaced by a smaller constant)
(2) does any such family contain a large family which is closed under unions?
January 22, 2016 at 10:36 am
It’s not quite clear to me what a counterexample means for (1). Obviously if only a constant fraction of pairs of sets have their union in the family, then the constant 1/2 has to be reduced, but it is not clear that there is a natural conjecture for how the new constant should depend on the fraction of unions we assume to be in the family. But maybe the precise question you have in mind, which looks interesting, is whether for every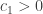 there exists
there exists 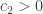 such that if a fraction
such that if a fraction 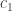 of pairs of sets in the family have their union in the family, then some element is contained in a fraction
of pairs of sets in the family have their union in the family, then some element is contained in a fraction 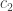 of the sets.
of the sets.
To prove this statement would be likely to be hard, since it is not known even if $c_1=1$. But as you say, it might be worth looking for a counterexample.
If that is indeed the question you mean, then presumably the motivation for (2), aside from its intrinsic interest, is that a positive answer to (2) would show that a positive answer to the question above would follow from a positive answer to the case, at least if “large” means “of proportional size”.
case, at least if “large” means “of proportional size”.
A thought about (2) is that a random family is probably a counterexample. If we just choose each subset of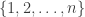 with probability 1/2, then approximately half the unions will belong to the family, but it looks as though the largest union-closed subfamily will be very small. So I think the best one can hope for with (2) is a subfamily that is somehow “regular”, in the sense that it resembles a random subfamily of a union-closed family, which would still be enough (given a suitable quasirandomness definition) to prove that some element is contained in a significant fraction of the sets, assuming that that is true for union-closed families.
with probability 1/2, then approximately half the unions will belong to the family, but it looks as though the largest union-closed subfamily will be very small. So I think the best one can hope for with (2) is a subfamily that is somehow “regular”, in the sense that it resembles a random subfamily of a union-closed family, which would still be enough (given a suitable quasirandomness definition) to prove that some element is contained in a significant fraction of the sets, assuming that that is true for union-closed families.
January 22, 2016 at 12:53 pm |
Two questions: 1) Does the Frankl’s conjecture extend when we replace the uniform distribution on the discrete cube by the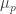 districution?
districution?
2) If the family is weakly symmetric, namely closed under transitive permutation group, or even if it is regular, namely every element belongs to the same number of sets , then the conjecture should apply to every element. Perhaps this is an easier case.
It is interesting to note that for weakly symmetric union closed families assuming also a yes answer for 1) we will get (by Russo’s lemma) that is monotone non decreasing with p. (like for monotone families.)
is monotone non decreasing with p. (like for monotone families.)
January 22, 2016 at 2:11 pm
Let me check I understand the first question. I take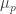 to be the distribution that assigns to each subset
to be the distribution that assigns to each subset 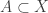 the probability of picking that set if elements of
the probability of picking that set if elements of  are chosen independently with probability
are chosen independently with probability  . If we take all subsets of
. If we take all subsets of  , then the probability that a random subset contains
, then the probability that a random subset contains  is
is  , so the optimistic extension of the conjecture would be that if
, so the optimistic extension of the conjecture would be that if  is union closed then there is some
is union closed then there is some  such that the probability that a
such that the probability that a 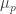 -random subset of
-random subset of  contains
contains  given that it belongs to
given that it belongs to  is at least
is at least  .
.
January 22, 2016 at 3:35 pm
The way I think about it which might be equivalent to what you say (otherwise we will have two variants at the price of one) is: Is there a k such that the Fourier coefficient with respect to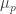 ,
,  is non positive. Of course we can ask if we can find an element which works simultaneously for all k.
is non positive. Of course we can ask if we can find an element which works simultaneously for all k.
(By Jeff’s heuristics the answer should be “no” for all these but I dont recall I thought about them.)
January 22, 2016 at 3:35 pm
I meant “for all p” not “for all k”.
January 22, 2016 at 8:47 pm |
Another modification of your first approach would be to ask if an average point in a separating family belongs to at least half the sets. But this is also false: consider the five sets ,
, 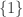 ,
,  ,
,  ,
, 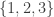 . An average point belongs to only
. An average point belongs to only  of the sets.
of the sets.
I wonder if Jeff Kahn’s ‘bet’ would apply to the conjecture of Poonen mentioned in the survey article (Conjecture 14). Or does that not qualify as a sufficient strengthening?
January 22, 2016 at 9:41 pm
Let me see whether I can test my correlation-minimizing guess on this example. I have that . We may as well average this matrix with its transpose, which gives
. We may as well average this matrix with its transpose, which gives  . So it’s clear that to minimize the sum
. So it’s clear that to minimize the sum 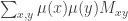 we want to take the uniform distribution (so as to minimize the diagonal contribution). So the example above demolishes the first of my two suggestions in the post. I’m not sure I’ve got the stomach to think about the entropy construction just at the moment, but my immediate thought now is to wonder what it might be possible to do about the above failure: somehow the correct distribution “shouldn’t” have given equal weight to 3. Can one convert this feeling of moral outrage into a better construction?
we want to take the uniform distribution (so as to minimize the diagonal contribution). So the example above demolishes the first of my two suggestions in the post. I’m not sure I’ve got the stomach to think about the entropy construction just at the moment, but my immediate thought now is to wonder what it might be possible to do about the above failure: somehow the correct distribution “shouldn’t” have given equal weight to 3. Can one convert this feeling of moral outrage into a better construction?
January 23, 2016 at 11:47 am
Yes, the problem is that being big makes up for
being big makes up for 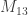 being small. So that way of defining
being small. So that way of defining  doesn’t work.
doesn’t work.
A still more naive idea would be to make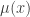 proportional to
proportional to 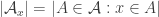 . But whether this works at all, or makes anything easier to prove, I don’t know. This would correspond to the following strengthening of the conjecture:
. But whether this works at all, or makes anything easier to prove, I don’t know. This would correspond to the following strengthening of the conjecture:  (where
(where  is the number of sets in
is the number of sets in  ). (The example above satisfies this.)
). (The example above satisfies this.)
March 7, 2016 at 3:16 pm
Apparenty the above strengthening is false: see this comment.
January 23, 2016 at 10:52 am |
That comment got completely messed up in format. I’ll replace the less-than signs with non-HTML and repost it shortly (and the version above can be deleted).
January 23, 2016 at 10:55 am |
The following false proof seems worth posting, even though I think other comments here already rule out the suggested strengthening from being true. The error is straightforward, so I’ll leave it as an exercise for the reader for 24 hours or so, or until anyone reveals it in a comment (which you should feel free to do if it helps the discussion).
Reformulate the set-family A as a 0-1 matrix, with columns being characteristic functions of member sets, and rows being elements. Call any 0-1 matrix “legitimate” if all columns are distinct and all rows have a 1.
The conjecture is now: in a legitimate matrix, if the set of columns is union-closed, at least one row has density >= 1/2.
Reexpress it as: in a legitimate matrix, if all rows have density < 1/2, the set of columns is not union-closed.
Now strengthen it as follows: in a legitimate matrix, if the matrix as a whole has density < 1/2, the set of columns is not union-closed.
Now assume a counterexample and find one with fewer rows. This will prove the strengthened conjecture by contradiction, since if there is only one row, it’s obvious.
Case 0: some row is entirely 1s. The remaining part of the matrix has lower density than the whole matrix, and is legitimate, so just remove that row and continue.
Case 1: some row has density >= 1/2 (but is not all 1s). Put that row on top, and sort the columns so that row has all its 0s first. Split the matrix into three submatrices: that row, the part under that row’s 0s, the part under that row’s 1s. Since the whole matrix density is < 1/2 and is a weighted average of the densities of these parts, at least one part has density < 1/2. By assumption it’s not the top row, so it must be one of the submatrices under it (which are legitimate). Pick that one and continue.
Case 2: no row has density >= 1/2. Put any row on top, and split the matrix as in Case 1. This time, just note that the matrix with its top row removed has density < 1/2 (since it’s made of rows of density < 1/2), which is a weighted average of the two submatrix parts, so we can pick one with density < 1/2.
QED (not counting the error I noticed, and any other errors I *didn’t* notice).
January 23, 2016 at 11:02 am
I forgot to say, about the submatrices, that they are also union-closed (like the hypothetical counterexample). That’s not the error (it’s correct).
January 23, 2016 at 11:29 am
I think I see one flaw: when we split the matrix into submatrices, the two submatrices under the first row might not be legitimate, since they may have rows without a 1?
January 23, 2016 at 5:36 pm
A disturbing aspect of the argument is that it doesn’t seem to use anywhere the hypothesis that the columns are distinct. Since we know that the strengthened statement is false when the columns are not required to be distinct, we should have a general flaw-identifying mechanism. (But perhaps I have missed a place where the hypothesis is genuinely used.)
January 23, 2016 at 10:04 pm
@Alec: that’s indeed the error I know about — “0-rows” (containing no 1s) can be produced. It’s a fatal error, but I’ll post below about ideas for possible ways around it. (If you find any *other* error, it’s one I don’t know about.)
@gowers: it does use the columns being distinct — in the base case (1 row). Otherwise we could have [[0, 0, 1]] of density 1/3. AFAIK it’s not disturbing that it only uses that in that one place; do you agree?
OTOH it is disturbing that it never uses the union-closed property. (So if it didn’t have the error, I think it would “prove” that almost any 0-1 matrix with distinct columns and density < 1/2 is a contradiction.)
It turns out that these issues might be related, in the sense that some of the ideas I'll post for dealing with 0-rows might have a way of making use of the columns being union-closed. More on this shortly.
January 23, 2016 at 11:02 pm
I added a long comment at the bottom, “About getting around 0-rows … (in part, by making use of the union-closed condition)”.
January 23, 2016 at 11:59 am |
Something I’d like to do is try to give a precise formulation to the question, “Does there exist a non-trivial averaging argument that solves the conjecture?” As I pointed out in the post, the obvious first attempt — does there exist a probability distribution on such that the average number of sets containing a random
such that the average number of sets containing a random 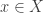 is at least
is at least 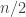 — is unsatisfactory, because if we allow probability distributions that are concentrated at a point, then the question is trivially equivalent to the original question. So what exactly is it that one is looking for?
— is unsatisfactory, because if we allow probability distributions that are concentrated at a point, then the question is trivially equivalent to the original question. So what exactly is it that one is looking for?
One property that I would very much like is a property that I mentioned earlier: that the distribution does the right thing if one blows sets up. We can express the property as follows. Given the set-system , let
, let  be the algebra that it generates (that is, everything you can make out of
be the algebra that it generates (that is, everything you can make out of  using intersections, unions and set differences). Let
using intersections, unions and set differences). Let 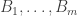 be the atoms of this algebra and define a set-system
be the atoms of this algebra and define a set-system  to be the set of all
to be the set of all  such that
such that  . Let me also write
. Let me also write  for
for 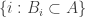 .
.
Now say that another set-system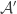 is isomorphic to
is isomorphic to  if
if  is isomorphic to
is isomorphic to  in the obvious sense that there is some permutation of the ground set of
in the obvious sense that there is some permutation of the ground set of  that makes it equal to
that makes it equal to  . And let us extend that by saying that
. And let us extend that by saying that  is isomorphic to
is isomorphic to  (with
(with  being the isomorphism — it is an isomorphism of lattices or something like that) and taking the transitive closure.
being the isomorphism — it is an isomorphism of lattices or something like that) and taking the transitive closure.
The property I would want is that the probability distribution one constructs for is a lattice invariant. That is, if two set systems become identical after applying
is a lattice invariant. That is, if two set systems become identical after applying  and permuting ground sets, then corresponding atoms get the same probabilities.
and permuting ground sets, then corresponding atoms get the same probabilities.
In particular, this seems to say that if permuting and
and  leads to an automorphism of
leads to an automorphism of  , then
, then  and
and  should be given equal probability. This is not enough to rule out the trivial argument though, since if some element is in half the sets, we can assign all the probability to that element and any other element that is indistinguishable from it.
should be given equal probability. This is not enough to rule out the trivial argument though, since if some element is in half the sets, we can assign all the probability to that element and any other element that is indistinguishable from it.
Another property I would like, but don’t have a precise formulation of, is “continuity”. That is, if you don’t change much, then the probability distribution doesn’t change much either.
much, then the probability distribution doesn’t change much either.
It feels to me as though it might be good to ask for some quantity to be minimized or maximized, as in my two attempts in the post.
And a final remark is that we don’t have to take the average number of sets containing a point: we could take the average of some strictly increasing function of that number. As long as that average is at least
of that number. As long as that average is at least 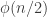 then we will be done.
then we will be done.
That is as far as I’ve got so far with coming up with precise requirements.
January 23, 2016 at 2:47 pm |
I wonder whether the following question is trivial-or the answer known: if one considers the set of N elements, to be specific, {1,2,…,N} and assigns to it the uniform measure, so p(k)=1/N, for k an element of this set, there are 2^N subsets. These sets contain elements of the original one more than once. If one chooses a set with some probability, is it known, how p(k) changes? One can imagine organizing these as a binary tree and trying to characterize paths along it-how would the property “closed under union” be expressed in this context?
January 23, 2016 at 4:24 pm
I don’t understand the question. You seem to have defined to be
to be  , so how can it change? Can you give a more formal formulation of what you are asking?
, so how can it change? Can you give a more formal formulation of what you are asking?
January 23, 2016 at 6:13 pm |
I’m sorry-what I’m trying to get at is how the set, whose elements are the subsets of the original set, that are union-closed could be constructed, from the set of all subsets of the original set and trying to think of a simple (maybe too simple) example. For, while p(k)=1/N for the original set, in my example, by selecting subsets, this may be different, within some collection of subsets, constructed by a given rule. I was trying to work through the first example of the survey article.
January 23, 2016 at 10:54 pm |
About getting around 0-rows in the “false proof” I gave above (in part, by making use of the union-closed condition):
Most of the arguments in the “false proof” extend to a weighted definition of “whole matrix density”, which uses a distribution on X (specified in advance) to weight the rows. Then if we knew which rows were going to turn out to be 0-rows (once we reached them in some submatrix with fewer columns — they were not 0-rows to begin with), we could specify their weights as 0; then we could remove those rows from a submatrix without increasing the density of the remaining part.
I know of only two problems with this:
1. since changing those weights changes how we evaluate submatrix density, it can change which submatrix we choose at any stage, perhaps at multiple stages much earlier than when the 0-row (which motivates the weight change) comes up. So if we make an argument of the form “when a 0-row arises, slightly lower that row’s weight and start over”, then several far earlier submatrix choices might change.
2. the possible existence of 0-columns means the recursion can end with one submatrix being a single 0-column. This was ruled out by having 0-rows, but since it can come up when we recurse, we have to deal with it somehow.
Issue (2) seems like a technicality, but I don’t know how to fix it or how serious it is.
Issue (1) is interesting. The problem with “adjust weights until they work” would be if we get into a “loop”; this seems possible, since submatrix choices change how we’ll want to adjust them. (And it must be possible, since as said before, fixing it (and issue (2)) would mean proving most density 1/3 matrices don’t exist.)
But the union-closed condition relates the rows of the two submatrices we choose between, at a given stage.
If the right submatrix (under 1’s) has row R all 0, then so must the left one (under 0’s), for the same R. (Otherwise we can construct a union of columns which should exist in the right one but doesn’t, taking any column on the right unioned with any column containing a 1 in row R on the left.)
So a 0-row on the right would be a 0-row on the left too, and thus a 0-row in the whole, and is therefore ruled out. Thus the right submatrix has no 0-rows, which means any change to this stage’s choice of left or right submatrix, motivated by finding a 0-row immediately afterwards, would be changing the choice from left to right (never from right to left).
Furthermore, I think a similar argument can say a similar thing about a choice made at an earlier stage, though I haven’t worked out exactly what it says, since this method of relating 0-rows should work for smaller submatrices too (defined by grouping columns based on the content of their first k rows, not only with k = 1 as before), provided their “indices” (content of first k rows) are related by the right one’s bits (matrix elements) being strictly >= than the left one’s bits.
So this gives me some hope that the union-closed condition can control the way row-weight changes affect the choice of submatrices, in a way that prevents “long term oscillations” in a strategy which gradually adjusts row weights to try to postpone the problem of finding a 0-row with nonzero weight (by reducing the weight of such rows).
January 23, 2016 at 11:00 pm
Minor clarifications in the above:
“This was ruled out by having 0-rows” -> “This is ruled out by such a submatrix having 0-rows”.
“submatrix choices change how we’ll want to adjust them” — by changing which rows end up being 0-rows when we reach them.
January 23, 2016 at 11:12 pm
I also guess that when lowering a row’s weight since it contains a 0-row (in the left submatrix) that might come up in the next stage, you can often increase some later row’s weight to avoid affecting any submatrix choices from earlier stages (by not changing the total weighted density of the current matrix you’re looking at); this change to two weights would then only change the upcoming choice, not any earlier choices.
January 23, 2016 at 11:17 pm
Wait, that last guess is wrong as stated, since different earlier choices were looking at rows widened by different sets of columns, so perhaps no single way of making compensating row-weight changes would work for all choices (and the suggested way, changing just one other weight, would not in general work for more than one of those choices). So I don’t know whether this possibility helps or not. In general I think it means you could fix the first j stages (i.e. prevent having to revise the first j choices) if you had j nonzero rows (below the top row) at that point. That’s a guess, not verified.
January 23, 2016 at 11:50 pm
About “issue (2)”:
A matrix corresponding to the 3-set family { empty set, S, X } can fit all the criteria (distinct columns, union closed, density < 1/2, no 0-rows) and yet exists, disproving the “strengthened conjecture” even with union closed columns taken into account. (And I think this example has already been given, somewhere in this discussion.)
So “issue (2)” above is indeed serious. Nonetheless it feels to me somewhat orthogonal to the given ideas for issue (1).
In this example, making it “separating” would handle it, as would making some equivalent condition about row weights; requiring density < 1/2 under *all* row weight distributions rather than just one would be too strong, but under *enough* row weight distributions (in some sense) could conceivably solve it.
Conclusion: both issues are serious, but the above ideas for issue (1) still seem interesting to me.
July 7, 2016 at 5:16 pm
If one row ‘majorizes’ the other, i.e. one element belongs to all the sets that the other one belongs to, then the lower Hamming weight row can always be deleted — this element is not needed in computing the maximum of densities #A_i / #A where A_i is the subfamily consisting of all the sets containing the element i. In other words, if the original matrix is a counterexample to the original non-strengthened conjecture, so has to be the new matrix, and vice versa. However, with the strengthened conjecture this relationship does not seem to hold, as the density of the whole matrix may go up. Perhaps this means the row of lower Hamming weight has to be taken with weight 0 into the distribution?
July 7, 2016 at 6:03 pm
My goal was to avoid 0-rows in the submatrices. But I guess it does not work. If we change the 0s into 1s where the minor and major row differ, and allow identical columns — this can not help for the base case, only hurt, in the only place where the distinctness of columns assumption is used. But unfortunately this change may turn a counterexample for the strengthened hypothesis into a non-counterexample (even if this is not the case for the original hypothesis).
January 24, 2016 at 4:40 pm |
It can be useful to have a stock of ‘extreme’ examples on which to test hypotheses, so here’s an example of an (arbitrarily large) family that has just one abundant set: for , let
, let  . Then
. Then  has
has 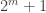 members; the element
members; the element 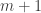 belongs to all but one of them; but everything else belongs to only
belongs to all but one of them; but everything else belongs to only 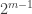 , which is just under half of them.
, which is just under half of them.
January 24, 2016 at 4:58 pm
Thanks for that — I’ll definitely bear it in mind when trying to devise ways of using to define a probability distribution on
to define a probability distribution on  for which an averaging argument works.
for which an averaging argument works.
January 24, 2016 at 9:50 pm |
Let me mention an idea before I think about why it doesn’t work, which it surely won’t. In general, I’m searching for a natural way of choosing a random element of not uniformly but using the set-system
not uniformly but using the set-system  somehow. A rather obvious way — and already I’m seeing what’s wrong with it — would be to choose a random set
somehow. A rather obvious way — and already I’m seeing what’s wrong with it — would be to choose a random set 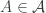 and then a random element
and then a random element  , in both cases chosen uniformly.
, in both cases chosen uniformly.
What’s wrong with that? Unfortunately, it fails the isomorphism-invariance condition: if we take the set system consisting of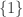 and
and 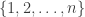 , then the probability that we choose the element 1 will be
, then the probability that we choose the element 1 will be  , which is not independent of
, which is not independent of  .
.
With Alec’s example above, the probability of choosing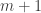 is going to be roughly
is going to be roughly 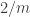 , because a random set that contains
, because a random set that contains 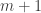 will have about
will have about  elements. This is sort of semi-promising, as it does bias the choice slightly towards the element we want to choose. I haven’t checked whether it makes the average number of elements OK.
elements. This is sort of semi-promising, as it does bias the choice slightly towards the element we want to choose. I haven’t checked whether it makes the average number of elements OK.
But if we were to duplicate all the other elements a large number of times, we could easily make it extremely unlikely that we would choose the element , so the general approach still fails. Is there some way of capturing its essence but having isomorphism invariance as well?
, so the general approach still fails. Is there some way of capturing its essence but having isomorphism invariance as well?
January 24, 2016 at 10:37 pm
A modification of the idea that I don’t have time to think about for the moment is to take the bipartite graph where is joined to
is joined to 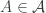 if
if  and find its stationary distribution. It’s not clear to me what use that would be, given that ultimately we are interested in the uniform distribution on
and find its stationary distribution. It’s not clear to me what use that would be, given that ultimately we are interested in the uniform distribution on  , but at least it feels pretty natural and I think satisfies the isomorphism condition.
, but at least it feels pretty natural and I think satisfies the isomorphism condition.
January 26, 2016 at 8:17 am
Let me try and recast that constructively. Let be a union-closed family with ground set
be a union-closed family with ground set  . Choose an arbitrary
. Choose an arbitrary 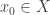 . Then define a sequence
. Then define a sequence 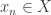 iteratively: given
iteratively: given 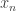 , choose
, choose  uniformly at random from
uniformly at random from  , and then choose
, and then choose 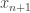 uniformly at random from
uniformly at random from  . Then the hope is that for sufficiently large
. Then the hope is that for sufficiently large  the expectation of
the expectation of  is at least
is at least 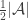 .
.
Is that right? It would be interesting to test this out on some examples.
January 26, 2016 at 9:11 am
Hmm, that doesn’t work: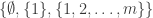 is an obvious counterexample.
is an obvious counterexample.
January 26, 2016 at 12:54 pm
Ah yes, I need to work out what I meant by “stationary distribution” there, since it clearly wasn’t the limiting distribution of a random walk on the bipartite graph where you go to each neighbour with equal probability (and have a staying-still probability to make it converge), as that does not satisfy the isomorphism-invariance condition.
Let me begin with a completely wrong argument and then try to do a Google-page-rank-ish process to make it less wrong. The completely wrong argument is that a good way to choose an element that belongs to lots of sets is to choose a random non-empty
that belongs to lots of sets is to choose a random non-empty 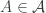 and then a random
and then a random  . Why might that be good? Because it favours elements that belong to lots of sets. And why is it in fact not good? Because it doesn’t penalize the other elements enough. The
. Why might that be good? Because it favours elements that belong to lots of sets. And why is it in fact not good? Because it doesn’t penalize the other elements enough. The  example illustrates this: although we pick
example illustrates this: although we pick  with probability very slightly greater than 1/2, that is not enough to tip the average … oh wait, yes it is. We choose 1 with probability
with probability very slightly greater than 1/2, that is not enough to tip the average … oh wait, yes it is. We choose 1 with probability 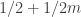 and all other elements with probability
and all other elements with probability  , so the expected number of sets containing a point is
, so the expected number of sets containing a point is  .
.
So I need to work slightly harder to find a counterexample. I’ll do that this afternoon unless someone has beaten me to it.
January 26, 2016 at 2:23 pm
As a first step, let me try to find a nice expression for the expected number of sets in that contain a random element of a random non-empty set in
that contain a random element of a random non-empty set in  . Let the non-empty sets in
. Let the non-empty sets in  be
be 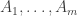 and let
and let  and
and  . Then if the randomly chosen set is
. Then if the randomly chosen set is 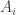 , the probability that
, the probability that 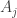 contains a random
contains a random  is
is  , so the expected number of sets containing a random
, so the expected number of sets containing a random  is
is  and the expectation of that over all
and the expectation of that over all  is
is  , which is a fairly bizarre expression.
, which is a fairly bizarre expression.
January 26, 2016 at 3:02 pm
Maybe it’s not as bad as all that actually. Let’s define the average overlap density with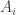 to be the average of
to be the average of 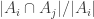 over all
over all  . This average is
. This average is 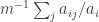 , so the expectation at the end of the previous comment is the sum over all
, so the expectation at the end of the previous comment is the sum over all  of the average overlap density with
of the average overlap density with 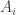 .
.
Although this quantity is not an isomorphism invariant, there are limits to what can be done to it by duplicating elements.
What about your example where consists of all subsets of
consists of all subsets of  that are either empty or contain
that are either empty or contain 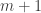 ? I think the average overlap density will be slightly greater than 1/2 (because almost all sets contain
? I think the average overlap density will be slightly greater than 1/2 (because almost all sets contain  ), but I can try to defeat that by duplicating the elements
), but I can try to defeat that by duplicating the elements 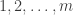 many times. Equivalently, I will put a measure on the set
many times. Equivalently, I will put a measure on the set  that gives measure 1 to all of
that gives measure 1 to all of 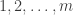 and measure
and measure  to
to 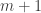 , and I will use that measure to define the overlap densities.
, and I will use that measure to define the overlap densities.
Now I need to be a little more careful with the calculations. I’ll begin by ignoring terms in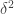 and hoping that the linear terms don’t cancel out. So if I pick a non-empty set
and hoping that the linear terms don’t cancel out. So if I pick a non-empty set  from the system, and if it has measure
from the system, and if it has measure  , then the average overlap density with
, then the average overlap density with  will be
will be
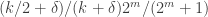 .
.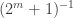 probability of choosing the empty set.
probability of choosing the empty set.
The last factor is there because there is a
For now I shall ignore that last factor, since it is the same for all sets, and I’ll put it back in at the end.
If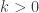 , then we can approximate
, then we can approximate 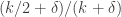 by
by  , while if
, while if  we get 1. So I find that I need to know the average of
we get 1. So I find that I need to know the average of 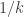 when each
when each  is chosen with probability
is chosen with probability  . I don’t know what this average is, and it doesn’t seem to have a nice closed form, so let’s call it
. I don’t know what this average is, and it doesn’t seem to have a nice closed form, so let’s call it  . That gives us an average overlap density (to first order in
. That gives us an average overlap density (to first order in  ) of
) of
 .
.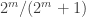 again, we get
again, we get
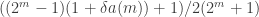 .
. tends to zero, this tends to
tends to zero, this tends to 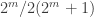 , so it seems that we have a counterexample.
, so it seems that we have a counterexample.
Now remembering about the factor
As
I think should be around
should be around 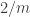 by concentration of measure. If that is correct, then for
by concentration of measure. If that is correct, then for  greater than around
greater than around  we’ll get an average overlap density greater than 1/2. So we really do have to do a lot of duplication to kill off the
we’ll get an average overlap density greater than 1/2. So we really do have to do a lot of duplication to kill off the 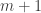 contribution. Of course, there may well be simpler examples where much less duplication is necessary.
contribution. Of course, there may well be simpler examples where much less duplication is necessary.
January 26, 2016 at 3:12 pm
I should remark that implicit in all that is a simple observation, which is the following. Define the average overlap density of the entire set system to be
to be
 ,
, is over the non-empty sets but the average over
is over the non-empty sets but the average over  is over all sets in
is over all sets in  . Then if the average overlap density is
. Then if the average overlap density is  , there must be an element contained in at least
, there must be an element contained in at least 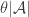 of the sets. This is true for any set system and not just a set system that is closed under unions.
of the sets. This is true for any set system and not just a set system that is closed under unions.
where the average over
In the case of the system the average overlap density is
the average overlap density is
 , which is very slightly greater than 1/2.
, which is very slightly greater than 1/2.
So here is a question: are there union-closed set systems with arbitrarily small average overlap density?
January 26, 2016 at 4:33 pm
I think we can get an arbitrarily small average overlap density. Here’s an example:
Take n >> k. We take and modify it a bit. Specifically, for every k-set
and modify it a bit. Specifically, for every k-set ![S \subset [n]](https://s0.wp.com/latex.php?latex=S+%5Csubset+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , define a new element
, define a new element  , and add it to exactly those elements of
, and add it to exactly those elements of  which contain
which contain  .
.
This family is union-closed. Also, nearly every set in it is dominated by the new elements , but each element
, but each element  is only in one in every
is only in one in every 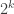 sets. So the average overlap density is only a shade over
sets. So the average overlap density is only a shade over 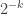 .
.
January 26, 2016 at 5:15 pm
I’m trying to understand this. Let’s take two disjoint -sets
-sets  and
and  . Then the modified sets will be
. Then the modified sets will be 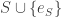 and
and  . Their union will be
. Their union will be  , which doesn’t seem to be of the form subset-
, which doesn’t seem to be of the form subset- -of-
-of-![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) union set-of-all-
union set-of-all- -such-that-
-such-that- -is-a-
-is-a- -subset-of-
-subset-of- . So either I’m making a stupid mistake (which is very possible indeed) or this family isn’t union closed.
. So either I’m making a stupid mistake (which is very possible indeed) or this family isn’t union closed.
January 26, 2016 at 5:19 pm
Oh! You are quite right, that family isn’t remotely union-closed. Back to the drawing board.
One particularly nice feature of this “average overlap density” strengthening is that the special exclusion for the family consisting only of the empty set becomes completely natural – as that family doesn’t have an average overlap density.
January 26, 2016 at 8:29 pm
I wonder if the average overlap density can ever be less than .
.
It attains the value for power sets, as well as some others, e.g.
for power sets, as well as some others, e.g.  . But it seems hard to find examples where it’s less than
. But it seems hard to find examples where it’s less than  .
.
January 26, 2016 at 9:13 pm
My longish comment above with the s in it was supposed to be an example of a union-closed family with average overlap density less than 1/2. It was a modification of an example of yours. To describe it more combinatorially, take a very large
s in it was supposed to be an example of a union-closed family with average overlap density less than 1/2. It was a modification of an example of yours. To describe it more combinatorially, take a very large  and take sets
and take sets 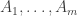 of size
of size  and a set
and a set  of size 1, all these sets being disjoint. Then
of size 1, all these sets being disjoint. Then  consists of the empty set together with all unions of the
consists of the empty set together with all unions of the 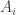 that contain
that contain  .
.
If I now pick a random non-empty set in the system, it consists of some union of the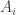 with
with 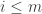 together with the singleton
together with the singleton  . The average overlap density with the set will be fractionally over 1/2 (by an amount that we can make arbitrarily small by making
. The average overlap density with the set will be fractionally over 1/2 (by an amount that we can make arbitrarily small by making  as large as we choose) if we intersect it with a random other set of the same form, but when we throw in the empty set as well, we bring the average down to just below 1/2 (by an amount proportional to
as large as we choose) if we intersect it with a random other set of the same form, but when we throw in the empty set as well, we bring the average down to just below 1/2 (by an amount proportional to 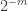 ).
).
The “problem” with this set system is that it is a bit like the power set of![[m]](https://s0.wp.com/latex.php?latex=%5Bm%5D&bg=ffffff&fg=333333&s=0&c=20201002) with the empty set duplicated — in a sense that is easy to make precise, it is a small perturbation of that.
with the empty set duplicated — in a sense that is easy to make precise, it is a small perturbation of that.
Now that I’ve expressed things this way, I’m starting to wonder whether we can do something more radical along these lines to obtain a smaller average overlap density. Roughly the idea would be to try to do a lot more duplication of small sets and somehow perturb to make them distinct.
Indeed, maybe one can take any union-closed set system , blow up every element into
, blow up every element into  elements, take unions of the resulting sets with some singleton, and throw in the empty set. It looks to me as though by repeating that with suitably large
elements, take unions of the resulting sets with some singleton, and throw in the empty set. It looks to me as though by repeating that with suitably large  one could slowly bring down the average intersection density to something arbitrarily small, but I haven’t checked, as I’m thinking as I write.
one could slowly bring down the average intersection density to something arbitrarily small, but I haven’t checked, as I’m thinking as I write.
January 26, 2016 at 9:21 pm
Ah yes, I was making a mistake: ignore my last comment!
January 26, 2016 at 9:53 pm
Actually, I’m a bit puzzled by your calculation. Suppose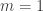 . (You don’t make any assumptions about
. (You don’t make any assumptions about  .) Then the set system (in full, before you replace the duplicates with the
.) Then the set system (in full, before you replace the duplicates with the  weighting) has the shape
weighting) has the shape 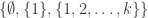 where
where  is large. But we already know that this has average overlap density more than
is large. But we already know that this has average overlap density more than  . This seems inconsistent with your conclusion, but I’m not sure where the mistake is.
. This seems inconsistent with your conclusion, but I’m not sure where the mistake is.
January 26, 2016 at 10:07 pm
Let me see what happens with . Now the sets (in the second version) are
. Now the sets (in the second version) are  , and
, and 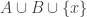 for two disjoint sets
for two disjoint sets  and
and  of size
of size  (disjoint also from
(disjoint also from  ).
). is
is  . The average overlap density with
. The average overlap density with 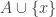 is
is 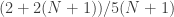 , as it is with
, as it is with 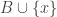 . And finally the average overlap density with
. And finally the average overlap density with 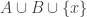 is
is  . To a first approximation (taking
. To a first approximation (taking  to be infinity) we get a total average of
to be infinity) we get a total average of  , so the initial sanity check is passed. But again it looks as though the averages are very slightly larger.
, so the initial sanity check is passed. But again it looks as though the averages are very slightly larger.
The average overlap density with
I have to do something else now, but I’m not sure what’s going on here either. But it’s a win-win — either the counterexample works, or the idea of using this as the basis for an averaging argument lives for a little longer.
January 27, 2016 at 9:12 am
I think I’ve seen my mistake, at least in the second version of the argument (Jan 26th, 9:13pm). I comment there that the set system “duplicates” the empty set. That is indeed true, but it gives rise to two competing effects. On the one hand, for each set that properly contains , the average overlap density is indeed very slightly less than 1/2 (because both
, the average overlap density is indeed very slightly less than 1/2 (because both  and
and  intersect it in a set of density almost zero). On the other hand, the average intersection density with the set
intersect it in a set of density almost zero). On the other hand, the average intersection density with the set  is almost 1, which has a tendency to lift things up.
is almost 1, which has a tendency to lift things up.
Ah, and in the first version of the argument I made a stupid mistake in my algebra. The expression towards the end for the average overlap density should have been

 to
to  .
.
the difference being the “+2” which I gave as “+1”. This is enough to tip the balance from being
So I’m definitely back to not knowing of an example where the average overlap density is less than 1/2.
January 27, 2016 at 9:53 am
For what it’s worth, I’ve run a program that generates random separating UC families and computes the a.o.d., and it hasn’t found any counterexamples, with equality occurring only for power sets.
(I don’t have a feeling yet for how much trust to place in such experiments. The generation algorithm I used depends on parameters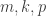 . It starts with a ground set of size
. It starts with a ground set of size  , generates
, generates  random subsets each containing each element with probability
random subsets each containing each element with probability  , and forms the smallest separating UC family containing them. I’ve tried various combinations of parameters, but haven’t run the program for very long. Anyway the experiment indicates that any counterexample would have to be quite structured.)
, and forms the smallest separating UC family containing them. I’ve tried various combinations of parameters, but haven’t run the program for very long. Anyway the experiment indicates that any counterexample would have to be quite structured.)
January 27, 2016 at 10:23 am
Additionally, for what little it’s worth, there are no counterexamples in (which is the largest powerset in which it is reasonable to enumerate the union-closed families).
(which is the largest powerset in which it is reasonable to enumerate the union-closed families).
January 27, 2016 at 11:28 am
Small correction to my description of the random generating algorithm: it doesn’t form the ‘smallest separating UC family containing’ the random sets (there may not be one); it forms the smallest UC family containing them and then reduces it by removing duplicates.
January 27, 2016 at 3:35 pm
I’ve had a thought for a potential way of making the conjecture nicer, but it risks tipping it over into falsehood.
Suppose we take two non-empty sets and
and  . Their contribution to the average overlap density is
. Their contribution to the average overlap density is
 .
.
 .
. and
and 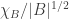 . What’s more, those functions are very natural: they are just the
. What’s more, those functions are very natural: they are just the 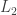 normalizations of the characteristic functions of
normalizations of the characteristic functions of  and
and  . Let me denote the normalized characteristic function of
. Let me denote the normalized characteristic function of  by
by  .
.
This is slightly unpleasant, but becomes a lot less so if instead we replace it by the smaller quantity
What’s nice about that is that, disregarding the factor 2, it is the inner product of the functions
Then I think another conjecture that implies FUNC, at least for set systems that do not contain the empty set, is that if is a union-closed family of that type, then
is a union-closed family of that type, then
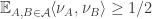 .
.
 .
.
But of course the left-hand side can be simplified: it is just
Just on the point of posting this comment, I think I’ve realized why this is a strengthening too far. The rough reason is that the previous conjecture was more or less sharp for the power set of a set , and then when you replace the average intersection density by this more symmetrical version you’ll get something smaller, because you’ll often have sets
, and then when you replace the average intersection density by this more symmetrical version you’ll get something smaller, because you’ll often have sets  and
and  of different size. But that doesn’t rule out proving something interesting by this method. For example, perhaps there is a constant
of different size. But that doesn’t rule out proving something interesting by this method. For example, perhaps there is a constant 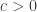 such that
such that
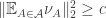
 .
.
for every union-closed set system
January 27, 2016 at 3:44 pm
A stress test. Let’s take a system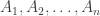 of nested sets with very rapidly increasing size. Then the inner product of any two of the
of nested sets with very rapidly increasing size. Then the inner product of any two of the  will be almost zero unless the two are the same set. So unfortunately this strengthened conjecture, even in its weakened form, is dead.
will be almost zero unless the two are the same set. So unfortunately this strengthened conjecture, even in its weakened form, is dead.
January 27, 2016 at 5:47 pm
Some sort of vector formulation is still possible, but it doesn’t really change much I think. We can define to be the
to be the 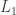 -normalized characteristic function (that is,
-normalized characteristic function (that is, 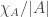 ), and then the claim is that
), and then the claim is that
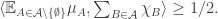
 and then a random
and then a random  , while the function on the right-hand side is just the function that counts how many sets you belong to. So it is not enough of a reformulation to count as a different take on the problem.
, while the function on the right-hand side is just the function that counts how many sets you belong to. So it is not enough of a reformulation to count as a different take on the problem.
The reason this doesn’t help much is that the function on the left-hand side is simply the probability measure you get by choosing a random
January 24, 2016 at 9:53 pm |
Over on the G+ post (https://plus.google.com/+TimothyGowers0/posts/QJPNRithDDM) one of the commenters suggested looking at the graph-theoretic formulation of Bruhn et al (Eur J. Comb. 2015), which I just added to the Wikipedia article (https://en.wikipedia.org/wiki/Union-closed_sets_conjecture#Equivalent_forms). According to that formulation, it’s equivalent to ask whether every bipartite graph has two adjacent vertices that both belong to at most half the maximal independent sets. So one possible class of counterexamples would be bipartite graphs in which both sides are vertex-transitive but in which the sides cannot be swapped, such as the semi-symmetric graphs. It seems like the union-closed set conjecture would imply that such highly-symmetric bipartite graphs always have another hidden symmetry, in that the graphs on both sides of the bipartition all appear in equally many maximal independent sets. Is something like this already known?
January 27, 2016 at 8:59 am
Apologies — it took me a while to notice this comment in my moderation queue (where it went because it contained two links).
January 24, 2016 at 11:02 pm |
Speaking of introducing probability measures, here’s another direction that might be worth thinking about.
The standard conjecture implicitly uses the counting measure to compare the size of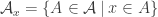 to the size of
to the size of  . What happens if one replaces this counting measure by something else?
. What happens if one replaces this counting measure by something else?
An extreme case is the probability measure supported on . In this case, there’s obviously no
. In this case, there’s obviously no  such that sampling from the measure results in an
such that sampling from the measure results in an  -containing set with probability
-containing set with probability 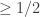 .
.
But explicitly excluding the empty set yields a seemingly more sensible question:
Conjecture: suppose that is a union-closed family and
is a union-closed family and  is a probability measure on
is a probability measure on  . Then there exists some
. Then there exists some 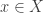 with
with  .
.
Of course, this may well have been considered before, and even if not, it may still be very easy to shoot down.
Thinking a bit further, I also wonder whether one can introduce a measure both on and on
and on  and impose some reasonable compatibility condition between the two.
and impose some reasonable compatibility condition between the two.
January 24, 2016 at 11:27 pm
That conjecture should easily turn out to be false, if one e.g. takes to be supported on singletons. Now I think that a more reasonable conjecture will turn the union-closure assumption into an assumption on $\mu$, such as this one:
to be supported on singletons. Now I think that a more reasonable conjecture will turn the union-closure assumption into an assumption on $\mu$, such as this one:
Condition: for every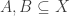 , one has
, one has 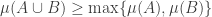 .
.
For example, the normalized counting measure of a union-closed family has this property.
Conjecture: for every probability measure on
on 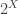 satisfying the condition, there is
satisfying the condition, there is 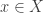 such that sampling from
such that sampling from  results in an
results in an  -containing set with probability
-containing set with probability 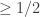 .
.
January 24, 2016 at 11:40 pm
Actually no, sorry: my condition was supposed to apply to all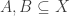 , and as such it is easily seen to be equivalent to monotonicity of
, and as such it is easily seen to be equivalent to monotonicity of  . In particular, the normalized counting measure of a union-closed family is not even an example… So I’ll rather shut up now.
. In particular, the normalized counting measure of a union-closed family is not even an example… So I’ll rather shut up now.
January 25, 2016 at 10:01 am
So here’s a strengthened conjecture which has the flavour of a problem in tropical geometry.
Conjecture: let![\mu : 2^X \to [0,1]](https://s0.wp.com/latex.php?latex=%5Cmu+%3A+2%5EX+%5Cto+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) be a probability distribution over subsets of $X$ in the sense that
be a probability distribution over subsets of $X$ in the sense that  . Suppose that for every
. Suppose that for every 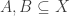 , one has
, one has
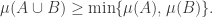
 results in an
results in an  -containing set with probability
-containing set with probability 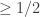 .
.
Then there is $x\in X$ such that sampling from
In the special case of being the normalized counting measure of a set family
being the normalized counting measure of a set family  , the additional assumption on
, the additional assumption on  holds if and only if
holds if and only if  is union-closed.
is union-closed.
What does this have to do with tropical geometry? Well, the assumption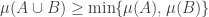 is a linear inequality over the min-plus semiring, while the normalization condition $\sum_A \mu(A) = 1$ is likewise a polynomial equation. Also, the conjectural conclusion can be rewritten as
is a linear inequality over the min-plus semiring, while the normalization condition $\sum_A \mu(A) = 1$ is likewise a polynomial equation. Also, the conjectural conclusion can be rewritten as

which is a polynomial inequality over the min-plus semiring.
Does this look worth thinking about or am I just ranting?
January 26, 2016 at 2:15 pm
Just to say that this does indeed look worth thinking about, but I don’t know anything about tropical geometry, so I don’t have a feel for what can be gained by casting the problem in this way. Are there some easily described tools from the area that have lots of applications, as there are in algebraic geometry?
January 26, 2016 at 6:20 pm
Unfortunately I don’t know enough about tropical geometry to know what kinds of tools it provides, but I’m now reading this wonderful introduction by Maclagan and Sturmfels: http://bookstore.ams.org/GSM-161 I’ll report back here in case that anything promising comes up.
January 25, 2016 at 5:13 am |
One can make some well known topological constructions which may be useful. These are cleaner for “intersection closed” systems (obtained by taking complements). These may be useful in assigning weights, or more generally making precise “depth” (whether the sets overlap a lot) and examples such as the one with a single large set.
Here is a sketch of the standard constructions and some simple observations.
1. We start with an intersection closed collection of sets X. This is partially ordered by inclusion.
2. We have the associated poset complex, namely with vertices elements of X (i.e., sets in our collection) and simplices corresponding to totally ordered sets.
3. This simplicial complex has a decomposition into `cell-like’ subsets associated to
associated to 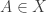 , namely those totally ordered sets with
, namely those totally ordered sets with  as the maximal element. These are contractible (as all simplices in
as the maximal element. These are contractible (as all simplices in  contain the vertex
contain the vertex  , but not actually cells.
, but not actually cells.
4. The nice thing here is that being intersection closed gives a statement about the cells . Namely, if
. Namely, if 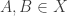 , then
, then  , and we can see that
, and we can see that  .
.
5. We can also associate subsets of the poset complex corresponding to points based on whether
based on whether 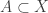 contains
contains  . These sets may have topology.
. These sets may have topology.
6. What may be useful is the “local homology” as well as “analysis like” constructions such as the PL Laplacian.
January 25, 2016 at 9:08 am
This looks interesting. I couldn’t find anything when I tried to look up what the PL Laplacian was. Is it possible to give a link or a brief explanation?
January 25, 2016 at 9:18 am
What I was thinking of was what is used for instance in
Ray, D. B.; Singer, I. M. (1973a), “Analytic torsion for complex manifolds.”, Ann. Of Math. (2) (Annals of Mathematics) 98 (1): 154–177
The philosophy is that for a finite simplicial complex, we can identify simplcial chains and co-chains as they are elements of a vector space and its dual, but we have a canonical basis given by simplices. So we have on the same space both a boundary $\partial$ and a co-boundary $d$. We can put these together and get a Hodge Laplacian:
$d\partial + \partial d$
On 0-forms this is a Laplacian (one of the terms disappears).
January 25, 2016 at 10:29 am |
I tried to come up with examples of union-closed (or intersection-closed) set systems to get a better feeling for the conjecture. Unfortunately the examples somewhat trivially satisfy FUNC.
The idea is to map elements i of sets to the i-th prime. Singleton sets will be mapped to primes, sets with more elements to the respective products. The set systems will then be (certain) subsets of
the i-th prime. Singleton sets will be mapped to primes, sets with more elements to the respective products. The set systems will then be (certain) subsets of 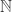 and vice versa. In case I was careful enough we end up with the following equivalent formulation of FUNC:
and vice versa. In case I was careful enough we end up with the following equivalent formulation of FUNC:
Let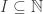 be a gcd-closed index set and let
be a gcd-closed index set and let 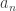 be a strong divisibility sequence. Then there is a prime
be a strong divisibility sequence. Then there is a prime  such that
such that  divides at most
divides at most  of the numbers in
of the numbers in 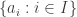 .
.
Unfortunately (for us, but not in general) there are results for many such sequences that ensure the existence of prime divisors which e.g. divide just the number with the largest index. Such (primitive) prime divisors make our examples (in a sense trivially) obey FUNC.
The story has a twist.
For many (if not all) strong divisibility sequences there is a dual sequence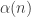 being the first index
being the first index  such that
such that  . This
. This  satisfies
satisfies  . FUNC then becomes: Let
. FUNC then becomes: Let  be a lcm-closed index set and let
be a lcm-closed index set and let 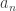 be a strong divisibility sequence with dual sequence
be a strong divisibility sequence with dual sequence  . Then there is a prime
. Then there is a prime  such that
such that  divides at least
divides at least  of the numbers in
of the numbers in  .
.
Let me close this with an example. The lcm-closed index set are the divisors of 20 and the strong divisibility sequence is the Fibonacci sequence. Then, by inspection, and by the lcm rule
and by the lcm rule 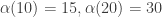 . The generated set system would then be
. The generated set system would then be 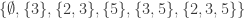 . Luckily this is union closed and thus the above might not be cmplete garbage. Again FUNC is easily true.
. Luckily this is union closed and thus the above might not be cmplete garbage. Again FUNC is easily true.
January 26, 2016 at 4:39 pm
While I still like the idea to construct (large) intersection closed set systems via strong divisibility sequences, the above is not going to work easily. This is why. Let be a gcd closed index set and
be a gcd closed index set and  be a strong divisibility sequence. The map
be a strong divisibility sequence. The map  that sends each
that sends each  to the set of all primes dividing generates an intersection closed set. For some index sets
to the set of all primes dividing generates an intersection closed set. For some index sets  will be injective. In this case the intersection closed set system satisfies FUNC somewhat trivially (at least I think so). For index sets with
will be injective. In this case the intersection closed set system satisfies FUNC somewhat trivially (at least I think so). For index sets with 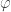 not injective it is not obvious to me how FUNC translates. If there is an element with low frequency in the image set system, is there a prime in the strong divisibility sequence that does not divide a lot of the
not injective it is not obvious to me how FUNC translates. If there is an element with low frequency in the image set system, is there a prime in the strong divisibility sequence that does not divide a lot of the 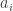 ?
?
Maybe its time for me to switch on the computer and generate some set systems via elliptic divisibility sequences (for that I need to know when an elliptic divisibility sequence is a strong divisibility sequence. That _must_ be known).
January 26, 2016 at 5:18 pm
That would be great (the switching on of the computer with all its consequences).
January 25, 2016 at 12:30 pm |
One half-baked idea for a generalisation:
Let . Then a rephrasing of “
. Then a rephrasing of “ is union-closed” is
is union-closed” is  . So, we generalise by making one of these
. So, we generalise by making one of these  s a
s a  . The right generalisation is not at all obvious, but baby steps that I’d like a counterexample to would be:
. The right generalisation is not at all obvious, but baby steps that I’d like a counterexample to would be:
If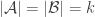 , and
, and  , then at least one of
, then at least one of  and
and  has an element in half of its sets.
has an element in half of its sets.
or
If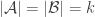 , and
, and  , then some element is in at least
, then some element is in at least  sets between
sets between  and
and  .
.
If those don’t fall easily, then perhaps there is a more interesting strengthening, where we make a statement about pairs and
and  of non-equal sizes, and/or with more varied limits on
of non-equal sizes, and/or with more varied limits on  .
.
January 25, 2016 at 1:07 pm
I’ve thought a little bit and can’t find a counterexample, even to the second statement. At one moment I thought I had one but then realized that it wasn’t at all — all it was was an example where the hypothesis is satisfied but neither nor
nor  is anything like union closed.
is anything like union closed.
The example is to partition into disjoint sets
into disjoint sets 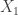 and
and 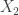 and to take
and to take  to consist of all sets that contain
to consist of all sets that contain 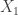 and
and  to consist of all sets that contain
to consist of all sets that contain 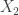 . If
. If  , then
, then  , but
, but 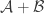 consists of the single set
consists of the single set  . However, every element belongs to 3/4 of the sets, so this isn’t even close to being a counterexample. But perhaps it is worth remarking that
. However, every element belongs to 3/4 of the sets, so this isn’t even close to being a counterexample. But perhaps it is worth remarking that  can be much smaller than either
can be much smaller than either  or
or  . This feels slightly odd. One could cure it by insisting that both
. This feels slightly odd. One could cure it by insisting that both  and
and  should contain the empty set, but then we need
should contain the empty set, but then we need  to equal
to equal  , which forces the two set systems to be equal.
, which forces the two set systems to be equal.
But maybe that slight oddness is nothing to worry about. So right now your proposed generalization seems pretty interesting, though that maybe because I haven’t made the right simple observation.
January 25, 2016 at 7:40 pm
Changing your example a little, let consist of sets that consist of all of
consist of sets that consist of all of 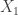 and a single element of
and a single element of 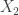 , and
, and  consist of sets that consist of all of
consist of sets that consist of all of 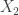 and a single element of
and a single element of 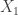 . Then
. Then  is still 1, but each element is in only just over 1/2 the sets between the two families.
is still 1, but each element is in only just over 1/2 the sets between the two families.
That feels slightly odd – we have a vastly stronger constraint on than the
than the  , but we haven’t gained anything above an element in half the sets in total.
, but we haven’t gained anything above an element in half the sets in total.
That makes me prefer the other statement, with the conjecture being that either or
or  has an abundant element. If
has an abundant element. If  , then at least one of the families has a universal element – it feels more promising that this stronger condition leads to a stronger conclusion.
, then at least one of the families has a universal element – it feels more promising that this stronger condition leads to a stronger conclusion.
January 25, 2016 at 8:49 pm
That makes good sense. It might be nice to try to guess at a conjecture for what should happen (with the second question) if ,
,  and
and 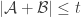 , perhaps under restrictions such as
, perhaps under restrictions such as  and perhaps not. If one could find a not obviously false conjecture, it could conceivably be useful, as something more general like that feels more amenable to an inductive proof.
and perhaps not. If one could find a not obviously false conjecture, it could conceivably be useful, as something more general like that feels more amenable to an inductive proof.
January 25, 2016 at 10:07 pm
Just to throw it into the mix, here’s a very similar example that, while it doesn’t disprove or even necessarily cast doubt onto these conjectures, might be helpful to have in the thought-box.
Let denote all sets of the form
denote all sets of the form 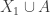 for some
for some 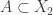 , together with all sets of the form
, together with all sets of the form  for some
for some  . Let
. Let  denote all subsets of
denote all subsets of 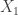 and all subsets of
and all subsets of 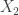 .
.
Then ,
,  , and
, and 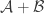 all have the same size,
all have the same size,  (indeed,
(indeed, 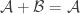 ), and every element is in precisely
), and every element is in precisely  of the sets from
of the sets from  and
and  .
.
January 27, 2016 at 4:24 am
If |\mathcal A + \mathcal B| = 1, then if we call X_1 the union of all sets in \mathcal A, which is a set in \mathcal A, and X_2 the union of all sets in \mathcal B, which is a set in \mathcal B, we have \mathcal A + \mathcal B=\{X_1\cupX_2\}. If \mathcal A does not have an universal element, let x_1\inX_1 and pick a set S\in\mathcal A such that x_1\not\in S. Since {S}\cup \mathcal B \subset \mathcal A + \mathcal B this means x_1\in B\cup S for all B \in \mathcal B and so x_1 is universal in \mathcal B.
January 25, 2016 at 3:11 pm |
I don’t have any deep insights but my first thought was to explore some randomly generated examples. I wrote the following code in a few minutes so its probably embarrassingly inefficient but perhaps someone else could improve it. It outputs random union-closed sets that have a low abundance. I will look into better ways of visualizing the output.
https://sagecell.sagemath.org/?q=xkqack
January 25, 2016 at 3:46 pm
It would be very nice to have a library of small examples we could use (and put on a Wiki page) in order to test conjectures.
January 28, 2016 at 5:02 pm
In a very similar vein, here is a Mathematica Manipulate that randomly generates union closed families, then plots the frequency distribution of the elements of the original set (after a rename/sort) within the family. It was interesting to see as the family size got larger, all elements of the original set seem to occur in just over n/2 sets within the family.
Manipulate[
X = Table[i, {i, 1, m, 1}];
powerSet = Subsets[X];
psLength = Length[powerSet];
randomSample = RandomSample[powerSet, r];
pairs = Subsets[randomSample, {2}];
munion = DeleteDuplicates[ Map[Apply[Union, #] &, pairs]];
mcounts = Sort[BinCounts[Flatten[munion], {1, m + 1, 1}]];
Column[{
Row[{“Set is “, X}],
(*Row[{“PowerSet is “,
powerSet}],*)
(*Row[{“RandomSample of PowerSet is “,
randomSample}],*)
(*Row[{“Pairs are “,pairs}],*)
Row[{“A union closed Family of Subsets with Cardinality “,
Length[munion], ” is “, munion}],
Row[{“Counts are “, mcounts}],
(*Row[{“Histogram is “,
Histogram[Flatten[munion],{1,9,1},
ImageSize\[Rule]{400,200},
GridLines\[Rule]{{},{Length[munion]/2, Length[munion]}}]
}],*)
Row[{“Ordered freqs are “,
ListPlot[mcounts,
Filling -> Axis,
ImageSize -> {400, 200},
PlotRange -> {0, Length[munion]},
GridLines -> {{}, {Length[munion], Length[munion]/2}}]
}]
}]
, {{m, 9, “Original Set Cardinality”}, 0, 19, 1}
, {{r, 3, “Random Sample Size”}, 0, 1000, 1}]
January 28, 2016 at 5:06 pm
Is it easy to describe how your random generation works? Do you pick a few random sets and take the union closure?
January 28, 2016 at 8:40 pm
Yes, that’s about it. I create the power set, take a random sample from the power set, then create the closure by taking the union of all pairs formed from the cartesian product of the sample with itself. The DeleteDuplicates, above, creates the family from this list of unions. Not the most efficient way, I’m sure, and I notice that the null set is never in the closure, also.
A slider in the Manipulate allows the size of the random sample to be changed interactively.
January 29, 2016 at 9:06 am
Rik,
The families created aren’t necessarily union-closed. The code only takes unions of _pairs_ of sampled sets. (It also discards the original sample.)
The following seems to work correctly. For efficiency, I’ve used bistrings (binary integers) to represent the sets.
Manipulate[
randomSampleInts = RandomInteger[2^m – 1, r];
ucFamilyInts =
Nest[DeleteDuplicates[BitOr @@@ Subsets[#, {1, 2}]] &,
randomSampleInts, IntegerLength[r, 2]];
ucFamilyBits = IntegerDigits[#, 2, m] & /@ ucFamilyInts;
elementCounts = Total@ucFamilyBits;
Column[{
Row[{"Base set is ", Range@m}],
Row[{"Cardinality of union closed family of subsets is ",
Length[ucFamilyInts]}],
Row[{"Counts are ", elementCounts}],
Row[{"Ordered freqs are ",
ListPlot[elementCounts, Filling -> Axis, ImageSize -> {400, 200},
PlotRange -> {0, Length[ucFamilyInts]},
GridLines -> {{}, {Length[ucFamilyInts],
Length[ucFamilyInts]/2}}]}],
Row[{"Union closed family is ",
Sort[Join @@ Position[#, 1] & /@ ucFamilyBits]}]
}]
, {{m, 9, "Base set cardinality"}, 0, 19, 1}
, {{r, 5, "Random sample size"}, 0, 100, 1}]
January 29, 2016 at 12:11 pm
Ah yes, thanks for the correction, and the far more efficient way of tackling the calculation. (Also thanks for the Wolfram Language lesson, most instructive.)
January 25, 2016 at 10:21 pm |
Regarding the suggested strengthening to a weighting on a union-closed family
on a union-closed family  such that
such that 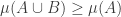 (so that there is an element
(so that there is an element  such that
such that  ), I thought briefly that it easily followed from FUNC, before I realised my error.
), I thought briefly that it easily followed from FUNC, before I realised my error.
In the spirit of polymath, I’ll record my erroneous proof here.
Suppose that this fails for some union-closed family , and some weight function
, and some weight function  with the above property. Assume FUNC holds. Choose such a failing
with the above property. Assume FUNC holds. Choose such a failing  with maximal
with maximal  .
.
By FUNC, pick an in at least half of the sets, but suppose
in at least half of the sets, but suppose 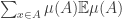 , so by maximality this strengthened FUNC does hold for
, so by maximality this strengthened FUNC does hold for 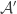 . Let
. Let  be as given by the strengthened FUNC.
be as given by the strengthened FUNC.
Then . Let
. Let 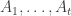 be the sets summed over in this index. If we can find
be the sets summed over in this index. If we can find  with
with  such that
such that  is distinct for distinct
is distinct for distinct  , then we’re done, because
, then we’re done, because  .
.
The problem is finding such magical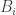 , that guarantee this uniqueness. At first I thought this was easy, because we have (if there are
, that guarantee this uniqueness. At first I thought this was easy, because we have (if there are  sets to begin with), that
sets to begin with), that  and there are
and there are 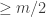 sets
sets  to choose from, so some kind of greedy choice works. But this appears to be nonsense, and the proof unsalvageable.
to choose from, so some kind of greedy choice works. But this appears to be nonsense, and the proof unsalvageable.
January 26, 2016 at 1:09 pm
After the word “suppose” in your fourth paragraph there is a mathematical expression about which you say nothing. What did you mean to write? Another question I had was about the maximality condition. What’s stopping you multiplying all the weights by 100? (I am of course asking these questions because I’m interested in what you write, and even more interested in what you meant to write!)
I think it would be interesting to decide whether weighted FUNC follows from FUNC itself. I had tried it too without getting anywhere. The idea I looked at was to try to compress the weights somehow until they were all the same, while not introducing a good element that wasn’t there before, but I couldn’t see a way of doing it.
January 26, 2016 at 5:29 pm
Ah yes, of course – I was implicitly taking (without loss of generality) , without loss of generality. This handles the ‘base case’ of the induction, since that becomes
, without loss of generality. This handles the ‘base case’ of the induction, since that becomes  , which is precisely FUNC.
, which is precisely FUNC.
The fourth paragraph has become oddly mangled. It should read:
By FUNC, pick an in at least half of the sets, but suppose that
in at least half of the sets, but suppose that  , so by maximality this strengthened FUNC does hold for
, so by maximality this strengthened FUNC does hold for 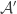 . Let
. Let  be as given by the strengthened FUNC.
be as given by the strengthened FUNC.
January 26, 2016 at 5:31 pm
How odd, it did it again. Let me try and adjust the LaTeX slightly to avoid this oddness. (and apologies for the repeated comments, but I couldn’t see a way to edit comments).
By FUNC, pick an $x$ in at least half of the sets, but suppose that $\sum_{x\in A}\mu(A)\mathbb{E}\mu(A)$, so by maximality this strengthened FUNC does hold for $\mathcal{A}’$. Let $y$ be as given by the strengthened FUNC.
January 26, 2016 at 5:32 pm
And again. Without any better ideas, I’ll just write it down with the LaTeX formatting.
By FUNC, pick an x in at least half of the sets, but suppose that \sum_{x\in A}\mu(A)\mathbb{E}\mu(A), so by maximality this strengthened FUNC does hold for \mathcal{A}’. Let y be as given by the strengthened FUNC.
January 26, 2016 at 5:35 pm
How, how silly of me. It didn’t like the less than and greater than symbols. This should now work.
By FUNC, pick an x in at least half of the sets, but suppose that . Then, if
. Then, if 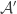 denotes the collection of sets in
denotes the collection of sets in  which do not contain
which do not contain  , it follows that
, it follows that 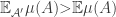 , so by maximality this strengthened FUNC does hold for
, so by maximality this strengthened FUNC does hold for 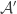 . Let
. Let  be as given by the strengthened FUNC.
be as given by the strengthened FUNC.
January 26, 2016 at 1:54 am |
A couple of simple observations regarding the topological approach, which seems to have some promise. As sketched above, we take an intersection closed collection of sets and look at the poset complex. We further assume that all pairs of points are separated, so points correspond to minimal non-empty sets in our collection.
1. In the collection {1}, {1, 2}, {1, 3}, the element that is not rare is {1}. But this is also an element that is not peripheral, in the sense that the complement splits. In general non-peripheral may mean complement not contractible, or have “large” topology.
2. The space cannot be, for example, a circle due to the intersection closed hypothesis.
3. The main point here is to show an existence result – in this case for rare elements, it is useful to be able to identity good candidates. The topology of the complement being simple seems promising.
January 26, 2016 at 6:46 pm
I’ve been wondering how to tell which vertices of the poset complex correspond to the original points (minimal non-empty sets).
Since the order complex of a poset is isomorphic to the order complex of the opposite poset, the order complex alone seems insufficient to tell us which vertices correspond to the points. (For example, take a power set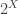 and its opposite.)
and its opposite.)
So in order to formulate (some version of) FUNC in terms of the order complex, we need to equip this order complex with some additional structure, right?
January 26, 2016 at 11:46 am |
One thing we can try to do is to consider weaker forms of the conjecture. Frankl’s conjecture asserts that every union closed family has a nonnegative correlation with some “dictatorship”. We can gradually replace “some dictatorship” by a larger class of objects. Lets call a family of sets antipodal if for every set S precisely one set among S and its complement is in the family. So we can ask:
1) Does every union-closed family has a nonnegative correlation with some antipodal weighted-majority family?
2) Does every union-closed family has a nonnegative correlation with some antipodal monotone function?
(We can also consider more general antipodal functions on the discrete.)
antipodal weighted majority function is a family where every element has a weight and a set is in the family if the sum of weights is larger than half the total weight, and is not in the family if the sum of weights is less than half).
January 26, 2016 at 1:01 pm
Is there a simple counterexample if we just take the “naive” family that consists of all sets of size at least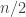 (with
(with  odd, say)?
odd, say)?
Yes there is. The usual examples works, since 2/3 of the sets will not be greater than
examples works, since 2/3 of the sets will not be greater than 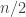 in size even if we take
in size even if we take  . And actually we could take
. And actually we could take  to be bigger than
to be bigger than  . So the weights clearly have to depend on
. So the weights clearly have to depend on  , which is of course a good thing.
, which is of course a good thing.
January 27, 2016 at 1:13 pm
If we just want to find a (non decreasing) monoton antipodal family with non negative correlation with our family union closed family F, maybe we can take the family G of all sets S such that: S contains more sets in F than its complement. Assuming there are no “ties” will G have nonnegative correlation with F?
January 26, 2016 at 5:55 pm |
Let just also record a general ‘recipe’ for constructing some non-obvious union-closed families. Let and
and  be two distinct union-closed families, each with maximal `universe’ set
be two distinct union-closed families, each with maximal `universe’ set  and
and  , respectively, and
, respectively, and  .
.
The following is also a union-closed family: every set in , every set of the shape
, every set of the shape  for
for 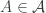 , every set of the shape
, every set of the shape 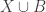 for
for 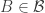 , every set of the shape
, every set of the shape 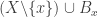 , for some choice of
, for some choice of  for each
for each 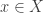 , and every set of the shape
, and every set of the shape 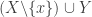 .
.
This can obviously be adjusted in a few ways. Why is it interesting? For example, applying it and
and 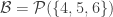 (both of which are fairly dull union-closed families) yields the more interesting union-closed family mentioned in http://mathoverflow.net/questions/138567/renaud-sarvate-limitation-on-frankls-conjecture/138570.
(both of which are fairly dull union-closed families) yields the more interesting union-closed family mentioned in http://mathoverflow.net/questions/138567/renaud-sarvate-limitation-on-frankls-conjecture/138570.
That is, it gives the example of Bruhn, Charbit, Schaudt, Arne Telle of a union closed family with a set of three elements, none of whose elements are abundant.
I haven’t gone much further, but perhaps something interesting can be said more generally about features of the type of union closed family this procedure generates, given that applying it to two trivial families already gives something interesting? Maybe an iterated application of this procedure is an easy way to generate some candidates for counterexamples.
Indeed, the simpler family of , every set of the shape
, every set of the shape  for
for 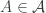 , every set of the shape
, every set of the shape 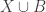 for
for 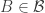 is still union-closed but simpler to analyse, and perhaps is still interesting to study.
is still union-closed but simpler to analyse, and perhaps is still interesting to study.
January 26, 2016 at 7:21 pm
To record what the (first, more elaborate) construction does to the abundancy of elements. Let denote the number of sets in
denote the number of sets in  ,
,  the number in
the number in  , and
, and 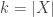 . Similarly, let
. Similarly, let 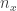 denote the abundancy of
denote the abundancy of  , for example.
, for example.
I’ll ignore constant factors here, since I’m thinking of . Then there are
. Then there are  sets in this new family, provided
sets in this new family, provided 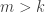 .
.
The abundancy of any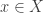 is roughly
is roughly  . The abundancy of any
. The abundancy of any 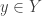 is roughly
is roughly 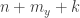 .
.
In particular, if is a union-closed family with the maximum abundancy
is a union-closed family with the maximum abundancy  , then if we do this construction with any
, then if we do this construction with any  with
with  , we ensure that no element of
, we ensure that no element of  is abundant (i.e. can’t satisfy the FUNC property).
is abundant (i.e. can’t satisfy the FUNC property).
In particular, this looks like a good way to rule out a lot of speculation along the lines of `if a union-closed family has some particular substructure, then that particular substructure must contain abundant elements’ – just choose some union-closed family with the desired structure, and apply this construction, which stops anything in
with the desired structure, and apply this construction, which stops anything in  being abundant.
being abundant.
This is precisely what the special case I mentioned above is doing, where `particular substructure’ means ‘a set with three elements’.
Of course, the loss of abundancy from is more than made up for here by the boost that everybody in
is more than made up for here by the boost that everybody in  gets. Maybe there’s a more careful construction which doesn’t boost the abundancy in
gets. Maybe there’s a more careful construction which doesn’t boost the abundancy in  too much, while still dampening
too much, while still dampening  .
.
January 27, 2016 at 9:27 am |
Consider the following:
There exists a such that for any union-closed family of
such that for any union-closed family of  sets there exists a pair of elements
sets there exists a pair of elements  and
and  such that the number of sets containing both
such that the number of sets containing both  and
and  is at least
is at least  .
.
Is there an obvious counterexample, or is this obviously equivalent to ‘weak FUNC’, which is that this holds considering just the sets including a single element?
January 27, 2016 at 9:34 am
Ah yes, this is obviously equivalent to weak FUNC – just take the union-closed subfamily of sets including an abundant element, and apply weak FUNC again.
January 27, 2016 at 10:25 am
Many thanks for all these interesting comments. A quick remark is that to get your LaTeX to compile, you need to write “latex” immediately after the first dollar sign. So for example to obtain you should write @latex \delta m@, except that those @ signs should be dollars.
you should write @latex \delta m@, except that those @ signs should be dollars.
January 27, 2016 at 2:25 pm |
Still thinking in terms of probability theory, let me try to introduce a slightly different point of view on the problem.
Let’s take the ground set to be![[n]=\{1,\ldots,n\}](https://s0.wp.com/latex.php?latex=%5Bn%5D%3D%5C%7B1%2C%5Cldots%2Cn%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) and encode a union-closed set family in terms of the associated normalized counting measure on the power set
and encode a union-closed set family in terms of the associated normalized counting measure on the power set ![2^{[n]}](https://s0.wp.com/latex.php?latex=2%5E%7B%5Bn%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Then any subset of
. Then any subset of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) corresponds to a vector in
corresponds to a vector in  . Via the measure, we are now working with a probability distribution over such vectors.
. Via the measure, we are now working with a probability distribution over such vectors.
Speaking in terms of components, this means that we are dealing with many
many  -valued random variables. Let me denote them
-valued random variables. Let me denote them  . The conclusion claimed by FUNC is that there exists an index
. The conclusion claimed by FUNC is that there exists an index  such that
such that ![P[Y_k =1] \geq 1/2](https://s0.wp.com/latex.php?latex=P%5BY_k+%3D1%5D+%5Cgeq+1%2F2&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Unfortunately, I don’t have a nice formulation of some version or generalization of the union-closure assumption. In case that such a formulation will be found, we can apply powerful tools from probability theory, such as the Lovász local lemma, in order to try and prove that![P[Y_k =1 ] < 1/2](https://s0.wp.com/latex.php?latex=P%5BY_k+%3D1+%5D+%3C+1%2F2&bg=ffffff&fg=333333&s=0&c=20201002) for all
for all  is incompatible with union-closure.
is incompatible with union-closure.
January 27, 2016 at 2:55 pm
I see now that a similar perspective was already contained in the original post, “look at the events for each
for each 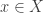 . In general, these events are correlated.”
. In general, these events are correlated.”
Is there anything interesting to be said about the sign of the correlation?
January 27, 2016 at 3:38 pm |
A quick comment to say that I have a general policy of starting new Polymath posts if existing ones reach 100 comments. I’ve started writing FUNC1 and made some headway with it, but probably won’t be able to finish it for 24 hours or so.
January 28, 2016 at 2:42 am |
I have a conjecture that would imply Frankl’s conjecture and it has the benefit of not involving union-closed families. It is quite strong and therefore likely to be false, but I present it here because I was unable to find a counter-example, even after some computer search for small examples. Incidentally, I asked this of Jeff Kahn and he also thought it was false but couldn’t give a counter example.
It was shown by Reimer that if you have a union-closed family and you perform the up-shifting operation to it for every element (For each
and you perform the up-shifting operation to it for every element (For each  such that
such that 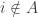 and
and 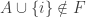 , add
, add 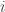 to
to 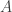 ), then you end up with an associated upward-closed set
), then you end up with an associated upward-closed set  and bijection
and bijection  with a curious property:
with a curious property:
For all ,
, ![[A, \phi(A)] \cap [B, \phi(B)] = \emptyset](https://s0.wp.com/latex.php?latex=%5BA%2C+%5Cphi%28A%29%5D+%5Ccap+%5BB%2C+%5Cphi%28B%29%5D+%3D+%5Cemptyset+&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where ![[X , Z] = \{ Y : X \subseteq Y \subseteq Z \}](https://s0.wp.com/latex.php?latex=%5BX+%2C+Z%5D+%3D+%5C%7B+Y+%3A+X+%5Csubseteq+Y+%5Csubseteq+Z+%5C%7D+&bg=ffffff&fg=333333&s=0&c=20201002) is an interval with respect to inclusion.
is an interval with respect to inclusion.
Frankl’s conjecture easily holds for all ground elements of an upward-closed family, and this curious property somehow implies that the sets of cannot be too much smaller than those of
cannot be too much smaller than those of  , or else there would be overlap in the intervals. So it is natural to ask whether this property alone is enough to ensure that Frankl’s condition holds for
, or else there would be overlap in the intervals. So it is natural to ask whether this property alone is enough to ensure that Frankl’s condition holds for  .
.
More formally, given any family , an upward-closed family
, an upward-closed family 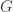 , and a bijection
, and a bijection  that satisfies the above property, does there exist an element appearing in at least half the sets of
that satisfies the above property, does there exist an element appearing in at least half the sets of 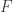 ?
?
I tried to look for small counter examples to a weaker form of this conjecture, by looping over all families $ latex F $ with few elements, applying the up-shifting operation, and seeing if the property held. Anyway, assuming I didn’t make any programming mistakes, I found no counter examples for families on at most 5 ground elements (as well as families of up to 11 sets on 6 elements).
January 28, 2016 at 10:49 am
This is an excellent question! Exploring Reimer’s not so difficult but very surprising arguments themselves is probably also a good idea. I also wonder if Reimer’s upset has non negative correlation with the original family.
January 28, 2016 at 11:30 am
Agreed. This question will definitely feature in my next post, in which I will list a number of statements that imply FUNC.
January 28, 2016 at 5:45 pm
I am wondering whether you implicitly intended your conjecture to also require of the bijection that A is included in
that A is included in 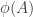 , since otherwise some of those inclusion intervals will be empty (and your test of the weaker form only covered this variant).
, since otherwise some of those inclusion intervals will be empty (and your test of the weaker form only covered this variant).
January 28, 2016 at 9:18 pm
Is this not a counterexample to your conjecture: and
and  , with
, with  ,
,  and
and  ?
?
January 28, 2016 at 9:23 pm
Alec, your is not upwards closed because it contains
is not upwards closed because it contains 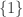 but doesn’t contain
but doesn’t contain 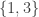 .
.
January 28, 2016 at 9:25 pm
Also, if you replace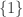 by
by 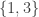 in
in  , then you get that
, then you get that  .
.
January 28, 2016 at 9:25 pm
Thanks. I misunderstood what ‘upward-closed’ meant. (Thought it just had to be superset-closed.)
January 28, 2016 at 9:27 pm
Now you’re confusing me. Doesn’t superset-closed mean that if a set is in then so are all its supersets? That’s exactly the property your set system lacked. We must be talking past each other somehow.
January 28, 2016 at 9:29 pm
Yes, I’m talking nonsense. I’m not sure what I was thinking there!
January 28, 2016 at 9:35 pm
Yes, I am also assuming that . Sorry for not saying it earlier. Also note that there are valid
. Sorry for not saying it earlier. Also note that there are valid  but such that
but such that  is not the result of up-shifting applied to
is not the result of up-shifting applied to  .
.
January 29, 2016 at 8:29 am
I’ve tested this on a few million random examples with the size of the ground set and the size
of the ground set and the size  of
of  and
and  satisfying
satisfying  and
and  , where
, where  has no abundant elements and
has no abundant elements and  is the result of up-shifting applied to
is the result of up-shifting applied to  ; and found none that satisfy the condition. Seems promising. It would be interesting to investigate examples where
; and found none that satisfy the condition. Seems promising. It would be interesting to investigate examples where  is not the result of up-shifting applied to
is not the result of up-shifting applied to  , but I don’t see an easy way to find those.
, but I don’t see an easy way to find those.
January 29, 2016 at 8:59 am
Here’s a naive suggestion that may well be complete nonsense as I haven’t thought about it properly. One could generate randomly by picking a few random sets (according to a distribution that looks sensible) and taking the upward closure. Then one could iteratively choose sets in G and try to remove elements from them, keeping going until it is no longer possible to remove any elements without violating the conditions that F and G must satisfy. (To be clear, when one removes an element from a set, the resulting set is the new set that corresponds to the one you removed an element from, which in turn corresponds, after some chain of removals, to a set in G.) In general I see no reason why the set F you get at the end should have an up-compression to G.
randomly by picking a few random sets (according to a distribution that looks sensible) and taking the upward closure. Then one could iteratively choose sets in G and try to remove elements from them, keeping going until it is no longer possible to remove any elements without violating the conditions that F and G must satisfy. (To be clear, when one removes an element from a set, the resulting set is the new set that corresponds to the one you removed an element from, which in turn corresponds, after some chain of removals, to a set in G.) In general I see no reason why the set F you get at the end should have an up-compression to G.
January 29, 2016 at 9:06 am
Regarding correlation between , could you define what you mean? If I take it to mean the correlation between the corresponding boolean functions and let
, could you define what you mean? If I take it to mean the correlation between the corresponding boolean functions and let  , then when
, then when  is small relative to
is small relative to 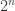 , we trivially have nonnegative correlation (just because most sets are in neither
, we trivially have nonnegative correlation (just because most sets are in neither  nor
nor  :
:
Since the largest set cannot rise, we always have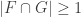 , and from this it follows that the correlation will be nonnegative for
, and from this it follows that the correlation will be nonnegative for  . Moreover, this is the regime we really care about for weak FUNC since for
. Moreover, this is the regime we really care about for weak FUNC since for 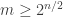 we have by Reimer’s result that the average set size is at least
we have by Reimer’s result that the average set size is at least 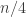 and hence some element appears in at least
and hence some element appears in at least 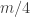 sets.
sets.
January 29, 2016 at 9:36 am
Tim: That sounds reasonable. I’ll try it out when I next have some time…
January 29, 2016 at 4:30 pm
Dear Igor, I mean .
.
January 29, 2016 at 4:32 pm
Or better written
January 29, 2016 at 5:44 pm
Dear Gil, Ok it is as I thought, so my previous comment applies. The problem is that if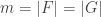 is too small, then it is enough for
is too small, then it is enough for 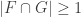 in order to get nonnegative correlation. It seems this kind of question is interesting only when
in order to get nonnegative correlation. It seems this kind of question is interesting only when  is on the order of
is on the order of 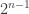 , as is the case with the dictator functions.
, as is the case with the dictator functions.
January 29, 2016 at 8:30 pm
Right, my initial ultra-weak version of Frankl is that every union-closed family has nonnegative correlation with maximal intersecting family. (I am not entirely sure how and if you can weaken it further in an interesting way giving up the “maximal” condition.”
January 29, 2016 at 2:41 pm |
[…] of sets of weight 1 is union closed and we obtain the original conjecture. It was suggested in this comment that one might perhaps be able to attack this strengthening using tropical geometry, since the […]
February 7, 2016 at 3:45 am |
[…] family there is an element that belongs to at lease half the sets in the family. Here are links to Post number 0 and Post number 1. (Meanwhile polymath10 continues to run on “Combinatorics and […]
August 7, 2017 at 9:02 am |
I have managed to show that if $\mathcal{F}$ is a union-closed family of subsets of $[n]$, containing at least a $(\frac{1}{2}-c)$ fraction of $2^{[n]}$, where $c$ is some small absolute constant, then there is an element that appears in at least half the members of $\mathcal{F}$. The proof uses Boolean-Analysis.
https://arxiv.org/abs/1708.01434
December 26, 2017 at 8:17 am |
[…] 11 was devoted to this question (Wiki, first post, last post). We mentioned the conjecture in the first blog post over here and several other times, […]
November 18, 2018 at 6:11 am |
Dear all, I am very much interested in this problem and I believe that this paper holds a valid proof. For now, I urge the community to take a look at this paper and if you find anything wrong with the proof, please say so. I believe that you will find it very interesting. Thank you!
November 18, 2018 at 6:12 am |
This is the link to the document. The key to solving the Frankl union-closed problem is based on extending the definition to multi-sets.
Click to access 1805.09695.pdf
November 18, 2018 at 9:44 am
This paper is hard to read because it uses language not like in the literature (Irreducible elements in a union-closed family has been defined in many papers already). Seems like the author needs to be more careful when reading other papers. For instance, “According to Poonen [1], the union-closed conjecture is false for some Ω(union-closed) satisfying |U(Ω)| = ∞. Therefore, the conjecture is investigated only for Ω satisfying |U(Ω)| < ∞." is exactly the opposite of what Poonen proves! He shows that the case |U(Ω)| = ∞ can be reduced to the case |U(Ω)| < ∞.
May 6, 2020 at 9:23 am |
Probably not of much use, but if I am not wrong, I believe that if in a family with $n$ sets, $n$ odd, with $m$ generators, there exists an element belonging to more than $m – \lfloor\log_2{\frac{n+1}{2}}\rfloor$ of its generators, then the family satisfies the Frankl conjecture.
See [this question on math.stackexchange](https://math.stackexchange.com/q/3646721/573047).
However, experimentally, 95% of families with universe of at most 3 elements have that property, but this drops already to 69% for families with universe of at most 5 elements.
June 1, 2021 at 8:05 am |
Significant contribution to Frankl conjecture – last contribution. Please consider this paper. Stay blessed everyone.
https://arxiv.org/abs/2105.14912
June 1, 2021 at 8:17 am |
Click to access 2105.14912.pdf
June 4, 2021 at 7:02 am |
I received comments from two combinatorists and the key revision to the article is definition (2.2) where $\in$ is replaced with $\subseteq$. The arxiv articles will be revised accordingly.
February 12, 2022 at 2:15 pm |
I wonder if rewriting the problem like in this post:
https://mathoverflow.net/questions/414690/proving-that-some-intersection-of-5-or-more-unions-is-non-empty-for-a-union/415344#415344
might lead somewhere.
September 25, 2022 at 6:37 pm
Is the following conjecture: “there does not exist a union closed family on n sets with all elements with frequency (n-1)/2” easier than the Frankl’s union closed sets conjecture?
See this question: https://mathoverflow.net/questions/430993/how-to-prove-that-there-does-not-exist-a-union-closed-family-of-n-sets-with-al?noredirect=1#comment1109221_430993
January 3, 2023 at 3:11 pm |
[…] He was encouraged by ideas that a group of mathematicians had explored years earlier in an open collaboration on the blog of a prominent mathematician named Tim Gowers. He also worked with a textbook by his […]
January 3, 2023 at 5:34 pm |
[…] He was encouraged by ideas that a group of mathematicians had explored years earlier in an open collaboration on the blog of a prominent mathematician named Tim Gowers. He also worked with a textbook by his […]
January 3, 2023 at 7:46 pm |
[…] He was encouraged by ideas that a group of mathematicians had explored years earlier in an open collaboration on the blog of a prominent mathematician named Tim Gowers. He also worked with a textbook by his […]
May 2, 2024 at 11:28 am |
“https://github.com/blitzDing/Frankle.git” there i provide a proof as a PDF. It’s only a little bit more than one Side. Thanx if u actually read it.
Ps: johnbernard@hotmail.de