The next Polymath project on this blog: some polls

For reasons that I have already gone into, I do not think that the origin-of-life project is suitable as the next Polymath project on this blog, though there seems to be enough enthusiasm for it that I am quite serious about giving it a try at some point in the not too distant future. The complexity-related project also no longer seems such a great idea for now. That leaves three candidates from amongst the problems that I have posted about recently: the project related to the polynomial-DHJ problem, the project related to the Littlewood problem, and the project to solve Erdős’s discrepancy problem. My impression is that for each of these three projects there is already a small group of highly interested people, and certainly my level of enthusiasm for each of these three problems is enough for me to be ready to devote plenty of time to it. (A theory I want to test is that if I post regularly and am not completely stuck, then that will be enough to keep the project feeling active and attracting contributions from other people as well, even if a proof does not appear to be round the corner.)

To help me decide which of the above three problems to go for, here are four polls.

Wiles meets his match

A brief return to the theme of mathematics in literature: I can’t resist sharing what is, by a long way, the silliest piece of fictional mathematics I have ever come across. It comes in “The Girl Who Played With Fire,” by the late Stieg Larsson, translated (not very well) by someone called Reg Keeling. Here is a little piece of advice for any author who wants to incorporate mathematics into a novel. If you don’t want what you write to be risibly unrealistic, it is not enough to read popular science books: you must also run what you write past a mathematician.

And here is the passage in question.

Erdős’s discrepancy problem

I’ve been pretty busy over the last month or so — hence my blog silence — and continue to be busy. But here is one more discussion of a problem that was on my earlier list of possible future Polymath projects. The problem in question is sometimes known as Erdős’s discrepancy problem. This will be a shortish post, because I don’t have much of a programme for solving the problem: if it were adopted, then we would be starting almost from scratch, but that could be an interesting experiment.

Here is the question.

Problem. Is it possible to find a -valued sequence and a constant such that for every and every ?

With the help of a little terminology we can ask this question in a slightly different way. If is a collection of subsets of a set and , define the discrepancy of to be the maximum value of over all . In our case, is the collection of all arithmetic progressions of the special form , and the question is whether there is any function that has bounded discrepancy for this . I say “bounded” rather than “finite” because one can define the function to be the discrepancy of with respect to all those sets in that are subsets of . Then the question is equivalent to asking whether there is any function for which is a bounded function of .

Problems related to Littlewood’s conjecture

This is the third in a series of posts in which I discuss problems that could perhaps form Polymath projects. Again, I am elaborating on a brief discussion that appeared in an earlier post on possible future projects. [Not for the first time in my experience, WordPress’s dates have gone funny and this was posted not on the 17th as it says above but on the 20th.]

An obvious objection to the Littlewood conjecture as a Polymath project is that it is notoriously hard. On its own that might not necessarily be a convincing argument, since part of the point of Polymath is to attempt to succeed where individual mathematicians have failed. However, a second objection is that the best results in the direction of the Littlewood conjecture, due to Einsiedler, Katok and Lindenstrauss, use methods that are far from elementary (and far from understood by me). I envisage this project as an elementary one, at least to begin with, so does that make it completely unrealistic? I shall try to argue in this post that there is plenty that could potentially be done by elementary methods, even if attempting to prove the conjecture itself is probably too ambitious.

Another advantage of tackling the conjecture by elementary means is that if we find ourselves forced to reintroduce the non-elementary methods that have led to the very interesting results of Einsiedler, Katok and Lindenstrauss, we will have a deeper understanding of those methods than if we had just passively learnt about them. I myself prefer to rediscover things than to learn them: it isn’t always practical, but it’s easier if you half bear in mind that they are there and have a vague idea about them.

The first unknown case of polynomial DHJ

In this post I want to discuss a combinatorial problem that is very appealing in its own right, but also important as a potential first step towards solving a central open problem in Ramsey theory. It is the second in a series of three posts (I may add to this number later, but three is what I have written or semi-written so far) that give further details about possible Polymath projects. This one was number 2 in the post in which I first discussed these projects. In that post, I said nothing beyond the fact that the project had close connections with the density Hales-Jewett theorem. Unlike the origin-of-life suggestion, this project is a straightforward mathematical one.

Let me very briefly indicate what the central open problem in Ramsey theory is. The density Hales-Jewett theorem, which has been discussed at great length on this blog, is the assertion that every dense subset of contains a combinatorial line (provided that is large enough in terms of and the density). This implies Szemerédi’s theorem.

Now there is an amazing generalization of Szemerédi’s theorem, due to Bergelson and Leibman, known as the polynomial Szemerédi’s theorem. This is the following assertion. For any 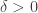and any choice of polynomials with integer coefficients and constant terms equal to zero, there exists 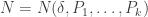such that every subset 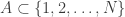of size at least 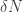contains a subset of the form with . To see that this generalizes Szemerédi’s theorem, just let (unless you feel that is more natural).

Another special case of this theorem is when and . Then one is trying to find a subset of the form 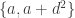, or in other words a pair of elements of that differ by a perfect square. This was proved independently by Sarkozy and Furstenberg, though my favourite proof is a more recent argument due to Ben Green that follows more closely the general structure of Roth’s proof of Roth’s theorem.

An obvious question now arises: is there a generalization of DHJ that implies both DHJ and the polynomial Szemerédi’s theorem? So far, the answer is no, and that is the central problem I was referring to earlier. However, we do at least know the colouring version: that is, there is a colouring statement that simultaneously generalizes the Hales-Jewett theorem and van der Waerden’s theorem. This is a result of Bergelson and McCutcheon — alternative proofs have been given by Mark Walters (who has the shortest and simplest argument) and Saharon Shelah (who has produced a primitive recursive bound).

A conversation about complexity lower bounds, X

This is the final post in the series about complexity lower bounds. It ends not with any grand conclusion, but just with the three characters running out of steam. The main focus of this final instalment is the Gaussian-elimination problem mentioned in earlier instalments (find an explicit nonsingular matrix over that needs a superlinear number of row operations to turn it into the identity). The discussion follows a familiar pattern, starting out with some ideas for solving the question, understanding why they are hopelessly over-optimistic, and ending with some speculations about why even this problem might be extremely hard.

Polymath and the origin of life

This is the first of a few posts I plan (one other of which is written and another of which is in draft form but in need of a few changes) in which I discuss various Polymath proposals in more detail than I did in my earlier post on possible projects.

One of my suggestions, albeit a rather tentative one, was to try to come up with a model that would show convincingly how life could emerge from non-life by purely naturalistic processes. But before this could become a sensible project it would be essential to have a more clearly defined mathematical question. By that I don’t mean a conjecture that Polymath would be trying to prove rigorously, but rather a list of properties that a model would have to have for it to count as successful. Such a list need not be fully precise, but in my view it should be reasonably precise, so that the task is reasonably well defined. It would of course be possible to change the desiderata as one went along.

In this post I’d like to make a preliminary list. It will undoubtedly be unsatisfactory in many ways, but I hope that there will be a subsequent discussion and that from it a better list will emerge. The purpose of this is not to start a Polymath project, but simply to attempt to define a Polymath proposal that might at some future date be an actual project. For two reasons I wouldn’t want this to be a serious project just yet: it seems a good idea to think quite hard about how it would actually work in practice, and someone who I hope will be a key participant is very busy for the next few months and less busy thereafter.

A conversation about complexity lower bounds, IX

This instalment has a brief discussion of another barrier to proving that PNP, known as algebrization. I don’t fully understand it, and therefore neither do my characters. (I’m hoping that maybe someone can help me with this.) But even a fuzzy understanding has some consequences, and the characters are led to formulate a simpler (and almost certainly already considered by the experts) problem that has the merit that when trying to solve it one is not tempted by proof techniques that would run up against the algebrization barrier. However, for all the usual reasons, this “simpler” problem looks very hard as well.

**************************************

🙂 I’m afraid I’m not yet ready to tell you what basic 3-bit operations do to quadratic phase functions.

8) In that case, can I instead mention something I read that looks relevant?

🙂 Sure, go ahead.

8) Well, you may remember my mentioning that Scott Aaronson and Avi Wigderson have a paper in which they introduce another barrier to lower bound proofs, which they call “algebrization”. If a proof can be algebrized, then it can’t prove that PNP.

A conversation about complexity lower bounds, VIII

In this next instalment, our characters discuss the norm you get by looking for the best possible correlation with a quadratic phase function. They end up discussing a heuristic argument that might, just conceivably, show that this norm is one of a wide class of norms that cannot possibly give rise to superlinear lower bounds. Along the way they have several thoughts, some of which are quite interesting, some not interesting at all, and some plain wrong. (The more interesting ones are mostly later on in the instalment.)

*******************************

🙂 Last time we met, I came to the understanding that if you build a norm by means of a formula of the form then there are two properties that might have that will give the norm an outside chance of being a useful quasirandomness norm for proving nontrivial lower bounds. The first is that the cardinality of should be superpolynomial in (or else there is a trivial polynomial-time algorithm for working out the norm). The second, which implies the first, but which I prefer to think of as a separate property, is there should not be some clever polynomial-time way of working out the norm—which, when has superexponential size would require one to exploit special properties of the particular set of functions.

As I see it, if you take to be the set of all quadratic phase functions, then you get a set that definitely has the first property and could well have the second. So I want to go back to thinking about this quadratic-correlation norm. Earlier I convinced myself that a random low-complexity function should not correlate with any quadratic phase function. But if for any fixed quadratic phase function I can get only an exponentially small probability of a huge correlation, and if there are superexponentially many quadratic phase functions, then perhaps we need to revisit this statement. Is it conceivable that every function of linear circuit complexity correlates quite heavily with a quadratic phase function?

Triple negatives and Conservapedia’s support for Hitler

In an entry entitled “Negatives” in his Modern English Usage, Henry Fowler gave an amusing collection of examples of blunders that had been made with them. (If you follow this link, you have to scroll down a page to find the article I’m talking about.) Unaware of this, though not surprised to see it, I have been making a little collection myself. Since this is supposed to be a maths blog, let me feebly justify posting it by saying that it is a reflection on the fact that (and at one point on the corollary that ).