Archive for the ‘Cambridge teaching’ Category

« Older Entries

A few analysis resources

March 12, 2014

This will be my final post associated with the Analysis I course, for which the last lecture was yesterday. It’s possible that I’ll write further relevant posts in the nearish future, but it’s also possible that I won’t. This one is a short one to draw attention to other material that can be found on the web that may help you to learn the course material. It will be an incomplete list: further suggestions would be welcome in the comments below.

A good way to test your basic knowledge of (some of) the course would be to do a short multiple-choice quiz devised by Vicky Neale. If you don’t get the right answer first time for every question, then it will give you an idea of the areas of the course that need attention.

Terence Tao has also created a number of multiple-choice quizzes, some of which are relevant to the course. They can be found on this page. The quiz on continuity expects you to know the definitions of adherent points and limit points, which I did not discuss in lectures.
(more…)

Posted in Cambridge teaching, IA Analysis | 4 Comments »

How do the power-series definitions of sin and cos relate to their geometrical interpretations?

March 2, 2014

I hope that most of you have either asked yourselves this question explicitly, or at least felt a vague sense of unease about how the definitions I gave in lectures, namely

\displaystyle \cos x = 1 - \frac{x^2}{2!}+\frac{x^4}{4!}-\dots

and

\displaystyle \sin x = x - \frac{x^3}{3!}+\frac{x^5}{5!}-\dots,

relate to things like the opposite, adjacent and hypotenuse. Using the power-series definitions, we proved several facts about trigonometric functions, such as the addition formulae, their derivatives, and the fact that they are periodic. But we didn’t quite get to the stage of proving that if x^2+y^2=1 and \theta is the angle that the line from (0,0) to (x,y) makes with the line from (0,0) to (1,0), then x=\cos\theta and y=\sin\theta. So how does one establish that? How does one even define the angle? In this post, I will give one possible answer to these questions.
(more…)

Posted in Cambridge teaching, IA Analysis | 36 Comments »

Differentiating power series

February 22, 2014

I’m writing this post as a way of preparing for a lecture. I want to discuss the result that a power series \sum_{n=0}^\infty a_nz^n is differentiable inside its circle of convergence, and the derivative is given by the obvious formula \sum_{n=1}^\infty na_nz^{n-1}. In other words, inside the circle of convergence we can think of a power series as like a polynomial of degree \infty for the purposes of differentiation.

A preliminary question about this is why it is not more or less obvious. After all, writing f(z)=\sum_{n=0}^\infty a_nz^n, we have the following facts.

  1. Writing S_N(z)=\sum_{n=0}^Na_nz^n, we have that S_N(z)\to f(z).
  2. For each N, S_N'(z)=\sum_{n=1}^Nna_nz^{n-1}.

If we knew that S_N'(z)\to f'(z), then we would be done.

Ah, you might be thinking, how do we know that the sequence (S_N'(z)) converges? But it turns out that that is not the problem: it is reasonably straightforward to show that it converges. (Roughly speaking, inside the circle of convergence the series \sum_na_nz^{n-1} converges at least as fast as a GP, and multiplying the nth term by n doesn’t stop a GP converging (as can easily be seen with the help of the ratio test). So, writing g(z) for \sum_{n=1}^\infty na_nz^{n-1}, we have the following facts at our disposal.

  1. S_N(z)\to f(z)
  2. S_N'(z)\to g(z)

Doesn’t it follow from that that f'(z)=g(z)?
(more…)

Posted in Cambridge teaching, IA Analysis | 13 Comments »

Taylor’s theorem with the Lagrange form of the remainder

February 11, 2014

There are countless situations in mathematics where it helps to expand a function as a power series. Therefore, Taylor’s theorem, which gives us circumstances under which this can be done, is an important result of the course. It is also the one result that I was dreading lecturing, at least with the Lagrange form of the remainder, because in the past I have always found that the proof is one that I have not been able to understand properly. I don’t mean by that that I couldn’t follow the arguments I read. What I mean is that I couldn’t reproduce the proof without committing a couple of things to memory, which I would then forget again once I had presented them. Briefly, an argument that appears in a lot of textbooks uses a result called the Cauchy mean value theorem, and applies it to a cleverly chosen function. Whereas I understand what the mean value theorem is for, I somehow don’t have the same feeling about the Cauchy mean value theorem: it just works in this situation and happens to give the answer one wants. And I don’t see an easy way of predicting in advance what function to plug in.

I have always found this situation annoying, because a part of me said that the result ought to be a straightforward generalization of the mean value theorem, in the following sense. The mean value theorem applied to the interval [x,x+h] tells us that there exists y\in (x,x+h) such that f'(y)=\frac{f(x+h)-f(x)}h, and therefore that f(x+h)=f(x)+hf'(y). Writing y=x+\theta h for some \theta\in(0,1) we obtain the statement f(x+h)=f(x)+hf'(x+\theta h). This is the case n=1 of Taylor’s theorem. So can’t we find some kind of “polynomial mean value theorem” that will do the same job for approximating f by polynomials of higher degree?

Now that I’ve been forced to lecture this result again (for the second time actually — the first was in Princeton about twelve years ago, when I just suffered and memorized the Cauchy mean value theorem approach), I have made a proper effort to explore this question, and have realized that the answer is yes. I’m sure there must be textbooks that do it this way, but the ones I’ve looked at all use the Cauchy mean value theorem. I don’t understand why, since it seems to me that the way of proving the result that I’m about to present makes the whole argument completely transparent. I’m actually looking forward to lecturing it (as I add this sentence to the post, the lecture is about half an hour in the future), since the demands on my memory are going to be close to zero.
(more…)

Posted in Cambridge teaching, IA Analysis | 38 Comments »

How to work out proofs in Analysis I

February 3, 2014

Now that we’ve had several results about sequences and series, it seems like a good time to step back a little and discuss how you should go about memorizing their proofs. And the very first thing to say about that is that you should attempt to do this while making as little use of your memory as you possibly can.

Suppose I were to ask you to memorize the sequence 5432187654321. Would you have to learn a string of 13 symbols? No, because after studying the sequence you would see that it is just counting down from 5 and then counting down from 8. What you want is for your memory of a proof to be like that too: you just keep doing the obvious thing except that from time to time the next step isn’t obvious, so you need to remember it. Even then, the better you can understand why the non-obvious step was in fact sensible, the easier it will be to memorize it, and as you get more experienced you may find that steps that previously seemed clever and nonobvious start to seem like the natural thing to do.

For some reason, Analysis I contains a number of proofs that experienced mathematicians find easy but many beginners find very hard. I want to try in this post to explain why the experienced mathematicians are right: in a rather precise sense many of these proofs really are easy, in the sense that if you just repeatedly do the obvious thing you will solve them. Others are mostly like that, with perhaps one smallish idea needed when the obvious steps run out. And even the hardest ones have easy parts to them.
(more…)

Posted in Cambridge teaching, IA Analysis | 17 Comments »

Introduction to Cambridge IA Analysis I 2014

January 11, 2014

This term I shall be giving Cambridge’s course Analysis I, a standard first course in analysis, covering convergence, infinite sums, continuity, differentiation and integration. This post is aimed at people attending that course. I plan to write a few posts as I go along, in which I will attempt to provide further explanations of the new concepts that will be covered, as well as giving advice about how to solve routine problems in the area. (This advice will be heavily influenced by my experience in attempting to teach a computer, about which I have reported elsewhere on this blog.)

I cannot promise to follow the amazing example of Vicky Neale, my predecessor on this course, who posted after every single lecture. However, her posts are still available online, so in some ways you are better off than the people who took Analysis I last year, since you will have her posts as well as mine. (I am making the assumption here that my posts will not contribute negatively to your understanding — I hope that proves to be correct.) Having said that, I probably won’t cover exactly the same material in each lecture as she did, so the correspondence between my lectures and her posts won’t be as good as the correspondence between her lectures and her posts. Nevertheless, I strongly recommend you look at her posts and see whether you find them helpful.

You will find this course much easier to understand if you are comfortable with basic logic. In particular, you should be clear about what “implies” means and should not be afraid of the quantifiers 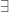\exists and \forall. You may find a series of posts I wrote a couple of years ago helpful, and in particular the ones where I wrote about logic (NB, as with Vicky Neale’s posts above, they appear in reverse order). I also have a few old posts that are directly relevant to the Analysis I course (since they are old posts you may have to click on “older entries” a couple of times to reach them), but they are detailed discussions of Tripos questions rather than accompaniments to lectures. You may find them useful in the summer, and you may even be curious to have a quick look at them straight away, but for now your job is to learn mathematics rather than trying to get good at one particular style of exam, so I would not recommend devoting much time to them yet.
(more…)

Posted in Cambridge teaching, IA Analysis | 24 Comments »

A little paradox

December 9, 2013

This post is intended as a footnote to one that I wrote a couple of years ago about the meaning of “implies” in mathematics, which was part of a series of posts designed as an introduction to certain aspects of university mathematics.

If you are reasonably comfortable with the kind of basic logic needed in an undergraduate course, then you may enjoy trying to find the flaw in the following argument, which must have a flaw, since I’m going to prove a general statement and then give a counterexample to it. If you find the exercise extremely easy, then you may prefer to hold back so that others who find it harder will have a chance to think about it. Or perhaps I should just say that if you don’t find it easy, then I think it would be a good exercise to think about it for a while before looking at other people’s suggested solutions.
(more…)

Posted in Basic logic, Cambridge teaching | 60 Comments »

A look at a few Tripos questions X

May 29, 2012

Since time is short, I am going to discuss a couple of Groups questions but in slightly less detail than I have been giving up to now: instead of working through the questions completely, I’ll try to zero in on the most important points. Because there wasn’t a separate Groups course until 2008, I am taking my questions from that year.

5E. For a normal subgroup H of a group G, explain carefully how to make the set of (left) cosets of H into a group.

For a subgroup H of a group G, show that the following are equivalent:

(i) H is a normal subgroup of G;

(ii) there exist a group K and a homomorphism \theta:G\rightarrow K such that H is the kernel of \theta.

Let G be a finite group that has a proper subgroup H of index n (in other words, |H|=|G|/n). Show that if |G|>n!, then G cannot be simple. [Hint: Let G act on the set of left cosets of H by left multiplication.]
(more…)

Posted in Cambridge teaching, IA Groups | 6 Comments »

A look at a few Tripos questions IX

May 26, 2012

Exam day approaches, so I’ve decided to prioritize. Instead of doing question 7C, which isn’t all that interesting (in the sense that it doesn’t give me much scope to emphasize principles of more general use in exams), I’m going to skip it, and instead, if I get time, go through a groups question or two. But first I will do the final Numbers and Sets question because it involves something a lot of people dislike: the inclusion-exclusion principle. It’s worth getting comfortable with this, because it comes up year after year (either in Numbers and Sets or in Probability). You may think that applying the principle requires some ingenuity. The aim of this post is to convince you that it can be done on autopilot.

8C. Let X be a finite set with n elements. How many functions are there from X to X? How many relations are there on X?

Show that the number of relations R on X such that, for each y\in X, there exists at least one x\in X with xRy, is (2^n-1)^n.

Using the inclusion-exclusion principle or otherwise, deduce that the number of such relations R for which, in addition, for each x\in X, there exists at least one y\in X with xRy, is

\displaystyle \sum_{k=0}^n(-1)^k\binom nk(2^{n-k}-1)^n.
(more…)

Posted in Cambridge teaching, IA Numbers and Sets | 3 Comments »

A look at a few Tripos questions VIII

May 24, 2012

Now for a question on modular arithmetic. As with countability, there is a very high chance of a question on this topic. [Added after the post was written: as usual I wrote down my thoughts about this question as I had them, and I didn’t spot the best approach to part (ii) of the question until after I had come up with some less good approaches. So my recommendations evolve through the post, with some of the later ones superseding some of the earlier ones.]

6C. (i) Prove Wilson’s theorem: if p is prime then (p-1)!\equiv -1 (mod p).

Deduce that if p\equiv 1 (mod 4) then

\displaystyle \Bigl(\bigl(\frac{p-1}2\bigr)!\Bigr)^2\equiv -1 (mod p).

(ii) Suppose that p is a prime of the form 4k+3. Show that if x^4\equiv 1 (mod p) then x^2\equiv 1 (mod p).

(iii) Deduce that if p is an odd prime, then the congruence

\displaystyle x^2\equiv -1 (mod p)

has exactly two solutions (modulo p) if p\equiv 1 (mod 4), and none otherwise.
(more…)

Posted in Cambridge teaching, IA Numbers and Sets | 4 Comments »

« Older Entries