The discussion in the last thread has noticeably moved on to new topics. In particular, multiplicative functions have been much less in the spotlight. Some progress has been made on the question of whether the Fourier transform of a sequence of bounded discrepancy must be very large somewhere, though the question is far from answered, and it is not even clear that the answer is yes. (One might suggest that the answer is trivially yes if EDP is true, but that is to misunderstand the question. An advantage of this question is that there could in theory be a positive answer not just for -valued functions but also for
-valued functions with
norm at least
, say.)
Another question that has been investigated, mostly by Sune, is the question about what happens if one takes another structure (consisting of “pseudointegers”) for which EDP makes sense. The motivation for this is either to find a more general statement that seems to be true or to find a more general statement that seems to be false. In the first case, one would see that certain features of were not crucial to the problem, which would decrease the size of the “proof space” in which one was searching (since now one would try to find proofs that did not use these incidental features of
). In the second case, one would see that certain features of
were crucial to the problem (since without them the answer would be negative), which would again decrease the size of the proof space. Perhaps the least satisfactory outcome of these investigations would be an example of a system that was very similar to
where it was possible to prove EDP. For example, perhaps one could find a system of real numbers
that was closed under multiplication and had a counting function very similar to that of
, but that was very far from closed under addition. That might mean that there were no troublesome additive examples, and one might even be able to prove a more general result (that applied, e.g., to
-valued functions). This would be interesting, but the proof, if it worked, would be succeeding by getting rid of the difficulties rather than dealing with them. However, even this would have some bearing on EDP itself, I think, as it would be a strong indication that it was indeed necessary to prove EDP by showing that counterexamples had to have certain properties (such as additive periodicity) and then pressing on from there to a contradiction.
A question I have become interested in is understanding the behaviour of the quadratic form with matrix . The derivation of this matrix (as something to be interested in in connection with EDP) starts with this comment and is completed in this comment. I wondered what the positive eigenvector would look like, and Ian Martin obliged with some very nice plots of it. Here is a link to where these plots start. It seems to be a function with a number-theoretic formula (that is, with a value at
that strongly depends on the prime factorization of
— as one would of course expect), but we have not yet managed to guess what that formula is.
I now want to try to understand this quadratic form in Fourier space. That is, for any pair of real numbers I want to calculate
, and I would then like to try to understand the shape of the kernel
. Now looking back at this comment, one can see that
Since the bilinear form is determined by the quadratic form
I’ll concentrate on the latter (which in any case is what interests me). So substituting
into the above formula gives me
The infinite sum is a geometric progression, so this simplifies to
Note that for each the integrand is bounded unless
is a multiple of
, and more generally is small unless
is close to a multiple of
and
is close to 0. So we do at least have the condition of being close to a rational with small denominator making an appearance here. (Why small denominator? Because then there will be more
such that
is a multiple of
.)
I plan to investigate the sequence 1, -1, 0, 1, -1, 0, … from this perspective. It takes the value at
. I shall attempt to understand from the Fourier side why this gives a sequence with such small discrepancy.
Before I finish this post, let me also mention a nice question of Alec’s, or perhaps it is better to call it a class of questions. It’s a little bit like the “entropy” question that I asked about EDP, but it’s about multiplicative functions. The question is this: you play a game with an adversary in which you take turns assigning values to primes. You want the resulting completely multiplicative function to have as small discrepancy as you can, whereas your adversary wants the discrepancy (that is, growth of partial sums) to be large. How well can you do? One can ask many variants, such as what happens if your adversary is forced to choose certain primes (for instance, every other prime), or if your adversary’s choices are revealed to you in advance (so now the question is what you can do if you are trying to make a low-discrepancy function but someone else has filled in half the values already and done so as badly as possible), or if you choose your values randomly, etc. etc. So far there don’t seem to be any concrete results, and yet it feels as though it ought to be possible to prove at least something non-trivial here.
One other question I’d like to highlight before I finish this post. It seems that we do not know whether EDP is true even if you insist that the HAPs have common differences that are either primes or powers of 2. The powers of 2 rule out all periodic sequences, but for a strange parity reason: for instance, if you have a sequence that’s periodic with period 72, then along the HAP with common difference 8 it is periodic with period 9, which means that the sum along each block of 9 is non-zero (because it is an odd number) and therefore the sums along that HAP grow linearly. Sune points out that the sequence is a simple counterexample over
, but it’s not clear what message we can take from that, given that periodic sequences don’t work in the
case. I like this question, because finding a counterexample should be easier if there is one, and if there isn’t, then proving the stronger theorem might be easier because HAPs with prime common differences are “independent” in a nice way.
Update: I intended, but forgot, to mention also some interesting ideas put forward by Gil in this comment. He has a proposal for trying to use probabilistic methods, and in particular methods that are suited to proving that rare events have non-zero probability when there is sufficient independence around, to show that there are many sequences with slow-growing discrepancy. It is not clear at this stage whether such an argument can be made to work, but it seems very likely that thinking about the problems that arise when one attempts to make it work will be fruitful.
February 24, 2010 at 2:34 pm |
I just realized that we have some very integer-like pseudointegers where the EDP is false, namely the set of integers not divisible by p for some prime p (the sequence is the Legendre character). I know that this is nothing new, we already knew that these examples told us something about what a proof of EDP could look like, but I didn’t think of them as pseudointeger (actually I did once but the two parts of my brain that knew that “the set of integers not divisible by p can have bounded discrepancy” and “the set of integers not divisible by p is a set of pseudointeger” where too far from each other).
I think these examples have discrepancy about at most (if I remember correctly) and the density of them is
(if I remember correctly) and the density of them is  . The next question is: Can we find pseudointegers with density 1 and bounded discrepancy? Or a weaker question: Can we find sets of pseudointeger with density arbitrary close to 1 and discrepancy <C for some fixed C?
. The next question is: Can we find pseudointegers with density 1 and bounded discrepancy? Or a weaker question: Can we find sets of pseudointeger with density arbitrary close to 1 and discrepancy <C for some fixed C?
February 24, 2010 at 4:51 pm
I think the following gives a set of pseudointegers with density 1 and a multiplicative sequence with discrepancy 2: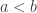 but b-a is infinitesimal (so they are not a subset of R. More about this later. I think of
but b-a is infinitesimal (so they are not a subset of R. More about this later. I think of  as a real number). We define
as a real number). We define 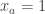 and
and  and let multiplicativity define the rest. So for any
and let multiplicativity define the rest. So for any 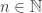 not divisible by 3 the numbers na and nb are close and
not divisible by 3 the numbers na and nb are close and  and
and 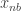 have opposite signs, so these doesn’t increase the discrepancy to more than 2. The only problem is at powers of a: Around
have opposite signs, so these doesn’t increase the discrepancy to more than 2. The only problem is at powers of a: Around 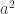 we have the numbers
we have the numbers  with
with  so we “create” a new prime
so we “create” a new prime 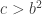 such that
such that 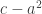 is infinitesimal, but infinitely larger than
is infinitesimal, but infinitely larger than 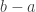 . Now everything is fine for
. Now everything is fine for  . Here
. Here 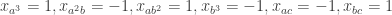 , but at
, but at  we get intro trouble again, so we need to add a new prime
we get intro trouble again, so we need to add a new prime 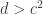 . Continuing this way, we get a set of pseudointegers with bounded discrepancy.
. Continuing this way, we get a set of pseudointegers with bounded discrepancy.
Start with the set of integers not divisible by 3. This have discrepancy 1 (I’m using the 1,-1,0,1,-1,0,… sequence) and density 2/3, so we need to increase the density. In order to do so, we add two primes a and b such that
Lets calculate the density. To begin with we have the set of integers not divisible by 3. This has density 2/3. The set of numbers an or bn, where n is a integer not divisible by 3, has density . The set of numbers on the form aan,abn,bbn or cn has density
. The set of numbers on the form aan,abn,bbn or cn has density  , and so on. Now the whole set has density
, and so on. Now the whole set has density
Where the nominator is A000123 (number of partitions of 2n into powers of 2). Since the sequence of nominators grows slower than some geometric sequence (e.g. using that it is less than the number of ordered partitions of 2n), we can choose a so that the density is 1.
using that it is less than the number of ordered partitions of 2n), we can choose a so that the density is 1.
This is of course not a subset of the real numbers as I used infinitesimal, but if we just choose very small numbers instead, think we can correct the errors when they arise. I think this shows that a proof of EDP must somehow use the additive structure of the integers.
February 24, 2010 at 5:01 pm
@Tim:
“Perhaps the least satisfactory outcome of these investigations would be an example of a system that was very similar to \mathbb{N} where it was possible to prove EDP.”
I’m not sure I understand you correctly. Do you mean that this wouldn’t be interesting or just that we should at least be able to get this result? I think that finding a set of pseudointegers where we can prove EDP is the only interesting pseudointeger-question left (when I say interesting I mean with relevances to EDP). Perhaps I have forgot some questions.
February 24, 2010 at 6:38 pm
It was a slightly peculiar thing for me to say, because I changed my mind as I was writing it. Initially I thought that finding such a proof wouldn’t shed any light on EDP itself, but by the end of the comment I had started to realize that it could do after all.
February 24, 2010 at 3:49 pm |
Going back to my graph-theoretic construction, I wanted to include a meaning for “completely multiplicative”.
This likely could be more elegant. I apologize for the mess.
Define everything as the comment, including the 4 extra conditions (it might be possible to do without some, but I haven’t had time to think about it). I will also call the set of edges from condition #1 the omega set, and the root node of that set to be the alpha node.
A node is called prime if the in-degree is 1; that is, the only edge incoming is from the omega set.
A node is a power if the in-degree is 2.
Consider all incoming edges to a particular node; trace the edges backwards to their root nodes. These are the divisors of the node.
Here is a prime factorization algorithm for the node n:
1. List the k divisors of n (excluding the alpha node) . Call the path of a divisor to be the traversal going from the divisor to n. Given any divisor a that has divisor b in its path, remove a from the list.
. Call the path of a divisor to be the traversal going from the divisor to n. Given any divisor a that has divisor b in its path, remove a from the list.
2. For any divisor that is not prime and is not a power on the list , connect the divisors of each of
, connect the divisors of each of  as a branching tree (again excluding the alpha node); again, given any divisor a that has divisor b in its path, remove a from the list.
as a branching tree (again excluding the alpha node); again, given any divisor a that has divisor b in its path, remove a from the list.
For any divisor that is a power on the list , connect the divisor that is not the alpha node c a multiple number of times m+1, where m is the number of times powers occur in the traversal between the divisor of c and c.
, connect the divisor that is not the alpha node c a multiple number of times m+1, where m is the number of times powers occur in the traversal between the divisor of c and c.
3. Repeat #2 until all divisors on the bottom of the tree are prime.
4. The set of divisors at the bottom of the tree is the prime factorization of n.
So, a graph is completely multiplicative if that multiplying the values of all the nodes in the prime factorization of a node n (including repeated nodes as ncessary) gives the value of the node n.
February 24, 2010 at 5:25 pm
There’s a bug in the algorithm: if n is already a power, it should jump to the “for any divisor that is a power on the list” process.
Also, an extra condition #5 should be added if we want multiplication to be a function: each node can be the root node of only one labelled set of directed edges.
February 24, 2010 at 4:47 pm |
Regarding Gill’s probabilistic approach https://gowers.wordpress.com/2010/02/19/edp8-what-next/#comment-6278
it might be a good idea to consider separate “bad” events for “sum is less than -C” and “sum is greater than C”
The “less than “-events along a given AP are clearly pairwise positively correlated, and likewise for the “greater than”-events. However the “less than”-events and “greater than”-events along an AP are negatively correlated.
To me mixing the two types of failure for the discrepancy bound seems to make things harder to keep track of. I guess I’m going more in the direction of the Janson inequalites than the local lemma here.
February 26, 2010 at 11:09 am
I think what I have in mind is to choose the locations of the zeros for the partial sum. We need to be able to show (1) that we can locate the zeroes of the partial sums where we want them, and then that (2) conditioned on such locations that the probabilities for “sum is greater than C” or “sum is smaller than -C” are very small.
For part (2) the probabilities may perhaps be small enough that we can use union bounds and not worry about dependenies.
For the location of zeroes part (1), we certainly need to be able to handle dependencies. And it seems that if we want to go below -discrepancy we will need to exploit positive dependencies (for the events of vanishing partial sums along intervals.) Indeed Janson’s inequalities may be quite relevant.
-discrepancy we will need to exploit positive dependencies (for the events of vanishing partial sums along intervals.) Indeed Janson’s inequalities may be quite relevant.
February 24, 2010 at 7:39 pm |
A couple of observations that will I hope make the calculations in the post make a bit more sense.
First, note that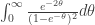 equals
equals  , which is infinite. Therefore,
, which is infinite. Therefore, 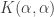 blows up when
blows up when  is equal to a rational number.
is equal to a rational number.
Next, note that the bilinear form derived from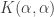 is given by the formula
is given by the formula
Now let’s continue to write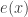 for
for 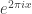 and let us also write
and let us also write 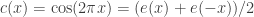 and
and  . Our basic example of a bounded-discrepancy sequence is (up to a constant multiple) the sequence
. Our basic example of a bounded-discrepancy sequence is (up to a constant multiple) the sequence  , which is begging to be understood from a Fourier perspective. Let us call this function
, which is begging to be understood from a Fourier perspective. Let us call this function  and let
and let 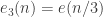 . Now
. Now 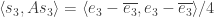 , which equals
, which equals
which, because of easy symmetry properties of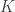 , is equal to
, is equal to
where (but I’d rather keep it as
(but I’d rather keep it as  , as the argument is perfectly general). Every time
, as the argument is perfectly general). Every time  is an integer, this gives us zero, and when
is an integer, this gives us zero, and when  is not an integer it gives us something fairly small. So in this way we (sort of) see the bounded average discrepancy coming about. I still need to think more about this calculation before I can say I fully understand it, or be confident that it isn’t rubbish in some way.
is not an integer it gives us something fairly small. So in this way we (sort of) see the bounded average discrepancy coming about. I still need to think more about this calculation before I can say I fully understand it, or be confident that it isn’t rubbish in some way.
February 24, 2010 at 9:27 pm |
If player one and player two alternate assigning signs to primes with one have the objective of forcing a discrepancy of four then the player trying to force a discrepancy of four will always win.
If player one and player two assign values to the primes of a multiplicative function and player one is trying to force a discrepancy of 4 and player 2 to prevent this player one will win.
Player one chooses to assign 2 the value 1 then player 2 must assign 3 the value -1 or the sum of 1 to 4 will be 4 after 3 is assigned the value 1.
Then player one assigns 5 the value 1 and since f(1),f(2),f(4),f(5) and f(8),f(9) and f(10) are positive the sum at 10 is at least 4 and we are done.
If player one and player two assign values to the primes of a multiplicative function and player two is trying to force a discrepancy of 4 and player 2 to prevent this player two will win.
First we will show that the first player must choose 2. If player one does not choose this then let the second player choose 2 and assign it the value 1 at player 2’s first move. Then the first two moves of player one must be assigning 3 and 5 the values -1. If not then player two will assign one of these the value one on player 2’s second move and either f(1),f(2),f(4),f(5) and f(8),f(9)
and f(10) are positive or f(1),f(2),f(3), and f(4) are positive and in either
case the discrepancy is 4.
So the first player must assign f(2) the value -1 on the first players first
move. Let the second player assign f(3) the value 1 on the second players first move. Now f(1),f(3),f(4),f(5),
f(9),f(12),f(15),f(16) are positive one of f(7) and f(14) is positive. So if the first player does not assign 11 and 13 the value -1 on the second and third moves then the second player can assign one of them value 1 and f(1),f(3),f(4),f(5),f(9),f(12),f(15),f(16), one of f(7) and f(14) and the number chosen make 10 positive values less than or equal to 16 which gives a discrepancy of four.So the second and third moves of the first player are choosing 11 and 13 and assigning them value -1. The second player assigns 7 the value 1 on the third move. Now f(1),f(3),f(4),f(5), f(9),f(12),f(15),f(16) f(7),f(20),f(21),f(22)f(25),f(26),f(27) and f(28) are positive and the discrepancy is at least 4 at 28 and we are done.
February 24, 2010 at 9:45 pm |
[…] Polymath5 By kristalcantwell There is a new thread for Polymath5. The pace seems to be slowing down a bit. Let me update this there is another thread. […]
February 25, 2010 at 11:55 am |
I want to follow up on this comment with some rather speculative ideas about why EDP might be true.
The annoying example we keep coming up against is 1, -1, 0, 1, -1, 0, …, which, as I have already pointed out, is given by the formula , where
, where  stands for
stands for 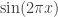 . Now perhaps something like the following is true. Given any
. Now perhaps something like the following is true. Given any  sequence (or indeed any sequence) we can decompose it as a linear combination of sequences of the form
sequence (or indeed any sequence) we can decompose it as a linear combination of sequences of the form  and
and  , where
, where  is rational. A simple proof is as follows. We can produce the characteristic function of the HAP with common difference d as the sum
is rational. A simple proof is as follows. We can produce the characteristic function of the HAP with common difference d as the sum 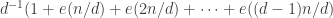 . And we can produce any function of the natural numbers as a linear combination of HAPs, just by solving an infinite system of linear equations that’s in triangular form. (Basically that is the proof of the Möbius inversion formula.)
. And we can produce any function of the natural numbers as a linear combination of HAPs, just by solving an infinite system of linear equations that’s in triangular form. (Basically that is the proof of the Möbius inversion formula.)
Let’s gloss over the fact that the decomposition is far from unique. It means that what I am about to say is not correct as it stands, but my hope is that it could be made correct somehow.
On the face of it, using cosines in a decomposition is likely to lead to large discrepancies, because not only are they periodic, but they are at their maximum at the end of each period, so the HAP with common difference that period (which is an integer if we are looking at for some rational
for some rational  ) is being given a linear discrepancy that we would hope could not be cancelled out. (This is where we would need a much more unique decomposition, since as things stand it can be cancelled out.) So perhaps one could prove that for a
) is being given a linear discrepancy that we would hope could not be cancelled out. (This is where we would need a much more unique decomposition, since as things stand it can be cancelled out.) So perhaps one could prove that for a  sequence to have any chance of having small discrepancy, it has to be built out of sines rather than cosines.
sequence to have any chance of having small discrepancy, it has to be built out of sines rather than cosines.
Now the problem with sines is that they keep being zero. So one could ask the following question: how large a sum of coefficients do you need if you want to build a sequence out of sines?
sequence out of sines?
I think the answer to this question may be that to get values of all the way up to
all the way up to  requires coefficients that sum to at least
requires coefficients that sum to at least  . My evidence for that is the weak evidence that the obvious way of getting a
. My evidence for that is the weak evidence that the obvious way of getting a  sequence does give this kind of logarithmic growth. Here is how it works.
sequence does give this kind of logarithmic growth. Here is how it works.
I know that gives me
gives me  values (after normalization) except at multiples of 3 where it gives me zero. To deal with multiples of 3, I first create the HAP with common difference 3 by taking
values (after normalization) except at multiples of 3 where it gives me zero. To deal with multiples of 3, I first create the HAP with common difference 3 by taking 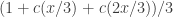 (which works because it’s the real part of
(which works because it’s the real part of  , which also works. That, however, is not allowed because I’ve used cosines. So I’ll multiply it by
, which also works. That, however, is not allowed because I’ve used cosines. So I’ll multiply it by  . The addition formulae for trigonometric functions tell us that
. The addition formulae for trigonometric functions tell us that 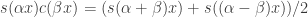 , so this results in a sum of sines with coefficients adding up to 1 (or
, so this results in a sum of sines with coefficients adding up to 1 (or  when we do the normalization). But this new sequence has gaps at multiples of 9. Continuing this process, we find that for each power of 3 we need coefficients totalling 1 (or
when we do the normalization). But this new sequence has gaps at multiples of 9. Continuing this process, we find that for each power of 3 we need coefficients totalling 1 (or  ) to fill the gaps at multiples of that power, which gives us a logarithmic bound.
) to fill the gaps at multiples of that power, which gives us a logarithmic bound.
So the following might be a programme for proving EDP, which has the nice feature of using the hypothesis in a big way.
hypothesis in a big way.
1. Show that any sequence that involves cosines in a significant way must have unbounded discrepancy. (One might add functions such as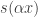 where
where  is irrational.)
is irrational.)
2. Show that any sequence involving sines must have a discrepancy at least as big as the sum of the coefficients of those sines.
3. Show that to make a sequence out of sines one must have coefficients that grow at least logarithmically.
sequence out of sines one must have coefficients that grow at least logarithmically.
As I say, before even starting to try to prove something like this, one would need to restrict the class of possible decompositions, so some preliminary thought is required before one can attempt anything like 1 or 2. Can anyone come up with a precise conjecture that isn’t obviously false? As for 3, it may be that one can already attempt to prove what I suggested above, that to get a sequence all the way up to
sequence all the way up to  requires coefficients with absolute values that sum to at least
requires coefficients with absolute values that sum to at least  .
.
February 25, 2010 at 7:03 pm
A small remark: If we only show (2) for finite sums of sines, it might still be possible to for an infinite sum of sines where the coefficients doesn’t converge to have bounded discrepancy. A sequence with bounded discrepancy can easily be written as a limit of sequences with unbounded discrepancy.
February 25, 2010 at 7:07 pm
I agree. For an approach like this to work there definitely needs to be some extra ingredient, which I do not yet see (and it is not clear that it even exists), that restricts the way you are allowed to decompose a sequence.
February 25, 2010 at 9:25 pm
This sounds interesting, but I have to ask: Do we have any reason to prefer to use sine functions rather than characteristic functions of APs?
February 25, 2010 at 9:52 pm
I’ve wondered about that, and will try to come up with a convincing justification for thinking about sines. However, that doesn’t mean that characteristic functions of APs shouldn’t be tried too. If we did, then perhaps the idea would be to show that using HAPs themselves is a disaster, and using other APs requires too many coefficients, or something like that.
On a not quite related note, does anyone know whether EDP becomes true if for each you are allowed to choose some shift of the HAP with common difference
you are allowed to choose some shift of the HAP with common difference  ? (We considered a related problem earlier, but here I do not insist that the shifts are consistent: e.g., you can shift the 2-HAP by 1 and the 4-HAP by 2.)
? (We considered a related problem earlier, but here I do not insist that the shifts are consistent: e.g., you can shift the 2-HAP by 1 and the 4-HAP by 2.)
February 26, 2010 at 10:54 am
I suppose the following concrete questions are relevant:
Conjecture 1 If a sequence of +1 -1 0 has bounded discrepency then, except for a set of density 0 it is periodic.
I do not know a counter example to:
Conjecture 2 If a multiplicative sequence of +1 -1 0 has bounded discrepency then it is periodic.
A periodic sequence with period r has bounded discrepency if the sum of elements with indices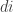 for every
for every  which devides
which devides  is 0. (In particular,
is 0. (In particular, 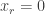 .) So it make sense to check the suggested conjecture 3 of fine tune it on such periodic sequences.
.) So it make sense to check the suggested conjecture 3 of fine tune it on such periodic sequences.
February 25, 2010 at 4:29 pm |
How about the periodic sequence whose period is 1 -1 1 1 -1 -1 1 -1 0
February 25, 2010 at 5:15 pm
I don’t understand your question.
February 25, 2010 at 6:02 pm
I was just curious about the sine decomposition (or sine/cosine decomposition) for the basic sequence and for “r-truncated
and for “r-truncated  ” where you make the sequence 0 if at integers divisible by
” where you make the sequence 0 if at integers divisible by  . (You mentiones the r=1 case and I wondered especially about r=2.)
. (You mentiones the r=1 case and I wondered especially about r=2.)
February 25, 2010 at 6:13 pm
I would decompose it by the method I mentioned above. That is, at the first stage I obtain the function 1 -1 0 1 -1 0 … as a multiple of s(n/3). I then obtain 0 0 1 0 0 1 0 0 1 … by taking (1+c(n/3)+c(2n/3))/3. I then convert that into 0 0 1 0 0 -1 0 0 0 … by pointwise multiplying it by s(n/9) (or rather ). By the addition formulae for sin and cos, that gives you the periodic sequence 1 -1 1 1 -1 -1 1 -1 0 recurring as a sum of sines, where the total sum of coefficients is
). By the addition formulae for sin and cos, that gives you the periodic sequence 1 -1 1 1 -1 -1 1 -1 0 recurring as a sum of sines, where the total sum of coefficients is  .
.
February 25, 2010 at 6:16 pm
so part 2) of the conjecture works ok for such trubcations?
February 25, 2010 at 7:57 pm |
I wanted to mention an approach to proving a lower bound similar to some of the ideas being discussed here. Consider the generalization of EDP to sequences of unit vectors. The problem is to find unit vectors so that
so that 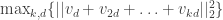 is bounded.
is bounded.
For sequences of length , this leads to the optimization problem: Find unit vectors
, this leads to the optimization problem: Find unit vectors  so as to minimize
so as to minimize 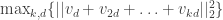 . This can be expressed as a semidefinite program (SDP) – a convex optimization problem that we know how to solve to any desired accuracy. Moreover, there is a dual optimization problem
. This can be expressed as a semidefinite program (SDP) – a convex optimization problem that we know how to solve to any desired accuracy. Moreover, there is a dual optimization problem
such that any feasible solution to the dual gives us a lower bound on the value of the (primal) SDP and the optimal solutions to both are equal.
The dual problem to this SDP is the following: Find values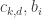
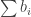 such that
such that 
 is positive semidefinite.
is positive semidefinite.
so as to maximize
and the quadratic form
The semidefinite program is usually referred to as a relaxation of the original optimization question over variables. Note that any feasible dual solution gives a valid lower bound for the original
variables. Note that any feasible dual solution gives a valid lower bound for the original  question. This is easy to see directly. Suppose that
question. This is easy to see directly. Suppose that  for all
for all 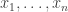 . In particular, it is non-negative for any
. In particular, it is non-negative for any  and for such values
and for such values  . Since
. Since  , there must be some
, there must be some 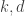 such that
such that 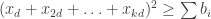 .
.
Now what is interesting is that for the vector discrepancy question for sequences of length , there is always a lower bound of this form that matches the optimal discrepancy. If the correct answer for vector discrepancy was a slowly growing function of
, there is always a lower bound of this form that matches the optimal discrepancy. If the correct answer for vector discrepancy was a slowly growing function of  , and if we could figure out good values for
, and if we could figure out good values for  and
and  to prove this, we would have a lower bound for EDP.
to prove this, we would have a lower bound for EDP.
Now the nice thing is that we can actually solve these semidefinite programs for small values of and examine their optimal solutions to see if there is any useful structure. Huy Nguyen and I have been looking at some of these solutions. Firstly here are the optimal values of the SDP for some values of
and examine their optimal solutions to see if there is any useful structure. Huy Nguyen and I have been looking at some of these solutions. Firstly here are the optimal values of the SDP for some values of  .
.
128: 0.53683
256: 0.55467
512: 0.56981
1024: 0.58365
1500: 0.59064
(I should mention that we excluded HAPs of length 1 from the objective function of the SDP, otherwise the optimal values would be trivially at least 1.) The discrepancy values are very small, but the good news is that they seem to be growing with , perhaps linearly with
, perhaps linearly with 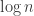 . The bad news is that it is unlikely we can solve much larger SDPs. (We haven’t been able to solve the SDP for 2048 yet.)
. The bad news is that it is unlikely we can solve much larger SDPs. (We haven’t been able to solve the SDP for 2048 yet.)
The main point of this was to say that there seems to be significant structure in the dual solutions of these SDPs which we should be able to exploit if we understand what’s going on. One pattern we discovered in the values is that the sums of tails of this sequence (for fixed d) seem to drop exponentially. More specifically, if
values is that the sums of tails of this sequence (for fixed d) seem to drop exponentially. More specifically, if 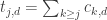 then
then 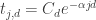 (approximately). It looks like the scaling factor
(approximately). It looks like the scaling factor  is dependent on
is dependent on  , but the factor
, but the factor  in the exponent is not. The
in the exponent is not. The  values in the dual solution also seem to have interesting structure. The values are not uniform and tend to be higher for numbers with many divisors (not surprising since they appear in many HAPs).
values in the dual solution also seem to have interesting structure. The values are not uniform and tend to be higher for numbers with many divisors (not surprising since they appear in many HAPs).
We should figure out the easiest way to share these SDP dual solutions with everyone so others can play with the values as well.
February 26, 2010 at 10:19 am
This looks like a very interesting idea to pursue. One aspect I do not yet understand is this. It is crucial to EDP that we look at functions that take values and not, say sequences that take values in
and not, say sequences that take values in ![[-1,1]](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) and are large on average. For example, the sequence 1, -1, 0, 1, -1, 0, … has bounded discrepancy. In your description of the dual problem and how it directly gives a lower bound, it seems to me that any lower bound would also be valid for this more general class of sequences. But perhaps I am wrong about this. If so, then where is the
and are large on average. For example, the sequence 1, -1, 0, 1, -1, 0, … has bounded discrepancy. In your description of the dual problem and how it directly gives a lower bound, it seems to me that any lower bound would also be valid for this more general class of sequences. But perhaps I am wrong about this. If so, then where is the  hypothesis being used?
hypothesis being used?
If it was in fact not being used, that does not stop what you wrote being interesting, since one could still try to find a positive semidefinite matrix and try to extract information from it. For example, it might be that the sequences that one could build out of eigenfunctions with small eigenvalues had properties that meant that it was not possible to build -valued sequences out of them. (This is the kind of thing I was trying to think about with the quadratic form mentioned in the post.)
-valued sequences out of them. (This is the kind of thing I was trying to think about with the quadratic form mentioned in the post.)
I have edited your comment and got rid of all the typos I can, but I can’t quite work out what you meant to write in the formula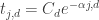 .
.
February 26, 2010 at 12:55 pm
Tim, the hypothesis is being used in placing the constraint
hypothesis is being used in placing the constraint  in the SDP. So a sequence with
in the SDP. So a sequence with  would be a valid solution but one with
would be a valid solution but one with 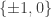 would not. The variables
would not. The variables  correspond to this constraint. In fact, it seems sufficient to use the constraint
correspond to this constraint. In fact, it seems sufficient to use the constraint  (the optimal values are almost the same). In this case, the dual variables
(the optimal values are almost the same). In this case, the dual variables  . In some sense, value of
. In some sense, value of  is a measure of how important the constraint
is a measure of how important the constraint  is.
is.
While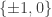 sequences are not valid solutions, distributions
sequences are not valid solutions, distributions
over such sequences which are large on average on every coordinate are valid
solutions to the SDP. So a lower bound on the vector question means that any distribution on sequences which is large on average on every coordinate must contain a sequence with high discrepancy.
The expression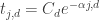 should not have a comma in the exponent, i.e. it should read:
should not have a comma in the exponent, i.e. it should read: 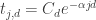 . Sorry for all the typos ! I wish I could visually inspect the comment before it posts (or edit it later).
. Sorry for all the typos ! I wish I could visually inspect the comment before it posts (or edit it later).
February 26, 2010 at 1:32 pm
Ah, I see now. This is indeed a very nice approach, and I hope that we will soon be able to get some experimental investigations going and generate some nice pictures.
February 26, 2010 at 1:56 pm
I mentioned that it looks like the optimal values of the SDP seem to be growing linearly with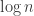 . If true, this would establish a lower bound of
. If true, this would establish a lower bound of  on the discrepancy of
on the discrepancy of  sequences. This is because for the vector problem, the objective function is actually the square of the discrepancy for integer sequences. The analog of integer discrepancy would be to look at
sequences. This is because for the vector problem, the objective function is actually the square of the discrepancy for integer sequences. The analog of integer discrepancy would be to look at  but in fact, the objective function of the SDP is the maximum of
but in fact, the objective function of the SDP is the maximum of 
In fact the growth rate for vector sequences could be different from the growth rate for integer sequences. I think we can construct sequences unit vectors of length such that the maximum value of
such that the maximum value of  is
is  . This can be done using the familiar 1,-1,0,1,-1,0,… sequence: Construct the vectors one coordinate at a time. Every vector in the sequence will have a 1 or -1 in exactly one coordinate and 0’s elsewhere. In the first coordinate we place the 1,-1,0,1,-1,0,… sequence. Look at the subsequence of vectors with 0 in the first coordinate. For these, we place the 1,-1,0,1,-1,0,… sequence in the second coordinate. Now look at the subsequence of vectors with 0’s in the first two coordinates. For these, we place the 1,-1,0,1,-1,0,… sequence in the third coordinate and so on. All unspecified coordinate values are 0. The first
. This can be done using the familiar 1,-1,0,1,-1,0,… sequence: Construct the vectors one coordinate at a time. Every vector in the sequence will have a 1 or -1 in exactly one coordinate and 0’s elsewhere. In the first coordinate we place the 1,-1,0,1,-1,0,… sequence. Look at the subsequence of vectors with 0 in the first coordinate. For these, we place the 1,-1,0,1,-1,0,… sequence in the second coordinate. Now look at the subsequence of vectors with 0’s in the first two coordinates. For these, we place the 1,-1,0,1,-1,0,… sequence in the third coordinate and so on. All unspecified coordinate values are 0. The first  vectors in this sequence have non-zero coordinates only amongst the first
vectors in this sequence have non-zero coordinates only amongst the first  coordinates. Now for any HAP, the vector sequence has bounded discrepancy in every coordinate. Thus the maximum of
coordinates. Now for any HAP, the vector sequence has bounded discrepancy in every coordinate. Thus the maximum of  for the first
for the first  vectors is bounded by
vectors is bounded by  .
.
February 26, 2010 at 3:04 pm
I like that observation. One could even think of it as a multiplicative function as follows. We take the function from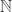 to
to  defined by the following properties: (i) if
defined by the following properties: (i) if  is congruent to
is congruent to  mod 3, then
mod 3, then  is the constant function
is the constant function  ; (ii)
; (ii)  is the function
is the function  ; (iii)
; (iii)  is completely multiplicative (where multiplication in
is completely multiplicative (where multiplication in  is pointwise).
is pointwise).
To be more explicit about it, to calculate you write
you write  as
as  , where
, where  is congruent to
is congruent to  mod 3, and
mod 3, and  is then the function
is then the function 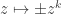 .
.
February 26, 2010 at 3:35 pm
Out of curiosity, let me assume that is given by a formula of the kind
is given by a formula of the kind 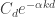 (which would give the right sort of behaviour for the tails). What does that give us for
(which would give the right sort of behaviour for the tails). What does that give us for 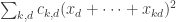 ?
?
Well, if then
then 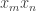 is counted
is counted  times, where the sum is over all common factors
times, where the sum is over all common factors  of
of  and
and  and over all
and over all  that exceed
that exceed  . For each fixed
. For each fixed  , … OK, I’ll change to assuming that the tail of the sum of the
, … OK, I’ll change to assuming that the tail of the sum of the  is given by that formula, so we would get
is given by that formula, so we would get  , and then we’d sum that over all
, and then we’d sum that over all  dividing
dividing  .
.
Now let me choose, purely out of a hat, to go for , so that when we sum over
, so that when we sum over  we get
we get  . This is not a million miles away from what I was looking at before, but now the task is much clearer. We don’t have to worry about the fact that some functions like 1, -1, 0, 1, -1, 0, … have bounded discrepancy. Rather, we must find some sequence
. This is not a million miles away from what I was looking at before, but now the task is much clearer. We don’t have to worry about the fact that some functions like 1, -1, 0, 1, -1, 0, … have bounded discrepancy. Rather, we must find some sequence 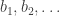 such that subtracting the corresponding diagonal matrix leaves us with something that’s still positive semidefinite, in such a way that the sum of the
such that subtracting the corresponding diagonal matrix leaves us with something that’s still positive semidefinite, in such a way that the sum of the  is large.
is large.
I haven’t checked in the above what the sum of the is, so I don’t know how large the sum of the
is, so I don’t know how large the sum of the  has to be. But, for those who share the anxiety I had earlier, the way we deal with the problem of the bounded-discrepancy sequences is that the sequence
has to be. But, for those who share the anxiety I had earlier, the way we deal with the problem of the bounded-discrepancy sequences is that the sequence  will tend to be bigger at numbers with many prime factors, to the point where, for example, the sum of the
will tend to be bigger at numbers with many prime factors, to the point where, for example, the sum of the  such that
such that  is not a multiple of 3 will be bounded.
is not a multiple of 3 will be bounded.
Here’s a simple toy problem, but it could be a useful exercise. Find a big supply of positive sequences of real numbers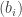 such that
such that 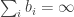 but for every
but for every  the sum of all
the sum of all  such that
such that  is not a multiple of
is not a multiple of  is finite.
is finite.
I’ve just found one to get the process going: take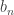 to be 1 if
to be 1 if 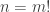 for some
for some  and 0 otherwise. So the question is to find more interesting examples, or perhaps even something closer to a characterization of all such sequences.
and 0 otherwise. So the question is to find more interesting examples, or perhaps even something closer to a characterization of all such sequences.
February 26, 2010 at 4:05 pm
The more I think about this the more I look forward to your sharing the values of the solutions to the SDP dual problem that you have found, especially if they can also be represented visually. You’ve basically already said this, but what excites me is that we could then perhaps make a guess at some good choices for the and the
and the  and end up with a much more tractable looking conjecture than EDP — namely, that some particular matrix is positive semidefinite.
and end up with a much more tractable looking conjecture than EDP — namely, that some particular matrix is positive semidefinite.
February 26, 2010 at 6:52 pm
Regarding the toy problem, here’s a slight generalization of your example: let (
( ) be any sequence of finite non-empty subsets of
) be any sequence of finite non-empty subsets of 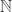 , and let
, and let 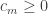 be any sequence such that
be any sequence such that  . Then the sequence
. Then the sequence
satisfies the condition (where is the characteristic function of
is the characteristic function of  ).
).
February 26, 2010 at 9:07 pm
To generalize a bit further: let (
(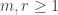 ) be a matrix of non-negative reals such that
) be a matrix of non-negative reals such that 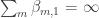 and
and  for all
for all  . Then let
. Then let 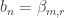 where
where  with
with  maximal.
maximal.
February 26, 2010 at 11:48 pm
One can greedily create such sequences as follows. First, choose a sequence of positive reals that sums to infinity. Next, arbitrarily choose a sequence with finite sum that takes the value
of positive reals that sums to infinity. Next, arbitrarily choose a sequence with finite sum that takes the value  somewhere, and put it down on the odd numbers. That takes care of the non-multiples of 2. Now we take care of multiples of 3 by choosing a sequence that has finite sum and takes the value
somewhere, and put it down on the odd numbers. That takes care of the non-multiples of 2. Now we take care of multiples of 3 by choosing a sequence that has finite sum and takes the value 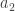 somewhere and placing it at the points that equal 2 or 4 mod 6 (that is, the non-multiples of 3 that have not had their values already assigned). Next, we deal with non-multiples of 5 by choosing values for numbers congruent to 6, 12, 18 or 24 mod 30 … and so on.
somewhere and placing it at the points that equal 2 or 4 mod 6 (that is, the non-multiples of 3 that have not had their values already assigned). Next, we deal with non-multiples of 5 by choosing values for numbers congruent to 6, 12, 18 or 24 mod 30 … and so on.
February 27, 2010 at 4:47 am
I have put some summary data of the SDP solutions at http://www.cs.princeton.edu/~hlnguyen/discrepancy/discrepancy.html .
.
The data mostly focus on the tails rather than
February 27, 2010 at 7:24 am
This comment got posted in the wrong spot earlier. Please delete the other copy.
The dual solutions for n=512,1024,1500 and the corresponding positive semidefinite matrices are available
here . Double click on a file to download it.
The files dual*.txt have the following format. values
values
Lines beginning with “b” specify the
b i
Lines beginning with “t” specify the tails
t k d
The files matrix*.txt have the following format: the ith line of the file contains the entries of the ith row of the matrix.
February 26, 2010 at 12:23 pm |
Gil, I meant to mention your ideas about creating low-discrepancy sequences probabilistically in my latest post, but forgot. I have now updated it. I would like to bring that particular discussion over to here, which is why I am writing this comment.
I am trying to come up with a purely linear-algebraic question that is nevertheless relevant to EDP. Here is one attempt. Let r be an integer, and let us try to build a sequence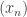 of real numbers such that for every
of real numbers such that for every  and every
and every  the sum
the sum  . That is, for every
. That is, for every  , if you break the HAP with common difference
, if you break the HAP with common difference  into chunks of length
into chunks of length  , then the sum over every chunk is zero.
, then the sum over every chunk is zero.
If is prime, then one way of achieving this is to create a sequence with the following three properties: (i) it is periodic with period
is prime, then one way of achieving this is to create a sequence with the following three properties: (i) it is periodic with period  ; (ii)
; (ii) 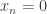 whenever
whenever  is a multiple of
is a multiple of  ; (iii)
; (iii) 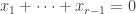 . If
. If  is composite, then the condition is similar but slightly more complicated. A general condition that covers (ii) and (iii) simultaneously is that for every factor
is composite, then the condition is similar but slightly more complicated. A general condition that covers (ii) and (iii) simultaneously is that for every factor  of
of  the sum
the sum 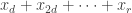 must be zero.
must be zero.
The set of all such sequences is a linear subspace of the set of all real sequences. My question is whether every sequence satisfying the first condition (namely summing to zero along chunks of HAPs) must belong to this subspace.
I have given no thought to this question, so it may have a simple and uninteresting answer.
Let me just remark that it is very important that the “chunks” are not just any sets of consecutive terms of HAPs, since then periodicity would follow trivially (because when you remove
consecutive terms of HAPs, since then periodicity would follow trivially (because when you remove 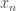 from the beginning of a chunk and add
from the beginning of a chunk and add 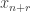 , you would need the sum to be the same). So, for example, if
, you would need the sum to be the same). So, for example, if 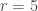 , then the conditions imposed on the HAP with common difference 3 are that
, then the conditions imposed on the HAP with common difference 3 are that  , that
, that  , and so on.
, and so on.
February 28, 2010 at 8:22 am
Sure, lets continue discussing it here along with the various other interesting avenues. The idea was to try to impose zeroes as partial sums along intervals of HAPs. If the distance between these zeroes is order k then in a random such sequence we can hope for discrepency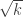 .
.
The value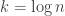 appears to be critical. (Perhaps, more accurately, $k=\log n \log\log n$.) When
appears to be critical. (Perhaps, more accurately, $k=\log n \log\log n$.) When  is larger the number of conditions is sublinear and the probability for such a condition to hold is roughly is
is larger the number of conditions is sublinear and the probability for such a condition to hold is roughly is 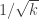 . So when
. So when 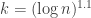 we can expect that the number of sequences satisfying the conditions is typically
we can expect that the number of sequences satisfying the conditions is typically  .
.
This give a heuristic prediction of (up to lower order terms, or perhaps, more accurately,
(up to lower order terms, or perhaps, more accurately,  ) as the maximum discrepency of a sequence of length
) as the maximum discrepency of a sequence of length  .
.
Of course, the evidence that this is the answer is rather small. This idea suggests that randomized constructions may lead to examples with descrepency roughly . In fact, this may apply to variants of the problems like the one where we restrict ourselves to square free integers. I will make some specific suggestions in a different post.
. In fact, this may apply to variants of the problems like the one where we restrict ourselves to square free integers. I will make some specific suggestions in a different post.
Regarding lower bounds, if is smaller than $\log n$ then the number of constrains is larger then the number of variables. So this may suggest that even to solve the linear equations might be difficult. Like with any lower bound approach we have to understand the case that we consider only HAP with odd periods where we have a sequence of discrepency 1. It is possible, as Tim suggested, that solutions to the linear algebra problem exists only if the imposed spacing are very structured which hopefully implies a periodic solution.
is smaller than $\log n$ then the number of constrains is larger then the number of variables. So this may suggest that even to solve the linear equations might be difficult. Like with any lower bound approach we have to understand the case that we consider only HAP with odd periods where we have a sequence of discrepency 1. It is possible, as Tim suggested, that solutions to the linear algebra problem exists only if the imposed spacing are very structured which hopefully implies a periodic solution.
February 27, 2010 at 7:14 am |
The dual solutions for n=512,1024,1500 and the corresponding positive semidefinite matrices are available here. Double click on a file to download it.
The files dual*.txt have the following format. values
values



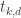
Lines beginning with “b” specify the
b
Lines beginning with “t” specify the tails
t
The files matrix*.txt have the following format: the th line of the file contains the entries of the
th line of the file contains the entries of the  th row of the matrix.
th row of the matrix.
February 27, 2010 at 12:52 pm |
Although the mathematics of this comment is entirely contained in the mathematics of Moses Charikar’s earlier comment, I think it bears repeating, since it could hold the key to a solution to EDP.
Amongst other things, Moses points out that a positive solution to EDP would follow if for large one could find coefficients
one could find coefficients  and
and 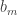 such that the quadratic form
such that the quadratic form
is positive semidefinite, the coefficients are non-negative and sum to 1, and the coefficients
are non-negative and sum to 1, and the coefficients 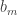 are non-negative and sum to
are non-negative and sum to  , where
, where  is some function that tends to infinity. Here, the sums are over all
is some function that tends to infinity. Here, the sums are over all 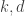 such that
such that 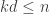 and over all
and over all 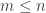 . The proof is simple: if such a quadratic form exists, then when each
. The proof is simple: if such a quadratic form exists, then when each 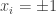 we have that
we have that 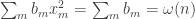 , and since the
, and since the  are non-negative and sum to 1 we know by averaging that there must exist
are non-negative and sum to 1 we know by averaging that there must exist 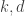 such that
such that 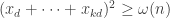 .
.
Here are a few things that are very nice about this.
(i) The condition that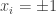 is used in an important way: if the
is used in an important way: if the 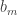 are mainly concentrated on pretty smooth numbers, then we will not be trying to prove false lower bounds for sequences like 1, -1, 0, 1, -1, 0, … since the sum of the
are mainly concentrated on pretty smooth numbers, then we will not be trying to prove false lower bounds for sequences like 1, -1, 0, 1, -1, 0, … since the sum of the 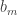 over non-multiples of 3 can easily be at most 1 or something like that.
over non-multiples of 3 can easily be at most 1 or something like that.
(ii) We can use semidefinite programming to calculate the best possible quadratic form for fairly large (as Moses and Huy Nguyen have done already) and try to understand its features. This will help us to make intelligent guesses about what sorts of coefficients
(as Moses and Huy Nguyen have done already) and try to understand its features. This will help us to make intelligent guesses about what sorts of coefficients  and
and 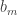 have a chance of working.
have a chance of working.
(iii) We don’t have to be too precise in our guesses in (ii), since to prove EDP it is not necessary to find the best possible quadratic form. It may be that there is another quadratic form with similar qualitative features that we can design so that various formulae simplify in convenient ways.
(iv) To prove that a quadratic form is positive semi-definite is not a hopeless task: it can be done by expressing the form as a sum of squares. So we can ask for something more specific: try to find a positive linear combination of squares of linear forms in variables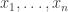 such that it equals a sum of the form
such that it equals a sum of the form
To do this, it is not necessary to diagonalize the quadratic form, though that would be one way of expressing it as a sum of squares.
In theory, therefore, a simple identity between two sums of squares of linear forms could give a one-line proof of EDP. It’s just a question of finding one that will do the job.
At this point I’m going to stick my neck out and say that in view of (i)-(iv) I now think that if we continue to work on EDP then it will be only a matter of time before we solve it. That is of course a judgment that I may want to revise in the light of later experience.
February 27, 2010 at 2:41 pm
Here is a very toy toy problem, just to try to get some intuition. The general aim is to try to produce a sum of squares of linear forms, which will automatically be a positive semidefinite quadratic form, from which it is possible to subtract a diagonal quadratic form and still have something positive semidefinite.
Here is a simple example where this can be done. Let us consider the quadratic form
in three variables and
and  . Here,
. Here,  is a small positive constant. Now this form is positive definite, since the only way it could be zero is if
is a small positive constant. Now this form is positive definite, since the only way it could be zero is if 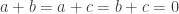 , which implies that
, which implies that  . But we want to quantify that statement.
. But we want to quantify that statement.
One possible quantification is as follows. We rewrite the quadratic form as
and observe that the part in the second bracket can be rewritten as . Therefore, the whole quadratic form is bounded below by
. Therefore, the whole quadratic form is bounded below by 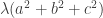 .
.
This isn’t a complete analysis, since if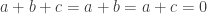 then
then  , so I haven’t subtracted enough. But I have to go.
, so I haven’t subtracted enough. But I have to go.
February 27, 2010 at 4:15 pm
Actually, for intuition-building purposes, I think the identity
is better, because it is very simple, and it shows how the “bunchedupness” on the left-hand side can be traded in for a diagonal part and something that’s more spread out. Now all we have to do is work out how to do something similar when we have HAPs on the left-hand side …
February 27, 2010 at 4:44 pm
Here’s an exercise that would be one step harder than the above, but still easier than EDP and possibly quite useful. I’d like to know what the possibilities are for subtracting something diagonal and positive from the infinite quadratic form
and still ending up with something positive definite, where is some constant less than 1. That is, I would like to find a way of rewriting the above expression as a sum of squares of linear forms, with as much as possible of the weight of the coefficients being given to squares of single variables.
is some constant less than 1. That is, I would like to find a way of rewriting the above expression as a sum of squares of linear forms, with as much as possible of the weight of the coefficients being given to squares of single variables.
Actually, I’ve seen one possible way of doing it. Note that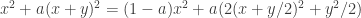 . That allows us to take the terms of the above series in pairs and write each pair as a square plus
. That allows us to take the terms of the above series in pairs and write each pair as a square plus 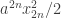 . So we can subtract off the diagonal form
. So we can subtract off the diagonal form
and still have something positive semidefinite.
However, it looks to me as though that is not going to be good enough by any means, because if we sum the coefficients in that kind of expression over all we are going to get something of comparable size to the sum of all the coefficients, which will be bounded. So we have to take much more account of how the HAPs mix with each other (which is not remotely surprising).
we are going to get something of comparable size to the sum of all the coefficients, which will be bounded. So we have to take much more account of how the HAPs mix with each other (which is not remotely surprising).
So I’d like some better examples to serve as models.
February 27, 2010 at 5:54 pm
If you were able to subtract off a large diagonal term from the expression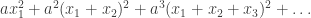 and still end up with something positive semidefinite, then this would serve as a lower bound for the discrepancy of the collection of subsets
and still end up with something positive semidefinite, then this would serve as a lower bound for the discrepancy of the collection of subsets  . But the minimum discrepancy of this collection is 1. Hence the sum of coefficients of the diagonal terms can be no larger than
. But the minimum discrepancy of this collection is 1. Hence the sum of coefficients of the diagonal terms can be no larger than 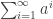 . (The ratio of the two quantities is a lower bound on the square discrepancy). The best you can do I suppose is to have
. (The ratio of the two quantities is a lower bound on the square discrepancy). The best you can do I suppose is to have  be very small, and subtract
be very small, and subtract  .
.
February 27, 2010 at 6:27 pm
I didn’t mean that just that form on its own would suffice, but that even if you add up a whole lot of expressions of that kind, one for each , the bound for the sum of the diagonal terms will be bounded in terms of the sum of all the coefficients. But I suppose your remark still applies: that is inevitably the case, or else one could prove for some fixed
, the bound for the sum of the diagonal terms will be bounded in terms of the sum of all the coefficients. But I suppose your remark still applies: that is inevitably the case, or else one could prove for some fixed  that the discrepancy always had to be unbounded on some HAP of common difference
that the discrepancy always had to be unbounded on some HAP of common difference  , which is obvious nonsense.
, which is obvious nonsense.
Let’s define the –part of the quadratic form that interests us to be
–part of the quadratic form that interests us to be  . And let’s call it
. And let’s call it 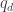 . Then it is absolutely essential to subtract a diagonal form
. Then it is absolutely essential to subtract a diagonal form  from
from 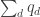 in such a way that we cannot decompose
in such a way that we cannot decompose  as a sum
as a sum  of positive semi-definite forms.
of positive semi-definite forms.
Maybe the next thing to do is try to find a non-trivial example of subtracting a large diagonal from a sum of a small number of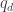 s. (By non-trivial, I mean something that would beat the bound you get by subtracting the best
s. (By non-trivial, I mean something that would beat the bound you get by subtracting the best 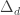 from each
from each 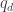 separately.)
separately.)
February 27, 2010 at 6:47 pm
We could get some inspiration from the SDP solutions for small values of . Note that we explicitly excluded the singleton terms from each HAP because that would trivially give us a bound of 1. So far, the best bound we have (for
. Note that we explicitly excluded the singleton terms from each HAP because that would trivially give us a bound of 1. So far, the best bound we have (for 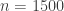 ) from the SDP is still less than 1. Getting a bound that exceeds 1 by this approach is going to require a very large value of
) from the SDP is still less than 1. Getting a bound that exceeds 1 by this approach is going to require a very large value of  . That being said, here are some dual solutions that have clean expressions:
. That being said, here are some dual solutions that have clean expressions:
This gives a lower bound of on the square discrepancy for
on the square discrepancy for  .
.
This gives a lower bound of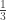 on the square discrepancy for
on the square discrepancy for 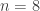 .
.
I don’t have proofs that these quadratic forms are non-negative, except that they ought to be if we believe that the SDP solver is correct.
February 27, 2010 at 7:23 pm
Of course, we can get a sum of squares representation from the Cholesky decomposition of the matrix corresponding to the quadratic form.
February 27, 2010 at 8:48 pm
The non-negativity of the first of those forms is a special case of what I said earler: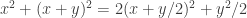 . I’ll think about the other one.
. I’ll think about the other one.
February 27, 2010 at 9:55 pm
The second form has the following decomposition:
We know that the SDP bound is for
for 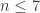 and jumps to
and jumps to  for
for 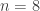 thanks to this quadratic form. Hence this decomposition is non-trivial in that it cannot be decomposed as a sum
thanks to this quadratic form. Hence this decomposition is non-trivial in that it cannot be decomposed as a sum 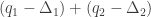 of positive semidefinite forms.
of positive semidefinite forms.
February 28, 2010 at 7:53 am
If we look at the Cholesky decomposition of the matrix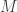 corresponding to the quadratic form computed by the SDP solver for n=1500 for inspiration for the sum of squares, there seem to be some interesting patterns going on there. Let
corresponding to the quadratic form computed by the SDP solver for n=1500 for inspiration for the sum of squares, there seem to be some interesting patterns going on there. Let  be the decomposition, and
be the decomposition, and 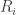 be the i-th row of
be the i-th row of 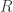 , then
, then 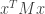 can be rewritten as
can be rewritten as  .
. 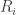 seems to put most of its weight on numbers that are multiple of i. The weight at the multiples of i decreases quickly as the multiples get larger. Among the non-multiples of i, there is also some pattern in the weights of numbers with common divisors with i as well. I have put some plots at http://www.cs.princeton.edu/~hlnguyen/discrepancy/cholesky.html
seems to put most of its weight on numbers that are multiple of i. The weight at the multiples of i decreases quickly as the multiples get larger. Among the non-multiples of i, there is also some pattern in the weights of numbers with common divisors with i as well. I have put some plots at http://www.cs.princeton.edu/~hlnguyen/discrepancy/cholesky.html
February 28, 2010 at 12:09 pm
Here’s another way of thinking about the problem. Let’s assume that we have chosen (by inspired guesswork based on experimental results, say) the coefficients . So now we have a quadratic form
. So now we have a quadratic form 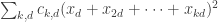 , and we want to write it in a different way, as
, and we want to write it in a different way, as 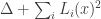 , where
, where  is shorthand for
is shorthand for 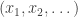 and for each
and for each 
 is some linear form
is some linear form 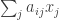 . Also,
. Also,  is a non-negative diagonal form (that is, one of the form
is a non-negative diagonal form (that is, one of the form 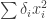 , and our aim is to get the sum of the
, and our aim is to get the sum of the 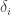 to be as large as possible.
to be as large as possible.
Instead of focusing on , I think it may be more fruitful to focus on the off-diagonal part of the quadratic form. That is, we try to choose the
, I think it may be more fruitful to focus on the off-diagonal part of the quadratic form. That is, we try to choose the 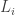 so as to produce the right coefficients at every
so as to produce the right coefficients at every 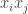 , and we try to do that so efficiently that when we’ve finished we find that the diagonal part is not big enough — hence the need to add
, and we try to do that so efficiently that when we’ve finished we find that the diagonal part is not big enough — hence the need to add  .
.
To explain what I mean about “efficiency” here, let me give an extreme example. Suppose we have a quadratic form in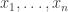 and all we are told about it is that the coefficient of every
and all we are told about it is that the coefficient of every 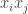 is 2. An inefficient way of achieving this is to take
is 2. An inefficient way of achieving this is to take  . If we do this, then the diagonal part is
. If we do this, then the diagonal part is  . But we can do much much better by taking
. But we can do much much better by taking 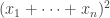 , which gives a diagonal part of
, which gives a diagonal part of 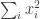 .
.
In the HAPs case, what we’d like to do is find ways of reexpressing the sum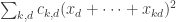 more efficiently by somehow cleverly combining forms so as to achieve the off-diagonal part with less effort. The fact that there are very long sequences with low discrepancy tells us that this will be a delicate task, but we could perhaps try to save only something very small. For instance, we could try to show that the form was still positive semidefinite even after we subtract
more efficiently by somehow cleverly combining forms so as to achieve the off-diagonal part with less effort. The fact that there are very long sequences with low discrepancy tells us that this will be a delicate task, but we could perhaps try to save only something very small. For instance, we could try to show that the form was still positive semidefinite even after we subtract  . (This would show
. (This would show 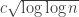 growth in the discrepancy, whereas we are tentatively expecting that it should be possible to get
growth in the discrepancy, whereas we are tentatively expecting that it should be possible to get  .)
.)
February 28, 2010 at 12:53 pm
What would it take, by this method, to show that the discrepency is > 2?
February 28, 2010 at 1:17 pm
If I understand correctly from Wikipedia, the Cholesky decomposition would attempt to solve the problem in my previous comment in a greedy way: it would first make sure that all the coefficients of were correct, leaving a remainder that does not depend on
were correct, leaving a remainder that does not depend on 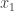 . Then it would deal with the
. Then it would deal with the 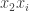 terms (with
terms (with 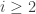 ), and so on. If this is correct (which it may not be) then it is not at all clear that it will be an efficient method in the sense I discussed above (though in the particular example I gave it happened to give the same decomposition).
), and so on. If this is correct (which it may not be) then it is not at all clear that it will be an efficient method in the sense I discussed above (though in the particular example I gave it happened to give the same decomposition).
February 28, 2010 at 1:23 pm
The answer to Gil’s question is that we’d need to choose the coefficients to sum to 1 and to be able to rewrite the quadratic form
to sum to 1 and to be able to rewrite the quadratic form 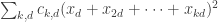 as
as 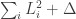 where the
where the 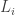 are linear forms and
are linear forms and  is a diagonal form
is a diagonal form 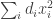 with non-negative coefficients
with non-negative coefficients 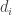 that sum to more than 4. (The 4 is because we then have to take square roots.)
that sum to more than 4. (The 4 is because we then have to take square roots.)
Indeed, if we can do this, then we see that if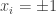 for every
for every  , then the quadratic form we started with takes value greater than 4, so by averaging at least one of the
, then the quadratic form we started with takes value greater than 4, so by averaging at least one of the 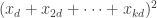 is greater than 4.
is greater than 4.
We know from the 1124 examples that this is not going to be easy, but the fact that we need to go up to 4 is encouraging (in the sense that 1124 is not as frighteningly large a function of 4 as it is of 2).
February 28, 2010 at 1:39 pm
As a tiny help in thinking about the problem, it is useful to note that the coefficient of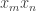 in the quadratic form
in the quadratic form 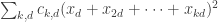 is
is 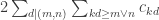 . If, following Moses, we write
. If, following Moses, we write 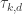 for
for  , then this becomes
, then this becomes  .
.
It’s a shame that this formula involves the maximum , but we might be able to deal with that by smoothing the truncations of the HAPs (as I did in the calculations in the EDP9 post). That is, one could try to prove that a sum such as
, but we might be able to deal with that by smoothing the truncations of the HAPs (as I did in the calculations in the EDP9 post). That is, one could try to prove that a sum such as  is large, which implies by partial summation that one of the sums
is large, which implies by partial summation that one of the sums  is large. This too raises technical problems — instead of summing over the coefficients we end up integrating (which isn’t a problem at all) but the integral of the coefficients is infinite. I call this a technical problem because it still doesn’t rule out finding some way of showing that the diagonal coefficients are “more infinite” in some sense, or doing some truncation to make things finite and then dealing with the approximations.
is large. This too raises technical problems — instead of summing over the coefficients we end up integrating (which isn’t a problem at all) but the integral of the coefficients is infinite. I call this a technical problem because it still doesn’t rule out finding some way of showing that the diagonal coefficients are “more infinite” in some sense, or doing some truncation to make things finite and then dealing with the approximations.
February 28, 2010 at 3:21 pm
One further small remark. The suggestion from the experimental evidence is that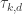 has the form
has the form 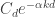 . However, we are not forced to go for the best possible form. So perhaps we could try out
. However, we are not forced to go for the best possible form. So perhaps we could try out  (and it is not hard to choose the
(and it is not hard to choose the  so as to achieve that). Then
so as to achieve that). Then 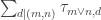 would equal
would equal  . That would leave us free to choose some nice arithmetical function
. That would leave us free to choose some nice arithmetical function 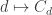 . For example, we could choose
. For example, we could choose  and would then end up with
and would then end up with 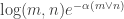 .
.
If we did that, then we would have the following question. Fix a large integer , and work out the sum
, and work out the sum  of all the coefficients
of all the coefficients  such that
such that  . Then try to prove that it is possible to rewrite the quadratic form
. Then try to prove that it is possible to rewrite the quadratic form  as a diagonal form plus a positive semidefinite form in such a way that the sum of the diagonal terms is at least
as a diagonal form plus a positive semidefinite form in such a way that the sum of the diagonal terms is at least  .
.
There is no guarantee that this particular choice will work, but I imagine that there is some statement about a suitable weighted average of discrepancies that would be equivalent to it, and we might find that that statement looked reasonably plausible.
February 28, 2010 at 8:44 pm
Since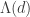 is non-zero only for prime powers, your choice of
is non-zero only for prime powers, your choice of  would prove that the discrepancy is unbounded even if we restrict ourselves to HAPs with common differences that are prime powers. Certainly plausible.
would prove that the discrepancy is unbounded even if we restrict ourselves to HAPs with common differences that are prime powers. Certainly plausible.
One comment on how large needs to be for this to prove that the discrepancy is
needs to be for this to prove that the discrepancy is  . If the trend from the SDP values for small
. If the trend from the SDP values for small  continues, it will take really really large
continues, it will take really really large  for the square discrepancy to exceed even 1 ! The increment in the value from
for the square discrepancy to exceed even 1 ! The increment in the value from 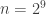 to
to 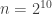 was a mere 0.014. At this rate, you would need to multiply by something like
was a mere 0.014. At this rate, you would need to multiply by something like 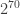 to get an increment of 1 in the lower bound on square discrepancy.
to get an increment of 1 in the lower bound on square discrepancy.
March 1, 2010 at 12:28 am
For exactly this reason, we had a discussion a few days ago about whether EDP could be true even for HAPs with prime-power common differences. Sune observed that it is false for complex numbers, since one can take a sequence such as . However, it is not clear what the right moral from that example is, since no periodic sequence can give a counterexample for the real case. But it shows that any quadratic-forms identity one found would have to be one that could not be extended to the complex numbers. But it seems that such identities do not exist: if we change the real quadratic form
. However, it is not clear what the right moral from that example is, since no periodic sequence can give a counterexample for the real case. But it shows that any quadratic-forms identity one found would have to be one that could not be extended to the complex numbers. But it seems that such identities do not exist: if we change the real quadratic form  into the Hermitian form
into the Hermitian form 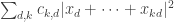 , the matrix of the form is unchanged, and the coefficient of
, the matrix of the form is unchanged, and the coefficient of 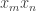 becomes the coefficient of
becomes the coefficient of  .
.
So if my understanding is correct, even if EDP is true for prime power differences, it cannot be proved by this method, and was therefore a bad choice.
was therefore a bad choice.
March 1, 2010 at 12:31 am
In fact, the reason I chose it was that I had a moment of madness and stopped thinking that , because I forgot that it was precisely the same as
, because I forgot that it was precisely the same as 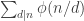 . (What I mean is that I knew this fact, but temporarily persuaded myself that it wasn’t true.) So I go back to choosing instead
. (What I mean is that I knew this fact, but temporarily persuaded myself that it wasn’t true.) So I go back to choosing instead  , in which case the quadratic form one would try to rewrite would be
, in which case the quadratic form one would try to rewrite would be 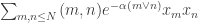 .
.
March 1, 2010 at 12:50 am
Another way to see this is that complex numbers can be viewed as 2 dimensional vectors: . If EDP does not hold for complex numbers for a subset of HAPs, then it does not hold for vectors for the same subset of HAPs. Hence we cannot get a good lower bound via the quadratic form.
. If EDP does not hold for complex numbers for a subset of HAPs, then it does not hold for vectors for the same subset of HAPs. Hence we cannot get a good lower bound via the quadratic form.
March 1, 2010 at 2:35 am
One observation about the : If only a subset of the
: If only a subset of the  are non-zero, we need to think carefully about where to place these non-zero values. A proof of this form would imply this: Consider any sequence where we place
are non-zero, we need to think carefully about where to place these non-zero values. A proof of this form would imply this: Consider any sequence where we place  values at locations
values at locations  such that
such that  , but are free to place arbitrary values (including
, but are free to place arbitrary values (including  ) at locations
) at locations  such that
such that  . Then the discrepancy of any such sequence over HAPs is unbounded.
. Then the discrepancy of any such sequence over HAPs is unbounded.
In particular, this rules out having non-zero values for only at
only at  , because an alternating $\pm 1$ sequence at these values (and zeroes elsewhere) has bounded discrepancy over all HAPs.
, because an alternating $\pm 1$ sequence at these values (and zeroes elsewhere) has bounded discrepancy over all HAPs.
One attractive feature of this approach is that the best lower bound achievable via a proof of this form is exactly equal to the discrepancy of vector sequences (for every sequence length ). But we ought to admit the possibility that the discrepancy for vector sequences may be bounded (even if it is unbounded for
). But we ought to admit the possibility that the discrepancy for vector sequences may be bounded (even if it is unbounded for  sequences). We know at least two instances where we can do something with unit vectors that cannot be done with
sequences). We know at least two instances where we can do something with unit vectors that cannot be done with  sequences. Are there constructions of sequences of unit vectors with bounded discrepancy ?
sequences. Are there constructions of sequences of unit vectors with bounded discrepancy ?
March 1, 2010 at 7:47 am
This is a minor point, but I think the choice actually ensures that the coefficient of
actually ensures that the coefficient of  is
is 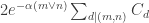 . Doesn’t change what we need to prove.
. Doesn’t change what we need to prove.
February 28, 2010 at 10:13 am |
Here is a proposed probabilistic construction which is quite similar to earlier algorithms, can be tested empirically, and perhaps even analyzed. Let be the lenth of the sequence we want to create and let
be the lenth of the sequence we want to create and let  be a real number. (
be a real number. ( 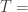
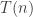 will be a monotone function of
will be a monotone function of  that we determine later.)
that we determine later.)
You chose the value of , $1 \le i \le n$, after you have chosen earlier values. For every HAP containing
, $1 \le i \le n$, after you have chosen earlier values. For every HAP containing  we compute the discrepency along the HAP containing i. We ignore those HAP so that the discrepency is smaller than T. For an HAP so that the discrepency D is larger than T, if the sum is negative we give weight (D/T) to +1 and weight 1 to -1. If the sum is negative we give the weight (D/T) to -1 and weight 1 to 1. (D is the absolute value of the sum.) (We can also replace D/T by a fixed constant, say 2.)
we compute the discrepency along the HAP containing i. We ignore those HAP so that the discrepency is smaller than T. For an HAP so that the discrepency D is larger than T, if the sum is negative we give weight (D/T) to +1 and weight 1 to -1. If the sum is negative we give the weight (D/T) to -1 and weight 1 to 1. (D is the absolute value of the sum.) (We can also replace D/T by a fixed constant, say 2.)
Now when we chose we compute the prduct of these weights for the choise +1 and for the choise -1 and choose at random according to these products.
we compute the prduct of these weights for the choise +1 and for the choise -1 and choose at random according to these products.
I propose to choose T as something like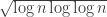 or a little bit higher. We want to find a T so that typically for every i only a small (perhaps typically at most 1) number of HAP will contribute non trivial weights. We experiment this algorithm for various ns and Ts.
or a little bit higher. We want to find a T so that typically for every i only a small (perhaps typically at most 1) number of HAP will contribute non trivial weights. We experiment this algorithm for various ns and Ts.
February 28, 2010 at 6:06 pm
Actually, when we move from the spacing k to the discrepency inside the intervals, we do pay a price from time to time. And it seems that if you consider n intervals as we do there will be intervals whose discrepency is larger than expected. This brings us back to the
larger than expected. This brings us back to the 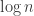 area.
area.
I still propose to experiment what I suggested in the previos post but would expect that this will lead to examples with discrepency in the order of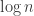 .
.
I see no heuristic arument that we can go below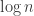 discrepency. But for certain measures of average discrepency the heuristic remains at
discrepency. But for certain measures of average discrepency the heuristic remains at  ).
).
March 1, 2010 at 9:54 am |
This is a response to this comment of Moses, but that subthread was getting rather long, so I’m starting a new one.
What you say is of course a good point, and one that, despite its simplicity, I had missed. Let me spell it out once again. If we manage to find an identity of the form
with all coefficients non-negative, the summing to 1 and the
summing to 1 and the 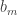 summing to
summing to  , then not only will we have proved EDP, but we will have shown a much stronger result that applies to all sequences
, then not only will we have proved EDP, but we will have shown a much stronger result that applies to all sequences 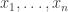 (and even vector sequences, but let me not worry about that for now).
(and even vector sequences, but let me not worry about that for now).
To give an example of the kind of implication this has, let us suppose that is any set such that
is any set such that 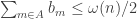 , then we must be able to prove that EDP holds for sequences that take the value 0 on
, then we must be able to prove that EDP holds for sequences that take the value 0 on  and
and  on the complement of
on the complement of  , since for such a sequence we know that
, since for such a sequence we know that
We know that there are subsets on which EDP holds. An obvious example is the set of all even numbers. As Moses points out, the set of all factorials is not even close to being an example. In general we do not have to stick to subsets: the experimental evidence suggests that we should be looking at weighted sets, where the discussion is a bit more complicated.
An obvious preliminary problem is to try to come up with a set of integers of density zero such that EDP does not obviously fail for sequences that are inside that set and 0 outside. Unfortunately, there is a boring answer to this. If EDP is true, then let
inside that set and 0 outside. Unfortunately, there is a boring answer to this. If EDP is true, then let  be such that all
be such that all  sequences of length
sequences of length  have discrepancy at least
have discrepancy at least  . Now take all integers up to
. Now take all integers up to  , together with all even numbers up to
, together with all even numbers up to 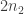 , all multiples of 4 up to
, all multiples of 4 up to 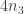 , and so on. The density of this set is zero and it has been constructed so that EDP holds for it.
, and so on. The density of this set is zero and it has been constructed so that EDP holds for it.
However, it may be that this gives us some small clue about the kind of sequence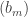 we should be looking for.
we should be looking for.
March 1, 2010 at 5:52 pm
Here is another attempt to gain some intuition about what is going on in the SDP approach to the problem. I want to give a moderately interesting example (but only moderately) of a situation where it is possible to remove a diagonal part from a quadratic form and maintain positive semidefiniteness. It is chosen to have a slight resemblance to quadratic forms based on HAPs, which one can think of as sets that have fairly small intersections with each other, but a few points that belong to a larger than average number of sets.
To model this, let us take a more extreme situation, where we have a collection of sets that are almost disjoint, apart from the fact that one element is common to all of them. To be precise, let us suppose that we have subsets
subsets 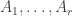 of
of 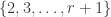 , each of size
, each of size  , with
, with  for every
for every  such that for every
such that for every 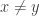 belonging to
belonging to 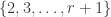 there is exactly one
there is exactly one 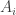 that contains both
that contains both  and
and  . Such systems (projective planes) are known to exist, though I may have got the details slightly wrong — I think
. Such systems (projective planes) are known to exist, though I may have got the details slightly wrong — I think  works out to be
works out to be 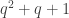 .
.
Now let us consider the quadratic form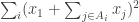 . Thus, we are adding the element 1 to each set
. Thus, we are adding the element 1 to each set 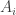 and taking the quadratic form that corresponds to this new set system. It is not hard to check that the coefficient of
and taking the quadratic form that corresponds to this new set system. It is not hard to check that the coefficient of 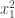 is
is  , the coefficient of
, the coefficient of  is
is 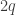 (because for each
(because for each  there turn out to be exactly
there turn out to be exactly  sets
sets 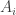 that contain
that contain  ), the coefficient of
), the coefficient of  is
is  when
when 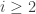 (for the same reason) and the coefficient of
(for the same reason) and the coefficient of 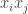 when
when 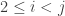 is 2.
is 2.
It follows, if my calculations are correct, that the form can be rewritten as
To me this suggests that a more efficient way of representing some average of squares over HAPs may well involve something like putting together bunches of HAPs that and replacing the corresponding sum of squares by sums of squares of linear forms that have weights that favour numbers that belong to many of the HAPs — that is, smoother numbers.
One problem is that we may have two numbers and
and  that are both very smooth but nevertheless
that are both very smooth but nevertheless 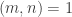 . But that may be where the bunching comes in. For example, perhaps it would be useful to take a large smooth number
. But that may be where the bunching comes in. For example, perhaps it would be useful to take a large smooth number  and look at all HAPs that contain
and look at all HAPs that contain  , and try to find a more efficient representation for just that bunch. (That doesn’t feel like a strong enough idea, but exploring its weaknesses might be helpful.)
, and try to find a more efficient representation for just that bunch. (That doesn’t feel like a strong enough idea, but exploring its weaknesses might be helpful.)
March 1, 2010 at 10:30 am |
While wondering about heuristic arguments for EDP I did a very simple calculation which leaves me somewhat puzzled.
Consider the set of all -valued sequences on
-valued sequences on 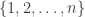 as a probability space, with all sequences having equal probability
as a probability space, with all sequences having equal probability 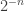 . Let
. Let 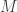 be the event ‘sequence is completely multiplicative’, and
be the event ‘sequence is completely multiplicative’, and  the event ‘partial sums are bounded by
the event ‘partial sums are bounded by  ’. Then
’. Then 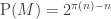 , and I think that
, and I think that 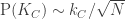 (for some constant
(for some constant  ).
).
If we were to assume that and
and  are independent, we would get
are independent, we would get 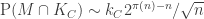 . Since
. Since 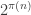 is much bigger than
is much bigger than  , this means we would expect there to be lots and lots of completely multiplicative sequences of length
, this means we would expect there to be lots and lots of completely multiplicative sequences of length  with discrepancy
with discrepancy  .
.
What puzzles me is not that the assumption of independence is wrong but just how wrong it is. If EDP is true, then the multiplicativity of a sequence must force the discrepancy to be large in a big way. Of course, we know that it forces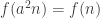 , so that the sequence ‘reproduces’ itself across certain subsequences, but this doesn’t seem enough to explain the above.
, so that the sequence ‘reproduces’ itself across certain subsequences, but this doesn’t seem enough to explain the above.
March 1, 2010 at 10:37 am
The probability that the partial sums are bounded are exponentially small, no?
March 1, 2010 at 10:58 am
I don’t suppose you’ll be satisfied with this answer, but part of the explanation is surely that if a sequence is multiplicative and has bounded partial sums, then it has bounded partial sums along all HAPs. So if that is impossible, then …
I see that that’s not much more than a restatement of the question. Perhaps one way to gain intuition would be to think carefully about the events “has partial sums between -C and C” and “is 2-multiplicative”, where by that I mean that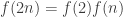 for every
for every  . Do these two events appear to be negatively correlated? (I can’t face doing the calculation myself.) It may be that the negative correlation doesn’t show up at this point, in which case this question will not help.
. Do these two events appear to be negatively correlated? (I can’t face doing the calculation myself.) It may be that the negative correlation doesn’t show up at this point, in which case this question will not help.
March 1, 2010 at 12:05 pm
Gil: unless I’m misunderstanding something, the probabiity of the partial sum being within a certain bound goes down as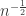 , corresponding to the height around zero of the density function of a Gaussian variable with mean zero and variance
, corresponding to the height around zero of the density function of a Gaussian variable with mean zero and variance  . (We actually want the maximum rather than the final height, but I think this behaves similarly.)
. (We actually want the maximum rather than the final height, but I think this behaves similarly.)
Tim: that sounds like a good idea; I’ll look at that…
March 1, 2010 at 12:31 pm
Alec, I think Gil is probably right. Intuitively, if you want to force a random walk to stay within [-C,C], then you will have to give it a nudge a positive proportion of the time, which is restricting it by an exponential amount. In the extreme case where C=1 this is clear — every other move of the walk is forced.
To put it another way, and in fact, this is a proof, you cannot afford to have a subinterval with drift greater than 2C. But for this to happen with positive probability, the subinterval needs to have size a constant times , so the probability that it never happens is at most something like
, so the probability that it never happens is at most something like  for some absolute constant
for some absolute constant  .
.
March 1, 2010 at 1:04 pm
Sorry, yes, you’re right. I was misinterpreting a result about the maximum value attained (as opposed to the maximum absolute value). That alleviates my puzzlement.
March 1, 2010 at 10:33 am |
Another technique which is fairly standard and may be useful in the lower bound direction is the “polynomial technique”. Say you want to prove that every long enough sequence has discrepency at least 3. Consider polynomials in the variables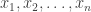 over a field with 7 elements. Now mod our by the equation
over a field with 7 elements. Now mod our by the equation 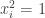 . We want to show that a certain polynomial is identically zero. The polynomial is:
. We want to show that a certain polynomial is identically zero. The polynomial is: 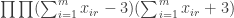 , where the products are over all r and all m smaller than n/r. Once we forced the identity
, where the products are over all r and all m smaller than n/r. Once we forced the identity 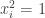 we can reduce every such polynomial to square free polynomial and what we need to show is that for large enough n this polynomial is identically zero.
we can reduce every such polynomial to square free polynomial and what we need to show is that for large enough n this polynomial is identically zero.
In case the formula wont compile: you take the product of all partial sums -3 times the same sum + 3, over all HAPs.
(If you prefer to consider polynomials over the field and not mod up by any ideal you can replace the by
by 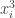 and add the product of all
and add the product of all  s as another term.)
s as another term.)
We use the fact that if the discrepency is becoming greater than 2 then some of the above sums will be +3 or -3 modulo 7.
On the one hand, it feels like simply reformulating the problem, but on the other hand, maybe it is not. Perhaps, the complicated product can be simplified or some other algebraic reason why such products ultimately vanish exist. This type of technique is sometimes useful for problems where we can think also of semi definite/linear programming methodsl.
I also share the feeling that at present Moses’s semidefinite program is the most promising.
March 1, 2010 at 2:15 pm |
A while back we were looking at multiplicative functions such that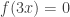 for all
for all  , and one question which was raised was wether a function of this type, with bounded discrepancy , must be the function 1, -1, 0, 1, -1, 0, 1, -1, 0,…
, and one question which was raised was wether a function of this type, with bounded discrepancy , must be the function 1, -1, 0, 1, -1, 0, 1, -1, 0,…
I could not see an intuitive reason for why this should be true, apart from just not managing to construct a counterexample. Has anyone looked more at this?
I used one of my old Mathematica program to search for a multiplicative function of this type, with , and while I had lunch it found an assignment to the first 115 primes which works up to n=630.
, and while I had lunch it found an assignment to the first 115 primes which works up to n=630.
Here is the values for the primes
{-1,0, 1, -1, 1, -1, 1, -1, -1, 1, -1, 1, 1, -1, -1, 1, -1, -1, -1, -1,
1, 1, -1, 1, 1, -1, 1, -1, 1, 1, -1, -1, 1, -1, -1, -1, 1, -1, -1, 1,
1, -1, -1, 1, -1, 1, 1, 1, 1, -1, 1, -1, 1, -1, 1, -1, 1, -1, -1, -1,
-1, 1, 1, 1, -1, -1, 1, 1, 1, 1, -1, -1, -1, 1, 1, 1, 1, -1, -1, -1,
1, -1, 1, -1, -1, -1, 1, -1, -1, -1, -1, 1, 1, -1, -1, 1, 1, 1, -1,
1, -1, -1, -1, 1, -1, -1, -1, 1, 1, 1, -1, -1, 1, -1, -1}
The function for all x is then
{1, -1, 0, 1, 1, 0, -1, -1, 0, -1, 1, 0, -1, 1, 0, 1, 1, 0, -1, 1, 0, \
-1, -1, 0, 1, 1, 0, -1, 1, 0, -1, -1, 0, -1, -1, 0, 1, 1, 0, -1, 1, \
0, -1, 1, 0, 1, -1, 0, 1, -1, 0, -1, 1, 0, 1, 1, 0, -1, -1, 0, -1, 1, \
0, 1, -1, 0, -1, 1, 0, 1, -1, 0, 1, -1, 0, -1, -1, 0, 1, 1, 0, -1, \
-1, 0, 1, 1, 0, -1, 1, 0, 1, -1, 0, 1, -1, 0, 1, -1, 0, 1, -1, 0, 1, \
1, 0, -1, -1, 0, 1, -1, 0, -1, 1, 0, -1, 1, 0, 1, -1, 0, 1, 1, 0, -1, \
1, 0, -1, -1, 0, 1, -1, 0, 1, 1, 0, -1, 1, 0, -1, -1, 0, 1, -1, 0, 1, \
-1, 0, 1, -1, 0, -1, 1, 0, 1, -1, 0, 1, -1, 0, -1, 1, 0, -1, 1, 0, 1, \
-1, 0, 1, -1, 0, -1, 1, 0, -1, 1, 0, -1, 1, 0, -1, -1, 0, 1, 1, 0, 1, \
-1, 0, 1, -1, 0, 1, -1, 0, 1, -1, 0, 1, -1, 0, 1, -1, 0, 1, -1, 0, \
-1, -1, 0, 1, 1, 0, 1, -1, 0, 1, -1, 0, 1, -1, 0, 1, 1, 0, -1, 1, 0, \
-1, 1, 0, -1, 1, 0, -1, -1, 0, 1, -1, 0, 1, -1, 0, -1, 1, 0, 1, 1, 0, \
-1, -1, 0, -1, 1, 0, 1, 1, 0, -1, -1, 0, 1, -1, 0, 1, -1, 0, -1, 1, \
0, -1, 1, 0, -1, 1, 0, -1, 1, 0, 1, -1, 0, -1, -1, 0, 1, -1, 0, 1, \
-1, 0, 1, 1, 0, -1, -1, 0, 1, 1, 0, 1, 1, 0, -1, -1, 0, 1, -1, 0, 1, \
1, 0, -1, -1, 0, 1, -1, 0, 1, 1, 0, -1, -1, 0, -1, 1, 0, -1, 1, 0, 1, \
-1, 0, 1, -1, 0, 1, -1, 0, 1, -1, 0, -1, 1, 0, -1, 1, 0, 1, 1, 0, -1, \
-1, 0, -1, 1, 0, -1, -1, 0, 1, 1, 0, 1, 1, 0, -1, -1, 0, -1, -1, 0, \
1, -1, 0, 1, -1, 0, 1, -1, 0, 1, 1, 0, -1, -1, 0, 1, 1, 0, -1, -1, 0, \
1, 1, 0, -1, -1, 0, 1, -1, 0, 1, -1, 0, 1, 1, 0, -1, -1, 0, 1, 1, 0, \
-1, 1, 0, 1, 1, 0, -1, -1, 0, -1, 1, 0, 1, -1, 0, 1, 1, 0, -1, -1, 0, \
1, 1, 0, -1, -1, 0, 1, -1, 0, 1, -1, 0, -1, 1, 0, 1, 1, 0, -1, 1, 0, \
-1, 1, 0, -1, -1, 0, -1, 1, 0, -1, -1, 0, 1, 1, 0, 1, -1, 0, -1, -1, \
0, 1, 1, 0, -1, -1, 0, 1, 1, 0, 1, 1, 0, -1, -1, 0, 1, -1, 0, -1, 1, \
0, -1, 1, 0, 1, 1, 0, -1, 1, 0, -1, 1, 0, -1, -1, 0, -1, 1, 0, -1, 1, \
0, 1, 1, 0, -1, -1, 0, 1, -1, 0, 1, -1, 0, 1, -1, 0, -1, 1, 0, -1, 1, \
0, 1, 1, 0, -1, 1, 0, -1, 1, 0, -1, -1, 0, -1, 1, 0, -1, -1, 0, 1, \
-1, 0, 1, -1, 0, 1, 1, 0, 1, 1, 0, -1, -1, 0, 1, -1, 0, -1, -1, 0, 1, \
1, 0, 1, -1, 0, -1, -1, 0, 1, 1, 0, 1, 1, 0, -1, -1, 0, -1, 1, 0, 1, \
-1, 0, -1, 1, 0, -1, 1, 0, 1, 1, 0, -1, -1, 0, 1, 1, 0, -1, -1, 0, \
-1, -1, 0, 1, 1, 0, 1, 1, 0
March 1, 2010 at 2:22 pm
The point of the example of course being that it is distinct from the unique example with discrepancy 1 even for small values of $x$. one will typically be able to construct trivial examples defined on the first
one will typically be able to construct trivial examples defined on the first  integers simply by changing the values at the primes closest to
integers simply by changing the values at the primes closest to  , since they are not affected by the multiplicative requirement.
, since they are not affected by the multiplicative requirement.
For a finite bound
March 2, 2010 at 8:22 am
One can get at least as far as 886 with a sequence like this of discrepancy 2 sending 5 to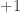 :
:
Here the following primes are sent to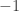 : 2, 7, 13, 19, 23, 31, 43, 47, 53, 61, 67, 73, 83, 97, 101, 107, 131, 139, 149, 151, 163, 167, 181, 191, 193, 199, 233, 239, 271, 277, 281, 283, 293, 313, 317, 349, 353, 359, 397, 401, 409, 419, 421, 431, 439, 443, 457, 463, 467, 509, 523, 547, 563, 571, 577, 587, 607, 613, 619, 631, 643, 647, 661, 677, 683, 691, 701, 709, 751, 787, 811, 823, 827, 829, 839, 859, 863, 883.
: 2, 7, 13, 19, 23, 31, 43, 47, 53, 61, 67, 73, 83, 97, 101, 107, 131, 139, 149, 151, 163, 167, 181, 191, 193, 199, 233, 239, 271, 277, 281, 283, 293, 313, 317, 349, 353, 359, 397, 401, 409, 419, 421, 431, 439, 443, 457, 463, 467, 509, 523, 547, 563, 571, 577, 587, 607, 613, 619, 631, 643, 647, 661, 677, 683, 691, 701, 709, 751, 787, 811, 823, 827, 829, 839, 859, 863, 883.
I can’t see much of a pattern, but there seems to be quite a bit of freedom to assign either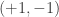 or
or  at twin-prime pairs
at twin-prime pairs 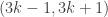 .
.
March 2, 2010 at 10:37 pm
That search finally terminated — so that is the longest such sequence we can get that sends 5 to +1.
March 3, 2010 at 9:03 am
Alec, could you try that with the value at 7 flipped instead? It would be interesting to see how much further one gets by following the discrepancy 1 function out to different primes.
March 3, 2010 at 9:54 am
OK, I’ll try that when I get back to my computer this evening.
March 5, 2010 at 7:49 pm
In this case (flipping the value at 7) the maximal length of sequence (or rather, the maximal length that is of the form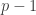 — which is what I should have said above too) is 946:
— which is what I should have said above too) is 946:
(Primes sent to -1 in this example: 2, 5, 7, 13, 17, 29, 37, 41, 43, 59, 67, 71, 79, 83, 89, 109, 113, 137, 139, 157, 167, 179, 191, 197, 211, 223, 227, 229, 251, 257, 269, 277, 281, 293, 311, 349, 353, 359, 379, 383, 389, 401, 421, 431, 443, 457, 467, 479, 487, 491, 499, 521, 541, 547, 557, 563, 569, 577, 587, 599, 617, 619, 641, 647, 653, 683, 701, 709, 719, 761, 769, 773, 787, 809, 811, 857, 859, 881, 911, 929, 937.)
I’ll kick off a search with 11 flipped, but won’t hold my breath for it to finish!
March 5, 2010 at 7:55 pm
Well, I’ll have to eat my words. It finished almost immediately, having got only as far as 330:
(Primes sent to -1: 2, 5, 13, 17, 23, 29, 41, 43, 47, 59, 71, 73, 83, 89, 101, 109, 113, 131, 137, 149, 173, 179, 181, 191, 211, 223, 227, 233, 239, 257, 263, 269, 281, 293, 311.)
I had assumed that the maximum length would be a monotonic function of the first prime flipped, but evidently not…
March 5, 2010 at 11:20 pm
I’ve now gone a bit further with this, and found:
It seems that flipping a prime of the form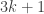 is much better than flipping a prime of the form
is much better than flipping a prime of the form 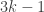 . (Perhaps this isn’t too surprising, as it means we don’t immediately require
. (Perhaps this isn’t too surprising, as it means we don’t immediately require 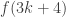 to change sign to keep the discrepancy at 2, but I’m not sure that fully explains it.)
to change sign to keep the discrepancy at 2, but I’m not sure that fully explains it.)
March 6, 2010 at 9:46 am
That’s an interesting sequence. I would not have expected the different :s to give such different lengths.
:s to give such different lengths.
However the fact that one can find sequences as long a the ones you have found for some primes, suggest that any proof showing that the maximum length is finite for any will have to be rather indirect, not giving a good bound for the maximum length.
will have to be rather indirect, not giving a good bound for the maximum length.
March 2, 2010 at 7:40 am |
As Tim pointed out earlier, the Cholesky decomposition is greedy and does not necessarily give an efficient decomposition into sum of squares that uses the diagonal sparingly. But I want to propose using it as a proof technique for positive semidefiniteness after we have subtracted out the diagonal terms. If we can prove that the Cholesky decomposition succeeds, this proves that the matrix is positive definite. Put differently, I want to try and figure out what values we can get away with without making the Cholesky decomposition procedure fail.
values we can get away with without making the Cholesky decomposition procedure fail.
Let’s review how Cholesky works. The goal is to represent positive definite matrix such that
such that  is a lower triangular matrix. If
is a lower triangular matrix. If  is the
is the  th row of
th row of  , the only non-zero coordinates of
, the only non-zero coordinates of  are in the first
are in the first  positions, and
positions, and 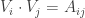 .
.
The algorithm proceeds thus: Having determined
Having determined  , the coordinates of
, the coordinates of  are determined thus:
are determined thus:  is completely determined by the condition
is completely determined by the condition  . Next,
. Next,  is determined by
is determined by 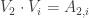 and so on. Finally,
and so on. Finally,  is determined by the constraint:
is determined by the constraint:  . The procedure succeeds if, for all
. The procedure succeeds if, for all  , in the computation of
, in the computation of  ,
,  .
.
Consider what happens if, for a particular , we subtract
, we subtract  from
from  and compute the new Cholesky decomposition. Since
and compute the new Cholesky decomposition. Since  is smaller,
is smaller, 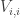 will become smaller. This in turn will increase the values of
will become smaller. This in turn will increase the values of 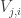 for
for  . This sets off a chain reaction and decreases
. This sets off a chain reaction and decreases  values for
values for  . If we subtract too much, we run the risk of the Cholesky decomposition failing. But if it does fail, we know for sure that we have ruined positive definiteness.
. If we subtract too much, we run the risk of the Cholesky decomposition failing. But if it does fail, we know for sure that we have ruined positive definiteness.
Now suppose we know the Cholesky decomposition of matrix . This might help us guess what diagonal terms we can safely subtract from
. This might help us guess what diagonal terms we can safely subtract from  . I’m hoping that the large diagonal
. I’m hoping that the large diagonal 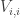 in the decomposition give us clues for where we can hope to subtract
in the decomposition give us clues for where we can hope to subtract  (although there are complex dependencies and subtracting a small amount from one location changes a whole bunch of other elements in the decomposition.)
(although there are complex dependencies and subtracting a small amount from one location changes a whole bunch of other elements in the decomposition.)
March 2, 2010 at 8:24 am
Here is a setting I want to think about, with some assumptions on various parameters slightly different from the ones that Tim proposed earlier. I’m going to repeat a few things from previous comments. Recall that we are interested in the quadratic form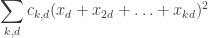
As before . Consider
. Consider  to be very small. We’ll use this to make some approximations. Say
to be very small. We’ll use this to make some approximations. Say  for all
for all  . (I hope this will turn out to be an easier setting to analyze and understand).
. (I hope this will turn out to be an easier setting to analyze and understand).
Note that .
.
Consider the symmetric matrix corresponding to the quadratic form above (i.e. the quadratic form is
corresponding to the quadratic form above (i.e. the quadratic form is  ). We hope to subtract a large diagonal term
). We hope to subtract a large diagonal term 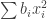 such that the remainder is still positive semidefinite. For
such that the remainder is still positive semidefinite. For 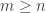 , the entry
, the entry  where
where  the number of divisors of
the number of divisors of  .
.
First, lets figure out the Cholesky decomposition for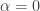 . In this case,
. In this case, 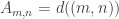 . This has a nice form which is obvious in retrospect:
. This has a nice form which is obvious in retrospect:  if
if 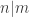 and
and 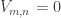 otherwise. In other words, the
otherwise. In other words, the  th column is the indicator function for the infinite HAP with common difference
th column is the indicator function for the infinite HAP with common difference  . It is easy to verify that
. It is easy to verify that  since
since 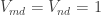 precisely when
precisely when  and
and  .
.
The next step is to figure out what the decomposition is for this setting of parameters with and very small. I want to obtain approximate expressions for the entries of the Cholesky decomposition as linear expressions in
and very small. I want to obtain approximate expressions for the entries of the Cholesky decomposition as linear expressions in  , i.e. by dropping higher order terms from the Taylor series. I’m hoping that the relatively structured form of the matrix will allow us to get closed form approximations for the entries of this decomposition, and further that, it will result in diagonal elements
, i.e. by dropping higher order terms from the Taylor series. I’m hoping that the relatively structured form of the matrix will allow us to get closed form approximations for the entries of this decomposition, and further that, it will result in diagonal elements 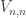 being relatively high for
being relatively high for  with many divisors. If so, this should help us subtract large
with many divisors. If so, this should help us subtract large 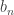 values for such
values for such  .
.
March 2, 2010 at 11:03 am
I tried calculating the coefficients of for the entries of the Cholesky decomposition of the matrix described above. (The constant term for each entry is given by the Cholesky decomposition for
for the entries of the Cholesky decomposition of the matrix described above. (The constant term for each entry is given by the Cholesky decomposition for 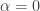 determined above).The computation of the
determined above).The computation of the  coefficients seemed too tedious (and error-prone) to do by hand, so I wrote some code to do it. Here is the output of the code for the first 100 rows of the decomposition. The format of each line of the file is
coefficients seemed too tedious (and error-prone) to do by hand, so I wrote some code to do it. Here is the output of the code for the first 100 rows of the decomposition. The format of each line of the file is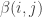
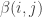 is the coefficient of
is the coefficient of  in the Taylor expansion of
in the Taylor expansion of 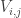 . It seems to match some initial values I computed by hand, so I hope the code is correct. I can’t say I understand what these values are, but it is reassuring to see that for
. It seems to match some initial values I computed by hand, so I hope the code is correct. I can’t say I understand what these values are, but it is reassuring to see that for  with many divisors,
with many divisors,
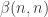 seems to be large. On the other hand it seems to be
seems to be large. On the other hand it seems to be
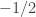 for prime
for prime  . I hope this means that we can subtract out large values of
. I hope this means that we can subtract out large values of 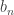 for
for  with many divisors while maintaining the property that the Cholesky decomposition continues to proceed successfully. To prove that Cholesky works, we will need to show upper bounds on
with many divisors while maintaining the property that the Cholesky decomposition continues to proceed successfully. To prove that Cholesky works, we will need to show upper bounds on  for
for 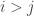 and lower bounds on the diagonal terms
and lower bounds on the diagonal terms 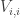 (for the decomposition of the matrix with the diagonal form subtracted out).
(for the decomposition of the matrix with the diagonal form subtracted out).
i j
where
Before we do that, we need to understand what these coefficients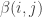 are and why the values
are and why the values 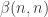 are large for
are large for  with many divisors. Any ideas ?
with many divisors. Any ideas ?
March 2, 2010 at 11:26 am
I’ve just had a look in Sloane’s database to see if there are any sequences that match the values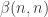 but had no luck (even after various transformations, such as multiplying by 2, or multiplying by 2 and adding 1). But it might be worth continuing to look.
but had no luck (even after various transformations, such as multiplying by 2, or multiplying by 2 and adding 1). But it might be worth continuing to look.
March 2, 2010 at 11:35 am
A couple of small observations. I think if we continue along these lines we will be able to get a formula for the diagonal values.
The observations are that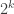 maps to
maps to  for every
for every  (so far, that is) and that
(so far, that is) and that 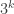 maps to
maps to  for every
for every  . I’ll continue to look at powers for a bit and then I’ll move on to more general geometric progressions (an obvious example being 3,6,12,24,48,96) and see what pops out.
. I’ll continue to look at powers for a bit and then I’ll move on to more general geometric progressions (an obvious example being 3,6,12,24,48,96) and see what pops out.
March 2, 2010 at 11:45 am
A formula that works when and gives the right value for k=0 and k=1 is that
and gives the right value for k=0 and k=1 is that 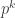 maps to
maps to  . I suspect it is valid for all prime powers but have not yet checked.
. I suspect it is valid for all prime powers but have not yet checked.
Maybe this looks more suggestive if we rewrite it as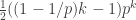 .
.
March 2, 2010 at 11:51 am
Very interesting. I’ve put up a file with only the diagonal entries upto 1000 here . It is tedious to look for diagonal entries in the earlier file. I’ve also included prime factorizations in the new file.
March 2, 2010 at 12:39 pm
Sorry — had to do something else.
But I’ve now checked the GP 3,6,12,… and we get the formula .
.
Next up, the GP 5,10,20,40,… which gives the formula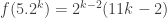 .
.
So I’d hazard a guess that . Let me do a random check by looking at
. Let me do a random check by looking at  . If my guess is correct, this should be
. If my guess is correct, this should be  and in fact it is … 134. Let me try that again. It should be
and in fact it is … 134. Let me try that again. It should be  . So I believe that formula now.
. So I believe that formula now.
March 2, 2010 at 12:50 pm
It’s taken me longer than it should have, but I now see that we ought to be looking not at but at
but at  . Somehow, this is where the “real pattern” is.
. Somehow, this is where the “real pattern” is.
When we get
we get 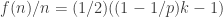 , and when
, and when  we get
we get  .
.
I think an abstract question is emerging. Suppose we know that, as seems to be the case, for any and
and  we have a formula of the kind
we have a formula of the kind 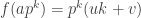 . With enough initial conditions, that should determine
. With enough initial conditions, that should determine  . We already have a lot of initial conditions, since we know that
. We already have a lot of initial conditions, since we know that 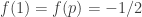 for every prime
for every prime  . Those conditions are enough to determine
. Those conditions are enough to determine 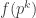 , but they don’t seem to be sufficient to do everything. For that I appear to need to know
, but they don’t seem to be sufficient to do everything. For that I appear to need to know  at all square-free numbers, or something like that.
at all square-free numbers, or something like that.
March 2, 2010 at 1:03 pm
For primes with
with  the formula appears to be
the formula appears to be
In keeping with the general idea of looking at , let me also write this formula as
, let me also write this formula as 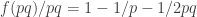 .
.
A small calculation, which I shall now do, will allow me to deduce the formula for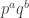 .
.
March 2, 2010 at 1:15 pm
Ok, I think we should have the diagonal values figured out soon, although understanding why these numbers arise will take more effort. Looking ahead, the hope was that large numbers are an indication that large can be subtracted out from those entries without sacrificing positive semidefiniteness. At this point, I don’t have a clue about how these
can be subtracted out from those entries without sacrificing positive semidefiniteness. At this point, I don’t have a clue about how these  should be picked. We can experiment with some guesses later.
should be picked. We can experiment with some guesses later.
Question for later: , for suitably small
, for suitably small  , we can pick
, we can pick  such that
such that 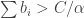 . At this point, I haven’t thought through why this should necessarily be the case. Is there a heuristic argument that we have enough mass on the diagonal to pull this through ?
. At this point, I haven’t thought through why this should necessarily be the case. Is there a heuristic argument that we have enough mass on the diagonal to pull this through ?
The hope is that for any
I am going to have to sign off for a while and get back to this later in the day.
March 2, 2010 at 1:36 pm
For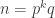 with
with  I get
I get
or equivalently
I’ll add to this comment when I get a formula for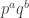 , which should be easy now.
, which should be easy now.
March 2, 2010 at 1:50 pm
All very interesting. Another thing to note about the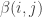 is that the fractional part is
is that the fractional part is  precisely when
precisely when  and
and  .
.
March 2, 2010 at 2:01 pm
I got the following formula for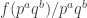 :
:
I have tried it out on and got the answer
and got the answer  , which was correct. So I believe this formula too.
, which was correct. So I believe this formula too.
Just to repeat what I am doing here, I am assuming that the function takes geometric progressions to arithmetic progressions and deducing what I can whenever I know what two values are. In this way, knowing
takes geometric progressions to arithmetic progressions and deducing what I can whenever I know what two values are. In this way, knowing  for prime powers and for products of two primes was enough to give me
for prime powers and for products of two primes was enough to give me  for all numbers of the form
for all numbers of the form 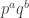 . Sorry — correction — I have assumed that only for GPs with prime common ratio. I haven’t looked at what happens when the common ratio is composite.
. Sorry — correction — I have assumed that only for GPs with prime common ratio. I haven’t looked at what happens when the common ratio is composite.
Come to think of it, if takes GPs with prime common ratio to APs, then
takes GPs with prime common ratio to APs, then 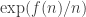 takes GPs with prime common ratio to GPs, which is a pretty strong multiplicativity property. That leads me to think that the eventual formula is going to be quite nice. I hope I’ll be able to guess it after working out
takes GPs with prime common ratio to GPs, which is a pretty strong multiplicativity property. That leads me to think that the eventual formula is going to be quite nice. I hope I’ll be able to guess it after working out 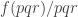 , or perhaps I’ll have to do
, or perhaps I’ll have to do  . But first I need some lunch.
. But first I need some lunch.
March 2, 2010 at 2:04 pm
Here’s a slightly more transparent way of writing the formula for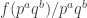 :
:
March 2, 2010 at 3:05 pm
Just before I dive into the calculations, let me make the remark that the signs are that the formula will be an inhomogeneous multilinear one in the indices. More precisely, I am expecting a formula of the following kind for when
when  and the primes
and the primes  are in increasing order:
are in increasing order:
March 2, 2010 at 3:52 pm
I’ve just wasted some time going about this a stupid way, which was to calculate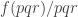 for several values and try to spot a pattern. But I now see that that was unlikely to be easy, since the dependence on
for several values and try to spot a pattern. But I now see that that was unlikely to be easy, since the dependence on  ,
, 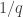 and
and 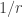 is trilinear. The values look quite strange too, but I have a new plan. That plan is to try to find a formula for
is trilinear. The values look quite strange too, but I have a new plan. That plan is to try to find a formula for 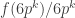 when
when  is a prime greater than 3. That should give me some coefficients of a linear function in
is a prime greater than 3. That should give me some coefficients of a linear function in  . If I repeat the exercise for one or two other small products of two primes, then it should be easyish to spot a formula for the coefficients, and then I’ll have a formula for
. If I repeat the exercise for one or two other small products of two primes, then it should be easyish to spot a formula for the coefficients, and then I’ll have a formula for 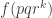 , which will be a good start. In fact, it will be more than just a start, as from that and the multilinearity assumption I’ll be able to work out all the rest of the values at products of three prime powers.
, which will be a good start. In fact, it will be more than just a start, as from that and the multilinearity assumption I’ll be able to work out all the rest of the values at products of three prime powers.
March 2, 2010 at 4:04 pm
Oh dear, for the first time I have run up against an anomaly in the data that may be hard to fit into a nice pattern. When is any of 7,11,13,17 or 19 the value of
is any of 7,11,13,17 or 19 the value of  is given by the formula
is given by the formula 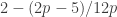 , but when
, but when  we get instead
we get instead  . But I’ll continue with this and try not to worry about
. But I’ll continue with this and try not to worry about 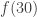 too much for now. (But I would love to learn that it was wrong and should have been 57.5 instead of 58.5.)
too much for now. (But I would love to learn that it was wrong and should have been 57.5 instead of 58.5.)
March 2, 2010 at 4:08 pm
I’ve added an even bigger file with diagonal entries upto 10,000 in this directory in case you are looking for more data points to verify guesses for formulae. The directory also contains the C code (cholesky.c) used to generate the lower triangular matrix of coefficients and another piece of code (cholesky2.c) to generate the diagonal entries only. I really hope the code is not buggy !
March 2, 2010 at 4:36 pm
Uh oh … I spotted a tiny problem in the code which could potentially affect the calculation for rows and columns greater than n/2. Except that for some mysterious reason it doesn’t. i.e. the output is exactly the same after fixing the “bug”. Basically, I was not setting the constant term in the Taylor expansion correctly for diagonal entries > n/2. It should have been 1 and was being set to 0 instead. This could potentially affect the calculation of the coefficient of for all entries in columns > n/2, but apparently it does not. I’m checking to see if there are any other issues.
for all entries in columns > n/2, but apparently it does not. I’m checking to see if there are any other issues.
March 2, 2010 at 4:55 pm
I looked over the code and as far as I can tell, it is correct. I now understand why the “bug” above did not really change anything.
March 2, 2010 at 5:16 pm
After further investigation, I no longer think the value at 30 is anomalous, but I have discovered (with much more effort than I thought would be needed, because the pattern is clearly subtler than I thought it would be) the following formula for . We know from earlier that
. We know from earlier that 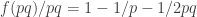 , so that gives us the value when
, so that gives us the value when  . If I call that value
. If I call that value  , then the formula, which is linear in
, then the formula, which is linear in  as we expect, is
as we expect, is
where is a binary operation that I do not fully understand. Let me tabulate the values that I have calculated so far:
is a binary operation that I do not fully understand. Let me tabulate the values that I have calculated so far:
I had to calculate a lot of values before I realized that there is a nice formula for this binary operation except if and
and  are consecutive primes. The formula is simply
are consecutive primes. The formula is simply 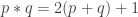 . But when
. But when  and
and  are consecutive we seem to get a little “kick” and the value is larger. In fact, by the time we get to
are consecutive we seem to get a little “kick” and the value is larger. In fact, by the time we get to  the kick is not all that little.
the kick is not all that little.
Anyhow, this observation partially explains the mysterious anomaly at 30, but really it replaces it by a bigger mystery: why should the values be sensitive to consecutiveness of primes?
Of course, at this stage I haven’t looked at all that many numbers, so I hope that I’ll be able to ask a more precise question in due course. So far, however, I don’t feel all that close to a formula for …
…
March 2, 2010 at 5:21 pm
Correction: the formula does not give the right value for either, so my understanding is worse than I thought. However, in a way that might be good news, since I found the idea of a formula that fails for consecutive primes a bit bizarre.
either, so my understanding is worse than I thought. However, in a way that might be good news, since I found the idea of a formula that fails for consecutive primes a bit bizarre.
March 2, 2010 at 5:45 pm
At some point I may ask whether somebody can write a piece of code to work out this binary operation that I am working out laboriously by hand. But for now, here are a few more values, which perhaps give us tiny further clues.
It looks as though a necessary and sufficient condition for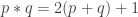 is that
is that 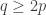 . What’s more, it looks as though
. What’s more, it looks as though 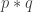 is constant before that. So the right formula should involve maxes and things.
is constant before that. So the right formula should involve maxes and things.
OK, here is my revised formula: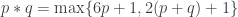 . Phew!
. Phew!
To test the earlier conjecture, let me try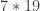 . It works out to be 53, which is indeed what it should be.
. It works out to be 53, which is indeed what it should be.
And to test the new conjecture, let me try . The prediction is 79. What I actually get is … 79. OK, I think I believe this formula now, but it will need quite a bit more slog to get a formula for
. The prediction is 79. What I actually get is … 79. OK, I think I believe this formula now, but it will need quite a bit more slog to get a formula for  from here. I’ve spent several hours on this: the calculations are certainly routine enough to do on a computer, so I wonder if anyone could take over at this point. For instance, it would be good to give a formula for
from here. I’ve spent several hours on this: the calculations are certainly routine enough to do on a computer, so I wonder if anyone could take over at this point. For instance, it would be good to give a formula for 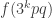 . Does it change behaviour according to whether
. Does it change behaviour according to whether 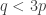 or
or 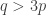 ?
?
March 2, 2010 at 9:16 pm
Here’s a plot of for
for  :
:

March 2, 2010 at 11:12 am |
These calculations (of Moses in the previous comment) look very interesting and potentially fruitful. Rather than trying to duplicate them, I will continue to do what I can to refine my speculations about what the coefficients and
and 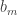 might conceivably look like.
might conceivably look like.
As has already been mentioned, an important constraint on the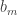 (aside from the essential one that the partial sums should be unbounded) is that if
(aside from the essential one that the partial sums should be unbounded) is that if  is a set for which EDP fails, then
is a set for which EDP fails, then 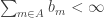 . Here I am saying that EDP fails for
. Here I am saying that EDP fails for  if there exists a sequence
if there exists a sequence 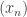 that takes
that takes  values on
values on  and arbitrary values on
and arbitrary values on  such that the HAP-discrepancy of
such that the HAP-discrepancy of 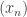 is bounded. This is a necessary condition on the coefficients
is bounded. This is a necessary condition on the coefficients 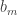 , since if
, since if 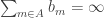 then we know that EDP is true for
then we know that EDP is true for  . (Once again, I am not being careful about the distinction between the large finite case and the infinite case.)
. (Once again, I am not being careful about the distinction between the large finite case and the infinite case.)
In fact, it is better to think about the complex case, or even the vector case, since the SDP proof, if it succeeds, automatically does those cases as well. So let me modify that definition to say that EDP fails for if there is a bounded-discrepancy sequence of complex numbers (or vectors) that has modulus (or norm) 1 everywhere on
if there is a bounded-discrepancy sequence of complex numbers (or vectors) that has modulus (or norm) 1 everywhere on  .
.
With this in mind, it is of some interest to have a good idea of which sets are the ones for which EDP succeeds. A trivial example is any HAP (assuming, that is, that EDP is true). An example of a set for which EDP fails is the complement of any HAP. Let me prove that in the case where the HAP has common difference 15 — it will then be clear how the proof works in general. For any
are the ones for which EDP succeeds. A trivial example is any HAP (assuming, that is, that EDP is true). An example of a set for which EDP fails is the complement of any HAP. Let me prove that in the case where the HAP has common difference 15 — it will then be clear how the proof works in general. For any  , let
, let 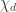 be a non-trivial character of the multiplicative group of residue classes mod
be a non-trivial character of the multiplicative group of residue classes mod  that are coprime to
that are coprime to  . Now define
. Now define  to be
to be  if
if  is coprime to 15,
is coprime to 15, 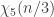 if
if  ,
,  if
if 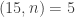 , and 0 if
, and 0 if  is a multiple of 15. Any HAP will run periodically through either all the residue classes mod 15, or all the residue classes that are multiples of 3, or all the residue classes that are multiples of 5, or will consists solely of multiples of 15. Whatever happens, we know that
is a multiple of 15. Any HAP will run periodically through either all the residue classes mod 15, or all the residue classes that are multiples of 3, or all the residue classes that are multiples of 5, or will consists solely of multiples of 15. Whatever happens, we know that  for every
for every  and every
and every  , and that
, and that  for every
for every  that is not a multiple of 15.
that is not a multiple of 15.
As Moses pointed out yesterday (to stop me getting carried away), if is the set of factorials, then EDP fails for
is the set of factorials, then EDP fails for  . That is because every HAP intersects
. That is because every HAP intersects  in a set of the form
in a set of the form  , which means that we can define
, which means that we can define 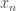 to be 0 if
to be 0 if  is not a factorial, and
is not a factorial, and  if
if 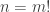 .
.
The main point of this comment is to give a slightly non-trivial example of a set for which EDP succeeds. By “non-trivial” I don’t mean mathematically hard, but just that the set is rather sparse. It is the set of perfect squares. (The proof generalizes straightforwardly to higher powers, and, I suspect, to a rich class of other sets, but I have not yet tried to verify this suspicion.)
To see this, one merely has to note what the intersection of with
with  is. The answer is that it is the set
is. The answer is that it is the set  , where
, where 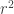 is the smallest multiple of
is the smallest multiple of  that is a perfect square. (That is, to get
that is a perfect square. (That is, to get  from
from  you multiply once by each prime that divides
you multiply once by each prime that divides  an odd number of times.) The proof that this is what you get is that a trivial necessary and sufficient condition for
an odd number of times.) The proof that this is what you get is that a trivial necessary and sufficient condition for  to divide
to divide 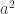 is that
is that 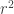 should divide
should divide 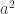 .
.
Now suppose that EDP failed for the set of perfect squares, and let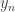 be the …
be the …
Hang on, my proof has collapsed. What I am proving is the weaker statement that EDP fails if you insist that the sequence is zero outside . Let me continue with that assumption, though the statement is much less interesting.
. Let me continue with that assumption, though the statement is much less interesting.
Now suppose that EDP fails for the set of perfect squares, and let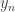 be the sequence that demonstrates this. Thus (because of our new assumption)
be the sequence that demonstrates this. Thus (because of our new assumption)  has modulus 1 for every positive integer
has modulus 1 for every positive integer  , and
, and  if
if  is not a perfect square. But then we can set
is not a perfect square. But then we can set 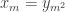 and we have a counterexample to EDP.
and we have a counterexample to EDP.
This comment has ended up as a bit of a damp squib, but let me salvage something by asking the following question. Suppose that the vector version of EDP is true and that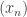 is a sequence such that
is a sequence such that  for every
for every  . Does it follow that
. Does it follow that 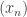 has unbounded discrepancy?
has unbounded discrepancy?
This may be a fairly easy question, since the squares are so sparse. (If it is, then the whole point of this comment is rather lost, but a different useful point will have been made instead.) For example, perhaps it is possible to find a sequence that takes the value 1 at every square and 0 or -1 everywhere else and has bounded discrepancy.
I think there is an interesting class of questions here. For which sets does there exist a function
does there exist a function  of bounded discrepancy that takes the value 1 everywhere on
of bounded discrepancy that takes the value 1 everywhere on  and 0, 1 or -1 everywhere else? As I did in the end of this comment, one can paste together different HAPs to produce an example with density zero, but are there any interesting examples? I would expect that as soon as
and 0, 1 or -1 everywhere else? As I did in the end of this comment, one can paste together different HAPs to produce an example with density zero, but are there any interesting examples? I would expect that as soon as  is reasonably sparse (in some sense that would have to be worked out — it would have to mean something like “sparse in every HAP”), it would be possible to use a greedy algorithm to prove that EDP fails. So here is a yet more specific question. Define a sequence
is reasonably sparse (in some sense that would have to be worked out — it would have to mean something like “sparse in every HAP”), it would be possible to use a greedy algorithm to prove that EDP fails. So here is a yet more specific question. Define a sequence 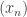 as follows. For every perfect square it takes the value 1. For all other
as follows. For every perfect square it takes the value 1. For all other  we choose
we choose 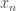 so as to minimize the maximum absolute value of the partial sum along any HAP that ends at
so as to minimize the maximum absolute value of the partial sum along any HAP that ends at  , and if we have the choice of taking
, and if we have the choice of taking 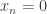 then we do. Thus, the first few terms of the sequence are as follows.
then we do. Thus, the first few terms of the sequence are as follows. 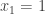 (since 1 is a square),
(since 1 is a square), 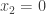 (since to minimize the maximum of
(since to minimize the maximum of  and
and  we can take
we can take  to be 0 or -1 and we prefer 0),
to be 0 or -1 and we prefer 0), 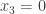 (for the same reason),
(for the same reason),  (since 4 is a square),
(since 4 is a square),  (since
(since  , so this makes the maximum at 5 equal to 1 rather than 2),
, so this makes the maximum at 5 equal to 1 rather than 2),  ,
, 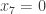 , and so on. Does this algorithm give rise to a bounded-discrepancy sequence? If not, is there some slightly more intelligent algorithm that does?
, and so on. Does this algorithm give rise to a bounded-discrepancy sequence? If not, is there some slightly more intelligent algorithm that does?