This is the first of a few posts I plan (one other of which is written and another of which is in draft form but in need of a few changes) in which I discuss various Polymath proposals in more detail than I did in my earlier post on possible projects.
One of my suggestions, albeit a rather tentative one, was to try to come up with a model that would show convincingly how life could emerge from non-life by purely naturalistic processes. But before this could become a sensible project it would be essential to have a more clearly defined mathematical question. By that I don’t mean a conjecture that Polymath would be trying to prove rigorously, but rather a list of properties that a model would have to have for it to count as successful. Such a list need not be fully precise, but in my view it should be reasonably precise, so that the task is reasonably well defined. It would of course be possible to change the desiderata as one went along.
In this post I’d like to make a preliminary list. It will undoubtedly be unsatisfactory in many ways, but I hope that there will be a subsequent discussion and that from it a better list will emerge. The purpose of this is not to start a Polymath project, but simply to attempt to define a Polymath proposal that might at some future date be an actual project. For two reasons I wouldn’t want this to be a serious project just yet: it seems a good idea to think quite hard about how it would actually work in practice, and someone who I hope will be a key participant is very busy for the next few months and less busy thereafter.
As a starting point, let me mention two ideas that are already out there and have attracted a lot of attention. One is the idea of cellular automata. A fairly general type of cellular automaton can be defined as follows. You have a graph (usually something like an infinite two-dimensional lattice), and at some points you have 1s and at other points you have 0s. You then let the system evolve in rounds according to some simple rule that is usually the same for every vertex. It might be something like this: if at least two of my neighbours are 1s then I will become a 1, and otherwise I will become a 0. It turns out that very simple rules can lead to extremely complicated and interesting behaviour.
What counts as complicated and interesting? Well, perhaps it is better to say what counts as dull. One possible form of dullness is if a system evolves to some state such as the all-1s state, or perhaps a big rectangle full of 1s with 0s outside, or an oscillation between two configurations. Another form of dullness is a system that tends to disperse the 1s until they form some fairly random looking bunch of 1s that never stops looking fairly random. But in between, there are systems that tend to evolve towards some kind of criticality, where you get fractal structures with organization at many different distance scales. One thing that interests people about cellular automata is that there are very simple rules that seem to want to evolve towards these nice “edge of chaos” patterns.
The second idea is self-organized criticality, which is a phenomenon exhibited by certain models in statistical physics — notably the so-called sandpile models. These are supposed to model what happens if you drop grains of sand one by one on to a pile. They will start to build up into a conical shape, but if the sides get too steep there are avalanches. The sizes of these avalanches vary, and if you plot the frequency of avalanches of various sizes, you find (experimentally at least) that they obey a power law. And power laws get people excited because they are what you find associated with critical phenomena. A typical sandpile model is something like this. You have a big square divided into a grid of small squares. You then set all squares equal to 0 except a few randomly chosen ones that you give small integers to. You then add 1 to the central square (let’s assume there is one), and after you have done so you have a rule that says that if any square has value at least 4 it must give 1 to each of its neighbours. This procedure you iterate until no square has value at least 4. (It can be shown that the order in which you do these operations doesn’t matter.) You then add 1 to the central square again, and keep going.
It turns out that the sizes of the “avalanches” that take place here (that is, how many iterations you have to do of the simple rule before all squares have value 0 to 3) also obey a power law, and also that systems such as these have a tendency to evolve towards interesting (that is, not too random and not too structured) configurations. That is, you can get critical phenomena without having to fine-tune some parameter. Again, this has got people excited as it seems to promise an explanation of how the complexity in nature could have started.
In the above description, I made the starting configuration random but after that the way the model evolved was deterministic. There are of course many different possible models, and in some of them the new “grains of sand” are dropped in random places. Again you get interesting critical behaviour.
Now as far as I know, with both cellular automata and sandpile models you get nice critical phenomena appearing, but while they give you pretty patterns they do not give you anything resembling an ecosystem. Yes, Conway’s game of life gives you glider guns and configurations that can reproduce themselves, but you have to set them up carefully in advance, and they don’t seem to do anything all that exciting. They also support universal computation, but again if you want to program the game of life to create an artificial-life simulator, you might as well use a much more powerful computer to do so. What a Polymath project would be looking for is a very simple system with the property that, regardless of the starting configuration, it would tend to develop and eventually produce something that looked like a complex ecosystem.
This brings me to a point that is worth making. The idea of this Polymath project would not be to produce yet another artificial life program, fascinating though those programs can be. One could think of it more like this: can one come up with a very simple model that almost always “self-organizes” and produces something that looks a bit like what you get with artificial life programs? In other words, we would be trying to model abiogenesis rather than evolution.
After that discussion, I think I can have a stab at saying what the properties are that would make a truly interesting and new model. (I am much less sure about the “new” part, and would be interested to hear from people with more knowledge about this kind of topic what the state of the art is.) Some of the properties below seem to be more important than others, but for now I won’t bother to distinguish between those that I regard as essential and those that are merely desirable.
1. It should be a dynamic model that evolves according to simple rules.
2. It should have a tendency to evolve towards patterns with a “critical” character — not too random and not too simple, with interesting features at many distance scales.
3. Probably it should be a somewhat randomized model (to give it a certain robustness). Here I am referring to the rules by which the model develops rather than the initial conditions, but perhaps the initial conditions should be randomized as well.
4. It should have a tendency to produce identifiable macroscopic structures.
5. It should be possible to classify these macroscopic structures in interesting ways. (That is, we would like to be able to say that certain structures look more or less the same as certain others, and ideally this similarity would be a bit more flexible than one just being a translation of another.)
6. These structures should interact with one another, and the interaction should sometimes be destructive (thereby providing some selection pressure).
7. With high probability, self-reproducing structures should eventually emerge. (Before posting this I showed it to Michael Nielsen, who made some interesting points. One of them is that experience in the actual universe suggests that perhaps there should be some fine tuning of parameters before the probability becomes high: after all, life does not evolve on all planets.)
I could go on, but the idea is that once you’ve got 6 and 7, and perhaps a few other properties (for instance, one might decide to have major environmental changes from time to time just to stimulate the development of the system), then natural selection can begin to operate.
Of course, the major challenge is 7. The most plausible route I can see to 7 is a purely probabilistic one: almost all configurations are not self-reproducing, but if a self-reproducing one ever does arise, then it will reproduce itself and start appearing all over the place. But in that case 5 is also a huge challenge. The kinds of structures one would ideally like are not things like the bullets from Conway’s glider guns, but larger configurations that can move about and that are defined more topologically. Indeed, that could be a huge and general problem: the geometry of just isn’t the same as the geometry of
, but a continuous model would be very difficult to design and simulate (or would it?). But perhaps there could be some cleverly chosen simple rule that would tend to protect “clumps” of 1s and allow them to move, and to do complicated things like rotating (whatever that can be made to mean in
). Or perhaps a complicated ecosystem could develop that was more
-like than
-like.
Here, incidentally, is a paragraph from the Wikipedia article on Conway’s game of life, which shows that it is not already an example of what I am talking about:
From a random initial pattern of living cells on the grid, observers will find the population constantly changing as the generations tick by. The patterns that emerge from the simple rules may be considered a form of beauty. Small isolated subpatterns with no initial symmetry tend to become symmetrical. Once this happens the symmetry may increase in richness, but it cannot be lost unless a nearby subpattern comes close enough to disturb it. In a very few cases the society eventually dies out, with all living cells vanishing, though this may not happen for a great many generations. Most initial patterns eventually “burn out”, producing either stable figures or patterns that oscillate forever between two or more states; many also produce one or more gliders or spaceships that travel indefinitely away from the initial location.
We would be looking for something a bit like the Game of Life, possibly randomized, with the important difference that it almost always got more and more complicated and more and more interesting.
Physics
There is one other property that I think would make a model more convincing as an argument for the probability of life arising out of non-life without any magic processes operating. I partly owe this thought to Michael Nielsen, who included the following two questions in a comment he made on the post where I originally mentioned this problem.
(1) How would you go about recognizing self-replicating beings?
(2) What sort of models are “reasonable”, in the sense of both reflecting what we know of physics, and being simple enough to be tractable? The Game of Life isn’t very physical, in that it disobeys many basic physical principles, like conservation of energy, conservation of mass, conservation of momentum, and so on.
One of the things that people often say about life, evolution, biological systems and the like is that they are ways of locally combatting the second law of thermodynamics. So perhaps one could add the following property as one that it would be very nice to have.
8. The general tendency for the model is to become more and more disordered, and eventually to end in heat death, but for there to be many local increases in order.
Of course, one would need to be clear what that meant. The other physical principles that Michael mentioned would also be good to have.
Here is a subproblem that occurs to me as I am writing this. It is connected with the thought that one would like macroscopic structures to have some tendency to survive. In the Game of Life, it seems that structures that survive do so almost by accident — they settle down into some sort of periodicity, say. But structures in the biological world are held together by physical forces, and they have identifiable boundaries and things like that. So one might try to develop a model that captures just this behaviour. As with the main problem, I’m not sure how to formulate this subproblem precisely, but let me have a go. Does there exist a model with the following properties?
(i) If you draw some large-scale shape (think of the 0s and 1s as black and white pixels, say, so the shape is on a much larger distance scale than the distance between two neighbouring points of the grid), it has a tendency to move “continuously”.
(ii) There is a tendency for mass and momentum to be conserved.
To give an idea of the kind of thing I mean here, let’s suppose that “mass” is represented by 1s, and you take a large annulus, place it over , and put a 1 at every grid point that lies in the annulus. Then in the interior circle of the annulus put a random scattering of not too many 1s. And then slightly move the annulus part, and slightly move all the little particles inside. If the first position of the annulus represents where some very simple structure is at time 1 and the second where it is at time 2, then conservation of mass and momentum would tell us to expect it to continue moving in the same direction (so it would be more sophisticated than a cellular automaton of the kind described earlier because its behaviour would depend not just on how it behaved an instant earlier), and to stay the same size. We might also have “forces” between neighbouring 1s that encouraged them to stay together somewhat, and so on.
Of course, as with Conway’s Game of Life, the idea would be to devise the simplest possible set of rules that did what one wanted (in this case preserve macroscopic shapes at least to some extent and allow them to move about reasonably flexibly but without distorting themselves too much). It would not be to try to create the most realistic model one could of the actual world.
Since writing the above paragraphs I’ve found out the following relevant facts. First this from the Wikipedia article on Life-like cellular automata:
Larger than Life is a family of cellular automata studied by Kellie Michele Evans. They have very large radius neighbourhoods, but perform `birth/death’ thresholding similar to Conway’s life. The LtL CA manifest eerily organic `glider’ and `blinker’ structures.
RealLife is the “continuum limit″ of Evan’s Larger Than Life CA, in the limit as the neighbourhood radius goes to infinity, while the lattice spacing goes to zero. Technically, they are not cellular automata at all, because the underlying “space” is the continuous Euclidean plane R2, not the discrete lattice Z2. They have been studied by Marcus Pivato.
Secondly, here is the paper by Marcus Pivato mentioned above.
Chemistry and the problem of scale.
By far the most famous contribution to our understanding of how life started is the Miller-Urey experiment, in which Miller and Urey attempted to simulate the chemical conditions that might have prevailed early on in the life of the Earth. They used electrodes to create lightning-like sparks that passed through a vapour that was formed of water, methane, ammonia and hydrogen, and found that they produced complex amino acids, which are essential building blocks of life.
What relevance would this experiment have for a computer simulation? My view is that one should not necessarily try to produce a virtual Miller-Urey experiment (complete with virtual lightning, virtual ammonia, etc.) but that the experiment does raise a couple of questions that it is essential to address.
A fundamental fact about life as it exists in the physical world is that it is carbon based. The great virtue of carbon is that its particular bonding properties allow it to combine with other atoms to form molecules that are large and complicated enough to encode highly sophisticated information. So an obvious question is this.
Question 1: Should one design some kind of rudimentary virtual chemistry that would make complicated “molecules” possible in principle?
The alternative is to have some very simple physical rule and hope that the chemistry emerges from it (which would be more like the Game of Life approach).
This is just one example of a general tension. The more features you design into a model, the less “universal” it becomes and the less convincing it is as a demonstration of the inevitability of life. However, one can also argue for at least some designed features. After all, if we want to explain the origin of life, it is not necessary to start with a virtual Big Bang and get from there to the possibility of complex molecules. It may be that designing rules to make complex molecules possible (and then arguing that with probability 1 this possibility is actually realized) is attacking the problem at the correct level.
I do not have a strong view about what the right answer to this question is. Obviously I would prefer the chemistry to emerge as if by magic, but that may be an unrealistic hope.
The second question does not arise directly out of the Miller-Urey experiment, but it is related.
Question 2: How large and how complicated should we expect “organisms” to be?
A real-world organism, even a micro-organism, is made out of more atoms than one could hope to simulate on a computer. (I am not certain that that last sentence is correct, but I would be very surprised if it wasn’t. Added later: Michael Nielsen tells me that there are rudimentary organisms that are so small that they could perhaps be simulated in full.) Moreover, although it has many levels of complexity, there will also be distance scales at which it is relatively simple. For example, if I look at my hand from a distance of about a yard, my skin looks smooth. Similarly, if I were to look through a powerful microscope at one of the cells of my hand, then the boundary of that cell would be reasonably smooth, rather than fractal-like. In general, it seems that if you look at a typical organism, it is not equally complicated at all distance scales, but is more like this: you take some small objects and put them together in a reasonably simple way to form bigger objects; you then use these bigger objects as building blocks for yet bigger objects; continuing this process for eight or nine (??) levels (perhaps if I knew more biology I would revise this number up considerably) you end up with a complex organism.
If that picture is roughly correct, then the number of “atoms” in a complex multicellular organism might be prohibitively large for a simulation. Is this a problem?
I think it shouldn’t be too problematic. Just as we are not trying to start with the Big Bang, neither are we trying to end with mammals. The main aim is to get to the point where evolution can take over. In particular, if a readily identifiable micro-organism appeared that could reproduce itself with small modifications, then the simulation would surely be declared a success.
Nevertheless, the question of scale remains. Would we want such a micro-organism to consist of a small handful of “pixels” that by some magic local rule gives rise to a copy of itself? Or would we want something much larger that had “smooth boundaries” at some distance scales and was composed of “complex molecules”? My inclination at the moment is to prefer the second for two reasons: it is less like the Game of Life (and therefore more likely to be novel and interesting) and it is closer to the life forms that we actually observe.
Added later: I haven’t quite made clear that one aim of such a project would be to come up with theoretical arguments. That is, it would be very nice if one could do more than have a discussion, based on intelligent guesswork, about how to design a simulation, followed (if we were lucky and found collaborators who were good at programming) by attempts to implement the designs, followed by refinements of the designs, etc. Even that could be pretty good, but some kind of theoretical (but probably not rigorous) argument that gave one good reason to expect certain models to work well would be better still. Getting the right balance between theory and experiment could be challenging. The reason I am in favour of theory is that I feel that that is where mathematicians have more chance of making a genuinely new contribution to knowledge.
November 7, 2009 at 12:29 am |
Life evolved in an environment where there is low entropy energy flowing in and higher entropy energy flowing out. Observationally such systems thrash around looking for maximum entropy production (MEPP: Maximum Entropy Production Principle). We also note that life increases the entropy production of the Earth (intelligent life even more so). So it seems like life is a part of Earth’s search for maximum entropy production. At any rate I suspect you need something which produces a lot of chaotic but self-organizing behaviour on various scales. You also need something (like carbon chains) that can get complex when it finds itself in an area of usefully low entropy. I’d also guess that you need a fractal dimension more than 2, if not all the way to 3.
November 7, 2009 at 8:46 am |
This isn’t directly applicable but might give some inspiration:
“Crystal Nights” is a short story by Greg Egan (online at http://ttapress.com/553/crystal-nights-by-greg-egan/ ) that describes a computer simulation of the evolution of consciousness. He doesn’t talk about how the first replicator in the story was made, but the way he sets up biology is interesting:
“The basic units of biology here were ‘beads’, small spheres that possessed a handful of simple properties but no complex internal biochemistry.”
The creatures in the story go on to physically rearrange their own beads as part of reproduction:
“…reproduction involved two Phites pooling their spare beads and then collaborating to ‘sculpt’ them into an infant, in part by directly copying each other’s current body plans.”
Getting all the way up from Miller-Urey amino acids to whatever the first self-replicator was seems hard. However, maybe a way to approach the problem would be to have the building blocks be larger, and a little more functional, like Egan’s beads.
If they get too functional, to the point at which one of the built-in axiomatic functions of a bead is to make a replica of itself, then this is too much like cheating, but perhaps we can attempt to simplify the axioms down from such a system rather than complicating the axioms up from Conway’s game of life. As the axioms for the beads get less directly about replication, one would expect the numbers of beads needed for a replicator to go up, but perhaps not so far up that it becomes impossible to simulate.
November 7, 2009 at 9:42 am |
Douglas Hofstadter suggested a genetic model in Gödel, Escher, Bach.
The emergence of complex systems probably has to be handled at a range of descriptive levels to keep the computing under control.
eg at two levels –
(i) (atomic) does this system give rise to entities with genetic properties?
(ii) (genetic) are these genetic properties sufficient to produce self-replication, survival etc?
Such a multi-level description – if one is computing at the genetic level – creates the opportunity for events at the atomic level to intrude as apparently random fluctuation/disturbances at the genetic level. One can then ask ‘how robust is this system against such “random” events’.
I think the fractal idea may be misleading, since it invites the suggestion that the description of the system will be similar on different scales. It may be necessary for the description to be radically different on different scales.
One really interesting question which may arise is ‘how fine-tuned do the parameters have to be to make this work?’.
November 7, 2009 at 6:23 pm |
There are some interesting comments here about levels, and that is clearly something that needs to be thought about hard. Henry, your idea of a top-down approach is an interesting one that chimes with thoughts I have had about how one could in principle argue convincingly that computers can do maths. The idea in the latter context is that if you want to argue that computers could have thought of a proof of theorem T, you don’t actually have to show how they would do the whole thing. Rather, all you have to do is show how a computer could, in reasonable time, come up with a reduction of T to problems that are strictly simpler. Then induction does the rest. To put it contrapositively, to demonstrate that computers cannot do maths, you would need to find a statement and a proof of that statement and argue that there is no algorithmic process that could have come up with the general structure of the proof. (A simple example might be if there was some “magic lemma” L such that both L and the implication of T from L are easier than T, but there was no convincing way of explaining how to come up with L. But how does one come up with such an example …?)
Returning to the question at hand, perhaps the right thing to try to do is identify something that deserves to be called “the level just below life”, where you have fairly complicated chemistry, say, or even proto-biology, but you don’t quite have structures that reproduce themselves. You then try to show that life does, with high probability (perhaps only if certain parameters are within friendly ranges), emerge from the promising soup of not-quite-life.
Having done that, the task is reduced to explaining the emergence of the promising soup, which is a strictly easier question. (It might not be easy, but it should be easier.) And perhaps there would be several levels before one got down to something like simple cellular automata.
Returning to the top-level question, perhaps one would be trying to devise something a bit like a cellular automaton, but where the basic objects are not bits, but complicated structures that can combine and split up in interesting ways.
Mark, obviously what I’ve just said also relates closely to your comment. I agree with your view that one should be cautious about fractals, though it does seem that a lot of people jump from “fractals can appear in simple processes” to “biological complexity can be the result of simple processes”. What biology clearly does exhibit is interesting features at many different distance scales, but that is of course not the same thing as fractal structure.
November 7, 2009 at 6:56 pm |
It looks like a step along the top down approach might have already been made. From http://en.wikipedia.org/wiki/Digital_organism :
“In 1996, Andy Pargellis created a Tierra-like system called Amoeba that evolved self-replication from a randomly seeded initial condition.”
A quick descriptive writeup is here: http://www.cs.manchester.ac.uk/~toby/writing/PCW/life.htm
The ‘beads’ here have a lot of built in structure, but it doesn’t quite seem like cheating:
“The genetic code of each cell is a sequence of up to 30 computer instructions, chosen from a repertoire of 16 possible instructions. These are based on standard operations such as ‘jump to address’, ‘copy contents of memory location A into memory location B’, and ‘compare registers and skip next instruction’. Pergellis has carefully designed his instruction set such that it is possible to create a self-replicating cell with only 5 instructions”
Producing the soup might not be easier in this kind of case, when so much of the copying structure is built in.
There is something to think about here, in what combination of simplicity of soup and surprisingness that the soup produces a self-replicator would be a satisfying answer to the question.
November 7, 2009 at 7:40 pm |
That’s a very interesting pair of references. As you say, what Andy Pargellis did is at a very high level, but it is pretty similar to the kind of thing I was describing in my previous comment. So maybe the appropriate first challenge is not getting self-replicating code from randomish code, but getting any kind of code at all from something that is interesting but that does not yet deserve to be called code.
To put that more negatively, what is unsatisfactory about Paregellis’s simulation is that the he doesn’t just create life-forms but he also creates an environment that knows how to interpret the life-forms as instructions for doing things. But how does that situation arise? Perhaps the main goal, at least to start with, shouldn’t be self-reproducing beings but the more basic phenomenon of structures that in some sense encode implementable instructions.
It could be that some fundamental questions would need to be addressed. For instance, we like to think about computational models, and there is a temptation to make them rather efficient. But the computational structures that could emerge through natural chemical processes are probably very different and full of huge redundancies. (At a higher level, these redundancies appear in Pargellis’s self-reproducing life-forms, which I find very interesting.) So perhaps one would need to think hard about computational models and about what it means for a structure to encode a set of instructions that can be implemented.
November 7, 2009 at 7:57 pm |
[…] https://gowers.wordpress.com/2009/11/07/polymath-and-the-origin-of-life/ […]
November 7, 2009 at 9:35 pm |
A few observations about stability and geometry:
It looks like Amoeba’s self replicators are something like combinations of up to 30 of the 16 instructions in a cell, which when run, copy themselves to other cells. They would therefore have reasonably good stability: their structure lives in one cell, and nothing much else in the environment will mess that structure up.
In contrast, meaningful structures in Conway’s game of life are very fragile. It doesn’t seem possible to create a “protective shell” around a structure, that can survive the kinds of random things that one might see in the environment. Similarly, if we move a small part of a structure a little, that change will generally destroy the entire structure.
This behaviour is very different from real life life (RLL), which has resilience and deals with lots of randomness. Everything happens probabilistically, and eventually the right protein and amino acid get together and the next step happens. Amoeba looks like it gets around this issue by having the cells generally protected from incursion from randomness: a cell with random code in it will be unlikely to do bad things to other cells.
Moving onto geometry: rigid geometric rules such as in Conway’s game of life would seem to be too fragile. Amoeba and other “code” life simulations work with only very basic geometric structure, perhaps the environment is a complete graph on some number of vertices, and in each vertex the structure is just a list of commands. In order to pare this back to a less code-like system we would have to break up the instructions, and with nowhere to “put” different parts of an instruction within one of the vertices, this seems difficult.
RLL has real 3d geometry of course, but the way that molecules combine has something of the features of the complete graph as well, in that it’s fine to just wait around until the right molecule bumps into the right receptor. Simulating millions of molecules bumping around is hard, but the effect is as if the receptor has a certain probability of meeting any of the “complete graph” of things sloshing around in the vicinity of it. Once however it does meet the right molecule the geometry of how the added molecule interacts with the existing structure really does matter.
This is connected somehow with the idea that there has to be different levels of “stickiness” of how different elements of the simulation interact: whether when two objects meet they glue together strongly, weakly, break apart some other connection or just bounce off. In Conway’s game of life there is only one level of this kind of interaction, which leads to the brittleness. In RLL there are a huge number.
November 8, 2009 at 5:38 am |
I have just a few quick, possibly disjointed, thoughts about this that are intended to be provocative.
Is an object a living thing if it is the only living thing in its environment? If so, what distinguishes it from a crystal? Certainly a crystal is self-organizing, even if passively so. I’ve always felt that the notion of a living thing requires a sub-notion of otherness, and that the duality of otherness is one of the most basic organizing principles in the soup of life we have on this planet. This is not philosophical speculation plucked out of thin air. Even a very young child realizes that virtually every other conscious being around them, whether other humans or the squirrel in the tree, has a sense of self and not-self. Indeed, without this sense of self and not-self we would probably experience severe hallucinogenic disorientation if we aren’t in fact quickly eaten by something else. But self/not-self is not exclusive to consciousness. Our entire immune system, from skin to cell walls to the highly complex set of cells and messaging cytokines that comprise the adaptive immune system, grapples with this every day in fending off viruses, bacteria, and parasites that degrade our self-integrity, possibly to death. Distinguishing between self and not-self is a tough problem for the immune system (and immunology), and failure is all too common when autoimmunity develops as an accidental byproduct of the adaptive immune system fighting infections. (One could also argue that the brain was originally an extension of the immune system, and inherited the self/not-self duality from the immune system.) Perhaps a living thing is that which actively maintains a stable morphology by playing the self/not-self game on many different levels.
I can’t leave without asserting that the self/not-self game does not imply that selfishness or super capitalism are the natural order of things; they are quite different things. My own immune system recently came to the fore of my thoughts when I wound up in the hospital at age 58 with a mystery infection that either looks, walks, and quacks like the measles I had fifty years ago, or was a biological warfare experiment.
November 8, 2009 at 12:57 pm |
Incidentally, I found quite a nice blog post on the origin of life and the various stages that might have been needed. The author of the post is very concerned to argue against creationists, but that argument isn’t a big feature of what he writes, which is mostly just interesting science. It can be found here.
November 8, 2009 at 1:55 pm |
[…] presentation of one possible near future polymath: the mathematics of the origin of life can be found on Gowers’s blog. Leave a […]
November 8, 2009 at 4:37 pm
I’d just like to mention that if you click on the link of the pingback above (which was created by Gil Kalai), not only do you get a rather nice volcano graphic, but if you click on that graphic you are taken to another web page that has a useful summary of current thinking about how life may have arisen.
November 8, 2009 at 8:31 pm |
I thought I would make a small comment about self-replicating systems: There is an old theorem of Kleene (Kleene’s second recursion theorem), a corollary of which is that in any sufficiently rich, general purpose programming language, there exist arbitrarily complex `quines’, which are programs that reproduce their own output when run on empty input — i.e. they self-replicate… in a sense. If one could interpret interacting collections of atoms as a type of “computer program”, and if the possible interactions are sufficiently rich (so that the laws of physics restricted to the particular domain under consideration effectively constitutes a general-purpose programming language), then it seems to me that arbitrarily complex self-replicating systems are guaranteed to exist. Of course, the property of self-replication is only necessary, not sufficient, for the system to be deemed “alive”.
November 9, 2009 at 10:23 pm
This idea that sufficiently rich systems contain the capacity for self-replication had occurred to me, and I was going to look it up. (NB pretty much every ‘sufficiently rich’ system can replicate some form of programming – albeit very inefficiently in some cases eg Conway’s Life).
Another version of programmed ‘life’ is seen in the repeated playing of the ‘Prisoner’s Dilemma’ – eg Axelrod’s “Evolution of cooperation” – which never really convinced me because the differences between good strategies are marginal – but it does show that there are robust survivors in a competitive environment.
Anyhow, there seem to me to be some ideas worth exploring:
(i) Conservation principles creating a competitive environment
(ii) Entropy – limiting the total order of the system
(the “Life” Glider Gun potentially produces unlimited order – good structure would perhaps avoid this)
(iii) And there is something less tangible about there being self-replicating systems which in some sense form open sets, rather than being isolated points. This would allow for the existence of resilient self-replicators.
November 8, 2009 at 8:31 pm |
I’m very intrigued by these ideas though concerned about “loose talk”. And speaking of loose talk, I have a few ideas I seldom voice to anyone (people look at me as though I am insane when I do). It concerns property 3 above…. If a system has some non-trivial randomness about the way it evolves, then for any fixed initial conditions the possible states at time N will be exponential in N (at least for a little while, until you run into constraints such as the ability of the system to harbor many distinct states). There will be so many states that even if the design is very bad, at least some of the states might be interesting, and look a lot like “life”. So the possibility of “life” doesn’t necessarily require a very good automaton. The only alternative I ever see discussed, though, is finding an automaton where “life” is inevitable, i.e. will arise with probability approaching 1. This seems to be what you are looking for here as well.
What if the physical universe isn’t like that, though? What if, in fact, the probabilities you get out of quantum mechanics produce life with a vanishingly small likelihood (albeit better than coin tossing, presumably)? You could think of all the states existing in parallel. Very few of them exhibit anything resembling life. But, the ones that do have life are the ones where the conscious entities (the “psychons”) are hanging out…because that’s where they want to be, where interesting things are going on–when wave functions collapse, they don’t divide, they go where things are more interesting.
The point about this is that if things did work this way, you wouldn’t run into any limitations in calculation resources….not existing in the physical universe and unbound by time constraints, psychons could in theory perform an enormous lookup or even cheat by being somewhat prescient…I suspect they could do this and still evade detection by suspicious experimenters; in brains for example the chaotic nature of the activity would make it virtually impossible to connect specific firings with their teleological import, so what on earth would you even test for?
A pessimistic viewpoint, but somewhat close to my viewpoint.
November 8, 2009 at 10:44 pm
I agree that what you call loose talk is a worry. One of the things I was hoping to discuss in this thread is whether there is any hope that a Polymath project could achieve anything. On the plus side, it does seem like a project where expertise of many kinds is required: knowledge of mathematics, chemistry, biology, programming, etc. But would it be possible to formulate questions that were precise enough for it to be clear when they had been solved? For example, one question that has already arisen is this: if it is correct to say that a biological system operates at many levels, then how many of those levels, and which ones, should one try to simulate? That seems like an important question, but can one do more than (i) discuss it in a loose way and express hunches about it, and (ii) experiment with some simulations and see what happens? If there is nothing in between — some kind of analysis of what is likely to work and why — then how might a project work?
I suppose one possibility might be that someone volunteers to write a program based on some ideas that emerge from the conversation, the program exhibits behaviour that one doesn’t completely expect, and then one attempts to understand the model well enough to explain why it behaves as it does, perhaps using that analysis to devise better models. But for that to work, we would need some skilled programmers, which I for one am definitely not.
November 9, 2009 at 2:08 am |
About which form of live we may find:
Many religions claim exsistence of spirits. Christianity tells about living spirits (in Bible the word spirit is literally translated “wind”). So Bible tells us that living winds exists.
BTW, I do not only believe in existence of spirits but also has seen some spiritual anomalies such as clouds taking form of some objects such as a cloud in the form of an airplane.
I assume that spirits are living creatures living in Navier–Stokes equations or in some variation of these equations. (But I may mistake, spirits could be alternatively bacteria living in clouds.) Further I will suppose that spirits are living solutions of Navier–Stokes equations.
Navier stocks equations are relatively simple to model. But if we search for spirits (living winds), we do not know what we are searching for. Do separate winds have geometrical shape? Are they “separated” from each other whatever this word means, or all spirits in one big organism? Are spirits small “fluctuations” on the ground of macroscopic wind structures? Do spirits communicate with each other trough sound waves? Or maybe electromagnetic waves in the ionosphere is a part of the life of spirits? After all in the current level of development of mathematics we know nothing about Navier–Stokes equations, how we could know anything about spirits?
Currenly the only way I know to find existence of a spirit is when it would show some intelligent sign, like the above mentioned airplane. Mathematically modelled spirits on current computers certainly cannot reach so high intelligence to understand what is an airplane and how to show it. So even if we will produce a spirit in a computer model, we do not know how to notice that it exists.
After all, if to believe Bible, spirits reached (or it was always so after big bang) the level of development so high that they may create protein life.
November 9, 2009 at 11:45 am |
A small thought I have is that a simulation might be something like this. You start off with a large number of extremely primitive “basic objects”, which one might think of as molecules. When I say “extremely primitive” I don’t mean that they are just single bits — either on or off. Rather, they have some very basic structure to them that affects how they interact. This is supposed to be some analogue of “chemistry”. They move about in a Brownian sort of way (as real molecules might), and when they get close they sometimes combine to form larger objects. The bonding rules, which I see as being randomized, depend on the internal structure of the objects. It is also possible for larger objects to split up into smaller ones: whether that happens would probably be partly dependent on some external temperature that could be one of the parameters that is to be set. (Incidentally, it occurs to me that rather than fine-tuning the external parameters, one might simply allow them to fluctuate, so that they would at least sometimes be in the right range.)
What I don’t yet see is how molecules themselves would form groups that were not themselves huge molecules. It seems as though there would have to be bonding rules corresponding to chemical reactions and different bonding rules that cause distinct molecules to stick together.
At the moment, it seems to me that the big leap is getting to the point where molecules can act as a kind of code that is “understood” by the rest of the system. But this shouldn’t be impossible, as Ernie Croot points out. After all, the whole point of computation is that it reduces complicated algorithms to a series of very simple mechanical steps. So perhaps if one had a “soup” of extremely primitive machines (things like, “If I see a particle of type B, I convert it into a particle of type A and become myself a particle of type C”) together with some mechanism for such machines to hook up with each other, they might combine (given the right selection pressures) to form much more complicated machines.
November 13, 2009 at 2:07 am
Catalysis seems to be a very important example of such a code in real systems. Effectively:
if catalyst present
then X and Y combine to form Z
else X and Y stay the same
November 13, 2009 at 2:50 am
And, of course, the reverse reaction can also be catalysed, e.g., Z disassociates to produce X and Y.
Much more complex reactions can also be catalysed, but to produce computational universality, these two simple types might come especially in handy.
November 11, 2009 at 11:44 am |
[…] 11, 2009 Hold your breath … Tim Gowers proposes a poymath project to answer the question about the origin of life scientifically […]
November 12, 2009 at 6:26 pm |
Cosma Shalizi has done some interesting work on the topic of self organization and attempting to come to a more formal understanding of what self-organization is. I’m not sure whether this is the same sort of life as people are thinking, but its certainly closely related. One idea that he discusses is thinking about the complexity of a time series in terms of the amount of information needed to predict future states. This could provide an interesting starting point.
intro-link plus lots of references towards the end:
http://cscs.umich.edu/~crshalizi/notebooks/self-organization.html
talk:
http://cscs.umich.edu/~crshalizi/Self-organization/soup-done/
phd thesis:
http://cscs.umich.edu/~crshalizi/thesis/
paper:
http://arxiv.org/abs/nlin.AO/0409024
November 12, 2009 at 7:08 pm |
(I meant to include this part in the original comment)
Self-organization, then is defined in terms of a dynamical system whose “statistical complexity” (measured in terms of the information required to infer future states) is increasing without outside intervention.
Intuitively, this seems a lot like life: for any living thing we need a tremendous amount of data and information to predict future states of the organism. One thing (among many) that is lacking in this sort of definition though, is a notion of homeostasis and self-reproduction.
I’m curious as to whether self-organizing systems merely become self-reproducing once they reach a particular point.
November 13, 2009 at 1:42 am |
On whether there are living organisms in the real world that could be simulated in full, let me add a remark qualifying my earlier comment: the smallest organisms that I know of which self-replicate autonomously are bacteria which are a few hundred nanometers on a side. (Viruses can be smaller, but don’t self-replicate without additional machinery). That’s a volume of tens of billions of cubic angstroms. Assuming conservatively that an atom occupies about a cubic angstrom, that means the total number of atoms will be at most tens of billions, and probably far less.
Now, to what extent it’s possible to simulate that depends on how much you’re willing to build in. My understanding is that first principles simulation even of, e.g., very simple proteins is well beyond us now. But if one took as given many of the empirically observed properties of the molecules involved (not to mention the surface physics, and so on), then the interesting point to take away is that the sheer number of particles is not itself prohibitive.
November 13, 2009 at 3:23 am |
I have been interested for a long time in this question so I can’t resist to comment.
First of all many comments indicate the need of some randomization to make the model less rigid. But what is the minimal complexity of a probability space that is enough for the formation of life?
(life itself is a low probability event if we look at life/space ratio in the universe)
Already in quantum mechanics the probability space seems to be of a higher complexity then just a bunch of independent events, let’s says, at the vertices of a certain grid.
But here is an even more drastic speculation:
Quantum mechanics is consistent with a branching model of the universe.
Such a model increases the probability enormously that in one branch interesting life forms appear. So the branching model is a much more complicated probability space, but it is almost impossible to model on computers.
This is of course just crazy speculation. I am also optimistic that a simple linear time model with local rules and randomization can produce surprising structures. An interesting try would be to allow some kind of “evolution” of the local rule itself.
November 13, 2009 at 5:56 am |
It seems to me that momentum conservation is perhaps not so essential for being “realistic”. After all, organisms living (walking) on the surface of the Earth do not see momentum being conserved; you can basically start moving from rest without needing to throw stuff in the opposite direction for propulsion. Of course this is because Earth is huge and you do not observe the momentum it gains when you start moving by pushing it with your feet. One may also argue that inter-organism interactions (collisions!) should be enforced to conserve momentum, even if “Earth-organism” interactions seemingly don’t. I guess my point (without going too much into these detailed issues) is, if you somehow end up with an artificial world with “interesting” “beings”, the violation of certain laws of physics may not necessarily be reason to discard it as unrealistic, and ignore the insights that can be gained from it. In other words, we certainly will do away with *some* laws of physics in the artificial world, and it may be worth thinking hard before deeming a law essential.
November 13, 2009 at 4:25 pm
I think that the main importance of conservation laws (in real life) is that they don’t let the system go “crazy”. But I agree that in computer simulations this can be controlled in other ways as well.
November 13, 2009 at 11:54 am |
[…] Polymath and the origin of life « Gowers’s Weblog […]
November 13, 2009 at 7:57 pm |
Shouldn’t you at least take a glance at the work of Manfred Eigen or Stuart Kauffman?
November 14, 2009 at 12:32 am
Absolutely. I’ve got Kauffman’s book (origins of order) and plan to read it before I’m too much older. I have to confess that I hadn’t heard of Manfred Eigen, though the name somehow rings a bell, so thank you for that and I will look into it. Obviously, one important preliminary is to come up with a goal that was not too close to things that have already been done.
November 13, 2009 at 8:32 pm |
I seriously doubt it, but maybe Gregory Chaitin has some useful thoughts in the subject here: http://www.cs.umaine.edu/~chaitin/jack.html
November 14, 2009 at 2:12 am |
[…] Polymath and the origin of life « Gowers’s Weblog (tags: math bio evolution complexity cellular-automata self-organisation self physics) […]
November 14, 2009 at 5:35 am |
3 Definition of Life
by
Jonathan Vos Post
Annotated text version with citations of graphic PDF Venn Diagram of September 2009
Version 1.0 of 9 Nov 2009, 4 pp., 1400 words
My graphic is a Venn Diagram. The three overlapping circles contain text summarizing these 3 main definitions: The diagram as whole gives my tentative “original” composite definition of life which combines the main 3 definitions given:
“A self-assembled, self-contained negentropic chemical system network of feedback mechanisms capable of undergoing Darwinian evolution.”
There was also a polygonal box with the following text, as the cited article initiated my composition of the diagram: “see pp.56 ff ‘What is Life’ of ‘Origin of Life’ by Alonso Ricardo & Jack W. Szostak, Scientific American, September 2009.”
I. Cybernetic Definition
“A network of inferior negative feedbacks (regulatory mechanisms) subordinated to a superior positive feedback (potential of expansion, reproduction).” [Korzeniewski, 2001]
Summarized for the graphic [by JVP] as: “A network of feedback mechanisms”
I had an arrow from the word CYBERNETICS pointing to this part of the circle, and an arrow pointing from it to a box containing the text: “Best fit to theory of ‘Metabolism First’ as opposed to ‘RNA First’ Biogenesis, network of catalysts which process energy.”
II. Schrödinger’s Physics Definition
Summarized for the graphic [by JVP] as: “Self-assemble against nature’s tendency towards entropy (disorder) (i.e. negentropy). [Note: this was historically the first of these]
I had an arrow from the word PHYSICS pointing to this part of the circle, and under the arrow the text: “Schrödinger also predicted before DNA structure known : 1-dimensional aperiodic crystal.”
I drew an arrow pointing to it to a box containing the text: “Self-assemble” as opposed to assisted self-assembly on mineral substrate such as Clay (Jim Ferris et al.)”
III. Chemistry Definition
“Life is a self-sustained chemical system capable of undergoing Darwinian evolution.” [Joyce]
Summarized for the graphic [by JVP] as: “Gerald Joyce’s ‘working definition’ adopted by NASA: ‘self-sustained chemical system capable of undergoing Darwinian evolution.’ Note: Panspermia allows the Darwinian evolution to have started on another planet or body.”
I drew an arrow pointing to it to a box containing the text: “If we leave out Gerald Joyce’s ‘chemical system’ we cannot simply exclude software ‘artifical life’ in silico — or more exotic substrates.
I drew an arrow pointing from that box to a box wit the text: “Questions: in regions combining only 1 or 2 of these definitions, what counterexamples are possible?”
There was also a rectangular box in the upper right hand corner which read: “Venn Diagram copyright © 2009 by Jonathan Vos Post.”
The overlapping areas of the Venn Diagram
I/II. Cybernetics + Physics
Summarized for the graphic [by JVP] as “self-assembled negentropic network of feedback mechanisms”
II/III. Physics + Chemistry
Summarized for the graphic [by JVP] as “self-assembled, self-sustained negentropic chemical system capable of undergoing Darwinian evolution.”
I/III. Cybernetics + Chemistry
Summarized for the graphic [by JVP] as “self-contained network of feedback mechanisms capable of undergoing Darwinian evolution.”
I/II/II. Cybernetics + Physics + Chemistry
“A self-assembled, self-contained negentropic chemical system network of feedback mechanisms capable of undergoing Darwinian evolution.”
Further clarifications and discussions.
To clarify Schrödinger’s Physics definition, although many non-physicists persist in stating that life’s dynamics somehow go against the tendency of second law (which states that the entropy of an isolated system tends to increase), the definition assuredly does not in any way conflict or invalidate this law. This is because the principle that entropy can only increase or remain constant applies only to a closed system (i.e. one which is adiabatically isolated, so that no heat can enter or leave). Whenever a system can exchange either heat or matter with its environment, both of which apply to the planet Earth and its ecosystem, an entropy decrease of that system is entirely compatible with the second law.
In more modern terminology, life is a dissipative system. A dissipative system is characterized by the spontaneous appearance of symmetry breaking (anisotropy) and the formation of complex, sometimes chaotic, structures where interacting particles exhibit long range correlations. The term dissipative structure was coined by Russian-Belgian physical chemist Ilya Prigogine, who was awarded the Nobel Prize in Chemistry in 1977 for his pioneering work on these structures, some of which rediscovered my research on what I call “enzyme waves.”
As chemist John Avery explains in his 2003 book Information Theory and Evolution, we find a presentation in which the phenomenon of life, including its origin and evolution, as well as human cultural evolution, has its basis in the background of thermodynamics, statistical mechanics, and information theory. The (apparent) paradox between the second law of thermodynamics and the high degree of order and complexity produced by living systems, according to Avery, has its resolution “in the information content of the Gibbs free energy that enters the biosphere from outside sources.” The process of natural selection responsible for such local increase in order may be mathematically derived directly from the expression of the second law equation for connected non-equilibrium open systems
The “Ferris et al” and clay text summarizes the fact that when free nucleotides are combined in water solution, they do not react at all. Hence various teams of scientists have searched for what types of activating groups and inorganic catalysts must have been involved in the polymer bonding process. Dr. Ferris, of Rensselaer Polytechnic Institute in Troy, New York, discovered one inorganic material which facilitates this reaction, namely montmorillonite clay. The specific structure of this clay can provide a medium on which the individual activated RNA units combine to form larger chains.
REFERENCES:
Avery, John (2003). Information Theory and Evolution. World Scientific. ISBN 981-238-399-9.
.
Dr. James P. Ferris. “Montmorillonite Catalysis of RNA Oligomer Formation in Aqueous Solution. A Model for the Prebiotic Formation of RNA.” Journal of the American Chemical Society. 1993, 155, 12270-12275.
James P. Ferris is Director, New York Center for Studies on the Origins of Life
Gerald Francis Joyce, “The RNA World: Life Before DNA and Protein”.
Professor Gerald Francis Joyce (born 1956) is a researcher at The Scripps Research Institute. His primary interests include the in vitro evolution of catalytic RNA molecules and the origins of life. He was elected to the National Academy of Sciences in 2001.
Joyce received his Bachelor of Arts from the University of Chicago in 1978, completed his M.D. and Ph.D. at the University of California, San Diego in 1984, and joined Scripps in 1989. Joyce, quoted in commentary in Science (1992): “Obviously, Harry [Noller]’s finding doesn’t speak to how life started, and it doesn’t explain what came before RNA. But as part of the continually growing body of circumstantial evidence that there was a life form before us on this planet, from which we emerged – boy, it’s very strong!”
Korzeniewski, Bernard (2001). “Cybernetic formulation of the definition of life”. Journal of Theoretical Biology. 2001 April 7. 209 (3) pp. 275–86.
Prof. Bernard Korzeniewski’s home page,
http://awe.mol.uj.edu.pl/~benio/
Faculty of Biochemistry, Biophysics and Biotechnology, Jagiellonian University, ul. Gronostajowa 7, 30-387 Kraków (Krakow), Poland
e-mail: benio@mol.uj.edu.pl
Alonso Ricardo and Jack W. Szostak, , “Origin of Life”, Scientific American, September 2009.
Schrödinger, Erwin (1944). What is Life – the Physical Aspect of the Living Cell. Cambridge University Press. ISBN 0-521-42708-8.
in the famous 1944 book What is Life?, Nobel-laureate physicist Erwin Schrödinger theorizes that life, contrary to the general tendency dictated by the Second law of thermodynamics, decreases or maintains its entropy by feeding on negative entropy. In a note to What is Life?, however, Schrödinger explains his usage of this term:
“Let me say first, that if I had been catering for them [physicists] alone I should have let the discussion turn on free energy instead. It is the more familiar notion in this context. But this highly technical term seemed linguistically too near to energy for making the average reader alive to the contrast between the two things.”
November 14, 2009 at 6:37 am |
More possibly relevant references are the books by Cairns-Smith,”Seven Clues to the Origin of Life”, and by Freeman Dyson, “Origins of Life”. I haven’t read the latter, and don’t know how useful it is. Cairns-Smith’s book was stimulating (but non-mathematical).
November 14, 2009 at 8:16 am |
I cite the mineral substrate theory elaborated by Cairns’Smith in my long submission. Also, to be historical:
Jonathan Vos Post
Charles Darwin’s famous passage in a letter he mailed to his close friend Joseph Dalton Hooker on March 29, 1863, in which he wrote that “…it is mere rubbish thinking, at present, of origin of life; one might as well think of origin of matter”. But yet, in a now famous paragraph in the letter sent to the same addressee on February 1st, 1871, he stated that “it is often said that all the conditions for the first production of a living being are now present, which could ever have been present. But if (and oh what a big if) we could conceive in some warm little pond with all sort of ammonia and phosphoric salts,—light, heat, electricity present, that a protein compound was chemically formed, ready to undergo still more complex changes, at the present such matter would be instantly devoured, or absorbed, which would not have been the case before living creatures were formed […]”.
Darwin, C. Written in 1871, published in 1887. The Life and Letters of Charles Darwin, including an autobiographical chapter, vol. 3. London: John Murray, 18.
November 14, 2009 at 8:09 pm |
Michael Nielsen made a very interesting comment about catalysis and its potential to be used as an element of code. It’s clear that very simple elements like that would be extremely useful.
Suppose, then, that we had a number of such elements that could enable us to simulate AND, OR and NOT gates, say. What would cause these basic computational operations to occur in a given order? Does anyone have any knowledge of how this happens in the biological world? (This may not be a very good question: perhaps the computational model that you get in biology is so different from the one we normally use — even if in theory of equal power — that we shouldn’t be thinking in terms of a long sequence of simple operations. But how in that case should the question be formulated?)
November 23, 2009 at 10:48 pm
On a note related to catalysis-as-computation, there’s a trick Nature uses that I think might be worth building into a model.
The context is the standard story in biology: the transcription of DNA into RNA into proteins, with a very simple dictionary being used to translate codons in the DNA into amino acids in the proteins. Something that long bothered me about this process is that it seemed redundant. If proteins are just defined by a deterministic mapping of codons to amino acids, then surely nature can either do without the codons, or without the proteins? There are many obvious practical responses to this question, but the ones I’ve heard somehow don’t seem very fundamental from an evolutionary perspective.
The answer seems to be that this is a trick Nature uses to store shapes inside a completely regular structure. The DNA double helix has a very regular (and easily copied) shape, while proteins have very complex shapes, shapes that are very important to their function. Protein-folding of course isn’t well understood, but very roughly most proteins end up in a low-lying state (or the ground state) of the polypeptide chain of amino acids making up the protein.
This seems to me like a terrific trick for encoding complex shapes inside a regular, easy-to-copy structure. Those complex shapes can then be used to build up computational models. Processes that might be reasonable to build into a simple model might be (a) transcription; and (b) the ability for molecules to find their ground state (or something close).
November 14, 2009 at 9:42 pm |
“Does anyone have any knowledge of how this happens in the biological world?” Well, my PhD dissertation included this question, and I have been presenting paperts at conferences on Complex Systems, where I listen to, and chair sessions on, Biologists, Chemists, Physicists, Mathematicians alike.
Short answer: I think that it is a philosophical category error to refer to the logic in a catalytic, autopoeitic, metabolic, or genetic regulatory network as ANY of {Analog, Digital} as it is very different from either. Hence it is Not Even Wrong to claim that AND, OR and NOT gates occur in living cells. However, as discussed in my Dissertation, one can BUILD AND, OR and NOT gates into a slightly modified living cell or even simpler system, which is part of what Synbio (Synthetic Biology) is about. The latter field being very active, with hundreds of teams of thousands of people, and parts kits available as trays of samples of dry DNA that is used to make the suite of hundreds of available parts, out of which people can build real (not simulated) wet biochemistry systems, which can indeed perform AND, OR and NOT gate functions in useful ways.
November 14, 2009 at 11:31 pm |
Your answer rather confirms my suspicions, and I think that means that one can begin to identify a subgoal that a Polymath project along these lines would have to have. It ties in with the question of how such a project would differ from what Andy Pargellis did. (See this comment for a link to a description of Pargellis’s work.) The way I see it, one would like to have some notion of a molecule encoding a set of instructions and those instructions being obeyed. One would also like these types of instructions to be powerful enough to simulate any computation. However, almost certainly the model of computation should be quite different from usual models, in stark contrast with Pargellis’s organisms, which were explicitly set up to be conventional (if primitive) computers.
The subgoal I was thinking of was to describe a computational model that was “biologically realistic”. From what you say, there may already have been important work along those lines, in which case I’d be interested to know of references.
If one could come up with such a model, then devising a process that led, with high probability, to implementations of the model emerging, would be an obvious next subgoal. I think only after those two subgoals had been achieved would it even make sense to think about trying to get to the stage of self-reproducing organisms, though Pargellis’s work suggests to me that maybe getting any sort of computation going is the more fundamental challenge, and that self-reproduction can be expected to emerge sooner or later once you have a set-up where the computations that take place can potentially increase in complexity.
Added later: I’ve just spotted this blog post. It doesn’t seem to be exactly what I’m talking about, but it’s certainly interesting and I think some of it is in the same ball park.
November 24, 2009 at 10:37 pm
One line of work on biological models of computation was initiated by Adleman’s famous paper about DNA computing:
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.54.2565&rep=rep1&type=pdf
The idea is very interesting, and relies a lot on rather general ideas of amplification and selection, ideas which I think are potentially very stimulating for any potential Polymath project. I’ve never worked through all the details, and there are places where my knowledge of biology needs to be brought up to snuff to follow the paper. Incidentally, Dick Lipton has a great blog post explaining how PCR amplification works: http://rjlipton.wordpress.com/2009/08/13/amplifying-on-the-pcr-amplifier/
Adleman’s work has been taken a lot further. The Wikipedia article is fascinating, and claims that there are now universality constructions extending Adleman’s original ideas (which were just for the Hamiltonian cycle problem), and much else besides:
http://en.wikipedia.org/wiki/DNA_computing
The top Google Scholar citations to Adleman’s paper also show several interesting leads:
http://scholar.google.ca/scholar?cites=9946731965107616971&hl=en&as_sdt=2000
Another interesting-looking line of work claims that chemical kinetics is Turing Universal:
Click to access PhysRevLett%2878%291190.pdf
November 15, 2009 at 8:31 pm |
Identifying criteria of success for this project requires identifying what is characteristic of life. I would argue that it is *not* necessarily natural selection acting on self-replicating entities. The simplest self-replicating entities may be so complex that they could not have arisen by chance in a finite universe. If so, then an alternative mechanism is required to explain their emergence. Granted, success in simulating life’s origins might always be recognized by the eventual emergence of self-replicating entities, but it may be that the path to such emergence is quite long. So it might be wise not to insist too strongly on property 7.
I would argue that a more generic view of what is characteristic of life is *the emergence of complexity from simple laws acting over long periods of time*. From this perspective, the first order of business would be to determine what precise notion of complexity is at work here. One can then evaluate the performance of any given model of life’s origins by whether and in what manner the appropriate measure of complexity increases. In other words, I’m proposing that property 2 should be emphasized and should be cashed out in terms of a measure of complexity.
It would be useful if someone who knows this field better than I do could provide the key references. The chapter entitled “Complexity and Evolution” in “Complexity, Entropy and the Physics of Information” edited by Wojciech Zurek is one.
November 23, 2009 at 10:20 pm
A problem with using self-replication as a criterion is that it becomes hard to distinguish from other phenomena which we ordinarily don’t regard as life. Crystal growth is one. In some sense the lattice structure is self-reproducing, but it’s hard to see that process as lifelike, as natural selection doesn’t seem to be in play.
(I don’t recall where I first heard this observation made, but it’s not mine. Might be from Cairns-Smith’s book.)
It would be interesting to precisely formulate the idea that natural selection acts. One idea that immediately comes to mind is that it should be possible to introduce small perturbations somehow while (a) preserving the self-replicating property; and perhaps (b) approximately preserving the phenotype. Even point (a) alone seems quite interesting, and worth attempting to make more precise.
November 15, 2009 at 8:40 pm |
One would like a measure of complexity that respects the following rough assessments: living objects are more complex than nonliving, Boeing 747s are more complex than mounds of dirt, and human beings are more complex than bacteria. What are some candidates for such a measure? Here are a few that I can think of, together with an assessment of their appropriateness. (I’ll consider the complexity of objects in a cellular automaton world rather than physical objects in the real world in order to sidestep the problem of providing a digital description of physical objects.)
i) Algorithmic complexity of the object
The algorithmic complexity of a binary string is the length of the shortest program that generates that string. More precisely, it is the shortest binary input which causes a particular universal Turing machine to produce that string as output. It was proposed by Solomonoff and independently by Kolmogorov and by Chaitin. One could obtain an associated measure of complexity for an object in a cellular automaton world as follows: draw a line around the object and calculate the algorithmic complexity of the pattern within the boundary. Repeating patterns will have low complexity, algorithmically random patterns will have high complexity, while the interesting objects that exhibit some order (the organisms and artefacts) will have an intermediate degree of complexity. So algorithmic complexity does not fit the bill. One would like a notion of complexity for which random patterns are not deemed the most complex.
ii) Algorithmic complexity of an equivalence class of objects
A possible solution to the problem outlined above is to define complexity for a class of objects that have the same function, rather than for a particular object. After all, one isn’t really interested in the relative complexity of a particular Boeing 747 and a particular pile of dirt, but rather of the set of things that function like a 747 and the set of things that function like a pile of dirt. There is a demarcation problem here — what counts as functioning like a 747 or a pile of dirt? This may be a difficult problem or it may be that the relative complexity is not so dependent on where the boundary is placed. In any case, let’s leave the demarcation problem aside for the moment. How should we define the complexity of an equivalence class of objects? A natural choice is to take the infimum of the algorithmic complexity of its members (this was first suggested to me by Robin Blume-Kohout). It may well be that the equivalence class containing random patterns contains pseudo-random patterns with low algorithmic complexity, while equivalence classes containing organisms and artifacts with specialized functions have no elements with low algorithmic complexity. In this case, the resulting measure of complexity would be of the sort one wants.
iii) Logical depth
Charlie Bennett has proposed a different way of trying to do justice to our intuitive notion of biological complexity. He defines a measure of complexity for a string, called “logical depth”, as the execution time of the shortest program that generates that string. Noting that one might achieve shorter running times with longer programs, Bennett also defines a more refined notion of logical depth: an object’s “s-significant depth” is the execution time of a program that generates the string and is no more than s bits larger than the shortest program. The idea here is that an object is complex in proportion to the amount of computational work required to generate it. This measure judges both repeating and random patterns to be of low complexity, because programs generating these run quickly. An ephemeris (a table indicating where planets and stars will be found in the sky on various dates) has small algorithmic complexity (because it can be deduced from initial conditions and simple laws of motion) but large logical depth (because it embodies a large number of calculations). An organism having a long evolutionary history is likely to embody more computational work than ones with a short history and consequently organisms on the branches of the evolutionary tree will be more complex, by this measure, than organisms on the roots. Bennett attributes the idea of logical depth to Chaitin and specifies a number of other related references. See http://www.research.ibm.com/people/b/bennetc/utmx.ps.
Unfortunately, none of these measures are computable, but they may motivate some computable measures that could be used to assess models.
November 15, 2009 at 10:02 pm |
The general question of coming up with a measure of complexity that assigns low complexity both to regular repeating patterns and to random patterns is one that has always interested me, and even has something of a tie-in to the questions I have worked on in additive combinatorics (where highly structured objects and highly random objects are easy to deal with and the problems come in between).
When it comes to static patterns of pixels, one can do things like taking some kind of transform (such as the Fourier transform, a wavelet transform, or something along those lines), truncating it, and looking at the algorithmic complexity of what remains. I’m not saying that that kind of idea is relevant here, but just that there are things one can imagine doing that are basically along the lines of what you suggest in (ii). (Here, the equivalence relation would be “is equal, when you truncate the ***** transform, to”.)
But I think that the real equivalence relation of interest is, as you suggest, something more like “does roughly the same as”.
Another problem that would bedevil any attempt to come up with a good definition is the same one that bedevils attempts to prove lower bounds in circuit complexity: there seems to be no observable difference between random and pseudorandom phenomena. This is, I think, a problem with any notion of algorithmic complexity. For example, a highly random arrangement of particles will behave very like (and therefore be equivalent to, according to the relation quasi-defined above) an extremely simple pseudorandom arrangement. Hang on … maybe that’s good news rather than bad, as we want it to count as having low complexity. But in some funny way it appears to have low complexity “for the wrong reason”.
I still think that a fundamental question is the following basic one: what would cause one to pick out some part of the model and say that it was “doing something”? At the lowest level one might build that in (e.g. one might have simple molecules that could react with one another) but the problem would then appear at the higher level of collections of molecules. If one is not clear about this, then it is hard to see how one can even get started with defining a useful measure of complexity.
November 16, 2009 at 4:08 am |
See also this link to an integer sequence I posted which is related to “Artificial Chemistry”
http://www.research.att.com/~njas/sequences/A101145
A101145 List of molecules in Hintze-Adami artificial chemistry (see comments for definition).
Arend Hintze and Christoph Adami, “Evolution of complex modular biological networks.”
PDF of latter is
Click to access 0705.4674.pdf
November 16, 2009 at 5:46 am |
one reference potentially worth considering, although largely unrelated to every other comment, is michael thompson’s recent book entitled, “Life and Action: Elementary Structures of Practice and Practical Thought.” in it, the author expounds on the difficulty of defining life in a meaningful and non-tautological way. it seems to generally be regarded amongst philosophical folk as revolutionary. i haven’t finished it yet, so i’m withholding judgement. it is entirely non-mathematical (at least, so far), but might be helpful with regard to defining our desiderata here for this project. anybody else have any thoughts on this?
November 19, 2009 at 2:16 am |
I’m part way through writing a monograph on complexity of biological networks. Specifically, neural networks (not just in the brain, my first example is the 1% of your neurons that are in your gut — could that be conscious?) and genetic regulatory networks and immune system networks and metabolic networks. In that light, and some of the discussion on this thread so far, I’ll note that this was just posted about 10 minutes ago and seems very on-topic.
arXiv:0911.3482 [ps, pdf, other]
Title: Complexity of Networks (reprise)
Authors: Russell K. Standish
Subjects: Information Theory (cs.IT)
Network or graph structures are ubiquitous in the study of complex systems. In a previous paper [arXiv:nlin/0101006], a complexity measure of networks was proposed based on the {\em complexity is information content} paradigm. The previously proposed representation language had the deficiency that the fully connected and empty networks were the most complex for a given number of nodes. A variation of this measure, called zcomplexity, applied a compression algorithm to the resuling {JVP: resulting} bitstring representation, to solve this problem. Unfortunately, zcomplexity proved too computationally expensive to be practical. In this paper, I propose a new representation language that encodes the number of links along with the number of nodes and a representation of the linklist. This, like zcomplexity, exhibits minimal complexity for fully connected and empty networks, but is as tractable as the original measure. This measure is extended to directed and weighted links, and several real world networks have their network complexities compared with randomly generated model networks with matched node and link counts, and matched link weight distributions.
November 19, 2009 at 4:50 pm |
What a great polymath project to cooperate if i had free time !!
I just can suggest one reading wich is a must regarding this matter: “The origins of life: from the birth of life to the origin of languaje” from Maynard-Smith and Szathmary. The whole thing is explained from a biological point of view but giving to the informational issues the attention they deserve. Also Kauffman ´s, wich was a pioner in biological theory is worth reading (e.g .auto-catalysis networks)…And add some quick comments:
1 If you want the model to be realistic the concept of level is fundamental. As a principle, no agent in a higher level can contradict the restrictions of the lower level (i.e. biological systems can not contradict physical laws). If not you can end with models wich are more game than life.
2 There is a consensus that the unit of life is the cell (and as it has been already pointed the simplest of cells are bacteria).
3 Cells are embedded in an environment and what they do is to extract energy from this environment and use this energy to self-mantain and replicate.
4 So any model for the origin of life must start with an input wich represents an inert physico-chemical environment with physical and chemical elements containing energy and end with an ouput wich are cell-like units.
5 Let´s see more concretelly what one would expect as ouput of the model. Let´s see a cell as a computational-robot system: the membrane would be the tape where the inputs are represented, the chemical and physical elements of the environement would be the inputs, the DNA is the memory where the inputs, the RNA are the processors and the proteins are the actuators. So the cell can be seeing as a parallel computing system. Computations are energy extraction from the environment.
6 I do not see replication per se as important. Non living flexible 3D·membranes duplicate naturally when you inject more fluid inside.·So the more energy an efficient cell gets from the environment the, quicker it will grow and naturally divide. Of course the dificult task for the cell and what must be explained by observers as us is how the cell controls this replication keeping the complex DNA-RNA-Proteins etc…machinery alive in both copies. As an aside commment, regarding duplication, one thing remains unexplained by some current biological theories: if the aim of the gene is maximize self-replication how is it the case that no cell has been found yet that effects multiplication i/o duplication ?
To conclude once you find the correct model to formalize the environment and the cells within it you will realise that the only possible path to understand the origins of life is to explain the main biological invariant wich is the non arbitrary four letters code and its semantics. And the the clue for this was already foresee by Darwin as J. Vos Post quotes: “…it is mere rubbish thinking, at present, of origin of life; one might as well think of origin of matter” (and i add of mind and of society).
November 19, 2009 at 6:03 pm |
I agree with proaonuiq. John Maynard-Smith’s books influenced me since my Caltech days (1968-1973) and through my PhD work. He was instrumental in the application of game theory to evolution and theorized on other problems such as the evolution of sex and signalling I also appreciated Szathmary’s work. Eörs Szathmáry (born 1959) is a Hungarian theoretical evolutionary biologist. Wikipedia summarizes:
Professor Szathmáry’s main achievements include:
* a mathematical description of some phases of early evolution;
* a scenario for the origin of the genetic code;
* an analysis of epistasis in terms of metabolic control theory;
* a demonstration of the selection consequences of parabolic growth;
* a derivation of the optimal size of the genetic alphabet;
* a general framework to discuss the major transitions in evolution.
I attended lectures early in grad school (i.e. 1973 and 1974)by Stuart Alan Kauffman (born 28 September 1939) who is an American theoretical biologist and complex systems researcher concerning the origin of life on Earth. My coauthors and I cite him and quote him frequently in our refereed papers not only in Mathematical Biology, but also in Mathematical Economics. We have told him that we expect him to win a Nobel prize.
I also agree and have spent consderable time dealing with the point that
“If you want the model to be realistic the concept of level is fundamental.” This raises extreme problems in computational effort, as there are on the order of 20 orders of magnitude in both time and space of systems and subsystems modeled. I have a long paper on quantifying these challenges, and literature survey on how they are being tackled by various research institutions.
There were some other points raised in proaonuiq’s comment which I find interesting, but do not feel impelled to explore tangentially at this time. However, I am not convinced at all that there is a unique “non arbitrary four letters code and its semantics” because we only have in vivo data from one planet sofar. The value of Theoretical Computational Biogenesis and Evolution is to be:
(1) inclusive enough to fit data from Life as We Know it (as John Holland did in his original Genetic Algorithm book which I “beta tested” and coded in grad achool, as I was the first to use GA to evolve working software in semantic space which solved existing unsolved problems in scientific literature);
(2) exclusive to the extent as being not so abstract as to be “more game than life”;
(3) allowing discovery of life-like systems which are unquestionably “Life As We Do Not Know It” — i.e. in a very different part of phase space from terrestrial life.
(4) The above applies at every level
(5) one can study “artificial Physics” (i.e. toy Quantum Mechanics, life embedded in higher deimensions and nonEuclidean spaces and the like, such as my work with Conway Game of Life in hyperbolic planes;
(6) One can study “artificial chemistry” as I cited earlier;
(7) One can study “artificial biochemistry” with analogues of enzymes and membranes;
(8) one can study artificial cells with different organelles and architrtectures;
(9) One can study artificial tissues;
(10) one can study artificial organs;
(11) One can study artificial organisms (i.e. the global race to completely simulate a sing;e E coli cell);
(12) One can study artificial ecosystems.
The vast problems associated with doing combinations of the above suggest that it is very important to focus the Polymath project at something that needs considerably less resources than all the computers in the world for a century.
The must-read fiction is by Greg Egan. Check his own web site. He is monumentally adept at dealing with these issues in fiction, and also coauthors Mathematical Physics with John Baez, and also makes wonderful interactive color 2-D and 3-D graphics.
November 23, 2009 at 2:29 am |
Sample of text from the arXiv paper that I cited here on 19 Nov 2009:
Complexity of Networks (reprise)
Russell K. Standish
Mathematics, University of New South Wales
Submitted to Proceedings of the National Academy of Sciences of the United States of America
In artificial life, the issue of complexity trend in evolution is extremely important[3: Mark A. Bedau, John S. McCaskill, Norman H. Packard, Steen Rasmussen, Chris Adami, David G. Green, Takashi Ikegami, Kinihiko Kaneko, and Thomas S. Ray. Open problems in artificial life. Artificial Life, 6:363–376, 2000.]. I have explored the complexity of individual Tierran organisms[22, 23: Russell K. Standish. The influence of parsimony and randomness on complexity growth in Tierra. In Bedau et al., editors, ALife IX Workshop and Tutorial Proceedings, pages 51–55, 2004. arXiv:nlin.AO/0604026.
24. Russell K. Standish. Complexity of networks. In Abbass et al., editors, Recent Advances in Artificial Life, volume 3 of Advances in Natural Computation, pages 253–263, Singapore, 2005. World Scientific. arXiv:cs.IT/0508075.], which, if anything, shows a trend to simpler organisms. However, it is entirely plausible that complexity growth takes place in the network of ecological interactions between individuals. For example, in the evolution of the eukaryotic cell, mitochondria are simpler
entities than the free-living bacteria they were supposedly descended. A computationally feasible measure of network complexity is an important prerequisite for further studies of evolutionary complexity trends.
November 23, 2009 at 4:23 pm |
I remind Kauffman Investigations were trully inspiring (though i´m not so sure that he is the kind of researcher a Nobel is awarded to). Besides Maynard-Smith, two researchers wich has contributed much to the field of biogenesis are Cairns-Smith and Cavalier-Smith (is there some ¿?-Smith involved in this project ?).
In any case i would like to suggest another book worth reading regarding the subject of this polymath project: “The chemistry of Life” from Steven Rose. It is an introduction to biochemistry, where you can see how life is best understood when you see it as an energy processor machinery (i do not want to be polemic but the replicators-gene as unit of selection view, so in vogue in or times, is clearly misleading).
I agree with J.Vos Post that, as usual when doing scientific modelling, the hardest task is to find the correct level of abstraction: too concrete and you are the Borges cartographist, too abstract you are doing pure mathematics (wich is great, but not the target).
What we would expect from a trully biological theory (and i´m not minimizing advances up to now, i think they are great) is to be able to answer questions such as: what kind of lifes are possible in nature ? In other words what variations are possible within life parameters ? For instance, is it possible to construct cells with:
Parameter a: different materials as those used by actual living objects (saccharides for energy, aminoacids for actuators, nucleic acids for memory and processors, and lipids for the tape) ? We do not know.
Parameter b: with an n letters code (with n diferent from 4) ?
Paremeter c: with m-plication (with m diferent from 2) ? We do not know.
Parameter d: with different methabolic paths ? I do not know.
Parameter e: using as energy keeper a molecule different than the ATP ? I do not know.
Other questions that a trully biological theory may answer are (though these are not related with biogenesis so i will not developpe in full here) are:
–Is evolution (i.e. the emergence of variation in life objects) endogenous or exogenous (i.e. driven totally by environment changes)? At present the current consensus seems to be that evolution is mainly exogenous (given an abiotic environment, if you could control it, you could get life of any parameter, any kind of organisms and species…. Again i do not want to be polemic, but I´m sure that as the trully biological theory advances, we will see that even in a constant environment life would have generated variation anyway: life is more the novelty looking for its niche than the niche creating the novelty.
–what kind of especies are possible ? We do not know.
–Wich is the correct unit of selection ? We do not know despite extensive discussion.
–What kind of organisms are possible ? In other words is the homeobox complex universal ?
To conclude, we (almost) have this kind of trully theoretical knowledge in physics (with permission of multiversists) and i assert it is also possible in biology. One just need to find the correct biological model (wich of course must be based on the correct physical model).
November 23, 2009 at 5:20 pm |
See Nov 2009 Physics Today, pp.13-14.
There have been threads and postings among my facebook friends on
this, at various levels of understanding. The point is, only 2% of
the Human Genome codes for proteins. 50% to 80% of human DNA is the so-called Non Coding Type or ncDNA which is transcribed into RNA
molecules of various sizes. The differentiation of cell types in
humans involves attaching a variety of epigenetic markings including
acetylization of the histone proteins that support the DNA in
chromosomes, or methylization of the nucleotides themselves at
specific sites on the cellular DNA of eukaryotes. What interests me
[JVP} in my research is that human memory may also be controlled by
epigenetic labeling. The Physics Today letter shows that it is theoretically by a complexity argument for all human memory to be related to epigenetic markers on DNA in neurons.
November 24, 2009 at 12:42 pm |
To quote you:
“Does there exist a model with the following properties?
(i) If you draw some large-scale shape (think of the 0s and 1s as black and white pixels, say, so the shape is on a much larger distance scale than the distance between two neighbouring points of the grid), it has a tendency to move “continuously”.
(ii) There is a tendency for mass and momentum to be conserved.”
…
How about the Universe? Under supersymmetry it to moves continuously if you change all the fermions to bosons and back again repeatedly.
November 24, 2009 at 2:09 pm
Hmm … I was hoping for a slightly smaller-scale model than that!
November 25, 2009 at 10:12 pm |
I’ve recently come across the concept of autocatalysis, which was invented by Stuart Kauffman. Does anyone reading this know how successful his theory is regarded as being? I understand that chemists have produced autocatalytic sets in the lab. It seems to me to be a wheel that Polymath would not want to end up reinventing.
November 25, 2009 at 10:37 pm |
Here’s an outline of a reasonably simple model that I believe has all of these properties, at least in some degree. It’s a simple abstraction of real biological systems – the model occurred to me as I was waking up this morning, probably because I’ve been thinking about real biological systems for another project.
Many details of the model are incompletely expressed, and need to be filled in (or simplified), but I hope the sense is clear. In the general spirit of Polymath it seemed worth sharing the model now despite these inadequacies.
The model is based on a two-dimensional square grid of cells.
There are 5 cell types, labelled 0,1,B,E and S. I’ll explain the notation shortly.
For the 0 and 1 cells, orientation matters. I’ll use 0 and 1 to denote the standard orientation, and and
and  to denote the upside down versions. The other two orientations I won’t need, and so won’t introduce any notation. Better notational suggestions would be most welcome.
to denote the upside down versions. The other two orientations I won’t need, and so won’t introduce any notation. Better notational suggestions would be most welcome.
For the other cell types, orientation does not matter, and I will use the same notation, regardless of orientation.
The basic idea is inspired by biochemistry. It’s to set simple rules for bonding between nearby cells to form “molecules”, and similar bonding rules for the molecules. I’m sure the rules I give can be dramatically simplified; this is the simplest abstraction of real living systems that occurred to me.
The B cells like to bond on to the left of 0 and 1 cells when they get close (this is in the standard orientation), giving B0 and B1.
In the upside down orientation, this gives us B and
B and  B.
B.
Furthermore, B and B0 molecules like to bond when they get close, bonding on the B’s (B is for bond) to form a new molecule:
B and B0 molecules like to bond when they get close, bonding on the B’s (B is for bond) to form a new molecule:  BB0
BB0
As do B and B1 molecules when they get close:
B and B1 molecules when they get close:  BB1
BB1
I’ll call these four-element molecules “links” – the idea is that a link corresponds to a single DNA base pair.
If we have an incomplete stack of links like so:
 B
B
 BB1
BB1
 BB0
BB0
 BB1
BB1
 BB0
BB0
 BB1
BB1
 BB1
BB1
 BB0
BB0
 BB1
BB1
 BB0
BB0
Then a B1 (or B0, if that’s appropriate) molecule likes to slot in:
I’ll call this a stack.
Both B0 and B1’s like to bond on top (or bottom) of a stack, to form a new incomplete stack.
The E cells like to bond together in groups of 4, linearly arranged: EEEE. Again, this rule or something like it can emerge from simpler rules. I’ll call this an endcap (E is for endcap).
Endcaps like to sit adjacent to one link, but not two. So you can easily get EEEE to sit on top and bottom of a stack, but stacks with endcaps won’t join together.
The last set of rules is designed to split apart stacks with double endcaps into two half stacks. It involves an S cell coming and bonding to the top of the third cell in an EEEE endcap. This then causes the entire stack to “split” apart (before the S unbonds). To be realistic, the split needs to propagate locally down the stack – various mechanisms can be imagined that allow this. The result is two “half stacks”, some distance from one another, preferably with a momentum that keeps them separate. The rules above will then ensure that each half-stack rapidly self-assembles into a full stack, given a reasonable background supply of B0 and B1 molecules.
With these rules, reasonable initial densities for the different cell types, and a fair amount of random interaction, you’ll see self-replicating entities pretty quickly. Stacks with endcaps will self-assemble, and then sooner or later be split apart into two halves by an S cell, and then each half will self-assemble complete copies, which will then be split apart, and so on.
It is easy to add a small stochastic element to this model to give a mechanism for mutation. Further changes will give a mechanism for lengthening or shortening stacks with endcaps.
Many simplifications suggest themselves – it’d be easy enough to get rid of the double B’s, for example, and use just a single bonding element. (In fact, it should be possible to get rid of the B’s altogether.)
Something not obviously in this model is a notion of natural selection. In an earlier comment I suggested a mechanism which could be used to take the above model and give rise to complex shapes and functional behaviour. I suspect the phenotype could be complex enough that natural selection could be said to act. That comment is here:
November 26, 2009 at 4:18 am
A few very minor observations:
(1) It’s possible this would work better in R^2, rather than on a discrete grid. In particular, working in R^2 gives a relatively natural way of thinking of the cells as essentially billiard balls bouncing around, and occasionally binding together as rigid bodies, or unbinding.
(2) For someone appropriately skilled, a model along these lines might be fun to code up, and play with. I know I’d love to see an apparently frothing see of chaos suddenly show replicators.
(3) The phenotype is rather simple – it looks to me like the main aspect of the phenotype will be the time required to replicate, which will be determined by the number of 1’s and 0’s in the “genome”, and the density and velocity of the respective cell types (especially 1s, 0s and Bs) in the environment. It’s possible there is some other aspect to phenotype that will also turn out to be important for selection, but I don’t see it right now. Whether any of this gives rise to evolutionarily interesting pressures, I can’t tell.
(4) It seems to me as though for suitable (but rather generic) assumptions about the parameters of the system, it ought to be rather easy to prove that self-replicating creatures will arise. In fact, it seems likely that rather tight bounds on the time could be proven.
(5) The respective densities of the different cell types will obviously be crucial. Roughly speaking, you want 0,1 and B to be common, and E and S to be rather rarer.
November 26, 2009 at 4:31 am
In the last comment, “see” should of course be “sea”. But I very much like “see of chaos” as an expression – one of the towns I grew up in could quite accurately be described as being within the see of chaos.
November 25, 2009 at 11:03 pm |
Much about this model can be simplified by eliminating the B’s and the orientations. One simply has rules allowing 0’s to pair, and 1’s to pair: 00 and 11, and for 0’s or 1’s to attach to the top of stacks of such pairs, e.g.:
1
00
11
00
00
11
A 1 is then the only thing allowed to bond into the missing space. The endcaps and splitting proceed more or less as before. It is necessary to prevent triples like 000 forming “horizontally” in the above stack, while allowing them vertically.
November 27, 2009 at 11:24 am |
Michael, it would be good to have a clarification of precisely what properties you see as being captured by this model. As I see it, what you’ve got is a simple mechanism for a string of code to reproduce: it gradually builds up, then splits down the middle, and then each free-floating half has a tendency to attract cells that join on and form a copy of what you had before the splitting. Is the idea that this would be a process that could underlie some larger-scale process that incorporated selection pressures, and with luck led to the code actually doing something?
November 27, 2009 at 9:13 pm
The model I outlined obviously has property 1.
I’m not sure the model has property 2 (not too random, not too simple, features at many length scales), but below I sketch an idea that suggests a simple extension of the model that would go a long way toward satisfying property 2. I’m not sure about the “features at many length scales”, though.
I’m not sure I understand property 3 (randomized model). Much about the model will be robust to a wide range of variation in initial conditions. It will also be somewhat robust against occasional exceptions to the rules I described, but that robustness will decrease as the size of the stacks increases.
I think it’s reasonable to say the model has property 4, if you regard these “zipped up” stacks as identifiable macroscopic structures. But maybe that’s not quite complex enough. The extended model sketched below will give rise to more complex shapes, although perhaps still not quite as much as one might hope.
I’m not sure I understand property 5, or whether this model has it.
If one grants the model has property 4, then property 6 (destructive interaction between macroscopic structures) seems like something that would either happen naturally in the model, or could easily be added. The splitting cell S has something of this flavour; you could imagine another cell D that would have an even more disruptive effect, perhaps splitting stacks into two halves, or otherwise ripping them up. Even just causing a mutation in the stack would be pretty interesting.
I believe property 7 is clear, and that a proof could probably be given for a discrete version of this model. For a version in R^2 that doesn’t seem so clear – the obvious sorts of properties you’d want would be related to ideas like ergodicity, which might well be true, but hard to establish rigorously.
There is an interesting subtlety about property 7, which is that that if the expected number of copies of a given stack is less than 1, then it’s not really clear that it deserves to be called self-replicating, since it will quickly “die out”. Whether that is the case seems like it will depend on the relative densities of the different cell types, and on details of the model that I haven’t fully specified. In any case, it seems clear that provided the density of S and E cells is low compared to the other cell types, this should not be a problem.
Coming back to the question of macroscopic structures, suppose you introduce two additional cells types, X and Y. These will play the role of amino acids. The idea is that X’s attach to 0’s, and Y’s to 1’s. When a whole chain forms on the side of a stack, the amino acid chain detaches, and then “folds”. The mechanism for folding could either be some simple local annealing rule, or maybe just a rule that says it goes straight to the ground state. (The same type of rules might possibly be used to enforce the bonding behaviour in the unextended model). To get interesting shapes one would need to think a bit about the form of the Hamiltonian for the chains, and possibly introduce more than two types of “amino acid”, but I think this should be fairly easy to achieve – the main idea is to set up competition between different types of interaction, forcing the chain to fold in interesting ways to minimize energy.
Note that if D cells could be incorporated into the proteins (maybe X’s turn into D’s once the protein detaches), then this gives a natural way of meeting property 6 – stacks can produce proteins which in turn can disrupt other stacks. You can imagine other “defensive” proteins evolving which would try to stop that from happening.
I hope I’ve been clear enough above. The model is obviously not well-specified at present, and is both too complex and inadequate in various other ways. For example, when the half-stack starts to reassemble, there are questions one might ask about how the reassembly works. How do the endcaps come back, for example? It’s easy enough to sort out this particular question, but it would be great to have a fully-specified model that’s very simple, easy to analyse, and hopefully prove some interesting theorems about.
November 27, 2009 at 10:05 pm
Let me try to explain property 5, or at least the thought behind it. If one is going to talk about structures reproducing themselves, one needs to know when two structures count as the same. In Conway’s game of life the answer is simple: they are the same if one is a translate of another (or perhaps also a reflection or rotation). But if one is talking about quite large structures, then the criterion for identity almost certainly wants to be looser than that: to take an extreme example, even if we had two identical twins who were completely identical, they certainly wouldn’t be translates of one another. So some kind of map with a strong continuity property seems more appropriate, or if the structures are not tied quite so much to the geometry then perhaps one would be looking for a more functional description of when two entities are the same. I was imagining a simulated primeval chemical soup and thinking about the problem of when one would count some part of it as being an entity in its own right and when one would count two entities as being the same, or belonging to “the same species”.
The structures you are talking about look as though their criterion for identity is that one can be translated to become the other, unless you work in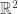 and make them bendy, in which case it is the order in which the different kinds of cells appear. Either way, it is a fairly rigid equivalence relation, but that is probably appropriate for the sorts of low-level structures you are considering.
and make them bendy, in which case it is the order in which the different kinds of cells appear. Either way, it is a fairly rigid equivalence relation, but that is probably appropriate for the sorts of low-level structures you are considering.
November 27, 2009 at 11:08 pm
Thankyou for the clarification.
I get the sense that you’re looking for another level of complexity beyond the features in the model I’ve sketched. Can you say what sorts of things you’d be looking for?
November 27, 2009 at 11:16 pm
I should perhaps qualify my last comment slightly to say “beyond the features that are obviously present in the model I’ve sketched”. My belief is that the power to get nontrivial shapes is likely to be extremely powerful, and to have consequences that are not at all obvious.
In a related vein, an interesting question might be whether there exists some abstracted model of protein folding along the lines I’ve suggested which has the property of “shape universality”, i.e., the ability to “program” an arbitrary shape.
November 29, 2009 at 10:20 pm
To follow up with some further thoughts on property 5, it may be that the right level to operate at is the “genetic” level. Different members of the same species tend to have DNA that is pretty close to being identical, while other species are further away.
Using a genetic criterion like this would avoid the problem of evolutionary convergence, where two species are superficially very similar because they evolved to fill the same ecological niche, but they actually have quite dissimilar genetics.
I suspect it’s also a simpler criterion to apply than any more functional criterion, since it involves only a comparison of digital information, and not more complex notions of shape, form, and so on.
November 27, 2009 at 10:46 pm |
I agree the two most recent comments by Gowers. (1) I am one of many who take autocatalysis, which was invented by Stuart Kauffman, and Kauffman’s broader theories, VERY seriously. That’s why I mentioned him in a much earlier comment. (2) I agree about “rigid” and “loose” equivalencies in simulated biological systrems. That is why I gave both a clutser of definition of Life (citing to major figures in the literature) and a sketch of the many levels over space and tim,e in which such systems exist and undergo dynamics. A robust and interesting simulation operates at many such levels, up through an ecosystem of interacting higher and lower vitual organisms. There are challnging important questions at each level. One or more seem to me appropriate for Polymath, and I take Gowers’ aims here very seriously.
November 27, 2009 at 11:32 pm |
Rather than have a long thread of replies I’m arbitrarily starting a fresh comment. But I’m replying to Michael’s recent question: what more am I looking for in a model than what looks as though it could come from his?
The answer at this stage is that I don’t have a clear idea. My impression is that there are several levels of complexity and that each level provides a sort of primeval soup for the next level up, if that makes sense. So perhaps one level is merely the possibility for complex molecules to form, join, and split up. Another much higher one is the ability for a sequence of digits to be encoded in a way that causes it to act on its surroundings in a way that is of potentially limitless complexity. Yet another would be the ability to reproduce. What I would ask of a “stage” (and if I am vague about anything it is because I’m not sure I know how to be more precise) is that you feed in objects of a certain “level” and the rules that apply at that stage are such that with high probability you get a good and varied supply of objects at the next level up. At a low level one might be doing some sort of artificial chemistry. At a higher level it might be more like what Pargellis was doing with his mini-programs. I realize that Jonathan VP has said much of this already in an earlier comment.
Anyhow, a sort of answer is that from any model I would look for the potential to produce objects that could serve as the basic building blocks for a higher-level model.
December 2, 2009 at 12:31 pm |
Just another quick suggestion for reading. From a CS perspective the tool of choice for modeling biological systems are the same wich are used to model concurrent systems (also of interest for physicists): process algebras or process calculi (CCS by Milner, CSP by Hoare, Petri Nets…).
A tutorial for bigraphs, a generalization of CCS by Milner,
http://www.cl.cam.ac.uk/~rm135/bigraphs-tutorial.pdf
To see how bigraphs are applied to model biological system a fresh (today´s) link
http://www.arxiv.org/html/0912.0034
and for comments about this systems in the n-category café:
http://www.golem.ph.utexas.edu/category/2009/08/the_pi_calculus.html
But i´m not sure how relevant these systems might be for the problem of the origin of life. Moreover the problem pointed by JvosPost (unmanageable complexity) might arise when using these models.
December 2, 2009 at 2:20 pm |
is is Another fresh (today´s) link, this time from the reality (biology) top-down approach. It is interesting how they divide the cell into three subsystems: proteonoma, metaboloma and transcriptoma (Should we speak about a fourth, the membranoloma ?). Elaborating on my previous comments in this thread, and in analogy with social systems i would say that proteins are to RNA what machines are to human agents or processors.
http://www.elpais.com/articulo/sociedad/vida/compleja/esperaba/elpepusoccie/20091126elpepusoc_18/Tes
Sorry, that the link is in spanish.
December 2, 2009 at 5:03 pm |
Yes, the science of Lipidomics has advanced considerably. There was a great paper in the PNAS classifying all lipids a few years ago. The “membranoloma” speculated by proaonuiq is indeed dealt with by Lipidomics, and the mebrane proteins (embedded in the cell or nuclear membranes and acting as pores, pumps, and informational interfaces for signals between outside the cell and inside the cell. There is also Chronomics, which deals with the timing, synchronization, clocks, and the like. Plus other -omics. So which have the problems are the low lying fruit, to polymathically solve and thus build the collaborative community and get the first publication, and based on that experience, how to work at more than one “level”?
December 2, 2009 at 5:38 pm |
While you are using cellular automaton as a primary example, I believe more of the properties you cite could be obtained by a network automaton (essentially a Life-like system on a graph). This is because many of the patterns from Life-like systems come from the grid itself which it is based, but in a network automaton both the edges and the values of the nodes can be changed. (I suppose the edges can even be weighted, but as far I know nobody has done any work with this.)
While I don’t have confidence that there will be a grand link between biological processes, I think it’d be possible to make a well-defined project involving network automatons that self-replicate.
December 2, 2009 at 6:37 pm |
I can’t find the diskette where this lived, but do have the Word attachment where I gmailed it to myself as backup. I broke loose 3 distinct papers, each of which was rejected for a different reason at the international conference mentioned, co-sponsored by Microsoft Research.
Picosecond to Lifetime to Gigayear and Single Molecule to Organism to Ecosphere in Computational Enzyme Kinetics and Proteomics
> by
> Jonathan Vos Post
> Computer Futures, Inc.
> 3225 North Marengo Avenue
> Altadena, CA 91001
>
> [Draft 11.0; 99 pages; 46,000 words; 8 May 06]
>
INTERNATIONAL CONFERENCE ON COMPUTATIONAL METHODS IN
SYSTEMS BIOLOGY
18-19 October 2006
> The Microsoft Research – University of Trento Centre
> for Computational and Systems Biology TRENTO – ITALY
> http://www.msr-unitn.unitn.it/events/cmsb06.php
>
ABSTRACT:
My research goal since 1973 has been a computational theory of protein dynamics and evolution which unifies mechanisms from picosecond through organism lifetime through evolutionary time scales. This unification effort included my Ph.D. dissertation work at the University of Massachusetts, Amherst, (arguably the world’s first dissertation on Nanotechnology and Artificial Life) and those chapters of that dissertation which have been modified and subsequently published as refereed papers for international conferences [Post, 1976-2004]. The unification must describe the origin of complexity in several regimes, and requires bridging certain gaps in time scales, where previous theories were limited (as with the breakdown of the Born-Oppenheimer approximation in certain surface catalysis and solvated protein phenomena). The unification also requires bridging different length scales, from nanotechnological to microscopic through mesoscopic to macroscopic. The unification at several scales involves nonlinear, kinetic, and statistical analysis connecting the behavior of individual molecules with ensembles of those molecules, and using the mathematics of Wiener convolutions, Laplace transforms, and Krohn-Rhodes decomposition of semigroups. Recent laboratory results in several countries, including the ultrafast dynamics of femtochemistry and femtobiology, which probe the behavior of single molecules of enzyme proteins, shed new light on the overarching problem, and confirm the practicality of that goal. The unification in contemporary terms requires building bridges – and compatible databases with interoperable software – between Genomics, Interactomics, Lipidomics, Metabolomics, Proteomics, Transcriptomics, and other fields. The challenges to 21st Century Computational Biology include the need to perform measurements and integrated simulations over 28 orders of magnitude of time, as a means to study and to understand better the emergent, collective behaviors of metabolic, regulatory, neural, developmental, and ecological networks.
>
>
> TABLE OF CONTENTS
> Abstract 1
> Table of Contents 2
> 1.0 Introduction 3
> 1.1 Motivation 3
> Table 1: Time Scales (see Appendix A) 5
> 1.2 Femtosecond to Picosecond 6
> 1.3 Picosecond to Nanosecond 10
> 1.4 Nanosecond to Microsecond 11
> 1.5 Microsecond to Millisecond 12
> 1.6 Millisecond to Second 12
> 1.7 Second to Kilosecond; my PhD Dissertation 13
> 1.8 Kilosecond to Megasecond 18
> 1.9 Megasecond to Gigasecond 18
> 1.10 Gigasecond to Terasecond 19
> 1.11 Terasecond to Petasecond 20
> 1.12 Petasecond to Exasecond 20
> 2.0 Challenges: Computational Systems Biology 21
> 2.1 Overall Problems Classified 21
> 2.2 Antireductionism and the E-cell project 32
> 2.3 Metabolomics 35
> 2.4 Metagenomics 39
> 3.0 Annotated References 62
> Appendix A: Biological Time Spans 97
December 3, 2009 at 7:02 pm |
This morning I found that the NIH had scanned to PDF one of my papers from 1980 which mentions the possibility of simulating an entire organism. Plus a good reference list.
http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2203661/?page=1
[Proceedings of the Annual Symposium on Computer Applications in Medical Care]
Proc Annu Symp Comput Appl Med Care. 1980 November 5; 1: 51–59.
PMCID: PMC2203661
Simulation of Metabolic Dynamics
Jonathan V. Post
To think that I wrote this 30 years ago, and that it was published 29 years ago. Many things have happened to distract me from this research: employment, marriage, parenthood being 3 major categories.
Another great advantage of Polymath: continuity as individual people drop in and out. The task exceeds what one person, or one academic department can do.
December 8, 2009 at 12:01 pm |
[…] Polymath and the origin of life Emergent systems (tags: math life computers simulation philosophy physics) […]
December 8, 2009 at 10:51 pm |
Nice work that suggests the origin of fractal/chaos in systems as simple as 3 neurons with feedback.
Mathematical Model of Simple Circuit in Chicken Brain Raises Fundamental Questions About Neural Circuitry
http://www.sciencedaily.com/releases/2009/12/091207095941.htm
“… On the one hand, there are the individual nerve cells whose membrane depolarization is at the basis of everything and on the other hand, there’s lyric poetry, serial murder and the calculus. In between there are hundreds of billions of nerve cells, with hundreds of trillions of connections. Scientists understand the bottom end and can say useful things about the top end, but getting from one end to the other is another story.”
“As they try, they argue continually and sometimes bitterly about levels of abstraction. If a model of the brain or part of the brain doesn’t abstract at all, it is quickly snarled in unintelligible complexity. On the other hand, if it abstracts too much, it offers little insight into the organ it purports to represent.”
“In work published in the online edition of Physical Review E on November 25th, biophysicists and theoretical physicists at Washington University in St. Louis describe an elegant compromise….”
I’d comment that similar chaotic behavior occurs in metabolic systems, where the Michaelis-Menten equations substitute for neural systems with Hodgkin–Huxley-type models.
December 11, 2009 at 3:15 pm |
[…] of Life – Revisited Roughly one month ago I have reported on Tim Gowers’s polymath project to model the origin of life. Now it is time to go back there and see what has […]
December 15, 2009 at 7:21 pm |
This article looks interesting:
http://www.nature.com/news/2009/091211/full/news.2009.1132.html
“Alberts simulated cellular parts such as motor proteins and actin filaments, programmed them to obey a few mathematical rules reflecting physical forces, and saw that they were able to reproduce their behaviour in cells on his computer screen. Biological systems are robust, he reasoned, so “all we really need to do, we hope, is get things about right, and we will see some emergent properties”.”
December 18, 2009 at 9:38 pm |
This is a wonderful paper, and of interest to us for the proposed polymath.
Self-assembly, modularity and physical complexity
S. E. Ahnert, I. G. Johnston, T. M. A. Fink, J. P. K. Doye, and A. A. Louis
http://arxiv.org/abs/0912.3464
We present a quantitative measure of physical complexity, based on the amount of information required to build a given physical structure through self-assembly. Our procedure can be adapted to any given geometry, and thus to any given type of physical system. We illustrate our approach using self-assembling polyominoes, and demonstrate the breadth of its potential applications by quantifying the physical complexity of molecules and protein complexes. This measure is particularly well suited for the detection of symmetry and modularity in the underlying structure, and allows for a quantitative definition of structural modularity. Furthermore we use our approach to show that
symmetric and modular structures are favoured in biological self-assembly, for example of protein complexes. Lastly, we also introduce the notions of joint, mutual and conditional complexity, which
provide a useful distance measure between physical structures.
December 21, 2009 at 10:44 pm |
An interesting-looking popular overview of some related questions:
Nick Lane, “Life Ascending: The Ten Great Inventions of Evolution”, W. W. Norton (2009).
The book has the following description at Google Books ( http://books.google.com/books?id=OhH-3DyLIt4C ):
“How did life invent itself? Where did DNA come from? How did consciousness develop? Powerful new research methods are providing vivid insights into the makeup of life. Comparing gene sequences, examining atomic structures of proteins, and looking into the geochemistry of rocks have helped explain evolution in more detail than ever before. Nick Lane expertly reconstructs the history of life by describing the ten greatest inventions of evolution (including DNA, photosynthesis, sex, and sight), based on their historical impact, role in organisms today, and relevance to current controversies. Who would have guessed that eyes started off as light-sensitive spots used to calibrate photosynthesis in algae? Or that DNA’s building blocks form spontaneously in hydrothermal vents? Lane gives a gripping, lucid account of nature’s ingenuity, and the result is a work of essential reading for anyone who has ever pondered or questioned the science underlying evolution’s greatest gifts to man.”
I’m going to order it.
December 23, 2009 at 2:55 am |
This comment is not in response to any comment, just to the general topic.
I don’t know if evolution is clearly defined.
Does evolution mean iteration?
Does it mean a stepwise walk through an algorithm?
It seems that most models of life have a starting point of defining a process or algorithm to be followed. In principle, if the process is deterministic, our perception of an evolving structure is purely artificial. The structure is truly 4-dimensional and is completely defined by the governing algorithm (or function). The algorithm than is the minimum entropy representation of the structure.
If algorithm is stochastic in some way, the question is whether we define a cutoff in significant digits of the probabilities used. If we do, then in principle we should be able to map out a branching structure, and it should still be countable (if N is the number of significant digits, then 10^N is the number of branches at each random number draw; if M is the number of random number draws, then 10^N^M will give me all potential configurations of the system). So in the case where I have a finite number of significant digits in my probabilities and as long as the random number draws are done in a series order, then my initial algorithm still is a minimum entropy representation of a much larger structure in some space.
These cases are uninteresting I think.
What is interesting are continuous space filling structures. So instead of seeing branches, we see fog. In some places the fog is more dense than in others. Self similar structures in the fog would be interesting I think.
December 23, 2009 at 10:33 pm |
… Gregory Chaitin… talking about a proposal for a new field he calls “metabiology”, which he defined in the talk (and on the website above) as “a field parallel to biology, dealing with the random evolution of artificial software (computer programs) rather than natural software (DNA), and simple enough that it is possible to prove rigorous theorems or formulate heuristic arguments at the same high level of precision that is common in theoretical physics.” This field doesn’t really exist to date, but his talk was intended to argue that it should, and to suggest some ideas as to what it might look like.
… One of the motivating ideas that he put forth was that there is currently no rigorous proof that Darwin-style biological evolution can work – i.e. that operations of mutation and natural selection can produce systems of very high complexity. This is a fundamental notion in biology, summarized by the slogan, “Nothing in biology makes sense except in light of evolution”. This phrase, funnily, was coined as the title of a defense of a “theistic evolution” – not obviously a majority position among scientists, but also not to be confused with “intelligent design” which claims that evolution can’t account for observed features of organisms. This is a touchy political issue in some countries, and it’s not obvious that a formal proof that mutation and selection CAN produce highly complex forms would resolve it. Even so, as Chaitin said, it seems likely that such a proof could exist – but if there’s a rigorous proof of the contrary, that would be good to know also!
Of course, such a formal proof doesn’t exist because formal proof doesn’t play much role in biology, or any other empirical science – since living things are very complex, and incompletely understood. Thus the proposal of a different field, “metabiology”, which would study simpler formal objects: “artificial software” in the form of Turing machines or program code, as opposed to “natural software” like DNA. This abstracts away everything about an organism except its genes (which is a lot!), with the aim of simplifying enough to prove that mutation and selection in this toy world can generate arbitrarily high levels of complexity….
December 24, 2009 at 2:12 am |
PLoS Biol. 2009 June; 7(6): e122.
Published online 2009 June 2. doi: 10.1371/journal.pbio.1000122.
PMCID: PMC2682484
Copyright Antonio Lazcano. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Mind the Gap!
Reviewed by Antonio Lazcano*
Facultad de Ciencias, Universidad Nacional Autónoma de México (UNAM), Mexico City, Mexico
* E-mail: alar@correo.unam.mx
S Rasmussen, MA Bedau, L Chen, D Deamer and NH Packard. editors 2008. Protocells: Bridging nonliving and living matter.
Cambridge (Massachusetts): MIT Press. 776p. ISBN: 978-0262182683. US$75.00
http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2682484/
In 1835, the French naturalist Felix Dujardin started crushing ciliates under the microscope and observed that the tiny cells exuded a jellylike, water-insoluble substance, which he described as a “gelée vivante” and which was eventually christened “protoplasm” by the physician Johann E. Purkinje and the botanist Hugo von Mohl. Fifty years after Dujardin’s observations, the possibility that living organisms were the evolutionary outcome of the gradual transformation of lifeless gel-like matter into protoplasm was so widespread that it found its way into musical comedies. In 1885, the self-important Pooh-Bah, Lord Chief Justice and Chancellor of the Exchequer, declared in Gilbert and Sullivan’s The Mikado that “I am in point of fact, a particularly haughty and exclusive person, of pre-Adamite ancestral descent. You will understand this when I tell you that I can trace my ancestry back to a protoplasmal primordial atomic globule.” …
December 26, 2009 at 1:44 pm |
I thought it might be a good starting point to find a good definition of life
http://www.thefreedictionary.com/life
life (lf)
n. pl. lives (lvz)
1.
a. The property or quality that distinguishes living organisms from dead organisms and inanimate matter, manifested in functions such as metabolism, growth, reproduction, and response to stimuli or adaptation to the environment originating from within the organism.
b. The characteristic state or condition of a living organism.
2. Living organisms considered as a group: plant life; marine life.
3. A living being, especially a person: an earthquake that claimed hundreds of lives.
4. The physical, mental, and spiritual experiences that constitute existence: the artistic life of a writer.
5.
a. The interval of time between birth and death: She led a good, long life.
b. The interval of time between one’s birth and the present: has had hay fever all his life.
c. A particular segment of one’s life: my adolescent life.
d. The period from an occurrence until death: elected for life; paralyzed for life.
e. Slang A sentence of imprisonment lasting till death.
6. The time for which something exists or functions: the useful life of a car.
7. A spiritual state regarded as a transcending of corporeal death.
8. An account of a person’s life; a biography.
9. Human existence, relationships, or activity in general: real life; everyday life.
10.
a. A manner of living: led a hard life.
b. A specific, characteristic manner of existence. Used of inanimate objects: “Great institutions seem to have a life of their own, independent of those who run them” (New Republic).
c. The activities and interests of a particular area or realm: musical life in New York.
11.
a. A source of vitality; an animating force: She’s the life of the show.
b. Liveliness or vitality; animation: a face that is full of life.
12.
a. Something that actually exists regarded as a subject for an artist: painted from life.
b. Actual environment or reality; nature.
December 28, 2009 at 2:20 am |
“An interesting-looking popular overview of some related questions:”
Recently i bought a book with, surprisingly, very similar view to mine.
I can not resist to quote it even if it is writen in spanish: “El siglo de la ciencia; nuestro mundo al descubierto” by J. Sampedro, first edition November 2009. He describes the situation of science at all relevant levels (physical, biological, neuromental and social).
After several uninteresting chapters about the physical levels, starts the parts concerning the biological levels which are specialy informative (the author is a biologist turned to jornalist, he dominates the biological literature in papers and gives really updated information and gives some hints for the target of this polymath). I liked his description of the transposon revolution and, at the social level, the chapter about music, that is the explanation about the almost universal diatonic and pentatonic scales.
More generaly, he says in the introduction: “Toda la ciencia, si se mira bien, versa sobre la autoorganización de la materia: quarks en atomos, moléculas en genes, neuronas en circuitos en cerebros en la apertura de Wall Street”. Sounds familiar ?
December 28, 2009 at 11:25 am
Just as a matter of interest, does he note that if you accept the division of the octave into twelve notes, then both the pentatonic and diatonic scales can be thought of as arithmetic progressions with common difference a perfect fifth? It seems to me that that is enough to explain their universality, so I would be suspicious of any social explanation.
From the point of view of this as a Polymath project, what I think we are looking for is twofold. First, we would like to divide the transition from non-life to life into several recognisable stages, so that we don’t find ourselves wanting to make a huge jump from molecules swilling about all the way to a self-reproducing organism. Second, we would like to identify a pair of consecutive levels and build a model that treats the ingredients that go into the first level as black boxes and climbs to the second level with high probability. Ideally we would like to do that for all pairs of consecutive levels, but some of them seem to have been done already. (But I see no harm in repeating previous work, especially if we could fit it all into a unified framework.)
December 28, 2009 at 6:37 pm |
“…does he note that if you accept the division of the octave into twelve notes, then both the pentatonic and diatonic scales can be thought of as arithmetic progressions with common difference a perfect fifth ?” Yes That´s approximativelly exactly his explanation.
This fact, which is surelly a topic for music experts, was unknown for me. As he explains the pentatonic (used in traditional music in Etiopia, West Africa, China, Indonesia, Vietnam, Korea, Philippines, Albania, Hungary and celt folk…) still was discovered first and later some cultures (first historical record in Ur, 4000 years ago) exploring “fifth paths” in the circulant graph of 12 sounds discovered the diatonic scale (for those interested in hearing this first diatonic song: http://www.amaranthpublishing.com/hurrian.htm).
As for the origin of life i agree that it is best to work in the minimum first jump …although i´ve seen the project is closed (wise decision!). By the way Another paragraph from Sampedro´s book hits the whole polymath idea
“En contra de lo que suele pensarse, las tormentas de cerebros (brainstorming) no son muy útiles para encontrar ideas innovadoras. La creatividad se fundamenta en el establecimiento de nexos entre conceptos alejados, pero esos nexos tienen que estar en la misma cabeza para ser útiles. Un poeta puede crear doce metáforas en media hora, pero doce poetas no escribirian ni una en todo el día. La áreas del cerebro se comunican mejor que las personas”.
In summary: he asserts that poly-projects are not productive. I do not know yet if i agree or not but this assertion seems to contradict previous results. In any case good luck with the next one !
January 5, 2010 at 1:24 am |
I do not see a challenge either to my previous annotated Definitions of Life, nor to this proposed Polymath from:
‘Lifeless’ Prions Capable of Evolutionary Change and Adaptation
ScienceDaily (Jan. 3, 2010) — Scientists from The Scripps Research Institute have determined for the first time that prions, bits of infectious protein devoid of DNA or RNA that can cause fatal neurodegenerative disease, are capable of Darwinian evolution.
The study from Scripps Florida in Jupiter shows that prions can develop large numbers of mutations at the protein level and, through natural selection, these mutations can eventually bring about such evolutionary adaptations as drug resistance, a phenomenon previously known to occur only in bacteria and viruses. These breakthrough findings also suggest that the normal prion protein — which occurs naturally in human cells — may prove to be a more effective therapeutic target than its abnormal toxic relation.
The study was published in the December 31, 2009 issue of the journal Science Express, an advance, online edition of the journal Science.
“On the face of it, you have exactly the same process of mutation and adaptive change in prions as you see in viruses,” said Charles Weissmann, M.D., Ph.D., the head of Scripps Florida’s Department of Infectology, who led the study. “This means that this pattern of Darwinian evolution appears to be universally active. In viruses, mutation is linked to changes in nucleic acid sequence that leads to resistance. Now, this adaptability has moved one level down — to prions and protein folding — and it’s clear that you do not need nucleic acid for the process of evolution.”
Infectious prions (short for proteinaceous infectious particles) are associated with some 20 different diseases in humans and animals, including mad cow disease and a rare human form, Creutzfeldt-Jakob disease. All these diseases are untreatable and eventually fatal. Prions, which are composed solely of protein, are classified by distinct strains, originally characterized by their incubation time and the disease they cause. Prions have the ability to reproduce, despite the fact that they contain no nucleic acid genome.
Mammalian cells normally produce cellular prion protein or PrPC. During infection, abnormal or misfolded protein — known as PrPSc — converts the normal host prion protein into its toxic form by changing its conformation or shape. The end-stage consists of large assemblies (polymers) of these misfolded proteins, which cause massive tissue and cell damage.
“It was generally thought that once cellular prion protein was converted into the abnormal form, there was no further change,” Weissmann said. “But there have been hints that something was happening. When you transmit prions from sheep to mice, they become more virulent over time. Now we know that the abnormal prions replicate, and create variants, perhaps at a low level initially. But once they are transferred to a new host, natural selection will eventually choose the more virulent and aggressive variants.”
Drug Resistance
In the first part of the study, Weissmann and his colleagues transferred prion populations from infected brain cells to culture cells. When transplanted, cell-adapted prions developed and out-competed their brain-adapted counterparts, confirming prions’ ability to adapt to new surroundings, a hallmark of Darwinian evolution. When returned to brain, brain-adapted prions again took over the population.
To confirm the findings and to explore the issue of evolution of drug resistance, Weissmann and his colleagues used the drug swainsonine or swa, which is found in plants and fungi, and has been shown to inhibit certain prion strains. In cultures where the drug was present, the team found that a drug-resistant sub-strain of prion evolved to become predominant. When the drug was withdrawn, the sub-strain that was susceptible to swainsonine again grew to become the major component of the population.
Weissmann notes that the findings have implications for the development of therapeutic targets for prion disease. Instead of developing drugs to target abnormal proteins, it could be more efficient to try to limit the supply of normally produced prions — in essence, reducing the amount of fuel being fed into the fire. Weissmann and his colleagues have shown some 15 years ago that genetically engineered mice devoid of the normal prion protein develop and function quite normally (and are resistant to prion disease!).
“It will likely be very difficult to inhibit the production of a specific natural protein pharmacologically,” Weissmann said, “You may end up interfering with some other critical physiological process, but nonetheless, finding a way to inhibit the production of normal prion protein is a project currently being pursued in collaboration with Scripps Florida Professor Corinne Lasmezas in our department.”
Quasi-Species
Another implication of the findings, according to the study, is that drug-resistant variants either exist in the prion population at a low level prior to exposure or are generated during exposure to the drug. Indeed, the researchers found some prions secreted by infected cells were resistant to the drug before exposure, but only at levels less than one percent.
The scientists show that prion variants constantly arise in a particular population. These variants, or “mutants,” are believed to differ in the way the prion protein is folded. As a consequence, prion populations are, in fact, comprised of multiple sub-strains.
This, Weissmann noted, is reminiscent of something he helped define some 30 years ago — the evolutionary concept of quasi-species. The idea was first conceived by Manfred Eigen, a German biophysicist who won the Nobel Prize in Chemistry in 1967. Basically stated, a quasi-species is a complex, self-perpetuating population of diverse and related entities that act as a whole. It was Weissmann, however, who provided the first confirmation of the theory through the study of a particular bacteriophage — a virus that infects bacteria — while he was director of the Institut für Molekularbiologie in Zürich, Switzerland.
“The proof of the quasi-species concept is a discovery we made over 30 years ago,” he said. “We found that an RNA virus population, which was thought to have only one sequence, was constantly creating mutations and eliminating the unfavorable ones. In these quasi-populations, much like we have now found in prions, you begin with a single particle, but it becomes very heterogeneous as it grows into a larger population.”
There are some unknown dynamics at work in the prion population that leads to this increased heterogeneity, Weissmann added, that still need to be explored.
“It’s amusing that something we did 30 years has come back to us,” he said. “But we know that mutation and natural selection occur in living organisms and now we know that they also occur in a non-living organism. I suppose anything that can’t do that wouldn’t stand much of a chance of survival.”
The joint first authors of the Science study are Jiali Li and Shawn Browning of The Scripps Research Institute. Other authors include Sukhvir P. Mahal and Anja M. Oelschlegel also of The Scripps Research Institute. Weissmann notes that after the manuscript was accepted by Science, an article by Ghaemmanghami et al. appeared in PLoS Pathogens that described emergence of prions resistant to a completely different drug, quinacrine, providing additional support to the Scripps Research team’s conclusions.
The Scripps Research study was supported by a grant from the National Institutes of Health and by a generous donation to the Weissmann laboratory from the Alafi Family Foundation.
Story Source:
Adapted from materials provided by Scripps Research Institute, via EurekAlert!, a service of AAAS.
Journal Reference:
1. Li et al. Darwinian Evolution of Prions in Cell Culture. Science, 2009; DOI: 10.1126/science.1183218
January 8, 2010 at 4:41 pm |
[…] further glance at ‘Polymath and the Origin of Life’ Polymath and the origin of life has finished its second month. Remember, Tim Gowers plans to set up a polymath project to explain […]
January 9, 2010 at 11:17 pm |
Vera Vasasa, Eörs Szathmáry and Mauro Santosa. Lack of evolvability in self-sustaining autocatalytic networks: A constraint on the metabolism-first path to the origin of life. PNAS, January 4, 2010 DOI: 10.1073/pnas.0912628107
Press release/summary at:
What Came First in the Origin of Life? New Study Contradicts the ‘Metabolism First’ Hypothesis
http://www.sciencedaily.com/releases/2010/01/100108101433.htm
ScienceDaily (Jan. 9, 2010) — A new study published in Proceedings of National Academy of Sciences rejects the theory that the origin of life stems from a system of self-catalytic molecules capable of experiencing Darwinian evolution without the need of RNA or DNA and their replication….
January 12, 2010 at 2:50 am |
I can’t bring myself to read this, as my crackp[ot alarms go off from the abstract. Anyone brave enough to tellus?
http://arxiv.org/abs/1001.1690
Title: Dynamical real numbers and living systems
Authors: Dhurjati Prasad Datta
Comments: AMS-latex 2e, 14 pages
Journal-ref: Chaos, Solitons, and Fractals, vol 20, issue 4, 705-712, (2004)
Subjects: General Mathematics (math.GM)
Recently uncovered second derivative discontinuous solutions of the simplest linear ordinary differential equation define not only an nonstandard extension of the framework of the ordinary calculus, but also provide a dynamical representation of the ordinary real number system. Every real number can be visualized as a living cell -like structure, endowed with a definite evolutionary arrow. We discuss the relevance of this extended calculus in the study of living systems. We also present an intelligent version of the Newton’s first law of motion.
January 12, 2010 at 9:38 pm |
http://news.bbc.co.uk/2/hi/science/nature/8452196.stm
A promising push toward a novel, biologically-inspired “chemical computer” has begun as part of an international collaboration.
The “wet computer” incorporates several recently discovered properties of chemical systems that can be hijacked to engineer computing power.
The team’s approach mimics some of the actions of neurons in the brain.
The 1.8m-euro (£1.6m) project will run for three years, funded by an EU emerging technologies programme.
The programme has identified biologically-inspired computing as particularly important, having recently funded several such projects.
What distinguishes the current project is that it will make use of stable “cells” featuring a coating that forms spontaneously, similar to the walls of our own cells, and uses chemistry to accomplish the signal processing similar to that of our own neurons….
January 12, 2010 at 10:58 pm |
Jonathan, i find this result as highly interesting and informative though i´ve not read it in deep. Thanks for pointing to it. It is not surprising that Szathmary is one of the authors.
“Vera Vasasa, Eörs Szathmáry and Mauro Santosa. Lack of evolvability in self-sustaining autocatalytic networks: A constraint on the metabolism-first path to the origin of life. PNAS, January 4, 2010 DOI: 10.1073/pnas.0912628107.
I copypasted the main conclusion:
Researchers concluded that this fundamental limitation of “compound genomes” should lead to caution towards theories that set metabolism first as the origin as life, even though former metabolic systems could have offered a stable habitat in which primitive polymers such as RNA could have evolved.
Researchers state that different prebiotic Earth scenarios can be considered. However, the basic property of life as a system capable of undergoing Darwinian evolution began when genetic information was finally stored and transmitted such as occurs in nucleotide polymers (RNA and DNA).”
No time now to extract its consequences…
August 21, 2010 at 3:14 pm |
I have recently come across the posts on the origin of life and would like to suggest a model of complex pattern formation which is relevant to the current discussion. The model is a theoretical sandpile model [1] where particles are added at the center and then distributed following simple rules. The final particle distribution forms beautiful complex patterns [1-4].
This model has the following properties mentioned by Prof. Gowers.
1. This is a dynamical model with simple local evolution rules.
2. It produces deterministic complex patterns with distinguishable features inside, at many distance scales.
3. Exact quantitative characterization is possible for some of the patterns and involves interesting mathematics like discrete analytic functions on Riemann surfaces, piece-wise linear approximants of continuous functions etc.[1,2]
4. There is certain extent of robustness.
The patterns when overlap, interact in an interesting way and produces new features which in some simple cases possible to analytically characterize. However the interactions are not dissipative and does not build selection pressure. Also the patterns do not self replicate.
The model is a cellular automata model of self-organized criticality and known as the Abelian sandpile model. A simple example is the following:
Step1: Consider an infinite grid of square cells, where each cell has a non-negative integer variable z(x) equal to the number of particles in that cell.
Step2: Each cell can contain at most three particles. If the number of particles in a cell exceeds the threshold then it is unstable and relaxes by giving away one particle to each of its four nearest neighbour cells.
Step3: Start with a periodic distribution of z(x), all bellow threshold. Then add N number of particles at a single cell and follow the above rule until all cells are stable.
The final distribution of the number of particles z(x) produces beautiful complex pattern in the large N limit. (see [1,2] for some examples of the patterns. Also see [3] for many variants of the model. Patterns for very large N can be found in D. B. Wilson’s page [4])
The most interesting property is the proportionate growth of the patterns. As more and more particles added, the pattern grows in size with the structures inside the pattern growing in proportion to each other. As a result the full pattern for different values of N looks almost the same, just their sizes are different (similar to the way baby animals grow in size). The important thing to notice is that the effective long distance communication between different parts of the pattern necessary for proportionate growth is achieved by simple local rules.
The original motivation for studying these patterns is them being a simple model of proportionate growth in animals. The nutrients are centrally fed. Then they are transported to different parts of the body and same nutrients get converted into chemicals forming different cellular structures (organs). This model has the same qualitative features.
The patterns are deterministic i.e. given the initial configuration there is always a unique pattern. A very large number of patterns can be generated this way by changing the initial configuration or the relaxation rule.
The patterns are robust against limited variations in the initial conditions. A large class of initial distribution of particles produce exactly same macroscopic structure. Similarly certain variations of the relaxation rules changes only the pattern for small N, but the large N picture remains almost the same.
When a small amount of randomness is added in the initial configuration, the boundary between the structures inside the pattern gets distorted. However the structures are still distinguishable and retains their overall shape. On the other hand a tiny amount of randomness in the relaxation rule completely destroys the pattern and turns into a circle of uniform density.
References:
[1] http://iopscience.iop.org/0295-5075/85/4/48002
[2] http://www.springerlink.com/content/l076631ph1375111/
[3] http://www.theory.tifr.res.in/~tridib/patterns.html
[4] http://research.microsoft.com/en-us/um/people/dbwilson/sandpile/
August 25, 2010 at 7:08 pm |
Hello everyone, I noticed that my “metabiology” proposal was mentioned above. That’s the idea of thinking of life as evolving software. I have recently been able to formulate this mathematically as a workable theory:
Click to access darwin.pdf
Here is the abstract:
To a mathematical theory of evolution and biological creativity
G. J. Chaitin
We present an information-theoretic analysis of Darwin’s theory of evolution, modeled as a hill-climbing algorithm on a fitness landscape. Our space of possible organisms consists of computer programs, which are subjected to random mutations. We study the random walk of increasing fitness made by a single mutating organism. In two different models we are able to show that evolution will occur and to characterize the rate of evolutionary progress, i.e., the rate of biological creativity.
Key words and phrases:
metabiology, evolution of mutating software, random walks in software space, algorithmic information theory
November 21, 2010 at 2:10 pm |
Here are a couple of videos of mechanical constructions that may be of interest. The first is I believe by Lionel and Shirley Penrose, and shows self replicating mechanical wooden “molecules”:
http://vimeo.com/10298933
The second, by Saul Griffith, is similar, but automates the random sloshing around of the components using robotics:
http://alumni.media.mit.edu/~saul/PhD/videos/rep5mer.mov
All of these via this reddit thread: http://www.reddit.com/r/technology/comments/e9egb/mechanical_self_replication_mindblown/
November 23, 2010 at 6:16 pm
A quick note to say thanks for these links — I enjoyed them.
January 25, 2011 at 11:39 am |
Hi Prof. Gowers,
Speaking about “edge of chaos patterns”, what do you think about this excerpt from Kocarev et. al., Phys. Rev. Lett. 93, 234101 (2004):
“The classical chaos is but a limiting pattern which is, nevertheless, very important both in the theory to compare with the real (quantum) chaos and in applications … The existence of the horseshoe is a fingerprint of chaos in continuous-space systems. In discrete-space systems, however, the existence of a set, on which the map is injection, and for which all periodic orbits are unstable, is a fingerprint of pseudochaos.” ps Ono announcement http://ams.org/news?news_id=1046
August 16, 2011 at 6:17 pm |
The following informative short review has just appeared, with many interesting links to recent research on the (biological) origin of life:
http://www.newscientist.com/article/mg21128251.300-first-life-the-search-for-the-first-replicator.html?full=true
January 19, 2013 at 4:40 pm |
Sorry for not quite on topic comment.
I was a creationist earlier, but more detailed study of Bible seems to show that there are more arguments pro evolution in Bible that arguments against evolution.
http://withoutvowels.org/wiki/Theology:Evolution wiki page is to collect all biblical arguments both pro and against evolution.
I think, what I’ve said about evolution also applies for abiogenesis.
January 19, 2013 at 5:00 pm
The most interesting number I heard yesterday at the TEDx on the Brain, at Caltech, was that there are 500 distinct protein species, roughly 50 copies of each molecule, at each of the 100 Trillion synapses in your brain… and that each has a half-life of only 24 hours, making 25,000 molecules per day per synapse being made via RNA. That is consistent with the figures I used in my 1973-1977 PhD Dissertation, as to how much information processing goes on in each living cell, my estimate at the time was 1 gigabit per second, roughly 90% of which was in the proteome.
But the -ome at the conference was the connectome, and Jeff Lichtman showed a slide of a definition of Connectomics, which one eventually noticed claimed to be from the 2019 edition of Merriam-Webster.
Video ranged from Joel Burdick’s sequences of totally paralyzed people operating multifingered robotic hands as prosthesis under direct brain-computer interface, to Pinky & the Brain.
I don’t see much in the Bible that deals with this level of description, though in Erasmus Darwin’s day the Koran was cited as a source for “Mohammedan Evolution.”
May 26, 2013 at 11:10 pm |
Have you read Fontana’s “The arrival of the fittest” and “The barrier of objects”? I believe that work addresses some of the objectives of this project
May 27, 2013 at 9:34 am
Thank you very much for that reference, which I was unaware of. It does indeed look very close to the kind of thing I was suggesting trying to do, so if a project like this ever gets off the ground, then reading and digesting those papers will be an essential first step. (So far I’ve only quickly looked through the first paper, so it wasn’t clear to me whether computer models have been built using their ideas that exhibit spontaneous self-organization.)
February 7, 2016 at 6:13 pm |
What if anything happened to the plan described in this article?
February 7, 2016 at 7:12 pm
Nothing. I still find these questions fascinating though, and would in principle be very interested in trying to do some serious work along these lines. Or when you say “this article” are you referring to the article by Fontana mentioned in the previous comment?
February 9, 2016 at 12:30 am
I was talking about this blog article. I think that simulating and understanding the origin of life is a good Polymath project because 1) it’s ambitious, 2) partial progress can still be interesting, 3) there’s room for many different approaches, 4) not only a few “experts” have the necessary technique to make significant progress, 5) there have been plenty of contests to create interesting artificial life forms, but not exactly what you’re proposing.
On the downside, the set of people who like doing Polymath projects seems to be almost disjoint from the people who like biology.
I’ve been thinking about biology lately, so I can imagine wanting to join a project like this, though I have my own idiosyncratic approach that might not fit in well.
April 4, 2016 at 12:36 am |
[…] I found some discussion made in Timothy Gowers’s Weblog. The book What is Life? by Erwin Schrödinger, although I don’t know much, also seems to […]
July 28, 2017 at 11:50 pm |
This article describes work on closely related ideas.
July 29, 2017 at 4:34 pm
Schrodinger’s famous book is the main one I cite in my Venn Diagram of published Definitions of Life; Physics circle.
.
3 Definitions of Life
by
Jonathan Vos Post
Annotated text version with citations of graphic PDF Venn Diagram of
September 2009
Version 1.0 of 9 Nov 2009, 4 pp., 1400 words
My graphic is a Venn Diagram. The three overlapping circles contain
text summarizing these 3 main definitions: The diagram as whole gives
my tentative “original” composite definition of life which combines
the main 3 definitions given:
“A self-assembled, self-contained negentropic chemical system network
of feedback mechanisms capable of undergoing Darwinian evolution.”
There was also a polygonal box with the following text, as the cited
article initiated my composition of the diagram: “see pp.56 ff ‘What
is Life’ of ‘Origin of Life’ by Alonso Ricardo & Jack W. Szostak,
Scientific American, September 2009.”
I. Cybernetic Definition
“A network of inferior negative feedbacks (regulatory mechanisms)
subordinated to a superior positive feedback (potential of expansion,
reproduction).” [Korzeniewski, 2001]
Summarized for the graphic [by JVP] as: “A network of feedback mechanisms”
I had an arrow from the word CYBERNETICS pointing to this part of the
circle, and an arrow pointing from it to a box containing the text:
“Best fit to theory of ‘Metabolism First’ as opposed to ‘RNA First’
Biogenesis, network of catalysts which process energy.”
II. Schrödinger’s Physics Definition
Summarized for the graphic [by JVP] as: “Self-assemble against
nature’s tendency towards entropy (disorder) (i.e. negentropy). [Note:
this was historically the first of these]
I had an arrow from the word PHYSICS pointing to this part of the
circle, and under the arrow the text: “Schrödinger also predicted
before DNA structure known : 1-dimensional aperiodic crystal.”
I drew an arrow pointing to it to a box containing the text:
“Self-assemble” as opposed to assisted self-assembly on mineral
substrate such as Clay (Jim Ferris et al.)”
III. Chemistry Definition
“Life is a self-sustained chemical system capable of undergoing
Darwinian evolution.” [Joyce]
Summarized for the graphic [by JVP] as: “Gerald Joyce’s ‘working
definition’ adopted by NASA: ‘self-sustained chemical system capable
of undergoing Darwinian evolution.’ Note: Panspermia allows the
Darwinian evolution to have started on another planet or body.”
I drew an arrow pointing to it to a box containing the text: “If we
leave out Gerald Joyce’s ‘chemical system’ we cannot simply exclude
software ‘artifical life’ in silico — or more exotic substrates.
I drew an arrow pointing from that box to a box wit the text:
“Questions: in regions combining only 1 or 2 of these definitions,
what counterexamples are possible?”
There was also a rectangular box in the upper right hand corner which
read: “Venn Diagram copyright © 2009 by Jonathan Vos Post.”
The overlapping areas of the Venn Diagram
I/II. Cybernetics + Physics
Summarized for the graphic [by JVP] as “self-assembled negentropic
network of feedback mechanisms”
II/III. Physics + Chemistry
Summarized for the graphic [by JVP] as “self-assembled, self-sustained
negentropic chemical system capable of undergoing Darwinian
evolution.”
I/III. Cybernetics + Chemistry
Summarized for the graphic [by JVP] as “self-contained network of
feedback mechanisms capable of undergoing Darwinian evolution.”
I/II/II. Cybernetics + Physics + Chemistry
“A self-assembled, self-contained negentropic chemical system network
of feedback mechanisms capable of undergoing Darwinian evolution.”
Further clarifications and discussions.
To clarify Schrödinger’s Physics definition, although many
non-physicists persist in stating that life’s dynamics somehow go
against the tendency of second law (which states that the entropy of
an isolated system tends to increase), the definition assuredly does
not in any way conflict or invalidate this law. This is because the
principle that entropy can only increase or remain constant applies
only to a closed system (i.e. one which is adiabatically isolated, so
that no heat can enter or leave). Whenever a system can exchange
either heat or matter with its environment, both of which apply to the
planet Earth and its ecosystem, an entropy decrease of that system is
entirely compatible with the second law.
In more modern terminology, life is a dissipative system. A
dissipative system is characterized by the spontaneous appearance of
symmetry breaking (anisotropy) and the formation of complex, sometimes
chaotic, structures where interacting particles exhibit long range
correlations. The term dissipative structure was coined by
Russian-Belgian physical chemist Ilya Prigogine, who was awarded the
Nobel Prize in Chemistry in 1977 for his pioneering work on these
structures, some of which rediscovered my research on what I call
“enzyme waves.”
As chemist John Avery explains in his 2003 book Information Theory and
Evolution, we find a presentation in which the phenomenon of life,
including its origin and evolution, as well as human cultural
evolution, has its basis in the background of thermodynamics,
statistical mechanics, and information theory. The (apparent) paradox
between the second law of thermodynamics and the high degree of order
and complexity produced by living systems, according to Avery, has its
resolution “in the information content of the Gibbs free energy that
enters the biosphere from outside sources.” The process of natural
selection responsible for such local increase in order may be
mathematically derived directly from the expression of the second law
equation for connected non-equilibrium open systems
The “Ferris et al” and clay text summarizes the fact that when free
nucleotides are combined in water solution, they do not react at all.
Hence various teams of scientists have searched for what types of
activating groups and inorganic catalysts must have been involved in
the polymer bonding process. Dr. Ferris, of Rensselaer Polytechnic
Institute in Troy, New York, discovered one inorganic material which
facilitates this reaction, namely montmorillonite clay. The specific
structure of this clay can provide a medium on which the individual
activated RNA units combine to form larger chains.
REFERENCES:
Avery, John (2003). Information Theory and Evolution. World
Scientific. ISBN 981-238-399-9.
.
Dr. James P. Ferris. “Montmorillonite Catalysis of RNA Oligomer
Formation in Aqueous Solution. A Model for the Prebiotic Formation of
RNA.” Journal of the American Chemical Society. 1993, 155,
12270-12275.
James P. Ferris is Director, New York Center for Studies on the Origins of Life
Gerald Francis Joyce, “The RNA World: Life Before DNA and Protein”.
Professor Gerald Francis Joyce (born 1956) is a researcher at The
Scripps Research Institute. His primary interests include the in vitro
evolution of catalytic RNA molecules and the origins of life. He was
elected to the National Academy of Sciences in 2001.
Joyce received his Bachelor of Arts from the University of Chicago in
1978, completed his M.D. and Ph.D. at the University of California,
San Diego in 1984, and joined Scripps in 1989. Joyce, quoted in
commentary in Science (1992): “Obviously, Harry [Noller]’s finding
doesn’t speak to how life started, and it doesn’t explain what came
before RNA. But as part of the continually growing body of
circumstantial evidence that there was a life form before us on this
planet, from which we emerged – boy, it’s very strong!”
Korzeniewski, Bernard (2001). “Cybernetic formulation of the
definition of life”. Journal of Theoretical Biology. 2001 April 7. 209
(3) pp. 275–86.
Prof. Bernard Korzeniewski’s home page,
http://awe.mol.uj.edu.pl/~benio/
Faculty of Biochemistry, Biophysics and Biotechnology, Jagiellonian
University, ul. Gronostajowa 7, 30-387 Kraków (Krakow), Poland
e-mail: benio@mol.uj.edu.pl
Alonso Ricardo and Jack W. Szostak, , “Origin of Life”, Scientific
American, September 2009.
Schrödinger, Erwin (1944). What is Life – the Physical Aspect of the
Living Cell. Cambridge University Press. ISBN 0-521-42708-8.
in the famous 1944 book What is Life?, Nobel-laureate physicist Erwin
Schrödinger theorizes that life, contrary to the general tendency
dictated by the Second law of thermodynamics, decreases or maintains
its entropy by feeding on negative entropy. In a note to What is
Life?, however, Schrödinger explains his usage of this term:
“Let me say first, that if I had been catering for them [physicists]
alone I should have let the discussion turn on free energy instead. It
is the more familiar notion in this context. But this highly technical
term seemed linguistically too near to energy for making the average
reader alive to the contrast between the two things.”
JVP\acp\3DefsLife.doc
l “Substrate-independent definition of Life,” ALIFEXV Proceedings
l Jonathan Vos Post
l
l Abstract
l This paper provides a substrate-independent definition of Life, and is provided here according to the formatting requirements for papers submitted to the 15th International Conference on the Synthesis and Simulation of Living Systems (ALIFEXV). I understand that MIT Press will publish the proceedings in a single online open-access volume. The proceedings will be assembled directly from Portable Document Format (PDF) files furnished by the authors. I have yet to scan my hand-drawn Venn diagram into PDF, but the text alone allows its reconstruction easily. The publication style used here is identical to the style of the ALIFE 14 conference to ensure uniformity over both conferences.
l Since we discuss systems on the borderline between “life as we know it,” and something else, what is mydefinition of Life?
l My graphic is a Venn Diagram. The three overlapping circles contain text summarizing these 3 main definitions: The diagram as whole gives my tentative ‘original’ composite definition of life which combines the main 3definitions given:
l “A self-assembled, self-contained negentropic chemical system network of feedback mechanisms capable of undergoing Darwinian evolution.”
l I draw a polygonal box with the following text, “see pp.56 ff ‘What is Life’ of ‘Origin of Life’ by Alonso Ricardo & Jack W. Szostak, Scientific American, September 2009.”
l
*************************************
l I. Cybernetic Definition
l “A network of inferior negative feedbacks (regulatory mechanisms) subordinated to a superior positive feedback (potential of expansion, reproduction).” [Korzeniewski, 2001]
l Summarized for the graphic as: “A network of feedback mechanisms”
l I draw an arrow from the word CYBERNETICS pointing to this part of the circle, and an arrow pointing from it to a box containing the text: “Best fit to theory of ‘Metabolism First’ as opposed to ‘RNA First’ Biogenesis, network of catalysts which process energy.”
l
*************************************
l II. Schrödinger’s Physics Definition
l Summarized for the graphic as: “Self-assemble against nature’s tendency towards entropy (disorder) (i.e. negentropy). [Note: this was historically the first of these]
l I have an arrow from the word PHYSICS pointing to this part of the circle, and under the arrow the text: “Schrödinger also predicted before DNA structure known : 1-dimensional aperiodic crystal.”
l There was an arrow pointing to it to a box containing the text: “Self-assemble” as opposed to assisted self-assembly on mineral substrate such as Clay (Jim Ferris et al.)”
l
*************************************
l III. Chemistry Definition
l “Life is a self-sustained chemical system capable of undergoing Darwinian evolution.” [Joyce]
l Summarized for the graphic as: “Gerald Joyce’s ‘working definition’ adopted by NASA: ‘self-sustained chemical system capable of undergoing Darwinian evolution.’ Note: Panspermia allows the Darwinian evolution to have started on another planet or body.”
l I draw an arrow pointing to it to a box containing the text: “If we leave out Gerald Joyce’s ‘chemical system’ we cannot simply exclude software ‘artificial life’ in silico — or more exotic substrates.
l I draw an arrow pointing from that box to a box wit the text: “Questions: in regions combining only 1 or 2 of these definitions, what counterexamples are possible?”
l
l Then there are the overlapping areas of the Venn Diagram:
l *************************************
l I/II. Cybernetics + Physics
l Summarized for the graphic as “self-assembled negentropic network of feedback mechanisms”
*************************************
l II/III. Physics + Chemistry
l Summarized for the graphic as “self-assembled, self-sustained negentropic chemical system capable of undergoing Darwinian evolution.”
*************************************
l I/III. Cybernetics + Chemistry
l Summarized for the graphic as “self-contained network of feedback mechanisms capable of undergoing Darwinian evolution.”
*************************************
l At the center, the triple overlap:
l I/II/III. Cybernetics + Physics + Chemistry
“A self-assembled, self-contained negentropic chemical system network of feedback mechanisms capable of undergoing Darwinian evolution.”
*************************************
“Let me add further clarifications and discussion. To clarify Schrödinger’s Physics definition, although many non-physicists persist in stating that life’s dynamics somehow go against the tendency of second law (which states that the entropy of an isolated system tends to increase), the definition assuredly does not in any way conflict or invalidate this law. This is because the principle that entropy can only increase or remain constant applies only to a closed system (i.e. one which is adiabatically isolated, so that no heat can enter or leave). Whenever a system can exchange either heat or matter with its environment, both of which apply to the planet Earth and its ecosystem, an entropy decrease of that system is entirely compatible with the second law.”
l In more modern terminology life is a dissipative system. A dissipative system is characterized by the spontaneous appearance of symmetry breaking (anisotropy) and the formation of complex, sometimes chaotic, structures where interacting particles exhibit long range correlations. The term dissipative structure was coined by Russian-Belgian physical chemist Ilya Prigogine, awarded the Nobel Prize in Chemistry in 1977 for his pioneering work on these structures, some of which rediscovered by me at the University of Massachusetts after my M.S. In Artificial Intelligence and Cybernetics, with “’enzyme waves.’” – the world’s first PhD Dissertation, what was later known as Alife and Nanotechnology.
“As chemist John Avery explains in his 2003 book Information Theory and Evolution,” said the Cyb, “we find a presentation in which the phenomenon of life, including its origin and evolution, as well as human cultural evolution, has its basis in the background of thermodynamics, statistical mechanics, and information theory. The (apparent) paradox between the second law of thermodynamics and the high degree of order and complexity produced by living systems, according to Avery, has its resolution “in the information content of the Gibbs free energy that enters the biosphere from outside sources.” The process of natural selection responsible for such local increase in order may be mathematically derived directly from the expression of the second law equation for connected non-equilibrium open systems.
“The ‘Ferris et al’ and clay text summarizes the fact that when free nucleotides are combined in water solution, they do not react at all. Hence various teams of scientists have searched for what types of activating groups and inorganic catalysts must have been involved in the polymer bonding process. Dr. Ferris, of Rensselaer Polytechnic Institute in Troy, New York, discovered one inorganic material which facilitates this reaction, namely montmorillonite clay. The specific structure of this clay can provide a medium on which the individual activated RNA units combine to form larger chains.”
l .
l References
l Avery, John (2003). Information Theory and Evolution. World Scientific. ISBN 981-238-399-9.
l Dr. James P. Ferris. “Montmorillonite Catalysis of RNA Oligomer Formation in Aqueous Solution. A Model for the Prebiotic Formation of RNA.” Journal of the American Chemical Society. 1993, 155, 12270-12275.
l James P. Ferris is Director, New York Center for Studies on the Origins of Life
l Gerald Francis Joyce, “The RNA World: Life Before DNA and Protein”.
l Professor Gerald Francis Joyce (born 1956) is a researcher at The Scripps Research Institute. His primary interests include the in vitro evolution of catalytic RNA molecules and the origins of life. He was elected to the National Academy of Sciences in 2001.
l Joyce received his Bachelor of Arts from the University of Chicago in 1978, completed his M.D. and Ph.D. at the University of California, San Diego in 1984, and joined Scripps in 1989. Joyce, quoted in commentary in Science (1992): “Obviously, Harry [Noller]’s finding doesn’t speak to how life started, and it doesn’t explain what came before RNA. But as part of the continually growing body of circumstantial evidence that there was a life form before us on this planet, from which we emerged – boy, it’s very strong!”
l Korzeniewski, Bernard (2001). “Cybernetic formulation of the definition of life”. Journal of Theoretical Biology. 2001 April 7. 209 (3) pp. 275–86.
l Prof. Bernard Korzeniewski’s home page,
l http://awe.mol.uj.edu.pl/~benio/
l Faculty of Biochemistry, Biophysics and Biotechnology, Jagiellonian University, ul. Gronostajowa 7, 30-387 Kraków (Krakow), Poland
l e-mail: benio@mol.uj.edu.pl
l Alonso Ricardo and Jack W. Szostak, , “Origin of Life”, Scientific American, September 2009.
l Schrödinger, Erwin (1944). What is Life- the Physical Aspect of the Living Cell. Cambridge University Press. ISBN 0-521-42708-8. In the famous 1944 book What is Life?, Nobel-laureate physicist Erwin Schrödinger theorizes that life, contrary to the general tendency dictated by the Second law of thermodynamics, decreases or maintains its entropy by feeding on negative entropy. In a note to What is Life?, however, Schrödinger explains his usage of this term:
“Let me say first, that if I had been catering for them [physicists] alone I should have let the discussion turn on free energy instead. It is the more familiar notion in this context. But this highly technical term seemed linguistically too near to energy for making the average reader alive to the contrast between the two things.”
JVP\new\3Life.doc.
.
February 7, 2019 at 5:52 pm |
I am Andy Pargellis and I <> noticed this blog which includes some references to my digital life platform, Amoeba. I recently wrote a follow-up paper with my coauthor, Benjamin Greenbaum. Ben and I studied the self-organization process that occurs in Amoeba.
The paper reference is:
“Self-Replicators Emerge from a Self-Organizing Prebiotic Computer World.”
Artificial Life 23: 318-342 (2017).
Basically, the originally random opcode basis set becomes biased during a self-organizing stage where “propagator sequences” of 3 to 5 opcodes propagate short code snippets that further propagate the sequences. Eventually, the memory space becomes filled with short propagator sequences that eventually coalesce and for the “initial ancestor.”
January 29, 2021 at 9:03 am |
[…] that would show convincingly how life could emerge from non-life by purely naturalistic processes. It was further discussed in this post. There was a lot of excitement around it but it did not lead to a polymath project, and I am not […]
March 16, 2022 at 6:43 pm |
[…] I found some discussion made in Timothy Gowers’s Weblog. The book What is Life? by Erwin Schrödinger, although I don’t know much, also seems to […]