I’m in the happy state of just having finished marking exams for this year. There is very little of interest to say about the week that was removed from my life: it would be fun to talk about particularly bizarre mistakes, but I can’t really do that, especially as the results are not yet known (or even fully decided). However, one general theme emerged that made no difference to anybody’s marks. There seems to be a common misconception amongst many Cambridge undergraduates that I’d like to discuss here in the hope that I can clear things up for a few people. (It is an issue that I have discussed already on my web page, but rather than turning that into a blog post I’m starting again.)
The question where the misconception made itself felt was one about functions, injections, surjections, etc. I noticed that a lot of people wrote things like, “If then
so
is well defined.” Now if you fully understand what a function is, then you will find this quite amusing: if
then trivially
by the very basic principle that you can substitute something for something else if the two things are equal to each other. (A famous type of counterexample to this from philosophy: two years ago, Michelle Obama was the wife of Barack Obama; Barack Obama is the president of the United States; two years ago, Michelle Obama was not the wife of the president of the United States. Yes yes, there are ways of explaining why this isn’t a real counterexample.)
But it seems only fair, if one is going to laugh at such sentences, to provide examples of functions that are well defined and functions that aren’t, so that the difference can be made clear. But now we have a problem: any putative example of a function that is not well defined is not a function at all. So it begins to seem as though all functions are well defined. But in that case, what are people doing when they check that a function is well defined?
The real question we are asking is this: when we use the words “well defined”, what are we referring to? It can’t be a function, because a function is a function is a function and that’s all there is to it. Is it something like “an attempted definition of a function”? That seems a bit odd: we define things, not definitions. If we wanted to say that a definition really did specify a function, then surely we would just say “This definition is good.” So what kinds of objects are there that are sometimes functions (if they are well defined) and sometimes not functions (if they are not well defined)?
To answer this, let me give a fairly standard example of a definition that feels as though it might define a function but in fact doesn’t. We’ll define a “gunction” as follows:
. That is,
takes two rationals and creates a new rational by adding the numerators and adding the denominators. For instance,
.
Why doesn’t this define a function? Well, , so it ought to be the case that if we replace
by
in the calculation just made, then we get the same answer. But actually we get
, which is not the same as
.
But doesn’t this show that what people were writing in their exam scripts is exactly what they should have been writing? I’ve just shown that is not well defined, and did I not do so by finding an example of rational numbers
,
and
such that
but
? Well, sort of, but in that case what function am I talking about? What does
even mean?
Let’s go back to how the gunction is defined, but with no presuppositions about what a gunction actually is. Suppose that
and
are rational numbers. Then to calculate
we choose integers
such that
and
, and output the answer
. As we’ve observed, there are many ways of choosing
and many possible distinct fractions
that could result. So what we have is not a function but a process that takes an element of
and gives us several possible answers.
Thus, a gunction is like a function but it can be multivalued. What is a multivalued function? Well, informally it is “a function that is allowed to take more than one value” such as the gunction defined by
. For some examples we could also allow gunctions not to be defined everywhere, as would happen here if we extended the domain of
to all of
. More formally, a multivalued function from
to
is a subset
of
such that for every
there is at least one
such that
. And a more general gunction is just any subset of
(otherwise known as a relation).
Let’s stick with the informal definition of a gunction from to
as being like a function except that it doesn’t have to take precisely one value for each
. The next question that arises is this: why bother with gunctions at all? Why take the risk of a bad definition? Why not just stick to functions so that everything is automatically well defined?
To answer this, let us go back to the rationals and see how we define the sum of two rationals. The most convenient definition is the obvious one: . Let us break that up into a composition of simpler operations. We start with a pair
of rational numbers. Next, we choose pairs
and
of integers such that
and
. Then we work out the integers
and
. Finally, we output the answer
.
Now the first stage of this process is a very clear example of a multivalued function, since for each pair there are many ways of choosing the pairs
and
. From then on, however, we are dealing with good old-fashioned functions. So we have just defined a gunction from
to
by composing a genuinely multivalued function from
to
with a function from
to
and then a function from
to
. (To be slightly more accurate we should say
rather than
.) The resulting object is a good example of a gunction that happens to be a function, but where that fact, rather than being trivial, is something that needs to be checked.
This example points us to the answer to our earlier questions. It often happens that the most convenient way of defining a function is to define it as a composition
, where
is a multivalued function and
is a function. For
to be a function, or, as we usually say, for
to be well defined, we need the following to hold: for every
and any two possible values
of
,
.
Why does this situation come up so often? Well, often and
are not just any old sets but sets of equivalence classes. For example, an element of
can be thought of as an equivalence class of pairs
, where
if and only if
. (And this is not just some strange abstract definition: it really is what we are doing when we deal with rationals, except that we happen to write
instead of
.) If we want to define a function
from
to
, then what do we do?
Let’s suppose that is the set of all equivalence classes of some equivalence relation
on a set
and that
is the set of equivalence classes of an equivalence relation
on a set
. Then often what we do is this: start with an equivalence class
of the relation
on
; choose an element
of
; apply some function
to the element
, obtaining an element
; let
be the equivalence class of
. We then say that
.
There is a natural multifunction from to
, namely the multifunction that takes the equivalence class
to any element
of
. The procedure we have just defined is the composition of that multifunction with a function from
to
and the quotient map from
to
. And what do we need to know about
if we want
to be a function? We must check that
whenever
, which is actually not all that different from what the candidates were writing in the exam. However, it is different: the difference between “is equal to” and “is equivalent to” makes the difference between a triviality and something that actually needs to be checked.
Notice that the multifunction from to
was in a sense the inverse of the quotient map from
to
(which equals
). This is another way of thinking about why gunctions/multifunctions arise naturally: they are, so to speak, inverses of functions that don’t have inverses. Or at least, that is a natural way for them to arise.
All this demonstrates that the conventional use of language, with sentences like “We must check that this function is well defined,” is extremely unfortunate: if you have been confused by it, then that is much more the terminology’s fault than it is yours. But it looks as though the terminology is here to stay, so the best advice I can give is that while you write “Let us check that this function is well defined,” you secretly translate it to yourself as “Let us check that this gunction really is a function” or, if that’s a bit too Dr Seuss for your tastes, “Let us check that this multivalued function is in fact a function.” And one last piece of advice, which would have saved a few precious seconds for many candidates on the exam that I’ve just marked: if you’ve just defined a function from to
by specifiying unambiguously what it does to each element of
, or if you’ve defined it as a composition of two existing functions, then it is automatically well defined and you don’t need to check anything. You don’t even need to say that you don’t need to check anything: it’s just a function and that’s all there is to it. The things that might fail to be well defined are multifunctions.
June 8, 2009 at 3:05 pm |
It’s okay and fun to make up words like “gunction”, or use a somewhat oxymoronic term like “multivalued function”, but the traditional term is “relation” — and students can be taught that a relation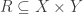 can be thought of also as a function taking elements of X to subsets of Y (or elements of the power set PY, if you like). Then the question becomes “is this relation a function?”.
can be thought of also as a function taking elements of X to subsets of Y (or elements of the power set PY, if you like). Then the question becomes “is this relation a function?”.
It seems to me that one of the first things taught in a course which deals with basic mathematical concepts is some facility with relational ideas. The hoary “calculus of relations” crops up far more often than most people let on.
June 8, 2009 at 4:46 pm |
I’d say your Obamas counterexample isn’t really one because you’ve introduced the qualifier “two years ago” which wasn’t in any of the hypotheses. Two years ago, Barack Obama *wasn’t* president, so Michelle Obama wasn’t the wife of the president. The only contradiction is in objects changing state over time.
The real issue here is referential transparency, the property that you can freely substitute things that are equal without changing the truth of propositions. And I think that’s better illustrated by this counterexample, adapted from Quine: You think Batman is a criminal menace. Unknown to you, Batman is Bruce Wayne. Would I be correct to say that you think Bruce Wayne is a criminal menace?
Also, what Todd said.
June 8, 2009 at 5:04 pm |
Another perspective, which is emphasized in constructive type theory, is that equality of two mathematical objects is not absolute, but relative to their type. Writing a=b in A to mean that a and b are equal as objects of type A, we then say that f is a function from A to B iff whenever a=b in A we have f(a)=f(b) in B. (Equality being reflexive, this implies that objects of A are mapped to objects of B by f.)
Your gunction g is then evidently a function from Z^2 * Z^2 -> Z^2, because it is composed of other such functions. The question is whether g is also a function from Q x Q -> Q, where Q is defined to be Z^2/~ as discussed. As your students seem to think, this _is_ a question of preservation of equality: we must check that if (u,v)=(u’,v’) in QxQ then g(u,v)=g(u’,v’) in Q! But when we unravel the definitions we see that the requirement is to show that if (u,v)~(u’,v’) then g(u,v)~g(u’,v’), which is not true, so g does not preserve QxQ-equality, even though it preserves Z^2xZ^2 equality.
This explanation avoids the need to discuss multifunctions or relations, and can be seen as validating the intuitions that the students have (somehow) acquired. Perhaps it falls short in some other respect?
June 8, 2009 at 5:16 pm |
Todd, one small comment about what you say. In one sentence you say that a relation can be thought of as a function, and in the next sentence you say that the question becomes whether it is a function. Obviously you mean two different things, but there is the potential there for people unfamiliar with these ideas to get confused. In fact, I think I’d argue against pointing out that a relation can be thought of as a set-valued function, because that makes the connection between relations and functions less clear rather than clearer: you’d then have to say that a function could be identified with a relation that took singleton values. I find it easier to say that a function is a multifunction that happens to be single-valued.
I prefer to use the term “relation” when I’m relating things and “function” when I’m operating on things, and I think that makes it more transparent to the beginner because it reflects more accurately what one actually does. For example, when I multiply two residue classes mod , I really do pick representatives, mutliply them, and take the residue class of the product. And the picking operation feels more like a dynamic process rather than the static fact that the representatives belong to the residue classes. Similarly, although one can compose relations, I find it less intuitive than “do
, I really do pick representatives, mutliply them, and take the residue class of the product. And the picking operation feels more like a dynamic process rather than the static fact that the representatives belong to the residue classes. Similarly, although one can compose relations, I find it less intuitive than “do  and then do
and then do  “.
“.
I’m saying all this from the perspective of somebody who dislikes the tendency to turn everything into sets. I see the need for it if one is going to prove the independence of CH or something like that, but I don’t want it interfering with the rest of my mathematical life. So for example I don’t like the idea that a function from to
to  is “really” a set
is “really” a set  of sets
of sets 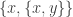 such that for every
such that for every 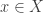 there is exactly one
there is exactly one 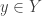 such that
such that 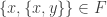 .
.
June 8, 2009 at 5:31 pm |
Robert, here’s another example. Suppose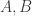 and
and  are groups and I’ve got homomorphisms
are groups and I’ve got homomorphisms 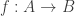 and
and 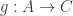 , and suppose that I now want to define a homomorphism
, and suppose that I now want to define a homomorphism 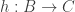 such that
such that 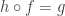 . I won’t always be able to do so, but one way I could try to do so is as follows. For each
. I won’t always be able to do so, but one way I could try to do so is as follows. For each  I find
I find  such that
such that 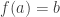 (which requires the hypothesis that
(which requires the hypothesis that  is a surjection) and I then let
is a surjection) and I then let  .
.
One of the first things I’ll need to do is check whether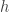 is well defined, for which I need that if
is well defined, for which I need that if  then
then 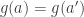 . I find it quite natural to think of this as asking whether the composition of the multifunction
. I find it quite natural to think of this as asking whether the composition of the multifunction 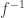 with the function
with the function  is single valued. I’m not sure how you would think about it: it seems a little unnatural to talk of
is single valued. I’m not sure how you would think about it: it seems a little unnatural to talk of  and
and 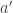 being equal “as things that go into
being equal “as things that go into  when you do
when you do  ” or something like that.
” or something like that.
But in general, I agree that what the students were doing is not completely incorrect: often they just need to replace “equal” by “equivalent”.
June 10, 2009 at 6:14 am
<>
And they need to do so on both the starting ensemble and the arriving one.
Your exemple still stands with f :E ->F is a function iff a==_E b => f(a) ==_F f(b). with the the equality on E defined on A/f. So this is correct.
But I agree it is suboptimal way to talk about wether a function is defined or not. The approach of transforming a function f to its equivalent on the set, which always exists along with its composition, seems much more elegant and natural.
What is needed I guess is to formalize the equivalence, so that everyone can use the fittest tool depending on the context.
December 19, 2010 at 6:17 pm
In your example, $f$ needs to be a surjection, as you say — so it’s reasonable to see elements of $A$ as *representations* of elements of $B$, via $f$ (just as a pair of integers is a representation of a rational number). Then it does seem reasonably natural to say things like “$a$ and $a’$ are equal, when seen as [representing] elements of $B$”. I.e.: as pairs of integers (1,3) and (2,6) are different, but seen as representing rationals, they’re equal.
June 8, 2009 at 6:54 pm |
since, on the tricki, search(“well defined” + “well-defined”) maps to ‘Your search yielded no results’, would you (or somebody!) place a note about this on there ??
i.e. relations on equivalence classes, and their well-definedness
June 8, 2009 at 8:13 pm |
An interesting math object can always be viewed in several different ways (they have different conceptual metaphors). Two of these ways can often be seen as different sides of a natural equivalence, and that may be worth pointing out in many cases (depending on the level of the class).
Relations from A to B are naturally equivalent to multivalued functions (functions from A to the powerset of B). To say they are the “same thing” is a kind of reductionism. As you say, you think of one when relating things and the other as operators.
The category of equivalence relations are naturally equivalent as a category (with the usual definition of morphism) to the category of partitions of sets. But “things are alike” is not the same metaphor as “disjoint sets of things”. In fact the category equivalence spells out how you change from one kind of thinking to the other.
Functions on the reals that satisfy the epsilon-delta definition are “the same thing” as functions for which inverse images preserve openness. But the conceptual images are strikingly different.
We need to teach students some meta-ideas:
1) It is good to have different conceptual metaphors for the “same kind of” math object. In fact it is essential.
2) But conceptual metaphors are dangerous. They suggest things that are true but also things that are false. (“Set as container” suggests that if x is an element of A and A is an element of B then x is an element of B. “A function with positive derivative is growing” is OK only if you are imagining moving from left to right on the graph!)
3) Discovering that two conceptual metaphors are related by a natural equivalence is great because then you know you the metaphors are not so likely to introduce errors (provided you really understand how the equivalence works.)
4) Reducing one kind of thing to another is good because it enables you to transfer your mental images from one to the other. It doesn’t mean you should forget the images for the kind being replaced.
June 8, 2009 at 9:37 pm |
This takes me back to Conway’s numbers in which equality is a defined relation, which is, in the end, a different language for equivalence classes – but it might provide interesting examples (is addition well-defined?)
June 8, 2009 at 11:06 pm |
Well put, Charles. I was indeed trying to suggest that relations, which is a word students may have already seen, can be thought of in more than one way, including as multifunctions. But your fuller explanation was much better.
I’d also like to say that I’m fully on the same page with Tim when he says “I’m saying all this from the perspective of somebody who dislikes the tendency to turn everything into sets.” The calculus of relations to which I alluded interests me less as an opportunity to turn everything into sets; rather I see it more along the lines of a form of algebra not unlike linear or matrix algebra, as was observed long ago by Peirce. But this is a subject for a different thread.
June 9, 2009 at 7:34 am |
Your students are right to say a function is defined iff a=b => f(a)=f(b)
Only they miss to define what equality means here !
Taking your example of g, it is a function from the set of couples of couples ((a,b), (c,d)) to the space of couples (e,f) : in this space (1,3) (2,6), so f( (1,3), (a,b)) f( (2,6), (a,b)) is not a problem.
As you said, it is not a function from Q, because (1,3) ==_Q (2,6) in that space. So the equality of your student should be subindexed by domain(f) (on both side..)
More generally, the problem is that we define function over a domain from a representation of an element of that domain.
And obviously, for a function to be well defined, the result should be independant from the particular representation we choose.
so f :E ->F is a function iff a==_E b => f(a) ==_F f(b)
June 9, 2009 at 10:39 am
” in this space (1,3) \neq (2,6), so f( (1,3), (a,b)) \neq f( (2,6), (a,b)) is not a problem.”
June 9, 2009 at 7:49 am |
If we are to compose a list of things to double check in a new fantastic proof one of the things on top of the list will be to check if functions (and other notions) are really well defined. (And that even if they are well defined, the definition allows to well define other functions/notions based on them.) The difficulty in understanding what is a well defined function extends from undergraduates to professional mathematicians. (Another thing I’d put on top of such list is to carefully double check every appearance of the word “clearly”.)
June 9, 2009 at 10:41 am |
I agree with Todd, and I’d like to elucidate:
In my dream world, students would be taught about “relations”, how “some relations are functions”, and “Relation inverse and composition of relations always exist, and while the composition of two functions is a function, the inverse of a function might not be a function”. (This is different, for me, than saying “the inverse *exists*”. The inverse exists always: it is all pairs s.t., …. but it might not satisfy the function properties.)
Which means that not only would they say “Let us prove that this relation is a function”, which is awesome in itself, but also that proofs like “recursive definition of functions” have something to prove: “There is exactly one relation which satisfies recursive definitions and it is a function” (given a good definition of what it means to have a recursive function definition).
This means that students, when wanting to prove a relation is a function, need not start with composition: they can define addition as all pairs: ([a/b, c/d], (ad+bc)/bd), and to check that it is “well-defined” (i.e., is a function and not just a general relation) they need to go through exactly the motions defined earlier: if a/b=a’/b’ and c/d=c’/d’, let’s check that the addition formula gives equal results. They need not add lots of boiler plate regarding equivalence classes and choosing equivalence elements (and while that might be *one* definition of Q, it’s not the only one…). They really only need to check that if (x,y),(x’,y’) are in the relation, and x=x’ then y=y’ — exactly what they long to do 🙂
June 9, 2009 at 3:08 pm |
I think there’s a lot of agreement here masquerading as disagreement. In particular, I think everybody understands what has to be checked when we show that addition on the rationals is well defined, and everybody understands that there are several different but complementary ways of looking at it.
I even share Moshez’s vision, closely related to Todd’s, that it would be good to teach people about a calculus of relations. One advantage of that is that it gets rid of a strange asymmetry: we talk a lot about whether functions are injections and/or surjections, but when it comes to the question of whether a relation is a function we try to sweep it under the carpet by banning all talk of non-functions. Geometrically, we are interested in how many times horizontal lines intersect the graph, but we insist that vertical lines intersect exactly once. And we discuss the rather artificial statement that a function is a surjection if and only if it has a right inverse, when in applications we don’t tend to use the fact that that right inverse is a function: it is usually more natural to take the inverse of the relation and compose it with something that turns it into a function.
So my only quibble is with the use of the word “relation”. I think what I would advocate is a more function-like word such as “multifunction” at least to start with. And then one could point out that multifunctions and relations were the same thing. I don’t think that’s pointless, because, as Charles Wells might put it, it gives us genuinely different conceptual metaphors, and that tends to be helpful.
Even this hardly counts as a quibble, since it is more or less the same as what Charles said and Todd enthusiastically endorsed.
To quibble with myself though, I can see that “multifunction” is not quite ideal for an arbitrary relation, because it could suggest that there always had to be multiple values. But right now I can’t think of a good word for a function-like object that can take any number of values, including no values at all. The best I can do is hopelessly clumsy: partially defined nondeterministic function. Maybe it is after all better to use the word “relation” but immediately stress that a relation can be thought of not just as a collection of statements relating objects, but also as a function-like process of transformation.
June 9, 2009 at 3:37 pm |
Hi Tim,
Have you given this example to nuclear physicists? If an object doesn’t arise in a natural way, e.g., primes in rational mechanics, then it is hard to understand.
June 9, 2009 at 4:36 pm |
Thanks for that balanced summary, Tim. It would indeed be nice to develop basic relational thinking in undergraduates, starting with different ways of picturing relations. The description of a relation as a subset of a cartesian product, while of course correct, is a bit bare-bones and not necessarily the best for picturing how relational composition works, at least not for beginners. The multifunction picture comes a bit closer, but my own inclination would be to take that further and draw a relation from a set to a set
to a set  as a bunch of arrows, with an arrow from
as a bunch of arrows, with an arrow from 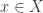 to
to 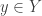 if they are
if they are 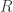 -related. This picture conveys something of the “function-like” way we’d like to think of relations.
-related. This picture conveys something of the “function-like” way we’d like to think of relations.
Then, composition of relations is a kind of Feynman-like “sum over all histories” process, where we can pun on the word “sum” by thinking of it as “some”. That is, in composing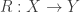 with
with 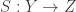 (these are relations, not functions), we consider any and all paths from an element
(these are relations, not functions), we consider any and all paths from an element 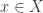 to an element
to an element  which pass through some intermediate
which pass through some intermediate 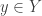 ; if there is some such path, then
; if there is some such path, then  holds. This has to be the simplest possible kind of “Feynman path-integral”, where we replace arithmetic in the complex numbers by “tropical arithmetic” in the set of values
holds. This has to be the simplest possible kind of “Feynman path-integral”, where we replace arithmetic in the complex numbers by “tropical arithmetic” in the set of values 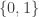 . In any event, we are giving a kind of pictorial description of the matrix formula
. In any event, we are giving a kind of pictorial description of the matrix formula
where now we are literally interpreting “sum” as “some”, and “product” as “and” (putting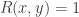 if
if 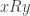 holds).
holds).
A lot of fun can be had with this. For example, the opposite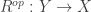 of a relation
of a relation 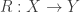 is given as the matrix transpose
is given as the matrix transpose 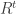 of
of 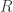 . A relation is
. A relation is 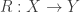 is “well-defined” (in the function sense) iff
is “well-defined” (in the function sense) iff 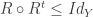 , where the right side denotes the identity matrix. It is “total” (meaning that for all
, where the right side denotes the identity matrix. It is “total” (meaning that for all  there exists
there exists  such that
such that 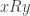 ) iff
) iff 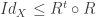 . Other functional concepts such as “injection” and “surjection” also receive elegant treatment in the matrix language.
. Other functional concepts such as “injection” and “surjection” also receive elegant treatment in the matrix language.
(I wonder, Tim, if your Cambridge colleagues Peter Johnstone or Martin Hyland ever introduce these sorts of ideas in courses at this level?)
June 9, 2009 at 6:00 pm |
When we say that a function is well defined, perhaps it would be more accurate to say that our definition is consistent. I have in mind the following example. Assume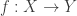 is a linear map between two vector spaces
is a linear map between two vector spaces  and
and  , consider two subspaces
, consider two subspaces 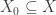 and
and 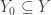 , and define the quotient map
, and define the quotient map 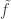 by the expression
by the expression 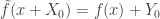 . This definition is consistent as far as
. This definition is consistent as far as 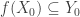 .
.
June 10, 2009 at 5:47 am
which is again an example where

where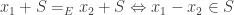 and the equivalent definition in F
and the equivalent definition in F
June 9, 2009 at 6:42 pm |
Here is another example from a paper entitled Norm estimates for the partial transpose map on the tensor product of matrices, by Tsuyoshi Ando and Takashi Sano (MR 2373130) . The partial transpose map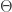 takes very tensor
takes very tensor  into the tensor
into the tensor 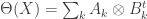 . Although the representation for
. Although the representation for  as a sum of elementary tensors is not unique, this definition is consistent.
as a sum of elementary tensors is not unique, this definition is consistent.
June 9, 2009 at 11:32 pm |
[…] 2009 — Charles Wells I recommend reading the discussion (to which I contributed) of the post “Why aren’t all functions well-defined?” on Gower’s Weblog. It resulted in an insight I should have had a long time […]
June 9, 2009 at 11:42 pm |
You could use the word “transformer” for a multivalued function. This doesn’t seem to clash with other usages. A linear transformation is a transformer, and so are integral transforms. The word transformer discourages confusing the transformer from any value. Thus a Fourier transform is an output of a transformer.
Some decisions about terminology need to be made.
Maybe a transformer should not be allowed empty output for some inputs. Then a transformer would be a kind of relation, but not any old relation. Don’t most things that are actually called multivalued functions have this property?
Given a transformer T, you could use the notation T(c) for the set of all outputs for input c, and T’c for an arbitrary output. You could use the syntax “Consider a T’2.”
There are two different ideas corresponding to “injective”: (1) The corresponding set-valued function is injective and (2) If c is different from d then no T’c is the same as any T’d.
By the way, I posted a kind of spin-off from this discussion here: http://sixwingedseraph.wordpress.com/2009/06/10/different-names-for-the-same-thing/
June 10, 2009 at 4:20 am |
miguel, your first example is a special case of what Tim’s been talking about; quotients are equivalence relations. (The case I had in mind was the even more specific case of defining a linear transformation on the space of Lebesgue-integrable functions and showing that it is well-defined on the quotient by null functions, which is where I saw phrases like “check that this function is well-defined” most often last semester.)
June 10, 2009 at 3:27 pm
Qiaochu, you are right, this is a special case of what Tim mentioned in the 15th paragraph when he talked about well-defined functions between quotients. Nicolas is right too, the equivalence relation is defined for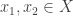 as follows:
as follows: 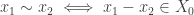 . My point is that in this special case, the statement that a function is well-defined makes a lot of sense (i.e. one has to check that
. My point is that in this special case, the statement that a function is well-defined makes a lot of sense (i.e. one has to check that 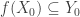 ), in contrast with the more general statement that
), in contrast with the more general statement that  , which doesn’t help much to illustrate what you understand by a well-defined function.
, which doesn’t help much to illustrate what you understand by a well-defined function.
Concerning the more specific case of a linear transformation on the space of Lebesgue-integrable functions, you probably were asked to check that if
on the space of Lebesgue-integrable functions, you probably were asked to check that if  vanishes almost everywhere, then so does
vanishes almost everywhere, then so does 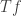 . This is something that every undergraduate should do at least once in a lifetime, although it is my particular opinion that, after all, this is just a question of burocracy.
. This is something that every undergraduate should do at least once in a lifetime, although it is my particular opinion that, after all, this is just a question of burocracy.
June 10, 2009 at 7:00 pm |
On the terminology front, I think we started off with mappings or maps, of which functions were a subset – but that might be too informal, and map(ping) probably has too many potentially conflicting formal and informal uses to be useful terminology here. But I do think that the basic terminology for a general relation ought to be a ‘high school’ type phrase, rather than something which sounds over-technical – because that is when the concept of relationships between sets is first introduced. This is the fundamental concept.
On the question of well-defined functions, another way of looking at the question is a function “from what” “to what”?
So on the rationals, one way of putting the question is whether a putative function function has the proper domain – whether it is a function from the rationals or not. Tim’s example is a function from ordered pairs, but cannot be factored through the rationals. The way the rationals appear brings the ideas of category theory into play.
The reals defined as cauchy sequences mod null sequences raise similar issues, but there is some theorem or lemma along the way that certain kinds of maps can be factored through this definition which guarantees well-definedeness in the cases we need.
So one question is whether there is a sufficiently standard way of proving well-definedness that we prove a lemma to cover the cases we need, or whether the examples given are effectively the proof which is necessary to guarantee well-definedness without thinking about it later on.
June 10, 2009 at 8:23 pm |
Here’s an example that shows the artificiality of insisting on functions. Let’s consider the proof of the isomorphism theorem for groups that says that if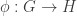 is a homomorphism, then the image of
is a homomorphism, then the image of  is isomorphic to
is isomorphic to  quotiented by the kernel of
quotiented by the kernel of  .
.
Here’s how it is often proved. Let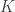 be the kernel of
be the kernel of  and let
and let  be an element of the quotient
be an element of the quotient 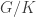 . Then define
. Then define 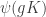 to be
to be 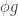 . We must now prove that
. We must now prove that  is a well-defined isomorphism. To do that we prove that if
is a well-defined isomorphism. To do that we prove that if 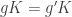 then
then 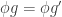 , which follows easily from the fact that
, which follows easily from the fact that 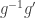 belongs to the kernel of
belongs to the kernel of  . We must also prove that it is an isomorphism, which is also easy.
. We must also prove that it is an isomorphism, which is also easy.
Here is an alternative proof. Obviously the work is going to be the same, so it is not a radically different argument and I am not claiming that it is. But let be the quotient map and let
be the quotient map and let 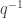 be its inverse, which is not a function but a multifunction, or relation, or whatever you feel like calling it. Then we define
be its inverse, which is not a function but a multifunction, or relation, or whatever you feel like calling it. Then we define  to be
to be 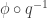 . We must check that
. We must check that  is a function, which means that we must check that if
is a function, which means that we must check that if 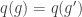 then
then 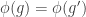 . But
. But 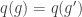 if and only if
if and only if 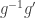 belongs to
belongs to 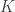 if and only if
if and only if 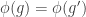 . Somehow, this second way of looking at it brings out the triviality of the result in a more transparent way, and we don’t have the silly business of defining a function, getting anxious that we might have done something stupid, and checking that we haven’t. Instead, we do the utterly obvious thing, given the maps we have around, of taking the only composition that can possibly do the job.
. Somehow, this second way of looking at it brings out the triviality of the result in a more transparent way, and we don’t have the silly business of defining a function, getting anxious that we might have done something stupid, and checking that we haven’t. Instead, we do the utterly obvious thing, given the maps we have around, of taking the only composition that can possibly do the job.
June 24, 2009 at 1:27 pm
Tim Gowers writes: “Let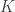 be the kernel of
be the kernel of  and let
and let  be an element of the quotient
be an element of the quotient 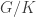 . Then define
. Then define 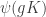 to be
to be 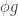 .”
.”
The psychological problem for me is in the phrase “define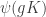 to be
to be 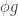 .”
.”
This is sort of an arrogant statement – not on Tim’s part, but for mathematicians generally. It suggests that we mathematicians are free to do what we darned well like! In this case we can, but as in Tim’s fractions example, sometimes we cannot.
I would suggest a softer and more humanly realistic type of language, such as: “Let us try to define a function latex \psi$ by the procedure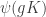 is
is 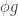 . Does this work? That is, if
. Does this work? That is, if 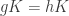 does it follow that
does it follow that 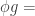 \phi g”.
\phi g”.
September 16, 2009 at 11:33 pm
re: mathematicians are arrogant and do whatever they like
Indeed, that I can play God is possibly the only reason why I cannot but do math!
June 14, 2009 at 10:28 pm |
All this seems much ado over nothing. Equality is not a very rigorous mathematical concept, it’s just some particular equivalence relation such that all the members of an equivalence class have the same value with respect to all properties that we happen to be studying.
June 15, 2009 at 10:01 pm |
Well there are different kinds of equivalences which are encompassed within the concepts of equality we use in mathematics. In some cases we learn to push the equivalence relations so far into the background that most of us don’t even realise they are there or reflect on their significance.
And then there are equivalence relations which emerge out of mathematical work, where the question (the ‘well-definedness question’) is effectively “is this equivalence relation compatible with that mathematical property?” (or “have I got my construction/definition right?”)
Thinking about this, I would suggest there are at least two different kinds of equivalence which do fade into the background.
One is the equivalence relation between ordered pairs of integers which represent the same rational number – an equivalence relation on a set.
A second is an embedding – eg taking Peano integers into rationals defined as ordered pairs, or taking rationals into reals defined as equivalence classes of Cauchy sequences, or the process of identifying a ground field as a subfield of an extension field.
But the question which seems to me to be raise in this thread is about when and how the well-denfinedness question arises.
June 15, 2009 at 10:58 pm |
Another question is a terminological one. Suppose that you were in charge of a contemporary Bourbaki and could start again with the basic concepts of mathematics, secure in the knowledge that the conventions you decided on would be widely adopted. Would you stick with the current terminology relating to functions?
I think I’d be tempted by a set of definitions that allowed one to say that every function has an inverse — it’s just that the inverse may not be a function. Then a surjection would just be a function whose inverse is a multifunction (where this means a function-like object where every has at least one image), an injection would be a function whose inverse is a partial function (I’d like to have nicer terms for these, but this is what they might be called now), and when we wrote
has at least one image), an injection would be a function whose inverse is a partial function (I’d like to have nicer terms for these, but this is what they might be called now), and when we wrote  we wouldn’t have to tell students that
we wouldn’t have to tell students that 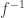 had no meaning. I may be wrong, but it feels to me as though doing things this way would be more natural and easier for students to understand.
had no meaning. I may be wrong, but it feels to me as though doing things this way would be more natural and easier for students to understand.
June 16, 2009 at 2:08 am
Dear Tim,
It is an interesting suggestion, which has certain merits. On the other hand, there are a couple of classical cases in which we do have (mildly, or occasionally) multi-valued inverses, namely square roots, and inverse trigonometric functions. The (potentially) multi-valued nature of these functions, when they appear in problems (say in a calculus course), is a fairly standard source of confusion and error, at least in my experience. Thinking about these examples makes me wonder if it wouldn’t be the case that changing the terminology/point-of-view wouldn’t just shift confusion and error from one place to another.
June 16, 2009 at 8:26 am
Perhaps. But perhaps it would be more honest to say that the square root is sometimes two-valued and sometimes no-valued, but that for various reasons it is convenient to restrict to just one value. If the potential multivalued nature of the functions causes confusion, then perhaps one could partially avoid that confusion by not trying to pretend that they are single valued.
An interesting moment would come when one introduced complex numbers. One could argue that thinking of the square root as a two-valued function would convey to the subconscious the sophisticated idea that interchanging and
and 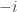 is an automorphism of
is an automorphism of 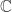 . By contrast, most people when they first see complex numbers think of
. By contrast, most people when they first see complex numbers think of  as “the” square root of
as “the” square root of 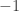 and of
and of 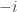 as minus that, even though that makes no sense at all.
as minus that, even though that makes no sense at all.
June 16, 2009 at 8:48 am
Of course in topology the rather basic idea that a function is continuous if the inverse image of an open set is open provides an example where a multi-valued inverse is allowed.
As to terminology, it would seem very useful to have a rather smoother way of talking about some of these things, which more easily and naturally reflects the mathematical reality. Some of the issues with multiple values live on Riemann Surfaces, for example.
With things like square roots is the terminology basically performing a holding function until the full mathematical shape of things is revealed, or is it intended to do more than this and point to an underlying way of thinking?
June 25, 2009 at 10:15 pm
How about “functoids” for partially defined functions, and perhaps “multifunctoids” for the general relation when viewed from a near-function point of view? So plus-or-minus square root would be a multifunctoid when you (attempt to) define it on the whole real line.
The most common mistake that I see from students in this area is when I ask them for the definition of an injective function. Often they insist that this means a function from
from  to
to  such that, for all
such that, for all 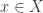 , there is a unique
, there is a unique 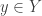 such that
such that 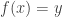 . One year I decided that a brief discussion of the differences between functions and multifunctions might help to eliminate this particular misconception. Unfortunately, I suspect that it just added to the confusion of many of the students (though this is hard to measure). I don’t plan to try this approach again in the near future.
. One year I decided that a brief discussion of the differences between functions and multifunctions might help to eliminate this particular misconception. Unfortunately, I suspect that it just added to the confusion of many of the students (though this is hard to measure). I don’t plan to try this approach again in the near future.
Joel Feinstein
June 18, 2009 at 6:22 pm |
For the sake of discussion, here’s an alternative point of view:
Introducing h(.) via some sentence of the form “Let h(x) = whatever”
is adding to our notation. We may then wish to show that this addition
has not invalidated the formal rules of manipulation that our notation
enjoyed before the addition — especially the rule that equals may be
substituted for equals. Thus claiming that “if a=b then h(a)=h(b)”
is a trivial instance of substitution is begging the question.
You wrote, “we define *things*, not *definitions*”. In the view I’m
trying to suggest above, we define notations, not things.
(You mention that substitution is a little more complicated in
philosophy, but there are plenty of complications even in math,
aren’t there? From “x=y and (forall x: g(x))” we cannot deduce
“(forall x: g(y))”, for example, but the most naive form of a
substitution rule would allow it.)
June 22, 2009 at 1:23 pm |
Well I still don’t understand the usefulness of gunctions and reason for dealing with them. f(a/b, c/d) is really tricky. Why not just define a beautiful f(a, b, c, d) and eliminate all the fuss and spare time for a coffee break :-)?
July 2, 2009 at 4:52 am
If ‘f’ is (say) adding rational, then the first representation is the more natural. There is the fundamental requirement that f be a proper function
(over the rationals). This constraint would not be natural in the second representation.
Also the gunction g(a/b, c/d) = (a+c)/(b+d) as a gunction is nice to demonstrate that the rationals are dense. g being a function it not required just that one can constructively find a rational between any two other rationals. The fact that equivalent rationals give different results actually kinda stengthens the argument. (This was my favorite ‘gunction’ from my high school days.)
June 22, 2009 at 10:06 pm |
The examples discussed in this thread so far are all about multivalued functions like the complex logarithm or equivalence relations.
I have in mind another situation were functions might not be well defined.
Let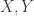 be two vector spaces and let
be two vector spaces and let 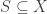 be a generating system. Then we may define a linear map
be a generating system. Then we may define a linear map 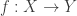 with prescribed values on
with prescribed values on  as long as
as long as  is a linearly independent set, for otherwise our definition may not be consistent.
is a linearly independent set, for otherwise our definition may not be consistent.
More generally, if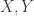 are two groups and
are two groups and  is a generating system then a homomorphism
is a generating system then a homomorphism 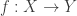 with prescribed values on $S$ can be well-defined assuming that there are no relations, so that
with prescribed values on $S$ can be well-defined assuming that there are no relations, so that  is a the free group with free generating set
is a the free group with free generating set  .
.
June 23, 2009 at 12:46 pm |
I have read this discussion with much interest. I am a Cambridge philosopher who works with Timothy Smiley on plural logic. We find many-valued functions important because they illustrate how plural rather than singular logic is a better vehicle for representing much mathematics (in plural logic, there are plural terms standing for more than one thing; a term formed from a functor expressing a many-valued function is plural). In our ‘Plural Descriptions and Many-valued Functions’ (Mind 114, (2005): 1039-68: http://mind.oxfordjournals.org/cgi/content/abstract/114/456/1039) we discuss the history of many-valued functions (e.g. they are there in Euler and Hardy), and their treatment by logicians. Up to the 1960s, there are two camps. Frege, Russell, Carnap and Church all thought the notion of a many-valued function was illegitimate (in the paper, we criticise their arguments). On the other hand, Tarski, Kleene, Rosser and Quine knew of them, do not object, but ignore them. As for the present day, many-valued functions have been eliminated by definition in logic textbooks, which seems to us a mistake. We also criticise a number of common ways to eliminate many-valued functions, e.g. by replacing functions by relations, replacing the many values by a set, or by changing the domain of arguments.
June 24, 2009 at 4:53 pm |
This is a response to Gary Davis’ comment. He says “The psychological problem for me is in the phrase ‘define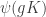 to be
to be 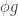 .'” The point is that when Tim wrote that statement he already knew that the definition worked. There is reader’s time and writer’s time.
.'” The point is that when Tim wrote that statement he already knew that the definition worked. There is reader’s time and writer’s time.
Gary Davis is engaging in the pretense that we should read a mathematical argument entirely in reader’s time. In fact it is much more efficient to skip around when you read it so that you know what is “coming up” (in reader’s time) as well as what has already happened. That is the way I read math and I think that is true of most other people.
For that reason I don’t regard the way Tim wrote the sentence as “arrogant”. But reasonable people may disagree about this.
June 25, 2009 at 5:50 pm |
As far as I’ve observed, many undergrads from non scientific disciplines don’t have a sound grasp of the meaning of a function.
The intuition which is being taught to them is that a function “gets a value and does some operation on it”. While that might but true for all single variable functions, there is usually not enough emphasis on the fact that it doesn’t work the other way around. The best work around I’ve been able to think about is to teach what an operation is in general and what operations are and aren’t functions. Of course, I’m in no teaching position so I haven’t been able to test this approach, though it does wonders to my pupils (I give private lessons).
I think the entire approach behind omitting formalities in favor of not overburdening the student, and trusting him to have robust intuition, is too optimistic to actually work.
Thanks for the detailed post, I’ll be sure to use these examples in the future.
June 30, 2009 at 2:19 am |
The discussion is illuminating to me but to go back to the world of the undergraduate students taking the exams who wrote: “If a=b then h(a)=h(b) so h is well defined.” Isn’t the issue that we have a set $E$, an equivalence relation $R$ , a function $f: E \to X$ and a desire to define a function $\bar{f} E/R \to X$ s.t $f = \bar{f} \circ p$ where p is the canonical mapping from $E$ to $E/R$. We define $\bar{f}$ by its action on an element of $E$ a representative of an equivalence class. In this case to show that $\bar{f}$ is well-defined , i.e. a function, we have to show that if $a \equiv b \left( \mod R \right)$ then $f(a) = f(b)$. This is what the student should have written. Godement’s Algebra discusses this in excruciating but very clear detail in Ch, 4, Sec. 3 and the case of fractions in Ch. 29, Sec. 1.
June 30, 2009 at 2:23 am |
The discussion is illuminating to me but to go back to the world of the undergraduate students taking the exams who wrote: “If a=b then h(a)=h(b) so h is well defined.” Isn’t the issue that we have a set , an equivalence relation
, an equivalence relation 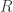 , a function
, a function 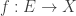 and a desire to define a function
and a desire to define a function 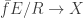 s.t
s.t 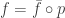 where p is the canonical mapping from
where p is the canonical mapping from  to
to 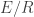 . We define
. We define 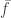 by its action on an element of
by its action on an element of  a representative of an equivalence class. In this case to show that
a representative of an equivalence class. In this case to show that  is well-defined , i.e. a function, we have to show that if
is well-defined , i.e. a function, we have to show that if  then
then  . This is what the student should have written. Godement’s Algebra discusses this in excruciating but very clear detail in Ch, 4, Sec. 3 and the case of fractions in Ch. 29, Sec. 1.
. This is what the student should have written. Godement’s Algebra discusses this in excruciating but very clear detail in Ch, 4, Sec. 3 and the case of fractions in Ch. 29, Sec. 1.
July 2, 2009 at 9:20 am
That wasn’t the issue in the exams. There I had students who defined functions in a normal context where there was no chance of any ambiguity and no equivalence classes to think about, and they still thought that it was necessary to go through some process of proving that their functions were well defined. So there really did seem to be some genuine confusion about it.
July 4, 2009 at 1:19 am |
In economics, “multi-valued functions” come up naturally, and are usually called “correspondences”. For example, given a price vector p and an amount of wealth w, one has a budget constraint B(p,w) = { x : 0 <= x , p*x <= w } (i.e. the set of bundles of goods one can afford). There is also the demand "function" x(p,w) which chooses an individual's optimal good from B(p,w), but it may not be single-valued since the solution to the optimization problem may not be unique. Similarly, there are "best response correspondences" in game theory, whose fixed points are exactly Nash Equilibria. Etc. etc.
February 17, 2010 at 8:43 pm |
[…] defined functions By bitsofmaths Motivated by the interesting article you can find here I explain how a function is usually defined based on relations. I think, dividing the […]
March 12, 2010 at 8:28 am |
[…] all functions are well defined functions.. You can know more about it from the following link, https://gowers.wordpress.com/2009/0…ns-well-defined/ The links has many examples hope that is what you wanted.. var pubId=24240; var […]
July 17, 2011 at 10:44 pm |
thank you everybody!
November 10, 2011 at 8:52 pm |
[…] If the phrase “well-defined” worries you in the above argument, then I recommend a post I once wrote about what it means. […]
February 16, 2012 at 5:20 am |
Thank you for your post and that webpage talking about the exact meaning of “well defined”.But I have some questions.I once read in a book(Analysis–Terence Tao),that book adopts an complete axiomatic method of constructing set theories and real number system.So that book involve a lot of stuff which deal with the check of some thing like “well defined”.While constructing ZF set theory,it define two set $A=B$ as the following:$A=B$ iff $\forall x\in A,x\in B$,and $\forall x\in B,x\in A$.Then a strange thing happen,it says that we should examine whether the equality of two sets are well defined,it says,If $A=B$,then $\forall x\in A$,we can easily gets $x\in B$,so it is well defined regarding the relationship “belong to”.I can’t find any thing like “multifunction” in this example,so I am a bit confused…
October 24, 2012 at 4:33 pm |
[…] recommend reading the discussion (to which I contributed) of the post “Why aren’t all functions well-defined?” on Gower’s Weblog. It resulted in an insight I should have had a long time […]
June 25, 2013 at 6:51 pm |
Reblogged this on Singapore Maths Tuition.
April 18, 2015 at 9:22 pm |
[…] https://gowers.wordpress.com/2009/06/08/why-arent-all-functions-well-defined/#more-605 […]
October 24, 2015 at 12:48 pm |
[…] The word “well-defined” is always a little tricky the first few times you meet it. What exactly does it mean? In fact, it can mean several things in different contexts. In the context of the sign it means the following: our definition of the sign homomorphism seems to depend on a choice, namely the choice of how we write as a product of transpositions. So if I made a different choice, would I get a different sign? That would not be a very good function! (In fact, it would not be a function.) So we have to check that the outcome, namely the , does not depend on this choice, but that we get the same outcome whichever choice we made. This is what “well-defined” means here: it really is a function. We met “well-defined”ness again later in the lecture and will meet it often again in the future. It can mean in different contexts: does the function really land where we say it lands? That is what it meant in the context of the bijection between and . Or: if we define something using a representative, do we get the same answer regardless of which representative we use (that is very close to the sense we used it today)? Look out for it in “Applications of Lagrange”, which we will start next time. You can also read an entry on well-definedness on Tim Gowers’ blog. […]
May 2, 2016 at 11:12 am |
[…] normal subgroups and quotient groups. He’s also written about what it means to say that a function is well defined, which was very relevant for today’s […]
July 28, 2016 at 5:22 pm |
Please, which meaning we shiould give to optimization when we admit that we have gunction and not function? It arises new questions to formulate maximum and minumum problems?
July 29, 2016 at 8:23 am
I don’t know the answer to this, but if you put “multivalued optimization” into Google, it becomes clear that there is a literature on the subject, though it looks quite technical.
December 12, 2016 at 5:23 pm |
Every instance that I can think of of needing to check that a function is “well defined” actually fits into this general framework:
Let pi: A \to B be a surjection. We are attempting to define a function f: B \to C. What we have is a function g: A \to C. Checking that f is “well defined” means that we need to check that if pi(a_1) = pi(a_2) then g(a_1) = g(a_2). In this case, g must factor through pi.
I advocate this viewpoint in this question on MathOverflow:
https://mathoverflow.net/questions/41955/does-any-textbook-take-this-approach-to-the-isomorphism-theorems
Can you think of any cases where we need to check that a function is well defined which does not fit into this framework? If not, I think forcing students to find out the “hidden” function pi, and use this “factorization theorem” every time they want to justify that a map is “well defined” might help to clear up some of these issues.
December 12, 2016 at 6:02 pm
In the language of multifunctions, this would be saying that I have a multifunction $pi^{-1}:B \to A$ and a function $g:A \to C$, and I want to define a function $f:B \to C$ by $f = g \circ \pi^{-1}$. I only get a function $f$ if all the different values of of $\pi^{-1}$ are identified after composition with $g$.
I like the “factorization” language better than the “multifunction” language because it sticks to just talking about “functions”, and it also prepares students for thinking about categorical arguments in the future.
May 1, 2017 at 11:07 am |
[…] about normal subgroups and quotient groups. He’s also written about what it means to say that a function is well defined, which was very relevant for today’s […]
July 3, 2019 at 9:01 am |
[…] we pick from the two colours we’re multiplying, because multiplication modulo n is well defined. We could have chosen -2 from dull green and 16 from mid purple, and multplied them to get -32, and […]
March 17, 2022 at 8:09 am |
[…] Because f(g_1)=f(g_2) impliedby g_1G_omega=g_2G_omega, the function f descends to (a.k.a., factors through) a function phi:G/G_omegatoOmega defined by phi(gG_omega):=gomega=f(g). (This is often phrased as “proving phi is well-defined”; see Timothy Gowers’s post about this.) […]