How many rotational symmetries does a cube have? This question can be answered in a number of ways. Perhaps the one that most readily occurs to people is this: each vertex can end up in one of eight places; once you’ve decided where to put it, there are three places you can put one of its neighbours; once you’ve decided where to put that, the rotation is determined, so the total number of rotations is .
Here’s another proof. Take one of the faces. It can go to one of six other faces, and once you’ve decided which face it will go to, one of the vertices on the face has four places it can go, and once you’ve decided that you’ve fixed the rotation. So the total number of rotations is .
And here’s another. Take one of the midpoints of the twelve edges. There are twelve places it can end up, and once you’ve decided where to put it, there are two choices for how you send the two endpoints of the original edge to the endpoints of the new edge. So the total number of rotations is .
And here’s yet another. Take a point half way between the centre of one of the faces and one of the vertices. (If the cube is the set of all points such that
and
all lie in the closed interval
, then we could, for instance, take the point
.) There are 24 places that that point can end up — the 24 points that are half way between the centre of some face and one of the vertices of that face. There is only one rotational symmetry that takes the original point to any given one of those 24 points. Therefore, the number of rotations of the cube is
.
If you understood those arguments, then you basically understand the orbit-stabilizer theorem, even if you think you don’t. To try to convince you of that, I’ll first show how to convert one of the proofs into a proof that explicitly uses the orbit-stabilizer theorem. I’ll then discuss how much you have to remember in order to remember the proof of the orbit-stabilizer theorem. As usual, I shall aim to show that the answer is “very little indeed”. However, routine proofs in abstract algebra have a somewhat different flavour from routine proofs in set theory and analysis, and as this one is a good representative example, it bears discussing in some detail. (Later I may try the same with the first isomorphism theorem, which you should be meeting fairly soon.)
To illustrate how to count symmetries using the orbit-stabilizer theorem, let me convert the proof that used faces. The obvious way to capture the idea of “which face a particular face goes to” is to let the symmetry group of the cube act on the faces of the cube. Then the set of places that a particular face can go to is nothing other than the orbit of that face. How does the group act on the faces? Well, any rotation of the cube will permute the faces, and that permutation is the one that corresponds to the rotation.
In the earlier version of the argument, we said that our chosen face can go to any one of six other faces. The fancy way of saying that is that the orbit of the chosen face is the set of all faces, which has size 6.
And in the earlier version of the argument, we said that once we had decided which face our chosen face would go to, there were four ways of lining up the vertices. This doesn’t quite correspond to a statement about stabilizers, but let us note for now that if the chosen face maps to itself, then we have four choices. So the stabilizer of our chosen face has size 4. Multiplying those two numbers together gives us 24.
The content of the orbit-stabilizer theorem is basically that if a group acts on a set
, then once you know how many ways there are of sending an element
of
to itself, you also know how many ways there are of sending it to any other element in its orbit. In the faces-of-the-cube example, knowing that there are four ways of rotating the cube so that a face
ends up where it was before tells us that there are also four ways of sending it to some other face
. And that is because “all faces look basically the same” from the point of view of the rotation group. In general, “all points of the orbit of
look basically the same” from the point of view of the transformations performed by the elements of
.
I’m going to give a few different proofs of the orbit-stabilizer theorem, not because they are fundamentally different, but because they have certain stylistic features that are worth commenting on. Also, it may be interesting to see how much variety is possible even when presenting a proof, even when the underlying argument is the same.
First, I’ll remind you of the statement we are trying to prove.
Theorem. Let be a group that acts on a set
, let
be an element of
, let
be the orbit of
and let
be the stabilizer of
. Then
.
In words, the size of the group is the size of the orbit times the size of the stabilizer.
Proof 1. For this proof I want to try to capture as closely as possible our intuition in the cube example that the set of rotations that takes one face to another is “just like the set of rotations that fix that face, but over at another place”. However, I’ll argue in general.
What am I trying to show in the abstract? I want to show that if belongs to the orbit of
, then the set of
such that
is the same size as
, which is the set of
such that
. (Here I’m slipping into the condensed notation and writing
instead of
or
. But it’s important to bear in mind that the “product”
is not the group operation, since it’s only
that belongs to a group. Rather, it is what one might call the group action operation, which has some nice group-like properties such as
and
.)
What is the most natural way to show that two sets have the same size? It’s to produce a bijection between them. (It isn’t the only way. Another is to calculate their sizes, possibly by completely different methods, and show that you get the same answer in both cases. But that is not an appropriate method here, since we’re not given enough information to calculate anything.)
Let me write for the set of
that take
to
. If I’m given an element of
, how do I turn it into an element of
? Well, in the faces-of-cube example, what I might do is this. I fix, once and for all, a rotation
that takes my initial face to the given face. And then, given a rotation that fixes the initial face, I compose it with
to get a rotation that takes the initial face to the given face.
Let’s try that with and
. Since
belongs to the orbit of
(by assumption), there is some
such that
. Now let me define a map from
to
by mapping
to
. Note that
takes
first to
(since
) and then to
(since
). Thus,
really does belong to
.
However, is the map we’ve just defined a bijection? Let’s see if we can prove that it’s an injection and a surjection. No, let’s not do that. Let’s try to find an inverse. Given an element of
, how might we convert it into an element of
? There’s only one thing we can even dream of trying at this point. Since
takes
to
and
also takes
to
,
takes
to
, as we want. So the map
takes
to
. Does it invert the previous map? Yes of course it does.
We’ve shown that for each there are precisely
elements of
that take
to
. But every element of
takes
to something in the orbit, so
, as we were trying to prove.
In case you found that off-puttingly long, here it is stripped of all the accompanying chat.
The real Proof 1. Let be an arbitrary element of
, and let
. Pick
and define a map
by
. The map
defined by
inverts
, so
for every
. But the sets
with
form a partition of
. It follows that
.
I cheated slightly there by not checking carefully that really does take
to
and that
really does take
to
. But those facts are easy enough to be left to the reader to do in his/her head.
That proof is so short that one might wonder why another proof could possibly be desirable. Well, it’s mostly an aesthetic point, at least as far as this proof is concerned, but there’s something a bit ugly about choosing that . Why? Because I didn’t say how to do it. So, for example, the way I chose
for one
might be completely unrelated to the way I chose it for another
. Wouldn’t it be nicer if there were some natural way of defining
in terms of
?
Well, yes it would, but it’s not that easy to do. Just think of the cube example. Suppose I take a face and I ask you to define, for each other face
, a rotation of the cube that takes
to
. I want you to do it in a nice systematic way. How might you do it? Well, if
then probably the most natural thing to do is take the identity. How about if
is one of the neighbouring faces to
? Perhaps the most natural thing there is to take a 90-degree rotation about an axis through the centre of the cube that’s parallel to the edge where
and
meet. But then what about the face opposite
? There are four ways of rotating the cube so that
lands up at the opposite face, and they are of two kinds: two of them are half turns about axes that go through the midpoints of two opposite faces, and the other two are half turns about axes that go through the midpoints of two opposite edges. (If you draw a diagram, I hope you’ll be able to see what I’m talking about here. It’s one of those things that may be easier to work out for yourself.) Anyhow, for each of these two types of half turn, there is absolutely nothing to choose between the two half turns of that type. So there just isn’t a natural way to choose a rotation for each face. As mathematicians might say, there isn’t a canonical choice.
So is that the end of the story? Not quite. There’s a useful principle that sometimes applies in this kind of situation. It says this.
This meme was embedded in my brain as a result of a nice Mathoverflow question, though I suppose I was aware of it less consciously before that. Let’s see how it plays out with our proof.
If I don’t choose just one , then what do I do instead? I choose all
that belong to
.
A problem then arises when I try to define a bijection from to
. Never mind, though. Let’s just define a map from
to
by sending
to
. Note that this is like what we did before, but we’re doing it for every
and not just one chosen
. And what’s nice about it is that we are now doing precisely the same thing for every
.
Let’s call our map . Obviously,
is not a bijection, but that doesn’t matter. We’re trying to show that it’s a bit like a putting together of
bijections. So what we’d like to show is that every element of
has exactly
preimages under
. That will tell us that
, which will imply that
.
So let’s take . How many preimages has it got? Well, a preimage of
is a pair
such that
. So I want to show that there are precisely
solutions of the equation
with
and
. But that’s easy: for each
there is precisely one possible
, namely
, which does indeed belong to
.
Let me again give the condensed version, just to convince you that what I’ve written doesn’t add up to a long proof. In fact, I don’t even need to bother to define the function .
Proof 2. Let be an arbitrary element of
and let
. For every
there is exactly one
such that
, namely
. It follows that every
can be written in
ways as
with
and
. Also,
for every
and every
. It follows that
. Therefore,
. But the sets
with
form a partition of
. It follows that
.
Here is a variant of the above argument that I like better.
Proof 3. Let be an arbitrary element of
and let
. Let
and let us see in how many ways we can write
with
and
. Well, for each
, there is exactly one
such that
, namely
. So we can write
in
ways. But also, for each
there is exactly one
such that
, namely
. This shows that we can write
in
ways. Therefore,
. But the sets
with
form a partition of
. It follows that
.
Or do I like it better? It’s starting to look, with its non-canonical choice of , a bit too like the first argument.
I still don’t feel as though I’ve arrived at the neatest and most symmetrical argument, and I’ve also not satisfied another urge, which is to prove that by finding a nice bijection between
and
. There are good reasons for the second problem, as I’ve already discussed, but I might be able to satisfy my urge by finding not a one-to-one correspondence, but something a bit more general and multivalued.
So let’s take a point . What can we do with it? We can use it to define the element
of
, but that doesn’t seem very exciting or helpful. What we’d really like is to define an element of
, which earlier we did by fixing some
and taking
. But that felt too non-canonical, so instead we preferred to take all
.
If we take all , then that’s saying that we can get from
to
in several different ways. So we seem to get a map from
to
, which is very simple: it takes
to
. But what’s the point of it? And where does
come in?
One way of making come in is to go one step further and let
act on
to create
. So now we’ve got a map from
to
, the map that takes
to
. How many preimages does an element
have?
I’m not going to answer that question (though I could) because once we’ve got to the point of mapping to
using the map above, we see that
isn’t really playing a role, so why not just focus on the map from
to
that takes
(which I was calling
above) to
? If
, then how many preimages does
have?
I won’t bother to answer that question either: it’s the same as asking how big the set is, and we’ve established already that that is
, so it wouldn’t be a particularly new proof that resulted. However, one remark that’s worth making is that the set
is a left coset of
. Probably the proof you were given in lectures was this.
Proof 4. We shall show that there is a bijection between and the set of left cosets of
. To do this, we map the left coset
to
. We must show that this is well-defined. But if
, then
, and therefore, since
is a subgroup,
. From that it follows that
, so
.
Since the number of left cosets of is
, we are done.
If the phrase “well-defined” worries you in the above argument, then I recommend a post I once wrote about what it means.
Here’s a different way of writing the above proof, where we think more about equivalence relations than about partitions.
Proof 5. Here are two equivalence relations on . For the first, I define
if
. For the second, I define
if
. Note that this is the same as saying that
and also the same as saying that
.
Now if and only if
if and only if
. So the two equivalence relations are the same. The number of equivalence classes for the first relation is obviously
and the size of each equivalence class for the second relation is obviously
, so the result is proved.
Let me make one final remark about the orbit-stabilizer theorem. Why, one might ask, is it a useful result? A rather general answer is that it gives us a relationship between three quantities, namely ,
and
, that allows us to determine any one of them from the other two. Situations crop up quite frequently in group theory where it is not very easy to see what one of these quantities is directly, but quite easy to calculate the other two. The orbit-stabilizer theorem then gives us the hard one too. For example, in the case of counting rotational symmetries of a cube, it isn’t easy to think of all the rotations unless you partition them in some nice way, such as looking at what they do to a particular vertex or face, which, as we saw before, amounts to counting orbits and stabilizers.
It’s not always that’s the tough one to get a handle on. For example, in question 10 of Examples Sheet 3 it’s the size of the orbit that isn’t obvious. (In general with the bunch of questions around there, I recommend thinking to yourself, “What is the orbit-stabilizer theorem giving me?”)
November 9, 2011 at 4:16 pm |
I wasn’t quite sure about the first proof for the rotational symmetries of a cube. Can you confirm that what you are doing is picking a line through one vertice and another vertice opposite that, then twirling it around this axis and this is what you mean when you say ”there are three places you can put one of its neighbours”?
thanks
November 9, 2011 at 6:42 pm
If I understand you correctly, then yes that is what I was saying. Let be your starting vertex and let
be your starting vertex and let  be another vertex. There’s definitely at least one rotation that takes
be another vertex. There’s definitely at least one rotation that takes  to
to  . Once you’ve found that, you can rotate the cube about the line that joins
. Once you’ve found that, you can rotate the cube about the line that joins  to the vertex opposite
to the vertex opposite  (exactly as you say) through any multiple of 120 degrees. That gives you three rotations that take
(exactly as you say) through any multiple of 120 degrees. That gives you three rotations that take  to
to  (since a composition of two rotations is a rotation). But the way I was thinking about it, I was describing those three rotations by taking a vertex
(since a composition of two rotations is a rotation). But the way I was thinking about it, I was describing those three rotations by taking a vertex  adjacent to
adjacent to  and considering where it could go if you already know that
and considering where it could go if you already know that  goes to
goes to  . Clearly it has to go to one of the three vertices adjacent to
. Clearly it has to go to one of the three vertices adjacent to  . Also, once you’ve decided where
. Also, once you’ve decided where  goes and where
goes and where  goes then the rotation is completely determined. (If you allow reflections as well, then this is no longer the case: there are two possible transformations that take
goes then the rotation is completely determined. (If you allow reflections as well, then this is no longer the case: there are two possible transformations that take  to
to  and
and  to some given neighbour of
to some given neighbour of  .)
.)
November 10, 2011 at 11:38 am |
And did you have trouble at first visualising that patricular rotation? I had to physically rotate a cube about that axis to convince myself of that symmetry.
November 10, 2011 at 12:48 pm |
In your first paragraph, you write:
Now in the image, We can go from (i) to (iii) via a rotation but not to (ii). Is there a easy way to see this without invoking orientations?
November 10, 2011 at 5:15 pm
I think you probably have to invoke orientations somehow, even if you disguise them. One way one might disguise them is to say something like this: imagine that you are walking from b to a in the first picture; then c is over to the right; the same must be true after a rotation; so once you’ve fixed a and b then you’ve fixed c and hence the whole linear map. (This is a bit like the right-hand rule applied to 0, a, b and c.)
November 10, 2011 at 3:11 pm |
I feel the orbit-stabilizer theorem is an example of a theorem whose proof is more interesting than its statement. The way I remember how to prove it is probably closest to proof 4. I think it is clearer to prove a stronger statement: that the group is partitioned into (equally sized) cosets of the stabiliser, and elements in the same coset send x to the same place, and elements in different cosets send x to different places. This statement is easy to remember and gives one a better insight into the structure of the group action, and the steps of proving the statement are quite easy. If you like you can notice that the stabiliser is a subgroup and then use existing knowledge about cosets of a subgroup (for example that that they are all the same size and the set of cosets partition the group).
November 10, 2011 at 4:57 pm |
I’m not sure Nayayas picture is correct because the orientation of the a and b is not reversed in all 3 pictures. Surely everything has to be reversed when you reflect?
November 11, 2011 at 11:49 am
I am not sure what you mean. To get (iii) from (i). Rotate \pi/4 about the central axis (connecting the midpoints of the top face and the bottom face) and then \2pi/3 about the diagonal of the cube through . To get (ii) from (i) rotate \pi/4 about the central axis and reflect along the plane containing
. To get (ii) from (i) rotate \pi/4 about the central axis and reflect along the plane containing 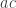 and normal parallel to
and normal parallel to 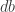 (this is still a reflection… to see this, notice that the det of the operation is +1.(-1)=-1)
(this is still a reflection… to see this, notice that the det of the operation is +1.(-1)=-1)
November 11, 2011 at 12:23 pm
The picture looks correct to me too.
November 10, 2011 at 6:23 pm |
Just a few small typos here: in the second proof you write “every u \in S_x” where it really should be “every u in S_xy”. And in the third proof you repeat “with h \in S_xy” twice.
Many thanks — fixed now.
November 13, 2011 at 3:45 pm |
There is an analogy between the orbit-stabilizer theorem and the following simple observation. If we have two isomorphic structures, there may yet be more than one isomorphism from one to the other. It is possible to view the action of the group on the faces of the cube in this way. To be precise, the number of isomorphisms from a structure to an isomorphic structure is equal to the number of automorphisms of the structure. We can prove this deep fact and the orbit-stabilizer theorem in essentially the same way, using elementary combinatorial arguments about directed graphs.
November 13, 2011 at 6:04 pm |
I wanted to give a simple, elegant application of the Orbit-Stabilizer theorem. This is an alternate proof of Cauchy’s theorem: if a prime ‘p’ divides the order of the finite group G, then G has an element ‘x’ of order p. This proof is due to James McKay (Monthly, 1959).
Consider the set S, a subset of GxGx…xG, the p-fold Cartesian product of G, where S = {(x_1, x_2, …, x_p): x_1*x_2*…*x_p = 1}. S is non-empty and in fact it is fairly easy to see that |S| = |G|^{p-1}.
Define an action of Z/p on S, where Z/p acts via cyclic permutations (as a subgroup of the symmetric group S_p). Then by the Orbit-Stabilizer theorem (and the fact that p is prime) every orbit of this action on S has size either 1 or p. An orbit of size 1 is a fixed point, and an element of S is fixed for all cyclic permutations if and only if it looks like (x,x,…,x). The collection of fixed points in non-empty; the element (1,1,…,1) is fixed. If there are ‘k’ fixed points, where k is at least 1, and ‘m’ orbits of size p, then we have
|S| = |G|^{p-1} = k + m*p
The left side is divisible by p so that implies that k>1. So there is a non-trivial element (x,x,…,x) in S (in fact at least p-1 such elements) such that x^p = 1 which is the required element of order p.
November 13, 2011 at 9:03 pm
I was going to write about that argument (which appears in one of the questions on the Cambridge examples sheet mentioned in the post) in a further post on group actions, but in the course of thinking about it, I came to the conclusion that it was a bogus application, in the sense that essentially the same argument can be written out more simply with no mention of the orbit-stabilizer theorem. It goes like this. (Most of it is the same as the argument as you’ve written it.)
1. The set S has size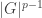 .
.
2. If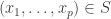 and
and 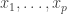 are not all equal, then all cyclic permutations of
are not all equal, then all cyclic permutations of  belong to
belong to  and are distinct. (This depends on
and are distinct. (This depends on  being prime.)
being prime.)
3. On the other hand if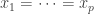 then all cyclic permutations are trivially equal.
then all cyclic permutations are trivially equal.
4. Hence, if we define two elements of to be equivalent if one is a cyclic permutation of the other, then the equivalence classes all have size 1 or p.
to be equivalent if one is a cyclic permutation of the other, then the equivalence classes all have size 1 or p.
5. Since belongs to
belongs to  , at least one equivalence class has size 1.
, at least one equivalence class has size 1.
6. Therefore, there must be another equivalence class of size 1, which implies that there is some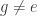 such that
such that  .
.
In this proof there is no need to mention the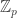 action, though I suppose implicitly it’s there. Similarly with orbits. But the real point is that there is absolutely no need to use the orbit-stabilizer theorem, since we can see directly what the sizes of the orbits are.
action, though I suppose implicitly it’s there. Similarly with orbits. But the real point is that there is absolutely no need to use the orbit-stabilizer theorem, since we can see directly what the sizes of the orbits are.
November 13, 2011 at 9:08 pm
Having just written that, I read what you wrote more carefully, and I now see that you do in fact use the orbit-stabilizer theorem to save a tiny bit of time, so I take back slightly what I’ve just written. In the argument I suggest above, you have to argue that if the sequence is equal to a cyclic permutation of itself, then we get some such that
such that  for every
for every  , and since every element of
, and since every element of 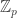 is a multiple of
is a multiple of  it follows that all the
it follows that all the  are equal. Your argument is that the stabilizer is a subgroup of
are equal. Your argument is that the stabilizer is a subgroup of 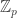 and hence has size 1 or p, from which it follows that the orbit has size 1 or p.
and hence has size 1 or p, from which it follows that the orbit has size 1 or p.
That still leaves me with the feeling that Cauchy’s theorem isn’t really an application of the orbit-stabilizer theorem: it’s more that a small part of the proof can be made slightly quicker (at the cost of making the argument look a bit more mysterious and magical).
November 14, 2011 at 1:26 am
I suppose one can get away with equivalence classes in this context but here is another example of the utility of the Orbit-Stabilizer theorem. Namely the Sylow theorems: let G be a finite group of order p^a*m, where p does not divide m and p prime.
Let S denote the collection of all subsets of G of size p^a. S has size p^a*m choose p^a. It is (if I may dare say this to you Tim) a relatively simple exercise in combinatorics to show that p does not divide |S| if p is prime. Now G acts on S by right multiplication. Since p does not divide |S|, there must be an orbit O = G(X) of the G-action of size not divisible by p. But by the Orbit-Stabilizer theorem |O| divides |G| and hence |O| divides m. Let G_X be the stabilizer of the subset X in O. Again by the Orbit-Stabilizer theorem, |G_X| = p^a*k, where k = m/|O|. On the other hand, for an element x in X, the set {xg: g in G_X} is a subset of X so |G_X| is at most |X| = p^a. Hence, G_X is a subgroup of G of size p^a, i.e., we have shown the existence of a Sylow p-subgroup.
Once can continue further: if C denotes the set of G conjugates of G_X (note now we considering a different action), then by considering the sub-action of G_X on C, one can show that G_X is the only fixed point (again using the Orbit-Stabilizer theorem) and hence all Sylow p-subgroups are conjugate. This also yields that the number of Sylow p-subgroups is congruent to 1 mod p, again by the O-S theorem, each orbit has size 1 or a power of p etc.
Of course there are other proofs of the above theorems but to my taste this seems quite elegant and one can see for instance why the number of Sylow p-subgroups is 1 mod p.
November 13, 2011 at 7:18 pm |
A variant of your proof 2 would give you a bijection, if you think that would be neater. Define a map from to
to  by sending
by sending 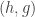 to
to  .
.
Another thought: You mention that the way to show that two sets are the same size is to find a bijection between them. I was trying to think how other proofs, such as proof 4, show that the two sets are the same size. The way it does it is by showing that the sets are equal to a pair of sets we know to be equal, a subgroup and one of its cosets. However, it is not much different, because we would show a bijection to prove that a subgroup is equal in size to one of its cosets, so all that is different here is that the use of the technique is buried in the proof of a result that we rely on.
A typo: Where you wrote “What we’d really like is to define an element of g”, I believe this should be “What we’d really like is to define an element of G”.
Thanks — fixed. (And I like that bijection.)
November 13, 2011 at 8:28 pm |
Suppose is defined as in my previous comment. Notice that the domains and co-domains of these maps are disjoint. The closest thing to a bijection from
is defined as in my previous comment. Notice that the domains and co-domains of these maps are disjoint. The closest thing to a bijection from 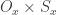 to
to  is, I believe,
is, I believe, 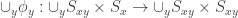 .
.
To get the theorem from this by counting, we need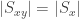 for all
for all  . (Admittedly, once you have that it is hardly worth bothering with the argument we are in the middle of.) Then we proceed as follows:
. (Admittedly, once you have that it is hardly worth bothering with the argument we are in the middle of.) Then we proceed as follows:
November 15, 2011 at 1:40 pm |
It’s worth pointing out here that the orbit-stabiliser theorem is robust enough that it can be stated and proved for arbitrary subsets of G, rather than for subgroups of G or (as here) G itself. This is something that became very useful to me early on – I recently chose to highlight it as Lemma 3.1 in http://arxiv.org/abs/1109.3550 .
December 10, 2011 at 12:58 am |
Minor typo: “So let’s take $u\in S_x$. How many preimages has it got?”
Should be: $u\in S_{xy}$.
December 10, 2011 at 5:42 pm |
[…] a small list of possible actions to draw on). Just before I finish, I’m going to look back at a comment on my previous post but one on group actions, which I deliberately didn’t read properly because I knew I was going to write this. It will […]
June 19, 2013 at 2:39 pm |
Can different groups share stabilizers? I’m asking because I’ve been studying Lie Theory, and I’ve learned how to calculate differential invariants for ODE’s of any order. You substitute these into the ODE and with a little algebra, out pops the invariant solution. It’s very nice. Last night I found a Riccati equation someone had solved using an exponential transformation, and I solved it using a stretching group and got the same answer. When I calculated the stabilizers of the exponential group (using Sophus Lie’s technique) I found it to have the same stabilizers as my stretching group. Does this mean that they are in fact the same group, and does it matter that these are infinite groups, not finite groups?
May 11, 2015 at 12:14 pm |
[…] Tim Gowers on the orbit-stabiliser theorem. And there are some useful summary notes here from Thomas Beatty. These lecture notes by Keith […]
April 5, 2016 at 6:00 am |
[…] category theory I am more comfortable with the first one. But I do not feel them. (Like in this post by Gowers he explains Orbit-Stablizer by moving a cube and with this picture you get the feeling […]
July 21, 2016 at 4:18 pm |
[…] Field Medallist Prof. Gowers has also written a nice post on the Orbit -Stabilizer Theorem and various proofs. […]
January 28, 2017 at 12:38 am |
Reblogged this on 茨之部屋.
January 11, 2018 at 6:38 pm |
A nice exercise is to compute the order C_n of the symmetry group of the n-cube. You can compute this by induction using the orbit stabiliser theorem. An n-cube has 2n faces of one lower dimension, so C_n = 2n * C_(n-1). This leads to C_n = n! 2^n. If reflections are not allowed, then n! 2^(n-1).
March 4, 2018 at 4:25 am |
[…] We note substantial discussion about that in a StackExchange post and links from it to a lengthy post by Tim Gowers. We will try our own explanation because it speaks right to aspects of the cycle […]
October 16, 2018 at 7:01 pm |
[…] theory than I do here, this is a good sequence: Group Actions I, which actually defines the things. Group actions II: the orbit-stabilizer theorem, which is about just what it says. Group actions III — what’s the point of them?, which has the […]
August 5, 2019 at 5:59 pm |
[…] other night before turning in, I read Tim Gowers’ post on the orbit-stabilizer theorem. It starts with an invitation to count the rotational symmetries of […]
August 27, 2021 at 3:35 pm |
“knowing that there are four ways of rotating the cube so that a face F ends up where it was before tells us that there are also *four* ways of sending it to some other face F’.”
should it be that
… there are *six* ways of sending it to some other face F’
?
August 27, 2021 at 3:47 pm
Never mind. Looking at the proof of the theorem, I see what this means: the cardinality of the stabilizer of a face F is the same as that of the set
of a face F is the same as that of the set  . In other words, “once you know how many ways there are of sending an element x of X to itself, you also know how many ways there are of sending it to any other element in its orbit.”
. In other words, “once you know how many ways there are of sending an element x of X to itself, you also know how many ways there are of sending it to any other element in its orbit.”
August 27, 2021 at 3:53 pm |
“The content of the orbit-stabilizer theorem is basically that if a group G acts on a set X, then once you know how many ways there are of sending an element x of X to itself, you also know how many ways there are of sending it to any other element in its orbit.”
Perhaps you really mean that “The content of *the proof* of the orbit-stabilizer theorem is basically …”, since in the quoted interpretation above, there is no “stabilizer” but only “orbit”.
August 27, 2021 at 4:22 pm
Okay. The quoted excerpt means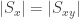 for any
for any 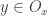 , i.e., the size of the stabilizer (
, i.e., the size of the stabilizer (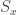 ) is the same as that of
) is the same as that of 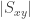 . (I would put this as an essential step of the proof of the theorem, rather than the theorem per se.)
. (I would put this as an essential step of the proof of the theorem, rather than the theorem per se.)
Once this is done and since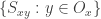 forms a partition of
forms a partition of  , the *theorem* follows.
, the *theorem* follows.