I now feel more optimistic about the prospects for this project. I don’t know whether we’ll solve the problem, but I think there’s a chance. But it seems that there is after all enough appetite to make it an “official” Polymath project. Perhaps we could also have an understanding that the pace of the project will be a little slower than it has been for most other projects. I myself have various other mathematical projects on the boil, so can’t spend too much time on this one, but quite like the idea of giving it an occasional go when the mood takes me, and trying to make slow but steady progress. So I’ve created a polymath13 category, into which this post now fits. I’ve also retrospectively changed the category for the previous two posts. I don’t think we’ve got to the stage where a wiki will be particularly useful, but I don’t rule that out at some point in the future.
In this post I want to expand on part of the previous one, to try to understand better what would need to be true for the quasirandomness assertion to be true. I’ll repeat a few simple definitions and simple facts needed to make the post more self-contained.
By an –sided die I mean a sequence in
(where
is shorthand for
) that adds up to
. Given an
-sided die
and
, I define
to be the number of
such that
and
to be
.
We can write as
. Therefore, if
is another die, or even just an arbitrary sequence in
, we have that
.
If and no
is equal to any
, then the sign of this sum therefore tells us whether
beats
. For most
, we don’t expect many ties, so the sign of the sum is a reasonable, but not perfect, proxy for which of the two dice wins. (With a slightly more complicated function we can avoid the problem of ties: I shall stick with the simpler one for ease of exposition, but would expect that if proofs could be got to work, then we would switch to the more complicated functions.)
This motivates the following question. Let and
be two random dice. Is it the case that with high probability the remaining dice
are split into four sets of roughly equal size according to the signs of
and
? I expect the answer to this question to be the same as the answer to the original transitivity question, but I haven’t checked as carefully as I should that my cavalier approach to ties isn’t problematic.
I propose the following way of tackling this question. We fix and
and then choose a purely random sequence
(that is, with no constraint on the sum) and look at the 3D random variable
.
Each coordinate separately is a sum of independent random variables with mean zero, so provided not too many of the or
are zero, which for random
and
is a reasonable assumption, we should get something that approximates a trivariate normal distribution.
Therefore, we should expect that when we condition on being zero, we will get something that approximates a bivariate normal distribution. Although that may not be completely straightforward to prove rigorously, tools such as the Berry-Esseen theorem ought to be helpful, and I’d be surprised if this was impossibly hard. But for now I’m aiming at a heuristic argument, so I want simply to assume it.
What we want is for the signs of the first two coordinates to be approximately independent, which I think is equivalent to saying (assuming normality) that the first two coordinates themselves are approximately independent.
However, what makes the question interesting is that the first two coordinates are definitely not independent without the conditioning: the random variables and
are typically quite strongly correlated. (There are good reasons to expect this to be the case, and I’ve tested it computationally too.) Also, we expect correlations between these variables and
. So what we are asking for is that all these correlations should disappear when we condition appropriately. More geometrically, there is a certain ellipsoid, and we want its intersection with a certain plane to be a circle.
The main aim of this post is to make the last paragraph more precise. That is, I want to take three standard normal random variables and
that are not independent, and understand precisely the circumstances that guarantee that
and
become independent when we condition on
.
The joint distribution of is determined by the matrix of correlations. Let this matrix be split up as
, where
is the
covariance matrix of
,
is a
matrix,
is a
matrix and
is the matrix
. A general result about conditioning joint normal distributions on a subset of the variables tells us, if I understand the result correctly, that the covariance matrix of
when we condition on the value of
is
. (I got this from Wikipedia. It seems to be quite tricky to prove, so I hope it really can be used as a black box.) So in our case if we have a covariance matrix
then the covariance matrix of
conditioned on
should be
.
That looks dimensionally odd because I normalized the random variables to have variance 1. If instead I had started with the more general covariance matrix I would have ended up with
.
So after the conditioning, if we want and
to become independent, we appear to want
to equal
. That is, we want
where I am using angle brackets for covariances.
If we divide each variable by its standard deviation, that gives us that the correlation between and
should be the product of the correlation between
and
and the correlation between
and
.
I wrote some code to test this, and it seemed not to be the case, anything like, but I am not confident that I didn’t make careless mistakes in the code. (However, my correlations were reasonable numbers in the range , so any mistakes there might have been didn’t jump out at me. I might just rewrite the code from scratch without looking at the old version.)
One final remark I’d like to make is that if you feel there is something familiar about the expression , then you are not completely wrong. The formula for the vector triple product is
.
Therefore, the expression can be condensed to . Now this is the scalar triple product of the three vectors
,
, and
. For this to be zero, we need
to lie in the plane generated by
and
. Note that
is orthogonal to both
and
. So if
is the orthogonal projection to the subspace generated by
, we want
to be orthogonal to
. Actually, that can be read out of the original formula too, since it is
. A nicer way of thinking of it (because more symmetrical) is that we want the orthogonal projections of
and
to the subspace orthogonal to
to be orthogonal. To check that, assuming (WLOG) that
,
.
So what I’d like to see done (but I’m certainly not saying it’s the only thing worth doing) is the following.
1. Test experimentally whether for a random pair of
-sided dice we find that the correlations of the random variables
,
and
really do appear to satisfy the relationship
corr.corr
corr
.
Here the are chosen randomly without any conditioning on their sum. My experiment seemed to indicate not, but I’m hoping I made a mistake.
2. If they do satisfy that relationship, then we can start to think about why.
3. If they do not satisfy it, then we can start to think about why not. In particular, which of the heuristic assumptions used to suggest that they should satisfy that relationship is wrong — or is it my understanding of multivariate normals that is faulty?
If we manage to prove that they typically do satisfy that relationship, at least approximately, then we can think about whether various distributions become sufficiently normal sufficiently quickly for that to imply that intransitivity occurs with probability 1/4.
May 20, 2017 at 11:32 am |
Just a quick change-of-basis argument that is indeed equivalent to X and Y being independent conditional on Z=0.
is indeed equivalent to X and Y being independent conditional on Z=0.
We can write jointly gaussian variables X,Z (for now with mean 0 and variance 1) as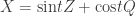 for some value t, where Z and Q are independent N(0,1).
for some value t, where Z and Q are independent N(0,1).
Then we can write third jointly gaussian variable Y as
 , where
, where  and
and  are independent N(0,1).
are independent N(0,1).
Then the covariances are
 ,
,
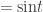 and
and
 .
.
As such it follows that if and only if
if and only if
 ,
,  or
or 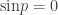 . Ignoring the first two cases for now,
. Ignoring the first two cases for now, 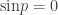 if and only if the distributions of X and Y conditional on Z=0 (which are
if and only if the distributions of X and Y conditional on Z=0 (which are
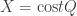 and
and  ) are independent.
) are independent.
May 20, 2017 at 11:39 am
This would be a lot clearer if I had used rather than which just disappears in latex.
rather than which just disappears in latex.
May 20, 2017 at 1:49 pm
I’m afraid the system completely swallows things up when you do that, so I’m unable to edit your comment. If you have a moment to write it again, that would be great, and then I’ll delete this one.
May 20, 2017 at 6:33 pm |
Given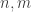 It is interesting to consider
It is interesting to consider  -sided dice which is a sequence of length
-sided dice which is a sequence of length  of integers between one and
of integers between one and  that sum up to
that sum up to 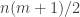 . (We can assume that either
. (We can assume that either  or
or 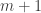 are even.) When we consider sequences rather than multiset the random model based on uniform probability distribution is slightly different. (I had the impression that the first post talked about random multisets while this post talks about random sequences.)
are even.) When we consider sequences rather than multiset the random model based on uniform probability distribution is slightly different. (I had the impression that the first post talked about random multisets while this post talks about random sequences.)
When without any constrain on the sum, this is essentially the model of approval voting. Then every three dice are transitive. Looking at
without any constrain on the sum, this is essentially the model of approval voting. Then every three dice are transitive. Looking at 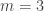 could be interesting and also on the case that
could be interesting and also on the case that  is fixed and
is fixed and  tends to infinity. (There the multiset model is asymptotically the same as the sequence model, and the probability of ties tends to 0.)
tends to infinity. (There the multiset model is asymptotically the same as the sequence model, and the probability of ties tends to 0.)
May 21, 2017 at 2:56 am
Quick note that if variables
variables 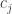 are independently drawn from some distribution, then the
are independently drawn from some distribution, then the and
and
 is simply
is simply  times the covariance of
times the covariance of  and
and  .
.
covariance of
It follows that the correlation coefficient of and
and  is the same as the correlation coefficient of
is the same as the correlation coefficient of  and
and  .
.
So the condition that and
and
 are independent subject to
are independent subject to
 should be equivalent to the condition that
should be equivalent to the condition that  and
and  are
are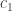 .
.
independent once you remove the components of each that are
dependent on
To be more clear on that, for each dice , define a number
, define a number 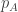 such that
such that  is statistically independent
is statistically independent when
when  is chosen uniformly from
is chosen uniformly from
 . Then I think the condition stated should be
. Then I think the condition stated should be and
and 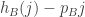 being
being
from
equivalent to
statistically independent.
As a second note: if X and Z are jointly Gaussian with mean 0, variance 1 and correlation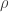 , then we can write
, then we can write 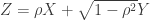 where X and Y are independent N(0,1).
where X and Y are independent N(0,1).
Then the event that X and Z are both positive depends only on which is
which is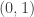 and
and 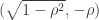 , so
, so .
.
the vector
uniform on the unit circle. In particular, it happens if that point is between
the probability is
As such if the signs of X and Z are independent, this probability is
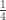 , which means
, which means  , so
, so
 .
.
May 20, 2017 at 11:35 pm |
Alright!
We have some good data to dig though.
First, this post contains data calculated using four different procedures for obtaining random dice. All dice are proper (values from 1 to n, sum constrained to n(n+1)/2), just different random selections. I will refer to the different random selection methods as follows:
sequence – uniform in unsorted sequence representation
multiset – uniform in multiset representation
sequence_walk – a random walk method, hopefully converges to same distribution as sequence method
multiset_walk – a random walk method, hopefully converges to same distribution as multiset method
==================================
How well do the random walk methods compare to their counterparts?
I had the number of steps scale as n log(n).
The fraction of intransitives and ties felt too summarized to get a good comparison, so I looked at the distribution of two measurements.
Comparison score:
for a given die A, randomly choose 100000 dice B and for each note the comparison score = number of roll pairs where A wins – number of roll pairs where B wins
graph for n=100 is here: http://imgur.com/a/UiKU3
L_1 distance from standard die:
calculated for 100000 randomly choose dice
graph for n=100 is here: http://imgur.com/a/YykOl
While previously we saw the fraction of k=4 intransitives was quite close comparing the sequence and multiset random model, these measurements both clearly distinguish between the two models.
The random walk distributions fall on top of their counterparts so closely that only statistical noise allows the colors of the covered curve to peek out now and then. So I’d say the random walk methods pass these tests nicely.
The sequence random method is fast enough that its random walk method is actually slower for the ranges I’ve looked at. However the multiset random walk is a huge improvement in speed. If we trust the multiset_walk method, we can now push to larger n sided dice.
==================================
Data on k=4 tournaments and fraction of ties
Calculated with multiset distribution, 100000 random dice each test.
n=50, tie=0.063590 intransitive=0.373510 (of non-tie = 0.398874)
n=100, tie=0.030920 intransitive=0.385000 (of non-tie = 0.397284)
n=150, tie=0.020690 intransitive=0.386690 (of non-tie = 0.394860)
n=200, tie=0.015290 intransitive=0.387660 (of non-tie = 0.393679)
So approaching towards ~ 0.39 is still visible.
Looking with the multiset random walk method, I also recorded the fraction of other tournament scores to try to see where the fraction is going.
———————-
n=100, tie=0.030870 intransitive=0.382700 (of non-tie = 0.394890)
[0, 1, 2, 3] 0.386940 (of non-tie 0.399265)
[0, 2, 2, 2] 0.101210 (of non-tie 0.104434)
[1, 1, 1, 3] 0.098280 (of non-tie 0.101411)
[1, 1, 2, 2] 0.382700 (of non-tie 0.394890)
———————-
n=200, tie=0.015500 intransitive=0.386350 (of non-tie = 0.392433)
[0, 1, 2, 3] 0.391660 (of non-tie 0.397826)
[0, 2, 2, 2] 0.102710 (of non-tie 0.104327)
[1, 1, 1, 3] 0.103780 (of non-tie 0.105414)
[1, 1, 2, 2] 0.386350 (of non-tie 0.392433)
———————-
n=500, tie=0.006130 intransitive=0.389120 (of non-tie = 0.391520)
[0, 1, 2, 3] 0.395030 (of non-tie 0.397466)
[0, 2, 2, 2] 0.105260 (of non-tie 0.105909)
[1, 1, 1, 3] 0.104460 (of non-tie 0.105104)
[1, 1, 2, 2] 0.389120 (of non-tie 0.391520)
———————-
n=1000, tie=0.002850 intransitive=0.391930 (of non-tie = 0.393050)
[0, 1, 2, 3] 0.394400 (of non-tie 0.395527)
[0, 2, 2, 2] 0.106880 (of non-tie 0.107185)
[1, 1, 1, 3] 0.103940 (of non-tie 0.104237)
[1, 1, 2, 2] 0.391930 (of non-tie 0.393050)
Just like in the previous calculations with sequence random dice, the fraction of intransitives increases to ~ 0.39
==================================
The fraction of ties goes to zero conjecture is intuitively clear, and the data is quite convincing. However for the other conjecture on randomness of tournaments, I am currently leaning towards this not being correct.
I think too much is being summarized in these fractions measurements, and enough details are being missed that it looks “almost” true, but not quite. So I explored for ways to show how the space of dice “looked” as viewed from each die.
The rough picture of these dice as suggested by the random tournament conjecture, is that except for rare dice that are washed out as n increases, the “space” as seen by comparisons from each die is practically equivalent and uncorrelated.
While not a disproof of the conjecture, we now know at least that this rough picture of equivalent dice is not correct. Consider the following graph:
http://imgur.com/a/mGL3Q
For a given die, the distribution of comparison scores to the other dice appears as a bell shaped distribution about 0. Tying is actually the peak of the distribution, the fraction of ties just goes down because it is only a sliver of the distribution for most dice.
This comparison “view” differs strongly across the dice, as the standard deviation of the bell curve seems strongly related to the L_1 distance from the standard die. In this sense, the standard die is just the limit of L_1 = 0, with the comparison scores fully peaked on ties.
If this picture is correct, the fraction of ties then goes to zero because the average distance from the standard die increases as n increases.
Now, it is still possible these score distributions become uncorrelated as n increases, but the result that the distributions for individual dice are already distinguishable with a distance parameter, makes it feel like the distributions would have to cleverly conspire to be uncorrelated. The k=4 data doesn’t seem to support such a conspiracy occurring, and I struggle for an intuitive reason to expect no correlation.
I will probably be busy for about the next week, but I should be able to run more tests in June.
May 22, 2017 at 9:49 pm
Oops, correction on:
“Data on k=4 tournaments and fraction of ties
Calculated with multiset distribution, 100000 random dice each test.”
I meant each calculation involved 100000 tests (4 random dice each test)
May 22, 2017 at 9:51 pm
I put the code on github in case someone wants to run similar calcuations (or just wants to use the random dice generation methods mentioned above).
https://github.com/perfluxion/dicetools
May 21, 2017 at 10:54 am |
So I ran some quick tests for 100-sided, 500-sided and 1000-sided dice, and the conditional correlations do not seem to be small.
I’ve put the code at http://ideone.com/5XmwVl so it can be verified.
May 21, 2017 at 3:33 pm
I’m glad someone else has independently come to this conclusion, as I wasn’t confident that my code was correct (partly, it has to be said, because I was particularly keen for the answer to come out differently).
If P. Peng’s experiment provides unanswerable evidence that the “beats” tournament is not after all quasirandom, then everything fits and I think we’ll have to conclude that for the sequences model the general conjecture is false. It’s still possible that the more specific one about the probability of transitivity for three dice is correct, but the natural way of proving it would be ruled out. And of course, there would still the multiset model to think about, and various questions one could try to answer about the sequences model in order to understand the tournament, even if it isn’t quasirandom.
May 21, 2017 at 5:04 pm
Just to be sure: If A beats B and B beats C then the probability for A to beat C is larger than 1/2 ? (What is this probability?)
May 21, 2017 at 5:28 pm
What this indicates is that the events “A beats C” and “B beats C” are unlikely to be independent for a randomly chosen (but fixed) A and B.
It may still be the case that for randomly chosen A, B and C, the events “A beats B”, “B beats C” and “C beats A” behave correctly.
But I think, if I understand correctly, if “A beats C” and “B beats C” are not independent for randomly chosen fixed A and B, then it is likely that given “A beats C_i” for 1<=i<=n and "B beats C_i" for 1<=i<n, it is likely that the correlation for A and B is positive, so it is more likely than not that B beats C_n, and the big conjecture (as I understand it) is that basically any edge of the domination graph is independent of all of the other edges.
May 21, 2017 at 8:50 pm
Dear Luke, I still don’t understand. Did you choose A and B at random and then computed the correlation for many choices of C? Or did you choose A, B and C at random (again and again) and computed the correlation for all these triples between A>C and B>C?
May 21, 2017 at 9:47 pm
This may be repeating what Luke said — I’m not quite sure — but if for almost all pairs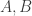 the events “
the events “ beats
beats  ” and “
” and “ beats
beats  ” are approximately independent (and each hold with probability approximately 1/2), then the whole tournament is quasirandom, since this condition is equivalent to the statement that the number of even (labelled) 4-cycles is roughly
” are approximately independent (and each hold with probability approximately 1/2), then the whole tournament is quasirandom, since this condition is equivalent to the statement that the number of even (labelled) 4-cycles is roughly 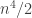 . But the condition that a triple
. But the condition that a triple 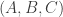 is intransitive with probability approximately 1/4 is weaker than full quasirandomness, so even if, as is looking distinctly possible for the sequences model, full quasirandomness fails, the transitivity statement could conceivably still hold.
is intransitive with probability approximately 1/4 is weaker than full quasirandomness, so even if, as is looking distinctly possible for the sequences model, full quasirandomness fails, the transitivity statement could conceivably still hold.
May 21, 2017 at 10:27 pm
Was not aware of that fact (if for almost all pairs A, B the events “A beats C” and “B beats C” are approximately independent and each hold with probability approximately 1/2 then the whole tournament is quasirandom).
To be very clear about what the computations I have done are, for each dice A there is a function (defined in the previous post on this blog) such that for all dice $C$, the amount by which A beats C is
(defined in the previous post on this blog) such that for all dice $C$, the amount by which A beats C is 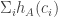 .
.
If for uniformly chosen from
from  , the variables
, the variables 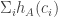 and
and
 are approximately jointly Gaussian, then the conditional distribution of the first given the second should be roughly the same as the first minus the linear regression of the first on the second. For each dice A, my program computes
are approximately jointly Gaussian, then the conditional distribution of the first given the second should be roughly the same as the first minus the linear regression of the first on the second. For each dice A, my program computes  and this linear regression
and this linear regression  , and then computes the difference
, and then computes the difference 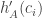 .
.
Now, for random dice A, B, suppose we assume that all three variables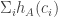 ,
,  and
and  are approximately jointly Gaussian. Then we wish for the two first distributions to have independent signs subject to the third being zero. Jointly Gaussian distributions (with mean 0) have independent signs iff they are independent, so we want the two condtiional distributions to be independent. By the previous paragraph, this is the same as wanting
are approximately jointly Gaussian. Then we wish for the two first distributions to have independent signs subject to the third being zero. Jointly Gaussian distributions (with mean 0) have independent signs iff they are independent, so we want the two condtiional distributions to be independent. By the previous paragraph, this is the same as wanting 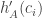 and
and 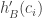 to be independent.
to be independent.
This is what I calculate. I generate random dice A and B, and compute the correlation of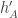 and
and 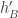 .
.
I possibly even do this correctly.
Interesting follow-up questions that I haven’t had time to investigate:
For a fixed random dice A, how similar are the distributions of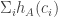 subject to
subject to  and of
and of
 with no conditions.
with no conditions.
The same for two fixed random dice A, B. Does the correlation over random dice C seem to be close to what is predicted by this logic?
May 21, 2017 at 5:30 pm |
I don’t think the numerical evidence against the conjecture is very convincing. There are very possibly lower order main terms which could unduly sway the evidence for small n. Is there any way to test million-sided dice?
May 21, 2017 at 6:17 pm
Assuming my code is right:
Testcase #1 of 1000000-sided die: Var1=83666677520.9489, Var2=58164194958.0453, Cov=-5142588342.6654, Corr=-0.0737
Testcase #2 of 1000000-sided die: Var1=170652385885.1353, Var2=383837502837.2842, Cov=-44340175731.3077, Corr=-0.1732
Testcase #3 of 1000000-sided die: Var1=95411567879.0051, Var2=411651017261.1688, Cov=23514160690.4223, Corr=0.1186
Testcase #4 of 1000000-sided die: Var1=129337519658.2799, Var2=482870174382.8414, Cov=103327042561.5577, Corr=0.4135
Testcase #5 of 1000000-sided die: Var1=63469236644.0365, Var2=190459144796.9994, Cov=36445058013.0572, Corr=0.3315
Testcase #6 of 1000000-sided die: Var1=247959398175.2720, Var2=374571837411.0212, Cov=-168707342617.3397,
Corr=-0.5536
Testcase #7 of 1000000-sided die: Var1=118527199199.1557, Var2=235795826705.5231, Cov=81219466247.5660, Corr=0.4858
Testcase #8 of 1000000-sided die: Var1=156142669182.8310, Var2=151112944593.1989, Cov=17976062335.7008, Corr=0.1170
Testcase #9 of 1000000-sided die: Var1=155578825797.1025, Var2=186257137173.6792, Cov=-85601110430.8644, Corr=-0.5029
Testcase #10 of 1000000-sided die: Var1=250084013516.8111, Var2=176570151724.8132, Cov=-37752750469.6730, Corr=-0.1797
Testcase #11 of 1000000-sided die: Var1=83525126083.2328, Var2=188512345761.9844, Cov=-3293101901.2540, Corr=-0.0262
Testcase #12 of 1000000-sided die: Var1=243148285063.8932, Var2=128526622114.4252, Cov=-109666564179.3167, Corr=-0.6204
Testcase #13 of 1000000-sided die: Var1=111797132874.2193, Var2=359613721671.0355, Cov=10839894699.5140, Corr=0.0541
Testcase #14 of 1000000-sided die: Var1=103272231129.6406, Var2=191318190359.1727, Cov=-8302571778.2218, Corr=-0.0591
Testcase #15 of 1000000-sided die: Var1=86787771777.1460, Var2=200071063872.5374, Cov=42895672072.9774, Corr=0.3255
Testcase #16 of 1000000-sided die: Var1=266654706016.3156, Var2=88389047630.7891, Cov=84162110644.4755, Corr=0.5482
Testcase #17 of 1000000-sided die: Var1=139457028923.0280, Var2=107994124793.1600, Cov=57593784095.0311, Corr=0.4693
Testcase #18 of 1000000-sided die: Var1=251366425435.1886, Var2=157545398985.3911, Cov=37697388546.0484, Corr=0.1894
Testcase #19 of 1000000-sided die: Var1=153786028139.5456, Var2=263080371691.1945, Cov=-67579189182.8782, Corr=-0.3360
Testcase #20 of 1000000-sided die: Var1=311433278205.4565, Var2=248353888692.7109, Cov=-5039875172.9270, Corr=-0.0181
May 21, 2017 at 9:52 pm
Just to check, are these the correlations between the random variables and
and  , where
, where 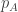 and
and  are as in your earlier comment? In other words, are they the correlations that ought to be zero in order for
are as in your earlier comment? In other words, are they the correlations that ought to be zero in order for  and
and  to become independent when we condition on
to become independent when we condition on  ?
?
May 21, 2017 at 10:01 pm
Yes.
May 21, 2017 at 11:15 pm
Dear Luke, Again, I dont understand these outcomes. You chose A and B at random (In these 20 testcases) and computed the correlation between A beats C and B beats C for many choices of C. And then we see sometimes positive correlation and sometimes negative correlation. It is still possible that if we take r random dice (starting with 3 and 4) and compute the tournament of which beats which this will converge to a random tournament. (I dont refer to low order terms. I just dont see the connection between this experiment and the statement – I think you need to take many random triples A B and C and compute the probabilities for A beats B; B beats C; and C beats A.
May 21, 2017 at 11:41 pm
My contention is that “A beats C” and “B beats C” not being approximately independent for randomly chosen A and B doesn’t contradict r random dice converging to a random tournament for any fixed r, but that it makes it very unlikely that this will be the case for all r.
Although, given what Tim said earlier, I think that if 4 random dice converge to a random tournament then the whole thing is quasirandom, which I assume would mean that “A beats C” and “B beats C” are approximately independent for almost all pairs A, B. (This paragraph is not something I am very comfortable with).
May 22, 2017 at 6:37 am
I agree that a crucial property would be
“For a randomly chosen A with probability close to 1/2 A beats a randomly chosen B”
If this fails (and the more delicate tests based on correlation for randomly chosen A and B) the conjecture is very implausible. (But checking directly random triples could be useful). It would be interesting to understand (in words) what property of A makes A more likely to beat many other dice and what properties of A and B leads to positive correlation or to negative correlation. Since all symmetric dice are tied it may be related to measures of asymmetry.
May 21, 2017 at 11:07 pm |
nudge … my post from yesterday appears stuck in moderation (maybe because it had several links to images and got marked as spam or something?)
May 22, 2017 at 12:09 am |
Let’s look at the case of 6-sided proper dice. There are 32 of them. Let’s toss out the standard die since it ties with everything and consider
{D1,… ,D31}={{6, 6, 6, 1, 1, 1}, {6, 6, 5, 2, 1, 1}, {6, 6, 4, 3, 1, 1},
{6, 6, 4, 2, 2, 1}, {6, 6, 3, 3, 2, 1}, {6, 6, 3, 2, 2, 2}, {6, 5, 5, 3, 1, 1}, {6, 5, 5, 2, 2, 1}, {6, 5, 4, 4, 1, 1}, {6, 5, 4, 2, 2, 2}, {6, 5, 3, 3, 3, 1}, {6, 5, 3, 3, 2, 2}, {6, 4, 4, 4, 2, 1}, {6, 4, 4, 3, 3, 1}, {6, 4, 4, 3, 2, 2}, {6, 4, 3, 3, 3, 2}, {6, 3, 3, 3, 3, 3}, {5, 5, 5, 4, 1, 1}, {5, 5, 5, 3, 2, 1}, {5, 5, 5, 2, 2, 2}, {5, 5, 4, 4, 2, 1}, {5, 5, 4, 3, 3, 1}, {5, 5, 4, 3, 2, 2}, {5, 5, 3, 3, 3, 2}, {5, 4, 4, 4, 3, 1}, {5, 4, 4, 4, 2, 2}, {5, 4, 4, 3, 3, 2}, {5, 4, 3, 3, 3, 3}, {4, 4, 4, 4, 4, 1}, {4, 4, 4, 4, 3, 2}, {4, 4, 4, 3, 3, 3}}
There are 31C3=4495 triples of these dice. Of these,
26 are intransitive triples, 2307 are transitive, and
2162 have a tie. Clearly this is a long way from the
“expected” 25% of intransitive triples, but the number
of sides is very small. Nevertheless we can look at
the intransitive triples and what we notice is that
certain dice and certain pairs of dice occur
inordinately often. For example D10 appears in 9 of
these 26 triples whereas D1, D16, D17, D20, D25,
D29, D30, and D31 don’t appear in any of them.
The list of the 26 triples is
{{14, 15, 19}, {13, 23, 24}, {13, 15, 23}, {12, 15, 19},
{11, 24, 27}, {11, 23, 28}, {11, 18, 19}, {10, 13, 23},
{9, 15, 19}, {8, 15, 19}, {8, 10, 22}, {7, 12, 13},
{7, 10, 23}, {7, 10, 14}, {6, 10, 23}, {5, 10, 22},
{4, 14, 19}, {4, 11, 21}, {4, 8, 10}, {3, 15, 24},
{3, 15, 19}, {3, 11, 26}, {3, 10, 22}, {3, 7, 10},
{3, 4, 11}, {2, 11, 26}}
where, for example, {14,15,19} means the triple
{D14, D15, D19}.
I don’t know if this is helpful or not but it may
have some bearing on the correlation calculations
being performed. I have a feeling that this lopsidedness
will persist for dice with many sides. I suspect that
there will be a smallish number of dice and pairs of
dice that contribute a lot to the intransitive total.
May 22, 2017 at 12:52 am
Thanks for the data! It occurs to me that we could try to learn a little more from all of those ties. If there’s at least one tie among dice A, B, and C then there are various distinct cases:
1) A ties B and both beat C
2) A ties B and both lose to C
3) A ties B, C beats A, and B beats C.
4) A ties B, A ties C, and B beats C
5) A, B, and C all tie pairwise.
Cases (1), (2) and (5) are weakly transitive in the sense that we could implement a tiebreaking scheme to create a linear order, though in case (5) the tiebreaker would be doing all the work. Cases (3) and (4) would be intransitive in this sense.
If it’s easy to extract from your data, could you tell us how many times each case arises?
May 22, 2017 at 3:01 am
Oops! What I wrote is wrong. There are actually 577 intransitive triples…
May 22, 2017 at 3:21 am
It should be 577 intransitive triples; 1385 transitive triples; 400 of type (1) above; 306 of type (2); 930 of type (3); 671 of type (4) which is two ties; and 226 of type (5) where all three dice tie.
May 22, 2017 at 4:08 am
The frequency of 6-sided dice in intransitive triples is
23, {5, 5, 4, 3, 2, 2}
24, {6, 4, 4, 3, 3, 1,
24, {5, 4, 4, 3,3, 2}
24, {4, 4, 4, 3, 3, 3}
29, {6, 6, 6, 1, 1, 1}
33, {6, 6, 4, 3, 1, 1}
45, {6, 4, 3, 3, 3, 2}
45, {5, 4, 4, 4, 3, 1}
49, {6, 4, 4, 3, 2, 2}
49, {5, 5, 4, 3, 3, 1}
50, {5, 5, 3, 3, 3, 2}
50, {5, 4, 4, 4, 2, 2}
54, {5, 5, 5, 2, 2, 2}
58, {6, 6, 4, 2, 2, 1}
58, {6, 5, 5, 3, 1, 1}
59, {6, 6, 3, 3, 2, 1}
59, {6, 5, 4, 4, 1, 1}
59, {6, 5, 3, 3, 3, 1}
59, {6, 5, 3, 3, 2, 2}
59, {6, 4, 4, 4, 2, 1}
59, {5, 5, 4, 4, 2, 1}
62, {5, 4, 3, 3, 3, 3}
62, {4, 4, 4, 4, 3, 2}
65, {6, 3, 3, 3, 3, 3}
65, {4, 4, 4, 4, 4, 1}
78, {6, 5, 4, 2, 2, 2}
78, {5, 5, 5, 3, 2, 1}
79, {6, 6, 5, 2, 1, 1}
79, {6, 5, 5, 2, 2, 1}
97, {6, 6, 3, 2, 2, 2}
97, {5, 5, 5, 4, 1, 1}
May 22, 2017 at 5:29 am
Tristram, 4) is not intransitive.
May 22, 2017 at 8:25 am |
Perhaps to test how good a dice is, we need to compare the dice with the symmetric dice. If A is much better than (n+1-A) then it will be “charismatic” and win against more than 50% symmetric dices, if A and B are both “charismatic” or both “anticharismatic” then they will have positive correlation compared to a random C etc.
May 22, 2017 at 9:36 am
I think what is going on is the following: we can expect that if a random dice A beats a random dice B then the gap between the number of pairs for which A beats B and the number of pairs for which B beats A is linear in n (say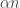 . (Square root of the total number of pairs.) Moreover, near the expected number the distribution is roughly uniform.
. (Square root of the total number of pairs.) Moreover, near the expected number the distribution is roughly uniform.
If we start with a random dice A then the expected gap between the number of pairs A beats another random dice B minus pairs that B beats A is also in expectation linear in n, (say the expectation is ).
).
So the values of will tilt the tournament described by several dice toward transitivity.
will tilt the tournament described by several dice toward transitivity.
The number of pairs for which A beats its symmetric pair (n+1-A) is also linear in expectation and perhaps it is well-correlated with .
.
May 22, 2017 at 9:11 am |
After the experimental results that suggest that full quasirandomness is probably false, I’ve written a quick piece of code to check this directly. That is, I pick a random pair of dice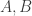 and then take a whole lot of random dice
and then take a whole lot of random dice  and see how many of them fall into the four possible classes, according to whether they beat A and whether they beat B. If the tournament is quasirandom, then we’d expect these four numbers to be roughly equal, but in my tests so far they don’t seem to be. For instance, with 100-sided dice and 10000 tests I’ve just obtained the numbers (3376,1523,1523,3330). The equality of the second and third numbers isn’t a bug in my program as it doesn’t always happen when I run it …
and see how many of them fall into the four possible classes, according to whether they beat A and whether they beat B. If the tournament is quasirandom, then we’d expect these four numbers to be roughly equal, but in my tests so far they don’t seem to be. For instance, with 100-sided dice and 10000 tests I’ve just obtained the numbers (3376,1523,1523,3330). The equality of the second and third numbers isn’t a bug in my program as it doesn’t always happen when I run it …
Length 100 is probably not long enough to be a convincing indication of anything, but one can at least say that a number of bits of not wholly convincing evidence are stacking up. Of course, these bits of evidence are not independent of each other, so it would still be very good to run this simple test with longer sequences. I’ll do a few more runs with my primitive program and report on the result, but it would be very interesting to look at longer dice and more tests.
May 22, 2017 at 9:38 am |
A few results with sequences of length 500 and 500 tests for each (A,B) (so the standard deviation for each number should be about 10).
(128, 121, 136, 113)
(147, 103, 112, 136)
(121, 133, 118, 123)
These don’t seem terribly conclusive in either direction.
OK, here are a few goes with 200 sides and 2000 tests (so standard deviation up to more like 20).
(514, 511, 457, 495)
(428, 568, 589, 397)
(506, 523, 454, 494)
(401, 615, 600, 362)
Some of these are so far from what quasirandomness would predict that my belief in full quasirandomness for the sequence model is almost extinguished — I don’t quite rule out that what we’re seeing is a small-numbers phenomenon, but I would have expected sequences of length 200 to be a bit closer to quasirandom than this if the quasirandomness conjecture were true.
Another thing it would obviously be good to do is the same simple test for the multiset model. Maybe I’ll try that later, but I have other things to do for a while.
May 22, 2017 at 10:04 am |
I thought it would be helpful to have an example of a tournament that is not quasirandom but where intransitivity occurs with the expected probability. I can actually exhibit a large class of such tournaments (and I think it may be possible to enlarge it quite a bit further).
Let be a positive integer and let
be a positive integer and let  be an antisymmetric set, meaning that
be an antisymmetric set, meaning that  if and only if
if and only if  . (I don’t care what happens to zero, since that makes a negligible difference to what follows.)
. (I don’t care what happens to zero, since that makes a negligible difference to what follows.)
Now define a tournament by putting an arrow from to
to  if
if 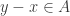 . In this case I’ll say that
. In this case I’ll say that  beats
beats  .
.
Writing for its own characteristic function, we can express the number of triples
for its own characteristic function, we can express the number of triples 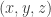 such that
such that  beats
beats  ,
,  beats
beats  and
and  beats
beats  as
as
which is equal to
If we change variables by replacing each variable by its negative, we see that this is also equal to
which by the antisymmetry of is equal (to make this work exactly, we could set
is equal (to make this work exactly, we could set  just for convenience) to
just for convenience) to
This last sum splits up into eight terms. The main term is simply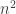 . A term that involves just one of
. A term that involves just one of  ,
,  or
or  gives
gives 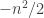 . A term that involves two of them gives
. A term that involves two of them gives  (since any two of the variables
(since any two of the variables  vary completely independently). And finally, the term that involves all three of
vary completely independently). And finally, the term that involves all three of  and
and  can be taken over to the left-hand side. So we get that
can be taken over to the left-hand side. So we get that
and hence that the number of triples we were counting is . Therefore, the number of intransitive triples is
. Therefore, the number of intransitive triples is 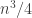 (since we can cycle round the other way too).
(since we can cycle round the other way too).
If we take a set such as
such as 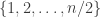 , then this tournament is very far from quasirandom, since vertices that are close to each other have very similar neighbourhoods.
, then this tournament is very far from quasirandom, since vertices that are close to each other have very similar neighbourhoods.
It might be an idea to try to think of a more general way of constructing tournaments like this, so that we have some kind of model for what might be going on with the dice: obviously we don’t expect the dice tournament to be based on a Cayley graph.
May 22, 2017 at 10:06 am
A small remark is that the little result in the previous comment can also be proved easily using Fourier analysis, the key fact, for those familiar with this technique, being that for each non-zero we have from antisymmetry that
we have from antisymmetry that  so
so  .
.
May 22, 2017 at 10:19 am |
As I was writing the previous comment I had a suspicion that it was completely unnecessary to restrict attention to Cayley graphs, and indeed the same proof works for general antisymmetric matrices.
To keep things consistent with what I did before, I’ll take the “adjacency matrix” of a tournament to be given by if
if  beats
beats  and 0 otherwise (rather than -1 otherwise).
and 0 otherwise (rather than -1 otherwise).
So now the number of triples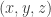 such that
such that  beats
beats  ,
,  beats
beats  and
and  beats
beats  is
is
By swapping the names of and
and  we get that this is equal to
we get that this is equal to
which by antisymmetry is equal to
The main term is . With just one “A” we sum
. With just one “A” we sum  times over all 1s in
times over all 1s in  , getting
, getting  . With a sum such as
. With a sum such as  we are summing over all
we are summing over all  the square of its outdegree. So if all outdegrees are
the square of its outdegree. So if all outdegrees are 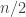 , then this gives us
, then this gives us 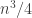 .
.
So with that assumption we get that
and with the cycles in the opposite direction we get that the probability of intransitivity is 1/4.
So it seems that it should be enough to prove that almost all dice beat roughly half of all the other dice.
May 22, 2017 at 10:59 am
Just a quick note that a simple double-counting proof has just occurred to me (based on a proof of the lower bound for the number of monochromatic triangles in a 2-coloured graph on n vertices) that not only is the correct proportion of transitive triangles implied by all the outdegrees being about a half, in fact these two statements are equivalent.
Count the number of triples (x, y, z) where x beats y and y beats z. This is clearly C(n,3) plus twice the number of transitive triangles (by counting via the distinct elements x, y and z) and is also equal to the sum of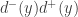 where these denote the indegree and outdegrees of y.
where these denote the indegree and outdegrees of y.
Since these two degrees sum to n-1, the count is at most n(n-1)^2/4, so the number of transitive triangles is at most n(n-1)(n+1)/24 (very close to the expected number in a random) with equality if every degree is about half.
May 22, 2017 at 11:03 am
Ah, I had wondered whether that might be the case. In a way it makes the original conjecture slightly less interesting — it’s no longer “really” about intransitivity — but I would still like it if we could prove it!
May 22, 2017 at 10:24 am |
Going back to the experimental evidence mentioned above, the numbers given are the number of such that the dice beating
such that the dice beating  are
are
( and
and  ,
,  ,
,  , neither).
, neither).
So for the intransitivity conjecture to be true, we would like the first and second numbers to add up to roughly half the total, and also the first and third numbers. So we want the outer two numbers to be roughly equal and the inner two numbers to be roughly equal. Apart from one slightly troubling run (which can probably be dismissed as a fluke) this seems to be happening reasonably well.
May 22, 2017 at 10:54 am
A few more runs picking a random die and counting how many times it wins and how many times it loses. Sequences of length 500, 2000 trials. Each pair is (number of times A wins, number of times A loses).
This looks pretty good to me. The second pair isn’t great, but that could be simply because the die in that case was slightly untypical and that the true probability of its beating a further die was a little bit less than 1/2.
May 22, 2017 at 11:01 am |
It feels to me as though we ought to be able to prove the “small” conjecture now, given the observation that it is sufficient for almost all dice to beat roughly half the other dice.
We already have a heuristic argument for this, namely the following. Let be a typical die. (I think this should mean something like that
be a typical die. (I think this should mean something like that 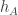 is not zero too much.) Then
is not zero too much.) Then  beats
beats  if
if 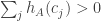 . But if
. But if  is chosen purely randomly (with no condition on the sum), then we expect the random variable
is chosen purely randomly (with no condition on the sum), then we expect the random variable
to approximate a bivariate normal with mean
with mean 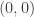 . And if this is the case, then when we condition on
. And if this is the case, then when we condition on 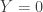 we should get a normal distribution, which will have a probability 1/2 of being greater than zero.
we should get a normal distribution, which will have a probability 1/2 of being greater than zero.
So if we can make this argument rigorous using Berry-Esseen type results, then we should be done.
To be clear, “done” means that we would have proved the conjecture about the frequency of intransitivity for the sequences model. If we can do that, it would be nice to push on and try to do the multiset model too.
May 22, 2017 at 11:05 am
And let me add that Bogdan Grechuk has already made a start on proving this.
May 22, 2017 at 11:13 am
One of the things that Bogdan needed to get the argument to work is some control on how large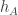 gets.
gets.
I think it should be possible to say something about this quite easily — though whether what I say is strong enough I haven’t yet worked out.
Suppose we choose a random die by choosing a purely random sequence and conditioning on its having the right total. For the purely random sequence,
by choosing a purely random sequence and conditioning on its having the right total. For the purely random sequence, 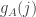 is a sum of
is a sum of  Bernoulli random variables with probability
Bernoulli random variables with probability 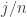 , so the probability that it differs from its mean
, so the probability that it differs from its mean  by more than
by more than 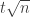 is going to be bounded above by
is going to be bounded above by 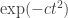 for some positive
for some positive  . So if
. So if  , the probability starts to be at most
, the probability starts to be at most  .
.
But when we condition on the sum being zero, this probability will multiply by at most or so, since the probability that the sum is correct is of order
or so, since the probability that the sum is correct is of order  . So I think we can safely say that for a typical die
. So I think we can safely say that for a typical die  , no
, no 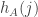 will be bigger than, say,
will be bigger than, say, 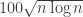 .
.
With another elementary argument I think we should be able to show that the sum of the squares of the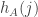 will not be too small. So maybe the ingredients are almost all in place.
will not be too small. So maybe the ingredients are almost all in place.
May 22, 2017 at 2:47 pm
Here’s the kind of elementary argument I’m talking about that should prove that the sum of the squares of the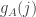 won’t usually be too small. Fix some
won’t usually be too small. Fix some 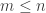 and let us consider just the values of
and let us consider just the values of 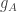 at
at  . The probability that
. The probability that  is at most
is at most 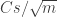 . More generally, the probability that
. More generally, the probability that 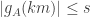 given the value of
given the value of 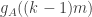 will be at most
will be at most 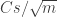 . So for lots of the
. So for lots of the  to be small we need a lot of unlikely events to happen, the probabilities of which are multiplied together.
to be small we need a lot of unlikely events to happen, the probabilities of which are multiplied together.
It seems at least possible that for suitably optimized choices of and
and  we’ll get a strong enough bound from this kind of argument. Indeed, if
we’ll get a strong enough bound from this kind of argument. Indeed, if  is something like
is something like  , then I think the above sketch should show that with very high probability
, then I think the above sketch should show that with very high probability  for at least half the values of
for at least half the values of  , which would give a lower bound for
, which would give a lower bound for 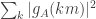 of
of  .
.
That looks unfortunate, but I now see that we can probably improve it quite substantially by observing that each time is large, it is probably surrounded by quite a lot of other large values (since the only way this could fail to be the case is if there are unexpected clusters in
is large, it is probably surrounded by quite a lot of other large values (since the only way this could fail to be the case is if there are unexpected clusters in  ).
).
May 22, 2017 at 3:10 pm
I’m getting slightly confused, which is partly because I think that in Bogdan’s comment in the place where he defined the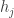 he forgot a power 1/2 in the denominator. That’s slightly better, and means that the lower bound I sketched for this denominator would be proportional to
he forgot a power 1/2 in the denominator. That’s slightly better, and means that the lower bound I sketched for this denominator would be proportional to 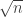 . So we need to gain a further factor of
. So we need to gain a further factor of  .
.
But suppose that we have some with
with  . Ah, there’s a useful property here, which is that
. Ah, there’s a useful property here, which is that 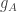 is increasing, so
is increasing, so 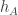 decreases by at most 1 when
decreases by at most 1 when  increases by 1. So we get
increases by 1. So we get  values of
values of  with
with  , which gives a lower bound for
, which gives a lower bound for 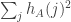 of
of 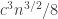 and therefore a lower bound for the square root of this of
and therefore a lower bound for the square root of this of  , which is a lot bigger than
, which is a lot bigger than 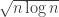 .
.
So it’s possible that we’re done, but I’ve only half understood Bogdan’s comment, so I’ll need to await confirmation. Also, my calculation above could turn out to be nonsense — it’s not carefully checked.
May 23, 2017 at 1:44 pm
I am sorry about “a power 1/2 in the denominator” (can you correct this?). As I noted in the comments to my post, control of maximal hj for a typical dice seems to be easy (thank you for adding the details, the observation that hj decreases by at most 1 indeed proves the statement), but, for the argument to work, Berry–Esseen theorem should remain correct for random vectors, while Wikipedia formulation is for the one-dimensional case only. I have asked for a reference with no response yet. So, I would not say we are done. But very close, one step away.
May 23, 2017 at 1:56 pm
Thanks for this clarification. I’ve added the 1/2 now.
This mathoverflow question points us to a multidimensional Berry-Esseen theorem. In particular, it looks as though Theorem 1.1 in this paper is probably what we want. Does it look strong enough to you? (I could probably work this out, but I think you’ll be able to do so a lot more quickly.)
May 23, 2017 at 3:24 pm
It looks to me as though we wouldn’t be quite there, because the 2D Berry-Esseen theorem needs to be discrete, and that raises certain considerations that may turn out to be non-trivial.
The theorem in the paper measures closeness to a Gaussian as the maximum discrepancy between the Gaussian probability of being a convex set and the probability of the given distribution being in that set. However, the convex set that we want to restrict to will be a one-dimensional set, and therefore very small.
The kind of problem this could cause is illustrated by the following simple example. Let be a random variable that has mean zero and is supported on a finite subset of
be a random variable that has mean zero and is supported on a finite subset of 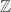 . Let
. Let 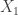 and
and 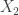 be independent copies of
be independent copies of  . Then a sum of
. Then a sum of  independent copies of
independent copies of 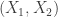 will approximate a normal distribution with mean
will approximate a normal distribution with mean 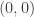 and a certain variance.
and a certain variance.
Now let’s suppose that![\mathbb P[X=1]](https://s0.wp.com/latex.php?latex=%5Cmathbb+P%5BX%3D1%5D&bg=ffffff&fg=333333&s=0&c=20201002) is non-zero. Then the normal distribution we converge to will assign non-zero probabilities to every point in
is non-zero. Then the normal distribution we converge to will assign non-zero probabilities to every point in 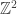 .
.
But if instead we start with a different random variable with the same mean and variance as but supported on the even numbers, then the normal distribution we converge to will assign zero probability to numbers with an odd coordinate and will make up for it by assigning more weight to points in
but supported on the even numbers, then the normal distribution we converge to will assign zero probability to numbers with an odd coordinate and will make up for it by assigning more weight to points in 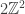 .
.
This is no problem when it comes to the probability of landing in a convex set, but it is more worrying when we condition on one of the coordinates being zero, which will lead to the probabilities being doubled, in a certain sense.
In our case, we should be OK, because the variable whose value we are conditioning on will not be supported in a residue class, but I think it means we may have to delve into the proof of the multidimensional Berry-Esseen theorem rather than just quoting it — unless of course someone else has proved a version that is better adapted to our purpose.
May 23, 2017 at 4:57 pm
I think the kind of statement we might want is that the distribution tends, in a suitable sense, to a distribution with a Gaussian type formula (that is, the probability of being at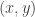 is something like
is something like 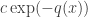 for some positive definite quadratic form
for some positive definite quadratic form  ) on some sublattice of
) on some sublattice of 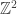 (or more generally
(or more generally 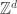 ).
).
May 23, 2017 at 5:46 pm
Thank you for the reference to 2D Berry-Esseen theorem. Indeed, it does not seem applicable, and the problem is much trickier than I thought. I do not think that the problem is because we have discrete distribution. In the continuous case, the fact that random vector (X,Y) is “close” to Gaussian in the sense that “the maximum discrepancy on convex sets” (as defined in the reference) is small, tell us nothing about the conditional distribution of X given Y=0, because P(Y=0)=0…
May 23, 2017 at 11:09 pm
An example. Fix a generic solution to the system of 5 equations:
to the system of 5 equations:  . Now, let random vector (X,Y) takes values
. Now, let random vector (X,Y) takes values  each with probability 1/3. Then
each with probability 1/3. Then  ,
,  ,
, 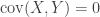 . Let
. Let 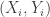 be i.i.d copies of this random vector,
be i.i.d copies of this random vector,  ,
,  . Then the joint distribution of
. Then the joint distribution of  converges to standard 2D normal. For example,
converges to standard 2D normal. For example, ![P[U_n>0, V_n>0]](https://s0.wp.com/latex.php?latex=P%5BU_n%3E0%2C+V_n%3E0%5D&bg=ffffff&fg=333333&s=0&c=20201002) converges to 1/4, etc.
converges to 1/4, etc.
However, in fact , where
, where 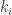 are frequencies for each value, and
are frequencies for each value, and 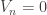 implies
implies  , hence
, hence 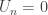 . So,
. So, ![P[U_n=0 | V_n=0]=1](https://s0.wp.com/latex.php?latex=P%5BU_n%3D0+%7C+V_n%3D0%5D%3D1&bg=ffffff&fg=333333&s=0&c=20201002) .
.
On the other hand, most of proof strategies we had for the dice problem, if worked, could also be used to prove that![P[U_n=0 | V_n=0]](https://s0.wp.com/latex.php?latex=P%5BU_n%3D0+%7C+V_n%3D0%5D&bg=ffffff&fg=333333&s=0&c=20201002) converges to 0, while
converges to 0, while ![P[U_n>0 | V_n=0]](https://s0.wp.com/latex.php?latex=P%5BU_n%3E0+%7C+V_n%3D0%5D&bg=ffffff&fg=333333&s=0&c=20201002) converges to 1/2…
converges to 1/2…
May 24, 2017 at 2:09 pm
It seems I have finally found the correct type of theorems we need: these are Discrete local limit theorems for random vectors. The original result is due to Richter (MULTI-DIMENSIONAL LOCAL LIMIT THEOREMS FOR LARGE DEVIATIONS), but the formulation there is complicated. A recent book is “Random Walk: A Modern Introduction” by Gregory F. Lawler and Vlada Limic, Section 2, Theorem 2.1.1. There are different estimates there, but, basically, the Theorem states that the for every single point x in the lattice, the probability that we will be exactly at x after n steps can be estimated from the corresponding normal distribution, plus some error term.
May 24, 2017 at 3:02 pm
Fantastic! I also came across the Lawler/Limic book but had not understood it well enough to see that it had what we wanted (assuming that that is indeed the case).
It seems to me that there will probably be some kind of technical lemma needed to argue that the probability that the entire random walk lives in a sublattice tends to zero. But probably this too follows reasonably easily from the fact that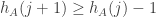 for every
for every  .
.
May 24, 2017 at 7:13 pm
Just as a reference for those following along who don’t have access to the Lawler/Limic book, Terry Tao gives a bit of related exposition in a blog post: https://terrytao.wordpress.com/2015/11/19/275a-notes-5-variants-of-the-central-limit-theorem/#more-8566. Hope it helps!
May 24, 2017 at 9:27 pm
That blog post is definitely worth a read, but let me add that everyone has access to the Lawler/Limic book.
May 25, 2017 at 12:05 pm
Ah, the second time when I thought we are almost done, I then see a problem. For fixed A and random j we have a 2-dimensional random vector (X,Y) taking values with equal chances. Note that for odd n it takes integer values only. Let
with equal chances. Note that for odd n it takes integer values only. Let  be i.i.d copies of (X,Y),
be i.i.d copies of (X,Y),  ,
,  .
.
For simplicity, let us talk about ties conjecture, for which it suffices to prove that![P[U_n=0 | V_n=0] = P[U_n = V_n = 0]/P[V_n=0]](https://s0.wp.com/latex.php?latex=P%5BU_n%3D0+%7C+V_n%3D0%5D+%3D+P%5BU_n+%3D+V_n+%3D+0%5D%2FP%5BV_n%3D0%5D&bg=ffffff&fg=333333&s=0&c=20201002) converges to $0$.
converges to $0$.
Let![p_n(u,v) = P[U_n=u, V_n=v]](https://s0.wp.com/latex.php?latex=p_n%28u%2Cv%29+%3D+P%5BU_n%3Du%2C+V_n%3Dv%5D&bg=ffffff&fg=333333&s=0&c=20201002) , and let
, and let  be an estimate of
be an estimate of  obtained by integrating density of standard normal distribution around point
obtained by integrating density of standard normal distribution around point 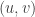 . Then
. Then ![p'_n(0,0)/P[V_n=0]](https://s0.wp.com/latex.php?latex=p%27_n%280%2C0%29%2FP%5BV_n%3D0%5D&bg=ffffff&fg=333333&s=0&c=20201002) converges to
converges to  , so all we need is to control the ratio
, so all we need is to control the ratio  .
.
Now, substituting x=(0,0) into the formula (2.5) on page 25 in the book, we get , while (again according to the book)
, while (again according to the book)  is of order $c/\sqrt{n}$. This seemed to clearly imply that
is of order $c/\sqrt{n}$. This seemed to clearly imply that  converges to $1$, and we would be done. The proof that
converges to $1$, and we would be done. The proof that ![P[U_n>0 | V_n=0]](https://s0.wp.com/latex.php?latex=P%5BU_n%3E0+%7C+V_n%3D0%5D&bg=ffffff&fg=333333&s=0&c=20201002) converges to 1/2 is similar.
converges to 1/2 is similar.
However, while the constant in Berry–Esseen theorem was universal (0.4748 works), the constant c in the formula (2.5) in the book seems to depend on our initial random vector (X,Y). In our case, the vector is not fixed but different for every n, so c depends on n, which makes the inequality meaningless.
So, we need a version of Local Central Limit Theorem, as in the book, but with all constants universal, and the dependence of the initial random vector (X,Y), if any, should be explicit (in terms of moments, etc.) It seems not easy to extract this from the proof in the book.
May 25, 2017 at 12:18 pm
I’m in the middle of a new post, which I’ll now have to tone down slightly, to make clear that there is still work to do (or a convenient result to find in the literature). My guess is that we don’t actually need a new idea, but rather we will have to go through the proof of the LCLT very carefully, extract some assumption we need about the random vector and then prove that for almost all
and then prove that for almost all  we have that assumption when
we have that assumption when  is
is 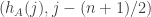 for a randomly chosen
for a randomly chosen  . The kinds of properties we might want are that the support of
. The kinds of properties we might want are that the support of 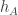 is quite small (about
is quite small (about 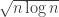 ) and that
) and that  is not concentrated in some sublattice of
is not concentrated in some sublattice of 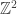 .
.
May 22, 2017 at 8:38 pm |
Gowers,
My comment from a couple days ago is still stuck in the moderation queue.
May 22, 2017 at 9:24 pm
Again, apologies about that, and a curse on WordPress. To make the comment easy to find, here is a link to it.
May 22, 2017 at 9:59 pm |
Tim, I am a little confused about where matters stand and what the empirical evidence indicates. Are we leaning toward a YES answer or a NO answer.
May 22, 2017 at 10:16 pm
Well, I may be wrong, but I personally am leaning towards the small conjecture being correct and the big conjecture being false, where these are the following.
Small conjecture: if beats
beats  and
and  beats
beats  then the probability that
then the probability that  beats
beats  is approximately 1/2.
is approximately 1/2.
Big conjecture: the tournament obtained by the relation “beats” is quasirandom.
We now know that the small conjecture is equivalent to the statement that almost every die beats approximately half the other dice, and the big conjecture is equivalent to the statement that for almost every pair of dice, the remaining dice are split into four approximately equal classes according to the four possibilities for which of the two they beat.
I’ve only really been thinking about the sequences model, but I think the experimental evidence is suggesting that the same should be true for the multisets model as well.
Also, I think we may already essentially have a proof of the small conjecture for the sequences model, but I’m waiting to see whether Bogdan Grechuk agrees with me about this.
May 23, 2017 at 7:36 pm
Ironically, the one thing I was rather certain about (based on the voting rules analogy) is that the big conjecture would follow from the small conjecture. Oh, well 🙂
May 23, 2017 at 11:22 am |
I’ve spent a little time thinking about how the argument, if it turns out to be OK, could be modified to deal with the multiset model as well. The bijection between multisets with values from
values from ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and subsets of
and subsets of ![[2n-1]](https://s0.wp.com/latex.php?latex=%5B2n-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) of size
of size  ought to be helpful here.
ought to be helpful here.
One thing it gives us quite easily is a way of proving statements about the function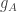 . For convenience I’ll take a set
. For convenience I’ll take a set ![A\subset[2n-1]](https://s0.wp.com/latex.php?latex=A%5Csubset%5B2n-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) of size
of size  as my basic object. Then if we list the elements of
as my basic object. Then if we list the elements of  as
as 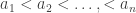 , the elements of the multiset are
, the elements of the multiset are  (with multiplicity equal to the number of times they appear in this list). I’ll call this multiset
(with multiplicity equal to the number of times they appear in this list). I’ll call this multiset 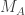 and I’ll write
and I’ll write 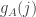 for the number of elements of
for the number of elements of 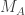 , with multiplicity, that are at most
, with multiplicity, that are at most  .
.
It doesn’t seem to be wholly pleasant to define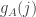 directly in terms of the set
directly in terms of the set  : it is the maximal
: it is the maximal  such that
such that  . However, we do at least have that the “inverse” is a nice function. That is, we know that the
. However, we do at least have that the “inverse” is a nice function. That is, we know that the  th largest face of the die
th largest face of the die 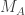 is
is  . And that is quite helpful. For instance, if instead of choosing a random
. And that is quite helpful. For instance, if instead of choosing a random 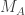 that adds up to 1 we instead choose a random subset of
that adds up to 1 we instead choose a random subset of ![[2n-1]](https://s0.wp.com/latex.php?latex=%5B2n-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) where each element is chosen independently with probability
where each element is chosen independently with probability  , then we would normally expect
, then we would normally expect 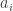 to be around
to be around 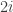 , and not to differ from
, and not to differ from 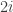 by much more than
by much more than  . So we get that for this completely random model that the
. So we get that for this completely random model that the  th largest face of the die typically has value close to
th largest face of the die typically has value close to  , and is well concentrated. If we now condition on the size of the set being
, and is well concentrated. If we now condition on the size of the set being  and the sum of the faces of the die being
and the sum of the faces of the die being 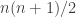 , this will not change too much. And now we can just invert and say the same about
, this will not change too much. And now we can just invert and say the same about 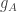 .
.
We also have that beats
beats  if the number of
if the number of 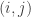 such that
such that  is greater than the number of
is greater than the number of 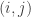 such that
such that  . This may turn out to be reasonably easy to work with — I’m not sure.
. This may turn out to be reasonably easy to work with — I’m not sure.
May 27, 2017 at 4:53 pm |
[…] to a statement that doesn’t mention transitivity. The very quick proof I’ll give here was supplied by Luke Pebody. Suppose we have a tournament (that is, a complete graph with each edge directed in one of the two […]
October 27, 2019 at 10:25 pm |
I’m sorry I did a mistake in my code, on the transitivity of $>>$ , I hope it wont appear, and that it did’nt yet made you lose some time…
October 27, 2019 at 11:15 pm
Fortunatelly the post I’m talking about was not posted (I had to register in between)
After identification of $A=(a_1,…,a_n)$ and $A^*=(n+1-a_n,…,n+1-a_1) $I was trying to build $>>$, an ” almost transitive ” relation between these classes (that are pair or singleton (if $A$ ties with $A^*$)) in such a hope that if $A$ beats $B$ and $B$ beats $C$, then the fact that $A$ beats $C$ only depends on $>>$
I made a mistake thinking I had this relation but the two very basic facts that I like are
1)$A$ beats $B$ iff $B^*$ beats $A^*$
2) If $A$ does not tie with $B$ then, either $A$ beats/defeats BOTH $B$ and $B^*$ either $B$ beats/defeats BOTH $A$ and $A^*$ so that we have a new relation on the quotient of all dies after identification of a die and its dual.
Then we have something like this : $X$ beats $Y$ that beats $Y^*$ that beats X^*$ (where $X,Y\in \left\{A,A^*,B,B^*\right\}$, and $X$ does not tie with $Y$)
Now if $X$ beats $X^*$ we have a transitive chain involving the four dies.., I kind of feel that an investigation on this might be intersting…