I’m not getting the feeling that this intransitive-dice problem is taking off as a Polymath project. However, I myself like the problem enough to want to think about it some more. So here’s a post with some observations and with a few suggested subproblems that shouldn’t be hard to solve and that should shed light on the main problem. If the rate of comments by people other than me doesn’t pick up, then I think I’ll simply conclude that there wasn’t sufficient interest to run the project. However, if I do that, I have a back-up plan, which is to switch to a more traditional collaboration — that is, done privately with a small number of people. The one non-traditional aspect of it will be that the people who join the collaboration will select themselves by emailing me and asking to be part of it. And if the problem gets solved, it will be a normal multi-author paper. (There’s potentially a small problem if someone asks to join in with the collaboration and then contributes very little to it, but we can try to work out some sort of “deal” in advance.)
But I haven’t got to that point yet: let me see whether a second public post generates any more reaction.
I’ll start by collecting a few thoughts that have already been made in comments. And I’ll start that with some definitions. First of all, I’m going to change the definition of a die. This is because it probably makes sense to try to prove rigorous results for the simplest model for which they are true, and random multisets are a little bit frightening. But I am told that experiments suggest that the conjectured phenomenon occurs for the following model as well. We define an -sided die to be a sequence
of integers between 1 and
such that
. A random
-sided die is just one of those chosen uniformly from the set of all of them. We say that
beats
if
That is, beats
if the probability, when you roll the two dice, that
shows a higher number than
is greater than the probability that
shows a higher number than
. If the two probabilities are equal then we say that
ties with
.
The main two conjectures are that the probability that two dice tie with each other tends to zero as tends to infinity and that the “beats” relation is pretty well random. This has a precise meaning, but one manifestation of this randomness is that if you choose three dice
and
uniformly at random and are given that
beats
and
beats
, then the probability that
beats
is, for large
, approximately
. In other words, transitivity doesn’t happen any more often than it does for a random tournament. (Recall that a tournament is a complete graph in which every edge is directed.)
Now let me define a function that helps one think about dice. Given a die , define a function
on the set
by
Then it follows immediately from the definitions that beats
if
, which is equivalent to the statement that
.
If the “beats” tournament is quasirandom, then we would expect that for almost every pair of dice the remaining dice are split into four parts of roughly equal sizes, according to whether they beat
and whether they beat
. So for a typical pair of dice
we would like to show that
for roughly half of all dice
, and
for roughly half of all dice
, and that these two events have almost no correlation.
It is critical here that the sums should be fixed. Otherwise, if we are told that beats
, the most likely explanation is that the sum of
is a bit bigger than the sum of
, and then
is significantly more likely to beat
than
is.
Note that for every die we have
That is, every die ties with the die .
Now let me modify the functions to make them a bit easier to think about, though not quite as directly related to the “beats” relation (though everything can be suitably translated). Define
to be
and
to be
. Note that
which would normally be approximately equal to
.
We are therefore interested in sums such as . I would therefore like to get a picture of what a typical sequence
looks like. I’m pretty sure that
has mean
. I also think it is distributed approximately normally around
. But I would also like to know about how
and
correlate, since this will help us get some idea of the variance of
, which, if everything in sight is roughly normal, will pin down the distribution. I’d also like to know about the covariance of
and
, or similar quantities anyway, but I don’t want to walk before I can fly.
Anyhow, I had the good fortune to see Persi Diaconis a couple of days ago, and he assured me that the kind of thing I wanted to understand had been studied thoroughly by probabilists and comes under the name “constrained limit theorems”. I’ve subsequently Googled that phrase and found some fairly old papers written in the typical uncompromising style and level of generality of their day, which leaves me thinking that it may be simpler to work a few things out from scratch. The main purpose of this post is to set out some exercises that have that as their goal.
What is the average of 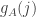 ?
?
Suppose, then, that we have a random -sided die
. Let’s begin by asking for a proper proof that the mean of
is
. It clearly is if we choose a purely random
-tuple of elements of
, but what happens if we constrain the average to be
?
I don’t see an easy proof. In fact, I’m not sure it’s true, and here’s why. The average will always be if and only if the probability that
is always equal to
, and that is true if and only if
is uniformly distributed. (The distributions of the
are of course identical, but — equally of course — not independent.) But do we expect
to be uniformly distributed? No we don’t: if
that will surely make it easier for the global average to be
than if
.
However, I would be surprised if it were not at least approximately true. Here is how I would suggest proving it. (I stress that I am not claiming that this is an unknown result, or something that would detain a professional probabilist for more than two minutes — that is why I used the word “exercise” above. But I hope these questions will be useful exercises.)
The basic problem we want to solve is this: if are chosen independently and uniformly from
, then what is the conditional probability that
given that the average of the
is exactly
?
It’s not the aim of this post to give solutions, but I will at least say why I think that the problems aren’t too hard. In this case, we can use Bayes’s theorem. Using well-known estimates for sums of independent random variables, we can give good approximations to the probability that the sum is and of the probability of that given that
(which is just the probability that the sum of the remaining
s is
). We also know that the probability that
is
. So we have all the information we need. I haven’t done the calculation, but my guess is that the tendency for
to be closer to the middle than to the extremes is not very pronounced.
In fact, here’s a rough argument for that. If we choose uniformly from
, then the variance is about
. So the variance of the sum of the
(in the fully independent case) is about
, so the standard deviation is proportional to
. But if that’s the case, then the probability that the sum equals
is roughly constant for
.
I think it should be possible to use similar reasoning to prove that if , then
are approximately independent. (Of course, this would apply to any
of the
, if correct.)
How is 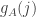 distributed?
distributed?
What is the probability that of the
are at most
? Again, it seems to me that Bayes’s theorem and facts about sums of independent random variables are enough for this. We want the probability of the above event given that
. By Bayes’s theorem, we can work this out if we know the probability that
given that
, together with the probability that
and the probability that
, in both cases when
is chosen fully independently. The last two calculations are simple. The first one isn’t 100% simple, but it doesn’t look too bad. We have a sum of
random variables that are uniform on
and
that are uniform on
and we want to know how likely it is that they add up to
. We could do this by conditioning on the possible values of the two sums, which then leaves us with sums of independent variables, and adding up all the results. It looks to me as though that calculation shouldn’t be too unpleasant. What I would recommend is to do the calculation on the assumption that the distributions are normal (in a suitable discrete sense) with whatever mean and variance they have to have, since that will yield an answer that is almost certainly correct. A rigorous proof can come later, and shouldn’t be too much harder.
The answer I expect and hope for is that is approximately normally distributed with mean
and a variance that would come out of the calculations.
What is the joint distribution of  and
and  ?
?
This can in principle be done by exactly the same technique, except that now things get one step nastier because we have to condition on the sum of the that are at most
, the sum of the
that are between
and
, and the sum of the rest. So we end up with a double sum of products of three probabilities at the end instead of a single sum of products of two probabilities. The reason I haven’t done this is that I am quite busy with other things and the calculation will need a strong stomach. I’d be very happy if someone else did it. But if not, I will attempt it at some point over the next … well, I don’t want to commit myself too strongly, but perhaps the next week or two. At this stage I’m just interested in the heuristic approach — assume that probabilities one knows are roughly normal are in fact given by an exact formula of the form
.
For some experimental evidence about this, see a comment by Ian on the previous post, which links to some nice visualizations. Ian, if you’re reading this, it would take you about another minute, I’d have thought, to choose a few random dice and plot the graphs
. It would be interesting to see such plots to get an idea of what a typical one looks like: roughly how often does it change sign, for example?
What is a heuristic argument for the “ beats
beats  ” tournament being quasirandom?
” tournament being quasirandom?
I have much less to say here — in particular, I don’t have a satisfactory answer. But I haven’t spent serious time on it, and I think it should be possible to get one.
One slight simplification is that we don’t have to think too hard about whether beats
when we are thinking about the three dice
and
. As I commented above, the tournament will be quasirandom (I think I’m right in saying) if for almost every
and
the events “
beats
” and “
beats
” have probability roughly 1/2 each and are hardly correlated.
A good starting point would be the first part. Is it true that almost every die beats approximately half the other dice? This question was also recommended by Bogdan Grechuk in a comment on the previous post. He suggested, as a preliminary question, the question of finding a good sufficient condition on a die for this to be the case.
That I think is approachable too. Let’s fix some function without worrying too much about whether it comes from a die (but I have no objection to assuming that it is non-decreasing and that
, should that be helpful). Under what conditions can we be confident that the sum
is greater than
with probability roughly 1/2, where
is a random die?
Assuming it’s correct that each is roughly uniform,
is going to average
, which if
is a die will be close to
. But we need to know rather more than that in order to obtain the probability in question.
But I think the Bayes approach may still work. We’d like to nail down the distribution of given that
. So we can look at
, where now the
are chosen uniformly and independently. Calling that
, we find that it’s going to be fairly easy to estimate the probabilities of
and
. However, it doesn’t seem to be notably easier to calculate
than it is to calculate
. But we have made at least one huge gain, which is that now the
are independent, so I’d be very surprised if people don’t know how to estimate this probability. Indeed, the probability we really want to know is
. From that all else should follow. And I think that what we’d like is a nice condition on
that would tell us that the two events are approximately independent.
I’d better stop here, but I hope I will have persuaded at least some people that there’s some reasonably low-hanging fruit around, at least for the time being.
May 12, 2017 at 10:00 pm |
The argument for why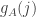 should not be precisely uniform seems persuasive on its own, but I decided to make sure in the first nontrivial case:
should not be precisely uniform seems persuasive on its own, but I decided to make sure in the first nontrivial case:  . There are five distinct multisets:
. There are five distinct multisets:  , and
, and  of respective multiplicities 6, 24, 6, 4, and 4 in the
of respective multiplicities 6, 24, 6, 4, and 4 in the  -tuples model. So by just counting I get that with the multiset model,
-tuples model. So by just counting I get that with the multiset model, ,
,  , and
, and 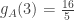 . With the tuples model, I get
. With the tuples model, I get  ,
,  , and
, and 
May 13, 2017 at 6:37 am |
If the distribution was random, then given a set of dice: D_1 > D_2 > D_3 > D_4 … > D_k we’d expect it to be probability 1/2 that D_k > D_1. Their example with n=6 k=3 looks close to this, but if we look further, some of them are quite away from that prediction.
k=4 and k=6 in particular look quite a bit off
Here is data exhaustively looking at all the set of dice that satisfy D_1 > D_2 > D_3 > D_4 … > D_k, and then check the relationship of D_1 to D_k (“win” means D_1 beats D_k).
n = 6
32 proper dice
——————–
n=6, k=3
total: 4417
win = 1756
lose = 1731
tie = 930
——————–
n=6, k=4
total: 50222
win = 11373
lose = 29888
tie = 8961
——————–
n=6, k=5
total: 548764
win = 218865
lose = 230555
tie = 99344
——————–
n=6, k=6
total: 5774214
win = 2791119
lose = 1911756
tie = 1071339
——————–
n=6, k=7
total: 58321842
win = 23702152
lose = 23575958
tie = 11043732
——————–
n=6, k=8
total: 563494040
win = 206137406
lose = 250564360
tie = 106792274
Also, it sounds like they are claiming that for k=4, the fraction of intransitives should approach C(4)/2^6 = 0.375. But their numerical evidence with n going up to 200 shows it monotonically increasing beyond that value.
May 13, 2017 at 10:01 am
That last comment of yours is interesting, so let me think about how worrying it is. They obtain their probabilities by doing a random sample of 1000 dice. If the true probability were exactly 3/8, then the variance of the number of intransitive quadruples observed would be so the standard deviation would be about 15 or so. Their last trial gave a probability of 0.392, so it’s about one standard deviation above what the conjecture would predict. So I think they are right when they say that the results are consistent with the conjecture — but they are clearly not enough to confirm it in a strong way.
so the standard deviation would be about 15 or so. Their last trial gave a probability of 0.392, so it’s about one standard deviation above what the conjecture would predict. So I think they are right when they say that the results are consistent with the conjecture — but they are clearly not enough to confirm it in a strong way.
It could be interesting to rerun these trials, or to perform similar and larger-scale experiments for the model we are now considering, just to reassure ourselves that we aren’t struggling to prove a false statement.
May 13, 2017 at 3:06 pm
With k=4 there are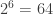 tournament graphs and 24 of them have a cycle of length 4. Our conjecture is that these 64 tournament graphs become equally probable in the large
tournament graphs and 24 of them have a cycle of length 4. Our conjecture is that these 64 tournament graphs become equally probable in the large  limit. With a small sample size like 1000, it is not surprising that the experimental ratio 0.392 that we found for
limit. With a small sample size like 1000, it is not surprising that the experimental ratio 0.392 that we found for  is above
is above  , and as Gowers pointed out it is about one standard deviation above. We’d definitely like to see more experiments on a larger scale.
, and as Gowers pointed out it is about one standard deviation above. We’d definitely like to see more experiments on a larger scale.
May 13, 2017 at 11:12 am |
I can run some experiments, but I’m not entirely sure I understand their statistics for k>3. For example the table with k=4, do they randomly choose 4 dice, check if any of the 4*3 pairs tie and if so reject it? and if there are no ties, then try all 4! permutations and see if any of those gives D_1 > D_2 > D_3 > D_4 > D_1 ? Or do I count it even if say D_2 would tie D_4 in that sequence? Or what about if there is a permutation in which it is not intransitive, just ignore that fact and only care if _some_ permutation of the 4 gives an intransitive sequence?
May 13, 2017 at 11:31 am
It looks to me as though they randomly choose four dice and look at the probability that the resulting tournament contains a 4-cycle. Of course, if there are any ties, then it isn’t a tournament, but that seems to happen with sufficiently low probability that it doesn’t affect things too much. So I think what one does with ties is up to you, as long as it is clear what has been done.
May 13, 2017 at 3:26 pm
Yes, that’s what we did. We looked at four random dice and made all pairwise comparisons. We counted the times that there were any ties among the 6 comparisons and we counted the number of times that the four dice formed an intransitive cycle. To determine that we simply looked for the cases that in the pairwise comparisons there were two dice with two wins each and two dice with one win each. That is, a tournament graph on 4 vertices has a 4-cycle if and only if the out-degrees are 2, 2, 1, 1.
May 13, 2017 at 8:30 pm
I looked for any ties in which case I marked it a tie and moved on the the next set of dice, and when there were no ties I tried all orders to get an intransitive sequence. This sounds equivalent to what you described but I just less efficient.
Results:
Fraction of ties are dropping as expected, but fractions having an intransitive cycle appear to still be increasing.
———————-
n=50, k=4
ntest=100000
tie=0.061320 intransitive=0.386040
———————-
n=100, k=4
ntest=100000
tie=0.031030 intransitive=0.389090
———————-
n=150, k=4
ntest=100000
tie=0.020720 intransitive=0.388750
———————-
n=200, k=4
ntest=100000
tie=0.015220 intransitive=0.391380
———————-
n=250, k=4
ntest=100000
tie=0.011780 intransitive=0.392990
I did a factor of 100 more tests, so roughly considering Poisson statistics I’d expect factor 10 improvement. The 1 sigma difference from before turned into 9 sigma.
Is there any reason to believe it would fluctuate around instead of just approaching the limit?
May 13, 2017 at 9:24 pm
Just to check, is this for the original multiset model or for the random-sequence-conditioned-on-sum model?
May 14, 2017 at 12:30 am
Good point. I am generating proper dice, but have not been consistent with the random selection.
The calculations I did a few posts back with n=6 k>=3, I constructed all the multisets and uniformly select from them.
For the calculations here with large n and k=4, I still generate random proper dice, but it would only be uniform sampling in random-sequence-conditioned-on-sum. I (possibly incorrectly) assumed this is what they used for the large n=200 dice calculations. This would indeed give a distribution different from uniformly sampling the multisets.
As n gets larger, would the difference of these distributions (for calculating the fraction of intransitives) become negligible?
Since there is a constraint, I randomly select n-1 values from [1,n], then determine the last value from the constraint if it is in range (otherwise toss the results and try again).
https://pastebin.com/j6hF0eWL
I actually dont know how to construct an algorithm to uniformly randomly select a constrained multiset without constructing all of them.
On another note. I noticed a stupid off-by-one error in my code when checking for ties (I accidentally never checked for ties with the last die). Fixing that roughly doubles the fraction of ties. But now my numbers don’t match the paper. However, this does then lower the fraction of intransitives.
So I can’t seem to match the paper now. Maybe they selected uniformly from the multisets somehow and this explains the difference?
I’d be curious to see the details of how that table was calculated.
I’m currently rerunning the calculation with 100000 tests.
May 13, 2017 at 12:16 pm |
Let me elaborate a little on the last section of the post. The aim is to show that for a typical , if
, if  is a random die, then the probability that
is a random die, then the probability that 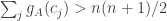 is roughly 1/2.
is roughly 1/2.
Let me define a purely random die to be one where we just choose a sequence uniformly from![[n]^n](https://s0.wp.com/latex.php?latex=%5Bn%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . So if
. So if  is a purely random die, we are interested in the event
is a purely random die, we are interested in the event ![P[X|Y]](https://s0.wp.com/latex.php?latex=P%5BX%7CY%5D&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where  is the event that
is the event that  and
and  is the event that
is the event that 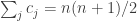 .
.
So it’s enough to understand the joint distribution of the random variables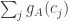 and
and  . This we would expect to be close to a 2D normal distribution.
. This we would expect to be close to a 2D normal distribution.
Before I go any further, are there any obvious examples of dice for which the probability is far from 1/2? What if, say,
for which the probability is far from 1/2? What if, say,  with probability 1/3$ and (approximately)
with probability 1/3$ and (approximately) 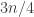 with probability 2/3? Then
with probability 2/3? Then 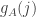 is
is  for
for 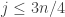 and
and  for
for  (roughly speaking). But we have already seen (not yet with a complete proof, but I’m sure it’s OK) that the entries
(roughly speaking). But we have already seen (not yet with a complete proof, but I’m sure it’s OK) that the entries 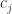 are approximately uniform, so the expectation of
are approximately uniform, so the expectation of 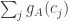 will be roughly
will be roughly 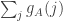 , which is
, which is  , which, if I’d been more careful, would be
, which, if I’d been more careful, would be 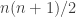 .
.
It’s beginning to look to me as though every die beats about half the others, but I’ll need to think a bit about whether that’s reasonable.
May 13, 2017 at 5:08 pm
It helps to think about the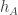 rather than
rather than 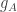 . Recall that
. Recall that 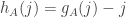 . Recall also that
. Recall also that 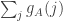 is
is
![\sum_i\sum_j\mathbf 1_{[a_i\leq j]}=\sum_i(n-a_i+1)](https://s0.wp.com/latex.php?latex=%5Csum_i%5Csum_j%5Cmathbf+1_%7B%5Ba_i%5Cleq+j%5D%7D%3D%5Csum_i%28n-a_i%2B1%29&bg=ffffff&fg=333333&s=0&c=20201002)
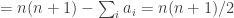 ,
,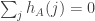 .
.
so
So if we now fix and let
and let  be random, then
be random, then 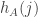 is a random variable with mean zero. Therefore, when we add lots of these together, we expect normal-type behaviour most of the time, but not so much if
is a random variable with mean zero. Therefore, when we add lots of these together, we expect normal-type behaviour most of the time, but not so much if 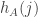 is zero almost all the time.
is zero almost all the time.
So I think a sufficient condition for to beat roughly half the other dice is going to be that
to beat roughly half the other dice is going to be that 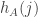 is not zero too much, and that should certainly happen for almost all
is not zero too much, and that should certainly happen for almost all  .
.
The reason it should be true is that if is purely random, then the distribution of the pair
is purely random, then the distribution of the pair 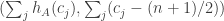 ought to be roughly a 2D normal distribution with mean
ought to be roughly a 2D normal distribution with mean 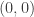 . But then fixing the second variable to be zero should lead to a normal distribution in the first, which has a probability 1/2 of being positive.
. But then fixing the second variable to be zero should lead to a normal distribution in the first, which has a probability 1/2 of being positive.
A bit of work would be needed to make this rigorous, but there’s a lot known about the speed of convergence to a normal distribution of sums of bounded independent random variables, so it ought to be doable.
May 18, 2017 at 4:33 pm
Let me try to add a bit more details on this. If is fixed and
is fixed and  is random, then
is random, then 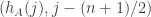 is a 2-dimensional random vector with mean
is a 2-dimensional random vector with mean 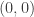 . By Multidimensional Central Limit Theorem https://en.wikipedia.org/wiki/Central_limit_theorem#Multidimensional_CLT , the (scaled) sum of N independent copies of it converges to 2D normal distribution as N goes to infinity, which would imply that the conditional sum of
. By Multidimensional Central Limit Theorem https://en.wikipedia.org/wiki/Central_limit_theorem#Multidimensional_CLT , the (scaled) sum of N independent copies of it converges to 2D normal distribution as N goes to infinity, which would imply that the conditional sum of  has a probability
has a probability  of being positive, and the probability
of being positive, and the probability  of being
of being  .
.
The problem is that, if is fixed, then
is fixed, then  is fixed as well, so we have “just”
is fixed as well, so we have “just”  copies of our random vector, not as much as we want. So, indeed, the question is about speed of convergence. Let
copies of our random vector, not as much as we want. So, indeed, the question is about speed of convergence. Let  be random variable taking values
be random variable taking values  with equal chances, where
with equal chances, where  . (We assume that
. (We assume that  , so that
, so that  .) Then
.) Then ![E[H_A]=0](https://s0.wp.com/latex.php?latex=E%5BH_A%5D%3D0&bg=ffffff&fg=333333&s=0&c=20201002) and
and 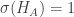 . Then, by Berry–Esseen theorem, https://en.wikipedia.org/wiki/Berry%E2%80%93Esseen_theorem
. Then, by Berry–Esseen theorem, https://en.wikipedia.org/wiki/Berry%E2%80%93Esseen_theorem
 , where
, where 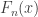 is the cdf of (scaled) sum,
is the cdf of (scaled) sum,  is the cdf of standard normal distribution, and
is the cdf of standard normal distribution, and  .
.
So, we need to show that . In fact, this is not always the case. For example, with
. In fact, this is not always the case. For example, with  ,
, 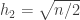 , and
, and  , we have
, we have ![E[H_A]=0](https://s0.wp.com/latex.php?latex=E%5BH_A%5D%3D0&bg=ffffff&fg=333333&s=0&c=20201002) and
and 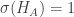 , but
, but  . However, for “typical” dice
. However, for “typical” dice  we would expect
we would expect  , which would imply the result.
, which would imply the result.
May 18, 2017 at 4:35 pm
Is it possible to preview the comment before posting? If I could, I would correct misprints like $\latex E[H_A]=0$ to![E[H_A]=0](https://s0.wp.com/latex.php?latex=E%5BH_A%5D%3D0&bg=ffffff&fg=333333&s=0&c=20201002) , etc.
, etc.
May 18, 2017 at 5:42 pm
Unfortunately there is no preview facility, but I am happy to do these corrections. Let me know if I’ve missed any.
May 19, 2017 at 10:00 am
Just search and replace \latex to latex. For now, I do not see the corrected text, and still see message “Your comment is awaiting moderation”.
The last step in my argument (control of maximal hj for a typical dice) seems to be easy. However, to make the argument fully rigorous, we need to refer to something like Berry–Esseen theorem (that is, control of speed of convergence to normal distribution), but for random vectors. I am sure this should be classical. Anybody knows the reference?
May 19, 2017 at 10:36 am
Sorry, your comment was indeed in the moderation queue (because it had two links) and I’ve now accepted it. Before a recent redesign, WordPress used to display to me the number of comments in the moderation queue, so I could spot when that number had increased and deal with it immediately. Unfortunately that feature has been removed, so it takes me longer to notice. If anyone does have a comment moderated, please feel free to let me know. (I can always delete any “I have a mod-queue comment” comments after they have served their purpose.)
May 13, 2017 at 4:28 pm |
Hello Professor Gowers,
Not sure if these are exactly what you asked for or if they’re still helpful, but here are three images showing different properties of the length 300 sequences.
Here we are assuming that your new hA sequences are the same as the old Vs from the previous post.
This first image is 100 raw sequences of length 300 where the sum of the sequence is 45150:
https://drive.google.com/file/d/0B8z2ZOOo7rKRQ3B4eHZPckp0elk/view?usp=sharing
This second image contains 100 of the calculated v sequences:
https://drive.google.com/file/d/0B8z2ZOOo7rKRNzRSbm8xOE5xZWc/view?usp=sharing
Finally, we include an image that just plots the sign(v) for the same 100 sequences:
https://drive.google.com/file/d/0B8z2ZOOo7rKRbTJoRzVVLXBqdG8/view?usp=sharing
We thought it was interesting that the long runs of same sign ( +, -, or 0 ) are not terribly rare.
If you’d like aggregate statistics for any of these properties ( count of runs by sign, or length of runs, or histograms of number of sign changes ) we have those as well.
May 13, 2017 at 5:37 pm |
These are comments on the first May 12 post.
In fact, I think that if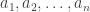 are chosen independently and uniformly from
are chosen independently and uniformly from ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , then the conditional probability that
, then the conditional probability that 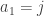 given that the average of the
given that the average of the 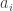 is exactly
is exactly 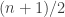 approaches uniform in some reasonable sense as
approaches uniform in some reasonable sense as  .
.
The question is really about the distribution of the face values over all the dice. I generated 1000 dice with 100 sides. The tallies of the 100,000 values look very uniform; they range from 929 to 1078 without any apparent tendency toward lower counts for either the small values near 1 or the large values near 100.
Here is a heuristic argument. The conditional probability is, by Bayes, equal to
is, by Bayes, equal to
 Here
Here 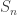 and
and 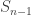 are the sums of
are the sums of  and
and 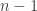 iid random variables uniform on
iid random variables uniform on ![[n].](https://s0.wp.com/latex.php?latex=%5Bn%5D.&bg=ffffff&fg=333333&s=0&c=20201002) Now
Now 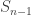 is approximately normal with mean
is approximately normal with mean  and
and  is within
is within 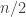 of that, which is about
of that, which is about 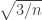 units of standard deviation. So, for large
units of standard deviation. So, for large  , the probability that
, the probability that  and the probability that
and the probability that  are roughly equal. Treating their quotient as 1, gives the approximation
are roughly equal. Treating their quotient as 1, gives the approximation 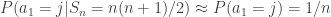 .
.
Also, there is a minor correction to make: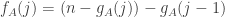 rather than
rather than  .
.
Minor correction now made — thanks.
May 13, 2017 at 6:29 pm |
I now realize that something I was hoping for is (i) probably false and (ii) not necessary.
What I hoped was that for almost all pairs of dice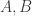 , the random variables
, the random variables 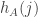 and
and 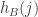 (where
(where  is chosen uniformly from
is chosen uniformly from 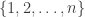 ) would be uncorrelated.
) would be uncorrelated.
One way of expressing that would be to say that the average

should be small.
But if we expand this out, we are looking at the average over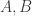 of
of
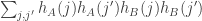 .
. and random
and random  ,
, 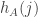 and
and  are positively correlated when
are positively correlated when  and
and 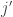 are close, and negatively correlated when they are far away. But that should then mean that if
are close, and negatively correlated when they are far away. But that should then mean that if 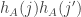 is positive, it’s more likely that
is positive, it’s more likely that  and
and 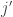 are close, and hence more likely that
are close, and hence more likely that  is positive. So I would expect the average above not to be small.
is positive. So I would expect the average above not to be small.
Furthermore, we have good reason to believe, and experiments to back it up, that for fixed
Why doesn’t this necessarily matter? It’s because what we care about is the marginal of the joint distribution of
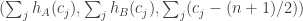
 , then for
, then for 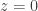 we have a standard 2D normal, but for other values of
we have a standard 2D normal, but for other values of  there is a tendency for both
there is a tendency for both  and
and  to be close to
to be close to  , which means that there is indeed a correlation between the first two variables. (One can of course establish that more rigorously by integrating over
, which means that there is indeed a correlation between the first two variables. (One can of course establish that more rigorously by integrating over  .)
.)
when we condition on the third coordinate being zero. If we assume that the joint distribution of all three variables is roughly normal, we are asking that the restriction of this distribution to the xz-plane should be rotation invariant. That is perfectly consistent with a correlation between the first two variables. If, for example, the density function is proportional to
I still haven’t got my head round what it would be saying if conditioning on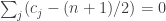 magically killed the correlation between
magically killed the correlation between  and
and 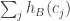 , so I don’t have a heuristic argument for why it might be the case.
, so I don’t have a heuristic argument for why it might be the case.
May 13, 2017 at 11:49 pm |
I’ve realized that there is a simple spectral characterization of quasirandom tournaments. One can associate with any tournament an antisymmetric matrix , where
, where 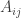 is 1 if there’s an arrow from
is 1 if there’s an arrow from  to
to  , -1 if there’s an arrow from
, -1 if there’s an arrow from  to
to  , and 0 if
, and 0 if  . (We can also allow ties and put zeros.)
. (We can also allow ties and put zeros.)
An even cycle in the sense of Chung and Graham corresponds to a rectangle of entries of which an even number are 1s, or equivalently a rectangle for which the product of the entries is 1. So the number of (labelled) even cycles is just the fourth power of the box norm of the matrix, which is the sum of the fourth powers of the absolute values of its eigenvalues.
Unlike in the graph case, where we have a symmetric adjacency matrix, the eigenvalues are not real. In fact, they are purely imaginary. So the spectral condition is that the sum of the fourth powers of the absolute values of the eigenvalues is small, which is easy to show is equivalent to the condition that the largest eigenvalue is small.
However, I don’t think this observation is going to help, as I can’t see a way of bounding the size of the largest eigenvalue that’s easier than trying to prove that even 4-cycles occur with the right frequency. (There’s also the small matter that this might not actually be true.)
May 14, 2017 at 11:33 am
Just wanted to note that something related was done here
Click to access tournament.pdf
May 14, 2017 at 3:26 pm
Thanks for pointing that out — I’m a bit surprised that Chung and Graham left it as an open problem though …
May 14, 2017 at 4:18 am |
Some basic results around the general conjecture:
I chose m=1000 dice with 300 sides uniformly at random, imposing the condition that all sides sum to . Performing a comparison between each of them, we produce an
. Performing a comparison between each of them, we produce an 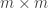 matrix where the color of each entry
matrix where the color of each entry  indicates if die
indicates if die  beat die
beat die  (blue), lost (red), or tied (black). As can be seen in the attached link, each die beats roughly 1/2 the other dice… More exactly, across the 1000 dice, the proportion each die won was:
(blue), lost (red), or tied (black). As can be seen in the attached link, each die beats roughly 1/2 the other dice… More exactly, across the 1000 dice, the proportion each die won was:
Mean: 0.497864
Variance: 0.000278389504
https://github.com/wbrackenbury/intransDice
Per Tim’s suggestion, I plan on investigating more unusual dice next that might bend these rules (the standard die with sequence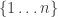 should tie all dice with the condition of summing to
should tie all dice with the condition of summing to  )
)
In terms of computational interest, if someone could take a look at the procedure I’ve coded for generating the dice, I would appreciate it… I generated random dice from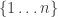 and simply selected the ones that met the sum condition, which took ~2+ hours on my laptop. If it would not interfere with the randomness, however, it would be more computationally feasible to start with the standard die and then “shuffle” the values of the faces. In this case, 1 is subtracted from one face and added to another face, and this is repeated enough times that the values should be shuffled somewhat, but the die itself still sums to the same value (function “generate1()” in the code). I’ll likely investigate how well this procedure functions in producing dice of this type going forward.
and simply selected the ones that met the sum condition, which took ~2+ hours on my laptop. If it would not interfere with the randomness, however, it would be more computationally feasible to start with the standard die and then “shuffle” the values of the faces. In this case, 1 is subtracted from one face and added to another face, and this is repeated enough times that the values should be shuffled somewhat, but the die itself still sums to the same value (function “generate1()” in the code). I’ll likely investigate how well this procedure functions in producing dice of this type going forward.
May 14, 2017 at 4:22 am
Also, could someone point me to a quick tutorial on using Latex in comments?…
May 14, 2017 at 8:18 am
I gave a link above to how I am generating random dice:
https://pastebin.com/j6hF0eWL
This is quick enough in practice that the main waste of time has actually been the comparison operation as it is naively O(n^2). Once I noticed this, I rewrote some of the routines so I can calculate comparisons in O(n) time. I’ve been able to look at much larger dice now.
Could you try reproducing the k=4, n=50,100,150,200 table from the paper? I’m getting a larger fraction of ties than what they report. So it would be nice to have another check.
May 14, 2017 at 8:32 am
I looked at your code. What I gave a link to is a faster version of your die generator inside of “generate(num, n)”.
So you are using the same random distribution of dice as I am. However we should keep in mind that this is slightly different that uniformly selecting amongst all distinct dice. That is because with that generate function there are several ways to ultimately obtain the sorted die [1,1,3,5,5], and only one way to obtain [3,3,3,3,3]. I don’t know how to uniformly sample multisets with a constraint though. And, hopefully, our method is fine for large n.
May 14, 2017 at 2:14 pm
Here’s the requested LaTeX tutorial. One example should suffice. If I want to create the expression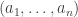 I write
I write
$ latex (a_1,\dots,a_n)$
but without the space after the first dollar sign.
May 14, 2017 at 3:49 pm
Thank you!
May 14, 2017 at 10:05 am |
Here’s a way of generating random multisets: I think it works but haven’t carefully checked that the distribution is uniform. I’ll illustrate it in the case . I first choose a random subset of
. I first choose a random subset of ![[2n-1]](https://s0.wp.com/latex.php?latex=%5B2n-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) (by randomly permuting the set and seeing where the first
(by randomly permuting the set and seeing where the first  elements end up). Then I fill in the remaining spaces with the numbers
elements end up). Then I fill in the remaining spaces with the numbers  . That gives me a sequence such as
. That gives me a sequence such as
I then stick a 1 on the front to get
Now I interpret the asterisks as telling me the number of each number that I need to take. For example, here we end up with the multiset . I chose two 3s because 3 was followed by two asterisks.
. I chose two 3s because 3 was followed by two asterisks.
Then to get dice one needs to discard sequences that don’t add up to the correct total.
May 14, 2017 at 11:35 pm |
Here are the latest results, after fixing the tie detection and also speeding up the comparisons so I can go to higher n. As the fraction of ties drops to zero, this lines up with my previous calculation. But it would be nice if someone could double check, because the fraction of ties is roughly twice what is reported in the paper. I’m not sure what they did different in the paper. Currently one guess is that they used a different distribution of selecting the dice and the difference really matters for ties for some reason. It would be nice if someone could verify.
———————-
n=50, k=4, ntest=100000
tie=0.119660 intransitive=0.353030
———————-
n=100, k=4, ntest=100000
tie=0.058790 intransitive=0.375170
———————-
n=150, k=4, ntest=100000
tie=0.039510 intransitive=0.380530
———————-
n=200, k=4, ntest=100000
tie=0.029060 intransitive=0.382880
———————-
n=250, k=4, ntest=100000
tie=0.023500 intransitive=0.384040
———————-
n=300, k=4, ntest=100000
tie=0.020200 intransitive=0.388710
———————-
n=400, k=4, ntest=100000
tie=0.014500 intransitive=0.391730
———————-
n=500, k=4, ntest=100000
tie=0.011690 intransitive=0.389740
———————-
n=700, k=4, ntest=100000
tie=0.008530 intransitive=0.391260
———————-
n=1000, k=4, ntest=100000
tie=0.005600 intransitive=0.390010
I will look into trying to randomly sample from multisets. Any idea I can think of involves tossing many of the results away, which is really inefficient. One straight forward way is to:
– randomly select an integer uniformly from [0,n]
– do this n times to build a list L
– treat the i-th entry (index starting with 1) as stating there are L[i] of number i
– toss if sum L[i] != n
– toss if sum i*L[i] != n*(n+1)/2
There is only one allowed sequence for each multi-set, and any sequence is equally likely, so this should be uniform. It will just be very inefficient computation wise.
This can be improved by reducing the initial range selecting for some of the entries (selecting n 1’s will always be rejected). And also attempting to pull the first constraint in for the final entry. But the last constraint will still toss a lot.
Gower’s method constructs the list to guarantee sum L[i] = n. So that is more efficient. But the last check will still toss a lot. It looks uniform, but I’d have to think about that a bit more.
I may try running the slow multiset method on small n to see if this even effects the results.
May 15, 2017 at 12:03 am
I’m pretty sure the method I suggested is uniform. Indeed, given a subset of![[2n-1]](https://s0.wp.com/latex.php?latex=%5B2n-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) of size
of size  , then procedure I described defines a multiset with
, then procedure I described defines a multiset with  elements (with multiplicity). Conversely, given a multiset with
elements (with multiplicity). Conversely, given a multiset with  elements we can recover a subset of
elements we can recover a subset of ![[2n-1]](https://s0.wp.com/latex.php?latex=%5B2n-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) with
with  elements. Again I’ll illustrate by example: given, say, the multiset
elements. Again I’ll illustrate by example: given, say, the multiset  , I create the sequence
, I create the sequence
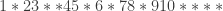 .
.
All I did there was put asterisks after each number with the number chosen to be the multiplicity of that number in the multiset.
I had an idea for how one might try to generate random multisets that add up to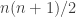 swiftly and almost uniformly. I don’t have a rigorous proof that it works, but it feels as though it might. It’s a very standard method of trying to generate random combinatorial structures efficiently: devising a suitable random walk. Given a multiset represented using numbers and asterisks, we can randomly choose a certain number of asterisks that appear just after numbers (other than 1) and swap them with those numbers. And then we can do the same but with asterisks that appear just before numbers. If we choose the same number of swaps both times, then we add and subtract the same number. And if we do this swapping operation a few times, then we ought to shuffle things up fairly quickly.
swiftly and almost uniformly. I don’t have a rigorous proof that it works, but it feels as though it might. It’s a very standard method of trying to generate random combinatorial structures efficiently: devising a suitable random walk. Given a multiset represented using numbers and asterisks, we can randomly choose a certain number of asterisks that appear just after numbers (other than 1) and swap them with those numbers. And then we can do the same but with asterisks that appear just before numbers. If we choose the same number of swaps both times, then we add and subtract the same number. And if we do this swapping operation a few times, then we ought to shuffle things up fairly quickly.
This is just one idea for a random walk — there may well be better ones.
May 15, 2017 at 1:35 am
The data in our paper is for the multiset dice model. I just ran a small test with n=50 and 5000 samples of four dice. There was at least one tie in about 12% of the samples, very close to your result. I have an idea why there are more ties with the n-tuple model. That is because the dice with fewer repetitions of face values (like the standard die that has no repetitions) are more likely to tie other dice and at the same time there are more versions of them in the n-tuples than in the multisets. For example, there are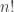 versions of the standard die in the n-tuple model but many fewer when there are a lot of repeated face values.
versions of the standard die in the n-tuple model but many fewer when there are a lot of repeated face values.
May 15, 2017 at 4:01 am
I tried to just brute force with the naive method, but it was way too inefficient.
So I used your 2n-1 method, but adapted it slightly (I didn’t do a full permutation).
– randomly select n-1 distinct numbers in range(2n-1)
– these “markers” separate the range into n regions
– count the number of unselected spots in each region -> gives multiplicity of each number on the die
– create die from that, and start over if sum is not n(n+1)/2
The changes due to the distribution are easily noticeable for small n, but surprisingly (to me at least) the effects can still be seen for larger n.
This multiset selection method is significantly slower than the distribution Will and I were using. The tests are slow enough that I had to drop down to only doing 1000 tests per n, but here are some preliminary results:
Method B: “uniform in multisets” distribution
———————
n=50, k=4, ntest=1000
tie=0.071000 intransitive=0.359000
———————
n=100, k=4, ntest=1000
tie=0.026000 intransitive=0.394000
———————
n=150, k=4, ntest=1000
tie=0.023000 intransitive=0.395000
———————
n=200, k=4, ntest=1000
tie=0.023000 intransitive=0.393000
for comparison, here was the results from the other distribution
Method A: “uniform in n numbers from [1 to n] conditioned on sum”
———————
n=50, k=4, ntest=100000
tie=0.119660 intransitive=0.353030
———————
n=100, k=4, ntest=100000
tie=0.058790 intransitive=0.375170
———————
n=150, k=4, ntest=100000
tie=0.039510 intransitive=0.380530
———————
n=200, k=4, ntest=100000
tie=0.029060 intransitive=0.382880
…
n=1000, k=4, ntest=100000
tie=0.005600 intransitive=0.390010
So even at n=100 the effects in the number of ties is still noticeable. However both show the fraction which are ties dropping to zero, and the fraction which are intransitive going to something ~ 0.39
I’m hoping the trend means the distribution does, in larger n, eventually not matter as much. I’ll try to get some more statistics, but it is going to be slow unless we come up with a faster way to generate large dice.
The paper explored different types of dice. But here, the results are for the same types of dice (“proper dice”), just a different sampling over them. Unless this difference dies out for large n, it feels like a hint about what is important for this conjecture.
Your randomwalk idea is similar to Will’s pip moving idea. That would be much more efficient if it turned out to be uniform. My hunch is that is not the case.
If we consider a graph of all the possible outcomes, and our choice of randomwalk algorithm dictates the edges that connect the outcomes, then if each step chooses uniformly among the possible edges, I don’t think the result would be uniform unless the graph has uniform degree. Consider the die [3,3,3,3,3]. In Will’s pip moving idea, we’d only have one place to move: [2,3,3,3,4]. In your idea, we’d have 123*****45, and can only end up moving to 123*****45,12*3***4*5, or 12**3*4**5. While a die like 1*2*3*4*5*, would have more options.
May 15, 2017 at 11:42 am
I find this number 0.39 that’s consistently showing up quite worrying. Have we got to the point where we can be fairly confident that the tournament is not quasirandom, at least in the case of random sequences with constrained sums?
May 15, 2017 at 11:47 am
See comment below for a random walk that converges to the uniform distribution (but I don’t have a proof that it does so quickly).
May 15, 2017 at 2:25 pm
To generate random multisets for the results in our paper we used Mathematica. The function RandomSample[Range[2 n – 1], n] gives a random subset of![[2n-1]](https://s0.wp.com/latex.php?latex=%5B2n-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) of size n. There is a bijection between multisets of
of size n. There is a bijection between multisets of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and subsets of
and subsets of ![[2n-1]](https://s0.wp.com/latex.php?latex=%5B2n-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) , where the multiset
, where the multiset  corresponds to the subset
corresponds to the subset  with
with 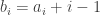 . The sum constraint
. The sum constraint  becomes
becomes  . So we generate random subsets until we get one whose sum is
. So we generate random subsets until we get one whose sum is 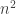 , and then we convert it to a multiset. It’s not terribly efficient, but even on an old laptop it takes about 1 second to generate 100 dice with 100 sides.
, and then we convert it to a multiset. It’s not terribly efficient, but even on an old laptop it takes about 1 second to generate 100 dice with 100 sides.
May 15, 2017 at 12:08 am |
I’ve written a bit of code that confirms my hunch that for a typical pair of random dice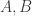 , the random variables
, the random variables 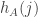 and
and 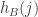 are quite strongly correlated. Here are some correlations obtained with sequences of length 1000: -0.23, 0.14, 0.71, -.13, -0.45. And I tried it once with sequences of length 10000 and got a correlation of 0.42.
are quite strongly correlated. Here are some correlations obtained with sequences of length 1000: -0.23, 0.14, 0.71, -.13, -0.45. And I tried it once with sequences of length 10000 and got a correlation of 0.42.
May 15, 2017 at 2:39 am |
One advantage of multisets over tuples that just occurred to me is that if we represent the set of dice as the integer points in a polytope, then with multisets, tying (respectively beating)
tying (respectively beating)  is just a quadratic equation (respectively inequality.) With tuples, the polytope is simpler but the condition for
is just a quadratic equation (respectively inequality.) With tuples, the polytope is simpler but the condition for  to tie/beat
to tie/beat  seems to be much more complicated.
seems to be much more complicated.
To wit, we can represent multiset dice as the integer points in the polytope . (Here
. (Here  is the number of sides showing
is the number of sides showing  .) If
.) If 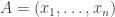 and
and  , then
, then 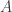 ties
ties  when
when  , and
, and  beats
beats  if we replace “equals” by “less than.” So to say that ties are rare is to say that few of the integer points in
if we replace “equals” by “less than.” So to say that ties are rare is to say that few of the integer points in 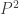 lie on a particular quadric hypersurface, which seems plausible enough though maybe just as difficult to prove as the original statement.
lie on a particular quadric hypersurface, which seems plausible enough though maybe just as difficult to prove as the original statement.
Tuple dice are just the integer points in the dilated and shifted standard simplex . But I don’t see how to express the condition of
. But I don’t see how to express the condition of  tying
tying  as any fixed-degree polynomial in the coordinates.
as any fixed-degree polynomial in the coordinates.
May 15, 2017 at 8:36 am |
[…] polymath-style project on non transitive dice (Wikipedea) is now running over Gowers blog. (Here is the link to the first […]
May 15, 2017 at 8:45 am |
Meta remark: as there is interest and nice participation, perhaps this should be considered as an official “polymath”?
May 15, 2017 at 1:52 pm
I can’t quite decide, or even (in the meta spirit) decide on a suitable decision procedure, but if things continue like this, then I agree that that will probably be the right thing to do.
May 15, 2017 at 9:23 am |
I was trying to think of a heuristic for when two dice beat each other, and came across a bit of a puzzle.
Handwavy yes, but here is the start:
Without the sum constraint, the die with the larger average is very likely to win (there are exceptions, but they are rare)
Not handwavy:
Because it only matters how the values of a roll compare (greater, equal, or less than), it doesn’t matter how large the differences are, so any monotonically increasing function over positive numbers, when applied to all values on the dice, should not change the comparison. For example adding a constant to all values on both dice, or squaring the values. Such a transformation will not change which die “beats” which.
Putting those together:
That suggests we could rank the constrained dice by the average of their square entries. But that would mean A beats B, and B beats C, implies it is more likely that A beats C than C beats A.
So something went wrong.
The handwavy part is true at least in some context. If we look at the tuple model without constraints, the average does strongly predict which die wins (at n=100, it is already ~ 98% correct).
However, the average of the squares, in the constrained tuple model, does not appear to predict anything (appears completely random).
Is this something special about the constrained sum dice?
I don’t really understand why the “average value” heuristic works in one case and gives zero information in the second case.
Anyway, maybe playing with “transformed” dice can help come up with new approaches.
May 15, 2017 at 11:38 am
I think a problem with the handwavy part is that the average is not a robust measure under arbitrary increasing transformations. To give a silly example, if it so happens that the maximum element of is bigger than that of
is bigger than that of  , but
, but  beats
beats  , we can make the average of
, we can make the average of  as large as we like by applying an increasing function that massively increases the largest element and leaves all the rest as they are. That’s a very special example, obviously, but the basic idea can be implemented in lots of ways. For example, your squaring idea gives an artificial extra weight to the larger values on the dice, so it’s quite similar.
as large as we like by applying an increasing function that massively increases the largest element and leaves all the rest as they are. That’s a very special example, obviously, but the basic idea can be implemented in lots of ways. For example, your squaring idea gives an artificial extra weight to the larger values on the dice, so it’s quite similar.
May 15, 2017 at 11:59 am |
Here’s a random walk that converges to the uniform distribution on multisets that add up to a given total. The (again standard) idea is to make the graph of the random walk regular by allowing loops. We then have a suite of moves, and we choose a random one. If it can’t be applied, we just don’t apply it.
So in my version with asterisks, one way we could do this is as follows. We randomly choose two places and
and  . We then consider exchanging whatever is in place
. We then consider exchanging whatever is in place  with whatever is in place
with whatever is in place 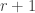 and also whatever is in place
and also whatever is in place  with whatever is in place
with whatever is in place 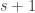 . If this results in a new multiset with the same sum, then we do both exchanges, and otherwise we leave the multiset as it is. Thus, we stick around for longer at multisets with fewer options, and that compensates for its being less easy to arrive at those multisets.
. If this results in a new multiset with the same sum, then we do both exchanges, and otherwise we leave the multiset as it is. Thus, we stick around for longer at multisets with fewer options, and that compensates for its being less easy to arrive at those multisets.
Again, there are many ways one could randomly change a multiset. Clearly the above approach will need at least steps to have any chance of mixing properly, and probably quite a few more than that. If we’re lucky, it might be about
steps to have any chance of mixing properly, and probably quite a few more than that. If we’re lucky, it might be about 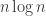 , as it is for the random walk in the discrete cube.
, as it is for the random walk in the discrete cube.
Would that represent a speedup? Well, to generate a random subset of![[2n-1]](https://s0.wp.com/latex.php?latex=%5B2n-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) of size
of size  takes roughly linear time, and if we then constrain the sum, we’ll be accepting sequence with probability roughly
takes roughly linear time, and if we then constrain the sum, we’ll be accepting sequence with probability roughly  . So the whole thing takes quadratic time to generate a random multiset. (I’m writing this without checking carefully what I’m saying.) If the random walk above, or something similar, converges in time
. So the whole thing takes quadratic time to generate a random multiset. (I’m writing this without checking carefully what I’m saying.) If the random walk above, or something similar, converges in time 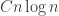 , then that’s a considerable saving.
, then that’s a considerable saving.
May 15, 2017 at 12:01 pm
If we can’t be bothered to estimate rigorously how long the walk takes to converge to uniform, we could at least test it by generating multisets this way and comparing the resulting statistics with those obtained from the uniform distribution.
May 15, 2017 at 2:07 pm
It occurs to me that this kind of idea could speed up the algorithms for the sequence model too. At the moment P. Peng’s procedure for generating a random die is to create a purely random sequence of length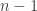 and then let the last entry be whatever it needs to be to make the sum equal to
and then let the last entry be whatever it needs to be to make the sum equal to 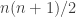 , discarding the sequence if that last entry isn’t between 1 and
, discarding the sequence if that last entry isn’t between 1 and  .
.
Now the standard deviation of the sum of numbers chosen uniformly from
numbers chosen uniformly from ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) is of order
is of order 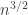 , so the probability of retaining the sequence is of order
, so the probability of retaining the sequence is of order  (since the “target” is of width
(since the “target” is of width  ). Thus, the time taken is going to be round about
). Thus, the time taken is going to be round about 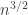 (maybe with a log factor thrown in as the time taken to get each random entry of
(maybe with a log factor thrown in as the time taken to get each random entry of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) ).
).
An alternative approach would be to start with the sequence and then take a random walk as follows. At each step, we randomly choose two coordinates
and then take a random walk as follows. At each step, we randomly choose two coordinates 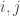 and a number
and a number 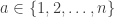 . We then add
. We then add  to the
to the  th coordinate and subtract
th coordinate and subtract  from the
from the  th coordinate, and move to the resulting sequence if the two new coordinates are still within the range 1 to
th coordinate, and move to the resulting sequence if the two new coordinates are still within the range 1 to  . If they are not, then we simply stay at the current sequence.
. If they are not, then we simply stay at the current sequence.
The probability that any given move will be accepted is always going to be bounded below by an absolute constant (I’m almost sure, though I haven’t sat down and proved this). I’m also pretty confident that this walk is enough like the standard random walk on the discrete cube that it will be close to uniform in total variation distance after order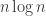 steps. So there is a potential saving of
steps. So there is a potential saving of 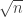 , which could be useful if the sequences are of length 1000.
, which could be useful if the sequences are of length 1000.
May 15, 2017 at 10:04 pm |
You suggest that a random dice A would have probability tending to 1/2 of beating a random other dice B, but is it not possible that even the worst choices of dice have probability tending to 1/2?
More formally, let p_N be the largest probability of A>=B (where B is chosen uniformly at random from N-dice), where A is an N-die. Is it plausible that p_N tends to 1/2?
Then it would certainly be true for a random die also.
May 15, 2017 at 10:51 pm
My computations say that given any distribution A on the integers 1 to 80 with mean 40.5, if we choose a random 80-dice B, the probability that A >= B is in the range 0.505475 to 0.506988.
The lower bound is attained by the distribution which can only take either 20 or 80, and the upper bound can take only 1 or 59.
May 15, 2017 at 11:07 pm
Roughly why I think this is true is that it seems the probabilities of a face of a random die being any value in the range 1 to N are all 1/N+O(1/N^2), so the probability of being less than equal to j is j/N+O(1/N) for all j, so the probability of being less than equal to A is E(A)/N+O(1/N)=1/2+O(1/N).
May 15, 2017 at 11:45 pm
I agree, and in fact suggested more or less this in an earlier comment. I think the only obstacle to a die beating roughly half of all the others is if it is very close to the die , which then creates lots of ties. Or are you saying that even when there are lots of ties, roughly half of the dice that do not tie should beat the given die and half of them should lose?
, which then creates lots of ties. Or are you saying that even when there are lots of ties, roughly half of the dice that do not tie should beat the given die and half of them should lose?
May 16, 2017 at 3:56 am
Yep, this was nonsense.
May 16, 2017 at 3:41 am |
I have nothing directly to add to the above (other than a great deal of enthusiasm!), but I will add “indirectly” that interesting generalizations of intransitivity to ternary relations also exist. Take for example the following set of five dice that I came up with a few years ago:
D_0 = {0,9,10,19,23,26,31,38,42,47,54,55,64,65,72,77,81,88,93,96}
D_1 = {1,8,13,16,20,29,30,39,43,46,51,58,62,67,74,75,84,85,92,97}
D_2 = {4,5,12,17,21,28,33,36,40,49,50,59,63,66,71,78,82,87,94,95}
D_3 = {2,7,14,15,24,25,32,37,41,48,53,56,60,69,70,79,83,86,91,98}
D_4 = {3,6,11,18,22,27,34,35,44,45,52,57,61,68,73,76,80,89,90,99}.
Here, given any three of the dice, D_x, D_y, D_z, it is the case that die D_(2*(x+y+z)) (mod 5) will roll a higher number than both of the other two dice with probability 1334/4000 when all three dice are rolled together, while each of the other two dice will roll the highest number with probability only 1333/4000. Consequently, every die beats every other die in some three-way contest.
Should any of you want, perhaps generalizing your questions to ternary relations over a set of five dice would be possible? Irrespective, it is great to see intransitive dice getting so much love!
May 16, 2017 at 8:09 pm |
We can define a simple n sided die without the condition on the sum of entries. My feeling is that the two models will be very similar w.r.t. the two main questions and in any case dropping the condition about the sum should make the problems much easier.
May 16, 2017 at 10:09 pm
I don’t think it’s true that the two models are similar with respect to the main questions. The problem is that if the sum of one die is a bit larger than average (by one standard deviation, say), then it becomes quite a bit more likely to beat other dice, so (with the help of Bayes’s theorem) knowing that A beats B and that B beats C makes it more likely that A beats C.
This paragraph comes from the paper of Conrey et al: “Finally, if we consider n-sided dice with face numbers from 1 to n but no restriction on the total, then random samples of three such dice almost never produce ties or intransitive triples. For example, in one run of 1000 triples of 50-sided dice there were three triples with a tie and three intransitive triples.”
May 16, 2017 at 10:26 pm
Hmm, so another try for an (potentially) easier to analyze model with (perhaps) the same answers is to drop the condition about the sum, but to normalize all values by dividing by the sum. (This would probably be easier to simulate.)
May 16, 2017 at 10:37 pm
According to the paper, experiments suggest that the proportion of intransitive triples drops from 1/4 to about 0.17 for that model. But it might be interesting to try to determine what this proportion actually is in the limit.
May 18, 2017 at 4:57 pm
Still another question: you can consider a model of multisets (or rather sequences) where orders matter, and, as we do, a model where order does not matter. Do we expect the same behavior for these two models.
May 16, 2017 at 11:27 pm |
Just a quick comment to say that although I have not been active on this project today, I do have a third post planned. It may take a little while to write though.
May 17, 2017 at 12:12 am |
Just to keep everyone updated, I ran tests on Dr. Gowers’ alternate method for generation of dice, i.e. “start with the sequence and then take a random walk as follows. At each step, we randomly choose two coordinates
and then take a random walk as follows. At each step, we randomly choose two coordinates  ,
, and a number
and a number 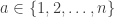 . We then add
. We then add  to the
to the  th coordinate and subtract
th coordinate and subtract  from the
from the  th coordinate, and move to the resulting sequence if the two new coordinates are still within the range 1 to
th coordinate, and move to the resulting sequence if the two new coordinates are still within the range 1 to  . If they are not, then we simply stay at the current sequence.”
. If they are not, then we simply stay at the current sequence.”
Notably, this method is much faster than the brute force method I have been using. The key question is whether this method converges to a uniform distribution with an acceptable number of steps.
I ran the algorithm with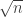 ,
,  ,
, 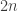 ,
, 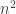 , and
, and 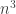 steps on the random walk for 1000 dice with 100 sides. Then, I ran the standard random generation method for 1000 dice with 100 sides.
steps on the random walk for 1000 dice with 100 sides. Then, I ran the standard random generation method for 1000 dice with 100 sides.
Comparing the total variation distance from the standard die between the 2 different generation methods produced some weird results, however, so I’m still tracking that down. I’ll try and upload my code at the github location I’ve been using (https://github/wbrackenbury/intransDice) so that people can double check my methodology. So, until I can verify the results, I would take the below with a grain of salt…
Brute Force
—————
Mean Total Variation Distance: 36.298
Variance, Total Variation Distance: 9.407196
Pip Shifting Method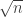 ): 5.4
): 5.4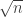 ): 24.25
): 24.25
————————
Mean TVD (
Var TVD (
Mean TVD ( ): 17.947
): 17.947 ): 122.722191
): 122.722191
Var TVD (
Mean TVD (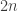 ): 19.422
): 19.422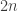 ): 132.347916
): 132.347916
Var TVD (
Mean TVD (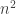 ): 21.672
): 21.672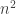 ): 133.872416
): 133.872416
Var TVD (
Mean TVD ( ): 21.484
): 21.484 ): 134.089744
): 134.089744
Var TVD (
————————
In short, as Dr. Gowers suggested, the method appears to converge between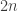 and
and 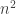 , which should be around
, which should be around 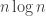 . The fact that it has such a high variance compared to the brute force method, however, seems problematic, which likely indicates a bug in my code. I’ll be working on that…
. The fact that it has such a high variance compared to the brute force method, however, seems problematic, which likely indicates a bug in my code. I’ll be working on that…
May 17, 2017 at 6:13 am
I think you accidentally committed the diceFuncs.pyc file instead of the python source.
May 17, 2017 at 6:24 am
You’re right, though I haven’t been able to commit the updated files because I was working on them from a different computer… the weird news is that, even after thoroughly debugging my code, the results still hold. I’ll find a way to commit the changes so others can figure out where I’m mistaken.
May 17, 2017 at 7:10 am
Should be updated now–the relevant functions are:
generate_pips() in testGen.py
test_results2() in testGen.py, and
test_res() in mainDice.py
The relevant pickle files needed for those were created in Python 3, so the interpreter might give you some lip about that, but otherwise, should be good to go.
May 17, 2017 at 8:57 am
It’s not clear to me what you mean here by “total variation distance”. What are you measuring?
May 17, 2017 at 9:45 am
In generate_pips, the line:
a = rd.randint(1, n)
should be in the for loop. Also a=n will never do anything in the for loop (so you were actually getting the standard die out 1/n of the time).
May 17, 2017 at 10:56 am
Ah, I think I see what you mean by “total variation distance”, but that isn’t standard usage, or what I meant. I was talking about a measure of distance between two probability distributions: the uniform distribution on -sided dice, and the distribution after a certain number of steps of the random walk. Roughly speaking, if the total variation distance is small, then any statistics you measure should give almost the same answer.
-sided dice, and the distribution after a certain number of steps of the random walk. Roughly speaking, if the total variation distance is small, then any statistics you measure should give almost the same answer.
But what you are doing is relevant, since one statistic is the average distance (in some suitable sense) from the standard die. So if you’re getting different answers for the random walk and for the genuinely uniform distribution, then that’s troubling. But since the random walk provably converges to the uniform distribution, I think there must be a mistake somewhere. Of course, it’s theoretically possible that the statistic appears to converge to one value but actually converges much later to a different value, but I’d be very surprised if that was actually what is happening here.
May 17, 2017 at 4:49 pm
Gotcha–understood. I’ll take a look at that next to ensure that the particular metric used here isn’t misleading in some way. Many thanks to P. Peng for finding the bug in the code: I have now fixed it, and ran tests for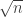 ,
,  ,
, 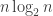 , and
, and 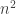 . I cut out
. I cut out  given that convergence did not change past
given that convergence did not change past 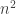 , and added in
, and added in 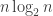 to see if the true point of convergence estimated by Dr. Gowers held as expected.
to see if the true point of convergence estimated by Dr. Gowers held as expected.
Brute Force
—————
Mean of metric: 36.298
Var of metric: 9.407196
Pip Shifting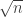 ): 5.943
): 5.943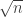 ): 6.505751
): 6.505751 ): 29.437
): 29.437 ): 10.092031
): 10.092031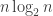 ): 36.311
): 36.311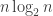 ): 9.458279
): 9.458279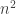 ): 36.427
): 36.427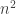 ): 9.458279
): 9.458279
—————
Mean of metric (
Var of metric (
Mean of metric (
Var of metric (
Mean of metric (
Var of metric (
Mean of metric (
Var of metric (
—————
Variance is now down to comparable levels. As such, if others agree, for future tests, I plan on generating dice via this method with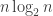 steps in the random walk, which should allow us to work much more quickly with higher sided dice. I’ll double check that these results hold true for the actual total variation distance. Pardon the ignorance, but could someone let me know which metric is the standard for TVD?
steps in the random walk, which should allow us to work much more quickly with higher sided dice. I’ll double check that these results hold true for the actual total variation distance. Pardon the ignorance, but could someone let me know which metric is the standard for TVD?
May 17, 2017 at 5:47 pm
Suppose you have a set X (in our case, the set of all -sided dice) and two probability distributions
-sided dice) and two probability distributions  and
and  . That is, given a die
. That is, given a die  , its probability of occurring is
, its probability of occurring is  in the first distribution and
in the first distribution and 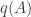 in the second. Then the total variation distance is (up to a factor 2)
in the second. Then the total variation distance is (up to a factor 2)  . It is not at all easy to estimate the total variation distance experimentally, since it requires you to sum over all dice, which becomes prohibitively expensive very quickly. Actually, I think I could probably give a formal proof, as the Markov chain in question is pretty simple. Alternatively, one can simply try out various statistical tests. For instance, one could estimate the probabilities of intransitivity and ties using the two distributions and see if the answers are more or less the same. The more tests that are passed, the more plausible it is that the two distributions are roughly the same.
. It is not at all easy to estimate the total variation distance experimentally, since it requires you to sum over all dice, which becomes prohibitively expensive very quickly. Actually, I think I could probably give a formal proof, as the Markov chain in question is pretty simple. Alternatively, one can simply try out various statistical tests. For instance, one could estimate the probabilities of intransitivity and ties using the two distributions and see if the answers are more or less the same. The more tests that are passed, the more plausible it is that the two distributions are roughly the same.
May 17, 2017 at 11:17 pm |
Haven’t seen anyone formally write down an approximate expression for the conditional probability, so here goes.
If X1, X2, …, Xn are uniformly chosen from {1, 2, …, n}, then the probability that X1 is i conditional on X1+X2+…+Xn = n(n+1)/2 is
proportional to the probability that X2+…+Xn is equal to
n(n+1)/2-i.
Now X2+…+Xn is a random variable of mean n(n+1)/2-(n+1)/2 and
variance (n-1)(n^2-1)/12.
Thus the conditional probability that X1 is i is approximately proportional to ,
, .
.
which is proportional to
So the conditional property is approximately proportional to
 . The sum of these values is clearly
. The sum of these values is clearly  , so the conditional property is approximately *equal* to
, so the conditional property is approximately *equal* to
A quick computer check verifies that these probabilities are within 10^-6 for n=80, and the cumulative probabilities are within 10^-5.
May 18, 2017 at 7:49 am |
Consider random dice . Let
. Let 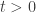 be a real number. Let
be a real number. Let  be a random dice conditioned on the relation
be a random dice conditioned on the relation
 with probability
with probability 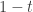 over all sides of the dice.
over all sides of the dice. a noisy version of
a noisy version of  with noise level
with noise level  . Let
. Let  be another, statistically independent from
be another, statistically independent from  random dice.
random dice.
We call
Let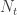 be the probability over
be the probability over 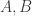 random dice and
random dice and  a random noisy version of
a random noisy version of  that
that  conditioned on
conditioned on 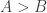 . The results for voting methods suggest that.
. The results for voting methods suggest that.
Conjecture: The following are equivalent.
For some fixed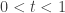 ,
,  as
as 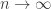 ,
,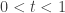 ,
,  as
as 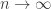 ,
, statistically independent from
statistically independent from  and
and  , the probability that
, the probability that 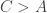 given
given  and
and  tends to 1/2 as
tends to 1/2 as  tends to infinity.
tends to infinity. random dice the tournament determined by them is pseudorandom as
random dice the tournament determined by them is pseudorandom as  tends to infinity.
tends to infinity. random dice the tournament determined by them is random as
random dice the tournament determined by them is random as  tends to infinity.
tends to infinity.
For every
Given another random dice
For every set of
For every set of
Moreover, there might be a direct simple relation between the probability in item 3 (three intransitive dice) and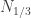 . For voting methods the various implications are quite easy.
. For voting methods the various implications are quite easy.
May 18, 2017 at 9:12 am |
The computer is still chugging away at better data for k=4 in the multiset uniformly random distribution.
In addition to checking if the ~ 0.39 fraction does hold up with better statistics, it will also give some probabilities the random walks can be compared against. It’s been running for a few days and looks like it will be done around the weekend.
While waiting on that, I wanted to see in detail what the comparison against an individual die looks like. Randomly choose one die, then compare many random dice against it, recording the number of roll pairs it wins – loses.
Here is a histogram:
http://imgur.com/a/GZ4P6
A “tie” is the most likely in the sense that it is (or is close to) the peak of the probability distribution. Ties go to zero with larger n just because there are so many other options. This fits with the descriptions so far, but is nice to see.
—
I’ve been struggling to figure out a way in which the proper dice are “special” as the randomness conjecture seems to rely so delicately on the model. I apologize if this has already been mentioned before but I noticed that in this model (unlike the improper dice), there is a concept of an “inverse” of a die.
There are three equivalent ways of looking at it:
– in the sorted tuple representation, compare how the values differ with the average value. Take the differences, negate them, add back to the average value (resort list).
– in the multiset representation (a list of counts of each number 1 to n), reverse the list
– in the sorted tuple representation, compare how the values differ from a standard die. Take the differences, negate them, reverse the list, and add back to the standard die.
Additionally, if we consider the comparison function f(x,y) to report the number of roll pairs that x wins – those that y wins, we have:
for all x,y:
f(x,y) = -f(y,x)
which also means
f(x,x) = 0
Now, denoting “-x” to be the inverse of a die, as defined above, it turns out:
f(x,y) = -f(-x,-y) = f(-y,-x)
So the inverse plays with the comparison nicely, as x < y means -y < -x
There are many dice besides the standard one that are equal to their inverse: x = -x.
For these special dice:
f(x,-y) = -f(x,y) (from the relations above)
Which means the set of dice equal to their inverse will compare to other dice in the set as zero (tie):
f(x,-y) = f(x,y) = -f(x,y) = 0
I haven't yet noticed any nice relation for f(x,y) to f(x,-y) in general. I'm hoping there is more structure in there to tease out.
May 18, 2017 at 8:55 pm
What if all, or at least “most”, ties come like that? If false, such a claim should be easy to refuse with a computer. If true, we could try to prove convergence to zero by considering the set of fixed points of this involution.
May 18, 2017 at 10:42 pm
I would be very surprised if that were the case, because if we assume the heuristic that everything behaves pretty randomly, then for a typical die you expect another die to tie with it with probability something like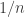 , whereas the probability that the other die is the inverse, or close to it, is much lower.
, whereas the probability that the other die is the inverse, or close to it, is much lower.
May 18, 2017 at 6:18 pm |
Since there has been some discussion of how to generate uniformly random dice, let me mention the dynamic programming + random walk approach that I used in my experiments (see my comment on the last post). I thought the technique was well known, but nobody here seems to have mentioned it so far. It uses two simple but elegant ideas: reduce uniform sampling to counting, and count using a recursive decomposition. These ideas go back quite a while – see Nijenhuis & Wilf’s classic 1975 book “Combinatorial Algorithms”, chapter 13. They’ve subsequently been used many times in computer science (to generate random words in regular and context-free languages, random solutions to Boolean formulas, etc.).
First counting. Let be the number of length-
be the number of length- sequences of integers between 1 and n that sum to
sequences of integers between 1 and n that sum to  . Then we have the recursive relation
. Then we have the recursive relation  (with the obvious base cases when
(with the obvious base cases when  or
or 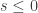 ). So we can compute the values of
). So we can compute the values of  for all
for all  and
and 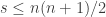 iteratively, starting with
iteratively, starting with  and moving upward. These are stored in a memoization table so that we don’t compute the same value multiple times.
and moving upward. These are stored in a memoization table so that we don’t compute the same value multiple times.
Once we can do counting, we can do uniform generation with a random walk as follows. Let’s write for convenience. Suppose that so far we have generated a sequence of length
for convenience. Suppose that so far we have generated a sequence of length  and sum
and sum  . Then there are
. Then there are 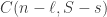 ways to complete the sequence to a full die, of which
ways to complete the sequence to a full die, of which 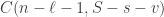 have
have  as the next element. So we extend the sequence with
as the next element. So we extend the sequence with  with probability
with probability  . Repeating this until a full die is produced yields a uniform distribution over all dice.
. Repeating this until a full die is produced yields a uniform distribution over all dice.
This technique produces an exact uniform distribution without needing rejection sampling (or having to wait for anything to converge), but it does use a lot of memory (for the memoization table, which has many entries and contains very large integers). It did work in my experiments, but for large n the table was gigabytes in size and awkward to handle (admittedly I didn’t try very hard to optimize anything).
May 19, 2017 at 2:43 pm |
In trying to organize the space of dice somewhat to get a handle on them, I have found that the “distance” characterization is quite useful
 .
.
In particular, considering the “standard” die to be the center of the space, and using the distance from it as a kind of radial distance.
Selecting a die A, the distribution of scores (number of roll pair wins – losses) from comparing to random dice, will be centered around 0 with the standard deviation depending strongly on the distance of A from the center.
For example here are three difference dice for n=100, at distance 30, 312, and 2450.
http://imgur.com/a/yEQI8
The last is the die with its values closest to average, and so is the furthest distance die from the center. Because it’s entries are all 50 or 51, there are strong undulations in the score due to ties if the comparison die happens to have the number 50 or 51 in it. If I used a larger histogram bin to smooth that out, it would look Gaussian.
The other extreme, dist=0 (the standard die), would be a zero width distribution since everything ties with it.
So the standard deviation of comparison scores for an individual die appear strongly correlated with that die’s distance from the standard die.
And here is a chart showing the distribution of distances when selecting uniformly in the multiset model, for n=100 (tested by selecting 100000 dice).
http://imgur.com/a/YoWL5
I haven’t yet calculated the distribution seen in the tuple model, but I have a feeling this is the measurement that would help distinguish it the most. Since the tuple model sees more ties, likely it means the distance distribution is shifted towards the center.
Will B, can you try your random walk generator and see how well it lines up with that distance distribution?
May 19, 2017 at 5:36 pm
Sure! Also, could you post your code for doing the dice comparison in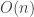 time? I was mocking up something similar that was essentially an adaption of the merge part of the standard MergeSort algorithm, but if you already have something, I’d rather use that.
time? I was mocking up something similar that was essentially an adaption of the merge part of the standard MergeSort algorithm, but if you already have something, I’d rather use that.
May 19, 2017 at 6:10 pm
Make an array of length n full of 0’s.
For each face of A, increment the corresponding element of the array by 1.
For i=2 to n, increase array[i] by array[i-1] for the accumulated totals.
Sum up the corresponding elements for B.
Something like that.
May 19, 2017 at 7:09 pm
Will B, oops I accidentally posted my reply in the larger thread.
May 19, 2017 at 7:53 pm
No worries–got it. I’ll code that up for future use and post it on the GitHub (though it might be a day or two…)
May 19, 2017 at 8:04 pm
Actually, I’m just now realizing something–pardon if I’m incorrect. It appears as though you’re working under the non-constrained sum model, while the pip-shifting generation method relies on a constrained sum model. I could use the standard generation method for dice to simply mirror your results, but I doubt that would accomplish as much. I’ll run a similar test to yours, but the variance in distance will likely be substantially lower…
May 19, 2017 at 8:04 pm
It appears as though you’re working under the non-constrained sum model, while the pip-shifting generation method relies on a constrained sum model. I could use the standard generation method for dice to simply mirror your results, but I doubt that would accomplish as much. I’ll run a similar test to yours, but the variance in distance will likely be substantially lower…
May 19, 2017 at 10:22 pm
I have taken a peak at some of the other dice types and random distributions, but the majority of discussion has been of proper dice, selecting using one of two different distributions (uniform in sequence representation, or uniform in multiset representation).
For the graphs above they were proper dice and random selection was done uniformly among the multisets. So this was not done using the code snippet I gave earlier. This was using something akin to the partition model Gowers suggested.
There are actually two distinguishing things here:
– the properties of dice (what values are allowed, and constraints on those values)
– the random distribution we use to select a random die
The snippet of code I shared previously was for:
– proper dice (allowed values are integers 1 to n, sum constrained to n*(n+1)/2)
– random selection was uniform in the “sequence” representation
Your original code was of this (dice type, distribution) as well.
Your random walk code we discussed before was also of this type.
The dice calculated for the graphs above were:
– proper dice
– random selection was uniform in the “multiset” representation.
Also, this would describe the dice and random distribution of the other random walk Gowers discussed.
The original conjecture was about uniformly selecting in the “multiset” representation. I was not being very careful at first, and implicitly assumed that because the conjecture was that in some sense the comparisons are as random as possible, that the sequence distribution should be fine (and it was easier for me to calculate). It is possible as n goes to infinity, the conjectures holds for both distributions. But I don’t know if results in one distribution can be used to prove the other or not.
So my last few results have been from selecting uniformly randomly in the “multiset” representation. I did this using an adapted form of Gowers suggested partition method. This should be slower than the random walk method, but for n up to about 200, I can still get reasonable statistics if i run code for a few days and I wanted some statistics that we knew for sure were selected uniform in multisets. Those calculations should finish today or tomorrow.
Anyway, I’ve been trying to be more clear now when I state results to also mention the distribution I used. If anything is confusing, or if I’m misusing terminology, don’t hesitate to point it out.
May 21, 2017 at 4:39 am
Gotcha, understood–might be worth looking at, then, since when I generated dice, I only ended up generating dice between 60 and 1,284. Because of that, I wasn’t able to mirror your results exactly. Perhaps there’s a smaller range of dice generated with the random walk?
Ran the tests based on the distance metric on the constrained sum case. I used the absolute distance as opposed to relative distance, so the graphs look slightly different. However, it seems to validate your conclusions: file is results_testDice_100s_70_200_650.png at github.com/wbrackenbury/intransDice. I generated 3 dice with distances 70, 200, and 650 from the standard die, and then generated 100000 dice, and measured their distances from each of those dice (red, blue, and green respectively for each of the distances). As seen in the figure, the distance from the standard die correlates strongly with distance from other dice, even with the random walk generation method. Could be useful for evaluating other hypotheses!
May 19, 2017 at 5:59 pm |
Here’s another question: what if you define a die roll as a probability distribution over [0,1]? (In other words, a “die roll” returns a real number in that interval). Are such dice transitive?
I’m not sure how you define a “distribution over distributions over [0,1]”, which I think you’d have to do.
Finite-sided dice could be modeled as having a spike in density at every possible value of the face (scaled to fit in [0,1]). But since that’s only a subset of possible “real-valued” dice, I don’t think answering this question would necessarily help with the original question.
I think that if you only consider continuously-valued dice, then ties have measure zero. That might not help, though (and takes it even further from the original question).
So I’m not at all sure that this helps answer the original question, but think it’s an interesting related question.
May 19, 2017 at 7:28 pm
As noted previously, we can scale the dice without changing their comparisons. So we can scale the dice with integer [1,n] to rational [0,1]. As n increases unbounded, this leads to a model of functions over rational values in [0,1] that matches the problem.
I think an issue with this approach is that the functions will not be continuous, and so doesn’t appear to make the problem nicer. And because it is discontinuous, I’m not sure what it would mean to leap to real values.
May 19, 2017 at 10:29 pm
This is something I have given some thought to but without successfully finding a continuous model that is still interesting. Here’s what I think is a natural attempt and why it doesn’t work.
For either the multiset or the n-tuple model, an n-sided die with face values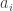 can be considered as a discrete probability measure on [0,1] by putting point masses of weight
can be considered as a discrete probability measure on [0,1] by putting point masses of weight 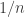 at
at  . Let
. Let 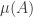 be the measure constructed from
be the measure constructed from  . Then consider sequences
. Then consider sequences 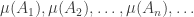 where the
where the  are chosen independently. Weak limits of these sequences would be good candidates for your “continuously-valued” dice. However, it must be that almost surely they converge weakly to the uniform (i.e., Lebesgue) measure on [0,1], and so in the limit all the dice are standard. I don’t really have a proof for this claim. It looks like the Glivenko-Cantelli theorem but with conditioning, since the sum restriction implies that the mean of
are chosen independently. Weak limits of these sequences would be good candidates for your “continuously-valued” dice. However, it must be that almost surely they converge weakly to the uniform (i.e., Lebesgue) measure on [0,1], and so in the limit all the dice are standard. I don’t really have a proof for this claim. It looks like the Glivenko-Cantelli theorem but with conditioning, since the sum restriction implies that the mean of 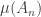 is
is  .
.
May 19, 2017 at 11:15 pm
I don’t have an interesting continuous model to suggest, but it is not obvious to me that the fact that for large a random die will look like the uniform distribution on
a random die will look like the uniform distribution on ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) completely kills all hopes of a limiting model where everything becomes exact. It’s just that the object would have to be something like an “infinitesimal perturbation” of the uniform distribution. But the model would have to be quite sophisticated I think, since we know that there are long-range correlations that result from the conditioning of the sum.
completely kills all hopes of a limiting model where everything becomes exact. It’s just that the object would have to be something like an “infinitesimal perturbation” of the uniform distribution. But the model would have to be quite sophisticated I think, since we know that there are long-range correlations that result from the conditioning of the sum.
May 20, 2017 at 8:03 am
We can keep fixed and consider sequences of
fixed and consider sequences of  real numbers between 0 and 1 conditioned on the sum being
real numbers between 0 and 1 conditioned on the sum being 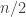 . This looks like an interesting simpler model. It is a limiting model for the case we have
. This looks like an interesting simpler model. It is a limiting model for the case we have  sided dice but number the sides by integers from one to
sided dice but number the sides by integers from one to  and
and  tends to infinity. if
tends to infinity. if  is odd we will never have ties and probably it will be easy to prove that the probability for ties always tends to zero. (I expect that my conjectured equivalence will hold for this variant as well.)
is odd we will never have ties and probably it will be easy to prove that the probability for ties always tends to zero. (I expect that my conjectured equivalence will hold for this variant as well.)
May 20, 2017 at 11:17 am
Just a note, Gil, that there will be no ties if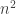 is odd, as we compare each face of one die with each face of another.
is odd, as we compare each face of one die with each face of another.
Another note that I tried generating dice made of n N(0,1) numbers conditioned on the sum being 0, and those are highly transitive. For 1000-sided dice, something like 1 in 10000 quadruples were non-transitive.
May 24, 2017 at 5:01 am
My apologies to P. Peng — your monotone scaling idea definitely includes the linear scaling I described as a special case. I missed this in my skimming of the comments. (I’m not sure where the most relevant place to reply is, but this seems reasonably nearby).
May 19, 2017 at 7:07 pm |
I don’t have access to the computers with the dice code at the moment. But I can describe what I did, which is probably more useful as I likely didn’t explain much in the code.
First, programming wise, the continual off by one thing is annoying so for the math below consider every value of the die -= 1. This doesn’t change any comparisons, and just makes the index of arrays or values discussed below not have +/- 1 everywhere.
Now, for the sequence representation it would also be nice to avoid even the n log n sorting hit. So convert directly from the sequence representation to the multiset representation, by stepping through the list, counting how many times you’ve seen each value. Now we have a list identifying the die using the multiset representation, where A[i] = (# of dice faces with value i).
We know the total of this list should be n.
Using that, step through the list, creating a new list where:
entry i holds a tuple that is ( multiset count, partially calculated score)
= ( # of dice faces with value i, (# of dice faces with value less than i) – (# of dice faces with value greater than i))
This whole thing took two trips through the list, so O(n) for conversion.
For lack of a better phrase, let’s call this representation the “fastdie” representation.
Now to compare two fastdie representations A and B, just sum up A[i][0] * B[i][1]. So O(n) for comparison.
This takes advantage of there only being n possible integer values in the initial die model, so will also be okay for the “unconstrained sum” dice model, but not improper dice nor the scaled real valued dice. If we pay the n log n to sort up front, then we should be able to compare those other representations in O(n) as well, but I have not written code for that.
As a side note, the partially calculated score in the fastdie representation is essentially Gower’s f_A(j) function.
May 19, 2017 at 7:51 pm |
If only for historical reasons, I thought I should mention that Martin Gardner wrote about this subject in SciAm (reprinted in “The Colossal Book of Mathematics”, ch. 22) where he gives this set of dice:
1: (0,0,4,4,4,4)
2: (3,3,3,3,3,3)
3: (2,2,2,2,6,6)
4: (1,1,1,5,5,5)
Each die beats the next one with a probability of 2/3, and die 4 beats die 1. Interestingly, the sums of the face numbers are 16, 18, 20 and 18: so the expectation value does not determine whether the next die is beaten or not!
There’s a reference in the article that might be interesting: R.P. Savage “The Paradox of Non-Transitive Dice”, Am. Math. Mo., Vol 101, May 1994, p429-36.
May 19, 2017 at 9:41 pm |
Can the set of all multi-sets of order with sum
with sum 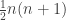 be equipped with a group structure that has
be equipped with a group structure that has 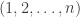 as neutral element and
as neutral element and 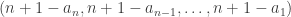 as inverse?
as inverse?
That would be nice, right? However, it is not hard to see that the answer in general is no. As a counter example consider e.g. all multisets of order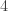 . There are
. There are 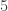 . The first three
. The first three  are fixed points for the above involution whereas the other two
are fixed points for the above involution whereas the other two  get mapped to each other. Since the only group of order
get mapped to each other. Since the only group of order 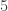 , the cyclic group, has exactly
, the cyclic group, has exactly  idempotent, we cannot equip our set of multi-sets with an operation that has the above properties.
idempotent, we cannot equip our set of multi-sets with an operation that has the above properties.
If its not a group, what else can it be? A cocycle? (I.e., there is a (meaningful) map from
from ![[n]\times [n]](https://s0.wp.com/latex.php?latex=%5Bn%5D%5Ctimes+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) to our set of multisets and a (meaningful) operation
to our set of multisets and a (meaningful) operation  on our multisets such that
on our multisets such that 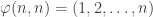 and
and  ) I do not know that, but while writing this I realize that the question I really have is actually very easy and the answer is probably well-known:
) I do not know that, but while writing this I realize that the question I really have is actually very easy and the answer is probably well-known:
Are there meaningful operations on the set of multi-sets?
July 14, 2017 at 11:54 pm |
Let me draw your attention to a related set of dice, “Lake Wobegon Dice,” which has the paradoxical property that each die is more likely to roll above the set average. The below paper included an exhaustive computer search through all three-die sets for the optimal such paradoxical dice. A great collaborative computer search would be to extend this to four such dice, so that novel statistics can be studied.
“Lake Wobegon Dice,” Jorge Moraleda and David G. Stork, College Mathematics Journal 43(2):152–159, 2012
October 12, 2017 at 2:14 pm |
[…] One of Tim Gowers’s blog posts on intransitive dice […]
October 14, 2017 at 3:21 pm |
[…] One of Tim Gowers’s blog posts on intransitive dice […]
January 6, 2021 at 9:53 am |
With the aforementioned suggestions it will make studying to play easier. Video clip Poker can be performed by one individual. The initial of these advantages is the reality that you can play from your own home.