Update: Nets Katz and Michael Bateman have posted a preprint to the arxiv that gives an improvement to the bounds for the cap-set problem. More on this later.
I have been extremely pleased with the response to my first post on the cap-set problem, in that various people have very generously shared their ideas about it. Indeed, Nets Katz has even posted a comment that may give an improvement to the bound by a factor of for some very small
(For reasons I have already explained, this would be very interesting if it worked.) This followed a previous comment in which he outlined some arguments that he had found with Michael Bateman that go a lot further than the ones that appeared in the section entitled “Sets with very weak additive structure” in my previous post.
Also, Ernie Croot, in addition to sketching a different very interesting approach to the problem, suggested that I should get in touch with Seva Lev, which I did. Seva has an example of a cap set that is interestingly different from the usual examples. I will discuss it in a moment.
My plan, by the way, is to try to understand the ideas in Ernie’s and Nets’s comments and then explain them in my own words in a future post. But I’m not yet ready to do that, so in this post I want to discuss some other aspects of the problem, including Seva’s example.
Seva’s example of a cap set.
Let me do that first. Regardless of what it may actually turn out to do for us, the example is a nice one. It’s defined as follows. Let We shall think of
as
where
is the field with
elements. Additively, this is the same as
of course, but it gives us some multiplicative structure that we can use to define our set. The definition of the set, which I’ll call
is very simple. Let
be an element of
that isn’t a square. Then we take the set of points of the form
(Note that
and
are all points of
so these points do indeed belong to
)
Why is a cap set? Well, if it contained an AP of length 3, then we would have elements
such that the following three points all belonged to
and formed an arithmetic progression.
Taking the sum of the first and third points and subtracting twice the second (which mod 3 is the same as adding the second) and using the fact that the third coordinates must be in arithmetic progression, we find that But that implies that
which contradicts the assumption that
was not a square. (More precisely, the only way not to get a contradiction is if
so the only APs are degenerate ones.)
What is interesting about this example? I won’t go into much detail, but will just point out a few of its features.
The only method I knew of for producing examples of cap sets until hearing from Seva was the following very simple-minded approach: take small examples and multiply them together. For example, the subset of
contains no non-trivial progression, so the set
doesn’t either. One can obtain slightly more interesting examples by starting with larger sets: if you have a cap set in
of size
where
then for arbitrarily large
you can find a cap set in
of size
Seva’s example has density so it does not answer the question of whether a density of
is possible. However, it does provide an example of a set that does not have an obvious product structure (and Seva has a proof of a rigorous statement to the effect that it does not have a product structure at all). Moreover, and this was one of Seva’s main points, the Fourier coefficients of the set are such that this set does not have any more bias on a codimension-1 subspace than is guaranteed by the simple Roth/Meshulam argument. In fact, it looks as though something similar is true for all small-codimension subspaces, for some suitable interpretation of “small”. However, because the density is exponentially small in the dimension, the example does not contradict the conjecture (or at least hope) that one can say something interesting after passing to a subspace of codimension that is a power of the logarithm of the density.
Thoughts provoked by Ben Green’s observation.
Recall the following question from the previous post.
Question 1. Let be a cap set in
of density
For which values of
and
can one prove that there must be an affine subspace
of
of codimension
such that the density of
inside
is at least
If one is feeling very optimistic, one might hope to be able to take for some absolute constant
and
But if that feels a bit too bold (and after Ben’s comment it does seem to be asking quite a lot to prove it, even if it is true) then one could tone down the hope a bit and ask for
to be
for some absolute constant
such as 4, say. Even this would be enough for a very substantial improvement to the Roth/Meshulam bound.
Now I’ve just realized that the question above is different from the one I actually asked. What I asked was the “off-diagonal” version of the question, where the initial assumption is not that is a cap set but that we have three sets
and
such that
contains no triple in arithmetic progression. Ben made the observation that any interesting bound for Question 1 can easily be converted into a bound for the codimension of a subspace contained in
where
is a dense set. The argument is as follows. If we have a positive answer to Question 1 for
and
(in the question I took
to be an absolute multiple of
so I am generalizing slightly here), then let
be a set of density
Either
is all of
or it misses out a point
In the latter case,
misses out 0, so applying Question 1 to the three sets
and
we find a subspace
of codimension
such that the density of
in
is at least
The number of iterations we can do of this argument is at most
by which time we have passed to a subspace of codimension at most
In particular, if
and
then
contains a subspace of codimension at most
Ben made the point that if is too small then this bound is better than the remarkable recent bound obtained by Sanders. He also hinted at the converse point that perhaps one might try to argue in the opposite direction, using Sanders’s ideas (which I shall come to soon) to show that Question 1 has a positive answer as long as
isn’t too small.
In order to investigate that possibility, we need to understand a bit about Sanders’s argument, and in particular the lemma of Croot and Sisask on which it depends. Rather than jumping straight in, I shall describe a proof strategy and then discuss whether it can be made to work.
Just before I do that, I’ll make an obvious comment given the discussion so far. It’s that I do not know of any technique for obtaining a density increment given that contains no non-trivial AP that does not work more generally, giving a density increment in
on the assumption that there are very few solutions to the linear equation
with
and
where
and
are sets of comparable density and
and
are non-zero. I can’t even think of a technique that might work. Until I can, or until somebody else can point me in the direction of such a technique, I shall look at the more general problem, which amounts to looking at what we can say about a set
if there is some convolution
that is very small on a set
with all of
and
of comparable density. (This approximates the hypothesis that
has density at most
where
is the density of
and of
)
A possible approach to obtaining good cap-set bounds.
If is a set of density
and
is not all of
then in particular
has density at most
Suppose now that we could find a subspace
such that
was approximately equal to
Recall that convolving
with
replaces the value
with the average of
over the coset
Thus, what we are supposing is that the convolution
tends to be approximately equal to its averaging projection, and therefore approximately invariant under translations by vectors in
Since has density at most
, there is a set of density
on which
takes the value 0. And since
we can say something like that there is a union of cosets of
of total density at least
on each of which
has small density.
All we actually need is that there should be one coset on which
is small. If we now pick any non-zero
then it cannot often be the case that the density of
is large in both
and
since otherwise we would add up a large number of reasonably large contributions to
in the coset
contradicting the fact that
was supposed to be small there.
Speaking very approximately, for each we can put
into
or
but not both. (That would be correct if
. I am claiming that it is approximately true if we only approximately have that assumption.) It follows that
must have at least double the density in some cosets (since it can intersect only half of them).
This sketchy argument would be of zero interest were it not for the fact that there is now a rather exciting new technique for obtaining statements of precisely the desired form. Having provided some motivation for finding approximate translation invariance of convolutions, let me now turn to the Croot-Sisask approach to obtaining it.
The Croot-Sisask lemma.
My aim in this section is not to give a full proof of the lemma, but merely to explain enough of the method to turn it into an exercise for anyone with a little experience in additive combinatorics. (I could try to spread the net a little wider, but my guess is that anyone who does not at least find the sketch below plausible enough to be persuaded that the result is correct will have lost interest in these posts by now.)
Suppose we have two subsets and
of
with densities
and
We want
to be approximately invariant under all the translates from some subspace. But let’s settle for less for the time being — we’ll merely try to get it to be approximately invariant under as many translations as we can, not worrying about whether those translations form (or contain) a low-codimensional subspace.
Why should have any translation invariance properties at all? One answer comes from Fourier analysis: the Fourier coefficients of
decay reasonably fast (they are absolutely summable), so we can approximate
in
(or indeed in any
-norm with
) by keeping only the part of the Fourier transform with large Fourier coefficients, of which, by Parseval, there are not too many. But a character on
is constant on cosets of a 1-codimensional subspace, so a linear combination of
characters is constant on cosets of a
-codimensional subspace. The problem with this argument is that
has to be rather large. I won’t go into details, but this kind of argument is nothing like strong enough to give an improvement to the cap-set bounds, or even to equal them.
Croot and Sisask have a different approach that does not involve the Fourier transform. To explain it, it will be helpful to normalize as follows: instead of considering the convolution I’ll consider the convolution
We can think of this probabilistically. Its value at
is the probability that
if you choose
uniformly at random from
Equivalently, you take all the sets
with
and take the average of their characteristic functions.
Suppose now that we could find a small such that
is approximately equal to
for a positive fraction
of all sets
of size
Then there must be some set
of size
such that
is approximately equal to
for a positive proportion of all translates
of
But if
is approximately equal to both
and
then
is approximately equal to
(Just to spell this out, if
is close to
then trivially
is close to
so the claim follows from the triangle inequality.)
How, then, are we to find a small set such that
There is an obvious answer: just pick a random small subset of
And this is exactly what Croot and Sisask do. Or rather, it’s almost exactly what they do, but because independent random variables are easier to handle, what they actually do is take
elements
from
uniformly at random (with replacement) and consider the function
If
are distinct (which they usually are) and we let
then this is indeed
To analyse how this works, consider the value at a point of the function
It is the average of
independent random variables, each of which involves picking a random
and setting the value to be 1 if
and 0 otherwise. That is, we have independent Bernoulli variables with mean
and variance at most 1.
How many of these do we need in order that their sample mean will, with high probability, be close to Well, the variance of the sample mean of
of them is at most
so at the very least we need this to be at most
To give an important example, suppose that
is a random subset of
of density
Then
is approximately
so we need
or
And a moment’s thought shows that this is trivially necessary: the convolution
is roughly constant, and since
has density
there is no hope of making it roughly constant if you take the average of fewer than
translates.
I haven’t actually said what kind of approximation I am talking about here, but it is sort of implicit in the fact that I looked at the value at an individual is that I am looking at an
approximation for some
And this is indeed what Croot and Sisask, and also Sanders, do.
Now let us think about two further aspects of the method: how large a set it gives, and whether that set has any useful structure. The answer to the first question is that there are ordered subsets of
of size
(where
is the density of
and
), so if we have chosen
such that for at least half of them we have
then we can find at least
of those that are translates of each other. So as a rule of thumb, the density of the set of good translates you get is
where
is the density of
and
is the size of your random samples.
In the case of the example where and
are random sets of density
this gives us a set of density
Even if that set is a subspace, it has codimension
so isn’t that good.
Before I discuss that further, let me quickly mention the matter of structure. Croot and Sisask observed that if you choose so that the approximations are all very good, by which I mean that we obtain a set
such that
is very close to
for every
then by the triangle inequality we still get pretty good approximations even if all we know about
is that it belongs to
for some not too large number of summands. But iterated sumsets have much more structure than arbitrary sets, a fact that was heavily exploited by Sanders (using Chang’s theorem).
However, the example above suggests that one might be able to do something else. After all, in that case is roughly constant, so it is roughly invariant under all translates. Can we get anywhere by understanding why the Croot-Sisask approach gives only a few of these translates?
Here is one natural thought that sheds some light on what goes wrong in the random example. Suppose we look for plenty of small sets such that
approximates
not in some
norm but in the
norm. Since all the translates of
are roughly equal in the
norm, this is going to be very easy — in fact, we can take
The triangle inequality will then give us plenty of values
such that
is small. But we know that the Fourier coefficients of
are absolutely summable. If the difference has small
norm on the Fourier side, then it must have small
-norm, so by Parseval we get some kind of bound on
This suggests that the problem with the argument might be that the intermediate step it aims for (an
bound) is too strong.
I haven’t checked what the bound is that comes out of the above argument, because in the next section I want to discuss an example that messes up all the thoughts I have had along these lines.
A killer example?
In this section I want to discuss an example that, to put things rather melodramatically, has been the bane of my life for many years. And I am not alone: for example, Nets Katz briefly alluded to it in one of his comments on my previous post. I am not yet well enough up on the new methods to know how damaging it is. I will say what I can about how I think the example might be dealt with, and will be very interested to know whether others have thoughts on the matter.
The basic idea behind the example is simple: take a random union of subspaces. Of course, there are some choices to be made here. We need to decide on the dimensions of the subspaces and the number that we shall take. Broadly speaking, if we take too many subspaces then their union will start to look like a fairly random set and we will no longer see its internal structure, whereas if we take too few then their union will be highly structured.
Suppose, then, that we take subspaces
of codimension
Since we have chosen them randomly, their pairwise intersections have codimension
(with high probability). A property that will be very handy will be if we can treat the union as though its characteristic function were just the sum of the characteristic functions of the
so we would like it if the measure of the intersections was small.
Let us write both for the subspace and for its characteristic function (a practice I was adopting above with the set
when I convolved it with
). Let
be the density of each
The density of the union of the
is, by the inclusion-exclusion formula, at least
which is approximately
provided
is substantially less than 1. So let us assume this. Note that the square of the
norm of the sum of the
is
(since the inner product of
with
is
when
and
when
). So with this condition on
and
we have that the union and the sum are approximately equal in
Let The next thing I want to look at is the convolution
Let
and assume that
which, as we have seen, implies that
is small. By an easy case of Young’s inequality it follows that
is small. I won’t bother with the precise calculation here — I’ll just feel free to use
instead of
.
Of course, is very easy to calculate: it is
Now
whereas if
then
is the constant function that takes value
everywhere. (This second assertion follows from the fact that
and
are subspaces of density
and that
) Therefore,
equals
I would like to choose and
so that the first term
is not tiny compared with the second term
Recall that we were talking about an
approximation. A typical non-zero value taken by
is
so we need
to be smaller than
for which in turn we need
to be at most
or so.
If we also want to be about
so that
has density
then it seems that a good choice is
and
So let us make that choice. Then for reasonably small
the function
is close to the function
In other words, instead of being a constant function, it is biased by having twice as much density as it should on the set
and slightly less everywhere else.
The rough point I want to make now is that is roughly constant only in directions that belong to almost all the subspaces
But that forces us down to a subspace of codimension
which is about
So it seems as though if we want a subspace
such that
then it has to have disappointingly large codimension.
Properties of the set A just constructed.
In this section I shall try to understand the set a bit better, and try to see as precisely as I can what proof methods it rules out. (That is very much the point here. Obviously, a union of subspaces does not threaten to be a cap set, but it does have annoying properties that show that certain lemmas one would like are false.)
To begin with, let us work out the Fourier transform of By our choices of
and
this is well approximated by the Fourier transform of the function
Let
be the annihilator of
for each
Then it is easy to check that the Fourier transform of
is
Recalling that
and noting that the subspaces
are disjoint except for
and have cardinality
this gives us
Fourier coefficients of size
Moreover, they span a subspace of dimension
which equals the Chang bound.
Next, let us observe that since is symmetric, the 3AP density of
is
which, by our discussion of
above, is approximately
This is significantly more than the
that one expects in the random case.
Next, let us think what happens when we pass to an affine subspace Our set then becomes the union
which has density at most
(where I am also using
to denote the uniform distribution on
). Let
be the annihilator of
Then
If intersects
in a subspace of dimension
then this works out as
If we fix the dimension of
to be
then by convexity if
then we maximize this by taking one
to be
and the rest to be zero. (I’m assuming that the
are in general position.) Thus, the best density increment we can get on an
-codimensional subspace is obtained by the obvious method of making that
-codimensional subspace contain one of the subspaces
That multiplies the density of that subspace by
and doesn’t affect the densities of the other
Next, let us think about translation invariance of Recall that this is approximately equal to
Now take a point
For what density of
do we have that
? Before we discuss that, we ought to decide how good we want the approximation to be. Since a typical value of
is around
it seems reasonable to ask for the difference to be small compared with
For this it is important not to choose
such that
and
Now the density of is around
(since we chose
and
to make this the case). If
then it is not possible for
and
both to belong to
and otherwise it is. So let
be the set of
such that
Then to a pretty good approximation,
has density around
It follows that unless belongs to at least half the
the density of points
such that
is small compared with
is at most
Since in the sketchy argument earlier I wanted to know
with reasonable accuracy on a set of density
and since the density of
that belong to half the
is extremely small, this example seems to show that there is a fundamental limitation to any argument that seeks to find a subspace
and prove that
is roughly constant on translates of
The above argument is a bit sketchy and I confess that I have not (yet) backed it up with precise statements and rigorous calculations. But I am reasonably confident that I am drawing the correct moral from it.
Some further observations concerning the above example.
1. There is an obvious analogue in of the set I have just constructed in
Instead of taking a random union of subspaces, one takes instead a random union of random Bohr sets (which will have predictable densities because they are defined by highly dissociated frequencies). This suggests that one ought to be able to prove the sharpness of Chang’s inequality in
without resorting to niveau sets. I plan to check this. (Alternatively, if anyone feels like doing some of the estimates, then perhaps there is scope for a joint paper here. The project would be to take the discussion of the previous paragraph, make it rigorous, and generalize it to all finite Abelian groups. Of course, all that would depend on its being correct in the first place.) [Added later: I’ve now realized that what I wrote here is wrong, since the example is weaker than the Chang bound. Chang’s inequality tells us that the number of dissociated frequencies where the Fourier coefficient is at least
is at most
whereas this union-of-subspaces example gives only
]
2. It is interesting to note that there is an easy way of getting a density increase for the set above, but getting the density to decrease is much harder. To get the density to increase, we pick on a subspace
and choose
in such a way that
If we want to decrease the density, then it looks as though we should choose
to be disjoint from
But this has a much smaller effect. This appears to demonstrate that the one-sidedness that both Nets Katz and I have run up against (and actually Seva Lev talks about it too) is a phenomenon that genuinely occurs. It also suggests that one might perhaps be able to find an interesting example by taking the complement of a union of subspaces, so that density increases become hard to obtain. However, I do not yet see how to make this thought work. (I can’t just take the complement of the set
above as that has density
But if I try to make it smaller, then the union and the sum are no longer roughly the same, so the example becomes harder to analyse. And now, a while later, I have made a fairly serious effort to analyse it and it seems to me to be hard to get the density to be small without the set becoming quasirandom.)
3. The main feature I would like to draw attention to in the above example is that it splits naturally into pieces, each of which has excellent translation-invariance properties. So a natural thing to try to do is find a general argument for splitting sets up into their “components” before attempting to apply an improved Croot-Sisask lemma. Alternatively, perhaps one can give an argument of the following kind: if a set contains pieces
and
that have low mutual additive energy, then
is roughly constant, which implies that
contains 3APs. If it does not contain such pieces, then
ought to have some unusual structure that prevents this. Perhaps, for instance, there must be many directions
such that
is unusually large, and perhaps that implies that we can obtain a better density increment than Roth-Meshulam gives.
4. The annoying example has a large spectrum that splits into subspaces. We know that we can in fact assume that no subspace can contain too many elements of the large spectrum. Could it be that we can obtain useful translation invariance of under the additional assumption that the large spectrum of
is “well-dispersed”?
As with my previous post, I end this one feeling as though there is much more to say. But I think my thoughts will be more organized if I leave it a few days, especially if I get some useful feedback on this post: I’ll be particularly interested in any ideas people might have for dealing with random unions of subspaces. Given that these cause difficulties for many of the ideas that occur to me, perhaps the title “What is difficult about the cap-set problem?” would have been more appropriate for this post than the last one.
January 19, 2011 at 9:20 am |
[…] (March 2009). Here are two “open discussion” posts on the cap set problem (first, and second) from Gowers’s blog (January 2011). These posts include several interesting Fourier theoretic […]
January 19, 2011 at 4:41 pm |
I have a further remark to make concerning the “killer example”, still based on the assumption that it has the properties I claimed it has. It is closely related to observation 2 above.
Suppose we want to try to prove that a set of density
of density  with no APs of length 3 must have a substantial density increase on some subspace of not very high codimension. It is tempting to try to prove a more general assertion, namely that if
with no APs of length 3 must have a substantial density increase on some subspace of not very high codimension. It is tempting to try to prove a more general assertion, namely that if  is any bounded function that averages
is any bounded function that averages  and
and 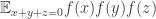 is significantly smaller than
is significantly smaller than  then
then  averages significantly more than
averages significantly more than  on some low-codimensional subspace.
on some low-codimensional subspace.
However, I think the “killer example” shows that this statement is false. It gives us an example of a set with density
with density  and with AP-density roughly
and with AP-density roughly  Now consider the function
Now consider the function 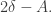 This again has density
This again has density  Its 3AP count is
Its 3AP count is  However, the fact that it is hard to obtain a density decrease for
However, the fact that it is hard to obtain a density decrease for  makes it hard to obtain a density increase for
makes it hard to obtain a density increase for 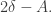
This shows that any proof that hopes to use a density-increment method to obtain a substantial improvement to the Roth-Meshulam bound must use in a crucial way the fact that the characteristic function of takes values in
takes values in ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) rather than, say, in
rather than, say, in ![[-1,1].](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D.&bg=ffffff&fg=333333&s=0&c=20201002) More suggestively, the balanced function of
More suggestively, the balanced function of  takes values in
takes values in ![[-\delta,1-\delta],](https://s0.wp.com/latex.php?latex=%5B-%5Cdelta%2C1-%5Cdelta%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002) and we must use the “one-sided” fact that its negative values cannot have large modulus.
and we must use the “one-sided” fact that its negative values cannot have large modulus.
Since this is potentially an important point, let me try to be more precise about what kinds of arguments the example rules out. To do that, I’ll bound from below the density of in an
in an  -codimensional affine subspace
-codimensional affine subspace 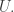 Let
Let  be the annihilator of
be the annihilator of  and let
and let 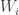 be the annihilator of
be the annihilator of 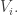 Then the density of
Then the density of  in
in  is
is 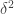 unless
unless  contains a point of
contains a point of  In the second case,
In the second case,  contains a vector capable of distinguishing
contains a vector capable of distinguishing  from
from 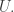 Whether or not it does so depends on whether we choose the right translate of
Whether or not it does so depends on whether we choose the right translate of  but the point is that the density of
but the point is that the density of  in
in  is roughly
is roughly 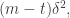 where
where  is the number of the
is the number of the 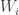 that are intersected by
that are intersected by 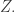 Since the
Since the 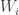 are assumed to be in general position, the density of
are assumed to be in general position, the density of  in
in  is at least roughly
is at least roughly  Thus, to get a density increase proportional to
Thus, to get a density increase proportional to  the number of dimensions we must lose is also proportional to
the number of dimensions we must lose is also proportional to 
If this is correct, it gives a test that should be applied to any attempted proof that tries to use a density-increment argument: does the argument generalize in a natural way to![[-1,1]](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) -valued functions? If it does, then the attempt will not improve on the Roth-Meshulam bound.
-valued functions? If it does, then the attempt will not improve on the Roth-Meshulam bound.
As with the post, this comment comes with a health warning: I haven’t written things up carefully so it is possible that what I am saying is nonsense.
January 20, 2011 at 11:46 am |
I’d like to point out briefly that the arguments of Nets Katz and Michael Bateman (and the more simple-minded arguments from my previous post) pass the test I discussed in my previous comment. That is, they exploit positivity in a crucial way. Let me spell this out.
It’s clear that what I have just said must be true, since one of the key facts driving what Nets was writing about is that you can’t have more than Fourier coefficients of size
Fourier coefficients of size 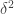 in a subspace of dimension
in a subspace of dimension 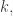 whereas the function I discussed in my previous comment had
whereas the function I discussed in my previous comment had 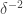 Fourier coefficients lying in a subspace of dimension
Fourier coefficients lying in a subspace of dimension 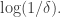 This isn’t a contradiction, because the function does not take values in
This isn’t a contradiction, because the function does not take values in ![[0,1],](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002) though it does take values in
though it does take values in ![[-1,1].](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D.&bg=ffffff&fg=333333&s=0&c=20201002) But let us see in more detail why it isn’t a contradiction.
But let us see in more detail why it isn’t a contradiction.
The argument for the bound goes like this. (I have already given it, and Nets has given it in a different form.) Suppose we can find a subspace
bound goes like this. (I have already given it, and Nets has given it in a different form.) Suppose we can find a subspace  of dimension
of dimension  such that for
such that for  values of
values of  the Fourier coefficient
the Fourier coefficient  has modulus at least
has modulus at least 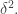 Then
Then  (The initial
(The initial 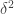 comes from the fact that
comes from the fact that  Now the restriction of
Now the restriction of 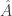 to
to  is the Fourier transform of
is the Fourier transform of  where
where  is the subspace annihilated by
is the subspace annihilated by  (so
(so  has codimension
has codimension  ). Therefore, by Parseval,
). Therefore, by Parseval, 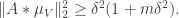 If
If  is substantially less than 1, then this roughly tells us that
is substantially less than 1, then this roughly tells us that  and therefore that there is an affine subspace of codimension
and therefore that there is an affine subspace of codimension  (a translate of
(a translate of  ) where
) where  takes at least the value
takes at least the value  which is the same as saying that the density of
which is the same as saying that the density of  in that affine subspace is at least
in that affine subspace is at least  It is here that I have used positivity: if I didn’t know that
It is here that I have used positivity: if I didn’t know that  was positive, then its
was positive, then its 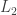 norm might be accounted for by some large negative values instead.
norm might be accounted for by some large negative values instead.
Now if we did Roth-Meshulam iterations, we would obtain a density increment of
Roth-Meshulam iterations, we would obtain a density increment of  whereas actually we have obtained
whereas actually we have obtained 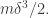 So the assumption that we cannot improve on Roth-Meshulam implies that
So the assumption that we cannot improve on Roth-Meshulam implies that  cannot be substantially bigger than
cannot be substantially bigger than  as claimed.
as claimed.
January 21, 2011 at 4:40 am |
Your construction of a union of a bunch of random subspaces made me think of a nice idea/result due to A. Blokhuis. Rather than write this all out, let me direct you to the following problem I posed at the ICM satellite conference on Analytic Number Theory:
Click to access icm_question3.pdf
See section 1.4 of the note. Basically, Blokhuis’s idea is an algebraic method that gives good bounds on the “union of subspaces” problem in that section (sec. 1.4).
Perhaps there is a way to combine Tom’s Bogolyubov theorem (or my work with Olof) with this algebraic approach to give a strong solution to the problem at the beginning of that note (since Tom’s result implies that sumsets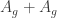 contain 99 percent of the elements of a large coset progression, one almost has that
contain 99 percent of the elements of a large coset progression, one almost has that  contains the union
contains the union  , where
, where  is some large subspace/subgroup with the
is some large subspace/subgroup with the  element removed). If so, then, as I comment, one would get strong upper bounds on the size of subsets in
element removed). If so, then, as I comment, one would get strong upper bounds on the size of subsets in 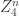 without 3APs, under a certain “uniformity assumption” (which perhaps can be removed) mentioned in the note.
without 3APs, under a certain “uniformity assumption” (which perhaps can be removed) mentioned in the note.
Assuming this could be done, it makes me wonder whether one could say something similar in — can algebraic and combinatorial/analytic methods be combined to attack the CAP set problem?
— can algebraic and combinatorial/analytic methods be combined to attack the CAP set problem?
January 24, 2011 at 6:08 am |
It is late so forgive me if what I write is not correct — but Lev’s example is a quadric surface S in A^3 over F = F_{3^m}, and I suppose what’s going on is that the non-squareness of lambda means that the two familes of lines contained in S are switched by the Galois group of F — in particular, there is no line at all defined over F and contained in S. But then, by Bezout, any line intersects S in at most two points. So I think something even stronger is true; that in Lev’s example, any F-arithmetic progression (i.e. a set of the form a + Fb with a,b in F^3) intersects S in at most two points. Any ordinary three-term arithmetic progression is contained in one of these.
January 27, 2011 at 11:16 am |
This is a bit of a non-comment, but I wanted to write some kind of acknowledgement of the comments of Ernie Croot and JSE above: I may not have thought of anything worth saying in response, but I found both of them interesting and thought-provoking.
January 28, 2011 at 7:49 am |
A comment to follow up on Jordan’s one. First, a set in with no three collinear points is called a cap because it looks like a cap (=hat like thing). An elliptic quadric (i.e. a quadric whose ruling is only defined in a quadratic extension) is a cap with
with no three collinear points is called a cap because it looks like a cap (=hat like thing). An elliptic quadric (i.e. a quadric whose ruling is only defined in a quadratic extension) is a cap with 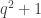 points (where
points (where  ). More surprising is the following theorem of B. Segre, if
). More surprising is the following theorem of B. Segre, if  is odd, then a cap in
is odd, then a cap in  whose is cardinality is at least
whose is cardinality is at least  (where
(where  is some constant I don’t remember) is contained in an elliptic quadric.
is some constant I don’t remember) is contained in an elliptic quadric.
January 28, 2011 at 8:19 am
Many thanks for this interesting comment. I have to confess that the hattishness of a set with no three collinear points doesn’t jump out at me, unless you are talking about subsets of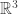 — is that the point?
— is that the point?
I was about to ask why the last statement doesn’t solve the cap-set problem, but suddenly realized that not containing three collinear points in is much stronger than not containing a line in
is much stronger than not containing a line in 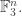 But that is an interesting result you mention.
But that is an interesting result you mention.
In case you are wondering why your latex didn’t initially come out, it is because you put backslashes in front of “latex”.
January 29, 2011 at 7:04 am
Thanks for fixing my latex. Yes, the terminology is supposed to evoke the geometry of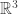 although it may not be necessarily true even there that a set with no 3 collinear points looks like a hat.
although it may not be necessarily true even there that a set with no 3 collinear points looks like a hat.
January 30, 2011 at 4:44 pm |
While we are on the topic of collinear points (and incidences), I thought I would mention a problem related to 3APs:
Problem. Can one encode three-term progressions in terms of point-line incidences in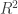 ? More specifically: suppose you are given a set of pairs
? More specifically: suppose you are given a set of pairs 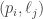 , which represents the fact that the point
, which represents the fact that the point  is on the line
is on the line  . Furthermore, suppose that this list of incidences may not be exhaustive in that there could be other point-line incidences in the drawing not accounted for by the list. Then, no matter how you draw the configuration of points and lines, so long as the incidences are respected, must the set of points
. Furthermore, suppose that this list of incidences may not be exhaustive in that there could be other point-line incidences in the drawing not accounted for by the list. Then, no matter how you draw the configuration of points and lines, so long as the incidences are respected, must the set of points  ALWAYS contain a 3AP?
ALWAYS contain a 3AP?
Take, for example, the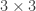 grid of
grid of 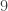 points, with
points, with  lines, each incident with three of those points. Some points are incident with
lines, each incident with three of those points. Some points are incident with 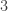 of those lines; some are incident with only
of those lines; some are incident with only  ; and one point is incident with
; and one point is incident with 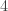 lines. It turns out that there are many OTHER ways of drawing the points and lines (uncountably many, even after accounting for affine transformations), besides the
lines. It turns out that there are many OTHER ways of drawing the points and lines (uncountably many, even after accounting for affine transformations), besides the 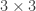 lattice grid, such that the
lattice grid, such that the 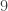 points do not contain a three-term progression. (It is a nice exercise to work out some examples!)
points do not contain a three-term progression. (It is a nice exercise to work out some examples!)
But what about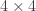 grids, or
grids, or 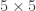 , etc.?
, etc.?
….
The original motivation of this problem was to find a way to convert problems about 3APs into incidence questions that could then be approached algebraically (e.g. using elliptic curves).
January 30, 2011 at 9:18 pm
I’m not sure whether I understand the problem correctly, but do you mean by three points forming an 3AP that one of them is the midpoint of the line segment joining the two other ones? If so (or also otherwise) could you, please, indicate a point/line-configuration that enforces the presence of a 3AP? At the moment I cannot think of any, mainly because there seem to be far too many projective maps that preserve incidence but tend to destroy the midpoint property. (To be more precise: Take a drawing of a given configuration, colour all points which are fourth harmonic points of collinear triples of points you have used yellow, consider a line avoing all these yellow points and send it to infinity.)
January 31, 2011 at 4:27 am
Christian,
“but do you mean by three points forming a 3AP that one of them is the midpoint…?” Yes, that is what I mean.
“Can you indicate a… ?” I don’t know of a single one! That’s my question — prove that one exists.
Assuming that the point-line incidence restrictions for all the lines associated to some grid pin down the grid structure up to affine transformations, it should be possible to decide this algebraically: in order to bypass the problems of multiple configurations due to affine transformations (which preserve incidences), one can anchor three of the points to be
grid pin down the grid structure up to affine transformations, it should be possible to decide this algebraically: in order to bypass the problems of multiple configurations due to affine transformations (which preserve incidences), one can anchor three of the points to be  and
and 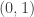 . Then, one can represent triples
. Then, one can represent triples  of collinear points by quadratic questions, which reflect the fact that the slopes of the segments
of collinear points by quadratic questions, which reflect the fact that the slopes of the segments 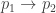 and
and  are equal. In principle, then, one can represent all the point-line incidences (using only the lines meeting three or more of the points) by a large number of these quadratic equations, which *should* have a unique solution (since the anchoring prevents multiple solutions coming from affine transformations). Perhaps one of these computer algebra packages (like MAGMA) can then verify that the equations indeed have a unique solution in the reals.
are equal. In principle, then, one can represent all the point-line incidences (using only the lines meeting three or more of the points) by a large number of these quadratic equations, which *should* have a unique solution (since the anchoring prevents multiple solutions coming from affine transformations). Perhaps one of these computer algebra packages (like MAGMA) can then verify that the equations indeed have a unique solution in the reals.
Assuming this is true (the incidence data for sufficiently large grids uniquely determines the structure of the grid up to affine transformations), a bigger and more interesting challenge would be to produce a set of point-line pairs where every line is incident to EXACTLY three points (i.e. not four or more), such that for any drawing of the incidence the points must ALWAYS contain a 3AP. I happen to believe it is possible to find such a configuration; in fact, I believe that projecting down a
must ALWAYS contain a 3AP. I happen to believe it is possible to find such a configuration; in fact, I believe that projecting down a  grid (and the associated lines hitting three points each) to the 2D plane (bijectively) will give such a configuration when the number of dimensions is large enough.
grid (and the associated lines hitting three points each) to the 2D plane (bijectively) will give such a configuration when the number of dimensions is large enough.
Why consider point configurations where every line meets exactly three points? Well, that has to do with ellitpic curves… another time, perhaps.
January 31, 2011 at 11:49 am |
Dear Ernie,
your argument involving a large number of quadratic equations sound compelling, but I still don’t see why the following rules out that, e.g. a grid, can enforce 3APs. The map
grid, can enforce 3APs. The map  preserves collinearity of points, so if we apply it to all points
preserves collinearity of points, so if we apply it to all points 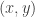 with integers
with integers 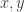 ranging from
ranging from  to
to  we get a copy of our grid. (I assume here that
we get a copy of our grid. (I assume here that  and
and  are linearly independent over the rationals, so that we do not divide by zero. It is also useful to assume these numbers to be algebraically independent for the sake of discussion. If one does not want to rely on that, one can replace them by two other “sufficiently general” real numbers). Now in the new drawing no point seems to be the midpoint of two other points (basically because this would tell us something non-trivial about
are linearly independent over the rationals, so that we do not divide by zero. It is also useful to assume these numbers to be algebraically independent for the sake of discussion. If one does not want to rely on that, one can replace them by two other “sufficiently general” real numbers). Now in the new drawing no point seems to be the midpoint of two other points (basically because this would tell us something non-trivial about  and
and  .)
.)
So it may be that the quadratic equations you produce are not very independent from one another. A possible reason for that, apart from getting only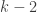 insted of
insted of  equations for any $ latex k$ collinear points might be hidden in results such as Pappus’ or Desargues’ theorem, which seem to tell us that sometimes one of these equations is entailed by eight or nine others in a non-trivial way. Hilbert’s Nullstellensatz suggests that these implication can be made rather explicit in single equations, which would incidentally yield – probably rather ugly – one-line-proofs of these two theorems.)
equations for any $ latex k$ collinear points might be hidden in results such as Pappus’ or Desargues’ theorem, which seem to tell us that sometimes one of these equations is entailed by eight or nine others in a non-trivial way. Hilbert’s Nullstellensatz suggests that these implication can be made rather explicit in single equations, which would incidentally yield – probably rather ugly – one-line-proofs of these two theorems.)
January 31, 2011 at 11:53 am
Oups, apart from that I failed to press the reply button, a crucial formula did not parse, so here is another attempt to write it down with slightly more English: The point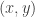 is mapped to
is mapped to  .
.
February 1, 2011 at 2:17 am
Dear Christian,
Wow! That’s fantastic. I had thought about various kinds of maps like you had described, but had somehow overlooked this particular possibility. I suppose it sinks my hope of encoding 3APs by incidences, but at the same time it means that problems about 3APs really are fundamentally different from incidence-type problems (at least superficially).
By the way, there is an old problem posed by T. Tao (and I think also J. Solymosi and others) appearing in the following (problem 4.6)
Click to access additivecomb.pdf
about classifying collections of points and lines with almost the maximal number of incidences. The fact that there are maps such as you describe suggests that the answer will not simply be “dense subsets of uniform grids”, but will instead be much more complicated.
February 1, 2011 at 11:44 am
Dear Ernie,
it seems to me that this kind of map is by far to general to imply anything interesting about the inverse question associated with the Szemerédi-Trotter thereom, except for that it suffices to classify the relevant configurations up to “projective isomorphisms”. By this I mean: These maps can be applied not only to grids, but to all configurations of points and lines, so in particular to those maximizing the number of incidences. By the way, I think I can do Problem 4.13 from your list, but probably that’s not new given that the list seems to be a few years old.
Best regards,
Christian.
February 2, 2011 at 3:27 pm
About that problem 4.13. Let’s continue this conversation off of this blog. Send me an email.
I guess I was being silly about the 3APs and incidences question, now that I think about it. I should have thought about the artist’s drawing of a horizon — that transformation preserves lines and incidences, but not 3APs.
But funnily enough I had asked this problem about 3APs to several people (including a geometer), and not one of them thought of using these projective transformations.
February 4, 2011 at 1:00 pm |
Concerning my example — here is an idea of how one could try to develop it further, to construct even larger caps. Let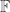 be the field of order
be the field of order 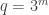 , and let
, and let 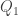 and
and 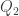 be quadratic forms over
be quadratic forms over  (more precisely, over
(more precisely, over 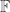 in five variables). Denote by
in five variables). Denote by  the set of common zeroes of
the set of common zeroes of 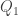 and
and 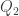 . Suppose that
. Suppose that  contains no (non-trivial) arithmetic progression \emph{with a difference from
contains no (non-trivial) arithmetic progression \emph{with a difference from  }, and consider the set
}, and consider the set

 is of the form
is of the form
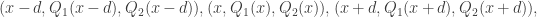
 and
and  for
for 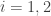 . The latter condition implies
. The latter condition implies  , whence
, whence  . But now the former condition along with the assumption that
. But now the former condition along with the assumption that  contains no arithmetic progressions with the difference in
contains no arithmetic progressions with the difference in  show that
show that 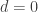 ! Thus,
! Thus,  is a cap, and we have
is a cap, and we have  . Can we choose
. Can we choose  , and
, and  so that
so that 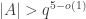 (as
(as  )? (What gives a hope that this is possible is that we do allow progressions in a vast majority of directions!) If so, we have constructed a cap in
)? (What gives a hope that this is possible is that we do allow progressions in a vast majority of directions!) If so, we have constructed a cap in  of size
of size  which, as far as I remember (I may well be wrong about it though), beats the best known constructions.
which, as far as I remember (I may well be wrong about it though), beats the best known constructions.
Any arithmetic progression in
where
February 11, 2011 at 10:34 am
I did a Monte Carlo with q=9, and I think found two quadratics whose zero-sets shared q points, all on a line through zero. (That is not surprising for homogeneous quadratics.)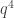 points in A, out of a total
points in A, out of a total 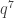 points, which is not as good as your other solution.
points, which is not as good as your other solution.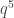 and you get your density
and you get your density
If that happened in other fields, it would allow
The only better result for this method would be if there are two quadratics whose only zero-point in common is the zero vector itself. In that case, the size of A would be
February 12, 2011 at 6:54 am
The Chevally-Warning Theorem (1936) says that any set of polynomials over a finite field, with more variables than the total of the degrees of the polynomials, has simultaneous zeros.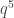 points.
points.
In our case, that means two quadratics in five variables have simultaneous non-trivial zeros, so A can’t have
Or three quadratics in seven variables have simultaneous non-trivial zeros, and again we can’t do better than your first solution.
Perhaps two quadratics in eight variables could have just q simultaneous zeros?
February 15, 2011 at 8:47 am
Consider two quadratics in four variables whose only common zero is the zero vector. They lead to a solution (w,x,y,z,Q1,Q2) with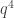 points, and the same density as Seva’s original example.
points, and the same density as Seva’s original example.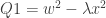 and
and  . where
. where  is not a square.
is not a square. multiplied together.
multiplied together.
I don’t know if they include new examples or not.
The only example I can think of is
Unfortunately, that is just two solutions
February 6, 2011 at 9:58 pm |
[…] Polymath6 has started. It is about improving the bounds for Roth’s theorem. See this post. Also there is a page on the polymath blog here. There is also a wiki here. Also see this post and this post. […]
June 14, 2011 at 9:53 pm |
[…] after many years, the Roth-Meshulam bound. See these two posts on Gowers’s blog (I,II). Very general theorems discovered independently by David Conlon and Tim Gowers and by Matheas […]
February 5, 2013 at 11:51 pm |
Regarding random union of subsets: It looks that if when we consider moving from V to a hyperplane, and then a codim 2 space and so on, the density-increase grows geometrically with the codimension, are there examples avoiding this feature?
July 8, 2020 at 5:00 pm |
[…] methods that for some ! This was very exciting. See these two posts on Gowers’s blog (I,II). This raised the question if the new method allows breaking the logarithmic barrier for […]
February 26, 2024 at 4:37 pm |
[…] In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had […]
February 26, 2024 at 4:46 pm |
[…] sonunda kullanacağı yaklaşım konusunda neden kötümser olduklarını tam olarak açıklayan 2011 tarihli bir blog gönderisine rastladığını […]
February 26, 2024 at 5:08 pm |
[…] In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had […]
February 27, 2024 at 3:01 am |
[…] In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had […]
February 27, 2024 at 3:09 am |
[…] In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had […]
February 27, 2024 at 7:39 am |
[…] In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had […]
February 27, 2024 at 10:48 am |
[…] In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had […]
February 27, 2024 at 10:51 am |
[…] In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had […]
February 27, 2024 at 11:02 am |
[…] In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had […]
February 27, 2024 at 12:32 pm |
[…] he and Kelley have been smartly on their approach to publishing, Kelley says he ran throughout a weblog put up from 2011 that defined precisely why mathematicians have been pessimistic in regards to the very manner that […]
February 27, 2024 at 1:21 pm |
[…] In fact, after he and Kelley were well on their way to publishing, Kelley says he ran across a blog post from 2011 that outlined exactly why mathematicians were pessimistic about the very approach that the two had […]
February 27, 2024 at 7:50 pm |
[…] he and Kelley had been properly on their solution to publishing, Kelley says he ran throughout a weblog put up from 2011 that outlined precisely why mathematicians had been pessimistic in regards to the very method that […]