An observation that has been made many times is that the internet is a perfect place to disseminate mathematical knowledge that is worth disseminating but that is not conventionally publishable. Another observation that has been made many times is that either of the following features can render a piece of mathematics unpublishable, even if it could be useful to other mathematicians.
1. It is not original.
2. It does not lead anywhere conclusive.
A piece of unoriginal mathematical writing can be useful if it explains a known piece of mathematics in a new way (and “new” here does not mean radically original — just a slightly different slant that can potentially appeal to a different audience), or if it explains something that “all the experts know” but nobody has bothered to write down. And an inconclusive observation such as “This proof attempt looks promising at first, but the following construction suggests that it won’t work, though unfortunately I cannot actually prove a rigorous result along those lines,” can be very helpful to somebody else who is thinking about a problem.
I’m mentioning all this because I have recently spent a couple of weeks thinking about the cap-set problem, getting excited about an approach, realizing that it can’t work, and finally connecting these observations with conversations I have had in the past (in particular with Ben Green and Tom Sanders) in order to see that these thoughts are ones that are almost certainly familiar to several people. They ought to have been familiar to me too, but the fact is that they weren’t, so I’m writing this as a kind of time-saving device for anyone who wants to try their hand at the cap-set problem and who isn’t one of the handful of experts who will find everything that I write obvious.
Added a little later: this post has taken far longer to write than I expected, because I went on to realize that the realization that the approach couldn’t work was itself problematic. It is possible that some of what I write below is new after all, though that is not my main concern. (It seems to me that mathematicians sometimes pay too much attention to who was the first to make a relatively simple observation that is made with high probability by anybody sensible who thinks seriously about a given problem. The observations here are of that kind, though if any of them led to a proof then I suppose they might look better with hindsight.) The post has ended up as a general discussion of the problem with several loose ends. I hope that others may see how to tie some of them up and be prepared to share their thoughts. This may sound like the beginning of a Polymath project. I’m not sure whether it is, but discuss the possibility at the end of the post.
Statement of problem.
First, a quick reminder of what the cap-set problem is. A cap-set is a subset of that contains no line, or equivalently no three distinct points
such that
or equivalently no non-trivial arithmetic progression
(Why it has this name I don’t know.) The problem is the obvious one: how large can a cap-set be? The best-known bound is obtained by a straightforward adaptation of Roth’s proof of his theorem about arithmetic progressions of length 3, as was observed by Meshulam. (In fact, the argument in
is significantly simpler than the argument in
which is part of the reason it is hard to improve.) The bound turns out to be
That is, the density you need,
is logarithmic in the cardinality of
This is why many people are interested in the problem of improving the bound for the cap-set problem: if one could, then there are standard techniques that often work for modifying the proof to obtain a bound for Roth’s theorem, and that bound would probably be better than
(at least if the improvement in the cap-set problem was reasonably substantial). And that would solve the first non-trivial case of Erdős’s conjecture that if
then
contains arithmetic progressions of all lengths.
If you Google “cap set problem” you will find other blog posts about it, including Terence Tao’s first (I think) blog post and various posts by Gil Kalai, of which this is a good introductory one.
Sketch of proof.
Next, here is a brief sketch of the Roth/Meshulam argument. I am giving it not so much for the benefit of people who have never seen it before, but because I shall need to refer to it. Recall that the Fourier transform of a function is defined by the formula
where is short for
stands for
and
is short for
Now
(Here stands for
since there are
solutions of
) By the convolution identity and the inversion formula, this is equal to
Now let be the characteristic function of a subset
of density
Then
Therefore, if
contains no solutions of
(apart from degenerate ones — I’ll ignore that slight qualification for the purposes of this sketch as it makes the argument slightly less neat without affecting its substance) we may deduce that
Now Parseval’s identity tells us that
from which it follows that
Recall that The function
is constant on each of the three hyperplanes
(here I interpret
as an element of
). From this it is easy to show that there is a hyperplane
such that
for some absolute constant
(If you can’t be bothered to do the calculation, the basic point to take away is that if
then there is a hyperplane perpendicular to
on which
has density at least
where
is an absolute constant. The converse holds too, though you recover the original bound for the Fourier coefficient only up to an absolute constant, so non-trivial Fourier coefficients and density increases on hyperplanes are essentially the same thing in this context.)
Thus, if contains no arithmetic progression of length 3, there is a hyperplane inside which the density of
is at least
If we iterate this argument
times, then we can double the (relative) density of
If we iterate it another
times, we can double it again, and so on. The number of iterations is at most
so by that time there must be an arithmetic progression of length 3. This tells us that we need lose only
dimensions, so for the argument to work we need
or equivalently
Can we do better at the first iteration?
There is a very obvious first question to ask if one is trying to improve this argument: is the first iteration best possible? That is, is a density increase from to
the best we can do if we are allowed to restrict to a hyperplane?
There is an annoying difficulty with this question, which is that the answer is trivially no if there do not exist sets of density that contain no arithmetic progressions. So initially it isn’t clear how we would prove that
is the best increase we can hope for.
There are two potential ways round this difficulty. One, which I shall adopt here, is to observe that all we actually used in the proof was the fact that So we can ask whether there are sets of density
that satisfy this condition and also the condition that
The other is to observe that a similar density increase can be obtained even if we look for solutions to
with
and
, where
and
are not assumed to be the same set. Now it becomes easy to avoid such solutions and keep the sets dense. If we do so, can we obtain a bigger density increase than the argument above (appropriately modified) gives? This again has become a question that makes sense.
The following simple example disposes of the first question. Let let
be a random subset of
of density
and let
be the set of all
such that their first
coordinates form a vector in
Then
has density
Let be the characteristic function of
Then it is not hard to prove that
unless
is supported in the first
coordinates. If this is the case, then as long as
the typical value of
is around
or around
It follows (despite the sloppiness of my argument) that
is around
If we could say that the typical value of was roughly its maximum value, then we would be done. This is true up to logarithmic factors, so this example is pretty close to what we want. If one wishes for more, then one can choose a set that is “better than random” in the sense that its Fourier coefficients are all as small as they can be. A set that will do the job is
(That sum is of course mod 3.) Again, the details are not too important. What matters is that there are sets with the “wrong number” of arithmetic progressions, such that we cannot increase their density by all that much by passing to a codimension-1 affine subspace of
Taking a bigger bite.
This is the point where I had one of those bursts of excitement that seems a bit embarrassing in retrospect when one realizes not only that it doesn’t work but also that other people would be surprised that you hadn’t realized that it didn’t work. But I’ve had enough of that kind of embarrassment not to mind a bit more. The little thought I had was that in the example above, even though there are no big density increases on codimension-1 subspaces, there is a huge density increase on a subspace of codimension Indeed, the density increases all the way to 1.
I quickly saw that that was too much to hope for in general. A different example that does something similar is to take a random subset of
(that is, with each element chosen with probability
), to take
to be the set of
with first
coordinates forming a vector in
and to let
be a random subset of
of density
(in
so each element of
is put into
with probability
). This set turns out to have a fairly similar size distribution for the squares and cubes of its Fourier coefficients, but now we cannot hope for a density increase to more than
even if we pass to a subspace of codimension
But that would be pretty good! We could iterate this process times and get to a density of 1, losing
dimensions each time. That would require
which would correspond to the best known lower bound for Roth’s theorem.
I won’t bore you with too much detail about the plans I started to devise for proving something like this. The rough idea was this: for each codimension- subspace
define
to be the averaging projection that takes
to
where
(The characteristic measure
of
is defined to be the unique function that is constant on
and zero outside
and that averages 1. The projection
takes
to
) Then I was trying expanding
in terms of its projections
It turns out that one can obtain expressions for the number of arithmetic progressions, and also a variant of Parseval’s identity. What I hoped to do was find a way to show that if we take
we can prove that there is some
such that
has order of magnitude
from which it follows straightforwardly that there is a density increase of order of magnitude
on some coset of
But how would such a result be proved? I had a few ideas about this, some of which I was getting pretty fond of, and as I thought about it I found myself being drawn inexorably towards an inequality of Chang.
Chang’s inequality.
It is noticeable that in the example that provoked this proof attempt, the large Fourier coefficients all occurred inside a low-dimensional subspace. Conversely, if that is the case, it is not too hard to prove that there is a nice large density increase on a small-codimensional subspace.
This suggests a line of attack: try to show that the only way that lots of Fourier coefficients can be large is if they all crowd together into a single subspace. A good enough result like that would enable one to drop down by more than one dimension, but not too many dimensions, and make a greater gain in density than is possible if one repeatedly drops down by one dimension and uses the best codimension-1 result at each step.
There is good news and bad news here. The good news is that there is a result of precisely this type due to Mei-Chu Chang: she shows that the large spectrum (that is, the set of such that
is large) cannot contain too large an independent set. (Actually, her result concerns so-called dissociated sets, but in the
context that means linearly independent.) The bad news is that the bound that comes out of her result does not yield any improvement to the bound for the cap-set problem: up to logarithmic factors, the number of linearly independent
for which
can have size
is around
, and even if we could somehow use that information to deduce that
has density 1 in a codimension-
subspace, we would end up proving a bound of
for the density needed to guarantee an arithmetic progression, which is considerably worse than one obtains from the much simpler Roth/Meshulam argument.
Let me briefly state (a slight simplification of) Chang’s inequality in the context. If
is a set of density
with characteristic function
then for any
the largest possible independent set of
such that
has size at most
For comparison, note that Parseval’s identity tells us that the number of with
cannot be more than
where
, which gives us a bound of
without the linear independence assumption.
Later we’ll think a little bit about the proof of Chang’s inequality, but first let us get a sense of how close or otherwise it comes to allowing us to improve on the bounds for the cap-set problem.
How might the structure of the large spectrum help us?
In this short section I will make a couple of very simple observations.
First of all, suppose that is a set of density
that contains no non-trivial arithmetic progression of length 3. Let
be the characteristic function of
Then as we have seen,
(That isn’t quite accurate, but it almost is, and it’s fine if we replace the bound by
say, which would not affect the arguments I am about to give.)
Now let us do a dyadic decomposition. For each positive integer let
be the set of all non-zero
such that
Then there are a few easy facts we can write down. First of all, by Parseval’s identity,
from which it follows that
Secondly, the contribution to the sum
from
such that
is, by Parseval again, at most
Thirdly, by the bound on the sum of the cubes of the Fourier coefficients, we have that
From this and the previous observation it follows that there exists such that
for some absolute constant
Thus, up to log factors (in ), there exists
such that the number of
with
is
This is a strengthening of the statement used by Roth/Meshulam, which is merely that there exists some
with
In combination with Chang’s theorem, and again being cavalier about log factors, this tells us that we have around values of
such that
and they all have to live in a subspace of dimension at most
So the obvious question now is this: can we somehow exploit the fact that the large spectrum lies inside some lowish-dimensional subspace?
A quick point to make here is that if all we want is some improvement to the Roth/Meshulam bound, then we can basically assume that since any larger value of
would allow us to drop a dimension in return for a larger density increase than the Roth/Meshulam argument obtains. However, let me stick with a general
for now.
If there are values of
all living in a
-dimensional subspace
such that
for each one, then
Therefore, the pointwise product of
with the characteristic function of
has
-norm squared equal to
It follows that the convolution of
with the characteristic measure of
, which is the function you get by replacing
by the averaging projection
of
defined earlier in this post, has
-norm squared equal to
Now never takes values less than
so the
-norm squared of the negative part of the projection of
is at most
Therefore, there must be some coset on which
averages at least
or so.
Thus, we can lose dimensions for a density gain of
Is that good? For comparison, if we lose just one dimension we gain
so losing
dimensions should gain us
Thus, the more complicated argument using the structure of the Fourier coefficients does worse than the much simpler Roth/Meshulam argument where you lose a dimension at a time.
When it is even easier to see just how unhelpful this approach is: to use it to make a density gain of
we have to lose
dimensions, whereas the Roth/Meshulam argument loses
dimensions in total.
Can Chang’s inequality be improved?
The next part of this post is a good example of how useful it can be to the research mathematician to remember slogans, even if those slogans are only half understood. For instance, as a result of discussions with Ben Green, I had the following two not wholly precise thoughts stored in my brain.
1. Chang’s inequality is best possible.
2. The analogue for finite fields of Ruzsa’s niveau sets is sets based on the sum (in ) of the coordinates.
The relevance of the second sentence to this discussion isn’t immediately clear, but the point is that Ben proved the first statement (suitably made precise) in this paper, and to do so he modified a remarkable construction of Ruzsa (which provides some very surprising counterexamples) of sets called niveau sets. So in order to come up with a set that has lots of large Fourier coefficients in linearly independent places, facts 1 and 2 suggest looking at sets built out of layers — that is, sets of the form where the sum is the sum in
and not the sum in
Incidentally, to the best of my knowledge, “fact” 2 is an insight due to Ben himself — no less valuable for not being a precise statement — though it is likely that others such as Ruzsa had thought of it too.
Let me switch to because it is slightly easier technically and I’m almost certain that whatever I say will carry over to
Let
be the set of all
such that
where
is an integer around
The density of this layer is about
for a positive absolute constant
Now let us think about its Fourier coefficients at the points
of the standard basis. By symmetry these will all be the same, so let us look just at the Fourier coefficient at
If we write
for the set of points
such that
then this is equal to the density of
minus the density of
The density of is half the density in
of the layer of points with coordinate sum
whereas the density of
is half the density in
of the layer with coordinate sum
So basically we need to know the difference in density of two consecutive layers of the cube when both layers are close to
The ratio of the binomial coefficients and
is approximately
or in our case around
Since the two densities are around
the difference is around
Thus, if we choose to be around
we have a set of density around
with around
Fourier coefficients of size around
Apart from the log factor, this is the Chang bound. (If we want a similar bound for a larger value of
then all we have to do is take a product of this example with
for some
)
Is this kind of approach completely dead?
Chang’s theorem doesn’t give a strong enough bound to improve the Roth/Meshulam bound. And Chang’s theorem itself cannot be hugely improved, as the above example shows. (With a bit of messing about, one can modify the example to provide examples for different values of .) So there is no hope of using this kind of approach to improve the bounds for the cap-set problem.
Or is that conclusion too hasty? Here are two considerations that should give us pause.
1. The example above that showed that Chang’s theorem is best possible does not have the kind of spectrum that a set with no arithmetic progressions would have. In particular, there does not exist such that, up to log factors,
Fourier coefficients have size at least
(If we take
then we get only
such coefficients.)
2. There are other ways one might imagine improving Chang’s theorem. For instance, suppose we are given Fourier coefficients of size
We know that they must all live in a
-dimensional subspace, but it is far from clear that they can be an arbitrary set of points in a
-dimensional subspace. (All the time I’m ignoring log factors.)
Let me discuss each of these two considerations in turn.
Is there an example that completely kills the density-increment approach?
Just to be clear, the density-increment approach to the theorem is to show that if a set of density
does not contain an arithmetic progression of length 3, then there is some subspace
of small codimension such that the density of
in
is at least
The Roth/Meshulam argument allows us to take
with a codimension of 1. If we could take
to be substantially more than
on a subspace of codimension
then we would be in excellent shape. Conversely, if we could find an example where this is not possible, then we would place significant limitations on what the proof of an improved bound could look like.
Again we face the problem of deciding what “an example” means, since we are not trying to construct dense sets with no arithmetic progressions. I find that I keep coming back to the following precise question.
Question 1. Let and
be three subsets of
each of density
Suppose that there are no solutions to the equation
with
and
For what values of
and
can we say that there must be an affine subspace
of codimension
such that the density of
in
is at least
?
The Roth/Meshulam argument implies that we can take and
The following example shows that we can’t do much better than
when
(I don’t claim that it is hard to improve on this example, but I can’t do so after five minutes of thinking about it). Pick
such that
(Again, one can obtain a larger
by taking a product.) Let
be a random subset of
of density
Then
has size bounded above by approximately
which means that it must miss around half of
so we can find
of the same density such that
Since is random, its non-trivial Fourier coefficients will be around
(Again, I am ignoring a log factor that is due to the fact that a few Fourier coefficients will be unexpectedly large. Again, quadratic examples can take care of this.)
Now note that in the above example we took to be proportional to
That means that if we are prepared to lose only
dimensions, we can get the density up to 1. So the obvious next case to think about is how big a density increase we can hope for if we are prepared to drop that many dimensions.
We certainly can’t hope to jump all the way to 1. A simple example that shows this is to let be a random subset of
of density
in
and to let
be a subset of
Then the relative density of
in an affine subspace
will be
approximately
or approximately
according to whether
is disjoint from
neither disjoint from nor contained in it, or contained in it — unless, that is, we are prepared to drop down to a very low dimension indeed, where the codimension depends on
Thus, the best density increase it is reasonable to aim for is one that is proportional to the existing density.
Putting these thoughts together, it is tempting to ask the following question, which is a more specific version of Question 1.
Question 2. Let and
be above. Can we take
proportional to
and
proportional to
?
If the answer to this question is yes, then it implies a bound for the problem of a huge improvement on the Roth/Meshulam bound of
Writing
for
we can rewrite this bound as
which is of the same form as the Behrend bound in
This is suggestive, but so weakly suggestive that I’m not sure it should be taken seriously.
I should stress that a counterexample to this rather optimistic conjecture would be very interesting. But it is far from clear to me where a counterexample is going to come from, since the examples that show that Chang’s theorem is best possible do not appear to have enough large Fourier coefficients to have no arithmetic progressions.
[Added later: Ben Green makes an observation about Questions 1 and 2 in a comment below, which demands to be mentioned here since it places them in a context about which plenty is known, including exciting recent progress due to Tom Sanders. Suppose that Question 2 has a positive answer, say. Let be a set of density
Then either
or there exists
such that
does not contain 0. In the latter case, we can set
and
equal to
and
equal to
and Question 2 tells us that there must be a codimension-
subspace (where
) inside which
has density
We cannot iterate this argument more than
times before reaching a density of 1, so
must contain a subspace of codimension at most
which is stronger than the best known result in this direction, due to Sanders.
However, Sanders’s result is in the same territory: he shows that contains a subspace of codimension at most a fixed power of
in this paper. Usually what you can do for four sets you can do for three — I haven’t checked that that is true here, but maybe somebody else has (Tom, if you are reading this, perhaps you could confirm it). Thus, even if it looks a bit optimistic to prove a positive answer to Question 2, one can still hope for a positive answer with the bound slightly weakened, to say
or something like that. Furthermore, the fact that Sanders has proved what he has proved suggests that there could be techniques out there, such as the Croot-Sisask lemma, that would be extremely helpful. (However, it is clear that Sanders, Croot and Sisask have thought pretty hard about what they can get out of these techniques, so a cheap application of them seems unlikely to be possible.)]
What can the large spectrum look like?
The following argument is excerpted from the proof of Chang’s theorem. Let be a set of density
and let
be the characteristic function of
Let
be a subset of
such that
for every
Let
be the function
and recall that
by the inversion formula.
Then
Also, for any and
such that
Hölder’s inequality tells us that
Now which is close to
when
is large, and within a constant of
when
reaches
.
In order to think about let us make the simplifying (and, it turns out, not remotely problematic) assumption that
is an even integer
Then a standard calculation (or easy use of the convolution identity) shows that
We therefore know that
is at least
To get a feel for what this is telling us, let us bound the left-hand side by replacing each Fourier coefficient by That tells us that
times the number of
-tuples
such that
is at least
Therefore, the number of these
-tuples is at least
Now a trivial lower bound for the number of the -tuples is
If the number is roughly equal to this lower bound, then we obtain something like the inequality
which implies that
For example, if and
then this tells us that we cannot have a subset
of the large spectrum of size
without having on the order of
non-trivial quadruples
Even this example (which is not the that Chang considers — she takes
to be around
) raises an interesting question. Let us write
for
Then if we cannot improve on the Roth/Meshulam bound, we must have (up to log factors) a set
of size
such that amongst any
of its elements there are at least as many non-trivial additive quadruples
as there are trivial ones: that is, at least
such quadruples.
Sets with very weak additive structure.
What does this imply about the set ? The short answer is that I don’t know, but let me give a longer answer.
First of all, the hypothesis (that every subset of size spans some non-trivial additive quadruples) is very much in the same ball park as the hypotheses for Freiman’s theorem and the Balog-Szemerédi theorem, in particular the latter. However, the number of additive quadruples assumed to exist is so small that we cannot even begin to touch this question using the known proofs of those theorems.
Should we therefore say that this problem is way beyond the reach of current techniques? It’s possible that we should, but there are a couple of reasons that I think one shouldn’t jump to this conclusion too hastily.
To explain the first reason, let me consider a weakening of the hypothesis of the problem: instead of assuming that every set of size spans at least
non-trivial additive quadruples, let’s just see how many additive quadruples that tells us there must be and assume only that we have that number.
This we can do with a standard double-counting argument. If we choose a random set of size our hypothesis tells us it will contain at least
non-trivial additive quadruples. But the probability that any given non-trivial additive quadruple
belongs to the set is
so if the total number of non-trivial additive quadruples is
then
must be at least
(counting the expected number of additive quadruples in a random set in two different ways). That is,
must be at least
This is to be contrasted with the trivial lower and upper bounds of
and
Here are two natural ways of constructing a set with that many additive quadruples. The first is simply to choose a set randomly from a subspace of cardinality
The typical number of additive quadruples if
is
so we want to take
and thus to take
The dimension of this subspace is therefore logarithmic in
which means that the entire large spectrum is contained in a log-dimensional subspace, which gives us a huge density increase for only a small cost in dimensions.
The second is at the opposite extreme: we take a union of subspaces of cardinality
for some
The number of non-trivial additive quadruples is approximately
so for this to equal
we need
to be
and
to be
Note that here again we are cramming a large portion of the large spectrum into a log-dimensional subspace.
So far this is quite encouraging, but we should remind ourselves (i) that there could be some much more interesting examples than these ones (as I write it occurs to me that finite-fields niveau sets are probably worth thinking about, for instance) and (ii) that even if the most optimistic conjectures are true, they seem to be very hard to prove with this level of weakness of hypothesis.
A quick remark about the second example. If we choose points at random from each of the
subspaces of size
then those points will span around
additive quadruples, so in total we will get around
additive quadruples. This is how to minimize the number of additive quadruples in a set of size
so in the second case (as well as the first) we also have the stronger property that every subset of size
contains at least
non-trivial additive quadruples.
Going back to the point that we are assuming a very weak condition, the main reason that that doesn’t quite demonstrate that this approach is hopelessly difficult is that we can get by with a very weak conclusion as well. Given the very weak hypotheses, one can either say, “Well, it looks as though A ought to be true, but I have no idea how to prove it,” or one can say, “Let’s see if we can prove anything non-trivial about sets with this property.” As far as I know, not too much thought has been given to the second question. (If I’m wrong about that then I’d be very interested to know.)
I’ve basically given the argument already, but let me just spell out again what conclusion would be sufficient for some kind of improvement to the current bound. For the purposes of this discussion I’ll be delighted with a bound that gives a density of (since that would be below the magic
barrier and would thus raise hopes for beating that barrier in Roth’s theorem too).
As ever, I’ll take to equal
so that we have around
Fourier coefficients of size around
If
of these are contained in a
-dimensional subspace
then the sum of squares of all the Fourier coefficients in
is at least
which gives us a coset of
in which the density is increased by
This is an improvement on the Roth/Meshulam argument provided only that
is significantly bigger than
or in other words
is significantly bigger than
So here is a question, a positive answer to which would give a weakish, but definitely very interesting, improvement to the Roth/Meshulam bound. I’ve chosen some arbitrary numbers to stick in rather than asking the question in a more general but less transparent form. But if you would prefer the latter, then it’s easy to modify the formulation below.
Question 3. Let be a subset of
of size
that contains at least
quadruples
Does it follow that there is a subspace of
of dimension at most
that contains at least
elements of
?
I talked about very weak conclusions above. The justification for that description is that we are asking for the number of points of in the subspace to be around the cube of the dimension, whereas the cardinality of the subspace is exponential in the dimension. So we are asking for only a tiny fraction of the subspace to be filled up. This is much much weaker than anything that comes out of Freiman’s theorem.
To give an idea of the sort of argument that it makes available to us that is not available when one wishes to prove Freiman’s theorem, let us suppose we have a set of size
such that no subspace of dimension
contains more than
points, and let us choose from
a random subset
picking each element with probability
Given any subspace of dimension the expected number of points we pick in that subspace is at most
and the probability that we pick at least
points is at most around
The number of subspace of dimension
that contain at least
points of
is at most
which is at most
If we take
to be
then the expected number of these subspaces that contain at least
points is less than 1.
On the other hand, if the number of additive quadruples in was at least
then the expected number in our random subset is at least
while the size of that subset is around
The precise numbers here are not too important. The point is that this random subset is a set of size
that contains
additive quadruples for some
such that no subspace of dimension
contains more than
points of
And we have a certain amount of flexibility in the values of
and
Thus, to improve on the bounds for the cap-set problem it is enough to show that having
additive quadruples implies the existence of a subspace of dimension
for some small
(or even smaller dimension if one is satisfied with a yet more modest improvement to the Roth/Meshulam bound) that contains a superlinear number (in the dimension of the subspace) of points of
This is promising, partly because it potentially allows us to use the stronger hypothesis that we were actually given about Recall that the
bound for the number of additive quadruples was actually derived from the fact that every subset of
of size
contains at least
non-trivial additive quadruples. So one thing we might try to do is assume that we have a set
of size
such that no subspace of dimension
contains more than
points of
and try to use that to build inside
a largish subset (of size
say) that has very few additive quadruples.
Let me end this section with a reminder that we have by no means explored all the possibilities that arise out of Chang’s argument. I have concentrated on the case (and thus
) because it is easy to describe and because it relates rather closely to existing results in additive combinatorics. But if it is possible to use these ideas to obtain a big improvement to the Roth/Meshulam bound, then I’m pretty sure that to do so one needs to take
to be something closer to
as Chang does in her theorem. The arguments I have been sketching have their counterparts in this range too. In short, there seems to be a lot of territory round here, and I suspect that not all of it has been thoroughly explored.
Is there a simple and direct way of answering Question 2?
Let me begin with a reminder of what Question 2 was. Let and
be three subsets of
each of density
Suppose that there are no solutions to the equation
with
and
Then Question 2 asks whether there is an affine subspace
of codimension
such that the density of
inside
is at least
The Roth/Meshulam argument gives us a density of in a codimension-1 subspace, and it does so by expanding and applying simple identities and inequalities such as Parseval and Cauchy-Schwarz to the Fourier coefficients. Now Fourier coefficients are very closely related to averaging projections onto cosets of 1-codimensional subspaces (a remark I’ll make more precise in a moment). Can we somehow generalize the Roth/Meshulam argument and look at an expansion in terms of averaging projections to cosets of
-codimensional subspaces, with
? Is there a very simple argument here that everybody has overlooked? Probably not, but if there isn’t then it at least seems worth understanding where the difficulties are, especially as quite a lot of the Roth/Meshulam argument does generalize rather nicely.
Expanding in terms of projections.
[Added later: While looking for something else, I stumbled on a paper of Lev, which basically contains all the observations in this section.]
For the purposes of this section it will be convenient to work not with the characteristic functions of and
but with their balanced functions, which I shall call
and
The balanced function of a set
of density
is the characteristic function minus
That is, if
then
and otherwise
The main properties we shall need of the balanced function are that it averages zero and that if it averages
in some subset of
then
has density
inside that subset.
Here is another simple (and very standard) lemma about balanced functions. Suppose we pick a random triple of elements of
such that
Then the probability that it lies in
is
This sum splits into a sum of eight sums, one for each way of choosing either the first or the second term from each bracket. But since and
all average zero, all but two of these terms disappear. For example,
is zero since it equals
which in turn equals
Thus, the probability in question is
In particular, if it is zero, then
Let be a linear subspace of
of codimension 1. Then
is of the form
for some
(which is unique up to a scalar multiple), where
stands for the sum
in
Let us write
for the function
defined by setting
to be the average of
over all
Thus,
is the averaging projection that maps a function to the nearest function that is constant on cosets of
Let us now relate this to the Fourier expansion of
I shall do it by a direct calculation, but it can be understood conceptually: if we restrict the Fourier transform to a subspace, then we convolve the original function by the annihilator of that subspace.
By the inversion formula, we have that
where Now let us pick a non-zero
and consider the sum
Note that we are adding up over all Fourier coefficients at multiples of Expanding the Fourier coefficients, we obtain the sum
The term in brackets is 3 when and 0 otherwise. If
is the subspace
then this says that the term in brackets is 3 if
and
lie in the same coset of
and 0 otherwise. Since the probability that they lie in the same coset is 1/3, this tells us that the sum is nothing other than
An additional observation, and our reason for using balanced functions, is that if averages zero, then
Therefore, in this case we have the identity
and also (by the inversion formula and the fact that the pairs partition the non-zero elements of
) the identity
where the sum is over all subspaces of codimension 1.
Since the functions form an orthonormal basis, we can also translate Parseval’s identity into the form
and more generally
What about counting arithmetic progressions of length 3? Well, expands as
Interchanging summation we obtain
Now the three functions
and
all average zero, and they are constant on cosets of
and
respectively. If
and
are not all equal, then the inner expectation must be zero. To see this, let
and
be vectors “perpendicular” to
and
respectively. Then
if and only if there exists
that cannot be written as
with
That is the case if and only if there is a multiple
of each of
and
such that
(Why? Well if there is such a multiple then it is obvious. Conversely, if
is not in
then there must be a linear functional
that vanishes on
but not at
If that linear functional is
then
must be a multiple of each of
and
) Such
exist if and only if
and
are all multiples of each other, which happens if and only if
and
are all equal.
Therefore, the AP count can be rewritten as
In words, the AP count is obtained by summing the AP counts over all codimension-1 averaging projections.
Now the size of that last expression is bounded above by
By the projections version of Parseval’s identity, the sum of those inner products is so the assumption that there are no APs in
implies that
Since and
are at most
we find that
which implies that there is a coset of some
in which
averages at least
(The factor 1/2 comes from the fact that
might have its
norm by virtue of
averaging
on a coset. But since
averages zero, we then get at least
on one of the other two cosets.)
What I have just done is recast the Roth/Meshulam argument in terms of averaging projections rather than Fourier coefficients — but it is basically the same argument. What was the point of doing that? My motivation was that the projections version gives me something I can generalize to subspaces of higher codimension.
Expanding in terms of higher-codimension averaging projections.
A lot of what I said in the last section carries over easily to the more general situation where we sum over higher-codimension averaging projections. Let us fix a and interpret all sums over subspaces as being over the set of all subspaces of codimension
Our first identity in the case
was
What happens for general ? Well,
Let us write for the number of codimension-
subspaces of
Then the number of codimension-
subspaces that contain
is
if
and
otherwise (since the probability that a random codimension-
subspace contains
is equal to the number of non-zero points in such a subspace divided by the total number of non-zero points in
). Therefore, the sum above works out as
The contribution from the second term is zero, since averages zero, so we get
Thus, is proportional to
with a constant of proportionality that is not too hard to estimate.
Next, let us prove a version of Parseval’s identity.
Now the number of subspaces containing depends on the dimension of the space spanned by
and
However, if we sum
over all pairs
then we get zero (since
averages zero). If we sum over all pairs of the form
for some
then we get zero, since every pair
can be written in
ways as
The same applies to pairs of the form
and pairs of the form
Finally, if we sum over pairs of the form
we get a multiple of
with a larger multiple (by a factor of roughly
) if
Putting this together, we find that is proportional to
again with a constant of proportionality that, with a bit of effort, one can estimate fairly accurately. Once again, this implies (by polarization or by generalizing the proof) that
is proportional to
Finally, let us prove that the AP count of is proportional to the sum of the AP counts of the projections. We have
The value of depends only on the dimension of the subspace spanned by
The sum of
over all
is zero. The sum over all
that satisfy a non-trivial linear relation
is zero unless
(because unless that is the case we can express any triple in the form
with
and
and the result is proportional to
). The sum over all
such that
is proportional to
Putting all this together tells us that
is proportional to as claimed. What is potentially significant about this is that if we can use it to show that there is some
of low codimension such that the AP count of
is reasonably large, then there must be some coset of
on which
has reasonably large average.
At this point, honesty compels me to mention that the above facts can be proved much more simply on the Fourier side — so much so that it casts serious doubt on whether one could get anything out of this “codimension- expansion” that one couldn’t get out of the normal Fourier expansion. All we have to do is point out that the Fourier expansion of
is the restriction of
to
and that if
sums to zero then
From this it follows easily that the Fourier transform of
is proportional to
that
is proportional to
and that
is proportional to
From those facts, the results above follow easily.
Thus, all we are doing by splitting up into the functions is splitting up the Fourier transform of
as a suitable average of its restrictions to the subspaces
(and using the fact that
— all non-zero points will be in the same number of subspaces
). How can that possibly tell us anything that we can’t learn from examining the Fourier transform directly?
The only answer I can think of to this question is that it might conceivably be possible to prove something by looking at some function of the projections that does not translate easily over to the Fourier side. I have various thoughts about this, but nothing that is worth posting just yet.
So what was the point of this section? It’s here more to ask a question than propose an answer to anything. The question is this. If it really is the case that for every AP-free set (or AP-free triple of sets ) there must be a fairly low-codimensional subspace
such that variations in density show up even after one applies the averaging projection
then it seems highly plausible that some kind of expression in terms of these expansions should be useful for proving it. For instance, we might be interested in the quantity
where
is the balanced function of
And perhaps we might try to analyse that by looking instead at
for some suitably chosen large integer
(to get a handle on the maximum but also to give us something we can expand and think about). The question is, can anything like this work? I don’t rule out a convincing negative answer. One possibility would be to show that it cannot give you anything that straightforward Fourier analysis doesn’t give you. A more extreme possibility is that the rather optimistic conjecture about getting a large density increment on a low-codimensional subspace is false. The latter would be very interesting to me as it would rule out a lot of approaches to the problem.
Conclusion.
I don’t really feel that I’ve come to the end of what I want to say, but I also feel as though I am never going to reach that happy state, so I am going to cut myself off artificially at this point. Let me end by briefly discussing a question I mentioned at the beginning of this post: is this the beginning of a Polymath project?
It isn’t meant to be, partly because I haven’t done any kind of consultation to see whether a Polymath project on this problem would be welcome. For now, I see it as very much in the same spirit as Gil Kalai’s “open discussion”. What I hope is that some of my remarks will provoke others to share some of their thoughts — especially if they have tried things I suggest above and can elaborate on why they are difficult, or known not to work. If at some point in the future it becomes clear that there is an appetite for collectively pursuing one particular approach to the problem, then at that point we could perhaps think about a Polymath project.
Should there be ground rules associated with an open discussion of a mathematical problem? Perhaps there should, but I’m not sure what they should be. I suppose if you use a genuine idea that somebody has put forward in the discussion then it is only polite to credit them: in any case, the discussion will be in the public domain so if you have an idea and share it then it will be date-stamped. If anyone has any further suggestions about where trouble might arise and how to avoid it then I’ll be interested to hear them.
January 11, 2011 at 3:51 pm |
I guess these are called “cap sets” because they cap the number of cards you can have in the Set game without having a set.
January 11, 2011 at 5:00 pm |
I was once told that cap-sets, which are investigated in various geometries, are called like this, since the shape of a cap (in the sense of headgear) resembles a form not containing three colinear points. Some other terms used in this context, e.g., oval or ovoid, seem to have a similar origin.
January 11, 2011 at 6:15 pm |
Tim,
Thanks for this interesting post. Here is a thought that occurred to me whilst reading it, and which I haven’t looked at in any detail yet. Your question 2 seems to be pretty close to some well-known unsolved problems connected with (and in fact stronger than) the polynomial Freiman-Ruzsa conjecture (PFR). In particular it is conjectured that A + B contains 99 percent of a subspace of codimension C log (1/\alpha), so if A + B doesn’t meet -C then C will definitely have some biases on subspaces of that kind of dimension. This conjecture implies the “polynomial Bogolyubov conjecture”, which is known to imply PFR but is not known to follow from it. I’ll have to think about how your question fits into this circle of ideas.
Actually, as I write this, it occurs to me that if your question holds then either A + A + A is everything or else A has doubled density on a subspace of codimension log (1/\alpha). So by iteration you get that A + A + A contains a subspace of codimension log^2 (1/\alpha), if I’m not mistaken. This is already better than known bounds for Bogolyubov-type theorems (there is a very recent paper of Sanders in which he gets log^4 (1/\alpha) I believe).
It would be interesting to know whether you can reverse the implication (P Bogolyubov => weak form of Q2 => improvements on cap sets) . I think Sanders and Schoen have done some work on related issues — if instead of solving x + y = 2z you want to solve x + y + z = 3w I think they have something new to say.Tom Sanders will be able to supply the details.
January 11, 2011 at 6:35 pm
I don’t quite understand your point about A+A+A here. If A has doubled density, I don’t see how you then iterate, because you no longer know about the densities of B and C. Also, although the result might be stronger than known Bogolyubov theorems (though that’s not a disaster as one could simply allow the codimension to be a bit larger), the assumption is a bit different.
Ah, in writing that I see a very elementary pint that I’d missed (despite knowing it in many other contexts), namely that what I’m assuming is strictly weaker than assuming that the density of A+A is at most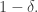 I’ll have a think about whether I want to modify what I’ve written.
I’ll have a think about whether I want to modify what I’ve written.
January 11, 2011 at 7:18 pm |
Tim,
On the first iteration I plan to take A = B and C = A – x, where x is some element not in A + A+ A. This gives me A’, a set with density 2\alpha on F_3^{n’} with n’ >= n – O(log (1/\alpha). Now if A’ + A’ + A’ is everything (in F_3^{n’}) I’m done; otherwise repeat. Doesn’t this work?
Ben
January 11, 2011 at 7:25 pm
In between replying to your previous comment and replying to this I had a bath, during which I understood properly what you were saying — and indeed it works.
January 11, 2011 at 10:08 pm |
Dear Tim,
I had in mind a somewhat different approach to improving upon the Roth-Meshulam bound that I think I can describe fairly painlessly: suppose that is a subset of
is a subset of  of density
of density  , where we take
, where we take  as close to
as close to  as we please and
as we please and  (the goal is to show that
(the goal is to show that 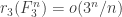 ). Then, of course, if
). Then, of course, if  is small enough the Roth-Meshulam approach will just fail to work. However, if you do about
is small enough the Roth-Meshulam approach will just fail to work. However, if you do about 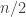 Roth iterations (passing to hyperplanes each time), what you will wind up with is a subspace
Roth iterations (passing to hyperplanes each time), what you will wind up with is a subspace  of dimension about
of dimension about 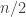 and a set
and a set  such that the following hold:
such that the following hold:
1. First, if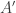 contains a 3AP in
contains a 3AP in  , then
, then  contains a 3AP in
contains a 3AP in  .
.
2. Let be the set of all
be the set of all 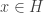 having at most
having at most  representations as
representations as 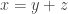 where
where  . Then, second, we have that
. Then, second, we have that 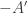 is a positive density subset (the density will be a function of
is a positive density subset (the density will be a function of  ) of
) of  . In other words,
. In other words, 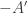 is a dense subset of a level-set of a sumset.
is a dense subset of a level-set of a sumset.
Now, if we knew that were roughly translation-invariant by a couple different directions
were roughly translation-invariant by a couple different directions  (where, say,
(where, say,  ), then we would expect that there exists
), then we would expect that there exists  such that
such that  , where
, where  . In other words, there is a shift of a low-dimensional (but not too low) subspace
. In other words, there is a shift of a low-dimensional (but not too low) subspace  that intersects
that intersects 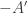 in many points. Upon applying Roth-Meshulam to this intersection we’d be done, since then
in many points. Upon applying Roth-Meshulam to this intersection we’d be done, since then 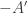 would contain a 3AP, implying that
would contain a 3AP, implying that 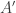 contains a 3AP, implying that
contains a 3AP, implying that  contains a 3AP.
contains a 3AP.
But could we show that is translation-invarant by many directions? Well, it turns out that my work with Olof is just barely too weak to do this — if we could improve our method only a tiny bit, we’d be done (basically, we would try to show that the function
is translation-invarant by many directions? Well, it turns out that my work with Olof is just barely too weak to do this — if we could improve our method only a tiny bit, we’d be done (basically, we would try to show that the function 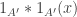 is roughly translation-invariant by a lot of directions, which would imply that various level-sets of this function are roughly translation-invariant; our method works so long as the density of
is roughly translation-invariant by a lot of directions, which would imply that various level-sets of this function are roughly translation-invariant; our method works so long as the density of 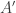 is just larger than about
is just larger than about 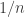 ).
).
What I plan to do is to generalize mine and Olof’s results so that we can work with densities somewhat below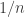 , and where I replace “translation-invarance” with some other property. I can prove *some* non-trivial things about the function
, and where I replace “translation-invarance” with some other property. I can prove *some* non-trivial things about the function 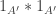 by generalizing our arguments in a trivial way (the sort of things that are pretty much hopeless to show using Fourier methods as we currently understand them); and I suspect that much more will follow once I have a chance to seriously think about it.
by generalizing our arguments in a trivial way (the sort of things that are pretty much hopeless to show using Fourier methods as we currently understand them); and I suspect that much more will follow once I have a chance to seriously think about it.
By the way… Seva Lev once emailed me some constructions of sets giving very little density gain under multiple Roth iterations. I forget what bounds he got exactly, however. Perhaps you should email him.
January 16, 2011 at 11:25 am
Ernie, I have trouble understanding your interesting-looking argument. Here are a few questions.
1. When you say that after n/2 Roth iterations you get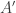 with certain properties, is that supposed to be obvious, or is there an argument you are not giving that tells us that
with certain properties, is that supposed to be obvious, or is there an argument you are not giving that tells us that 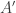 has properties that we cannot assume for the original set
has properties that we cannot assume for the original set  ? Either way, how are these n/2 Roth iterations helping us?
? Either way, how are these n/2 Roth iterations helping us?
Actually, that’s my only question for now. I get a bit lost in the paragraph after your property 2, so if you felt like expanding on that, it would also be very helpful.
January 16, 2011 at 10:42 pm
[1. When you say that after…]
Actually, that part is fairly easy to do. Starting with a subset A of having density about
having density about  , two things can happen: either all the non-trivial Fourier coefficients are smaller than about
, two things can happen: either all the non-trivial Fourier coefficients are smaller than about  , or there is at least one that is larger than this in magnitude. If we are in the former case, then just writing the number of 3APs in terms of Fourier coefficients we quickly see that
, or there is at least one that is larger than this in magnitude. If we are in the former case, then just writing the number of 3APs in terms of Fourier coefficients we quickly see that  contains 3APs. And if we are in the latter case, just doing one Roth iteration will boost the relative density (on a hyperplane) by a factor
contains 3APs. And if we are in the latter case, just doing one Roth iteration will boost the relative density (on a hyperplane) by a factor 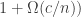 .
.
Now let’s suppose that we do this for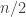 iterations, and that for each iteration we can *always* find a Fourier coefficient where we can do a little better: instead having one of size at least
iterations, and that for each iteration we can *always* find a Fourier coefficient where we can do a little better: instead having one of size at least  , we always find one of size at least
, we always find one of size at least  , resulting in a magnification in the density after each iteration by a factor
, resulting in a magnification in the density after each iteration by a factor  . When we do this
. When we do this 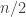 times, we end up with a set whose relative density inside
times, we end up with a set whose relative density inside 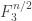 (assume
(assume  is even) has size
is even) has size
That density is just large enough that the standard Roth-Meshulam bound guarantees that our set has 3APs.
So either we prove that our set has 3APs by the th iteration, or else at *some* iteration all the non-trivial Fourier coefficients are
th iteration, or else at *some* iteration all the non-trivial Fourier coefficients are  times as large as at the principal character.
times as large as at the principal character.
Now, if we find ourselves in this latter case, then it means we have passed to a set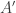 that is fairly quasirandom inside some space
that is fairly quasirandom inside some space 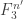 , where
, where  . It is *so* quasirandom, in fact, that standard arguments show that
. It is *so* quasirandom, in fact, that standard arguments show that  for all but at most
for all but at most 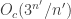 places
places  (here,
(here,  is normalized to just be the count of the number of solutions
is normalized to just be the count of the number of solutions 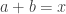 ,
,  ).
).
If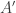 contains no 3APs, then for any
contains no 3APs, then for any  we must have
we must have 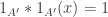 (there is always the trivial solution
(there is always the trivial solution 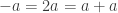 ). What this means is that if
). What this means is that if 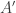 has no 3APs, then
has no 3APs, then 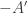 must be a subset of those
must be a subset of those 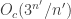 places where
places where  . And in fact, this means that
. And in fact, this means that 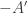 is then a positive-density subset of a particular level-set of
is then a positive-density subset of a particular level-set of 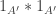 !
!
If we just knew that this level set was roughly a union of cosets of some subspace of not-too-low-dimension, then one of those cosets would intersect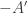 in a positive density of elements… and then we’d be done. Alas, my work with Olof is just barely too weak to show this — if the set
in a positive density of elements… and then we’d be done. Alas, my work with Olof is just barely too weak to show this — if the set 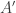 were just of slightly higher density a direct application of our methods would indeed show exactly what we need (covering by cosets).
were just of slightly higher density a direct application of our methods would indeed show exactly what we need (covering by cosets).
Tom’s recent work on Bogolyubov seems like the obvious idea to try at this point, since it even works with very low-density sets. However, his result only shows that there is a large subspace meeting the set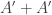 in a high proportion of the points of that subspace; it does *not* show that the level-sets of
in a high proportion of the points of that subspace; it does *not* show that the level-sets of 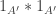 can be *covered* by cosets of that subspace. I have actually thought some on Tom’s proof, and it seems that it is too “local” to get this type of conclusion without some modifications.
can be *covered* by cosets of that subspace. I have actually thought some on Tom’s proof, and it seems that it is too “local” to get this type of conclusion without some modifications.
Fortunately, I don’t think we have quite reached the limit of what my work with Olof can achieve…
January 16, 2011 at 10:43 pm
Oops… everywhere I wrote $latec A^(0)$ I should have written .
.
January 17, 2011 at 6:02 am
Also, where I wrote , I meant
, I meant 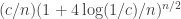 . (Too bad wordpress doesn’t allow one to edit ones comments.)
. (Too bad wordpress doesn’t allow one to edit ones comments.)
January 17, 2011 at 9:04 am
That non-feature of WordPress is indeed very irritating.
I’m in the middle of a new post, and, interestingly, some of what you write above is very similar to things that I have written in the post. I won’t say more for now, but will try to finish the post as soon as I can.
January 13, 2011 at 10:18 pm |
The problem is indeed fascinating. One basic example is all 0,1 vectors. One idea I thought about variations of this example which may be useful was this: suppose that n is a power of 4 and let the n coordinates organized at the leaves of a 4-regular tree. When the variables are labeled 0, 1, 2 label inductively each internal vertex 2 if at least 2 of the sons is labeled 2. Otherwised label it 0 or 1. Consider all vectors of 0,1,2, so that the root is labelled 0 or 1. for three such vectors x y and z there is a son of the root they all are labeled 0 or 1 this goes all the wat to a single variable they all ar elabeled 0 and 1. so there is now x+y+z=0. The point is to find example base don somehow importing some Boolean function we have.
January 13, 2011 at 10:33 pm
(this was a bit silly since in a coordinate with no 2 the three entries can still be the same. in any case, I had the vague hope that using some sircuits or formulas expressing relations between the coordinates may lead to interesting examples. )
January 14, 2011 at 6:51 am |
Sorry, part of my post seems not to have appeared. There’s an unfortunate skip between d/N^2 and S. I think it is because blogger
gets upset when it sees two less than signs together. I have replaced my double
less thans with less thans.
Let me try again.
Dear Tim,
Michael Bateman and I have worked, unsuccessfully, quite a bit on the cap set problem along the lines which you suggest. The spectrum of a capset with no increments better than Meshulam’s in fact has much better structure than your blog post suggests. It has largish subsets which are close to additively closed but not quite close enough by our bookkeeping to get an improvement.
Let us suppose that is a capset of size almost
is a capset of size almost  in
in 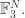 Let
Let  be the set of frequencies where
be the set of frequencies where  shows bias of at least almost
shows bias of at least almost 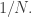 It can never be much more than
It can never be much more than  or we automatically have a better increment. You show that
or we automatically have a better increment. You show that 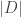 is about
is about  and that
and that  has at least
has at least  additive quadruples. But, in fact, the situation is much sharper than this because
additive quadruples. But, in fact, the situation is much sharper than this because  has no more than
has no more than  additive quadruples. Moreover, things don’t get better when you look at higher tuples.
additive quadruples. Moreover, things don’t get better when you look at higher tuples.  has at most
has at most 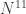 sextuples,
sextuples, 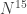 octuples and so forth.
octuples and so forth.
Here’s a sketch of a proof. We have the Fourier argument which appears in your post controlling how much spectrum can be in a subspace. In particular, a subspace of dimension may contain no more than
may contain no more than  elements of the spectrum. (At least this is true for
elements of the spectrum. (At least this is true for  where none of the Meshulam increments are substantially better than the first.)
where none of the Meshulam increments are substantially better than the first.)
This tells us a lot about how linearly independent must be small random selections from If I have already selected
If I have already selected  elements from
elements from  at random without replacement and I am about to select a
at random without replacement and I am about to select a 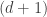 st, then the span of the elements I have already selected is at most
st, then the span of the elements I have already selected is at most 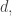 so the probability that the
so the probability that the 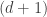 st element lives in the span is at most
st element lives in the span is at most 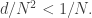 Thus if I take a random selection without replacement of almost
Thus if I take a random selection without replacement of almost  elements, then they have a good chance (better than
elements, then they have a good chance (better than  ) of being linearly independent and indeed the probability that they have nullity
) of being linearly independent and indeed the probability that they have nullity  is exponentially decreasing in
is exponentially decreasing in  We let
We let 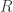 be this random selection and we ask ourselves how many
be this random selection and we ask ourselves how many  -tuples come entirely from elements of
-tuples come entirely from elements of  We choose a maximal linearly independent set of all vanishing linear combinations of elements of
We choose a maximal linearly independent set of all vanishing linear combinations of elements of 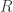 which consist of at most
which consist of at most 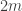 elements of
elements of  This set consists of at most
This set consists of at most  elements because
elements because 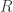 has nullity
has nullity 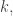 so it involves at most
so it involves at most  elements of
elements of  Therefore there are at most
Therefore there are at most 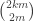 many
many  -tuplets in
-tuplets in  This grows only polynomially in
This grows only polynomially in  with
with  fixed. Therefore the expected number of
fixed. Therefore the expected number of  -tuplets is bounded above by a constant depending only on
-tuplets is bounded above by a constant depending only on 
However suppose that has many more than
has many more than 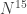 octuplets. For some
octuplets. For some 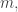 it will have substantially more than
it will have substantially more than 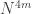
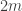 -tuplets and therefore, the expected number of
-tuplets and therefore, the expected number of 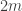 -tuplets in
-tuplets in 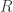 will be more than a constant. This is a contradiction.
will be more than a constant. This is a contradiction.
So we really can expect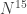 octuplets in
octuplets in  and no more. What good does that do? A hint at the answer lies in a paper of mine with Paul Koester which has been getting a fair amount of attention lately. In that paper, what Paul and I did was to try to quantify the structure of nearly additively closed sets by how much they get better when you add them to themselves. The result was in any case to get slight better energy than one might expect for a subset of the sumset. The extremes of the range of examples we had in mind were a) random set + subspace and b) random subset of subspace. In the case a) the sumsets never get better – the subspace stays the same and the random set expands. Let us call that, for the sake of this message, the additively non-smoothing case. The example b) is just the opposite. Add it to itself once and you get whole subspace. In our paper, we put every additive set somewhere in a continuum between these two examples. However, if we know in advance that there no more octuplets than Holder requires, then we have no additive smoothing and this means we are stuck close to example a). Let me show a little more rigorously how this works in our present situation.
and no more. What good does that do? A hint at the answer lies in a paper of mine with Paul Koester which has been getting a fair amount of attention lately. In that paper, what Paul and I did was to try to quantify the structure of nearly additively closed sets by how much they get better when you add them to themselves. The result was in any case to get slight better energy than one might expect for a subset of the sumset. The extremes of the range of examples we had in mind were a) random set + subspace and b) random subset of subspace. In the case a) the sumsets never get better – the subspace stays the same and the random set expands. Let us call that, for the sake of this message, the additively non-smoothing case. The example b) is just the opposite. Add it to itself once and you get whole subspace. In our paper, we put every additive set somewhere in a continuum between these two examples. However, if we know in advance that there no more octuplets than Holder requires, then we have no additive smoothing and this means we are stuck close to example a). Let me show a little more rigorously how this works in our present situation.
We have a set of size
of size  with at least approximately
with at least approximately  quadruples and at most
quadruples and at most 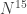 octuples. I will aim at something very modest which is not nearly strong enough to imply a cap set improvement but which seems a great deal stronger than the structure you have indicated in your post. Namely there is a subset
octuples. I will aim at something very modest which is not nearly strong enough to imply a cap set improvement but which seems a great deal stronger than the structure you have indicated in your post. Namely there is a subset  of
of  with the size of
with the size of  at least
at least  so that there is
so that there is 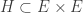 with
with 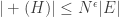 and with
and with 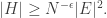 [We can do a little better but still not enough to do any good.]
[We can do a little better but still not enough to do any good.]
I have written my claim so that I never have to be self-conscious about dyadic pigeonholing. [And by the bookkeeping I can do, much of this falls apart without it. I omit all logs that appear. This is in fact a problem.]
Thus, I can start out with a set so that
so that 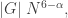 so that the sums in
so that the sums in  are all popular: that is
are all popular: that is 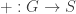 with
with 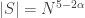 and I assume each sum is represented
and I assume each sum is represented 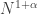 ways and each element
ways and each element 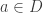 appears as a summand in
appears as a summand in  sums.
sums.
As in my paper with Koester for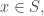 we define the set
we define the set ![D[x]](https://s0.wp.com/latex.php?latex=D%5Bx%5D&bg=ffffff&fg=333333&s=0&c=20201002) to consist of all summands of
to consist of all summands of 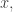 or if you
or if you![D[x] = (x-D) \cap D.](https://s0.wp.com/latex.php?latex=D%5Bx%5D++%3D++%28x-D%29++%5Ccap++D.&bg=ffffff&fg=333333&s=0&c=20201002)
prefer
Now we consider the expression
Clearly, this expression counts triples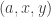 with
with ![a \in D[x]](https://s0.wp.com/latex.php?latex=a+%5Cin+D%5Bx%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![a \in D[y].](https://s0.wp.com/latex.php?latex=a+%5Cin+D%5By%5D.&bg=ffffff&fg=333333&s=0&c=20201002) Since each a participates in
Since each a participates in  sums, the expression clearly adds to
sums, the expression clearly adds to  Now again we uniformize assuming the entire sum comes from terms of size
Now again we uniformize assuming the entire sum comes from terms of size 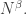 Thus there are
Thus there are 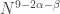 many pairs
many pairs 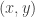 so that
so that ![D[x] \cap D[y]](https://s0.wp.com/latex.php?latex=D%5Bx%5D+%5Ccap+D%5By%5D&bg=ffffff&fg=333333&s=0&c=20201002) has size
has size 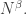
What does this mean?
If is in both
is in both ![D[x]](https://s0.wp.com/latex.php?latex=D%5Bx%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![D[y],](https://s0.wp.com/latex.php?latex=D%5By%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002) we have
we have 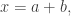
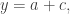 thus
thus 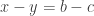 and this happens in
and this happens in  different ways.
different ways.
Thus we have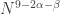 pairs
pairs  with
with  differences.
differences.
Applying Cauchy Schwarz, we get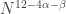 additive quadruples in
additive quadruples in 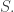
Applying the fact that each element of has
has 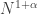 representations as pairs in
representations as pairs in 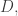 we get
we get 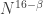 additive octuples in
additive octuples in  Since we have no more than
Since we have no more than 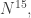 this tells us that
this tells us that  On the other hand, we know
On the other hand, we know 
If which is ,for instance, true in the case
which is ,for instance, true in the case
 then we're done. The sets
then we're done. The sets ![D[x]](https://s0.wp.com/latex.php?latex=D%5Bx%5D&bg=ffffff&fg=333333&s=0&c=20201002) have
have To be precise, we find a typical
To be precise, we find a typical ![D[x]](https://s0.wp.com/latex.php?latex=D%5Bx%5D&bg=ffffff&fg=333333&s=0&c=20201002) to be almost invariant under
to be almost invariant under  distinct shifts and therefore to be almost additively closed.
distinct shifts and therefore to be almost additively closed.
to essentially belong to disjoint blocks of size
What if is much smaller than
is much smaller than  ? Then we ask how many differences
? Then we ask how many differences  do we have with
do we have with  representations. It is at most
representations. It is at most  since any more would imply too many additive quadruples in D. On the other hand, assuming that
since any more would imply too many additive quadruples in D. On the other hand, assuming that 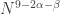 pairs
pairs  have fewer than
have fewer than 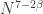 differences would imply more than
differences would imply more than 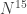 octuples in
octuples in  again a contradiction. Thus we have exactly
again a contradiction. Thus we have exactly  such differences which means we can replace
such differences which means we can replace  by
by 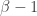 which is smaller. We iterate until
which is smaller. We iterate until  stabilizes.
stabilizes.
However, it is not at all clear to me how this structure helps us. The easy Plancherel bound tells us no more than in a space of dimension
in a space of dimension  which doesn't say much about additively closed sets of size
which doesn't say much about additively closed sets of size  in the spectrum. If
in the spectrum. If  is really close to
is really close to  I can do something with a two step process where I first pass to a relatively low codimension subspace with no large negative increments and then do Plancherel again in a less lossy way. However this falls apart once the density of the spectrum in the subspace gets too small relative to the size of the spectrum so applying Freiman together with the losses from pigeonholing sinks me.
I can do something with a two step process where I first pass to a relatively low codimension subspace with no large negative increments and then do Plancherel again in a less lossy way. However this falls apart once the density of the spectrum in the subspace gets too small relative to the size of the spectrum so applying Freiman together with the losses from pigeonholing sinks me.
Best,
Nets
January 14, 2011 at 11:28 am
A useful link seems to be:
Click to access 0802.4371v1.pdf
Regards,
Christian.
January 15, 2011 at 4:34 pm
Perhaps Nets’s most interesting comment can be made into a separate post?
January 15, 2011 at 4:56 pm
I absolutely agree, and am going to try to process it. Actually, even without it I’ve got enough material for at least one more post. When my six-week-old daughter lets me, I shall get writing.
January 14, 2011 at 1:59 pm |
[…] and so it is interesting to see what motivates him to write a blog about mathematics. This latest post goes a large way to explaining why. He starts by speculating about the features of some piece of […]
January 16, 2011 at 7:32 am |
I have another mathematical post to make and I have been instructed that to produce tex output I should write “latex”
after left dollar signs. I have never tried this before and am worried that I may have misunderstood
so I apologize in advance if this post has the extraneous word “latex” appearing over and over again.
I now think I have a heuristic for getting an improvement in the capset problem along the lines must have size at most
must have size at most 
 but really small (think
but really small (think  .) Let me try to describe it. The rough idea will
.) Let me try to describe it. The rough idea will .
.
that a capset
for some fixed small
be to take
Fourier transforms fiberwise on subspaces for more than one way of decomposing the underlying space
thus the description will require a bit of notation. Because of the nature of the result I am
aiming for, I will be perpetually ignoring constants of size
Let me begin by recalling the Fourier argument which says that in any subspace of dimension $d$ there are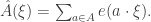 $
$
at most $Nd$ elements of the spectrum. I am in the habit of normalizing everything in the wrong way so bear with me.
We define the Fourier transform
$
Now we let be a subspace of
be a subspace of  of dimension
of dimension  with
with  a lot smaller than
a lot smaller than
 . And we let
. And we let  be a
be a on the space
on the space . Thus on each affine subspace
. Thus on each affine subspace  for
for
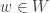 , we cannot have a positive increment stronger than
, we cannot have a positive increment stronger than  . That is,
. That is,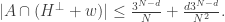 $
$ the expression
the expression  .
.
subspace of dimension
side which is transverse to the annihilator
$
We denote by
Now using Plancherel, we have that $
$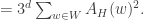 $
$
$
$
Now we break up as the disjoint union
as the disjoint union  , where
, where $
$
$
For , we have the estimate
, we have the estimate 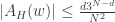
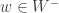 , we merely have the estimate
, we merely have the estimate 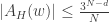
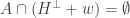 and is indeed what we should expect
and is indeed what we should expect $
$ elements
elements  of
of 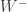 for which
for which $
$
whereas, unfortunately for
which is what happens when
given the negative bias of $\hat A(\xi)^3$. However, we also know by cancellation that
$
Thus the worst case happens when there are about
$
In that case, we have $
$
$
Since an element of the the spectrum is a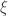 for which
for which  , there are at most
, there are at most
 such elements in the subspace
such elements in the subspace  .
.
Now let us recall where we were at the end of my previous post. The spectrum (and indeed any nearly full subset of it) and indeed of any nearly
and indeed of any nearly factors is additively nonsmoothing mod
factors is additively nonsmoothing mod  factors. This guarantees
factors. This guarantees and possibly larger which has nearly maximal energy.
and possibly larger which has nearly maximal energy. which is nearly additively closed
which is nearly additively closed . Thus we have a subset of size at least almost
. Thus we have a subset of size at least almost  contained
contained . Let us call the subspace $H$ and the subset of the spectrum
. Let us call the subspace $H$ and the subset of the spectrum  .
. as if it is a subspace. And we’d like to think of the spectrum as being
as if it is a subspace. And we’d like to think of the spectrum as being  with
with
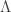
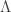 of size
of size so that for each element
so that for each element  , we have that
, we have that  has
has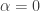 case, where zero always means
case, where zero always means  . If we had too large
. If we had too large estimate.]
estimate.]
of
tight capset up to
us that the spectrum has a subset of size at least
Applying Balog-Szemeredi-Gowers this gives us a subset of size almost
(that is the doubling constant is
in a subspace of dimension
We think of
a random set. This isn’t quite true, but it’s approximately true in the sense that there’s a
about
large intersection with the
spectrum. [Notice that we are in the
a set nearly additively closed, we would already violate the
So we’re in the situation I was unhappy about in the last post, namely the subset of the spectrum has almost in
of the spectrum has almost in
 elements in a space of dimension
elements in a space of dimension  and it does not violate the
and it does not violate the  bounds
bounds elements of
elements of 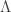 , say
, say

 , I get a subspace
, I get a subspace  with dimension no more than
with dimension no more than 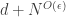 .
. which is a lot more than
which is a lot more than  but still very,very small. Then the beautiful thing
but still very,very small. Then the beautiful thing are contained in
are contained in  and disjoint for different
and disjoint for different  ‘s.
‘s. is tight for the
is tight for the  bound on spectrum it contains. What is really quite amazing about this
bound on spectrum it contains. What is really quite amazing about this ‘s I picked and different choices give us spans with trivial intersection.
‘s I picked and different choices give us spans with trivial intersection.
 .
.
but is merely almost tight
for it. However it gets better. If I choose randomly
and I take their span with
We can choose
this to be some
is that large parts of each
Thus the
subspace
is that this is true no matter which random
This is going to lead to a contradiction of information we have about the spectrum of intersections of
with translates of the annihilator of
How does this work, well we look on the space side. I define the fibers with respect to , namely
, namely  .
. with
with  which has the same dimension as
which has the same dimension as  and is transverse to
and is transverse to
 . We try to understand
. We try to understand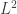 norm of increments on
norm of increments on  is tight. What is this
is tight. What is this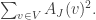 $
$ and another resolution
and another resolution . Namely
. Namely $
$
Then we introduce a subspace
the meaning of the estimate that the space side of the
sum
$
Well, there’s some martingale stuff going on here. There is one resolution at the scale of
by
$
What’s the upshot of this. Each (and I use the term each in a very kind of way) of the fibers
kind of way) of the fibers 
 bound as well. Now it isn’t surprising that this is possible.
bound as well. Now it isn’t surprising that this is possible. is a cap set in its own right. So its spectrum looks like a subspace plus random set.
is a cap set in its own right. So its spectrum looks like a subspace plus random set. ‘s so that they don’t contribute too
‘s so that they don’t contribute too .) But what’s very weird is that the subspace part of the
.) But what’s very weird is that the subspace part of the ‘s has to be contained in the span of
‘s has to be contained in the span of 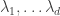 .
.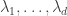 and different choices with very high
and different choices with very high
loose fraction with denominator
have to be tight with respect to the
Each fiber
(The subspace parts have to look different for different
large a subspace part to the spectrum of
spectrum for the tight
But this is true independent of the choice of
probability give us nontrivial intersection. (This is basically the same probabilistic calculation that
gave us the additive non-smoothing.) That means that the fibers $A^w$ can’t have any subspace part to their spectrum
which is at last a contradiction.
Now a word of caution. I am prone to delusions and as Gina says, the capset problem fights back. This is maybe the third time
in the last month that I felt sure it was licked. So the whole thing might not survive being written down. The difference
this time is that there’s an open discussion going on. So surely the sin of making a fool of myself has already been committed.
But what’s interesting are the ground rules. The argument can be written down rigorously by anyone as long as this post is cited.
That’s great! Do I have any volunteers? Or do I have to do it?
January 16, 2011 at 11:10 am |
Well, there have been fewer comments than I expected on this post, but their quality has been remarkably high. Many thanks to all who have generously shared their extremely interesting ideas here. Nets, your approach looks exciting, but I am having some difficulty understanding it. I don’t know how much that’s me (I can be pretty slow on the uptake, as my initial response to Ben’s comment demonstrated) and how much it is the way you explained your ideas.
Since it is not very helpful to you if I simply say that I found it hard to follow, let me try to pick out some specific points where I struggle.
Actually, even this isn’t completely easy to do, because I sometimes found that I was following things line by line but without a very clear idea of where I was going, so that by the time I got there I no longer knew where I was, so to speak. So one thing that would be immensely helpful would be a short global view of your argument, one where you say something like, “If we could do A, B and C then we would be done because D. But it turns out that we can do A, B and C’, and C’ is sufficiently like C for some small improvement to be possible.”
Leaving that problem aside, here are a few points where I had trouble in your first post.
It took me a while to work out that “shows bias of at least almost 1/N” meant that the bias was a fraction 1/N of the size of D, so in absolute terms. In general, I think this kind of slightly non-standard loose terminology (which of course we all use extensively when we are thinking privately) can make communication a bit less clear. If you say instead that you are considering all frequencies
in absolute terms. In general, I think this kind of slightly non-standard loose terminology (which of course we all use extensively when we are thinking privately) can make communication a bit less clear. If you say instead that you are considering all frequencies 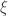 such that the Fourier coefficient
such that the Fourier coefficient  is at least
is at least  (or whatever it is with your normalization) then the reader can translate that into his/her preferred private language). Or you could give us both the precise version and the imprecise version. I’m dwelling on this one example not because it deserves this much attention but because it is representative.
(or whatever it is with your normalization) then the reader can translate that into his/her preferred private language). Or you could give us both the precise version and the imprecise version. I’m dwelling on this one example not because it deserves this much attention but because it is representative.
Next comes a more philosophical point. You say that the situation is much sharper because there are no more than additive quadruples. Now when I came up with the
additive quadruples. Now when I came up with the  figure, I wanted it to be as large as possible, so the fact that it can’t be larger doesn’t seem like an obvious help. On further reflection I assume that the point is that if you can produce an upper bound of
figure, I wanted it to be as large as possible, so the fact that it can’t be larger doesn’t seem like an obvious help. On further reflection I assume that the point is that if you can produce an upper bound of  as well, then you’re in some kind of extremal situation, and that should force the set to have some structure that can be exploited. That is, one can hope for an argument of the following kind.
as well, then you’re in some kind of extremal situation, and that should force the set to have some structure that can be exploited. That is, one can hope for an argument of the following kind.
(i) We know that there are at least additive quadruples by argument A.
additive quadruples by argument A.
(ii) We know that there are at most additive quadruples by argument B.
additive quadruples by argument B.
(iii) Therefore, all inequalities are sharp.
(iv) Therefore, if there is no improvement to the bound at all, then the set looks like this, which leads to a contradiction.
(v) Now relaxing very slightly, we obtain a contradiction even if we can’t improve by some small factor that tends to infinity with N, which means that we have improved the Roth/Meshulam bound.
Is that the kind of thing you mean when you say that the situation is much sharper? And why does it help to have few sextuples, octuples, etc.? (I think that gets answered later on, so I’m not insisting on an answer here.)
I’m slightly confused by the bound of . I thought it was anything that was substantially larger than
. I thought it was anything that was substantially larger than  But reading on, I think the point is that you’re only actually using the bound of
But reading on, I think the point is that you’re only actually using the bound of  even though the stronger bound holds. Is that right?
even though the stronger bound holds. Is that right?
The next paragraph took me a while to follow (however easy it seemed in retrospect). With just a few extra words it would have been much quicker. Those extra words are as follows.
The next bit that holds me up: “we ask ourselves how many -tuples come entirely from elements of
-tuples come entirely from elements of 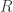 .” What does this mean? I think I could eventually understand the rest of this paragraph (probably by not looking at it and trying to work out the argument for myself) but with just a bit more guidance I’d find it ten times easier.
.” What does this mean? I think I could eventually understand the rest of this paragraph (probably by not looking at it and trying to work out the argument for myself) but with just a bit more guidance I’d find it ten times easier.
However, let me believe you that there are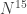 additive octuples at most. What use is that? You give an intuitive idea in the next paragraph, which I don’t really understand because I am insufficiently familiar with your paper with Koester (a situation I hope to remedy soon). However, you go on to be more precise, which is great.
additive octuples at most. What use is that? You give an intuitive idea in the next paragraph, which I don’t really understand because I am insufficiently familiar with your paper with Koester (a situation I hope to remedy soon). However, you go on to be more precise, which is great.
Next problem: I don’t know what means. I’m guessing it’s got something to do with sums within
means. I’m guessing it’s got something to do with sums within  or something like that. In fact, let me guess that that’s exactly what it is: the size of the set
or something like that. In fact, let me guess that that’s exactly what it is: the size of the set  is at most
is at most  That looks sort of promising, since it’s extremal if you ignore the
That looks sort of promising, since it’s extremal if you ignore the  factor.
factor.
I’m assuming that in the next paragraph there’s a sign missing. That is, it should say “
sign missing. That is, it should say “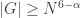 “. Another of the small things that keep holding me up: what is
“. Another of the small things that keep holding me up: what is  ? Looking back through the post, I see no mention of any
? Looking back through the post, I see no mention of any 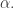 My best guess is that you are taking an arbitrary
My best guess is that you are taking an arbitrary  (and if I look a long way ahead I see that this guess is confirmed) but it would be hugely helpful to be told that. Individually, none of these things is a problem, but I find that they accumulate until I somehow no longer feel that I’m standing on solid ground.
(and if I look a long way ahead I see that this guess is confirmed) but it would be hugely helpful to be told that. Individually, none of these things is a problem, but I find that they accumulate until I somehow no longer feel that I’m standing on solid ground.
I know with this paragraph that I could work out what happens fairly easily, so I’ll happily trust the numbers you write down.
Over the next few paragraphs I get slowly lost, even though I can’t put my finger on any point that seems unclear. It’s just that I have to hold too much in my head. For example, by the time you say “we know that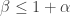 ” I am too muddled to see the argument, even though it is obvious from the way you write that it is a triviality. Is it that the
” I am too muddled to see the argument, even though it is obvious from the way you write that it is a triviality. Is it that the ![D[x]](https://s0.wp.com/latex.php?latex=D%5Bx%5D&bg=ffffff&fg=333333&s=0&c=20201002) have size
have size  and therefore their intersections have at most this size?
and therefore their intersections have at most this size?
On reading once again, I see that (I’m almost sure) I misunderstood something rather important. When you said that you assumed that the entire sum comes from terms of size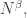 did you actually mean from terms of size zero or
did you actually mean from terms of size zero or 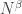 ? (That is the only way I can make sense of your “disjoint blocks” comment later on.)
? (That is the only way I can make sense of your “disjoint blocks” comment later on.)
Can you say explicitly what “this structure” works out to be that you discuss in the last paragraph? It would be very helpful to the reader who hasn’t followed the details of the argument up to that point.
Very briefly, looking at the next post of yours, I see one crucial point where a precise definitely would be hugely helpful. You say, “is additively nonsmoothing mod factors”. Could you tell us exactly what this means?
factors”. Could you tell us exactly what this means?
I have to say that I don’t understand why you aren’t already done once you have a subset of size almost contained in a subspace of dimension
contained in a subspace of dimension  Let me give the argument and you can tell me what’s wrong with it, unless I notice for myself when I write it.
Let me give the argument and you can tell me what’s wrong with it, unless I notice for myself when I write it.
The way I normalize things (so that Fourier coefficients are at most 1 in modulus), you are defining the spectrum to be the set of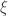 such that the Fourier coefficient at
such that the Fourier coefficient at 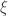 has modulus at least
has modulus at least 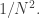 Suppose we have
Suppose we have  such points in a subspace
such points in a subspace  of dimension
of dimension  Then the sum of the squares of the (non-zero) Fourier coefficients over that subspace is at least
Then the sum of the squares of the (non-zero) Fourier coefficients over that subspace is at least  Therefore, the
Therefore, the 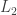 norm of the balanced function of the set convolved with the characteristic measure
norm of the balanced function of the set convolved with the characteristic measure  of
of  has square at least
has square at least  Therefore, the square of the
Therefore, the square of the 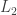 -norm of the characteristic function of the set convolved with
-norm of the characteristic function of the set convolved with  is at least
is at least  which means that the
which means that the 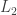 -norm itself is at least approximately
-norm itself is at least approximately  or something like that. OK, I now understand that for this to be better than Roth/Meshulam, we need
or something like that. OK, I now understand that for this to be better than Roth/Meshulam, we need 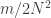 to be better than
to be better than  or
or  to be better than
to be better than  which is the bound you give (up to the constant factor).
which is the bound you give (up to the constant factor).
In fact, I made a mistake in my post. If you just look at the balanced function, you can conclude that there is a significant density change just with the hypothesis that you have substantially more than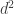 elements of the spectrum in a subspace of dimension
elements of the spectrum in a subspace of dimension  But it could be a decrease rather than an increase. If you insist on an increase, then the bound isn’t so good.
But it could be a decrease rather than an increase. If you insist on an increase, then the bound isn’t so good.
Going back to the second post now that I’ve sorted that out for myself, I’d be hugely grateful if you could provide some kind of overview of the proof. It’s difficult to describe exactly what I mean, as I sometimes feel the need for more detail and sometimes less. I think the ideal is something short but precise (i.e., it is short but it tells you what it isn’t saying, so to speak).
I wouldn’t have bothered with this long comment if I weren’t very interested in understanding what it is you have to say here.
January 16, 2011 at 12:07 pm |
Tim,
Let me try to take things a few points at a time. This way there will be more posts of lower quality. 🙂
There is an argument which says there are at least $ latex N^7$ quadruples which you gave. (I actually first learned it in a slicker form from Bateman but maybe I don’t have to repeat his version of the argument now.) This numerology comes from having
comes from having  spectrum which follows when we assume the cap set has density
spectrum which follows when we assume the cap set has density
 so if we try to rule out density more than
so if we try to rule out density more than
 then factors of $N^{\epsilon}$
then factors of $N^{\epsilon}$
start to appear in the lower bound for quadruples but keeping track
of them is very tedious, at least for me, so I won’t.
Now there is a very easy argument that says at most spectrum and at least
spectrum and at least  quadruples implies at least
quadruples implies at least
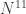 sextuples, at least
sextuples, at least 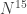 and so forth.
and so forth.
I assume everyone is familiar with this, because it is just Holder on
the Fourier transform of the spectrum and is a poor man’s version
of Plunnecke.
However, I claim there is also an argument that says there are at most
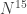 octuplets. (Don’t worry about why this helps yet. It
octuplets. (Don’t worry about why this helps yet. It
does. If that seems counterintuitive, maybe that’s the part which is FN.)
The reason there are at most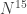 octuplets is that if there
octuplets is that if there type factors) then
type factors) then there are at least
there are at least 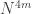
 elements of the spectrum (i.e probability
elements of the spectrum (i.e probability
 for each one) then I will get some 2m-tuplets
for each one) then I will get some 2m-tuplets
are more (by at least
for some not too large
2m-tuples. That means that if I randomly select slightly fewer
than
but this is a contradiction because I expect my selection to be
linearly independent. [I do this argument a little more rigorously in the
first post. It’s based on the dN bound.]
About the dN bound: I expected it to be a d^2 bound too at first. But then
I noticed much to my chagrin that it is only a dN bound, because
we have a good upper bound on how much more dense the capset
can be in a subspace – positive increments – but no good upper bound
on how much less dense it can be. This is explained carefully in the second post.
Broad outline: We show that the spectrum of size N^3 is random + structured where the random part is of size N^2 and the structured part . This is done basically in the
. This is done basically in the
is of size N. The structured part has around N^3 quadruplets and so lives in a subspace of size
first post. The second post explains why this is enough.
Now I come back to what I consider your main question. Why does an
upper bound on octuplets help. The reason is that it is saying that Plunnecke is sharp. That is, the set is expanding additively as much as
possible. That means that the structured part is already full. It isn’t rapidly becoming more structured as we add it to itself. This gives us a fast shortcut for identifying the structured part. It is the set of summands
for a given popular sum. To my knowledge, this idea was first used
in my paper with Koester. It is quite handy. I give a fairly rigorous
description in my first post.
alpha is of course a parameter which tells us how many pairs the quadruples come from. An example to worry about is N random uncorrelated subspaces of size N^2. Then we have N^5 pairs,
those are pairs in the same subspace, giving N^7 quadruples. Of
course we can rule out this example by the Nd bound.
By the way I played a little fast and loose with alpha in my first post.
It can be as large as 2 and I implicitly assumed it was less than 1.
In our favorite example, a random set of N^2 + a subspace of N, we
actually get N^4 pairs, those pairs whose difference is in the subspace
giving N^7 quadruples, so alpha is a little in the eye of the beholder.
There is some duality between the summands and the sums. When
alpha is small, the set of summands leaves the sums invariant and hence
it is structured. When alpha is large, the sums leave the summands invariant and hence they are structured.
I hope this helped a little. I can write more posts aimed at more specific questions. Or I could write a paper, but this might take a week…
January 17, 2011 at 8:12 am |
I think that trying to push the 3^n/n bound using additional structure which we can prove or expect for sets which come close to the bound is extremely interesting.
Is there any heuristic argument how far such an approach can go in a very optimistic scenario?
A problem that I regard as somewhat analogous is about traces of families of sets. The question is what is the density of a family F of subsets of {1,2,…,n} that guarantees the existence of a set S of size 3n/4 so that the trace of F on S (=the family intersection of sets in F with S) contains at least half the subsets of S.
Iteratively raising the density argument shows that density 1/n^c suffuces for some small c. The best conjectural structure theorems my lead to 1/n^c for every c or a little beyond that. The best examples suggests that maybe density rho^n for rho<1 (and very close to 1 suffices).
Both in this trace problem, the cup set problem and the 3-AP problem I see no reason to believe why the examples represent the truth. (But I know that, at least for Roth's problem, this is a common view.)
January 17, 2011 at 11:44 am
Gil,
I don’t have a lot of intuition for this trace problem. I’d have to think much harder about it even to understand your analogy.
The reason I see no hope of using the method I’ve been suggesting to get is that one loses control
is that one loses control a bit but not the nature of the result.)
a bit but not the nature of the result.)
better than
of the Fourier spectrum if things are worse. It is interesting that even the
polynomial Freiman Ruzsa theorem does not help. (It would improve
the
The reason I think such a result would be fun is that I’ve been nursing
a vague hope that this might suggest a way of improving Sander’s result past the log barrier. But I haven’t thought about that seriously either.
Today I’m going to not be inhibited by this conversation and start on a rigorous draft of using the method described in my first two posts for the capset problem. Usually this will cause me to encounter some difficulty.
If it does, I will try to inform you guys as quickly as possible so that the ritual floggings can begin.
January 18, 2011 at 7:38 pm
Gil–
In response to the question
“Is there any heuristic argument how far such an approach can go in a very optimistic scenario?”
I have the following. (My apologies if I misunderstand the kind of thing you want to be optimistic about.) It is along the lines of Tim’s argument using Chang’s theorem to obtain structural information on the spectrum of a capset. It suggests, in the very optimistic scenario you request, that the density of the capset should be less than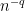 for any positive
for any positive  . Exactly how much further it goes is another story.
. Exactly how much further it goes is another story.
The value of this argument depends on your level of optimism. The optimistic scenario requires that one be able to make strong statements about the structure of sets with a large number of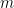 -tuples. So this sketch proves a statement of the form “Even very small capsets have spectrum with many
-tuples. So this sketch proves a statement of the form “Even very small capsets have spectrum with many 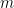 -tuples.” The optimism is required to believe that something can be done with this information. Perhaps nothing can. At the least, this argument together with the argument in Nets’ earlier post shows that spectra
-tuples.” The optimism is required to believe that something can be done with this information. Perhaps nothing can. At the least, this argument together with the argument in Nets’ earlier post shows that spectra 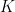 with approximately
with approximately 
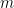 -tuples play an important role.
-tuples play an important role.
January 18, 2011 at 7:39 pm
(part 2)
More precisely, we prove
Lemma 1 Suppose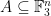 is a capset with density
is a capset with density 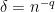 . Then there exists a set
. Then there exists a set 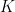 and
and  such that
such that 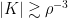 , such that
, such that  for all
for all 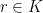 , and such that for each even
, and such that for each even 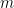 , the number of
, the number of 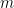 -tuples in
-tuples in 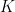 is greater than
is greater than
All but the last claim of the lemma are mentioned in Tim’s original post.
As in the original post, is the capset and
is the capset and  is the characteristic function of
is the characteristic function of  . We assume that
. We assume that 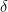 is the density of
is the density of  . Suppose
. Suppose  . As noted in the post, by an iteration argument we may assume that for all
. As noted in the post, by an iteration argument we may assume that for all 
for otherwise there is a hyperplane with unusually large intersection with the capset
and hence that (up to a loss that is logarithmic in
where
which is essentially the notation used in the original post. This implies that
Further, for every
Hence
Now we introduce a sum over
By using Holder’s inequality, we may estimate the sum on the right by
For even
(A slightly technical point: the last claim is only correct because the set
The quantity
which implies
But we know that
by our definition of
As long as
(for otherwise there is a hyperplane with unusually large intersection with
This is true only when
When
January 18, 2011 at 7:50 pm
Since two of my formulas apparently don’t parse (and since I don’t know why) I will post the original latex for them here. Many apologies for the terrible readability, but if you’ve read this far then you probably won’t mind translating.
First non-parsing formula:
“…and interchange sums to see that
\rho \delta |K_{\rho}| \lesssim 3^{-n} \sum _{x\in \mathbb {F} _3 ^n } \sum _{r\in K_{\rho}} [1_A (x) \one _{P_r} (x) – {1\over 3} 1 _A (x) ]. ”
Second non-parsing formula:
“estimate the sum on the right by
\delta ^{1-{1\over m}} \left( 3^{-n} \sum _{x\in \mathbb {F} _3 ^n } \left| \sum _{r\in K_{\rho}} [ \one _{P_r} (x) – {1\over 3} 1 _A (x) ] \right|^m \right)^{1\over m}”
After quite a bit of experimenting, I eventually discovered that WordPress doesn’t recognise the \one macro. I’ve changed them to 1s — Tim.
January 19, 2011 at 9:00 am
Many thanks, Michael. This is very interesting.
January 17, 2011 at 10:02 am |
In particular, I am interested in the following class of examples: You start is a family of m-subsets of {1,2,…,n}. For every set S in
of m-subsets of {1,2,…,n}. For every set S in  associate a family
associate a family as follows. Choose at random a 0,1,2- vector
as follows. Choose at random a 0,1,2- vector 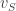 of length n.
of length n. 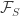 is the set of all 0,1,2-vectors that disagree with
is the set of all 0,1,2-vectors that disagree with 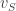 for $\latex i \in S$ and agree with
for $\latex i \in S$ and agree with 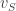 for
for  . So this is a family of size
. So this is a family of size 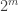 and you take $\cal F$ as the union of all these families. Of course you have to specify what m is and more importantly how the family $\cal G$ is selected.
and you take $\cal F$ as the union of all these families. Of course you have to specify what m is and more importantly how the family $\cal G$ is selected.
January 29, 2011 at 5:08 pm
To Michael Bateman.
I do not understand why are you use absence of AP3.
It is known that all you say is true for an arbitrary set A.
Certainly
\delta \rho |K_\rho| \le \sum_{x\in K_rho} |\cap{A} (x)|
for any A.
January 29, 2011 at 5:18 pm
Ilya–
The estimate in display (3) is not true for an arbitrary set, and neither is the estimate on \rho .
Michael
January 19, 2011 at 9:20 am |
[…] Roth theorem (March 2009). Here are two “open discussion” posts on the cap set problem (first, and second) from Gowers’s blog (January 2011). These posts include several interesting […]
January 30, 2011 at 5:40 pm |
I do not understand. You do not use (3), actually.
If \rho \sim \delta (we are interested in the case) then
|K_\rho| \sim 1/\delta^3 and by T.Gowers’ estimate before
\rho^m |K_\rho|^m \sim |K_\rho|^{2m/3} that is ezactly your bound.
I misunderstand, sorry.
February 1, 2011 at 4:47 pm
(3) is used in the orginal post as well, about 20 lines into the section called “Sketch of Proof”.
February 6, 2011 at 9:58 pm |
[…] this post. Also there is a page on the polymath blog here. There is also a wiki here. Also see this post and this […]
June 14, 2011 at 9:53 pm |
[…] after many years, the Roth-Meshulam bound. See these two posts on Gowers’s blog (I,II). Very general theorems discovered independently by David Conlon and Tim Gowers and by Matheas […]
June 28, 2011 at 11:56 pm |
[…] no non-trivial arithmetic progression (Why it has this name I don’t know.)"(source: https://gowers.wordpress.com/2011…)This answer .Please specify the necessary improvements. Edit Link Text Show answer summary […]
June 30, 2011 at 12:38 am |
Why is a cap set so named?…
Looks like Tim Gowers, who is among the few people I could find using that terminology, doesn’t know either. “First, a quick reminder of what the cap-set problem is. A cap-set is a subset of that contains no line, or equivalently no three distinct po…
December 18, 2015 at 2:04 pm
The definition of a cap is inspired from that of an arc, a set of points in the finite projective (or affine) plane no two of which are collinear. The classical examples of arcs in projective planes are the conics, which are usually draw like a “cap”. That could be the reasoning behind it. The oldest paper on caps that I have been able to locate is that by Raymond Hill “On the largest size of cap in S5,3
Rend. Accad. Naz. Lincei, 54 (8) (1973), pp. 378–384”. Also see this: http://www.sciencedirect.com/science/article/pii/0012365X78901206
September 10, 2012 at 11:28 pm |
[…] conjecture is true or false, but one thing that we do know is that it is a popular blog topic (see here, here, here, and the end of this […]
October 13, 2013 at 8:37 pm |
[…] proof in full details. A good place to see a detailed sketch of the proof is in this post What is difficult about the cap-set problem? on Gowers’ […]
June 14, 2014 at 9:08 pm |
[…] the cap set problem see e.g. here, here and here. There is some similarity between problem and techniques between additive combinatorics […]
December 18, 2015 at 2:16 pm |
Regarding “Why it has this name I don’t know.”:
The definition of a cap is inspired from that of an Arc (https://en.wikipedia.org/wiki/Arc_(projective_geometry)), a set of points in the finite projective (or affine) plane no two of which are collinear. The classical examples of arcs in projective planes are the conics, which are usually draw like a “cap”. And in fact, it’s pretty common to draw any arc like a conic. That could be the reasoning behind calling such a set a cap.
The oldest paper using the term caps that I have been able to locate is that by Raymond Hill “On the largest size of cap in S5,3 Rend. Accad. Naz. Lincei, 54 (8) (1973), pp. 378–384”, which may have some answers. Also see this: Caps and codes (http://www.sciencedirect.com/science/article/pii/0012365X78901206).
May 17, 2016 at 11:50 pm |
[…] that survived even after a lot of effort from several mathematicians (see this, this, this and this). Ultimately, just like the finite field Kakeya problem, it succumbed to the polynomial method. I […]
May 19, 2016 at 12:58 pm |
[…] as I’ve got a history with this problem, including posting about it on this blog in the past, I feel I can’t just not react. So in this post and a subsequent one (or ones) I want to do […]
July 8, 2020 at 5:00 pm |
[…] methods that for some ! This was very exciting. See these two posts on Gowers’s blog (I,II). This raised the question if the new method allows breaking the logarithmic barrier for […]