It is not at all clear to me what should now happen with the project to solve the Erdős discrepancy problem. A little while ago, it seems that either the project ran out of steam, or else several people, at roughly the same time, decided that other things they were doing should take higher priority for a while. Perhaps those are two ways of saying the same thing.
But they are not quite the same: as an individual researcher I often give up on problems with the strong intention of returning to them, and I often find that if I do return to them then the break has had an invigorating effect. For instance, it can cause me to forget various ideas that weren’t really working, while remembering the important progress. I imagine these are common experiences. But do they apply to Polymath? Is it possible that the EDP project could regain some of its old vigour and that we could push it forward and make further progress? Is it conceivable that it could go into a different mode, where people contributed to it only occasionally? (A problem with that is that one of the appeals of a polymath project is checking in to see whether there are new ideas, or whether people have reacted to your comments. It is not clear to me that this appeal works if it is substantially slowed down.)
Anyhow, as Terry Tao might put it, this situation can be regarded as an opportunity to add a new datapoint to the general polymath experiment. Recently the following conjunction of circumstances occurred: I found myself on a plane, my laptop battery lasts a fraction of the time it should, and all the films on offer were either unappealing or too appealing (meaning that I’d been looking forward to seeing them but didn’t want to waste them by watching them in aeroplane conditions). I therefore found myself with several hours to think about mathematics. It was just like the old days when I didn’t have a laptop and there would only be a couple of films, both terrible. So I thought about EDP. Now I would like to avail myself of the opportunity to obtain a new datapoint by writing my thoughts, such as they were, down in a post and seeing whether anyone feels like joining or rejoining the discussion. I have plenty of questions, some of which may be fairly easy: I hope that will be a good way of tempting people.
A brief reminder of some of the ideas we have been thinking about.
Since one of the aims of this post is possibly to attract newcomers to the project, let me briefly recap one or two things, including a statement of the problem. We define a homogeneous arithmetic progression, or HAP for short, to be a set of the form for some pair of positive integers
. Given any sequence
, we define its HAP-discrepancy, or discrepancy for short (since in this context we will almost always be talking about HAP-discrepancy and not any other kind of discrepancy) to be the maximum of
over all HAPs
. Erdős’s discrepancy problem is the annoyingly simple sounding question of whether it is possible that one can find arbitrarily long
sequences with bounded discrepancy. That is, does there exist a constant
such that for every
there is a
sequence of length
and discrepancy at most
?
When we started work on the problem, my perception was that a major difficulty was that the problem relied heavily on the sequence taking values in . There is a very simple example that appears to demonstrate this: the sequence
. It is easy to check that the discrepancy of this sequence (even the infinite sequence) is 1, and yet it takes values of modulus 1 two thirds of the time. This is a pity, because the usual analytic methods tend to give results that can be generalized from purely combinatorial statements (typically involving sequences that take just two values) to more general analytic ones (typically involving sequences that satisfy some analytic condition such as a norm bound).
A more general question.
One of the main pieces of progress to come out of the original discussion was Moses Charikar’s observation that it is possible to attack the problem analytically after all. The trick is to use a weighted norm that tends to give more weight to numbers when they have more factors. For instance, a multiple of the example mentioned above shows that there is no hope of proving that the discrepancy is unbounded for every sequence such that
. However, there appears to be no reason in principle that one could not prove that the discrepancy was always at least
for a sequence
such that
is unbounded. If one could do that, then it would imply EDP, since for
sequences we have
for every
.
There has been quite a bit of discussion about how one might be able to find such a set of weights and prove the result, but so far we have not succeeded. Rather than repeating what the possible methods of proof might be, I would like to suggest focusing on the problem of choosing the weights, because it seems to me that there is plenty of opportunity here to get further insights into the problem.
To repeat: in order to prove EDP we need to find a system of weights such that
is unbounded above and such that every sequence
has discrepancy at least
. The problem I would like to focus on for a while is this: find a good candidate system of weights. That is, find weights that do not obviously fail to work. What I hope is that if we look at several systems of weights and manage to show that they do not work (by constructing increasingly clever sequences
) then we will eventually settle on a system of weights that does work. If we can do that, then we will have split the problem into two and solved one of the two parts. And we have ideas about how to do the other part. (Roughly speaking, we want to find a way of decomposing a diagonal matrix: the two parts of the problem are to choose the diagonal matrix and to find the decomposition.)
Which systems of weights are definitely bad?
For the remainder of this post I want to make a start (or rather, a restart, since much of what I say can be found in the earlier discussions) by thinking about what is wrong with certain systems of weights. It will be convenient to rephrase the problem slightly: let us ask for a system of weights such that the discrepancy of an arbitrary real sequence
is always at least
(where
tends to infinity as
tends to infinity). That way we care about the weights only up to a scalar multiple, so we do not have to normalize them carefully in advance.
The sequence 1, -1, 0, 1, -1, 0, … shows that we cannot take for every
. (I have already said this above, in a very slightly different way.) Indeed, its discrepancy is 1, but
would be around 2/3 if we took
for every
. And the ratio of these two is not unbounded.
The same sequence disposes of many other systems of weights. For example, suppose we were to choose randomly to be 1 with probability
and
otherwise. Then with very high probability
would be close to
and
would be close to
. Therefore, once again we would have a quantity that is close to 2/3 for the ratio, which does not tend to zero.
Indeed, any system of weights that is not concentrated in the multiples of 3 will have the same defect, for precisely the same reason. To put that more precisely, suppose that Then with
as above, we have
while the discrepancy of the sequence
is 1. Thus, for the weights
to yield a proof of EDP we need
This simple observation can be generalized in many directions. For instance, it is easy to prove in a similar way that we need It is also easy to prove in a similar way that we need
A general message from this argument is this: the weights
must be strongly concentrated on numbers with many factors. And when one thinks about this, it is not too surprising: the numbers with plenty of factors are precisely the numbers that belong to many HAPs and therefore the numbers
for which it should be in some sense difficult to incorporate a large real number
into a sequence
with low discrepancy (because there are likely to be many constraints on
).
But let us stay for the moment with elementary observations rather than thinking about what sequences there are that are concentrated on numbers with many factors. We know that for every the proportion of the total weight of the
on values of
such that
but
is
. One way of achieving that is to
and to choose a set
that contains, for each
, exactly one element that is divisible by
but not by
. One could then let
if and only if
If is the set
then it is easy to find an appropriate sequence
: just let
if
for even
,
if
for odd
, and 0 otherwise. The intersection of any HAP with
is either empty or takes the form
so this sequence has a discrepancy of 1, while
However, if consists of an arbitrary number that is equal to 1 mod 3, an arbitrary number that is equal to 3 mod 9, and so on, then many more HAPs can intersect
and I have not come up with a method of constructing bounded-discrepancy sequences with a substantial restriction to
Let me ask this as a formal question. It doesn’t seem to be trivial, but I cannot believe that it is especially hard either.
Question. Let be a subset of
such that for every
there is no element of
that is congruent to
mod
and at most one element that is congruent to
mod
Must there be a sequence of bounded discrepancy that takes values
everywhere on
?
It is not in fact necessary for the sequence to take values everywhere on
in order to show that the characteristic function of
is unsuitable. However, since I expect such a sequence to exist, I have stated the question in this stronger form. Probably one can also ask for the sequence to take values
or 0 outside
I should briefly explain why I have not asked the more general question of whether it is possible to prove that no small set can work (as opposed to a set that is forced to be small by the divisibility conditions above). That is because cardinality on its own is not enough: for example, one could take
to be a HAP of length
, and then to find a sequence of bounded discrepancy that takes
values on
would be equivalent to finding a counterexample to EDP. The idea here is to show that for certain sets
one can exploit the freedom of a sequence outside
to make the discrepancy small.
Nevertheless, there might be a condition of the following kind: perhaps if has the property that it cannot intersect a HAP of length
in more than
elements, then it cannot serve as a system of weights for EDP. And I don’t have any particular reason to think that
is the right function here — perhaps one could prove a similar result for significantly faster-growing functions.
A candidate for a good system of weights.
I’d now like to resurrect an idea that I mentioned at some point earlier in the discussion. It’s a suggestion for a sequence of weights that seems to me to have some chance of working. And if it doesn’t work for some obvious reason, then it feels like the kind of idea that could be modified in various ways to get round preliminary objections.
Let me start with two ideas that don’t work. The first is to take for every
. We have seen that this doesn’t work — indeed, the proportion of weight it attaches to multiples of 3 is not
The second is a feeble attempt to get round this obvious problem with the first. We want to give extra weight to numbers with more factors, so how about defining to be
, the number of factors of
?
To see that this does not work is slightly harder, but only slightly. Again we shall show that this system of weights does not concentrate on multiples of 3. (Of course, we care about multiples of other numbers too, but if it doesn’t work for 3 then we’re already in serious trouble.) To see this, let us first consider how to estimate This we can rewrite as
since each
contributes 1 to the sum for each multiple
of
that is at most
And this we can approximate by
which is roughly
(I won’t bother to analyse how good an approximation that is.)
Now let’s consider what happens if we estimate in a similar way. This time, we can approximate the sum as
since if
is a multiple of 3 we get no contribution, and if
is not a multiple of 3, we get a contribution of 1 for each multiple of
that is not a multiple of 3, and there are about
of those. So the sum works out to be around
Now this is 4/9 of the entire sum, so the usual sequence
shows that setting
does not work.
Nevertheless, we do seem to have achieved something: with this choice of we have given less than average weight to non-multiples of 3. The problem is that we have not gone far enough. Now one way of thinking of
is that it is
. A way that one might think of attaching yet more weight to numbers with plenty of factors would be to define
to be
This can be rewritten as
That is, it counts pairs
such that
and
A fairly simple calculation similar to the one done above shows that this function again attaches too much weight to non-multiples of 3, but it is an improvement on the previous function. The constant function 1 attaches weight 2/3 to the non-multiples of 3, the function
attaches weight 4/9, and the function
attaches weight 8/27 (or 4/9 of what it should if it were unbiased).
This suggests, correctly, that we can obtain the desired weight if we iterate this process an unbounded number of times. This leads to two suggestions for a system of weights. The first is to choose some slow-growing function
and take the function
(which is defined inductively by the formula
Another is to iterate until a fixed point is reached, though for this the definition must be modified somewhat. We obviously cannot find a positive function
such that
but we can find a function
such that
Indeed, if we set
then the first few values are
Let me now just write the sequence: it goes
This sequence can be found on Sloane’s database. (It’s sufficiently natural that I’d be perturbed if it couldn’t.) I haven’t yet understood everything it says there about it, but there appear to be some facts there that might conceivably be of use.
So here is an obvious question: is there some reason that it cannot work in a proof of EDP? Let me say once again what this means. For this function to work in a proof of EDP we would need to be able to prove an inequality that said that for every sequence the HAP-discrepancy is always at least
So to prove that it does not work it is sufficient to find a sequence (I’ve been assuming it will be real, but even a vector-valued sequence would do) of bounded discrepancy such that
for some constant
that is independent of
One possible reason for its not working might be that it grows too fast, or perhaps has a subsequence that grows too fast. Let me try to explain what might conceivably go wrong.
To do this, we need a more explicit definition of . It can be defined as follows:
is the number of sequences
such that
and for each
we have
. Here we include the empty sequence as a sequence. (An equivalent definition would be to ask for sequences that start with 1.) It is easy to check that this function satisfies the relation
and the initial condition
. And to see how it works in a concrete case, let's take
. The possible sequences are (), (2), (3), (4), (6), (2,4), (2,6) and (3,6).
In general, working out is slightly complicated. If
for some prime
, then we can take any subset of
in increasing order, so
If
is a product
of distinct primes, then for each
there is a one-to-one correspondence between the sequences of length
that we can take and the set of surjections from
to
. Indeed, given a surjection
, define
to be the product of all
such that
and take the sequence
. Conversely, from the sequence we can recover the
and hence the function
, which has to be a surjection since the sequence is strictly increasing.
Unfortunately, there is no nice formula for the number of surjections from a set of size to a set of size
, but we can think of
as being a function that behaves fairly like
.
So how big can be if
? The biggest it can be for a prime power is
, since the best possible case is
. As for products of distinct primes, the best we can do is if we take the first
primes. The product of these we can sloppily estimate to be about
, which is around
, which in turn is around
. By contrast,
is around
, so in this case
appears to be much smaller than
. However, it is also a lot bigger than 1, so it would appear that the weight attached to a big power of 2 does not by any means dominate the sum.
Given that evidence, I find it not quite clear whether we should be happy with the function as already defined, or whether we should consider weighting it in some way so as to make it roughly the same size throughout the range. At this stage it is perhaps enough to say that we have the option of attempting the latter. (I am mindful of the experimental evidence discovered by Moses and Huy, which suggests that the optimal function has a tail that shows some kind of exponential decay. I don't have any kind of theoretical argument for that.)
How might one prove the result we want?
In my previous post on EDP, I suggested various techniques for finding delicate examples. One of them was recursion, which I rather dismissed. However, I am interested in it again now, not least because the function above has a natural recursive definition.
How might that lead to a proof? Well, here’s a suggestion. Suppose we find a non-trivial way of writing the identity matrix as a linear combination , where the
and
are HAPs and
is the rank-1 matrix with xy-entry equal to 1 if
and
and 0 otherwise. We know that this will not be a useful decomposition of the identity. However, the formula
can be rewritten
where
if
and
if
. It follows that the diagonal matrix
that has
down the diagonal can be expressed as a sum
, where
is the diagonal matrix that takes the value
at all multiples of
apart from
itself, and 0 everywhere else. (To see this, note that
)
If we have a way of decomposing the identity (for all ) then we can subtract the matrix that’s 1 at (1,1) and 0 everywhere else, to obtain the matrix
And then we can use the same method to obtain decompositions of all
and finally we can take an appropriate linear combination to obtain the matrix
So far, this achieves nothing much, but note that our decompositions involve negative as well as positive coefficients. If we can do it in a way that involves many HAPs with many common differences, then perhaps there is some hope that there will be significant cancellation so that the decomposition of
is more efficient than the decompositions of the individual matrices
Further remarks.
I’ll start by briefly pointing out that if the above approach is to work, then it will have to use HAPs that are not “full”. (By a full HAP I mean one of the form ) That is because the sequence that is 1 up to
and
thereafter has bounded discrepancy on all full HAPs. More generally, for a decomposition of a diagonal matrix to work, it must lead to a discrepancy proof for the class of HAPs used in the decomposition, so one should not try to build the matrix out of some restricted class of HAP products unless there is a chance that the theorem is still true for that restricted class.
A second remark is essentially the same as this recent comment of Gil’s. It’s that we already know that the extremal examples — by which I mean long sequences with low discrepancy — have to have some kind of multiplicative structure. This information ought to help us make our guesses. At the time of writing I don’t have a clear idea of how it would narrow down the search, so in order to pursue this thought, the first thing to do would be to consider exactly that question: if you have information about what the worst sequences are like, how does that affect the possible matrix decompositions?
Could the weights be multiplicative?
Since it’s relevant to that last question, let me mention a system of weights I thought of that doesn’t seem to work, but that might perhaps be salvageable. The idea is to define weights such that
for every
and
An instant problem with that idea is that it seems to be hard to concentrate the weights on multiples of 3. Indeed, either tends to infinity, or the sum of the first
weights tends to zero as a proportion of the sum of the first
weights. That is because
by multiplicativity.
The second condition essentially means that the sequence should grow faster than any power of . But if we set
to be the same for every prime
, as seems quite natural, then we find that the sequence grows at most polynomially (since the biggest we can get is at powers of 2, and
would be
which is a power of
). So we seem to be forced to take
to be a “constant” that tends to infinity. But then, if some back-of-envelope calculations are correct (but I’m far from sure about this), the weight of the sequence is too concentrated on large powers of 2. In fact, I think it may even be concentrated at just the single largest power of 2 less than
, which is obviously disastrous.
So it looks as though multiplicative sequences are out, but this claim needs careful checking as it could be rubbish. (One way it could be rubbish is if it is possible to salvage something from the idea by having different values at different primes, but at the moment I’m not very convinced by that idea.)
A rather vague general question.
The following question is important, even if hard to make precise: how much does the choice of the weights matter?
Let me at least try to pin the question down a little bit. We know that there are certain simple constraints that the have to satisfy, and also that these constraints narrow down the choice quite a bit. However, they do not seem to determine the weights anything like uniquely. It is quite possible that with a bit more thought we could come up with some more constraints. In fact, that is clearly something we should try to do, so let me interrupt the discussion to ask that more formally.
Question. Are there some other kinds of constraints that the must satisfy?
In relation to this question, it is worth looking at this comment of Sune’s, and the surrounding discussion.
Even if the answer is yes, it is clear that the constraints will not completely determine the sequence . (Why? Well, given one matrix decomposition that works, one can build other ones out of it in artificial ways. I leave that as an easy exercise.) But do they come close? For example, is there some low-dimensional space such that every system of weights that works is a small perturbation of a sequence in that space?
I don’t really care about that as a mathematical question so much as a strategic question. From the point of view of solving EDP, can we afford to be reasonably relaxed about the choice of the and focus our attention on the decomposition, or will we find that the desired decomposition does not exist unless we choose the
extremely carefully?
A summary of what I have said above.
I hope very much that it will be possible to revive the EDP discussion, even if the pace is slower than before. It seems to me that an excellent topic to concentrate on for a while would be the question of how to find a system of weights such that the square of the HAP-discrepancy of every sequence
is always at least
Amongst the subquestions of this question are whether the sequence I suggested above has a chance of working, “how large” the set of sequences that could work is, and whether there are constraints of a completely different kind from the ones considered so far.
I have considered real sequences, but if a sequence of weights is to work, we also need the inequality to generalize to vector-valued sequences. That is, we need the square of the discrepancy of to be at least
A further question of interest is whether generalizing to vectors introduces interesting constraints that are not felt if one just looks at scalar sequences.
June 21, 2010 at 9:11 pm |
Let me repeat my last comment from EDP14 which perhaps is better placed here.
In the recent two related approaches of Mozes’ SPD and of Gowers’s repreentation of diagonal matrices we somehow hope that the SPD and LP problem “will do all the work”. (I think this is also the case for the ideas in EDP15.)
However, in earlier discussions we gained some additional information on how an example of bounded discrepency should look like. In particular, Tao’s argument suggests that a counterexample will have diminishing correlation with every character on every HAP. (Terry proved it for multiplicative sequences but we can expect that this extends to general sequences.)
Maybe it can be fruitful to add the condition of “small correlation with a caracter on every HAP” to Mozes’ SPD or Gowers’s LP, and hope that the SPD will more rapidly give good bounds and oerhaps allow to detect some pattern with such extra assumption. At the time, dealing with (say) multiplicative functions with diminishing correlation with every character lookes appealing.
Talking about sequences with diminishing correlation with every nontrivialcharacter, suppose that you have a multiplicative sequence with REALLY small correlation with every character. (E.g. whan you take the correlation for sequences of size n it is as small as n^{-beta} for beta>0. what can you say then about the discrepency?
June 21, 2010 at 9:22 pm
Gil, I am intrigued by what you write (as I said in the post above) but can you say in more detail what it means to add the small-correlation condition to the SDP or LP? I don’t fully understand this.
June 21, 2010 at 9:43 pm
Tim, my comment is related to some early result of Terry but maybe I missed or forgot something. If I remember correctly while the low-diecrepency examples are rather periodic i.e. they have high correlation with a non trivial character there was an argument showing that for the multiplicative case a bounded discrepency sequence cannot have substantial correlation with a non trivial character.
If I “translate” this statement to a general sequence it seems appealing (and perhaps provable) that when a sequence has bounded-away-from-zero correlation with a nontrivial character on some HAP then it has unbounded discrepency.
So we can try to add the condition: the sequence has a small correlation with every non trivial character on every HAP to the SDP. Actually, you suggested something similar in EDP8:to start with the case that the sequence is quasirandom. So the question is now that we are equiped with SDP and SP ideas (EDP10 and EDP12) can we add some sort of quasirandomness condition to these programs.
June 22, 2010 at 10:29 am
Here is a thought about how that might work in practice — but let me know if it is not the kind of thing you had in mind.
Suppose we wanted to use the decomposition-of-diagonal approach. The idea, roughly, is to write a diagonal matrix with unbounded trace as a linear combination of HAP products with bounded sum of absolute values of coefficients. Then a simple argument shows that every sequence must have unbounded correlation with some HAP. If we want to show this under the additional hypothesis that the sequence does not correlate with a non-trivial character, then that is equivalent to showing that every sequence correlates either with a HAP or with a non-trivial character. So one could try decomposing a diagonal matrix into products not just of HAPs but also of non-trivial characters. This ought to be strictly easier, but still very interesting.
sequence must have unbounded correlation with some HAP. If we want to show this under the additional hypothesis that the sequence does not correlate with a non-trivial character, then that is equivalent to showing that every sequence correlates either with a HAP or with a non-trivial character. So one could try decomposing a diagonal matrix into products not just of HAPs but also of non-trivial characters. This ought to be strictly easier, but still very interesting.
June 21, 2010 at 9:50 pm |
Since writing the post above, I have had a small further thought about the function (the one defined recursively by the formula
(the one defined recursively by the formula  and
and  ). It strikes me that that formula depends only on the multiplicities of the primes in the prime factorization of
). It strikes me that that formula depends only on the multiplicities of the primes in the prime factorization of 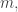 whereas from the constraints one might expect a function that also depended on the primes themselves.
whereas from the constraints one might expect a function that also depended on the primes themselves.
On second thoughts, that’s not what I want to say. In fact, I like the function as it is, but let me say why I thought for a moment that I didn’t like it, and why I have changed my mind (back, I now realize, to what it was before).
Roughly what do we expect the ratio of to
to  to be? This is asking how much bigger we expect a random
to be? This is asking how much bigger we expect a random 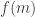 to be if we condition on
to be if we condition on  being divisible by 3. I think that this increases the expected number of prime factors by some positive constant that would probably be between 0 and 1 (I’d be interested in a rigorous proof of this), and if so then since the expected number of prime factors is around
being divisible by 3. I think that this increases the expected number of prime factors by some positive constant that would probably be between 0 and 1 (I’d be interested in a rigorous proof of this), and if so then since the expected number of prime factors is around  and since
and since  behaves a bit like the factorial of the number of prime factors (it’s different if they are not distinct, but usually they will be mostly distinct) that ought to increase the expected value of
behaves a bit like the factorial of the number of prime factors (it’s different if they are not distinct, but usually they will be mostly distinct) that ought to increase the expected value of  by a factor of around
by a factor of around 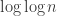 . So we do seem to get the small weight on non-multiples of 3. (Note, however, that if these very crude heuristics are correct, then it looks as though this set of weights cannot prove better than a bound of
. So we do seem to get the small weight on non-multiples of 3. (Note, however, that if these very crude heuristics are correct, then it looks as though this set of weights cannot prove better than a bound of 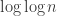 .)
.)
Now if is bigger, then we do not need the weight to be quite so concentrated on multiples of
is bigger, then we do not need the weight to be quite so concentrated on multiples of  (since the sequences we know of that are supported on non-multiples of
(since the sequences we know of that are supported on non-multiples of  and have bounded discrepancy have discrepancy something like
and have bounded discrepancy have discrepancy something like  so the larger
so the larger  is, the less impact such sequences have on the set of possible sequences of weights). But this is good, because it isn’t quite so concentrated on multiples of
is, the less impact such sequences have on the set of possible sequences of weights). But this is good, because it isn’t quite so concentrated on multiples of 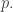
Let me try to justify that claim. Some further heuristic arguments in the post suggest that on average grows more slowly than any power of
grows more slowly than any power of 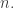 (The rough idea of the proof would be that it is smaller than any power of
(The rough idea of the proof would be that it is smaller than any power of  for products of distinct primes, even in the worst case, and other numbers such as powers of 2 are just too rare to make a significant difference. All these “facts” are things that could be worth proving rigorously — I wouldn’t expect it to be all that hard.) This means that the ratio of
for products of distinct primes, even in the worst case, and other numbers such as powers of 2 are just too rare to make a significant difference. All these “facts” are things that could be worth proving rigorously — I wouldn’t expect it to be all that hard.) This means that the ratio of  to
to  will be roughly
will be roughly  unless
unless  is
is  So if
So if  is bounded above by a constant
is bounded above by a constant 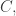 then
then  is about
is about  which means that the latter is about …
which means that the latter is about …
Actually, I’m about to prove a nasty contradiction. I’ve had this trouble a few times, so let me say what it is, in case somebody can tell me where the heuristic argument is going wrong. My problem is this.
1. It looks as though on average grows more slowly than any power of
grows more slowly than any power of 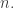
2. It ought to follow that for any prime ,
,  is approximately
is approximately 
3. But multiplying a number less than by
by  ought on average (unless
ought on average (unless  is fairly large) to increase
is fairly large) to increase  of that number by about
of that number by about  or at least by some factor that tends to infinity.
or at least by some factor that tends to infinity.
4. But since everything is positive, that is a contradiction, since it would show that is greater than
is greater than 
So I need to look more carefully at how behaves. But can anyone see which of the above highly non-rigorous arguments is wrong?
behaves. But can anyone see which of the above highly non-rigorous arguments is wrong?
June 22, 2010 at 2:14 pm
I don’t understand 4. What is m?
June 22, 2010 at 4:23 pm
Sorry, 4 was a complete mess. It should have read as follows.
4. But since everything is positive, that is a contradiction, since it would show that is greater than
is greater than 
June 22, 2010 at 7:40 pm
Plotting f seems to indicate that the ‘bad’ candidates are multiples of 24 (e.g. f(192)=256 or f(240)=368) and that n^-1 sum_{i=1}^n f(i) grows faster than n^1/2. So maybe we should have a closer look at step 1 of the argument.
June 22, 2010 at 8:38 pm
Indeed, it appears that is a (very slowly) increasing function of
is a (very slowly) increasing function of  . I’ve plotted it up to
. I’ve plotted it up to  here.
here.
June 22, 2010 at 8:42 pm
(For avoidance of doubt, I don’t mean ‘increasing’ in a strict sense; I mean that the tendency is to increase.)
June 22, 2010 at 9:17 pm
OK I’ll try to think of a theoretical argument for that, unless someone else does first. Basically it’s good news though. If I read it correctly, it’s saying that the function grows very slightly quicker than any polynomial, which is necessary if the above contradiction is to be avoided without sacrificing 3 (which I’d rather not sacrifice if possible). But it would also mean that there was no possibility of the whole sum being dominated by a tiny handful of values.
June 22, 2010 at 10:12 pm
It’s not quite saying that grows faster than any polynomial: it is still possible that
grows faster than any polynomial: it is still possible that  for some
for some  …
…
June 22, 2010 at 11:13 pm
Alec, what happens to your plot if you have the x-axis in log scale ? Or is there any other scaling for the plot that suggests the rate of growth of the function ?
June 23, 2010 at 12:17 am
Ah, I didn’t look at the plot and interpreted “very slowly increasing” to mean “tending to infinity very slowly”.
June 23, 2010 at 6:19 am
Moses: here is a plot of the same function with on a logarithmic scale.
on a logarithmic scale.
If does grow on average like
does grow on average like 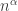 , we can make a guess at what
, we can make a guess at what  should be. (Perhaps this even constitutes a hand-waving argument why it should be so.) We have
should be. (Perhaps this even constitutes a hand-waving argument why it should be so.) We have  , which has a simple pole at
, which has a simple pole at  . But
. But  , which has a simple pole at
, which has a simple pole at  . So we might expect
. So we might expect  . This at least appears consistent with the graph.
. This at least appears consistent with the graph.
June 23, 2010 at 2:29 pm
Alec, what does your data say about versus
versus  ?
?
June 23, 2010 at 4:09 pm
I’ve just had another attempt at thinking about the growth rate of and come to a similar conclusion for a different reason. Whether that constitutes convincing evidence I don’t know …
and come to a similar conclusion for a different reason. Whether that constitutes convincing evidence I don’t know …
Here is the argument. We are interested to estimate which equals the sum over k of the number
which equals the sum over k of the number  of k-tuples
of k-tuples  such that
such that  and
and  Let's estimate
Let's estimate  by thinking about how many such
by thinking about how many such  -tuples have at least one
-tuples have at least one  equal to
equal to 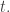 An upper bound for this is
An upper bound for this is  (to be a bit cavalier about integer parts), since the maximum ratio can occur in
(to be a bit cavalier about integer parts), since the maximum ratio can occur in 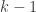 places, and once you know where it occurs you get the rest by finding a sequence of length
places, and once you know where it occurs you get the rest by finding a sequence of length 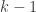 of numbers that divide each other, with the maximum number in the sequence at most
of numbers that divide each other, with the maximum number in the sequence at most  This is an upper bound because it overcounts sequences where
This is an upper bound because it overcounts sequences where  occurs more than once.
occurs more than once.
Now So
So 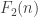 is at most
is at most  which is roughly
which is roughly 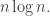 I would expect this process to stabilize at some point. If we make the assumption that it stabilizes at some power
I would expect this process to stabilize at some point. If we make the assumption that it stabilizes at some power  then we ought to have (if we ignore the factor
then we ought to have (if we ignore the factor  on the grounds that it is much smaller than
on the grounds that it is much smaller than 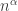 ) something like that
) something like that  which is roughly
which is roughly  So we get
So we get 
This is consistent with what Alec says above, since he is looking at the average of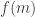 up to
up to  while I am looking at the sum.
while I am looking at the sum.
June 23, 2010 at 8:00 pm
Moses: is this the kind of thing you mean? These are plots of for
for  up to
up to  , for
, for  .
.
June 23, 2010 at 8:19 pm
Here are the same data with plotted on a logarithmic axis. From these, I’d say it looks fairly likely that the ratios are tending to zero — in other words, that
plotted on a logarithmic axis. From these, I’d say it looks fairly likely that the ratios are tending to zero — in other words, that  is concentrated on multiples of
is concentrated on multiples of  (for each prime
(for each prime  )…
)…
June 23, 2010 at 8:19 pm
Oops: link.
June 23, 2010 at 8:33 pm
Even more convincing is a log-log plot.
June 24, 2010 at 12:32 am
Very convincing indeed !
June 24, 2010 at 6:47 am
I don’t have time to check this now, but it seems to me possible that an adaptation of Tim’s argument above might show that , where
, where  : instead of
: instead of  we would be counting the
we would be counting the  -tuples
-tuples  such that
such that  and
and  .
.
June 24, 2010 at 10:34 am
Alec, many thanks for those plots. Let me now ask once again why they don’t imply a contradiction. (I must, once again, be missing something obvious.)
Here’s why I think they do lead to a contradiction, even though I know they can’t.
1. If grows like
grows like  then
then  is approximately
is approximately 
2. If is a typical number, then
is a typical number, then  should be
should be  (I think this is the incorrect statement, but I’ll try to justify it below.)
(I think this is the incorrect statement, but I’ll try to justify it below.)
3. It follows that is much bigger than
is much bigger than  an obvious contradiction.
an obvious contradiction.
Ah, at the moment that I start to try to justify 2, I think I see where I am going to fail. The crude argument was this: a typical number has about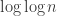 prime factors, most of which are distinct; if
prime factors, most of which are distinct; if  has
has  distinct prime factors then
distinct prime factors then 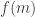 is something that behaves a bit like
is something that behaves a bit like 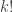 ; therefore, multiplying by a prime should increase the value of
; therefore, multiplying by a prime should increase the value of  by something like
by something like 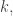 which is usually around
which is usually around 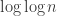 , which tends to infinity.
, which tends to infinity.
However, behaves rather differently at prime powers: we know that
behaves rather differently at prime powers: we know that  So in this extreme case, if
So in this extreme case, if  is a power of
is a power of  then
then  giving us a ratio that does not tend to infinity.
giving us a ratio that does not tend to infinity.
Now we also know, more or less, that is concentrated on smooth numbers. So we will expect, for instance, that almost all the measure of
is concentrated on smooth numbers. So we will expect, for instance, that almost all the measure of  will be concentrated on numbers
will be concentrated on numbers  such that
such that  for some
for some  that tends to infinity with
that tends to infinity with  (possibly very slowly). I haven’t checked, but it now seems a highly plausible guess — since I don’t otherwise see how to avoid a contradiction — that if a high power of 3 divides
(possibly very slowly). I haven’t checked, but it now seems a highly plausible guess — since I don’t otherwise see how to avoid a contradiction — that if a high power of 3 divides 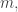 then
then 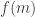 is not
is not 
If we want to get a feel for how behaves, then proving this last fact rigorously would seem to be quite a good idea. If nobody here can do it in the near future, then I’ll post a question on Mathoverflow.
behaves, then proving this last fact rigorously would seem to be quite a good idea. If nobody here can do it in the near future, then I’ll post a question on Mathoverflow.
June 24, 2010 at 12:15 pm
I now have a nonrigorous argument that does indeed suggest that is usually not all that much bigger than
is usually not all that much bigger than 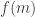 when
when 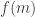 itself is large. It feels like a better argument than some of my earlier nonrigorous arguments, in that there might be some hope of making it precise.
itself is large. It feels like a better argument than some of my earlier nonrigorous arguments, in that there might be some hope of making it precise.
The argument goes like this. A typical for which
for which 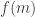 is large will have many small factors. In particular, factors like 2 and 3 will occur with high multiplicity. Let us now define a bipartite graph as follows. The vertices on one side are strictly increasing
is large will have many small factors. In particular, factors like 2 and 3 will occur with high multiplicity. Let us now define a bipartite graph as follows. The vertices on one side are strictly increasing  -tuples (where
-tuples (where  does not have to be the same for each vertex) of numbers
does not have to be the same for each vertex) of numbers  such that each
such that each 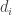 divides the next,
divides the next,  , and
, and  The vertices on the other side are the same but with
The vertices on the other side are the same but with  replaced by
replaced by  We join
We join  to
to  if there exists
if there exists  such that
such that  for every
for every  and
and  for every
for every  (It would perhaps have been nicer to define these sequences by the ratios of successive
(It would perhaps have been nicer to define these sequences by the ratios of successive  )
)
The degree of each vertex is obviously
is obviously  In the reverse direction, the degree of
In the reverse direction, the degree of  is equal to the number of
is equal to the number of  such that
such that  At this point rigour flies out of the window: it seems reasonable to guess that for the ultra-smooth
At this point rigour flies out of the window: it seems reasonable to guess that for the ultra-smooth  s that we are looking at, and for a typical value of
s that we are looking at, and for a typical value of  (if we choose a random
(if we choose a random  satisfying the conditions), a constant proportion of the ratios
satisfying the conditions), a constant proportion of the ratios  are divisible by 3. If that is so, then a simple double-couting argument tells us that the number of vertices on the
are divisible by 3. If that is so, then a simple double-couting argument tells us that the number of vertices on the  side is at most a constant times the number of vertices on the
side is at most a constant times the number of vertices on the  side. Since we sort of know that the conclusion must be true, this feels like a fairly plausible explanation for it. But I'd still like to understand better why so many ratios are divisible by 3.
side. Since we sort of know that the conclusion must be true, this feels like a fairly plausible explanation for it. But I'd still like to understand better why so many ratios are divisible by 3.
June 24, 2010 at 8:48 pm
I think that the only modification to Tim’s argument above needed to calculate the exponent in
in  is the replacement of
is the replacement of  by
by  . If the argument is correct then
. If the argument is correct then  must satisfy
must satisfy  . This gives
. This gives  ,
,  ,
,  , and
, and  . I’m not hugely confident about this, but it appears consistent with the graphs.
. I’m not hugely confident about this, but it appears consistent with the graphs.
June 25, 2010 at 8:22 am
This sounds reasonable. Do you see a way to estimate and more generally,
and more generally,  ? These estimates would lend confidence to Tim’s assertion that almost all the measure of
? These estimates would lend confidence to Tim’s assertion that almost all the measure of  should be concentrated on numbers
should be concentrated on numbers  such that
such that  .
.
June 25, 2010 at 9:04 am
The only thought I have at the moment is that it may be useful to get some kind of handle on the generalization of — call it
— call it 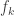 for the moment — defined by
for the moment — defined by  . Note that
. Note that  . Then I think we have
. Then I think we have  , since given an ordered factorization of
, since given an ordered factorization of  each new factor
each new factor  can be combined with one of the existing
can be combined with one of the existing  factors or inserted in one of the
factors or inserted in one of the 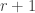 gaps.
gaps.
June 25, 2010 at 9:48 am
Sorry, I’ve just realized that’s wrong. It isn’t the choose function that we want, it’s a more complicated partition function…
June 21, 2010 at 10:46 pm |
[…] Polymath5 By kristalcantwell There is a new thread for Polymath5 here. […]
June 22, 2010 at 4:55 am |
I hope that you’ll succeed at restarting this project, but unfortunately I don’t have too much time the next month (due to exams, IMO, and IMC), but I probably can’t resist thinking about the problem from time to time.
In the post you ask for “system of weights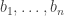 such that the discrepancy of an arbitrary real sequence
such that the discrepancy of an arbitrary real sequence 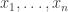 is always at least
is always at least  (where
(where  tends to infinity as n tends to infinity).” It is not clear to me if you allow the
tends to infinity as n tends to infinity).” It is not clear to me if you allow the  ’s to depend on n (in this case there is no reason to divide by
’s to depend on n (in this case there is no reason to divide by  . This is (1) below) or not (in this case we are really considering a infinite sequence
. This is (1) below) or not (in this case we are really considering a infinite sequence  . This is (3) below).
. This is (3) below).
1. The most general version of this approach is to find a sequence (indexed by n) of (longer and longer finite) sequences such that any real sequence
such that any real sequence  has discrepancy at least
has discrepancy at least  and such that the sums of the
and such that the sums of the  ’s tends to infinity (or at least is unbounded) as
’s tends to infinity (or at least is unbounded) as 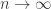 . If this is not possible, Moses’ approach cannot work.
. If this is not possible, Moses’ approach cannot work.
2. Finding an infinite sequence of finite sequences is complicated, so we want to simplify things. One thing we could do is to require the to not depend on
to not depend on  . In this case we are just using an infinite sequence
. In this case we are just using an infinite sequence  and for each n we only look at the first n terms. However, our experimental results suggest that for fixed n in (1),
and for each n we only look at the first n terms. However, our experimental results suggest that for fixed n in (1),  is large for some large values of i. That is, the size of
is large for some large values of i. That is, the size of  depends on the size of
depends on the size of  (and of course the number of divisors of i). That suggests that this cannot work.
(and of course the number of divisors of i). That suggests that this cannot work.
3. One possible solution is the one Gowers use in this post (dividing by ). Is this a new idea?
). Is this a new idea?
4. Another possibility is to let be a sequence over the rational numbers in
be a sequence over the rational numbers in ![(0,1]](https://s0.wp.com/latex.php?latex=%280%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) or
or 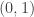 instead of over the integers. Here the idea is that you can find a sequence
instead of over the integers. Here the idea is that you can find a sequence  to use in (1) by looking at
to use in (1) by looking at  in this approach.
in this approach.
Any other suggestions?
Clearly 1 is stronger that 2, 3, and 4 (meaning that if you can find a sequence to use in 2, 3 or 4, you can find one to use in 1), but what is the relative strength of 2, 3, and 4? I think I would prefer to work on 3, but I can’t really justify it.
About the vector-question: Isn’t it trivial that a weight system works for vectors iff it works for real numbers?
June 22, 2010 at 8:19 am |
One interesting property of Tim’s function that is mentioned on Sloane’s database is that its Dirichlet inverse is the sequence
that is mentioned on Sloane’s database is that its Dirichlet inverse is the sequence  . (So
. (So  .) Functions with Dirichlet inverse bounded by 1 are a kind of generalization of completely-multiplicative
.) Functions with Dirichlet inverse bounded by 1 are a kind of generalization of completely-multiplicative  -valued functions: see this wiki page. This one has the extra property of being non-negative. I wonder how special that is.
-valued functions: see this wiki page. This one has the extra property of being non-negative. I wonder how special that is.
June 22, 2010 at 10:04 am
Here’s another argument where I get stuck and can’t see what I’m doing wrong. Perhaps you can help out.
The inductive definition of is that
is that  where
where  if
if 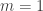 and
and  otherwise. Now it seems to me that the normal rate of growth of
otherwise. Now it seems to me that the normal rate of growth of  is slower than polynomial, with the occasional abnormally high value, but that
is slower than polynomial, with the occasional abnormally high value, but that  for every
for every 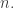 If that is correct, then the Dirichlet series
If that is correct, then the Dirichlet series  converges at the very least when
converges at the very least when  and almost certainly when
and almost certainly when  (All these assertions are unchecked facts, and given that I’m about to run into difficulties, the chances that some of them are wrong are quite high.)
(All these assertions are unchecked facts, and given that I’m about to run into difficulties, the chances that some of them are wrong are quite high.)
Now the inductive definition seems to tell us that since the Dirichlet series associated with
since the Dirichlet series associated with  is
is  and
and  is the Dirichlet convolution of itself with
is the Dirichlet convolution of itself with  But that is ridiculous — it would tell us that
But that is ridiculous — it would tell us that  was zero whenever
was zero whenever  and hence, since it is analytic, zero everywhere where the series converges.
and hence, since it is analytic, zero everywhere where the series converges.
I’m obviously making some silly mistake here, but I just can’t see what it is.
June 22, 2010 at 11:20 am
I think the flaw in your argument is that the inductive definition you wrote down is false for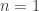 . Taking this into account, the correct relation is
. Taking this into account, the correct relation is  , which gives
, which gives  .
.
June 22, 2010 at 12:05 pm
Thanks!
June 22, 2010 at 10:52 am |
If your EDP project is stalled, can we start a new polymath project in near future?
I think this my conjecture is a good candidate for the next polymath project:
June 24, 2010 at 5:08 am
Goodbye, Porton!
June 25, 2010 at 2:27 am |
I tried to post this in the appropriate thread above, but I couldn’t make it work. So, let me just say that it is not hard to show that for some constant $c$, with
for some constant $c$, with  . This follows from the fact that
. This follows from the fact that  has no poles in
has no poles in  aside from
aside from  , hence the Weiner-Ikehara Tauberian theorem applies. To see my statement about poles, note that for any fixed real
, hence the Weiner-Ikehara Tauberian theorem applies. To see my statement about poles, note that for any fixed real  , the function
, the function  is nonnegative, and vanishes only at $t=0$.
is nonnegative, and vanishes only at $t=0$.
June 25, 2010 at 8:26 am
Ah, thanks. Now I am much more confident that where
where  . Let
. Let  be
be  if
if  and zero if
and zero if  . Then for all
. Then for all 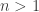 ,
,  where
where  is 1 if
is 1 if 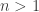 and
and  , and zero otherwise. So, writing
, and zero otherwise. So, writing  , we have
, we have  , so that
, so that  . Now if my understanding is right, we just need to check that
. Now if my understanding is right, we just need to check that  has no poles to the right of our
has no poles to the right of our  .
.
June 27, 2010 at 7:09 pm
Alec, this will indeed always work – is pole-free to the right of
is pole-free to the right of  and only has a pole at $s=\alpha_p$ on the line
and only has a pole at $s=\alpha_p$ on the line  .
.
June 25, 2010 at 10:08 am |
If it is correct that the function is concentrated at numbers
is concentrated at numbers  that are divisible by high powers of small primes, then estimating
that are divisible by high powers of small primes, then estimating  at products of distinct primes may not be all that important to us. However, I went to a bit of effort to do so yesterday, so let me report what I came up with. (Incidentally, I’m sure that everything I say in this comment is either known or incorrect.)
at products of distinct primes may not be all that important to us. However, I went to a bit of effort to do so yesterday, so let me report what I came up with. (Incidentally, I’m sure that everything I say in this comment is either known or incorrect.)
Suppose, then, that Then the sequences we are counting are in one-to-one correspondence with ordered partitions of
Then the sequences we are counting are in one-to-one correspondence with ordered partitions of 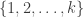 into non-empty sets. For instance, given the partition
into non-empty sets. For instance, given the partition  one sets
one sets  and then one sets
and then one sets  for
for 
Now the ordered partitions of![[k]=\{1,2,\dots,k\}](https://s0.wp.com/latex.php?latex=%5Bk%5D%3D%5C%7B1%2C2%2C%5Cdots%2Ck%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) into
into  non-empty sets are in one-to-one correspondence with the surjections from
non-empty sets are in one-to-one correspondence with the surjections from ![[k]](https://s0.wp.com/latex.php?latex=%5Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) to
to ![[r].](https://s0.wp.com/latex.php?latex=%5Br%5D.&bg=ffffff&fg=333333&s=0&c=20201002) The normal way of counting these is to use the inclusion-exclusion formula, applied to the sets
The normal way of counting these is to use the inclusion-exclusion formula, applied to the sets  where
where 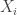 is the set of functions from
is the set of functions from ![[k]](https://s0.wp.com/latex.php?latex=%5Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) to
to ![[r]](https://s0.wp.com/latex.php?latex=%5Br%5D&bg=ffffff&fg=333333&s=0&c=20201002) that miss
that miss 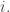 This tells us that the number of surjections is
This tells us that the number of surjections is
Now this formula as it stands is not much use to us because what we really want to know is the approximate number of surjections, and here we have an exact formula with a lot of cancellation. So let us do some approximating. If we take out a factor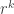 then a typical term will be
then a typical term will be  If we then approximate
If we then approximate  by
by  we end up approximating the whole sum by
we end up approximating the whole sum by
which, by the binomial theorem, equals
As a quick sanity check, let us see what happens in the extreme cases and
and  In the first case we get
In the first case we get  This is not very good, because we should be getting
This is not very good, because we should be getting 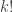 , which is more like
, which is more like  And it’s even worse when
And it’s even worse when  when we should get zero but in fact get a non-zero answer.
when we should get zero but in fact get a non-zero answer.
Leaving those problems aside for now, let’s see what happens when is small. Then we get almost exactly
is small. Then we get almost exactly  since
since  is much smaller than
is much smaller than 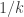 (and therefore
(and therefore  is almost exactly 1). This is what we would hope, since almost every function from
is almost exactly 1). This is what we would hope, since almost every function from ![[k]](https://s0.wp.com/latex.php?latex=%5Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) to
to ![[r]](https://s0.wp.com/latex.php?latex=%5Br%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a surjection when
is a surjection when  is small.
is small.
Continuing to pretend that the first estimate was a good one, let us think about how to maximize for given
for given  Clearly if
Clearly if  is small enough for the second term to be approximately 1, then we want to increase it. To see roughly where the maximum occurs, let us take logs. That gives us
is small enough for the second term to be approximately 1, then we want to increase it. To see roughly where the maximum occurs, let us take logs. That gives us  At the maximum,
At the maximum,  will be reasonably small (if
will be reasonably small (if  is large) so we can probably approximate
is large) so we can probably approximate  by
by  which gives us
which gives us  To maximize that let’s differentiate the part in the brackets, which gives us
To maximize that let’s differentiate the part in the brackets, which gives us  For that to be zero, we need
For that to be zero, we need  Unfortunately,
Unfortunately,  has no positive solutions. But perhaps that is not really unfortunate and is just telling us that the number of surjections is biggest when
has no positive solutions. But perhaps that is not really unfortunate and is just telling us that the number of surjections is biggest when 
Another sanity check: how many surjections are there from![[k]](https://s0.wp.com/latex.php?latex=%5Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) to
to ![[k-1]](https://s0.wp.com/latex.php?latex=%5Bk-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) ? This is not too hard to calculate because we know that precisely one value must be taken twice, and all the others must be taken once. The number of ways of choosing the value to be taken twice is
? This is not too hard to calculate because we know that precisely one value must be taken twice, and all the others must be taken once. The number of ways of choosing the value to be taken twice is  The number of ways of choosing the two preimages of that value is
The number of ways of choosing the two preimages of that value is  The number of ways of choosing the rest of the function is
The number of ways of choosing the rest of the function is  . So it looks as though the number of surjections is
. So it looks as though the number of surjections is  which is definitely bigger than
which is definitely bigger than 
I’ve got myself into a muddle once again. A possible explanation is that the number of surjections is maximized when And in fact, I have a suggestion of why that might be. Perhaps the number is maximized when
And in fact, I have a suggestion of why that might be. Perhaps the number is maximized when  is as big as possible such that almost all functions from
is as big as possible such that almost all functions from ![[k]](https://s0.wp.com/latex.php?latex=%5Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) to
to ![[r]](https://s0.wp.com/latex.php?latex=%5Br%5D&bg=ffffff&fg=333333&s=0&c=20201002) are surjections. Indeed, I find this pretty plausible. The probability that a function is not a surjection is at most
are surjections. Indeed, I find this pretty plausible. The probability that a function is not a surjection is at most  or about
or about  That is small as long as
That is small as long as  is much smaller than
is much smaller than  or
or  is much smaller than
is much smaller than  This tells us that
This tells us that  can go up to about
can go up to about  (which is not
(which is not  but I now don’t believe that any more). The number of surjections we get should then be roughly
but I now don’t believe that any more). The number of surjections we get should then be roughly  Except that that is
Except that that is  which is a lot smaller than
which is a lot smaller than  which is roughly
which is roughly 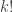 .
.
My sanity checks seem to have resulted in insanity, so I’d better stop this rambling comment and see if I can find the answer somewhere, or if anyone knows it. (As I said at the beginning, it must surely be known.)
June 25, 2010 at 2:01 pm
I’ve tried posting a question on Mathoverflow to see whether anyone has any idea. So far, some relevant information has been given but no definitive answer yet.
June 25, 2010 at 2:25 pm
Here is how I had tried to calculate this earlier.
We want the value of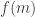 for
for  . This is a function
. This is a function  where
where  is the number of prime divisors of
is the number of prime divisors of  . Then it is not hard to see that
. Then it is not hard to see that  satisfies the recurrence relation
satisfies the recurrence relation  . The first few values of
. The first few values of 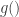 are
are  and so on.
and so on.
Let’s rewrite the recurrence relation in the following way:
Now define , then
, then  satisfies the recurrence:
satisfies the recurrence:
Consider the generating function $a(x) = \sum_{n \geq 0} a(n) x^n$. Then, from the recurrence relation for , we have the following condition:
, we have the following condition:  . In order to verify this, we need to check the coefficient of
. In order to verify this, we need to check the coefficient of 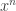 on both sides of the claimed equality. Assuming this is correct, we get:
on both sides of the claimed equality. Assuming this is correct, we get:  which implies $a(x) = 1/(2-e^x)$. So
which implies $a(x) = 1/(2-e^x)$. So  should be the coefficient of
should be the coefficient of 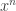 in the Taylor series of
in the Taylor series of  around 0. Let’s try to get an expression for this coefficient.
around 0. Let’s try to get an expression for this coefficient.
So , the coefficient of
, the coefficient of 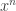 in this expression ought to be
in this expression ought to be
 . Recall that the actual function we wanted was
. Recall that the actual function we wanted was  . Hence we get:
. Hence we get:
I have no idea why this expression is an integer for positive integers , except that it must be if the calculations are correct. If this is correct, then we can get an approximate expression for
, except that it must be if the calculations are correct. If this is correct, then we can get an approximate expression for  by looking at the largest term in the summation.
by looking at the largest term in the summation.  is maximized for $n \log t – t \log 2 = 0$ which means
is maximized for $n \log t – t \log 2 = 0$ which means  , so
, so  .
.
As a sanity check, going back to the generating function , I plugged in the expression $1/(2-e^x)$ into sage and computed the first few terms of the Taylor series expansion. This yielded
, I plugged in the expression $1/(2-e^x)$ into sage and computed the first few terms of the Taylor series expansion. This yielded
The numerators of the fractions in the expression above are the values of , and they seem to match the values obtained from the recurrence relation for
, and they seem to match the values obtained from the recurrence relation for  . Also plugging in the sequence
. Also plugging in the sequence  into Sloan’s database, you get the sequence A000670 .
into Sloan’s database, you get the sequence A000670 .
June 25, 2010 at 3:12 pm
I made a mistake in estimating from the expression
from the expression
The term in maximized for
in maximized for  , i.e.
, i.e.  , and this gives the approximation
, and this gives the approximation  .
.
June 25, 2010 at 3:25 pm
That’s interesting. Since , it is (as it has to be) bigger than
, it is (as it has to be) bigger than  but it is a very similar kind of function. I like the argument too.
but it is a very similar kind of function. I like the argument too.
June 26, 2010 at 10:31 am
There is a function such that
such that  for all primes
for all primes  not dividing
not dividing  . We have
. We have  , and we now know a bit about the growth of this, but it would be useful to understand the growth of
, and we now know a bit about the growth of this, but it would be useful to understand the growth of  more generally. This would allow us, for example, to test whether some easily-defined sequences with low discrepancy can actually ‘break’
more generally. This would allow us, for example, to test whether some easily-defined sequences with low discrepancy can actually ‘break’  as a candidate for a proof of EDP, or not.
as a candidate for a proof of EDP, or not.
Note that depends only on the multiplicities in the prime facrtorization of
depends only on the multiplicities in the prime facrtorization of  . Here are some simple cases:
. Here are some simple cases:  for
for 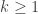 (and
(and  );
);  ; and in general when
; and in general when  is a product of distinct primes,
is a product of distinct primes,  is described by Sloane’s A098348. (Click on the keyword ‘tabl’ towards the bottom of that page to see the sequence formatted as a table: row
is described by Sloane’s A098348. (Click on the keyword ‘tabl’ towards the bottom of that page to see the sequence formatted as a table: row  shows
shows  as a function of
as a function of  when
when  is a product of
is a product of  distinct primes).
distinct primes).
June 26, 2010 at 10:47 am
Richard Stanley has now given a useful answer to my Mathoverflow question. It is very similar to Moses’s answer above.
June 26, 2010 at 11:26 am |
One question I would very much like to know the answer to is this. Suppose we choose an “ -random” integer between 1 and n. What is its prime factorization like? By an
-random” integer between 1 and n. What is its prime factorization like? By an  -random integer I mean that we choose the number
-random integer I mean that we choose the number  with probability
with probability  What I suspect is that such a number will, with fairly high probability, be divisible by large powers of all small primes.
What I suspect is that such a number will, with fairly high probability, be divisible by large powers of all small primes.
We now understand at prime powers and we understand it pretty well at products of distinct primes. Perhaps the next case is products of two prime powers. I’ve made a start thinking about this, and in the Polymath spirit I’m going to report on my half-formed thoughts rather than trying to push them to a conclusion first.
at prime powers and we understand it pretty well at products of distinct primes. Perhaps the next case is products of two prime powers. I’ve made a start thinking about this, and in the Polymath spirit I’m going to report on my half-formed thoughts rather than trying to push them to a conclusion first.
Let’s take the number If we consider the ratios between successive terms of the sequences we are counting, these all take the form
If we consider the ratios between successive terms of the sequences we are counting, these all take the form  with
with 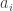 and
and  non-negative integers and at least one of
non-negative integers and at least one of 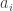 and
and  not zero. So we need to count the number of pairs of sequences
not zero. So we need to count the number of pairs of sequences  and
and  such that
such that  ,
,  and at least one of
and at least one of 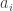 and
and  is non-zero.
is non-zero.
Given such a sequence, we can form a 23-sequence as follows. For each in turn we write
in turn we write 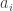 2s followed by
2s followed by  3s. It is clear that every 23-sequence with
3s. It is clear that every 23-sequence with  2s and
2s and  3s can be created in this way (e.g. we could make every single ratio be either 2 or 3), so the number of sequences is at least
3s can be created in this way (e.g. we could make every single ratio be either 2 or 3), so the number of sequences is at least  . However, this creation is very far from unique. For example, the sequence 2233232 can be split up as 2, 233, 23, 2 (leading to the four ratios 2, 18, 6, 2) or as 22, 33, 2, 3, 2 (leading to the five ratios 4, 9, 2, 3, 2). So what additional information do we need to get from the 23-sequence to the ratio sequence? Obviously, we need to know where the prime factorization of one ratio ends and the prime factorization of the next ratio begins. To do this, we need to add an extra symbol such as |.
. However, this creation is very far from unique. For example, the sequence 2233232 can be split up as 2, 233, 23, 2 (leading to the four ratios 2, 18, 6, 2) or as 22, 33, 2, 3, 2 (leading to the five ratios 4, 9, 2, 3, 2). So what additional information do we need to get from the 23-sequence to the ratio sequence? Obviously, we need to know where the prime factorization of one ratio ends and the prime factorization of the next ratio begins. To do this, we need to add an extra symbol such as |.
Now it’s not quite as simple as just adding |s wherever we feel like it, because between two |s you are never allowed to go from a 3 to a 2. Actually, the words “between two |s” were redundant there. I think the rule is that we can take any sequence of 2s, 3s and |s, provided 3 is never followed by 2. To test that, let me pick a fairly random such sequence: 23|33|2|223|233|3|2. That corresponds to the sequence of ratios 6, 9, 2, 12, 18, 3, 2. And in the opposite direction I take the ratios and form the sequence in the obvious way.
I’ve missed out one further condition, which is that you are never allowed two |s in a row. So the question becomes the following. How many 23|-sequences are there with 2s and
2s and  3s such that 3 is never followed by 2 and | is never followed by |, and such that the sequence is not allowed to begin or end with |? This sounds to me like a pretty standard problem in enumerative combinatorics, probably treatable with generating functions. I’ll have a think about it myself.
3s such that 3 is never followed by 2 and | is never followed by |, and such that the sequence is not allowed to begin or end with |? This sounds to me like a pretty standard problem in enumerative combinatorics, probably treatable with generating functions. I’ll have a think about it myself.
June 26, 2010 at 12:05 pm
A small further observation, which lends some support to the idea that should be concentrated on numbers with many small prime factors, but not so many that they are all identical.
should be concentrated on numbers with many small prime factors, but not so many that they are all identical.
First, observe that to get a valid sequence of 2s, 3s and |s, one can take a sequence of 2s and 3s with 2s and
2s and  3s and insert |s into it. The only rules about the insertion process are that you should insert at most one | into each gap (and nothing before or after the sequence) and that every time the sequence goes from a 3 to a 2 you must insert a |. That means that the number of possible insertions is 2 raised to the power the number of places in the sequence where you do not go from a 3 to a 2.
3s and insert |s into it. The only rules about the insertion process are that you should insert at most one | into each gap (and nothing before or after the sequence) and that every time the sequence goes from a 3 to a 2 you must insert a |. That means that the number of possible insertions is 2 raised to the power the number of places in the sequence where you do not go from a 3 to a 2.
Let’s consider the number Then there must be at least
Then there must be at least  places in the sequence where you do not go from 3 to 2 (with equality for the sequence 32323232…) and usually rather more than this. So
places in the sequence where you do not go from 3 to 2 (with equality for the sequence 32323232…) and usually rather more than this. So  is at least
is at least  (for the number of 23-sequences) times
(for the number of 23-sequences) times  (for the number of possible insertions per sequence), or around
(for the number of possible insertions per sequence), or around  . That is
. That is  is at least
is at least  or so. This is significantly bigger than
or so. This is significantly bigger than 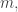 from which we learn that to maximize
from which we learn that to maximize  (or, perhaps more interestingly,
(or, perhaps more interestingly,  ) we definitely do not want to take
) we definitely do not want to take  to be a power of 2.
to be a power of 2.
Needless to say, the estimates just made can be improved, but even now they are good enough to make this point.
June 26, 2010 at 12:12 pm
A further quick thought. If we take to be
to be  , what are the valid sequences that result? This time we make sequences out of 2s, 3s, 5s and |s. The rules are that 2 never follows 3 or 5 and 3 never follows 5, and otherwise they are the same as before. Obviously this generalizes.
, what are the valid sequences that result? This time we make sequences out of 2s, 3s, 5s and |s. The rules are that 2 never follows 3 or 5 and 3 never follows 5, and otherwise they are the same as before. Obviously this generalizes.
June 26, 2010 at 3:27 pm |
Going back to sequences of 2s, 3s and |s, here are some more calculations that give quite a good idea of how many there are.
What I’m going to do is count something slightly different. I’ll count all length-n sequences of 1s, 2s and 3s (with 1 playing the role of |) such that 32 and 11 never appear. Let’s call this number f(n), and for i=1,2,3 let be the number of sequences of length n that end with i. Then we have the following recurrence relations:
be the number of sequences of length n that end with i. Then we have the following recurrence relations:  ,
,  and
and  Writing
Writing 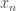 for the vector
for the vector  we find that
we find that  and
and  where
where  is the matrix
is the matrix 
The largest eigenvalue of this matrix is, if my calculations are correct, a cubic irrational that lies beween 2 and 3. So the growth rate of is
is  for some
for some  between
between  and
and 
Now the here is not the same as the combined number of 2s and 3s in the sequence. However, we can get a feel for this by calculating the eigenvector that corresponds to the largest eigenvalue. It will tell us the proportions of 1s, 2s and 3s in a typical sequence (since we can think of these proportions as being the distribution after
here is not the same as the combined number of 2s and 3s in the sequence. However, we can get a feel for this by calculating the eigenvector that corresponds to the largest eigenvalue. It will tell us the proportions of 1s, 2s and 3s in a typical sequence (since we can think of these proportions as being the distribution after  steps of a random walk, which will converge very rapidly to the stationary distribution). So if we want
steps of a random walk, which will converge very rapidly to the stationary distribution). So if we want 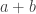 to be about
to be about  then we can multiply our previous
then we can multiply our previous  by
by  where
where  is the proportion of 1s in a typical sequence. (Of course, this isn’t exact, but it’s close.)
is the proportion of 1s in a typical sequence. (Of course, this isn’t exact, but it’s close.)
By working through the technicalities here, I think one can get pretty good bounds for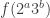 when
when  and
and  are in their typical proportions. And I think we can also say that they are in their typical proportions
are in their typical proportions. And I think we can also say that they are in their typical proportions  -almost all the time.
-almost all the time.
June 26, 2010 at 3:32 pm
Actually, I want to modify one thing I said there. What we care about is not the value of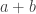 but the value of
but the value of  which needs to be less than
which needs to be less than  However, the remark about the typical ratio of
However, the remark about the typical ratio of  and
and  still stands, I think, so to work out the typical values of
still stands, I think, so to work out the typical values of  and
and  subject to the condition that
subject to the condition that  we can use the ratio of
we can use the ratio of  to
to  and the inequality
and the inequality 
June 26, 2010 at 3:49 pm
On second thoughts, I’m worried about what I just said. The eigenvector tells us about the ratios of the number of sequences ending in a 2 and the number ending in a 3. It does not tell us about the ratio of the number of 2s to the number of 3s in a typical sequence. Indeed, that should tend to 1, since the reverse of a sequence that works gives us a similar sequence but with 23 forbidden instead, so symmetry seems to preclude any bias.
But that observation doesn’t sit very well with the inequality We ought to be punished to some extent for choosing 3s, because that will cause the length of the sequence to go down. I’ll discuss this a bit more in my next comment.
We ought to be punished to some extent for choosing 3s, because that will cause the length of the sequence to go down. I’ll discuss this a bit more in my next comment.
June 26, 2010 at 4:05 pm |
In this comment I want to suggest a (probably standard) method for estimating the number of sequences of the kind I’ve been considering above, but somehow forcing the ratio of the number of 2s to the number of 3s to be approximately some prescribed value. As I commented here, if you take the uniform distribution on sequences of length that satisfy the conditions, then you should get about the same number of 2s as 3s. So how can one change this?
that satisfy the conditions, then you should get about the same number of 2s as 3s. So how can one change this?
One way is to count sequences with weights. Suppose we weight a sequence by where
where  is the number of 2s and
is the number of 2s and  is the number of 3s. Now let
is the number of 3s. Now let  be the total weight of sequences of length
be the total weight of sequences of length  , and split
, and split  up into
up into  as before. Our new matrix is
as before. Our new matrix is 
I can’t see in my head what to do next. Either I’ll have to go away and think about this, or someone reading this will know, or be able to work out, how the argument should go.
June 26, 2010 at 5:03 pm |
From the inductive definition of , it follows that the values of
, it follows that the values of  (for distinct primes
(for distinct primes 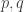 ) are given by the formulae
) are given by the formulae  (
( ),
),  , and for
, and for  ,
,  . This is Sloane’s A059576, called there the ‘summatory Pascal triangle’. I don’t quite understand the principal definition stated on that page, but there are a few formulae that may be helpful in calculating the asymptotics. The generating function is given as
. This is Sloane’s A059576, called there the ‘summatory Pascal triangle’. I don’t quite understand the principal definition stated on that page, but there are a few formulae that may be helpful in calculating the asymptotics. The generating function is given as  .
.
June 26, 2010 at 7:08 pm
Here is the calculation for the generating function of (
( distinct primes). Writing
distinct primes). Writing  and
and  if and only if
if and only if  for all
for all  , for
, for  we have
we have  , so that
, so that  , and
, and  . In terms of the generating function
. In terms of the generating function  , we can note that the right-hand side is a convolution with
, we can note that the right-hand side is a convolution with  , and so write
, and so write  , which implies that
, which implies that  .
.
June 26, 2010 at 10:14 pm
That’s nice. I feel as though if I were more used to generating functions (or perhaps just if I sat down and thought for a while) then I’d be able to get from here to a good answer to the question I mentioned earlier: what does the prime factorization of a typical -random number look like? More precise questions are as follows.
-random number look like? More precise questions are as follows.
1. If you choose a random from
from 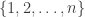 with probability
with probability  then what is the expectation of the sequence
then what is the expectation of the sequence  such that
such that  ?
?
2. How concentrated are the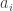 about their means?
about their means?
3. Roughly how quickly do they decay with ?
?
A decent answer to 1 should yield a decent answer to 3. My hunch, and hope, is that the answers to 2 and 3 are that they are pretty concentrated and that they decay pretty fast. The reason I’d like that is that it would make much more plausible my unproved assertion that if you take a typical and a typical sequence
and a typical sequence 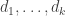 of increasing divisors of
of increasing divisors of 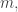 then a positive fraction of the
then a positive fraction of the 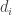 will be divisible by 3.
will be divisible by 3.
It occurs to me that this question could be investigated experimentally. I don’t know how large an one would need to take in order to get results that were genuinely informative, and the numbers would be large, so high-precision arithmetic (or some judicious approximations) might be needed. But just to see a large bunch of numbers generated according to the above probability distribution could give us a very good feel for the function
one would need to take in order to get results that were genuinely informative, and the numbers would be large, so high-precision arithmetic (or some judicious approximations) might be needed. But just to see a large bunch of numbers generated according to the above probability distribution could give us a very good feel for the function  I think.
I think.
June 27, 2010 at 12:27 am
Minor observation: using Alec’s generating function (assuming the generalization to infinitely many variables ), and substituting $z_i = (p_i)^{-s}$ gives an alternate proof of the fact that
), and substituting $z_i = (p_i)^{-s}$ gives an alternate proof of the fact that  (Alex had mentioned this in a comment above).
(Alex had mentioned this in a comment above).
June 27, 2010 at 7:46 pm
That is an interesting observation, and it generalizes a bit: if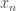 is a completely-multiplicative sequence, and
is a completely-multiplicative sequence, and  , then
, then  . Of course if
. Of course if 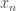 is completely multiplicative then so is
is completely multiplicative then so is  , so if we fomally set
, so if we fomally set 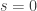 then it starts to look suggestive in relation to the original problem.
then it starts to look suggestive in relation to the original problem.
Regarding Tim’s question about the -random frequencies of exponents of different primes: the distribution is easy enough to compute exactly, and I have done so up to
-random frequencies of exponents of different primes: the distribution is easy enough to compute exactly, and I have done so up to  . These graphs show
. These graphs show  plotted against
plotted against  , for
, for  , where
, where  is the exponent of
is the exponent of  in the factorization of
in the factorization of  .
.
June 27, 2010 at 10:21 pm
Those are very nice. I realize that I was getting muddled when I said that the numbers would be very large — I was confusing the dependence on with the dependence on the number of prime factors of
with the dependence on the number of prime factors of 
What I find interesting so far is that the graphs for 2 and 3 seem to be exhibiting the kind of behaviour one might hope for — perhaps even approaching a normal distribution, though this is scant evidence for such a strong conjecture.
I’d still be interested to know the behaviour for much larger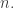 One way that one might try to analyse it is by devising a suitable random walk through the set of all sequences
One way that one might try to analyse it is by devising a suitable random walk through the set of all sequences  or equivalently through the set of all sequences
or equivalently through the set of all sequences  such that each
such that each 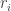 is a positive integer and
is a positive integer and  If we could devise it so that the stationary distribution was uniform and the walk was rapidly mixing, then we would be able to sample randomly with very large values of
If we could devise it so that the stationary distribution was uniform and the walk was rapidly mixing, then we would be able to sample randomly with very large values of  and thereby get a very good feel for the distribution.
and thereby get a very good feel for the distribution.
The sort of walk one might try is this. Suppose you are at the sequence Choose a random prime
Choose a random prime  less than or equal to
less than or equal to 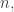 a random number
a random number  from the set
from the set  and a random positive integer
and a random positive integer  less than or equal to
less than or equal to 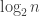 .
.
If then
then
……if and
and  then divide
then divide 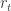 by
by 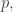
……else do nothing.
If then
then
……if then
then
…………if then multiply
then multiply  by
by 
…………else do nothing
……else if then
then
…………if then move to the sequence
then move to the sequence 
…………else do nothing
……else do nothing.
One not very nice aspect of this algorithm is that the probability of dividing by a prime is rather small at any given stage, so the time taken to reach the stationary distribution is more -like than
-like than 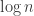 -like. I don’t know if there is an ingenious way round this. But perhaps even an
-like. I don’t know if there is an ingenious way round this. But perhaps even an  -like algorithm could be run up to values of
-like algorithm could be run up to values of  of a few million or so.
of a few million or so.
Unless I’ve made a silly mistake, the stationary distribution of that algorithm is uniform over all valid sequences. My reasoning is that we can think of it as a multigraph with loops that is regular of degree
I forgot to say that I have no proof about its speed of convergence. However, if all we are looking for is an experiment to try, then we don’t really care whether we have a rigorous proof that it converges rapidly, as long as it seems plausible that it should. (But the latter is important — if there were some bottleneck, then it would lead to genuinely misleading results.)
June 28, 2010 at 8:30 am
A small thought — is it possible that the distributions in Alec’s graphs (see previous message but one) are Poisson?
June 28, 2010 at 6:47 am |
I have a conjecture regarding the behaviour of as
as 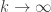 , which I’ll try to explain.
, which I’ll try to explain.
Let be the number of distinct prime factors of
be the number of distinct prime factors of  , and let
, and let  be the number of prime factors of
be the number of prime factors of  counted with multiplicity. (For example,
counted with multiplicity. (For example,  and
and  .)
.)
The conjecture is that for any ,
,  .
.
In terms of the notation used above for the generating function, this is saying that , when all of the
, when all of the 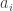 are positive. This is true for
are positive. This is true for  , and seems consistent with the calculations I’ve done for
, and seems consistent with the calculations I’ve done for 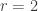 . (For example, the conjecture implies that
. (For example, the conjecture implies that  ; we have
; we have  .)
.)
The form is suggested by analogy of the formula with the integral formula
with the integral formula  , which has solutions of the form
, which has solutions of the form  ; by symmetry all the
; by symmetry all the 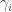 must be equal.
must be equal.
The actual factor comes from the fact that the generating function has a pole at
has a pole at  , so that its coefficients must grow as
, so that its coefficients must grow as  .
.
These are rather vague justifications, but perhaps they can be fleshed out, or perhaps an altogether different proof is possible.
June 28, 2010 at 7:55 am |
I wanted to go back to some of the calculations we were doing earlier because I think they might yield some answers about the prime factorization of -random numbers. In particular, I think we can conclude that the power of a small prime that divides an
-random numbers. In particular, I think we can conclude that the power of a small prime that divides an  -random number is
-random number is  .
.
I am going to repeat a bunch of things from previous comments of Tim and Alec. Recall that we had estimated where
where  is such that
is such that  . Consider
. Consider  where
where  is the largest
is the largest  such that
such that  . Note that
. Note that  where
where  is such that
is such that  ,
,  . If we determine that
. If we determine that  for all
for all  and
and  ).
). 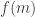 is equal to the number of divisor sequences of
is equal to the number of divisor sequences of  , and say
, and say  is the number of such sequences of length
is the number of such sequences of length  ; also
; also  .
.
A divisor sequence of (with
(with  ) can be mapped uniquely to a divisor sequence of
) can be mapped uniquely to a divisor sequence of  by simply dividing each term of the sequence by the highest power of
by simply dividing each term of the sequence by the highest power of  that divides it. This is a many-one mapping. Let’s estimate the number of pre-images that a divisor sequence of
that divides it. This is a many-one mapping. Let’s estimate the number of pre-images that a divisor sequence of  has in this mapping. This number is a function of the length
has in this mapping. This number is a function of the length  of the sequence and
of the sequence and  . Roughly speaking, we need to distribute
. Roughly speaking, we need to distribute  copies of
copies of  in the given divisor sequence – each of these copies could either fall between elements of the given divisor sequence or they could multiply existing elements of the sequence. I claim the number of pre-images is roughly
in the given divisor sequence – each of these copies could either fall between elements of the given divisor sequence or they could multiply existing elements of the sequence. I claim the number of pre-images is roughly  – the number of ways of interleaving the
– the number of ways of interleaving the  copies of
copies of  in the existing sequence of length
in the existing sequence of length  is
is  and then each copy has the option of merging (multiplying) with the element immediately to the right of it. That gives the factor
and then each copy has the option of merging (multiplying) with the element immediately to the right of it. That gives the factor  . If one of the copies of
. If one of the copies of  is the last element of the sequence, then it does not have this option of multiplying to the right, hence this is a slight overestimate.
is the last element of the sequence, then it does not have this option of multiplying to the right, hence this is a slight overestimate.
So . Hence
. Hence  (ignoring floors). Note that
(ignoring floors). Note that  , the length of the divisor sequence, is at most
, the length of the divisor sequence, is at most 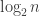 , hence
, hence  . What we really wanted to do was find a value
. What we really wanted to do was find a value 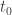 , such that
, such that  for all
for all  . From our estimate, it looks like
. From our estimate, it looks like  should suffice (for suitable constant
should suffice (for suitable constant  ).
).
If all this is correct we conclude that an -random number is divisible by
-random number is divisible by  .
.
June 28, 2010 at 8:07 am
Some parts of my comment above came out garbled. In reading it, replace the last few lines of the second para (beginning with “If we determine that”) with the following text:
If we determine that for all
for all  and
and  ).
). 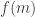 is equal to the number of divisor sequences of
is equal to the number of divisor sequences of  , and say
, and say  is the number of such sequences of length
is the number of such sequences of length  ; also
; also  .
.
A divisor sequence of …
June 28, 2010 at 8:09 am
uh oh … the intended fix is garbled in exactly the same way. I give up.
June 28, 2010 at 8:19 am
Did the garbled bit contain less-that or greater-than symbols? WordPress has trouble parsing those inside Latex expressions, so you have to render them as ‘& l t ;’ and ‘& g t ;’ (closing up the spaces) — which, oddly enough, WordPress can parse inside Latex.
June 28, 2010 at 8:38 am
Unfortunately, WordPress garbles not just the output but also the input, sometimes chopping out quite a bit of text, so I’m unable to edit it. But I think Alec’s diagnosis and cure are both right.
One thing I’ve noticed is that sometimes one can get away with the usual symbols. I have a feeling that the problems really start to arise if you have a less-than symbol followed a bit later by a greater-than symbol. I think WordPress gives much higher precedence to that pairing than it does to dollars, and therefore gets itself into difficulties.
June 28, 2010 at 8:50 am
Something that slightly troubles me about this estimate is that it looks as though a typical -random number is greater than
-random number is greater than 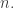 The log of
The log of  is
is  The sum of that over
The sum of that over  is roughly the same as the sum of
is roughly the same as the sum of  over
over  since the
since the  exactly cancels out the sparseness of the primes. So it seems that the sum tends to infinity. If we stop the sum at some
exactly cancels out the sparseness of the primes. So it seems that the sum tends to infinity. If we stop the sum at some  at a point where it is distinctly bigger than
at a point where it is distinctly bigger than  then the product of
then the product of  over all
over all  has logarithm greater than
has logarithm greater than  so it is greater than
so it is greater than 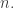 For
For  large enough (so that the approximations are valid for all primes up to the constant
large enough (so that the approximations are valid for all primes up to the constant  ) this appears to be a contradiction.
) this appears to be a contradiction.
If I’m not making some silly mistake, I wonder if there is some tweak to your argument that would avoid the problem. (I can’t really tell until we get the missing text …)
June 28, 2010 at 8:57 am
Assuming that the answer to that last question is yes (and the end of Moses’s argument does look at a first glance as though it allows a certain flexibility), then that and Alec’s graphs make me wonder whether the largest power of that divides an
that divides an  -random
-random  is aymptotically Poisson with mean
is aymptotically Poisson with mean  for some suitable constant
for some suitable constant  that depends on
that depends on  only. If so, then it’s tempting to make it genuinely Poisson and see what happens. Normally this would make certain calculations much nicer. I don’t have any indication of how that might apply in our case, so this is a thought to go on the back burner for now.
only. If so, then it’s tempting to make it genuinely Poisson and see what happens. Normally this would make certain calculations much nicer. I don’t have any indication of how that might apply in our case, so this is a thought to go on the back burner for now.
June 28, 2010 at 11:50 am
In answer to Tim’s question about the contradiction from the estimate: yes, it does look like I miscalculated in the very end (and there could be other errors too). Let me try to do it a little more carefully. The final lower bound for the power of was based on this calculation:
was based on this calculation:
So we need:

I used the approximation . Also, although I did not calculate this before, it looks like the approximation
. Also, although I did not calculate this before, it looks like the approximation  may be reasonable. Substituting, the condition we need is:
may be reasonable. Substituting, the condition we need is:
The condition should be satisfied for all , so the lower bound on the power of
, so the lower bound on the power of  we get from this argument is
we get from this argument is
 .
.
June 28, 2010 at 9:28 pm
I’ve taken the computation a bit further (to , with
, with  ), and also fitted Poisson distributions with the same mean to the data. The plots are here.
), and also fitted Poisson distributions with the same mean to the data. The plots are here.
The fit is remarkably good for ; for some reason it is a bit less good for
; for some reason it is a bit less good for  .
.
The mean values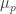 of the exponents were about 5.840, 2.316, 0.836 and 0.442 for 2, 3, 5 and 7 respectively. To test Moses’s theory, we can calculate
of the exponents were about 5.840, 2.316, 0.836 and 0.442 for 2, 3, 5 and 7 respectively. To test Moses’s theory, we can calculate  , where
, where  satisfies
satisfies  . The values of this ratio for 2, 3, 5 and 7 are about 1.27, 1.06, 1.01 and 0.99 respectively. Despite the seeming anomaly with
. The values of this ratio for 2, 3, 5 and 7 are about 1.27, 1.06, 1.01 and 0.99 respectively. Despite the seeming anomaly with 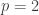 , I think these are very encouraging.
, I think these are very encouraging.
June 28, 2010 at 10:08 pm
Wow, thanks for doing that. Odd about 2, and almost odder about the rest fitting so well. I suppose if one were greedy then one could check that the distributions were independent …
There do seem to be some ways in which 2 is anomalous for this problem, such as the fact that we can’t use characters mod 2 to create bounded-discrepancy examples. I wonder if in some way that underlies what’s going on. (Having written that, I realize that I was accidentally assuming that there is a deep connection between f and HAP-discrepancy, which we haven’t yet demonstrated.)
June 28, 2010 at 10:49 pm
The prime 2 is a problem in a very simple way. There is a trivial sequence (-1 on odd, +1 on even) which works for every HAP with odd difference. No-one has yet given an example (sorry if I’ve missed it), even for a set of at least two primes including 2, of a sequence which is bounded on every HAP where the difference is only divisible by those primes.
Maybe there are some clues here as to why 2 blocks some of the otherwise obvious solutions.
June 28, 2010 at 10:58 pm
You’re saying that we don’t know, for example, whether every sequence has unbounded discrepancy on a HAP with common difference of the form
sequence has unbounded discrepancy on a HAP with common difference of the form  ? If we don’t have a counterexample to that, then we should probably look quite hard for one.
? If we don’t have a counterexample to that, then we should probably look quite hard for one.
June 28, 2010 at 11:16 pm
Actually, I now think we did have an example for common differences of the form but I can’t find where it was in the discussion. The idea was to construct a sequence with the property that
but I can’t find where it was in the discussion. The idea was to construct a sequence with the property that  for every
for every  and to keep the partial sums bounded. To do that, one divides it up into blocks of 6. When you get to a new block of 6 of the form
and to keep the partial sums bounded. To do that, one divides it up into blocks of 6. When you get to a new block of 6 of the form  you’ve decided on the value of
you’ve decided on the value of  at
at 

 and
and  so you’ve only got two more choices. I think you can prove if you do this inductive construction properly that the choices you’ve made so far are not all the same, so you can keep the sum over the block down to zero. Or perhaps you do something to make sure you’ll always be OK. In fact, I think that’s it — you also insist that
so you’ve only got two more choices. I think you can prove if you do this inductive construction properly that the choices you’ve made so far are not all the same, so you can keep the sum over the block down to zero. Or perhaps you do something to make sure you’ll always be OK. In fact, I think that’s it — you also insist that 
 and
and  should never all be the same. That ensures that the block will be OK, and you can make sure that this condition continues to be satisfied.
should never all be the same. That ensures that the block will be OK, and you can make sure that this condition continues to be satisfied.
June 28, 2010 at 11:05 am |
Yes indeed the WordPress problem seems to be with less-than and greater-than symbols. Here is the correction again. Replace the last few lines of the second para (beginning with “If we determine that”) with the following text:
If we determine that for all
for all  then we could conclude that an
then we could conclude that an  -random number is divisible by
-random number is divisible by  . (Since the total contribution to
. (Since the total contribution to 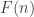 from numbers
from numbers  such that $p^{t_0} \nmid m$ is negligible). So our goal will be to estimate
such that $p^{t_0} \nmid m$ is negligible). So our goal will be to estimate  .
.
Consider an such that
such that  . Then
. Then  and
and  . We can build divisor sequences for
. We can build divisor sequences for  from divisor sequences for $m/p^t$. (For our purposes, a divisor sequence of
from divisor sequences for $m/p^t$. (For our purposes, a divisor sequence of  is a sequence
is a sequence  such that $d_i > 1$ and
such that $d_i > 1$ and  ).
). 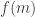 is equal to the number of divisor sequences of
is equal to the number of divisor sequences of  , and say
, and say  is the number of such sequences of length
is the number of such sequences of length  ; also
; also  .
.
A divisor sequence of …
June 28, 2010 at 12:16 pm |
I want to add in a thought that’s somewhat orthogonal to the present discussion (no pun intended — why there might even be considered to be a pun will become clear).
Once we’ve chosen the weight sequence our goal is to bound the discrepancy of every sequence
our goal is to bound the discrepancy of every sequence 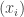 below in terms of
below in terms of  So we are living in a Hilbert space with inner product
So we are living in a Hilbert space with inner product  One sign that we were on the right track with the function
One sign that we were on the right track with the function  might be if we managed to find a nice set of functions that were
might be if we managed to find a nice set of functions that were  -orthogonal. And by “nice” I think I almost certainly mean “built out of HAPs in a simple way”.
-orthogonal. And by “nice” I think I almost certainly mean “built out of HAPs in a simple way”.
A candidate for such a set of functions is functions that alternate 1 and -1 along HAPs with prime common difference. (These can easily be built out of two HAPs, one with common difference and the other with common difference
and the other with common difference  ) And we can also throw in functions with common difference a power of 2. (Note that we still don’t have an example that shows that we cannot get large discrepancy along a HAP with a difference that is either prime or a power of 2. This is vaguely encouraging.)
) And we can also throw in functions with common difference a power of 2. (Note that we still don’t have an example that shows that we cannot get large discrepancy along a HAP with a difference that is either prime or a power of 2. This is vaguely encouraging.)
Now obviously there aren’t enough of these functions to build every single sequence. But perhaps we can use these functions to build the “significant part” of every sequence (that is, the part with high -weight) and extend them to an orthonormal basis (give or take the technicality that the functions may not be exactly orthogonal, but we could choose
-weight) and extend them to an orthonormal basis (give or take the technicality that the functions may not be exactly orthogonal, but we could choose  to be divisible by the first few primes and a reasonably high power of 2) in some way that doesn’t matter too much since its only function is to deal with sequences of such low norm that they obviously have discrepancy bigger than that norm.
to be divisible by the first few primes and a reasonably high power of 2) in some way that doesn’t matter too much since its only function is to deal with sequences of such low norm that they obviously have discrepancy bigger than that norm.
This is all a bit vague for now, but I think there are some promising apsects to it.
June 28, 2010 at 4:53 pm
I’ve just realized that my candidate for a nice system of orthogonal functions fails quite badly. For example, consider the sequences
0 -1 0 1 0 -1 0 1 0 -1 0 1 …
and
0 0 -1 0 0 1 0 0 -1 0 0 1 0 0 -1 0 0 1 …
The pointwise product of these two is
0 0 0 0 0 -1 0 0 0 0 0 0 1 0 0 0 0 0 -1 0 0 0 0 0 1 …
The -integral of this sequence is large, because the
-integral of this sequence is large, because the  -weight of numbers that are 6 mod 12 is much smaller than the
-weight of numbers that are 6 mod 12 is much smaller than the  -weight of numbers that are 0 mod 12.
-weight of numbers that are 0 mod 12.
So how do we create orthogonal sequences? Indeed, how do we create a natural example of a sequence with -integral that is zero, or at least small? [Added after writing the rest of the post: I recommend skimming rather quickly through this, as I’m not sure it really gets anywhere but it shows a kind of idea that I think could be useful to us if we could get it to work better.]
-integral that is zero, or at least small? [Added after writing the rest of the post: I recommend skimming rather quickly through this, as I’m not sure it really gets anywhere but it shows a kind of idea that I think could be useful to us if we could get it to work better.]
One thought that might be worth pursuing is to copy the inductive process that led to the function but starting with a different “seed sequence”. Let me try to explain what I mean by this.
but starting with a different “seed sequence”. Let me try to explain what I mean by this.
To create we start with the constant sequence 111111111…, and more generally, once we have defined
we start with the constant sequence 111111111…, and more generally, once we have defined  we define
we define  to be
to be  What would happen if we started instead with the sequence
What would happen if we started instead with the sequence  ?
?
Actually, I don’t think that’s going to work, because the inductive procedure is going to tend to lead everything towards a single fixed point. (That doesn’t seem to be quite true, but I think it’s almost true, meaning that the relationship between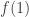 and the rest of
and the rest of  can change, but that’s about it.)
can change, but that’s about it.)
Maybe the thing to do is change the inductive definition to something like I think that might have a chance of giving something interesting. I haven’t checked, but the kind of thing I’d be hoping for would be that the non-inductive definition would be a sum over all sequences, and sequences of length
I think that might have a chance of giving something interesting. I haven’t checked, but the kind of thing I’d be hoping for would be that the non-inductive definition would be a sum over all sequences, and sequences of length  would now have a weight of
would now have a weight of 
Except that that’s not very good, because for an -typical number
-typical number  one might expect a random sequence of increasing divisors of
one might expect a random sequence of increasing divisors of  to have a length that was fairly uniformly distributed modulo any small integer.
to have a length that was fairly uniformly distributed modulo any small integer.
One final suggestion. Perhaps the way to build functions that are approximately orthogonal in the -weighted
-weighted 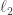 norm is to take functions of the form
norm is to take functions of the form  for some
for some 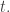 To be precise, we take the function
To be precise, we take the function  (which has norm
(which has norm  ) and the candidate for a collection of nicely orthogonal functions is
) and the candidate for a collection of nicely orthogonal functions is  The
The  -inner product of
-inner product of  and
and  is
is 
All this is extremely speculative, and therefore 99% likely to be wrong, though I hope that if wrong it might lead to something less wrong. But let me try to justify why one would want to take these functions.
First of all, if you have an orthonormal basis in the usual sense, then
in the usual sense, then  equals the identity. The reason we can’t just use this straight off is that we can’t build an orthonormal basis efficiently (that is, with small coefficients) out of HAPs. Now the function
equals the identity. The reason we can’t just use this straight off is that we can’t build an orthonormal basis efficiently (that is, with small coefficients) out of HAPs. Now the function  is designed in a HAP-ish sort of way, so there is some hope that it, or its square root, can be built efficiently. And functions like
is designed in a HAP-ish sort of way, so there is some hope that it, or its square root, can be built efficiently. And functions like  can be approximated quite well by functions that are constant on long intervals, since
can be approximated quite well by functions that are constant on long intervals, since  grows slowly. So the functions
grows slowly. So the functions  above look potentially buildable out of HAPs.
above look potentially buildable out of HAPs.
Now the functions and
and  are far from orthogonal in the usual sense, again because
are far from orthogonal in the usual sense, again because  grows so slowly (so the terms from
grows so slowly (so the terms from 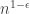 to
to  will be roughly constant). But it’s not completely obvious to me that they are not approximately
will be roughly constant). But it’s not completely obvious to me that they are not approximately  -orthogonal (though in the opposite direction it’s even less obvious, I have to admit). We know that almost all powers of 2 that are less than
-orthogonal (though in the opposite direction it’s even less obvious, I have to admit). We know that almost all powers of 2 that are less than  are less than
are less than  and similarly for more general kinds of numbers such as numbers of the form
and similarly for more general kinds of numbers such as numbers of the form  Could it be that the
Could it be that the  -measure is actually (and rather counterintuitively) concentrated on fairly small numbers? If so, then perhaps the
-measure is actually (and rather counterintuitively) concentrated on fairly small numbers? If so, then perhaps the  -measure “orthogonalizes” the functions
-measure “orthogonalizes” the functions  and
and  (provided of course that
(provided of course that  and
and  are sufficiently far apart).
are sufficiently far apart).
I am prepared for this suggestion to be quickly demolished — I don’t have good evidence for the assertion that -measure is concentrated on small numbers, and a priori the assertion itself is not very plausible. On balance, I don’t think I believe it.
-measure is concentrated on small numbers, and a priori the assertion itself is not very plausible. On balance, I don’t think I believe it.
June 28, 2010 at 5:36 pm
On second thoughts, I think I should have taken the functions and not bothered to multiply them by
and not bothered to multiply them by  Some of what I said above wasn’t quite right, even before it started to look unhelpful anyway.
Some of what I said above wasn’t quite right, even before it started to look unhelpful anyway.
But let me say slightly more about the thoughts that lay behind the mistake. Suppose we had an -orthonormal basis
-orthonormal basis  The
The  -orthonormality would tell us that
-orthonormality would tell us that  which would tell us that the functions
which would tell us that the functions  formed an orthonormal basis in the usual sense. From this, if my calculations are correct, it follows that if
formed an orthonormal basis in the usual sense. From this, if my calculations are correct, it follows that if  then
then  gives us the diagonal matrix with
gives us the diagonal matrix with  down the diagonal.
down the diagonal.
June 29, 2010 at 11:23 am |
I think I now have a much clearer and more concise version of what I was struggling to say in my previous block of comments.
Suppose we have an orthonormal basis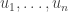 of
of  and let
and let  be the diagonal matrix with entries given by
be the diagonal matrix with entries given by 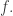 Then I claim that if we set
Then I claim that if we set  for every
for every  then we have
then we have 
To check this, let us evaluate the left-hand side at We get
We get  which (since the columns of a row-orthogonal matrix are orthogonal) equals
which (since the columns of a row-orthogonal matrix are orthogonal) equals  if
if  and 0 otherwise, which is what we wanted.
and 0 otherwise, which is what we wanted.
How might this observation be useful? Well, for normal AP-discrepancy one can start with a decomposition where the
where the 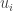 are trigonometric functions. This fails badly for HAP-discrepancy because a trigonometric function can be efficiently split up into a linear combination of APs, but it can’t be efficiently split up into a linear combination of HAPs.
are trigonometric functions. This fails badly for HAP-discrepancy because a trigonometric function can be efficiently split up into a linear combination of APs, but it can’t be efficiently split up into a linear combination of HAPs.
But if we weight a trigonometric function by multiplying its entries pointwise by then things could perhaps change quite a bit, since the bits that are hard to make out of HAPs will be given much smaller weight than the bits that were easy. So perhaps the decomposition-of-identity proof of Roth can be modified to become a decomposition-of-
then things could perhaps change quite a bit, since the bits that are hard to make out of HAPs will be given much smaller weight than the bits that were easy. So perhaps the decomposition-of-identity proof of Roth can be modified to become a decomposition-of- proof of EDP.
proof of EDP.
June 29, 2010 at 3:40 pm
Let me say very slightly more about that last suggestion. The idea would be this. We would start with the decomposition where
where  for every
for every  and
and  As in the proof of Roth’s discrepancy theorem, written out here with an
As in the proof of Roth’s discrepancy theorem, written out here with an  bound by Kevin O’Bryant, we then decompose each
bound by Kevin O’Bryant, we then decompose each 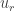 efficiently into characteristic functions of APs. However, in this case instead of trying to make them as long as possible, we give them lengths that tend slowly to infinity.
efficiently into characteristic functions of APs. However, in this case instead of trying to make them as long as possible, we give them lengths that tend slowly to infinity.
As in the Roth proof, there should be plenty of cancellation in the coefficients, which is crucial to the success of that proof and obviously would be here too. But here we face an additional difficulty, which is that most of the APs we have decomposed into are not HAPs.
What I am hoping, though it may be a rather desperate hope, is that if instead we do something very similar but for the functions then the total weight of the non-homogeneous APs that we use will be small enough that we can replace that part of the decomposition by something much more trivial (such as decomposition into HAPs of length 1).
then the total weight of the non-homogeneous APs that we use will be small enough that we can replace that part of the decomposition by something much more trivial (such as decomposition into HAPs of length 1).
Everything depends in a crucial way on the numbers, and at the time of writing I don’t have an intuitive idea of how that is likely to go. (Naturally, the most likely outcome is that a first attempt at getting the numbers to work will fail dismally, but if we were lucky then it might suggest a refined approach with a better chance of working.)
June 30, 2010 at 6:32 am
I haven’t quite figured out where this is headed, but I just wanted to recall th column is the HAP of common difference
th column is the HAP of common difference  and remove the diagonal part except for the (1,1) entry. Tim pointed out that
and remove the diagonal part except for the (1,1) entry. Tim pointed out that  is an eigenvector of this matrix.
is an eigenvector of this matrix.
a comment that Tim made when he first suggested this particular function as a possible candidate for the diagonal. Consider the matrix whose
Given this connection and the fact that this matrix is defined in terms of HAPs,
is there any useful information in this matrix for constructing the diagonal representation we are hoping for ? e.g. does the singular value decomposition of this matrix suggest anything ?
June 30, 2010 at 10:51 am
I’ve thought about this a bit further, and this is where I’ve got to.
In the representation-of-diagonals approach to Roth’s AP-discrepancy theorem, one does a trivial estimate, which results in no improvement to the trivial bound, and then one exploits cancellation to gain on the trivial estimate. Looking at it more closely, I see that the fact that the trivial estimate gives rise to the trivial bound is actually a coincidence: if you take (the lengths of the APs into which you decompose) to be smaller than
(the lengths of the APs into which you decompose) to be smaller than 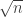 then you no longer get the trivial estimate but something worse than the trivial estimate.
then you no longer get the trivial estimate but something worse than the trivial estimate.
Just to clarify, in this proof we are trying to represent the identity as a linear combination of AP products with absolute values of coefficients adding up to less than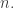 The trivial estimate allows us to do so with absolute values adding up to around
The trivial estimate allows us to do so with absolute values adding up to around  which just happens to equal
which just happens to equal  when
when  The extra cancellation then gains a factor of
The extra cancellation then gains a factor of  which for Roth’s theorem leads to a bound of
which for Roth’s theorem leads to a bound of  for the sum of the coefficients. The discrepancy is obtained by dividing
for the sum of the coefficients. The discrepancy is obtained by dividing  by this sum and taking the square root, giving the
by this sum and taking the square root, giving the  bound. Unfortunately, when
bound. Unfortunately, when  it gives us nothing.
it gives us nothing.
However, we know that the correct bound for Roth is and it did look as though it should be possible to work out the cancellations more efficiently and obtain an improvement to the trivial bound by a factor of
and it did look as though it should be possible to work out the cancellations more efficiently and obtain an improvement to the trivial bound by a factor of  rather than just
rather than just  If this is indeed possible, then it would give a bound of
If this is indeed possible, then it would give a bound of 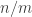 for the sum of the coefficients, and a discrepancy bound of
for the sum of the coefficients, and a discrepancy bound of  which makes more sense, since it interpolates correctly between the results we know for
which makes more sense, since it interpolates correctly between the results we know for 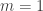 and strongly suspect for
and strongly suspect for  So I now feel that it is becoming a priority to stop being lazy and to try to push the representation-of-diagonals approach through for Roth until it matches the correct bound. (An additional motive for this is that it would be an interesting result in itself — perhaps even interesting enough to publish.)
So I now feel that it is becoming a priority to stop being lazy and to try to push the representation-of-diagonals approach through for Roth until it matches the correct bound. (An additional motive for this is that it would be an interesting result in itself — perhaps even interesting enough to publish.)
If all that can be got to work, here’s how I imagine we go from there. (The word “imagine” is carefully chosen, as the argument I have in mind may well be purely imaginary.) We decompose the identity efficiently into a sum of AP products of length for some
for some  that tends to infinity very slowly. Note the crucial fact that the common differences of these APs will also be bounded above by a number that tends to infinity very slowly. This gives us a very small but non-trivial AP-discrepancy lower bound. We then modify the decomposition to get a decomposition of the diagonal matrix with
that tends to infinity very slowly. Note the crucial fact that the common differences of these APs will also be bounded above by a number that tends to infinity very slowly. This gives us a very small but non-trivial AP-discrepancy lower bound. We then modify the decomposition to get a decomposition of the diagonal matrix with  down the diagonal (in the manner described in the comment to which this is a reply). Now some of the APs used in this decomposition will be (segments of) HAPs, and others won’t. But if
down the diagonal (in the manner described in the comment to which this is a reply). Now some of the APs used in this decomposition will be (segments of) HAPs, and others won’t. But if  is small enough, so that the common differences are very small — only just bigger than constant — then
is small enough, so that the common differences are very small — only just bigger than constant — then 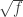 should give very much smaller weight, on average, to the non-homogeneous parts. Indeed, the fraction ought to be smaller than
should give very much smaller weight, on average, to the non-homogeneous parts. Indeed, the fraction ought to be smaller than  So I’m hoping we can replace the non-homogeneous APs we use by trivial decompositions into singletons and not suffer for it.
So I’m hoping we can replace the non-homogeneous APs we use by trivial decompositions into singletons and not suffer for it.
At the moment, I don’t have a convincing argument that tells me that this approach couldn’t work. So I’m feeling as though we need to start to get a bit technical. Of course, I don’t mean that absolutely everything needs to be proved — at this stage it would be fantastic if we could prove a result conditional on the Roth thing working out and various plausible facts about being true. Then we would have reduced the whole problem to a couple of technical lemmas.
being true. Then we would have reduced the whole problem to a couple of technical lemmas.
Moses, that was an interesting thought and I’ve been thinking about it, but I haven’t come up with anything worth saying in this comment. Perhaps it would be worth working out the SVD of the matrix for some large just to see what it looks like. A slightly similar thought I had was to take the inner product I defined earlier (in the weighted
just to see what it looks like. A slightly similar thought I had was to take the inner product I defined earlier (in the weighted 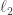 space using
space using  as weights) and do Gram-Schmidt orthogonalization. But I don’t have a good candidate for the basis that should be orthogonalized.
as weights) and do Gram-Schmidt orthogonalization. But I don’t have a good candidate for the basis that should be orthogonalized.
July 1, 2010 at 3:15 pm |
With reference to the programme suggested in my previous comment, I thought I’d mention that I am in the middle of writing a note (under the Polymath pseudonym) about the representation-of-diagonals approach to Roth’s AP-discrepancy theorem. The main differences between this note and Kevin’s contribution to the wiki are (i) that I’ve written it paper form (in LaTeX) and (ii) that I’m intending to push the argument to give the bound it ought to give: if you decompose into APs of length then the resulting discrepancy bound should be
then the resulting discrepancy bound should be  , and the biggest
, and the biggest  you can take is
you can take is 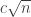 . I’m almost certain I know how to do this, but it will take a small effort to sort out all the details.
. I’m almost certain I know how to do this, but it will take a small effort to sort out all the details.
I’m doing this because it is necessary to sort out what happens with small if there is to be any hope of modifying the proof to give something for HAPs rather than APs.
if there is to be any hope of modifying the proof to give something for HAPs rather than APs.
July 1, 2010 at 10:24 pm
I look forward to the writeup. In reference to your earlier comment here , I’m not sure I follow your intuition for why getting the lengths of the APs to tend to infinity slowly is useful for getting a result for HAP discrepancy. Maybe I’m being daft (and admittedly I haven’t worked through the the details of the Roth proof carefully), but why does having
of the APs to tend to infinity slowly is useful for getting a result for HAP discrepancy. Maybe I’m being daft (and admittedly I haven’t worked through the the details of the Roth proof carefully), but why does having  small ensure that the common differences are small too ?
small ensure that the common differences are small too ?
July 1, 2010 at 10:52 pm
I hope I haven’t made a silly mistake, but plays a dual role in the proof. In order to approximate a trigonometric function
plays a dual role in the proof. In order to approximate a trigonometric function  , I convolve it with (a multiple of) an arithmetic progression
, I convolve it with (a multiple of) an arithmetic progression  with common difference
with common difference  . For this to work, we choose
. For this to work, we choose  such that
such that  is at most
is at most  , and that allows us to take the length of
, and that allows us to take the length of  to be
to be  . It’s because we need
. It’s because we need  to be at most
to be at most  that
that  has to be at most
has to be at most  .
.
Thus, in brief, is actually given as the bound on the common differences, and it requires a comparable bound on the lengths for the proof to work.
is actually given as the bound on the common differences, and it requires a comparable bound on the lengths for the proof to work.
July 2, 2010 at 3:42 pm
I hope this link will work. It’s very much a first draft, so I’ve been a bit lazy in places (not with the details of the proof, but with the accompanying explanations of what is going on). At some point I’ll update it, or if anyone else feels like doing so they are welcome and I can send the source file.
I’ve just checked, and the link does work. I haven’t mentioned in the write-up that I used the extra flexibility that is provided by an observation of Moses, which is that it is not necessary to represent a diagonal matrix — it’s enough to find an efficient representation of a matrix , where
, where  is diagonal and
is diagonal and  is positive semidefinite. It turned out to be very helpful not to have to make the decomposition exactly equal to the identity. I haven’t thought about how this would affect any generalization to an HAP version with
is positive semidefinite. It turned out to be very helpful not to have to make the decomposition exactly equal to the identity. I haven’t thought about how this would affect any generalization to an HAP version with  down the diagonal instead of 1.
down the diagonal instead of 1.
I also have a question: is this proof essentially the same as Roth’s original argument? I don’t know because I haven’t looked at the original argument.
Update: I’ve noticed that the statement of Lemma 3.1 is wrong (though the proof is a proof of the correct statement). The answer should be 1 rather than 1/N. I’ve tried to replace the file by a corrected version, but it’s failing to work, for reasons that I simply don’t understand. I’ll try some crude fix later.
July 2, 2010 at 8:10 pm
One crude fix to the file update issue would be to use a different filename.
July 2, 2010 at 11:20 pm
I was hoping to avoid that, but have given up the attempt. The link is now to the corrected file. (I hope I won’t have to keep doing this every time I update the file.)
July 2, 2010 at 11:24 pm
One way to handle a shared tex file is to use scribtex. This still requires some action on your part to share the file, so it isn’t as free-range as a wiki would be. (To get access, I’d need a free scribtex account, and you’d need to add my username to the file’s share list.)
July 2, 2010 at 11:53 pm
Kevin, I’ve followed as much of your suggestion as I can, meaning that I’ve got myself a free scribtex account and uploaded the file as it currently is. I’m happy to share the file with anyone who’s interested.
July 3, 2010 at 12:12 am
My scribtex username is “obryant”. I haven’t used scribtex in awhile; it looks much more polished now than last summer. It also looks like the number of collaborators might be severely limited. /Something/ like this should be around and useful for the write-up stage, instead of “passing the token” and the wiki.
July 3, 2010 at 12:18 am
Well, you’re added now. If the limited numbers become a problem we can think again about what to do.
July 3, 2010 at 12:18 am
Well, you’re added now. If the limited numbers become a problem we can think again about what to do.
July 3, 2010 at 6:43 am
I’ve just created a Scribtex account — could you add me, please? My username is ‘obtext’.
July 3, 2010 at 8:12 am
I was going to do just that, but I now discover that the limited-numbers issue has kicked in already: if I have a free account then I’m allowed up to … er … one collaborator per project.
July 3, 2010 at 3:42 pm
ONE?!?
July 3, 2010 at 5:07 pm
Yes, it does seem to be a limit of one on the free account, unfortunately. I’ve done a bit of searching and found a couple of other options (latexlab and monkeytex), but I haven’t got either to work. I suppose a partial solution would be simply to post the Latex source on the wiki.
July 3, 2010 at 5:22 pm
OK I’ve done that. You can get to it via the following sequence of links: Polymath5 wiki — General proof strategies — representation of diagonals — after which it is clear what to go for.
July 3, 2010 at 10:05 pm
Thanks, that works. I’ve made a minor edit. (In case anyone isn’t aware, by clicking on ‘history’ at the top of the document and selecting two revisions you can see how they differ.)
July 3, 2010 at 8:52 am |
[…] – Roth’s theorem (again) Tim Gowers has published a new proof of Roth’s theorem (link to Polymath5) as part of the project. He extends previous polymath work from Kevin Obryant […]
July 3, 2010 at 9:40 pm |
[…] see this comment and the responses to […]
July 4, 2010 at 6:36 am |
I perhaps have missed something, but are we worrying solely about the 3 case? Won’t
1,1,-1,-1,0,1,1,-1,-1,0 …
be bound by 2?
July 4, 2010 at 7:39 am
Jason, the discrepancy of that sequence is indeed bounded, but that’s OK, because the ratio is about
is about  .
.
July 4, 2010 at 7:41 am
Sorry, I wrote when I meant
when I meant 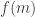 .
.