This post is about a result that has recently been proved in my old stamping ground of the theory of Banach spaces. When I set up this blog, I wasn’t expecting to write a post about Banach spaces, but the result I want to talk about is one of those rare and delightful events when a problem that you thought you might well never live to see solved is solved. And since Banach space theory is one of the less fashionable areas of mathematics, the result may well not get the publicity it deserves: this is an attempt to counteract that to a small extent.
To explain the significance of the result, it will help to talk about a Banach space that Bernard Maurey and I constructed almost 20 years ago. At the time, this was a good candidate for the “nastiest known Banach space”, in a sense that it had almost no non-trivial structure.
What does this mean? Well, one obvious sort of structure that one likes in a Banach space is symmetry, which we detect by finding operators from the space to itself. A Hilbert space is an extreme example of a space with lots of structure: one has a huge group of unitary matrices, as well as an abundance of projections. Moreover, all the subspaces of a Hilbert space look like the space itself. Thus, one way of saying that a Banach space has structure is to say that the space
of continuous linear operators from
to
is large.
The space that Maurey and I constructed has the property that every operator in
is of the form
, where
is a scalar,
is the identity, and
is a strictly singular operator. The formal definition of a strictly singular operator is that you cannot restrict to an infinite-dimensional subspace on which it is an isomorphic embedding. To put that another way, for every infinite-dimensional subspace
of
and every
you can find
such that
and
. (The idea is that you can’t “make it non-singular” by restricting to a subspace.)
Now there are all sorts of theorems about strictly singular operators that show that we can regard them as in some sense “small”. For example, it is easy to see that a non-trivial projection (by which I mean that both and
are infinite-dimensional) is not of the form
. Also, if
is Fredholm with index
and
is strictly singular, then
is Fredholm with index
. These two facts implied that
could not be decomposed as a direct sum
in such a way that the projections on to
and
were continuous (and in fact every subspace of
had that property), and also that
was not isomorphic to any proper subspace of itself (since any isomorphism from
to a proper subspace would have to be Fredholm with non-zero index, whereas
is Fredholm with zero index).
Now most people, if you ask them what they would understand by an operator being “small”, would not say “strictly singular”. In fact, most people haven’t even heard of strictly singular operators. The usual notion of smallness is compactness: an operator is considered to be small if the closure of the image of the unit ball is compact. In particular, if an operator has finite rank, then it is compact, and one can think of compact operators as “almost” having finite rank (though this raises subtle questions to do with the approximation property, which I won’t go into here). It turns out that the strictly singular operators and the compact operators on a Hilbert space are the same, which perhaps explains why strict singularity is not such a well-known concept. In general, a compact operator must be strictly singular but there are strictly singular operators that are not compact.
An obvious question this raised was whether the space Maurey and I had constructed admitted an operator that was strictly singular but not compact. If not, then we would have a space with the even stronger property that every operator was of the form with
compact. However, as Androulakis and Schlumprecht eventually showed in 2003, that space does have non-compact strictly singular operators.
Since the construction of the original space, many variants have been constructed, which managed to combine its lack-of-structure properties with “nice” properties such as uniform convexity. (That particular result was proved by Valentin Ferenczi.) In particular, one person, Spiros Argyros, made this area his own, and with various collaborators proved a variety of remarkable results, both positive and negative, about spaces of this kind.
All this brings me back to the main subject of this post. When I thought about how one might try to build a space on which every operator is of the form , I came to the conclusion that this was such a strong property for the space to have that there might even be a proof that no such space existed. But I was unable to get anywhere at all with the problem — in either direction.
Fast forward to the end of 2008, when I received an email from Spiros Argyros to say that he and Richard Haydon had constructed a space on which every operator is a multiple of the identity plus a compact operator. Apparently they did this some months earlier, but the news hadn’t filtered through to me.
Now you might ask, if the strictly singular operators are the same as the compact operators on a Hilbert space, and if strictly singular operators do much of what compact operators do, does the new space of Argyros and Haydon have properties (besides the basic property they proved) that have not yet been shown for any other Banach space? The answer to this question is a resounding yes, but to explain this I need to give a bit more background.
One of the biggest problems in functional analysis is the invariant subspace problem , which asks whether for every operator on a Hilbert space
there is a proper closed subspace
such that
. Even the corresponding question for Banach spaces is very hard, but operators without invariant subspaces have been constructed for various Banach spaces in amazing work of Per Enflo and Charles Read. Meanwhile, the problem for Hilbert spaces remains stubbornly open.
Now one might speculate that the result is hard to prove because it is in fact false. And one might even speculate that it is false for every Banach space. However, the example of Argyros and Haydon shows that the situation is more complicated. A famous result of Lomonosov shows that every operator that commutes with a non-zero compact operator must have an invariant subspace. And obviously commutes with
if
is non-zero, or trivially has an invariant subspace if
. From this we conclude that every continuous linear operator on the space of Argyros and Haydon has a non-trivial invariant subspace, the first space for which such a result is known.
What this shows is that you can’t hope to find a counterexample for a general Banach space, because in a sense a general Banach space doesn’t have to have enough operators for there to be any chance at all of a counterexample. (This reminds me slightly of a problem that a different space Maurey and I “solved”. A Banach space is called prime if for every continuous projection
with infinite rank,
is isomorphic to
. It was known that
spaces and
were prime, and the question was whether there were any other prime spaces. Maurey and I constructed a variant of our original space that was isomorphic to all its finite-codimensional spaces but did not admit any non-trivial projections. So it was prime by virtue of there not being enough projections for it to have a decent chance of not being prime.)
Thus, the Argyros-Haydon space has very definitely taken over as the new “nastiest known Banach space”.
If you want to join this race, there is still one unsolved problem, which arises when one tries to imagine what the strongest possible nonexistence-of-operators result could be. If you’re given a Banach space , then you automatically have all multiples of the identity. Also, the Hahn-Banach theorem allows you to define a wide range of finite-rank operators, and they are all continuous. (To define a rank-one operator, pick a vector
and a linear functional
and map
to
. Then add these rank-one operators together to get arbitrary finite-rank operators.) Thirdly, since
is a Banach space, if you take a bunch of rank-one operators
such that
, then the sum
is continuous. The question that’s still open is whether there must be any operators besides these trivial examples. An absolutely convergent sum of rank-one operators is called a nuclear operator, so we can ask this question in a different way: does there exist a Banach space such that every operator is of the form
, where
is nuclear?
It would be interesting to know what Argyros and Haydon think the answer to this question is likely to be: I have no idea myself, but would secretly quite like it if someone managed to construct just a very slightly nontrivial operator on an arbitrary (separable) Banach space. On the other hand, if someone gave an example where that couldn’t be done, then it would be the ultimately structureless Banach space, and that would be pretty good as well. (It’s tempting to say that the Argyros-Haydon space is already the ultimate space, and that this one would be beyond ultimate.)
I think the preprint of Argyros and Haydon isn’t yet up on the web. As soon as it is, I’ll add a link to it.
Update 24/3/09: the paper is now available on the arXiv.
February 7, 2009 at 10:36 pm |
Fascinating result! It helps explain to “outsiders” like myself why the invariant subspace problem for Hilbert spaces is so hard.
Here is a question. This result sounds very interesting to me, but I think I am in the minority among mathematicians. Why is it that, as you put it, Banach space theory is not very fashionable?
There was a thread in sci.math.research last year in which Sergei Akbarov argued that the theory of topological vector spaces is dead and will continue to remain dead for all time. Stephen Montgomery-Smith said he didn’t know much about TVS but said similar things about Banach spaces, the basic complaint being that a field consisting only of horrible counterexamples is not healthy, and is removed from “reality.” I had a gut feeling that there was something amiss about these criticisms, because they sounded similar to criticisms that have been leveled against subjects like recursion theory or large cardinals, which I strongly believe are misguided. But while I know a little about recursion theory and large cardinals, I know zero about TVS theory. What is your view of these criticisms?
February 7, 2009 at 11:28 pm |
Tim, looking at what Stephen Montgomery-Smith writes, I’d say that he has two basic complaints. One is the one you mention, and the other is that the Banach spaces that are used in more concrete parts of analysis are, as he puts it, “trivial” from the abstract point of view. So what he means by “removed from reality” is that even though we no know that, for example, not every Banach space admits operators apart from compact perturbations of multiples of the identity, with any Banach space that “arises in nature” we can see instantly that it has many interesting operators.
I myself would not try to justify the result of Argyros and Haydon by arguing that perhaps their construction will arise unexpectedly in a completely different context. I just think there is room in the world for what you might call pure pure mathematics as opposed to applied pure mathematics. I do think it is a weakness of a field if it is too pure in this sense, but sometimes a result is just so intrinsically interesting that it transcends all such considerations.
I would also want to add that, as I argued in The Two Cultures of Mathematics, one should be wary of judging a field just based on its direct influence on other areas, because there are more subtle ways in which one field can benefit another. For example, it can inculcate habits of thought that turn out to be just the right habits for some other field, even if the results themselves are not directly applied. The theory of Banach spaces is notable in that regard: there are many people who used to work in the area but gradually drifted away and are now finding that the expertise that they built up has indirectly but importantly helped them to do excellent work in other areas.
Another point is that Banach space theory has always been rather unfashionable, even when people hoped that the main open problems might have positive answers. I think the reason for that has more to do with the lack of structure of an arbitrary Banach space (as opposed to say a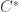 -algebra). This might also be part of the explanation for why set theory is unfashionable. Combinatorics is another low-structure subject of course, and used for that reason to be unfashionable too, but it has hugely benefited in recent years from its associations with computer science (to mention just one area of obvious importance), and I think nobody who knows what they are talking about could describe it as an isolated subject (even if it has some isolated pockets, but that applies to all areas of mathematics).
-algebra). This might also be part of the explanation for why set theory is unfashionable. Combinatorics is another low-structure subject of course, and used for that reason to be unfashionable too, but it has hugely benefited in recent years from its associations with computer science (to mention just one area of obvious importance), and I think nobody who knows what they are talking about could describe it as an isolated subject (even if it has some isolated pockets, but that applies to all areas of mathematics).
February 8, 2009 at 4:51 am |
I think Tim’s speech on the importance of mathematics at the millennium meetings (see http://www.youtube.com/watch?v=BsIJN4YMZZo) is beautiful explanation for why it is important to study problems without apparent applications. I highly recommend it.
February 8, 2009 at 6:01 am |
At least around here in the middle east, Banach space theory is vert fashionable…
February 8, 2009 at 12:56 pm |
Perhaps it is no coincidence that I have visited Israel many times …
February 8, 2009 at 4:05 pm |
This nice post reminded me of the very intriguing question raised by Tim at the end of his ICM 94 lecture (which I have read recently), where he remarks that the nonclassical Banach spaces (exhibiting strong counterexamples to various properties) have norms which are seem difficult to compute (in the complexity sense, with recursive definitions), and he asks:
“It is tempting to ask whether there is a meta-theorem that states that a norm that is in some sense directly defined must give a space that has some ell_p-space or c_0 as a subspace. (…) it could be that there is, waiting to be discovered, a theory of `easily described’ Banach spaces and linear operators very different indeed from the theory of general spaces as outlined in this paper.”
I wonder if there’s been any progress or work in this direction? It certainly sounds extremely interesting!
February 8, 2009 at 4:39 pm |
the space of Spiros-Hoyden is also the first Banach space for which every bounded quasinilpotent operator is compact.
Now, is this Banach space reflexive and separable as in the case of H.I Banach space constructed by T. Gowers and B. Maurey?
February 8, 2009 at 5:01 pm |
Emmanuel, I’m glad you’ve brought that up, because I thought it might make a very good polymath project. I very much doubt that it’s something that anyone is actively thinking about at the moment, and I have some questions that could probably be cleared up by people who know more logic than I do. (To solve the problem one needs to formulate it, but all I have so far is some arguments that show that certain ways of formulating it don’t work. However, reverse mathematicians may be able to tell me of some logical system where only very very weak forms of induction are possible. If so, then we could be in business.)
Liverpool: I’ve just refreshed my memory, and the space of Argyros and Haydon is separable but not reflexive. In fact, remarkably, its dual is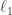 .
.
February 8, 2009 at 5:05 pm |
what is the strange also on the space of Spiros (Argyros)-Hoyden is that the West decomposition of Riesz operators is trivial, because this last class coincides with the ideal of compact operators.
Now is the dichotomy theorem of Gowers a very best criterion for the classification of Banach spaces or we can find a finer criteria?
February 8, 2009 at 5:09 pm |
I don’t think that in Banach spaces theory we can construct a Banach space as a limit (in a certain sense!) of quasi-Banach space.
February 8, 2009 at 5:41 pm |
Rich and poor Banach spaces can have the same properties, indeed in
L(l_p) or L(c_o), compact operators are the only closed two-sided ideal as in L(Argyros-Hoyden space), this is the same case of rich and poor men!!!! (hahaha)
February 8, 2009 at 8:41 pm |
Dear Tim,
I’d be very much interested in hearing more about your thoughts (that you think they don’t work) on the meta-problem Emmanuel brought up. Do you intend to share those? Indeed, the question of formulating the problem could make a fine polymath project.
February 9, 2009 at 3:06 am |
The best-known logical systems where only very very weak induction is possible go by the name of “systems of bounded arithmetic.” These are closely related to computational complexity classes. Before diving into the somewhat technical definitions of bounded arithmetic, it may be good to ask first, does it seem that what you’re looking for are spaces that are “polynomial-time computable” in some sense?
February 9, 2009 at 4:37 pm |
Here’s another thought—perhaps descriptive complexity might be more relevant than bounded arithmetic.
For certain kinds of objects, like graphs and groups, there’s a meaningful notion of “first-order definable properties.” First-order definable properties of graphs are easy to compute, and there are a lot of nice theorems in this area. I think there’s also some theorem to the effect that any subgroup of a group that is first-order definable has to be normal (not sure of the exact statement, though).
Thus one could try to talk about first-order definable classes of Banach spaces. The difficulty here is that it’s not clear what the first-order objects and relations should be. In a graph, it’s clear that the vertices of the graph should be the first-order objects and the edge relation should be the only relation. In the case of Banach spaces it’s not so clear. And maybe this is one of the things you already tried and found wanting?
February 9, 2009 at 10:11 pm |
Can someone recommend a good, reasonably up-to-date, and introductory text or set of lecture notes on functional analysis? Thanks!
February 9, 2009 at 10:47 pm |
Tim, it’s difficult to answer your questions without going into quite a lot of detail about the definition of Tsirelson’s space. But perhaps I can give it a try. The elements of the space are infinite real sequences (though the definition works in the complex case as well). Given a vector and a finite subset
and a finite subset  of
of 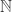 , we write
, we write  for the sequence that’s
for the sequence that’s  in
in  and 0 outside
and 0 outside  . We also write
. We also write 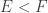 if the maximum element of
if the maximum element of  is less than the minimum element of
is less than the minimum element of  . To work out the norm of a vector
. To work out the norm of a vector  , you take the maximum over all
, you take the maximum over all  and all sequences
and all sequences  of the quantity
of the quantity 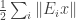 , and you also take the maximum of that with the
, and you also take the maximum of that with the 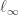 norm.
norm.
Now this looks like a rather strange definition because the norm is defined in terms of itself. However, it is not circular but inductive: as you split a vector up, the sizes of the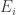 s get smaller and smaller, since if they don’t then you would be saying that
s get smaller and smaller, since if they don’t then you would be saying that  , which would imply that
, which would imply that 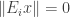 , and then you would have done better to take the
, and then you would have done better to take the 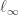 norm.
norm.
An alternative way of looking at this is to look at all possible ways of splitting the support of up, and then all possible ways of splitting those pieces up, and so on until you get down to singletons. If you do that, you find that you are taking the maximum over a certain set of trees (their vertices are finite subsets of
up, and then all possible ways of splitting those pieces up, and so on until you get down to singletons. If you do that, you find that you are taking the maximum over a certain set of trees (their vertices are finite subsets of 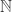 , their edges join sets to subsets, and their leaves are singletons) of a particular calculation associated with
, their edges join sets to subsets, and their leaves are singletons) of a particular calculation associated with  and the tree. This sounds as though it could potentially give rise to an NP-complete problem: given a vector
and the tree. This sounds as though it could potentially give rise to an NP-complete problem: given a vector  supported on
supported on 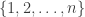 , approximate its norm to within
, approximate its norm to within 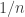 . I don’t know whether anything much is known about that, but I do know that it’s not the definition I’m looking for. The reason is that you can pick a very very slowly growing function
. I don’t know whether anything much is known about that, but I do know that it’s not the definition I’m looking for. The reason is that you can pick a very very slowly growing function  and insist not that
and insist not that 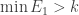 but instead that
but instead that  . If you do that, then unless the support of
. If you do that, then unless the support of  is very large indeed you can split it up into lots of pieces, and you find that you have to have vectors of absolutely enormous support to get at all far away from the
is very large indeed you can split it up into lots of pieces, and you find that you have to have vectors of absolutely enormous support to get at all far away from the 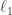 norm. In terms of trees, you find that the number of trees you have to consider in order to evaluate the norm of a vector that’s supported on
norm. In terms of trees, you find that the number of trees you have to consider in order to evaluate the norm of a vector that’s supported on 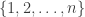 can be made as small-growing a function of
can be made as small-growing a function of  as you like. But the proof that the space doesn’t contain
as you like. But the proof that the space doesn’t contain 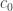 or
or 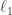 is just a tiny modification of the proof for Tsirelson’s space itself.
is just a tiny modification of the proof for Tsirelson’s space itself.
The problem is to find a definition of “explicitly definable” that doesn’t allow an inductive definition such as I’ve just outlined (and there are many others that do similar things), and that doesn’t allow you to take a maximum over some trees as a way of pretending that you aren’t doing induction. On the other hand, it should be generous enough to allow things like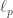 spaces, Sobolev spaces, Lorentz spaces, etc. When you’ve played around with these spaces for a while, you really get the feeling there is some definition out there, but nobody has come up with it yet. I can’t remember now what my various failed ideas were (other than the computational complexity one), but one problem I had is that you can’t really do anything without a bit of induction, and as soon as you allow a bit, it’s hard not to find that you can, in some devious way, define Tsirelson’s space with it. It’s here that I thought someone like you might be able to help.
spaces, Sobolev spaces, Lorentz spaces, etc. When you’ve played around with these spaces for a while, you really get the feeling there is some definition out there, but nobody has come up with it yet. I can’t remember now what my various failed ideas were (other than the computational complexity one), but one problem I had is that you can’t really do anything without a bit of induction, and as soon as you allow a bit, it’s hard not to find that you can, in some devious way, define Tsirelson’s space with it. It’s here that I thought someone like you might be able to help.
February 10, 2009 at 12:29 am |
Yor,
Part III of the book Analysis and Logic
Analysis and Logic by Ted Odell gives a very nice overview of Banach space theory including HI spaces and such. It is not a textbook but many of the fundamental ideas and questions are presented very well.
February 10, 2009 at 3:41 am |
Timothy Chow wrote:
I think there’s also some theorem to the effect that any subgroup of a group that is first-order definable has to be normal (not sure of the exact statement, though).
If you’re allowing constants (which is usual) then that’s certainly not true. For instance, any centralizer is obviously definable, but centralizers are often not normal.
The theorem sounds very reasonable if you don’t allow constants, though. Could you point me to a reference?
Actually, on second thoughts, perhaps it’s obvious. If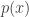 is a predicate with no constants and
is a predicate with no constants and 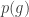 holds then it’s clear that
holds then it’s clear that 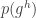 holds for any
holds for any 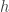 . So I suppose the theorem is just “Any definable (without constants) set is a union of conjugacy classes.”
. So I suppose the theorem is just “Any definable (without constants) set is a union of conjugacy classes.”
February 10, 2009 at 4:02 am |
For the same reason, any definable (without parameters) subgroup must in fact be characteristic (invariant under all automorphisms).
February 10, 2009 at 6:12 am |
Yor, another book that I’ve found very helpful is “Linear Analysis” by Bela Bollobas. It makes a point of emphasizing the finite dimensional point of view, which is rather clarifying and something many older texts lack.
February 10, 2009 at 10:15 pm |
Tim,
Did you check the Argyros-Haydon result? I am worried that nobody checked it and it isn’t available online. Are you sure that it is correct?
February 12, 2009 at 12:54 am |
Bob Solovay, John Harrison and I have been doing some work over the past few years on decidability for first order theories of (real) Banach spaces that may be of interest. We work with the obvious two-sorted first-order language for normed spaces with a sort for the scalars and a sort for the vectors.
There is a brief announcement of part of our work in an extended abstract of mine that you can find at http://www.lemma-one.com/papers/70.pdf. This includes a short sketch of our proof that there is a primitive recursive reduction of second order arithmetic to the theory of any class of Banach spaces or normed spaces that includes all spaces of some given finite or infinite dimension d >= 2. So all these theories are (“very”) undecidable.
We are near to completion of a longer account which includes more information on the degrees of unsolvability of these theories. We have a Skolem-Loewenheim theorem stating that any model V of a sentence in the normed space language has an elementary substructure W that is a real normed space with at most 2^omega vectors (i.e., with a Hamel basis of cardinality <= 2^omega). W can be taken to be a Banach space if V is a Banach space. Using this one can show that the theory of arbitrary Banach spaces or normed spaces is many-one equivalent to the set of Pi^2_1 sentences in third order arithmetic. The theory of finite-dimensional Banach spaces turns out to be many-one equivalent to the set of truths of second order arithmetic.
Analogous theories of Hilbert spaces or inner product spaces are all decidable. It also turns out that any first order property of Hilbert spaces that is true in all finite-dimensional spaces is true in all inner product spaces (complete or not). By contrast, there are first order sentences that are satisfiable but only in infinite-dimensional Banach spaces (e.g., the assertion that the space is non-trivial but the unit disc contains no extreme points). There are also sentences that are satisfiable but only in incomplete normed spaces (this is bit more difficult: we wittle bits off the unit ball in the incomplete space of finitely non-zero sequences of reals under the euclidean norm so that a Cauchy sequence with no limit becomes definable by simple geometric criteria).
February 12, 2009 at 1:36 pm |
Hi Yor,
Sometimes I find the book by Erwin Kreyszig, Introductory Functional Analysis with Applications, helpful. It does depend on the taste.
February 12, 2009 at 7:06 pm |
>In fact, remarkably, its dual is \ell_1.
There is some description of L_1-preduals of Lazar and Lindenstrauss (which does not make these spaces less interesting, of course, say Gurarij space is also L_1-predual, and this one). The characterisation is in terms of some specific matrices, which correspond to the finite-dimensional embeddings of l_infty’s. Is it known, how to decribe the incredible space of Argyros-Haydon in these terms?
February 13, 2009 at 1:16 am |
Hi Fedor,
I think perhaps you are thinking of _isometric_ preduals when you speak of the Lazar-Lindenstrauss characterisation? A Banach space whose dual is isometric to $\ell_1$ necessarily contains a complemented subspace isomorphic to $c_0$ (this result is due to M. Zippin), and therefore admits uncountably many nontrivial projections. The space constructed by Argyros and Haydon has its dual isomorphic to, but not isometric to, $\ell_1$. Note that it is a $\mathcal{L}_\infty$ space not containing $c_0$ (or any other space with any unconditional basis).
That brings me to my next point. The main ingredient in the Argyros-Haydon construction – aside from the ‘usual’ techniques involved in constructing HI spaces – is the Bourgain-Delbaen construction. In their paper, Bourgain and Delbaen give the first examples of $\mathcal{L}_\infty$ space not containing $c_0$, and with a number of other unusual properties. Much later Richard Haydon showed that the somewhat reflexive examples of Bourgain and Delbaen are in fact $\ell_p$-saturated for some $1< p < \infty$. Now Argyros and Haydon have succeeded in modifying this construction in such a way to exclude not only $c_0$ as a subspace, but any unconditionality whatsoever. For the Bourgain-Delbaen construction, you could look at their original paper or at Bourgain’s Lecture Notes in Mathematics book on the subject. Also, the B-D construction was later generalised by Bourgain and Pisier.
I had wondered some time ago whether the somewhat reflexive BD spaces might be simple – that is, $X$ is simple if $L(X)$ has only one nontrivial ideal, the compact operators – and prime, because they have many ‘smallness’ properties (including their Szlenk index being as small as possible). It seems now that, as far as the simplicity property goes, the Argyros-Haydon variant goes way beyond that! As far as primeness of the Argyros-Haydon space goes, I guess that will depend only upon whether it is isomorphic to its hyperplanes (though they do not address this in the preprint I have seen).
Philip Brooker.
February 13, 2009 at 1:19 am |
It wouldn’t be isomorphic to its hyperplanes because every operator is either compact or Fredholm with index zero. Maurey and I had this issue with our space, which is partly what motivated us to construct a variant where the space was isomorphic to its hyperplanes but not to its infinite-codimensional subspaces. I don’t know whether a similar modification of the Argyros-Haydon space is possible.
February 13, 2009 at 9:27 am |
Now the question: is it possible to construct a Banach space not hereditarily indecomposable which satisfies the scalar plus compact problem? Nothing that this is possible for the case of Banach spaces such that every bounded operator can be written under the form scalar I + strictly singular operator, some examples were constructed by V.Ferenczi, S.Argyros and Manoussakis.
February 17, 2009 at 12:45 am |
I’m still not sure I completely understand Tsirelson’s space, but at first glance it seems like it might require the weak Koenig lemma. This states that every infinite binary tree has an infinite branch.
If the existence of Tsirelson’s space does indeed require WKL, then we’re in business. The usual “base system” for reverse mathematics is known as RCA_0, which can’t prove WKL, although it’s strong enough to do a lot of mathematics in.
I’ll pose the question on the Foundations of Mathematics mailing list to see if someone there can answer this question definitively.
February 17, 2009 at 5:27 am |
Could it have something to do with fixed point property of
(certain class of) order preserving maps on partially ordered sets?
There is a general argument used to show the existence of of norms
of norms  on
on 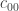
 is monotone normalized and
is monotone normalized and 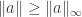 ,
,  . Put a partial order
. Put a partial order 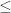 on
on
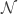 by
by 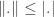 if
if  for all
for all
 . So
. So  is the minimum and
is the minimum and 
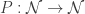
 admits a smallest fixed point. The
admits a smallest fixed point. The to be
to be 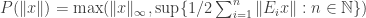 where
where 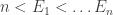 . Of course,
. Of course,
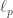 norms are also fixed points of some (rather trivial) maps
norms are also fixed points of some (rather trivial) maps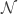 . So perhaps we are looking for axioms where the
. So perhaps we are looking for axioms where the
Tsirelson’s type norms due to Odell and Schlumprecht (see Prop 2.1):
Consider the collection
for which
is the maximum of the poset. Then if
is order preserving, then
proof proceeds with transfinite induction and uses the compactness
of dual balls. For instance, for Tsirelson’s space we can take the
map
on
existence of fixed points of `genuine’ maps depends upon.
February 17, 2009 at 6:31 pm |
Dear Philip,
thank you for the explanation! I was confused by the verb “is”.
March 1, 2009 at 7:21 pm |
A few other interesting (and difficult) problems left open by the Argyros-Haydon construction:
1) Does there exist a reflexive space satisfying \lambda + K?
1′) Does there exist a reflexive space on which every diagonal operator is \lambda + K?
In this direction Argyros and collaborators have constructed a quasi-reflexive space (codim 1 in the double dual) on which every diagonal operator is \lambda + K.
2) Does there exist a space X such that for every Y subspace of X and every T:Y \to X can be written as \lambda inclusion + K?
Argyros-Haydon space does not solve this problem: Since it is saturated (i.e. every subspace contains a further subspace isomorphic) with the original Gowers-Maurey space (or a close relative), the Androulakis-Schlumprecht result gives a strictly singular non-compact operator on this subspace.
The fact that the dual of Argros-Haydon space (AH) is isomorphic to \ell_1 is important in showing that it satisfies \lambda +K. Since every weakly compact operator on \ell_1 is compact, the same is true for every operator on AH.
March 6, 2009 at 9:35 am
Hi Kevin,
that’s an interesting list of open problems. Another open problem (as far as I am aware) that has been studied in recent years is of course whether there is a compact Hausdorff space L such that every operator on C(L) is scalar+compact.
About your final comment, I am not very far along with reading the Argyros-Haydon paper (I’ve got a thesis to bury!), but it did catch my attention in the introduction that they say that their proof doesn’t actually use the Schur property of \ell_1. I guess it’s possible that an earlier version of the proof did, or that it is there in disguise.
June 16, 2009 at 5:35 pm
There is a mistake in my first post, I was recalling a conversation and hadn’t reread the paper. It seems that, rather than what I said, they have a lemma which says that whenever an operator goes to zero along RIS’s it has to go to zero along block sequences (and therefore must be compact). This has something to do with X being a script L-infty space.
I don’t know if every strictly singular operator on an \ell_1 predual (or HI \ell_1 predual) is compact, but this seems like an interesting question.
February 5, 2010 at 4:53 am
I’ve been meaning to come back here for ages and address the embarrassing mistake in my post above: there is of course no such thing as a compact Hausdorff space L such that every operator on C(L) is scalar+compact! I figured this out for myself soon after posting the message above, and later found out further that this is noted in a paper of Koszmider. I guess that I had my fifteen minutes of public brain fart when I posted the message above.
Regarding your later comment Kevin, I have also wondered whether every strictly singular operator on a space whose dual is isomoprhic to \ell_1 is compact; so +1 to your remark that it is an interesting question.
November 23, 2010 at 4:12 am
It turns out that a space with dual isomorphic to $\ell_1$ can have noncompact, strictly-singular operators: http://arxiv.org/pdf/1011.4776 (the author is Richard Haydon’s student).
March 6, 2009 at 4:35 am |
Hi friends,
I loved the discussion above. But, is it reasonable to ask if there exists a Banach space on which every bounded operator is of the form I+K? That is, with scalar 1?
March 6, 2009 at 8:44 am
No — take twice the identity for example. (Of course, the space is assumed to be infinite dimensional.)
March 6, 2009 at 4:34 pm |
Ok, Gowers. But, let me formulate precisely what I’m thinking on this.
Question: Does there exists a Banach space X on which every bounded operator in L(X)\ span{I} is of the form I+K?
March 6, 2009 at 4:52 pm
No — take a non-zero finite rank operator T and consider the operator 2I+T. More generally, the class of bounded operators is closed under scalar multiplication so either you need to ask an inhomogeneous question or look for a homogeneous answer.
March 6, 2009 at 7:54 pm |
Thanks for your answers.
March 24, 2009 at 2:15 am |
The Argyros-Haydon paper has just appeared on the arXiv: arxiv.org/pdf/0903.3921
Philip.
May 27, 2009 at 4:18 am |
Rumour has it that the Banach algebra of bounded linear operators on the Argyros-Haydon space is amenable… this would make it the first known Banach space with this property. The proof apparently uses result(s) of Niels Gronbaek, Barry Johnson and George Willis on amenability of K(X) (the algebra of all compact operators on the Banach space X).
May 30, 2009 at 7:13 pm |
Philip, the GJW paper can also be found (at least in preprint form) on the arXiv, see http://arxiv.org/abs/math.FA/9209211
I am writing this comment in a short gap before having to dash across town, so haven’t (re)read the paper carefully. But it would seem that one uses Theorems 4.2 and 4.3 of GJW together with the fact that the Argyros-Haydon space has dual isomorphic to l^1. (You also need to know that the unitization of an amenable algebra is amenable, but that is relatively trivial, if that makes sense…)
February 10, 2010 at 3:04 am |
Looking at Dan Freeman’s (Texas A&M) web site, it says that he, Haydon, Odell and Schlumprecht have shown that every uniformly convex Banach space embeds in a Banach space for which every operator is scalar-plus-compact. As noted there, this implies that spaces for which every operator is scalar-plus-compact need not be hereditarily indecomposable, and that there exists a Banach space containing \ell_2 and for which every operator has a nontrivial invariant subspace. Pretty impressive stuff.
October 9, 2010 at 11:01 am |
what is the form of essential spectra of operators defined on exotic Banach spaces?
Is it possible to construct other (not H.I or Q.H.I Banach spaces) such that bounded operators have as essential spectra finite points and circles, arcs, cantor’s sets or in general sets which does not contain any boundary of open sets in the complex plane?
January 28, 2013 at 1:19 am |
Dear Tim,
It appears that Carl Cowen and Eva Gallardo have solved the invariant subspace problem for operators on Hilbert space. I posted a remark about this on my blog http://cafematematico.com
Best,
Miguel
January 28, 2013 at 9:37 am
That’s very interesting. Do you know whether they have made a preprint publicly available?
January 28, 2013 at 1:36 pm
I asked Eva for a preprint but she said they are not circulating the preprint yet and that it has been with the referee for seven weeks. You may ask her to send you a preprint. Her email address is : eva(at)gallardo(at)mat(dot)ucm(dot)es. Carl’s email address is cowen(at)math(dot)purdue(dot)edu.
February 4, 2013 at 9:58 pm |
Dear Tim,
I heard that Donald Sarason has found a gap in the proof.
Best,
Miguel
August 10, 2013 at 4:51 pm |
Is it possible to construct on the space of Gowers-Maurey a strictly singular operator without invariant subspace (necessary this operator is quasinilpotent)?
August 11, 2013 at 10:10 pm
I think Charles Read (from Leeds University) has done this. At any rate, he did something similar, and would be able to tell you whether it is known.
August 14, 2013 at 12:40 pm |
The construction of Charles read is based on the weighted shift operators, unfortunately this is not possible in the case of algebra of bounded linear operators on X_GM, but I know that on this space, we can construct a strictly singular which is not polynomially compact, is this operator the good answer for my question and why? notice that an operator without invariant subspace does not commute with any non zero compact operator, but I think that the converse is not true in general, On the space X_GM, are theses two properties equivalent? On the space of Argyros-Haydon this is true.
August 14, 2013 at 11:10 pm
Ah, the result I was thinking of was that there exists a strictly singular operator with no non-trivial closed invariant subspace. This shows that one can’t answer your question just from the fact that every operator on X_GM is a multiple of the identity plus a strictly singular operator.
So I don’t know the answer to your question and I suspect that it is not known.
August 15, 2013 at 2:50 am |
“The theory of Banach spaces is notable in that regard: there are many people who used to work in the area but gradually drifted away and are now finding that the expertise that they built up has indirectly but importantly helped them to do excellent work in other areas.”
How is this different from other areas? And why did they drift away? Does that mean that people in Banach spaces are so smart, or research in Banach spaces is not very exciting anymore?
September 2, 2013 at 1:08 pm |
On the space X_GM, is it possible to construct a strictly singular (not compact) with infinite eigenvalues such that the sum of modules of these eigenvalues (computed with their multiplicities) is equal to infty. Notice that the example of operator constructed by Androulakis and T. Schlumprecht concerning strictly singular not compact on X_GM is quasinilpotent.
October 2, 2013 at 7:55 pm |
Is it possible to characterize smooth functions from X_GM (or open sets in X_GM) to X_GM?
October 6, 2013 at 3:35 pm |
there is lots of interesting commentary by WTG and commenters about the relative interest in/importance of particular subbranches eg banach spaces etc. what sometimes in politics is called “inside baseball”. eg this comment
it is fun to study the “relative importance of misc fields” in math or other technical sciences eg physics, computer science. in some ways it does revert to a talk of “scientific fashion”. one of the best commentaries on this subj is Kuhns perspective which has not been surpassed much. in some ways it is both highly meaningful (we are looking at nothing less than the evolutionary path of scientific development) and also meaningless (like papparazi chasing various stars/celebrities).
what is also interesting is that it can be of such high importance to scientific development but yet also seems to get low attention as a particular field of study. Kuhn is looked on with suspicion and criticism by a lot of “hard core” scientists/researchers. it is, admittedly, a kind of “meta science”.
re the above quote, it is difficult to find actual citable refs for opinions like the above, eg in papers/books. it comes from practitioners in the field who rarely are willing to go on the record in scientific papers as talking about such subjects. WTG’s papers do have some of this style eg “two cultures of mathematics”, one of my favorites. just want to say “thx for this attn”. its one of those undeservedly at-times-low-status subjects/angles. but hey, lots of the greats participated in this sort of “navel-gazing”. Hardy is at the top of the list.
some more musings on this subject wrt Erdos, [status of] computer science/combinatorics in/vs mathematics, future development etc in this blog: erdos 100, tribute to a brilliant contrarian, also partly inspired by WTGs blog contents & “two cultures” paper.
October 6, 2013 at 3:43 pm |
(oops) that link does have some musings on the status of combinatorics/CS wrt other math areas; here is a sort of part II link which quotes WTG directly, incl an semi-infamous quote “combinatorics is the slums of topology” by whitehead, adventures & commotions in automated thm proving. and a big point to be made is that blogs are great emerging medium for this kind of behind-the-scenes materials & again many thx to WTG & his high stature for making that all a )( tiny bit more respectable by personal participation =)
November 5, 2013 at 8:46 am |
If X is a separable Banach space, then the set of compact operators on X is BORELIAN in the set of linear bounded operators on X equipped with its strong topology denoted by L_s(X), the result is it true for the set of stricly singular operators on X and why?
December 18, 2013 at 10:40 am |
Is it possible to construct an infinite dimensional Banach space such that every Riesz operator can be written under the sum of finite rank operator and a quasinilpotent operator?
November 22, 2014 at 5:52 pm |
HI or QHI or exotic Banach Spaces have or not the FIXED POINT PROPERTY? the result is true for Banach spaces having 1-unconditional basis.
October 13, 2015 at 3:54 pm |
Riesz operators have West decomposition on the space of Schlumprecht space S and the space of Gowers-Maurey X_GM, the reflexivity gives that the result is also true on their dual.
April 2, 2016 at 7:48 am |
[…] breakthrough by Argyros and Haydon settling the long-standing scalar-plus-compact problem (see Gowers’s blog entry for some background) shows that there is a space with the property that the only possbile spectra […]
December 3, 2018 at 2:46 pm |
The Banach space X_GM has or not fixed point property (FPP) for nonexpansive mappings which is in this case equivalent to weak fixed point property!!!
July 25, 2020 at 8:46 am |
If X is a Hilbert space then every bounded linear operator which is power compact is written under the compact + nilpotent operator. This result was proved by Olsen (1980) in a difficult paper. Is this result a characterization of Hilbert spaces? In other words, is it possible to find another infinite dimensional Banach spaces for which this result is true!!! What is the situation of l_p or L_p spaces or at least if p is even.