Without anyone being particularly aware of it, a race has been taking place. Which would happen first: the comment count reaching 1000, or the discovery of a new proof of the density Hales-Jewett theorem for lines of length 3? Very satisfyingly, it appears that DHJ(3) has won. If this were a conventional way of producing mathematics, then it would be premature to make such an announcement — one would wait until the proof was completely written up with every single i dotted and every t crossed — but this is blog maths and we’re free to make up conventions as we go along. So I hereby state that I am basically sure that the problem is solved (though not in the way originally envisaged).
Why do I feel so confident that what we have now is right, especially given that another attempt that seemed quite convincing ended up collapsing? Partly because it’s got what you want from a correct proof: not just some calculations that magically manage not to go wrong, but higher-level explanations backed up by fairly easy calculations, a new understanding of other situations where closely analogous arguments definitely work, and so on. And it seems that all the participants share the feeling that the argument is “robust” in the right way. And another pretty persuasive piece of evidence is that Tim Austin has used some of the ideas to produce a new and simpler proof of the recurrence result of Furstenberg and Katznelson from which they deduced DHJ. His preprint is available on the arXiv.
Better still, it looks very much as though the argument here will generalize straightforwardly to give the full density Hales-Jewett theorem. We are actively working on this and I expect it to be done within a week or so. (Work in progress can be found on the polymath1 wiki.) Better even than that, it seems that the resulting proof will be the simplest known proof of Szemerédi’s theorem. (There is one other proof, via hypergraphs, that could be another candidate for that, but it’s slightly less elementary.)
I have lots of thoughts about the project as a whole, but I want to save those for a different and less mathematical post. This one is intended to be the continuation of the discussion of DHJ(3), and now DHJ(k), into the 1000s. More precisely, it is for comments 1000-1049.
March 10, 2009 at 1:32 am |
Metacomment.
Appropriate timing of note:
Cantwell.949: A Moser set for n=5 has 124 points
March 10, 2009 at 3:37 am |
1000. DHJ(k)
A small comment: from experience with hypergraph regularity, I would imagine that DHJ(k) will not follow exactly from DHJ(k-1), but from something more like DHJ(k-1,k), and so the induction hypothesis may need to have an additional parameter than just k. (For instance, the simplex removal lemma for 3-uniform hypergraphs requires, at base, something resembling the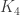 -removal lemma for graphs rather than the triangle removal lemma for graphs. While the
-removal lemma for graphs rather than the triangle removal lemma for graphs. While the 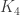 -removal and triangle removal lemmas have nearly identical proofs, I don’t think one can easily deduce the former from the latter if the latter is a black box.)
-removal and triangle removal lemmas have nearly identical proofs, I don’t think one can easily deduce the former from the latter if the latter is a black box.)
March 10, 2009 at 10:37 am
1000.1 An comment: you mean of course DHJ(k-2,k).
comment: you mean of course DHJ(k-2,k).
I think the jury is still out on whether we need to prove the full DHJ(k-2,k) before doing DHJ(k) or whether passing to subspaces the whole time makes it unnecessary. I’m hoping for the latter, but am ready to switch if we have to.
An comment: you are now our official powers-of-ten champion …
comment: you are now our official powers-of-ten champion …
March 10, 2009 at 7:20 am |
1001. Line and equal-slice distributions in![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) .
.
It seems to me that the right generalization of the “another useful equivalent definition” of equal-slices on![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is as follows:
is as follows:
Pick![z \in [k]^n](https://s0.wp.com/latex.php?latex=z+%5Cin+%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) from the equal-slices distribution. Form
from the equal-slices distribution. Form ![x^i \in [k-1]^n](https://s0.wp.com/latex.php?latex=x%5Ei+%5Cin+%5Bk-1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) by changing all the
by changing all the  ‘s in
‘s in  into
into  ‘s, for
‘s, for  . Finally, let
. Finally, let  be a random permutation of the
be a random permutation of the 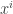 ‘s.
‘s.
Certainly the set is a combinatorial line, which is degenerate only if
is a combinatorial line, which is degenerate only if  had no
had no  ‘s.
‘s.
I believe that each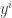 is individually distributed as equal-slices on
is individually distributed as equal-slices on ![[k-1]^n](https://s0.wp.com/latex.php?latex=%5Bk-1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , but I can’t quite seem to prove it to myself at this late hour. Anyone want to prove or disprove?
, but I can’t quite seem to prove it to myself at this late hour. Anyone want to prove or disprove?
(If it’s true, there must be some slick way to see it, like “break up a necklace of beads into
beads into  pieces, then pretend you did it in one the
pieces, then pretend you did it in one the 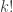 different orders, then…” etc.)
different orders, then…” etc.)
March 10, 2009 at 7:21 am
1001.1. That was me writing; forgot to log in.
March 10, 2009 at 9:12 am
1001.2 I’m pretty sure it’s false. In fact, isn’t it obviously false, since the expected number of s in
s in 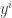 is twice the expected number of any j for
is twice the expected number of any j for  ?
?
However, I think what can be proved is that the distribution on each individual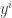 is not importantly different from the equal-slices distribution, in that the collection of dense sets is the same in both cases. This is analogous to what happens in the corners problem, where the number of corners containing a point is different from point to point (even if we start off with a triangular grid) but this doesn’t matter because the discrepancy between the uniform measure of a set and the point-in-random-corners measure of a set depends only on the measures and not on
is not importantly different from the equal-slices distribution, in that the collection of dense sets is the same in both cases. This is analogous to what happens in the corners problem, where the number of corners containing a point is different from point to point (even if we start off with a triangular grid) but this doesn’t matter because the discrepancy between the uniform measure of a set and the point-in-random-corners measure of a set depends only on the measures and not on  .
.
March 10, 2009 at 10:41 am
1001.3 However, I think I may be misunderstanding what you have written, since I don’t quite see why you bother to permute the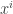 s (given that they were already distributed in a way that is permutation-invariant — or at least that’s how it appears to me from what you say).
s (given that they were already distributed in a way that is permutation-invariant — or at least that’s how it appears to me from what you say).
March 10, 2009 at 4:41 pm
1001.4. Oops, yes, I think what I meant to say was “Pick a permutation on
on ![[k-1]](https://s0.wp.com/latex.php?latex=%5Bk-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) and then form
and then form  , where by
, where by  we mean permute the
we mean permute the  -sets of
-sets of 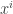 according to the permutation
according to the permutation  .”
.”
I will write a new comment on this topic later today.
March 10, 2009 at 7:49 am |
1002. 895 again.
Okay, maybe the book proof of Szemeredi goes through DHJ, but I hope not…I was trying before to get someone to bite on trying something potentially simpler than DHJ (3) that would still prove the corners theorem via the Ajtai-Szem method. (And in particular didn’t use Szemeredi’s theorem as a lemma.) Of course, being the token ergodic theorist, you can probably guess that I would like someone to bite so I don’t have to try to check myself, because I am woefully slow and error prone when it comes to such things. So let me try again…I’ll just think out loud and if none of this makes any sense, everyone can feel free to ignore.
What if I take as my basic object pairs of
of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . A diagonal is a set
. A diagonal is a set  , where
, where  is multi-set union and
is multi-set union and  is some fixed multi-set (of multiplicity no greater than 2 in each element). A corner is a triple of the form
is some fixed multi-set (of multiplicity no greater than 2 in each element). A corner is a triple of the form  , where
, where  can be a set plus an anti-set (an antiset is like a set where every element has a multiplicity of -1).
can be a set plus an anti-set (an antiset is like a set where every element has a multiplicity of -1).
Okay, let be a set of pairs of density at least
be a set of pairs of density at least  , i.e.
, i.e.  . Now, for some rather small, or at least not-so-big
. Now, for some rather small, or at least not-so-big  , most of the whole space is covered by diagonals whose “multiplicity 2-or-zero” (for the defining multiset
, most of the whole space is covered by diagonals whose “multiplicity 2-or-zero” (for the defining multiset  ) set of indices has size no bigger than
) set of indices has size no bigger than  .
.
Diagonals of this sort have at least members. Take one of these diagonals
members. Take one of these diagonals  on which
on which  is dense, say of relative density at least
is dense, say of relative density at least  . If
. If  is corner-free, then any pair of the form
is corner-free, then any pair of the form  , where
, where  and
and 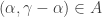 is forbidden. That should be something like
is forbidden. That should be something like  forbidden pairs, and these pairs lie in a Cartesian product. This should mean that
forbidden pairs, and these pairs lie in a Cartesian product. This should mean that  has a density increment on some other Cartesian product, call it
has a density increment on some other Cartesian product, call it 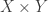 .
.
The next step is presumably to use the multidimensional Sperner’s theorem to carve almost all of up into subgrids of some large but fixed size
up into subgrids of some large but fixed size  . (Here a subgrid is a collection
. (Here a subgrid is a collection  .) I wasn’t really anticipating how hard this would be but maybe you can use the iteration method we use to carve 1-spaces up. Now that I am thinking about this finally, maybe one can do it all in one go. Namely, you can always find
.) I wasn’t really anticipating how hard this would be but maybe you can use the iteration method we use to carve 1-spaces up. Now that I am thinking about this finally, maybe one can do it all in one go. Namely, you can always find  with combined size at most
with combined size at most  such that the probability that
such that the probability that  and
and  is above some constant
is above some constant  . So for those pairs
. So for those pairs  where you get the containment you were shooting for, remove those grids from
where you get the containment you were shooting for, remove those grids from  and keep them as part of your partition; partition the other pairs into
and keep them as part of your partition; partition the other pairs into  classes according to the value taken on the subgrid associated with that pair. Each of these classes is the intersection of
classes according to the value taken on the subgrid associated with that pair. Each of these classes is the intersection of  with a subgrid and we iterate…just like in the proof of DHJ. And, I guess that’s it. Assuming all of the above is correct, you get an increment on a subgrid.
with a subgrid and we iterate…just like in the proof of DHJ. And, I guess that’s it. Assuming all of the above is correct, you get an increment on a subgrid.
It’s almost 3 here and too late to check so I will apologize in advance if something is amiss.
March 10, 2009 at 9:18 am
1002.1 Randall, is your problem the same as Jozsef’s in comment 2? In one of the very early comments I tried to translate that one into set-theoretic language and ended up with something pretty similar. This is mainly to say that I agree that it’s worth seeing whether Szemerédi can be done without going the whole way to DHJ. For now I’m going to concentrate my efforts on DHJ(k) but will follow what you have to say with interest. I suppose there are two issues: can DHJ be avoided, and is the resulting proof substantially simpler?
March 10, 2009 at 3:39 pm
1002.2 Yes, it was intended to be the same (not sure whether Jozsef intended to allow inverted corners, but I am here). Oh, yes…I see your comment 7. That looks to be exactly the interpretation I am employing.
Well, perhaps Terry will wake up and say whether the alleged proof I gave is really a proof or can be made into a proof. (And whether it’s simpler than what we have already.) Since he composed and typed the breakthrough post (837?) in eighteen minutes, perhaps he’ll be able to do this despite being very busy with other things.
On a more general philosophical note, Tim, to we ergodic theorists (who have trouble with subscripts appearing on the numbers capital N appearing in proofs), the dynamical proof of van der Waerden (not that of Furstenberg and Weiss but the easy one, due to Blszczyk, Plewik and Turek) is much more pleasant than any proof I have seen of HJ. (Actually, I have long wanted to see a proof, even an unpleasant one, of HJ that made efficacious use of non-metrizable topological dynamics.)
March 10, 2009 at 6:58 pm
1002.3 Obviously I meant “efficacious use of *metrizable* topological dynamics”. There exist proofs using non-metrizable topological dynamics (e.g. Furstenberg and Katznelson’s proof). It may not be possible, or it may require some non-commutative stuff like in the FK proof of DHJ. There is a Bergelson-Leibman proof that tried to use recurrence for continuous maps of compact metric spaces, but it was realized after the paper appeared that neither continuity of the transformations nor completeness of the space was actually ever used.
March 11, 2009 at 7:34 pm
1002.4 No induction….
I think the idea I had to prove Szemeredi via Ajtai-Szem type argument using Jozsef’s formulation from comment 2 is dead in the water at k=3.5. The problem I don’t see a way around is that there don’t seem to be enough corners at k=3 to forbid enough points at k=4. Obviously not a problem for DHJ since the number of lines at k=3 is 4^k which is equal to the number of points at k=4.
Oh well…if the above is correct (nobody checked?) it may be the simplest proof of the corner’s theorem, at least.
March 25, 2009 at 8:57 pm
Hmm…I finally had a look at the above myself, and it seems to be complete garbage for (at least) two reasons…. Perhaps now I am convinced that the DHJ proof is the right one for Szemeredi after all. (Maybe.)
March 10, 2009 at 10:49 am |
Metacomment: because of more spam problems on the wiki, you now have to be registered on it and logged in if you want to edit the main page.
March 10, 2009 at 4:41 pm |
[…] experiment in doing math research on his blog. It sounds like it was a resounding success! Timothy Gowers announced on his blog that he is pretty convinced that the crowd on his blog has come up with a new proof of the density […]
March 10, 2009 at 7:10 pm |
Metacomment.
This might be a good time to set up a “meta” thread to deal with issues not directly related to finishing off the proof of DHJ(3)/DHJ(k) [1000-1049] or of computing DHJ-type numbers in small dimension [900-999]. For instance, this seems like a good time to face issues concerning writing up the results, how to perform proper attribution, etc. (At a more frivolous level, there was a suggestion on the wiki to come up with a logo for that wiki; I think that might be a fun topic for the meta thread. More generally, discussion of the strengths and weaknesses of the wiki, or the threaded format, etc. would be apropos at this time, I think.)
March 10, 2009 at 7:45 pm
OK what I’ll do is get on and write a post that I’ve been intending to write, in which I discuss general meta-issues that have arisen out of how things have gone. I think there’s a lot to talk about, so comments on that should be a natural place for discussing these issues amongst others.
March 10, 2009 at 7:43 pm |
1003. Austin’s proof
I’ve managed to digest a key ingredient in Austin’s proof (Lemma 6.1 of http://arxiv.org/abs/0903.1633 ) which may be of interest here. Roughly speaking, it says that 1-sets and 2-sets (say) are always “locally independent” of each other. A more precise statement is the following. Let![f: [3]^n \to [-1,1]](https://s0.wp.com/latex.php?latex=f%3A+%5B3%5D%5En+%5Cto+%5B-1%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) be 02-insensitive (e.g. it is the indicator function of a 1-set), and let
be 02-insensitive (e.g. it is the indicator function of a 1-set), and let ![g: [3]^n \to [-1,1]](https://s0.wp.com/latex.php?latex=g%3A+%5B3%5D%5En+%5Cto+%5B-1%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) be 01-insensitive (e.g. it is the indicator of a 2-set). Suppose also that
be 01-insensitive (e.g. it is the indicator of a 2-set). Suppose also that ![{\Bbb E}_{x \in [3]^n} f(x) g(x)](https://s0.wp.com/latex.php?latex=%7B%5CBbb+E%7D_%7Bx+%5Cin+%5B3%5D%5En%7D+f%28x%29+g%28x%29&bg=ffffff&fg=333333&s=0&c=20201002) is large. Then f has large average on large-dimensional spaces, or (equivalently) correlates with a 012-low influence function (a function which is almost invariant under any interchanges between 0, 1, and 2).
is large. Then f has large average on large-dimensional spaces, or (equivalently) correlates with a 012-low influence function (a function which is almost invariant under any interchanges between 0, 1, and 2).
Proof. Let x be a random string![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , let
, let ![A \subset [n]](https://s0.wp.com/latex.php?latex=A+%5Csubset+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) be a random medium-sized set of indices, and let
be a random medium-sized set of indices, and let  be the string in
be the string in ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) formed by replacing all occurrences of 0 or 2 in A with 0. If A is not too large, then
formed by replacing all occurrences of 0 or 2 in A with 0. If A is not too large, then  is still roughly uniformly distributed in
is still roughly uniformly distributed in ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , and so
, and so
But as f is 02-insensitive,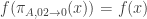 . As g is 01-insensitive,
. As g is 01-insensitive, 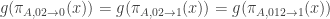 , where
, where 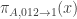 is the string formed by sending every digit of x in A to 1. Thus
is the string formed by sending every digit of x in A to 1. Thus
Freezing A, we thus conclude that f has large mean on many |A|-dimensional subspaces; alternatively, we see that f correlates with the 012-low influence function (if we choose A in a suitably Poisson manner).
(if we choose A in a suitably Poisson manner).
A corollary of this is that if one has a 1-set A and a 2-set B which are “strongly stationary” in the sense that their average local density on medium-sized subspaces is close to their global density, then A and B are roughly independent, thus the density of the 12-set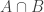 is roughly the density of A multiplied by the density of B.
is roughly the density of A multiplied by the density of B.
As one might imagine, this fact is extremely useful for doing any sort of “counting lemma” involving 12-sets.
To be continued…
March 10, 2009 at 7:44 pm
A small correction: where I said that f and g could be indicators of 1-sets and 2-sets respectively, it might be better to think of them as the balanced functions of a 1-set and 2-set, i.e. the indicator minus the density.
March 10, 2009 at 7:55 pm
1003.2
Incidentally, this framework also gives a short proof of “lack of lines implies correlation with a local 12-set”. With the notation as before, observe that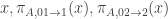 will form a combinatorial line with high probability if A is not too small. Thus if
will form a combinatorial line with high probability if A is not too small. Thus if  is a set with no lines and density
is a set with no lines and density  then
then
But if we freeze A and the coordinates outside of A (thus passing to an |A|-dimensional subspace), then ,
,  are indicators of a 2-set and a 1-set respectively, and the claim follows.
are indicators of a 2-set and a 1-set respectively, and the claim follows.
March 10, 2009 at 11:50 pm
1003.3 Terry, I’m trying to digest 1003.2. It seems to me that the displayed line is true only if there are many x such that and
and 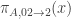 both belong to
both belong to 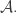 In the previous proof this was done with the help of Sperner and that seemed necessary. I’m not sure where the Sperner step is appearing in what you’ve written.
In the previous proof this was done with the help of Sperner and that seemed necessary. I’m not sure where the Sperner step is appearing in what you’ve written.
March 10, 2009 at 9:54 pm |
1004. Random lines/equal slices for DHJ(k+1).
I think what I wrote in 1001 was correct. Let me restate it here for clarity:
Let![z \in [k+1]^n](https://s0.wp.com/latex.php?latex=z+%5Cin+%5Bk%2B1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) be drawn from equal-slices. Form the string
be drawn from equal-slices. Form the string ![v^j \in [k]^n](https://s0.wp.com/latex.php?latex=v%5Ej+%5Cin+%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) by changing all
by changing all  ‘s in
‘s in  to
to  ‘s, for
‘s, for  . Finally, pick a random permutation
. Finally, pick a random permutation  on
on ![[k]](https://s0.wp.com/latex.php?latex=%5Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) and define strings
and define strings  , for
, for  .
.
Then each string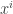 is distributed as equal-slices on
is distributed as equal-slices on ![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . Further, since
. Further, since 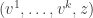 is a combinatorial line (“in order”), we also have that
is a combinatorial line (“in order”), we also have that 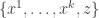 is a combinatorial line (possibly “out of order”).
is a combinatorial line (possibly “out of order”).
The proof is here; I’ll wikify it soon.
March 10, 2009 at 10:12 pm
1004.1. Wikified here. Hopefully this will help with the generalization of line-free sets correlating with 12-sets.
March 10, 2009 at 10:56 pm
1004.2 Ryan, I’m still struggling with the statement of what you are proving. Suppose k=2. Then I pick![z\in[3]^n](https://s0.wp.com/latex.php?latex=z%5Cin%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) from equal slices and form the strings
from equal slices and form the strings  and
and  by turning the 3s of
by turning the 3s of  into 1s and 2s, respectively. Then I randomly decide whether to interchange
into 1s and 2s, respectively. Then I randomly decide whether to interchange  to
to  . Now let’s look at the event that the number of 1s in
. Now let’s look at the event that the number of 1s in  is between
is between  and
and  If I choose
If I choose  according to equal-slices that is
according to equal-slices that is  . But if I choose it by starting with z, then either I start with about that number of 1s and change the 3s to 2s, or I start with about that number of 2s and change the 3s to 1s. The probability seems to me to be smaller because
. But if I choose it by starting with z, then either I start with about that number of 1s and change the 3s to 2s, or I start with about that number of 2s and change the 3s to 1s. The probability seems to me to be smaller because  is being asked to have rather a lot of 1s or rather a lot of 2s. Since you’ve got a wikified proof, what I’m asking here is for an explanation of where I’m going wrong.
is being asked to have rather a lot of 1s or rather a lot of 2s. Since you’ve got a wikified proof, what I’m asking here is for an explanation of where I’m going wrong.
March 10, 2009 at 11:53 pm
1004.3. Hmm, I’m not quite sure what I can say to help.
In your example, when you pick from equal-slices on
from equal-slices on ![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) “in the normal fashion”, then as you say the event
“in the normal fashion”, then as you say the event  = “number of
= “number of  ‘s in
‘s in  is in
is in ![[.49n, .51n]](https://s0.wp.com/latex.php?latex=%5B.49n%2C+.51n%5D&bg=ffffff&fg=333333&s=0&c=20201002) ” occurs with probability exactly
” occurs with probability exactly  .
.
When you pick it in the funny way, through, , what is the probability? As you say, half the time
, what is the probability? As you say, half the time  is formed by changing
is formed by changing  ‘s
‘s 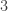 ‘s to
‘s to  ‘s. In this case,
‘s. In this case,  occurs iff
occurs iff  had between
had between  and
and 
 ‘s. The other half of the time,
‘s. The other half of the time,  is formed by changing
is formed by changing  ‘s
‘s 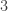 ‘s to
‘s to  ‘s. In this case,
‘s. In this case,  occurs iff
occurs iff  had between
had between  and
and 
 ‘s-and-
‘s-and-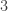 ‘s-together, iff
‘s-together, iff  had between
had between 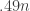 and
and 
 ‘s.
‘s.
Clearly the probability has between
has between  and
and 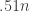
 ‘s is the same as the probability
‘s is the same as the probability  has between
has between  and
and 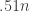
 ‘s. So we are reduced to asking why this probability is indeed
‘s. So we are reduced to asking why this probability is indeed  .
.
Well, I’m not sure what to say, except that it is. It comes from the fact that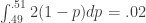 , where
, where 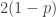 is the density of the first component in a uniform draw from the
is the density of the first component in a uniform draw from the 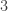 -simplex. Note that this integral is a bit of a “coincidence”, because it is not true that, e.g.,
-simplex. Note that this integral is a bit of a “coincidence”, because it is not true that, e.g., 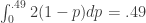 .
.
The reason this all works is a bit easier to understand in the case of ; see this explanation in the older wiki article on equal-slices.
; see this explanation in the older wiki article on equal-slices.
March 11, 2009 at 12:16 am
1004.4 Thanks — I think I’m starting to get it now.
March 10, 2009 at 9:55 pm |
1005. Quantitative bounds?
Is our understanding of the density-increment proof of DHJ(3) good enough that we can venture a probable quantitative bound for n in terms of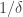 ? Naively I am expecting tower-exponential behaviour (with the height of the tower being either polynomial or exponential in
? Naively I am expecting tower-exponential behaviour (with the height of the tower being either polynomial or exponential in 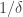 ).
).
March 10, 2009 at 11:08 pm
1005.1 I’m pretty sure it’s a tower. The rough reason is that when we drop to a subspace we obtain that subspace by applying multidimensional Sperner, which I think restricts its dimension to the log of the previous dimension. But I think the density increase we can get that way is good, so I think the bound should be a tower of height polynomial in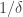 and therefore not worse than what you get out of the Ajtai-Szemerédi proof of the corners theorem.
and therefore not worse than what you get out of the Ajtai-Szemerédi proof of the corners theorem.
Also, if we’ve got the stomach for it, we could think about trying to Shkredovize the argument and beat Shelah’s bound for the colouring DHJ(3). That would be a serious undertaking though, as it would require us to understand the global obstructions rather than just the local ones.
March 10, 2009 at 10:27 pm |
1006. Equal-slices.
I wonder: can we mostly work in the equal-slices measure for the whole proof (of DHJ(3), say)? What are the advantages of the uniform distribution?
March 10, 2009 at 11:12 pm
1006.1 My take on this is that equal-slices measure is very good when you want to mix random points and random lines, but the uniform measure is better when you want to restrict to subspaces. Roughly, the reason for the latter is that if you start with equal-slices and restrict a few coordinates, then the distribution on the resulting subspace becomes much more like a uniform one, or a suitably weighted uniform one. For example, if you’re told that a point’s restriction to the first m coordinates has roughly equal numbers of 1s, 2s and 3s, then with very high probability it belongs to a slice with roughly equal numbers of 1s, 2s and 3s, so the distribution in that (n-m)-dimensional subspace is roughly uniform.
It’s possible that we could argue that we can restrict to subspaces and get an equal-slices density increase, but I think we would still have to go via uniform, so in the end I don’t see a compelling argument for doing that.
March 11, 2009 at 12:08 am
1006.2. That’s a good point. I guess I was idly hoping that the fact that equal-slices is exactly equal to a (fairly natural) mixture of uniform distributions on subspaces might allow us a clever way to stay entirely in the equal-slices world.
March 11, 2009 at 12:55 am |
1007. DHJ(k)
I think I’ve now proved (though with details a bit hazy at a couple of points) the analogue for k of the fact that line-free sets in![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) correlate locally with 12-sets. The proposed argument can probably be tidied up in a few places. I haven’t yet thought about whether any of the rest of DHJ(k) is going to present problems, but it feels as though we’re closing in on it pretty rapidly. That’s my lot for today though.
correlate locally with 12-sets. The proposed argument can probably be tidied up in a few places. I haven’t yet thought about whether any of the rest of DHJ(k) is going to present problems, but it feels as though we’re closing in on it pretty rapidly. That’s my lot for today though.
March 11, 2009 at 1:20 am |
1008. Re: 1003.3
Yes, you’re right, one also needs Sperner. Without it, what one gets is that if is uniformly distributed with respect to 12-sets, then
is uniformly distributed with respect to 12-sets, then
and then one has to use DHJ(2) to say that the RHS is large (which one can do, after letting A vary in a sufficiently Poisson-like manner).
I would imagine that the same thing works in higher k, perhaps this is already implicit in 1007.
March 11, 2009 at 1:49 am |
[…] Problem solved (probably) Without anyone being particularly aware of it, a race has been taking place. Which would happen first: the comment count […] […]
March 11, 2009 at 5:38 am |
1009. Equal-slices distribution.
I think the following is an easier explanation of what I wrote.
Claim: Pick![z \in [k]^n](https://s0.wp.com/latex.php?latex=z+%5Cin+%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) according to equal-slices. Then pick
according to equal-slices. Then pick ![J \in [k-1]](https://s0.wp.com/latex.php?latex=J+%5Cin+%5Bk-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) uniformly and form
uniformly and form  by changing all the
by changing all the  ‘s in
‘s in  to
to 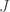 ‘s. Then
‘s. Then  is distributed according to equal-slices on
is distributed according to equal-slices on ![[k-1]^n](https://s0.wp.com/latex.php?latex=%5Bk-1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Note: it’s helpful to think of ‘s as
‘s as  ‘s.
‘s.
Proof sketch via coupling: Draw a circle of dots. Place bar(1) uniformly at random in the
dots. Place bar(1) uniformly at random in the 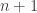 slots. Then place bar(2) uniformly at random in the resulting
slots. Then place bar(2) uniformly at random in the resulting 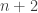 slots. Etc., placing
slots. Etc., placing  bars. Pick
bars. Pick ![J \in [k-1]](https://s0.wp.com/latex.php?latex=J+%5Cin+%5Bk-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) uniformly. Look at the arc of dots following bar(k) clockwise, up until the next bar. Fill in these dots with
uniformly. Look at the arc of dots following bar(k) clockwise, up until the next bar. Fill in these dots with  ‘s. Look also at the arc of dots preceding bar(k) counterclockwise, up until the next bar. Fill in these dots with
‘s. Look also at the arc of dots preceding bar(k) counterclockwise, up until the next bar. Fill in these dots with 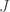 ‘s. Next, for each of the remaining
‘s. Next, for each of the remaining 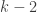 arcs of dots, fill it all with the same digit — using up the remaining digits
arcs of dots, fill it all with the same digit — using up the remaining digits ![[k-1] \setminus \{J\}](https://s0.wp.com/latex.php?latex=%5Bk-1%5D+%5Csetminus+%5C%7BJ%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) in some arbitrary way. Finally, delete the bars, cut the circle to make it a segment, and then randomly permute the whole sequence of digits. We claim the resulting sequence is distributed as equal-slices on
in some arbitrary way. Finally, delete the bars, cut the circle to make it a segment, and then randomly permute the whole sequence of digits. We claim the resulting sequence is distributed as equal-slices on ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , and therefore we can take it as
, and therefore we can take it as  .
.
Now forming from
from  is the same as doing the above procedure but using
is the same as doing the above procedure but using 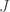 ‘s where we were using
‘s where we were using  ‘s before. But really, happens under this new procedure? You place
‘s before. But really, happens under this new procedure? You place 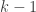 bars as if you were doing equal-slices on
bars as if you were doing equal-slices on ![[k-1]^n](https://s0.wp.com/latex.php?latex=%5Bk-1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) ; then you throw in a phantom extra bar but only use it insofar as deciding to call the arc it lands in the
; then you throw in a phantom extra bar but only use it insofar as deciding to call the arc it lands in the 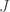 -arc; then you define the other
-arc; then you define the other 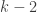 arcs according to the digits in
arcs according to the digits in ![[k-1] \setminus \{J\}](https://s0.wp.com/latex.php?latex=%5Bk-1%5D+%5Csetminus+%5C%7BJ%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) , etc. Now granted, the arc chosen to be the
, etc. Now granted, the arc chosen to be the 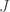 -arc is not uniformly distributed among arcs — it’s biased towards the longer arcs. But who cares, since
-arc is not uniformly distributed among arcs — it’s biased towards the longer arcs. But who cares, since 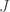 is uniformly random on
is uniformly random on ![[k-1]](https://s0.wp.com/latex.php?latex=%5Bk-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) ?
?
March 11, 2009 at 6:01 am |
1010. “Varnavides”-DHJ(k). (Sorry for the scare quotes, but it strikes me as funny somehow to name this concept after a person.)
Tim, I can’t quite follow what you wrote at the end of your proof sketch that line-free sets in![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) correlate with lower-complexity sets. I was wondering if you could clarify. In particular, as you say it seems we need to show that DHJ(k) actually implies Varnavides-DHJ(k) under some appropriate measures.
correlate with lower-complexity sets. I was wondering if you could clarify. In particular, as you say it seems we need to show that DHJ(k) actually implies Varnavides-DHJ(k) under some appropriate measures.
As you suggest, it seems that equal-slices is what to hope for here (it works pretty well for at least!). In other words, we may hope that if
at least!). In other words, we may hope that if ![A \subseteq [k]^n](https://s0.wp.com/latex.php?latex=A+%5Csubseteq+%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) has equal-slices measure
has equal-slices measure  then if you choose an “equal-slices-combinatorial-line” (i.e., draw from equal-slices on
then if you choose an “equal-slices-combinatorial-line” (i.e., draw from equal-slices on ![([k] \cup \{\ast\})^n](https://s0.wp.com/latex.php?latex=%28%5Bk%5D+%5Ccup+%5C%7B%5Cast%5C%7D%29%5En&bg=ffffff&fg=333333&s=0&c=20201002) ) then there is some
) then there is some  chance that all
chance that all  points are in
points are in  .
.
Looking at that statement now I worry slightly that it is a bit optimistic. Well, let’s hope it’s true, and let me ask, Tim, about what you wrote.
I guess I don’t quite understand what’s going on with the parameter . On one hand, I assume it’s to be “small” (although still perhaps
. On one hand, I assume it’s to be “small” (although still perhaps 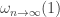 ), because otherwise bounding the number of lines in
), because otherwise bounding the number of lines in ![[k]^M](https://s0.wp.com/latex.php?latex=%5Bk%5D%5EM&bg=ffffff&fg=333333&s=0&c=20201002) by
by 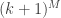 looks worrisome.
looks worrisome.
On the other hand, this makes me worry a bit about bullet-point 3: if is supported on
is supported on  -dimensional subspaces then somehow I don’t expect that a set of lines
-dimensional subspaces then somehow I don’t expect that a set of lines 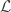 being large under
being large under  should mean it’s large under a more “global” measure on lines such as equal-slices.
should mean it’s large under a more “global” measure on lines such as equal-slices.
Quite likely I’m mistaking your argument or missing something — would you be able to clarify? Thanks!
March 11, 2009 at 1:16 pm
1010.1 Ryan, the argument is so sloppily written (little more than a declaration that my gut feeling is that it works) that it is good that you apply a little pressure of this kind. I think I have answers to your specific queries, but that’s not the same as a proof. But maybe it will tip you over to believing that it works.
First of all, my parameter M is not supposed to tend to infinity. As I said in the write-up, it’s meant to be the smallest integer such that we have DHJ(k) with density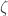 , where
, where 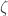 depends only on the equal-slices density
depends only on the equal-slices density  of the set inside which we’re trying to find lots of combinatorial lines.
of the set inside which we’re trying to find lots of combinatorial lines.
So what about your second worry? The point here is that the M-dimensional subspaces I’m averaging over are absolutely not local. Instead, they’re supposed to be far more tailored to equal-slices. What I’m not doing is fixing almost all coordinates and taking M small wildcard sets, or something like that. Instead, I’m randomly choosing the sizes of the M wildcard sets (which I allow to add up to 1, so there are in fact no fixed coordinates at all) and then uniformly at random choosing a line from the resulting subspace. That’s why I’m hoping that the resulting measure on lines is sufficiently global in character.
March 11, 2009 at 8:00 am |
1011. A Shelah-type argument
I’m quite optimistic that a Shelah type argument might work for the general DHJ(k) problem. It’s late evening and I had a hard day, so I’m not sure how far can I go with the argument tonight. Let me give some basic definitions first. In![k^{[n]}](https://s0.wp.com/latex.php?latex=k%5E%7B%5Bn%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) two points are neighbours if they have same coordinates everywhere but in one position where one is k-2 and the other is k-1. For a subset
two points are neighbours if they have same coordinates everywhere but in one position where one is k-2 and the other is k-1. For a subset ![S\subset k^{[n]}](https://s0.wp.com/latex.php?latex=S%5Csubset+k%5E%7B%5Bn%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) the space
the space ![k^{[n]}](https://s0.wp.com/latex.php?latex=k%5E%7B%5Bn%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) is fliptop if a point p is in S iff any neighbour of p is also in S. (I will wikify it if the argument turns out to be useful) Our goal is to find a large fliptop subspace which is dense. By induction there will be a k-1 combinatorial line which gives a full combinatorial line because of the fliptop property of the subspace. I will follow Shelah’s strategy with some extra conditions to make it (hopefully) work for the density version.
is fliptop if a point p is in S iff any neighbour of p is also in S. (I will wikify it if the argument turns out to be useful) Our goal is to find a large fliptop subspace which is dense. By induction there will be a k-1 combinatorial line which gives a full combinatorial line because of the fliptop property of the subspace. I will follow Shelah’s strategy with some extra conditions to make it (hopefully) work for the density version.![S\subset k^{[n]}](https://s0.wp.com/latex.php?latex=S%5Csubset+k%5E%7B%5Bn%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) is c-dense and we already know the subspace version of DHJ for k-1. Partition [n] into m consecutive intervals of lengths
is c-dense and we already know the subspace version of DHJ for k-1. Partition [n] into m consecutive intervals of lengths 
Suppose that
We will repeat two steps to get a subspace eventually. The first one should keep the density high and the second will provide the fliptop property.![k^{[l_m]}](https://s0.wp.com/latex.php?latex=k%5E%7B%5Bl_m%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) there is a certain number of points in S with that tail. Select the points from
there is a certain number of points in S with that tail. Select the points from ![k^{[l_m]}](https://s0.wp.com/latex.php?latex=k%5E%7B%5Bl_m%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) which are tails of at least
which are tails of at least 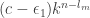 elements of S. The set of such points is denoted by H1. Applying the induction hypothesis we know that
elements of S. The set of such points is denoted by H1. Applying the induction hypothesis we know that ![k^{[l_m]}](https://s0.wp.com/latex.php?latex=k%5E%7B%5Bl_m%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) will contain a d1-dimensional subspace where every element avoiding (running) coordinate k-1 are from H1 (so it has many extensions that are in S).
will contain a d1-dimensional subspace where every element avoiding (running) coordinate k-1 are from H1 (so it has many extensions that are in S). such equivalence classes. Therefore if
such equivalence classes. Therefore if  then we have a Sperner pair, two points where the set of k-1 coordinates of a point contains the other point’s set of k-1 coordinates. It defines a combinatorial line in the subspace and we will work with this line in the following steps.
then we have a Sperner pair, two points where the set of k-1 coordinates of a point contains the other point’s set of k-1 coordinates. It defines a combinatorial line in the subspace and we will work with this line in the following steps. . I will continue, but I would like to read over first what I wrote.
. I will continue, but I would like to read over first what I wrote.
Step one: For any point in
Step two: Consider the elements of the d1-dimensional subspace where every coordinate is k-1 or k-2. We say that two such points are equivalent if they are the tails of the same subset of S. There are no more than
We will repeat steps one and two in
March 11, 2009 at 8:56 am
1011. contd.
Let us denote the k points of the combinatorial line selected previously by (indexed by the running coordinates.)
(indexed by the running coordinates.)![k^{[l_{m-1}]}](https://s0.wp.com/latex.php?latex=k%5E%7B%5Bl_%7Bm-1%7D%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) .
.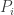 it is the tail of at least
it is the tail of at least  elements of S where
elements of S where 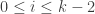 . There are two cases; either there are many such points or there is a tail of at least
. There are two cases; either there are many such points or there is a tail of at least  elements of S. (More careful calculations are needed, but let me sketch the argument first.) If there are enough points, the there is a d2-dimensional subspace in
elements of S. (More careful calculations are needed, but let me sketch the argument first.) If there are enough points, the there is a d2-dimensional subspace in ![k^{[l_{m-1}]}](https://s0.wp.com/latex.php?latex=k%5E%7B%5Bl_%7Bm-1%7D%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) where every point without coordinate k-1 is from H2.
where every point without coordinate k-1 is from H2.![t\in k^{[n-l_m-l_{m-1}]}](https://s0.wp.com/latex.php?latex=t%5Cin+k%5E%7B%5Bn-l_m-l_%7Bm-1%7D%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) ,
,  is in S iff
is in S iff  is in S. There are no more than
is in S. There are no more than  such equivalence classes. If
such equivalence classes. If  then there is a Sperner pair, two points where the set of k-1 coordinates contains the other point’s set of k-1 coordinates. It defines the second combinatorial line in the subspace and we will work with the two lines in the following steps. Let us denote the k points of the new combinatorial line by
then there is a Sperner pair, two points where the set of k-1 coordinates contains the other point’s set of k-1 coordinates. It defines the second combinatorial line in the subspace and we will work with the two lines in the following steps. Let us denote the k points of the new combinatorial line by 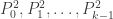
Step one: select set H2 from
Select a point if with any
Step two: Consider the elements of the d2-dimensional subspace where every coordinate is k-1 or k-2. We say that two such points, a and b. are equivalent if for any element
March 11, 2009 at 6:18 pm
There are a few typos in the argument. I should fix them eventually, but let me mention her one which might be quite misleading; “There are no more than such equivalence classes.” actually, there are no more than
such equivalence classes.” actually, there are no more than  such equivalence classes. Similarly, in the second iteration There are no more than
such equivalence classes. Similarly, in the second iteration There are no more than 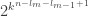 such equivalence classes.
such equivalence classes.
March 11, 2009 at 9:00 am |
I’ll continue tomorrow morning, but I hope that what I wrote makes sense and maybe someone will tell me if this plan is feasible or not.
March 11, 2009 at 9:20 am
1012.1 I’ve just read through it and nothing jumps out at me as wrong, or obviously not going to work. I suppose my one worry is a metaworry, which is that many people must have tried to produce a density version of Shelah’s argument, and there doesn’t seem to be any sign of an obstacle in the above sketch. On the other hand, a balancing metareassurance is that you have a record of finding dazzlingly simple arguments.
I haven’t yet thought about the part where you write “more careful calculations are needed”.
Perhaps another reason to be hopeful is that one way of explaining what Shelah did is to say that he changed an inductive argument from deducing HJ(k) from HJ(2) with the repeated help of HJ(k-1) to deducing HJ(k) from HJ(k-1) with the repeated help of HJ(2), and there is no obvious reason to think that that cannot be done for density as well.
Anyhow, if it works … amazing!
March 11, 2009 at 12:54 pm |
1013. Shelah.
I took the car to be serviced today, which resulted in a long walk to work, during which I pondered Jozsef’s argument. I can’t see a problem, but neither have I thought it through fully. So I want to try to assess its feasibility by seeing if I can sketch it. (Of course, Jozsef has already sketched it, but there’s no harm in having more than one sketch, and if I manage to sketch it without looking any further at what he wrote, then it might make us feel better in the way that people feel better about computer-assisted proofs if more than one person does the computer part and different programs are used.)
What is remarkable about Jozsef’s proposal if it works is that it is so similar to what Shelah did: it would make it very mysterious that the proof had not been discovered earlier (which would add another layer of mystery to the already remarkable fact that Shelah’s proof was itself not discovered earlier).
The idea is this. Suppose that we are trying to prove DHJ(k) with density . We begin by choosing some parameters. First, we choose
. We begin by choosing some parameters. First, we choose  so large that DHJ(k-1) is true with density
so large that DHJ(k-1) is true with density 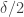 . That is, we assume as an inductive hypothesis that every subset of
. That is, we assume as an inductive hypothesis that every subset of ![{}[k-1]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk-1%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) of density at least
of density at least 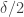 contains a combinatorial line.
contains a combinatorial line.
Next, we choose a very rapidly increasing sequence of integers (though in the context of some proofs of this kind the rate of increase is not too bad — this proof should result in a primitive recursive bound for DHJ(k), one level beyond a tower, just like Shelah’s)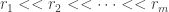 . (Jozsef called them
. (Jozsef called them 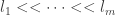 but on my screen an
but on my screen an  is just a vertical line so I’ve changed the notation.)
is just a vertical line so I’ve changed the notation.)
We shall repeatedly apply the following averaging argument: if are integers between 0 and 1, and the average of the
are integers between 0 and 1, and the average of the 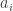 is
is  , then at least
, then at least 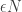 of the
of the 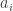 are at least
are at least  The proof is trivial (by contradiction).
The proof is trivial (by contradiction).
Now let and think of
and think of ![{}[k]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as
as ![{}[k]^{r_1}\times\dots\times[k]^{r_m}.](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Br_1%7D%5Ctimes%5Cdots%5Ctimes%5Bk%5D%5E%7Br_m%7D.&bg=ffffff&fg=333333&s=0&c=20201002) Let
Let  be a subset of
be a subset of ![{}[k]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  For each
For each ![y\in[k]^{r_m},](https://s0.wp.com/latex.php?latex=y%5Cin%5Bk%5D%5E%7Br_m%7D%2C&bg=ffffff&fg=333333&s=0&c=20201002) let
let ![\mathcal{A}_y=\{x\in[k]^{n-r_m}:(x,y)\in\mathcal{A}\}.](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BA%7D_y%3D%5C%7Bx%5Cin%5Bk%5D%5E%7Bn-r_m%7D%3A%28x%2Cy%29%5Cin%5Cmathcal%7BA%7D%5C%7D.&bg=ffffff&fg=333333&s=0&c=20201002) Then the average density of
Then the average density of  over
over ![y\in[k]^{r_m}](https://s0.wp.com/latex.php?latex=y%5Cin%5Bk%5D%5E%7Br_m%7D&bg=ffffff&fg=333333&s=0&c=20201002) is
is  , so the density of
, so the density of  such that
such that  has density at least
has density at least 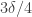 is at least
is at least 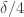 .
.
Let be the set of all
be the set of all ![y\in[k]^{r_m}](https://s0.wp.com/latex.php?latex=y%5Cin%5Bk%5D%5E%7Br_m%7D&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that  has density at least
has density at least 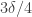 . By the pigeonhole principle, we can find a subset
. By the pigeonhole principle, we can find a subset  of
of  of density at least
of density at least  such that
such that  is the same for every
is the same for every  .
.
Let us define a ”binary subspace” to be a set where you fix some of the coordinates and allow the remaining ones to take the values k-1 and k. If t is small enough, and if you choose a random binary subspace of![{}[k]^{r_m}](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Br_m%7D&bg=ffffff&fg=333333&s=0&c=20201002) by randomly choosing t coordinates to be the variable ones and randomly fixing the others, and if you then choose a random point in one of these random binary subspaces, the result will be very close to the uniform distribution on
by randomly choosing t coordinates to be the variable ones and randomly fixing the others, and if you then choose a random point in one of these random binary subspaces, the result will be very close to the uniform distribution on ![{}[k]^{r_m}](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Br_m%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Therefore, by an easy averaging argument we can find a binary subspace inside which the density of
. Therefore, by an easy averaging argument we can find a binary subspace inside which the density of  is at least
is at least 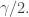 (Note that for this to work we need
(Note that for this to work we need  to be large enough in terms of
to be large enough in terms of  and
and  .) And then by Sperner’s theorem we can find two points in the binary subspace that form a combinatorial line (in the
.) And then by Sperner’s theorem we can find two points in the binary subspace that form a combinatorial line (in the ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) sense but with
sense but with 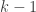 and
and  replacing 1 and 2, or 0 and 1 if you prefer).
replacing 1 and 2, or 0 and 1 if you prefer).
We can extend this binary combinatorial line to a full combinatorial line in![{}[k]^{m_r}](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Bm_r%7D&bg=ffffff&fg=333333&s=0&c=20201002) , by allowing the wildcards to take the values
, by allowing the wildcards to take the values  as well. The result is a …
as well. The result is a …
OK, this is the first point at which I’ve got stuck, though I think Jozsef may have dealt with the difficulty I am facing. Time to end this comment and start a new one.
March 11, 2009 at 1:06 pm |
1014. Shelah
The problem with what I was doing just above is this. I’ve just defined a line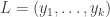 in
in ![{}[k]^{m_r}](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Bm_r%7D&bg=ffffff&fg=333333&s=0&c=20201002) , and I know that the sets
, and I know that the sets 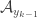 and
and  are the same. However, I don’t know anything about
are the same. However, I don’t know anything about 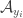 for
for  and it would be a serious problem if e.g. they turned out to be empty.
and it would be a serious problem if e.g. they turned out to be empty.
However, I’ve ignored Jozsef’s step 1, which is perhaps his main new idea. He begins by using DHJ(k-1) to pass to a subspace where has density close to
has density close to  for all sequences
for all sequences 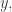 provided only that they do not have any (variable) coordinate equal to
provided only that they do not have any (variable) coordinate equal to  . (This can be done by an averaging argument similar to the one I used above to get dense binary subspaces — this time one wants dense (k-1)-ary subspaces.)
. (This can be done by an averaging argument similar to the one I used above to get dense binary subspaces — this time one wants dense (k-1)-ary subspaces.)
But now I’ve reached the point where I don’t understand Jozsef’s argument. How do I know that it is not the case that is empty whenever one of the variable coordinates of
is empty whenever one of the variable coordinates of  is equal to k? I don’t see it at the moment, so I think I’d better wait for Jozsef to wake up.
is equal to k? I don’t see it at the moment, so I think I’d better wait for Jozsef to wake up.
March 11, 2009 at 5:47 pm
1014.1 Dear Tim, I don’t think that we need that is dense if one of the variable coordinates is equal to k. This is actually a crucial observation, that’s why we need the fliptop property. At the last step, when only
is dense if one of the variable coordinates is equal to k. This is actually a crucial observation, that’s why we need the fliptop property. At the last step, when only 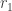 remains, one word of
remains, one word of 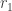 spans a dense subset of the
spans a dense subset of the 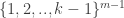 part of the subspace. By induction there is a line, and by the fliptop property there is an extension to k. Note that the fliptop property was defined by considering running coordinates k as well, however it wasn’t sensitive for density in any ways.
part of the subspace. By induction there is a line, and by the fliptop property there is an extension to k. Note that the fliptop property was defined by considering running coordinates k as well, however it wasn’t sensitive for density in any ways.
March 11, 2009 at 7:15 pm
1014.2 I’m still mystified. In Step 1, let’s choose a subspace such that for every sequence that avoids running coordinate
that avoids running coordinate  , there is a set of density almost
, there is a set of density almost  of
of  such that
such that  . Now we go to Step 2. Nothing we’ve done so far stops
. Now we go to Step 2. Nothing we’ve done so far stops  being empty for every
being empty for every  that does involve
that does involve  . So we choose our Sperner pair and have two points
. So we choose our Sperner pair and have two points  and
and 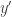 (where
(where 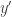 is obtained from
is obtained from  by changing some of the
by changing some of the 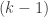 s to
s to  s). How can that help? Indeed, it seems that
s). How can that help? Indeed, it seems that  could be empty for every point in the combinatorial line you select.
could be empty for every point in the combinatorial line you select.
March 11, 2009 at 7:59 pm
Tim – I have to go to the University now, where I will rethink your question again, but I think that the answer is that it is not possible that you switch a running coordinate to k from k-1 and the density drops because the two points are neighbours. I will get back to you soon.
March 11, 2009 at 8:02 pm
Jozsef, that gives me time to be more precise about my question. See comment 1016 below.
March 11, 2009 at 7:21 pm |
[…] northern Israel. Coming back I saw two new posts on Tim Gowers’s blog entitled “Problem solved probably” and “polymath1 and open collaborative mathematics.” It appears […]
March 11, 2009 at 7:39 pm |
1015. A bit off-topic
“If this were a conventional way of producing mathematics, then it would be premature to make such an announcement — one would wait until the proof was completely written up with every single i dotted and every t crossed — ”
hmmm, maybe we should regard it premature also in this new mode. What do the rules say?
“but this is blog maths and we’re free to make up conventions as we go along.
So I hereby state that I am basically sure that the problem is solved”
Congratulations! I must admit that even if a full k=3 proof will take 200 more comments and several more weeks the success of the project exceeded my expectations.
“(though not in the way originally envisaged).”
Actually, this is a lovely aspect and a sign of success of the open collaboration idea, isn’t it?
March 11, 2009 at 7:49 pm
1015.1 Gil, I feel slightly awkward about it, and won’t feel entirely happy until it’s written up in the conventional way. But if one regards a write-up as having a tree structure, then it’s all there on the wiki down to the small sticks, and only a few leaves are missing. Somehow there don’t seem to be any points where one says “I don’t quite see it but I’m sure it works.” It’s more like “I do see it but it’s slightly tedious to write out in full.” Despite that, I wouldn’t have written what I wrote if it had not been for the fact that other participants seem to share my confidence. But for now I will keep the “(probably)”.
March 11, 2009 at 8:12 pm |
1016 Shelah
Jozsef, I’m still trying to follow your argument in 1011. Let me try to be completely precise about where it seems to me to go wrong. Of course, it could be me who is going wrong.
Consider the following example. I take a random subset S of![{}[k]^{r_m}](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Br_m%7D&bg=ffffff&fg=333333&s=0&c=20201002) and then take the set
and then take the set  of all sequences in
of all sequences in ![{}[k]^{r_1+\dots+r_m}](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Br_1%2B%5Cdots%2Br_m%7D&bg=ffffff&fg=333333&s=0&c=20201002) such that the final part lies in S. This set has density 1/2. Now I apply your step 1, and it happens that the
such that the final part lies in S. This set has density 1/2. Now I apply your step 1, and it happens that the 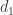 -dimensional subspace I choose has the following property: every point with all running coordinates less than k belong to S, and all other points belong to the complement of S. (With high probability such a subspace exists, and no steps have been taken to avoid it.)
-dimensional subspace I choose has the following property: every point with all running coordinates less than k belong to S, and all other points belong to the complement of S. (With high probability such a subspace exists, and no steps have been taken to avoid it.)
Then the pigeohole argument gives you that all the points with running coordinates less than k can be joined to anything you like in![{}[k]^{r_1+\dots+r_{m-1}}.](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Br_1%2B%5Cdots%2Br_%7Bm-1%7D%7D.&bg=ffffff&fg=333333&s=0&c=20201002) However, if you take any line given by the application of Sperner, then both its top two points must involve a k and give the empty set. Therefore, the whole line gives the empty set (meaning that if your mth part belongs to the line then you don’t belong to
However, if you take any line given by the application of Sperner, then both its top two points must involve a k and give the empty set. Therefore, the whole line gives the empty set (meaning that if your mth part belongs to the line then you don’t belong to  ). So at the second stage of the iteration I don’t see how you can do Step 1 (because of the “with any
). So at the second stage of the iteration I don’t see how you can do Step 1 (because of the “with any 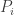 ” requirement).
” requirement).
March 11, 2009 at 8:52 pm
Tim, what you wrote is perfectly right with the exeption that in step one I never consider running coordinates larger than k-1. (with my old notation “larger than k-2”) So, in your example fliptop means that the neighbours given by the last (m-th) k, k-1 pair are simultaneously not in S. I’m still not sure that the argument works, but I don’t see any serious problem yet.
March 11, 2009 at 10:40 pm
I have office hours now, so I will beging to write up the argument and if I won’t have too many students to show up then I will post the sketch in an hour or so.
March 11, 2009 at 10:49 pm
Just to try to be more explicit still, let’s imagine that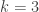 and
and 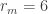 . Suppose that all sequences of six 0s and 1s are the tail of every preceding sequence, and that the two points
. Suppose that all sequences of six 0s and 1s are the tail of every preceding sequence, and that the two points 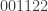 and
and 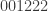 are the tails of precisely the same set of sequences, so you choose as your line the line
are the tails of precisely the same set of sequences, so you choose as your line the line 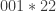 . It seems to me that there is no reason for any point in that line to be the tail of any previous sequence.
. It seems to me that there is no reason for any point in that line to be the tail of any previous sequence.
A separate question: is the aim to construct in each![{}[k]^{r_i}](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Br_i%7D&bg=ffffff&fg=333333&s=0&c=20201002) a line
a line 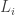 in such a way that the product of the lines is fliptop (that is, insensitive to changing 1s to 2s when k=3), and
in such a way that the product of the lines is fliptop (that is, insensitive to changing 1s to 2s when k=3), and  is dense in that product? My difficulty is that I don’t see the relevance of a statement about
is dense in that product? My difficulty is that I don’t see the relevance of a statement about  when the line
when the line 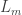 might have 2 as one of its fixed coordinates.
might have 2 as one of its fixed coordinates.
March 11, 2009 at 11:42 pm
I see now. One should be more careful with the selection of the fliptop lines. I still think that it is duable, but it seems that we have to consider more subspaces. I don’t have much time, but I will think about it.
March 12, 2009 at 1:36 am
I should stress here that I definitely think this is worth attempting. Even if it turns out not to work 100% straightforwardly, the following question exists and is clearly an interesting one. You have a set![\mathcal{A}\subset[k]^n](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BA%7D%5Csubset%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  . How large a subspace
. How large a subspace  can you find such that
can you find such that  has density at least
has density at least 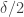 in the subspace, and membership of
in the subspace, and membership of  in the subspace does not change if you flip a
in the subspace does not change if you flip a  to a
to a 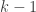 ? I do not see any philosophical reason for that being significantly harder than Sperner plus induction, though such a reason might emerge I suppose.
? I do not see any philosophical reason for that being significantly harder than Sperner plus induction, though such a reason might emerge I suppose.
March 11, 2009 at 10:43 pm |
1017. Varnavides-DHJ(k).
In 1010.1, Tim wrote “What I’m not doing is fixing almost all coordinates and taking M small wildcard sets, or something like that. Instead, I’m randomly choosing the sizes of the M wildcard sets (which I allow to add up to 1, so there are in fact no fixed coordinates at all) and then uniformly at random choosing a line from the resulting subspace.”
Tim, I think I get it now; as usual I was misinterpreting the word “subspace” and was thinking you were doing what you said you weren’t doing 🙂 I agree now that the sketch looks relatively solid. Let me see if I can fill in some “leaves”, as you say.
March 11, 2009 at 10:50 pm
Great — I’m off for a couple of hours and won’t be able to do much more today, if anything.
March 11, 2009 at 11:40 pm |
1018. Is Equal-Slices of Equal-Slices equal to Equal-Slices?
Suppose we want to try to prove Varnavides-DHJ(3); as in #1010, let’s try to show that if![A \subseteq [3]^n](https://s0.wp.com/latex.php?latex=A+%5Csubseteq+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) has equal-slices density
has equal-slices density  , and we choose a random combinatorial line by drawing its template from equal-slices on
, and we choose a random combinatorial line by drawing its template from equal-slices on ![([3] \cup \{\ast\})^n](https://s0.wp.com/latex.php?latex=%28%5B3%5D+%5Ccup+%5C%7B%5Cast%5C%7D%29%5En&bg=ffffff&fg=333333&s=0&c=20201002) , then with probability at least $\eps(\delta) > 0$ the whole line is in
, then with probability at least $\eps(\delta) > 0$ the whole line is in  (assuming
(assuming  is sufficiently large).
is sufficiently large).
Tim’s strategy for this involves, among other things, picking a combinatorial subspace of dimension with no free coordinates, according to some distribution
with no free coordinates, according to some distribution  ; then drawing a point from that subspace (thought of as
; then drawing a point from that subspace (thought of as ![[k]^M](https://s0.wp.com/latex.php?latex=%5Bk%5D%5EM&bg=ffffff&fg=333333&s=0&c=20201002) ) from some other distribution,
) from some other distribution,  .
.
It would be particularly helpful if the overall distribution is equal-slices on![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . Also helpful would be if $lambda \nu$ is a relatively “natural” distribution; also
. Also helpful would be if $lambda \nu$ is a relatively “natural” distribution; also  should have full support. (It’s also not essential that
should have full support. (It’s also not essential that  generates subspaces with exactly
generates subspaces with exactly  dimensions, but never mind that for now.)
dimensions, but never mind that for now.)
Here is perhaps the simplest possible proposal: Let be equal-slices on
be equal-slices on ![[M]^n](https://s0.wp.com/latex.php?latex=%5BM%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , and let
, and let  be equal-slices on
be equal-slices on ![[k]^M](https://s0.wp.com/latex.php?latex=%5Bk%5D%5EM&bg=ffffff&fg=333333&s=0&c=20201002) .
.
The question is: might combining these two actually give equal-slices on![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) precisely?! I will submit some evidence in a reply to this post.
precisely?! I will submit some evidence in a reply to this post.
March 11, 2009 at 11:53 pm
1018.1. Evidence.
Well, my first piece of “evidence” is that in these simple probability matters, sometimes things just turn out nicely 🙂
Here is slightly more rigorous evidence… (I would try to simply give a proof, but I haven’t the time to work on it this evening, so I thought I’d quickly throw it out there.)
For my poor brain, let me fix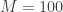 and fix
and fix  ,
, ![[k] = \{R, G, B\}](https://s0.wp.com/latex.php?latex=%5Bk%5D+%3D+%5C%7BR%2C+G%2C+B%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) (red, green, blue).
(red, green, blue).
We can think of the “outer” equal slices as choosing uniformly, then drawing from the resulting product distribution on
uniformly, then drawing from the resulting product distribution on  . We can think of the “inner” equal slices as choosing
. We can think of the “inner” equal slices as choosing  uniformly, then changing each
uniformly, then changing each  to
to  with probability
with probability 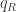 ,
,  with probability
with probability  , and
, and  with probability
with probability  .
.
If you think about it a minute, you see that the final is string is drawn from a randomly chosen product distribution on
on 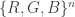 . That’s good! If we could just show that that
. That’s good! If we could just show that that  is indeed distributed as “uniform on the
is indeed distributed as “uniform on the 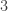 -simplex” we’d be done.
-simplex” we’d be done.
So how is it chosen? Well, we think of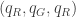 as being chosen first. Then, think of
as being chosen first. Then, think of  as being independent Exponential
as being independent Exponential ‘s. (Of course, this does not give
‘s. (Of course, this does not give 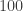 numbers adding to
numbers adding to  , but we use these numbers as proportions, rather than probabilities.)
, but we use these numbers as proportions, rather than probabilities.)
Then gets generated by putting each
gets generated by putting each  into the “R” bucket with probability
into the “R” bucket with probability 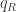 , into the “G” bucket with probability
, into the “G” bucket with probability  , and into the “B” bucket with probability
, and into the “B” bucket with probability  . Finally, you add up all the Exponentials in each bucket, and
. Finally, you add up all the Exponentials in each bucket, and  is proportional to these totals.
is proportional to these totals.
So what is the distribution on the three bucket totals? It shouldn’t be too hard to really work it out, but let me write heuristically here. Once is fixed, we expect about
is fixed, we expect about  of the independent Exponentials to go into the R bucket, and similarly for G and B. (Even moreso do we expect this if
of the independent Exponentials to go into the R bucket, and similarly for G and B. (Even moreso do we expect this if 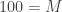 is huge.) And thinking of
is huge.) And thinking of  as still huge, we’re adding up a huge number of i.i.d. Exponentials, so the CLT will imply that the sum will almost surely be very close to
as still huge, we’re adding up a huge number of i.i.d. Exponentials, so the CLT will imply that the sum will almost surely be very close to  . Similarly, the sum in the G bucket will almost surely be very close to
. Similarly, the sum in the G bucket will almost surely be very close to 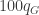 , and again for B.
, and again for B.
But in this case, the proportions will be really close to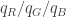 I.e., almost surely it seems
I.e., almost surely it seems  will be very nearly
will be very nearly  . But
. But  is distributed uniformly on the
is distributed uniformly on the 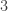 -simplex, as desired!
-simplex, as desired!
March 12, 2009 at 6:00 am
1018.2. I don’t think it’s exactly correct, but I still hope some variant is…
March 12, 2009 at 6:29 am |
1019. ENDS of ENDS = ENDS.
I think I’ve got it now. Define a distribution on -partitions of
-partitions of  called
called  -Equal Non-Degenerate Slices (
-Equal Non-Degenerate Slices ( -ENDS): To get it, take
-ENDS): To get it, take  dots in a line, consider the
dots in a line, consider the 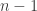 gaps between them, and place
gaps between them, and place 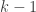 bars in these gaps, uniformly from among the
bars in these gaps, uniformly from among the 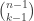 many possibilities (i.e., “without replacement”). Then the intra-bar blocks of dots correspond to
many possibilities (i.e., “without replacement”). Then the intra-bar blocks of dots correspond to  positive integers
positive integers  which add up to
which add up to  . Associating block
. Associating block 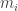 to character
to character ![i \in [k]](https://s0.wp.com/latex.php?latex=i+%5Cin+%5Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) , we get a distribution on “Non-Degenerate” slices (each character appears at least once). We can extend this to a distribution on
, we get a distribution on “Non-Degenerate” slices (each character appears at least once). We can extend this to a distribution on ![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as usual, just by randomly permuting the string.
as usual, just by randomly permuting the string.
This is actually a kind of convenient variant on equal-slices, because when you’re using equal-slices to pick combinatorial lines, it’s a bit annoying to have to worry about the unlikely case of getting wildcards.
wildcards.
Anyway, I think it’s now easy to see that if you do -ENDS, and then you do
-ENDS, and then you do  -ENDS on that (as described in #1018), then you just get
-ENDS on that (as described in #1018), then you just get  -ENDS, exactly. Because all that’s really happening is that you’re picking
-ENDS, exactly. Because all that’s really happening is that you’re picking  bar-spots uniformly, and then you’re picking
bar-spots uniformly, and then you’re picking 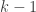 of those
of those  bars to be the “final bars”, uniformly. So that’s just the same as picking
bars to be the “final bars”, uniformly. So that’s just the same as picking 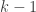 bars uniformly to start with.
bars uniformly to start with.
I think. Once again, it’s late.
March 12, 2009 at 6:30 am |
1019.1. “Formula does not parse” above is “(n-1 choose k-1)”. [Fixed]
March 12, 2009 at 7:13 am |
1019.2. Some googling reveals this paper (among others) which discusses in its Section 2 the proper nomenclature for this stuff, as well as related probability distributions.
k-ENDS -> “random composition into k parts”; the consequent distribution on strings is “random ordered partition into k parts”.
dots -> “balls”
bars -> “walls”
March 12, 2009 at 10:21 am |
1020 DHJ(k)
Ryan, that all looks like good news — it would be very nice if we could get the technicalities to run smoothly so that they don’t obscure the main ideas, and your comments above give me hope that it will be possible.
I’ve got 25 minutes to spare so I’m going to try to explain why I think that DHJ(k) is basically done too. I’m assuming for this that the proof that a line-free set correlates locally with a set of complexity k-2 is going to work out now, which seems likely, as it’s been sketched down to a pretty fine level of detail and you’ve scrutinized the parts that looked most likely to go wrong if anything was going to.
In order to explain how I think the rest of the proof will go, what I need to do is explain the difference between the proof for DHJ(k) and the proof of DHJ(3) outlined on the wiki here.
Analogue of Step 1. We need to replace 1-sets by what I call -sets. These are sets $\latex \mathcal{B}$ such that
-sets. These are sets $\latex \mathcal{B}$ such that  if and only if
if and only if 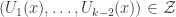 for some suitable collection
for some suitable collection  of disjoint (k-2)-tuples of sets and
of disjoint (k-2)-tuples of sets and  stands for the set of places where x takes the value i. To save writing, I’ll call these simple sets. So the next obvious aim is to prove that a simple set can be approximately partitioned into subspaces. Once that’s done, I think it is fair to say that the rest of the proof is exactly as in the k=3 case.
stands for the set of places where x takes the value i. To save writing, I’ll call these simple sets. So the next obvious aim is to prove that a simple set can be approximately partitioned into subspaces. Once that’s done, I think it is fair to say that the rest of the proof is exactly as in the k=3 case.
The one other thing that needs to be changed in Step 1 is that the appeal to the multidimensional Sperner theorem has to be replaced by an appeal to multidimensional DHJ(k-1), a proof of which is sketched on the wiki here. Otherwise, the changes are trivial: 3 becomes k, and![\mathcal{U}\otimes[2]^n](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BU%7D%5Cotimes%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) becomes our simple set
becomes our simple set  (I admit that I haven’t been through Step 1 line by line checking what I’m saying — that would use up more than my 25 minutes.)
(I admit that I haven’t been through Step 1 line by line checking what I’m saying — that would use up more than my 25 minutes.)
I’ve looked through Step 2 and I think all the changes needed are of the trivial variety (changing 3s to ks and that kind of thing). It might be nice at some point to write an abstract version of this argument, since what we’re using seems to be very general — that we can partition![{}[k]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into subspaces very conveniently, that the structure of good sets is preserved when we do so, that dense good sets contain lots of subspaces — that kind of thing.
into subspaces very conveniently, that the structure of good sets is preserved when we do so, that dense good sets contain lots of subspaces — that kind of thing.
Step 3. And now we do the same trick as we did in DHJ(3) except that we have to apply Step 2 k-1 times instead of twice. The end result is that a set of complexity k-2 can be almost partitioned into subspaces, and that’s what we’re looking for.
March 12, 2009 at 4:46 pm |
1021. Varnavides.
Hi Tim, I think the -ary proof that line-free sets correlate with simple sets is now done to about 100% satisfaction in my mind. I’ll try to wikify some details later, but to illustrate the simplicity with which it’s working out, here is a complete proof of Varnavides:
-ary proof that line-free sets correlate with simple sets is now done to about 100% satisfaction in my mind. I’ll try to wikify some details later, but to illustrate the simplicity with which it’s working out, here is a complete proof of Varnavides:
Assume we have DHJ(k).
Technicality: I want to say that a combinatorial line is (also) “degenerate” if the fixed coordinates do not use each character from![[k]](https://s0.wp.com/latex.php?latex=%5Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) at least once. Deducing DHJ(k) with this very slightly stronger notion of degeneracy is trivial.
at least once. Deducing DHJ(k) with this very slightly stronger notion of degeneracy is trivial.
Proof of Varnavides: Assume![A \subseteq [k]^n](https://s0.wp.com/latex.php?latex=A+%5Csubseteq+%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) has density
has density  under the “uniform
under the “uniform  -composition” distribution (i.e., equal-slices conditioned on the slice having at least one of each character). Let
-composition” distribution (i.e., equal-slices conditioned on the slice having at least one of each character). Let  denote the least integer such that DHJ(k) guarantees the existence of a nondegenerate line in any subset of
denote the least integer such that DHJ(k) guarantees the existence of a nondegenerate line in any subset of ![[k]^M](https://s0.wp.com/latex.php?latex=%5Bk%5D%5EM&bg=ffffff&fg=333333&s=0&c=20201002) with uniform
with uniform  -composition density at least
-composition density at least 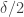 .
.
Think of choosing![x \in [k]^n](https://s0.wp.com/latex.php?latex=x+%5Cin+%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as first drawing a random
as first drawing a random  -dimensional subspace
-dimensional subspace  from the uniform
from the uniform  -composition distribution, and then drawing
-composition distribution, and then drawing  randomly from
randomly from ![V \cong [k]^M](https://s0.wp.com/latex.php?latex=V+%5Ccong+%5Bk%5D%5EM&bg=ffffff&fg=333333&s=0&c=20201002) according to the uniform
according to the uniform  -composition distribution. Since
-composition distribution. Since 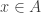 with probability at least
with probability at least  , we know that with probability at least
, we know that with probability at least 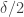 over the choice of
over the choice of  , the
, the  -uniform composition density of
-uniform composition density of  is at least
is at least 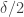 . Call such
. Call such  ‘s “good”. By DHJ(k) we know that for any good
‘s “good”. By DHJ(k) we know that for any good  , there is a (nondegenerate) line inside
, there is a (nondegenerate) line inside  .
.
Now suppose we choose a random line in $[k]^n$ according to the uniform
in $[k]^n$ according to the uniform  -composition distribution. We claim that it is entirely within
-composition distribution. We claim that it is entirely within  with probability at least
with probability at least ![\delta/[2 M^{k/2} (k+1)^M]](https://s0.wp.com/latex.php?latex=%5Cdelta%2F%5B2+M%5E%7Bk%2F2%7D+%28k%2B1%29%5EM%5D&bg=ffffff&fg=333333&s=0&c=20201002) . To see this, again think of
. To see this, again think of  as being drawn by first choosing
as being drawn by first choosing  , and then drawing a random line in
, and then drawing a random line in  according to uniform
according to uniform  -composition. With probability at least
-composition. With probability at least 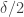
 is good, in which case there is at least one nondegenerate line in
is good, in which case there is at least one nondegenerate line in 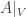 . The probability
. The probability  is picked to be it is at least
is picked to be it is at least ![1/[M^{k/2} (k+1)^M]](https://s0.wp.com/latex.php?latex=1%2F%5BM%5E%7Bk%2F2%7D+%28k%2B1%29%5EM%5D&bg=ffffff&fg=333333&s=0&c=20201002) , since the least probability under uniform
, since the least probability under uniform  -composition of
-composition of  is at least this quantity (er, or something like that).
is at least this quantity (er, or something like that).
March 12, 2009 at 4:51 pm
1021.1. That was me again, not logged in. I wanted to add that we can complete the whole “line-free implies correlation with simple set” proof exclusively in this uniform -composition measure rather easily, I think. The only thing to really check is that if you choose a
-composition measure rather easily, I think. The only thing to really check is that if you choose a  fraction of the coordinates
fraction of the coordinates  randomly, do uniform-
randomly, do uniform- -composition on
-composition on  , and then independently do uniform-
, and then independently do uniform- -composition OR uniform-
-composition OR uniform-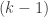 -composition on
-composition on  , then the overall probability distribution has total variation distance at most
, then the overall probability distribution has total variation distance at most  from the usual global uniform
from the usual global uniform  -composition distribution. Which is, I’m pretty sure, true.
-composition distribution. Which is, I’m pretty sure, true.
March 12, 2009 at 10:58 pm |
1022. Shelah
While I wait for reaction about how we should go ahead with writing things up (see this comment), I want to continue thinking a bit about whether the proof we have could be Shelah-ized. Terry said in a comment some time ago that he is a big fan of translating things back and forth between combinatorial and ergodic languages. I (in common with just about every mathematician) am a big fan of “completing the square,” by which I mean completing puzzles of the form “A is to B as C is to ??” For example, “corner is to combinatorial line as large grid is to ??” the answer to which turned out, not completely expectedly, to be “![{}[2]^k](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5Ek&bg=ffffff&fg=333333&s=0&c=20201002) for some large
for some large  “. And that was just one part of a bigger such puzzle: “the Ajtai-Szemerédi proof of the corners theorem is to the triviality that a dense subset of
“. And that was just one part of a bigger such puzzle: “the Ajtai-Szemerédi proof of the corners theorem is to the triviality that a dense subset of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) contains two distinct points as ?? is to the proof of Sperner’s theorem.”
contains two distinct points as ?? is to the proof of Sperner’s theorem.”
So here I would like to think about the puzzle, “The colour-focusing proof of the Hales-Jewett theorem is to Shelah’s proof of the Hales-Jewett theorem as the proof we now have of DHJ(k) is to ??”
The reason I am drawn to this is that I once lectured both proofs of the Hales-Jewett theorem and came to a very clear understanding of the relationship between them, which I’ll have to reconstruct, but I remember it as being natural enough that it will be easy to reconstruct. When I have a spare moment, I’ll write something about this on the wiki, but for now let me just say that Shelah’s basic idea can be interpreted as follows: whereas the old proof of HJ(k) used HJ(k-1) to reduce the problem to the almost trivial HJ(2), Shelah’s new proof used HJ(2) to reduce the problem to HJ(k-1). As I say, I’ll justify that at some point, but here I just want to take that thought and have a stab at applying it to DHJ(k) instead.
Of course, I’m not sure that it’s possible to do so, but just having the goal in mind does, I think, suggest some questions. For instance, here’s a place in the proof where DHJ(k-1) comes into the proof of DHJ(k). One first passes to a subspace, which we’ll notate as though it is the whole space, such that the density of is almost
is almost  and the density of
and the density of  in
in ![{}[k-1]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk-1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is still positive. Writing
is still positive. Writing  for
for ![\mathcal{A}\cap[k-1]^n](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BA%7D%5Ccap%5Bk-1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , we use
, we use  to construct a dense set
to construct a dense set  of complexity
of complexity 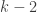 that is disjoint from
that is disjoint from  . It doesn’t matter too much what all this means: the main point is that once we have a set of complexity
. It doesn’t matter too much what all this means: the main point is that once we have a set of complexity 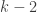 we are able to hit it with DHJ(k-1).
we are able to hit it with DHJ(k-1).
So a natural question, if we are trying to Shelah-ize, is whether we can construct some set of complexity 1 (which means it’s hittable with DHJ(2), aka Sperner) and thereby, somehow, create a fliptop subspace inside which is dense. Recall that a fliptop subspace is one inside which if you change any coordinate with value k-1 to a k, then you don’t change whether the point x belongs to the set
is dense. Recall that a fliptop subspace is one inside which if you change any coordinate with value k-1 to a k, then you don’t change whether the point x belongs to the set  . So if your set is dense in such a subspace (or rather, dense in the
. So if your set is dense in such a subspace (or rather, dense in the ![{}[k-1]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk-1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) part of the subspace) then you can hit it with DHJ(k-1) and finish off the proof immediately. Because DHJ(k-1) is used just as the inductive step and not as some part of an iterative procedure for getting to the inductive step, a proof of this kind should be far better quantitatively.
part of the subspace) then you can hit it with DHJ(k-1) and finish off the proof immediately. Because DHJ(k-1) is used just as the inductive step and not as some part of an iterative procedure for getting to the inductive step, a proof of this kind should be far better quantitatively.
In my next comment I shall think about the following question: are there any complexity-1 sets that can be derived from a set ? For now, I don’t care whether we can actually use them.
? For now, I don’t care whether we can actually use them.
March 12, 2009 at 11:40 pm |
1023. Shelah.
Continuing on from 1022, a completely simple-minded idea would be to pass to a subspace such that is dense in
is dense in ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) and still had density almost
and still had density almost  . (I’m just going to assume that that’s fine.) If we write
. (I’m just going to assume that that’s fine.) If we write  for
for ![\mathcal{A}\cap[2]^n,](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BA%7D%5Ccap%5B2%5D%5En%2C&bg=ffffff&fg=333333&s=0&c=20201002) then what set
then what set  can we construct from
can we construct from  ?
?
In the other argument, we looked at all sequences such that, for every
such that, for every  , if you change all
, if you change all  s to
s to  s then you get a sequence in
s then you get a sequence in  . Here, it is clear, we are going to have to do a much more radical collapsing of the sequence. One possibility, which may be nonsense, would be to convert all non-1 coordinates into 2s. In other words, we let
. Here, it is clear, we are going to have to do a much more radical collapsing of the sequence. One possibility, which may be nonsense, would be to convert all non-1 coordinates into 2s. In other words, we let  be the set of all x such that the 1-set of x is equal to the 1-set of some sequence in
be the set of all x such that the 1-set of x is equal to the 1-set of some sequence in  .
.
In the other argument, we then argued that is disjoint from
is disjoint from  if it does not contain a combinatorial line. What happens here? Well, bearing in mind that (using the Shelah proof as a guide) we are not trying to go straight for a combinatorial line, but rather for a fliptop subspace, we should perhaps assume as our hypothesis that
if it does not contain a combinatorial line. What happens here? Well, bearing in mind that (using the Shelah proof as a guide) we are not trying to go straight for a combinatorial line, but rather for a fliptop subspace, we should perhaps assume as our hypothesis that  does not contain such a subspace.
does not contain such a subspace.
Turning that round, we would want to prove that if intersects
intersects  then it contains a fliptop subspace. (This doesn’t sound true, but let’s see what’s wrong with it first.)
then it contains a fliptop subspace. (This doesn’t sound true, but let’s see what’s wrong with it first.)
For to intersect
to intersect  we need a sequence
we need a sequence  such that if you convert all its non-1s into 2s, then you get a sequence of 1s and 2s that also belongs to
such that if you convert all its non-1s into 2s, then you get a sequence of 1s and 2s that also belongs to  . Why should that be interesting? I don’t know.
. Why should that be interesting? I don’t know.
But suppose instead that we managed to find quite a large subspace S of such points. Then if x belonged to and had a variable coordinate equal to 2, we would … no, I don’t see where this goes.
and had a variable coordinate equal to 2, we would … no, I don’t see where this goes.
Part of the problem is that I seem to be going for the fliptop subspace to be contained in , whereas what I should be aiming for is merely that
, whereas what I should be aiming for is merely that  is dense in the fliptop subspace (which actually seems to be a flipbottom subspace).
is dense in the fliptop subspace (which actually seems to be a flipbottom subspace).
I’m going to stop this comment here — I hope I’ve demonstrated the flavour of the argument that I think might conceivably exist.
March 12, 2009 at 11:41 pm
1023.1 I should have added the remark that the set has complexity 1.
has complexity 1.
March 12, 2009 at 11:45 pm |
1024. Austin’s proof
I’ve written down an informal (and sketchy) combinatorial translation of the k=3 case of Austin’s argument at
http://michaelnielsen.org/polymath1/index.php?title=Austin%27s_proof
It’s actually very much in the style of the proof of the triangle-removal lemma, especially if one takes an analytic perspective rather than a combinatorial one and talks about decomposing functions rather than regularising graphs. In particular, it’s best to avoid thinking in the classical language of vertices and take a more “point-less” approach in the spirit of probability theory or ergodic theory (or operator algebras, for that matter), thus for instance one should think about averages of products of functions rather than counting triangles etc. One reason for shifting one’s thinking this way is that it allows one to think about strong stationarity in a civilised way, whereas this concept becomes really difficult to work with if one insists on holding on to concrete vertices and edges. (In classical combinatorial language, being strongly stationary is like saying that a certain graph is a “statistically equivalent” to the subgraph formed by restricting of its vertex set from a big space such as [3]^n to a randomly chosen subspace; but defining what “statistically equivalent” means precisely is sort of a pain unless one decides to give up on vertices altogether.)
It’s also clear that this proof will end up being messier than the pure density-increment proof (though cleaner than a finitisation of the Furstenberg-Katznelson proof), and give worse bounds, in large part because one has to apply Graham-Rothschild (with parameters given in turn from a Szemeredi-type regularity lemma!) to get the initial strong stationarity properties. It looks possible to use density increment arguments as a substitute for Graham-Rothschild, but this is still going to have quite lousy bounds.
March 12, 2009 at 11:55 pm
1023.1 Information-theoretic approach
Hmm, it occurs to me now that the information-theoretic approach to the regularity lemma that I laid out in
http://front.math.ucdavis.edu/math.CO/0504472
(where I “regularise” random variables using Shannon entropy) is actually well suited to this problem, and may lead to a relatively slick (albeit alien-looking) proof. What I may do at some point is begin by showing how by playing around with conditional Shannon entropies of various random variables, one can establish the triangle removal lemma, and I believe that this proof may extend relatively painlessly to the case under consideration. More on this later…
March 12, 2009 at 11:47 pm |
1025. Always the uniform-ordered-partition distribution.
Following up on my comment #1006, I feel somewhat sure that we can work entirely within the uniform-ordered-partition distribution (i.e., “equal-nondegenerate-slices”). I’m going to try to write it down now to be sure, but if it’s correct, it should mean that “DHJ(k)=>Varnavides”, “DHJ(k)=>multidimensional-DHJ(k)”, and hopefully also “line-free sets correlate with simple sets” can all be proved with simple arguments.
More precisely, they will be the same simple arguments we have now, but with no annoyances due to all the tedious passing back and forth between various distributions via subspaces.
March 12, 2009 at 11:54 pm
1025.1 Wow — I very much hope you’re right about this. I suppose the bit that would be hardest (but not obviously impossible) would be “simple sets can be almost partitioned into subspaces”. In the uniform measure you are then done, but in other measures you can’t instantly argue that a set of density inside the simple set must have density almost
inside the simple set must have density almost  on one of the subspaces.
on one of the subspaces.
But that could well be just another little task to add to your collection. Now the idea would be to prove that the measure on a simple set can be written as a positive linear combination of the measures on subspaces. If that too can be done cleanly in the UOPD/ENS then we are in fantastic shape.
March 13, 2009 at 12:26 am |
1026. Does triangle removal imply DHJ(3)?
A wild thought this one, especially as it’s close to an idea I had several years ago and couldn’t get to work. But with the benefit of a bad memory (something that is very helpful in mathematics, in my view) I now can’t see what is wrong with it.
The idea is sort of ridiculous. Let’s pass to a subspace in which, notating it as![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) ,
,  has average density at least
has average density at least  in the slices up to
in the slices up to  , where
, where  is much smaller than
is much smaller than  . Sorry — by that I mean slices where the 1-set and 2-set are of size at most
. Sorry — by that I mean slices where the 1-set and 2-set are of size at most  .
.
The hope now is that the disjointness graph becomes dense (because two sets of size are almost always disjoint), so we can just apply the usual triangle-removal lemma. My one reason for not completely dismissing this idea is that when I tried it all those years ago I did not have the concept of equal-slices measure to play with.
are almost always disjoint), so we can just apply the usual triangle-removal lemma. My one reason for not completely dismissing this idea is that when I tried it all those years ago I did not have the concept of equal-slices measure to play with.
Unfortunately, it doesn’t become dense. Only the UV-part of it is dense (because it is just the 1-set and the 2-set that I am assuming to be small).
Let me ask a slightly different question, which probably has a fairly easy answer, and that answer will probably kill off this little idea. Given points in
points in ![{}[3]^N](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5EN&bg=ffffff&fg=333333&s=0&c=20201002) (where
(where  can be as big as you like), how many combinatorial lines can they contain?
can be as big as you like), how many combinatorial lines can they contain?
March 13, 2009 at 1:07 am
Well, if you don’t care about the dimension, then the number of lines might be Just take 0-1 sequences as i zeros followed by n-i ones (for every i) and 0-2 sequences where the zeros are followed by two-s. For any pair of such 0-1 sequences there is a third 0-2, giving a line. So this number itself won’t show that your plan won’t work.
Just take 0-1 sequences as i zeros followed by n-i ones (for every i) and 0-2 sequences where the zeros are followed by two-s. For any pair of such 0-1 sequences there is a third 0-2, giving a line. So this number itself won’t show that your plan won’t work.
March 13, 2009 at 1:17 am
I don’t understand — large should mean surely? Or perhaps
surely? Or perhaps  but with the three bipartite graphs dense.
but with the three bipartite graphs dense.
March 13, 2009 at 2:10 am
Probably I don’t understand the question. Isn’t it so that two points define the line uniquely. In any case, my example won’t work.
March 13, 2009 at 3:29 am
As it happened before, I didn’t read your post carefully. It is an extremely busy period for me; heavy teaching, committees, etc. So, I’m just writing those “half baked remarks” as Boris would say. I will try to refrain from that in the future.
March 13, 2009 at 2:24 am |
1027. A single distribution?
In preparation for trying to justify what I wrote in 1025, I have written this document explaining the distribution. I’ll wikify it if and only if this scheme works out and proves helpful 🙂
March 13, 2009 at 7:22 am
1027.1 I wrote some more here but I’ve gotten too sleepy to finish tonight. I’ll try to finish tomorrow and explain it properly in a post, but I have to go out of town tomorrow too…
March 13, 2009 at 9:30 am |
1028.
I will make my first visible visit on this side of the project by asking one of the stupid questions discussed in the metathread.
Regarding the question from 1026. As far as I understand any pair of points specify a unique line. if that is the case n points can specify at most Cn^2 lines.
Now if we have a set of points and a set of lines where every pair of points specify a unique line we have the beginnings of a projective plane, but a projective plane has the same number of points and lines.
So is there another known nice family of combinatorial objects which instead maximises the gap between the number of points and lines?
March 13, 2009 at 9:59 am |
1029
Klas, your “stupid” question has exposed the stupidity (without inverted commas) of mine — it’s not what I meant to ask. Let me have another go.
The way we prove Sperner using equal-slices measure can be thought of like this. We partition the measure on![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into measures where the set of combinatorial lines is dense. Each measure is obtained by taking a random permutation of
into measures where the set of combinatorial lines is dense. Each measure is obtained by taking a random permutation of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and taking all intervals in that permuted set, and then any two points with non-zero measure define a combinatorial line.
and taking all intervals in that permuted set, and then any two points with non-zero measure define a combinatorial line.
So a vague version of what I am trying to ask is whether we can somehow find dense structures inside![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) and play a similar game, this time exploiting the corners theorem. However, I don’t have a sensible precise version of this question, which perhaps suggests that the answer is no.
and play a similar game, this time exploiting the corners theorem. However, I don’t have a sensible precise version of this question, which perhaps suggests that the answer is no.
March 13, 2009 at 12:47 pm |
1030. Shelah
Another idea. Instead of struggling to preserve the density of by constructing just one fliptop subspace, perhaps we can partition the whole of (or almost the whole of)
by constructing just one fliptop subspace, perhaps we can partition the whole of (or almost the whole of) ![{}[k]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into fliptop subspaces. Then in at least one of them
into fliptop subspaces. Then in at least one of them  would have density almost
would have density almost  and we would be done by induction.
and we would be done by induction.
Actually, that’s not quite right unless we’re rather careful, because in order to apply induction we need to be dense in the
to be dense in the ![{}[k-1]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk-1%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) part of the fliptop subspace. Let me not worry about this for the time being.
part of the fliptop subspace. Let me not worry about this for the time being.
Instead, I’d like to think about whether some kind of argument like the one we’ve used for partitioning 1-sets into subspaces could do the job here. I can’t see it in advance so I’ll just try to plunge in.
Let m be a medium-sized integer — much smaller than n, but much larger than 1 — and write![{}[k]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as
as ![{}[k]^{n-m}\times[k]^m.](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Bn-m%7D%5Ctimes%5Bk%5D%5Em.&bg=ffffff&fg=333333&s=0&c=20201002) By the pigeonhole principle we can find a subset
By the pigeonhole principle we can find a subset  of
of ![{}[k]^{n-m}](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5E%7Bn-m%7D&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  such that for every
such that for every 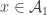 the set of
the set of ![y\in[k]^m](https://s0.wp.com/latex.php?latex=y%5Cin%5Bk%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) such that
such that  is the same. Let that set be
is the same. Let that set be  , and find a big subspace
, and find a big subspace 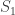 in
in ![{}[k]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) that is fliptop with respect to
that is fliptop with respect to  . Then all the subspaces
. Then all the subspaces  such that
such that 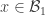 are fliptop. (They could be disjoint from
are fliptop. (They could be disjoint from  , but we don’t care about this.) Let us include them in our attempted partition and remove them from
, but we don’t care about this.) Let us include them in our attempted partition and remove them from ![{}[k]^n.](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En.&bg=ffffff&fg=333333&s=0&c=20201002) Note that we have removed a positive proportion (depending on
Note that we have removed a positive proportion (depending on  ) of
) of ![{}[k]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as a result of this.
as a result of this.
We now partition![{}[k]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) according to the part that belongs to
according to the part that belongs to ![{}[k]^m.](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5Em.&bg=ffffff&fg=333333&s=0&c=20201002) The result is a number of subspaces of the form
The result is a number of subspaces of the form ![S_y=\{(x,y):x\in[k]^{n-m}\}.](https://s0.wp.com/latex.php?latex=S_y%3D%5C%7B%28x%2Cy%29%3Ax%5Cin%5Bk%5D%5E%7Bn-m%7D%5C%7D.&bg=ffffff&fg=333333&s=0&c=20201002) If
If 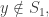 then we have not thrown away any of
then we have not thrown away any of  and we just repeat the first step. However, if
and we just repeat the first step. However, if  then things are more complicated, because we have thrown away some of
then things are more complicated, because we have thrown away some of  and are therefore not allowed to use that part in any new cell that we want to add to the attempted partition.
and are therefore not allowed to use that part in any new cell that we want to add to the attempted partition.
At this point I think it helps to imagine that we’ve somehow managed to deal with this problem for several iterations. What position would we expect to be in then? Well, we’d have restricted to some subspace (of codimension where r is the number of iterations completed), and we would want to find a big chunk (which would be a union of fliptop subspaces) to remove. Hmm, it doesn’t seem to work, since by this stage I’m needing to find a big orderly chunk of subspaces inside a set over which I have pretty well no control.
where r is the number of iterations completed), and we would want to find a big chunk (which would be a union of fliptop subspaces) to remove. Hmm, it doesn’t seem to work, since by this stage I’m needing to find a big orderly chunk of subspaces inside a set over which I have pretty well no control.
March 13, 2009 at 3:58 pm |
1031. New distribution.
This writeup is practically the same, but I think it sets things up the best. It’s a bit long, but that was mainly just to convince myself what I was saying is correct.
The gist is this:
The basic objects are length- lists (ordered) of nonempty sets, where the sets’ union is
lists (ordered) of nonempty sets, where the sets’ union is ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Such lists are in obvious correspondence with the set of “nondegenerate” points in
. Such lists are in obvious correspondence with the set of “nondegenerate” points in ![[m]^n](https://s0.wp.com/latex.php?latex=%5Bm%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) (where a point is degenerate if it does not include each character at least once).
(where a point is degenerate if it does not include each character at least once).
The basic operations are: 1. = randomly permute the list. 2.
= randomly permute the list. 2.  = do a random “coagulation”: pick $i \in [m-1]$ uniformly, and merge the
= do a random “coagulation”: pick $i \in [m-1]$ uniformly, and merge the  th set into the
th set into the  th set (shrinking the list length to
th set (shrinking the list length to  ).
).
The basic distribution is: Start with the length- list
list  . If we first apply a
. If we first apply a  operation, and then apply
operation, and then apply 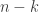 consecutive
consecutive  operations, we get a length-
operations, we get a length- list, which corresponds to a point in
list, which corresponds to a point in ![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . This is our basic distribution on strings. It is (one can show) the “equal-nondegenerate-slices” distribution.
. This is our basic distribution on strings. It is (one can show) the “equal-nondegenerate-slices” distribution.
Finally, note that if we only did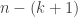 of the
of the  operations, we’d get a string
operations, we’d get a string ![\lambda \in [k+1]^n](https://s0.wp.com/latex.php?latex=%5Clambda+%5Cin+%5Bk%2B1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , which we think of as
, which we think of as ![([k] \cup \{\star\})^n](https://s0.wp.com/latex.php?latex=%28%5Bk%5D+%5Ccup+%5C%7B%5Cstar%5C%7D%29%5En&bg=ffffff&fg=333333&s=0&c=20201002) ; i.e., a combinatorial line (template). If we were to further apply the
; i.e., a combinatorial line (template). If we were to further apply the  operation to this, we’d get one of the
operation to this, we’d get one of the  points on this line, uniformly at random. And, note that
points on this line, uniformly at random. And, note that  is a string in
is a string in ![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) distributed according to our basic distribution.
distributed according to our basic distribution.
—-
I’m quite sure that at the very least, Varnavides and Multidimensional DHJ(k) become “trivial” now. The proof of line-free sets in![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) correlating with simple sets was already pretty simple assuming these two tools, but I’m hoping it also gets a paragraph proof now.
correlating with simple sets was already pretty simple assuming these two tools, but I’m hoping it also gets a paragraph proof now.
Of course, I further hope that this helps simplify the “other half” of the proof, namely the density-increment argument. I’d like to think more about it except I’m going to visit family for a few days and will likely not get the chance.
March 14, 2009 at 9:41 am
Ryan, the link to your write-up isn’t working. I’m looking forward to seeing it …
March 13, 2009 at 4:08 pm |
1032. Shelah/wikification
I’ve now put on the wiki a very slight modification of the usual proof of the (colouring) Hales-Jewett theorem, together with Shelah’s proof. The purpose of the exercise is to show just how similar the two proofs really are: one uses HJ(k-1) to get you down to HJ(2), while the other one uses HJ(2), in pretty well exactly the same way, to get you down to HJ(k-1). If I’d been feeling silly enough, I would have interpolated between the two cases and written a general argument for how to use HJ(s) to get you down to HJ(k-s+1), which can quite clearly be done. (Indeed, it’s so clear that it can be done that maybe what’s already there can be thought of as doing it by giving enough examples to make clear what the general case is.)
I bothered to do this partly because I find it historically interesting that it took such a long time for Shelah’s proof to be discovered, and I think that presenting the two proofs side by side in that way makes it really quite mysterious. But my main motive is to try to get people interested in the process of Shelahification of the proof we (probably) have of DHJ(k). If the induction can be turned upside down so easily in the colouring version, I will need a pretty convincing argument to persuade me that it cannot be done for the density version. And if it can be done, it would be really good to do it because the bounds would drop from Ackermann to primitive recursive.
The proofs are on the page about the colouring Hales-Jewett theorem.
March 13, 2009 at 4:34 pm
Isn’t it so that the iterations give you a k-(k-1) fliptop space, then a (k-1)-(k-2) fliptop space in the smaller cube so on? Then if you check any line, it is fliptop for any consecutive pairs, so it is monochromatic. I was wondering if a statistical variant would work or not; Take an almost fliptop subspace (many neighbours have the same colour) and a smaller almost fliptop subspace so on. At the end if at least one line is pairwise fliptop then we are done.
March 13, 2009 at 7:43 pm
Jozsef, I’m not sure if this is what you’re asking, but on the wiki I presented Shelah’s argument in terms of flipbottom subspaces instead of fliptop ones.
March 13, 2009 at 8:18 pm
Tim, I just changed the notation there. I should have followed yours. While I think that I understand Shelah’s proof completely, I’m not sure that I see exactly the limits of the technique. For example, it seems to me that we don’t use that the points of every neighboring pair have the same colour. For example if 11111… is blue and 21111… is red in the first fliptop subspace, it won’t make any trouble later as the line defined by the two elements is outside of the next subspace. In general, every point with coordinate 1 has exactly one “semi-neighbour” which is important in the iteration, where the 1-s are replaced by 2-s. But I don’t see an easy way to consider the important pairs only.
March 13, 2009 at 8:29 pm
Yes, I had a similar thought soon after writing up the wiki page. I modified the usual proof so as to ensure, unnecessarily, that it reduced HJ(k) to HJ(2). But the usual colour-focusing proof doesn’t need that full strength. I therefore suspect that it is possible to modify the Shelah proof so that instead of producing a fliptop subspace you produce a subspace with some weaker property. But I haven’t tried to work out any details, or even to convince myself that it’s definitely possible.
March 13, 2009 at 6:31 pm |
[…] combinatorial proof of the density Hales-Jewitt theorem (DHJ). Big congratulations to them, because the problem is solved, probably. Summarizing why he spent his time on this particular problem, Terry Tao wrote: I guess DHJ is […]
March 13, 2009 at 8:15 pm |
1033. Shelah
I’m still just throwing out guesses here (and seeing whether I get anywhere with them in real time — no luck so far) and here’s another one.
In the argument we have now, we could present it as saying that we try to find a combinatorial line, and if we can’t then we get correlation with a set of complexity k-2. If we are going to try to Shelah-ize, then we’re very much hoping to find a fliptop subspace (or perhaps, as Jozsef suggests above, something slightly weaker but still sufficient) where is still dense. So perhaps we should plunge in and try to construct such a subspace, but instead of being completely determined to succeed, we should hope that either we will succeed or we will get correlation with a set of complexity 1.
is still dense. So perhaps we should plunge in and try to construct such a subspace, but instead of being completely determined to succeed, we should hope that either we will succeed or we will get correlation with a set of complexity 1.
The first step of what I was trying to do in 1013, following Jozsef in 1011, was as follows. Write![{}[k]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as
as ![{}[k]^r\times[k]^s](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5Er%5Ctimes%5Bk%5D%5Es&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where  is much bigger than
is much bigger than  . For each
. For each ![y\in[k]^s,](https://s0.wp.com/latex.php?latex=y%5Cin%5Bk%5D%5Es%2C&bg=ffffff&fg=333333&s=0&c=20201002) define
define  to be
to be ![\{x\in[k]^r:(x,y)\in\mathcal{A}\}.](https://s0.wp.com/latex.php?latex=%5C%7Bx%5Cin%5Bk%5D%5Er%3A%28x%2Cy%29%5Cin%5Cmathcal%7BA%7D%5C%7D.&bg=ffffff&fg=333333&s=0&c=20201002) We would like to find
We would like to find 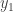 and
and 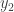 that differ only in a few places where coordinates that were k-1 in
that differ only in a few places where coordinates that were k-1 in 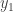 are k in
are k in 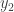 , such that
, such that  So far so good, but we would also like
So far so good, but we would also like  to have density almost as big as the starting density when restricted to
to have density almost as big as the starting density when restricted to ![{}[k]^r\times L](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5Er%5Ctimes+L&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where  is the unique combinatorial line that contains both
is the unique combinatorial line that contains both 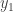 and
and 
Now if we can’t do this, then we potentially get an interesting set inside which has reduced density. It’s formed as follows: for each pair
has reduced density. It’s formed as follows: for each pair 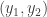 as above, form the line
as above, form the line  , and take the union
, and take the union  of all those lines.
of all those lines.
Ignoring for now the fact that the union is not an arithmetic operation, so we can’t actually conclude without extra work that if has reduced density on every
has reduced density on every ![{}[k]^r\times L](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5Er%5Ctimes+L&bg=ffffff&fg=333333&s=0&c=20201002) that it has reduced density on
that it has reduced density on ![{}[k]\times X,](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5Ctimes+X%2C&bg=ffffff&fg=333333&s=0&c=20201002) let’s see whether
let’s see whether  has any good structure, such as low complexity.
has any good structure, such as low complexity.
A sequence![z\in[k]^s](https://s0.wp.com/latex.php?latex=z%5Cin%5Bk%5D%5Es&bg=ffffff&fg=333333&s=0&c=20201002) belongs to
belongs to  if and only if we can find some
if and only if we can find some  and some subset
and some subset  of the j-set of
of the j-set of  such that when we overwrite
such that when we overwrite  with (k-1)s or ks, we get two points
with (k-1)s or ks, we get two points 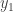 and
and 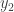 with
with  Hmm, that doesn’t seem to have low complexity. Back to the drawing board.
Hmm, that doesn’t seem to have low complexity. Back to the drawing board.
March 13, 2009 at 8:47 pm
Just a technical remark; when you cut![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into two parts the you can play with the densities. The density of A is c, say. If any
into two parts the you can play with the densities. The density of A is c, say. If any 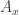 or
or  had density larger than
had density larger than  then we can go there and repeat. That means that the density of x that
then we can go there and repeat. That means that the density of x that 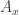 is at least
is at least  is almost 1, I think.
is almost 1, I think.
March 13, 2009 at 8:48 pm |
1034. Shelah
Time for a very vague thought indeed. Maybe the mistake in our thoughts so far about a density version of Shelah’s proof is that we’re still using colourings too much. Is there some “density equivalent” of a fliptop subspace?
To get a handle on this question, let us try to focus on the property that’s good about fliptop subspaces: that if you ever find a line with all the points up to k-1 of the same colour, then the whole line must be monochromatic. The obvious density version of that would be that if the first k-1 points belong to then so does the kth.
then so does the kth.
One immediate small observation is that for this to be the case, all we need is that if you change some (k-1)s to ks, you don’t go out of . We don’t mind if this operation takes you in to
. We don’t mind if this operation takes you in to  . But is there perhaps some much more general circumstance under which we can deduce that
. But is there perhaps some much more general circumstance under which we can deduce that  contains a line from the fact that
contains a line from the fact that ![\mathcal{A}\cap[k-1]^n](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BA%7D%5Ccap%5Bk-1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) does? Or perhaps from the fact that
does? Or perhaps from the fact that ![\mathcal{A}\cap[k-1]^n](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BA%7D%5Ccap%5Bk-1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) contains lots of combinatorial lines? In the latter case, what is the set of points that
contains lots of combinatorial lines? In the latter case, what is the set of points that  will be forced to avoid?
will be forced to avoid?
I have to go now, but at first glance it still doesn’t look as though there are any super-low-complexity sets floating about.
March 14, 2009 at 4:47 am |
1035. Austin’s proof w/o Ramsey theory or density increment
I’ve written up a more or less complete proof of DHJ(3) using a (rather abstract) triangle-removal approach, based on Austin’s proof, at
http://michaelnielsen.org/polymath1/index.php?title=Austin%27s_proof_II
I found that stationarity is not used as much as I had previously thought, and can in fact be obtained by a simple energy increment argument and the pigeonhole principle rather than more high-powered Ramsey-theoretic tools such as Graham-Rothschild.
The argument is a bit tedious though. It follows the approach to triangle removal used for instance in my reworking of the hypergraph removal lemma, in particular, heavily using lots of conditional expectation computations, rather than the traditional language of cleaning out “bad” cells and then counting both “non-trivial” and “trivial” triangles in the surviving cells. But there are some distracting complications due to the multiplicity of scales, and the presence of some additional random choices (basically, one has to choose some random index sets I to flip from 0 to 2, etc). One has to make the whole argument “relative” or “conditioned” to these random choices, which makes the argument look stranger than it normally does.
The bounds seem to be tower-exponential in nature – not so surprising, being based on triangle removal. Amusingly, if one used uniform measure rather than equal-slices measure, one would be forced to make a double tower-exponential, because of the fact that each new scale would have to essentially be the square root of the previous. Hooray for equal slices measure!
I’m pretty sure the density-increment argument is going to end up being shorter and simpler than this one, but I’m putting the triangle removal proof here for completeness.
I’ll be travelling overseas shortly, and so I’ll probably be contributing very little for the next week or two.
March 14, 2009 at 12:20 pm |
[…] even though it touches on my central topics of maths and communication. Now with its preliminary success feels like a good time to do so. […]
March 14, 2009 at 12:57 pm |
1036. Graham-Rothschild
A quick pair of closely related questions: is the density version of Graham-Rothschild known, and do we now have the tools to prove it (whether or not it is known)?
For the benefit of anyone who can’t be bothered to look it up on the wiki, the Graham-Rothschild theorem is like the Hales-Jewett theorem except that the basic objects are combinatorial subspaces of some fixed dimension rather than points. For instance, a special case is that if you colour the lines in![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with finitely many colours, then there is a combinatorial subspace of dimension m such that all the lines in that subspace have the same colour — provided n is big enough in terms of m and the number of colours.
with finitely many colours, then there is a combinatorial subspace of dimension m such that all the lines in that subspace have the same colour — provided n is big enough in terms of m and the number of colours.
It may be that the question is easy. For instance, suppose we think of a combinatorial line in![{}[k]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as a point in
as a point in ![{}[k+1]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5Bk%2B1%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with coordinates that belong to the set
with coordinates that belong to the set 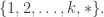 If we then find in our dense set
If we then find in our dense set  of such lines an m-dimensional subspace, what does that translate into? It gives us some wildcard sets
of such lines an m-dimensional subspace, what does that translate into? It gives us some wildcard sets 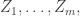 each of which can be converted into an element of this alphabet, and it also gives us some fixed coordinates. The problem is that the fixed coordinates can be equal to
each of which can be converted into an element of this alphabet, and it also gives us some fixed coordinates. The problem is that the fixed coordinates can be equal to  , so we do not end up with all the lines in some combinatorial subspace.
, so we do not end up with all the lines in some combinatorial subspace.
At first this looks problematic: given a dense subset of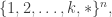 we can’t hope to find a subspace inside it with no fixed coordinates equal to
we can’t hope to find a subspace inside it with no fixed coordinates equal to  , since
, since  might consist of all points with at least one coordinate equal to
might consist of all points with at least one coordinate equal to  . However, that’s not a problem, because our entire space consists of points with at least one
. However, that’s not a problem, because our entire space consists of points with at least one  (since they are combinatorial lines).
(since they are combinatorial lines).
So here’s a DHJ(3) variant. Suppose you have a dense subset of
of ![{}[3]^n.](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En.&bg=ffffff&fg=333333&s=0&c=20201002) Must there be an m-dimensional subspace S such that all the fixed coordinates are equal to 1 or 2, and every point in S that includes at least one 3 is an element of
Must there be an m-dimensional subspace S such that all the fixed coordinates are equal to 1 or 2, and every point in S that includes at least one 3 is an element of  ?
?
March 14, 2009 at 1:28 pm
Just realized that the formulation of that last question was a bit careless, since the usual example of a set with roughly equal numbers of all three coordinates is a counterexample to this when m=2. So it’s not instantly obvious what a density version of Graham-Rothschild would even say, but I hope that with the help of equal-slices measure one might be able to formulate a decent statement.
March 14, 2009 at 10:16 pm
Generally, these Ramsey theorems are either “projective” (Schur, Hindman, Ramsey), “affine” (van der Waerden, HJ) or “projective/affine” (Graham-Rothschild, Carlson, CST). Nothing with a projective aspect will typically have a “naive” density version, though I don’t know exactly what you are shooting for here. (Presumably you don’t mean something that the set of words having an odd number of 3s would be a counterexample to.)
March 14, 2009 at 10:58 pm
Hi Randall, It is an interesting question if these problems have density versions or not. Let’s consider Schur’s thm. Ben Green proved that if a subset of [n], S, has only a few, , solutions to x+y=z in S then one can remove o(n) elements from S to destroy all solutions. This might be viewed as a density version of Schur’s theorem. On the other hand I don’t see a simple way to deduce Schur’s theorem from this density version. I tried it as it might give a bound on the triangle removal lemma, but without success.
, solutions to x+y=z in S then one can remove o(n) elements from S to destroy all solutions. This might be viewed as a density version of Schur’s theorem. On the other hand I don’t see a simple way to deduce Schur’s theorem from this density version. I tried it as it might give a bound on the triangle removal lemma, but without success.
March 14, 2009 at 5:05 pm |
1037. Uniform ordered partition measure.
Here is the corrected link from 1031; in other words, add “.pdf” to the broken link. I think this measure will work well with the Graham-Rothschild problem described above; again, I’ll try to write more in a few days when I get back home.
March 14, 2009 at 5:06 pm
1037.1 Drat, I keep botching it! It’s here.
March 14, 2009 at 7:17 pm |
1038. Subspace implies line
A simple argument shows that DHJ(k) implies d-dimensional subspaces in![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) for any dense subset (with large enough n). I remember seeing a wiki article about this, but I was unable to find it this morning. It is also true that a subspace theorem implies DHJ. That looks fairly trivial but let me explain it; I want to show that the following statement is equivalent to DHJ(k): “There is a constant,
for any dense subset (with large enough n). I remember seeing a wiki article about this, but I was unable to find it this morning. It is also true that a subspace theorem implies DHJ. That looks fairly trivial but let me explain it; I want to show that the following statement is equivalent to DHJ(k): “There is a constant,  that for every d there is an n that any c-dense subset of
that for every d there is an n that any c-dense subset of ![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) contains a d-dimensional subspace.”
contains a d-dimensional subspace.”![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as
as ![[k]^r\times[k]^s](https://s0.wp.com/latex.php?latex=%5Bk%5D%5Er%5Ctimes%5Bk%5D%5Es&bg=ffffff&fg=333333&s=0&c=20201002) , where s is much bigger than r. For each
, where s is much bigger than r. For each ![y\in [k]^s](https://s0.wp.com/latex.php?latex=y%5Cin+%5Bk%5D%5Es&bg=ffffff&fg=333333&s=0&c=20201002) , define
, define  to be
to be ![\{x\in[k]^r:(x,y)\in\mathcal{A}\}](https://s0.wp.com/latex.php?latex=%5C%7Bx%5Cin%5Bk%5D%5Er%3A%28x%2Cy%29%5Cin%5Cmathcal%7BA%7D%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) .
.![y\in [k]^s](https://s0.wp.com/latex.php?latex=y%5Cin+%5Bk%5D%5Es&bg=ffffff&fg=333333&s=0&c=20201002) , that
, that  is empty. Suppose that
is empty. Suppose that  is large, line-free, and its density is
is large, line-free, and its density is  where
where  is the limit of density of line-free sets and
is the limit of density of line-free sets and 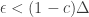 . We can also suppose that no
. We can also suppose that no  has density much larger than
has density much larger than  as that would guarantee a combinatorial line. But then the density of Y is at most 1-c, so there is a c-dense set Z
as that would guarantee a combinatorial line. But then the density of Y is at most 1-c, so there is a c-dense set Z ![Z=[k]^s-Y](https://s0.wp.com/latex.php?latex=Z%3D%5Bk%5D%5Es-Y&bg=ffffff&fg=333333&s=0&c=20201002) such that any element is a tail of some elements of
such that any element is a tail of some elements of  . For every
. For every  choose an x
choose an x ![x\in [k]^r:(x,y)\in\mathcal{A}](https://s0.wp.com/latex.php?latex=x%5Cin+%5Bk%5D%5Er%3A%28x%2Cy%29%5Cin%5Cmathcal%7BA%7D&bg=ffffff&fg=333333&s=0&c=20201002) . This x will be the colour of y. It gives a
. This x will be the colour of y. It gives a ![[k]^r](https://s0.wp.com/latex.php?latex=%5Bk%5D%5Er&bg=ffffff&fg=333333&s=0&c=20201002) colouring on Z. By the initial condition Z contains arbitrary large subspaces, so by HJ(k) we get a line in
colouring on Z. By the initial condition Z contains arbitrary large subspaces, so by HJ(k) we get a line in  .
.
I would like to show the direction that the statement above implieas DHJ(k). The other direction is already wikified.
As before, write
Let Y denote the set of
March 15, 2009 at 5:06 pm
I’ve find Tim’s post about DHJ(k) implies subspace DHJ(k).
http://michaelnielsen.org/polymath1/index.php?title=DHJ(k)_implies_multidimensional_DHJ(k)
The right title of the post above would be “Weak subspace DHJ(k) implies DHJ(k)”.
March 14, 2009 at 11:33 pm |
1039 Graham-Rothschild
I’ve got a new attempt at a density version of Graham-Rothschild that might have a chance of being true. I realized that equal-slices measure wouldn’t rescue the previous version, since the set of lines with wildcard set of size approximately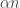 is a counterexample.
is a counterexample.
As I write, I realize that my new attempt fails too. Basically, if you’ve got a 2D subspace then you must have lines with wildcard sets of sizes x, y and x+y, so a density version looks as though it would have to imply a density version of Schur’s theorem, which is of course false. (I realize that I am sort of repeating what people have already said in their replies to 1036.)
Maybe one could go down the route Jozsef implicitly suggests and try proving that if is a set that contains few m-dimensional subspaces, then one can remove a small number of elements from
is a set that contains few m-dimensional subspaces, then one can remove a small number of elements from  and end up with no m-dimensional subspaces. I’m not sure that I feel like trying this though …
and end up with no m-dimensional subspaces. I’m not sure that I feel like trying this though …
March 15, 2009 at 10:52 am |
1040.
Since the density of a subset of [k]^n is quite insensitive to the removal of an element, at least for large n, a set with positive density will contain many lines. How many lines can be guaranteed, as a function of the density and n?
From the equal-slices proof of Sperner it is not hard to get a lower bound for DHJ(2) so I’m curious as to what can be said for DJH(3).
March 15, 2009 at 6:33 pm |
1041. Line-free sets correlate locally with complexity-1 sets
I would like to go back to one important part of the DHJ(3) proof, to analyze it from a slightly different angle. Let us consider our set , a dense subset of
, a dense subset of ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , as a subset of
, as a subset of 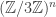 . Build a graph on
. Build a graph on  as follows; The vertex set is
as follows; The vertex set is  and two vertices, a and b, are connected iff for c: a+b+c=0 c is also in
and two vertices, a and b, are connected iff for c: a+b+c=0 c is also in  . If
. If  was dense then there are many edges in any typical subspace. Now DHJ is equivalent to the statement that there are two connected elements of
was dense then there are many edges in any typical subspace. Now DHJ is equivalent to the statement that there are two connected elements of  with the same set of 3-s and that one’s set of 1-s contains the 1-s of the other. This model leads us to a density Sperner problem.
with the same set of 3-s and that one’s set of 1-s contains the 1-s of the other. This model leads us to a density Sperner problem.
It just turned out that I have to go somewhere right now. I will come back in a few (4+) hours.
March 15, 2009 at 11:38 pm
1042. The distribution.
Hmm. In fact, it may be even better to view strings in![[k]^n](https://s0.wp.com/latex.php?latex=%5Bk%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) being generated in the time-opposite way from the one I described. Specifically, equal-slices and its nondegenerate variant are the same as the following Polya-Eggenberger urn process:
being generated in the time-opposite way from the one I described. Specifically, equal-slices and its nondegenerate variant are the same as the following Polya-Eggenberger urn process:
[Non-degenerate version:] Start with one of the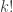 permutations of the string
permutations of the string  . Repeat the following
. Repeat the following 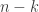 times: pick a random character in
times: pick a random character in ![[k]](https://s0.wp.com/latex.php?latex=%5Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) with probability proportional to the number of times it appears already in the string. Now insert that character into a random place in the string.
with probability proportional to the number of times it appears already in the string. Now insert that character into a random place in the string.
[Equal-slices version, I think:] Same, except: a) start with the empty string; b) for the purposes of proportionality, pretend there is a phantom copy of each of the characters.
characters.
This yet-another viewpoint on the equal-slices distribution helps with making “subspace arguments” (which the uniform distribution was good for): the point is, if you do a -color Polya urn process for
-color Polya urn process for  steps and
steps and 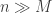 , then the final distribution hardly depends at all on what happened in the first
, then the final distribution hardly depends at all on what happened in the first  steps.
steps.
Will write more when I get back in two days.
March 15, 2009 at 11:57 pm |
1042. Density increasing and an analog problem
(This is a little off topic) Let me mention a problem which I thought of as analogous to Roth/cap set where the gaps between lower and upper bounds are similarly shocking and the current density increasing arguments cannot help; (It is related to old work of mine with Kahn and Linial and also to some more recent work with Shelah that we did not publish.)
you have a subset A of of density c and you would like to find a combinatorial subcube F of dimension 0.9n so that the projection of A to F is of large density say 0.99. In other words, we want to find a set of 0.9n coordinates so that for a fraction 0.99 of the vectors supported on this set we can find a continuation on the other coordinates that is in A. (We usually talk here about restriction to a subcube/subspace and not about projections. But traditionally sections and projections are not unrelated.)
of density c and you would like to find a combinatorial subcube F of dimension 0.9n so that the projection of A to F is of large density say 0.99. In other words, we want to find a set of 0.9n coordinates so that for a fraction 0.99 of the vectors supported on this set we can find a continuation on the other coordinates that is in A. (We usually talk here about restriction to a subcube/subspace and not about projections. But traditionally sections and projections are not unrelated.)
By a density increasing argument doing it one coordinate at a time it was known from the late 80s that this can be achieved if c is for
for  or so. A conjecture by Benny Chor asserts that
or so. A conjecture by Benny Chor asserts that  is good enough!
is good enough!
I think it is a little analogous to Roth (or cap set)
a few points:
1) The proof is also by a slow density increasing argument (you reduce the dimension by one every time) and there are examples the such an argument cannot be improved.
2) There are some conjectures (by Friedgut and others) which may explain why we can get the density down to for every
for every  maybe even
maybe even 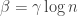 but no plans beyond it.
but no plans beyond it.
3) There are alarming examples by Ajtai and Linial of Boolean functions descibed by certain random depth 3 circuits (that Ryan already mentioned) that may (or a varian of) give a counter example. It is complicated to check it.
I admit that the analogy with density increasing argument for Roth-type problems is not very strong: this problem is about projection to subcubes and there it is about restrictions to subspaces or similar creatures; But there may be some connecion.
In particular I would try subsets described by low depth small size circuits (with operations over {0,1,2}) as candidates for counter examples for the most ambitious conjectures regarding Roth and cap sets.
(On the positive side maybe more sophisticated density increasing arguments of the kind we talk about here can be used in this problem.)
March 16, 2009 at 3:12 am |
1043. Graham-Rothschild
From 1036: ” A quick pair of closely related questions: is the density version of Graham-Rothschild known, and do we now have the tools to prove it (whether or not it is known)?
For the benefit of anyone who can’t be bothered to look it up on the wiki, the Graham-Rothschild theorem is like the Hales-Jewett theorem except that the basic objects are combinatorial subspaces of some fixed dimension rather than points. For instance, a special case is that if you colour the lines in with finitely many colours, then there is a combinatorial subspace of dimension m such that all the lines in that subspace have the same colour — provided n is big enough in terms of m and the number of colours. ”
I doubt there is density version of the Graham-Rothschild theorem. If one fixes a coordinate and deletes all lines that has a constant coordinate at that point then that will only lower the number of lines by a constant factor but it will prevent the formation of any two dimensional space with all its lines monochromatic as in that case the intersection of the moving coordinates of all of the lines is the null set.
March 16, 2009 at 3:19 am |
1044. Density theorems and Ramsey theorems
Density theorems are stronger than Ramsey theorems. Any density theorem can be converted to a Ramsey theorem as follows. One sets the density less than 1/r and gets a large enough configuration so that the if the density is greater than 1/r there will be the desired result than for any r coloring there will be one color with density 1/r or more and we will have a monochromatic configuration in that color.
March 16, 2009 at 5:49 am |
1045. Density Schur Theorem
I have just remembered the counterexample for a density version of Schur’s theorem. One just takes the odd numbers, they have density 1/2 but since the sum of two odd numbers is even there are no triples a,b,c in the set such that a+b=c.
March 16, 2009 at 7:54 am
The fact that the density version of Schur’s theorem is false implies that density Graham-Rothschild is false — see 1038.
March 16, 2009 at 11:36 am |
1046. Bad news and good news.
Bad news: our proof of DHJ(3) is wrong!
Good news: it isn’t too hard to fix.
But it’s still quite amusing that nobody noticed that Substep 2.2 of the write-up on the wiki of the crucial lemma that a dense 1-set can be almost completely partitioned into subspaces was nonsense as presented. I’ve left the old version there as a cautionary tale. Fortunately, the reason for the mistake was that I had translated the corresponding part of Terry’s argument in a sloppy way — the argument itself was sound. But it did give me a bit of a scare …
March 16, 2009 at 6:28 pm
1046.1 Good news and polymath….
Well, perhaps it will be somewhat reassuring that the changes you have made seem to be only adding more detail, and that, from the ergodic perspective at least, it was natural to omit said detail; loosely translated (and unless I misunderstand), what you seem not to be checking more carefully is that when you remove the fibers (over some factor) that recur under a subspace, what you have left is still measurable with respect to that subspace. So perhaps the good news is actually that polymath is like math with a net. (In which case the bad news is the danger than everyone involved will internalize that piece of good news to the point where it becomes a problem.)
March 16, 2009 at 6:32 pm
I of course meant (a) “now” to be checking more carefully, and (b) measureable with respect to that “factor”.
March 16, 2009 at 1:09 pm |
1047. Wikification
I have now wikified an abstract version of the iterative argument that was wrong before. From the abstract point of view the property that I was forgetting about was the all-important sigma-algebra property. This version should be fine now and is intended to be sufficiently general to deal with DHJ(k) as well. The argument could be sharpened up a bit towards the end — I ran out of energy.
March 16, 2009 at 1:17 pm |
Metacomment. I’ve created a thread for comments 1050-1099, so this one should draw to a close.
March 20, 2009 at 9:29 pm |
[…] week, Gowers announced that the problem was “probably solved”. In fact, if the results hold up, the project […]
March 24, 2009 at 5:27 pm |
[…] project, as of February 20, 2009. The project, which began around February 2, 2009, has now been declared successful by Gowers. While the original aim was to find a new proof of a special case of an already proved theorem, the […]
March 25, 2009 at 9:13 am |
[…] (as a little spin off to the polymath1 project, (look especially here and here)) if you have any thoughts about where the truth is for these problems, or about how to […]
March 26, 2009 at 1:41 am |
[…] to an online collaborative approach, then kicked things off with a blog post. Six weeks later, the main problem he proposed was declared (essentially) solved. However, the project still continues apace, especially at threads at Terry Tao’s […]
April 28, 2009 at 9:27 pm |
[…] (probably),” Nature Physics, 5: 237, April 2009 . Hay una entrada en el blog de Tim con el mismo título. Más allá de la demostración la experiencia muestra a los jóvenes que se inician en la […]
July 2, 2009 at 10:17 am |
Thank you. best information for me.
July 23, 2009 at 9:47 am |
[…] polymath projects After the success of the first polymath project (see also here and here as well as the project wiki), there are now […]
May 1, 2010 at 7:45 pm |
[…] subprojects of the Polymath Project progressed quickly. On March 10, Gowers announced that he was confident that the polymaths had found a new combinatorial proof of DHJ. Just 37 days […]
September 20, 2010 at 2:18 am |
[…] papers, but platforms like OpenWetWare clearly show that this is doable, and initiatives like the Polymath projects demonstrate that it may even be beneficial to the topic — an aspect that is especially […]
April 8, 2011 at 8:57 pm |
[…] to the Hales-Jewett theorem — and, several hundred comments later, announced that they had succeeded. Here’s the paper. Buoyed by this success, the group has set up a Polymath Wiki to expedite […]
April 26, 2011 at 3:41 pm |
[…] to go because, to paraphrase Michael Nielsen’s account of Tim Gowers’ synopsis of the initial Polymath project, doing science in the open is to traditional science like driving is to pushing a […]
May 19, 2011 at 4:24 pm |
[…] way to go because, to paraphrase Michael Nielsen’s account of Tim Gowers’ synopsis of the initial Polymath project, doing science in the open is to traditional science like driving is to pushing a […]