In this post I want to discuss some general issues that arise naturally in the light of how the polymath experiment has gone so far. First, let me say that for me personally this has been one of the most exciting six weeks of my mathematical life. That is partly because it is always exciting to solve a problem, but a much more important reason is the way this problem was solved, with people chipping in with their thoughts, provoking other people to have other thoughts (sometimes almost accidentally, and sometimes more logically), and ideas gradually emerging as a result. Incidentally, many of these ideas are still to be properly explored: at some point the main collaboration will probably be declared to be over (though I suppose in theory it could just go on and on, since its seems almost impossible to clear up every interesting question that emerges) and then I hope that the comments will be a useful resource for anybody who wants to find some interesting open problems.
The sheer speed at which all this happened contributed to the excitement. In my own case it led to my becoming fairly obsessed with the project and working on it to the exclusion of almost everything else (apart, obviously, from things I absolutely had to do).
But how does what happened compare with my initial fantasy about what might happen? Looked at from that point of view, it was more successful in some ways and less in others.
On the plus side, the mathematical result of the project has far exceeded what I thought would be possible in a mere six weeks. I deliberately set a rather modest aim: to explore just one approach to DHJ(3). In retrospect, this seems not to have been the right decision, though it may have been quite good as a starting point, since in the end we moved off into other directions that were more fruitful (not that I completely rule out a proof along the lines first envisaged, especially given some of the tools that we have now developed). Anyhow, these initial restrictions were quietly abandoned, and it looks as though we have proved a stronger result than seemed remotely feasible then. (More precisely, if we had managed to get my initial suggestion to work, it would probably have been unpleasant, though not impossible, to generalize.)
Also on the plus side, the project has been genuinely collaborative, and has led, to a remarkable extent, to the kind of efficiency gains that I was hoping for. To give one example, Randall McCutcheon made some very useful comments, but they were in the language of ergodic theory, which I understand only in a very limited way. But Terence Tao is a master at translating concepts back and forth between combinatorics and ergodic theory, so I was able to benefit from Randall’s contributions indirectly.
But something I found more striking than the opportunity for specialization of this kind was how often I found myself having thoughts that I would not have had without some chance remark of another contributor. I think it is mainly this that sped up the process so much.
I could go on, but from the point of view of discussion I am more interested in the way that the project fell short of my expectations, and there is one way that stands out. There seemed to be such a lot of interest in the whole idea that I thought that there would be dozens of contributors, but instead the number settled down to a handful, all of whom I knew personally. (Actually, Randall, I know of you so well that I feel as though I know you but I can’t quite remember whether we have met — hope to do so soon.)
This raises two questions. (<rant> By the way, it doesn’t beg any questions at all. </rant>) Why did it happen like this, and does it matter?
I would be very interested to hear from anyone who thought that they might like to contribute but ended up not doing so. I have spoken to one or two people like that, so I know of at least one reason, which I suspect may be the most important: it’s that the number of comments grew so rapidly that merely keeping up with the discussion involved a substantial commitment that not many people were in a position to make. I definitely intend to start another polymath project, but next time I think we may have to have some policy such as writing up all useful insights on the corresponding wiki before we allow ourselves a new comment thread, so that anybody who wants to join the discussion can read about the progress in a condensed and organized form. Or perhaps we should just artificially slow ourselves down. Or perhaps it will just naturally be slower second time round.
Another possible reason is that the problem I chose lent itself more naturally to a smaller collaboration, since in order to be well placed to think about the density Hales-Jewett theorem it was a huge help to be familiar with, and to have thought hard about, other related results. So the pool of potential collaborators was not as large as it might have been (though it was still substantially larger than the number of people who did contribute). The next problem I have in mind is less like that: it should be possible to contribute with virtually no prior knowledge.
A third possible reason is that there are a lot of experts out there who could in principle have contributed but who just aren’t part of the blogosphere in any serious way. Amongst them are probably several people who would not in any case feel comfortable about airing their thoughts so publicly.
Does it matter? In a way no: this smaller collaboration has worked very well, and, as several people have commented, it has provided, for possibly the first time ever (though I may well be wrong about this), the first fully documented account of how a serious research problem was solved, complete with false starts, dead ends etc. It may be that the open nature of the collaboration was in the end more important than its size. I can even imagine solo polymath-type projects, where somebody thinks online just to interest anyone who might be interested.
Another thing I have found good about the project is that it has made it possible to work hard without having the sensation of working hard. There are some people who have brains that they seem to be able to split into three or four parts that can work independently, one part solving problems, another digesting the literature, another blogging, another giving lecture courses. My own brain works in series rather than in parallel, but now that I have found a way of simultaneously blogging and carrying out research I can do two things at the same time by identifying them.
However, there is still a part of me that would like to see whether a much bigger collaboration might be possible. I think a lesson of this one is that a big collaboration would need an extra level of organization, so that it was possible to work on part of the project without keeping track of the whole of it. But finding a good way of doing that would be quite a challenge: when we tried to split this discussion into separate threads, it didn’t really work, except for the thriving thread on DHJ numbers on Terry’s blog, which worked because it was a more or less disjoint enterprise from the one here.
There are some other questions that need discussing, such as the best way to write results up, what appropriate conventions should be for referring to work here, and so on. Comments on these and other practical questions are also welcomed.
March 10, 2009 at 10:54 pm |
I do think that one obstacle for me is that the dialogue was not done via some sort of mailing list. There are people (such as I) who try to not open the web browser for fear of getting distracted by the internet, but who can handle having their email client open constantly. Also, that would naturally obviate the whole clunky “threading vs no threading” debate. It would be easy to host such through google groups or via whatever service you have planned to host the wiki.
March 10, 2009 at 11:14 pm |
I’m pleased to see that someone else still cares about “begging the question”.
I suspect that the way most people use email would make a purely email-based approach less suitable than the existing one, but perhaps a sensible thing would be to give people the option of receiving email updates – of course, one can already subscribe to the comments here by email, but I suspect there are better ways of implementing this.
March 11, 2009 at 6:08 am
I dunno, I’m kinda with Utahraptor on this one.
March 11, 2009 at 6:54 pm
I see Ryan’s Utahraptor and raise him a (fictionalized) Barack Obama.
March 11, 2009 at 12:02 am |
I wanted to contribute, but the timing was not right for me to focus on this effort, so I was merely watching. I did notice this comment of yours, which agrees with my experience in such collaborations:
—-
But something I found more striking than the opportunity for specialization of this kind was how often I found myself having thoughts that I would not have had without some chance remark of another contributor. I think it is mainly this that sped up the process so much.
—-
What is really funny is when misinterpretation of what a collaborator was saying is the key to passing a roadblock in my thinking — scientific progress is so often accidental.
March 11, 2009 at 12:27 am |
The project was definitely successful from my standpoint. I’m sort of an amateur with just an undergraduate degree in math (mostly complexity theory) and before this project I’d never heard of Ramsey theory, Szemeredi, combinatorial lines, or anything like that. So I couldn’t really contribute (aside from the comment on the wiki about having a logo). But at the same time it was immensely exciting to watch the collaboration take place, which inspired me to really get back into math. In particular I’m really sold on this entire field now of ramsey theory/probabilistic combinatorics.
The linear format of the blog was wonderful in that it enabled my inspiration to come via observing the process of research. And the wiki was great too, since over the past two weeks I’ve been catching up on all of the pre-requisite math to actually understand what’s going on. While the “easier” proof of the corners theorem by Ajtai-Szem was a big moment for Tim et.al., it was also a great moment for me because it solidified my whole understanding of the project – afterwards I went back and read through many of the comments again to better interpret the discussion. So to me, the real value of the project was simply that intermediate steps were being written up, rather than the usual “write up only when you have a paper to publish”. And indeed it was inspiring to know that I could contribute in principle, it was just that any contribution I could make would have been redundant.
I’ve been experimenting now, offline, with little steps on things like trying to characterize the configurations of form {a+f(x), b+g(x)} that can be found in N, using the techniques I learned from observing the project. It would still be quite a long time before I would feel confident in contributing to the project, without a lot more context and a better understanding of the notation. Math, like chess, has a rather well-defined continuum of ability (although it is more multifaceted), so 1) the most experienced and talented simply manipulate more advanced concepts, and 2) in this case, the Tim was already more than capable of solving the question himself, just using the help and input of others. At the same time, the obvious capabilities of Tim, et.al. was also a major part of what drove my excitement on the project (the other part was the general notion of an open and well-attributed style of math research).
An optimistic speculation is the following: that given that the set of all existing available human knowledge is enough to solve a certain problem, then it will be solved under the polymath system very rapidly – i.e. first every person spools in their knowledge, the sum is enough, then the answer comes out by some form of efficient mixing.
One interesting type of problem to try is the kind that is very accessible, but seems to require much creativity or outside-the-box thinking (whereas DHJ was more towards the level of dissection). One might negatively call this “recreational math”, but by removing the need to try to learn a whole field of research math, perhaps I would have been able to contribute. And recreational math is likely in my opinion to turn up interesting connections, especially given the distributed brain available via polymath.
There is also the idea of posing a question that doesn’t satisfy the criteria “Tim could just solve it himself if somebody told him a few good ideas” – for instance the Goldbach conjecture. Then I definitely might have been tempted to make some number of comments, although with high likelihood they would have been useless. However, optimistically all of the obvious “faq” like comments would be addressed early and incrementally, so newcomers would be able to quickly get up to speed by reading through “all of the obvious things that an amateur might try that fail” (which is separate from “things that a professional tried and failed that were also interesting enough to write a paper about or be in the princeton companion”).
A couple problems that would arise in opening up the subject matter to a broader audience, are 1) wading through huge amounts of spam and 2) lack of control over any kind of community. We certainly can’t predict what would happen. On the flip side I believe Tim found that casually reading through even non-relevant comments might cause him to have a brilliant idea. At any rate I truly feel that there is some potential future where much of “the current state of research mathematics” is written out on wikis like the polymath wiki, as a result of projects like polymath1 – and that would be a remarkable advance.
March 11, 2009 at 12:28 am
I mean {a+f(x), a+g(x)}.
March 11, 2009 at 12:56 am
Also sorry – pointlessly long and redundant with Tim who thinks like me but more powerfully.
March 11, 2009 at 12:52 am |
“the problem I chose lent itself more naturally to a smaller collaboration, since in order to be well placed to think about the density Hales-Jewett theorem it was a huge help to be familiar with, and to have thought hard about, other related results”
This excluded me. The barrier to entry was too high (or at least I evaluated it as too high at the start of the discussion) and I had other things I could be doing, even as spectacularly exciting as this sounded.
“it should be possible to contribute with virtually no prior knowledge” – I await this eagerly. 😀
March 11, 2009 at 12:56 am |
In my case I was intrigued by the project enough to take a look, but ended up not contributing. I think mainly this was because I was intimidated by the amount of background material it seemed necessary to know to make an effective contribution. And to a lesser extent, I didn’t contribute because I had other research that I needed to finish up and get written up within that time frame, and didn’t want to let myself get distracted from that.
But also, I don’t have a strong feeling (and still really don’t) why DHJ(3) is worth spending so much effort to prove — don’t get me wrong, I’m happy that you seem to have succeeded, I’ve used Ramsey theory more than once in my own research so I’m a believer in the value of that area of mathematics in general, and I trust your taste in problems. It’s just that I haven’t seen enough explicit motivation for that specific problem to get myself to spend the effort to learn the background material and to think about the problem at the obsessive level needed to make progress. And now it seems like you might be able to extend the proof to DHJ(k) in general, but at the start it seemed more like “here’s a special case of a known result that we might be able to get a different proof of that’s more combinatorial than the previous proof” and it was hard to get excited about that.
March 11, 2009 at 2:03 am
I guess DHJ is known to experts in the field to be an interesting question, partly because it implies a number of other deep theorems (e.g. Szemeredi’s theorem, which was for instance a key tool in my result with Ben that the primes contain arbitrarily long arithmetic progressions), but also because it (until very recently) was one of the most prominent density Ramsey theorems that could only be proven by ergodic theoretic techniques. I myself am a big believer in exploiting more systematically the connections between ergodic theory, combinatorics, and Fourier analysis, and so this project was certainly very appealing to me. Besides, historically every new proof of Szemeredi’s theorem has led to a substantial amount of progress and activity in at least one subfield of mathematics; now that we have yet another proof (the fifth genuinely new proof of Szemeredi, by my count), one can hope that the tools developed here will have some applicability elsewhere.
March 11, 2009 at 1:35 am |
The project involved too much background that’s unrelated to what I work on. Earlier on in grad school I might have plunged into learning it to try to follow (because the polymath idea is something I’d really enjoy), but now that I have so many other things I’m working on I couldn’t really make that commitment. If it were something that touched on a subject I already knew I would have tried to get involved.
I think one of the real benefits of this project is that young graduate students in the future will be able to read through the comment archives and see how top mathematicians actually think and approach a problem. So often the key steps are done in private that it’s hard to learn how people actually solve problems.
March 11, 2009 at 2:33 am |
I think the type of ad hoc structure we had here (with threads, wikis, spreadsheets, comment numbering systems, etc. rigged up as we went along) allowed us to scale up the size of the collaboration from the traditional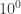 or so people to closer to
or so people to closer to 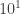 (plus maybe up to
(plus maybe up to  mostly silent audience members). But I don’t think the format we have would scale up by any further orders of magnitude; there would just be far too much activity concentrated in one place to be able to keep current unless one was basically devoted full time to the project.
mostly silent audience members). But I don’t think the format we have would scale up by any further orders of magnitude; there would just be far too much activity concentrated in one place to be able to keep current unless one was basically devoted full time to the project.
But one could imagine that, instead of having one massive polymath project with 100+ active contributors, one could have ten loosely related polymath projects sharing some common resources (e.g. a common wiki), with 10+ active participants in each, and a scattering of people involved in two or more of the projects at a time, and being able to import and export ideas and questions (and manpower) from one project to an adjacent project whenever it becomes necessary. (A polypolymath project, in other words.) This seems to be the most practical way to scale up even further, though it is going to be a long time, I think, before these sorts of collaborations become routine enough that we can reach that rung in the hierarchy.
March 11, 2009 at 4:13 am |
Dear Tim,
Like Toby, I was pleased by the aside rant on “begging the question”.
I have followed the developments here quite closely, although the subject
matter was too far from things I know about for me to be able to contribute.
I think that when one has several top experts thinking hard about the question
and posting several times a day, it certainly creates a barrier to others entering
the discussion: when significant ideas are clearly being generated and discussed at a
rapid rate, trying to absorb them, so as to be able to comment fruitfully to move the discussion forward, could easily be a full-time commitment, which many potential
contributors (on any topic) are not in a position to make.
In the initial discussion of the project, the idea was proposed that the project
would create its own brain, by using just a small number of bits from many contributors individual brains. I don’t think that it worked out like this: clearly at least some key contributors devoted many of the bits of their own brains to the project. (You acknowledge this about yourself in your post.)
But I don’t think either of these points (which are really the same point, I guess) is necessarily a negative. Clearly the project generated a fantastically successful collaboration, and seeing it documented online I think was exciting for many (certainly for me). It’s easy to imagine that this online record will be valuable in many different ways: for students wanting to learn about the field, or just wanting to learn how research is done; from a history and philosophy of science mathematics perspective; as inspiration; and surely in other ways too.
I don’t think that it’s a trivial thing to have found a successful new model for mathematical collaboration, what one might call open collaboration (massive or not).
Congratulations to you and to all the contributors to the project!
Best wishes,
Matt
March 11, 2009 at 4:48 am |
Regarding the amount of background knowledge required, while on the thread here it did stray through intimidating territory (I could read most of it but I didn’t feel comfortable enough to contribute), on Terry’s blog the arguments (though elaborate in the case of Moser) were relatively elementary.
March 11, 2009 at 5:34 am |
To open up a somewhat different topic, it seems that both of the main mathematical threads of this project are nearing the end of the “research” phase and thus approaching the “writing” phase. Thus far we have been using the wiki to hammer out drafts of various bits and pieces of the argument, and allowing a certain amount of loose language, vaguely defined terms, etc. in order to not get bogged down in technicalities. This is fine for getting a sketch of all the main mathematical points written up, but it seems infeasible to do the same for writing the publication-quality papers that will presumably eventuate from this project, especially given that it is not so easy to convert wiki HTML to LaTeX or back. On the other hand, the wiki would be a great place to do version control, and a running blog thread can serve for proofreading and other writing suggestions.
Given that one of the main contributions of this project has been to open up the process of mathematical research a bit, I suppose we can try to do the same for the process of mathematical writing. I don’t know if there is any collaborative software out there that would let us write up a LaTeX document like a wiki, but we can perhaps use cruder and more ad hoc methods, e.g. someone uploads a skeleton TeX and PDF file of a paper to be discussed, and after a while “control” of the paper (or of sections of the paper) gets handed to another participant, with various fragments of the paper eventually being merged together at some point. (Most of my traditional collaborations use some permutation of this method.)
The one technical obstacle I see so far is that the wiki we have right now doesn’t easily support uploading of TeX and PDF files. I suppose we can improvise using our own separate web pages (we have already been doing this on my polymath threads, especially with regards to computer data) to hold various versions of the draft paper, and keeping track of all these versions at some page on the wiki.
March 11, 2009 at 5:54 am
Jacques Distler has modified a wiki software called instiki so that there is a “one click” option to convert a given page in LaTeX:
http://golem.ph.utexas.edu/instiki/show/HomePage
Apparently, it is not hard to set up a wiki using this software.
March 11, 2009 at 6:24 am
Even better would be a wiki software in which one uses LaTeX as the markup language. Unfortunately, I don’t think something like this exists.
March 11, 2009 at 10:52 am
I have heard of Latexki, “a collaboration tool to create LaTeX documents”. Seems to fit the bill.
March 13, 2009 at 3:36 pm
I’ve written an online collaborative LaTeX editor called ScribTeX which might suit your needs:
http://www.scribtex.com
Congratulations on all the work you’ve done here!
March 19, 2009 at 9:37 am
Mercurial is your friend:
http://www.selenic.com/mercurial/wiki/
I’ve set it up before when my old hoster didn’t allow me to install things on the server. So, I did a local install to my $HOME and it worked just fine.
I know that every person I’ve talked to in research is adverse to such things. But, learning two or three commands and using them is a fair bit more convenient than manually keeping track of versions, manually uploading them, etc, etc, etc.
Of course, CVS/SVN/etc would be fine as well. It’s just that Mercurial requires *much* less from the IT guy/department/whatever. So, it can be a DIY project as well.
March 11, 2009 at 5:43 am |
I would mostly just like to give a big “thank you” to Tim for doing this. I didn’t really even know what a blog was, and found out about your polymath experiment rather by accident, through a student’s offhand comment. It is probably the case that many people who would like to have known about it, didn’t know about it.
March 11, 2009 at 7:55 am |
Congratulations to all of you on a job well done over the past weeks!
March 11, 2009 at 9:56 am |
What I’m wondering about is whether one thing that made this project to work for you (on which my most sincere congratulations) wasn’t specifically the fact that this problem had both very limited appeal to a wider audience (from the DAMTP side of things DHJ(3) looks rather arcane) and a rather high barrier to entry in terms of prior knowledge.
If you were to try this kind of project with a well-known problem whose formulation is comprehensible to a wider audience (say the Ulam series, the normality of Pi, or some such), wouldn’t you have to worry about drowning in crank “contributions” that would make moderation of the discussion a rather time-consuming task?
March 11, 2009 at 4:02 pm
I have been thinking about how a polymath of the normality of pi specifically would look. There are (are as far as I know) only two plausable approaches:
1. Getting a full understanding of the research related to the BBP formula. It’s possible a simple push will get the rest of the way, but I personally believe the reason why the formula exists needs to be better understood. Furthermore it needs generalization; I believe there are other BBP-type formulas out there, and if they can all be brought together, it ought to be possible to have multiple ways of obtaining a specific digit of pi, making a normality proof more plausable.
2. Working from the end of continued fractions, which could be connected to normality (although nobody has successfully done so). Very few people likely have the initial background knowledge required, so this would likely start as a “reading seminar” type post and move from there.
If discussion was restricted to one of these two with the actual normality of pi on the “back burner”, likely there wouldn’t be too many interruptions from cranks.
March 11, 2009 at 7:18 pm
Moderation of the discussion can be done on a lower level than contribution to the discussion; for instance, given any broad subject on Wikipedia, there are probably only a few dozen people who regularly contribute actual content, but there are likely several hundred with less knowledge of the subject or access to sources who clean up the articles, discuss improvements on the talk page, etc.
Tim and Terry have both pointed out that there were considerably many more of us “watching from the sidelines” than there were making substantial contributions to the project, and I feel as if their eventual role might be to perform low-level moderation. I certainly don’t know much about the BBS formula, but I feel like I could distinguish between an expert and a crank pretty well most of the time.
March 15, 2009 at 8:03 pm
Two blog posts this weekend discuss the BBP formula in further depth:
Foxmaths (near the end, mentions how the formula was discovered)
Gödel’s Lost Letter and P=NP (about the complexity class of the algorithm)
March 11, 2009 at 12:03 pm |
From one or two of the comments here it seems that I should have said more about the motivation for DHJ(3). The reason I didn’t is that I belong to a corner of mathematics where it’s just obvious that this is a problem worth studying. Terry has explained the main reasons for this (in his reply to D. Eppstein above). DHJ(3) was an example of the kind of problem Erdos was famous for: if you come to it cold you may wonder why anyone should be interested, but there are indications that it will be more or less impossible to solve without having ideas of much more general applicability.
March 11, 2009 at 1:51 pm |
I followed the initial pointer from Terry’s blog, and read the first hundred or so posts. No doubt a lot went over my head, but I got a couple of the referenced papers and tried to read them.
Terry identified some elementary questions for his blog, and I found I could contribute to that. It was great fun, firstly as an extended puzzle, and secondly puzzle-solving as a team game.
I am light-years from being able to contribute to the actual DHJ, and I am sure Terry could have done all we did by himself much more quickly, but thankyou Tim and Terry for this project.
March 11, 2009 at 2:51 pm |
A couple other observations:
1. In some cases I believe there was an “expert momentum” thing going on that made me not want to contribute. For example, once the solution on Moser got moving I felt no need to try to contribute, because the people hacking at it (Kristal, Michael, Terry, people providing computer data) were doing such a good job a solution seemed inevitable. (It was highly entertaining to watch. I fantasize about R(5,5) being solved this way.)
2. Related to that is the possibility of working out a solution, but being beaten to the punch. This made me feel nervous working on Fujimura’s problem.
3. There was on occasion where I hit some notational snag because it was explained in an earlier message. For example, I didn’t fully grasp the equal-slices notation at first.
March 11, 2009 at 6:33 pm |
Polymath projects might benefit from better publicity. I know it’s been mentioned that there exist potential collaborators who aren’t active in the blogosphere or who otherwise are unaware that this project exists; there are certainly steps that could be taken to promote awareness of this project in the mathematical community. Perhaps some of the more prominent contributors could begin giving talks about the nature of the project and interesting results and questions that arose as a consequence of it? Actually, the idea of an army of lecturers giving talks on the results in the wiki all over the country sounds pretty good (although perhaps this should wait until the “writing” phase is over?).
One issue with increased publicity would be an increase in crank comments, but a system designed to handle a greater order of magnitude of collaborators would need to handle this anyway. But I think it would be worth it, especially if, say, a non-mathematician heard about polymath who had a particularly good idea about how to organize future projects properly.
March 11, 2009 at 7:21 pm |
[…] two new posts on Tim Gowers’s blog entitled “Problem solved probably” and “polymath1 and open collaborative mathematics.” It appears that ”polymath1” have led to a new proof for the density version of […]
March 11, 2009 at 7:37 pm |
It recently occurred to me that the polymath project may well represent a personal milestone: for years (ever since I wrote two joint papers with Bernard Maurey) my Erdos number has been 4, and in a silly way I was quite proud of managing to be an Erdos-style combinatorialist with an unusually high number. However, if polymath starts publishing, as I assume it will, what is my Erdos number then? There are two questions here. The first is to evaluate m=min EN was a participant in the polymath project
was a participant in the polymath project The second is to decide whether if we publish as a collective without giving individual names on the paper (which is my preferred convention) this reduces my Erdos number to m+1 (if m+1 is less than 4).
The second is to decide whether if we publish as a collective without giving individual names on the paper (which is my preferred convention) this reduces my Erdos number to m+1 (if m+1 is less than 4).
March 12, 2009 at 5:20 am
No paper with Bela?
March 11, 2009 at 7:37 pm |
I wish I could have contributed, but I’m not so much an expert in additive combinatorics as an interested undergrad, and the high barrier to entry and level of time commitment meant that I couldn’t.
Another potential application for polymath-style collaboration might be to try to develop a well-defined but underexplored area of mathematics, rather than working toward a concrete goal as in this instance. This has a few obvious disadvantages (it’s nearly impossible to tell when it’s “done,” for example, and the likelihood of going off on wild-goose chases and not realizing it is considerably higher) but it might also lower the barriers to entry, since one wouldn’t have to be familiar with a lot of specific literature or even with the entirety of the project thus far, and the community can more-or-less automatically adjust its goals as it goes along. I’m not at all sure this would work (and I’ve no idea what would be worked on), but it’d be interesting to see how open collaboration would extend to theory-builders rather than just problem-solvers.
March 11, 2009 at 7:42 pm |
What struck me, watching the discussion with interest, was the real insight this gave into the processes of mathematical problem solving. With this in mind I would suggest that the bibliographies on the Wiki could be expanded to include more basic introductory works, which will be well known to active participants, but which might help observers to follow the arguments a little more closely – maybe doing a little of this as you go along, but also – if this is to remain as a record in cyberspace – as consolidation. Where would an intelligent student who knows little about the field need to begin?
March 11, 2009 at 8:05 pm |
Here are some scattered thoughts about the very successful polymath1:
A) I hope the current project will continue to the DHJ(k) and perhaps some other topics around cup-sets/Roth/Szemeredi’s etc. (Including discussing: what is the true value for Roth/cup set problem.)
B) Here are 4 questions regarding open collaboration like this:
1) Was it too hectic?
2) Need such a project be orchestrated. (Is it more like a bunch of musicians playing together or in turns or like an orchestra or like a Jass band).
3) Will such open collaborations make the community more polarized or less? (And is it beneficial.)
4) Is it “macho.” (I.e., another aspect of our profession which is more inviting to men compared to women.)
C) I’d love to see an open collaboration around Hirsch’s conjecture (or better its combinatorial version. See here http://gilkalai.wordpress.com/2008/12/01/a-diameter-problem-7/ ) It looks overall within reach.
March 11, 2009 at 8:16 pm
Gil, I had the thought today, which I had somehow not noticed, that the vast majority of people who comment on mathematical blogs are male. The percentage seems to me to be far higher than the percentage of interested mathematicians who are male. So I too am a bit concerned about 4.
I actually can’t think of a single comment made by a woman on this blog, but I hope that’s either because I’ve forgotten about it or that some pseudonyms and anonymous comments have in fact belonged to women.
March 12, 2009 at 5:08 am
What about Kristal Cantwell (major contributor on the 700’s/900’s thread)? I’m just guessing from the name.
March 12, 2009 at 3:23 pm
I think there is a certain tendency for men and women to segregate, and this tendency may be stronger on the internet than one might expect from other contexts. I don’t have any numbers to back this up, but anecdotally at least, it seems that a blog written by a woman will have disproportionately many links to and from blogs written by women, and similarly for men, even after one allows for subject matter. Perhaps this also applies to frequent commenters on blogs. So it’s possible that the picture the average male or female blogger would get ‘locally’ will give a biased estimate of the internet as a whole.
I have seen a few blogs by women who are interested in mathematics, but in most cases the authors seem to be either students or amateur mathematicians, rather than more established figures. This may or may not have something to do with the overall demographics of the maths community.
March 11, 2009 at 9:48 pm |
Gil and Jozsef have Erdos #2 (via Noga and Jaroslav respectively). (I myself am #3, via multiple paths.)
I quite like the idea that the Polymath1 wiki will morph over time into a general resource for Ramsey theory, while still containing of course with a historical record of progress in the Polymath1 project. I added the classic Graham-Rothschild-Spencer book to the references; of course we can encourage more additions. I’ve forked the bibliography off of the (protected) main page so that it can be more easily added to, at
http://michaelnielsen.org/polymath1/index.php?title=Bibliography
contributions are of course welcome!
I have also, partly for my own amusement, set up a timeline of events and key milestones in the polymath1 project so far at
http://michaelnielsen.org/polymath1/index.php?title=Timeline
March 12, 2009 at 5:11 pm
As do Randall (via Hindman) and I (via Bollobas or Saks). Tim & Terry, you’re the outliers 🙂
March 11, 2009 at 9:52 pm |
Dear Tim,
I think that the project was a rather nice idea, but I was not able to keep up with many of the comments, as I have so many other responsibilities right now that take up my time (committee work, teaching, writing research papers). This is the main reason I didn’t post anything on your blog; but, there was also the issue of not wanting to write something obviously wrong (upon looking at it later) to such a visible blog as yours, though I suppose one could post anonymously.
Two more comments: it seems to me that there are some types of solutions to math problems that start with risky ideas, that
don’t look like they will go anywhere, but do. Such ideas are not likely to be entertained by others in a blog like this. In other words, the solutions that the blog approach seems good at uncovering are those reached by small steps, using standard ideas, that lots of people agree look viable.
My second comment is that I worry that if this type of blog approach to doing research becomes popular, it could have negative professional repercussions. For my own case, I am glad you chose the DHJ problem, instead of the F_3 cap set problem (improve Roth-Meshulam), which is a problem I (and many others) have devoted years to attempting to solve. It would be somewhat demoralizing to see that problem solved in six weeks of massive collaborative effort; and, it could negatively affect one in other ways (grant support, salary, etc.). Of course, one can always try to find alternate proofs; but, it has been my experience that there is much more respect for solutions to old, stubborn problems, than there is for new proofs.
March 11, 2009 at 10:19 pm
Ernie, your points are interesting — in particular, the one about the particular problem chosen. I too would love to solve the F_3 cap set problem, and there are other problems like that, that a lot of people are very keen on, where doing it collaboratively would risk putting people in a difficult position (whether to share their ideas, or just hope that the multiple collaboration is unsuccessful). I shall try to avoid such problems. But I’d be interested to know whether you would find it more demoralizing to see one of your all-time favourite problems solved quickly in this way than it would be just to see it solved by someone else using the conventional approach.
March 12, 2009 at 12:39 am
Dear Tim,
I think I would be more demoralized by a large group solving it than an individual. Also, if the problem were solved by an individual in this way, these negative feelings would be quickly replaced by awe and admiration for that person; but, with a group solving the problem, it would be harder for me to know where to place my respect — groups are impersonal. That said, as far as the DHJ problem is concerned, I rather liked all of the ideas that people had, and have respect for everyone involved. The proof turned out to be very beautiful indeed!
March 12, 2009 at 10:04 pm
Here’s a related difficulty. Suppose I take the attitude, “If you can’t beat ’em, join ’em.” That is, when I see Polymath getting interested in one of my problems, I decide to join Polymath. Even if things work out beautifully from a mathematical point of view—say my ideas prove to be critical, while at the same time I could not have had those ideas without the input of others, and the problem is solved when it might not have been solved otherwise—it might not work out well from the point of view of getting credit. I’ve already encountered the following reaction from some people when I tell them about polymath1: “Oh, that just proves once again that Gowers and Tao are geniuses.” It confirms a suspicion I had before polymath1 really got started—few people are going to sort through the 1000 comments to assess the value of individual contributions. Most will make snap judgments, and the easiest snap judgment to make is that the handful of famous people involved did all the really important stuff.
It reminds me of the famous Alpher-Bethe-Gamow paper. It’s fairly well known that there were only two “real” contributors to the paper, and the third author was thrown in just for the sake of the pun. Since Bethe and Gamow are famous, many people assume that Alpher was the pseudo-author. In fact Bethe was the pseudo-author and Alpher had to fight the misconception his whole professional life, becoming quite bitter about it, especially since he had foreseen the problem at the very beginning and had vehemently objected to adding Bethe (but was ultimately unable to stop Gamow).
March 12, 2009 at 10:21 pm
By the way, I want to add that I think polymath1 was a great idea and a great success and I hope there will be more projects like it in the future. Collaborative efforts like this appeal to my personal temperament a lot, and I failed to jump into polymath1 only because I didn’t have the requisite background. But I’m keenly aware that my enthusiasm for Polymath comes partly from the fact that I’ve reached a point where I have the luxury of not worrying about having to prove to people that I’m a capable researcher. Polymath is a good thing for mathematics as a subject, but at least in the short term it could be a threat to anyone who needs to prove their worth to others.
March 11, 2009 at 11:11 pm |
Though I originally I planned to contribute, and even posted some minor comments in the beginning, I dropped out for two main reasons:
1) Keeping up with what the huge volume of comments that contained half-baked ideas required a lot of time.
2) I felt that my efforts duplicate the efforts of the others participants in polymath. By the time I finished a thought, someone would sometimes already post something quite similar. I figured that my time is better spent on problems that do not get as much attention.
Boris
March 13, 2009 at 10:07 am
Boris, I wondered why you had dropped out. Of course, it’s entirely your decision whether it was the best use of your time, but I cannot agree that the comments that you made were minor. In particular, your comments on obstructions to uniformity were a significant contribution to the discussion at that point, for which many thanks.
March 15, 2009 at 11:16 pm
I second what Time said about forbiding minors. I think sets satisfying equations proposed by Boris may be useful both as obstructions for unifrmity and as actual examples for sets avoiding various structures (lines etc.) Sort like the pre Behrend examples. Actually I once unoticedly duplicated a comment Boris made and felt quite proud about it…
March 11, 2009 at 11:18 pm |
It occurs to me that one thing that was missing from the polymath project, which was a list of ways in which casual participants could help contribute (i.e. without first reading hundreds of comments to catch up). I’ve put a preliminary list of this type at the bottom of the main wiki page. It doesn’t have many suggestions right now (basically, contribute to the bibliography, or to the discussion here)), but perhaps it could be expanded.
March 12, 2009 at 12:46 am
We definitely could use more visualizations (I think Thomas Sauvaget is the only one so far who has depicted c_n visually), although things would first have to be packaged in such a way that a casual participant could understand and make such a thing.
March 12, 2009 at 12:58 am |
Tim – an example of a woman commenting on this blog:
March 12, 2009 at 1:29 am
Ah yes — I’d forgotten about Carrie, whom I know and who has an interesting blog of her own.
March 12, 2009 at 8:21 am |
It’s true that I am female, but I am not a mathematician by calling, so it may still be that no female mathematician has commmented. I haven’t done any proper research into this question but I have the impression that in philosophy there are a fair number of female bloggers and blog commentators (fair given the proportion of philosohers who are women). If there is a discrepancy between our disciplines it would be interesting to know why.
March 12, 2009 at 9:00 am |
A comment purely on practical matters. I suggested earlier that a forum might be better than a blog for this type of project but got – justifiably! – shot down because I couldn’t produce one. Well, I can now. [bbPress](http://bbpress.org) is a forum system built by the same people that designed wordpress, and it’s designed to live happily side-by-side with wordpress. I’ve managed to adapt one of the wordpress LaTeX plugins for use with bbPress so it is now possible to have a LaTeX-enabled forum. If you, or anyone else, wanted to do another polymath problem and wanted to try a forum format then I’d be happy to help with setting it up.
March 12, 2009 at 11:49 am |
A thought that’s a mixture of practical and fundamental. It seems that, quite understandably, some people were reluctant to contribute because they didn’t want to seem foolish. I remember the feeling of liberation I had when I became sufficiently established not to mind asking stupid questions in seminars, but it definitely didn’t happen immediately — as a beginning graduate student I’d have been mortified to ask a question that had an answer that was obvious to most people, or that revealed some misunderstanding of what the speaker was saying. And it doesn’t seem to be enough to say, as I did at the beginning of the project, that “stupid” comments are welcome.
I’ve been wondering whether there might be a way of dealing with this, by having some kind of area where people can make comments less publicly. For instance, there could be a place where everyone could post comments, but only a few moderators could read them. These moderators would then email the posters of comments, and responses could range from “Great idea — you should definitely go public on this one” at one end of the spectrum to something like “If you look at comment 126, you will see that this has already been discussed, and it doesn’t work” at the other.
That way, people could make comments without the risk of seeming foolish, except perhaps to the small team of moderators who would be chosen for their great kindness and understanding.
At the moment, the main snag I can see with this idea is the possible difficulty of finding the moderators — it could be quite a bit of work. On the other hand, maybe that work would itself be a good way of getting involved.
March 12, 2009 at 5:43 pm
I think having that sort of gating is a terrible idea. To my mind one of the advantages of a polymath approach is that the person who has an idea doesn’t need to be the same person who realizes its a good idea or the person who makes it work. Recently in a smaller collaboration we had something where A suggested an idea, B gave a very compelling explanation of why it probably wouldn’t work, A bought the explanation so dropped the idea, and C didn’t buy the counterargument and went off and did the calculation, and low and behold it worked. If A or B had been the gate keeper here then progress wouldn’t have been made.
March 12, 2009 at 5:57 pm
Again, I wasn’t suggesting it for all comments — definitely not. I was suggesting it only as a means of getting useful comments out of people who would otherwise have remained silent (in which case something less than perfect is better than nothing at all). But even for this it may be suboptimal — a possibly better solution is suggested below.
March 13, 2009 at 12:55 am
Why on earth would anyone be afraid of making a stupid comment when it is possible to do so anonymously or pseudonymously (as I am doing)? If a shy junior researcher want to later get a share of the credit they can use a genuine email address, which can be used to authenticate them later.
This is a non-issue.
March 12, 2009 at 1:01 pm |
Personally, I think I’d feel MORE awkward having a moderator tell me which of my submissions were good than simply throwing them out to the world. But I’m pretty unembarrassed by asking questions in general, so maybe the policy shouldn’t be built around my preferences.
Another option would be for participants to choose a pseudonym if they think they may be posing a naive question.
March 12, 2009 at 1:48 pm
The idea would be that some people would feel like you, and would post in the normal way, whereas this other space would be a different option for the benefit of people who felt the other way — if there were any.
March 12, 2009 at 3:51 pm
I’m going to have to agree here from my experience as a K-12 teacher — having a moderator check first would make people even more sheepish.
The best thing to overcome that is to have a “critical mass” of people asking stupid questions.
I know I asked at least one (there was some point I needed clarified in one argument that turned out to be trivial) but there were a couple others that came up I never posted not because I was afraid, but I didn’t want to interrupt the flow of thought. (Having threading helps with this.)
I was going to cite the super-optimist conjecture I made (which was disproved in something like 10 minutes) as another stupid comment, but the semi-optimist conjecture based on it seems extremely promising, which demonstrates another reason it’s ok to ask stupid questions.
March 12, 2009 at 4:47 pm
I agree that the critical mass idea is better, if it happens. Also, moderators needn’t be in the position of judges — they could just offer a bit of feedback and leave it up to the potential commenter to decide what to do.
Another idea, perhaps better, would be to have different comment threads, but not so much for different subject matter as for different purposes. For instance, one could have a mainly expository thread, where people could post comments like, “X wrote`by an argument similar to Shelah’s proof of the Hales-Jewett theorem. Does anyone know a good reference for that?” and somebody else might respond by sketching the proof, preferably on the wiki. And on that thread, someone who didn’t know about the area might feel happier to post a comment like, “The discussion has left me behind for now, but can someone tell me why a simple-minded argument like this doesn’t work?” and follow it with an explanation of an approach that the poster knew had no chance of working. Such a comment might be unsuitable for the main thread, because it would interrupt the flow, but nevertheless valuable as a way of improving the collective understanding of the problem.
Anyhow, my proposal was just meant as a zeroth approximation. Perhaps this new one could serve as a first.
March 12, 2009 at 6:05 pm
While I still would prefer stupid questions to new material be addressed in the main thread (due to it being likely others may have the same question, and also to help build the critical mass) I can see a expository thread being useful for those trying to catch up with earlier material. I can’t imagine posting a question about something that happened back in the 200s long after the thread has been closed. Even asking about something that happened only 50 comments back likely seems awkward to the casual observer.
Concurrent to that, the expository thread might help those simply trying to learn the subject in question (when Ryan’s comments started jumping past my knowledge I would have liked to ask about some the concepts at a more elementary level).
March 12, 2009 at 8:27 pm
Just to leave my note on the balancing side, Tim’s original idea would indeed work for my personality – I would feel comfortable exposing my incomplete thoughts in a private forum to get exactly the kind of feedback Tim proposes (either “ah you have an incomplete misunderstanding”, or “that’s interesting post it to the blog and take credit”).
March 13, 2009 at 2:41 pm
John, I’ve been thinking about your dilemma: instead of a thread would it help to have someone offer an open an email address designed for moderation? Then you can get a private message about if it should be put in the thread, yet because it’s a side feature it shouldn’t get anyone nervous about posting to the main thread.
However, saying all that, I’m still against it. Let me give a specific example why.
In the other thread I just made a “semi-optimist conjecture” which is a perfect example of a stupid comment a moderator might shoot down — it only is true by violating something in the original definitions we’ve been working with.
However, because it was based on experimental data (why I formed it in the first place), it led Terry to realize something was wrong and Klas to spot the bug in the program he was using.
A moderator not might not notice that connection, and we’d never spot the problem and we’d still be using the bad data.
In other words, even the most basic-premise-violating of stupid comments may yield something useful.
March 13, 2009 at 4:48 pm
I have to agree with Jason both on the specific example and on the general principle: “dumb” questions should be encouraged (in addition to “smart” questions, of course :-).
March 12, 2009 at 6:09 pm |
> I definitely intend to start another polymath project
How about allowing all interested parties to record their e-mail
addresses somewhere to be notified when this new project starts off?
> I would be very interested to hear from anyone who thought that they
> might like to contribute but ended up not doing so.
One of the reasons for me is that the project was spread in a pretty
chaotic way between half-a-dozen+ threats, and just browsing all these
threads systematically is a lot of work! It was probably a good idea to
keep the project non-linear, but it would be great to have this
non-linearity well-organized. (No practical suggestions though as to
exactly how to organize it.)
Another reason is the absence of appropriate references and the fact that
not all participants always made enough effort to be clear and present
appropriate context. As a curious example: I know from Tim’s
introduction to this thread that the problem seems to be solved, but I do
not know where to look for the solution! (Is it in the “second outline of a
density-increment argument”? I can only guess!)
March 12, 2009 at 8:26 pm |
This comment is mainly aimed at the participants in polymath1, though others may have useful thoughts about it.
It does seem very much as though we should be writing up a complete proof of DHJ(k). Up to now, the policy has been that whoever can first be bothered to write something up (on the wiki) does so, but I think for the actual paper a bit more planning is required, both of the write-up itself (how to organize the paper into sections and subsections, etc.) and of how we go about producing it. To get the discussion started, here are a few thoughts.
1. I have one or two very strong, but I think uncontroversial, views about the style of the paper: basically, it should be as easy to understand as possible, and aimed at a reader who is not necessarily an expert in additive combinatorics. So if anybody else writes part of the paper and I find it hard to understand, I will have a strong desire to rewrite it. I also like to err on the side of putting in too much detail of proofs rather than too little. (So not too many “it is easy to show that”s and the like.)
2. If, as seems to be the case, the proof has a nice modular structure, then we should work it out in advance. Then in principle different people could write (first drafts of) different modules.
3. I wouldn’t in fact mind writing the whole lot, at least if I could consult people from time to time. (I’m thinking particularly of Ryan and some of his nice arguments that should make parts of the proof run much more smoothly.) So I don’t think anyone should do any writing unless they would positively like to. But if they would positively like to, then I think we should share the writing in some appropriate way.
I’m sure I had some other thoughts, but they temporarily escape me and I’ve got to go for now.
March 12, 2009 at 9:11 pm |
Like many others, I followed the project at the beginning of the threads but since I didn’t have a particular expertise to draw on to start making comments, and then had other work/duties to take care of, I couldn’t continue reading thoroughly all the comments.
But this is definitely a very remarkable project. I actually think of it as a great illustration of how research works, which may be enormously useful by being completely open (so it can be given as example to people wondering what research is like…). Even if the framework and the number of people involved was very purposely different from the usual way mathematical research evolves, I still see a lot of similarities.
March 12, 2009 at 9:11 pm |
Congratulations to all who worked on this project! I think that the solution of DHJ(3) will help spread the word and probably any follow up project will have more initial participants and if that level persists throughout the pace will be faster. I worked mostly on the thread on DHJ numbers. I enjoyed my experience I can’t think of any major changes I want made. I suspect with time and increasing number of participants a lot of small changes will occur to make things run smoother as problems come up and are solved.
March 12, 2009 at 11:09 pm |
Regarding writing: what I plan to do soonish for the small-n side of the project is to plonk down on the wiki a skeletal outline of what the paper should look like (basically, section headings with a description of what would go inside them). This would not be in LaTeX, but just informal English at this point. Then the various stakeholders in the project can debate moving around the outline until it stabilises. At that point, I am envisaging converting the outline to a LaTeX template (to use as a baseline), and then have people contribute sections. At some late stage, these sections will be merged into a single paper. This plan may evolve depending on how impractical it becomes to do all this.
I don’t know yet what to do with the “Author” field of a paper. It is tempting to go the Bourbaki route and just have “A. Polymath” as the author (but presumably we will still need a human as the corresponding author, and of course in the main text of the paper we will expand out Polymath into a set of humans). On the other hand, for the purposes of citation counts, etc., which are (for better or for worse) valued in certain job evaluation metrics, we may need to put the names of participants in the author field. But then the question arises where one draws the line – does everyone who contributed a comment get billed as an author? It’s a bit of a delicate issue. And, for the reasons that Timothy mentioned above, there is the danger of the authorship list degenerating over time to something like “Gowers et al.”.
I suppose this issue must already come up in the physical and life sciences, where one routinely has papers with dozens of authors involved. I wonder how they deal with this problem…
March 12, 2009 at 11:26 pm
I’d be happy to do something similar for the large-n side, if others were happy to let me. Of course, that too would be just a starting point for debate.
I had imagined that the author would be Polymath, and that instead of mentioning authors there would be a link to the blog. (Or perhaps, since the blog has my name on it, it would be better to have a link to the wiki instead.) I am reluctant to have any names on the paper, for precisely the “Where do you draw the line?” reason: excluding anybody is very much not in the spirit of the project, but appearing on MathSciNet as a result of one small remark doesn’t make much sense either. It’s a knotty problem. I had imagined that on my CV I would put polymath papers to which I felt I had made a serious contribution in a separate section on my publication list, together with an explanatory note.
I can see that this comment is not going to be the end of this particular conversation.
March 13, 2009 at 12:12 am
I would not be too defeatist about existing metrics for measuring contributions to a collaborative exercise like this. It is a new way of doing things, and an experiment in opening up new possibilities.
This has two implications – those who contribute to the early efforts, and make worthwhile contributions, will register for the novelty value – and their contribution is overt and public. People can see exactly who has contributed and how.
If the Polymath way of doing things takes off so it becomes a regular way of doing collaborative mathematics, the metrics will have to change to take this new way of working into account.
It would be a real shame if the bold approach to doing mathematics were stifled by a belief that the structures could not be changed. I know structures can be conservative and appear rather stupid and unresponsive – but they can be challenged too.
[And on moderation – I can imagine, maybe some time hence, research grants approved to fund the moderation of some polymath project – the challenge, given the comments about people being busy, is to find a funding model which encourages participation – thus speaks the accountant]
March 13, 2009 at 12:12 am
On the credit issue:
I would probably vote for the “Bourbaki” method, for a couple of reasons: One, it’s relatively fair; I’m not sure it could lead to any significantly hurt feelings. Two, I believe it’s what Tim originally proposed, so one might argue that by contributing to the project, people were implicitly accepting his original rules. Three, I agree with Tim that it’s fine if a person lists their participation in a polymath project on their CV if they felt it was significant.
I would also be okay with the anybody-and-everybody-in-the-authors-list (alphabetized) method; in this case, if a person really felt they hadn’t contributed, they would be free to ask for their name to be removed. Personally, I don’t think it’s overly nonsensical to have dozens of people credited on mathscinet (why not? is my opinion), but I can certainly understand the position that it is.
I’d probably be against how they do it in the physical and life sciences, which I believe is to order the authors by some kind of importance measure.
March 18, 2009 at 6:05 pm
Terry – On the issue of how the physical sciences deal with it, it’s very common to just refer to the name of a collaboration. For example, it’s well known that the top quark was discovered by the CDF collaboration at FermiLab: http://en.wikipedia.org/wiki/Collider_Detector_at_Fermilab
I’m not a high energy physicist, so I don’t entirely understand how this impacts on jobs, but I imagine the main impact is to make letters of recommendation more important. My understanding is that the big collaborations have internal report series they use to help organize the collaborations internally. These would seem to play a role analogous to the blog and wiki discussion in Polymath, albeit far less open.
March 13, 2009 at 12:00 am |
Could we hold off on the actual writing for at least a little bit? I feel it might make the final paper significantly better if the ideas gestated slightly.
I certainly have had the experience of figuring out a complicated proof of a theorem and happily writing out the 30-page proof, only to see later that it could have been done in 10 pages, and more clearly, if I had taken the time to think the argument out carefully.
I mean, it doesn’t hurt to write the 30-page proof immediately, but it could lead to some wasted effort.
March 13, 2009 at 12:03 am
Having seen the wonderful cleaning up that you appear to be managing to do, I agree with you. I was slightly rattled by Gil Kalai’s suggestion that perhaps it was wrong to declare the problem (probably) solved, but my confidence in the proof increases with each comment you post (not to mention each time I revisit the argument and find no nasty surprises).
March 13, 2009 at 12:15 am
Well, like Gil I am also too nervous as a rule to declare any result proved until the last t is crossed, but that’s why I’m trying to go through the whole thing now slowly…
March 13, 2009 at 2:44 am |
I think it went really well… I know nothing about the field, but you solved a hard problem really quickly.
I think it had a lot to do with the “celebrity power” of Tim and Terry, though…
Like a lot of other people, I wish for a polymath project closer to what I actually do… and I have a concrete suggestion.
There are lots of problems involving combinatorics of Jacobi diagrams. These form a graded vector space over a field F (usually Q) spanned by finite graphs whose vertices have valence 1 or 3, and whose trivalent vertices are oriented (clockwise or counterclockwise), modulo a couple of local relations (called AS and IHX). See e.g. http://cornellmath.wordpress.com/2007/12/18/chord-diagrams-understanding-the-4t-relation/
They arise in quantum topology for knots and 3-manifolds. I think that some of these problems would make great polymath problems, and not only because I am personally interested in them, but because these problems admit many different avenues of attack (quantum algebra methods, number theory methods, combinatorics…), are accessible, have significant implications in quantum topology, and (I think) are beautiful. For example, can any Jacobi diagram be expressed via AS and IHX as a sum over F of planar Jacobi diagrams? (conjecture of S. Duzhin) Do all Jacobi diagrams with an odd number of 1-valent vertices vanish modulo AS and IHX?
March 13, 2009 at 9:19 am
1. If you were to start such a project, and if you assured me that there would be no danger of it rolling all over some research student’s PhD thesis, then I would be happy to give it lots of publicity on this blog.
2. If you were to explain the problems in clear and purely combinatorial ways (or perhaps combinatorial with just a hint of algebra …) then I might even try to participate.
The same goes for anyone else who thinks they might like to start an open collaboration. But 1 is quite important — I think we need procedures for dealing with this problem, and I don’t think we’ve thought through it properly yet.
March 13, 2009 at 9:15 am |
A quick remark that something I think we really ought to do soon is trawl through the various comment threads, pick up any interesting looking loose ends, and organize them properly on a wiki page. Many questions arose in the discussion that would still be well worth answering — an obvious example being to try to find global obstructions for sets that contain the wrong number of lines in equal-slices measure (I still hope that such sets correlate with 12-sets) — and there is a danger that they will get buried.
At some point, I imagine polymath1 will quieten down a bit, and investigating some of these problems could be a good way for new people to get involved. But a decent wiki page with proper explanation/motivation for the problems would undoubtedly help with that.
March 13, 2009 at 5:57 pm
Also we might get together a list of general suggestions for how people think polymath should be done in general. (Not jeopardizing a students thesis, for example.) One thought regarding your idea to make a list of new problems: it might be a good idea to keep the scope of any particular “polymath no. n” blog as narrow as possible (while maintaining a more general-purpose wiki). My idea is that participants in a blog pursuing proof of X agree to an implicit “social contract” whereby they don’t think too hard about X non-publically (and almost certainly don’t publish a proof of X, or at least a proof of the type being pursued in the project, on their own); if a blog pursuing X starts taking Y, Z and W indiscriminately under its umbrella, in addition to X, it might complicate the terms of said “contract”.
March 13, 2009 at 11:53 am |
[…] Polymath1 and open collaborative mathematics « Gowers’s Weblog […]
March 13, 2009 at 5:42 pm |
[…] Polymath1 and open collaborative mathemathics. O Polymath foi um experimento tentando resolver um problema de matemática colaborativamente, por […]
March 14, 2009 at 12:20 pm |
[…] Tim Gowers […]
March 14, 2009 at 1:29 pm |
A couple of questions, one about the polymath and one on the math.
First, as a reader who couldn’t follow in real time but was able to understand some postings long after their heydey, I wonder: how does one make a belated contribution to the discussion (not the proof)? Should one email the people principally involved with a given technical point, or not bother, or …?
Second, in the analysis of pure combinatorial Shelah-type arguments, probabilistic methods were still used as a source of intuition on what should be true. This raises, and does not beg, the question: are there any theorems whose Ramsey (pure combinatorial existence) version is true but whose Szemeredi (density) version is known or suspected to be false? Or are Ramsey results generally just waystations to the more intuitive but often harder to prove density statements?
March 14, 2009 at 1:43 pm
A quick answer to the second question: the density version of Ramsey’s theorem itself is false: a complete bipartite graph has density 1/2 but contains no triangle. Another well-known example of a colouring statement with no density counterpart is Schur’s theorem: if you colour the integers from 1 to (a sufficiently large) n with r colours then you can find x, y and z, all of the same colour, such that x+y=z. The odd numbers show that the density version is false. The question of when the Szemerédi phenomenon occurs and when it doesn’t is quite an interesting one.
March 14, 2009 at 1:44 pm |
For me the exciting parts seem to be the simpler proof and the need to rewrite in accessible language to enable people to join in. Maybe this can be made one of the explicit goals of the project. Not just to create new maths but to work on making mathematics that can be accessible.
I say the same thing, but in a more long winded way here.
Edmund
March 14, 2009 at 11:16 pm |
[…] Posted an item Michael Nielsen: Polymath1 and open collaborative mathematics « Gowers’s Weblog (via delicious) […]
March 15, 2009 at 6:45 am |
Now that the polymath1 project is well on track to a successful conclusion, perhaps it is now safe to raise the question of how one would deal the situation of a “failed” polymath project – one in which the problem turned out to be frustratingly out of reach of the available mathematical technology, or which somehow never accumulated enough momentum. I suppose that one of two things could happen: either a consensus would arise that the project should be closed, with any publishable partial results written up, or else the pace would simply slow down to a crawl, with most participants giving up and moving on to other activities. I suppose either outcome is not too bad (though it is never much fun to concede defeat, especially publicly), though the second outcome may become a problem if it “blocks” other mathematicians who want to have their own go at the problem, but for one reason or another are disinclined to do so via the polymath. At what point after a lull in activity would the problem be considered “fair game” again? Or can a polymath project perform the mathematical equivalent of “squatting” on a particular problem indefinitely?
March 15, 2009 at 11:03 am
Here’s what I wrote on this topic in the “official rules”.
14. If it becomes clear that the discussion has run out of steam, then anything that is worth writing up will be written up (this may well be a collaborative process) and submitted to the arXiv, for use by anybody who wishes to use it.
It’s not clear to me what should count as “worth writing up”, however, or whether a result that is interesting enough for the wiki but not interesting enough to be submitted to a journal has anything to gain from being polished and put on the arXiv. I suppose the test could be whether any of the participants feel like doing it.
More importantly, I didn’t say how we would decide whether a project had run out of steam. This has the potential to be a difficult issue, because it could well happen (as it does with conventional research projects) that the project would run out of steam more for social than mathematical reasons. That is, there might be a lot of promising ideas floating about, but not the energy to deal with them. And then there are several choices.
The first, which is the one I had imagined, is that somebody would post a comment saying, “I think I’ve reached my limit on this project,” and everyone else would rapidly agree, the wiki would be tidied up, and the resources created would be free for anyone to use as they saw fit (with, one hoped, a convention that if you made crucial use of an idea you found on polymath-n, you would credit polymath-n in your paper).
Another would be not to declare the project officially closed, but to leave it hanging there, so that if someone had an idea that could revive it again, it would continue, possibly with a rather different set of participants.
To avoid the risk of blocking of the kind you talk about, one could mix the two: if people wanted to contribute ideas via blog comments, they could do that, and if they wanted to make private use of polymath-n ideas they could do that too.
Incidentally, I’d also like to make the point that a number of the perceived difficulties with polymath are ones that already exist in conventional ways of doing things: the difference is just one of degree. For example, a PhD student can work on a problem, make quite a bit of progress, and be beaten to the finish by a much more experienced mathematician, or group of mathematicians, who becomes interested in the problem: that has happened to lots of people I know. And if people write a joint paper, there is a tendency to assume that the best known authors are the ones who have made the main contributions. I’m not saying that we shouldn’t take these difficulties seriously — we definitely should — but I don’t think they are deal-breakers.
On the subject of the PhD-wrecking problem, one might even make a case for polymath being better than the current system, because as things are at the moment there is no way of checking whether you are risking ruining someone’s life when you work on a problem, whereas because polymath is out in the open, there is the opportunity to check first.
And the same is true of the misguided-apportioning-of-credit problem: whatever else you might say, there is much more information to go on if the research has been fully public. (For instance, X might say, “Look, I am not as famous as Y, but go and read comments 345, 347, 382 and 383 and you will see that I contributed an idea that was enthusiastically taken up by the other contributors and was essential to the solution.”)
March 15, 2009 at 7:47 am |
1) I think with a large collaboration of this kind we can aim not only for success in settling the problems (which is, of course, the central goal) but also for higher standards in explaining the proof, improving the argument, making sure it is locally correct and detailed (hyperlinks can even allow to give details that are necessary for some while obvious for others), and in the exposition level of the paper. Since everything is in the open there is no preasure to rush on these matters.
2) I think the general rule for having research in the open is that at any point what was achieved or presented openly can be used by other mathematicians who want to have their own go at the problem or use some ideas for other purposes. Of course, if the project looks successful it can be optimal to join in in the open effort.
3) There are many interesting questions regarding such projects. Large open collaboration turned out too be, apparently a valuable resource; An important issue is how (and who is) to decide on a project; there are various issues regarding credits (and influence) which are of interest in ususal academic research that are of special interest here.
Of course, we should not forget also the joy and effectiveness of standard, often face-to-face collaboration. And of working alone.
4) More specifically to this project. Ernie wrote: “For my own case, I am glad you chose the DHJ problem, instead of the F_3 cap set problem (improve Roth-Meshulam), which is a problem I (and many others) have devoted years to attempting to solve. It would be somewhat demoralizing to see that problem solved in six weeks of massive collaborative effort; and, it could negatively affect one in other ways (grant support, salary, etc.).”
I think part of the reason for success here is that many people had some thoughts on the problem and related problems for year. So also for the cap set problem indeed quite a few people thought about it and worked on it and it is possible that an open discussion of avenues that were tried can by itself be useful.
5) In some sense the mode of work in the TCS (FOCS/STOC) community (and other very hot and hectic areas) is similar to open discussion mode (except that the posts are papers).
March 15, 2009 at 11:24 pm
I’ve been thinking about your point 4. I am one of the many people who has tried to solve the F_3 cap set problem, and I can’t help wondering, like you, whether enough people have enough slightly different thoughts about it that a largish open collaboration might work very well for it. I’m not actually suggesting it for the time being, but for my own part I’d rather be part of a big team who solved that problem than have a five percent chance of solving it individually before anyone else managed.
But that raises another issue. What if lots of people have had thoughts about a problem and there is considerable overlap between the thoughts? We wouldn’t want a silly race where people tried to post reasonably obvious ideas before anyone else in order to claim credit for them. I have a possible solution for this, which is to begin by setting up a wiki. The understanding would be that until the collaboration started in earnest one would put on the wiki only ideas that pretty well any expert who had thought hard about the problem would be likely to have had, so one would not in any way be claiming credit for them (but one might wish to stop others claiming credit for ideas that should rightly be considered reasonably standard). And only after all the standard ideas were there would one begin the search for genuinely new ones.
Another thought that occurs to me is that we could take some popular problem like the F_3 cap set problem and announce that polymath was going to attempt it, but only after some time lag such as two years. Then anybody who felt that they had made some serious progress that they didn’t want to share would have ample opportunity to explore their ideas and see whether they could push through to a solution; potential newcomers to the problem would have plenty of advance warning that the start of the polymath project was approaching, so they would know the risks in attempting it; and others might like time to think hard about the problem as individuals in order to be able to contribute better to the collective effort when the time came.
March 16, 2009 at 8:50 am
Dear Tim,
Regarding notorious problems like improving bounds for Roth or for the cap set problem. Maybe what is needed most is an open (candid) discussion about how people (mainly experts) see what the state of the art is. The most promising direction I am aware of for the cap set problem is the result by Sanders about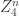 So what could be useful for people in the field (also in terms of expected future credit) is if this results and the new techniques are discussed and explained. (This can be a sort of follow up to the introduction of the problem in Terry’s blog and not necessarily a full fledge polymath effort.)
So what could be useful for people in the field (also in terms of expected future credit) is if this results and the new techniques are discussed and explained. (This can be a sort of follow up to the introduction of the problem in Terry’s blog and not necessarily a full fledge polymath effort.)
But even with a full fledge polymath cap set or Roth project I see higher probability that such a project will not lead to an improvement of the known bounds (as I am not sure if the technology is in place) but rather will give some better platform for researcher who will work on it in the future. and I see little chance for off-scale improvements of upper bounds.
There are ideas which seem long-shots in terms of the results they are expected to give. Exploring them openly (not necessarily in the polymath mode) may be helpful in shooting them down. (And may lead to some byproducts. And maybe maybe to success.)
For example, you mentioned (in this remark ) in a discussion of Elkin’s result the following:
“I recently came up with a slightly different way of proving Roth’s theorem, which I haven’t actually written up properly so can’t guarantee the correctness of, but it looks from that argument as though there is a chance of using strong bounds for Freiman’s theorem (which seem highly plausible, even though nobody has yet managed to prove them) to obtain Behrend-type bounds in Roth. Even this might be a good ‘open source’ project, though it would be too technical to be massively collaborative.”
The possibility that a different proof of Roth (even slightly-so) combined with plausible but strong bounds of Freiman Thm will push the known upper bounds for Roth to the Behrend territory represents such a spectacular possibility that I think exploring it openly or otherwise should be great. Again in view of the spectacular expected result I see more chance that the idea will somehow be shot down (or will show unexpected but not easily applicable equivalence between Roth and Freiman theorems). But there is also the probability that it will work.
March 15, 2009 at 5:45 pm |
[…] second piece that got me thinking was Tim Gower’s dicussion of the experience of the Polymath project (via Michael Nielsen). For those who missed this, the project aimed to […]
March 16, 2009 at 4:28 pm |
Judging from the way the young people are communicating these days maybe we should make the next polymath via SMS’s
March 16, 2009 at 5:04 pm
Th@ wd B gr8. We cd prv sm 1drfl lMas & thms th@ wA.
March 16, 2009 at 5:32 pm
Great! And I could use my grant money to buy a cell phone at last, as I would use it for research. (A fancy one, like my son’s)
March 18, 2009 at 9:12 pm |
It’s not surprising that you knew all of the collaborators:
Ramsey’s Theorem says that if you have 6 collaborators or more, you would guarantee that three people are either mutually acquainted or mutually strangers 😉
March 18, 2009 at 10:58 pm |
I think that a app on facebook would be just as valid…
what would be cool is a blog entry that got posted in facebook/myspace/mobile that could be tracked…
glad you all had fun !
regards
John Jones
http://www.johnjones.me.uk
March 19, 2009 at 7:46 am |
[…] I learn that the massively collaborative math project that I wrote about a while ago has reached successful conclusion: … the mathematical result of the project has far exceeded what I thought would be possible […]
March 19, 2009 at 9:50 am |
Without having individual names on the paper, how exactly are people supposed to build a reputation again? Are potential employers supposed to troll through thousands of posts on such projects making sure that someone isn’t lying about being a contributor? What about *when* these threads cease to exist? Because, storage is quite fragile and thinking that backups don’t fail and that companies will keep data around forever, or even be in business or the product will be the same, in say, 20 or 50 years, is rather naive. In other words, expecting an exceedingly high quality product that doesn’t change how it works and to have an eternal life expectancy, especially when that product is free, isn’t exactly reasonable.
In all honesty, it’s great that you guys showed that what I said last time around was true, but now you’re going to have to finally address practical issues surrounding this method of research. You can start with answering the above questions.
March 19, 2009 at 10:38 am
Reid, I wish I had a complete and fully satisfactory answer to your first question (about credit) but I don’t. If collaborations like this become a mainstream activity then procedures will need to be developed. There is an optimistic point of view, which is espoused by Mark Bennet in a comment above, which is that the present systems of apportioning credit will adapt to fit mathematical practice. I think he may be right, but there could be an awkward transitional period, and that could be very important if it happens to be you who are not getting the credit you should. But I suppose the bottom line is that nobody’s forced to contribute to an online collaboration (at least if people are careful to avoid the PhD-spoiling danger that we’ve discussed already).
Incidentally, Terry Tao wrote a timeline of what he described as some of the highlights of the project. If that became a regular practice then it would make it much easier for people to get a feel for who had done what, since they wouldn’t have to trawl through all those comments. Of course, that presents its own problems: who decides which events qualify as highlights, and on what basis? (Actually, that made me a little uncomfortable about the timeline, but eventually I decided that its utility outweighed that problem, especially as the timeline can be freely edited if anyone feels that a comment has been wrongly left out.)
You’ve already mentioned the storage problem, and I took your comment seriously: a few days ago I made a backup on my computer of my entire blog, and I plan to make further copies of it on other systems. I hope that the chances of everything failing simultaneously are sufficiently remote that the record of the solution will be safe.
March 19, 2009 at 6:05 pm
Reid,
As I commented earlier, the first of the problems you mention is already faced by large-scale collaborations in other communities, such as high-energy physics and astrophysics. My understanding is that it’s addressed largely by letters of recommendation. Many of those collaborations also have internal (private) working papers that play a role not dissimilar to the role played by blog comments and wiki edits in the Polymath1 project. Those internal reports are not necessarily used directly by hiring committees, but they play an indirect role through the letters of recommendation.
The second problem – preservation and data integrity – is very interesting. Last year, Google announced a service for experimentalists to store scientific datasets, and then axed it just a few months later. I doubt anyone lost data as a result – it wasn’t around long enough that anyone was relying on it – but it’s sobering as an example of the kind of problem you’re talking about.
Over the long run, I’m confident this problem will be solved. There are many people in the academic library community and at funding agencies who see long-term preservation of digital data as part of their job. It takes time to develop the necessary infrastructure, though, and at present those people are still working out what needs to be preserved. Their work has resulted in systems like CrossRef and the digital object identifier (DOI) system, now used by many journals to provide permanent URLs for papers. If Polymath-style projects become common, I have no doubt this commnity wil be interested in helping properly archive the information.
March 20, 2009 at 2:16 am
If polymaths become common, there is an issue that might come up — a polymath where *nobody* is a senior researcher.
March 31, 2009 at 4:06 pm
Just to follow up on the question of preserving the blog record again, this type of question is being discussed now in the library and related communities, see e.g., http://www.gavinbaker.com/2009/03/30/preservation-for-scholarly-blogs/ and http://cavlec.yarinareth.net/2009/03/31/blog-preservation/
March 19, 2009 at 10:02 am |
I should mention that the above came off disturbingly more arrogant that intended. Sorry.
March 19, 2009 at 1:41 pm |
Regarding apportioning credit, I think that it’s important to remember that (at least within acedemia) the most important aspect of a job candidate’s application is their letters of recommendation. Potential employers won’t necessarily have to examine the record themselves to determine the extent of a candidate’s contribution to Polymath; rather, it’s reasonable to expect that this will be documented in the candidate’s letters.
It is already quite common practice, in the case when a candidate has done important collaborative work with a more senior figure in their field, to ask that senior person for a letter, with the goal being to try to determine the role of the candidate in the collaboration. One could presumably do the same in the case of Polymath: ask one
of the senior figures whose contribution to the project was not in doubt for a letter,
which would then address the significance of the candidates contribution.
We should bear in mind that if a candidate only makes relatively minor contributions to the project, then the role of their work on Polymath won’t in any case be the main pillar of support of their application: they will presumably have other more major work
on which their reputation, and the strength of their application, rests. And if they did contribute significantly, then the problem doesn’t seem that different from the already existing problem of determining how to apportion credit for joint work with senior figures in the field, and as I indicated, we already have a standard method for dealing with this problem.
March 19, 2009 at 4:30 pm |
[…] proof of the density Hales-Jewett theorem. Some six weeks (and nearly 1000 comments) later, Gowers has declared the project a success, and some of the ideas have already been written up as a […]
March 20, 2009 at 6:24 pm |
Perhaps the “first order questions” regarding open collaboration of this kind is: Does it have a good chance to work at all? does it has unique advantages compared to traditional ways of collaborating? And is it overall a good way of collaboration compared to more traditional ways.
I think the answer for the first question is a surprisingly clear ‘yes’.
The issue of credits is sort of second order. It is important and it is interesting also in the context of traditional ways of doing science. It is also interesting as an academic problem and it almost bring us back to influences. Understanding the influence of a player on the outcome of a correlated process or function is a complicated issue. What is the influence of a player on the outcome in football, of a musician in a symphonic concert? trying to understand the influence of players and trying to create a good insentive system of credits is not the same thing. (There are notion of influences for non product distributions and interesting studies for them. I think there is often a basic uncertainty involved when it comes to the influence of a player on a complicated process.)
one rule I though could be handy in order not to make the discussion too hectic (and to internally competative) is that every remark will be published after a delay which will be a random variable (say exponential) with expectation of 12 hours (negotiable) and when it will be publishe also the time of sub,ission will be noted. Bit it is probably a bad idea.
March 20, 2009 at 9:29 pm |
[…] The original hope was that the project would be a “massive collaboration”. Let’s suppose we take the number above (23) as representative of the number of people who made notable mathematical contributions, bearing in mind that there are obviously substantial limitations to using the timeline in this way. (The timeline contains some pointers to notable general comments, which I have not included in this count.) It’s certainly true that 23 people is a very large number for a mathematical collaboration – a few days into the project, Tim Gowers remarked that “this process is to normal research as driving is to pushing a car” – but it also falls well short of mass collaborations such as Linux and Wikipedia. Gowers has remarked that “I thought that there would be dozens of contributors, but instead the number settled down to …. […]
March 22, 2009 at 5:48 am |
I suppose I should have said something earlier, as the last comment is a few days old – oh, well, this is what my weekends are for anyway…
I only recently found that a project like this existed – previously the only projects I saw were completely unrelated to mathematics, and I now wish that I had looked around earlier. I hope to be able to contribute soon – as a first-year graduate student with no research experience (and a degree that only took two years) I’m not sure how much I’ll be able to contribute, but this seems to be a very efficient way of getting work done and I’m very excited to see what can happen next.
JB
March 22, 2009 at 7:00 am |
@Matthew Emerton:
I think you’re confusing where you’re working with academia in general. I should also point out that there more major work isn’t really provable in a tractable way unless credit is properly given.
I also think you are being exceedingly naive that this would even show up in there letters. Because, the distributive nature of the way “poly-math” is done means that the candidate is likely to have done a fair bit of this work (if not all) not including people where (s)he is physically working.
@J. Broll:
There are reasons listed above as to why this particular problem *seemed* to be very efficient. I would suggest you read the post and its commentary again.
I find it stunning that you old guys, that already have tenure, can’t see the importance of obtaining proper credit. It might not matter to you, or you can’t see the HR/lying/etc problems now, but if this takes off, with the delusional aspect of those now coming up, you’ll *really* start to see it if this is handled improperly.
I should also ask the practical question: what happens when one runs out of names for the pseudonym the work will be published under? Because, no group will have the exact same contributing members and thus demand another new name given. How would this be managed across the Mathematics community as a whole? As in, what about duplicate names? Etc, etc, etc.
Come on guys. This isn’t about idealism. This is about practicality.
March 22, 2009 at 7:09 am |
@gowers:
The highlights thing is actually quite a problem. After all, politics is everywhere and I’ve been bit in the … before even when discussing black and white issues with Maths. So, who writes the highlights will have a great impact especially if the person… dislikes a member of the group. This can even be subconscious. Highlights is also extra work that would be better spent on working on other problems or writing up. Also, if anyone could edit it, then where’s the integrity of that document? What’s to stop people from freely adding things that, in no way shape or form, are highlights? Given such loose restrictions on editing, it would need to be constantly watched for “defacement.”
Essentially, highlights only works in ideal cases and will fail the real world test. In general of course.
March 22, 2009 at 7:20 am |
@Michael Nielsen:
Regarding your reply to me (and pretty much every one else’s), am I the only one that is disturbed the the over use of assumptions in your (these) repl(y|ies)?
I should also mention that if you look at that experimental papers, which have… lots of people working on them, they *all* *do* get there names on it. Credit where credit is due.
@all:
But, as I’ve said, I have no problem with this type of discussion. The problem is that, as Terry Tao has echoed, it doesn’t scale. Among other things that I’ve mentioned before. Saying that a solution is forthcoming (assumption) isn’t good enough. Specifically for credit, especially since preserving credit, on the paper itself, is extremely easy.
March 22, 2009 at 7:22 am |
@Jason Dyer:
Seriously. Come on.
March 22, 2009 at 6:30 pm
? I don’t understand the nature of your reply.
A consortium of, say, 50 first-year graduate students could discover something significant (especially if they start with a topic with not much known about it in the first place.)
March 22, 2009 at 7:01 pm
The three 1930s students Erdös, Klein and Szekeres are a concrete example of a fruitful collaboration between non-seniors. Certainly three exceptional students, but there will be more of them.
March 22, 2009 at 5:40 pm |
Dear Reid,
I didn’t understand exactly what you were getting at in the sentence “there [sic] more major work … ”. I was presuming that they (a beginning researcher who is also a contributor to a Polymath project) will be doing other mathematics as well, which they will be publishing under their own name (so that the issue of credit doesn’t arise).
But I do think that you might be underestimating the importance of letter writing in the current academic environment, and also the amount of attention that prospective employers pay to the question of evaluating joint work, especially when the authors
are at different levels of seniority.
You talk about idealism versus practicality, but I don’t think it is a question of idealism
to expect that letters of recommendation will reflect the reality. In the current system,
beginning researchers rely on the good faith and good will of their senior colleagues to write evaluations that accurately reflect their contributions to their field; letters of recommendation are the basic currency for academic jobs and promotions. This system surely doesn’t work perfectly, but it seems to work reasonably well, and is in any case the system that we have. And I don’t see that the situation with Polymath is so radically different. (Maybe the latter point is where our disagreement lies?)
Regards,
Matthew
March 24, 2009 at 5:27 pm |
[…] a subsequent blog post, Gowers gave his own summary of the project as well as what he thinks about the future potential of […]
March 25, 2009 at 3:22 am |
I’m more a programmer than a mathematician, but it was interesting watching progress being made.
It seems to me that a bottleneck was the moderators’ job. When people suggested a possible proof, or conjectured that some other lemma would suffice, someone (you, Terry Tao, or someone else) at some point had to see if it made sense. Although since it’s a blog, there were more people looking who might spot a bug; but it wouldn’t always be obvious when a step was incorrect.
In the glorious future of flying cars, perhaps the blog format could be integrated with a proof-checking system; many people have been thinking about related things. Many of the ideas involved have been around for a while, but this still hasn’t taken off on a large scale, and so advice from working mathematicians might be helpful.
March 26, 2009 at 3:48 pm |
[…] in mathematics tagged Intellectual property, mathematics at 9:48 am by waynezwhirled Is Polymath1 the intellectual analog to OPM (other people’s […]
March 26, 2009 at 5:58 pm |
[…] group blog on math, physics and philosophy and Tim Gowers blog, where a mathematics paper has been succesively conceived and submitted mostly through blog discussions. How I wish to have been smart enough to know more such math and […]
March 31, 2009 at 1:51 pm |
Overall I think the issue of credit for contributors in open collaborative work is not so problematic. I expect that the handfull of people with crucial influence will have ample credit; Also the issue of individual researchers who are engaged with similar projects may not be too bad. Such open collaboration had potential to help (probably more than to harm) these separate efforts as well.
One difficulty I see is that people will be hesitant to partake in open collaboration, especially a hectic and competative one, because it may harm their reputation. There are serious issues of “cost of opportunity” that were expressed already: is this a good way to spend the time of an individual researcher? Is this a good way to spent efforts of many researchers all on the same issue? There is also a deeper issue of a shift (that can be artificial) of the attention of the community towards few problems.
May 25, 2009 at 7:17 pm |
[…] time, not to mention mental organization, to follow several such projects at all closely. One of Tim’s take away lessons from the project seemed to be that it shrank in number of participants faster than he expected. And […]
May 25, 2009 at 11:22 pm |
Matthew:
I think you may be somewhat too optimistic about the role of letters of recommendation. At a research university with a sizable department who will have someone in the candidate’s general area(s) of research, I have no doubt that appropriate evaluation of letters can and usually will take place. However, at a regional state university or lower-tier liberal arts college where an applicant for tenure is trying to count a significant contribution to a large collaboration as one of two or three papers expected for tenure, there may simply be no one who could understand the letter of recommendation and what it says about the tenure applicant’s contribution.
August 1, 2009 at 8:27 am |
[…] was playing with the idea of attempting a “polymath”-style open collaboration (see here, here and here) aiming […]
December 23, 2009 at 12:06 am |
Prof. Gowers, can I ask a few quick questions? I’m a business academic fascinated by this successful example of ‘crowdsourcing’ a problem, and would love to learn a bit more about it so that I can blog about it intelligently.
You say in your post that “the number [of primary contributors] settled down to a handful, all of whom I knew personally…” This raises (yes, NOT ‘begs’) a couple questions for me:
* How large was this ‘handful?’ How big was the cohort of primary contributors? I’m sorry if you gave this number somewhere above; I couldn’t find it.
* How many of this cohort had you previously collaborated / coauthored with?
* How many of this cohort did you know, or at least suspect, had both the knowledge and the enthusiasm necessary to be effective collaborators on this effort? In other words, were cohort members the first, or among the first, people you would have contacted to work on this problem in the old-fashioned way? Or did at least some of them surprise you when they showed up on this polymath project? To ask the question differently, what does the Venn diagram look like of the polymath cohort and the cohort of people you would have called up to work on this problem in the old-fashioned way?
I hope these questions make sense to you, and I hope I’m not being too presumptuous or intrusive on your time to pose them here. Any answers, or any pointers to a place where they’ve been answered, would be very much appreciated. Thank you!
– Andrew McAfee, MIT
December 30, 2009 at 5:42 pm |
[…] second piece that got me thinking was Tim Gower’s dicussion of the experience of the Polymath project (via Michael Nielsen). For those who missed this, the project aimed to […]
October 22, 2011 at 4:38 am |
[…] group blog on math, physics and philosophy and Tim Gowers blog, where a mathematics paper has been succesively conceived and submitted mostly through blog discussions. How I wish to have been smart enough to know more such math and […]
October 26, 2021 at 1:04 pm |
You wrote this article very well. Very knowledgeable. Thanks for sharing this article
Visit dreamteach.co.uk!
October 26, 2021 at 1:04 pm |
Wow , i learned something new here. i wish you will post more article just like this one
Visit abacustrainer.com!