It has become clear that what we need in order to finish off one of the problems about intransitive dice is a suitable version of the local central limit theorem. Roughly speaking, we need a version that is two-dimensional — that is, concerning a random walk on — and completely explicit — that is, giving precise bounds for error terms so that we can be sure that they get small fast enough.
There is a recent paper that does this in the one-dimensional case, though it used an elementary argument, whereas I would prefer to use Fourier analysis. Here I’d like to begin the process of proving a two-dimensional result that is designed with our particular application in mind. If we are successful in doing that, then it would be natural to try to extract from the proof a more general statement, but that is not a priority just yet.
As people often do, I’ll begin with a heuristic argument, and then I’ll discuss how we might try to sharpen it up to the point where it gives us good bounds for the probabilities of individual points of . Much of this post is cut and pasted from comments on the previous post, since it should be more convenient to have it in one place.
Using characteristic functions
The rough idea of the characteristic-functions approach, which I’ll specialize to the 2-dimensional case, is as follows. (Apologies to anyone who knows about this properly for anything idiotic I might accidentally write.) Let be a random variable on
and write
for
. If we take
independent copies of
and add them together, then the probability of being at
is
where that denotes the -fold convolution.
Now let’s define the Fourier transform of , which probabilists call the characteristic function, in the usual way by
.
Here and
belong to
, but I’ll sometimes think of them as belonging to
too.
We have the convolution law that and the inversion formula
Putting these together, we find that if random variables are
independent copies of
, then the probability that their sum is
is
.
The very rough reason that we should now expect a Gaussian formula is that we consider a Taylor expansion of . We can assume for our application that
and
have mean zero. From that one can argue that the coefficients of the linear terms in the Taylor expansion are zero. (I’ll give more details in a subsequent comment.) The constant term is 1, and the quadratic terms give us the covariance matrix of
and
. If we assume that we can approximate
by an expression of the form
for some suitable quadratic form in
and
, then the
th power should be close to
, and then, since Fourier transforms (and inverse Fourier transforms) take Gaussians to Gaussians, when we invert this one, we should get a Gaussian-type formula for
. So far I’m glossing over the point that Gaussians are defined on
, whereas
and
live in
and
and
live in
, but if most of
is supported in a small region around 0, then this turns out not to be too much of a problem.
The Taylor-expansion part
If we take the formula
and partially differentiate times with respect to
and
times with respect to
we obtain the expression
.
Setting turns this into
. Also, for every
and
the absolute value of the partial derivative is at most
. This allows us to get a very good handle on the Taylor expansion of
when
and
are close to the origin.
Recall that the two-dimensional Taylor expansion of about
is given by the formula
where is the partial derivative operator with respect to the first coordinate,
the mixed partial derivative, and so on.
In our case, ,
, and
.
As in the one-dimensional case, the error term has an integral representation, namely
,
which has absolute value at most , which in turn is at most
.
When is the random variable
(where
is a fixed die and
is chosen randomly from
), we have that
.
With very slightly more effort we can get bounds for the moments of as well. For any particular
and a purely random sequence
, the probability that
is bounded above by
for an absolute constant
. (Something like 1/8 will do.) So the probability that there exists such a
conditional on
(which happens with probability about
) is at most
, and in particular is small when
. I think that with a bit more effort we could probably prove that
is at most
, which would allow us to improve the bound for the error term, but I think we can afford the logarithmic factor here, so I won’t worry about this. So we get an error of
.
For this error to count as small, we want it to be small compared with the second moments. For the time being I’m just going to assume that the rough size of the second-moment contribution is around . So for our error to be small, we want
to be
and
to be
.
That is giving us a rough idea of the domain in which we can say confidently that the terms up to the quadratic ones give a good approximation to , and hence that
is well approximated by a Gaussian.
The remaining part
Outside the domain, we have to do something different, and that something is fairly simple: we shall show that is very small. This is equivalent to showing that
is bounded away from 1 by significantly more than
. This we do by looking more directly at the formula for the Fourier transform:
.
We would like this to have absolute value bounded away from 1 by significantly more than except when
is quite a bit smaller than
and
is quite a bit smaller than
.
Now in our case is uniformly distributed on the
points
. So we can write
as
.
Here’s a possible way that we might try to bound that sum. Let and let us split up the sum into pairs of terms with
and
, for
. So each pair of terms will take the form
The ratio of these two terms is
.
And if the ratio is , then the modulus of the sum of the two terms is at most
.
Now let us suppose that as varies, the differences
are mostly reasonably well distributed in an interval between
and
, as seems very likely to be the case. Then the ratios above vary in a range from about
to
. But that should imply that the entire sum, when divided by
, has modulus at most
. (This analysis obviously isn’t correct when
is bigger than
, since the modulus can’t be negative, but once we’re in that regime, then it really is easy to establish the bounds we want.)
If is, say
, then this gives us
, and raising that to the power
gives us
, which is tiny.
As a quick sanity check, note that for not to be tiny we need
to be not much more than
. This reflects the fact that a random walk of
steps of typical size about
will tend to be at a distance comparable to
from the origin, and when you take the Fourier transform, you take the reciprocals of the distance scales.
If is quite a bit smaller than
and
is not too much smaller than
, then the numbers
are all small but the numbers
vary quite a bit, so a similar argument can be used to show that in this case too the Fourier transform is not close enough to 1 for its
th power to be large. I won’t give details here.
What is left to do?
If the calculations above are not too wide of the mark, then the main thing that needs to be done is to show that for a typical die the numbers
are reasonably uniform in a range of width around
, and more importantly that the numbers
are not too constant: basically I’d like them to be pretty uniform too.
It’s possible that we might want to try a slightly different approach, which is to take the uniform distribution on the set of points , convolve it once with itself, and argue that the resulting probability distribution is reasonably uniform in a rectangle of width around
and height around
. By that I mean that a significant proportion of the points are hit around
times each (because there are
sums and they lie in a rectangle of area
). But one way or another, I feel pretty confident that we will be able to bound this Fourier transform and get the local central limit theorem we need.
May 31, 2017 at 7:08 am |
For one-dimensional probability distributions, there is a refinement to the Central Limit Theorem that gives an upper bound to the error made in using the CLT to approximate a sum of ‘n’ iid random variables. It’s known as the Berry-Esséen theorem, and goes back to the 1940s . The error bound depends on the absolute 3rd moment of one of the ‘n’ iid random variables, which must be finite.
May 31, 2017 at 8:26 am
I discussed that in the previous post: see the section entitled “Why are we not immediately done?”. The problem with the Berry-Esseen theorem for this application is that while it gives you a good approximation to the distribution function, it is not sufficiently good to tell the difference between discrete and continuous random variables. Here we have a pair of random variables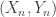 , a sum of
, a sum of  independent copies of
independent copies of  , and we are interested in events such as
, and we are interested in events such as 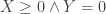 . If
. If  and
and  were continuous random variables, this would have probability zero, but since they take values in
were continuous random variables, this would have probability zero, but since they take values in  , it has positive probability, and we would like to be able to estimate it. It is for that kind of purpose that LCLTs are useful.
, it has positive probability, and we would like to be able to estimate it. It is for that kind of purpose that LCLTs are useful.
One approach to LCLTs that’s in the literature is to use the Berry-Esseen theorem together with a separate argument that the distribution is “flat”, in the sense that if you change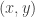 by a small amount, then the probability of landing at
by a small amount, then the probability of landing at 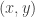 does not vary by much. Then one can estimate probabilities by using the Berry-Esseen theorem to get the probability of being inside some small region and the flatness to get the probabilities of the individual points in that region (which are roughly the same and have a known sum, so can be calculated). Although I chose to use characteristic functions above, I think that approach could work as well.
does not vary by much. Then one can estimate probabilities by using the Berry-Esseen theorem to get the probability of being inside some small region and the flatness to get the probabilities of the individual points in that region (which are roughly the same and have a known sum, so can be calculated). Although I chose to use characteristic functions above, I think that approach could work as well.
May 31, 2017 at 10:38 am |
I’ve noticed a subtlety that makes part of my sketch in the post above not correct as stated. I claimed that it was probably the case that for a typical the numbers
the numbers 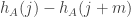 should be pretty evenly distributed in a range of width about
should be pretty evenly distributed in a range of width about 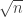 .
.
Here’s why one might think that is true. Suppose we add 1 to . Then to the given number we will add
. Then to the given number we will add 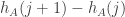 and subtract
and subtract 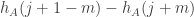 . But
. But 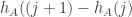 is the multiplicity with which
is the multiplicity with which 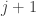 occurs in
occurs in  , and we would expect these multiplicities to behave like independent Poisson random variables of mean 1. So what we have here looks like a random walk where each step is given by a difference of two independent Poisson random variables. After several steps, the distribution should be approximately Gaussian, but what we’re interested in is not the distribution of the end point, but rather the distribution of a random point of the random walk. And this is a somewhat more slippery object.
, and we would expect these multiplicities to behave like independent Poisson random variables of mean 1. So what we have here looks like a random walk where each step is given by a difference of two independent Poisson random variables. After several steps, the distribution should be approximately Gaussian, but what we’re interested in is not the distribution of the end point, but rather the distribution of a random point of the random walk. And this is a somewhat more slippery object.
If we want to use the technique of pretending variables are independent, proving that something holds with very high probability, and then conditioning on an event that isn’t too unlikely, that limits what we can hope to prove here. For example, the probability that the normal random walk stays positive for steps is of order
steps is of order  , so if we then condition on an event of probability
, so if we then condition on an event of probability  we cannot rule out that this will happen. And in fact, I think that these kinds of things actually will happen: it seems that conditioning the sum of
we cannot rule out that this will happen. And in fact, I think that these kinds of things actually will happen: it seems that conditioning the sum of  to be
to be 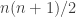 makes it quite likely that
makes it quite likely that 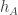 will be broadly positive for the first half and broadly negative for the second, in which case
will be broadly positive for the first half and broadly negative for the second, in which case 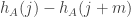 would be broadly positive.
would be broadly positive.
However, for the purposes of bounding the Fourier coefficient, we don’t need to nail down the distribution too precisely: we just need it to avoid having “silly” properties such as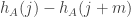 always being even. I’d also quite like to know that it doesn’t take the same value too many times.
always being even. I’d also quite like to know that it doesn’t take the same value too many times.
To that end, here’s a simple question to which the answer is probably known, but a quick Google search didn’t reveal it to me. Suppose we take a standard one-dimensional random walk for steps. Let
steps. Let  be the number of times the origin is visited. For what value of
be the number of times the origin is visited. For what value of  does
does ![\mathbb P[Z\geq t]](https://s0.wp.com/latex.php?latex=%5Cmathbb+P%5BZ%5Cgeq+t%5D&bg=ffffff&fg=333333&s=0&c=20201002) become smaller than
become smaller than 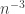 ? (The 3 there is just some arbitrary constant that’s safely bigger than 1.) I would expect the answer to be something like
? (The 3 there is just some arbitrary constant that’s safely bigger than 1.) I would expect the answer to be something like 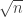 times a logarithmic factor, since we would expect the walk to wander around in an interval of width of order
times a logarithmic factor, since we would expect the walk to wander around in an interval of width of order 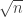 , not necessarily visiting all of it, but not being too concentrated on any one part of it.
, not necessarily visiting all of it, but not being too concentrated on any one part of it.
May 31, 2017 at 11:03 am |
There’s probably a much nicer way of doing things, but I think for the question in the last paragraph of the comment above, the following fairly crude approach should give a bound that’s just about OK for the purposes we need. It’s to get some kind of estimate for the th moment of
th moment of  , where
, where  is a positive integer that one optimizes. The random variable
is a positive integer that one optimizes. The random variable 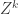 counts ordered
counts ordered  -tuples of points at which the origin is visited. There are
-tuples of points at which the origin is visited. There are 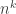 possibilities for their x-coordinates. If we take one of these
possibilities for their x-coordinates. If we take one of these  -tuples and call it
-tuples and call it 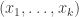 (putting them in increasing order), then the probability that we’re zero at
(putting them in increasing order), then the probability that we’re zero at 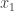 (ignoring parity, which in any case doesn’t apply to the random walk we’re ultimately interested in) is about
(ignoring parity, which in any case doesn’t apply to the random walk we’re ultimately interested in) is about 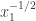 . Then the probability that we’re zero at
. Then the probability that we’re zero at  given that we’re zero at
given that we’re zero at 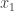 is about
is about 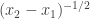 , and so on. For a typical
, and so on. For a typical  -tuple, this should give us something like
-tuple, this should give us something like 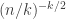 (though it will often be somewhat bigger, so some care would be needed for this part of the argument). So ignoring a constant factor that depends on
(though it will often be somewhat bigger, so some care would be needed for this part of the argument). So ignoring a constant factor that depends on  (which will be important when we optimize), it looks as though the
(which will be important when we optimize), it looks as though the  th moment should be something like
th moment should be something like 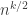 .
.
Therefore, by Chebyshev, the probability that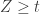 should be bounded above by something like
should be bounded above by something like 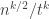 . If we want that to be at most
. If we want that to be at most 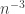 , then we need
, then we need  to be at least
to be at least 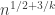 . This will be multiplied by a constant factor that depends on
. This will be multiplied by a constant factor that depends on  , but it should give us an upper bound of
, but it should give us an upper bound of  .
.
May 31, 2017 at 11:26 am |
Maybe we should do one more “random walk iteration”? Fix some j, and let be a random vector taking n values
be a random vector taking n values 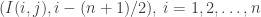 with equal chances, where
with equal chances, where 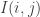 is an indicator function:
is an indicator function: 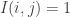 if
if 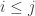 and
and 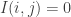 if
if  . Assume that we can prove some sort of local central limit theorem for this very simple random walk. Then we can control the probabilities like
. Assume that we can prove some sort of local central limit theorem for this very simple random walk. Then we can control the probabilities like 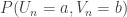 , where
, where 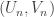 is the sum of n i.i.d. copies of
is the sum of n i.i.d. copies of  . But
. But 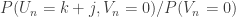 is exactly the probability that
is exactly the probability that 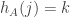 for random dice A.
for random dice A.
With indicator function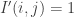 if
if 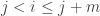 but
but 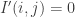 otherwise we should be able to control
otherwise we should be able to control 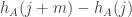 in a similar way.
in a similar way.
May 31, 2017 at 11:54 am
That could be useful, but would it give us information about the typical behaviour of the distribution of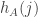 ? We want to know not just what the probability is that it takes a given value, but quite a lot about how those probabilities for different
? We want to know not just what the probability is that it takes a given value, but quite a lot about how those probabilities for different  depend on each other.
depend on each other.
May 31, 2017 at 7:22 pm |
If you have weak dependence of your variables, particularly if there’s symmetry between them, it might be worth trying Stein’s method https://statweb.stanford.edu/~souravc/beam-icm-trans.pdf as an alternative to controlling the characteristic function. For example, you can get the Berry-Esseen rate for independent variables fairly easily.
Unfortunately, I don’t know how easy it is to get a local limit theorem using Stein – it tends to be used to control total variation.
June 4, 2017 at 1:31 pm |
I came up with a possible definition of “sampling a probability density defined on [0,1]” (or at least, sampling from countably-many points in that interval). Such dice seem to be transitive, _if_ you center their expected value.
I’m not quite sure this is relevant; I think it might be, though, because some of the discussion seems to involve the difference between continuous and discrete probability variables. Even if it doesn’t help settle the question, I think it’s an interesting sidelight.
It’s on Github at
Click to access fuzzyDice.pdf
(Actually, my main motivation for doing this was that I like the description “fuzzy dice” 🙂
June 6, 2017 at 7:45 pm
This looks interesting, but I’m not sure I’m understanding. Can you explain a bit more about your model?
I’m not familiar with R, so I don’t quite follow the details of this generation (or the comparison function). But it roughly appears to generate a continuous function on [0,1] with length_scale scaling the derivatives so as to affect the length scale over which the function values are roughly equal. Is that understanding at least close?
Unless I misunderstood your model, it sounds like the only difference is that in the large n limit, this model yields a continuous distribution where-as the discrete dice would represent a discontinuous distribution. If that is the only difference, then somehow the intransitivity _depends_ on the discontinuity!? Somehow normalized continuous functions on [0,1] are almost totally ordered (ties and exceptions to ordering are of probability 0), where-as normalized discontinuous functions are almost perfectly “not ordered”? Is there some simple reason this should be obvious? If true, this seems fascinating and non-intuitive to me.
Would this mean that in the large n limit, if an idea doesn’t somehow capture the essential “discontinuities”, and instead approximates it as something smooth, it is bound to fail to describe the discrete dice?
So I hope you continue poking at this continuous model of dice to pull out some more information. It sounds interesting and could also be telling us something important.
June 5, 2017 at 12:09 pm |
A short numerical experiment about last paragraph of the post. I have selected n=10,000, took uniform distribution of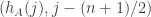 as suggested, convolved it once with itself, and plot the graph: x axes is
as suggested, convolved it once with itself, and plot the graph: x axes is 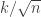 for
for  , and y axes is the number of times
, and y axes is the number of times 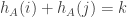 subject to
subject to 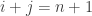 . The graph is http://imgur.com/Gpf2MiJ (not sure how to upload it here). Does it look like “close” to being about 100 for every k in this interval ?
. The graph is http://imgur.com/Gpf2MiJ (not sure how to upload it here). Does it look like “close” to being about 100 for every k in this interval ?
June 5, 2017 at 2:08 pm
It looks close in the sense I intended, yes. We know it has to be supported in a rectangle of width of order and height of order
and height of order 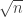 . If almost no points occur with probability greater than
. If almost no points occur with probability greater than 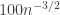 , that forces the distribution after two steps of the random walk to be pretty spread out, and then a local CLT should be achievable — though there’s still the problem of making sure that the distribution isn’t concentrated in a sublattice.
, that forces the distribution after two steps of the random walk to be pretty spread out, and then a local CLT should be achievable — though there’s still the problem of making sure that the distribution isn’t concentrated in a sublattice.
June 9, 2017 at 4:23 am |
A clarification about the continuous model: when I sampled (a sort of) “continuous” dice, with no restriction on their expected value. they didn’t seem transitive. However, when I forced their expected value to be 0.5, they did seem transitive.
This seems vaguely analogous to forcing the sum of discrete dice to be n-choose-2, but other than that, this may not be relevant to whether discrete dice are intransitive, or not.
June 9, 2017 at 11:33 am |
(Hopefully the Latex code works…)
Maybe some other approach to bound the Fourier transform focusing on
the direct differences.
Consider the Fourier transform
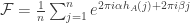
(I drop the constant shift in the second component, because it only
adds a constant factor with modulus one)
Let
with the convention . Then
. Then
With this
Let
Then we can rewrite the Fourier transform as
As , the absolute value can be bounded as
, the absolute value can be bounded as
The sum consists of summands and each of it is at most
summands and each of it is at most  . Hence
. Hence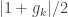 as
as , then
, then 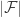 is strictly bounded away
is strictly bounded away .
.
if we can bound a positive fraction of the summands
strictly less than
from
As an illustration, assume that the dice is such that there exist
is such that there exist and
and 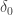 and
and 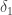 such that
such that
constants
and
and
(I guess that could already be true for a typical dice , but
, but for a typical dice seems approachable.)
for a typical dice seems approachable.)
otherwise the argument could easily be refined. Moreover, looking at
the distribution of
Then for around
around  (in the torus topology),
(in the torus topology),
there exists a constant such that
(if we are not close to , the modulus of the Fourier transform is easily bounded
, the modulus of the Fourier transform is easily bounded ).
).
away from
This shows
and
With the constants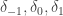 , we can then easily
, we can then easily
bound the Fourier transform as
This seems pretty good to me, because we only need a bound when
 is relatively large (in particular I guess significantly
is relatively large (in particular I guess significantly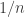 ) and this shows that
) and this shows that
larger than
for an appropriate constant .
.
N.B.: We can recover the approach sketched in the post, in a th neighbouring term,
th neighbouring term,
generalised setting by comparing the term
i.e. writing the sum as
so that we need to bound terms of the form
where
In the above approach it was taken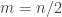 , but for refined
, but for refined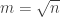 could be more helpful.
could be more helpful.
estimates maybe
June 9, 2017 at 3:49 pm
I just tried to code up some rejection sampling and unless I have done some coding error, it seems to me that actually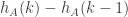 nearly always takes the values
nearly always takes the values 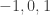 and rarely only slightly larger values (typically well less than 10). So the plotting suggests that the approach with the
and rarely only slightly larger values (typically well less than 10). So the plotting suggests that the approach with the 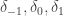 should work.
should work.
The used python code is below:
import numpy as np
import numpy.random
import matplotlib.pylab as plt
def sample(n):
“””Sample a dice”””
while True:
dist = numpy.random.randint(1,n+2,n)
if np.sum(dist) == n*(n+1)/2:
return dist
def delta(dist, k):
“””Return the first component of Delta_k”””
return np.sum(dist==k) – 1
n = 10000
dist = sample(n)
kList = np.arange(n) + 1
deltaList = np.array( [delta(dist, k) for k in kList] )
# Plot directly
plt.figure()
plt.plot(kList, deltaList)
plt.xlabel(‘k’)
plt.ylabel(‘$\Delta_k$’)
# Histogram plot
if deltaList.min() < 0:
deltaListP = deltaList – deltaList.min()
binData = np.bincount(deltaListP)
binLabels = np.arange(len(binData)) + deltaList.min()
plt.figure()
plt.bar(binLabels, binData / n)
plt.xlabel('Value of $h_A(k)-h_A(k-1)$')
plt.ylabel('Frequency')
June 9, 2017 at 6:31 pm
That’s interesting: I expected the distribution to be roughly Poisson, or rather that the probability that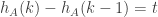 should be roughly
should be roughly 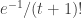 for
for 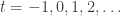 . Is that consistent with your data?
. Is that consistent with your data?
June 26, 2017 at 12:57 am
I’ve realized while trying to write up the proof that you make a false statement above, when you say
“Then for around
around  (in the torus topology),
(in the torus topology),
there exists a constant such that
That final bound should be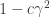 , and unfortunately that weakens the bound to the point where it is no longer good enough. However, that just means that looking at successive differences is insufficient, and I’m pretty sure that I am on track to complete the proof with a more complicated argument that looks at longer-range differences. I’m travelling at the moment, so it will probably take me a week or two to have a complete draft of the write-up.
, and unfortunately that weakens the bound to the point where it is no longer good enough. However, that just means that looking at successive differences is insufficient, and I’m pretty sure that I am on track to complete the proof with a more complicated argument that looks at longer-range differences. I’m travelling at the moment, so it will probably take me a week or two to have a complete draft of the write-up.
June 9, 2017 at 9:41 pm |
The guess that is roughly
is roughly 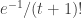 seems pretty consistent with the samples (I took n=5000 and n=10000). If you sample from that it is very unlikely to get anything bigger than say 10. That at least sounds to me that it is likely to get a positive fraction with the
seems pretty consistent with the samples (I took n=5000 and n=10000). If you sample from that it is very unlikely to get anything bigger than say 10. That at least sounds to me that it is likely to get a positive fraction with the 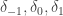 .
.
Just for the record: By the definition one finds immediately that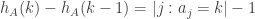 (I guess that was the intuition behind the Poisson distribution). Basically I guess the only question is whether the conditioning destroys anything, but that seems unlikely to me.
(I guess that was the intuition behind the Poisson distribution). Basically I guess the only question is whether the conditioning destroys anything, but that seems unlikely to me.
June 10, 2017 at 4:38 pm |
I’ve just read your earlier comment a bit more carefully and it looks interesting and useful. I’m quite busy at the moment, and it’s that rather than any diminishing enthusiasm that has caused me not to comment much for a few days. I definitely intend to make a serious effort to finish off this argument, unless someone else has already done it by the time I’m ready.
June 14, 2017 at 12:32 pm |
After the recent comments of Helge Dietert above, I think we’ve got to the point where it is worth trying to write something up. I will have a go at this, and when I either have a draft or get stuck, I’ll share the resulting file and see whether anyone else would like to rewrite parts of it, add to it, etc. And if we end up with a complete proof, we can think about whether we want to push on and try to solve the problem for the multiset model, and also try to disprove the stronger conjecture that the tournament is quasirandom.
June 18, 2017 at 10:35 pm |
I have made a start with a write-up. I can’t quite claim that we have a proof, though I think we probably do. I had intended to post a complete draft, but it went more slowly than I had hoped, and now I have a very busy couple of weeks ahead and will be unable to spend time on this for a while. If anyone feels like doing some writing — either improving what’s there already or adding to it — I’ll be happy to send the source file. Just let me know.
This is what I have done so far.
June 26, 2017 at 2:32 pm
Noticed small typo: on page 5, believe you meant to write that the mean of (gA(j),j-(n+1)/2) is (0,0), instead of the mean of (gA(j),j.
June 27, 2017 at 7:22 am
Thanks for that and indeed that is what I meant to write — I’ve now corrected it.
June 19, 2017 at 3:45 pm |
One step that was missing in the write-up has now, I think, essentially been filled. I asked a closely related question on Mathoverflow and have received a useful answer that will I think easily translate over into our context (to give a lower bound for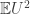 — see draft for definition of the random variable
— see draft for definition of the random variable  ).
).
June 28, 2017 at 10:59 pm |
A thought has occurred to me that might make a nice addition to the write-up. I think it ought to be possible to generalize the proof to show that if and
and  are random sequences conditioned with
are random sequences conditioned with  conditioned to have sum
conditioned to have sum 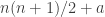 and
and  conditioned to have sum
conditioned to have sum 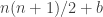 , then if
, then if  for some absolute constant
for some absolute constant 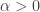 , which is the typical order of magnitude of the difference of two sums of
, which is the typical order of magnitude of the difference of two sums of  random elements of
random elements of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , then
, then  beats
beats  with probability
with probability 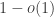 . If this is true, it will be prove rigorously something that the experimental evidence already shows, namely that intransitivity is extremely rare for purely random elements of
. If this is true, it will be prove rigorously something that the experimental evidence already shows, namely that intransitivity is extremely rare for purely random elements of ![[n]^n](https://s0.wp.com/latex.php?latex=%5Bn%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . That’s because whether or not
. That’s because whether or not  beats
beats  will depend almost entirely on which has the larger sum, which is of course a transitive relation.
will depend almost entirely on which has the larger sum, which is of course a transitive relation.
July 3, 2017 at 4:52 pm |
Because uniform random “constrained sum sequence dice” can be viewed as just a non-uniform random selection from “proper/multiset dice”, is there a way to carry over the sequence results to give a response on the original conjecture on proper dice?
Maybe for instance by pulling on the thread that the non-uniform weighting changes the weights equally on (die A) and (inverse die A)?
July 4, 2017 at 7:33 am
I’m keen to think about this once the write-up is finished, which I hope will be soon. I certainly hope that the multiset version will turn out not to require a substantial new idea.
July 22, 2017 at 4:17 pm |
At last I have finished a first draft of the write-up. There are a lot of slightly fiddly estimates, so there is a high chance of minor errors, but I’m fairly sure the argument is robust and basically correct. (But it’s definitely necessary to check this, and I’d rather that checking was done by a fresh pair of eyes.) Anyhow, it can be found here.
It still needs a bibliography, some comments about the experimental evidence for the stronger quasirandomness conjecture, and I also think we should try to solve two further problems. The first is the question of whether we can prove rigorously that the stronger quasirandomness conjecture is false, and the second is whether we can use similar techniques to prove the weaker conjecture for the multisets model. And one other thing that I very much want to add is a rigorous proof that if you just take random elements of![[n]^n](https://s0.wp.com/latex.php?latex=%5Bn%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , then which die wins is with very high probability determined by the sum of the faces of the dice: that is, the die with the bigger sum almost certainly wins. I think that should in fact be quite a lot easier than what is proved in the draft so far — it just needs doing, as it explains why in the unconstrained model the experimental evidence suggests that one gets transitivity almost all the time.
, then which die wins is with very high probability determined by the sum of the faces of the dice: that is, the die with the bigger sum almost certainly wins. I think that should in fact be quite a lot easier than what is proved in the draft so far — it just needs doing, as it explains why in the unconstrained model the experimental evidence suggests that one gets transitivity almost all the time.
July 22, 2017 at 4:42 pm
I forgot to add that in the write-up there is a proof of a lower bound for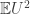 which is then not used. That is because I erroneously thought I was going to use it, and haven’t quite taken the step of deleting it (which involves a small amount of reorganization).
which is then not used. That is because I erroneously thought I was going to use it, and haven’t quite taken the step of deleting it (which involves a small amount of reorganization).
July 23, 2017 at 10:56 am
Thank you for the update. May I ask for a small clarification? Theorem 7.2 is formulated for A being random die (that is, random element of![[n]^n](https://s0.wp.com/latex.php?latex=%5Bn%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with sum
with sum 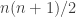 ). The proof starts with assuming that A is a random element of
). The proof starts with assuming that A is a random element of ![[n]^n](https://s0.wp.com/latex.php?latex=%5Bn%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) (that is, without any condition on the sum), but then the condition is used in the proof (for example, when we say that G is even function, we assume that the mean of G is 0). At which point of the proof A stops being random element of
(that is, without any condition on the sum), but then the condition is used in the proof (for example, when we say that G is even function, we assume that the mean of G is 0). At which point of the proof A stops being random element of ![[n]^n](https://s0.wp.com/latex.php?latex=%5Bn%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) and becoming random die?
and becoming random die?
July 23, 2017 at 4:05 pm
Hmm, that may be a slip. I’ll have to think about it.
July 23, 2017 at 4:18 pm
OK, let me think aloud.
The idea of the proof was to prove that has certain properties with sufficiently high probability that when we condition on the sum being zero it still has those properties. The main properties are the following two.
has certain properties with sufficiently high probability that when we condition on the sum being zero it still has those properties. The main properties are the following two.
1.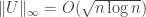 .
.
2. The characteristic function of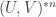 is very small when
is very small when 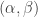 are not both small.
are not both small.
I think that in the rest of the argument I don’t use probabilistic arguments, but just these properties. So what I have written is not expressed clearly but I think it is correct.
What I think I should have done is got to the end of Section 5 and then fixed an that had the desired properties, together with a sum that is equal to
that had the desired properties, together with a sum that is equal to 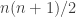 , noting that almost all random
, noting that almost all random  -sided dice have this property (which is the main content of Section 5). After that, probabilistic arguments would be banned and the rest of the paper should be deterministic. I need to check, but I think that the only reason certain statements after Section 5 are true only with high probability is that they make use of statements in Section 5 that themselves hold with high probability.
-sided dice have this property (which is the main content of Section 5). After that, probabilistic arguments would be banned and the rest of the paper should be deterministic. I need to check, but I think that the only reason certain statements after Section 5 are true only with high probability is that they make use of statements in Section 5 that themselves hold with high probability.
So, to summarize, thank you for picking that up, and at the moment I am fairly confident that it will be easy to correct.
July 23, 2017 at 4:41 pm
I’ve now updated the link in the comment that starts this thread, so that it links to an updated file. I hope it is now OK.
July 23, 2017 at 10:14 pm
I now have a sketch proof for the result that in the “purely random” model of -sided dice — that is, the model where a random
-sided dice — that is, the model where a random  -sided die is just a random element of
-sided die is just a random element of ![[n]^n](https://s0.wp.com/latex.php?latex=%5Bn%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) — transitivity almost always occurs. I’ll be travelling tomorrow, but will try to add this result to the write-up in the next day or two after that. As I suspected, the proof is short, and does not need a local central limit theorem — just easy tail bounds for sums of independent random variables.
— transitivity almost always occurs. I’ll be travelling tomorrow, but will try to add this result to the write-up in the next day or two after that. As I suspected, the proof is short, and does not need a local central limit theorem — just easy tail bounds for sums of independent random variables.