This post is intended to accomplish several things at once. First and foremost, I want to explain (not just in the post) why I have been interested in Borel determinacy and in the natural proofs barrier. Roughly speaking (or should I say tl;dr?) I think that Martin’s proof of Borel determinacy has features that might just conceivably offer a way past that barrier.
As long-term readers of this blog will be aware, the P versus NP problem is one of my personal mathematical diseases (in Richard Lipton’s sense). I had been in remission for a few years, but last academic year I set a Cambridge Part III essay on barriers in complexity theory, and after marking the essays in June I thought I would just spend an hour or two thinking about the problem again, and that hour or two accidentally turned into about three months (and counting).
The trouble was that I had an idea that has refused to die, despite my best efforts to kill it. Like a particularly awkward virus, it has accomplished this by mutating rapidly, so that what it looks like now is very different from what it looked like at the beginning of the summer. (For example, at that stage I hadn’t thought of trying to model a proof on the proof of Borel determinacy.) So what am I to do?
An obvious answer is this: expose my ideas to public scrutiny. Then if there is a good reason to think that they can’t be made to work, it is likely that that reason will come to light more quickly than if I, as one individual with judgment possibly skewed by my emotional attachment to the approach, think about it on my own.
But what if they can be made to work? Do I want to make them public in their current only partially developed state? I’ve thought about this, and my view is that (i) it is very unlikely that the ideas will work, not just because it is always unlikely that any given attack on a notoriously hard problem will work, but also because there are certain worrying analogies that suggest, without actually conclusively demonstrating, that the approach has a good chance of running into a certain kind of well-known difficulty (roughly, that I’ll end up not managing to show that the parity function is simpler than an arbitrary function) and (ii) if, by some miracle, the approach does work, I’ll have put enough into it to be able to claim a reasonable share of the credit, and I’ll probably get to that stage far more quickly and enjoyably than if I work secretly. So in the first case, I gain something precious — time — and in the second case I also gain time and end up with an amount of credit that any sensible person ought to be satisfied with. [Confession: I wrote that some time ago and then had some further ideas that made me feel more optimistic, so I worked on them on my own for another two or three weeks. I’m going public only after starting to feel a bit bogged down again.]
And of course, if I go down the public route, it gives me another chance to try to promote the Polymathematical way of doing research, which on general grounds I think ought to be far more efficient. This is a strong additional motivation.
There is one question that I will not be able to suppress so I might as well get it out of the way: if the problem did get solved this way, then what would happen to the million dollars? The answer is that I don’t know, but I am not too bothered, since the situation is very unlikely to arise, and if it does, then it’s the Clay Mathematics Institute’s problem — they have a committee for making that kind of decision — and not mine. And I think it would be very wrong indeed if the existence of a prize like that had the effect of making research on a major mathematical question more secret, and therefore more inefficient, than it needed to be.
I have two remaining anxieties about going public. One is that it looks a bit attention grabbing to say that I’m working on the P versus NP problem. It’s probably a hopeless thing to ask, but I’d like it if this project could be thought of in a suitably low-key way. What I have at the moment has not yet been sufficiently tested to count as a serious approach to the problem: as I’ve already said, complexity experts may be able to see quickly why it can’t work. Of course I dream that it might turn into a serious approach, but I’m not claiming that status for it unless it survives other people’s attempts to kill it off. To begin with, one should probably think of Polymath9 as devoted to the question, “Why could nothing like this work?” which is rather less exciting than “Please help me finish off my proof that PNP.” (However, I think the approach is different enough from other approaches that a sufficiently general explanation of why nothing like it can work would be of some interest in itself.)
The other is that I may have missed some simple argument that immediately demolishes the approach in its entirety. If someone points out such an argument, it will sting a bit, and it makes me feel quite apprehensive about clicking on the “Publish” button I see in front of me. But let me feel the fear and do it anyway, since it’s probably better to feel embarrassed when that happens than it is to spend another two or three months working on an approach that is doomed to fail uninterestingly.
An experiment with a slightly different way of doing Polymath
Although multiple online collaboration has not been widely adopted as a way of doing research, there have been enough different quite serious projects, each one with its own distinctive characteristics, to provide some evidence of what works and what doesn’t. Let me mention three examples that in different ways have worked. I think that Polymath1 (the density Hales-Jewett theorem) worked well partly because we started with not just a problem, but also the beginning of an approach to that problem. (The approach later changed and eventually had little in common with how it had been when it started, but having a clear starting point was still helpful.) Polymath3 (the Erdős discrepancy problem) started with just a statement of the problem to be tackled, and did not end up solving it, but I still count the project as a success of a kind, in that we rapidly reached a much better understanding of the problem, found plenty of revealing experimental data, and generated a number of interesting subquestions and variants of the initial question. More recently, Polymath8 (improving Zhang’s bound for prime gaps) worked well because the problem was not a yes/no question. Rather, it was a how-far-can-we-push-this-proof question, very well suited to a group of people looking together at a paper and reaching an understanding of the arguments that allowed them to improve the bound significantly. It was also good to undertake a project that was guaranteed to produce at least something — though I think the current bound is probably better than most people would have predicted at the beginning of the process.
Having said all that, there are some aspects of the Polymath projects so far that have left me not fully satisfied. I don’t mean that I have been positively dissatisfied, but I have been left with the feeling that more could be achieved. For one thing, it is slightly disappointing that there have not been more projects. (I bear some responsibility for this, since I have not been involved in any Polymath projects for quite a while, apart from a brief attempt to revive Polymath3.) I think there are various reasons for this, some of which it may be possible to do something about.
My original fantasy was that it would be possible for lots of people to make small contributions to a project and for those small contributions to add up almost magically to something greater than the sum of its parts. I think that to a small extent that happened, in the sense that reading other people’s comments was quite unexpectedly stimulating. However, I came to think that there was significant room for improvement in the way that a Polymathematical discussion takes place. At the moment it principally takes place in two ways: as a sequence of comments on blog posts, and as a wiki that is gradually built up by the participants. But neither of these conveys in a truly transparent way the logical structure of the discussion, or makes it easy for new people to join the discussion once it has got going. What I would like to see is the gradual building up of what I call a proof discovery tree. I don’t have a precise definition of this concept, but the rough idea is this. You start with the initial question you are trying to answer. You can’t just write down the answer, so you have to find new questions to ask. (At the very beginning they will be extremely hazy questions like, “What could a proof of this statement conceivably look like?”.) Those questions will probably generate further questions, and in that way one builds up a tree of questions. When one has gone deep enough into the tree, one starts to reach questions that one can answer. Sometimes the answer will have the effect of telling you that you have reached a dead end. Occasionally it will transform your approach to the entire problem.
I think something like that is a reasonable description of the research process, though of course it leaves a lot out. I also think that with modern technology it is possible to record one’s attempt to prove a result in a tree-like format rather than in the linear format that is encouraged by paper and pen, or even by TeX files, blog posts and the like.
What would be the advantage of writing notes on proof attempts in a tree-like form? I think there is one huge advantage: if at some point you feel stuck, or for some other reason want others to join in, then setting out your thoughts in a more structured way could make it much easier for others to take up where you left off rather than having to start from scratch. For example, when you stop, there will probably be a number of leaves of your proof-discovery tree that are not dead ends, but rather are questions that you just haven’t got round to answering. If you ask the questions in isolation (on Mathoverflow, say), then they will seem fairly unmotivated. But if they live on a proof-discovery tree, you can follow a path back to the root, seeing that the question asked was motivated by an earlier question, which itself was motivated by an earlier question, and so on. Or, if you just want to add a new leaf to the proof-discovery tree, you can ignore all that motivation (or perhaps skim it briefly) and simply try to answer the question.
Would it be practical for people to keep adding leaves to a tree like this? Wouldn’t it all get a bit out of hand, with people disagreeing about what constitutes an appropriate link from an existing vertex? I think it might. One way round that problem is the following. There is an informal discussion that takes place in the usual way — with comments on blog posts. But the participants also keep an eye on a somewhat more formal proof-discovery tree that develops as the discussion progresses, and if somebody makes a comment that looks as though it could be developed into a useful new node of the tree, it is proposed for a sort of “micro-publication”. If it is accepted, then whoever is moderating the discussion adds it to the proof-discovery tree, possibly rewriting it in the process. The node of the tree comes with links to the comment that inspired it, and the name of the author of that comment. So this process of micro-publication provides a similar kind of motivation to the one that traditional publication provides, but on a much smaller scale.
TiddlySpace
Is there any good software out there for creating a proof-discovery tree of this kind? I asked this question on Google Plus and got a variety of helpful answers. I opted to go with the third answer, given by Robert Schöftner, who suggested TiddlySpace with a MathJax plugin. If you’re the kind of person to whom that sounds complicated, you should take the fact that I managed to get it to work fairly easily as strong evidence that it is not. And I’ve fallen in love with TiddlySpace. It feels very unhealthy to have written that, but also, given the amount of time I’ve spent with it, not too wide of the mark.
Its main advantage, as I see it, over a traditional wiki is that a “tiddler”, which roughly corresponds to a wiki page or short blog post, is not on a separate web page. Rather, it forms part of a “tiddlyspace”, roughly speaking a collection of interlinked tiddlers, that all live on the same page and can be opened and closed as you like. Amazingly (to me at any rate), you can open, close, create and edit tiddlers even when you are offline, without losing anything. When you’re next online, everything gets saved. (I imagine if you close the page then you will lose everything, but it’s not exactly challenging not to do that.) One can also add nice gadgets such as what they call “sliders” — boxes you click on to make some text appear and click on again to make it disappear. I’ve used that in a few places to make it convenient for people to be reminded of definitions that they may have forgotten or not seen.
Now I’m not trying to say that everyone should use TiddlySpace. I’m sure people have very strong views about different kinds of wiki software being better than others. But I would like to encourage people to try writing their research attempts in a tree-like format, so that if they don’t succeed in solving a problem but do have interesting ideas about it, then they can present their incomplete proof attempt in a nice way. If you prefer some other software to TiddlySpace, then by all means use that instead.
As a matter of fact, TiddlySpace, while having a lot in common with what I have often thought would be great to have, also lacks a few features that I’d really like. I have included a tiddler with a site map that indicates the tree structure of all the pages by suitably indenting the titles. But what I’d prefer is a much more graphical representation, with actual nodes and links. The nodes could be circles (or perhaps different shapes for different kinds of pages) with text in them, and could increase in size as you hovered over them (like the icons on the dock of a Mac if you have too many of them) and open up if you clicked on them. Similarly, the edges would have text associated with them. So it might look more like the stacks project visualizations.
If writing up proof attempts became standard practice, and if somewhere there was an index of links to incomplete proof-discovery trees, then people who wanted something to think about could search through the leaves of the proof-discovery trees for problems that look interesting and well-motivated. (Maybe the Selected Papers Network could be used for this indexing purpose, though these would not be papers in any traditional sense.) In that way, collaborations could start up. Some of these might be very open and public. Others might be much quieter (e.g. someone emails the author of the proof-discovery tree with an answer to a question, and that leads to a private collaboration with the author). Also, even if every path of a proof-discovery tree led to a dead end, that would still be a useful document: it would give a detailed and thorough record of a proof attempt that doesn’t work. That’s something else that I’ve long thought would be a nice thing to have, partly because it may save time for other people, and partly because even a failed proof attempt may contain ideas that are useful for other problems. Also, as I found with Polymath1, there is the surprising phenomenon that other people’s ideas can be immensely stimulating even if you don’t use them. So even if my ideas about the P versus NP problem turn out to be fruitless, there is a chance, as long as they are not completely ridiculous (a possibility I cannot rule out at this stage), that they could provoke someone else into having better ideas that lead to interesting progress on the problem. If they do that for you, maybe you could buy me a drink some time.
For the above reasons, I see the publication (in the sense of making public on the internet) of partial proof-discovery trees as one possible way of getting Polymathematical research to become more accepted. Each such “publication” would be a kind of proposal for a project, as well as a record of progress so far. I also think that “micro-publishing” contributions to a proof-discovery tree have the potential to provide a motivation that is similar to the motivation that drives people to answer questions on Mathoverflow: it offers slightly more of a reward than you get from people responding to a comment you have made on a blog.
Yet another potential advantage of writing partial proof-discovery trees is that if you present your ideas so far in a structured format, it can result in a much more systematic approach to your own research. You may go from, “Oh dear, all this is getting complicated — I think I’ll try another problem,” to “Ah, now I see how all those various ideas link up (or don’t link up) — I think there is more to say about that leaf there.” I have found that when writing down my ideas about games and the P versus NP problem. So there is something to be said for doing it, even if you have no intention of making your thoughts public. (But what I would like to see in that case is people eventually deciding that they are unlikely to add to their private proof-discovery trees and making them public.)
Because I’m keen to see whether something like this could work, I have spent a couple of weeks taking my thoughts from over the summer (which I had written into a LaTeX file that stretched to 80 pages — in the interests of full disclosure I might make that file public too, though it is disorganized and I wouldn’t particularly recommend reading it), throwing out some of them that seemed to go nowhere, and putting the rest into a tree-structured Tiddlyspace wiki. I have tried to classify the tiddlers themselves and (more importantly) the links between the tiddlers. Most tiddlers are devoted to discussions of questions, so the link classifications are saying for what kind of reason I pass from trying to answer one question to trying to answer another. (Some simple examples might be that I want to try the first non-trivial case, or that I want to see whether a generalization of the original statement has a chance of being true.) I haven’t put as much thought into this link classification as I might have, so I am very open to suggestions for how to improve it, especially if these would make the connections clearer. (I can foresee two sorts of improvements: reclassifications of links within the scheme as it now is, and revisions to the scheme itself.) The result of doing that was to stimulate a lot more thought about the approach, so I’ve added that to the tree as well. A link to the whole thing can be found at the end of this post.
A proposal for Polymath9
To summarize, this is what I suggest.
1. The aim of the project is either to dispose quickly of the approach I am putting forward, by finding a compelling reason to believe that it won’t work (I have tried to highlight the most vulnerable parts, to make this as easy as possible — if it is possible) or to build on the existing partial proof-discovery tree until it yields an interesting theorem. While the big prize in the second (and much less likely) case would of course be to prove that PNP, there are more realistic weaker targets such as finding any property that follows “interestingly” from a function’s having low circuit complexity. In the first case, there is the prospect of finding a new barrier to proving lower bounds. For that one would need the approach to fail for an interesting reason. I explain below why I don’t think the approach obviously naturalizes, so there seems at least some chance of this.
2. I will give anyone who might be interested a week or two to browse in my partial proof-discovery tree. There is quite a lot to read (though I hope that its tree structure makes it possible to understand the approach without reading anything like everything), so I won’t open a mathematical comment thread for a while. (I’ve got other things I need to do in the meantime, so this works quite well for me.) However, before that starts I would very much welcome comments about the use I have made of TiddlySpace. I wanted to create a document that set out a proof attempt in a more transparent way than is possible if you are forced into a linear structure by a TeX document, but what I’ve actually produced was not planned all that carefully and I think there is room for improvement.
3. Once the comment thread is open (on this blog), I’ll act as a moderator in the way described above: if someone (or more than one person) provides input that would make a good page to add as a new leaf to the tree, then I will “micro-publish” that page. I don’t want to be too dictatorial about this, so I will welcome proposals for inclusion — either of your own questions and observations or of somebody else’s. I will make clear who the author is of each of these “micro-publications”. If I do not give credit to somebody who deserves it (e.g. if I base a page on a blog comment that builds on another blog comment that I had forgotten about) then I will welcome having that pointed out.
4. A typical “page” will consist of a question that is motivated by an existing page, together with a discussion of that question. If other questions arise naturally in that discussion, can’t be answered instantly, and seem worth answering, then they will be designated as “open tasks”. An open task can become a page if somebody makes enough observations about it to reduce the task to subtasks that look easier. (This does not have to be a logical reduction — it can simply be replacing the initial task by something that deserves to be attempted first.)
5. As a rule of thumb, if a question arises during the writing of a page that is sufficiently different from the question that the page is about that it is most naturally regarded as a new question, then it gets a new page. But this is a matter of judgment. For example, if the question is very minor and easy to answer, then it probably counts as more of a remark and doesn’t deserve a page to itself.
6. The underlying principle behind a link is this. You have a page discussing a question. If you can argue convincingly that the right approach (or at least a good approach) to the question is to think about another question or questions, then the argument forms the main content of the page, and the subquestion or questions form the headings for potential new pages. Links are classified into various types: if your link cannot be classified easily but is of a clearly recognisable type that does not belong to the current classification system, then I will consider adding that link type.
7. The main criterion for micro-publication is not the mathematical quality of the proposed page, but the suitability of that page as a new leaf of the tree. This principle reflects my conviction/prejudice that a good piece of mathematics can always be broken up into smaller units that are fairly natural things to try. I want to use the proof-discovery tree as a way of encouraging the process of exploring reasonably obvious avenues to be as systematic as possible. So I will normally insist that any proposed leaf is joined to an existing node by means of a link of one of a small number of types I have listed. (The list can be found over at the TiddlySpace space.) I will consider proposals for new link types, but will accept them only if there are compelling reasons to do so — which there may well be to start with.
8. If maintaining the partial proof-discovery tree becomes too much work to do on my own, then I will consider giving editing rights to one or more “core” participants. But to start with I will be the sole moderator.
A brief summary of the approach
There is a lot to read on my TiddlySpace. If you’d rather have some idea of what’s there before investing any time in looking at it, then this section is for you. I’ll try to give the main idea, though not fully precisely and without much of the motivation. If that gets you interested, you can try to use the proof-discovery tree to understand the motivation and a lot more detail about the approach.
The main idea, as I’ve already said, is to try to find a proof that relates to sets of low circuit complexity in the same way that Martin’s proof of determinacy relates to Borel sets. There are two instant reactions one might have to this proposal, one pessimistic and one optimistic. The pessimistic reaction is that the analogy between Borel sets and sets of low circuit complexity has already been explored, and it seems that a better analogue for the Borel sets is sets that can be computed by polynomial-sized circuits of constant depth. This fits with the fact that there is no natural Borel analogue of the parity function, and the parity function cannot be computed by polynomial-sized circuits of constant depth.
The optimistic reaction is that Martin’s proof is different enough from the proof, say, that the set of graphs containing an infinite clique is not Borel, that there is a chance that the objection just given does not apply. In particular, to prove that Borel sets of level are determined, one needs to apply the power set operation to the natural numbers roughly
times, and the statement that all analytic sets are determined (analytic sets corresponding to NP functions) needs large cardinal axioms. Could this be peculiar enough to enable us to find some non-natural analogue in the finite set-up?
An important thing to stress is that the property that I hope will distinguish between sets of low circuit complexity and random sets (or, even better, some set in NP, but for now I am not really thinking about that) is not an analogue of determinacy. That’s because it is a very easy exercise to show that the intersection of two determined sets does not have to be determined. (Roughly speaking, each set may have a nice part and a nasty part, with the nice parts disjoint and the nasty parts intersecting.) For this reason, Martin can’t prove determinacy by showing that the class of determined sets is closed under complements and countable unions and intersections. Instead what he does is prove inductively that Borel sets can be lifted to much simpler sets in such a way that (i) it is easy to show that the simpler sets are determined and (ii) it follows from that that the original sets are determined.
I won’t give all the definitions here, but the condition that is needed to get (ii) to work is basically this: given any set in the lifted game for which one of the players has a winning strategy, the same player has a winning strategy for the image of that set in the original game.
For various reasons, I’m convinced that certain features of the analysis of the infinite game have to be modified somewhat. The pages of my TiddlySpace set out my reasons in gory detail, but here let me simply jump to the set-up that I have been led to consider.
Basic definitions
I define a complexity structure to be a subset of a set
. I call the union of the
the alphabet associated with the structure. Often I consider the case where
. The maps between complexity structures that I consider (if you like, you can call them the morphisms in my category) are maps
such that for each
, the coordinate
depends only on
. To put that another way, if
is another complexity structure, the maps I consider are ones of the form
. I call a subset of a complexity structure
basic if it is of the form
for some
and some
. The motivation for the restriction on the maps is that I want the inverse image of a basic set to be basic.
The non-trivial basic sets in the complexity structure are the coordinate hyperplanes
and
. The circuit complexity of a subset of
measures how easily it can be built up from basic sets using intersections and unions. The definition carries over almost unchanged to an arbitrary complexity structure, and the property of maps ensures that the inverse image of a set of circuit complexity
has circuit complexity at most
.
Given a complexity structure , we can define a game that I call the shrinking-neighbourhoods game. For convenience let us take
to be
for some positive integer
. Then the players take turns specifying coordinates: that is, they make declarations of the form
. The only rules governing these specifications are the following.
- Player I must specify coordinates from
to
.
- Player II must specify coordinates from
to
.
- At every stage of the game, there must be at least one
that satisfies all the specifications so far (so that the game can continue until all coordinates are specified).
Note that I do not insist that the coordinates are specified in any particular order: just that Player I’s specifications concern the first half and Player II’s the second.
To determine who wins the game, we need a payoff set, which is simply a subset . Player I wins if the sequence
that the two players have specified belongs to
, and otherwise Player II wins. I call a set
I-winning if Player I has a winning strategy for getting into
and II-winning if Player II has a winning strategy for getting into
. (Just in case there is any confusion here, I really do mean that
is II-winning if Player II has a winning strategy for getting into
. I didn’t mean to write
.)
Because the game is finite, it is determined. Therefore, we have the following Ramseyish statement: given any 2-colouring of a complexity structure , either the red set is I-winning or the blue set is II-winning. (Normally with a Ramsey statement one talks about containing a structure of a certain kind. If we wanted to, we could do that here by looking at minimal I-winning and minimal II-winning sets.)
Given a complexity structure , I define a lift of
to be a complexity structure
together with a map
that satisfies the condition set out earlier. I define a lift to be Ramsey if
is a winning subset of
whenever
is a winning subset of
, and moreover it is winning for the same player. A more accurate name would be “winning-set preserving”, but I think of “Ramsey” as an abbreviation for that.
This gives us a potential method for showing that a subset is I-winning: we can find a Ramsey lift
such that
is simple enough for it to be easy to show that it is a I-winning subset of
. Then the Ramsey property guarantees that
, and hence
, is I-winning in
.
The definition of a Ramsey lift is closely modelled on Martin’s definition of a lift from one game to another, though there are also some important differences that I will not discuss here.
Now let me say what the property is that I hope will distinguish sets of low circuit complexity from some set in NP. I stress once again that this is a rather weak kind of hope: I think it probably won’t work, and the main reason I have not yet established for certain that it doesn’t work is that the definition of a Ramsey lift is complicated enough to make it fairly hard to prove even rather simple facts about it. However, I think the difficulties are reasonable ones rather than unreasonable ones. That is, I think that there are a number of questions that are tricky to answer, but that should yield reasonably quickly. I do not think that the difficulties are a disguised form of the usual difficulties connected with circuit complexity. So the most likely outcome of opening up the approach to public scrutiny is that the answers to these smaller questions will be found and they will not be what I want them to be.
An important example
To explain the property, let me first give an example of a Ramsey lift that converts every subset of into a basic set. I will take
to be the set of sequences
with the following properties.
- There exists
such that
is an ordered pair of the form
, where
and
is a I-winning subset of
with a winning strategy that begins with the move
.
- For every other
,
is an element of
.
- For every
,
is an ordered pair of the form
, where
,
, and
.
.
The map is the obvious one that takes the sequence above to
.
Given a set , its inverse image
is equal to the set of all
such that
for some
. This is a basic subset of
, as claimed earlier.
It remains to show that is a Ramsey lift of
. Let
be a I-winning subset of
and let
be a winning strategy for Player I for getting into
.
Suppose that Player I’s first move is of the form for some
and some I-winning subset
for which
is the first move of a winning strategy. Player II can now play an arbitrary move of the form
, where
,
, and
. Since
is a winning strategy for getting into
, the result will always be a win for Player I. Therefore, for every
with
there exists
with
. Let
be the set of sequences
such that
. Then
. So a winning strategy for Player I for
is to begin with the move
and then to play the rest of the strategy that gets into
, which will get her into
.
Now suppose that Player I’s first move is of the form . This time, Player II is free to choose an arbitrary
such that
and play the move
. After that, Player I is guaranteed to produce a sequence in
, which implies that
contains all sequences
with
. Therefore, Player I has a winning strategy for
, since she can simply start with the move
.
Now let be a II-winning subset of
and let
be a winning strategy for Player II for getting into
. Then for every opening move
that Player I might choose to make, Player II can defeat that move. It follows that there exists
with
such that the sequence
belongs to . Therefore, for every Player I winning set
there exists
such that
. It follows that Player I does not have a winning strategy for
, so Player II does have a winning strategy for
.
The potential distinguishing property
I called that an important example because it gives us a “trivial upper bound” on the size we need to have if we want to find a Ramsey lift from
to
that makes a set
simple. The lift above makes every single subset of
into a basic set. Note that this bound is quite large: there are doubly exponentially many winning sets
. (Slightly less obviously, there are doubly exponentially many minimal winning sets. I haven’t written out a full proof of this, but here is why I believe it. If you take a random set with a certain critical probability, then it should be a I-winning set, but it should not be possible to remove lots of elements from it and still have a I-winning set. Therefore, we need to have a collection of sets of density almost as big as the critical probability such that almost every set with the critical probability has a subset in the collection. That should make the collection doubly exponential in size. It would be good to make this argument rigorous.)
What I would like to prove is something like this. There is one part of what I want that is unfortunately a little vague, which is the definition of “simple”. I’ll discuss that in a moment.
- If a set
has polynomial circuit complexity, then there exists a Ramsey lift
of
with
such that
is simple and the cardinality of
is much less than doubly exponential.
- If
is a random subset of
, then with high probability the smallest Ramsey lift that makes
simple is doubly exponential.
- There exists an NP set
such that
the smallest Ramsey lift that makessimple is doubly exponential.
If one could prove 1 and 3, then one would have shown that PNP. If one could prove 1 and 2, then one would have exhibited a non-trivial property that distinguishes between functions of polynomial circuit complexity and random functions. That in itself would not prove that P
NP, but it might point the way towards other methods of defining “unnatural” properties, which is a necessary first step towards proving that P
NP.
I’ll say once again that I don’t yet consider this to be a serious approach, even if I ignore the problem that I don’t yet know what a “simple” set is. Given a precise definition of “simple” (and I have some candidates for this), I have just exhibited a pair of statements the conjunction of which would imply that PNP. However, for an observation that
to count as a serious approach to proving
, there are two other properties one wants. The first is good evidence that
is actually true, which I do not have — I do not count my failure to disprove it so far as good evidence, and the analogy with Martin’s theorem has certain drawbacks that make me think that it is likely that either 1 will be false, or else 1 will be true but only because all sets can be efficiently lifted, so that both 2 and 3 will be false. The second requirement is some reason to believe that
might be easier to prove than
. Here I think the implication above fares slightly better: while I have no idea how to prove lower bounds on the “Ramsey-lift complexity” of a set, the fact that proving upper bounds doesn’t seem to be easy for sets of low circuit complexity suggests that if one did manage to prove such upper bounds, one would have a reduction of the problem that didn’t feel trivially equivalent in difficulty to the original problem, though it might in practice turn out to be very hard as well. If further thought about 1-3 led people to believe that they were likely to be true after all, then and only then would I want to say that this was a serious approach. But as I’ve said several times now, I think that is fairly unlikely.
A key question I’d like to know the answer to is whether there is an efficient (that is, much smaller than doubly exponential) Ramsey lift for the parity function, or rather the set of points with an odd number of 1s. The reason is that it looks to me at the moment as though the most likely thing to go wrong will be that the most efficient lift blows up rapidly as the circuit complexity of a function increases — so rapidly that it becomes doubly exponential for circuits of linear size. (All we would need for this is for the size of
to square at each increase by 1 in the length of a straight-line computation. Obviously, slightly weaker statements would also suffice.) If that is indeed the case, it may well be that what determines the size of the smallest lift is closely related to the noise sensitivity of the set
, in which case the parity function is a good one to use as a test.
Another possibility for a cheap demolition of the whole approach is if you can spot a simple Ramsey lift that converts an arbitrary set into a basic set and needs an alphabet of only exponential size. I haven’t really tried to find such a lift, so I could easily have missed something obvious.
What is a simple set?
For Martin a simple set was one that is open and closed. The best analogue I can think of for the notion of an open set is the following. Let be a complexity structure. Call a subset of
–basic if it is an intersection of
basic sets, and call it
–open if it is a union of
-basic sets. Call it
–closed if its complement is
-open. Then we could look at sets that are
-open and
-closed for some suitably small
.
But how small? The only natural candidates seem to be 1,2 or something around , but there appear to be difficulties with all these choices.
Why not define a set to be simple if it is basic? I have a problem with that, which is that if it is too easy to lift a set to a basic set, then we will probably be able to lift all the coordinate hyperplanes in (which are basic already) to sets of the form
— that is, to sets that are not just basic but defined by restrictions of the first coordinate. But if we can do that, then all sets lift to basic sets in
.
An exercise
If you want an even easier question to think about than the one above about the parity function, I have not yet even managed to determine whether one particular lift works. Here’s how it is defined. I take the set of all sequences of the form
, where
and
is the parity of
. The map
takes this sequence to
. Thus, the game in
is the same as the game in
except that when Player II specifies the
th coordinate, he must also commit himself to a particular parity
and to playing his last move to ensure that
has this parity.
This extra condition on Player II should disadvantage him, so there should be payoff sets that Player I can get into if Player II has the extra restriction but cannot get into otherwise. I’m pretty sure it will be easy to find such a payoff set, but my first few attempts have failed, so I have not managed to do it yet. I do have a heuristic argument that suggests that a suitably chosen random set ought to be an example, so one approach would be to make that argument rigorous.
One can also consider small variants of the above lift, for some of which it is not at all clear that a random set should work, so what I’d really like to see is either a proof that some simple variant is in fact, contrary to expectations, a Ramsey lift, or an argument that is sufficiently general to rule out a large class of similar constructions.
Why wouldn’t the approach naturalize?
For anyone wondering whether to invest any time in helping me think about my approach, this is of course the key question. It’s hard to say for sure that the approach wouldn’t naturalize. Perhaps one could come up with a clever criterion that would say which sets can be efficiently lifted. But I’m fairly confident that the property “there exists a complexity structure with an alphabet of significantly less than doubly exponential size and a map
that takes I-winning sets to I-winning sets and II-winning sets to II-winning sets such that
is simple” is not easy to reformulate as a property with polynomial (or quasipolynomial, or anything at all small) circuit complexity (in the truth table of
). In fact, I think it is not even in NP, since we existentially quantify over
and
but then require
to have a property that holds for a very large class of rather complicated subsets of
. So even if we allow
to be “only exponential” in size (which is not required by the approach), the natural formulation of the property appears to be
.
Of course, it’s one thing to write down a strange property, and quite another to expect it to hold for functions of low circuit complexity. But the fact that I have been strongly motivated by the proof of Borel determinacy gives me some small reason to hope that a miracle might occur. It is in the nature of miracles that it probably won’t occur, but the subjective probability I associate with it is far enough from zero that I don’t want to give up on it until I am absolutely sure that it won’t.
I should add that even if the property I have given above does not work, it may be that some related property does, as there are various details that could be changed. For example, we could replace the classes of I-winning and II-winning sets by other classes of sets and ask for our maps to preserve those.
Link to the current version of the proof-discovery tree
Finally, here is the proof-discovery tree as I have developed it so far. To get started, I recommend clicking on “PvsNP Sitemap” in the toolbar at the top of the page. Even if the approach collapses almost immediately, I hope you may enjoy looking at it and getting an idea of what can be done on TiddlySpace.
October 24, 2013 at 7:36 pm |
I have been really intrigued by P=?NP : “How could we ever know that the NP-complete apparently hard problems really are beyond polynomially hard, given that asymptotically an infinite number of algorithms or programs are a priori possible/candidate poly-time solvers of some NP-complete decision problem?” I figure my time is limited for hard mathematical work, but I’m interested in following along. I happen to also have a WordPress Blog; would you give me permission to “Reblog” this post? A “Reblog” resembles a “reprint” in publishing: all content, author name, blog name and publication date are “re-published” faithfully , with a hyper-link to the original blog post (here, in this case). David Bernier
October 25, 2013 at 4:06 pm
I have no objection to that.
October 25, 2013 at 2:05 pm |
Reblogged this on Pink Iguana and commented:
Link back to Appel’s Verification result and Gowers’s crowd sourcing proofs, and try to determine given something like Knight Capital Programming fail, how do you even write the theorem to be automatically proved so you don’t drop 450 million USD.
October 25, 2013 at 3:30 pm |
If this project results in an interesting theorem (but probably not one which separates P from NP) I propose that it be named the “TiddlyTheorem”.
(Declaration: No conflict of interest.)
October 25, 2013 at 8:41 pm |
Reblogged this on meditationatae.
October 28, 2013 at 8:03 pm |
I am possibly not following the shrinking-neighborhoods game. Let me imagine a “sample play”:
Suppose m = 1, n = 2, and the payoff set sequences are 01 and 10. The starting sequence is unspecified, “–“.
If Player I starts, the possibilities are “1-” and “0-“. Then Player II can play “11” or “00” and win.
If Player II starts, the possibilities are “-1” and “-0”. Then Player I can play “01” or “10” and win.
Is this accurate?
October 28, 2013 at 8:14 pm
That comment was mine. Here would be (I think?) the I-winning and II-winning sets for the n=2 game:
I-winning
{00, 01}, {11, 10}, {11, 01, 10}, {00, 01, 10}, {00, 11, 01}, {00, 11, 01, 10}
II-winning
{00}, {11}, {01}, {10}, {00, 11}, {00, 10}, {11, 01}, {01, 10}
Again, is this accurate?
October 28, 2013 at 8:32 pm
What you said in your first comment is correct, except that I am assuming that Player I always starts.
The second comment isn’t quite right though. Player I can start with or
or 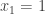 , so any II-winning set must have at least one sequence starting with a 0 and one sequence starting with a 1. That condition is also sufficient, so the four pairs you list under II-winning are the four minimal II-winning sets.
, so any II-winning set must have at least one sequence starting with a 0 and one sequence starting with a 1. That condition is also sufficient, so the four pairs you list under II-winning are the four minimal II-winning sets.
The two minimal winning sets for Player I are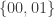 and
and  , i.e., the first two sets that you list. That’s because whatever Player I’s first move is, the set must contain both sequences that start that way.
, i.e., the first two sets that you list. That’s because whatever Player I’s first move is, the set must contain both sequences that start that way.
October 28, 2013 at 10:32 pm |
[…] Polymath 8 is working towards publication and it looks like Polymath 9 might be starting up. See the post: https://gowers.wordpress.com/2013/10/24/what-i-did-in-my-summer-holidays/ […]
October 29, 2013 at 6:05 pm |
I see no reason why not to use standard wiki software like MediaWiki. It is possible to create trees of pages in wikis simply by creating a list of links to “subpages” and on subpages create a link to “upper level”. Well, it involves manual creating a link from a subpage to its parent, but that is not much work.
I have no experience with TiddleSpace but it looks like it puts the entire tree on one page. I suspect the tree may grow too big.
Well, maybe you are right and it’s better to see the entire tree on one page. Good luck.
October 29, 2013 at 6:08 pm |
Dear Gowers, I want to ask you for an advise.
I am an amateur mathematician.
I have created a new theory (and put it into book form) in the field of general topology.
By the way I’ve “discovered” a big number of new open problems.
Will putting it at TiddleSpace help my research (by welcoming others who probably need first read my book)?
Or will it just a loss of time to put my problems in this form?
October 29, 2013 at 6:11 pm
The trouble is to contribute to my theory is possible only after reading my book, as otherwise one would even not understand my questions. And even if one understand one need to stay on my shoulders 🙂
October 29, 2013 at 6:28 pm
If you’ve already written a book about your theory, I think the marginal benefit of rewriting that book in TiddlySpace form is unlikely to be substantial.
October 29, 2013 at 6:38 pm
I never thought to rewrite my book in TiddlySpace form. But I think about writing my partial proofs (not in the book) of open problems in the book.
October 30, 2013 at 10:44 am |
Tim, crazy thought about simplicity measure (of cause not well defined, and not necessary the best, and is not well described).
Suppose your subsets can be described by the set of polynomial equations of degree d. write down all monomials up to degree d . expand the set of polynomial equations describing the constraints by multiplying by monomials from
. expand the set of polynomial equations describing the constraints by multiplying by monomials from  and taking them modulo the current set of equations. After few steps you get saturated system.
and taking them modulo the current set of equations. After few steps you get saturated system.
The complexity measure is the ratio between the size of null space of saturated system and the size of .
.
The linear system is easy: the ratio is close to 0. and say partition problem
and say partition problem  for saturation. The complexity is
for saturation. The complexity is  .
.
The simple NP-complete problems can be encoded as
The complexity of the subset is the minimum simplicity across all possible encoding. It is also possible to define measure with respect to d+1, so that non-linearity of the system appears in the problem, and use as the measure the size of null-space itself, without normalization.
October 30, 2013 at 5:15 pm |
It is not clear to me that the number of minimal winning sets is a double exponential. The minimal winning sets seem to have a lot of symmetry when we look at lower dimensions and possibly induction can preserve that symmetry and that would provide a bound that makes it smaller than any double exponential. Also I think that I can establish the density of a minimal set by induction and in fact the exact number of points and that most random arrangements of this number of points will not be winning sets so a proof by random methods may be difficult.
October 30, 2013 at 6:44 pm |
I believe I have an answer to your exercise when n = 6. .
. , sequences where
, sequences where  .
.
Let the payoff set include:
(Condition A) all sequences where
(Condition B) out of the sequences where
If Player I starts at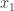 , condition A forces Player II to play at
, condition A forces Player II to play at 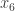 and make a parity choice. Now condition B means that Player II no longer has any control over the parity (since Player II’s only chance to win now is for
and make a parity choice. Now condition B means that Player II no longer has any control over the parity (since Player II’s only chance to win now is for  ) so Player I can use his or her turns to make the parity the opposite of what Player II chose. If it wasn’t for the parity choice, Player II would have won.
) so Player I can use his or her turns to make the parity the opposite of what Player II chose. If it wasn’t for the parity choice, Player II would have won.
October 30, 2013 at 6:50 pm
Scratch that: I need an extra condition so Player I can exploit the situation if Player II doesn’t immediately respond to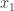 . Be back later.
. Be back later.
October 30, 2013 at 7:42 pm
Attempt #2, n = 6. Apologies for any typos. .
. , sequences where
, sequences where  .
. and
and  , sequences where
, sequences where  and
and 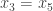 .
.
Let the payoff set include:
(Condition A) all sequences where
(Condition B) out of the sequences where
(Condition C) out of the sequences where
Player I starts at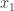 . Condition A will force
. Condition A will force 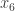 to be a non-parity changing mood. Condition B also indicates neither
to be a non-parity changing mood. Condition B also indicates neither 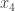 nor
nor  can change parity. Hence Player II has no parity control after the first move.
can change parity. Hence Player II has no parity control after the first move.
If Player II continues at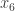 so Player I can use his or her turns to make the parity the opposite of what Player II chose. (This is Player II’s “out” which will allow the set to be winning in the unmodified version of the game.)
so Player I can use his or her turns to make the parity the opposite of what Player II chose. (This is Player II’s “out” which will allow the set to be winning in the unmodified version of the game.)
If Player II continues at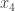 , following condition C Player I matches at
, following condition C Player I matches at  . If Player II continues at
. If Player II continues at  , then Player I matches at
, then Player I matches at 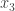 and wins. If Player II continues at
and wins. If Player II continues at 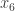 , then Player I continues at
, then Player I continues at 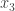 such that
such that  , forcing Player II to make
, forcing Player II to make  and being defeated by condition B.
and being defeated by condition B.
If Player II instead continues at , a similar argument applies.
, a similar argument applies.
November 2, 2013 at 11:33 am
Thank you for this example. I have micro-published it. Let me know if there is anything you would like changed in what I have written.
November 4, 2013 at 4:38 pm
On the tiddly (I hope I am using the right word) the indices are a bit messed up, half the time 4 should be 6 (or the other way around).
November 4, 2013 at 5:17 pm
Thanks — I changed the indices around but forgot some of them. I hope it’s OK now. (At any rate, it is more OK than it was before.)
November 2, 2013 at 2:24 pm |
Hi, this is awesome stuff.
I’m one of the maintainers and primary developers of TiddlySpace. I’m extremely happy to see the value you are getting out of it. It would be fantastic to start a conversation to figure out ways of making TiddlySpace more useful for you and people who would like to do similar things. There are a lot of features that don’t make themselves immediately obvious and functionality which needs a push to take it from prototype to useful.
I’m personally very interested in opening up academic publishing and discourse to a wider audience, especially using web based tools.
Please contact me if you have the time and interest to talk about it more.
November 3, 2013 at 12:01 pm
At the moment, the main additional feature I would like is a nicer way of displaying how the pages link together than the sitemap that I have created. One person suggested something called mindmaps, but I couldn’t get it to work, and I’m not quite sure it’s what I have in mind anyway.
November 3, 2013 at 10:45 pm
I’ll have a think and ask around about sitemap ideas.
In the meantime I figured out how to make the mathjax show up properly from outside TiddlyWiki when viewing a single tiddler.
November 3, 2013 at 11:40 pm
I’m confused by this. If I log out of TiddlySpace and then click on one of the links to individual Tiddlers on my blog, it renders fine, and always has done (I’ve checked in the past). I can’t work out how to make it not work. Is the fix you talk about something that you have added in your capacity as a developer, or is it something I need to do?
November 4, 2013 at 11:12 am
I’ve thought of another thing it would be nice to have. It would be good if one could look at the Tiddler one is editing while editing it. I don’t mean that I would want a display that continually updated itself as one wrote (though that would be great), but simply a convenient way to look at the most recently saved version.
One reason that would be nice is that at the moment if I make a mistake in the LaTeX, I have to hold in my head what and roughly where the mistake was when I click on “edit”. It can sometimes be a bit tedious to do that in a way that it would not be tedious if I could see the compiled text at the same time as the edited text.
November 4, 2013 at 3:33 pm
On the single tiddlers: There are two ways to link to individual tiddlers:
There’s the permalink into a TiddlyWiki that you’re familiar with.
There’s also a first class link to that tiddler directly, outside of TiddlyWiki. For your use you may never need to use that link, but it is one that search index systems might stumble upon so may get exposed via searches. So having it render the math might be worthwhile.
With regard to viewing the tiddler while editing it’s likely you could include what’s in the ViewTemplate in the EditTemplate. That’s the sort of thing that the the tiddlywiki google group could probably provide a good answer for. The boring but workable way to accomplish the same thing without additional code would be to put to browser windows side by side.
November 4, 2013 at 2:07 pm |
[…] Gowers Proposed and launched a new polymath proposal aimed at a certain approach he has for proving that […]
November 4, 2013 at 11:28 pm |
What would you mean if I put my problem (whether the category of continuous maps between endofuncoids is cartesian closed) in your Tiddle?
It is questionable however whether it is worth doing, because to start one need first read my book. I realize that not many people will go read it.
I spend some time attempting to prove this conjecture, but failed.
Dear Gowers, what you advise on this? Should I make a tiddler for this my problem? If yes, in your tiddler or to create my own?
November 4, 2013 at 11:46 pm
I suggest you don’t put your own, completely unrelated, work into the framework that Tim has built for his project and the subsequent Polymath9 project.
November 4, 2013 at 11:49 pm
David Roberts, Gowers’s wiki is called “Open maths notebooks”. The name suggests that it is open for other math projects. The final decision is by Gowers however and I want to hear his opinion.
November 9, 2013 at 11:35 pm |
“As long-term readers of this blog will be aware, the P versus NP problem is one of my personal mathematical diseases (in Richard Lipton’s sense). ”
this is an amusing blog by lipton & have cited it myself in my own blog. however, the ref to P vs NP as a “disease” imho while obviously facetiously intended is imho somewhat, to some degree, in poor taste. yes I know this is a joke. but if it really is a joke, Id like to ask a question on tcs stackexchange, which am sure would probably get voted down– what are cases of complexity theorists referring to their own field in disparaging and near-derogatory terms?
have seen this in multiple cases. of course its due to frustration of lack of progress/results (in many ways not all that much better than those found by shannon 1/2 century ago).
yes, obviously this is “inside baseball” and experts need to have some leeway to talk about it informally/casually esp in blogs & informal communication etc. but on the other hand, lots of ppl are listening to these blog including students and possible future researchers.
another point is that P vs NP is not an abstract problem like many others lipton cites as “diseases”. it has huge practical implications, possibly almost more so than almost any other math problem. can anyone think of a math problem with greater practical implications? maybe a theorem in thermodynamics? to me P vs NP actually has a lot of analogies to thermodynamics theorems on work/energy/information– ie almost an as-yet undiscovered law of physics.
in short its an elite/superb problem of highest calibre. a better analogy for public purposes would be Everest in its pre-summitted state. we can all agree on that, right? doesnt that sound much better? or say, if you are really pessimistic, Olympus Mons on Mars. but even NASA is planning to visit mars one day.
June 2, 2015 at 4:20 pm |
[…] facetiously/ jokingly sometimes as a “disease” or “virus” (RJlipton, Gowers, Tao, etc) and this is partly in reference to all the bogus proof attempts. the $1M claymath prize […]
August 31, 2015 at 11:30 pm |
[…] Polymath 8 is working towards publication and it looks like Polymath 9 might be starting up. See this post. […]
November 1, 2016 at 10:01 am |
Dear Timothy Gowers,
I was browsing on TiddlySpace just now, and I saw an announcement that they are shutting down in December. I do not know if you are aware of this. You might want to back up all that you have written about the P vs NP approach.
November 1, 2016 at 2:16 pm
Wow, thanks for letting me know. It’s a pity, but fortunately I know one or two other initiatives that could end u being adequate substitutes.
November 1, 2016 at 2:31 pm |
My pleasure. I am thinking myself about how to create the “hypertext” interface to proofs that Lampert talks about in his articles on structured proofs [1]. I think the TiddlyWiki interface is very suitable for that, but it doesn’t seem trivial to generate tiddlers automatically from a TeX source. (I am very much willing to restrict the TeX syntax to a minimum of LaTeX and some theorem/definition environments + Lampert’s pf2 package.)
What are the alternative initiatives that you mentioned. Would you please share more?
[1] http://research.microsoft.com/en-us/um/people/lamport/pubs/proof.pdf
September 4, 2021 at 11:09 am |
Regarding what should happen to any money won from the Clay mathematic institute in the eventuality such a collaboration where you can’t apportion credit easily? My personal belief is that far too much money is spent on posh buildings named after rich businessmen and dead while men in order to increase ‘prestige’. I have a most excellent concept – the Julia Robinson/Grace Hopper/Chien-Shiung Wu/Hypatia/Ada Lovelace etc. etc. etc. ecovillages for fundamental questions.
There has been a crash in the economy, and many supermarkets have excessive landbanks they are ‘saving for the future economic boom which isn’t going to happen’ and these landbanks often have planning permission (current or expired) for supermarkets on greenfield sites not far from University small towns, so the land which you could easily get planning permission for could be bought up cheaply. Luxury glamping pods only cost £5000 each and can be erected quickly – frequently they are made from ecologically sustainable materials.
An excellent person to approach to coordinate the project might be Simon Ambrose – an entrepreneur who came runner-up in one of the editions of ‘The Apprentice’ run by Sir Alan Sugar., and who has extensive experience running a property management business. Surallan has a lot of rich friends, possibly including the dragons from Dragons Den – a ‘real-life gameshow for entrepreneurs seeking in vestment’. Many of these dragons have philanthropic interests and could provide excellent mentoring on the project.
For example, one of the major logistical issues would be ‘how to link the glamping caravans to large computers via optial fibres , and Peter Jones, one of the dragons owns a telecommunications company – perhaps he could be convinced to delegate a couple of his engineers to look into logistical issues. These supermarket landbanks are frequently located near to industrial sites, which would be excellent places to warehouse the computers.
Of course, if P does really equal NP, then these intelligence agencies are going to find that they don’t have the monopoly on spying, so maybe there is the opportunity to use their enormous pre-existing computers (already under heavy security guard) for purposes far more useful to humanity than the spying on of all our personal correspondence.
These eco-villages should of course attempt to avoid the Town versus Gown dichotomy, and integrate into their local area. For example – if there is to be free food for the scientists, then the leftovers should go to eg. food-cycle etc. Offices of maths professors are cleaned far too often, and these underpaid and exploited cleaners frequently move papers and personal items to the great annoyance of the maths professors. There are many ways to accomplish the cleaning of offices in a fairer and more equitable manner than this system of wage slavery – e.g. the running of caravan parks is a popular profession for those looking to ‘get away from the city’ whether that be via landscape gardening, caravan park management. Initiatives in the UK such as WEA, Open University, the underfunded further education sector should be supported.
You must read the book by Virginia Woolf ‘A Room of One’s Own’ – PhD students are always forced to share offices, which isn’t necessary in our WIFI connected world. The seminars can be held in Yurts, with second-hand furniture (the British Heart foundation might be able to help with logistics – they have a whole network of 2nd hand UK furniture shops) for hot-desking and collaboration when the students and professors wish to be sociable. But for those wishing to be alone to think about maths then it should not only be the Professors who have their own glamping caravan.
Furthermore, there must be a ‘family-friendly’ section of the ecovillage (complete with childrens’ playground) for those researchers/teachers who wish to comibine their maths careers with having a family. However I am not such an expert at how to design this as I do not have children. Don’t forget to create some fellowships in collaboration with the network of Syrian former academics who have sought asylum in the UK, and also other refugees – not just the asylum seekers – the economic immigrants should not be discriminated against – they have frequently faced much hardship in their countries of origin, and are frequently the most hardworking and talented people around – the main problem being how to avoid ‘brain-drain’ from poor countries – so an exchange system should be set up.
I have less knowledge of what should be supported outside of the UK, but some ideas which maybe I’ll comment on sometime.