Having a blog gives me a chance to defend myself against a number of people who took issue with a passage in Mathematics, A Very Short Introduction, where I made the tentative suggestion that an abstract approach to mathematics could sometimes be better, pedagogically speaking, than a concrete one — even at school level. This was part of a general discussion about why many people come to hate mathematics.
The example I chose was logarithms and exponentials. The traditional method of teaching them, I would suggest, is to explain what they mean and then derive their properties from this basic meaning. So, for example, to justify the rule that xa+b=xaxb one would say something like that if you have a xs followed by b xs and you multiply them all together then you are multiplying a+b xs all together. Then, having established this rule, you would turn to the rule log(ab)=log(a)+log(b) and justify it by raising 10 (or e if you’d got on to that) to both sides, arguing that you get ab in both cases. This would itself be justified by the rule for exponentiation and the rule that 10log a=a. To justify that last rule you would shout at the children that this is what log means.
And yet, amazingly, at least 90 percent of children will get lost by that explanation, and will go on to make mistakes such as log(a+b)=log(a)+log(b). Could there be a better way?
Here’s a different way, at any rate. Perhaps it shouldn’t replace the traditional way, but it could certainly supplement it. It’s to admit, frankly, that the notion of multiplying a string of a xs together does not make sense when a is anything other than a positive integer and to focus from then on on the properties of the exponential and logarithmic functions, and especially the rules xa+b=xaxb and log(ab)=log(a)+log(b). If these were presented as in some sense defining the concepts of exponentiation and logarithms, then a number of traditional mistakes would be less likely to occur (and when they did, you could just say, “You’ve forgotten the definition” rather than, “You don’t understand the meaning of this concept if you could make a mistake like that”). Moreover, when pupils went on to do simple exercises, like working out the logarithm of the square root of x, they would be more likely to be guided to the correct proof: that the defining property of the square root, y, of x, is that y2=x; that this in turn means yy=x; that the log rule then tells you that log(y)+log(y)=log(x); so log(y)=log(x)/2.
Those who criticized this view tended to think that I was advocating pure rote learning rather than understanding. Actually, I was suggesting that a true understanding of a sophisticated concept such as the exponential function involves letting go of the intuitive meaning (once it has served its purpose of telling you the rules you want the function to satisfy) and using the defining properties instead.
Behind that suggestion is a more general claim, which is that mathematicians greatly underestimate the extent to which they think syntactically rather than semantically. When you work with the log function, it feels as though you are somehow in direct contact with the function, but this feeling is as much of an illusion as the feeling that you are actually seeing a cube when you decide to visualize it. (You don’t agree that that is an illusion? Then what colour was the one you just visualized?) When you actually write an argument using logs, you almost always use the familiar properties of the function (including more advanced properties, such as that it grows slowly) and not this direct contact with the meaning of the function. To put that more precisely, you don’t have to say to yourself things like, “This is the number x such that, if I raise e to the power x, I get a.” You don’t even need to say that when you take exp of a log—you just use the syntactic rule that exp and log cancel.
I write this expecting that it will still be an unpopular view. But I think I can defend it (or some suitably reexpressed version of it).
September 13, 2007 at 1:20 pm |
I very much like this suggestion of teaching logs and exps in this way to high-school kids. I agree the kids would probably perform much better, and it is a very good point that “you forgot the definition” is much less demotivating than “you don’t understand the concept”. Just wondering though—is it always possible to define elementary functions by simple equations? For x^a for example, is x^a the only function F(x,a) on two variables satisfying F(x,a+b) = F(x,a) F(x,b)?
By the way, there is a rather famous logician called Jean-Yves Girard who actively advocates removing completely the difference between syntax and semantics from logic, and indeed, from the foundations of mathematics altogether. He has written various elaborations of his ideas, which I find unfortunatly unpenetrable.
October 19, 2012 at 4:38 am
Watch my YouTube video, It relates to what you are taking about. My video will show a better alternative solution for Logarithms. I believe my solution to be unique.
September 13, 2007 at 2:03 pm |
This is a tangent, but it’s not an illusion that you “see” a cube when you mentally picture it–at least not completely. Old experiments with mental rotation tasks, as well as new evidence from brain imaging, show that mental imagery is very closely linked to “real” imagery and is indeed a tool the brain uses to solve problems.
September 13, 2007 at 2:07 pm |
Some thoughts.
1. I learned the rearrangement of equations when at school, using a heuristical method that involved rules for manipulating them. Thus the following move
a = bc
a/c = b
I learned as a rule: if you shift the thing multiplied over to the other side, stick it underneath. Only much later when I read Euclid (as a postgraduate philosopher) did I understand why this should work. An equation literally represents an equality: what’s on the left is the same in some respect, or identical to what is on the right. So, if you do something to one side, and do the same thing to the other side, you still have an equality.
The second thought process is more abstract and, in a way, far more difficult to understand than the first. Curiously so, because the second way is supposed to be the most fundamental way of following the inference through: if you do it the second way, you cannot but ‘see’ how the a/c = b follows of necessity, almost logically, from a = bc.
So, now having children of secondary school age, and needing to help them with mathematics and science, I proceeded to teach them using methods that involved the second way of thinking. Use clear definitions always, show what each term means, then show how to move by steps of thought that are intuitively clear and logically obvious &c.
The result was a complete disaster and soon abandoned. I found it was much easier to teach them mechanical methods of doing things. They don’t understand why these methods work, they just do them. Later on, when they’ve had enough practice they kind of see why it works.
On the other hand, the beauty of mathematics is the ‘seeing’ of how one thing follows from another, which the first way of thinking doesn’t really help with. I preferred the ‘traditional’ way of explaining exponentiation as it ‘really’ shows you why it works. The ‘syntactic’ explanation, by contrast, doesn’t really show you what’s going on.
2. The Stoics also thought that logic should be reduced to syntax. They said that the essence of the syllogism depends on words, but not on their meanings. If therefore the words are changed the syllogism ceases to exist.
September 13, 2007 at 2:17 pm |
Dear Anonymous,
I can’t remember where I saw it, but some time ago I was disturbed for at least two reasons to read about a remarkable experiment where they did something like forcing monkeys to look at images, injecting them with some kind of dye, and cutting their brains open to find actual copies of the images. (The details may be wrong, but that’s the general idea.) So I’m forced to admit that you’re right that visualization and vision are closely linked. But perhaps I can weaken that weakening of my case by appealing to a multitude of other experiments that show that vision itself is not the immediate, direct contact with an object that it seems to be. When it comes to mathematics, visualization clearly plays a very important role, as does its link with vision. But I’m inclined to think that these are mainly important as very good short cuts: they make certain mathematical facts obvious by providing a much better “notation” for them. To give an example, it is easy to “see” that if you attach a handle to a torus then you obtain a two-holed torus; to prove it rigorously is not particularly hard, but it would be quite difficult to write out a proof in a way that would be easy for somebody else to read.
September 13, 2007 at 2:23 pm |
Minor typos: The occurrence of “log(a+b)=log(a)+log(b)” in the third paragraph should probably be replaced by the correct rule. Also, there is an unmatched closing parenthesis in the penultimate paragraph.
Regarding your main point, you could make the same argument at a more basic level of mathematics, say, elementary algebra. The reason so many students will cancel the a’s in an expression of the form (a + b)/a is not that they don’t understand the distributive law, it’s that they haven’t absorbed basic algebraic manipulations at a purely syntactic level.
Regarding the feel of being in direct contact with the logarithm, long exposure and familiarity are what lead to that feeling, of course. Imagine, as a thought experiment, that precalculus textbooks started introducing (say) the (real) Lambert W function shortly after exponential functions and logarithms, with many routine exercises requiring the manipulation of the function via its defining properties. In such a case, it’s not difficult to imagine a future generation of mathematicians and scientists who viewed it as yet another elementary function.
September 13, 2007 at 2:45 pm |
Quite often in cases like this I will present a concept both ways: I will give a formulaic way of thinking, followed by a more detailed explanation. For logarithms, I tend to appeal to inverses and geometric thinking; I will also refer to slide rules. Students tend to be fascinated by slide rules, and the concepts within translate directly to log-log or semi-log graph paper.
I will keep re-emphasizing the syntactic version for those students who need it that way and explore the concept deeper for those that have an easier time understanding in a more conceptual sense. One can’t presume the same method works for every student. As an example from earlier in math, many students are happy with the midpoint formula being given as a direct formula to memorize, but there are always a few that will have puzzled looks until I explain it’s simply the average of the x values followed by the average of the y values. These students will say ‘oh, now it’s easy’ while the students who are content with the formula will plug away at that instead.
re William: As far as one-on-one tutoring goes, you should of course pick the individual method that works best and stick with it. Differentiated instruction is only needed for teaching en masse.
September 13, 2007 at 3:13 pm |
>> When it comes to mathematics, visualization clearly plays a very important role, as does its link with vision.
This immediately suggested the topic of blind mathematicians, and lo, I found a thread on the maths history site about this.
http://mathforum.org/kb/thread.jspa?threadID=383014
Where I learned to my surprise that Hilary Putnam is blind, though he is a logician.
September 13, 2007 at 3:23 pm |
In response to William on manipulating equations, I’d like to mention that I remember well from my own experience that I didn’t truly understand why it worked until I’d been doing it for years. The thing that made me finally understand THAT THE TWO THINGS ARE EQUAL SO OF COURSE YOU CAN DO THE SAME!!! was realizing that I had not really stopped to think why it was OK to add two equations together when solving simultaneous equations. Later, when teaching linear algebra, I tried to pass on this insight, but I very much doubt I managed: when you try to explain it, what you say has that quality of being so trivial that it’s almost impossible to get across why you are bothering to say it.
September 13, 2007 at 3:33 pm |
This reminds me of the saying famously attributed to von Neumann – “You don’t understand mathematics, you just get used to it.”. Is there any research on what actually works when teaching mathematics? There is a paper (“The camel has two humps” – http://www.cs.mdx.ac.uk/research/PhDArea/saeed/paper1.pdf) that claims there is a large chunk of the population who just cannot learn programming, and no teaching method makes much of a difference. They even propose a simple test. Has anything similar been claimed (or refuted) for teaching mathematics?
Jeremy Henty
PS: Tim, the best blogs have a preview option. Enable it if you can.
September 13, 2007 at 3:53 pm |
Happy to enable previewing but a brief search through Options doesn’t seem to get me anywhere. Can anyone advise me? And also about how to edit comments I make (as opposed to initial posts, which I have found easy to edit)?
September 13, 2007 at 3:56 pm |
Is it not von Neumann who is reputed to have said “In mathematics you don’t understand things. You just get used to them.”? I’ve often found myself wondering to what extent this is true, so I’m glad it’s been brought up for discussion.
September 13, 2007 at 3:58 pm |
Another thing I need to get used to is the idea of refreshing a blog before posting anything to it. Sorry to repeat what you said, Jeremy.
September 13, 2007 at 4:31 pm |
>> when you try to explain it, what you say has that quality of being so trivial that it’s almost impossible to get across why you are bothering to say it.
Very eighteenth century! You may be interested in Thomas Reid’s account of Aristotle’s Logic, where he makes similar remarks about the futility of logic (the traditional variety, of course – mathematical logic was 100 years later) and the corresponding superiority of mathematics. The link is here
http://uk.geocities.com/frege@btinternet.com/joyce/reid_aristotle.htm#C4%20Sec%20V
The anchor should take you to the relevant section, but if it doesn’t work, page down to the contents, and find the link to “Section V ON THIS THEORY, CONSIDERED AS AN ENGINE OF SCIENCE”. He notes, for example, that the conversion, A is greater than B, therefore B is less than A, does not fall within the rules of conversion given by Aristotle or the Logicians, and that even the simple reasoning, A is equal to B, and B to C, therefore A is equal to C, cannot be brought into any syllogism in figure and mode.
September 13, 2007 at 5:17 pm |
For editing comments: if you’re logged in, there should be an ‘edit’ link at the top of each comment, next to the date and time of posting.
September 13, 2007 at 5:32 pm |
As one of the proprietors of another WordPress blog, I’ve had no luck with turning on comment preview. This is among the 20 little things wordpress.com won’t let you do, which should in theory be possible, so perhaps they’re the appropriate people to be lobbying.
September 13, 2007 at 6:40 pm |
Dear Tim,
I guess there is a fundamental transition in mathematical learning when one realises that what mathematical objects are (and how they are constructed) may be less important than what mathematical objects do (e.g. what properties they obey). At the undergraduate level, I see students struggle with such concepts as abstract vector spaces for these reasons; the definition of a vector space, being property-oriented rather than constructive, does not resemble the mathematical definitions they have seen earlier in their education (though it does resemble some definitions they would have seen in non-mathematical contexts). This is a particular stumbling block when one wants to convince them that, say, real functions on [0,1] form a vector space.
I guess the one drawback with a property-oriented approach to logarithms is that the uniqueness of a logarithm is not at all clear (and the existence of a logarithm still requires the traditional definition).
Incidentally, you can put latex in your posts to get nice equations such as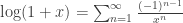 ; this, to me, is one of the key advantages of wordpress over other blog options. See
; this, to me, is one of the key advantages of wordpress over other blog options. See
http://faq.wordpress.com/2007/02/18/can-i-put-math-or-equations-in-my-posts/
September 13, 2007 at 11:55 pm |
Tim, Ben – I see working Comment Preview on other blogs so often that I assumed it must be easy to enable in WordPress. Looks like I was wrong!
Terry – Yes it’s vital to teach people they mustn’t assume that any apparently plausible set of properties defines a unique operation. Perhaps some standard fallacies could be used to show why this is so important? Such as the ones that exploit the ambiguity of sqrt(z) for complex z to introduce an extra minus sign?
(Let’s see if LaTeX works in comments: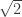 .)
.)
September 14, 2007 at 12:52 am |
>>Only much later when I read Euclid (as a postgraduate philosopher) did I understand why this should work. An equation literally represents an equality: what’s on the left is the same in some respect, or identical to what is on the right. So, if you do something to one side, and do the same thing to the other side, you still have an equality.
Being a sophomore in high school now, I’d only understood the reasoning behind many mathematical concepts last year, when I took a college computer science course and Algebra II simultaneously. Taking a computer science class taught me to think more logically instead of just going through the processes that I’d learned years before. With my computer science instructor forcing me to map out every process in my code and explain how and why each step in the process was crucial, I was finally able to understand the meanings behind the rules I had to memorize in maths.
Teachers no longer teach logic in maths class; they just tell students to memorize a rule, but don’t explain why it’s important. So, when students make a mistake, it really is because they don’t understand the concept. Your second suggestion of teaching might be harder to implement at first, but it definitely pays off later.
September 14, 2007 at 2:45 am |
Tim,
Although you are undoubtedly in a better position to know than I am, I’m nevertheless surprised that you refer to the “semantic” approach as “traditional”; my impression is just the opposite — that the “meanings” of mathematical objects have traditionally been given very short shrift.
The most striking (and, I would say, egregious) example of this is perhaps a subject that has already been alluded to, viz. linear algebra (and its applications in multivariable calculus). In the “traditional” approach, one performs formal computations with matrices, without any acknowledgement (at least at first) of the fact that the matrices represent homomorphisms of vector spaces. As a consequence, the definition of matrix multiplication seems like an artifice cooked up out of thin air — an excessively complicated one at that — rather than a natural, inevitable consequence of the fact that we’re talking about the composition of linear maps. The “traditional” proof of the existence of eigenvalues, invoking the characteristic polynomial defined in terms of determinants, is virtually a caricature of itself (it would have been a good candidate for inclusion in that famous book Mathematics Made Difficult) — as is the presentation of the multivariable chain rule (where one is presented with a near-incomprehensible formula involving hordes of indices rather than being told that “the derivative of a composition is the composition of the derivatives”), and the inverse/implicit function theorem (with talk about Jacobian determinants being nonzero rather than about derivatives being isomoprhisms), etc.
My distaste for this approach, in addition to deriving from my interest in things infinite-dimensional, where e.g. determinants simply aren’t involved, probably has a lot to do with the fact that the semantics are what I care about in the first place. (I wouldn’t be interested in matrices, for example, but for their interpretation as linear transformations.) The beauty of pure syntax resides in the fact that it allows one to contemplate multiple semantic interpretations, and thus to make previously unsuspected connections between apparently separate ideas; this is for me the point of category theory, for example. To be useful for this purpose, however, syntax has to be kept simple, lest the manipulative difficulties get in the way of semantic contemplation.
I actually don’t think your point about logarithms has to do with syntax versus semantics so much as with different choices of semantics. In effect, I read you as advocating that be conceived abstractly as a homomorphism relating the multiplicative structure of the real numbers to the additive structure — rather having that property follow as a consequence of another, more concrete, definition. (Or at least, that one should adopt the abstract conception as soon as one has seen that the property in question is a consequence of the concrete definition.)
be conceived abstractly as a homomorphism relating the multiplicative structure of the real numbers to the additive structure — rather having that property follow as a consequence of another, more concrete, definition. (Or at least, that one should adopt the abstract conception as soon as one has seen that the property in question is a consequence of the concrete definition.)
September 14, 2007 at 9:09 am |
All sorts of interesting points there. About Terry’s point that as well as abstract properties you need to establish existence and uniqueness: obviously this is correct, though for a first presentation of logarithms, to schoolchildren, I think it can be safely swept under the carpet, as, if they just assume it, they will be making a correct assumption. Actually, I suppose existence should have something said about it, but not so much, “It can be proved rigorously that there exists a function with these properties,” as something more like “It may seem a bit strange that you can actually extend the definition of exponentiation to non-integer exponents, but, amazingly, you can.” James is right to draw my attention to the fact that I am blurring two distinctions — abstract/concrete and syntax/semantics. I think both are relevant here, but right off the top of my head I’m not quite sure which is more important for the particular matter of teaching logarithms. However, I stand by my statement that it is common for mathematicians to underestimate the extent to which their thinking is syntactical. A third interesting point is how to teach linear algebra. I think that is such a big subject in its own right that it deserves a separate post, so I’ll put one up in a moment.
Now please excuse a little experiment: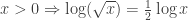 ;
;
I would like to emphasize things from time to time. Thanks: a huge step taken towards true maths bloggership.
September 14, 2007 at 10:04 am |
Thinking about this, I wonder if the distinction between semantics and syntax is as clear as we assumed before. Here’s a definition of the exponential
(A) a^n = a1.a2.a3…an
The digits following the a’s are meant to be subscripts, and simply ‘count’ the number of times we are applying the operator ‘times’, represented by the dot. The mental grasp required here is to understand what the ‘n’ represents, and is not any different from understanding multiplication. Indeed, if we replaced the caret by a ‘times’ sign, and the times sign by a plus, then we have a definition of multiplication.
(B) a^(m+n) = a1.a2.a3…a(m+n)
The move to (B) requires only a mental grasp of substitution. We don’t have to know what ‘m+n’ represents at this point.
(C) a1.a2.a3…a(m+n) = a1.a2.a3…a(m) . a1.a2.a3…a(n)
Now we move to the equivalence in question. How is it a ‘semantic’ move? Surely it’s no different to the move that young children make, called ‘counting on’. We have a sum, say
5 + 4
‘counting on’ is something they don’t grasp until reception or year 1 (age 5-6), perhaps later. They have to get the knack of saying ‘6 7 8 9’ while at the same time counting ‘1 2 3 4’. I remember from my brood how difficult this was. But (C) is the same. You count m times, applying the times operator as you go (doesn’t matter what this operator means). Then you count to m+1 to m+n, simultaneously ‘counting on’ 1 to n in parallel.
So the question is, in what sense is the first ‘traditional’ explanation a ‘semantic’ one?
September 14, 2007 at 10:33 am |
Here’s what I’d say to William on syntax and semantics. I agree that it’s not easy to say what there is to mathematical meaning over and above syntax, at least if you want to satisfy a philosopher. But suppose you are happy with an informal, and not terribly rigid, distinction. Then I think it is possible to say something useful. A first bash at it would be that you are operating semantically if all the syntax takes place at a lower level. For instance, even if the intuitive argument for is, at bottom, syntactic, you will not see that unless you start to pick it to pieces. (And even then, most people would have in their head a picture of what goes on when
is, at bottom, syntactic, you will not see that unless you start to pick it to pieces. (And even then, most people would have in their head a picture of what goes on when  and
and  or something like that — once there’s a model there I call it semantic.) Whereas, once
or something like that — once there’s a model there I call it semantic.) Whereas, once  and
and  stop being positive integers you just apply the rule, so it’s more syntactic. Actually, one thing I don’t understand about your comment: are you saying that counting on is syntactic? I can see arguments on both sides: it can be a mechanical process, but something seems to have to click inside a child (an intuitive understanding of why it works, perhaps?) before they can do it, and perhaps that should be called semantic. Here’s a second attempt at a definition (but again not too precise a definition). Syntactic thought is symbolic manipulation, whereas semantic thought involves a mathematical/mental model of what the symbols are talking about. (Where it gets complicated is that one might argue that mental models are encoded in some kind of brain syntax. That’s why I think an informal distinction is probably the best one can hope for.)
stop being positive integers you just apply the rule, so it’s more syntactic. Actually, one thing I don’t understand about your comment: are you saying that counting on is syntactic? I can see arguments on both sides: it can be a mechanical process, but something seems to have to click inside a child (an intuitive understanding of why it works, perhaps?) before they can do it, and perhaps that should be called semantic. Here’s a second attempt at a definition (but again not too precise a definition). Syntactic thought is symbolic manipulation, whereas semantic thought involves a mathematical/mental model of what the symbols are talking about. (Where it gets complicated is that one might argue that mental models are encoded in some kind of brain syntax. That’s why I think an informal distinction is probably the best one can hope for.)
September 14, 2007 at 11:02 am |
The syntax / semantics distinction is notoriously obscure. You mention one way of characterising it, but immediately qualify it by an obvious objection. Another way is to distinguish between rules which are very simple, and those which are very complicated (think of Google translator, and where it goes wrong, against the much more complicated system of rules that human translators use).
‘Counting on’ is clearly a simple rule that you could program a computer to follow, thus ‘syntactic’ in one sense.
September 14, 2007 at 2:04 pm |
[…] of very important discussions on the pedagogy of elementary mathematical topics (specifically logarithms and linear algebra). You can read my contributions here and […]
September 16, 2007 at 12:03 pm |
[…] How should logarithms be taught? « Gowers’s Weblog […]
September 18, 2007 at 8:38 pm |
Uniqueness of course only holds if you assume continuity. The fun starts once you drop that assumption (and brings you right into your “what is a definition” discussion if you try to come up with concrete counter examples).
September 21, 2007 at 2:35 pm |
[…] Maße mit mathematisch-konzeptionellen Fragen in Verbindung stehen. Als Beispiel sei hier nur der Beitrag “How should logarithms be taught?” erwähnt, in dem er den wahrscheinlich nicht so […]
September 24, 2007 at 12:27 am |
What about extending this to ‘calculus for engineers’? To take a trivial example, you would say, when x = t^2 dx/dt = 2t ‘as a rule’ and move on without a mention of epsilon, delta or even of Sylvanus P. Thompson and his shuffling dts. Leave all that to the mathematicians, engineers are trusting folk. They will believe you have got the fundamentals right.
Simpler rule – ‘Mathematica rules’.
There has to be some way to stop all those potential advanced math users moving into media studies or Macdonald University.
Hide the plumbing?
October 4, 2007 at 2:05 am |
I consider this whole discussion worthwhile just because I had no idea I could put LaTeX in my blog postings and comments. That’s outstanding. When one Fields medalist comments on the blog of another Fields medalist, I guess good things are bound to happen.
December 14, 2007 at 6:51 pm |
gowers Says (September 13, 2007 at 3:23 pm)
“In response to William on manipulating equations, I’d like to mention that I remember well from my own experience that I didn’t truly understand why it worked until I’d been doing it for years. The thing that made me finally understand THAT THE TWO THINGS ARE EQUAL SO OF COURSE YOU CAN DO THE SAME!!! was realizing that I had not really stopped to think why it was OK to add two equations together when solving simultaneous equations.”
Gosh, if I ever needed proof that my brain is wired differently from that of a top mathematician, here it is (btw, I am not even a mediocre mathematician).
How on earth could you go on for years just relying on applying “syntactic” rules without relying on the “semantic” fact you capitalized?
I would have flunked out of middle school!
A generation later: I have been relying very heavily on the capitalized fact to explain things to my 9yrs old daughter and not only it is working fine: it seems the only thing that works.
December 15, 2007 at 3:06 pm |
very interesting, but I don’t agree with you
Idetrorce
September 12, 2008 at 3:31 pm |
[…] Gower’s weblog […]
October 10, 2008 at 12:17 am |
“THE TWO THINGS ARE EQUAL SO OF COURSE YOU CAN DO THE SAME!!!”
Sorry to comment so late, but seeing that makes me feel better about how embarrassingly long it took me to realise this! I remember my school teacher saying ‘and now we add 2 to both sides’ or something and finally actually taking it in, and everyone looking at me like I was a moron cos I was supposed to be the clever one – but no, i’d just been chucking the variables ‘over the fence’ for years.
I like maths for the rare semantic insights, but it takes me so painfully long i’m resigned to huge amounts of syntactic muddling along.
October 11, 2008 at 1:22 am |
Hi,
Oh I love this kind of discussion. On Williams comments about equation, when I was in second year high school in a kinda outback fishing village in Philippines, one of the math subjects is algebra I discovered my first love, numbers. My impression on education there at that time about 30 yrs ago is pretty much like an old fashion american style a basic 3 r’s (writing, reading and arithmetic) and lots of drills in exercises. So my teacher introduced equation the first time and the first axioms relating to equation namely: axioms of addition, subtraction, multiplication and division, as a start. What you do in the left hand side of the equation you do in the right and everything will be fine.
Really reminds of democracy, you do same thing on both sides of the equation and you can start at the very beginning 1 = 1 .But 1 has many guises and faces and that the start of the story.
I did my Electrical Engineering degree in Manila just to get close to math and love of science. Now living in Sydney done my grad dip in Computer Science in University of New South Wales. Life passes by, now I am back to my first love, numbers.
October 17, 2008 at 2:03 am |
For what it’s worth I wrote a free 113 page pdf on the teaching of logarithms… http://www.mathlogarithms.com
Please access and comment.
Dan Umbarger
December 10, 2008 at 7:19 pm |
PLEASE SEND ME NEW WAYS OF TEACHING LOGARITHM IN COLLEGE SCHOOLS TO AID MY RESEARCH WORK
February 25, 2009 at 5:08 am |
Since log and exp are related in what is arguably the most intimate way two functions could be related with respect to their inner mechanics (i.e. inverse relationship), I don’t think any true understanding will be acquired until both are understood, with respect to the other.
My suggestion would be to teach log and exp as functions that give one information about a given tree diagram. Let’s say this tree exists out there in the Platonic realm, and log and exp are instruments that show us different aspects of it.
Exp is a function that says; given a branch factor b and the number of levels x, tell me how many leaf nodes = y are on the tree.
Log is a function that says; given a branch factor b and the number of leaf nodes y on the tree, tell me how many levels = x there are.
It then becomes clear that the number of levels x (returned by log()) grow arithmetically with respect to the branch factor b (think vertically), while the number of leaf nodes y (returned by exp()) grows geometrically with respect to the branch factor b (think horizontally).
Of course, this becomes less clean when you are dealing with reals instead of integers.
February 7, 2012 at 7:56 pm |
i want to teach probability
June 28, 2013 at 7:34 pm |
Reblogged this on Singapore Maths Tuition.
October 2, 2020 at 11:53 am |
Reblogged this on 站点标题.
September 14, 2021 at 12:24 pm |
[…] Article URL: https://gowers.wordpress.com/2007/09/13/how-should-logarithms-be-taught/ […]