Update: comments on this post are now closed, since my latest post would compromise any further contributions to the experiment.
Most of this post consists of write-ups of proofs of five simple propositions about metric spaces. There are three write-ups per proof, and I would be very grateful for any comments that you might have. If you would like to participate in the experiment, then please state your level of mathematical experience (the main thing I need to know is whether you yourself have studied the basic theory of metric spaces) and then make any comments/observations you wish on the write-ups. The more you say, the more useful it will be (within reason). I am particularly interested in comparisons and preferences. For each proof, the order of the three write-ups has been chosen randomly and independently.
It would also be useful if you could rate each of the 15 write-ups for clarity and style. So that everyone rates in the same way, I suggest the following rating systems.
Clarity.
-2 very hard to understand
-1 hard to understand
0 neither particularly hard nor particularly easy
1 easy to understand
2 very easy to understand
Style.
-2 very badly written
-1 badly written
0 neither badly written nor well written
1 well written
2 very well written
I stress that ratings should not be regarded as a substitute for comments and observations, or vice versa. What I really need is both comments and numerical ratings.
I do not want people to be influenced by the answers that other people give, so all comments on this post will go to my moderation queue. When I have enough data for the experiment, probably in a week or so, I will publish all the comments (unless for some reason you specifically request that your comment should not be published).
The more people who participate, the more reliable the results of the experiment will be. I realize that it may take a little time, so thank you very much in advance to everybody who agrees to help. (Update 26th March: I now have over 30 responses; they have been very helpful indeed, so I am extremely grateful for those. If they keep coming in at a similar rate over the next few days it will be wonderful.)
The write-ups.
Problem 1. Let and
be open sets in a metric space. Then
is open.
1(a) We want to show that for all in
, there exists
such that the open ball
is contained in
.
Let .
is in
, so
is in
and
is in
. Since
and
are open, there exist
such that
and
. Let
. Then
is contained in
, so it’s contained in
. Similarly,
is contained in
, so it’s contained in
. So
. So
is open.
1(b) For arbitrary , let
. Consider an arbitrary
. As
are open there are
such that
and
. Take
. Then
and
. So
. We’ve proved that for any
there is an open ball (
in this case) that contains
and is inside
. So
is open.
1(c) Let be an element of
. Then
and
. Therefore, since
is open, there exists
such that
whenever
and since
is open, there exists
such that
whenever
. We would like to find
s.t.
whenever
. But
if and only if
and
. We know that
whenever
and that
whenever
. Assume now that
. Then
if
and
if
. We may therefore take
and we are done.
Problem 2. Let and
be metric spaces, let
be continuous, and let
be an open subset of
. Then
is an open subset of
.
2(a) Let be an element of
. Then
. Therefore, since
is open, there exists
such that
whenever
. We would like to find
s.t.
whenever
. But
if and only if
. We know that
whenever
. Since
is continuous, there exists
such that
whenever
. Therefore, setting
, we are done.
2(b) Let . We seek
such that the open ball
is contained in
.
, so
.
is open, so we know that for some
,
. Since
is continuous, there exists
such that for all
,
; i.e.,
. So
if
; i.e.,
. So
is open.
2(c) Take any . We have
. As
is open, there is an open ball
in
. Because
is continuous, there is some
such that for any
,
belongs to
. Hence, for such
,
. So
. So
. We’ve proved that every point in
has an open ball neighbourhood. So
is open.
Problem 3. Let be a complete metric space and let
be a closed subset of
. Then
is complete.
3(a) Consider an arbitrary Cauchy sequence in
. As
is complete,
has a limit in
. Suppose
. Because
is closed,
belongs to
. We’ve proved that every Cauchy sequence in
has a limit point in
. So
is complete.
3(b) Let be a Cauchy sequence in
. Then, since
is complete, we have that
converges. That is, there exists
such that
. Since
is closed in
,
is a sequence in
and
, we have that
. Thus
converges in
and we are done.
3(c) Let be a Cauchy sequence in
. We want to show that
tends to a limit in
.
Since is a subset of
,
is a Cauchy sequence in
. Since
is complete,
, for some
. Since
is a closed subset of
, it must contain all its limit points, so
. So
in
. So
is complete.
Problem 4. Let and
be metric spaces and let
and
be continuous. Then the composition
is continuous.
4(a) Let , and let
. We need to show that there exists
such that for all
,
.
is continuous, so there exists
such that for all
,
.
is continuous, so there exists
such that for all
,
. But then
, as desired. So
is continuous.
4(b) Take an arbitrary . Let
and
. Using continuity of
, for any
, there is some
such that if
(for
), then
. As
is continuous, there is some
such that if
(for
), then
. So for any
we’ve found
such that if
, then
and therefore
. Hence
is continuous.
4(c) Take and
. We would like to find
s.t.
whenever
. Since
is continuous, there exists
such that
whenever
. Since
is continuous, there exists
such that
whenever
. Therefore, setting
, we are done.
Problem 5. Let and
be sets, let
be an injection and let
and
be subsets of
. Then
.
5(a) Take . So there is some
and
such that
. As
is injective,
and
are equal. So
. So
.
5(b) Suppose . Then, for some
,
and
. So
. Since
is injective,
, so
, so
. So
.
5(c) Let be an element of
. Then
and
. That is, there exists
such that
and there exists
such that
. Since
is an injection,
and
, we have that
. We would like to find
s.t.
. But
if and only if
and
. Therefore, setting
, we are done.
March 25, 2013 at 10:26 am
Just a few comments from me, rather than any deep analysis, as I have a backlog of refereeing to catch up on at the moment!
I can see that the differences are intended to be subtle rather than blatant. On a quick look through, there are many places where I would do something slightly different myself, but I didn’t see places where I would take any significant number of marks off in an exam.
I think that some comments might depend on context. For example, in 1(a) it looks as if one should at least say that a and b are >0, but might or might not need to specify that they are real numbers, depending on what students are used to at that point.
In 1(b), the inclusion of the definition of the open ball appears unnecessary, assuming this notation is already standard.
I usually don’t like using the word “any” because of potential ambiguity, though I think there is no issue here. (Probably more of an issue in 4(b).) I try (but often fail) to avoid the word “contains” (because of the element/subset distinction), and “is inside” is new to me.
Traditionally we avoid starting a sentence with a mathematical symbol, but this doesn’t affect the clarity of the argument.
In problem 3, I note that there appears to be more than one usage of the term “limit point” of a set in the literature. This rarely affects proofs, though!
In problem 4, I would always put brackets round to form or else write
or else write  . None of the three arguments do that, so perhaps this is unnecessary.
. None of the three arguments do that, so perhaps this is unnecessary.
I prefer the “suppose” of 5(b) to the “Let” and the “Take”, because the relevant set might be empty, But the multiple occurrences of “so” are slightly grating. Again, it is fairly widely accepted to use “Let” even when the set might be empty. I am not so sure about “Take”.
The use of theta as a positive real number here appears to me to be a little unusual, rather than incorrect. It is probably better to stick to more traditional usage: if taken to extremes one could define continuity of a function delta by insisting that for all points epsilon in the space and all f>0, there exists g>0 …
March 25, 2013 at 10:39 am
(I am a maths PhD, no longer in academia but still with business cards saying “Mathematician” on them. I am familiar with the basic theory of metric spaces.)
General remark: in some pairs a major difference is that one uses more words while the other uses more symbols. I find the latter harder to read here purely “optically”. I suspect (without actual evidence) that this is partly a matter of typesetting, and that in a context — e.g., textbook, TeXed lecture notes — where text and mathematics are more consistent in look there would be less difference in readability. I don’t think that’s the whole story, though; punctuation (hence sentence structure) is easier to see amidst text than amidst mathematical symbols.
You will notice that I much prefer to minimize mathematical notation when doing so brings no loss in conciseness. This is probably an idiosyncrasy, and you may choose to discount appropriately. If the choice of topic is representative, the audience would presumably be easily intimidated by such things, which could be an argument for minimizing notation (don’t scare them) or having plenty (get then used to it). I’m just going with my gut :-).
I find clarity and style very difficult to disentangle; in mathematical writing, good style is mostly *about* clarity.
1. +1,0,-1 for clarity; 0,-1,-2 for style.
(c) is really terrible *unless*, maaaaybe, the intention is to combine it with something more approachable to show how one can go back to basics and use the epsilon-delta definitions. (a) and (b) are of course very close to identical; (b) is worse mostly because of poor naming (r,r’,R much worse than a,b,r). I don’t have strong feelings about the words-versus-symbols difference between (a) and (b). Including the definition of B_r, as in (b), may be a good or a bad thing depending on the audience.
I would actually prefer to see this done with scarcely any notation at all. “Consider any point x in AnB. Some ball at x lies wholly within A, and some ball at x lies wholly within B. Whichever of the two has smaller radius lies wholly within AnB. In other words, for every point of AnB there’s a ball there inside AnB, so AnB is open.”
2. -1,0,1 for clarity; -2,-1,0 for style.
2(a) is like 1(c): raw epsilons and deltas. This never works. 2(b) is like 1(b): a bit of an intimidating thicket of notation. It doesn’t have the gratuitously bad variable names, though.
As with 1, it feels like it could be clearer with less notation; a brief attempt suggests that the result might actually be clearer only to those already familiar enough with the field not to need to be given a proof in the first place.
3. -1,-1,0 for clarity; 0,0,1 for style.
I don’t like any of these very much. I think using a rather than x for the points of the sequence is better. No need for the fussy subscript in (a). There’s a “garden-path” sentence in (b) that really doesn’t help. (c) has very much the right idea, but I think it’s too notation-heavy.
“We must show that any Cauchy sequence in A converges to a point in A. Well, any Cauchy sequence in A is also a Cauchy sequence in X, which is complete, so it converges to a point in X. But A is a closed subset of X, so any limit of points in A itself lies in A, and we’re done.”
4. I strongly dislike all three. The right way to prove this is to first prove that f is continuous iff inverse images of open sets are open (at which point you can add the bonus remark that there’s a more general setting in which this is the usual *definition* of continuity), and then say: the inverse image of an open set under gof is f^-1(g^-1(open)) = f^-1(open) by continuity of g = open by continuty of f.
I’m afraid I give them all -2 for both clarity and style; maybe -1 for (c) on one or both counts. Probably all could be improved with a judicious diagram.
5. Clarity: 1,2,0; style: -1,1,-1. Both (a) and (c) have what must be deliberately contrary choices of notation (e.g., elements y in X and x in Y). (c) is too verbose and has a bit of garden-pathiness for the same reason as the sentence I complained about in 3(b), for the same reason. (In general: never say “Since p, q, and r, s” because at first it looks as if you’re saying “Since p, q”.)
I wonder again about a very notation-light proof. “Any element of f(A) n f(B) has preimages in both A and B. But by injectivity it has only one preimage, which therefore lies both in A and in B, [].” Not so good for real novices who’ll blanch at the word “preimage”.
March 25, 2013 at 10:46 am
Here are my answers and comments.
Previous exposure to metric spaces: yes (but never had to teach that yet).
Comments beforehand: unless mistaken, the likely context is that of recent comments on your Two Cultures ideas. I’ve tried to answer regardless of this, but perhaps especially informative participants would be Part II and Part III students who have not read your blog nor your Two Cultures paper (that might mean printing out this blog post and hand it to a few of them).
Problem 1: , and this is implicitely used in proof b and c (at first, I thought “what is
, and this is implicitely used in proof b and c (at first, I thought “what is  ?”), but this is not the main reason why I feel they are badly written, it’s more to do with the flow of the argument. I especially like proofs that start with “we want to show that”.
?”), but this is not the main reason why I feel they are badly written, it’s more to do with the flow of the argument. I especially like proofs that start with “we want to show that”.
-proof a: clarity=2 style=2
-proof b: clarity=1 style=-1
-proof c: clarity=0 style=-1
Comment: the statement of the problem does not have a name for the metric space. Usually in exercices it is
Problem 2: for an element of
for an element of  is a little disturbing,
is a little disturbing, 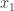 and
and  would have been better, but this is not the main reason, again it is its verbose aspect that makes it badly written in my opinion (the final part “Therefore, setting” is especially ‘antiflow’).
would have been better, but this is not the main reason, again it is its verbose aspect that makes it badly written in my opinion (the final part “Therefore, setting” is especially ‘antiflow’).
-proof a: clarity=0 style=-1
-proof b: clarity=2 style=2
-proof c: clarity=-1 style=0
Comment: in proof a the use of
Problem 3: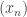 a sequence in
a sequence in  .
.
-proof a: clarity=2 style=1
-proof b: clarity=2 style=0
-proof c: clarity=2 style=0
Comment: it is more difficult to have a preference here, if anything writing limits with an arrow is more upsetting than calling
Problem 4: is akward (but I don’t like the
is akward (but I don’t like the  of proof a either, I’d prefer
of proof a either, I’d prefer  or
or  which to me are more neutral) but otherwise the proof is fine. Proof c is especially poorly written (where is
which to me are more neutral) but otherwise the proof is fine. Proof c is especially poorly written (where is  ? and so on…).
? and so on…).
-proof a: clarity=2 style=2
-proof b: clarity=2 style=1
-proof c: clarity=0 style=-2
Comment: in proof b the notation
Problem 5:
-proof a: clarity=2 style=0
-proof b: clarity=2 style=2
-proof c: clarity=0 style=0
Comment: after reading proof b the flaws of proof a become even more evident, so I’ve altered its mark in retrospect.
March 25, 2013 at 12:05 pm
Mathematical Experience – Part IA Maths, so no experience with metric spaces yet (although the timing of this seems peculiar, seeing as the Met and Top course is next term, and then you would be able to get feedback from a large number of Part IA/IB students)
Problem 1:
a) Clarity – 0, Style – -1
b) Clarity – 0, Style – 1
c) Clarity – 2, Style – 1
Comments:
While this may only be a consequence of having never studied metric spaces before, but I preferred c) much more mainly because it worked directly from the definition of what an open set is – after this I was able to understand the argument in a) and b) much better, although I still preferred the proof by the definition. The main difference between a) and b) is that in a), the usage of the subset symbol seemed fairly inconsistent (sometimes you would use the symbol, and others you would say “is contained in”), and such a mix of using/not using notation was fairly confusing.
Problem 2:
a) Clarity – 1, Style – 1
b) Clarity – 0, Style – 0
c) Clarity – 0, Style – -1
Comments:
c) has inconsistent usage of symbols/not using symbols, this time for the “a member of” symbol. While in b) the basic idea of the proof is appreciated, I can’t really understand what is happening with the open balls (probably because this is the first time I’ve seen them), whereas with a), the sequencing of ideas seems more natural seeing as the proof is effectively a “just do it” (as Imre Leader would say) proof.
Problem 3:
a) Clarity – 2, Style – 1
b) Clarity – 2, Style – 2
c) Clarity – 2, Style – 2
Comments:
Possibly because the actual idea behind the proof is incredibly simple, all three proofs are fairly clear in what they are doing. As for the style, in a) noting that the “n” subscript is a natural number is not hugely necessary, and the use of “lim” while on paper works just as well as an arrow, on a computer screen on one line it looks worse and can be slightly distracting.
Problem 4:
a) Clarity – 1, Style – 1
b) Clarity – -1, Style – -2
c) Clarity – 1, Style – 0
Comments:
In b), the use of “primes” makes the proof incredibly awkward to read, which is not helped by the “swapping around” of elements within the metric (i.e., writing d(x,y) < a *mumble something* implies d(f(y),f(x)) < b). With c, the use of brackets to show composition of functions is slightly harder to read than just using the circle symbol – if we were not using the composition inside something already in brackets, either would suffice.
Problem 5:
a) Clarity – 2, Style – 1
b) Clarity – 2, Style – 2
c) Clarity – 1, Style – 1
Comments:
In c), the inconsistent usage of the "an element of" symbol is slightly irritating, and the line beginning "Since f is an injection…" reads as if to say f(y)=x and f(z)=x because f is an injection, rather than using that f is an injection to show that y=x. Otherwise, the other two proofs are fine, although using a and b for the elements of A and B is much more obvious when reading the proof as compared to using y and z.
March 25, 2013 at 12:29 pm
I have studied topology of metric space.
As a general remark, I prefer not to include to many “inline” formulas.
I will first rate the write-ups and then give more specific comments
1(a) clarity: 2 style: 1
1(b) clarity: 0 style: 0
1(c) clarity: -2 style: -1
2(a) clarity: 1 style: 1
2(b) clarity: 0 style: 0
2(c) clarity: 2 style: 1
3(a) clarity: -1 style: 1
3(b) clarity: 1 style: 1
3(c) clarity: 0 style: 0
4(a) clarity: 1 style: 1
4(b) clarity: 1 style: 1
4(c) clarity: 1 style: 1
5(a) clarity: 1 style: 2
5(b) clarity: 1 style: 1
5(c) clarity: 0 style: 0
———————
Problem 1.
1(a) I would have written something like:
Since $x\in A, and $A$ is open, there exists $a$ such that $B_a(x)\subset A$. Similarly, there exists $a$ such that $B_b(x)\subset B$. Let $r=\min(a,b)$…
Indeed, defining a and b is harder on the reader than defining a and then b.
I also think that what you do in 2(b) i.e. say where we are going, is very good.
Let $x\in A\cap B$. We seek $c>0$ such that $B_c(x)\subset A\cap B$.
1(b) I would not have included the definition of open ball. If the reader does not already know what anopen ball is, then he probably does not understand anything at all. This just makes the proof longer which is bad because only difficult statement have long proofs, right ?
Otherwise, I think that using a and b for the radius is better than r and r’ because it helps keep track of which balls are included in which sets. Furthermore, I tend to use r’ when r’ is defined after r and it depends on r, which is not the case here and thus makes it less readable.
1(c) Inlining the definition of ball is just plain wrong.
———————
Problem 2.
Altough I prefer 2(c), what is really important is how continuity in $x$ was defined. If if was defined by \forall \epsilon, \exists \delta, s.t. d(x,y)<\delta implies that d(f(x), f(y))0$. Since $g$ is continuous, there exists $\gamma>0$ such that $g(B_\gamma(f(x)))\subset B_\epsilon(g(f(x)))$. Similarly, there exists $\delta>0$ such that $f(B_\delta(x))\subset B_\gamma(f(x))$. But then $g(f(B_\delta(x)))\subset B_\epsilon(g(f(x)))$, which proves that $g\circ f$ is continuous.
———————
Problem 5.
The 3 proofs are very similar, and quite simple. I think that 5(a) is the best, and that 5(c) is much too verbose.
March 25, 2013 at 12:32 pm
It looks like my comments on Problems 3 and 4 avec disapeard. I repost. Please do not publish both my posts.
I have studied topology of metric space.
As a general remark, I prefer not to include to many “inline” formulas.
I will first rate the write-ups and then give more specific comments
1(a) clarity: 2 style: 1
1(b) clarity: 0 style: 0
1(c) clarity: -2 style: -1
2(a) clarity: 1 style: 1
2(b) clarity: 0 style: 0
2(c) clarity: 2 style: 1
3(a) clarity: -1 style: 1
3(b) clarity: 1 style: 1
3(c) clarity: 0 style: 0
4(a) clarity: 1 style: 1
4(b) clarity: 1 style: 1
4(c) clarity: 1 style: 1
5(a) clarity: 1 style: 2
5(b) clarity: 1 style: 1
5(c) clarity: 0 style: 0
———————
Problem 1.
1(a) I would have written something like:
Since $x\in A, and $A$ is open, there exists $a$ such that $B_a(x)\subset A$. Similarly, there exists $a$ such that $B_b(x)\subset B$. Let $r=\min(a,b)$…
Indeed, defining a and b is harder on the reader than defining a and then b.
I also think that what you do in 2(b) i.e. say where we are going, is very good.
Let $x\in A\cap B$. We seek $c>0$ such that $B_c(x)\subset A\cap B$.
1(b) I would not have included the definition of open ball. If the reader does not already know what anopen ball is, then he probably does not understand anything at all. This just makes the proof longer which is bad because only difficult statement have long proofs, right ?
Otherwise, I think that using a and b for the radius is better than r and r’ because it helps keep track of which balls are included in which sets. Furthermore, I tend to use r’ when r’ is defined after r and it depends on r, which is not the case here and thus makes it less readable.
1(c) Inlining the definition of ball is just plain wrong.
———————
Problem 2.
Altough I prefer 2(c), what is really important is how continuity in $x$ was defined. If if was defined by \forall \epsilon, \exists \delta, s.t. d(x,y)<\delta implies that d(f(x), f(y))0$. Since $g$ is continuous, there exists $\gamma>0$ such that $g(B_\gamma(f(x)))\subset B_\epsilon(g(f(x)))$. Similarly, there exists $\delta>0$ such that $f(B_\delta(x))\subset B_\gamma(f(x))$. But then $g(f(B_\delta(x)))\subset B_\epsilon(g(f(x)))$, which proves that $g\circ f$ is continuous.
———————
Problem 5.
The 3 proofs are very similar, and quite simple. I think that 5(a) is the best, and that 5(c) is much too verbose.
March 25, 2013 at 12:36 pm
There exists an intonation in most mathematical writing like this that seems to boom from the clouds in a deified godspeak with Let and Thus and We Seek. Math suffers from the formal arrogance this heightened language is laced with… Solution? What would Euler do? X is a.function of simplicity and humility.
Metric spaces, brief overview, unobfuscated dot dot dot, next line, Intention is allow x to be, dot, dot, dot, Reason, Result – include the reader as participant rather than Mr. Sinai audience, ps.
March 25, 2013 at 12:44 pm
Problem 1.
(a) is the easiest to understand, say 2, but has some problems. There’s an actual error – B\sub{x}(a) where there should be B\sub{a}(x) – and the use of B for both one of the sets and a ball is potentially confusing (though I didn’t notice that on a first reading and I realise this is pretty standard nomenclature). So 1 for style.
(b) I prefer (a)’s statement of the approach at the beginning of the proof rather than the end. Say 1 for clarity. Reuses r in potentially confusing fashion. Too many “arbitrary x”s at the beginning. Say 1 for style too.
(c) This is two lines longer than (a) or (b), which is not a good sign, and it just seems more complex. Say 0 for clarity. Seems ok for style, though I don’t like the “s.t.” abbreviation. Maybe a 1 too.
I’m finding it hard to separate the clarity of the proof from the style of its presentation. It comes down in a way to “first impressions” versus “close reading”.
March 25, 2013 at 1:08 pm
[…] If you’ve some time to spare, go and take part in the experiment over at Gowers’s weblog. […]
March 25, 2013 at 1:39 pm
This looks like fun. I’ll go problem by problem, as I have time, if that is all right.
I have studied metric spaces, but would be a bit rusty at writing proofs.
@T
Problem 1
(a)
“Let x \in A \cap B. x is in A \cap B…” I find this potentially confusing. It (almost) repeats the same thing, but with no explanation as to why; so if you are not familiar with this already, you might think there is a significant step here, and spend time trying to figure out what it is. On the other hand, the reader is expected to understand ” B_a(x)” without comment, but if you need to explain that x \in A \cap B means x is in both A and B, surely you need to explain more about your open balls.
Clarity 1
Style 0
(b)
This one works for someone who knows the background already and wants a sketch proof. If you don’t understand it to start with, you will be wondering, what is this “arbitrary x” at the beginning? What is this *other* “arbitrary x” in A \cup B? It is fine for a quick introduction to some more advanced text, but not for a text that teaches metric spaces.
Clarity -1
Style 0
(c)
I can see this working, if a lecturer is speaking and drawing diagrams. It is harder to follow, if you have just the text. It seems to chatty for an introduction to an advanced text, but if teaching metric spaces, you have to ask what all the unexplained conditions mean. Why is \theta>0? Wait a minute, what is this \theta again?
Clarity -1
Style 0
March 25, 2013 at 2:19 pm
I’m at my fifth year of mathematical studies. I know the theory of metric spaces very well.
General observation: I think that the claim at the beginning of the write-up is useful only for complicated propositions; my ratings are therefore influenced by the low complexity of these statements.
1(a) Clarity: 1 Style: -1
In the first sentence there is B_x(r) instead of B_r(x).
1(b) Clarity: 1 Style: 1
1(c) Clarity: -2 Style: -1
2(a) Clarity: -1 Style: 0
2(b) Clarity: 1 Style: -2
There is again a B_x(r); there is a sentence beginning with formulas, and there are a logical symbol (\Rightarrow) and some “id est” in text.
2(c) Clarity: 1 Style: 0
3(a) Clarity: 2 Style: 2
Even if I don’t like the last sentences, I think that this write-up has the best notation (x_n and \lim).
3(b) Clarity: 2 Style: 1
3(c) Clarity: 1 Style: 0
4(a) Clarity: -1 Style: -2
Again, I can’t stand logical notation in text and sentences beginning with formulas.
4(b) Clarity: 2 Style: 1
I don’t like parenthesis in a proof.
4(c) Clarity: 1 Style: -1
Metric spaces? Uh? I’d say set theory.
5(a) Clarity: 2 Style: 2
5(b) Clarity: 2 Style: 1
5(c) Clarity: 0 Style: 0
March 25, 2013 at 2:20 pm
My mathematical experience is minimal. I did A level in 1975, have studied a certain amount of logic and set theory on account of doing philosophy, and have picked up bits and pieces of mathematical knowledge unsystematically. So I know what metric spaces and topological spaces are, but could not reel off the main results, let alone prove them.
All of the explanations struck me as beautifully written, so I have awarded 2 for style to all of them. This may, however, reflect the fact that I have not read enough mathematics to make refined judgements of style.
1. I noticed straightaway that I was influenced by the fact that I read these in order, 1(a) then (b) then (c). (a) was perfectly clear, so I could interpret (b) and (c) in the light of that knowledge. That may have made (b) and (c) easier to follow than they would otherwise have been. I take it that the reason why you ordered the explanations in the examples randomly and independently, was to compensate for this kind of effect.
1(a). Clarity 2, style 2. So long as the reader has already come across the concept of an open ball, this is very easy to follow. You just visualize balls with fuzzy surfaces (in the sense that there is no last point that is within the ball, so no smooth shiny surface). I would only suggest one amendment. This is to remind the reader that the open balls in A and in B are both centred on x, so that one is a (proper or improper) subset of the other, so we can just take the smaller one, or either one if they are identical. For a moment, I had the mistaken thought that we could not just do this, because we would have no guarantee that either of the balls would be within the intersection of A and B.
1(b). Clarity 1, style 2. This one makes it clearer how we construct the open ball we want, but doesn’t get us into the visualization so early.
1(c). Clarity 0, style 2. I found this one the hardest to follow, because it does not encourage visualization, and because it introduces a lot of variables. On the other hand, I suspect that it is the most rigorous. Does that make it the best example of style for serious students of mathematics to imitate?
2(a). Clarity 1, style 2.
2(b). Clarity 0, style 2.
2(c). Clarity 2, style 2.
In 2, (c) was the easiest to follow, and I think this is because it encourages visualization. I think that the readability of these examples is heavily influenced by how the notion of continuity is spelt out, with (b) making it most obscure for the lay reader, although that may also be the most rigorous expression of the notion.
3(a). Clarity 1, style 2.
3(b). Clarity 1, style 2.
3(c). Clarity 2, style 2.
This time, in judging clarity, I was heavily influenced by whether the proof struck me as convincing. The result is one, the correctness of which is not obvious to the lay reader. It is easy to have an intuitive feeling that the limit of a Cauchy sequence could lie just outside A. So if the proof does not dispel this feeling, the reader is left thinking that there must be something missing from his or her reading of the proof, so it must be hard to understand (since it is most unlikely that the fault lies with the writer of the proof), even if the precise difficulty in understanding is unclear. This is what gives 3(c) the edge for me. It spells out that a closed set contains all its limit points. Of course, the reader needs to know why that is so, in order not to think that the proof is a circular argument. I guess that one pedagogical aim is to give an intuitive sense of the relationship between “in a closed set, you can’t always go a little bit further and stay within the set”, and “in a Cauchy sequence, for any degree of closeness to the limit, there is a term in the sequence such that beyond that term, all terms are at least that close to the limit”.
4(a). Clarity 2, style 2.
4(b). Clarity 0, style 2.
4(c). Clarity 1, style 2.
(a) has the great advantage that it starts with an easily comprehensible statement of the strategy of the proof. (c) comes next in clarity, because it also indicates what we are after (the necessary delta) before showing how to find it.
I think that one reason why (a) and (c) are clearer than (b) is that they make use of universal quantifiers, explicitly in (a) (“for all”) and implicitly in (c) (“whenever”). They thereby encourage the reader to think in terms of little chunks of domains and of images, rather than in terms of individual points close to the x, y and z that are mentioned at the start of (b).
So far as I can see, the essence of (a) and (c) is, “Continuity means that we can take an arbitrarily small chunk of Z, with z somewhere in it, and then find a non-zero chunk of Y, with y in it, such that all values in the chunk of Y are taken by g to values in the chunk of Z. We can repeat the exercise on that chunk of Y, to get us to a non-zero chunk of X, with x in it. Then we could work our way forwards along the chain, from anywhere within the chunk of X, and find ourselves within the chunk of Z. So at each stage working backwards along the chain, from Z to X, we may have to make a chunk very small, but we can always find one. We may have to shrink chunks by multiplying their sizes by some very small positive numbers, but not by zero; and multiplying by two positive numbers in succession is multiplying by a positive number.” That story may be a bit slapdash at the end, with the idea of multiplying the size of a chunk by a number, since we are talking about many more things than stretches of the real line. But it is an easily comprehensible story, and I think it is one that (a) and (c) encourage the reader to imagine.
5(a). Clarity 1, style 2.
5(b). Clarity 2, style 2.
5(c). Clarity 0, style 2.
(b) strikes me as clearer than (a) for two reasons. The minor one is that its final sentence makes explicit the move from having found the result for the particular y, to the general conclusion about the inclusion of one set within another. The major one is that in (a), x is used for an image: x = f(y) and x = f(z). If y had been used in that role, and if we had had y = f(x) and y = f(w), then there might have been very little to choose between (a) and (b). This reflects the fact that everyone is brought up with y = f(x), not with x = f(y).
(c) also suffers from the use of x as an image. But it is also made less clear by the detour via u, the element in the intersection of A and B. This is one occasion where I feel that clarity is hindered, rather than helped, by spelling everything out. We could do what is done in (a), and go straight to y being in the intersection, since it equals z.
March 25, 2013 at 2:42 pm
I am familiar with basic metric theory.
(1a) 2
(1b) 2
(1c) 0
(2a) 1
(2b) 2
(2c) 0
(3a) 2
(3b) 1
(3c) 0
(4a) 0
(4b) -1 (first f(y’) should be g(y’))
(4c) 1
(5a) 2
(5b) 2 (clear, but sounds too informal)
(5c) 0
March 25, 2013 at 4:21 pm
Should we email you our response, or just post it as a comment?
March 25, 2013 at 4:39 pm
I studied algebra, geometry and topology on graduate level, with emphasis on topology. That was 20 years ago though, and I haven’t used it since, nor have I really kept up with the fields.
Nevertheless, these 5 propositions are basic enough that I understand them without having to consult my textbooks.
As a summary, I would like to say that I find none of them particularly hard to understand, nor particularly badly written. They seem fairly run of the mill for proofs of propositions to me 🙂
On to the individual write ups then:
1(a)
clarity: 2
style: 1
This is the best of the three. I like that it states the objective up front. That gives the proof a clear goal.
It’s also the shortest, while using the least number of variables. It flows nicely, the logic is easy to follow.
One point off for style for the repeated “So …. So …”.
1(b)
clarity: 1
style: 1
Not too bad. Explicitly restating the definition of “open ball” without actually naming it that (but referring to it by name later on) reads a bit awkward.
Summarizing the proof at the end is a nice touch.
1(c)
clarity: 0
style: 0
Too many variables. The use of open balls in the other two clearly wins over using only the metric on the space. A little abstraction goes a long way 😉
2(a)
clarity: 0
style: 1
Doesn’t clarify its objectives.
2(b)
clarity: 0
style: 1
States its objective upfront. Good.
Uses “so …” four times. Bad.
The main argument is a long string of symbols. Not very clear.
2(c)
clarity: 1
style: 1
This is the best of the three. Flows well, nice balance between words and symbols.
Summarizes its argument at the end. Good.
Slight overuse of “So…”.
3(a)
clarity: 2
style: 2
Very good.
3(b)
clarity: 2
style: 2
Very good as well. There’s something about this one I find slightly less attractive than 3(a), but I can’t quite put my finger on it.
3(c)
clarity: 2
style: 1
Quite good.
States its objective upfront. Good.
Flows nicely.
Overuse of “Since…” and “So…”
4(a)
clarity: 1
style: 1
States its objective upfront. Good.
My eyes are starting to glaze over at this point, so I’m going to rush through them a bit. Sorry 😦
4(b)
clarity: 1
style: 1
4(c)
clarity: 1
style: 1
I like this one the best, I think. Possibly because it’s the shortest.
5(a)
clarity: 2
style: 2
Short and to the point. Good.
5(b)
clarity: 2
style: 1
So, so, so. So.
5(c)
clarity: 1
style: 1
Oddly, the English in this one is more varied, which I find a plus. But it needs more symbols to get its point across, which detracts from the clarity.
Wow. I forgot how tedious these little proofs got after a while. I guess I wasn’t cut out for mathematics after all. Which is why I’ve become a software developer, because source code is much more readable 😉
All in all, they were all pretty decent. There’s not a lot of wiggle room to make these little proofs excellent rather than just good. I guess it’s a fine balance between brevity and terseness.
Hope this helps,
Rhesa
(I had no idea commenting on wordpress would be so annoying, if you don’t already have a login there. ugh)
March 25, 2013 at 5:01 pm
So, I’ve just graduated from UC Davis with a BS in math. I’ve done graduate level math courses. But I’m a little rusty (I currently work as a programmer, not a mathematician, alas!).
Solution 1(a). Style: -1, Clarity: -2.
The choice of notation seems bad ( re-uses the letter
re-uses the letter  which…to me, that’s a misdemeanor!). The real felony is the switch in notation to
which…to me, that’s a misdemeanor!). The real felony is the switch in notation to 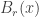 , since the function’s argument should be a non-negative real number, the subscript should be the point in the metric space…but no?
, since the function’s argument should be a non-negative real number, the subscript should be the point in the metric space…but no?
The horrible assumption made by the author (of the proof, not the blog!) seems to be: the metric space is a subset of the reals. This isn’t always true! (E.g., a 2-dimensional vector space over the reals.)
I do appreciate the “roadmap” given in the first sentence. That’s the only positive thing I can say.
For this style to work, it should be in a more “blogger” style…that is to say, each “major step” should be a new paragraph. (Lamport outlines this style in his article on proofs [pdf].)
There’s a lot of circuity, which doesn’t clarify the situation. I end up taking the conclusion more on faith than the proof….
Solution 1(b). Style: 0, Clarity: 0.
The strategy appears to be the same as 1(a), but it’s written better. The author commits the same wrong-doing when re-using symbols, but avoids the felony mixing up subscripts with function arguments. Hence this proof works for any metric space, not just a subset of the reals.
The penultimate sentence is a nice summary of what has been done, but the last sentence is unnecessary (we should know this is the definition of “open”!).
Solution 1(c). Style: 1, Clarity: 1.
This is the best of the three proofs. I have only slight suggestions for improvement (e.g., third sentence should begin with “Since is open…”, just cut “Therefore…”).
is open…”, just cut “Therefore…”).
Solution 2(a). Clarity: -2, Style: -2.
I don’t think this proof is even correct…otherwise every proof for a continuous function simply becomes “Set
proof for a continuous function simply becomes “Set 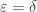 , and voila!”
, and voila!”
It’s rather confusing to see where the author is heading.
Solution 2(b). Clarity: 0, Style: -2
It’s nice the author provides a roadmap. Also it’s swell the author remains general.
It’s horrifying the author begins sentences with symbols.It’s felonious the author mixes up notation again! Subscripts and function arguments switched, evil! Were I a professor, I’d be tempted to use a spray bottle…
But I am fairly confident the proof works (alas, not confident enough to say “I know the proof works!”).
Solution 2(c). Clarity: 1, Style: 2
The author doesn’t provide a roadmap (arguably, this should go before a proof, and not in it!)…but unlike the others, this is an enjoyable read.
The author doesn’t seem to be a felon: she or he uses notation properly. This really pleases me after the first two proofs!
Although the author isn’t as pedantic as the first two, the author is consistent with the amount of details provided.
Personally, I like it because it forces me to stop and say after each sentence “OK, so this is asserted to be equivalent to [this or that property]…how can I see that?” It forced me to think about these properties, and that precise quality helped me learn mathematics.
Solution 3(a). Clarity: -1, Style: 0.
The style is neither pleasant nor dreadful.
But the proof scares me: I don’t understand, or recall, how we can justify this sentence “Because is closed,
is closed,  belongs to
belongs to  “.
“.
Solution 3(b). Clarity: 0, Style: 1
I know just enough logic to be dangerous! The indices on the sequence need to be clarified as belonging to the naturals or integers, otherwise we have problems with index sets that are “Too huge”.
That problem aside, the proof is superior to the first. But again, I am forced to take the result on faith rather than reason: we know in
in  …but there’s no reason to suppose
…but there’s no reason to suppose  .
.
At least, not to a paranoid mathematician!
Solution 3(c). Clarity: 2, Style: 2
This is the only proof that clearly told me what they were doing, where they were going, and why what they say is true.
It provided enough detail to indicate what properties to recall, but avoided needless pedantic rambling.
Each sentence appeared to lead logically to the next, leaving me with no doubts about the proof’s “truthiness”.
Solution 4(a). Clarity: -1, Style: -1
Although a roadmap is given, and the author follows it, the entire proof could be summed up as a commutative diagram. Actually, that’s how I translated the proof…
The style is horrible (using symbols at the beginning of a sentence: nooooo!).
Solution 4(b). Clarity: 0, Style: 0
This proof flows better than the first one, although it seems to be the same argument.
Solution 4(c). Clarity: -1, Style: 0
I believe the proof follows the same strategy as the others…but it’s not as clear.
The phrasing “Take and
and 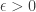 ” suggests an existential quantification, rather than a universal one…the vital words “Take any/arbitrary…” should be used.
” suggests an existential quantification, rather than a universal one…the vital words “Take any/arbitrary…” should be used.
But this proof left me with doubts concerning with respect to what happens when we restrict our focus of to the image of
to the image of  ?
?
Solution 5(a). Clarity: 0, Style: 0
Doesn’t this proof imply ?
?
Solution 5(b). Clarity: 1, Style: 1
This proof flowed far better than the first, easing my doubts, reminding me the proof was only for a subset not equality.
Solution 5(c). Clarity: -1, Style: -1
The approach seems convoluted, needlessly pedantic. *sigh*
March 25, 2013 at 5:26 pm
Background – undergraduate math major; I have familiarity with the basics of metric spaces.
Here is the list of what I consider to be the best proofs, along with reasons. If you wish, you can rate these all as 2’s and the unlisted ones as -2’s.
1(a): The balls are more geometric, which I prefer to (c). I prefer (a) to (b) for three reasons: first, the variable names $a$ and $b$ are nicer than $r$ and $r’$; second, the definition of open ball in (b) is unnecessary and breaks the flow; and (b) is also unnecessarily verbose in places.
2(c): More concise than the other two, and uses open balls which is nicer than all the $d(x,y)$’s in my view.
3(a): (b) is obviously funny because it should say “converges in $X$. (c) is too verbose.
4(c): (b) and (a) are much too verbose.
5(a): The other two are too verbose, (b)’s extra sentence is unnecessary, and a hindrance to the flow of reading. I prefer the variable choices of $x, a, b$ in (b), though.
March 25, 2013 at 5:50 pm
1(a): Clarity 2, Style 2
1(b): Clarity 0, Style -1. What’s X? the first sentence just confuses me. Does the definite depend on the set X that x is from, yet it isn’t a parameter? Ignoring the first sentence it is okay though in terms of clarity.
1(c): Clarity 2, Style 0. Too verbose. Some of the steps should be skipped, as sometimes too many steps like that are overwhelming.
2(a): Clarity -1, Style 2. I can’t think of a particular fault, but it seemed to me hard to read. I sort of kept reading it without taking it in.
2(b): Clarity 1, Style 2. OK, less variables to keep track of than in (a), but still could do better.
2(c): Clarity 2, Style 2. Very clear and easy to read. Less to keep in mind, assumptions and aim very clear and how they fit together immediately obvious.
3(a) & (b): These two read identically to me. Clarity 1, Style 1.
3(c): Clearer, as it says what first and separates the assumptions slightly better. Clarity and Style both 2.
4(a): Clarity 2, Style 1. I would make the minor remark that I intuitively wanted function calls to bind more tightly than function composition, but even then the line is unambiguous. The proof is really straightforwardly presented though.
4(b): Clarity 0, Style 1. Too many variables.
4(c): Clarity 1, Style 2. Slightly harder to read than (a), which surprised me as I thought f(g(x)) would be simpler than the function composition symbol. Theta somehow made it harder to understand too.
5(a): Clarity 1, Style 2.
5(b): Clarity 1, Style -1. ‘so’ has lost all meaning to me after reading that sentence. Otherwise it seems so similar to (a).
5(c): Clarity 2, Style 1. The ‘that is’ actually mades it more confusing as it separates a statement from its conclusion too much. Otherwise it is the most straightforward way.
My background: I did the Cambridge 1B course in Metric and Topological spaces and originally learnt the material from Mendleson as a sixth former.
As you may have seen, I don’t think the style of any of them is particularly bad.
March 25, 2013 at 6:41 pm
Mathematical experience: I’m a master student in mathematics (so I’m familiar with metric spaces).
I’ve noticed that two things have a big influence on my appreciation of the write-ups:
1. Giving an outlook at the beginning of the proof increases clarity. (e.g. 3c: first two sentences). However, such an outlook is superfluous when it is almost as long as the proof itself (e.g. 5c: last three sentences). In the latter case, I consider the outlook to be bad style.
2. The balance between text and formulas should be appropriate.
Some things are more easily said in words. (E.g. “the open ball B_x(r)” (1a) is better than “let $B_r(x):=\{y\in X|d(y,x)<r\}$" (1b), at least as long as it is clear which is the radius and which is the center of the ball.)
Other things are better expressed in a formula. (E.g. "B_r(x)\subset A" (1b) is much more readable than "$u \in A$ whenever $d(x,u)<\eta$" (1c).)
My ratings (Write-up; clarity; style):
1a 1 -1
1b 0 0
1c -2 -1
2a -2 -1
2b -1 -1
2c 0 0
3a 1 0
3b -1 0
3c 2 1
4a 0 -1
4b -1 -1
4c 1 0
5a 2 1
5b 0 -1
5c -1 -1
My preferences are 1a, 2c, 3c, 4c, 5a.
March 25, 2013 at 6:58 pm
Doesn’t 1a have a typo? Don’t you want to say Bsubr(x) instead of Bsubx(r), in the first sentence?
March 25, 2013 at 7:26 pm
Experience: familiar with basic properties of metric spaces.
Problem 1answer (a) Clarity: 0 Style: 0
Problem 1answer (b) Clarity: 1 Style: 1
Problem 1answer (c) Clarity: -1 Style: -1
Problem 2 answer (a) Clarity:-1 Style: -1
Problem 2 answer (b) Clarity: 0 Style: 0
Problem 2 answer (c) Clarity: 1 Style: 1
Problem 3 answer (a) Clarity: 1 Style: 1
Problem 3 answer (b) Clarity: -1 Style: -1
Problem 3 answer (c) Clarity: 0 Style: 0
Problem 4 answer (a) Clarity: 0 Style: 0
Problem 4 answer (b) Clarity: 1 Style: 1
Problem 4 answer (c) Clarity: -1 Style: -1
Problem 5 answer (a) Clarity: 1 Style: 1
Problem 5 answer (b) Clarity: 0 Style: 0
Problem 5 answer (c) Clarity: -1 Style: -1
I consider it important to have a particular group of readers in mind and to write for them.
March 25, 2013 at 7:33 pm
Background: entering undergraduate university course next year but am familiar with introductory analysis/metric topology.
1.
(a) C:2, S:2
(b) C:0, S:1
(c) C: -1, S:-1 ((a) is perfect because it invokes the least amount of technicalities while still being perfectly explanatory, while (c) is bad because it regurgitates the definition of openness too many times for no reason, while (b) is in between)
2.
(a) C:-1, S:0
(b) C:1, S:2
(c) C:2, S:2 (I like (c) best because I prefer continuity in terms of open balls rather than distances. (b) seems to use a hybrid of the two definitions of continuity and is nice stylistically but maybe it’s better to stick with one of the definitions)
3.
(a) C:2, S:2
(b) C:2, S:2
(c) C:2, S:1 (here I thought that the three proofs were almost indistinguishable; I could not tell the difference at all between (a) and (b), and (c) was worse in that it was a little redundant)
4.
(a) C:1, S:1
(b) C:0, S:0
(c) C:2, S:2 ((c) was easiest to follow. I’m not sure why I found (b) so hard to follow but I think it was because of the rate at which variables were introduced. (a) was alright but I think it’s clearer if composition notation (o) is not used)
5.
(a) C:2, S:1.
(b) C:2, S:2
(c) C:2, S:1 ((a) and (b) are extremely clear and concise. (c) is more verbose without actually making anything easier to understand. the only difference between (a) and (b) as far as I can tell is that (b) matches the element names to the names of their spaces, which is always better I think)
I hope the comments weren’t too long or too short.
March 25, 2013 at 9:21 pm
I’m an assistant professor of mathematics (combinatorics in particular). So I’ve studied the basics of metric spaces.
1(a) The first line is great because it states the goal while also setting notation for the rest. The second paragraph could easily be shortened, but is fine. I also like the naming of the radii.
Clarity: 2. Style: 1.
1(b) Fine, but doesn’t state the goal as 1(a) and r, r’, R aren’t particularly inspired names for the radii.
Clarity: 1. Style: 0.
1(c) What’s with the strange Greek letters? More importantly, not using balls adds to the logical difficulty, I think.
Clarity: -1. Style: -2.
2(a) Same complaints as 1(c).
Clarity: -1. Style: -2.
2(b) Beginning sentences with mathematical symbols and using the “implies” symbol in text.
Clarity: 0. Style: -2.
5(a) I’m not a big fan of starting sentences with “so”, especially not twice in a row.
Clarity: 2. Style: -1.
3(a) Generally fine, though lacks the things I like about the other two.
Clarity: 1. Style: 0.
3(b) I like naming the sequence a_n.
Clarity: 1. Style: 1.
3(c) I particularly liked stating that a_n is Cauchy in X and repeating the definition of a closed subset.
Clarity: 2. Style: 2.
4(a) Starting sentences with math again.
Clarity: 0. Style: -2.
4(b) Introducing y and z seems unwise to me because later things like f'(x) are needed.
Clarity: 0. Style: 0.
4(c) Far and away my favorite of the three. I might rewrite the last sentence as “Setting delta=theta completes the proof”.
Clarity: 2. Style: 2.
5(a) I’m not a big fan of starting sentences with “so”, especially not twice in a row.
Clarity: 2. Style: -1.
5(b) Good choices for variable names. Same problems with “so”s as 5(a) though.
Clarity: 2. Style: 0.
5(c) The goal is never stated and the last sentence doesn’t make it clear what has been proved. Also, the variable names seem chosen to purposely confuse the reader.
Clarity: -1. Style: -2.
March 25, 2013 at 10:15 pm
I’d rather not rate them individually, because they’re all too notation-heavy for my taste and I think the differences in clarity and writing style are too small compared to that. I’d rather point out some particular issues that I see with the writeup:
1(a) repeats “so…so…so…so”. I think a more varied vocabulary would sound less awkward.
1(b): uses “arbitrary” and “any” as quantifiers. This is a bad idea, since they are more ambiguous than the usual “every/all” and “there exists”.
1(a) and 1(b) both use a capital B for two unrelated purposes, never a good idea.
1(c) avoids those mistakes but gets too lost in unimportant details; for instance, taking a whole sentence to point out that an element of the intersection is also an element of each of the two intersected sets, and repeating several whole sentences for the two sets rather than simply noting that the situation is symmetric.
In 2(a), I don’t understand why you would abbreviate “s.t.” and then spell out “if and only if”. It seems inconsistent. And “we know that” is usually just meaningless noise.
In 2(b), the notation-heaviness (of all the proofs so far) leads to unfortunate juxtapositions where it is unclear whether some marks are mathematical operators or sentence punctuation; “U.U” for instance.
The use of notation as a substitute for language leads to grammatical inconsistencies in 2(c) (and likely earlier, but this is where I first noticed it). Should we read $x\in S$ as “x in S” (a noun phrase) or “x is in S” (a verb phrase)? Some uses go one way, some another. And 2(c) also uses “some” as a quantifier, another ambiguous substitute for every/exists.
In 3(a), I don’t like the phrasing in the sentence defining x, “Suppose lim=x”. To me that looks too much like x is something that already has a value I should know, and that I am now making an assumption that this previously-defined value happens to equal a certain limit. It doesn’t look like a definition. And anyway it would be much more simple to pack the definition into the previous sentence: “has a limit x in X”.
In 3(b), I think the preconditions of the sentence beginning “Since A is closed” could be combined reasonably naturally into a single clause, avoiding the need for the near-content-free combining phrase “we have that”: “Since a is the limit of a sequence in the closed set A, it belongs to A.”
3(c) again has the awkward “so…so…so”
I’ll stop here, since I’m clearly not giving you data in a format for which completeness would be helpful.
March 25, 2013 at 10:47 pm
I’m a fourth-year grad student in computer science with a BS in mathematics, and most of my work has been in algorithms, computational geometry, and machine learning. I haven’t *studied* the theory of metric spaces but I am familiar with much of the framework. My CS bias probably makes me prefer brevity. By “math” I usually mean “math typesetting.”
1a.
2 for clarity. It proceeds clearly.
1 for style. I’m not fond of extraneous intros like “we want to show that …” and it’s a bit redundant in a couple places.
1b.
1 for clarity. Overall good, but I’d much rather see $\subset$ reserved for proper/strict subsets and $\subseteq$ used otherwise. I get a bit tripped up when I see $\subset$ used for possibly equal sets.
-1 for style. I know what the open ball is, and the concluding remarks are too lengthy. I don’t like capitals for constants. The addition of $\subset A$ and $\subset B$ in the middle sentence is unnecessary. Too much math, it makes the line breaks awkward.
1c.
-2 for clarity. No. Just no. The Greek letters are really out of place and the sentences run on. It’s a mess.
-2 for style. It just looks like a stream of consciousness.
—
2a.
-2 for clarity. I had to fight to pick out some basic concepts like open balls. Why aren’t $\epsilon$ and $\delta$ used for continuity?
0 for style. Seems more structured than 1c, but it’s too wordy and uses the same words repeatedly.
2b.
1 for clarity. This proof is really tight but slightly too “mathy.” $\epsilon$ and $\delta$ for continuity feels “right,” so it doesn’t trip me up like 2a.
0 for style. Overall the math style is nice (and a lot of it is necessary for clarity) but makes line breaks awkward.
2c.
2 for clarity. This would fit well in an introductory text.
0 for style. What’s with the micro-sentences? The last two sentences could be made into a much shorter single sentence.
—
3a.
0 for clarity. Tight, but it feels like there’s something missing re: limit points + closed sets.
2 for style. No unnecessary math, the ideas flow nicely.
3b.
2 for clarity. Tight and feels complete.
1 for style. Like 3a, but the “have that”s felt awkward.
3c.
0 for clarity. The order of arguments is distracting.
0 for style. Zzzzzzzz.
—
4a.
2 for clarity. This is exactly how it should go.
1 for style: math is a bit dense for the line breaks.
4b.
-1 for clarity. I know the proof but this is confusing me — it’s disorganized.
0 for style. Not much to say here.
4c.
2 for clarity. Also very straightforward.
1 for style. Should use $\delta’$ instead of $\theta$.
—
5a.
2 for clarity. Very clear.
2 for style. Very snappy.
5b.
2 for clarity. Very clear.
1 for style. To many “so”s.
5c.
0 for clarity. The redundancy detracts from the clarity.
0 for style. This is an easy proof, made more complicated by the presentation.
Hope this helps, feel free to contact me if you need me to clarify anything I said.
March 26, 2013 at 12:17 am
Hello. I am a first year graduate student with initial graduate real analysis, general topology, and algebra classes complete, currently taking complex analysis, linear algebra, and algebraic topology. This is an interesting experiment and I hope that my comments help.
Problem 1. I think that (a) is the clearest. Its advantage, in my eyes, is that the motivation for the train of thought followed in the proof is stated immediately, which makes it much easier to understand the proof on the first readthrough. My nitpick here is that writing “x is in A and x is in B” is more verbose than “x \in A and x \in B” without improving clarity. Ending by stating the result which was asked for gives a sense of completeness. One last nitpick: “… so it’s contained in B” is an ambiguous reference; the meaning will most likely be clear, but perhaps not for a reader very new to proofs. 1 for style and 1 for clarity, and I would assign 2 for both if my nitpicks were accepted.
(b) reviews the definition of an open ball, which would presumably already have been introduced and likely does not help. Furthermore, states only at the end of the proof what was achieved and is somewhat verbose in doing so. The motivation for what was done before completing the proof is perhaps not entirely clear. 0 for style and 1 for clarity.
(c) mixes variable names from different alphabets, which, for me, still causes a mental context switch. Perhaps this is not a problem for most others, I do not know, but I personally found it to be an unnecessary distraction. I also think that to speak solely in terms of distances rather than in terms of open balls adds an unnecessary step of removal from the core concept that an open set contains a neighborhood of each of its points, which damages clarity. -1 for style and -1 for clarity.
————————
Problem 2. I would abbreviate my comments by saying that, for me, 2b is like 1a, 2c is like 1b, and 2a is like 1c, and I would rate accordingly. I think that I see how you have structured this, so I’d like to address a different aspect.
I commented that I thought that 2b/1a benefit from stating what we are looking to prove before proving it. I think that this would be beneficial to, say, an undergraduate student but might be unnecessary for a graduate student or above, though perhaps I am biased about the fact that I have had to do these exact proofs multiple times by now. If I had to write these proofs for a general audience rather than for a homework problem, I would pursue the style of 2b/1a pretty closely, I think.
————————
Problem 3. I would rank (c) most highly. It states the goal in the first sentence, states what has been proven at the end, and is the only of the three proofs that explicitly states and makes use of the fact that a closed set contains its limit points, which is a critical part of the proof. The only stylistic nitpick is that beginning a sentence with “so” sounds stilted to me and that I would choose to instead say “Therefore, A is complete” to highlight that we have reached the result we are looking for.
3a: 0, 0
3b: 1, 1
3c: 2, 2
————————
Problem 4. I do not think that I have any comments here not of a type I’ve made above, except that this proof is much nicer using the topological definition of continuity.
————————
Problem 5. In (a), “Take x \in …. So there is” does not make sense to me, stylistically, as a way to start a proof. Aside from that, this proof is concise and works well. The only change I might make would be to name the points being chosen based on their set membership, i.e. “some a \in A” instead of “some y \in A.” I have found that that approach makes it easier to follow a proof. Perhaps writing “f(z) = x = f(y)” might make the applicability of injectivity clearer. Lastly, it is not necessarily immediately clear that the desired conclusion follows from the last line of the proof, which detracts. 1 for style and 1 for clarity.
(b) is the winner, to me, here. Naming of points is consistent and easy to follow, f(a) = f(b) is clearly stated immediately before using injectivity, and the desired conclusion clearly follows and is clearly stated. 2 for clarity and 2 for style.
(c) loses from the fact that “f(z) = x and f(y) = x” requires a moment, even just a small one, to notice that f(z) = f(y). 0 for style and 1 for clarity.
March 26, 2013 at 12:54 am
My experience: Graduate student in Number Theory, I’ve done many analysis courses in my undergrad, so I think I’ve mastered the basic analysis involved here.
My format:
Question: Clarity of a / Style of a, Clarity of b / Style of b, …
1: 1/2 , 0/0, 2/0.
I think that both a) and b) are easy to understand but they don’t explain how to choose r (resp. R). That’s why c) gets one point more on clarity. The shortest and best written is a). b) is the same content-wise but is harder to read: e.g. the chains of inclusions should be written out. Also, the aim of the proof is stated at the end which makes it a bit less clear here.
2: 2/2, 2/-1, 2/1
I think b) is badly written. The first sentences of the second paragraph begin with a mathematical symbol which makes it harder to read. It is a bit repetitive (e.g. it ends with i.e. .. So .. i.e. .. So). Answer c) states the aim at the end but is still well written.
3: 2/1, 1/1, 1/0
I don’t like that b) and c) take a as the limit of a_n. This suggests that a is in A but it’s a really crucial for the readers understanding to see that a priori the limit is just in X and only A closed implies a \in A. For c) I don’t think it’s necessary to state the aim at the beginning of such a short proof.
4: 2/-1, -2/0, 2/2
The long implications in a) make the formatting quite horrible to look at, maybe it would be better to write them in extra lines (like the $$ command does in Latex), also $p\in X$ is a weird choice of letter. The notation in b) makes it very unclear. Why define y=f(x), z=g(y) when it is easy to write out the few times it is used.
5: 2/2, 2/0, 0/-2
All answers are very clear: My favourite choice of letters would’ve been x\in X, a\in A, b\in B but none of the answers does it. a) is still very good. The wording in c) is very bad as it repeats things (like f(y)=x and f(z)=x both times separately), makes the answer unnecessarily long and therefore less clear.
March 26, 2013 at 2:18 am
I’m familiar with metric spaces (I’m a researcher in theoretical computer science – computational geometry in particular)
1(a): Clarity: 1. Style: 0 (repeated use of So is a little disconcerting)
(b): Clarity: 0. Style 0
(c) Clarity: -1 Style 0 (by the third one, the proof is using what I think is excessive formality when colloquial english would have done fine)
2(a): Clarity: -1
(b): Clarity: 1
(c): Clarity 0:
The style doesn’t vary a lot, and indeed appears related to the clarity. Nevertheless, I’ll do a global style 0. Sadly, the arguments, while more or less clear, seem clunkily written :)).
3(a): Clarity: 0
(b): Clarity: 0
(c): Clarity: 1 (I had forgotten that a closed set contains all its limit points, and the clarification helped)
global style: 1: somehow I liked these arguments better. I think I like a lower density of math symbols when it can be avoided.
4(a): Clarity: 0
(b): Clarity: -1 (I think introducing the extra symbols y,z was distracting
(c): Clarity: 1 (this was better than (a) because the \circ symbol always makes me wonder which order to apply them in, and the direct g(f(.)) notation is clearer).
Style: 1
5(a): Clarity: 1
(b): Clarity: 0
(c): Clarity: -1
Style: 0
March 26, 2013 at 2:40 am
I am a theoretical computer scientist. I have encountered metric spaces, but I haven’t taken a course that covers it.
I just thought I’d give some general comments on the proofs. I hope they help. In the first question, I liked the first proof best. It seems close to the way I would explain it. I like the picture with balls instead of distances.
I also noticed that for all the problems, I liked proofs with more words and fewer symbols. I liked some of the verbose proofs better than the succinct ones. They sometimes even repeated what had to be proved in different words, which was excellent.
March 26, 2013 at 6:44 am
About me: I’m a math grad student at Brown University. I know about metric spaces.
Problem 1
I have little preference between writeups (a) and (b). I like that (b) defines the notation for a ball of radius around the point
around the point  . But I may also be biased as I’ve used that notation, and not the reversed notation used in (a). I really like that (a) opens with the exact statement of proof and labels his radii to match the ball. So for [clarity, style], I give (a) a [2,1], (b) a [1,1], and (c) a [-1,-2]. With regards to (c), I thought it was hard to follow. Had I not known the idea behind the proof already, I think I would have gotten lost in the wash of variables.
. But I may also be biased as I’ve used that notation, and not the reversed notation used in (a). I really like that (a) opens with the exact statement of proof and labels his radii to match the ball. So for [clarity, style], I give (a) a [2,1], (b) a [1,1], and (c) a [-1,-2]. With regards to (c), I thought it was hard to follow. Had I not known the idea behind the proof already, I think I would have gotten lost in the wash of variables.
Problem 2
I have a preference for (b), similar to my preference for (a) in Problem 1. The opening statement gives guidance to the rest of the proof. I’d give (b) a [2,2] this time around. Then comes (a), even though I think it would be clearer to use balls explicitly rather than to mention only distances. I like that (a) makes it very apparent where continuity is used. I find (c) roughly comparable to (a) in terms of my preference, but somehow I don’t like how and
and  are introduced and used wrt continuity. Thus (a) gets a [1,1] and (b) gets a [1,0].
are introduced and used wrt continuity. Thus (a) gets a [1,1] and (b) gets a [1,0].
Problem 3
I have a strong preference for (c). I still like the opening phrase giving guidance to the rest. But I’d like to contrast the small amount of punctuation in (c) compared to (b). All the commas and implied voice-stops in (b) annoy me as a reader. I also really dislike the explanation that the is in
is in  given in (b); it’s wordy and has bad flow. I think that all three are very clear, but they differ a lot in terms of style. I give (c) a [2,2], (a) a [2,1], and (b) a [2,-1].
given in (b); it’s wordy and has bad flow. I think that all three are very clear, but they differ a lot in terms of style. I give (c) a [2,2], (a) a [2,1], and (b) a [2,-1].
Problem 4
By now it comes as no surprise to me that I prefer (a). Clear opening statement and proof. (a) gets a [2,2]. I then like (b). Again, I think that all three are pretty clear, and it’s mostly style that separates them. One thing I see that I don’t like about (c), and for that matter the styles similar to (c) in the other problems, is the unnecessary generality: in particular, the separate justifications for and
and  due to the definition of continuity only to set them equal at the end – I know it’s true, but why introduce extra variables if they aren’t really used? (b) gets a [2,1], and (c) a [1.-1].
due to the definition of continuity only to set them equal at the end – I know it’s true, but why introduce extra variables if they aren’t really used? (b) gets a [2,1], and (c) a [1.-1].
Problem 5
I like (a) the most. I think it’s clear and it flows, and it gets a [2,2]. I essentially like (b) just as much, with one exception: the ‘so…,so…. So…’ bit. So (b) gets a [2,0]. But I slightly dislike (c). It’s wordy and long. While I like it when we have those introductory statements, I don’t like them in the middle of the proof (it seems). So (c) gets a [1,-1].
I see that I never gave a -2 for clarity. I don’t know what would be necessary for that, I suppose.
March 26, 2013 at 8:06 am
Level: familiar with metric spaces.
Ratings:
1a) style 2, clarity 2
1b) style 1, clarity 1
1c) style 1, clarity 1
2a) style 1, clarity 1
2b) style 2, clarity 2
2c) style 1, clarity 2
3a) style 1, clarity 2
3b) style 2, clarity 2
3c) style 2, clarity 2
4a) style 2, clarity 2
4b) style 1, clarity 1
4c) style 2, clarity 2
5a) style 2, clarity 2
5b) style 2, clarity 2
5c) style 1, clarity 1
Comments: Basically I find all proof accessible and well written. I was distracted by unneccessary words like “arbtitrary”. If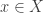 then there is no reason to say that
then there is no reason to say that  is arbritrary.
is arbritrary.
In some proofs the variable names are more pleasing; bad choices: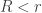 since
since  is "larger" than
is "larger" than  . If
. If  and $latex
and $latex  , why use
, why use  as radii and not
as radii and not  or
or 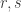 (i.e. consecutive letters commonly used for small real quantities).
(i.e. consecutive letters commonly used for small real quantities).
I had felt no preference for or against the usage of "so we are done", "we would like to show that" (although I have the feeling that the latter is more appropriate for more complicated or longish arguments than for one-liners).
Also I did not feel a preference for or against longer sentences vs. shorter sentences (no sentence was so long that it distracted from the argument).
Although I usually get distracted if sentences start with variable names and not with words, I did not feel this distraction that much here on the blog. Probably I am in a different reading mode on a blog and in a book.
I made no bad ratings since I have read the proofs as as if they were submitted exercises sheets (for some reason) and comparing to what I have read there, all proofs are definitely good.
Probably off-topic comment: The type in 1a) was not intended? Anyway, I only noticed it on second reading.
in 1a) was not intended? Anyway, I only noticed it on second reading.
March 26, 2013 at 8:44 am
I have a masters degree in mathematics and currently do research in
applied geometry. I am familiar and comfortable with the basic theory
of metric spaces, but I don’t have experience in teaching it.
I am not sure how to distinguish clarity from style. A relative
ranking of preference would be much easier for me than the two
absolute rankings requested. I generally avoid the limits of any
absolute ranking: something can always be better or worse than
anything I have imagined. I’ll allow half point increments.
Problem 1:
order of preference: a,b,c
a: style 1.5, clarity 1
b: style 1, clarity 1
c: style 0.5, clarity 0.5
I appreciate the style of stating what is to be done (a). Other than
that, it is difficult to see the difference between (a) and (b). The
fact that a capital ‘R’ was used for the smaller radius in (b)
irritated me, but I didn’t even notice that the centre and radius were
switched in the definition of the ball in (a).
The argument with balls is much easier for me to parse than the
distance-based argument of c.
Problem 2:
preference: b,c,a
I’ll just leave the absolute rankings as in the corresponding (order
of preference) solutions of Problem 1. This time I noticed the
centre-radius switch in (b).
I am now suspecting that there is going to be an attempt to make me
exhibit a bias for a style that I preferred in prob 1, in spite of
subtle degeneration of the quality of the response (or amelioration in
the quality of the others).
3:
c,a,b
I find c and a similar in quality, but continue to prefer the style of
c.
4:
a: style: 1, clarity 1
b: style: 0.5, clarity 1
c: style: 1.5, clairty 1.5
What happened to the balls? I think I rank c,a,b. I appreciated the
attempt in (b) to name variables according to the space they occupy,
but it didn’t seem to help.
5:
a,b,c
Solution c seems particularly bad this time.
March 26, 2013 at 12:10 pm
I’ve studied metric spaces at a university math course.
Problem, style, clarity, comments
1(a), 1, 1, B_x(r) wasn’t defined
1(b), -1, 1, I didn’t like the word arbitrary. I also found the mix of small and large alphabet for the radius irritating.
1(c), 1, 2, My favourite description, but somehow felt a bit long. Perhaps defining balls would shorten it a bit.
Problem, style, clarity, comments
2(a), 0, 2, I liked the fact that you state what you want to find
2(b), -1, 1, B_x(r) wasn’t defined. I didn’t like “i.e.”. I liked \in better than “is an element of”
2(c) 2, 0, I found the sentence “there exist \delta > 0 such that … f(y) belongs to” confusing.
Problem, style, clarity, comments
3(a), 1, -1, Needed to know that Cauchy sequences imply completeness
3(b), 1, 2, Not much separating this from 3(c)
3(c), 2, 2, I liked that you stated what you want to show.
Problem, style, clarity, comments
4(a), 2, 2, Stated what you want to show
4(b), -1, 1, Felt a bit informal
4(c), -1, 1, I didn’t like the setting of \delta=\theta
Problem, style, clarity, comments
5(a), -1, 0, Felt abrupt
5(b), -1, 0, I think the “so” is somehow not nice
5(c), 1, 2, In contrast to previous questions, I found setting u=y nice here.
March 26, 2013 at 1:45 pm
[…] An experiment concerning mathematical writing | Gowers’s Weblog. […]
March 26, 2013 at 1:45 pm
Nice experiment. I will be interested to see the results. I am just curious if you are going to gather data about what mathematical fields your participants belong to. (Or other such data.)
March 26, 2013 at 2:09 pm
I am an undegraduate/graduate student from Germany. I know about the basics of topological and metric spaces. The statements involved were clear to me.
General comments (after having read all the write-ups):
(A) I personally like proofs where the ideas are presented concisely while carrying out the correctness is left to the reader. I find, it has a rather stimulating effect. Another advantage is that proofs are kept short which is motivating.
(B) I also like to think and read about mathematical statements in the coarsest level possible, e.g. I prefer “⊂” over “∈”. (In my experience, coarser levels are simpler to think about. They are often accompanied by abstraction.)
(C) I’m in favour of short outlines of strategy in some of the proofs.
(D) To me, the use of “whenever” indicated equivalence. I needed a bit to realise what it meant. But then again, I’m not a native speaker of English.
On problem 1:
• My ratings are:
• 1(a) – Clarity: 2, Style: 2.
• 1(b) – Clarity: 1, Style: 0.
• 1(c) – Clarity: -2, Style: -1.
• In proof 1(a), it should be $B_r (x)$ and not $B_x (r)$. (Or is this typo intended?)
• I would even go shorter with 1(a) by using “∈” and “⊂” more often.
• In proof 1(c), I needed some time to parse “whatever”, cf. (D).
• In accordance with comment (A), I’d prefer 1(a) over 1(b) over 1(c).
On problem 2:
• My ratings are:
• 2(a) – Clarity: -1, Style: -1.
• 2(b) – Clarity: 1, Style: 1.
• 2(c) – Clarity: 2, Style: 1.
• The use of “whatever” in proof 2(a) threw me off this time, cf. (D).
• Again, in proof 2(b), it should be $B_r (x)$ and not $B_x (r)$.
• In proof 2(b), the first use of “i.e.” was a bit confusing for a second since I immediately refered it to the previous statement which was the implication itself, not its consequence.
• Again I would go even shorter with 2(c) by writing “since f is continuous, f( B_δ(x) ) ⊂ B_ε (f(x)”, directly, cf. (A), (B).
• In accordance with comment (A), I’d prefer 2(c) over 2(b) over 2(a).
On problem 3:
• My ratings are:
• 3(a) – Clarity: 1, Style: 1.
• 3(b) – Clarity: 1, Style: 1.
• 3(c) – Clarity: 2, Style: 2.
• Not much to say here. The difference between the proof styles nearly vanishes, maybe because the statement is so utterly clear and straightforward to prove.
• No real preferences.
On problem 4:
• My ratings are:
• 4(a) – Clarity: 1, Style: 1.
• 4(b) – Clarity: -2, Style: -1.
• 4(c) – Clarity: 2, Style: 1.
• In proof 4(b), the definitions of y and z are more confusing than clarifying. And generally, there are too many symbols.
• In proof 4(c), again I refered “but then” to the previous statement, which was the implication, not the consequence.
• Strangely, the use of “whatever” felt very appropriate this time, clarifying the proof.
• This time I prefer 4(c) over 4(a) over 4(b).
On problem 5:
• My ratings are:
• 5(a) – Clarity: 2, Style: 1.
• 5(b) – Clarity: 2, Style: 2.
• 5(c) – Clarity: 1, Style: 0.
• Both 5(a) and 5(b) are fine, 5(c) is too long.
I’m looking forward to your evaluation of the experiment (which you will hopefully post). I’m very interested in that.
March 26, 2013 at 2:26 pm
I have studied the basics of metric spaces – enough to follow
all the given proofs fairly easily.
1(a) Good WTS statement initially. Nice working
with open balls, and a nice balance of leaving out
low-level details that the reader should be able to
supply. Clarity +2, Style +2.
1(b) I prefer a WTS statement to orient the reader – this
proof lacks one. Context would determine whether the
definition of an open ball is necessary for the average
reader. The wording “We’ve proved that…” should be
changed to “We’ve proven that…” It sounds and looks
more natural. Still quite clear, but I would deduct a
point for style. Clarity +2, Style +1.
1(c) I see no need to use Greek letters when English ones
will do fine. Theta, in particular, is typically used more
for angles, so its use here could confuse. There is a
procedural error: delta is used before it is defined. Of
course, a reader could see that there is no real issue here,
but stylistically, delta should be defined before it used.
Finally, I find open balls a tad more intuitive than using
the metric. Clarity +1, Style +1.
(a) is the best proof, in my opinion, for Problem 1.
2(a) This proof required some staring on my part to comprehend.
Again, I find a WTS statement very helpful in orienting the
reader towards the goal, much like in physics problems where you
want to identify the target variable (that is, what it is for
which you wish to solve). Clarity +1, Style +1.
2(b) Nice WTS statement, again using open balls. To close the loop,
I think it would have been preferable to say that “Delta is the
r we seek.” However, this is not too great a strain on the reader.
Clarity +2, Style +2.
2(c) This is probably the most direct proof. I would prefer a WTS
statement, but staying with open balls is clearer to me than using
the metric. To me, the directness of this proof more than offsets
the lack of WTS statement. Clarity +2, Style +2.
(c) is the best proof for Problem 2.
3(a) No WTS statement, but it’s quite a direct proof. Clarity +2,
Style +2.
3(b) Again, quite direct. This is a fairly simple theorem,
so lengthy proofs are not necessary. Prefer WTS statement, but
it’s not bad. Clarity +2, Style +2.
3(c) This is the clearest of the Problem 3 proofs.
Nice WTS statement paraphrasing the conclusion of the theorem.
Unfortunately, the word “so” is used too often for my taste near the end
of the proof. Substitute some therefore’s or thus’s to relieve the tedium.
Clarity +2, Style +1.
Despite too many so’s, I prefer (c) for Problem 3.
4(a) I prefer $(g \circ f)(x)$ for function composition, or better yet,
$g(f(x))$, as in the 4(c) proof. The double-justification is forcing some
very large, unnatural gaps in the lines of these proofs. I’d recommend
just doing a left-justification. Good WTS statement. One thing it would be
good to know is the author’s use of surjectivity. It appears that
the author identifies y with f(p), but this should be explicit. Also, the
imbalanced expressions inside the metric are disconcerting. My eye wants
to see symmetry; that is, I don’t want to see something like
d(f(g(h(x))),z), but more like d(f(g(x)),f(g(y))).
Clarity +1, Style +1.
4(b) This proof suffers from a few of the same defects as 4(a): imbalanced
expressions inside the metric. This makes it difficult to keep track of
where various expressions live. Clarity +1, Style +1.
4(c) Good WTS statement, and nice balanced expressions inside the metric.
Also, I prefer the g(f(x)) notation to the circle notation. This is
definitely the best of these proofs. Clarity +2, Style +2.
(c) is the best for Problem 4.
5(a) Quite straight-forward and clear. Could use something other than “so”
twice in a row, but this is minor. Clarity +2, Style +2.
5(b) I like the matching of lowercase to uppercase, showing more clearly than
5(a) where the variables live. However, there are even more “so’s” in a row
here. Relieve the tedium! Clarity +2, Style +1.
5(c) This proof has the same kind of backwards trick to it that makes
some of the other proofs less clear than they might be. It generally
has good style, although I’d prefer a WTS statement. Clarity +1, Style +2.
I think I prefer (a) for Problem 5.
March 26, 2013 at 3:17 pm
First, here are my ratings. I suspect if I did them they’d come out rather differently. For each I list my clarity rating then my style rating.
1(a): 1, 0
1(b): 0, 2
1(c): -1, 1
2(a): 0, 1
2(b): 1, 1
2(c): 0, 2
3(a): 1, 2
3(b): 0, 2
3(c): 2, 2
4(a): 1, 1
4(b): 1, 1
4(c): 1, 2
5(a): 1, 1
5(b): 1, 2
5(c): 2, 1
Second, some very general comments. It’s hard to separate clarity from style, since I think clarity is one of the main aspects on which the style of mathematical writing should be judged. It’s also difficult to judge these write-ups without knowing the background of the intended audience. It’s easy enough to assume they’re students in a course covering such material for the first time, but I might prefer different write-ups depending on the details of what they’ve seen before — how much have they already worked with continuity in metric spaces, with open balls, or with injectivity? In addition, my judgement of style depends on knowing how the write-up will be presented. I really dislike sentences which begin with mathematical symbols in textbooks or papers (and took off style points for that), but I’m more relaxed about it in lectures.
Now to more specifics. Assuming that the audience is relatively inexperienced with the material, I highly favor write-ups which begin by pointing out what it is that needs to be proved. I generally dislike the pattern of stringing together several statements and then announcing “We’ve proved that…” (which I find students sometimes react to with unpleasant surprise — “Wait, what?”), but with two major caveats. First, the third alternative is to make no such comment at either the beginning or end, which makes it easy for students to understand nothing, but without recognizing that they’ve understood nothing. Second, the pattern of trying this, trying that, and then looking to see what you’ve actually proved more closely mimics (some of) how actual mathematical research gets done, and it can be good to expose students to that way of thinking (as opposed to the more algorithmic approach of earlier classes).
The approach of working with a parameter whose value is to be set later is one that I often like, partly because it can help avoid clutter and partly because it makes it less mysterious how someone came up with the proof in the first place. I thought these particular examples, though, were simple enough that that device didn’t add much.
I took off some points for notation choices. In 1(a), it’s extremely confusing that a and b are not elements of A and B, but are real numbers, and there’s nothing immediately indicating what kind of thing they are. Also in 1(a) two inconsistent notations for balls are used (changing the locations of the center and radius). In 3(b) it’s potentially misleading that a is not assumed a priori to be in A, and there’s no visual clue of that (such as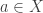 ). I gave my lowest marks to 1(c), which — compared to 1(a) and 1(b) — I found to be an excellent case study in how the terminology and notation for open balls can simplify that topic; this again depends, however, on whether the audience knows that terminology.
). I gave my lowest marks to 1(c), which — compared to 1(a) and 1(b) — I found to be an excellent case study in how the terminology and notation for open balls can simplify that topic; this again depends, however, on whether the audience knows that terminology.
Finally, I assume you’re not interested here merely in these write-ups per se, but I wonder whether you want to get at mathematical writing issues relevant specifically at the level of these write-ups, or more generally. I’ve judged the write-ups with my own undergraduate students in mind as an audience. On the other hand, maybe you’re also thinking about how we write research papers for colleagues, and the level of the material in the write-ups was dictated by wanting to work within the intersection of all mathematicians’ backgrounds. In that case I would revise my comments starting from “Now to more specifics” significantly, and say that any of the general patterns is generally acceptable, and the writer should favor whichever pattern seems to fit the logic of the proof most naturally.
March 26, 2013 at 3:52 pm
I have an undergraduate degree in maths (joint honours with computer science), which is 10 years out of date. I have never specifically studied metric spaces.
1a) it was apparent that the introductory statement serves as a definition of ‘open set’ – this helped to define the problem and strategy more clearly.
Given the introductory statement mentions a requirement on B_x(r), and the conclusion talks about B_r(x) – it was difficult to understand whether we had acheived the stated goal – it feels like there is some logical step missing.
1b) A clear definition of B makes this easier to follow. I preferred the style of this one compared to the other two – it followed my own initial logical process. It was unclear at first that r and r’ could be arbitrary rather than the smallest or largest such values (“there exist”, as used in the other proofs, would have been more familiar).
1c) seems to be the most thorough logical treatment, but the long sentences are confusing and make it difficult to follow step by step. The statement “we are done” feels extremely unpleasant. It would be nicer to state what is done, and why.
March 26, 2013 at 7:07 pm
——————————————————————————-
I have a very old (1986) B.A. in math. As part of another degree. I also took courses in real analysis (Rudin’s “Principles”) and point-set topology (instructor notes). I am familiar with the metric space concepts involved in your proofs.
(It would be interesting to know whether the proofs were intended to be proofs by a teacher/textbook (to help students understand the material) or proofs by a student (to demonstrate his/her understanding of the concepts). For my comments below, I assume that the proofs were intended to be from a
teacher or textbook to help students understand the material.)
——————————————————————————-
Problem 1, General Comments:
Proof 1(a) starts by declaring what we need to do to solve the problem. This declaration is useful, because it sketches the direction of the proof and gives students a path to guide their thoughts as they try to understand how the pieces of the proof line up along that path. Because a direction or rationale of the proof was given at the outset, students can always refer back to it if they get lost along the way; i.e., they can say, “Now what is it that we need to do?” I think it’s very helpful to provide students with this mental map of where they’re going, so they can always have the chance to see things at a glance and then take their time in figuring out how each of the details of the proofs fits into the larger picture.
Proof 1(b) dives right in without the kind of “map” that proof 1(a) lays down, with the result that students might have more trouble at the outset. They might wonder why the proof starts where it does and where the proof is going. Proof 1(b) essentially gives the rationale of the proof at the end of the proof, rather than at the beginning of the proof, as does proof 1(a). As a student,
I would prefer to know up front what the proof is trying to accomplish and why.
Proof 1(c) doesn’t state explicitly why all of its steps, taken together, constitute a proof of what needs to be established. In contrast to proofs 1(a) and 1(b), proof 1(c) doesn’t state its logic at the beginning or at the end.
Proofs 1(b) and 1(c) include details about open balls that I feel distract from the *idea* of the proof, because the details encourage/force the student to focus on the trees and miss the forest. Sure, the trees are there, but for this problem, proof 1(a) does a much better job of conveying, with a well staked-out rationale, the essentials of what is going on.
For me, none of the three proofs gives a sufficient intuition of what’s going on. For instance, there’s a *reason* why it makes sense to consider the smaller of two particular radii when considering which radius to use for the open ball that clinches the argument. I think the proofs would be better if they
explicitly dealt with the intuition behind the arguments (A student might ask, “Why are we introducing this minimum value here? What’s that got to do with anything?”) and the visual appeal of open balls.
1(a)
Clarity: 1
Style: 1
1(b)
Clarity: 0
Style: 1
1(c)
Clarity: -1
Style: -1
——————————————————————————-
Problem 2, General Comments:
Each of the three proofs mentions some kind of connection between a particular object (an open ball that is constructed about an arbitrary point in the inverse image of U and that is contained in the inverse image of U) and the rationale for why the existence of that object suffices to establishes the intended result (that the inverse image of U is open).
Proofs 2(a) and 2(c) begin by considering an arbitrary point in the inverse image of U, but without saying why they’re doing that or where they need to go once they’ve done that. Proof 2(b) also starts out with an arbitrary point in the inverse image of U, but it then says immediately where it’s going from there, which implicitly explains both why it started with that arbitrary
point and why finding the object it seeks will establish the needed result.
Proof 2(a) explicitly uses metrics, rather than open balls, to describe the open sets involved in the proofs. Proof 2(b) starts with open balls, switches to metrics, then returns to open balls. Proof 2(c) uses open balls throughout.
Proofs 2(a) and 2(b) seem to muddy the waters too much: proof 2(a) requires unnecessary metric gymnastics, and proof 2(b) needlessly switches between the intuition of open balls and the details of metrics.
Proof 2(c) is more straightforward for me. It is roughly like proof 1(a) except that proof 2(c) states its rationale at the end, whereas proof 1(a) gives its rationale at the outset.
2(a)
Clarity: -1
Style: -1
2(b)
Clarity: 0
Style: 0
2(c)
Clarity: 0
Style: 1
——————————————————————————-
Problem 3, General Comments:
None of these proofs begins with something like “To show that A is complete we need to show that every Cauchy sequence in A converges to a point in A,” though proof 3(c) comes close to explaining this at the outset, as does proof 3(a) at its end.
For me, proof 3(a) does a better job with notation than does proof 3(c). Proof 3(a) uses “x-notation” for the initial Cauchy sequence in A and then later establishes that because A is closed the limit of this “x-sequence” must be in A. Proof 3(a) uses “a-notation” for the initial Cauchy sequence. Because of this notation, I have to do slight double-take when I see that ‘a’ is
in X and then, oh yeah, it’s also in A, because A is closed. (Using ‘a’ instead of ‘x’ for the limit causes me to implicitly suppose that ‘a’ is already in A, and so I wonder for a moment why that fact needs to be proved.)
If proof 3(a) started with “To show that A is complete we
need to show that every Cauchy sequence in A has a limit point in A,” and if it said, “Because A is closed, x belongs to A (since a closed set contains all its limit points)” I would give it a 2 for clarity and a 2 for style. As it stands now, Proof 3(a) comes “within epsilon” of hitting the sweet spot for me.
Proof 3(b) doesn’t give a rationale for what it’s doing. It’s not an awful proof, though.
3(a)
Clarity: 1
Style: 1
3(b)
Clarity: 0
Style: 0
3(c)
Clarity: 1
Style: 0
——————————————————————————-
Problem 4, General Comments:
For me, proof 4(a) works best, because it lays out early the rationale for the subsequent steps, and it then proceeds to use the given information in a simple chain-like fashion to reach the needed conclusion.
My brain recoils from proof 4(b), starting with the second sentence and all the needless and distracting primes in the notation. I can barely force myself to follow the proof, the notation is so distracting.
Proof 4(c) starts out well by laying out what needs to be done. But it ends poorly, setting delta equal to theta, and forcing me to backtrack to understand why that completes the proof. I find myself having to ask, “Now what are delta and theta again, and exactly how are they being used? And how does setting them equal to each other complete the proof?”
4(a)
Clarity: 1
Style: 1
4(b)
Clarity: -2
Style: -2
4(c)
Clarity: -1
Style: -1
——————————————————————————-
Problem 5, General Comments:
Though none of the proofs says why we start out with x in the intersection of f(A) and f(B), or where we need to go with that information, it may be safe in this case to assume that the student knows (though a reminder wouldn’t hurt).
Proof 5(a) takes a bit of a jump when, after noting that y and z are equal, it says that y is in the intersection of A and B. This jump isn’t necessarily a bad thing, since it gives the reader “fair” brain practice in connecting different pieces of the proof together.
Proof 5(b) moves slowly in small steps, using perhaps the most familiar form of the fact that f is injective. Proof 5(b) also explicitly ends with a statement of exactly what we were asked to prove, so it’s quite tidy in that sense.
Most of proof 5(c) follows proof 5(b), but with more verbiage that doesn’t help clarify (for me) what is going on. Proof 5(c) ends with another “setting this equal to that and we’re done,” which requires too much back-tracking to understand. Also, for this proof and the others that end with “setting
this equal to that and we’re done” – there’s no good reason I can think of to end the proof this way. The problems were provable by much more perspicuous methods.
5(a)
Clarity: 0
Style: 0
5(b)
Clarity: 1
Style: 1
5(c)
Clarity: -1
Style: -1
March 26, 2013 at 7:30 pm
I have a graduate degree in engineering, but I took a class in real analysis many years back. In general, I liked proofs where the logic was more linear, but this doesn’t always seem possible, such as in the last example. I may have marked down some in which I had partially forgotten the definitions and the terms weren’t re-defined. Here are my comments.
1(a) Very easy to understand. The introductory sentence was very helpful in visualizing the problem.
Clarity: 2
Style: 1
1(b) The open ball was more intuitive for me than the ball definition, although that might not be an issue is someone is used to reading these proofs. I didn’t like how you had to remember that r and r’ correspond to A dn B respectively and then it was slightly confusing for the big R to be smaller than the small r’s.
Clarity: 0
Style: 1
1(c) Using eta and theta introduces the variables u and v which are never used again. In addition, you need to remember that eta and theta correspond to u and v and correspond to A and B. The definition of intersection feels redundant and the key point is delayed until the last line.
Clarity: -2
Style: -2
2(a) Using the eta and delta makes more sense in this case where continuity is the key factor. I still don’t like having to set delta to theta in the last step.
Clarity: 0
Style: 1
2(b) The section on continuity seemed a bit rushed. While logically sound, there seemed to be more jumps in the last line that weren’t immediately obvious.
Clarity: -1
Style: -1
2(c) It starts off very well. The definition of continuity is the clearest in this example, but then the proof seems to move backwards to get to the conclusion. If there were some way of combining (b) and (c), that would probably be the clearest solution.
Clarity: 0
Style: 2
3(a) Straightforward and moves in a logical direction. The statement that x belongs to A does not seem to be clearly justified.
Clarity: 1
Style: 2
3(b) It makes sense, but is repetitive and seems to move backwards and forwards in the logic.
Clarity: 1
Style -1
3(c) I like how this solution really breaks down the definitions of a complete metric space and closed subset, only it is slightly repetitive.
Clarity: 2
Style: 1
4(a) I really like how this one lays it out and then moves backwards from epsilon to delta to gamma and then forwards again. I wonder if it’s possible to do it without going in both directions, but this proof is what I had imagined in my mind.
Clarity: 2
Style: 1
4(b) Major negative points for using epsilon’ when you could have used another variable. Similarly, I don’t like the additional x’ and the y’ variables, although x’ makes a little bit of sense in the definition of continuity.
Clarity: -2
Style: -2
4(c) This is straightforward and seems very similar to (a), but the layout in (a) just seems slightly easier to read.
Clarity: 2
Style: 0
5(a) The writing is fine, but I don’t like how the last two statements seem to jump back and forward in the logic.
Clarity: 0
Style: 1
5(b) The first two statements were fine, but I got lost after that the first time reading it. It seemed like a jump going from a in A intersect B to y in f(A intersect B).
Clarity: -1
Style: -2
5(c) I like how the injection was very clearly laid out. The ending was still slightly confusing, but this proof broke it down a little more than the others did.
Clarity: 1
Style: 1
March 26, 2013 at 7:56 pm
experience: math/cs major in early 80s, CS prof. took topology using munkres; not current with the defns, but they come back.
My opinions on writing are strongly influenced by G. Gopen, see his article with Swan on the science of scientific writing (www.docstyles.com/library/ascience.pdf) or his book ‘A sense of structure’. You are likely familiar with these, since one of the variants appears to be ‘context first,’ which is one of his emphases.
Clarity Style Proof Comments
2 1 1a: verbose, but clear. Good style; I would need less detailed reminders of the definition in a context in which I had been recently using them.
1 -1 1b: notation-heavy, but still clear. Style points deducted for lack of consistency in naming ball radii, and for not saying ball B_r(x) …, which would at least give a single word clue as to how the notation is to be read and understood.
-1 -2 1c: uses language of conditionals where the prover can make a choice. The specific choice is made later, forcing the reader to reread everything to make sure the choice worked. Didn’t like it.
-2 1 2a: does not put context first, forcing me to reread once I discover where it is going
2 1 2b: verbose, but very clear.
1 1 2c: notation heavy, but still clear since I’m quite used to proofs of this style.
2 0 3a: definitions come last, unfortunately.
1 1 3b: definitions discovered as you go. verbose.
2 2 3c: definitions (and context) first. verbose, but very clear.
1 1 4a: context is stated first. All proofs of this use a lot of notation, but this is fairly clear.
-1 -2 4b: no signposting at all.
0 -1 4c: notation heavy, including defining two variables for the same thing, does say where it is trying to go, but must still read twice since a key choice is made at the end.
1 1 2a: shortest would have given +1 to style, but I didn’t see a need to change from injection to injective.
1 1 5b: fine, but some unnecessary notation.
0 -1 5c: too verbose and choice made at the end.
March 26, 2013 at 9:01 pm
1(a): 1, 1
1(b): 1, 1
1(c): -1,-1
2(a): -1.-1
A running theme in 1(c) and 2(a): I don’t like implicit quantification of the form “we know that y in A whenever d(x,y) < eta" and "u in U whenever d(f(x),u) < eta". I prever y and u in examples like this to be more formally introduced.
2(b): -1,0
I don't like what's happening in the sentence "i.e. f(z) in B_epsilon(f(x)) subset U". Just before it, there's a "for all x in Z, [something] implies [something else]", and the "i.e." bit is only unwinding a condition implied by [something else]. A semicolon is too little to connect these things together, as I see it.
2(c): 1,1.
What I'm taking from this is that there is an interesting gap in what I like to read, versus what I want students to produce. I know metric spaces, and I like reading proofs that don't force me through the triangle inequality every time. I find the notation for B_e(x) (where e is a positive real, and x is in the metric space) very helpful, and the elementary "set calculus" of balls, when taken for granted, cleans up proofs a lot. And I like it when students use this to clean up their proofs. But at the same time, in my teaching, I tend to push students who are seeing this the first time, who do their best to avoid nested "for all" statements and bare-bones applications of metric space axioms, to be clearer about what they are saying. Instead of "So f(x) \in U", for example, I'd like "By the definition of the set f^(-1)(U), we know f(x) in U." And maybe even I'd like some of the reasoning with balls explained by passing reference to the general facts about balls being used. (Even though I would not want to teach out of a textbook that wrote proofs this way!) Students learn or at least copy from each other, and I don't want weaker students getting the impression from stronger students that proof-writing is just writing series of "right" assertions, with no justification. For the same reason, I am almost at the point where use of the word "any" (as in "for any y in B_delta(x)") is not acceptable in student writing. Even though I *only* object to it in student writing. When strong students use "any", the less strong students will blur the details between "any" meaning all, and "any" meaning just one.
3(a) 0, 0.
This answer was on the borderline of poorly written to me but I would probably let it slide in a class. Ideally, a well written answer would be one that weaker students can learn from— or at least be reminded of facts from. So if this proof could recite a general relationship of closedness to containing sequential limits (whether it's by definition, or a theorem), I would love it.
3(b) -1, -2
I seem to care less than most about the importance of good notation, but experience tells me that a student who lets "a" denote the element of X that they're about to prove is really in A, will either (1) write obviously false statements immediately after, or (2) write a list of correct statements, with no indication of why any statement on the list is true, or any indication of how the statements in the list fit logically together, except what you can infer from the linear ordering of the statements on the page, and perhaps connecting words like "So" and "Because" and "Therefore". This proof, of course, was of type (2).
3(c) 1,0
I don't like the "a_n to a, for some a in X" ordering of quantifiers and try to teach away from it wherever possible. I like letters to be introduced before any statements are made about them. But other than that I liked this proof. OK, I wouldn't have chosen "a" to denote the element of X, but I loved "Since A is a closed subset of X, it must contain all its limit points." That is what I like to read in proofs. Correct statement _with a justification_ that I can read.
4(a): -1,0. I don't know why this was so hard for me to read, but it was.
4(b): 1,0.
4(c): 1,1.
5(a): 1,1. I would have gone to 2 for the quality, only I don't like "f(y) = f(z) = x. As f is injective, …" because a student reading it might think that f(y) and f(z) being equal to x was more important than f(y) and f(z) being simply equal, for the purpose of applying the fact that f was injective. Also, rather than just showing that every element of P is an element of Q, I like a proof to say at the end, "So P is a subset of Q." Or to say somewhere in the middle, that it suffices to show that an arbitrary element of P is an element of Q.
5(b): 2,2.
This is the closest to how I would like students to write this proof. It is probably too much to ask for a little reminder line explaining the reason for "a in A intersect B, so y in f(A intersect B)." It is just by definition (both of y, and of the set f(A intersect B)). But I like it when people draw attention to when they are using definitions and not anything more complicated.
5(c): 2,1.
This proof was a little symbol-heavy for me and it had the problem mentioned in the second half of my comments to 5(a).
March 26, 2013 at 9:38 pm
A fuller reply to come, but in 1(a), is for
for  an intentional misprint?
an intentional misprint?
March 26, 2013 at 10:36 pm
Problem 1.
1(a) Clarity 1. Style -2
Ignoring mispring at the beginning of the second line ( where
where  is meant), style points lost for the clumsy repetition at the beginning of the second para, and too many “so”s. I don’t at all mind contractions in general, but “it’s” here is unnecessary when “is” would be better.
is meant), style points lost for the clumsy repetition at the beginning of the second para, and too many “so”s. I don’t at all mind contractions in general, but “it’s” here is unnecessary when “is” would be better.
1(b) Clarity 1/2. Style 0
Style points lost for introducing idea of ‘open ball’ at the end rather than, more naturally, at the beginning (and would the initial explicit definition be needed at this stage?). But proof is natural.
1(c) Clarity 0. Style 0
Quite laborious to no gain: why avoid the nice image of the open ball?
Problem 2.
2(a) Clarity -1. Style 0
2(b) Clarity -1, Style -2.
For a start, why throw in an arrow instead of if/then? All a bit clumsy, to my eyes.
2(c) Clarity 2, Style 1
Giving a little less detail (leaving the reader to recall, if necessary, why continuity has the stated application) in fact makes the proof-idea clearer. Nice unlaboured variation “hence”/”so”/”so”/”we’ve proved that”.
Problem 3
3(a) Clarity 0, Style -1
Ugly to use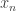 for points in
for points in  , and quite unnecessary to subscript
, and quite unnecessary to subscript  .
.
3(b) Clarity 1, Style 0
3(c) Clarity 2, Style 1
Spot on: beautifully clear. Only loses a style point for starting three sentences in a row “Since”.
Problem 4
4(a) Clarity, 1, Style 0/1
In some ways the best, but the modern notation for function composition [at least as rendered here, though perhaps that’s not the best test] isn’t easy to read, and again I don’t like sprinkling arrows for vernacular ifs.
4(b) Clarity 0/1, Style 0
Clarity is obscured by bad style choices (I had to check back for e.g. )
)
4(c) Clarity 1, Style 1/2
Clear proof-idea, and the old-style notation for function composition makes this more readable. But could, as in 4(a), have avoided play with
Problem 5
5(a) Clarity 1, Style -1
This is such an easy proof, it would be difficult to do it very unclearly — but the unmnemonic choice of variables knocks off style points.
5(b) Clarity 2, Style 1
Very nice, except for a style point meanly docked for three “so”s in a row …
5(c) Clarity 0, Style 0
Laboured to the point of making things harder not easier.
March 26, 2013 at 10:46 pm
[…] his blog, Timothy Gowers has asked for comments on some variant proofs, three proofs apiece in response to five basic problems in the elementary theory of functions, […]
March 27, 2013 at 5:40 am
Hi Prof. Gowers,
I can’t understand in which perspective you wish us to rate, I mean, most of my Maths knowledge is by self study, so at that time I wished the authors should write each and every detail, but now after coming to grad school, I feel bored to read such clearly written proofs. Like before grad school I liked Dummit Algebra, now I like Serge Lang Algebra book.
Can you give some clarity about this, I mean, who are the perspective readers? So that I can give my ratings depending.
March 27, 2013 at 7:18 am
1(a)2,2 Even though it’s “wrong” because of the backwards ball, it still gets “full marks” because the intent is clearly expressed.
(b) 2,1 Loses half a style point because the ball definition should not be necessary and another half for the lack of initial motivation.
(c) 1,1 Loses two style points because of the lack of motivation and because the failure to use ball language makes it harder to read but gets one back for consistently using greek letters for numbers and latin for points (which might have made for an improvement in (a))
2(b,c,a)=1(a,b,c) in scores (though not exactly for the same reasons) except that for 2(a) I’d change the clarity score to 0 (or maybe even -1)
3(c,b,a)=1(a,b,b) except that in 3(b) the first mention of a should make clear that it is initially only known to be an element of X so maybe the clarity score should go down to 1.5
4(c,a,b)=1(a,b,c) except that in 4(c) x should be identified as a point rather than a positive number, and it might be nicer to have space-identifying subscripts on the d’s and to use x and x’ (as in 4(b)) rather than x and y for the two points in space X, and it would look less like a proof of uniform continuity if expressed in terms of balls centered at x, f(x), and g(f(x)). In 4(a) the pattern might be clearer if the ordering of x and p matched that of f(x) and y. The wrong reference to f(y’) in 4(b) is more damaging than the errors in 1(a) and 4(c) because the multiplicity of symbols makes it harder to see what is going on, so here again I’d downgrade the clarity score.
5(b,a,c)=1(a,b,c) except that for 5(c) I’d lower both scores for the unnecessary complication of introducing yet a third name for the common value of y and z.
March 27, 2013 at 10:46 pm
Level of experience: postgraduate. Yes, know this stuff. (Knew!)
1a. Style 2, Clear 2. I liked this. The notation won’t generalise to more than 2 sets, however, we are only asked to prove it for 2 sets so that’s OK.
1b. Style -2, Clear 0. This is like a “proper mathematician” dressed up 1a in lots of notation but it gets in the way and I stop seeing little round balls. I feel I ought to like it more than 1a but I don’t! It adds nothing to define the ball notation, if you are going to use the d(x,y) notation at all then the ball adds nothing.
1c. Style 0, Clear 0. I do like that this starts from the basic definitions, but it is so verbose. (Explaining the meaning of intersection twice is a nice touch!!) Would be good cut to half the number of lines. Also given that we have 2 sets A and B I would have used “a” and “b” rather then “eta” and “theta” – anything to keep things simple.
2a Clear -2, Style -2. I didn’t like this. Better with x and x’ instead of x and y. Also, it’s too heuristic ie it sets down the order it was thought up in. I’d like to think that this helps comprehension. Certainly the opposite is often true, that a logical, here-are-the-axioms approach can bury comprehension but here things feels thin and stretched by the punchline. The other two versions do better to introduce continuity earlier. And, the sentence about continuity is convoluted.
2b Clear 1, Style 1. (I guess that’s a typo with the 2 notations of the balls.) Not helpful to mix balls and metrics, better one or the other. But, helpful to start
by stating where the proof is headed.
2c Clear 1, Style 2.
3a Clear 1, Style 1 because the {n in N} and the definition of the limit point are a bit excessive. Clear 1 because better to define the sequence as in 3b and 3c.
3b Clear 1, style 1.
3c Clear 2, style 2. Careful and clear to me.
4a,b Clear -1, Style -1. I got lost in all the extra variables.
4c Clear 2, Style 2. Working backwards from the definition works. This is kind of crude and brutal, but it doesn’t get between me and the basic idea of continuity and I can picture it how I want. 4a,b look more elegant and helpful but I have to remember all those extra variables and my thinking energy gets mopped up in following the author in the details, less is available for thinking about the problem.
5a. Clear 0, Style -1.
5b. Clear 2, Style 2. Much better choice of variables than 5a but a bit verbose relative to 5a.
5c. Clear -2, Style -2. Awful. Verbose and bad choice of variables.
March 27, 2013 at 11:56 pm
Problem 1. Version a is much easier to read overall, except for the typo. You mean Bsubr(x), I believe. From version 2, I got the notion of r being the radius, which came from a distance between points. But I was confused about the set X that’s first mentioned. I never made it through version c because of the use of greek letters whose names I can’t remember.
a: C: -1, S: 0
b: C: 1, S: 1
c. C:-2, S; -1
I’ll stop there. It’s all hard going for me.
March 28, 2013 at 6:14 am
1 a) +2 clarity, +1 style.
b) +1 clarity, +2 style.
c) +1 clarity, +1 style.
I liked the first answer better than the other two. Though there is a certain repetition in it that the style of the second avoids. For me a blend of the simpleness of the first with a more straightforward written of the second would be the ideal.
2 a) +2 clarity, +1 style.
b) 0 clarity, 0 style.
c) +1 clarity, +1 style.
The first seems more linear to understand than the other two. In the second the heavy use of i.e. takes a little out of the style.
3 a) +1 clarity, +2 style.
b) +1 clarity, +1 style.
c) +2 clarity, +2 style.
I found the third argument more linear than the first two. It also is the more precise among the three and it spell out in words the definitions of each property used in the steps of the proof.
4 a) 0 clarity, 0 style.
b) +1 clarity, +1 style. [I believe that there is a typo on line 3, shouldn’t it be d(g(y’),z)?]
c) +2 clarity, +2 style.
I rather two and three than one, because of their symmetry. But the notation and repeated change of variables name makes 2 a little more cumbersome than number 3.
5 a) +2 clarity, +1 style.
b) +1 clarity, 0 style.
c) +1 clarity, -1 style.
Number one is the quicker and clearer argument. I think that the third though very much explained ends up having too many words. Two actually is very similar to one, however strangely less appealing.
Remark, I guess my grades were very relative – I always started trying to have a +2 for the best among the three and going down from there. So I don’t know how they may compare in absolute to the others.
March 28, 2013 at 6:16 am
Sorry I forgot to state my mathematical experience, I am a Phd student in Math.
March 28, 2013 at 5:22 pm
(Rating for clarity, I am basing my answers on how I (being a lecturer) find the write-ups, not how I think it might be clear to a student learning the material for the first time).
1(a) Clarity 2 Style 2
1(b) Clarity 2 Style 1
1(c) Clarity 1 Style 1
2(a) Clarty 1 Style 0
2(b) Clarity 2 Style 2
2(c) Clarity 2 Style 2
3(a) Clarity 2 Style 1
3(b) Clarity 2 Style 0
3(c) Clarity 2 Style 1
4(a) Clarity -1 Style 0
4(b) Clarity -1 Style -1
4(c) Clarity 1 Style 1
(Maybe I was getting tired reading. Could be that you were getting tired writing?)
5(a) Clarity 2 Style 1
5(b) Clarity 2 Style 2
5(c) Clarity 0 Style 0
March 28, 2013 at 7:38 pm
I’ve got a diploma in math, and that included lectures on topology and metric spaces.
1a: Clarity=1, Style=1. Too wordy for my taste. For example, I’d prefer “A \subseteq B” to “A is contained in B”, especially for such simple relations as \subseteq.
1b: Clarity=0, Style=-1. Although the meaning is clear, X hasn’t been defined before it was used. So I spent some seconds searching for its definition. The -1 for style is due to using r, r’ and R: In my opinion, variable names of variables that are “symmetric” in meaning should convey that symmetry. For example, in 1a you used a and b for the radii, which I prefer since a) it directly reminds you that a is the radius in A and b is the radius in B, and b) ‘a’ and ‘b’ are similar but different letters. In contrast, r and r’ don’t show the relation to A and B and they don’t feel as symmetric. To me r’ is some special version of r, and not something that is conceptually equal to r. Also using lower case for r and r’ and upper case for R is not my taste. I prefer using the same “type” of letters for the same objects, e.g. lower case greek letters for reals, lower case latin letters for integers, upper case latin letters for sets, etc. Also, describing at the end of the proof what we want to prove simply doesn’t help. Put the explanation at the top (like in 1a) or leave it out.
1c: Clarity=0, Style=1. I think the B_x(a) notation is easier to understand then the d(x, u) < a.
2a: Clarity=0, Style=2. I like the writing, but would again prefer the ball notation.
2b: Clarity=1, Style=2.
2c: Clarity=2, Style=-1. The writing feels bumpy, especially at the beginning (e.g. sentences 1 and 2 feel totally unconnected). Easy to understand, though.
3a: Clarity=2, Style=1. Short and precise. The last two sentences should be formulated as a motivation at the beginning instead.
3b: Clarity=2, Style=0. Sounds like the proof of someone who's just picked up the subject. E.g. it's important that (a_n) converges in X.
3c: Clarity=2, Style=2. I like this one best for 3. Intention is stated at the beginning, reasoning is clear and well written.
4a: Clarity=2, Style=1.
4b: Clarity=1, Style=-1. Same issues with variable names as 1b.
4c: Clarity=2, Style=2. This is like 4a, just written a bit better. It has more flow and manages to avoid long formulas.
5a: Clarity=2, Style=2. Short and precise.
5b: Clarity=1, Style=1. The reasoning is less fluid than in 5a.
5c: Clarity=2, Style=0. Too wordy for my taste.
I would prefer to prove those problems that only require a topological space without any references to metrics. I think the proofs are more elegant without all those epsilons 🙂
March 28, 2013 at 11:57 pm
I am acquainted with metric spaces. I think I tend to find it easier to follow those proofs that correspond closer to the picture I would scrawl on the back of an envelope when visualising the question and seeking a proof. This exercise suggests to me, additionally, that on the whole I prefer clear English to symbols when these are reasonable alternatives.
1(a) 2; 2; (b) 0; -1; (c) -1; -2
2(a) -1; -1; (b) -1; -1; (c) 2; 2
3(a) 1; 0; (b) 0; 0; (c) 2; 2
4(a) 1; 0; (b) 2; 2; (c) 1; 0
5(a) 2; 2; (b) 2; 1; (c) 1; -1
(Incidentally, your clarity/style distinction raises interesting questions. I had drafted some thoughts on that, but you did not invite them.)
March 29, 2013 at 12:08 pm
My Experience – I’m a physiscist, although not working as scientist any more. But I still try to learn new stuff every now and then, things I never had the opportunity to learn at university. This includes some pure math as well as physics
Writeup Clarity Style
1a 2 1
1b 1 1
1c -2 -1
2a 0 -2
2b 2 1
2c 1 2
3a 0 -1
3b 1 1
3c 2 1
4a 2 2
4b -2 -2
4c 1 0
5a 2 2
5b 0 -1
5c 1 0
Some additional remarks
(1) In a certain sense, none of the proofs was really readable. In fact I found reading them remarkably difficult with regard to the (simple) content. [i.e. my rating for clarity is not absolut but only relative]
I think the reasons are
– to much math within the text, i. e. no strucuture that supports/guides the reader when he is following the argument. Such structure needs space but paper is cheap. Publishers may not like that but what do they gain if no one is buying their stuff because it is unintelligible?
– to much text: symbolic notation like => (used in 4a) makes reading often much easier (if not used too often …).
– in some cases bunches of different (or better: superfluous) objects (epsilon, delta, theta, eta in 1c, 2a and 4c) makes it difficult to follow the argument. What is going on, what does this object stand for etc. – all becomes suddenly confusing.
(2) I think the general style of writing should always depend very much on the audience. If the proofs are part of a monograph for experts it might be fine to keep them short without to many frills. If it’s written for “students” ( on whatever level) i think it’s very different. My minimum requirement for a readable proof is always an introductuory paragraph like in (1a) or (4a) which explains what the proof attempts to do. This is one of the resons why my rating for them is high.
On some reason this is rarely the case in many textbooks. Even worse, such explanation are mostly given in trivial cases only. If the proof is difficult and the argument is more involved, this lenghty beast is usually shortened. And this almost always starts with removing everything that serves the understanding of the reader. No explanation (why, how, what’s the next step), many implicit assumption etc. (see e.g. the proof of the Zassenhaus Lemma in Lang’s Algebra)?
(3) I absolutly hate “slick” proofs. They hide everything (motivation, idea, etc.), explain nothing and leave the reader completly baffled. Most of the time they are pure magic and they give no clue at all why the theorem is true. My personal favourite is the proof of the implicit function theorem with the contraction lemma – it works but it gives no hint at all why. All geometric intuition is thrown out of the window.
As I see it – the only purpose of a slick proof in a textbook is to show off. Alternative views might give new insights, but only if you an expert (i.e. it’s ok for mongraphs). Everybody else, in particular someone who is trying to learn something new fights most of the time with understanding (content, derivation,proof). He has better things to do than to admire a pompous author.
Happily none of your writeups belonged to this class – I would have rated it as -3/-3.
March 30, 2013 at 11:42 am
Experience: Maths bachelors degree (including metric spaces) 15 years ago
Ratings given as [clarity, style]
I don’t know if it makes a difference but problems 1, 3 and 4 were obvious to me (and the proofs went along the lines that I expected), whereas 2 and 5 were non-obvious.
1a: [2,2]
1b: [1, -1] choice of terminology was poor – why r prime?
1c: [0, 0] rather than leveraging the concept of an open ball this one was more from first principles, but this meant too many etas, thetas, deltas and nus were going on which I was struggling to hold in my head
2a: [0, 0] introduced theta for no good reason I could see.
2b: [0, 1] flipped between using open balls and a more direct definition of openness – epsilon got too much prominence in the proof, slightly clouding things for me. The “i.e.” section added nothing and only served to distract me slightly.
2c: [1, 1]
3a: [2, 2] didn’t like the “suppose” when what you’re doing is giving something a name, I would have used “call”
3b: [2, 1] again, the “that is” section seemed unecessary and just served to make me check whether I agreed with the “that is” rather than moving on with the proof. I would delete the words “we have than a_n converges”. Also, by this point I’m started to get irrationally irritated by “we are done” at the end of proofs.
3c: [2, 2]
4a: [2, 2]
4b: [-1, -2] the choice of names for things is all over the place. Why let y = f(x) – why not just use f(x) throughout? The substitution introduces an extra name to keep in my mind for only the tiniest increase in brevity of some of the expressions. Givening things names is only useful when the name is significant shorter than the thing it refers to, or some kind of summary of a number of steps.
4c: [2, 2] theta is mildly superfluous.
5a: [1, 2] I can see all of the steps work, but this doesn;t feel obvious from this proof.
5b: [2, 2] somehow this one makes me feel the results is right. Maybe it’s just that now I have two proofs? Or maybe it’s the use of a and b rather than y and z has let me keep track of things in my head more easily.
5c: [0, 0] OK, so now I’m pretty sure it the choice of terminology/labels that makes the difference, because this one is very confusing for me trying to keep track of which elements are in which sets.
March 31, 2013 at 11:14 pm
My background is computer science and physics. My experience with metric spaces is limited to self study from Rudin.
All of the proofs were straight forward but I found the wording of some distracting from the core idea.
Problem 3 was the most confusing because I wasn’t that familiar with the definition of a complete metric space and the fact that a closed set contains all its limit points.
1. 2, -1, -2
2. -2, 2, 2
3. -2, -2, 2
4. -2, 2, -1
5. 2, 2, -1
March 31, 2013 at 11:38 pm
Graduate student in mathematics.
Prob1
1(b) and 1(c) look lengthy and wordy. Besides, the “open ball” language is easier to read than the argument.
argument.
Rating Clarity Style
1(a) 2 2
1(b) 1 1
1(c) 0 0
Prob2
The “open ball” language in 2(b) and 2(c) is much more straightforward. For the sake of proving “open set”, one does finally need “open balls”. I need to “translate”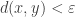 as
as  for understanding the proof.
for understanding the proof.
2(a) 1 1
2(b) 2 2
2(c) 2 2
Prob3
The third one is more of "algorithm" style. The second one is wordy.
3(a) 1 1
3(b) 0 0
3(c) 2 2
Prob4
4(a) and 4(b) are ugly long and hard to read. Every step in 4(c) is straigtforward and immediately from the definition.
4(a) -1 -2
4(b) -1 -2
4(c) 2 2
Prob5
5(c) is wordy. 5(a) is straightforward to read.
5(a) 2 2
5(b) 1 1
5(c) 0 0
April 1, 2013 at 4:46 pm
Experience level : PhD student. I studied the theory (and more than once).
Thank you so much for thinking about these issues seriously.
1a. Clarity 1, style -1.
Notation is screwed up (confusion between radius and centre of the ball), and the radiuses are written a and b, a notation which suggests elements of the sets A and B, which only adds to the confusion.
1b. Clarity 2, style 2
(what we are doing could perhaps be stated at the start and not at the end ? I don’t know. In any case it’s a clean proof.).
1c. Clarity 0, style -2
Too many useless notations : clutters working memory. Unnecessarily complex.
2a. Clarity -1, style -2.
Inverse images tend to be confusing : one should be very consistent with the notations (using x, x’,… for elements of X and y, y’,… for elements of Y) and here they are very bad. using y for an element of X should be forbidden and using u is not very helpful.
2b. Clarity 0, style -1.
Confusion between centre and radius again, but here could easily pass unnoticed (no confusing notation). However one should use ball notation everywhere and not just occasionally : the constant switch between balls and inequalities is painful.
2c. Clarity 2, style 2.
Here I am not disturbed by the final recapitulation. I think stating the goal at the start is not important here (as opposed to 1b) as the proposition is less elementary (students would be more familiar with openness), but a final recapitulation is clean and helpful.
3a. Clarity 2, style 2.
(But the sentence « suppose lim x_n = x » is superfluous : one could write « .. has a limit x in X » in the previous sentence.)
3b. Clarity 0, style -2.
Writing a_n and a kind of presupposes that both sequence and limit are in A : confusing. In this context defining the limit as a wthout stating which set it a priori belongs to is downright perverse. (I dislike sentences like « Since P, P’ and P”, we have Q » : in a quick reading I tend to see P’ as a consequence and need to start again).
3c. Clarity 1, style -1.
Again, writing a_n and a kind of presupposes that both sequence and limit are in A : confusing. But less serious since a is defined as merely being in X and the argument is clearer. The expressions « tends to a limit in A » and especially « càontains all its limit points » are sloppy.
4a. Clarity 1, style -1.
4b. Clarity 1, style -1.
There is a typo f(y’) instead of f(y). The use of the notation y in the first step is helpful, but the use of the notation z not that much and only hides the typo ; and the notation y is unnecessary in the second step.
4c. Clarity 2, style 2.
The use of y for an element of X does not disturb me here although I would probably have written x’. The proof is straightforward and keeps notations at a minimum.
5a. Clarity 1, style -1.
The use of x, y and z causes cognitive dissonance.
5b. Clarity 2, style 2.
5c. Clarity 1, style -2.
Cognitive dissonance and too many notations. The insistence on the meaning of intersection is superfluous : it breaks the flow of the argument. Plus, I dislike sentences like « Since P, P’ and P”, we have Q », cf 3b.
April 2, 2013 at 2:26 am
Interesting experiment! I’d like to try. Experience: second year PhD student but algebraist ;), knows metric spaces well.
Problem 1.
a) Clarity: 1
Style: 1
b) Clarity: 0
Style: -1
c)Clarity: -2
Style: -2
Comments: The first proof is the easiest to read by far. The notation a,b for A and B resp. is good. Introducing the definitions as in 1(b) is awkward and cumbersome. The writing style of 1(c) is strange (“therefore” in the second sentence is unclear). The last one is reminiscent of students struggling with the definitions.
Problem 2.
a) Clarity: -1
Style: -1
b) Clarity: 1
Style: 1
c)Clarity: 1
Style: 1
Comments: 2(b) is good in that it states what we are trying to prove in the notation _to be used_! This is always helpful. 1(a) is a mess, but I feel that the lack of line breaks is not helping
Problem 3.
a) Clarity: 2
Style: 1
b) Clarity: 0
Style: 1
c)Clarity: 2
Style: 2
Comments: 3(a) and 3(c) are good. I prefer (c) in that the letter _a_ is used but I prefer (a) in that the limit notation is clearer!
Problem 4.
a) Clarity: 0
Style: -2
b) Clarity: 1
Style: 1
c)Clarity: 2
Style: 2
Comments: The first one contains the implication symbol, which is too many symbols and overall I had a hard time reading it. (b) Is better but too many primes. The third is the best as it uses the fewest symbols and variables. One of the worst types of mistakes in mathematical writing is to introduce new symbols when it is unnecessary.
Problem 5.
a) Clarity: 2
Style: 2
b) Clarity: 0
Style: 1
c)Clarity: -1
Style: -2
Comments: The first is the best as it has the fewest words. The second takes too long to state f(a) = f(b). 5(c) is the worst as it doesn’t put the f(y) = f(z)! Also it states the definition of intersection which is too verbose.
April 2, 2013 at 11:37 am
I’ve taken a basic analysis course (first 4-5 chapters of Rudin) so have seen all these theorems before. That said, a number of them required a minute’s thought before the proof-idea resurfaced in my mind.
1(a)
Clarity – 2
Style – 2
Comment – this is how I think of the proof upon seeing the question and pondering it for a second or two. Provided you’ve previously defined an open ball, this is great.
1(b)
Clarity – 1
Style – 1
Having extra definitions within proofs almost tautologically makes things more difficult to understand.
1(c)
Clarity – 0
Style – 1
This feels like reading C code as opposed to Python code 🙂 All those d’s and eta’s for me make it much harder to get a feel for the idea behind proof.
2(a)
Clarity – 0
Style – 1
I would make very similar comments to 1(c). Because I couldn’t quite remember how the proof went, I skipped this after a few seconds and read the ones below 🙂
2(b)
Clarity – 1
Style – 2
Still too much LaTeX 🙂 But this is definitely a lot easier than 2(a), especially given the first two sentences.
2(c)
Clarity -2
Style -2
This is the proof I went to to jog my memory, and it was very clear. The visual image stirred up by the use of open balls is to me very compelling.
3(a)
Clarity – 2
Style -2
Again, I had to stop and find the argument for myself, which probably took 20 seconds. I then read this and it felt like I was reading my own thoughts. Very clear.
3(b)
Clarity – 1
Style -1
I felt this needlessly repeated itself. Also, you said (a_n) converges without saying that it must converge somewhere in X as you did in (a). This small statement, putting bounds on where this mysterious point of convergence could be, adds a huge amount of concreteness. After all, that’s all we care about – where the point of convergence is.
3(c)
Clarity – 1
Style -1
Rudin has a lot of these A implies B, B implies C, C implies D, etc. proofs, and personally I feel it takes away the clarity. Here we have 3 sentences which all begin with the word ‘Since’ and two with the word ‘So’, which for me horribly disrupts the flow and overall picture of the argument.
4(a)
Clarity – 2
Style – 2
Very easily jogged my memory. The first paragraph is excellent.
4(b)
Clarity – 1
Style – 2
I didn’t mind this proof, it is clear enough. Making the substitution for z and y brings some concreteness.
4(c)
Clarity –0
Style – 1
My least favourite 🙂 Why do you need to bring in \theta ?
Meta-comment: where are the open balls in Q4? 😀
5(a)
Clarity – 2
Style – 2
It took me a minute to figure why we needed injectivity. This proof highlights this straight away and gets straight to the point.
5(b)
Clarity – 1
Style – 1
Not too bad, but similar problems to 3(c): while 5(a) has only 3 occurrences of ‘so’, this proof has 4, plus one ‘since’ and one ‘then’ :D.
5(c)
Clarity – 0
Style – 1
I said for 4(b) I liked the definition of z and y. Perhaps this is because they’re the 2 points crucial to the proof and are worth focusing the mind’s eye on. Here though, defining y and z is not necessary and just puts extra strain on the memory.
Overall Comments: I think it’s fair to say I enjoyed the proofs which:
Appealed to geometrical or ‘higher-order’ ideas. I again make the link to computer programming: while C is closer to the ‘machinations’ of the hardware, higher-order constructs like classes in Python make everything so much simpler to quickly understand 🙂
Length: In almost every case, the shortest proof with the least LaTeX was my favourite.
April 15, 2013 at 10:30 am
[…] March 25th, this is exactly the question that Fields medalist Timothy Gowers asked his blog readers about this and four other theorems. The comments flooded with ratings and discussions of the […]
May 3, 2013 at 7:55 pm
[…] 1 An experiment concerning mathematical writing | Gowers’s Weblog […]
October 10, 2013 at 9:40 pm
[…] readership to guess which was which. (The undergrad was commonly confused with the computer!) Click here for the original experiment and here for the results. Overall, this Turing-type test shows that the […]
April 30, 2014 at 7:50 am
[…] https://gowers.wordpress.com/2013/03/25/an-experiment-concerning-mathematical-writing/ […]
October 24, 2015 at 6:47 pm
[…] proof program for generating proofs of certain kinds of theorems. Yours truly submitted one comment for that […]