I had a mathematical conversation yesterday with a 17-year-old boy who is in his second year of doing maths A-level. Although a sample of size 1 should be treated with caution, I’m pretty sure that the boy in question, who is very intelligent and is expected to get at least an A grade, has been taught as well as the vast majority of A-level mathematicians. If this is right, then what I discovered from talking to him was quite worrying.
The purpose of the conversation was to help him catch up with some work that he had missed through illness. The particular topics he wanted me to cover were integrating , or
as he called it, and integration by parts. (Actually, after I had explained integration by parts to him, he told me that that hadn’t been what he had meant, but I don’t think any harm was done.) But as we were starting, he asked me why the derivative of
was
, and what was special about
.
That seemed like a good preliminary conversation to have, so I said, “OK, let’s try to differentiate from first principles and see what happens.” He didn’t know what I meant by “from first principles” so I tried to give him a nudge, by saying, “If you didn’t know the derivative of
, then how would you go about working it out?”
At this point, he suggested . To be fair to him, he wasn’t saying that he knew that this was correct. Nevertheless, this was an interesting piece of cognitive dissonance, given that we were trying to understand why the derivative of
was
. But what bothered me more than the fact that he said it was the fact that he couldn’t see why it wasn’t right. And what bothered me perhaps even more than that was the fact that he should think of “from first principles” as mechanically applying the
rule.
In an effort to get past that, I asked, “Yes, but what does the derivative actually mean?” He had no answer. So I drew a graph of an arbitraryish function, labelled it , drew a point on the curve, and asked him what the derivative meant. I think he did then say that it was the gradient of the curve at that point. (I don’t think he used the word “tangent”.) I asked how we could go about working that out. He suggested
. I said, “So to work out the derivative you just divide by
— is that it?” He laughed and said no.
It was time to go back to basics, so I asked him how you work out the gradient of a straight line. He said, “Rise over run”, terminology that I either never knew or had completely forgotten — but the meaning was obvious. I then asked what the difficulty was when the line wasn’t straight, to which he replied that the gradient was changing all the time. So what could we do about that? He suggested taking a point not too far away and working out the slope of the line joining that to the point in question.
Now we were getting somewhere. I had already drawn a line segment going up from a point on the x-axis marked until it hit the curve. I did the same for a line segment going up from a point marked
and asked what the rise and run were. He correctly got the answers
and
. I then said that as
got smaller and smaller, the curve got more and more straight, so
was a formula for the derivative .
“Have you really never seen that before?” I asked. He denied it, but when I pressed him, he eventually conceded that he probably had seen it, but that if so, then it would have been clearly flagged up as something that he didn’t need to know, because there wouldn’t be questions about it on the exam.
It’s that that bothered me enough to make me need to get it off my chest in the form of a blog post. It hardly needs spelling out what was wrong with the argument that his teacher gave (if his teacher did in fact give that argument — I cannot be certain about this, though the mere fact that that was the message that got across is bad enough) but I’m going to anyway. Let’s suppose that your aim is simply to do well at maths A-level and that there are no questions that test your familiarity with the formula for the derivative of an arbitrary (nice) function at an arbitrary point. Which is better?
1. Don’t make any effort to learn and understand the formula, but simply learn a few basic examples of derivatives (polynomials, exponentials, logs, trig functions) and rules for differentiating combinations (linearity, product rule, quotient rule, chain rule) and you should be able to differentiate anything that comes up in the exams.
2. Learn what the derivative means, derive the formula for the derivative of an arbitrary function at an arbitrary point, calculate a few derivatives from first principles, derive the product rule, quotient rule and chain rule, and then learn how to use them to differentiate combinations.
The answer is that if you are capable of doing 2, then 2 is far better. And the boy I was talking to was certainly capable of doing 2. Why is it better? Because (and this is something I plan to devote a blog post to at some point) memory works far better when you learn networks of facts rather than facts in isolation. If you don’t really understand what differentiation is all about, then the fact that the derivative of is
is a completely different fact from the fact that the derivative of
is
. But if you’ve derived them both from first principles (I’ll come back to what I said about
in a moment), then they are related: we have a process we do to the functions
and
and this is what comes out. Of course, another reason is that if you forget something, you have a chance of rederiving it, but that’s a slightly different point. Your knowledge of a piece of maths is far more grounded if you know how it is derived, or at least have some memory of the derivation, even if you have no problem remembering the fact in question. Even if you forget the details of the derivations, just having seen them has a major effect on binding together the facts you know.
After I had explained differentiation in the abstract, I suggested that we should try differentiating from first principles. Or as I put it, “Let’s apply this formula in the case
. What do we get then?” To my further dismay, he didn’t immediately know what to do. “If
, then what is
?” I asked. I can’t remember what his response was, but it wasn’t
. He floundered and made wild guesses, not really understanding what I was asking. Again, something quite serious seemed not to have been done by his school, though I couldn’t give a precise diagnosis in this case — something along the lines of understanding the notion of a function well enough to talk about an abstract function
and see that it could have many instantiations.
Anyhow, once that point was cleared up (not necessarily for good, but for then anyway) we got through the differentiation of without further trouble. Again he denied having seen that derivation — maybe it was at that point that he said the thing about not needing to know it for the exam.
The general point here is of course that A-levels have got easier and schools have a natural tendency to teach to the test. If just one of those were true, it would be far less of a problem. I would have nothing against an easy A-level if people who were clever enough were given a much deeper understanding than the exam strictly required (though as I’ve argued above, for many people teaching to the test is misguided even on its own terms, since they will do a lot better on the exam if they have not been confined to what’s on the test), and I would not be too against teaching to the test if the test was hard enough.
How about differentiating ? Well, after a couple of false starts we got to the expression
I asked what could be done with . Quite a bit of prompting was needed to get him to say
. Then I asked what could be done with
. A lot of prompting was needed to get the answer to that question. (I had to ask what he would do with
.) Anyhow, we eventually got to
I decided just to point out that the last limit was the derivative of at 0. I also pointed out that the entire argument so far worked just as well for the function
, whatever the (positive) value of
. I then drew some pictures for different
, pointing out that some of them crossed the y-axis with a slope less than 1 and others with a slope greater than 1 and that
was the one where it actually equalled 1. He asked me why the slope was exactly 1 for
, which was a good opportunity for me to try to explain that that was getting things the wrong way round, and that
was chosen precisely to make that work. (Of course, the question would make very good sense the way he asked it if we had already defined
in some other way, but I’m not sure he had. Certainly, I remember this as the definition of
when I was at school, and I remember feeling slightly uncomfortable about it.)
There was plenty more of our conversation, though not much more to say about it. I accidentally fell into a derivation of the product rule, which again I think he had not seen. That was part of my preparation for deriving the formula for integration by parts. When I had done that, I went through an example or two. One of the examples I tried was from
to
. (He thought
was
, by the way, but was OK when we did it in degrees.) We got the answer
. I then felt annoyed not to be able to see why the answer had to be 1. I still haven’t got round to thinking about that.
I also discussed integrating by the method I call guess-and-adjust. You guess
because one part of what the product rule gives you is correct and you might be able to deal with the other part. Differentiating you get
. “What can we do to get rid of that 1?” He suggested
. We tried that, saw why it didn’t work, and then got to the right answer.
He managed to integrate between
and
with no help at all, so I think he got the basic idea, though whether he’ll hold on to it I don’t know.
Another thing I discovered was that he was very shaky on the chain rule. When I asked him what the chain rule said, he didn’t know what I was talking about. Eventually I got a glimmer of recognition out of him by writing down . But the idea that if you want to differentiate
you first pretend that
is a single variable with respect to which you are differentiating and then correct what you’ve just done by multiplying by the derivative of
was completely foreign to him. We looked at a few examples but they’ll need reinforcing at some point. It was yet another illustration of the general principle that if you forget about understanding what’s going on and concentrate on mechanical manipulations, you’ll forget how to do even the mechanical manipulations.
November 20, 2012 at 1:21 pm |
It seems that the American education approach is spreading overseas.
November 20, 2012 at 4:16 pm
If you’re talking about the topic of derivatives specfically, I have never seen a high school calculus class that doesn’t start as outlined in #2. Also (riffing on Cliff’s comment below) there is a special emphasis on function notation and I can’t imagine a US book leaving it out. The new Common Core (adopted by most of the US) has an entire section devoted to functions.
If you’re talking about a tendency in general to have formulas-without-justification, sure, although again I’d have to add qualifications depending on what specific topic you mean. While education is not a zero-sum game, as more things get jammed into the curriculum there’s things that will get left out.
Also, current US
trends are in reverse: one of the goals of Common Core is to have a “no mysteries” approach where everything is justified. It may even be overkill the other way (ex.: HSG-C.A.1 Prove that all circles are similar.)
November 20, 2012 at 1:49 pm |
I had a very similar conversation with a first year mechanical engineering student some years ago, when I was tutoring 1st year mathematics.
The student always got an answer of 1 for the fundamental limit theorem, because a) he claimed not to have seen it, b) did not understand functional notation, i.e. (f(x+h) – f(x))/h = h/h = 1
I refused to believe him, and checked with a friend who taught A level mathematics. She explained that it is no longer required to teach the fundamental limit theorem, or functional notation, and that many teachers (as they don’t understand it) chicken out and teach differentiation as a look-up table.
November 20, 2012 at 3:14 pm |
[…] Growsing justly about bad maths pedagogy. […]
November 20, 2012 at 3:14 pm |
[…] Growsing justly about bad maths pedagogy. […]
November 20, 2012 at 4:01 pm |
I think that the weakest link in calculus education is the concept of a function; it is incredibly fundamental to the subject, but looks so innocuous (especially to someone with enough mathematical training to understand it) that it is easy to gloss over it in favour of what looks to be more “substantial” (and also “testable”) components of calculus, such as integration by parts or the chain rule (and also, there can be the unsupported assumption that because students would “already have seen” the concept of a function in high school algebra, there’s no need to review it thoroughly).
(In general, I think fundamentals are too often given short shrift in order to advance prematurely to applications of said fundamentals. When I teach undergraduate real analysis, for instance, I like to spend a fair amount of time on construction of number systems, before getting to the limits and the deltas and epsilons. Unfortunately, the most basic topics are often the hardest to teach correctly…
November 20, 2012 at 4:24 pm
In the UK we tend to distinguish calculus from analysis fairly sharply, probably because we have the academic tradition of distinguishing pure and applied mathematics and treating them equally. I think there are two approaches to calculus (as opposed to analysis) which are both reasonable. One is to be careful about definitions of functions, and differentiability etc, along the lines of doing introductory analysis. Another is to consider variables x, y, z etc as denoting physical quantities and asking how they vary with respect to each other in a given situation. Then you get notions like dy/dx rather than f'(x) as primitive. While pure mathematicians tend to want to emphasize the functions method, wasn’t it only invented in the 19th century, and prior to that mathematicians had been perfectly capable of doing calculus the way physicists do it now?
One can be fairly rigorous with the dy/dx syntactic manipulation approach, as a set of formal rules (essentially differential algebra) augmented by some physical explanations of what the rules mean. Of course one cannot be completely rigorous without explaining the real numbers, but we are talking about school level calculus here, not analysis. I am not arguing that this is the best method for teaching calculus in schools, but I don’t see that it is without merit.
Currently I am teaching analysis to first-year undergraduates and yes, I started with the axioms of real numbers before moving on to sequences, series, and then eventually we will get to functions, differentiability and so on. It would not be at all feasible to teach the students this way if they were not also being taught calculus at the same time, in a much less rigorous fashion.
November 20, 2012 at 4:26 pm
I’d argue the derivative definition in particular is a rather new use of functions compared to past courses. While students have have seen the input being modified, it was in context of transformations in a way where the generality could be ignored. (Clarification: I mean while students have seen f(x-h) as “a horizontal transformation by h” they only need to use h as a placeholder and not as a general variable in any further algebraic manipulations as occurs in calculus.) Some books try to remedy this by introducing the derivative formula specifically as an exercise, but given how disconnected it is from the rest of the material I suspect only .01% of students recall seeing it once they get to calculus.
The upshot is while student might be familiar with functions but unfamiliar enough with how they are being used they are essentially a new topic when using them for the derivative. I certainly try to steer things with a nod to future calculus classes when I teach the topic, but the topic just doesn’t have enough interconnectivity at the pre-calc level to give it solid footing.
November 23, 2012 at 3:45 pm
Just last week a student asked me why when given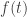 and asked to find the derivative via
and asked to find the derivative via  , “we are allowed to set
, “we are allowed to set 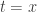 and
and  at the same time”. It appears that someone drilled into him the convention that a function must be followed by its argument and the only way to interpret
at the same time”. It appears that someone drilled into him the convention that a function must be followed by its argument and the only way to interpret 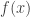 is “substitute
is “substitute 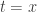 into
into 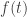 , which was how the function was originally defined”. I was unfortunately unsuccessful in disabusing him of that notion. (Explaining arithmetic in Swiss-French is not my strong suit.)
, which was how the function was originally defined”. I was unfortunately unsuccessful in disabusing him of that notion. (Explaining arithmetic in Swiss-French is not my strong suit.)
December 19, 2012 at 11:17 am
Dear Prof.Tao,
I have to say that the construction of the real number system is the hardest part of your book “Analysis” .It took me a semester’s time to mastered it well.By the way,I teach it myself using your book,maybe some tutorials may help me to understand,i,e,the comments in your blog post http://terrytao.wordpress.com/books/analysis-i/ .The hardest part of the construction of the real number system is to understand the principle of the construction,not those details.
February 7, 2014 at 3:26 pm
I think it would be interesting to try developing an understanding of derivatives and functions from more tangible experiences first, and then moving into the abstract symbols.
For example, have students measure their displacement and their velocity for a variety of fairly simple motions, and then look for comparisons and patterns between the two sets of data (perhaps by graphing them), and then use these observations to build a inductive understanding of the relationship between distance functions and velocity functions, and then extend this understanding to a variety of different functions AND then talk about secant lines, etc…
Even if you skip the notation, the idea of the secant line converging to a tangent line is completely accessible to students, especially if you use numerical examples.
As for students who do not understand graphs at all, I developed this tool to help jump start classroom discussions: http://davidwees.com/graphgame/
November 20, 2012 at 4:07 pm |
I’m a current A Level Maths student, and I can relate to everything in this blog post. It irritates me that we rarely derive stuff (I’ve looked up derivations myself…). I would add that it is better in Further Maths lessons, I guess because we’re an interested audience. I’m a subscriber to your “networks of facts” learning method, whilst my friends are “just learn for the exam”-ites, and I’m forever helping them with things that I remember through originally deriving them (And I get far better grades…).
Also, if you want reassurance on the standards of mathematics in 17/18 year-olds, I’d suggest looking up the Sixth Term Examination Paper (STEP). It is an exam (that I’ll be taking in 7 months time) that top universities for Mathematics (like Cambridge and Warwick) use to sift out better candidates, and they test proper mathematical reasoning and not just the monkey-with-a-pencil application of formulae.
November 20, 2012 at 4:42 pm |
A future net archeologist will deduce, by looking at this post, that the A-level was the worst in education circa year 2000. Correlated with abundant evidence that successful people (like entrepreneurs, politicians or media stars) had mainly B or C grades in school, the archeologist will advance the hypothesis that a good education was essential for public success at the beginning of the third millenium.
November 20, 2012 at 4:52 pm |
I was taking maths A level about five years ago, and everything in this article was certainly true then. If you look at the official Edexcel textbooks from that period – and most likely modern ones too – you will be absolutely horrified.
Many things are left completely unproved. Often things too advanced for the course are quietly shoved under the carpet rather than explicitly glossed over. For example, after finding the usual solutions to a second order linear ODE, there is no suggestion at all that proving no other solutions exist is even necessary. Or that a rigorous definition of a limit is necessary. There are also no questions in the textbooks that require anything beyond a straightforward application of the material.
Some areas of the course are, as far as I can tell, completely useless – I’ve never seen a mathematician use intrinsic coordinates. (They used to be used in a proof in M6, then M6 was axed and no-one bothered removing them.) Other areas of the course are ruined in the teaching. For example, FP3 had a lengthy unit on matrices covering eigenvalues and eigenvectors. No matrices of size larger than 3×3 were covered, almost every result stated was either left unproved or proved algebraically only in the 2×2 and 3×3 cases, the relation between matrices and linear maps was left as a sidenote rather than the point of the entire business, and there were no questions in the entire book applying linear algebra to other areas of mathematics. Not even a relation to solving simultaneous equations. So students were being asked to calculate the eigenvalues of a matrix with no reason whatsoever to believe that eigenvalues were useful or important in or outside of mathematics.
And don’t even get me started on D1 and D2, which consist of *literally* stepping through algorithms on the examination. As in, the question will ask you to carry out quicksort on a given list. No questions about time and space requirements beyond a vague knowledge that bubble sort is worse than quicksort, no questions about proving correctness, no thought whatsoever. Sometimes proofs of correctness are given in the textbook, sometimes they aren’t.
The only reason A level gave me any mathematical abilities worth mentioning was that I got sufficiently angry with the poor quality of the taught material that I started reading university-level stuff on my own. And that was only possible because I was lucky enough to go to a school which had university-level stuff in the library – many potential mathematicians aren’t so lucky, and textbooks are expensive.
November 20, 2012 at 4:54 pm |
I’m pretty sure that when I did A-level (the first iteration of Curriculum 2000) we had to do first principles differentiation.
I think the most important point is not just that omitting this makes it harder to remember “facts” about calculus, but that if you don’t get taught this, you get no conceptual understanding of calculus whatsoever. It’s no wonder kids ask why maths is relevant; if they understood what calculus actually was it wouldn’t be too great a leap to see how it was important for, say, clever things in science.
November 20, 2012 at 5:29 pm |
There are obviously big problems with A-level maths but I’m sure that all the things Prof. Gowers has mentioned are in fact in the A-level somewhere (apart from the e^h-1/h limit which, if I remember correctly, is just claimed to be 1). The student must have either not been paying attention, have forgotten or have a really bad teacher. I think the difficulty of the exams themselves is a bigger issue (Just look at a STEP paper to see what they could be like).
If you think this is bad, imagine being a Physics teacher and not being allowed to use calculus at all!
November 20, 2012 at 5:55 pm
I’d be amazed if they weren’t in the syllabus. The problem is that the exams make it possible to teach differentiation as a meaningless algebraic operation, or (what I think actually happened) to discuss the derivations briefly but put far greater emphasis on the algebraic side, to the point where you actually tell people that it doesn’t matter if they don’t understand the derivations. And that is a temptation that many teachers find hard to resist: it offers less to their pupils, but it feels safer. So the fault lies with the assessment, and the effect that the assessment has on teaching.
Related to this is something I’ve noticed with plenty of students: they find it very hard to understand how the fundamental theorem of calculus could be a theorem. For them, integration is just reversing the algebraic process of differentiation and adding an arbitrary constant, so saying that differentiating and integrating gets you back to the function you started with (up to a constant) is tautologous.
November 20, 2012 at 6:49 pm
My colleagues teaching calculus define an indefinite integral to be an antiderivative (and some of them may have learned it that way in Cambridge). Then they define definite integrals in terms of indefinite ones, and then they show that definite integrals of positive functions are the same as the area under the graph. I am sure this is also the way I was taught at school, about 18 years ago. I don’t see anything fundamentally wrong with doing things that way. You don’t get the most general notion of integral, but then you don’t with Riemann’s definition either. What you get is good enough for most purposes. That said, I think giving different definitions of differentiation and integration and then proving the fundamental theorem of calculus is much more elegant.
November 23, 2012 at 3:54 pm
A short note on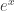 : in many a calculus textbooks (at least in the States)
: in many a calculus textbooks (at least in the States) 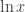 is defined to be the antiderivative of
is defined to be the antiderivative of  and
and 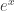 its inverse function. Of course, via the chain rule this implies that
its inverse function. Of course, via the chain rule this implies that 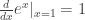 .
.
Then there are the textbooks that define the exponential function as the solution to the ODE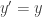 and the natural logarithm its inverse. As a result a student sitting two different courses of calculus sometimes end up writing some hilariously circular arguments.
and the natural logarithm its inverse. As a result a student sitting two different courses of calculus sometimes end up writing some hilariously circular arguments.
November 20, 2012 at 7:28 pm |
As a current school teacher (with a good Cambridge maths training and more), I am constantly torn between the needs of the examination and the need to teach mathematics. The current A-level (though it has essentially been this way for many years) is very much a course in “mathematics for science/engineering/…”; there is very little “Pure Mathematics” within it.
Part of my question is who we are teaching maths to: the vast majority of our students will not end up becoming mathematicians. It is sad that the time pressures of the curriculum (the AS course has to be completed in 2 terms) leaves precious little time with single maths groups to do much “real” mathematics. Also, the large heterogeneous groups now studying A-level tend to require significant time to even learn the mechanics of the techniques. I would *love* to be able to teach much more about the foundations of the subject, the purpose of the subject, problem-solving within mathematics and so on, but the time is too limited.
For the specific example of calculus, the definition of differentiation is fundamental to the subject, and I always introduce differentiation to my classes via the limiting concept. (My approach, though, is to draw graphs at different scales, so we talk about “zooming in” until the graph looks like a straight line; this also allows us to easily understand later on why $y=|x|$ has no derivative at the origin.) However, turning this into symbols becomes hard; the algebraic fluency of early year 12 students is frequently shaky, and they struggle with it. We do derive the derivative of $x^2$ from first principles, but then students panic and ask the inevitable question: “Will this be in the exam?” Well, of course you need to understand it to get anywhere in maths, but you’ll never be explicitly tested on it at A-level. I cannot derive the derivative of anything more complicated at this stage – we do observe the “$x^n$ differentiates to $x^{n-1}$ as a pattern, though. When I have the opportunity, I teach integration in the order: find the area under $y=x^2$ from $x=0$ to $x=a$ for different values of $a$, using the trapezium rule, until we observe a useful pattern. With a strong group (further mathematicians, usually), we then try to understand why this is the case, and deduce that the area under the curve (which I define to be integration) can be found by anti-differentiation, and hence one of the fundamental theorems of calculus falls out. Sadly, though, Edexcel decides to define integration as anti-differentiation in C1 and then as areas under curves in C2, culminating in the trapezium rule.
I have tried to derive the product rule for some groups, but with limited success: even some further maths groups are too weak to cope with the derivation. (And this is without touching the analysis required to prove it rigorously, just expanding $f(x+\delta x)g(x+\delta x)-f(x)g(x)$ and using linear approximations.) We learn $e^x$ “experimentally”, estimating the derivative of $y=a^x$ by eye, then getting Autograph to draw it, and then tweak the value of $a$ until the derivative is the same as the graph itself – that gives us our definition of $e$.
Someone commented above about how meaningless the syllabus is – indeed, I agree! I would love to see a huge chunk of calculus thrown out in favour of a small module on elementary number theory and (real) proof, or something similar, but that is unlikely to happen in my lifetime.
The gripes continue;
November 20, 2012 at 7:30 pm
sorry – got cut off at the end, there: just wanted to say that I would love to see some of the calculus replaced by, say, some elementary number theory (with real proofs!), but that is unlikely to happen any time soon!
November 20, 2012 at 10:31 pm |
Not sure if this is of any comfort, but if what you describe is typical of the UK, it’s a lot worse in other places. In Norway, where I currently find myself teaching a class of (very bright) 16-year olds, the notion of proof has been completely removed from the school curriculum, except for some side remarks in the textbooks. In fact, it is perfectly possible to go through all of school (up to age 19) with top grades in the most advanced mathematics courses, without ever writing down a single proof. Even the formula for solutions of a quadratic equation is normally presented without proof, and to attempt a proof of the chain rule in class is just unthinkable. I am told that they were doing epsilon-delta proofs in school 40 years ago, but back then, only the most talented students would sit in the advanced maths course.
As for making choices as a teacher, Julian describes precisely what the problem is – we are extremely pressed for time, and choosing to include proofs and proper definitions would mean having to exclude other topics, which, unlike proofs, appear in the all-important end-of-year exam.
So I guess my point is that while it is possible that your young friend has been badly taught, it is more likely that the teacher did what she had to do in order to get the majority of ordinary students through the exam with decent grades. It all comes back to the politics determining the curriculum – who are the people actually making these decisions? Are there any mathematicians involved?
Just some observations, from someone who spent almost 4 years doing a PhD in pure maths in a pavilion not far from you 😉
November 21, 2012 at 5:34 pm
Hi Andreas,
That’s a gloomy picture you present. How will they ever learn motivic cohomology?
More seriously, your post makes me wonder which countries are doing a reasonable job of teaching mathematics at school level. It seems plausible that having good models to point at would help in trying to reform (or at least maintain) the curriculum in countries where standards seem to be continually in decline.
December 8, 2012 at 9:31 am
… and same is the picture in India, where high school curriculum is so dull and boring without the proofs. Obviously, how can we expect anybody to be interested in the subject where there is a rote learning of formulas and in order to have success in the exam students generally solve 4-5 questions that involve the simple application of that formula.
Not just on school level, but same is the situation at under graduation level.
And I’m totally agreed with Andreas that “It all comes back to the politics determining the curriculum – who are the people actually making these decisions? Are there any mathematicians involved?”
Really a pathetic situation of present day school curriculum.
November 2, 2014 at 5:23 am
Hi Andreas,
I totally agree with your statement
“So I guess my point is that while it is possible that your young friend has been badly taught, it is more likely that the teacher did what she had to do in order to get the majority of ordinary students through the exam with decent grades”.
Teaching proofs/first principles and assesing students on these aspects would mean fewer good grades at the end of the day and our society or at least the powers that be decided that we should not go along such paths.
November 21, 2012 at 12:22 am |
I am extremely sorry that this is off topic, but has anyone read my comment on EDP27? It appears people usually read the comments when they see a new post, but not if its been up a while (I posted my comment a month ago, which was around a month after the post first came up. No one has said anything about it yet.).
Just so I am not utterly off topic, a similar experience happened to me as I was helping a friend review calculus (I’m in the US, so we call the courses ‘algebra’, ‘calculus’, etc.) before this school year. Apparently, he got through the course by memorizing the formulae before the tests without really knowing why they were true. I think he did well on the standarized AP exam (although I didn’t actually ask him). However, he did not remember the formulae he had memorized before, and obviously could not rederive them, since this was not taught. With a lot of bumps on the way, we got ourselves through the definition of derivative, proofs of the ‘sum rule’, the product rule, the chain rule (that took forever), and the derivatives of some functions. Hopefully, he remembers some of this. Throughout, I got the impression he was thinking that while this stuff was interesting, it was not really necessary, and that the formulae we got at the end were the important things which he needed to remember.
November 21, 2012 at 1:37 am |
[…] Today, 21:37 Thought this Tim Gowers post was quite […]
November 21, 2012 at 2:50 am |
I have, in the past, had similar experiences while one-on-one sessions on geometry and algebra, and have lamented about the state of education in our country (India). Your post seems to point to a rather disturbing universality of the schooling problem. Could it be that a single teacher imparting education to a large number of pupils (it’s close to 100 in many classrooms, here, not sure what the numbers are in the UK), is really the incorrect way of doing it?
November 21, 2012 at 4:22 am |
Forgive me for not having much original to say, but the comment about networks of facts made me think of the chapter The Relation of Mathematics to Physics in Feynman’s The Character of Physical Law, where he stresses that mathematics is not just a language, but a language plus logic and that the logical reasoning is important: `If you do not appreciate the mathematics, you cannot see, among the great variety of facts, that logic permits you to go from one to the other’. (In his example, the two facts are that the gravitational force is directed towards the Sun & planets sweep out equal areas.)
I think it is always tempting to teach the facts, rely on memorization, and suppress the logic, which is both slow (for most of us) and error-prone.
November 21, 2012 at 5:55 am |
Though I am very young at age still I happened to discuss mathematics with my classmates in engineering. I figured ouot the same thing among them. Since I was not very good at mugging up stuffs, i usually try to find up basics of everything which I believe is quite helpful for deriving any formula. But these days people find it easier to maintain short notes in pocket than getting to the basics.
November 21, 2012 at 7:17 am |
Here in the US, teaching at a respectable, but not top-tier, university, I routinely provide all (or at least most) of the conceptual content in my calculus courses, including derivations of derivatives and definite integrals via Riemann sums, etc. Any attempts to later test understanding of anything other than rote computational skills is inevitably disastrous except among the very top tier of students. This semester, I’ve gone so far as to prepare regular summaries of all the “main ideas” covered in class to save the students the chore of having to decide for themselves what’s important. It’s helped a little, but not much. And many of these students are seeing calculus for the second time, having already taken calculus classes in high school, some of them even getting respectable scores on AP exams.
What seems to me to be the real problem (at the university level in the US) is that students arrive with the idea that math isn’t something that you think about – it’s something where someone gives you a recipe and you follow it. I try explaining to them that, as pointed out in the post, it’s actually easier to learn something if you understand what’s going on than if you just try to blindly memorize formulas. I also try to instill the idea that if you don’t understand what it is you’re doing, there’s no point learning to do it since you’ll never be able to apply it (though of course to them, the application is the exam).
I’m honestly a little shocked that this state of affairs comes as a surprise to the author of the original post; it’s what I’ve seen every day for years. Actually, I find it eerie how closely the described conversation matches what happens in class everyday, from the attempts to apply the wrong rules in the wrong situations, to the arbitrary guessing, to the ultimate lack of understanding of the basic underlying vocabulary that should have been put in place years ago.
November 24, 2012 at 5:00 pm
‘What seems to me to be the real problem (at the university level in the US) is that students arrive with the idea that math isn’t something that you think about – it’s something where someone gives you a recipe and you follow it.’
Exactly correct. For the vast majority of A-Level students, plugging numbers into formulas and following arbitrary rules is *exactly* what maths is.
November 21, 2012 at 9:48 am |
“Because (and this is something I plan to devote a blog post to at some point) memory works far better when you learn networks of facts rather than facts in isolation.”
I distinctly remember thinking about this as a teenager, although I don’t remember if the idea emerged spontaneously or it is something a teacher told me. It seemed such a powerful notion that I was surprised that the teachers didn’t make a bigger deal of it. (Actually, there were some subjects where the presentation of the material was so incoherent that I felt I was being hoodwinked.)
Having a systematic view actually saves intellectual effort on balance, even from the narrow perspective of being able to display one’s knowledge of the A-level syllabus (provided that you start systematising far enough in advance). Perhaps this is how it should be sold to time-starved teachers and students.
November 21, 2012 at 10:48 am |
The specification for A level includes “The derivative of $f(x)$ as the gradient of the tangent to the graph of $y = f (x)$ at a point; the gradient of the tangent as a limit” which one would think would be fine.
But my impression is that this, and other aspects of the A level syllabus which concern principles and rigour, are not assessed properly by the examining boards. This is a large part of the current problem: the exam boards don’t do what they’re supposed to, and no one polices them at this level of detail.
The upshot is that this is something that good teachers teach and poor ones – and those expected by their school above all to teach to the test – don’t.
Incidentally, this would make first-principles differentiation a dangerous topic to use when interviewing prospective undergrads — it might elicit the quality of their teachers more than their own brightness.
November 24, 2012 at 8:10 pm
Looking at the current (to January 2013) MEI syllabus, the module (C2) which introduces differentiation and the idea of the derivative as a limit only requires students to be able to differentiate $kx^n$ for constant $k$ (for integer and rational $n$) and sums of such functions. The product rule and chain rule are not introduced until the next module, C3.
Also, ridiculously, at C3 one is taught the derivatives of sin and cos (and exp and log), but the formulae for cos(x+y) and sin(x+y) are not introduced until module C4.
Those, by the way, are the only derivatives which must be memorized for the exams; other derivatives one might reasonably require are given in the formula book, as is the quotient rule.
In short, the very structure of the MEI course militates against learning the basic properties of the derivative and then cementing that knowledge by calculating derivatives of basic functions from first principles.
November 21, 2012 at 10:54 am |
For many of my students (in US) that have struggled with calculus I was able to detect one source of the problem: extremely poor algebraic skills. One example, admittedly quite singular: I had a student who wrote 1/2+2/3=3/5.
For most of them the situation is not that dramatic. They are simply incredibly slow at performing basic algebraic manipulations such as, adding fractions, multiplying polynomials, adding rational functions. This could be lethal during a midterm. Tests in US seem pretty long to me, and given that many are multiple choice one minor computational error can have damaging consequences. Asking my students to compute the derivative of $1/(x+1)^2$ from “first-principles” would be considered mean.
This basic routine that we take for granted is not there for many of my otherwise bright students. I feel that I am asking a group of non-English speaking people to savor Shakespeare without asking them to memorize some words. (For disclosure, English is not my native tongue, and I still struggle with Shakespeare.)
That is why I am not fully sold on the Common Core movement. I don’t know how many practicing mathematicians were involved in setting-up this new approach. In any case, here is a critique of this new approach from The Atlantic.
http://www.theatlantic.com/national/archive/2012/11/a-new-kind-of-problem-the-common-core-math-standards/265444/
November 21, 2012 at 11:05 am |
Instead of deriving things, maybe it would be quicker and more fun to appeal to their intuition. Exponential functions are dramatic, because they out-pace polynomials and because they come up in topical issues like population growth or radio-active decay. If we are lucky, the students will just see that the rate of change of a population should be proportional to the population.
Similarly, for the product rule they could imagine a particle moving on a plane and consider the rate of change of the area of the rectangle.
In both cases, we can see *why* something is true rather than having a proof. Sometimes I find proofs very unsatisfying, because I can understand every step of the proof and still not get a feel for why it is true. Or, on other occasions, the proof is for something obvious and I can’t see why it wouldn’t be true in the first place.
November 21, 2012 at 12:18 pm
I like that rectangle idea — not something I’d ever thought of. However, I did think of something else in a similar spirit recently, which was a justification for the derivatives of sin and cos. If you imagine a particle with position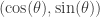 , then it is on the unit circle at an angle of
, then it is on the unit circle at an angle of  above the x-axis. It therefore moves at constant speed round the unit circle, and since when
above the x-axis. It therefore moves at constant speed round the unit circle, and since when  it has gone round once, and since the circumference of the circle is
it has gone round once, and since the circumference of the circle is 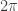 , that speed is 1.
, that speed is 1.
Now the velocity of the particle is (intuitively clearly) tangent to the circle and pointing anticlockwise. Therefore, the velocity vector is a positive multiple of . If the multiple is
. If the multiple is  , then the speed is
, then the speed is 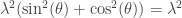 , and since we know that to be 1 it follows that
, and since we know that to be 1 it follows that  . Therefore, the velocity is
. Therefore, the velocity is  . Resolving into components we get that the derivative of
. Resolving into components we get that the derivative of  is
is  and that the derivative of
and that the derivative of  is
is  .
.
November 21, 2012 at 2:40 pm
Regarding the cos/sin derivation you may be interested in this paper:
The Spider’s Spacewalk Derivation of sin’ and cos’
It also has a “proof without words” version at Math Overflow.
January 19, 2013 at 6:57 pm
Tim, that particle moving on a circle is elegant. I like it. It rests on both differentiation-as-rate-of-change, and the as yet unmentioned area of mathematics which was at the heart of mathematical teaching until recently: geometry. When you say ‘I don’t think he used the word “tangent”’, you reveal that geometric visualization is an important part of your toolbox, and you expect to find it in others.
I have watched my son, now 13, learning maths at school, and he hasn’t yet picked up a compass, unless I’ve asked him to. Could he construct a line at right angles to a point on another line? Barely. Draw an equilateral triangle? Maybe. A regular hexagon? Probably not. Could he explain why the compass construction of an equilateral triangle produced an equilateral triangle? I doubt it. But that is the door I used to logic and proof.
When I was doing A-levels, we were shown how to integrate exp(-x^2) using the Cartesian to Polar transformation, and the machinery involved is complex: without geometry, it would have been harder to justify what we were doing.
So I think that leaving out both geometry and logic is at the root of the issue. And think of all the spectacular 20th century results in proof theory!
There’s been a similar forgetting in Physics: by the time he’s 18, my son will not have been exposed to any concepts from physics after about 1870. If he follows the syllabus, he will not have done any experiments with waves, so he will not have seen two slit interference, or the photoelectric effect. His teachers will provide him with no deeper an understanding of thermodynamics than a 19th century chemist could get.
Dos this mean it is time to extend the three-year first degree to four years, in order to catch up?
November 21, 2012 at 12:43 pm |
Also Feynmann gave a nice explanation of the fact that,in order to understand physics,you don’t need to waste a huge amount of memory to remember all the correct formulas,but by the opposite you should get the really general principles,and then train your guess,imagination,and logic to get everything from that(and he remark the power of analogy in this process,indeed if i remember well it’s just before to see how the laplacian comes up in many,apparently different, places in physics),with the power of what he called “triangulation”. In a similar spirit, Andrè Weil in his autobiography remarked that memory is the “art of forgetting” redundant information. All this is really fundamental. It would be interesting,if you make a blog post about this as you said,if you can show this phenomenon also at an high level of intellectual production,rather then just about the basic,to show how this,at the variation of cognitive scale,is an intellectual invariant. Bye
November 21, 2012 at 7:03 pm |
I am a mathematics student and while helping out my definitely smart smaller brother I was subject to the same astonishment – let me list it:
1) He did not know how the derivative is defined and in some elementary cases calculated.
2) While looking at the aforementioned definition of the derivative, it turned out that he was not able to calculate $f(x+h)=(x+h)^{2}$ but responded by $x^{2}+h$ as did maybe the person you had your discussion with.
3) As a corollary he had no idea what the chain rule is and in particular it took me about an hour to explain why the quotient rule is superfluous.
Me and my flatmate – a mathematical physicist – concluded in my brother’s absence that all this boils down to “he did not understand the concept of a function”. In Switzerland the last two years are almost entirely spent on real analysis and it is very irritating that it should be possible to obtain a sufficient mark when not understanding this concept.
This lack became (much more understandably) more apparent, when I wanted to explain where the “defined up to a constant” in the primitive comes from by writing down two primitives as integrals and calculating/drawing the difference between them.
What I want to say is the following: from my point of view the focus is completely flawed. If somebody graduates from high school with the aim to go to university (this being implicit) and study a subject where he or she will have to be able to integrate $x\log x$, he or she will have to do at least a condensed mathematics course where they will quickly learn/recall techniques. Nobody else will ever have to integrate $x\log x$ “in real life”. The time had better be spent on trying to make sure that the students understand the concepts. At least they should have a proper idea of what a function is after two years of single variable real analysis. Is there any way to seriously expect less than that?
November 21, 2012 at 11:35 pm |
There have been comments here about students’ grasp of the notion of a function. Thomas Forster, in the introduction to his book Logic, Induction and Sets (CUP 2003), comments that the eighteenth century did not have the notion of an arbitrary function, that individuals acquire their mathematical concepts in the order in which mathematics as a whole came to acquire them (ontogeny recapitulates phylogeny, as he remarks), and that school mathematics is pretty much stuck at the eighteenth century stage. There is a gap between the concept of an arbitrary function as mathematicians define it when they are being careful, and the general idea of a function with which most of us can make do (which I assume was around in the eighteenth century), but even allowing for that, Forster’s remarks may be relevant.
November 22, 2012 at 8:10 am |
[…] understand the author’s concern, but at the same time I also agree with the common sentiment that there really isn’t any need […]
November 23, 2012 at 3:25 pm |
There is a basic assumption here that the student’s teacher must have omitted all discussion of derivatives from first principles, or at best explained them poorly, because otherwise he would have remembered about it. I am not actually convinced by that.
I think that people generally have a remarkable ability to completely forget about things that they did not properly absorb when they first heard them. I remember at least one occasion as an undergraduate when I suddenly understood something, and complained to my friends that everything would have been much clearer if the lecturer had explained it that way in the first place, only to find later that the lecturer had indeed explained it that way, and I had even written it down, but then forgotten.
Just now I was explaining some linear algebra to a student. I know that she is diligent and competent and that she was in the lecture a couple of days ago where I explained exactly the same things. She clearly had not understood the first time, but beyond that, I think she genuinely did not remember having heard it before.
There is plenty of experimental evidence to show that human memory just does not work as well as we like to think it does. Unfortunately that does not lead to any easy conclusion about more effective ways to teach mathematics, but I think it is the reality.
November 23, 2012 at 4:43 pm
On my side this is not assumed. I am perfectly aware of this possibility. What I saw as a problem is the emphasis which is put on technicalities. I have the impression that “how to differentiate x^n” pops up in class far more frequently than “what is the differential”, which tends to distort the student’s point of view as well. And I stand by my point: the examples discussed could safely be less and the “more complicated” ones should rather result in extra credits. This opens up time to give two or three different discussions of derivatives and friends.
November 23, 2012 at 6:18 pm
I also didn’t assume it, which is why at one point I wrote (in brackets), “if his teacher did in fact give that argument — I cannot be certain about this, though the mere fact that that was the message that got across is bad enough”.
A textbook was brought to my attention today that calculates the gradient of the relevant chord as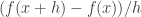 , says a little something about
, says a little something about 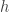 getting small, and then, quite remarkably, just quotes the fact that the derivative of
getting small, and then, quite remarkably, just quotes the fact that the derivative of 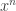 is
is  , claiming that the proof is long and beyond the scope of the book. Just in case anyone thinks that’s reasonable, it doesn’t even do
, claiming that the proof is long and beyond the scope of the book. Just in case anyone thinks that’s reasonable, it doesn’t even do 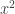 . So it gives the general formula but doesn’t show a single example of how to apply it. It would be entirely reasonable, if calculus was presented to you like that, to forget all about the formula.
. So it gives the general formula but doesn’t show a single example of how to apply it. It would be entirely reasonable, if calculus was presented to you like that, to forget all about the formula.
By the way, I have often had the “why didn’t anyone explain it like that?” feeling coupled with the “perhaps they did” feeling. So I completely agree with your main point.
November 25, 2012 at 5:00 pm
Indeed it’s really good and efficient that there is some resistence to inteoriorize some point of view,and we forget things that not come from our active mind,but just from listening a lecturer or someone else. In this way we can learn things in our own way,and we don’t have the problem of abbundancy of unchecked point of view in our mind,that would be a really inefficient one! This says that our memory work in a right direction for the intelligence,so,probably,better then how many people belive
November 23, 2012 at 5:36 pm |
[…] evidence for my theory that too much pre-college math instruction is thought up by people who don’t like […]
November 24, 2012 at 1:29 am |
This does not bode well for the future, and I’m afraid the problem is not limited to maths. For instance, there seem to be a lot of programmers who learn programming the way A-level students learn math: they just learn to follow recipes and stick things together like lego blocks. This is easily seen on Q&A forums like StackOverflow. People routinely ask questions which reveal a frightening lack of understanding of the basics, like what a compiler does, or what a local variable is, or what is the relationship between value, variable and memory location.
November 24, 2012 at 1:13 pm |
Why would people not be taught how to derive these formulas? I’ve taught myself things like calculus from a textbook and I always made sure I understood how to derive formulas since if I forget them I can just rederive them. It makes learning them both more interesting and much easier as it doesn’t rely on excessive memorisation.
November 24, 2012 at 2:37 pm |
As an A level math student in Singapore I am taught the rationale/proof for each formula. Unfortunately though, there is a tendency for us as students to dismiss this section of the lesson as irrelevant and jump straight into memorising the formula. I suppose fundamentally it’s not about the curriculum but the myopic attention students lavish upon grades, or the grade-focused atmosphere of the A-levels.
November 24, 2012 at 2:57 pm |
I must confess that as an Indian student, I have seen a similar situation-in fact, the situation is arguably acute because most of my class mates are preparing for engineering entrance exams.So, learning the subject right is least important for most. The cram schools or the “coaching centres” as well as the schools they study in rarely discuss calculus rigorously.
I have had a terrible experience in this regard-very often,I get into argument with teachers over the lack of rigour in mathematics and I have been rudely rebuked and told to either accept it or wreck my exams.I did write a blog post on this issue yesterday before I discovered this better post here.
I personally believe this sloppy attitude is because of teaching to the test. Tests are best when they are subjective and non-routine but I doubt if holding Olympiad-type tests is practical enough.
November 24, 2012 at 2:58 pm
My name is somehow being displayed incorrectly.It should instead be Sabyasachi Mukherjee.
November 24, 2012 at 5:27 pm |
[…] See this too:I wish I had found it […]
November 25, 2012 at 10:48 am |
I am a teacher of sixth form mathematics. Part of the problem here is that the boost in the number of sixth form mathematicians nationwide has come at the expense of quality. The good mathematicians are as good as they ever were, but now half the class need not have a strong grasp of fractions or even basic mental arithmetic (neither of these are required to get a good grade at GCSE). As a result, sixth form Maths classes likely have a far bigger spread of ability than ever before. How are teachers to deal with this?
I do always teach differentiation from first principles to my classes, but how long I spend on it will depend upon the ability of the students before me. If a majority of them are incapable of developing a significant understanding of what is going on in a reasonable time, I cannot justify spending lots of lesson time on this. I need to spend the time with them differentiating 5/2 x^(2/7) with respect to x because so many of them can’t multiply 5/2 by 2/7 in their head and certainly cannot subtract 1 from 2/7 without lots of practice. In the end, we teachers get judged on how our students do in exams and while I would be delighted if differentiation from first principles were formally tested, it is hardly surprising if some teachers in certain circumstances gloss over it. What else should they do? I am not necessarily defending, Tim, how the lad you describe was taught, but part of the explanation MAY be that he is in a class with a majority of far less able mathematicians aiming for lower target grades (or he MAY have a lousy teacher, or both).
As for the argument that seeing the derivation helps memory and helps get more marks, I agree with that for the students that have a significant understanding. If they don’t have much of a clue then then they would do better in the exam if they kept practising doing 2/7 minus 1.
To a certain extent I see a dialogue going on here between exceptional mathematicians (or at least competent ones!) who erroneously assume all or even most students are like they were.
November 25, 2012 at 2:48 pm
Many thanks for telling us about your experience. I don’t want what I write to be taken as a criticism of what teachers like you are doing in difficult circumstances. It’s more a criticism of the circumstances themselves. Something has gone wrong if we are trying to teach calculus to people for whom subtracting 1 from 2/7 is a challenge.
The advantage of the current situation is held to be that many more people are choosing to do maths A-level. Is that an advantage if they are learning things without properly understanding them? It’s genuinely hard to say, and something that needs to be thought about.
In an ideal world, before doing calculus one should be very comfortable with handling fractions, multiplying out brackets, and working out equations of straight lines (as well us understanding what gradients are) given various bits of information (such as two points on the line). I’ve probably missed out a few things there. Oh yes, one shouldn’t differentiate trig or exponential functions without being comfortable with the addition formulae for those. If somebody isn’t comfortable with the prerequisites, then is it better to spend time getting them comfortable, or should one press on regardless? My own experience with university maths was that sometimes doing a course that built on a course that I hadn’t properly understood helped me to get to grips with the important parts of the earlier course, but that one could only go so far with that. And building on a secure foundation was hugely preferable if one could manage it.
November 25, 2012 at 3:11 pm
A lot of maths A-Level is taught as mechanical formulas to learn and use. Even the quadratic formula is not always proved,and instead is merely stated as a formula to be learned.
And a fair few of the exam questions are of the type. ‘Find the equation of the tangent to the curve y = 3x^2-6x + 3 at the point where x = 2.’
But that can be done very easily on any computer graphing program.
So if students learn to do such questions mechanically , without any understanding of the principles involved, and passed the exam, what have they gained?
You may as well just teach them to use a computer graphing program. They would get accurate answers all the time, with just as much or as little understanding of the actual maths involved as now.
November 26, 2012 at 10:57 am |
Thanks Gowers for this post. While discussing with many students I have found that calculus is the most mysterious of topics for them. The reason is that most of the students (almost all barring a few) don’t try to read the concepts of calculus (perhaps teachers also don’t dwell much on these topics).
For the majority calculus represents a series of non-sensical mechanical rules of differentiation and integration. When we further dig down we find that the process of mechanical rules has started from high school algebra (identities and formulas) and somehow the same pedagogical approach is used to teach calculus.
Some educators try to use the geometrical reasoning to explain fundamental concepts of calculus, but this has a side effect that students take it as a rigorous proof. I believe some notion of real numbers and limit concept must be provided at length before jumping onto the mechanical rules of integration and differentiation. Also the student should be told to appreciate calculus as something different from algebra (that there are much interesting operations beyond +, -, /, *).
November 26, 2012 at 1:14 pm
I don’t think limits need to be treated formally before calculus is started, but I do think an informal understanding is needed that is correct for a restricted class of nice enough functions. For example, to differentiate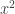 one needs to understand the statement that
one needs to understand the statement that  tends to
tends to 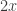 as
as 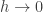 . If one sees lots of examples like that, one may come away with the impression that if a function tends to a limit, then it must be monotonic in intervals on either side of that limit. And that, though wrong, isn’t particularly harmful. Indeed, it is only “wrong” because of the particular choice we make of how to formalize the notion of “limit”. In principle, one could insist on monotonicity and the resulting definition would be adequate for most school purposes. (However, it would be very inconvenient theoretically: for instance, the sum of two locally monotonic functions doesn’t have to be locally monotonic.)
. If one sees lots of examples like that, one may come away with the impression that if a function tends to a limit, then it must be monotonic in intervals on either side of that limit. And that, though wrong, isn’t particularly harmful. Indeed, it is only “wrong” because of the particular choice we make of how to formalize the notion of “limit”. In principle, one could insist on monotonicity and the resulting definition would be adequate for most school purposes. (However, it would be very inconvenient theoretically: for instance, the sum of two locally monotonic functions doesn’t have to be locally monotonic.)
I’m not suggesting that at school one should formalize the notion differently. Rather, one should not formalize it and one should instead be satisfied with the intuitive fact that “gets closer and closer to
“gets closer and closer to 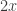 as
as 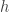 gets closer and closer to 0″. The rest can be built on this foundation, and the foundation can be made more secure later on with epsilons and deltas.
gets closer and closer to 0″. The rest can be built on this foundation, and the foundation can be made more secure later on with epsilons and deltas.
November 26, 2012 at 9:23 pm |
Young people should not be taught half-truths – when they ask “Will I need to know that for the exam?” The question ought to be – which exam, which application, which future? You need to know it to understand maths, physics, chemistry, engineering, how things change, how to describe the world in the most accurate way human beings have ever discovered. Understanding is an essential currency of education – what is the point (I had an A level student once for whom this was a live question) of knowing how to solve a quadratic equation by tapping numbers into a calculator without understanding the solutions? It gets you through the exam, it is not education.
When I was at school, differentiating simple functions came in O-level.
November 26, 2012 at 9:56 pm |
Tim, what risks you take when you try to teach the “unformalized” calculus, can be best seen here: http://milesmathis.com/expon.html.
It’s horrible what some minds can conceive if they start to think that what they hear in school is the “real mathematics” when it isn’t.
November 26, 2012 at 11:04 pm
I think that what I advocate might be something like this. When you differentiate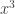 , say, you need to prove that
, say, you need to prove that  as
as 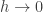 . But
. But 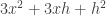 is continuous (because it’s a nice function and doesn’t have an obvious jump — this part is informal but nevertheless true) and equals
is continuous (because it’s a nice function and doesn’t have an obvious jump — this part is informal but nevertheless true) and equals 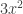 when
when 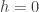 . Therefore, the limit is indeed
. Therefore, the limit is indeed 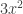 .
.
To make that proof rigorous, it is sufficient to define “continuous” and prove that polynomials are continuous. In other words, the argument is basically correct. Of course, there are nasty objects out there like differentiable functions with derivatives that are not continuous, but the point I’m making is that one can present calculus at a school level in a way that explains what is going on, with explanations that can be converted into rigorous proofs, as opposed to explanations that have to be discarded and replaced by completely different arguments.
November 27, 2012 at 4:54 am |
I’m against black-box methods to teach differentiation. In times past, the concepts around “the differential” dy when y depends on the independent variable x were respectable enough to appear in differential calculus exercises at the beginning level. Before the abstract, general purpose functional notation $f(x)$ became commonly used, many special cases had been given a special notation, e.g. $sin(x)$, $log(x)$ and others. I wonder if the general purpose, generic, $f(x)$ notation might have appeared (in extensive use) around the time of Euler; it could have been before, say starting with Leibniz.
This leaves me with a question: should A-level maths aspire to mathematical rigour as with Cauchy’s epsilon-delta definition of limits?
November 27, 2012 at 5:58 am |
I would like to make a quick and maybe not very constructive comment on the implicit discussion about the correct amount of mathematical rigour and abstraction: it seems to me – not mainly in this discussion – that the standing assumption is that more rigour goes hand in hand with reduced understanding. One can also hear rather often that our understanding of the topic does not mainly stem from Cauchy formalism but is due to the intuitive correctness of the statements.
I do not entirely agree with that although I do not have any studies at hand which I can cite. My point of view is that mathematics was tackled intuitively by a few selected people which should can by no means be taken as the representative of a student. Furthermore these selected minds even derived plenty of wrong conclusions while trying to tackle the issues at hand using a non epsilon-delta approach (if I am not mistaken, I am thinking of the discussion about the extension of the logarithm to -1 among Bernoulli, Leibniz and Euler – none of us would dare to state that either of the first two was of too limited mental capacity). Of course this was research and hence there are many more pitfalls from an objective point of view. Still, these exist and I think one is more prone – particularly if one is not particularly talented – to fall victim to any of these pitfalls if one can not use formal arguments to exclude certain strategies.
My point basically is: an increase in rigour could help, not damage, the diligent student which does not bring along all the mathematics by him- and herself anyway.
If ever I will become a teacher, I will teach vector spaces as vector spaces, not as arrows, just to make sure that the students know there are basically two and only two possible operations. Nothing else.
November 27, 2012 at 7:11 am |
Dear Sir,
This was a great post.
Did you tell the young boy while you were explaining the first principles, the difference between thinking abt the value of (2*x*h+h*h)/h when h is approaching zero compared to substituting h equal to zero. Because that will make him think abt what is a limit, and also what is meant by approaching and what are the different ways to approach a limit? Ofcourse the fact that one can approach smoothly assumes a sort of continuity in numbers and assumes the validity of infinitesimal and infinity which is integral to calculus. Then we need to step back and look at the arithmetic number sequence which is what we are dabbling with when we say x*x and the geometric curve and see if there is a correspondence. Now we are into Dedekind land. Dedekind was born more than 60 years after Newton died. And Newton differentiated using the ‘first’ principles.
So what I am trying to say is – where do we draw the line? What is really the first principle?
The thing is some people are content to know the formula for differentiating x^n and feel that, that is their first principles. Once you know the building block derivatives, the application of product and chain rule, then if you treat them as your first principles and dont find the need to plumb further as these are enough to get things done in whatever you are doing – (passing an exam or building a bridge), then they seem to have found their comfort level and find no utility in plumbing further for the limited objective they chose to do calculus.
Every person’s comfort level is different like Descartes’ and Newton’s comfort level seemed different from Dedekind’s or Cantor’s
Regards, Sridhar
November 27, 2012 at 8:45 am |
I fully agree with Sridhar’s remark about the difference between “h is approaching zero” and “substituting h equal to zero”. If a student is able to understand this fundamental difference he is already a step ahead many other students.
G H Hardy tried to drive down this same point again and again in his famous “A Course of Pure Mathematics”, but unfortunately this book never became a pedagogical success. Now most of the students don’t even know of this great masterpiece. Also this is not preferred at all by any of the teachers or professors in most schools and colleges.
Calculus needs more thinking along the lines of understanding the order relation on the number line rather than doing algebraic operations. I think focus on such topics should be given sufficient space in secondary classes so that the student is well prepared for an introduction to calculus.
Another technique which my teacher told me when I was studying calculus myself is this:
“To calculate limit of f(x)/g(x) when x tends to a, first put x = a, if the expression evaluates fine then f(a)/g(a) is the limit. But in most questions it will happen that f(a) = g(a) = 0. In that case first simply the expression f(x)/g(x) into such a form as p(x)/q(x) where q(a) is not zero. Then p(a)/q(a) is your desired limit”.
Now this rule works fine for most of algebraic / trigonometric limits and in fact is the case when calculating a derivative. But the rule misses the whole point that “limit” is a “not a value” of function which can be obtained by substituting some particular value of the independent variable.
My own preferred approach to demonstrate limits is by using calculator. To convince the student that (sin(x))/x tends to 1 as x tends to 0, simply start evaluating (sin(x))/x for x = 0.1, 0.01, 0.001, 0.0001 till your calculator starts giving the answer 1. The idea of f(x) approaching some value A when x approaches a is the crucial step in understanding of calculus concepts. Taking a non-obvious example and showing this behavior on a calculator gives some amount of confidence to the student. Once the student has some confidence that this is expected behavior of the function, you can present a proper proof.
November 27, 2012 at 9:14 am |
Tim, unfortunately, it only works for polynomials. In all other cases, you have those “faith-based limits”, like sin(h)/h when h->0. And even then, people like Miles see that for polynomials, there is a much (conceptually) simpler approach, based on finite differences. Of course, you can say that “they just don’t understand”. But I argue that they reach the best conclusion given the education they get. And it’s very sad.
Try to read http://milesmathis.com/calcsimp.html. I know it’s very hard to read for a professional mathematician like you, but you have to, if you want to propose a certain way of teaching calculus. Because then you see what people really start to think, if they are taught that way.
November 27, 2012 at 9:19 am |
Another interesting example is addition of numbers which are taught to kids.
Say adding 14+27. We add 7 and 4 and get 11. We write 1 below as the right most digit of the result and then carry over 1. Now we add 1 and 1 and 2 and get 4 and write it as the second digit from right and then we get 41. This is the process we teach the kids when they add numbers. And a similar but a little more complex process for multiplication of 14 and 27.
We do teach the kids to an extent the concept of units place, tens place and 100s place when we write a number but rarely we relate that knowledge and teach why this multiplication method , they use to multiply, works. Ask any one why this method works, people will scratch their heads for a bit before they wrap their minds around it. So this is not too trivial.
Infact in thirteenth century they would have computed 27*14 in a quite a different way of doubling 27 and the doubling it again and doubling it again. Then they have 27*2 = 54 and 27*4 = 54* 2= 108 and 27*8 = 108*2 = 216. Now they have a set of numbers which they can use to create 27*14. By adding 54, 108 and 216 they get 378. This was just some 700 years ago much much after Pythagoras, Euclid and Archimedes. The effective understanding of the principle of position was a relatively recent occurrence before which a lot of complex mathematics have already been accomplished.
Again the question we ask is when we teach a child, the multiplication method, does he or she needs to clearly understand the principle of position and how the multiplication method works due to the associative property of addition or is it something he unravels at a later time as a nirvana moment.
It is always a difficult choice as to where to stop plumbing and how much emphasis needs to be given to certain fundamental concepts.
To learn to drive a car, do we necessarily need to know how the clutch and the accelerator along with the gear works or how the brake works?
In software when we want to write say an application to run on a particular operating system we are given an application programming interface (API) to use the services provided by the underlying operating system. The application programmer then uses that to write his or her application by calling the routines or functions available in the API. We dont really need to bother abt how a function actually does what it does as long as it does as mentioned in the interface specification.
Similarly the API for the calculus is the building block derivatives like for instance the derivative formulae for X^n, trig functions, exponential functions and then the chain rule and the product rule. This is your API. When you are asked to derive, you use this API and derive.
Like children did addition quite well without understanding why it worked the way it worked, similarly young adults use the Calculus API or toolkit if you will and calculate their derivatives really not bothering how the initial formulae came about and why the other rules like chain and product rules are valid.
Ofcourse there might be some special situations when your toolkit would breakdown and then suddenly you wouldnt have anything to fall back on to tackle that situation – like say a brake failure.
As long as that doesnt occur some might think – Why bother?
November 27, 2012 at 12:02 pm
The difference between learning long multiplication as an unjustified mechanical process and learning differentiation as a purely algebraic operation (start with a few key examples that you learn by heart and derive the rest using the product rule, chain rule, etc.) is that when people learn long multiplication they already understand what multiplication means (because they’ve learned to multiply much smaller numbers), whereas if you learn differentiation as an algebraic process then you don’t know what it means. Or rather, some people do but you’re not forced to and many people don’t.
When I was at school, I was shown a proof that the derivative of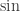 is
is  , based on the result that
, based on the result that 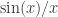 tends to 1 as
tends to 1 as  tends to 0. I found it quite hard and didn’t remember it, getting by perfectly satisfactorily with the knowledge that
tends to 0. I found it quite hard and didn’t remember it, getting by perfectly satisfactorily with the knowledge that 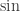 differentiates to
differentiates to  . However, I did at least know what that statement meant, and could see that it was plausible by thinking about the graphs of
. However, I did at least know what that statement meant, and could see that it was plausible by thinking about the graphs of 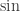 and
and  , and so on. It’s that additional level of understanding that is very important.
, and so on. It’s that additional level of understanding that is very important.
To pursue the car analogy, an algebraic approach to calculus might be like a rigid rule that says you should change up into third gear when you reach 20mph. That rule will let you down badly if you are climbing a steep hill. To drive properly, you don’t have to understand how the gears work, but you do have to understand what the point of the different gears is.
November 27, 2012 at 3:44 pm
@Sridhar: That’s a somewhat oversimplified view of historical multiplication. I might recommend the list at 25+ Ways to Multiply.
@gowers: In any case, I think the best way to force understanding of the third gear (so to speak) is not to make abstract arguments/analogies but to put questions on the test (in your case the A levels, in the US case the AP or IB tests) that require that understanding. For example, take a look at question 3a from this free-response from the Calculus BC (2009). [Using a graph with no equation given, “Is f differentiable at x = 0? Use the definition of the derivative with one-sided limits to justify your answer.”] A student used to just cranking through the chain rule will have difficulty. Since apparently the derivative definition is on the syllabus for A levels, why not put questions to match it on the test?
November 28, 2012 at 2:29 am
@gowers
Thank you for the reply. I see your point. But I have to say I still have a nagging contention in my mind regarding where a teacher should draw the line in explaining things to students.
One might feel not explaining why the multiplication method works is fine as long as one knows what is multiplication while some might feel at some point at the school level, the mechanics of the multiplication method needs to be explained.
One might feel that it is ok to just instruct what are the different situations you should use the different gears & how to use in those situations while some might feel it is better to explain at some basic level why a gear is needed in a vehicle.
The basic question is : Is there a teaching principle by which the teacher can know where to draw the line considering the capacity of the students and also the time available?
Would the following tenets be useful and can be taken as a basis to guide the teacher in unravelling a particular concept to the student?
1. Make the student appreciate the need for the concept discussed
2. Guide the student in such a manner he himself comes up with the first principle to approach it
I am just thinking aloud here. Let us look at differentiation and see how that can be done?
Step 1: Making the student appreciate the need.
Differentiation can be defined at a high level as computation of the rate of change and in the area of motion, an example is speed – rate of change of position. I would think rather than start with a curve, a physical example related to the world could introduce the student to derivatives with more ease. With the example of speed, the student’s general intellect is satisfied to an extent as to what is that you are calculating here and the need for it. Generally when one asks the student how to calculate the speed of a car, he would use the distance traveled and divide it by the time taken to travel that distance and calculate the average speed. It is a start, but though average speed is good, what we are actually interested is in the instantaneous speed, (the slope of the tangent). That is the entry point into the real significance of differentiation.
Here fortunately the student does understand instantaneous speed more viscerally because of the speedometer unlike say the tangent and its slope. He knows the speed in the speedometer is different from average speed and he knows it changes constantly and so he concludes in his mind, what is shown at any point of time is the instantaneous speed. And hence with this thought he starts to appreciates the difference.
I think with this we have satisfied the first step where the student appreciates the need for a derivative, in this case instantaneous speed.
Step 2: Making the student find a way to come up with the first principle formulae
So now the student will think : Well now as we know that the speedometer shows the instantaneous speed, how does the speedometer calculate the instantaneous speed? If we can look inside how Speedometer calculates, can we really know how differentiation works?
Digression (simplified view of the history and working of speedometer) : “Till 1980s we had analog speedometers which used eddy currents generated by a rotating magnet attached to the drive shaft and that “really” measured the slope of the tangent (instantaneous speed) and didnt do averaging. While recently we have electronic speedometers, which actually work on averaging by calculating the number of pulses (a pulse arrives for every rotation of the drive shaft) in a given time and what is calculated is conceptually not really the slope of the tangent but some kind of an averaging done within a very very short span of time. No limits or calculus is needed here to explain the working of electronic speedometer. But one needs calculus to explain the Analog speedometer as it depends on the relationship between motion of a magnet and the electricity it generates”
So interestingly though the analog speedometer gives a feel for the need for differentiation, it is truly a case of circular reference. Physics used calculus to explain the working of the speedometer. So if we look inside the speedometer obviously we find calculus and derivatives there as we put it there in the first place.
So though speedometer gives the feel for the derivative, it doesnt give the basic technique to calculate it. There we are left with a stumbling block in Step 2.
Then possibly we try to appeal to his intuition and try to frame it in a little more abstract manner as we have already given him some intuitive feel for this thing called derivative. One could define instantaneous speed depends on the distance travelled in an instant. The speed will be the distance travelled in an instant divided by duration of the instant. And it is not too farfetched to think if we reduce the duration of the instant to a very low value then then we tend to truly instantaneous speed. This line of argument would appeal to the human mind as in a way this is what the electronic speedometer does.
So we have :
Speed = Distance travelled in an instant/ Duration of an instant = (Distance travelled after an instant – Distance travelled before the instant)/Duration of an instant.
This seem more like our first principle formulae.
Till then we seem to make sense, but now we make a jump and ask the student the question – what is the value of this expression when the instant is so small that is “almost” zero.
A student with no exposure to calculus will in all probability equate when the instant is almost zero to the instant being zero in his mind and would conclude the distance travelled in such an instant will also be zero. He might think when the distance travelled is zero, when the change itself is zero, what do we mean by rate of change? In that durationless instant when there is no movement, how can we talk abt rate of movement? A student would have these confusing thoughts like possibly say Zeno had.
So what does the teacher at this juncture say to the student?
Say the teacher changes tact and approaches this again with a different example, say the curve example, then here again, the student would say when the run is almost zero, the rise is also almost zero and substituting zero in their minds for the numerator and denominator, he will get back to the same confusion.
So now without much ado, to resolve this, the teacher takes an example of x^2 and shows how the numerator becomes 2xh + h^2. And then now we can cancel the zero creating miscreant h from denominator and numerator and then we are left with just (2x + h)/1. And now if we make h tend to zero, we are left with 2x.
This seems to a student like a magic trick as only a moment ago he seemed to have a valid confusion of zeroes but now somehow those zeroes have vanished and he is still left with a slight discomfort on the way it was resolved.
Should the teacher now draw a line here and proceed with the chain and product rule?
The question is, Is Step 2 really done? Should we talk abt limits in detail now to take away his confusion? But if we start talking abt limits, then even in that there would be some point like this where we might need to talk abt a more fundamental concept … where does it end? Where does the teacher draw the line?
Is it a subjective decision?
November 29, 2012 at 9:28 am
Thank you for this thoughtful comment. The outline you give of how to teach differentiation is just the kind of thing I would advocate, and the pedagogical problem you draw attention to at the end — how it can be that the 0/0 problem has magically disappeared — is an interesting one.
To tackle it, I think epsilons and deltas are not the answer (at school level, that is). I think I might start by “proving” that 0/0 equals 1 and then “proving” that it equals 0 and then “proving” that it equals 2. The style of proof would be “Twice any number divided by that number is always 2, so 0/0 must be 2.”
Having done that, I would rephrase these “proofs” in terms of functions such as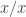 and
and 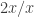 . I would say that you can’t directly substitute
. I would say that you can’t directly substitute  in, but there is a unique sensible value for the function at 0 if you want to give it one.
in, but there is a unique sensible value for the function at 0 if you want to give it one.
Then I’d look at a non-constant function such as and ask what they thought the obvious value for that should be at 0. And I’d ask why that was the obvious value.
and ask what they thought the obvious value for that should be at 0. And I’d ask why that was the obvious value.
There are two answers one can imagine here. One is that you can simplify the function to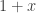 , and in that function you can substitute
, and in that function you can substitute 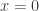 . I think that for school-level maths that is quite satisfactory when it works. The other answer would be more like, “It gets closer and closer to 1 when
. I think that for school-level maths that is quite satisfactory when it works. The other answer would be more like, “It gets closer and closer to 1 when  approaches 0, so 1 is the obvious value to pick.”
approaches 0, so 1 is the obvious value to pick.”
I was about to write that to force them to think the second way as well as the first, I might give them an example such as , but then I realized that you can of course simplify that to
, but then I realized that you can of course simplify that to  and substitute in
and substitute in 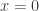 . Maybe the simplest example that can’t be dealt with in a simple algebraic way is
. Maybe the simplest example that can’t be dealt with in a simple algebraic way is 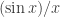 . Unfortunately, that would be quite a hard example to analyse, though maybe one could get somewhere by drawing the obvious diagram and pointing out that a certain arc and a certain side of a triangle appear to have very similar lengths when the angle is small.
. Unfortunately, that would be quite a hard example to analyse, though maybe one could get somewhere by drawing the obvious diagram and pointing out that a certain arc and a certain side of a triangle appear to have very similar lengths when the angle is small.
November 29, 2012 at 2:06 pm
Thank you for the reply.
I totally agree that at this point to remove the discomfort abt 0/0 we shouldnt talk abt epsilons and deltas and confuse the school student. A better approach is to find a way to resolve his discomfort abt 0/0 through certain verbal reasoning.
I like your approach.of first letting the student loosen his mind up on 0/0 and ‘proving’ that 0/0 is such an expression that it can take any value depending on the situation. It is like a joker in a card game.
In a game of Rummy, you let the joker to assume the value of a particular card depending on the other cards you have with you to complete a sequence. Similarly you need to evaluate the situation and guess an unique sensible value for ‘0/0’.
The key to finding which unique value ‘0/0’ assumes in a particular situation is by looking at the values this function (x + x^2)/x assumes at places where x is very close to zero (left and right of it) and then guess what value the function is going towards and will attain when it reaches zero. In this case we land with 1. Or in other words what value if it takes at zero would it form a nice sequence along with the values left and right of it. Just like Rummy!
Infact (sin x)/x should definitely be dealt with. Because in an simple algebraic example we have the shortcut of cancelling variables from the numerator and denominator while an example like sin x/x brings more value to the act of finding this unique sensible value for ‘0/0’.
I think the phrase you used – “unique sensible value” is a very good phrase to describe it.
Thank you for the insight.
November 29, 2012 at 2:40 pm
It is very normal, I think, to define the derivative of f at x to be the limit of [f(x+h)-f(h)]/h as h tends to 0, but not to give a precise definition of limit, instead relying on some intuition like “the unique sensible value”. I think this is good practice for two reasons. One is that giving a precise definition of limit using epsilontics is not practically possible in a first course in calculus. The second is a more philosophical reason – there is more than one way to formalise the definition of limit. Epsilontics gives one way, non-standard analysis another, and presumably one could find other methods as well. So while the notion of limit is, I believe, fundamentally important, the precise way of formalising it as epsilontics is not.
December 6, 2012 at 6:46 am
Thank you very much for the great ideas on how to motivate calculus in your second post. As a PhD student, I know I will have to teach calculus soon and I have trouble thinking of ways to make the subject interesting to my students, who will probably not be science-oriented, let alone mathematicians.
November 29, 2012 at 4:40 am |
Hehe! “I still haven’t got round to thinking about that.” Nice pun.
I was reading a post by Gowers about an interaction with a student. In it, I think, the main moral was that understanding was more important than manipulations. On the other hand, in it he asked an student. “what can we do to uv+u?” I think the student was right to not know what to answer. There are many things we could do to uv+u. I think it is often ignored in teaching math to give together the trick and the goal that it achieves. Even if these are given, it is more often forgotten to try to describe the features of the contexts in which the trick can be applied because it leads to the goal. I think the question, for the student to be able to answer, if he has never seen it before, should be: What can we do to uv+u if we want to get ____? Of course, what Gowers was trying to say is that he was surprised that the student hasn’t seen it before. But what I am trying to point out, is that it shouldn’t be forgotten to put together the question of “what can we do here” with “to get _______”. One cannot remember a trick without having first the purpose of the trick. One cannot use a trick without first getting some idea of when, in what contexts, the trick is going to fulfill the purpose.
November 29, 2012 at 9:30 am |
Reblogged this on Memoirs of a misunderstood teen.
November 29, 2012 at 5:02 pm |
The dependency structure of mathematics curricula seems dense: more advanced concepts tend to rely on a large subset of the less advanced concepts. If this is so, then teaching of mathematics tends to be inherently brittle: it is subject to catastrophic failure if just one part of the earlier syllabus has not been mastered. Failures propagate and may leave a learner unable to grasp big chunks of a more advanced course.
I do not think mathematics is inherently densely interdependent. It seems to me that alternative ways of deriving concepts have been pruned out of the syllabi, perhaps to free up time for covering concepts that are “deeper”, or to deal with more heterogeneous groups of learners. Pruning “unnecessary” concepts leads to an efficient dependence graph, but one that is prone to failure.
Would this not largely explain many of the observations made here?
December 2, 2012 at 3:51 am |
“…they will do a lot better on the exam if they have not been confined to what’s on the test.”
Wherein lies the tragedy induced by the Kafkaesque Ofsted and its hoard of destructive bureaucrats hissing “performance evaluation … kpisss … passs ratesss preciousss…” and other poisonous incantations into the ears of the struggling teachers. It can only get worse if the lessons of the past are any guide.
December 2, 2012 at 11:21 am |
I think you mean “horde”, although it is intriguing to think Ofsted might be hoarding destructive bureaucrats, while other public bodies have to cope with a shortage of them.
December 4, 2012 at 4:05 am
Quite right. Most unfortunate – it’s as bad as the sort of thing that one sometimes gets from Guardian journalists. There is, of course, no need to hoard bureaucrats – the supply is endless.
December 4, 2012 at 8:20 pm |
[…] a very dispiriting new blog post by Tim Gowers about the dire state of school maths teaching in the UK. I’m a bit surprised, though, that […]
December 5, 2012 at 2:51 pm |
I taught high school mathematics (in the U. S.) for 5 years–4 years in the late 1970s and 1 year recently. I continue to tutor high school math students in all subjects (including Calculus), having done so for decades. Much of value has been posted. I want to add only that in my tutoring and my teaching, Prof. Gowers’s experience with his student has been all too common for me. In fact, your approach to this student’s ignorance is exactly as I would have done in that circumstance, and the experience you had is the most probable outcome, yet, I continue to try.
The dispiriting part, for me, is the utter lack of curiosity in the students. This condition is dispiriting to me because it indicates that the natural curiosity of children has been crowded out by needs that are only indirectly, and sometimes inversely, related to learning: status, money, approval (peer and parental), “success” (getting the “right” answer), and the like.
In the U. S., in some states (e. g., Florida, where I live, now), many, if not most, elementary (primary) school and middle school (grades 6-8) teachers are barely capable of performing the arithmetic operations they teach to their students; they certainly have no grasp of mathematical discovery, verification or proof, in short, exploration, and don’t seem to value it and the varieties of outcomes. Got to get that answer! As with any parent or educated person, I have ideas on how to fix this problem, but, I have no indication as to whether they would be successful and for whom they would be successful. There are moments when I doubt whether I understand the phrase, “successful mathematics education.”
December 5, 2012 at 3:24 pm |
One other comment: as a former teacher, I can say that the most challenging aspect of teaching for me was devising tests that tested the students’ grasp of what (I believed) I was teaching at various depths of understanding, while conforming to the time constraints of the testing period and encouraging my students to “think it through” from first principles (definitions and other theorems) or explore alternative strategies, if they didn’t have an immediate insight that led them to a solution or a proof.
During my most recent teaching experience, I found that the faculty had essentially “given up” on attempting to teach using discovery and that topic tests rarely differentiated among different types or depths of understanding. The “hard” problems were simply versions of simple problems with more operations required to find the value of x. Our primary concerns were to complete the state-dictated syllabus and coach our students to pass the FCAT (Florida Comprehensive Assessment) near the beginning of the final nine weeks. We allocated two solid weeks to direct preparation for this test and used prior year tests and a study guide published by the testing authority (a textbook publisher, btw) as the basis for this preparation. Sadly, the students and parents demanded this approach and the administration (and many faculty) supported it.
December 6, 2012 at 7:10 am |
This post made me think about learning vectors and matrices in the old P6. As John had already noted, we were taught the manipulations without any mention of linear transformations (or maybe they were discussed but I forgot). The first time I remember learning about linear transformations was actually in between my Cambridge interviews – I had an hour of waiting time, and a Part III student calmed my nerves (but kept me in the mathematical mood) by explaining what matrices are for. And I was very happy to see why matrices multiply in that funny way. Yet I feel it was better for me to have learned the manipulations and the theory separately. Learning both together would be a lot of material to swallow at once (as I know from seeing my students struggle), and, having familiarised myself with the computations, I can experiment with examples whenever I was confused with the theory (during the Part IA course). It is unsettling when you know neither what the theory means, nor how to actually get any answers out.
Of course it would be best if students could do the manipulations, and also prove things from first principles. But when it becomes too much for them, the situation you described is sadly the case.
December 6, 2012 at 10:03 am
That’s an interesting point. I too had the experience of learning and getting comfortable with matrix multiplication long before I had the faintest idea why it was defined that way, and I think that worked reasonably well.
December 8, 2012 at 5:23 pm
Because my experience learning mathematics has been unconventional, my exposure to matrices was diametrically opposed to the typical sequence, as described in Ms. Pang’s posts. I took two university courses in linear and matrix without knowing what a matrix is, never having seen a matrix in any context other than data tables in books.
I struggled mightily with the concepts precisely because I was completely unfamiliar with the objects under discussion. It was rather like learning how an internal combustion engine works without ever having seen, used or worked on one or even being able to recognize, without investigation the tools I needed to do the work. Our textbook (Serge Lange) was little help – terse, shall we say. I had to invest an inordinate amount of time learning about what matrices an represent, their geometrical motivation, etc.
The notion that concepts can be taught directly and alone is bankrupt. I know that’s a straw man in this discussion. But, we must be careful to balance the particular with the general and to asses which level of generality is appropriate (Gowers’s and Mahadevan’s comments about differentiating polynomials to depict the structure of proof in differentiation are exactly on target). One idea with which pre-university students struggle is generalization. One can start to teach this idea early in their “careers”, but, I haven’t encountered explicit discussion or instruction of it in textbooks or classrooms. By teaching and practicing reaching general forms from specific example, even as early as first-year algebra, we can prepare students for the notion of a proof and educate/train them in the process of discovery. Linear equations, sequences, series, geometrical patterns (Euler’s formula, e. g.) are a good place to start. And, it’s useful in many other subjects, not just science and mathematics.
December 7, 2012 at 10:14 pm |
My school maths exam happened today and Wednesday and went quite well. I realised I had a better-written textbook in my room which the school doesn’t use, and managed to understand the mystery language of C3/C4.
December 8, 2012 at 7:58 pm |
There are a few models of measuring mathematical ability which bear reflection in the context. The IMO, for example, gives four and a half hours to three questions – basically, the idea is if you can do it, you will have the time to do it.
Then there is the traditional (and I understand a-bit-under-pressure) Cambridge method with alphas, betas and gammas – an alpha showing that the candidate has really got the idea sufficiently to tackle an unfamiliar problem.
Then there is the idea of levels, supposedly embedded in the National Curriculum – the idea of whether a young person has passed a level of understanding or proficiency.
In principle, all of these are resistant to any system of adding up marks – in each case (particularly the first two and in theory the third) trivial mistakes are heavily discounted in an attempt to test real understanding and proficiency.
Assessment is a huge issue, and the “objectivity” of mark schemes and percentages needs some serious challenge.
December 11, 2012 at 12:12 am |
I’m a second year undergrad in maths at Cambridge and having gone down I’m doing a bit of work experience at my old school’s maths department: this involves going to classes, trying to observe from the teachers’ points of view, and going around helping people where necessary. Having read this post before starting last week, I have noticed many things, but here are some particular things that I have noticed. Based on conversations with people from other schools, I believe they are very general and not specific to this school.
I’ve been working with a few sixth form further maths classes, and they are coming up to their Edexcel C1 and C2 exams which they are sitting in January, so sadly they’re having to rush things a bit. One class did integration last week, trying to find the area under a graph, but sadly there was no explanation of why this is the inverse problem of differentiation. (The teacher did not even mention the words “Fundamental Theorem of Calculus”, but merely suggested that interested students may look at the relevant parts in the textbook. The relevant parts in the textbook are shaded, indicating that they don’t need to be learnt for the exam.)
This afternoon, a teacher was absent so I ended up taking the lesson. This was another class doing C2 and they asked me to tell them about geometric sums, so I did. We covered finite sums in a few minutes, but when we moved on to infinite sums I realised that they had not met the term “limit” or the symbol “lim” before. I didn’t give a rigorous description (no epsilontics, statement without proof that r^n -> 0 for |r| < 1, etc.) I think they now understand geometric series, but given that they did differentiation before this, it does put a big question mark over how the teacher had covered that topic if they had not met limits.
One chapter of the textbook was titled "Proof". This chapter gave examples of using (and often abusing) the implication symbols, followed by a few exercises to practise on. Pupils from one class mentioned that they had been told to "read it at home" (ahem), to save lesson time.
I can offer another instance of Professor Gowers' anecdote, above, of pupils failing to understand that, if you are given f(x) = x^2 – 3x + 2 (say) then you can substitute whatever you want for x. This was in relation to using the remainder and factor theorems (that when the polynomial f is divided by (x-a), the remainder is f(a), and that (x-a) is a factor of f iff f(a) = 0).
Like I say, based on what I've seen at another school, and on conversations with people sitting or having sat A-Levels from other schools, the above seem to be epidemic.
December 11, 2012 at 1:35 pm |
Your A level student is typical, and the problem is he is arguably being perfectly rational given his interests and motivations: as an A level student, why would you want to learn how to differentiate from first principles when it’s much easier (and sufficient for passing exams) to learn a few formulas?
Even if it was given more attention in the syllabus, the vast majority of students are going to realise pretty quickly that they don’t need to understand it and therefore won’t try to.
The issue is far more to do with how children learn maths throughout school, which leads to them lacking sufficient motivation or independence to want to understand the concepts properly, than it is to do with the A level syllabus.
December 12, 2012 at 6:25 pm |
I am looking forward to your future post on networks of facts!
December 13, 2012 at 8:44 am |
@John:
I do agree that it has to do with how children are taught that affects their motivation. That’s why if we want people to be more interested in understanding the theory, we must do something about the way they are evaluated from ground up.
Most people respond much more to consequences than idealism.
—
Here’s my suggestion. Since most people are never going to apply much of the maths they learn in school to their daily lives (except for arithmetics and possibly statistics & probability), the WHOLE syllabus should be changed so that students will learn how to discover solutions instead of being given formulas to use.
80% of the exam marks will be allocated to theory and discovery, 20% to application of formulas. For optional Math subjects that are more applied-oriented, this can be changed to 60%/40%. Applied mathematics courses should NEVER be allowed to replace the pure mathematics courses at high school level.
This syllabus should be implemented as early as 10 years old, right about the time that according to Piaget’s theory of cognitive development, children are able to think logically about concrete objects and events, and about to transition to developing their abstract thinking.
The greatest price of this is that the teachers who are not competent in the theory part of mathematics will have to be trained, and this may be a cost that most schools will not be willing to fund.
Other than that, most of the textbooks will have to be re-constructed, and the beginning batches of students may suffer from the lack of study materials.
Ultimately it is those people who are interested in mathematical discovery that will benefit the most, but at least such a syllabus will foster a better understanding of what math really is about, and hopefully garner appreciation from more individuals.
December 16, 2012 at 11:31 am |
I’ve taught Mathematis in secondary schools in the UK, China and Germany. It’s true that the A-Level examinations (especially Edexcel board) are basically very algorithmic, and promote little thinking.
Whilst many are disgusted by the view of Mathematics solely being taught as a service to the Sciences, the situation is even worse in many international schools at the pre-16 level under the guise of IB MYP Mathematics. Here the subject is relegated to a humanities curriculum, with common criteria for assessment.
Cynically speaking, if you are articulate and can explain how you don’t understand Mathematics you can pass MYP Mathematics with a strong grade without the most basic understanding of algebra.
On the other hand, at the post-16 level (IB Diploma) all students must study some Mathematics. At the lowest level (Mathematical Studies) students cover differentiation from first principles, and formal logic. For the IB Diploma (Higher Level), the course content is a lot higher than A-Level and the questions involve a lot more problem-solving, and more conceptual understanding. (Although strangely enough formal logic does not feature in the Higher Level syllabus).
This idea of only covering content if it’s on the syllabus is, IMHO, a much more English problem than exists for example in Asia.
December 17, 2012 at 10:32 pm |
same here with IIT-JEE coaching classes in India. Not limited to maths of course, hackery in physics and in organic chemistry reaction mechanisms.
Had a chemistry teacher who once asked about the futility of remembering the derivation of chemical equations pointed out dryly that since an equation(don’t remember the name) didn’t contain a volume term, the nearest ocean could work as a buffer solution with little effort.
December 19, 2012 at 8:09 am |
Perhaps the following anecdote might help explain part of this problem. My wife is a Music teacher in a local school, and she was approached by the Head of Mathematics asking if I would like to see that morning’s Advanced Higher Maths paper – the Scottish equivalent of A-level. She also asked my wife if I would be good enough to give her speciman answers to the questions, as she felt that none of the other teachers were confident enough about the material! She was going to do the questions that evening and would like to compare answers with another mathematician. The school has a mathematics department with about 8-10 staff.
December 20, 2012 at 6:31 am
I am working as a teacher and I must say that the work load increases from year to year without a reasonable compensation. Believe it or not, that makes me feel very incompetent from time to time.
December 23, 2012 at 5:57 am |
Reminds me of all of my High School education. – and I was always at the top of my class, and I STILL had no actual understanding of the material.
Thanks for the good post. It was the first one I read, but I think I’ll be back.
December 24, 2012 at 6:54 pm |
I did A level maths (pure and applied) in the early fifties, soon after they were introduced. My son did A level maths in the 80s, and one of my grandsons is doing them now. I thought my son’s course lacked depth, but was much wider than my course, My grandson’s course seems to lack both depth and width. My own teachers had all graduated before the war. They had been taught by people who were strongly influenced by Victorian mathematicians – Todhunter in particular. I was taught rigorously, certainly from first principles, but not with a more modern outlook on functions, limits, etc.
December 25, 2012 at 6:23 am |
Most of the students think that maths of A level is very much tough. And their most toughest part is integration and differentiation. But if we solve maths of A level or any maths through step by step , then i dont think that it is too hard to understand. Main thing is that student must have their basics strong.
SUZZANE
December 25, 2012 at 8:46 am |
I was once in an high school Maths class where the teacher gave us a problem beyond the standard curriculum but still related to the topic being taught. The reaction of one of the students was that it was not necessary because it was not in the syllabus. It then made me think about the education system and the way it narrows the creativity of a student. But also considering the average amount of students in a class, the limited time given to teachers to teach a concept and the several other subjects the student has to study, I have seen it would be very difficult for most students and teachers to cope with the requirement to fully understand the basics. What I would suggest is a change in the system to concentrate more on the basics and then, providing problems where the students would be required to bring everything they have learnt to solve these problems – similar to an Olympiad but not as difficult though.
December 27, 2012 at 2:46 am |
I am a big believer of learning on a “need-to-know basis”. Most biology students view calculus as a pre-Med (or pre-Pharm) requirement that is quickly forgotten after the class or standardized exam; not surprisingly their understanding is purely mechanical. It is a different experience when the students learn calculus as part of a medical physiology class, something they need-to-know if they want to become a practicing intern.
I would like to see a greater integration of the math and science classes.
December 27, 2012 at 4:23 am |
With so many cogent replies already I hesitate to add more, but a point that has not been raised is the role of administrators — deans, associate deans, chairs, and the like — in encouraging this level of ignorance. I am a successful research mathematician and dedicated teacher who was priviliged to study at some of the best universities in the USA. I was teaching far more than “need to know” (which is a silly concept because nobody knows what a student will need to know in 10 years anyway). The students complained. I persisted. The dean threatened. I persisted. The dean amplified the threats. I persisted. The dean made it clear that I would teach rote or die, so to preserve my skin (that is to say health insurance) I began to skip the proofs and the rigor and even the joy of connecting two seemingly unrelated ideas. The students responded quite enthusiastically and now there is talk of a teaching award for me. All because I stopped teaching.
January 2, 2013 at 12:06 am |
Politics will often hinder education, and any pursuit of the truth.
But if there comes a time where politics can cooperate with us to produce an effective education system, the first thing one can do is to reduce the scope of the syllabus and then focus on increasing understanding.
January 2, 2013 at 12:16 am |
Decreasing the scope doesn’t reduce quality nor hinder a student’s progress from high school math to undergraduate math.
Decreased scope means more time to induce understanding of the basic ideas, as most of us can tell.
For those who have no intention of furthering their mathematical education, they will likely forget most of the procedures they were taught in high school. For those who pursue a mathematical education, they will likely cover some of the topics in the previous grade in K-12, and cover some of the topics in K-12 in freshman year respectively. (An interesting question would be, why is this necessary? Because the syllabi makers probably know that students don’t understand the ideas, so they have to reintroduce them to prevent students from forgetting!)
Hence, it is unnecessary to introduce so much width to high schoolers.
On a side note, even if a student has much to cover as a result of a reduced scope in high school, 1) if he understands the basic ideas he can probably find a solution himself, and 2) those who aspire to succeed will find a way to cover them anyway!
January 11, 2013 at 10:32 pm |
A level mathematics relies too much on exam approach rather than mathematics itself, students don’t ask why because that’s not what they are awarded for (you are being given marks for doing, not for understanding), I am personally an A level student and I find it rather disturbing, where finding a student that understands what he is actually doing is difficult (this may be only problem at my college but I assume it’s not just my college that has that issue)
January 17, 2013 at 3:18 am |
I don`t mean to be saying something that is rather tangential. But is not the approach to use definition of ln x as the area under the curve y=1/x from 1 to x, and then invoke fundamental theorem of calculus to differentiate it and to differentiate e^x using differentiation of inverse of a function the preferred way of approaching the question you raised.
Another approach is to define e^x as the solution of the differential equation f` – f = 0 with the initial condition f(0)= 1, which I believe is the answer that you were trying to explain to the student.
I do find it curious that learning to use a tool and learning to understand how and why a certain tool works are probably challenges of a different cognitive level, which is why the student was probably lost. Of course I am no real educator (other than some experience at teaching and learning myself) at least not someone who has in depth studied psychology of (learning) mathematics, but it seems fair to say from my experience that understanding why and how a tool (such as derivative) works from using the definitions at least for the problem you were addressing, has something to do with the fact that definition of e^x itself is puzzling. So there is a tertiary cognitive complication.
I am curious what your (or anyone`s) opinion or experience is regarding this matter.
January 17, 2013 at 1:21 pm |
These are some half-formed thoughts that might be of interest to those who worry about mathematics being taught in terms of applications.
I teach aerospace engineering in a leading UK department, although I grew up in Ireland, taking my A-Level equivalent maths there in the mid 80s, and studied at Trinity College Dublin. I learned about limits (fairly rigorously) as part of learning calculus at school, and learned to calculate derivatives from first principles using the idea of a limit. At university, I had three years of maths from mathematicians who gave us rigorous analysis (real and complex), calculus, numerical methods, and linear algebra. In the work I do now, I find myself using a lot of those ideas as assumed knowledge, without needing to worry about them too much.
My students, on the other hand, have largely taken A-Level mathematics and get two years of mathematics from staff in an engineering department. I suspect that the problems arise from their A-Level background, because they do not have routine fluency in certain ideas. For example, in teaching a little orbital mechanics, the equation $d^2u/d^\theta^2 + u =0$ arises ($\theta$ is azimuthal angle, $u=1/r$ where $r$ is the orbital radius). This should be a routine problem to solve, since it is a standard second order differential equation. Many students do not recognize this until I write $x”+x=0$ underneath it.
The problem seems to be that students do not learn maths as maths, but as a bag of tricks, with one trick for each application. I learned mathematics without applications (which has its own problems), but got a command of ideas which have been useful to me ever since, and which save a lot of time. If you have the idea of `orthogonality’, in the sense of `inner product space’, a wide range of methods become obvious, for example the use of a Proper Orthogonal Decomposition in turbulence analysis.
On the other hand, I think there is something to be said for mechanical application of rules (if you understand where those rules have come from). The great power of mathematics in engineering, say, is that once you have written the problem down, a series of mathematical operations, which need have no connection to physical reality, can be used to give you an answer. If you have some fluency in a reasonable set of mathematical ideas, you can make progress in a wide range of problems, and understand why some things are harder than others.
January 19, 2013 at 5:16 am |
the problem is because mugging up the formulas without thinking about why, how….
January 21, 2013 at 9:51 pm |
While reviewing the Cambridge International A Level Maths course
for possible advance placement at the University of Alberta,
I was struck by the fact the curriculum content contains
the comment “(the technique of differentiation from first principles
is not require).” Prof Gowers’s blog and the comments that follow it
lead me to conclude some A-level instructors have taken this as
license to gloss over the limit definition of the derivative.
February 28, 2013 at 1:40 pm |
[…] […]
March 1, 2013 at 6:43 pm |
I am neither a math teacher or a mathematician. zzephod from Mathhelp.com refered me to your blog, in response to a comment of mine. I found your blog interesting. It was curious that your example was the same one I was asking about. You makes the distinction between teaching how to understand math and teaching mechanical manipulations (which I was calling “cheap tricks”). I can share at least one student’s reaction — mine — to this distinction. When I was taking high school algebra we started coming to some things that didn’t make immediate intuitive sense to me. The first one was that a minus times a minus equaled a plus. In one way I could understand this, yet it seemed to me that if the minus and the plus areas on a number line were symmetrical extensions from 0, then the way it worked should be symmetrical on each side of 0. (If this makes sense.) I asked about this and was told that I needed to simply accept it and do the problems. As other things came up that also weren’t intuitive to me, things that I was just to accept, I turned off on the whole process and stopped making an effort to learn algebra. A very similar thing happened with Physics. It had to do with the speed of light being the same as measured from earth regardless of the speed at which different sources of the light were traveling in relation to the earth. This made no sense whatsoever to me. It was impossible, and I told the physics teacher it was. He said that it simply was true. I argued with him. It wasn’t true of anything else, I pointed out. I was eventually told I just had to accept it. And at that point I turned off on physics. Much later I learned about the special theory of relativity — and then about the general theory and then quantum physics, etc. This was fascinating stuff, which I could more or less grasp intuitively, but not mathematically. I regretted my earlier turning off on math and some 50 years after those fateful high-school courses, I took a pre-calculus and then a calculus course. They have hardly made me a math wizard. But learning this this math does promise to give me the tools for a better understanding of some fascinating stuff.
I think if my teachers had been teaching understanding rather than rules, I would have eaten it up.
jedson
March 9, 2013 at 1:57 pm |
[…] I end this post I want to say something else. Timothy Gowers (a very famous mathematician) wrote the following in his blog sometime […]
March 21, 2013 at 4:02 pm |
One of my greatest disappointments with the modern teaching of calculus (at least in the U.S.) is that (except in honors courses) the definition of a limit is no longer taught. To my mind the epsilon-delta definition of a limit is a pinnacle of modern thought, and most of calculus rests on the pillar of limits.
Of course, to teach the definition of a limit well, you need to ask students to work out examples, and many examples require manipulating a few inequalities. Adeptness in manipulating inequalities is not a skill that much time is spent on or that most students can readily acquire. But this isn’t necessary for the students to work out a few simple examples of the definition of the limit that don’t push inequality skills very far.
In my experience the only way to teach the epsilon-delta definition of the limit — assuming that the heuristic idea of a limit has already been conveyed — is to linger over each one of the four clauses in it until its meaning is crystal-clear. I suspect one reason this definition has been dropped is that unless each clause is lovingly lingered over, the definition will just be stated as a whole, and that is a lot for even a bright student to grasp in one swallow.
But to leave out the epsilon-delta definition of the limit from calculus courses is a crying shame.
March 21, 2013 at 4:39 pm |
Leaving aside the question of whether limits ought to be taught (I myself agree that at university level it is a great pity not to do so), it is interesting to think about how to do the “lingering” you talk about. One component of the process that I think is helpful is to look at a few key examples of convergent and non-convergent sequences (or functions if one is doing those limits). For example, one could write down the following four sequences:
1, 0, 1, 0, 1, 0, …
1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, …
1, 1/2, 1/3, 1/4, 1/5, …
1, 0, 1/2, 0, 0, 1/3, 0, 0, 0, 1/4, 0, 0, 0, 0, 1/5, …
Pretty well everyone would agree that the first two do not converge, and the second two converge to zero. Then one could ask people to justify that. Of particular importance is that the last sequence is not “getting closer and closer to zero”. “Yes,” someone might object, “but the amount by which it messes about gets smaller each time.” Maybe that would be the moment to write down a sequence such as
1/2, 0, 1, 0, 0, 1/4, 0, 0, 0, 1/3, 0, 0, 0, 0, 1/6, …
just to be annoying. And eventually one might just manage to provoke a few people into formulating something close to the correct definition.
March 28, 2013 at 12:16 am |
Your observation about the difficulty of remembering isolated facts vs networks of facts may help explain why people are so bad at remembering the names of people they meet at an event.
Often one meets someone at an event, and they tell you their name, and one starts a conversation about where they work, how they know the host of the event, where they live etc.
At the end of the conversation it’s often the case that one’s forgotten their name, despite remembering many of the other facts they told you – facts such as where they work, what they think of their boss etc.
It may be that these latter facts, the ones that one remembers, stick in one’s mind because they are part of a network of facts that the person tells you. Their name, on the other hand, is an isolated fact that they tell you, one that’s unconnected with any of the other facts that were discussed in the conversation.
April 3, 2013 at 4:36 pm |
[…] Questo discorso mi sembra di averlo già sentito/vissuto (spiacenti per l’inglese: non ce la farei a tradurlo tutto in tempi ragionevoli). […]
June 10, 2013 at 8:38 am |
Hi, I am a mere 17 year old taking the a level syllabus; an amateur if you will.
d/dx (e^x) = lim h-> 0 (e^x.e^h – e^x)/(h)
This can be factored into
e^x lim h-> (e^h -1)/(h) as you have mentioned.
Now this is then equal to 1.
My question is this ; suppose you replace e with say a number , a. Then, why does
lim h->0 (a^x -1)/(h) not equal to 1. What makes it so different?
I would also like to add that I do NOT want an answer that says that this is experimentally proven. That would be a disgusting and frankly speaking dishonest answer.
Also what does a number, b, raised to the number of an irrational mean? For instance,
a^ root 2 =???
The way I would do it is as follows;
Let a^ root 2 = b
Then raising again to the power of root 2,
a^2 = b^ root 2
But this is (in hindsight) plain stupid.
I have therefore accepted the fact that we can only approximate a^ root 2. ( in passing , I am tempted to ask, how can we prove that a^root 2 is an irrational?)
Consider also the proof that root 2 is an irrational number.
Suppose root 2 is rational.
Then by default, root 2 = p/q where p and q are elements of the integer set and q not equal to 0. Let p/q be a fraction in its simplest form. Then,
2q^2 = p^2
Then p can be replaced by 2k
Therefore,
q^2 = 2k^2
Then q must be even.
But p/q is a fraction in its simplest form.
Therefore, this is a contradiction and root 2 is an irrational ( Q.E.D)
Now I want to generalize this proof and prove that root a is irrational where a is an element of positive real numbers and a not equivalent to n^2 where n is an element of rational numbers.
This proof however is still not good enough. What about the generalization nth root of a is an irrational where a is an element of real numbers ( for odd nth) and a not equal to m^n
for m an element of rational number?
I would also like to ask what root 2 means and how we can draw out root 2 if it cannot be measured fully? (The drawing is easy; simply draw a right angle with sides 1 and 1 and the hypotenuse will be root 2) my question is what is the meaning of such a number physically? This also applies to the number pi. The circumference of a circle is given by the formula C = 2 x PI x R.
Consider r to be a rational number .
Then C is an irrational.
What does that mean physically ? How can we draw something that cannot be measured?
Thanks
June 10, 2013 at 12:55 pm
Hi Edward!
These are interesting questions, indeed. Are you aware of the “Ask NRICH” bulletin board at nrich.maths.org? That is a forum on which questions like this can be discussed – I do recommend that you post your question there, and you’ll get a series of good answers.
Julian
June 10, 2013 at 2:57 pm
Thanks a bunch! Appreciate it.
June 23, 2013 at 5:35 pm |
Reblogged this on Singapore Maths Tuition.
June 24, 2013 at 6:26 pm |
True, A-level is getting easier but the ‘First Principles’ of Maths is less emphasized. As a result, 99% of students who score distinction by drilling mechan
June 24, 2013 at 6:41 pm
… by drilling mechanically.
Another observation of A-level Calculus teaching, it never teaches students to be rigorous. Before applying all kinds of techniques to integrate, first check the domain of definition in which whether the function is defined? continuous? If the function is not continuous, then integration stops because it is not integratable over that domain (or interval).
In French lycées Baccalaureat, this rigorous practice is very much emphasized. When I was a student then in France, the professor yelled at me because I started straight to integrate without the prior check of integratability over the domain of definition and continuity.
July 25, 2013 at 4:29 pm |
Hi Tim, thanks for your response. I am also very much interested in Math education which I think could be made fun and enjoyable for students, just like they enjoy learning music, literature or science. Math should not be taught in such boring and scary pedagogical way in all schools in the world.
You are welcome to visit my blog tomcircle.wordpress.com, I would be honored if you find any idea useful to you.
Best regards,
Cornelius Goh
On Thu, Jul 25, 2013 at 2:32 AM, Gowers’s Weblog wrote:
> ** > this website commented: “Hi, i think that i saw you visited my website > thus i came to �return the favor�. I am trying to find things to enhance my > web site! I suppose its ok to use some of your ideas!!” >
July 25, 2013 at 10:31 pm
I’m afraid that’s a spam comment rather than something I wrote. I hope it doesn’t mean that this blog has been hacked into. Does the commenter provide an email address?
Nevertheless, thank you for your contributions to this discussion, and your blog looks nice.
July 26, 2013 at 2:04 pm
I see. No email address indicated in the comment.
Thanks for visiting my blog.
July 28, 2013 at 11:44 am |
Reblogged this on Math Online Tom Circle and commented:
Many insightful points on A-level Math. In some Junior Colleges there are close to 100% students scoring distinction in A-level Math just to show that either the exams papers is too easy or students are too smart to spot questions from past-year papers and drill to score perfect marks. Do the students learn the real math to prepare them for university education?
November 15, 2013 at 9:35 am |
I agree with tomcircle. In most of the cases, our teachers are using outdated teaching methods which students do not take much interest in. The books too are not very well written. Our education system is supposed to pay attention to this issue as soon as possible.
April 19, 2014 at 6:08 pm |
[…] An A-level student (if you’re Tim Gowers); […]
November 19, 2014 at 8:44 pm |
I am a current A-level Maths student. So far we have derived everything you have spoken about in this blog. I think it’s unfair that you say all these things based on your interaction with one student and I can tell you that if I was put under the kind of pressure you put the student under by not asking completely clear questions, I would get the answer wrong, even though I understand everything you are talking about. Also, I understand the concept of deriving differentiation but I have never heard of the term “first principles”. This seems to be a name that you “just learn”, which you are so against. I think this student (or just me) would have known how to answer the question if you explained it, not used the term “first principles”.
November 20, 2014 at 12:45 pm
Well I did say right at the start that a generalization from a sample of 1 should be treated with caution. Also, when it became clear that this student didn’t know what I meant by “from first principles” I immediately rephrased the question, so I don’t think his saying that the derivative of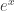 was
was  and then being unable to see what was wrong with it can be explained by any lack of clarity in what I was asking. I asked, “How would you work out the derivative of
and then being unable to see what was wrong with it can be explained by any lack of clarity in what I was asking. I asked, “How would you work out the derivative of 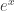 ?” Is that unclear in some way that I cannot see? And, as I said in the post, it seems that he had been shown how to differentiate from first principles: the problem was not that he hadn’t been shown it but that he had been told that he didn’t need to know it for the exams, which he took as an invitation to forget about it.
?” Is that unclear in some way that I cannot see? And, as I said in the post, it seems that he had been shown how to differentiate from first principles: the problem was not that he hadn’t been shown it but that he had been told that he didn’t need to know it for the exams, which he took as an invitation to forget about it.
November 20, 2014 at 6:12 pm
There are people who do maths with me who still do not know many simple concepts so it is not necessarily a reflection on teaching style but could be lack of deep understanding of maths. Also lots of people doing maths A level in my year are doing it to pursue other careers such as medicine and not maths. Therefore, it is better for other careers just to know how to apply lots of concepts and not to deeply understand much fewer concepts. For lots of people (not me) maths is just a stepping stone and I don’t think people like this should be forced to understand every mathematical equation.
December 29, 2014 at 5:46 pm |
In my views ,most of teachers of mathematics in Pakistan do not have basic concepts regarding relations. that is why concept of function remains weak.
January 24, 2015 at 11:14 am |
[…] Gowers (2012) on maths. A Fields Medallist and Cambridge professor, Tim Gowers, described some problems with Maths A Level and […]
January 27, 2015 at 5:55 pm |
[…] (2012) on maths. Tim Gowers, Cambridge professor and Fields Medallist, described some problems with Maths A Level and […]
April 2, 2015 at 6:53 am |
When the examiners stop testing a concept, the teachers are not eager to teach the concept and eventually the students stop learning the concept.
Or perhaps when the examiners stop testing a concept, the students are not eager to learn the concept, and eventually the teachers stop teaching the concept.
The cycle gets more vicious when the generation of students become the generation of teachers …
… until the examiners start testing the concept again.
March 18, 2016 at 10:49 pm |
Reblogged this on Function of Thyme and commented:
Saving this one for later.
March 21, 2016 at 5:57 pm |
Is it possible to “understand” math?
Yes, it is. If you learn math by memorizing formulas and applying them over and over, you’re not ever going to understand anything. You’re not going to have a sudden epiphany one day. Read your textbook. Although most high school textbooks are absolu…
May 23, 2016 at 12:24 am |
I think the problem with the the exams as they stand is you have to get to a point where you have memorized the derivative/intergral whatever it may be by heart simply to have enough time to finish in the time allowed. Deriving something I find to not really be a good use of time in the exam. So teachers I guess try to focus on the memorising first so students can at least finish and we students being lazy go with that’ll do if we are getting A/A* in tests. Personally, I cannot remeber a thing without it being in context so looked up how it all pieced together in my own time. This leads quite nicely onto my argument that they should make the exams twice as hard but have no time limit. How is someones mathmatical ability tested thoroughly when to finish the paper you pretty much have to be writing consistently, which means there is no time for logical deduction or any interesting questions to be included. No wonder everyone thinks maths is boring when all we are doing is memorising stuff not thinking!
Written from the perspectie of an AS Maths/Further Maths student.
November 13, 2017 at 4:01 am |
Late to the party.I learned calculus not long ago.I used two books; Lang and Keisler.I found Keisler’s method (using infinitesimals) more intuitive and easier to work with from first principles.It also greatly clarifies Leibniz’ notation, at least at this introductory level.
October 7, 2020 at 1:24 pm |
Hello: what you have essentially rediscovered is the difference between instrumental and relational learning. There are two – very different – subjects being taught under the name “mathematics”. The following article by Skemp is absolutely wonderful at describing this. I think the instrumental approach permeates even university level mathematics – many students are unable to construct very simple examples or counterexamples in subjects like real analysis, which require relational learning.
Click to access Richard_Skemp.pdf
June 7, 2021 at 12:38 pm |
Many years ago, whilst helping out on 1st year remedial mathematics at a Redbrick University (we only took students with an A in mathematics!), I had an identical conversation. Not believing the student when he said he had never seen the fundamental theorem I checked with the school and found that as teaching the fundamental theorem was discretionary they used look-up tables. The conversation was also difficult as it emerged the student didn’t understand the concept of “functions”.