If you were looking for a clue about this year’s winner, you could perhaps have paid attention to the curious incident of my recent Mathoverflow question.
“But you haven’t asked any Mathoverflow questions recently.”
That was the curious incident.
Anyhow, it was wonderful to be told that Endre Szemerédi was to be this year’s winner. I won’t say any more in this post, but instead refer you to the Abel Prize website and to the written version of the talk I gave, which was intended for non-mathematicians.
Gowers's Weblog 
March 21, 2012 at 1:46 pm |
[…] A prize and for what explained. […]
March 21, 2012 at 2:14 pm |
[…] “The Work of Endre Szemeredi” de Timothy Gowers encontra-se disponível a partir deste artigo do seu blogue. Partilhar isto:TwitterGostar disto:GostoBe the first to like this . Deixe um […]
March 21, 2012 at 3:28 pm |
Reblogged this on Room 196, Hilbert's Hotel.
March 21, 2012 at 5:41 pm |
Well done Norwegian Academy.
March 22, 2012 at 8:14 am |
Why is it a clue that you asked no question on Mathoverflow?
March 22, 2012 at 8:29 am
That’s a reasonable question. The comment was a joke that only a small proportion of readers could be expected to get, so I’ll now explain it. Last year, I was talking about John Milnor, and I couldn’t understand why his famous result about exotic spheres wasn’t obviously false. So I asked a related question on Mathoverflow, without revealing why. So this year my failure to ask a question could have been taken as a sign that I was more familiar with the work of the winner, as was indeed very much the case. But it would have been a silly argument, as I wouldn’t have dared to ask about an unfamiliar topic. So there were in reality no circumstances in which I could have used Mathoverflow to help me this year.
March 22, 2012 at 8:43 am |
Thanks for the explanation, Tim.
And I’m very happy to learn that you are a Holmes aficionado …
March 22, 2012 at 9:57 am |
I predicted the winner correctly (for the first time in ten years)! My clue was that Terence Tao told me a few years ago that Endre Szeméredi is his favorite mathematician. The interview is here (in Dutch): http://www.wiskundemeisjes.nl/20070426/de-favoriete-nog-levende-wiskundige-van%E2%80%A6-11/
Your talk was excellent yesterday, I liked it even better than the written version.
March 22, 2012 at 5:23 pm |
[…] Fellow math blogger, Tim Gowers, was in charge of giving a talk for non-mathematicians (i.e. journalists and such) about Dr. Szemerédi’s research. A tough challenge which Dr. Gowers adroitly pulls off. You can read the text on his blog here. […]
March 22, 2012 at 7:53 pm |
Before the announcement I looked at your recent questions, noticed there were none, thought that perhaps Terence Tao was picked (I know little combinatorics so I could not value Szemerédi’s achievements myself), then thought more probable that you had decided not to ask publicly, knowing that you would reveal you were giving the popular talk. This made sense especially if you were going to be a regular presenter, to avoid a guessing game. Then I made the Tarski joke because I could not think of a logician for the Abel prize -now I think perhaps Hrushovsky, Shelah, a computer scientist, a set theorist. The big question is: why “mereological sum”?
Also I would be curious to know how many nonmathematicians looked at the public lecture, what they think about it and how it influenced them.
March 23, 2012 at 10:06 am
The mereological sum business was another thing not to be taken too seriously. I wanted to be very careful not to give anything away, including the number of winners (which can be greater than 1). My initial impulse was to refer to a set of mathematicians, but that isn’t correct: the Abel Prize is not awarded to a set. So I wanted to do something like the following operation: take a set of mathematicians and remove the curly brackets. So my question was this. If I take some mathematicians, form a set out of them, and remove the curly brackets, then what is the relationship between what I now have and the mathematicians I started with? I think the answer is that I have their mereological sum, though I wouldn’t be too surprised if a philosopher read this and told me I was wrong.
March 23, 2012 at 6:23 pm
Thanks alot for the explanation. I really should have understood that by myself. I guess philosophy requires too much rigor for me.
Thank you.
March 23, 2012 at 6:39 pm
On a second thought, I think “union of mathematicians” would be the appropriate counterpart of “mereological sum of mathematicians”, because “set of mathematicians” implies that you take the set of recipients (say using the axiom of separation), not the union of the recipients (the set made of all elements in at least one of them, whatever that may mean). And in mereology the counterpart of “set of…” would actually also be “set of…”, as a mereological object.
March 23, 2012 at 10:07 pm
Perhaps the difficulty of deciding how to describe the situation in a way that allows for an award to one mathematician, and also an award to a greater number of mathematicians, arises out of a decision to regard the prize as an abstract entity.
The prize money is straightforward. It consists of a pile of kroner, and we can think of each mathematician taking a part of the pile (an improper part when there is only one winner).
The prize itself is different. If we think of an entity, the prize, being awarded to more than one mathematician, we have to worry about curly brackets and mereological sums. But we could avoid this if we did not think in terms of an entity which was won by other entities, and thought only in terms of properties of the winner or winners. That is, we could describe people as Abel-Prize-winners, without thinking that there had to be an Abel Prize that they, or a set of them, or a mereological sum of them, had won.
This approach is not free of philosophical difficulties. Nothing is, not even nothing. And it would contradict clause 2 of the statutes of the prize: ” … en internasjonal pris … “.
March 23, 2012 at 4:38 am |
Tim
Thanks very much for your written talk – I enjoyed it very much.
I think there may be a small correction:
“pair up the rocks in L with the rocks in R” should be “pair up the rocks in L with the rocks in H” I think?
March 23, 2012 at 10:07 am
No prizes for working out how I made that mistake …
Anyway, thanks for pointing it out. I’m not sure whether I can change the version on the Abel Prize website, but with a bit of effort I can change the version linked to from this blog. Maybe I’ll wait a bit to see whether any other errors get picked up.
March 23, 2012 at 7:56 am |
[…] yesterday the Abel prize Laureate 2012. http://www.abelprize.no/ Congratulations, Srac! (See also this post on Gowers’s […]
March 24, 2012 at 6:18 am |
A couple of additional typos in the written version:
– “Some ‘elementary’ proof are amongst the hardest…” (should be “proofs”)
– “I’m just going to repeat that is elementary in the technical sense…” (missing “it”)
– “…computer program that was able learn from experience” (missing “to”)
Thanks for sharing the talk!
March 31, 2012 at 5:02 am |
Tim, do you agree with the following interpretation of your essay
“Gowers speaks about a possible scenario of the development of mathematics in his essay “Rough structure and classification” (published in a special issue of “Geometric and Functional Analysis” in 2000 or 2001). See Section 2 entitled “Will mathematics exists in 2099?” He outlines a scenario in which mathematicians are gradually replaced by computers. This essay cannot be separated from his more famous essay “The two cultures in mathematics”, published nearly simultaneously. All supporting examples for his scenario belong to his “second culture”, which is more or less coinciding with the Hungarian style combinatorics. His attempts to approach some issues of the first culture along the lines outlined by him failed abysmally. A Wigner-shift to the Hungarian combinatorics would make his scenario a much more probable one. Indeed, it would be not very surprising if a Szemeredi-Gowers-like mathematician could be surpassed by computers (assuming that Gowers’ own description of his style in “Two cultures…” is correct), very much like Kasparov was surpassed by a very primitive by the current standards computer. But it is hard to imagine that Serre or Milnor can be ever approached by a computer.”
Taken from a comment thread here
http://www.blogger.com/comment.g?blogID=4049018105272921172&postID=8690732893167971234
March 31, 2012 at 1:11 pm
I agree with some of it, disagree with some of it, and am not sure about some of it. The main point of agreement is that I am very interested indeed in the possibility of getting computers to do a lot of what can currently only be done by mathematicians. I do not know what “His attempts to approach some issues of the first culture along the lines outlined by him failed abysmally” is referring to. I don’t recall having made any serious attempt in this direction. I disagree with some of the disparaging remarks about Hungarian-style combinatorics that you did not reproduce here. Also, the writer seems to have a picture of me as a wheeler-dealer that I don’t recognise.
But the most interesting question is whether Serre or Milnor can be approached by a computer. The first thing I’d say is that that’s setting the bar very high: by and large Serre and Milnor can’t be approached by humans either, except in very rare cases. So the real question (for me) is whether there is something about first-culture mathematics that means that computers would necessarily be terrible at it, as opposed to merely not the best in the world. The difficulty I have here is that I am not sufficiently trained in that kind of mathematics to be able to think about this question by analysing carefully how I do it. I’d love to be able to do more, but in the end I think my efforts are better spent on thinking about how computers would do the kind of maths I myself do.
I’d be very interested indeed if somebody who works in more of a first-culture sort of area took the view that computers ought to be able to do that too. (Actually, Gromov strongly believes that computers can take over, and he has plenty of first-culture experience.)
April 3, 2012 at 9:00 am
Computers obviously cannot replace human beings, Godel and Turing prohibit this. But of course it is intersting to which extent computers may help mathematician to solve their problems, how low is the complexity of the “real-life” mathematical questions. So, Timothy really has a point here, and I don’t see why one who loves “first” culture (may be it is second actually?!), and who obviously hasn’t succeeded in building any theories (great mathematicians never go down for condescending way of talking to others), would start casuistry about “computers replacing people”.
April 3, 2012 at 10:28 am
I’d query your use of the word “obviously”, since only a small minority of mathematicians and philosophers agree with Penrose that Gödel and Turing’s arguments demonstrate that there is something that humans can do that computers can’t.
April 3, 2012 at 12:32 pm
To Anonymous:
Here is a quote from Gowers’ GAFA Visions essay.
“In the end, the work of the mathematician would be simply to learn how to use theorem-proving machines effectively and to find interesting applications for them, This would be a valuable skill, but it would hardly be pure mathematics as we know it today.”
If this is not “computers replacing mathematicians”, then what it is?
April 3, 2012 at 12:59 pm
To Timothy Gowers:
The quoted by Anonymous comment requires some clarifications after being transferred here. You understood me partially correctly, partially not, and partially attributed to me something that I never said or even thought (namely, a picture of you as a wheeler-dealer). Unfortunately, a proper reply will hardly fit in this narrow column (sorry, the pun is not intended). It is already two standard pages long. I will try to find a suitable place to post it. Here I will say just a few words.
What you called the main point of agreement at least now hides the main point of disagreement. In the above quote from your GAFA Visions paper you seem to agree that using computers is not (pure) mathematics. But it is hard to understand how such a mathematician as you may be interested in eliminating mathematics. Anyhow, some people (including me) love mathematics in the original sense of this word as opposed to assisting computers.
I agree that the most interesting question is the one about Serre and Milnor. Are they humans or some kind of superhumans? But it leads nowhere, we have to assume that they are humans, as we do with respect to all similarly looking creatures.
Finally, after being charmed for several years by your essay about two cultures and studying some part of that presumed second culture as a result, I come to the conclusion that there is no two cultures, there is only one (pure) mathematics.
April 3, 2012 at 9:51 pm
Let me try to answer you when you say, “But it is hard to understand how such a mathematician as you may be interested in eliminating mathematics.” I’ll start from the premise that such an elimination (that is, an elimination resulting from a computer program that can do mathematics as well as we can and much more quickly) is possible. Thus, I’m trying to explain why if it is possible, then I am interested in it. Whether or not it is possible is a separate question.
The main reason I think it is worth trying to do an elimination of this kind is that the challenges along the way seem to me to be fascinating. It will be impossible to program a computer to prove theorems without a deep understanding of the theorem-proving process, and that, it seems to me, is an understanding that is worth striving for: I rebel against the idea of accepting that we rely on mysterious and irreducible flashes of characteristically human genius, and I want to know what is going on.
If it did turn out to be possible to get computers to do mathematics, then something I value would of course be lost. But there have been many such losses as technology has improved, and nobody would argue that those losses outweigh the gains. A recent example has occurred in the humanities: it used to be a mark of a good scholar in the humanities that they knew a huge amount and could therefore make connections that other people wouldn’t spot. That ability is still useful of course, but the vast amount of data that is now available online and searchable has made it far less important than it used to be. I can well imagine a recently retired clever-connection spotter thinking ruefully that what gave him/her such pleasure throughout an entire career would now be something that one could do just by typing a few words into Google. But we wouldn’t want to give up Google for that kind of reason.
Similarly, if it turns out that computers can do maths, then I think that things like the activity of sitting around for two weeks struggling to prove a lemma and only then realizing that there is a counterexample would come to seem as quaint as writing a PhD thesis by hand and paying somebody to type it up. And a generation of people would grow up knowing that computers could answer their mathematical questions (not all of them obviously, but the ones that humans might have been able to answer) and wouldn’t miss the hard slog that had previously been necessary.
There’s a very important qualification here, concerning how the programs actually work. If they are something like Deep Blue, using huge searches as a substitute for human understanding (which I actually don’t think is possible, so this is a rather hypothetical qualification), then something important would definitely be lost. So my requirement of a computer program that I would be happy (if a bit wistful) to see taking over is that it should be able to explain its thought processes in a way that humans can understand — at least when such explanations exist.
April 3, 2012 at 10:19 pm
Dear Tim,
You say “nobody would argue that those losses outweigh the gains”. I think I understand what you mean and am a bit surprised: I see alot (I couldn’t easily give numbers) of people arguing against technology making humans obsolete, in several ways claiming “it’s not the same result”, or “it was nice to do it by hand” (say chorizo), or “it was happier times back when humans did that”, or generally when humans used less technology.
I personally like all technology, without having thought about the issue thoroughly, but I think those are complicated and grave matters -so I plan to think about them more.
April 4, 2012 at 5:53 am
To Timothy Gowers:
Your explanation of this particular point is understandable, but not without serious qualifications. First of all, if this is your motivation, you are not mathematician anymore. You are a scientist, interested in a particular phenomenon. Mathematics is only partially a science; to a big extent it is an art. If your project succeeds, this art will disappear, in accordance with what you said in your GAFA Visions paper.
If you agree that you are not a mathematician anymore, then that my question is answered, but there will be other questions.
Second, your project is doubtful even for a scientist. Not all scientific and/or technological projects should be pursued, and not all of them are beneficial for the humanity. Imagine that A-bomb and H-bomb were created without the justification of the WWII and later of the Cold War, just out of scientific curiosity (many people consider this to be very objectionable even with these justifications), and then, of course, were tested, as the scientific method requires. Or imagine somebody working on a global weapon capable to turn the whole Earth into dust, and then testing it (for the sake of the argument, let us assume that it is impossible to deliver this weapon to another planet).
I would be surprised if you will not find such a research objectionable. Your goals are more moderate, of course: only to eliminate some kind of human activity. Still, your project is an experiment on human subjects, and now there are very strict rules for such experiments.
The Deep Blue example is quite relevant. The development of the chess-playing software started with exactly the same motivation you suggested: to understand how humans play chess. The success of Deep Blue told us nothing about this; it plays chess in a completely different manner than humans. Note that chess is, as G. Hardy mentioned in his famous book, a part of mathematics, only a very uninteresting one from the mathematical point of view. It is only natural to expect that if your project succeeds, the result will be almost the same. We will learn nothing about how humans prove theorems. But while chess survives as an entertainment, mathematics will not survive, since it cannot support itself as a form of entertainment.
April 4, 2012 at 7:55 am
I don’t have the space to explain why in detail, but I do not believe that anything like a Deep Blue approach to mathematics can be successful. I therefore think that the only way to program a computer to prove theorems is to get it to mimic closely how humans prove theorems. Therefore, I couldn’t disagree more when you say, “If your project succeeds, the result will be almost the same. We will learn nothing about how humans prove theorems.” One of my main reasons for interest in this is to learn about how humans prove theorems.
April 4, 2012 at 11:18 am
To Timothy Gowers:
Certainly, your explanations would be of interest not only for me. I hope you will have an occasion to write them down. Your claim contradicts all the experience of the humanity: successful technologies do not imitate the ways humans do things. Steam power, electricity, cars, planes, phones, computers, computers playing chess do not imitate humans. In any case, it is hard to accept this as a justification for your dangerous experiment: even in your own opinion, it can be justified only if your will get a particular outcome. The people who build the Deep Blue were interested in creating a tool to be used (of course, the chess was only a toy problem from the very beginning). The works in way different from humans, but it does not matter for the tool-designer. These issues are discussed in the book of Feng-hsiung Hsu, the system architect of Deep Blue. But as you say now, you are interested only in demonstrating that the most advanced intellectual human activity is not really human (Deep Blue did not demonstrated this for chess, and this wasn’t a goal).
After this short exchange of comments the question if you still consider yourself to be a mathematician emerged as the most intriguing one.
April 4, 2012 at 7:17 pm
I’m not sure it’s as intriguing as all that. I consider myself a mathematician because I try to solve mathematical problems. But probably the question you’re really asking is whether the activity of trying to work out how to program a computer to solve mathematical problems is itself mathematics. That is, would I still be a mathematician if I was devoting 100% of my time to trying to develop such a program? One could ask the same question of the process of trying to understand how somebody thought of a proof, or could have thought of it. Both activities involve thinking hard about how humans do mathematics, which is not itself mathematics. However, it is an activity that cannot be done well without significant mathematical experience (at least if my thesis that the Deep Blue approach won’t work is correct), and I don’t rule out that it might be possible to develop a formal model of “discoverable mathematical proof” that would turn the not fully mathematical question “How did anyone think of that?” into “Exhibit a discoverable [in the formal sense] proof of that.” I don’t claim to have such a model right now.
April 4, 2012 at 11:24 pm
To Timothy Gowers:
Of course, I am aware that you are working on some mathematical problems, and not only try, but actually solve some. In this sense you are a mathematician; and there is no much sense in discussing this triviality. The question is little bit more complicated than form you gave to it, but let start with your version. If you devote all your time to your program, then, as you say, you will exclude the Deep Blue approach, and will use your mathematical experience. I think that using the past mathematical experience cannot qualify you as a mathematician in this hypothetical situation. If some mathematician starts working on the Wall Street, she/he inevitably will use his past mathematical experience. Still, we usually say about such people “he/she quit mathematics and now works for Goldman-Sachs”. As all other people, mathematician can and do change their profession to some other sometimes.
But my question was not this one; I asked exactly what I wanted. It seems that your program of eliminating mathematicians is of very high value for you. In your explanations above with respect to the question “how such mathematician as you can be interested in eliminating mathematics” you presented yourself as a scientist, not as a mathematician. It seems that this scientific (presumably, it may be not) problem outweighs your recent work in mathematics. It seems that for you mathematics is a sort of an entertainment you are good at (like some people play chess or climb mountains), but for you the *real* problem is “can we replace mathematicians by computers, and if we can, how we do this”. For me this is hardly compatible with being a mathematician
April 5, 2012 at 4:36 am
sowa: Your argument rests on a definition of “mathematician” that is not universally accepted. Some people talk about “quitting mathematics” when they refer to leaving the academic mathematical world, but professional research mathematics is far from the only place where mathematics is done. While the word “mathematician” is sometimes used in an exclusive sense you seem to indicate (but have not precisely defined), one may also use the word “mathematician” to mean anyone who is skilled or educated in mathematics, or someone who uses mathematics as a fundamental part of day-to-day life.
At any rate, why are you wasting your time telling mathematicians that they aren’t mathematicians on the internet, when you could be using your antagonistic skills for far greater pursuits, like running for political office?
April 5, 2012 at 5:44 am
To Scott Carnahan:
I am not sure why are you wasting your time trying to tell some person on the internet how he should use his presumable skills. Anyhow, the answer to your question is very simple: I love mathematics, I am interested in the continuation of its existence, and I am not interested at all in holding a political office.
You don’t know my definition of a mathematician; I pointed out in my very first comment that the proper reply is quite long and does not fit in the comments here. If not the insinuations of the first Anonymous, I would try to write down my ideas carefully and to find a proper place to post them. Now many of them are already mentioned in the comments.
I do not think that one can be considered a mathematician only if he or she belongs to the academic world, although it seems that earning a living in some other way is not compatible nowadays with doing research in mathematics (it is well know that it was compatible sometimes at some places).
In any case, that is the point of arguing about what definition is the right one? There are some qualities which are necessary for being a mathematician in “my sense”. It is not my personal definition, it is the one a learned from other people either directly or through their writings. It seems to me now that I was influenced most by my Ph.D. thesis advisor and by writings of A. Weil and J. Dieudonne (who once usggested another definition, more suitable for his goals). Answering the question if somebody is a mathematician in this sense could be enlightening even if you adhere to another one.
The issue is not if the definition I use is universally accepted (in any case, such issues are not decided by a vote, this is not politics). The issues at hand are what is mathematics, is it valuable for the human race, would it be good to sacrifice it for the sake of scientific curiosity alone, etc.
April 2, 2012 at 4:02 pm |
Good text!
“to” missing in the sentence
[…] a computer program that was able learn from experience […]
April 4, 2012 at 11:34 am |
“Serre and Milnor can’t be approached by humans either, except in very rare cases.”
Really? Both are renowned for the clarity of their mathematics, besides anything else. With Milnor this is even official; he has a Steele Prize for exposition.
“it used to be a mark of a good scholar in the humanities that they knew a huge amount and could therefore make connections that other people wouldn’t spot. That ability is still useful of course, but the vast amount of data that is now available online and searchable has made it far less important than it used to be. I can well imagine a recently retired clever-connection spotter thinking ruefully that what gave him/her such pleasure throughout an entire career would now be something that one could do just by typing a few words into Google.”
I do not doubt that connection-spotting in mathematics is currently valued highly. In my own low-level experience (and the principle of mediocrity suggests that this is wide-spread; I am not Gel’fand) this is a matter of knowing one thing, or bunch of things, seeing another, and then recognizing a similarity, or parallel, or analogy. But “knowing” very often means “having some hazy acquaintance with or memory of”; how is this kind of knowledge to be uploaded to a database, when the person knowing it scarcely knows it themselves? And often the useful output is just as vague as the input: “Hmm, that reminds me, but of what exactly?”. Processing this imprecision is, currently, a crucial part of doing mathematics; when do you expect databases to be able to handle it as well as we do?
April 4, 2012 at 7:10 pm
That’s a very good question that I have certainly thought about but will not have a good answer to without thinking about it a lot more (and not necessarily even then).
I think you misinterpreted my remark about Serre and Milnor. I meant that only very few humans can do mathematics of the depth and originality of that of Serre and Milnor. I did not mean that very few humans can understand what they did.
April 4, 2012 at 11:52 pm
To Another Anonymous and Timothy Gowers:
I think that can add some perspective to the Serre-Milnor question. By the way, Serre also got a Steele Prize for expository writing (for “Arithmetics”). The quality of writing is indeed relevant here. Both of them wrote (and still write!) very clearly. The way they wrote their papers and books helps tremendously to understand not only why the results are true, but also that the results (not always their own) are natural and inevitable. Later on both of them wrote extremely interesting accounts of how they were lead to discover their Fields medal results. So, they are “approachable” not only in the sense that we can easily read their remarkable books and papers. We can also get a lot of insight into how their results were discovered.
So, the answer to my question above is that Serre and Milnor are humans. It was to some extent a rhetorical question. As I said, the answer “yes, they are humans” is true by much more general reasons than outlined here. The choice of these two mathematicians was not my; they were mentioned in the original post of avzel on blogspot as mathematicians with whom E. Szemeredi cannot be even compared. I indeed had some candidates for being superhuman (it does not matter if Serre or Milnor were among them), and even had discussed this issue online (but this was a private conversation). My current position is that they are all humans both by the general reasons, and that this also follows form an analysis of their work, their historical context, etc., even if they did not provided as with such good clues as Serre and Milnor did. Such an analysis is very rarely done. For example, Galois work if sometimes presented as coming out of sky, but this is not true (despite an irreducible revelations is present, but it is usually present in the works of much lower level too.)
April 4, 2012 at 11:07 pm |
About Serre and Milnor: if I misinterpreted you, it was because the word “approached” is ambiguous.
More substantively, my question of imparting vague knowledge to a computer or database is one on which the AI people have been stuck for 55 years. This is not a criticism of AI; the problem is worth being stuck on. And I am no luddite; were connection-spotting to be mechanized that would be a huge intellectual advance. But *why* do you think progress might be possible here when it has been elusive elsewhere?
April 5, 2012 at 11:57 am
Apologies — I didn’t mean to suggest that the misinterpretation was your fault.
As for the more substantive question, it isn’t one that I can answer briefly, partly because I don’t have a satisfactory answer at all, and partly because the answer I do have is not all that brief. But let me try to give an unsatisfactory summary of my unsatisfactory answer.
Basically, what you are asking is why I think that this formidable AI problem might be less formidable in the particular context of automatic theorem proving. Part of the reason is the general one that I think that all formidable AI problems become a little less frightening in this context, because to do mathematics we don’t have to handle large amounts of messy real-world data. How might this play out for the particular problem of spotting vague (but real) connections? Here is one idea. It is too simple to do everything — let me make that very clear before I start — but I think that it is powerful enough that it could be used to spot at least some vague connections, including ones that are of genuine mathematical interest.
I’ll illustrate the idea with two examples. The first is very simple indeed. Suppose we have just been told the definition of a group and are given as an exercise to prove the cancellation law, that
implies 
. Somehow we have to think of multiplying both sides on the right by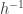 
and then applying associativity, which is problematic (from the point of view of coming up with a general method for solving problems) because it makes the two sides of the equation more complicated before it simplifies them. And if we’re allowed to do that, then why are we not allowed to do all sorts of other things that make problems more complicated?
The reason the approach feels natural to a human is almost certainly that they have seen cancellation laws before. The very notation for groups reminds us of multiplication of real numbers (or other numbers if you prefer), so we might think, “This looks like the multiplicative cancellation law for numbers, so perhaps we can imitate the proof of that. But how can one `divide both sides by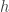
‘? Ah, we could think of the identity as a bit like 1, and then the inverse is a bit like a reciprocal. So maybe multiplying both sides by 
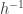would work.” At that point, being completely unfamiliar with the group axioms, we still need to check that our approach works, but that is a much easier problem. So our spotting of an analogy has been hugely helpful.
The key to finding this analogy was to recognise the more general concept of a cancellation law and then to search one’s memory for other examples of cancellation laws. At that point, the problem is reduced to smaller questions like, “What is the analogue of division?” that can be answered more automatically. (For instance, the “reciprocal” of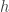
“ought” to be the 
that satisfies 
. And this turns out to exist and to be a good answer.)
This comment is getting long, so I’ll continue in a new comment.
April 5, 2012 at 1:40 pm
One might well object to the example I’ve just given by saying that it isn’t an example of a vague connection, since it is in fact completely precise. All I’ve done is take a familiar cancellation law — the multiplicative law for the non-zero reals — and generalized it to groups. I think that a lot of interesting mathematics can be done by generalizing, or by finding common generalizations, but sooner or later we will end up in situations where we exploit vague resemblances that we do not know how to turn into common generalizations. How might searching for those be automated?
Let me attempt a partial answer to that, by discussing another example. A useful lemma in additive combinatorics is the following. A dissociated set in an Abelian group is a subset
such that if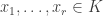 
, then no two of the sums 
, where each 
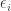is 0 or 1, are equal. (Other definitions are possible, but this one will do for my purposes here.) Suppose now that you have a subset 
of an Abelian group 
and 
does not contain any dissociated set of size greater than 
. What can be said about 
?
A natural reaction to this question is to spot that the definition of a dissociated set resembles that of a linearly independent set in a vector space. It is therefore reasonable to make the vague conjecture that
ought in some sense to be 
-dimensional. And once one has had that thought it is natural to speculate that a maximal dissociated subset of 
ought in some sense to “span” 
. And it is in fact easy to show that this is true in the following sense. If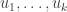 
is a maximal dissociated subset of 
, then every element of 
can be written in the form 
, where each 
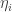is 0, 1 or -1. The proof is essentially the same as the corresponding proof is for vector spaces: if 
is not spanned in this sense, then one checks that it can be added to the dissociated set without losing the dissociativity.
Before writing this, I realized that one can with a bit of effort come up with a slightly artificial statement that simultaneously generalizes this lemma and the statement that a maximal linearly independent subset of a vector space is also a spanning set. However, that isn’t really the point, since it is not via that common generalization that one spots the connection. So what is going on?
I suggest that when we spot connections that are not wholly precise, what we are doing is finding common generalizations that can be written in a precise language (and therefore in principle handled by a computer) even if they are not precisely interpreted or universally true. For example, the common generalization here might be something like, “If you’ve got a maximal subset for which all combinations are distinct, then that subset generates the whole set.” There is then some work to be done: what is a combination? what does “generates” mean? etc. However, that is lower-level work, and should be easier than the preliminary spotting of the connection.
So what I would suggest is that a program for spotting connections would take precise mathematical statements and rewrite them in vaguer and vaguer language. My hope would be that many statements that start out distinct would become identical after a few stages of this process, and that is how vague connections would be spotted.
The big question for me is how far a method like that can take us. I’m convinced that it can do a lot, but I do not have a good reason to think that it can do everything. Indeed, I would expect many people to react at this point by saying, “That’s all very well for those simple examples, but what about X?” where X is a more sophisticated example. I’d be very interested in examples of vague connections that do not look as though they could be spotted in this way — or rather, I’d be interested in simple examples of such connections. If they involve a lot of sophisticated mathematical machinery, then it is not clear that the difficulty is not principally in the sophistication of the machinery.
April 6, 2012 at 9:54 pm |
I would like to add my grain of salt to the ongoing discussion on Gowers’s idea that computers may eventually replace mathematicians in some future. I dont know what computers will be in the future and they maybe able to do miraculous things, as in science fiction. I love science fiction, but I do not want to discuss it here. I do not want to speculate about quantum computing either. I assume that future computers will remain Von Neuman machines for a long time to come. They will be faster, have a bigger memory and they will be programmed differently.
Experience shows that mathematical thinking is depending on the alternation of two kinds of activities. One is about developing a mental picture of the problem, an intuition of its nature. The other is about making a calculation, as in algebra or formal logic. The two activities are performed alternatively as in a dance. A calculation is guided by an intuition, and the intuition is confirmed or rejected by a calculation. Few mathematical progresses can be made by using intuitions or calculations alone. Computers are very good at computing and they can help us doing mathematics, like a pen and a piece of paper. But they have no intuition, no consciousness. They are mindless mechanical machines.
I claim that we do not understand the nature of consciousness. Of course, we are making progress in studying the brain. But artificial intelligence seems to show that the brain does not need to be conscious to perform its tasks. So why should the brain produces consciousness? Consciousness is the blind spot of modern science.
April 7, 2012 at 6:57 am
My view is that the brain is just as much of a “mindless mechanical machine” (the apparent contradiction in terms is deliberate), and yet it somehow produces consciousness. That makes me optimistic (at least in the long term) about what computers might be able to do.
April 7, 2012 at 6:35 pm |
Maybe one needs to be a bit more clear about what ‘long-term’ and ‘possible’ are supposed to mean in order for this discussion to get further?
I think no-one who understands basic computer science would seriously claim that it is impossible for a computer to do something arbitrarily closely resembling human thought (whether you believe that is equivalent to being human, or genuinely self-conscious, or simply clever simulation seems to me to be a religious matter, and I’m not). If nothing else, one could in principle simulate the entire workings of a brain (noting that with current technology we cannot determine these workings well enough, but there isn’t any reason why it should stay impossible). So in principle we can replace Serre with a computer simulation, and it would no doubt show incredible intuitive abilities. But in practice, we do not have anything like the hardware to do this, nor are we likely to get it any time soon (i.e. here long-term could mean centuries)
On the other hand, it seems unlikely that simulating one particular computer which happens to run a desired algorithm is the best way to run the algorithm. So one could hope to somehow abstract the algorithm and run it on something more like current technology. In principle there is no reason why this shouldn’t work, and there is probably no reason why we should not be able to do it in a year’s time: it’s likely the solution will be simple (as compared to say the Windows code-base). But it’s probably also true that solutions to most major mathematical problems are similarly simple. I think it’s fair to compare the situation to the P=NP conjecture: nothing we have tried comes close, the only results we really have are of the form ‘this approach cannot work’. We still might solve it next year, but we probably won’t.
As some kind of middle ground, it’s possible we could develop a program which produces the kind of results we want but without our understanding how it works; evolutionary algorithms aren’t new, some of them really solve things in unexpected ways (I remember a decade or so back there was an FPGA circuit which solved a problem in a way which the researchers didn’t understand until they tried the same circuit with a different component layout: this didn’t work, and eventually it was realised that two neighbouring but unconnected components on the FPGA had a capacitance which was critical to the function but wasn’t ‘supposed’ to exist). Since these things are basically massively parallel maybe one could run an evolutionary algorithm in the style of SETI@home and get something useful. But it’s neither clear how one would design a scoring function for the algorithms being evolved, nor how long it would take.
April 7, 2012 at 6:36 pm |
To sowa:
If computers would be able to solve important mathematical problems and develop important mathematical structures/tools, then this wouldn’t prohibit you from doing mathematics nor would it destroy mathematics as an art. Quite the opposite, it would just put mathematics on the same scale with other arts – you have to do it out of your free time, and you only get payed when you do something very beautiful. Anyone who really loves mathematics, would still do mathematics. There would be even extra joy coming from the facts that 1) you have a mighty collaborator 2) much more (also beautiful) mathematics gets done 3) mathematics is potentially much more widely used.
So in fact, your accusations towards prof. Gowers of not being a real mathematician could using a Tolstoian argument be very easily turned against yourself.
April 8, 2012 at 9:27 am
To Hans:
First of all, since than claiming that somebody is not a mathematician, but “only” a scientist is an “accusation”? Is it now a sort of crime not to be a mathematician?
Pure mathematics exists as other arts anyhow. You are paid only when you did something other people like a lot. If you do not manage to produce something like this in your early years, you are out of the profession. The experience shows that it is nowadays impossible to do pure mathematics in your free time, as it was possible, say, to Fermat. Other jobs are too demanding, and mathematics requires prolonged concentration, which is not compatible with regular jobs.
In fact, most of traditional arts had disappeared during the last century. The modern paintings are essentially a kind of financial instruments. Still, a lot of people may appreciate visual arts and may pay for them for the pleasure and not as an investment. The situation in sports is similar. A lot of people appreciate chess even if they only know the rules. There is quite a lot or rich people among of them, and they played an essential role in supporting chess.
The situation with mathematics differs dramatically. The good current mathematics can be appreciated only by other professional mathematicians. You can do something incredibly beautiful, but it will be understood and appreciated first by a half-dozen of your closest colleagues. Even later, when a result finds its way in research monographs and then advanced level textbooks, the appreciation remains inside of the mathematical community. So, there is no outside source of support for this kind of beauty, and the mathematical community relays on at least potential usefulness of its production, as opposed to its artistic value.
Next, about the joy. There will be a joy of doing something better than a computer did. This kind of you exists without computers also; one may prove a theorem better than it was done the first time. But this joy is not comparable with the joy of doing something first time. What to do? Keep your ideas in secret from assistants to theorem-proving machines? They will spoil the joy anyhow, reproducing your result within a day.
I fail to see how a computer can be a mighty (or not) collaborator in the sort of mathematics I like. Computer may help to prove some theorem, like to (in)famous 4 colors conjecture, but there is nothing beautiful there.
I also fail to see why we (the human race) may need more mathematics. We already have too much. And why this computer mathematics will be beautiful. All beauty I ever seen in the output of computer was injected into it by humans before the computer started working.
The idea that pure mathematics is useful and is actually used is a fortunate (for mathematicians) misconception. The heart of pure mathematics, the proofs, is not needed for any applications. A heuristic argument together with an experimental verification is always sufficient.
April 7, 2012 at 8:09 pm |
I thank you Tim Gowers for expressing your position. I agree that the humain brain can be “mindless” in a rethorical sense (I am often mindless myself). You wrote that the brain can “somehow produces consciousness”. I would like to understand what you mean. Let me propose a thought experiment. One can imagine a universe parallel to ours, ruled by the same physical laws, with a planet supporting life like ours and everything exactly the same except for one thing: all animals and humans on this planet would be totally unconscious. This bizarre hypthesis is not absurd, since artificial intelligence is teaching us that consciousness is not essential to intelligence. Also, the hypothesis does not seem to contradict the laws of physics that I know. It follows from this thought experiment, that the presence of conciousness in our universe cannot be deduced from the law of physics as we know them. At this point, there are many possible positions. One would say that the idea of consciousness is an illusion of language. This is tantamout to saying that we are zombies. Another would say (as I do) that consciousness is real but we dont know what it is.
What do you mean when you write that the brain “somehow produces consciousness”?
April 7, 2012 at 10:27 pm
The zombie argument is a well-known argument in the philosophy of mind, and so is any response I am likely to think of. Like many philosophers (Daniel Dennett being a well-known example), I take the view that if a quasi-human on another planet had a brain that worked according to the same physical laws (complete with neurons firing etc.) then it would be conscious. In other words, I believe that consciousness is an emergent phenomenon and not some mysterious non-physical thing that can be added or subtracted.
In case I’m misunderstood, I don’t think consciousness is a black and white phenomenon. So if you had a sequence of ever more sophisticated computer programs, starting with today’s programs and ending with something that had software more or less identical to our brain’s software, I’d say that these programs would start out with virtually nothing that deserved to be called consciousness and would end up as conscious as we are. In between, they would have something intermediate.
April 8, 2012 at 1:26 pm
I thought the following are far from being settled:
1) The brain is indeed a computational device
2) The hard problem of consciousness is no more a problem and as Dennett says there is no such thing as Qualia.
Also, if we were to simulate ‘doing mathematics’, would it be like simulating the weather or like simulating addition?
April 8, 2012 at 4:16 pm
@Nyaya It is true that there are many who do not accept 1) or 2). However, there is a strong case for saying that 1) is true in a trivial sense if you believe in current physics — the brain is a physical system and physical systems can in principle be simulated computationally. The question then becomes whether it is a computational device in a less trivial sense: roughly, that we can hope to simulate it well enough on a computer to reproduce its outward behaviour — to which some, including me, would add the requirement that the software should be basically the same. (That is, I wouldn’t be happy with brute-force methods that just happened to give the same output, not that I believe that is remotely practical.)
As for 2), my view is that very strong arguments have been put forward against qualia by Dennett and others, and nothing I have ever read has come close to countering them. So I agree that it is not settled, but it seems to me that it ought to have been settled. (I feel the same way about climate change, though my respect for people who believe in qualia is infinitely greater than my respect for people who don’t believe in man-made global warming.)
April 8, 2012 at 3:09 am |
I thank you Tim Gowers for your reply. I am not a professionnal philosopher and I was not aware that my argument is standard. Anyway, it is a very natural argument and I am glad you have given an answer. I agree that consciousness is not a black and white phenomenon and that it is in some sense emerging. But I find the notion of emergence too vague and universal to be the basis of a real scientific explanation of the phenomenon. In any cases, if we succeed in constructing robots that behave intelligently, they better be unconscious. Because they will likely be used as servants, slaves, guards, soldiers and what? They will be reponsible of all the bad work. I would hate to know that my computer is suffering because it is computing for me days and nights.
April 8, 2012 at 9:45 am
To André Joyal:
Being conscious and being able to suffer (or to love, which are two sides of the same coin) seem to be completely independent phenomena.
In general, it is fairly amusing to learn that modern thinkers had only repackaged some century-old ideas of a well known political leader, V.I. Lenin. The metaphor of zombies may be new, but the idea of consciousness as an emergent phenomenon is worked out in his writings; it did not appeared to be so natural at the time.
April 8, 2012 at 9:59 pm
I thank you Sowa for the reference to Lenin and for expressin your view. You wrote that “Being conscious and being able to suffer seem to be completely independent phenomena”. Your are surely not saying that pain can exist without the consciousness of that pain? Are you saying that a conscious person may be devoided of emotion? A psychologist would probably diagnose this person as a psychopath. Of course, we may imagine that this person is a nice guy like Spock in Star Trek, but this is pure fiction. In your reply to Hans, you wrote that pure mathematics may be regarded as a form of art. I completely agree with you. Good mathematics allways carries an aesthetic emotion. Mathematicians are not purely rational minds. They are more like artists exploring the beauty of pure reason. It seems foolish to think that mathematical beauty can be fully rationalised. This is why we may never be able to replace mathematicians by intelligent machines. Why should we try?
April 8, 2012 at 10:57 pm
To André Joyal:
To be more precise, I am quite sure that one can conscious person devoid of emotions. Yes, such persons are usually classified as psychopaths (if they are not smart enough to hide this quality). By some estimates, about 5% of the population is such (I have no idea how accurate is this estimate, but at least it agrees with my own experience). But they are considered as humans, of course.
In the other direction the question is more subtle. Is it possible to suffer without being conscious? I believe that this is possible, at least to some extent. Let us look, for example, at sufficiently distant (in the biological sense) from us animals. It seems obvious that they can suffer, can be attracted to their mate or to a human, etc. But it doesn’t seem to be clear that they are conscious and if they are, to what degree. With the “emerging phenomenon” theory, if one wants a coherent point of view, one has to accept that *everything* is conscious, only to different degrees. Even stones, an even an electron should have a rudiment of consciousness. This is one of the issues Lenin recognized and dealt with. If we take such a position, the question disappears.
If one takes some other position, then it is natural to think that consciousness is needed for experiencing emotions. This only shifts the question. What is consciousness? I must admit that I don’t know what exactly the (post)modern philosophers understand by the consciousness. But nowhere had I seen a serious discussion of the following issue: is consciousness is just a receiver, a passive entity getting information from outside of it? Or it is also a transmitter, or, to put it better, is it active and creative? Personally, I believe that one cannot suffer without a receiver, but one can without a transmitter.
Starting with the words “In your reply to Hans”, I agree with every word you said, and don’t see any need for any qualifications or clarification. Here we are in complete agreement, including the last phrase “Why should we try?”
April 9, 2012 at 2:00 am |
@Sowa: In your reply to Hans, you wrote: “I also fail to see why we (the human race) may need more mathematics. We already have too much.”
I dont share your pessimism. Possibly because I am optimistic by nature,
It is true that mathematics is now too vast for one human been to know it all. It is expanding at an exponential rate (I would like to know the rate). More mathematics is produced every year (maybe every week) than what I can learn in my lifetime. The quality of the average mathematical paper seems to be going down. The number of mathematicians may double during the next 25 years, largely due to the contributions of developing countries like India and China (25 years is a rough estimate) . These developements will affect the mathematical culture (they are surely influencing it already). Mathematical knowledge appears increasely fragmented the barriers between the fields higher.
The traditional culture inherited from the age of enlightenment is under enormous stress, it maybe gone already. But something new may emerge from the ashes of the old culture. Can we figure it out? What we should do?
@Gowers: I am very interested in knowing your opinion on this. But my question could be out of the context you have created for this discussion. Please, let me know.
April 9, 2012 at 3:16 am |
To André Joyal:
Well, you quite nicely detailed what I meant: why there is “too much” mathematics.
I may add that the quality of mathematical papers is going down independently of developing countries. Take any top journal, like “Annals of Mathematics” or any other. During the last 20 years, the number of pages per year in “Annals” increased 3-fold, I think. There is no noticeable presence in “Annals” of mathematicians from China or India (I mean working there, not ethnicity). Most of the authors work in US, UK, rarely in France, and sometimes in other European countries. The number of positions did not increased, it is actually decreased. Inevitably, the level of “Annals” went down quite noticeably.
I don’t think that the quoted remark qualifies me as a pessimist (may be I am, but not because of this opinion). My point is there is no inherent good in producing more mathematics. It is not needed for applications (I already said this here: proofs are not needed, even in physics). Given the situation you outlined, more mathematics will serve no good for any individual mathematician. Today there is no way to learn in 100 years any sizable fraction of the already existing mathematics I would like to know (in particular, know about).
Craig Smorynski suggested about 25-30 years ago that mathematicians need to slow down the production new results for a while, and to put in order the things presumably done already. There are huge gaps in the literature, and many papers are hardly understandable. There are many examples from many branches of mathematics. The most distressing is the fact the some results or proofs are apparently lost despite their discoverers are still alive and well. They are just not interested in their old (and, occasionally, even new) results anymore.
I would like to stress that I am not speaking about the production of an average mathematician, I speak about superhuman insights of some of our contemporaries. Also, let me repeat, I am interested in the beauty of these insights and do not care much if a particular statement is true or not (probably, the generalized Riemann hypothesis is an exception, may be the only one).
April 9, 2012 at 4:34 am
@Sowa: You wrote that “Smorynski suggested about 25-30 years ago that mathematicians need to slow down the production new results for a while, and to put in order the things presumably done already” I feel exactly the same. Not that we should entirely stop producing new results, but that we should spend a lot of time reorganising what we already know, simplifying it, explaining it to others, learning other fields, reading old papers, writing introductory books, mastering the applications, etc. I am tempted call it SLOW MATHEMATICS, the opposite of FAST MATHEMATICS (like SLOW FOOD is the opposite of FAST FOOD). A fast mathematicians must write his papers quickly because he is in a rat race. His goal is to publish as much papers in a year as he can. His position and career are depending on that. Many mathematicians I know would love to slow down but they can’t. The value of slow mathematics is hardly recognized. We may be approaching the point where fast mathematics will destroy mathematics by turning it into a meaningless game, a pure rat race. Could slow mathematics save mathematics and mathematicians?
April 9, 2012 at 5:29 am
@André Joyal: I cannot agree more. I appreciate a lot when mathematicians do these slow things, and try to such things when possible. I like a lot learning other fields, and very happy when somebody writes an introduction aimed to mathematicians (and advanced graduate students). I found reading old papers be extremely illuminating even if the material is already in textbooks. I even had a couple of projects for introductory books (based on my graduate courses), but during last few months I realized that the mathematical books publishing may disappear sooner than I finish any of my projects.
I do not really understand why do we have this rat race. It seems that it is a fairly recent phenomenon. Personally, not very long ago I had the luxury to develop a little theory in the course of seven years after publishing only an announcement, devoted to this theory only partially. (I did publish papers about other things.) The final result is a very short monograph; a rat race would force me to publish it as nearly 10 papers, which would be overlapping and interconnected in a complicated way.
Could it be the case that we do compete for a smaller and smaller number of positions in pure mathematics? But what about people with tenure? What forces them to continue this race?
April 9, 2012 at 9:43 pm
Sowa wrote: “Could it be the case that we do compete for a smaller and smaller number of positions in pure mathematics?”
Probably so.
Higher education has expanded a lot during the second part of last century, starting after WWII. But the expansion seems to have slowed down recently. Let me discuss the general context. It is quite clear that we are now living in an era of triomphant capitalism, despite the lasting recession created by the financial system. I would like to give you a small example. In Canada (where I live) the grant agency supporting mathematical research is the NSERC (the Natural Sciences and Engineering Research Council). The freshly reelected Harper government (conservative) stated in his last budget, that “from now the NSERC will concentrate its energy to serve exclusively the priorities of the enterprises”. Wow!
Happily, the popularity of the Harper goverment is rapidly decreasing.
I would like to make it clear that I am not against capitalism. Surely, capitalism can be good, since it encourages initiatives and inovations via competion. But unreined capitalism is dangerous, it may destroy everything including itself. This is why democratic societies must impose stringent rules on corporations (like anti-monopolistic laws).
You wrote: “But what about people with tenure? What forces them to continue this race?”
I guess by self interest. Again, I would like to make it clear that self interest and competion can be good for academia. The problem here is that the rules governing academic research have been fixed a long time ago according to a pattern which is now partly outdated. The explosion of mathematical research does not translate into a broadening of the mathematical culture, except possibly for a very small number of peoples, if any. I fear that mathematics may eventually collapse on itself if it does not broaden its intellectual base. I feel strange when I meet someone who knows everything about nothing and nothing about everything. Hopefully, the danger will be recognised on time and the rules will be changed. Peoples contributing to the developpement of general mathematical culture should be better rewarded by the system.
Some efforts have been made in the past to unify and broaden the mathematical culture of the time. The Bourbaki group is famous. Despite their rigor, the mathematics of Bourbaki are poorly motivated and the applications are absent from the books. The Soviet Encyclopedia of Mathematics edited by Vinogradov is probably a better tentative, but I know it less. I guess that it has contributed to the dominance of russian mathematics during the last 20 years. The “Princeton Companion to Mathematics” edited by Tim Gowers is the latest example I know. Thank you Tim, your book is beautifully! I hope that Tim will not mind if I criticise his book a bit. I believe the book should have paid more attention to category theory, since it is possibly the most important tool for unifying mathematics.
Modestly, I would like to formulate a dream that many mathematicians have today. A new collective effort to present and unify mathematics should be undertaken. It should dawrf all previous efforts and it should be open ended. It should use the internet.
I dont know how such a collective effort may start. I would love to contribute to it with my modest means.
April 10, 2012 at 2:02 am
@André Joyal:
Instead of venturing into the political philosophy of capitalism, I would prefer to stay closer to mathematics. Things similar to what you wrote about NSERC do happen in its US equivalent, NSF, and even on the level of the Division of Mathematical Science. But I don’t see how this may be related to capitalism, triumphant or not, or to what party is in the power. Both agencies are purely socialist institutions and function in a way characteristic for socialist institutions. For example, exactly the same words as you quoted could be said by some USSR Communist Party apparatchik overseeing sciences, and, I believe, they were said many times.
While young non-tenured people may be forced to enter this rat race by external to mathematics circumstances, like the shortage of the new positions, the rat race of tenured people is a phenomenon internal to mathematics and we have nobody to blame except ourselves. Who is rewarded is determined by us by a very trivial reason: no administrator or an NSF officer can distinguish good mathematics from bad and even an expository work from purely original research (a good expository work requires a lot of creativity, in fact). Well, perhaps there are or at least were some exceptions in NSF, usually some former mathematicians (but usually even former mathematicians are not exceptions). Anyhow, any grant award, any promotion decision, and any salary rise eventually depends on the peer review. I think that there is no need to change the rules. Instead of this, we should change our own priorities, what we do recognized and what we do not.
My defense of Bourbaki turned out to be fairly long, and I posted it at another place. Also, I would like to defer my critisism of Encyclopedias and of the “Princeton Companion to Mathematics” for another occasion.
I do not have any big expectations for big collective online projects. To date, Bourbaki is the only example of a successful expository collaboration of several people. The Bourbaki enterprise is not reproducible, at least without some dramatic changes in the attitudes of the mathematical community, and even with an appropriate change, only very rarely.
What needs to be done collectively is exactly the change of attitude. We should appreciate the expository work much more than now, write enthusiastically about such work in letters of reference, say to the authors more often that they are doing very valuable work, etc. Then much more individuals or two-three authors together will start to write expositions, and, may be some bigger online projects will eventually mature.
As of your idea of dwarfing all previous efforts, I must say that I subscribe to Freeman Dyson’s maxim: “Small is beautiful”.
April 10, 2012 at 3:55 pm
@Sowa. I agree with what you said. I have streched the connection between academic life and globalisation too far, at least for the sake of the present discussion. I am beginning to worry that we may be abusing the hospitality of our host. We could discuss elsewhere. You are welcome to to contact me. You know my real name.
April 10, 2012 at 9:18 pm
@André Joyal:
Yes, I already suspected that we are abusing the hospitality of our host. We may move to one of my Google places:
http://owl-sowa.blogspot.com .
The top post is for your comments. I suspect that you missed the reference to my previous post there with my comments about Bourbaki. Here the links are not very visible unless given in the http:// form.
I am planning to use that blog for a discussion of other issues related to this post of T. Gowers.
My experience showes that a discussion in comment is more convenient than an exchange of e-mails, since the whole thread is at one place. I plan to write you later (right now I have to go, anyhow). I am not announcing my identity here by completely unrelated with the discussion issues. I am prepared to stay by my words under my real name.
April 13, 2012 at 5:30 pm |
Tim
Thank you very much for your written talk – I enjoyed a lot.
April 16, 2012 at 5:22 pm |
I would like to correct a factual error I made in my reply to Sowa April 9, 2012. I wrote that the Harper government has decided that This was wrong! The
government actually decided that I have confused the NSERC with the NRC!
http://www.nrc-cnrc.gc.ca/eng/index.html
http://www.nserc-crsng.gc.ca/index_eng.asp
I apologise. The former is supporting pure mathematics, not the latter. The new policy of the government does not seem to be as bad as I thought. There is something to worry however, since the NRC is supporting a wide variety of scientific researchs, including research in biology and environment.
December 13, 2012 at 10:34 am |
[…] and Terry Tao have set a fine example in their expositions of the works of Fields Medalists or Abel Prize laureates. These are among the most interesting and important posts out there, I […]
April 2, 2013 at 5:11 pm |
hi all, found this post belatedly. sowa pointed to the dialog on computer-based mathematics. there are many related areas here including computer assisted vs automatic theorem proving, the role of human vs computer in mathematics, etcetera. have been studying this subject for many years. a few thoughts.
it seems to me there is a lot of debate around here about competitive approaches eg “the two cultures” and “mathematicians vs computers” which at extremes border on adversarial. this shows up a lot in sowa’s writing. lets all take a deep breath. think about symbiosis & cooperation. its the natural/higher/global order between the society of mathematicians and between them and computers. its a feedback loop.
if you read gowers original paper on “rough structure and classification”, the interesting dialog with the computer is particularly *collaborative*. it is sowa that is emphasizing that computers could make human mathematicians obsolete and putting words into the mouth of gowers [this pattern continues on newer blogs on this site].
computers will never replace mathematics just as the field of chess has been *strengthened* with the advance of computer power.
it appears to me there will always be a tension between very difficult proofs that are *objectively* “true” but inscrutable and it will always take humans to rearrange and reorient the same proof in different ways, also called psychological “chunking”, that *subjectively* are more understandable and yes, *aesthetic*.
in this way there is a strong similarity to architecture and refactoring code from the field of software development. think this core analogy [between proofs and coding] will continue to become more prominent and strengthened in the future even with major advances in automated thm proving.
over the years Ive been looking at a particular model for human vs computer theorem proving. its the collatz conjecture. in some ways a toy problem, but in other ways, possibly the precursor to a new style of computer-assisted mathematics in a remarkable style.
along these lines: have some preliminary, promising results on the collatz conjecture related to computational analysis & am looking for volunteer(s) for a project that would bring about this new order into reality. needed: mathematical background, programming ability, and enthusiasm for pushing the [extreme?] boundaries of mathematical and scientific knowledge. the idea is to apply very deep new technical principles to a “toy” problem but only as a start, a prototype or “proof of principle” on the way to grander plateaus…
plz reply on my blog if interested!
December 20, 2019 at 3:02 pm |
Hi, thanks for the info. I pine for to advise you to look here