I am still very busy at the moment and do not expect to be able to get down to any serious polymathematics for a few weeks, at least. And in any case, there are two Polymath projects going on at the moment, so I am not in a huge hurry to start another. (The projects are Gil Kalai’s on the polynomial Hirsch conjecture and Terence Tao’s on finding primes deterministically.)
Having said that, a common complaint about the first Polymath project was that it got started so rapidly that it was very easy to get left behind. So for my next project I would like to do two things. First, I want to get a sense of which, out of many potential projects I have in mind, would appeal to enough other people for there to be a good chance of finding a core of people ready to put in an effort similar to the effort that some people put into DHJ. (A similar core of regular contributors has developed for Terry’s polymath4: I wonder if this will happen for all projects that get off the ground.) And secondly, having chosen a new project, I want to write several introductory posts to give people a chance to get up to speed before the project properly starts. The way things are looking at the moment, I think it’s unlikely that I’ll start a project before November, but the preliminary posts might come out earlier.
In this post, I will say very briefly what some of these possible projects are, and will also report on a conversation I had recently with Jordan Ellenberg, during which he told me some thoughts about Polymath that I found extremely interesting. In fact, let me do that first.
Jordan is interested in the question of what it is that motivates people to check websites regularly, and his answer is that the websites need to be constantly changing (like a blog that gets lots of posts and comments) rather than static (like a wiki or a home page). Of course, this is not a new observation, and of course Jordan wasn’t claiming that it was, but it does have some consequences for Polymath projects. For instance, Jordan’s view was that, however regularly a Polymath wiki is updated, people are far less likely to spend time reading it carefully than they are to check a Polymath blog, even if they are interested in finding out about the problem being tackled. The reason is that we all have 101 bits of mathematics that it would be good to learn about, and as soon as reading the wiki begins to feel like hard work, we won’t really have a strong reason for doing that piece of hard work rather than any other. This doesn’t invalidate the wiki, since it is very useful when making blog comments to be able to refer to the wiki for basic definitions and results rather than having to explain them every time, and it is also useful to put arguments on the wiki once they start to become more precise and technical. But I think I agree with Jordan that it is unrealistic to suppose that if there are good explanations on the wiki, then that will enable people to get up to speed and join a Polymath project at a late stage.
I myself would draw another conclusion, which is partly based on my experience of following polymath4 and making occasional casual contributions. On the Polymath blog, a very high level of threading is allowed, with the result that the order of comments is very different from their chronological order. This makes it substantially harder to check what has been added recently than it would be if there were no threading. It’s not impossible, since one has a list of recent comments, but it does reduce the feeling of a polymathematical thought process unfolding over time. I know that there is disagreement about this, but I am going back to the view that there should be no threading at all, though I might be ready to compromise and have threading down to depth 1, with the understanding that it should be used for brief local replies only.
There was plenty more to our conversation, but the take-home message was that we should think very carefully about the psychology of what one might call website addiction, that quality that some websites have that cause one to check them obsessively, and should try to harness it as efficiently as possible. It could be that it is this that really distinguishes a Polymath collaboration from a conventional collaboration, where it is all too easy to be lazy and take ages. Certainly, I experienced something of this addiction during polymath1 (as my wife will testify).
To state the requirement precisely, what a successful Polymath project needs is to be appealing in a fairly addictive way to enough people for the benefits of multiple collaboration to be truly felt. From the experience of Polymath1, I think it could be enough to have a nucleus of four or five people who are enthused by the project, keep up with what is going on, and maintain the momentum by making regular contributions.
I also had an interesting correspondence with Michael Nielsen in which I suggested that one reason for Polymath1 not fizzling out might have been that I started with a fairly detailed plan of attack, even though the eventual proof turned out to be quite different. He said that that was certainly a factor in the success of Linux: Linus Torvalds didn’t start by saying, “Hey guys, wouldn’t it be nice to develop a free operating system collaboratively,” but rather he got things started with a rudimentary system. And apparently there are many other examples like that. However, he also noted that Terry Tao’s mini-polymath was remarkably successful despite almost no initial input from Terry (since he already knew a solution). Despite this example, I think it is probably an advantage, even if not a necessity, for a project to start with a clear plan.
What then are the possible projects that I have in mind? I have two 20-page documents describing them, but here I will just give a quick digest of some of them, in the hope of narrowing down the possibilities (even though I think all of them have the potential to be good projects, and I would probably return to the ones that were weeded out) and getting some sort of feedback.
1. Littlewood’s conjecture and related problems.
Littlewood’s conjecture is a major open problem, about which there are some highly non-trivial results. It states that if and
are any two real numbers, and
, then there exists a positive integer
such that
. Here,
denotes the difference between
and the integer closest to
. The usual pigeonhole argument implies that for every
there exists
such that
, so the conjecture is asking for just a tiny improvement to this trivial bound if instead of looking at one real number we look at two simultaneously. For the conjecture to be false, there would have to be a pair
such that whenever
threatened to get close to an integer,
was safely far away, and vice versa.
Polymath seems suited to problems that can be tackled in an elementary way, which, given the non-elementary nature of the progress that has been made so far on Littlewood’s conjecture (the highlight of which is a proof by Einsiedler, Katok and Lindenstrauss that the Hausdorff dimension of the set of counterexamples to the conjecture is zero), might make it seem as though it was an unsuitable problem. Briefly, my reasons for nevertheless wanting to tackle it are (i) I have formulated a number of related problems that seem easier, and (ii) I have ideas for how to tackle the problem in an elementary way, and I believe that we could learn a lot from trying to get them to work, even if we failed.
An advantage of this project is that I already have quite a bit of material that could quickly be turned into initial posts, plenty of ideas to explore, etc. The fact that the problem itself is notoriously hard is not, in my view, a reason for not attempting it, since there are lesser goals, such as thinking about the related problems and improving our understanding of the main problem, that it would still be very good to be able to attain.
2. A DHJ-related project.
I will say very little about this project, except that its main advantage (which not everybody would consider an advantage) is that it is sufficiently closely related to DHJ that some of the expertise built up during that project could well be useful to this one. And it is an extremely interesting problem, so interesting that I am reluctant to put it in the public domain unless there is a real chance that it will be chosen as a polymath project. (Sorry, that’s a bit of my traditional possessive monomathic personality coming out there.) On the negative side, I don’t have much in the way of preliminary attacks on the problem, though this would I think be compensated for by the closeness to DHJ. (I should stress, however, that it is different enough from DHJ that a solution would be a serious mathematical advance.)
3. Four Erdös-style combinatorial problems.
Apologies for the non-Hungarian umlaut—I don’t know how to do Hungarian ones in WordPress. I am going to lump the next four projects together, since they are all beautiful problems of an extremal-combinatorics flavour. I will do little more than state the problems. I do not have plans of attack for these, though I have a few small ideas and preliminary observations about 3a that could provide some kind of starting point. However, for each problem I have a hunch that Polymath could really get its teeth into it.
3a. Erdös’s discrepancy problem.
Let be a sequence of
s and let
be a positive integer. Must there exist positive integers
and
such that
?
This is such a weak thing to ask, and seems so likely to be true, that I have the feeling that the reason the problem is still open is that people have not pushed quite hard enough. So perhaps a multipush is what is required. Having said that, I know various observations that show that there probably isn’t a truly easy solution to the problem. (For instance, it is possible to construct sequences where has to be exponentially large in terms of
, so many styles of argument that would tend to give quadratic bounds are ruled out. I could expand on this in a future post.)
3b. The Erdös-Hajnal conjecture.
This is a gorgeous problem in Ramsey theory. As is well-known, the Ramsey number is exponential in
. However, the graphs that demonstrate this are random graphs, and therefore they contain induced copies of all small graphs. By how much does the bound improve if one disallows this? More precisely, let
be a positive integer and let
be a graph. Erdös and Hajnal conjecture that there is a constant
such that if
is any graph with at least
vertices that does not contain any induced copy of
, then either
or
contains a clique of size
.
The usual bounds for off-diagonal Ramsey numbers prove the result when is a clique, and it is also known for certain classes of graphs. The simplest open case is where
is a pentagon. In other words, if
has
vertices and does not contain five vertices
such that each
is joined to
but not to
(mod 5), then it is not known whether the largest clique in
or
must have size at least
.
3c. Frankl’s union-closed conjecture.
This is a notorious question, and possibly the least likely to yield to a Polymath approach (it feels as though there might be a burst of ideas, none of which would work, followed by disillusionment, or else, if we were very lucky, a single bright idea from one person that essentially solved the problem, but I could be wrong). Let be a collection of sets that is closed under taking unions. Must there be an element that is contained in at least half the sets? (The extremal case is if
consists of all subsets of a
-element set, in which case there are
sets and no element is contained in more than
of them.)
3d. The delta-systems problem.
This question is due to Erdös and Rado. A delta system is a collection of sets such that all the sets
(with
) are equal. Equivalently, there exists some set
such that
for every
, and the sets
are disjoint.
Delta systems appear quite often in extremal combinatorics, and it would be good to know how many sets of size you need before you are guaranteed to find a delta system of size
. However, this is another notorious problem. Even when
, it is wide open, and Erdös offered 1000 dollars for a solution to the following problem: does there exist a constant
such that for every
and every system of at least
sets of size
, there must exist three of them that form a delta system? (The best known upper bound is more like
.)
4. Non-mathematical projects.
There are many fascinating questions that are not strictly speaking mathematics but that nevertheless appeal to many people who are mathematically inclined. It occurs to me that some of these could be ideal for Polymath, since one of the difficulties of Polymath — the need to communicate complicated mathematical ideas — is lessened. I will give two examples of the kind of thing I have in mind. I don’t expect either of these to be the next Polymath project, but I might be interested in tackling one or other of them in the future.
4a. Developing a non-boring chess-playing program.
I have great respect for the achievements of Deep Blue and similar programs, but I cannot avoid being disappointed by the heavy use that such programs make of brute-force searches. It feels to me as though the real problem — how do good chess players do what they do — remains unanswered. So I am interested in the following question: how good a chess-playing program is possible if the amount of memory space allowed is very restricted, and the amount of calculation is also limited?
What might a Polymath project devoted to this question be like? Well, it could start by trying to frame the question in a more abstract way. One would like to find a method of programming that applied to all games of a certain type (things like Othello, Go, etc.) and not just chess. The sort of method that I find exciting is an evolutionary strategy: one just sets the computer playing against itself, or perhaps against itself and against humans, and tries to set things up so that there is an evolutionary pressure that selects for good tactics. The major problem there is to come up with a notion of game-playing program that splits up into smaller bits (which one can think of as “genes”) that can be modified without just wrecking the whole program. And one wants to do that without imposing serious limitations on what the program can end up looking like. These are formidable challenges, and issues that many people have thought about. But I’m not sure that pure mathematicians have thought about them all that much, and perhaps some interesting new ideas could come out of a Polymath project on the subject.
4b. The origin of life.
This is even more absurdly ambitious than 4a, but why not? One of the major open problems in science is to give a plausible explanation of how life started: it seems to be much easier to explain how complex life forms evolved from simple ones than it is to explain how the simple ones evolved (if that is the right word) from nothing.
I think there is the potential for mathematicians to shed light on this problem, by coming up with a mathematical model and proving (not necessarily rigorously — perhaps one would be satisfied with convincing heuristic arguments and computer simulations) that it had a tendency to lead to extremely complex behaviour.
What about Conway’s game of Life, one might ask? Well, that is clearly a huge step in the direction I am talking about. But it doesn’t quite do what I said in the previous paragraph: what it does is demonstrate that some initial configurations lead, under some very simple rules, to complex behaviour. What I would find more convincing would be a somewhat randomized dynamic model, such as the kinds of models one sees in statistical physics, that not only can get very complex, but does so with some positive probability (which one could quite easily convert into a probability very close to 1). I recently attended a fascinating talk by Stanislav Smirnov in which he talked about sandpile models. These are models of the process where one drops sand on a pile, which grows but also gives rise to avalanches of various sizes. Apparently, statistical physicists find these models exciting because they naturally seem to give rise to complicated fractal patterns, whereas most models seem to be stable in the ordered regime or the completely chaotic regime and not at the boundary between them.
So a more precise question is this: can one devise some simple model that people could run on their computers that would start from virtually nothing and almost always lead to an interesting artificial eco-system? Such a model would provide powerful support for the hypothesis that life is a high-probability event rather than an extraordinary miracle that defies scientific explanation.
Of course, there must already have been a great deal of work on this question, and there are many variants on the game of Life. So a preliminary task would be to find out about that in order to see what would count as an important advance. (I suppose it is even worth thinking about whether a suitable choice of random starting position for the game of Life, with perhaps a very slight randomization of the game itself, would do the job.)
The reason I think this might make a good Polymath project is that whereas one person’s wild speculation can often be just that — wild speculation — if a large number of people made speculations and criticized and refined other people’s speculations, the result could perhaps be much more interesting.
5. A tentative approach to complexity lower bounds.
This has emerged only very recently as a suitable project. One of the features of the P versus NP problem that is rather intimidating is that theoretical computer scientists have proved a number of rigorous results that say “No proof that P does not equal NP could look like this.” And it seems to be hard to come up with a sketch of an argument that doesn’t “look like this” (though there is at least one serious proposal, due to Ketan Mulmuley).
Recently, however, I thought of an approach that could conceivably avoid some of these “barriers in computational complexity”. At the moment I’m almost sure (but not quite certain) that it wouldn’t be able to prove that P does not equal NP, but I haven’t yet managed to rule out its being able to solve another major problem in the area: to find a function in NP that has superpolynomial formula size. This is still a very long shot of course, but the nature of the subject is such that even reaching a good understanding of why an approach doesn’t work is cause for celebration, so I think the ideas are worth investigating. And I think that reaching this kind of good understanding would be quicker and more enjoyable if done polymathematically. I should say that I’ve tried reasonably hard to demolish the approach myself, but each time I think I’ve succeeded I find some desperate way of rescuing it. However, at least one of these demolition attempts does make it look highly likely that a certain measure of complexity that I have looked at can be large for polynomially computable functions. I shall continue to attack the approach, so it may be that by the time I would have been ready to start the project it won’t exist any more.
[UPDATE 19/9/09: I have now had a further realization that makes me extremely pessimistic about the idea. I will continue to think about it, but if your preference is/was for 5, it would still be good to think carefully about your second choice.]
There is a tiny tiny chance that the approach actually works, and a further minuscule chance that, despite the strong evidence to the contrary, it could then lead to a proof that PNP. This conjunction of two miracles is so unlikely that it is scarcely worth bringing up a difficult issue that would arise, but it is an amusing issue that will have occurred to almost anyone reading this, so let me do so. That is the question of what would happen to the Clay million dollars if one of their problems was solved polymathematically. I can think of a few possible answers. One might be simply to declare in advance that if that happened then Polymath would give the money to charity, or come up with ten 100,000-dollar problems, or in some other way not try to distribute the money to the individual participants. But then there might be a strong temptation for people to break off and work individually. Another answer might be just to rely on the Clay Foundation to solve the problem of apportioning credit — in their small print they already have something about possibly sharing prizes if the ideas that go into a solution are spread amongst different papers by different authors.
I don’t know if either of these solutions would work, but I do think that it would be a terrible pity if the existence of the Clay prize provided a disincentive to work on their problems in a potentially productive way.
From the point of view of suitability for Polymath, I think this project is a good one, since, as with the Littlewood problem, I have some detailed posts already written, in the form of a five-part dialogue between three mathematicians, one of whom specializes in proposing ideas, one in criticizing them, and the third in asking for fuller explantions from time to time. There is a good chance that complexity experts will be able to shoot it down almost immediately (indeed, the one thing that bothers me about this as a project is that it could be slightly embarrassing — it’s somewhat embarrassing even to admit to thinking about it): if so, nothing much is lost and we can move straight on to another project. But if the approach survives the initial scrutiny of the TCS crowd, then one thing it has going for it is that it is of a kind that would appeal to additive combinatorialists. Since there are already many people interested in both theoretical computer science and additive combinatorics, there is an excellent pool of potential participants: perhaps one or two of them could become addicted in the Ellenberg sense.
I have a disclaimer similar to the one I had at the start of DHJ: the official aim of this project would be to see whether one particular idea for proving complexity lower bounds has anything going for it. Of course, it would be great if the answer was provably yes, but there are many lesser outcomes that would still be interesting. (I would even be interested, if disappointed, to be told that the approach has already been tried.) I would also like to have my argument that it cannot prove that P=NP made rigorous: it seems to be quite an interesting and purely mathematical problem to do that.
Conclusion.
A few weeks ago, the Littlewood project was the one that appealed to me most. Now I am moving towards the one on complexity lower bounds (despite simultaneously feeling a bit uneasy about even mentioning it, and despite the fair chance that it’s based on an idea that will rapidly be seen to get nowhere). But all of them appeal to me quite a bit, or I wouldn’t have suggested them. I think the two non-mathematical projects are perhaps best left alone for the time being — I just mention them to raise the possibility that Polymath could be used for broader projects that are not completely mathematical. Amongst the projects in 2 and 3, I think my not terribly strong order of preference is 2 and 3a (equal first), followed by 3d, 3b, 3c. Funnily enough, or perhaps not so funnily, my order of preference is basically the same as the order of how many preliminary thoughts I have about the problems — i.e., on how well they do by the clarity-of-initial-plan criterion.
So now I’d like to get some feedback. I’m particularly interested in getting a sense not just of which projects people would like to see tackled, but which projects people feel they could make a serious contribution to and would be prepared to devote plenty of time to. I realize I haven’t given enough information for it to be easy to judge, but I hope I’ve at least said enough for people to decide their approximate level of enthusiasm.
September 17, 2009 at 12:47 am |
I’d quite like the Littlewood problem or Erdos 3a) – but this comes from a position of being naively attracted to the statements, rather than any experience or understanding of the perils involved. (Fools rush in where angels fear to tread, as some cove said.) But in both cases I’d hope to try and get involved, if only to try and contribute to the lesser goals and sub-problems.
September 17, 2009 at 12:50 am |
Preference order: 3b, 3a, 2.
September 17, 2009 at 1:38 am |
I’d be happy to try contribute to any of the 4 combinatorial problems, and Littlewood’s conjecture.
September 17, 2009 at 3:58 am |
Bring on number 5!
September 17, 2009 at 9:10 am
I second.
September 17, 2009 at 3:35 pm
I third.
September 17, 2009 at 4:04 am |
I would vote for 5 first, then 2, then 3a/c/d.
September 17, 2009 at 4:51 am |
[…] Gowers has been thinking about his next polymath proposal, and he has recently written about the possible projects that he has in mind. One of the project involves a new approach to proving circuit lower bounds. […]
September 17, 2009 at 8:35 am |
3a seems interesting, and maybe the most likely to fall to a polymathematical attack. Frankl’s conjecture seems like the type of problem that isn’t particularly parallelizable, and wouldn’t work well for polymath. At least right now, I’m more interested in seeing problems solved than exploring the boundaries of what polymath can do, so I guess my top preferences are 1 and 3a (tied), with a preference against 3c.
That said, I’d be happy to try to contribute to any of the given mathematical projects (although I might well end up dropping out early on if the approaches move too far away from what little I know, as happened with the finding primes project).
I do have a small concern with #5, which is essentially that, while a good approach to circuit lower bounds would very likely lend itself to an online community working on it, if the approach turns out not to be good then the project might not be as successful in a non-mathematical sense. (I should make clear that I’m not just talking about whether it can prove P != NP here, but whether it can even give much weaker separations.) Certainly there’d be work, and likely interesting work, in nailing down exactly how powerful a method is, but it wouldn’t attract as much interest as a possible approach to P != NP or even to, for instance, quadratic lower bounds for SAT. So I’m interested, but I think I’d want to see more before committing myself to it (which, of course, I guess I would if the project actually got started.)
September 17, 2009 at 9:46 am
I half share your worry about #5, but I think that the nature of the project is that if the basic idea isn’t a good one, then that should become clear pretty quickly. So interest in the project wouldn’t have to be sustained for all that long. And if no CS experts made remarks like “That kind of idea has been tried by many people and is a well-known dead end” or “Your proof proposal naturalizes/arithmetizes/relativizes in the following non-obvious (or even obvious) way”, then perhaps a second phase would start, where a few people would be interested enough to start thinking in more detail about the mathematical problems involved.
I still haven’t given up trying to convince myself that it can’t work, so it’s still quite possible that I’ll be forced to withdraw this particular proposal.
September 17, 2009 at 2:55 pm |
[…] Future polymath projects. […]
September 17, 2009 at 3:01 pm |
You’re probably already aware of this, but if you’re willing to wait until September 30th for the Google Wave beta, waves are threaded but have a playback feature that allows you to keep track of new updates to the wave chronologically.
As far as the problems, I’m a fan of 1 and 3c, but like Harrison my participation will be strongly limited by what I know.
September 17, 2009 at 4:22 pm
I didn’t know that. Do they also support LaTeX?
September 17, 2009 at 10:40 pm
I saw a demo of the LateX robot in Wave at Science Online London 2009 (http://www.scienceonlinelondon.org/) a few weeks back. There’s a low quality version of the live demo to view at http://vimeo.com/6374118 where the discussion of LaTeX is between 10 – 13 mins in.
Another alternative I was thinking of would be to use FriendFeed (http://friendfeed.com/) and hack together a greasemonkey script (http://en.wikipedia.org/wiki/Greasemonkey) with the code from LaTeXMathML (http://math.etsu.edu/LaTeXMathML/). In fact it might already be out there, but I haven’t had a chance to check yet; if not I shouldn’t think it would take no more than a weekend of hacking to get something working. A good place to see example FF threads (no LaTeX though) is http://friendfeed.com/ff-for-scientists
As I CompSci I have to say that I’d be keen to see proposal 5 get going.
September 17, 2009 at 3:47 pm |
My preference order: 5, 1, 3b, 3a
September 17, 2009 at 4:49 pm |
I think Richard Stallman might have a bit to say about your Linux analogy. Although I wonder, was GNU widely used before the rudimentary Linux kernel, I’m too young to know?
September 17, 2009 at 5:01 pm
I’m a bit hazy on my history there and am not trying to downplay Richard Stallman’s contribution. But the point remains that the most famous ever open-source project had an initial framework on which to build, rather than starting completely from scratch.
September 17, 2009 at 9:37 pm
Yes, parts of GNU were widely used before Linux existed. That’s certainly true of GNU emacs, for example, which I think I first encountered in 1987 or 1988, several years before Linux existed.
The original claim to fame of Linux was that it was an OS kernel. GNU didn’t have a kernel, although they’d been promising one for many years by the time Linux appeared. Torvalds released the code for a simple kernel, and that caused a huge amount of interest, initially mostly in the Minix community. Minix was an academic / teaching OS written by Andrew Tannenbaum, but not free at that time. My (possibly faulty) memory is that the initial release of the Linux OS kernel was just 1200 lines of code, but grew rapidly, and became far more feature complex. Basically, Torvalds provided something just interesting enough to stimulate others to be willing to contribute; it wasn’t pure vapour. Seems like a good model for Polymath Projects, too.
September 17, 2009 at 10:27 pm
I think my real problem is that I don’t know what an OS kernel is …
September 17, 2009 at 10:39 pm
The term kernel seems to be a bit flexible. But the main point is that it’s the core part of an OS, doing stuff like basic memory and process management, containing the basic device drivers (so you have a functional screen, a keyboard, etc). GNU added crucial software like the GNU C compiler (gcc) on top of that, which is obviously pretty important to an OS that hopes to be portable.
September 17, 2009 at 5:12 pm |
My preference order: 2, 5, 3b, 3a.
September 17, 2009 at 5:51 pm |
With regards to GNU and Linux I found this from http://www.gnu.org/gnu/gnu-linux-faq.html#why:
“Why do you call it GNU/Linux and not Linux?
Most operating system distributions based on Linux as kernel are basically modified versions of the GNU operating system. We began developing GNU in 1984, years before Linus Torvalds started to write his kernel. Our goal was to develop a complete free operating system. Of course, we did not develop all the parts ourselves—but we led the way. We developed most of the central components, forming the largest single contribution to the whole system. The basic vision was ours too.
In fairness, we ought to get at least equal mention.”
September 17, 2009 at 5:53 pm |
I am very interested in #5.
Without knowing your approach, I can say that in any attempt at lower bounds there is always a chance that it runs into a very significant obstacles (in particular the “natural proofs” barrier). But it has been the case in the past that we can learn from such obstacles. So, the record of this attempt, whether successful or not may turn out to be a very useful resource.
Also, this may be exactly the type problem that can benefit from joining together people with very different expertise, who don’t often collaborate.
September 17, 2009 at 6:13 pm
I should say that the approach was designed specifically as one that would get round the natural proofs barrier. However, I cannot discount that it might be naturalizable in a clever way. But if that is not the case, then there is the possibility that it will lead to the formulation of a new barrier, which would be very nice of course. Having said that, it could be that it fails just because it fails, and not for some interestingly generalizable reason.
September 18, 2009 at 12:41 am
That sounds very interesting! Would you mind sharing if it’s the largeness or constructivenss condition that you bypass*? In any case, there’s an easy oracle procedure to check if the approach has already been tried before or is must fail for some simple reason.
An important asset we computer scientist can bring to this project is our lax standard for success 🙂 More seriously, even if all we end up is showing that a formula size lower bound follows from a mathematical conjecture that you have reason to believe for other reasons, than I think that would be very good. (There are very few results like that with one of the nicest being Ran Raz’s recent work on elusive functions.)
—-
* For the people not familiar with the “Natural Proofs” barrier of Razborov and Rudich, they showed that essentially all proof methods for lower bounds have the property that they show that a function f is hard by showing that f does not belong in a set S, where S is a “nice set” that bounds the set of all easy functions, in the sense that S contains, say, at most half of all functions (this is known as “largeness”) and a function’s membership in S can be computed in time polynomial in the truth table of the function (this is known as “constructiveness”). They showed that such bounds will not be able to show that f is outside any complexity class that contains pseudorandom functions, and under a variety of cryptographic assumptions, very simple classes contain such functions.
condition (i.e., proof that ends up re-proving that a random function is hard) or constructiveness (i.e., proof
September 18, 2009 at 12:48 am
I had a typo: This is the oracle procedure I referred to.
September 18, 2009 at 8:04 am
I still like the basic intuition that low-complexity functions should have some “simplicity” property that distinguishes them from random functions. So I am very reluctant to abandon the largeness condition, and have instead abandoned the constructiveness condition. (However, my argument that the property I am considering is not constructive is far from conclusive — I say why I think it isn’t obviously constructive, but I haven’t tried hard to find a non-obvious algorithm for it. This is one of several potential weak points that would need to be attacked before one could start to think about the proposal more positively.)
September 18, 2009 at 11:26 am
To add to my last remark — I had a sudden realization this morning that if my property worked, then I could probably convert it into a constructive property that also worked. For a few minutes I thought that I’d just killed the whole idea, and then I realized that the constructive property would fail the largeness condition. So it seems that the answer to your question is in fact that my approach could be formulated so as to bypass either, but fortunately not both. All this is conditional on the unproved hypothesis that GPP TU. (For those who don’t know, GPP stands for “Gowers’s proposed property” and TU stands for “totally useless”.)
TU. (For those who don’t know, GPP stands for “Gowers’s proposed property” and TU stands for “totally useless”.)
September 18, 2009 at 1:37 pm
I very much like the idea of a potential non-constructive method, since I believe at the end the kind of functions we’ll want to prove lower bounds for (e.g. SAT) are very “unstructured” and so don’t leave much room for a non-large method. (Although of course if an approach works to prove a lower bound for some function F0 then you can always rephrase the property as the constructive but non-large property of computing F0..)
While it’s useful to keep natural proofs as a guide, I think it’s very dangerous to discard an approach prematurely just because it seems to succumb to this barrier. After all, 99% of the proof could be “natural” and you only need one minor component that’s not natural for things to work.
September 17, 2009 at 9:57 pm |
I’ll certainly follow projects 1-3, and am happy to help out in whatever ways I can, but doubt that I could contribute much to the core mathematical discussion, beyond occasional kibitzing.
4b is a problem I worked on a little some years ago, with very similar ends in mind: I wondered if it might be possible to use computer simulations or heuristic arguments to go beyond the famous Miller-Urey experiments. (http://en.wikipedia.org/wiki/Miller%E2%80%93Urey_experiment ) I didn’t get very far, beyond learning a bit about what’s known of the origin of life (not much). I’d certainly enjoy an extended open discussion of the problem, and, depending on the turn it took, might have useful contributions to make to a full-fledged project.
I’d be very interested in problem 5, although whether I could contribute would depend upon the details of the approach you are suggesting.
September 17, 2009 at 10:00 pm
Incidentally, something very nice about 4b is that it leads easily to many fascinating subproblems:
(1) How would you go about recognizing self-replicating beings?
(2) What sort of models are “reasonable”, in the sense of both reflecting what we know of physics, and being simple enough to be tractable? The Game of Life isn’t very physical, in that it disobeys many basic physical principles, like conservation of energy, conservation of mass, conservation of momentum, and so on.
And so on – it’s a great problem.
September 17, 2009 at 10:20 pm |
The people who really understand addictiveness seem to be the people who make games. Witness World of Warcraft – I’ve seen news reports of people who have apparently died after neglecting to sleep for several days so they could continue playing the game. (I don’t think you want Polymath that addictive.)
The most addictive open source project I’ve heard of borrows a key idea from the games. It’s the Matlab Programming Competition (http://www.mathworks.com/contest/). The idea is that a problem is posed, e.g., the travelling salesman problem. People submit programs to solve the problem throughout the week of the competition. When submitted the programs are automatically scored against a suite of test data – for TSP, the score would be better for fast programs that find short routes. The scoring is done more or less instantaneously, and the score goes up on a leaderboard. The clever twist is that anyone can then download the program, tweak it, and resubmit as their own, leapfrogging to the top of the leaderboard, for example.
The result is a fast and furious competition, with people constantly leaping over one another. It’s apparently fantastically addictive – here’s a quote from one participant:
“I started to become `obsessed’. At home, although I am a father of three children, my full-time job was working on the contest. I worked maybe 10 hours after work each day. On Thursday it was clear that I wasn’t going to be able to work seriously (for my job), so I took a day off on Friday.”
I think the combination of the automated scoring (meaning instant feedback) and radical openness (meaning you’re always just one improvement away from the top of the leaderboard) is probably a pretty good way of making things addictive.
I don’t immediately see how to use this pattern for mathematical problem-solving. In fact, I’m not sure you really want to. But I think it’s interesting food for thought.
September 17, 2009 at 10:25 pm |
[…] primes deterministically was launched over the polymathblog. (September 2009) Tim Gowers wrote a preliminary post about possible problems for the October 2009 […]
September 17, 2009 at 10:34 pm |
[…] Tim Gowers devote a post to several proposals for a polymath project in October. Leave a […]
September 17, 2009 at 10:48 pm |
Here is part of a definition of the kernel of an operating system:
“In computing, the ‘kernel’ is the central component of most computer operating systems. Its responsibilities include managing the system’s resources (the communication between hardware and software components).[1] Usually as a basic component of an operating system, a kernel can provide the lowest-level abstraction layer for the resources (especially memory, processors and I/O devices) that application software must control to perform its function. It typically makes these facilities available to application processes through inter-process communication mechanisms and system calls.”
It is from:
http://en.wikipedia.org/wiki/Kernel_(computing)
The note referred to by the [1] in the quoted text is to:
Wulf, W.; E. Cohen, W. Corwin, A. Jones, R. Levin, C. Pierson, F. Pollack (June 1974). “HYDRA: the kernel of a multiprocessor operating system”. Communications of the ACM 17 (6): 337–345. doi:10.1145/355616.364017. ISSN 0001-0782.
That articles is available at:
Click to access p337-wulf.pdf
September 18, 2009 at 1:00 am |
Hi Tim,
although I am not what a mathematician would call “a mathematician”, I’d be interested in following 4b. I’m a grad student in dynamical systems, so I am not sure if I could commit to a significant time expenditure, as I do have my day-job-research to work on. But it’s something I was interested in while doing my undergrad work, and I believe I am sufficiently good at simulating, speculating, and perhaps some maths too, to at least follow, if not contribute, to 4b.
September 18, 2009 at 2:21 am |
I think I will not be able to contribute more than casually to the next polymath project due to other time commitments (including, of course, Polymath4), so my opinion should be discounted somewhat, but it would be good to have a project distinct in nature and in operation from existing ones in order to get more data points (for instance, I agree with the proposal to have different threading and wikification strategies for different polymaths, as it is still not yet clear what is the optimal mix). In particular, it might be good to favour topics other than combinatorics, analytic number theory, and convex geometry (Polymath1, Polymath4, Polymath3). Project 5 seems quite ambitious but also highly worthwhile, and rather different from existing projects, so might be a good choice in that respect. On the other hand, the 1 and 3 projects seem to have a higher chance of producing at least a partial success, or at least an increased understanding of the problem.
September 18, 2009 at 4:59 am |
I was looking forward to see this list since Tim mentioned it some weeks ago and even tried to guess what’s on it and now I enjoy very much the list of problems itself. Probably all these problems deserve a separate detailed post, a round of discussion and a serious consideration. (Practically, if the next project starts sometime in November and require some preliminary posts the decision should come rather soon).
I agree that having a definite programme as some sort of anchor was helpful for the success of polymath1. To which of the problems in the list is there a programme/ plan for attack?
September 18, 2009 at 8:15 am
To 5 there is a very definite plan of attack (which, while it is an advantage, could also mean that people would quickly see why it had no hope of working, in which case I would not be in favour of saying, “Well, hey, let’s just see if we can solve a massively difficult lower-bound problem anyway!”). To 1 I have a lot of material to get started, but it’s more in the form of tempting (I hope) related problems, some of which might be substantially easier than Littlewood itself, but which might shed some light on it, and might lead to an approach. In other words, I don’t have a vague programme for solving the Littlewood conjecture, but I do have a platform to get started, and it is conceivable that after a bit of work some such programme could emerge. About 3a, I just have a few initial observations about why certain approaches don’t work, and about what a successful argument might have to be like. They could perhaps trigger some ideas in other people. About 3b there’s quite a lot I could write, but it’s mostly failed ideas. (However, I think writing down failed ideas is useful for getting other people thinking.) At this stage, 3c and 3d are just problems that I like — I’m not sure I have much of interest to say about them.
September 18, 2009 at 9:51 am |
Just out of curiosity, about how many people have read this post so far? The aim being to infer what is preventing readers from commiting to this next Polymath, or at least commenting.
Focussing only on would-be participants (i.e. discarding casual non-mathematician blog readers) here are some potential reasons:
(a) they have the expertise and a prefered project, but don’t have time at all;
(b) they have the expertise, a prefered project, and time, but refuse to commit themselves for some reason (e.g. would prefer a slow pace like Polymath4 rather than a fast one as you seem to suggest);
(c) they have time, but work in other areas and would prefer other projects;
(d) they have time, have expertise in other areas (or are grad students), are willing to be serious, but cannot possibly be sure to come up with anything substantial here.
Perhaps a poll would help? If the number of readers is low, maybe one should try to popularize more this blog post (could one use some mailing lists, say for complexity experts, and so on?)
September 18, 2009 at 5:25 pm |
I’m a casual non-mathematician blog reader. I would like to say there’s a good chance I’d try to participate in any of these projects, but I know from experience that’s just not true. My best guess is that I would read the work on 1 or 5 with great interest and *maybe* end up thinking hard about parts of them, read the work on 4a or 4b with great interest and think hard about parts of them and participate in at least initial discussions since that’s closer to what I actually *do* regularly, and probably only skim over the work on 2, 3a, 3b, 3c, and 3d before deciding it’s not worth getting up to speed to read with great interest.
September 18, 2009 at 9:05 pm |
I like all the polymath suggestions. I particularly like 4 (because it would be the first polymath project that the public at large could appreciate) 5, and 3a. I worry though that because 4 will likely require lots of computer simulation, it won’t attract as many people as other projects — it is not easy to see how people could contribute precise ideas (other than to share some qualitative descriptions of how various systems behave) to project 4.
With project 5 I imagine there will be a lot of contributors, but those with the right sort of detailed technical knowledge will quickly dominate the discussion. One upside is that of all the polymath projects proposed thus far, if one based around problem 5 succeeds it would have the greatest impact of them all (in my opinion).
Problem 3a is just the right sort that would attract lots of contributors, and I would think could be solved by a concerted effort (in fact, when I was a grad student, I recall solving some variant of this problem — probably not the actual problem — using the Large Sieve and some facts about the roots of Littlewood-type polynomials. Though, that was maybe 12 years or so ago, so it is probably lost now.).
And now I have to meet with some students, and then hopefully tomorrow I can write something for the polymath4 project…
September 18, 2009 at 10:23 pm |
I like 3a and 1 because they are the ones I think I’d have most chance of understanding – and polymath is a spectator enterprise too.
I think 5 would be most interesting, if it were anything like Polymath 1, because even if it failed rather quickly on the first idea, it might catalyse some thinking about ‘proofs which are not like this’ and generate a number of related ideas – which would be rather exciting.
Some work has (inevitably) been done on 4a (chess) in specialised circumstances, and even brute force search programmes have databases of openings and endgames. I have David Levy’s Computer Chess Compendium of late 1980s somewhere on my shelf, which has some interesting articles on both depth first and plan guided chess computers – it looks as though there is a recent reissue, though I haven’t noted whether there is any substantial updating of the original.
The use of databases and depth first search is governed, of course, by the fact that storage and speed have become cheaper very quickly over time. One interesting question would be whether depth first is still the most efficient use of these resources. There is a pay-off between static evaluation of a position based on some function, and evaluation by calculating to greater depth (which is another way of evaluating the same position). Back in the 1980s simple static evaluations were being used, because the resource cost of more complex evaluations was too great. And this in turn drives depth first approaches.
So as well as the issue of replicating intelligence (whether this is done efficiently or not), there is the issue of how best to use the kind of computing resources available to identify good moves. And if the two are different this may throw some interesting light on the theory of artificial intelligence.
September 18, 2009 at 11:10 pm
The big leap that cracked higher levels of Go-playing ability was to add the same sort of Monte Carlo simulations that have long been in backgammon and other games of chance. A limited-resource chess machine might try something similar.
(That said, the topic doesn’t terribly interest me even though it oddly is the one I know most about on the list. I guess I feel like it is too much a “done” topic and anything produced will be a novelty rather than a real advance.)
September 19, 2009 at 3:44 pm |
I’m sorry to say that I am now much less sure about 5: see update I’ve put there. But I need to think a bit more before rejecting it as a possible project.
September 20, 2009 at 12:03 am |
My background is more in simulation via software (math/physics background), with some odd biology experience thrown in (physician). For these reasons, 4b and 4a are more interesting to me, but I’m generally taken by your entire approach to these problems, and interested in all the listed projects.
(By the way, thanks so much for the Princeton Companion…what a wonderful read…)
September 20, 2009 at 5:01 am |
I’d cast my vote for the four problems that make up 3 … each has the benefit that the statement is easy enough for anyone to understand, yet obviously each has resisted solution for many years.
Some new ideas from other areas of mathematics may be just what is needed to help, but a priori we don’t know where those ideas might come from, which seems to be them ideal polymath projects..
September 20, 2009 at 3:54 pm |
Amir Ban post’s on computerized chess (and some comments from his lecture mentioned over the remarks) can give some interesting background for problem 4-a (btw, I dont like the use of “non-boring” in the title of the problem.)
September 20, 2009 at 4:27 pm
I’m happy to retract my use of “non-boring”. What I mean by “boring” is a brute-force search or a big look-up table or something like that (so in fact one reason I’m not too fond of real chess is the idea of having to learn lots of openings if one wants to get good). But I fully recognise that even if current chess-playing programs use a lot of brute-force searches, there is a lot more to them than that. What I mean by “non-boring” is something that works much more like a human being, and I think one way of formalizing that is what I suggested, namely allowing the program to use very little storage space indeed (since we don’t seem to be able to store much in our short-term memories — but to be clear, the program itself could be quite large and difficult to specify, just as our brains are complicated) and also not allowing it to take very long, so brute-force searches are not allowed either. Maybe this could be captured by a model such as log space and a time that would be linear if you applied a similar program to an chessboard.
chessboard.
September 20, 2009 at 4:30 pm |
Going back to 5, I think I really have killed it off now. What I’ll probably do is post my thoughts anyway, just as an example of the kinds of ideas that get you nowhere (and just in case they prompt anybody else to have related ideas that do better). It’s conceivable that there could be a useful polymathematical discussion about whether there are any general lessons to be learned from the failure of this particular approach, though even that is not clear to me at this stage. I’m mentioning this to make clear that I’m still interested in knowing how people react to the other proposals.
September 20, 2009 at 9:03 pm |
Casting a vote for 3b as the project I would be most likely to participate in (though I will follow any of them).
September 21, 2009 at 6:21 pm |
The problems in 3 are interesting and I’d certainly participate. All of them are the `sort’ that I’d think about.
Problem 1, on the other hand, is outside my comfort zone and too famously difficult for me to consider on my own. That’s why I vote for it.
September 21, 2009 at 7:47 pm |
Regarding 4a, a common alternative to “boring” minimax search + heuristic scoring function is to learn the scoring function automatically from data. If the function is good enough, you could skip the search entirely. Samuels did that in 1952 for checkers by having his program learn the scoring function from the matches against itself. More recently people are applying learning approach to Go, where branching factor is too large to be able to search to sufficient depth. http://books.nips.cc/papers/files/nips19/NIPS2006_0223.pdf
September 22, 2009 at 3:18 am |
[…] 09: Frankl’s conjecture was proposed, among other problems, for a “polymath […]
September 22, 2009 at 3:24 am |
[…] 09: The Erdos-Rado sunflower (Delta-system) conjecture was proposed by Tim Gowers, among other problems, for a “polymath […]
September 22, 2009 at 10:26 pm |
[…] Gowers’s Weblog Mathematics related discussions « Possible future Polymath projects […]
September 22, 2009 at 10:43 pm |
Your proposal for having one-level threads is (technically if not in spirit) very similar to mailing lists and Google groups. The latter is fairly easy to setup and it offers (by default) a web-view, RSS, and the possibility to subscribe to emails.
Also, some forums allow each user to choose between a threaded and a flat view. (If a user is not logged in then one view is chosen by default.) I don’t know how hard would be to set up such a forum, nor what exactly needs to be done.
September 29, 2009 at 12:22 pm |
Problem 1 gets my vote: it looks perfect for this kind of project, as it seems potentailly amenable to approaches of many different kinds (combinatorial, group-theoretic, analytic, number-theoretic…).
October 5, 2009 at 5:25 pm |
In regards to possibly using wave for polymath, while wave looks interesting there are several drawbacks. One is that there are a lot of problems with the latex implementation. Another is that it is not available to all people yet so there would be people trying to use without having seen it previously. I think it would be good to use it in the long term but there has to be greater availability and a better latex implementation before it is used for an actual project.
October 6, 2009 at 4:30 pm |
I like a lot the discussion stages and I hope we will have a chance to discuss some of the problems offered here. From various reasons I tend to think now that problem 3a is most suitable for a next polymath.
October 6, 2009 at 10:37 pm |
On 4a – is “non-boring” akin to a kind of Turing Test? So that the computer “explains” not just that the move selected is the one with the highest score, but in terms of intelligible goals and plans?
The reverse question then is whether the heuristics used by human chess players compensate for the inability to do quick calculations of all variations, or whether they represent knowledge or insight in some real and measurable way.
Underlying this is how closely it is possible to replicate the ‘best’ move – what would be done with perfect knowledge or a complete analysis – with some kind of easier computation. This is not to distant from the questions which are being posed in complexity theory.
October 24, 2009 at 4:26 pm |
I would be interested in #2, as a polymath, a dramatic dialog or even less. Though I fear I will miss it entirely if it ever does become a polymath, because I don’t monitor blogs closely. Any chance there could be an email list that gets pinged whenever a polymath project gets officially announced?
October 28, 2009 at 3:55 am |
Very good this is blog.
October 30, 2009 at 10:35 pm |
I’ve been thinking about 1 in very general terms, and it would be interesting to get some understanding of what makes this problem hard – it looks as if the bound ought to be tighter, and there ought to be some natural generalisation to r dimensions rather than just the two (the natural generalisation might come from understanding the bound better).
What is interesting is that it seems possible to prove for simple cases (rational and quadratic) and for complex cases (unbounded partial quotients). Normally a problem cracks under this kind of pressure from both ends. So there is something unusual going on here, which suggests that – even though the problem looks simple – there might be some deeper understanding to discover.
November 4, 2009 at 8:52 pm |
Recently, there has been a good deal of investigation by the
US Federal trade comission against bloggers and website owners
for not revealing advertising revenue, or potential
relationships with advertising networks.
What are your thoughts about how this could impact
the blogging world?
November 7, 2009 at 6:31 pm |
[…] Polymath and the origin of life By gowers This is the first of a few posts I plan (one other of which is written and another of which is in draft form but in need of a few changes) in which I discuss various Polymath proposals in more detail than I did in my earlier post on possible projects. […]
November 14, 2009 at 7:23 pm |
[…] so far) that give further details about possible Polymath projects. This one was number 2 in the post in which I first discussed these projects. In that post, I said nothing beyond the fact that the project had close connections with the […]
November 20, 2009 at 8:44 am |
[…] Problems related to Littlewood’s conjecture By gowers This is the third in a series of posts in which I discuss problems that could perhaps form Polymath projects. Again, I am elaborating on a brief discussion that appeared in an earlier post on possible future projects. […]
December 8, 2009 at 10:14 am |
[…] planned to study the polynomial Hirsch conjecture. In order not to conflict with Tim Gowers’s next polymath project which I suppose will start around January, I propose that we will start polymath3 in mid […]
December 17, 2009 at 1:09 pm |
[…] continue to be busy. But here is one more discussion of a problem that was on my earlier list of possible future Polymath projects. The problem in question is sometimes known as Erdös’s discrepancy problem. (To any […]
March 17, 2010 at 7:34 pm |
[…] of polytopes over this blog. There are several proposed projects on the polymath blog and on Gowers’s blog. The polymath concept was mentioned as an example of a new way of collaborating and doing science […]
June 13, 2010 at 8:32 am |
I would suggest you to study the “magic” world of a DiGraph under x^2-2 modulo a Prime number. The main tree of such a DiGraph is used for the Lucas-Lehmer Test for Mersenne and Fermat numbers. Moreover, for other more complex numbers, like k*2^n+/-1, there is the Lucas-Lehmer Riesel Test. However, no one has ever been able to produce a fast primality test for a number which is not of the form: N+/-1, where N can be easily (or partly) factored.
For Wagstaff numbers ( (2^q+1)/3 ), it “seems” that using a cycle of the DiGraphe under x^2-2 could lead to build a primality proof for such numbers: we have a conjecture and some computing success. A proof is needed… H.C. Williams and Samuel Wagstaff had a look at this.
Apart the Wagstaff numbers, studying the properties of the cycles that appear in a DiGraph under x^2-2 may lead to interesting and useful properties dealing with primality proof, I think.
Read more at: http://trex58.wordpress.com/math2matiques/ and http://tony.reix.free.fr/Mersenne/SummaryOfThe3Conjectures.pdf .
Regards,
Tony
December 1, 2010 at 8:11 pm |
Perhaps clicking into http://www.resurrectingcommonsense.com then linking to Economics 911 would present a problem worthy of consideration. When n-dimentional modeling in a limited resource domain environment became the priority intiative for dozens of DARPA funded projects in the 1980’s a generation of Polymath disciples were drafted into quasi-military service or worse. Enjoy the read. You never know when the truth might turn out to be stranger than fiction.
January 24, 2011 at 4:46 pm |
[…] I did not see how that one worked, but was pretty curious when Gowers was ready to start a new polymath project. This time he suggested several possible topics. This choice reflected the range of his personal […]
November 13, 2011 at 8:54 pm |
psychiatry educational background…
[…]Possible future Polymath projects « Gowers's Weblog[…]…
February 15, 2013 at 4:24 pm |
[…] for polymath projects appeared on this blog, in this post on Gowers’s blog, and in several other […]
March 18, 2013 at 5:35 am |
I like 1. and 3a. Also, 4a and 4b. In artificial intelligence, there was a hope of programs that would learn, and I don’t think that project worked well for games. Concerning Littlewood’s Conjecture, others and myself looked at sup_{a, b in [0,1]x[0,1]} min_{k= 1 … n} k || ka|| ||kb|| for n up to about 60 in my case; this was dicussed in the xkcd forums; etaoin shrdlu went up to n=10^5 or so in a few hours:
http://forums.xkcd.com/viewtopic.php?f=17&t=80338#p2880874
August 30, 2014 at 6:23 pm |
new very promising property on collatz conjecture discovered. invitation to collaborators
October 28, 2015 at 4:51 pm |
[…] will start over this blog in about a week. (This is one of the project proposals by Tim Gowers in this post.) Quanta magazine has an article on important progress by Maria Chudnovsky, Irene Lo, […]
October 30, 2015 at 4:19 pm |
btw nielsens book on cyber/ “networked” science is really great/ engaging/ imaginative/ compelling & wish more ppl would read/ cite/ review it. the idea of “incentives” is quite significant. you talk about basic ideas about “cyber-stickiness” associated with web sites. dynamics like changing content, nonthreaded conversations etc. that is all certainly part of the problem. to me to word “incentives” mainly makes me think of “scientific grants” which is a tricky topic.
however your talk about a sort of “ongoing conversation” in threads reminds me of “chat” rooms on stackexchange, maybe a sort of “limit case” of highly active comment threads. they seem to be very underutilized. unfortunately cyber chat has a reputation or impression of frivolity or superficiality or shallowness. that can occur but it also seems to have untapped potential. one way to think of it is merely as a cyberspace-based “room” that contains conversations of whoever visits. a key dynamic is that stackexchange chat rooms support asynchronous conversations fairly well. have been dabbling in this area for a few yrs now and wrote up a summary of different ppl/ conversations, hope some find it interesting & would encourage more participation/ experimentation in these rooms. they are very open, easy to use, and archived, etc, & have many other useful features.
November 2, 2015 at 9:38 pm |
[…] project. It is one of the nine projects (project 3d) proposed by Tim Gowers in his post “possible future polymath projects”. The plan is to attack Erdos-Rado delta system conjecture also known as the sunflower conjecture. […]
January 31, 2016 at 3:36 pm |
[…] questions were offered along with the Erdos discrepancy problem and the Erdos-Hajnal conjecture in this 2009 post by Tim. In fact, some people participate both in polymath10 and polymath11. The acronym for […]
February 29, 2016 at 6:02 am |
[…] questions were offered along with the Erdos discrepancy problem and the Erdos-Hajnal conjecture in this 2009 post by Tim. In fact, some people participate both in polymath10 and polymath11. The acronym for […]
August 13, 2016 at 8:23 pm |
[…] closed set conjecture (Proposed by Dominic van der Zypen; Also one of the proposals by Gowers in this post). […]
March 20, 2020 at 3:38 am |
[…] para la resolución de la conjetura. En 2009 el medallista Fields Timothy Gowers propuso en su blog estudiarla en el marco de los proyectos colaborativos Polymath. Estos proyectos pretenden atacar […]
March 20, 2020 at 11:08 am |
[…] para la resolución de la conjetura. En 2009 el medallista Fields Timothy Gowers propuso en su blog estudiarla en el marco de los proyectos colaborativos Polymath. Estos proyectos pretenden atacar […]
January 12, 2021 at 7:34 pm |
“If has
has  vertices and does not contain an induced pentagon, then it is not known whether the largest clique in
vertices and does not contain an induced pentagon, then it is not known whether the largest clique in  or
or 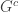 must have size at least
must have size at least 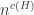 .”
.”
This has now been proved by Maria Chudnovsky, Alex Scott, Paul Symour and Sophie Spirkl, and they rely on recent results by Janos Pach and Istvan Tomon.
January 12, 2021 at 7:45 pm
January 29, 2021 at 9:03 am |
[…] the success of Polymath1 and the launching of Polymath3 and Polymath4, Tim Gowers wrote a blog post “Possible future Polymath projects” for planning the next polymath project on his blog. The post mentioned 9 possible projects. (Three […]
February 20, 2021 at 4:11 pm |
[…] the success of Polymath1 and the launching of Polymath3 and Polymath4, Tim Gowers wrote a blog post “Possible future Polymath projects” for planning the next polymath project on his blog. The post mentioned 9 possible projects. (Four […]
March 26, 2024 at 10:06 am |
Just let me welcome this topic from the approach of formal ontologies and from another starting point but in the same direction: Storing the theory of a particular subject area in one place and maintaining it (including formalization) through collective efforts is easily possible with the modern development of technology. The concentration and verification of knowledge achieved in this case should give a powerful ordering of theoretical knowledge, which will facilitate their formalization, i.e. mathematical notation, and therefore algorithmic processing in many cases, up to the semi-automatic proof of various kinds of consequences, for example, theorems. This message describes what the framework of the theory is, intended for unified storage and collective accumulation of its results.
https://www.researchgate.net/publication/374265191_Theory_framework_-_knowledge_hub_message_1