I will give only a rather brief summary here, together with links to some comments that expand on what I say.
If we take our lead from known proofs of Roth’s theorem and the corners theorem, then we can discern several possible approaches (each one attempting to imitate one of these known proofs).
1. Szemerédi’s original proof.
Szemerédi proved a proof of a one-dimensional theorem. I do not know whether his proof has been modified to deal with the multidimensional case (this was not done by Szemerédi, but might perhaps be known to Terry, who recently digested and rewrote Szemerédi’s proof). So it is not clear whether one can base an entire argument for DHJ on this argument, but it could well contain ideas that would be useful for DHJ. For a sketch of Szemerédi’s proof, see this post of Terry’s, and in particular his discussion of question V. He also has links to comments that expand on what he says.
Ajtai and Szemerédi found a clever proof of the corners theorem that used Szemerédi’s theorem as a lemma. This gives us a direction to explore that we have hardly touched on. Very roughly, to prove the corners theorem you first use an averaging argument to find a dense diagonal (that is, subset of the form that contains many points of your set
). For any two such points
and
you know that the point
does not lie in
(if
is corner free), which gives you some kind of non-quasirandomness. (The Cartesian semi-product arguments discussed in the 400s thread are very similar to this observation.) Indeed, it allows you to find a large Cartesian product
in which
is a bit too dense. In order to exploit this, Ajtai and Szemerédi used Szemerédi’s theorem to find long arithmetic progressions
and
of the same common difference such that
has a density increment in
. (I may have misremembered, but I think this must have been roughly what they did.) So we could think about what the analogue would be in the DHJ setting. Presumably it would be some kind of multidimensional Sperner statement of sufficient depth to imply Szemerédi’s theorem. A naive suggestion would be that in a dense subset of
you can find a large-dimensional combinatorial subspace in which all the variable sets have the same size. If you apply this to a union of layers, then you find an arithmetic progression of layer-cardinalities. But this feels rather artificial, so here’s a question we could think about.
Question 1. Can anyone think what the right common generalization of Szemerédi’s theorem and Sperner’s theorem ought to be? (Sperner’s theorem itself would correspond to the case of progressions of length 2.)
Density-increment strategies.
The idea here is to prove the result by means of the following two steps.
1. If does not contain a combinatorial line, then it correlates with a set
with some kind of atypical structure that we can describe.
2. Every set with that kind of structure can be partitioned into (or almost evenly covered by) a collection of combinatorial subspaces with dimension tending to infinity as
tends to infinity.
One then finishes the argument as follows. If contains no combinatorial line, then find
such that
is a bit denser in
than it is in
. Cover
with subspaces. By averaging we find that the density of
is a bit too large in one of these subspaces. But now we are back where we started with a denser set
so we can repeat. The iteration must eventually terminate (since we cannot have a density greater than 1) so if the initial
was large enough then we must have had a combinatorial line.
One can also imagine splitting 1 up further as follows.
1a. If contains no combinatorial line, then
contains too many of some other simple configuration.
1b. Any set that contains too many of those configurations must correlate with a structured set.
This is certainly how the argument goes in some of the proofs of related results.
Triangle removal.
This was the initial proposal, and we have not been concentrating on it recently, so I will simply refer the reader to the original post, and add the remark that if we manage to obtain a complete and global description of obstructions to uniformity, then regularity and triangle removal could be an alternative way of using this information to prove the theorem. And in the case of corners, this is a somewhat simpler thing to do.
Ergodic-inspired methods.
For a proposal to base a proof on at least some of the ideas that come out of the proof of Furstenberg and Katznelson, see Terry’s comment 439, as well as the first few comments after it. Another helpful comment of Terry’s is his comment 460, which again is responded to by other comments. Terry has also begun an online reading seminar on the Furstenberg-Katznelson proof, using not just the original paper of Furstenberg and Katznelson but also a more recent paper of Randall McCutcheon that explains how to finish off the Furstenberg-Katznelson argument.
Suggestion. I have tried to do a bit of further summary in my first couple of comments. It would be good if others did the same, with the aim that anyone who reads this should be able to get a reasonable idea of what is going on without having to read too much of the earlier discussion.
Remark. There is now a wiki associated with this whole enterprise. It is in the very early stages of development but has some useful things on it already.
February 13, 2009 at 11:30 am |
500. Inverse theorem.
This is continuing where I left off in 490. Let me briefly say what the aim is. I am using the disjoint-pairs formulation of DHJ: given a dense set of pairs
of pairs  of disjoint sets, one can find a triple of the form
of disjoint sets, one can find a triple of the form  ,
, 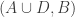 ,
, 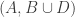 in
in  with all of
with all of 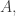
 and
and  disjoint. Here “dense” is to be interpreted in the equal-slices measure: that is, if you randomly choose two non-negative integers
disjoint. Here “dense” is to be interpreted in the equal-slices measure: that is, if you randomly choose two non-negative integers  with
with  , and then randomly choose disjoint sets
, and then randomly choose disjoint sets  and
and  with cardinalities
with cardinalities  and
and  , then the probability that
, then the probability that  is at least
is at least  .
.
Now I define a norm on functions![f:[2]^n\times[2]^n\rightarrow\mathbb{R}](https://s0.wp.com/latex.php?latex=f%3A%5B2%5D%5En%5Ctimes%5B2%5D%5En%5Crightarrow%5Cmathbb%7BR%7D&bg=ffffff&fg=333333&s=0&c=20201002) as follows. (Incidentally, this is the genuine Cartesian product here, but pairs of sets will not make too big a contribution if they intersect.) First choose a random permutation
as follows. (Incidentally, this is the genuine Cartesian product here, but pairs of sets will not make too big a contribution if they intersect.) First choose a random permutation  of
of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Then take the average of
. Then take the average of 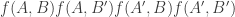 over all pairs
over all pairs 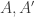 of initial segments of
of initial segments of ![\pi[n]](https://s0.wp.com/latex.php?latex=%5Cpi%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and all pairs
and all pairs  of final segments of
of final segments of ![\pi[n]](https://s0.wp.com/latex.php?latex=%5Cpi%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Finally, take the average over all
. Finally, take the average over all  .
.
A few things to note about this definition. First, if you choose the initial and final segments randomly, then the probability that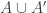 is disjoint from
is disjoint from 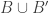 is at least
is at least  (and in fact slightly higher than this). Second, the marginal distributions of
(and in fact slightly higher than this). Second, the marginal distributions of  and
and 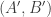 are just the slices-equal measure. Third, for any fixed
are just the slices-equal measure. Third, for any fixed  the expectation we take can also be thought of as
the expectation we take can also be thought of as 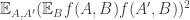 , so we get positivity. If we take the fourth root of this quantity and average over all
, so we get positivity. If we take the fourth root of this quantity and average over all  then we get a norm, by standard arguments. (I’m less sure what happens if we first average and then take the fourth root. I’m also not sure whether that’s an important question or not.)
then we get a norm, by standard arguments. (I’m less sure what happens if we first average and then take the fourth root. I’m also not sure whether that’s an important question or not.)
Given a set of density
of density  (as a subset of the set of all disjoint pairs, with slices-equal measure), define its balanced function
(as a subset of the set of all disjoint pairs, with slices-equal measure), define its balanced function ![f:[2]^n\times[2]^n\rightarrow\mathbb{R}](https://s0.wp.com/latex.php?latex=f%3A%5B2%5D%5En%5Ctimes%5B2%5D%5En%5Crightarrow%5Cmathbb%7BR%7D&bg=ffffff&fg=333333&s=0&c=20201002) as follows. If
as follows. If  and
and  are disjoint, then
are disjoint, then  if
if  and
and 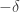 otherwise. If
otherwise. If  and
and  intersect, then
intersect, then 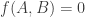 . Then
. Then  if we think about it suitably. And the way to think about it is this. To calculate
if we think about it suitably. And the way to think about it is this. To calculate 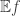 we first take a random permutation of
we first take a random permutation of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Then we choose a random initial segment
. Then we choose a random initial segment  and a random final segment
and a random final segment  . Then we evaluate
. Then we evaluate  . This is how I am defining the expectation of
. This is how I am defining the expectation of  .
.
Though I haven’t written out a formal proof (since I am not doing that — though I think a general rule is going to have to be that if a sketch starts to become rather detailed, and if nobody can see any reason for it not to be essentially correct, then the hard work of turning it into a formal argument would be done away from the computer), I am fairly sure that if a dense set contains no combinatorial lines and
contains no combinatorial lines and  is the balanced function of
is the balanced function of  then
then  is bounded away from 0.
is bounded away from 0.
That was just a mini-summary of where this uniformity-norms idea may possibly have got to. Because it feels OK I want to think about the part that feels potentially a lot less OK, which is obtaining some kind of usable structure where has a large average, on the assumption that
has a large average, on the assumption that  is large.
is large.
February 13, 2009 at 11:48 am |
501. Inverse theorem.
What I would very much like to be able to do is rescue a version of the conjecture put forward in comment 411. The conjecture as stated seems to be false, but it may still be true if we use the slices-equal measure. In terms of functions, what I’d like to be able to prove is that if is at least
is at least  , then there exist set systems
, then there exist set systems 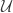 and
and 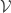 such that the density of disjoint pairs
such that the density of disjoint pairs  with
with 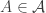 and
and  is at least
is at least 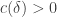 and the average of
and the average of  over all such pairs is at least
over all such pairs is at least  . (The first condition could be relaxed to positive density in some subspace if that helped.)
. (The first condition could be relaxed to positive density in some subspace if that helped.)
I’m fairly sure that easy arguments give us the following much weaker statement. If you choose a random pair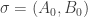 according to equal-slices measure, then you can find set systems
according to equal-slices measure, then you can find set systems  and
and  with the following properties.
with the following properties.
(i) Every set in is disjoint from
is disjoint from 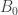 and every set in
and every set in  is disjoint from
is disjoint from  .
.
(ii) The set of disjoint pairs such that
such that  and
and 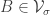 is on average dense in the set of disjoint pairs
is on average dense in the set of disjoint pairs  such that
such that 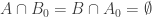 .
.
(iii) For each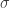 the expectation of
the expectation of  over all disjoint pairs
over all disjoint pairs 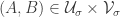 is at least
is at least  .
.
If this is correct, then the question at hand is whether one can piece together the pairs to form two set systems
to form two set systems 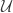 and
and 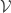 such that the density of disjoint pairs
such that the density of disjoint pairs  with
with 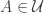 and
and  is at least
is at least 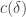 and the average of
and the average of  over all such pairs is at least
over all such pairs is at least  .
.
February 13, 2009 at 12:36 pm |
502. Inverse theorem.
In this comment I want to explain slightly better what I mean by “piecing together” local lack of uniformity to obtain global obstructions. To do so I’ll look at a few examples.
Example 1 Terry has already mentioned this one. Let be a function defined on
be a function defined on 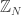 . Suppose we know that for every interval
. Suppose we know that for every interval  of length
of length  we can find a trigonometric function
we can find a trigonometric function  such that
such that 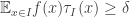 . Can we find a trigonometric function
. Can we find a trigonometric function  defined on all of
defined on all of 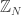 such that
such that 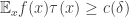 ? The answer is very definitely no. Basically, you can just partition
? The answer is very definitely no. Basically, you can just partition 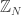 into intervals of length a bit bigger than
into intervals of length a bit bigger than  and define
and define  to be a randomly chosen trigonometric function on each of these intervals. This will satisfy the hypotheses but be globally quasirandom.
to be a randomly chosen trigonometric function on each of these intervals. This will satisfy the hypotheses but be globally quasirandom.
Example 2 Now let’s modify Example 1. This time we assume that has trigonometric bias not just on intervals but on arithmetic progressions of length
has trigonometric bias not just on intervals but on arithmetic progressions of length  (in the mod-
(in the mod- sense of an arithmetic progression). I don’t know for sure what the answer is here, but I think we do now get a global correlation. Suppose for instance that
sense of an arithmetic progression). I don’t know for sure what the answer is here, but I think we do now get a global correlation. Suppose for instance that  is around
is around  . Then if we choose random trigonometric functions on each interval of length
. Then if we choose random trigonometric functions on each interval of length  , they will give rise to random functions on arithmetic progressions of common difference
, they will give rise to random functions on arithmetic progressions of common difference  . So the frequencies are forced to relate to each other in a way that they weren’t before.
. So the frequencies are forced to relate to each other in a way that they weren’t before.
Example 3. Suppose that is a graph of density
is a graph of density  with vertex set
with vertex set  of size
of size  . Suppose that
. Suppose that  is some integer that’s much smaller than
is some integer that’s much smaller than  and suppose that for a proportion of at least
and suppose that for a proportion of at least  of the choices
of the choices  of
of  vertices you can find a subset
vertices you can find a subset  of size at least
of size at least  such that the density of the subgraph induced by
such that the density of the subgraph induced by  (inside
(inside  ) is at least
) is at least  . Can we find a subset
. Can we find a subset  of
of  of size at least
of size at least 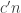 such that the density of the subgraph induced by
such that the density of the subgraph induced by  is at least
is at least 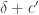 ?
?
The answer is yes, and it is an easy consequence of standard facts about quasirandomness. The hypothesis plus an averaging argument implies that contains too many 4-cycles, which means that
contains too many 4-cycles, which means that  is not quasirandom, which implies that there is a global density change. (Sorry, in this case I misstated it — you don’t actually get an increase, as the complete bipartite graph on two sets of size
is not quasirandom, which implies that there is a global density change. (Sorry, in this case I misstated it — you don’t actually get an increase, as the complete bipartite graph on two sets of size 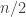 illustrates, but you can get the density to differ substantially from
illustrates, but you can get the density to differ substantially from  . If you want a density increase, then you need a similar statement about bipartite graphs.)
. If you want a density increase, then you need a similar statement about bipartite graphs.)
Example 4. Suppose that is a random graph on
is a random graph on  vertices with edge density
vertices with edge density  . Let
. Let  be a subgraph of
be a subgraph of  of relative density
of relative density  . Then one would expect
. Then one would expect  to contain about
to contain about 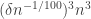 labelled triangles. Suppose that it contains more triangles than this. Can we find two large subsets
labelled triangles. Suppose that it contains more triangles than this. Can we find two large subsets  and
and  of vertices such that the number of edges joining them is substantially more than
of vertices such that the number of edges joining them is substantially more than  ?
?
Our hypothesis tells us that if we pick a random vertex in the graph, then its neighbourhood will on average have greater edge density than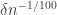 . So we have a large collection of sets where
. So we have a large collection of sets where  is too dense. However, these sets are all rather small. So can we put them together? The answer is yes but the proof is non-trivial and depends crucially on the fact that the neighbourhoods of the vertices are forced (by the randomness of
is too dense. However, these sets are all rather small. So can we put them together? The answer is yes but the proof is non-trivial and depends crucially on the fact that the neighbourhoods of the vertices are forced (by the randomness of  ) to spread themselves around.
) to spread themselves around.
Question. Going back to our Hales-Jewett situation, as described at the end of the previous comment, is it more like Example 1 (which would be bad news for this approach, but illuminating nevertheless), or is it more like the other examples where the non-uniformities are forced to relate to one another and combine to form a global obstruction?
February 13, 2009 at 5:23 pm |
503. Combining obstructions.
I want to think as abstractly as possible about when obstructions in small subsets are forced to combine to form a single global obstruction. For simplicity of discussion I’ll use a uniform measure. So let be a set, let
be a set, let 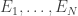 be subsets of
be subsets of  , and let us assume that every
, and let us assume that every 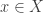 is contained in exactly
is contained in exactly  of the
of the 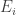 . Let us assume also that the
. Let us assume also that the 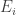 all have the same size (an assumption I’d eventually hope to relax) and that a typical intersection
all have the same size (an assumption I’d eventually hope to relax) and that a typical intersection  is not too small, though I won’t be precise about this for now.
is not too small, though I won’t be precise about this for now.
For each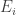 let
let ![g_i:E_i\rightarrow[-1,1]](https://s0.wp.com/latex.php?latex=g_i%3AE_i%5Crightarrow%5B-1%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) be some function. Then one simple remark one can make (which doesn’t require anything like all the assumptions I’ve just made) is that if we can find
be some function. Then one simple remark one can make (which doesn’t require anything like all the assumptions I’ve just made) is that if we can find  that correlates with many of the
that correlates with many of the 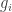 , then there must be lots of correlation between the
, then there must be lots of correlation between the 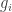 themselves. To see this, recall first that
themselves. To see this, recall first that 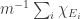 is the constant function 1. Therefore,
is the constant function 1. Therefore, 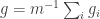 is a function that takes values in
is a function that takes values in ![{}[-1,1]](https://s0.wp.com/latex.php?latex=%7B%7D%5B-1%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Furthermore,
. Furthermore, 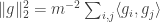 . Since
. Since 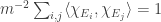 , and we can rewrite it as
, and we can rewrite it as 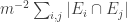 , we find that on average
, we find that on average 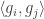 must be a substantial fraction of its trivial maximum
must be a substantial fraction of its trivial maximum 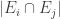 . If
. If  is large, so that the diagonal terms are negligible, then this says that there are lots of correlations between the
is large, so that the diagonal terms are negligible, then this says that there are lots of correlations between the 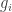 .
.
In my next comment I will discuss a strategy for getting from this to a globally defined function, built out of the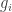 , that correlates with
, that correlates with  and is likely to have good properties under certain circumstances.
and is likely to have good properties under certain circumstances.
February 13, 2009 at 7:13 pm |
504. Combining obstructions.
Tim – Before you define a general local-global uniformity, please let me ask a question. For extremal set problems it was very useful – and we used it before – to take a random permutation of the base set [n] and considering only sets which are “nice” in this ordering. For example, let us consider sets where the elements are consecutive. If the original set system was dense, then in this window, that we had by a random permutation, is a dense set of intervals. Here we can define/check uniformity easily. Disjoint sets are disjoint, and one can also analyze intersections. I didn’t do any formal calculations, however this window might give us some information we want and it is easy to work with. (We won’t find combinatorial lines there, so I don’t see direct a proof for DHJ, but it’s not a surprise …)
February 13, 2009 at 9:06 pm |
505. Uniformity norms:
The ergodic proof of DHJ reduces it to an IP recurrence theorem. Now, for an IP system setup, we can easily define analogs of the (ergodic) uniformity norms. So, let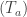 be a measure preserving IP system;
be a measure preserving IP system;  ranges over finite subsets of the naturals. Put
ranges over finite subsets of the naturals. Put 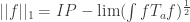 . Now let
. Now let  be the projection onto the factor that is asymptotically invariant under
be the projection onto the factor that is asymptotically invariant under 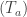 ; we can write
; we can write 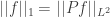 if we like. Now put
if we like. Now put 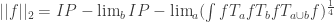 . (This should look awfully familiar.) Presumably, if
. (This should look awfully familiar.) Presumably, if 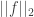 is small, where
is small, where  is the balanced version of the characteristic function of a set, then the set should have, asymptotically, the right number of arithmetic progressions of length 3 whose difference comes from some relevant IP set (or something like that). On the other hand, if
is the balanced version of the characteristic function of a set, then the set should have, asymptotically, the right number of arithmetic progressions of length 3 whose difference comes from some relevant IP set (or something like that). On the other hand, if 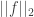 is big,
is big,  must correlate with….well, let’s just say if
must correlate with….well, let’s just say if  is big then
is big then  correlates with a rigid function, that much is easy. At any rate I think the above may be on the right track. I may try to translate from ergodic theory to a more recognizable form, but right now a baby is waking up behind me….
correlates with a rigid function, that much is easy. At any rate I think the above may be on the right track. I may try to translate from ergodic theory to a more recognizable form, but right now a baby is waking up behind me….
However, I will say this much…there is no conventional averaging in any proof of any ergodic IP recurrence theorem (IP limits serve that purpose in this context). Also, there are extremely strong analogies between the uniformity norms on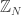 and the uniformity norms in ergodic theory (actually…to me it’s not really an analogy; these are exactly the same norms). Although no norms are defined in ergodic IP theory, there could be…what does a norm stand in for? To an ergodic theorist, the dth uniformity norm is a stand-in for d iterations of van der Corput. In the IP case, we do in fact use d iterations of a version of van der Corput. If the correlation holds to form, the above norms may well be the ones to be looking at.
and the uniformity norms in ergodic theory (actually…to me it’s not really an analogy; these are exactly the same norms). Although no norms are defined in ergodic IP theory, there could be…what does a norm stand in for? To an ergodic theorist, the dth uniformity norm is a stand-in for d iterations of van der Corput. In the IP case, we do in fact use d iterations of a version of van der Corput. If the correlation holds to form, the above norms may well be the ones to be looking at.
February 13, 2009 at 9:08 pm |
505. Combining obstructions.
In my previous post I said that we won’t see combinatorial lines in a random permutation. Now I’m not that sure about it. So, here is a simple statement which would imply DHJ (so it’s false most likely, but I can’t see a simple counterexample) If you take a dense subset of pairwise disjoint intervals in [n] then there are four numbers a, b, c, d in increasing order that [a,b],[c,d] and [a,c],[c,d] and [a,b],[b,d] are in your subset.
The rough numbers – counting the probability that there is no such configuration in a random permutation – didn’t give me any hint. I have to work with a more precise form of Stirling’s formula. I need time and I will work away from the computer. (I have to leave shortly anyways)
February 13, 2009 at 9:18 pm |
506.
The “simple statement” above is clearly false, just take pairs where
one interval is between 1 and n/2 and the second is between n/2 and n. But I think this is not a general problem for our application where we might be able to avoid such “bipartite” cases.
February 14, 2009 at 1:07 am |
507.
Tim,
Regarding your Example 2 in 502 above, here is a cheat way to get a global obstruction. If you correlate with a linear phase on many progressions of length sqrt{N} then you also have large U^2 norm on each such progression. Summing over all progressions, this means that the sum of f over all parallelograms (x,x+h,x+k,x+h+k) with |k/h| \leq \sqrt{N}, or roughly that, is large.
But even if you only control such parallelograms with k = 2h this is the same as controlling the average of f over 4-term progressions, and one knows that is controlled by the *global* U^3 norm and hence by a global quadratic object (nilsequence). That will allow you to “tie together” the frequencies of the trig polys that you correlated with at the beginning, though I haven’t bothered to think exactly how. One just needs to analyse which 2-step nilsequences correlate with a linear phase on many progressions of length sqrt{N}, and it might just be ones which are essentially 1-step, and that would imply that f correlates globally with a linear phase.
BY the way much the same argument shows that if you have large U^k norm on many progressions of length sqrt{N} (say) then you have large global U^{2^k -1} norm.
Ben
February 14, 2009 at 1:13 am |
508. Ergodic-mimicking general proof strategy:
Okay, I will give my general idea for a proof. I’m pretty sure it’s sound, though it may not be feasible in practice. On the other hand I may be badly mistaken about something. I will throw it out there for someone else to attempt, or say why it’s nonsense, or perhaps ignore. I won’t formulate it as a strategy to prove DHJ, but of what I’ve called IP Roth. If successful, one could possibly adapt it to the DHJ, k=3 situation, but there would be complications that would obscure what was going on.
We work in $X=[n]^{[n]}\times [n]^{[n]}$. For a real valued function $f$ defined on $X$, define the first coordinate 2-norm by $||f||^1_2=(\iplim_b\iplim_a {1\over |X|}\sum_{(x,y)\in X} f((x,y))f((x+a,y))f((x+b,y))f((x+a+b,y)))^{1\over 4}$. The second coordinate 2-norm is defined similarly (on the second coordinate, obviously). Now, let me explain what this means. $a$ and $b$ are subsets of $[n]$, and we identify $a$ with the characteristic function of $a$, which is a member of $[n]^{[n]}$. (That is how we can add $a$ to $x$ inside, etc. Since $[n]$ is a finite set, you can’t really take limits, but if $n$ is large, we can do something almost as good, namely ensure that whenever $\max\alpha<\min\beta$, the expression we are taking the limit of is close to something (Milliken Taylor ensures this, I think). Of course, you have to restrict $a$ and $b$ to a subspace. What is a subspace? You take a sequence $a_i$ of subsets of $[n]$ with $\max a_i<\min a_{i+1}$ and then restrict to unions of the $a_i$.
Now here is the idea. Take a subset $E$ of $X$ and let $f$ be its balanced indicator function. You first want to show that if *either* of the coordinate 2-norms of $f$ is small, then $E$ contains about the right number of corners $\{ (x,y), (x+a,y), (x,y+a)\}$. Restricted to the subspace of course. What does that mean? Well, you treat each of the $a_i$ as a single coordinate, moving them together. The other coordinates I’m not sure about. Maybe you can just fix them in the right way and have the norm that was small summing over all of $X$ still come out small. At any rate, the real trick is to show that if *both* coordinate 2-norms are big, you get a density increment on a subspace. Here a subspace surely means that you find some $a_i$s, treat them as single coordinates, and fix the values on the other coordinates.
February 14, 2009 at 1:19 am |
509. Quasirandomness.
Jozsef, re 504, what you describe is what I thought I was doing in the second paragraph of 500. The nice thing about taking a random permutation and then only looking at intervals is that you end up with dense graphs. The annoying thing is that these dense graphs don’t instantly give you combinatorial lines. However, they do give correlation with a Cartesian product, so my hope was to put together all these small dense Cartesian products to get a big dense “Kneser product”. At the moment I feel quite hopeful about this. I’ve got to go to bed very soon, but roughly my planned programme for doing it is this.
Suppose you have proved that there are a lot of pairwise correlations between the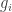 . Then I want to think of these
. Then I want to think of these 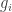 as unit vectors in a Hilbert space and find some selection of them such that most pairs of them correlate. Here’s a general dependent-random-selection procedure for vectors in a finite-dimensional Hilbert space. Suppose I have unit vectors
as unit vectors in a Hilbert space and find some selection of them such that most pairs of them correlate. Here’s a general dependent-random-selection procedure for vectors in a finite-dimensional Hilbert space. Suppose I have unit vectors 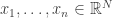 . Now I choose random unit vectors
. Now I choose random unit vectors 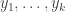 and pick all those
and pick all those  such that
such that 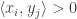 for every
for every  . The probability of choosing any given
. The probability of choosing any given  is obviously
is obviously 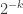 . Now the probability that
. Now the probability that 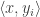 and
and  are both positive is equal to the proportion of the sphere in the intersection of the positive hemispheres defined by
are both positive is equal to the proportion of the sphere in the intersection of the positive hemispheres defined by  and
and 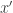 , which has measure
, which has measure 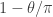 , where
, where  is the angle between
is the angle between  and
and 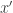 . So the probability of picking both
. So the probability of picking both  and
and 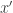 is
is  . So if
. So if 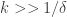 and we have lots of correlations of at least
and we have lots of correlations of at least  , then we should end up with almost all pairs that we choose having good correlations. It is some choice like this that I am currently hoping will give rise to a global obstruction to uniformity.
, then we should end up with almost all pairs that we choose having good correlations. It is some choice like this that I am currently hoping will give rise to a global obstruction to uniformity.
The more I think about this, the more I am beginning to feel that it’s got to the point where it’s going to be hard to make progress without going away and doing calculations. I don’t really see any other way of testing the plausibility of some of the ideas I am suggesting.
February 14, 2009 at 8:37 am |
510. Stationarity
The reading seminar is already paying off for me, in that I now see that the random Bernoulli variables associated to a Cartesian half-product automatically enjoy the stationarity property, which will presumably be useful in showing that those half-products contain lines with positive probability. (I also plan to write up this strategy on the wiki at some point.)
Let’s recall the setup. We have a set A of density in
in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) that we wish to find lines in. Pick a random x in
that we wish to find lines in. Pick a random x in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , then pick random
, then pick random 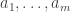 in the 0-set of x, where
in the 0-set of x, where 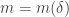 does not depend on n. This gives a random embedding of
does not depend on n. This gives a random embedding of ![{}[3]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) into
into ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , and in particular creates the strings
, and in particular creates the strings 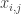 for
for 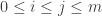 , formed from x by flipping the
, formed from x by flipping the 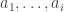 digits from 0 to 1, and the
digits from 0 to 1, and the 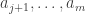 digits from 0 to 2. I like to think of the
digits from 0 to 2. I like to think of the 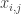 as a “Cartesian half-product”, which in the m=4 case is indexed as follows:
as a “Cartesian half-product”, which in the m=4 case is indexed as follows:
0000 0002 0022 0222 2222
1000 1002 1022 1222
1100 1102 1122
1110 1112
1111
Observe that form a line whenever
form a line whenever 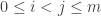 . We have the Bernoulli events
. We have the Bernoulli events 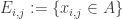 .
.
We already observed that each of the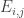 have probability about
have probability about  , thus the one-point correlations of
, thus the one-point correlations of 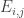 are basically independent of i and j. More generally, it looks like the k-point correlations of the
are basically independent of i and j. More generally, it looks like the k-point correlations of the 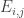 are translation-invariant in i and j (so long as one stays inside the Cartesian half-product). For instance, when
are translation-invariant in i and j (so long as one stays inside the Cartesian half-product). For instance, when 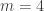 , the events
, the events 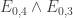 and
and  (which are the assertions that the embedded copies of 0000, 1000 and 0002, 1002 respectively both lie in A) have essentially the same probability. This is obvious if you think about it, and comes from the fact that if you take a uniformly random string in
(which are the assertions that the embedded copies of 0000, 1000 and 0002, 1002 respectively both lie in A) have essentially the same probability. This is obvious if you think about it, and comes from the fact that if you take a uniformly random string in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) and flip a random 0-bit of that string to a 2, one essentially gets another uniformly random string in
and flip a random 0-bit of that string to a 2, one essentially gets another uniformly random string in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) (the error in the probability distribution is negligible in the total variation norm). Indeed, all the probabilities of
(the error in the probability distribution is negligible in the total variation norm). Indeed, all the probabilities of 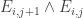 are essentially equal for all i,j for which this makes sense. And similarly for other k-point correlations.
are essentially equal for all i,j for which this makes sense. And similarly for other k-point correlations.
I don’t yet know how to use stationarity, but I expect to learn as the reading seminar continues.
February 14, 2009 at 9:42 am |
511. Local-to-global
Re 502 Example 2 and 507, I think I now have a simple way of getting a global obstruction in this case, but it would have to be checked. Suppose that is a function that correlates with a trigonometric function on a positive proportion of the APs in
is a function that correlates with a trigonometric function on a positive proportion of the APs in 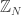 of length
of length  . Here
. Here  could be very small — depending on the size of the correlation only I think.
could be very small — depending on the size of the correlation only I think.
Now suppose I pick a random AP of length 3. Then it will be contained in several of these APs of length , and if
, and if  is prime each AP of length 3 will be in the same number of APs of length
is prime each AP of length 3 will be in the same number of APs of length  . At this stage there’s a gap in the argument because lack of uniformity doesn’t imply that you have the wrong sum over APs of length 3, but it sort of morally does, so I think it might well be possible to deal with this and get that the expectation of
. At this stage there’s a gap in the argument because lack of uniformity doesn’t imply that you have the wrong sum over APs of length 3, but it sort of morally does, so I think it might well be possible to deal with this and get that the expectation of 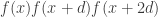 is not small — perhaps by modifying
is not small — perhaps by modifying  in some way or playing around with different
in some way or playing around with different  . And then we’d have a global obstruction by the
. And then we’d have a global obstruction by the 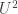 inverse theorem.
inverse theorem.
Alternatively, instead of using APs of length 3, it might be possible to use additive quadruples but under the extra condition that there is a small linear relation between
but under the extra condition that there is a small linear relation between  and
and  . That would give a useful positivity. I haven’t checked whether lack of uniformity on such additive quadruples implies that the
. That would give a useful positivity. I haven’t checked whether lack of uniformity on such additive quadruples implies that the 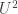 norm is large, but the fact that 3-APs give you big
norm is large, but the fact that 3-APs give you big 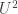 is a promising sign.
is a promising sign.
February 14, 2009 at 5:15 pm |
512. Stationarity.
Just a small note on Terry.#510: Is there any particular reason for choosing the indices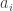 from the 0-set of the initial random string
from the 0-set of the initial random string  ?
?
If not, the probabilistic analysis might be very slightly cleaner if we simply say, “Choose random coordinates
random coordinates 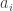 and fill in the remaining
and fill in the remaining  coordinates at random. Now consider the events
coordinates at random. Now consider the events 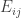 …”
…”
February 14, 2009 at 9:57 pm |
513. Stationarity
Yeah, you’re right; I was rather clumsily thinking of the base point x as being the lower left corner of the embedded space, when in fact one only needs to think of what x is doing outside of the variable indices. (I’ve updated the wiki to reflect this improvement.)
February 15, 2009 at 8:06 am |
514. DHJ(2.6)
Back in 130 I asked a weaker statement than DHJ(3), dubbed DHJ(2.5): if A is a dense subset of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , does there exist a combinatorial line
, does there exist a combinatorial line 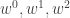 whose first two positions only
whose first two positions only  are required to lie inside A? It was quickly pointed out to me that this follows easily from DHJ(2).
are required to lie inside A? It was quickly pointed out to me that this follows easily from DHJ(2).
From the reading seminar, I now have a new problem intermediate between DHJ(3) and DHJ(2.5), which I am dubbing DHJ(2.6): if A is a dense subset of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , does there exist an r such that for each ij=01,12,20, there exists a combinatorial line
, does there exist an r such that for each ij=01,12,20, there exists a combinatorial line 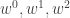 with exactly r wildcards with
with exactly r wildcards with 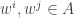 ? So it’s three copies of DHJ(2.5) with the extra constraint that the lines all have to have the same wildcard length. Clearly this would follow from DHJ(3) but is a weaker problem. At present I do not see a combinatorial proof of this weaker statement (which Furstenberg and Katznelson, by the way, spend an entire paper just to prove).
? So it’s three copies of DHJ(2.5) with the extra constraint that the lines all have to have the same wildcard length. Clearly this would follow from DHJ(3) but is a weaker problem. At present I do not see a combinatorial proof of this weaker statement (which Furstenberg and Katznelson, by the way, spend an entire paper just to prove).
February 15, 2009 at 3:53 pm |
515. Different measures.
Terry, I’m not sure I understand your derivation of slices-equal DHJ from uniform DHJ. For convenience let me copy your argument and then comment on specific lines of it.
Suppose that![A \subset [3]^n](https://s0.wp.com/latex.php?latex=A+%5Csubset+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) has density
has density  in the equal-slices sense. By the first moment method, this means that A has density
in the equal-slices sense. By the first moment method, this means that A has density  on
on  on the slices.
on the slices.
Let m be a medium integer (much bigger than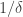 , much less than n).
, much less than n).
Pick (a, b, c) at random that add up to n-m. By the first moment method, we see that with probability , A will have density
, A will have density  on the
on the  of the slices
of the slices  with
with  ,
,  ,
, 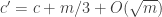 .
.
This implies that A has expected density on a random m-dimensional subspace generated by a 1s, b 2s, c 3s, and m independent wildcards.
on a random m-dimensional subspace generated by a 1s, b 2s, c 3s, and m independent wildcards.
Applying regular DHJ to that random subspace we obtain the claim.
One of my arguments for deducing slices-equal from uniform collapsed because sequences belonging to non-central slices are very much more heavily weighted than sequences that belong to central ones. I don’t understand why that’s not happening in your argument (though I haven’t carefully done calculations). Consider for example what might happen if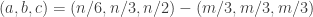 . Then the weights of individual sequences in the slices of the form
. Then the weights of individual sequences in the slices of the form 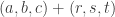 go down exponentially as r increases and as t decreases, even if
go down exponentially as r increases and as t decreases, even if  is close to
is close to 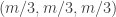 . Or am I missing something?
. Or am I missing something?
In general, there seems to be a difficult phenomenon associated with the slices-equal measure, which is that unless you’re lucky enough for to contain bits near the middle, it will be very far from uniform on all combinatorial subspaces where it might have a chance to be dense. Worse still, it doesn’t restrict to slices-equal measure on subspaces.
to contain bits near the middle, it will be very far from uniform on all combinatorial subspaces where it might have a chance to be dense. Worse still, it doesn’t restrict to slices-equal measure on subspaces.
February 15, 2009 at 5:28 pm |
516. Different measures.
On second thoughts, I do now follow your argument!
February 15, 2009 at 6:29 pm |
517. Different measures
I’ve put a summary of the different measures discussion on the wiki at
http://michaelnielsen.org/polymath1/index.php?title=Equal-slices_measure
(More generally, I will probably be more silent on this thread than previously, but will be working “behind the scenes” by distilling some of the older discussion onto the wiki.)
February 15, 2009 at 9:43 pm |
DHJ (2.6):
Here’s what looks like a combinatorial proof, modulo reduction to sets and Graham-Rothschild being kosher (at least no infinitary theorems are used). Put everything in the sets formulation, where you have sets $B_w$ of measure at least $\delta$ in a prob. space. (No need for stationarity.) Now color combinatorial lines $\{ w(0),w(1),w(2)\}$ according to whether $B_{w(0)}\cap B_{w(1)}$, $B_{w(0)}\cap B_{w(2)}$ and $B_{w(1)}\cap B_{w(2)}$ are empty or not (8 colors). By Graham-Rothschild, there is an $n$-dimensional subspace all of whose lines have the same color for this coloring. Just take $n$ large enough for the sets version of DHJ (2.5).
February 15, 2009 at 10:59 pm |
519.
Dear Randall, I like this proof, but I am a little worried that A is still dense on the subspace one passes to by Graham-Rothschild. If A is deterministic, it may well be that the space one passes to is completely empty; if instead A is random, then the Graham-Rothschild subspace will depend on A and it is no longer clear that all the events in that space have probability .
.
February 16, 2009 at 12:40 am |
520.
Terry…the subspace doesn’t depend on the random set A. What I am proving is the (b) formulation, not the (a) formulation. There seems to be some disconnect between the language of ergodic theory and the language of “random sets”, so let me try to translate: one reduces to a subspace where, for each ij=01,12,02, one of the following two things happens:
1. for all variable words w over the subspace, the probability that both w(i) and w(j) are in A is zero.
2. for all variable words w over the subspace, the probability that both w(i) and w(j) are in A is positive.
If you still think there is an issue about a density decrement, just read my proof as a proof of the (b) formulation…there, you can’t have a density decrement upon passing to a subspace because all the sets B_w have density at least \delta.
February 16, 2009 at 1:50 am |
521.
Oh, I see now. That’s a nice argument – and one that demonstrates an advantage in working in the ergodic/probabilistic setting. (It would be interesting to see a combinatorial translation of the argument, though.)
I’ll write it up on the wiki (on the DHJ page) now.
February 16, 2009 at 5:35 am |
522. DHJ(2.6).
Hmm, I see how this is a bit trickier than DHJ(2.5). For example, for any of the three pairs you can probably show that if
pairs you can probably show that if 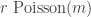 for some moderate
for some moderate  then there is at least an
then there is at least an  chance of having an “
chance of having an “ pair” at distance
pair” at distance  . But the trouble is, these could potentially be different measure
. But the trouble is, these could potentially be different measure  sets, and since they’re small it’s not so obvious how to show they’re not disjoint.
sets, and since they’re small it’s not so obvious how to show they’re not disjoint.
As an example of the trickiness, let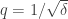 , assumed an integer. Perhaps $\latex A$ is the set of strings whose 0-count is divisible by
, assumed an integer. Perhaps $\latex A$ is the set of strings whose 0-count is divisible by  and whose 1-count is divisible by
and whose 1-count is divisible by  . Now 02-pairs have to be at distance which is a multiple of
. Now 02-pairs have to be at distance which is a multiple of  , and 12-pairs have to be at a distance which is a multiple of
, and 12-pairs have to be at a distance which is a multiple of  . So you have to be a bit clever to extract a common valid distance, a multiple of
. So you have to be a bit clever to extract a common valid distance, a multiple of 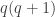 .
.
February 16, 2009 at 8:01 am |
Ryan,
Can you explain more your approach in comment 477. ?
February 16, 2009 at 8:38 am |
524. DHJ(2.6)
A small observation: one can tone the Ramsey theory in Randall’s proof of DHJ(2.6) a notch, by replacing the Graham-Rothschild theorem by the simpler Folkman’s theorem (this is basically because of the permutation symmetry of the random subcube ensemble). Indeed, given a dense set A in![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) we can colour [n] in eight colours, colouring a shift r depending on whether there exists a combinatorial line with r wildcards whose first two (or last two, or first and last) vertices lie in A. By Folkman’s theorem, we can find a monochromatic m-dimensional pinned cube Q in [n] (actually it is convenient to place this cube in a much smaller set, e.g.
we can colour [n] in eight colours, colouring a shift r depending on whether there exists a combinatorial line with r wildcards whose first two (or last two, or first and last) vertices lie in A. By Folkman’s theorem, we can find a monochromatic m-dimensional pinned cube Q in [n] (actually it is convenient to place this cube in a much smaller set, e.g. ![{}[n^{0.1}]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5E%7B0.1%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) ). If the monochromatic colour is such that all three pairs of a combinatorial line with r wildcards can occur in A, we are done, so suppose that there is no line with r wildcards with r in Q with (say) the first two elements lying in A.
). If the monochromatic colour is such that all three pairs of a combinatorial line with r wildcards can occur in A, we are done, so suppose that there is no line with r wildcards with r in Q with (say) the first two elements lying in A.
Now consider a random copy of![{}[3]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) in
in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , using the m generators of Q to determine how many times each of the m wildcards that define this copy will get. The expected density of A in this cube is about
, using the m generators of Q to determine how many times each of the m wildcards that define this copy will get. The expected density of A in this cube is about  , so by DHJ(2.5) at least one of the copies is going to get a line whose first two elements lie in A, which gives the contradiction.
, so by DHJ(2.5) at least one of the copies is going to get a line whose first two elements lie in A, which gives the contradiction.
February 16, 2009 at 8:59 am |
p.s. I have placed the statement of relevant Ramsey theorems (Graham-Rothschild, Folkman, Carlson-Simpson, etc.) on the wiki for reference.
February 16, 2009 at 2:22 pm |
525. Strategy based on influence proofs
Let me say a little more (vague) things about possible strategy based on mimmicking influence proofs. We want to derive facts on the Fourier expansion of our set based on the fact that there are no lines and let me just consider k=2 (Sperner). Suppose that your set A has density c and you know that there is no lines with one wild cards. This gives that
 . (In a random set we would expect
. (In a random set we would expect  ; anyway this is of course possible.)
; anyway this is of course possible.)
Next you want to add the fact that there are no lines with 2 wild cars.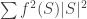 or some other indormations.
or some other indormations.
The formula (in fact there are few and we have to choose a simple one) for the number of lines with two wild cards i and j and the conclusion for the Fourier coefficients are less clear to me. Maybe we can derive conclusions on the higher moments
Here, we do not want to reach a subspace with higher density but rather a contradiction. In the ususal influence proofs the tool for that were certain inequalities asserting that for sets with small support the Fourier coefficients are high. This particular conclusion will not help us but the inequalities can help in some other way.
If indeed we are getting from the no line assumptions that the Fourier coefficients are high and concentrated this may be in conflict with facts about codes. Namely that our A will be a better than possible code in terms of its distance distribution. Anyway the first thing to calculate would be a good Fourier expression for the number of lines with 2 wildcards.
February 16, 2009 at 3:18 pm |
526. DHJ(2.6).
Thanks for the observation about using Folkman’s Theorem, Terry, it looks quite nice. I have some other ideas about trying to give a Ramsey-less proof based on Sperner’s Theorem; I’ll try to write them soon.
February 16, 2009 at 3:52 pm |
527. Fourier approach to Sperner.
Gil, here area few more details re #477. First, I see I dropped the Fourier coefficients at the beginning of the post, whoops! What I meant to say is that if you do the usual Fourier thing, you get the probability of is
is
The intuition here is that since is tiny, hopefully all the terms involving a positive power of
is tiny, hopefully all the terms involving a positive power of  are “negligible”. Obviously this is unlikely to precisely happen, but if it were true then we would get
are “negligible”. Obviously this is unlikely to precisely happen, but if it were true then we would get
a noise stability quantity. Now there are something like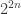 terms we want to drop, so it would be hard to do something simple like Cauchy-Schwarz. My idea is one from a recent paper with Wu. Think of
terms we want to drop, so it would be hard to do something simple like Cauchy-Schwarz. My idea is one from a recent paper with Wu. Think of  as a quadratic form over the Fourier coefficients of
as a quadratic form over the Fourier coefficients of  . I.e., think of
. I.e., think of 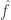 as a vector of length
as a vector of length 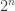 and think of
and think of
where is a matrix whose
is a matrix whose 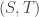 entry is the obvious expression from above with
entry is the obvious expression from above with  ‘s and
‘s and  ‘s and so on. Our goal is to find two similar-looking matrices
‘s and so on. Our goal is to find two similar-looking matrices 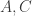 such that
such that 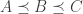 , meaning
, meaning 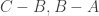 are psd. Then we get
are psd. Then we get 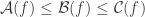 . (I see I’ve used
. (I see I’ve used  for two different things here; whoops.)
for two different things here; whoops.)
To be continued…
February 16, 2009 at 3:53 pm |
528. Fourier approach to Sperner.
Let me explain what I hope will be; the matrix
will be; the matrix  will be similar.
will be similar.
Let be the 2×2 matrix with entries
be the 2×2 matrix with entries 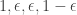 . This is like a little “
. This is like a little “ -biased
-biased  -noise stability” matrix. Let
-noise stability” matrix. Let 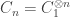 . Similarly, let
. Similarly, let 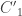 be the 2×2 matrix with entries
be the 2×2 matrix with entries 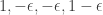 and define
and define 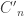 . Finally, let
. Finally, let 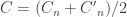 . The quadratic form associated to
. The quadratic form associated to  should be that average of two noise stabilities I wrote in post #477, except with noise rate
should be that average of two noise stabilities I wrote in post #477, except with noise rate  , not
, not 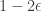 .
.
My unsubstantiated claim/hope is that indeed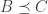 . Why do I believe this? Uh… believe it or not, because I checked empirically for
. Why do I believe this? Uh… believe it or not, because I checked empirically for  up to 5 with Maple. 😉 Sorry, I guess this isn’t how a real mathematician would do it. But I hope it can be proven.
up to 5 with Maple. 😉 Sorry, I guess this isn’t how a real mathematician would do it. But I hope it can be proven.
To define the matrix , do the same thing but set
, do the same thing but set 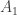 to be the 2×2 matrix with entries
to be the 2×2 matrix with entries  , etc. So eventually I hope to sandwich
, etc. So eventually I hope to sandwich 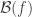 between the average of the
between the average of the  -biased
-biased  -noise stabilities of
-noise stabilities of  and the average of the
and the average of the  -biased
-biased 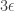 -noise stabilities of
-noise stabilities of  .
.
PS: Although it may work for Sperner, I’m less optimistic ideas like this will work for DHJ. The trouble is, in a distribution on comparable pairs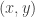 for Sperner, there is *imperfect* correlation between
for Sperner, there is *imperfect* correlation between  and
and  . Roughly, if you know
. Roughly, if you know  , you are still unsure what
, you are still unsure what  is. On the other hand, in any distribution on combinatorial lines
is. On the other hand, in any distribution on combinatorial lines 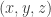 for DHJ, there is *perfect* correlation between
for DHJ, there is *perfect* correlation between 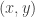 and
and  (and the other two pairs). If you know
(and the other two pairs). If you know  and
and  , then you know
, then you know  with certainty. This seems to break a lot of hopes to use “Invariance”-type methods like those in Elchanan’s follow-on to MOO. This is related to the fact that there is no hope to prove a generalization of DHJ of the form, “If
with certainty. This seems to break a lot of hopes to use “Invariance”-type methods like those in Elchanan’s follow-on to MOO. This is related to the fact that there is no hope to prove a generalization of DHJ of the form, “If  are two subsets of
are two subsets of ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  , then there is a combinatorial line
, then there is a combinatorial line 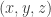 with
with  and
and 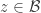 .”
.”
February 16, 2009 at 5:10 pm |
529. Ramsey-less DHJ(2.6) plan.
Here is a potential angle for a Ramsey-free proof of DHJ(2.6). The idea would be to soup up the Sperner-based proof of DHJ(2.5) and show that the set of (Hamming) distances where we can find a 01-half-line in
of (Hamming) distances where we can find a 01-half-line in  is “large” and “structured”.
is “large” and “structured”.
So again, let be a random string in
be a random string in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) and condition on the location of
and condition on the location of  ‘s 2’s. There must be some set of locations such that
‘s 2’s. There must be some set of locations such that  has density at least
has density at least  on the induced 01 hypercube (which will likely have dimension around
on the induced 01 hypercube (which will likely have dimension around  ). So fix 2’s into these locations and pass to the 01 hypercube. Our goal is now to show that if
). So fix 2’s into these locations and pass to the 01 hypercube. Our goal is now to show that if  is a subset of
is a subset of  of density
of density  then the set
then the set  of Hamming distances where
of Hamming distances where  has Sperner pairs is large/structured. (I’ve written
has Sperner pairs is large/structured. (I’ve written  here although it ought to be
here although it ought to be  .)
.)
Almost all the action in is around the
is around the  middle slices. Let’s simplify slightly (although this is not much of a cheat) by pretending that
middle slices. Let’s simplify slightly (although this is not much of a cheat) by pretending that  has density
has density  on the union of the
on the union of the 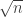 middle slices *and* that these slices have “equal weight”. Index the slices by
middle slices *and* that these slices have “equal weight”. Index the slices by ![i \in [\sqrt{n}]](https://s0.wp.com/latex.php?latex=i+%5Cin+%5B%5Csqrt%7Bn%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , with the
, with the  th slice actually being the
th slice actually being the  slice.
slice.
Let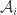 denote the intersection of
denote the intersection of  with the $i$th slice, and let
with the $i$th slice, and let 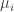 denote the relative density of
denote the relative density of 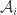 within its slice.
within its slice.
To be continued…
February 16, 2009 at 5:10 pm |
530. Ramsey-less DHJ(2.6) plan continued.
Here is a slightly wasteful but simplifying step: Since the average of the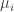 ‘s is
‘s is  , a simple Markov-type argument shows that
, a simple Markov-type argument shows that 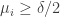 for at least a
for at least a 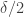 fraction of the
fraction of the  ‘s. Call such an
‘s. Call such an  “marked”.
“marked”.
Now whenever we have, say, marked
marked  ‘s, it means we have a portion of
‘s, it means we have a portion of  with a number of points at least
with a number of points at least  times the number of points in a single middle slice. Hence Sperner’s Theorem tells us we get two comparable points
times the number of points in a single middle slice. Hence Sperner’s Theorem tells us we get two comparable points 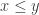 from among these slices.
from among these slices.
Thus we have reduced to the following setup:
There is a graph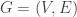 , where
, where ![V \subseteq [\sqrt{n}]](https://s0.wp.com/latex.php?latex=V+%5Csubseteq+%5B%5Csqrt%7Bn%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) (the “marked
(the “marked  ‘s”) has density at least
‘s”) has density at least 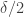 and the edge set
and the edge set  has the following density property: For every collection
has the following density property: For every collection 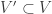 with
with  , there is at least one edge among the vertices in
, there is at least one edge among the vertices in 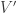 .
.
Let be the set of “distances” in this graph, where an edge
be the set of “distances” in this graph, where an edge 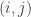 has “distance”
has “distance” 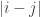 . Show that this set of distances must be large and/or have some useful arithmetic structure.
. Show that this set of distances must be large and/or have some useful arithmetic structure.
February 16, 2009 at 9:57 pm |
I wonder if the following “ideology” can be promoted or justified: A set without a line with at most r wildcards “behaves like” an error correcting code with minimal distance r’ where r’ grows to infinity (possibly very slowly) when r does. for k=2 of course we do not get en error correcting codes but when we have to split the set between many slices points from different slices are far apart so it is a little like a bahavior of a code. for k=3 this looks much more dubious but maybe has some truth in it.
February 16, 2009 at 10:40 pm |
532. Need for Carlson’s theorem?
Terry’s reduction to a use of Folkman instead of Graham-Rothschild, as well as his ideas for increasing the symmetry available, got me thinking there might be a way to reduce to a situation where you are using Hindman’s theorem instead of from Carlson’s theorem in the entire proof. Here is my first attempt…perhaps others can check if this makes sense. Fix a big $n$ and let $A$ be your subset of $[k]^n$ that you want to find a combinatorial line in. Let $Y$ be the space $2^{[k]^n}$, that is, all sets of words of length $n$. $U^i_j$ is the map on $Y$ that takes a set $E$ of words and interchanges 0s and js in the ith place to get a new set of words, namely the set $U^i_j E$. (Some of the words in $E$ may be unaffected; in particular, if no word in $E$ has a 0 or j in the ith place, $E$ is a fixed point.) Now let $X$ be the orbit of $A$ under $G$, the group gen. by these maps. It seems that to find a combinatorial line in any member of $X$ will give you a line in $A$. Let $B=\{ E:00…00\in E\}\subset X$. In general, for $U\subset X$, define the measure $\mu(U)$ to be the fraction of $g$ in $G$ such that $gA\in U$. This should give measure to $B$ equal to that of the relative density of $A$, and I am thinking the measure is preserved by the $U^i_j$ maps. If all of this is right, then things are simpler than FK imagined, because we have that $U^i_j$ commutes with $U^k_l$ for $i\neq k$, which should allow for the use of Hindman in all places were before Carlson was used. In particular, it allows for the use of Folkman in any finitary reduction (rather than Graham-Rothschild). And, in the case of Sperner’s Lemma, well, that becomes a simple consequence of the pigeonhole principle. (Because it’s just recurrence for a single IP system.) To be a bit more precise, in the $k=3$ case, I want to prove that there is some $\alpha\subset [n]$ such that $\mu(B\cap \prod_{i\in \alpha} U^i_1 B\cap \prod_{i\in \alpha} U^i_2 B)>0$ and conclude DHJ (3). The point is you get to IP systems much more easily with the extra commutativity assumption.
Sorry for the ergodic wording. Really at this state I am just hoping someone will check to see if everything I am saying is wrong for some simple reason I have overlooked. If not, we can write up a trivial proof of Sperner and a simplified version of $k=3$ and go from there.
February 16, 2009 at 11:10 pm |
533. Well it seems that was wrong…the maps don’t take lines to lines. Can anyone else think of a way to preserve some of the symmetry that Terry has gotten in the early stages?
February 17, 2009 at 12:08 am |
534. Folkman’s theorem
Back in 341 and in some following comments I tried to popularize Folkman’s theorem as a statement relevant to our project. I didn’t find a meaningful density version yet, however Tim pointed out that statements like Ben Green’s removal lemma for linear equations might work. It would be something like this; If the number of IP_d-sets is much less than what isexpected from the density, then removing a few elements one can destroy all IP_d sets. In the next post I will say a few more words about the set variant of Folkman’s theorem, however I’m not sure that this 500 blog series is the best forum for that.
February 17, 2009 at 12:41 am |
535. Folkman’s theorem
on second thought I decided not to talk about Folkman’s theorem here, since this blog is about possible proof strategies for DHJ. I will try to find another forum to discuss some questions on Folkman’s theorem.
February 17, 2009 at 6:27 pm |
536.
Jozsef: I guess this is the best forum we have right now (we tried splitting up into more threads earlier, but found that all but one of them would die out quickly). I can always archive the discussion at the wiki to be revived at some later point.
I wanted to point out two thoughts here. Firstly, I think I have a Fourier-analytic proof of DHJ(2.6) avoiding Ramsey theory. Firstly, observe that the usual proof of Sperner shows that the set of wildcard-lengths r of the combinatorial lines in a dense subset of![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) contains a difference set of the form A-A where A is a dense subset of
contains a difference set of the form A-A where A is a dense subset of ![{}[\sqrt{n}]](https://s0.wp.com/latex.php?latex=%7B%7D%5B%5Csqrt%7Bn%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Using the deduction of DHJ(2.5) from Sperner, we see that the set of wildcard lengths of combinatorial lines whose first two points lie in a dense subset of
. Using the deduction of DHJ(2.5) from Sperner, we see that the set of wildcard lengths of combinatorial lines whose first two points lie in a dense subset of ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) also contains a similar difference set. Similarly for permutations. So it comes down to the claim that for three dense sets A, B, C of
also contains a similar difference set. Similarly for permutations. So it comes down to the claim that for three dense sets A, B, C of ![{}[\sqrt{n}]](https://s0.wp.com/latex.php?latex=%7B%7D%5B%5Csqrt%7Bn%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) , that A-A, B-B, C-C have a non-trivial intersection outside of zero.
, that A-A, B-B, C-C have a non-trivial intersection outside of zero.
This can be proven either by the triangle removal lemma (try it!) or by the arithmetic regularity lemma of Green, finding a Bohr set on which A, B, C are dense and pseudorandom. There may also be a more direct proof of this.
Secondly, I think we may have a shot at a combinatorial proof of Moser(3) – that any dense subset A of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) contains a geometric line rather than a combinatorial line. This is intermediate between DHJ(3) and Roth, but currently has no combinatorial proof. Here is a sketch of an idea: we use extreme localisation and look at a random subcube
contains a geometric line rather than a combinatorial line. This is intermediate between DHJ(3) and Roth, but currently has no combinatorial proof. Here is a sketch of an idea: we use extreme localisation and look at a random subcube ![{}[3]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) . Let B be the portion of A on the corners
. Let B be the portion of A on the corners  of the subcube, and let C be the portion of A which is distance one away (in Hamming metric) from the centre
of the subcube, and let C be the portion of A which is distance one away (in Hamming metric) from the centre 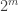 of this subcube. The point is that there are a lot of potential lines connecting one point of C with two nearly opposing points of B. I haven’t done it yet, but it looks like the number of such lines has a nice representation in terms of the low Fourier coefficients of A, and should therefore tell us that in order to be free of geometric lines, A has to have large influence. I am not sure where to take this next, but possibly by boosting this fact with the Ramsey theory tricks we can get some sort of contradiction.
of this subcube. The point is that there are a lot of potential lines connecting one point of C with two nearly opposing points of B. I haven’t done it yet, but it looks like the number of such lines has a nice representation in terms of the low Fourier coefficients of A, and should therefore tell us that in order to be free of geometric lines, A has to have large influence. I am not sure where to take this next, but possibly by boosting this fact with the Ramsey theory tricks we can get some sort of contradiction.
February 17, 2009 at 8:04 pm |
Here is a nice example I heard from Muli Safra. (It’s origin is in the problem of testing monotonicity of Boolean functions.) Consider a Boolean function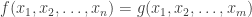 where
where 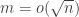 and
and  is a random Boolean function. When you consider strings x and y that correspond to two random sets S and T so that S is a subset of T with probability close to one f(x) = f(y) because almost surely the variables where S and T differs miss the first m variables. We can have a similar example for an alphabet of three letters.
is a random Boolean function. When you consider strings x and y that correspond to two random sets S and T so that S is a subset of T with probability close to one f(x) = f(y) because almost surely the variables where S and T differs miss the first m variables. We can have a similar example for an alphabet of three letters.
February 17, 2009 at 8:06 pm |
537. DHJ(2.6)
Hi Terry, re your #536: great! this is just what I was going for in #529 & #530… But one aspect of the deduction I didn’t quite get: in my #530, you don’t have the differences from all pairs in , just the ones where you have an “edge”. So do you produce your set
, just the ones where you have an “edge”. So do you produce your set  by filtering
by filtering  somehow? Or perhaps I’m missing some simple deduction from the proof of Sperner.
somehow? Or perhaps I’m missing some simple deduction from the proof of Sperner.
February 17, 2009 at 8:20 pm |
538. Fourier of line avoiding sets.
Thanks a lot for the details, Ryan, it is very interesting. I think that using Maple is the way a real mathematician will go about it!
As for my vague (related) suggestions: There is a nice Fourier expression of subsets of without a combinatorial line with one wild cards. But already when you assume there is no lines with one and two wildcadrs its get messy. (In particular these scare expressions
without a combinatorial line with one wild cards. But already when you assume there is no lines with one and two wildcadrs its get messy. (In particular these scare expressions 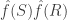 .)
.)
Maybe there would be a nice expression for sets in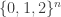 without a combinatorial line with one wildcard. This can be nice.
without a combinatorial line with one wildcard. This can be nice.
Another little (perhaps unwise) question regarding avoiding special configurations of “small distance” vectors. Suppose you look at subsets of without two distinct sets S and T so that S\T has precisely twice as many elements as T\S. Does this implies that the size of the family is
without two distinct sets S and T so that S\T has precisely twice as many elements as T\S. Does this implies that the size of the family is  ? (Again you can take a slice.)
? (Again you can take a slice.)
April 10, 2011 at 8:24 am
The problem about Sperner theorem which is mentioned in the the last paragraph was completely reolved by Imre Leader and Eoin Long, their paper Tilted Sperner families http://front.math.ucdavis.edu/1101.4151 contains also related results and conjectures.
February 17, 2009 at 8:24 pm |
538. Moser(3).
For this problem I think it might be helpful to go all the way back to Tim.#70 and think about “strong obstructions to uniformity” of the following form: dense sets for which
for which 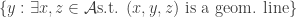 is not almost everything.
is not almost everything.
February 17, 2009 at 9:06 pm |
540.
Re: Sperner: if A is a dense subset of![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , then a random chain in this set is going to hit A in a dense subset of its equator (which is the middle
, then a random chain in this set is going to hit A in a dense subset of its equator (which is the middle  of the chain, which has length n). If A hits this chain in the
of the chain, which has length n). If A hits this chain in the 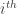 and
and 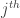 positions, then we get a combinatorial line with j-i wildcards. This is why the set of r arising from lines in A contain a difference set of a dense subset of
positions, then we get a combinatorial line with j-i wildcards. This is why the set of r arising from lines in A contain a difference set of a dense subset of ![[\sqrt{n}]](https://s0.wp.com/latex.php?latex=%5B%5Csqrt%7Bn%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Incidentally, I withdraw my claim that the joint intersection of A-A, B-B, C-C can be established from triangle removal – but the arithmetic regularity lemma argument should still work.
Finally, for Moser, I agree with Ryan’s 538 – except that I think one should restrict y to be very close to the centre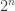 of the cube
of the cube 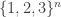 , otherwise y is only going to interact with a small fraction of the points of the cube and I don’t think this will be easily detectable by global obstructions. I still haven’t worked out what goes on when y is just a single digit away from
, otherwise y is only going to interact with a small fraction of the points of the cube and I don’t think this will be easily detectable by global obstructions. I still haven’t worked out what goes on when y is just a single digit away from 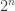 but I do believe it will have a nice Fourier-analytic interpretation.
but I do believe it will have a nice Fourier-analytic interpretation.
February 17, 2009 at 9:07 pm |
Metacomment.
I’d just like to chip in here and say that I’ve been devoting most of my polymath1 energies to developing the associated wiki. If anyone else has any thoughts that are in a sufficiently organized state to make wiki articles (they don’t have to be perfect of course) then it would be great. It will make it much easier to keep track of what we know, what we’ve asked, what we think we might be able to prove and roughly how, etc. So far, I think Terry and I are the only two contributors. The other thing I wanted to say is that I get the sense that other people are doing a certain amount of thinking away from the blog. I’ve got to the point where I want to do this too (and report back regularly if I come up with anything) but I don’t want to do it if others are in fact not doing so. Anybody care to tell me? It somehow feels as though we’ve got to the stage where a certain amount of private thought is needed to push things further, but because I formulated rule 6 I have felt obliged to stick to it. (Gil, I know you are relaxed about all this.)
February 17, 2009 at 9:20 pm |
541. Cave man methods:
Here’s a curious low-tech trick to get difference sets to intersect: suppose you have sets A, B, C of density d. Let m>1/d and use ramsey’s theorem to choose n so that for any 8-coloring of the 2-member sets of an n element set, you get an m element set whose 2-member sets are of one color. Now color {x,y}, x1/d, the x_i+A cannot all be disjoint, hence x_j-x_i is in A-A for some, hence all, i,j and similarly for B-B, C-C.
February 17, 2009 at 9:24 pm |
541. Cave man again:
I see stuff in what are interpretted as comment brackets gets left out! Let’s try this again.
Here’s a curious low-tech trick to get difference sets to intersect: suppose you have sets A, B, C of density d. Let m>1/d and use ramsey’s theorem to choose n so that for any 8-coloring of the 2-member sets of an n element set, you get an m element set whose 2-member sets are of one color. Now color {x,y}, x less than y, according to which of A-A, B-B, C-C y-x is in. Pass to an m member set {x_1,…,x_m} whose 2-member subsets are of one color for this coloring. Since m is greater than 1/d, the x_i+A cannot all be disjoint, hence x_j-x_i is in A-A for some, hence all, i,j and similarly for B-B, C-C.
February 17, 2009 at 9:28 pm |
542. Metacomment.
I too feel like trying out longer calculations off the blog from time to time. Tim, why don’t you go ahead and try the ones you’re thinking of? Perhaps we can just report here how the calculations go…
February 18, 2009 at 6:11 am |
Metacomment.
I think there may be some tension here between the objective of solving the problem by any means necessary, and the objective of trying to see whether a maximally collaborative approach to problem-solving can work. I would favour a relaxed approach at this point; it seems that we are already getting enough benefit from the collaborative forum here that we don’t need to be utterly purist about keeping it that way. And I think things are moving to the point where, traditionally, one of us would simply sit down for an hour or two and work out a lot of details at once.
February 18, 2009 at 6:19 am |
543. Moser(3)
Hmm, there do seem to be some obstructions to uniformity here that are annoying. For instance, if m is an odd number comparable to 0.1 n, and A is the set of points in {1,3}^n which have an even number of 3’s in the first m positions, and B is the set of points formed by taking 2^n and changing one of the last n-m positions to a 1 or a 3, then there are no geometric lines connecting A, B, and A despite A having density 0.5 and B having density 0.9 in {1,3}^n and the radius 1 Hamming ball with centre 2^n respectively. On the other hand, A has a lot of coordinates with low influence wrt swapping 1 and 3; if 1 and 3 were completely interchangeable then Moser(3) would collapse to DHJ(2), so perhaps there is something to exploit here.
Randall: I’m beginning to realise that if one wants to hold on to permutation symmetry on the cube, then one can’t use Ramsey theorems such as Graham-Rothschild or Carlson, as the symmetry is broken when one passes to a combinatorial subspace (the wildcard lengths are unequal). So it may actually not be a good tradeoff.
February 18, 2009 at 8:15 am |
Metacomment. I also agree that we need some off-line calculations, and we can keep the spirit of point 6 (asking not to go away for weeks to study some avenue) by participants trying to document and describe what they try to do and what they do (even if unsuccessful) in short time intervals.
February 18, 2009 at 10:00 am |
Metacomment. I think we all basically agree about off-line calculations. At some point fairly soon I will try to do some, but I will be careful to follow Gil’s suggestion. I will write a comment in advance to say what I am going to do, and I will report back frequently and in detail on what results from the calculations. (I may give less detail about the things that don’t work, but even there I will try to give enough detail to save anyone else from needing to go off and repeat my failures.)
Briefly, the kinds of things I’d like to do are to write out a rigorous proof that a quasirandom set (in a sense that I have defined on the wiki) must contain many combinatorial lines, and to try to deduce something from a set’s not being quasirandom. I’d also like to play around with Fourier coefficients on![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with equal-slices measure and try to prove that the only obstruction to Sperner in that measure is lots of low-influence variables. I won’t get down to either of these today, if anyone has any remarks that will potentially stop me or change how I go about it.
with equal-slices measure and try to prove that the only obstruction to Sperner in that measure is lots of low-influence variables. I won’t get down to either of these today, if anyone has any remarks that will potentially stop me or change how I go about it.
February 18, 2009 at 1:47 pm |
544. Corners(1,3)
Over at the wiki I have written about a special case of the corners problem that is like DHJ(1,3). It’s corners when your set A is of the form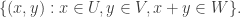 Can anyone see an elementary proof that a dense set of this kind contains a corner? I can prove it fairly easily if I’m allowed to use Szemerédi’s theorem, so at least the transition from one to two dimensions is elementary, but I’d rather a fully elementary proof. My account of the problem (and of DHJ(1,3)) can be found here.
Can anyone see an elementary proof that a dense set of this kind contains a corner? I can prove it fairly easily if I’m allowed to use Szemerédi’s theorem, so at least the transition from one to two dimensions is elementary, but I’d rather a fully elementary proof. My account of the problem (and of DHJ(1,3)) can be found here.
February 18, 2009 at 4:49 pm |
Metacomment.
I should point out that over at the 700 thread, things have already advanced to the point where we have already had several people run programs to get the latest upper and lower bounds (and writing programs is not something that one can really do collaboratively, at least not with the structures in place right now).
February 18, 2009 at 11:12 pm |
545. Fourier analysis on equal-slices![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002)
This isn’t the calculation I was talking about, as this one was possible to do in my head. I don’t yet know where we could go with this, but it felt like a good idea to think about how Walsh functions behave with respect to equal-slices measure. (I used to call this slices-equal measure, which I feel is slightly more correct, but in the end I have had to concede that “equal-slices” trips off the tongue much better.) In particular, I wondered about orthogonality.
The calculation turns out to be rather pretty. Let’s write for the Walsh function associated with the set
for the Walsh function associated with the set  . That is,
. That is,  is 1 if x has an even number of 1s in A, and -1 if it has an odd number of 1s in A. Then
is 1 if x has an even number of 1s in A, and -1 if it has an odd number of 1s in A. Then  .
.
Therefore, the inner product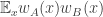 is equal to
is equal to 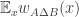 , so what we really care about is the expectation of individual Walsh functions. In the case of uniform measure, these expectations are all zero except when A is the empty set, and this implies the orthogonality of the Walsh functions.
, so what we really care about is the expectation of individual Walsh functions. In the case of uniform measure, these expectations are all zero except when A is the empty set, and this implies the orthogonality of the Walsh functions.
It turns out to be quite easy to think about the value of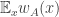 when expectations are with respect to equal-slices measure. This is because we can rewrite the expectation over
when expectations are with respect to equal-slices measure. This is because we can rewrite the expectation over ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as the expectation over all permutations
as the expectation over all permutations  of
of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and all integers
and all integers  between
between  and
and  (in both cases chosen uniformly) of the sequence
(in both cases chosen uniformly) of the sequence  such that
such that  is 1 if and only if
is 1 if and only if 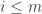 . (In set terms, we randomly permute
. (In set terms, we randomly permute ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and then pick a random initial segment.)
and then pick a random initial segment.)
Suppose that has cardinality
has cardinality  . Then the calculation we need to do is this: what is the probability that if you choose a random subset
. Then the calculation we need to do is this: what is the probability that if you choose a random subset ![B\subset[n]](https://s0.wp.com/latex.php?latex=B%5Csubset%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) of size
of size  and take a random
and take a random 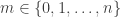 , then
, then  will have an even number of elements less than or equal to
will have an even number of elements less than or equal to  ? (If the probability is
? (If the probability is  , then
, then 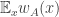 will be
will be  for every set
for every set  of size
of size  .)
.)
Now if is odd and
is odd and  is even, then we can replace
is even, then we can replace  by
by 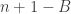 and we can replace
and we can replace  by
by 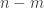 and the number of elements of
and the number of elements of 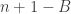 that are at most
that are at most 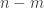 is the number of elements of
is the number of elements of  that are greater than
that are greater than  . Also,
. Also,  cannot equal
cannot equal 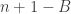 . Therefore, there is a bijection between pairs
. Therefore, there is a bijection between pairs 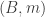 that give an odd intersection and pairs
that give an odd intersection and pairs  that give an even intersection. So the probability is
that give an even intersection. So the probability is 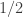 in this case, and we find, as we want, that
in this case, and we find, as we want, that 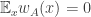 .
.
From this we find that is orthogonal to
is orthogonal to 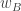 whenever
whenever  and
and  have different parities (assuming that
have different parities (assuming that  is even, which we may as well).
is even, which we may as well).
If has even cardinality, things do not work so well. Consider, for example, the case where
has even cardinality, things do not work so well. Consider, for example, the case where  consists of two elements. Here we choose a random
consists of two elements. Here we choose a random  and a random set
and a random set 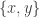 and ask for the probability that an even number of x and y are at most
and ask for the probability that an even number of x and y are at most  . For fixed
. For fixed 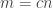 the probability is approximately
the probability is approximately  , which integrates to
, which integrates to 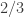 . So we get
. So we get 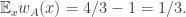
Another way to think of this is that x and y divide up![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) into three subintervals, each of expected size
into three subintervals, each of expected size  , so the probability that
, so the probability that  lands in the middle subinterval is on average
lands in the middle subinterval is on average 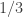 . This second way is quite useful, as it shows that for general even
. This second way is quite useful, as it shows that for general even 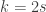 we will get approximately
we will get approximately  for the probability of an even intersection and therefore
for the probability of an even intersection and therefore 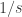 for
for 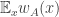 .
.
So we end up not with an orthonormal basis but with something fairly nice: a basis that splits into two sets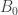 and
and 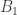 of vectors, one for even parity sets and one for odd parity sets, such that every vector in
of vectors, one for even parity sets and one for odd parity sets, such that every vector in 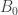 is orthogonal to every vector in
is orthogonal to every vector in 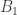 , and vectors
, and vectors  and
and 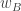 in the same set are nearly orthogonal except if the symmetric difference of
in the same set are nearly orthogonal except if the symmetric difference of  and
and  is small.
is small.
February 18, 2009 at 11:59 pm |
546. Fourier analysis and Sperner obstructions.
Now I want to try to do a similar calculation to see if we can say anything about obstructions to Sperner in the equal-slices measure. The model will be this. Let be a bounded function defined on
be a bounded function defined on ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . Now we pick a random pair of sets
. Now we pick a random pair of sets  by first picking a random permutation
by first picking a random permutation  of
of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and then picking two random initial segments of the permuted set. Then we take the expectation of
and then picking two random initial segments of the permuted set. Then we take the expectation of  . I am interested in what we can say if this expectation is not small. The dream would be to show that almost all the influence on
. I am interested in what we can say if this expectation is not small. The dream would be to show that almost all the influence on  comes from just a small set.
comes from just a small set.
Clearly the calculation we want to do is this: we pick two sets and
and  and work out the expectation of
and work out the expectation of 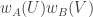 over all pairs
over all pairs  chosen according to the distribution above.
chosen according to the distribution above.
I think it is fairly clear that this expectation will be small if either of or
or  is large, by the arguments of the previous post. This is promising, but I don’t know that I can see, without going off and calculating, whether it will be small enough to give us something useful (particularly as I’m not quite sure what substitute we will have, if any, for Parseval’s identity). If
is large, by the arguments of the previous post. This is promising, but I don’t know that I can see, without going off and calculating, whether it will be small enough to give us something useful (particularly as I’m not quite sure what substitute we will have, if any, for Parseval’s identity). If  and
and  are both small, then there is quite a bit of dependence between
are both small, then there is quite a bit of dependence between 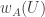 and
and 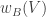 , or so it seems. For example, if
, or so it seems. For example, if  has size 2,
has size 2,  has size
has size 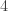 ,
,  , and for a particular permutation the probability that an initial segment contains an even number of elements of
, and for a particular permutation the probability that an initial segment contains an even number of elements of  is close to 1, then that permutation bunches
is close to 1, then that permutation bunches  up to one of the two ends of the interval, so
up to one of the two ends of the interval, so  behaves like a set of size 2 and the probability of getting an even intersection with
behaves like a set of size 2 and the probability of getting an even intersection with  is roughly 2/3.
is roughly 2/3.
This is all suggesting to me that lack of uniformity in Sperner implies that a few variables have almost all the influence. If any influence experts think they can see where these thoughts would be likely to lead, then I’d be interested to hear about it. Otherwise, this is one of the private calculations I’d like to do. If it worked, then we would have some modest evidence for what I very much hope will turn out to be the case: that with equal-slices measure the only obstructions to uniformity for DHJ(3) come from sets of complexity 1 (which are defined in the discussion of DHJ(1,3) on this wiki page. This would be because of the fluke that Sperner-type obstructions happened to correlate with sets of complexity 1.
February 19, 2009 at 6:25 am |
547. Equal slices measure / Sperner.
Hi Tim. I’m still not 100% on board for equal-slices measure 🙂 but…
1. If I’m not mistaken, it’s the same as first choosing![p \in [0,1]](https://s0.wp.com/latex.php?latex=p+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) uniformly, and then choosing from the
uniformly, and then choosing from the  -biased product distribution on
-biased product distribution on  . Thinking of it this way might help with Fourier methods, since they tend to mate nicely with product distributions.
. Thinking of it this way might help with Fourier methods, since they tend to mate nicely with product distributions.
2. When you say “obstructions to …”, do you mean obstructions to having probability close to for the event
for the event 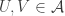 or for probability close to
or for probability close to 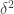 ? The former may be difficult, since any monotone
? The former may be difficult, since any monotone  will lead to probability close to
will lead to probability close to  , and there are an awful lot of monotone functions.
, and there are an awful lot of monotone functions.
If you are interested in the standard product measure (as opposed to equal-slices) then the Fourier calculations from #477 and company seem like they could lead to a pretty good understanding of density-Sperner for a small Poisson number of wildcards. But I’m not currently sure if understanding density-Sperner really helps at all for understanding HJ or even Moser. (I may say more on why I feel this way later; I’m feeling a bit gloomy about Fourier approaches right now…)
February 19, 2009 at 8:12 am |
[…] between the uniform distribution and the equal-slice distribution plays a role in a recent project discusses on Gowers’s […]
February 19, 2009 at 8:36 am |
Yes, integrating over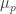 is a nice way to think about equal-slices probability. It would be interesting to come up with a good orthonormal basis of functions w.r.t. the equal slices probability. (Indeed, we have such functions for every
is a nice way to think about equal-slices probability. It would be interesting to come up with a good orthonormal basis of functions w.r.t. the equal slices probability. (Indeed, we have such functions for every 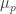 .)
.)
I would be very interested to see a good understanding of density Sperner with small number of Poisson number of wild-cards. (I tried to do some computation and I do not see how to proceed right now even with Sperner.)
February 19, 2009 at 11:35 am |
549. Sperner obstructions
Ryan, that is indeed a nice way of thinking about equal-slices measure, and thanks for reminding me about monotone functions, which, despite a number of your previous comments, had slipped out of my mind. I must try to think what the most general phenomenon is, of which monotone functions are a particularly nice manifestation. (For example, the intersection of an up-set and a down-set is likely to be highly non-quasirandom for Sperner.) Better still, it would be good to generalize that to subsets of![{}[3]^n,](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En%2C&bg=ffffff&fg=333333&s=0&c=20201002) where I don’t find it completely obvious what one should mean by a “monotone” set. (Of course, one can come up with definitions, but I’d like a definition with a proper justification.) In general, however, it seems to me that anything even remotely monotone-like in
where I don’t find it completely obvious what one should mean by a “monotone” set. (Of course, one can come up with definitions, but I’d like a definition with a proper justification.) In general, however, it seems to me that anything even remotely monotone-like in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) ought to correlate with a set of complexity 1.
ought to correlate with a set of complexity 1.
February 19, 2009 at 1:38 pm |
550. Equal-slices orthonormal basis
Ryan, I completely understand your not being 100% convinced by equal slices probability. I myself am in the position of (i) very much wanting it to do something good and (ii) feeling that it would be a bit of a miracle if it did.
I’ve been thinking about Gil’s question of finding a nice orthonormal basis of functions with respect to equal-slices density, and have just come up with a guess. In the true polymath spirit I will present the guess and only after that see whether it actually works. I’ve got a good feeling about it though (because I scientifically inducted from 2 to the general case).
Here are my initial desiderata. I would like a set of functions (sort of pseudo-Walsh functions), one for each subset
(sort of pseudo-Walsh functions), one for each subset ![A\subset[n]](https://s0.wp.com/latex.php?latex=A%5Csubset%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , such that, regarding the elements of
, such that, regarding the elements of ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as subsets of
as subsets of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , the value of
, the value of  depends only on the cardinality of
depends only on the cardinality of  . I would also like them to be orthogonal in the equal-slices measure. (I think this could be enough to nail the functions completely, but I’m just going to guess a solution. If it turns out to be rubbish then I’ll go away and try to solve some simultaneous equations.)
. I would also like them to be orthogonal in the equal-slices measure. (I think this could be enough to nail the functions completely, but I’m just going to guess a solution. If it turns out to be rubbish then I’ll go away and try to solve some simultaneous equations.)
There is more or less no choice about what to do with singletons: up to a constant multiple, I’ve basically got to define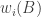 to be
to be  if
if 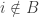 and
and  otherwise. Since the equal-slices weight of
otherwise. Since the equal-slices weight of  is equal to that of its complement, this function averages zero in the equal-slices measure, and is therefore orthogonal to the constant function 1 (which is what we have to choose for
is equal to that of its complement, this function averages zero in the equal-slices measure, and is therefore orthogonal to the constant function 1 (which is what we have to choose for  when
when  is empty).
is empty).
Things get more complicated with pairs. As I argued in an earlier comment, if you just choose the usual Walsh function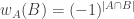 then with equal-slices measure you get that the average of the function is
then with equal-slices measure you get that the average of the function is 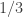 (when
(when  ). And that was basically because if you randomly choose two points in
). And that was basically because if you randomly choose two points in ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and then choose a random
and then choose a random  between
between  and
and  , then the probability that exactly one of your two random points is less than
, then the probability that exactly one of your two random points is less than  is approximately
is approximately 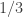 instead of
instead of 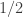 . So the nicest thing to do seems to be this (always assuming that
. So the nicest thing to do seems to be this (always assuming that  for this discussion): we define
for this discussion): we define  to be 1 if
to be 1 if 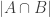 is 0 or 2 and
is 0 or 2 and 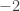 if
if 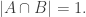
Now let’s jump straight to the guess. I won’t bother normalizing anything so I’m aiming for orthogonality rather than orthonormality. If then I’d like
then I’d like  to be
to be 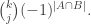
OK, now let me begin the probably painful process of checking this guess. FIrst of all, this set of functions is no longer closed under pointwise multiplication, but that was always going to be too much to ask, since otherwise the functions would have determined everything and we’d have ended up with the usual Walsh functions. This has the annoying consequence that it’s not enough just to check that
would have determined everything and we’d have ended up with the usual Walsh functions. This has the annoying consequence that it’s not enough just to check that  has average zero when
has average zero when  is non-empty. And I have to admit that at this stage I’m just hoping for a big slice of luck (no cheesy pun intended).
is non-empty. And I have to admit that at this stage I’m just hoping for a big slice of luck (no cheesy pun intended).
What, then, is the product ? Hmm, I think it’s going to be beyond me to do this straight up on to the computer, so now I really am going to do an offline computation. I’ve got various things coming up so it may be an hour or two before I can report back. (Also, I want to check that the expectation of
? Hmm, I think it’s going to be beyond me to do this straight up on to the computer, so now I really am going to do an offline computation. I’ve got various things coming up so it may be an hour or two before I can report back. (Also, I want to check that the expectation of  really is zero. I’m satisfied that it is approximately zero, but it would be much nicer to have exact orthogonality.)
really is zero. I’m satisfied that it is approximately zero, but it would be much nicer to have exact orthogonality.)
February 19, 2009 at 3:52 pm |
551. Equal slices and orthonormality
Oh dear, just noticed, before getting round to any calculation, that this idea is dead before it’s even got going. If for each we want
we want  to depend on
to depend on 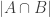 only, then as I pointed out above we need
only, then as I pointed out above we need  to be the usual Walsh function when
to be the usual Walsh function when  is a singleton. But for two such functions to be orthogonal we then need their pointwise product to average zero as well. But their pointwise product is the usual Walsh function associated with a set of size 2, and the whole motivation for this line of enquiry was that those Walsh functions did not average zero in the equal-slices measure.
is a singleton. But for two such functions to be orthogonal we then need their pointwise product to average zero as well. But their pointwise product is the usual Walsh function associated with a set of size 2, and the whole motivation for this line of enquiry was that those Walsh functions did not average zero in the equal-slices measure.
This shows that my two desiderata above are inconsistent. In my next comment I’ll give a suggestion for what to do.
February 19, 2009 at 5:00 pm |
552. Equal slices and orthonormality
It seems to me that Ryan’s way of looking at equal-slices density is too good to ignore, so instead of asking what the most natural orthonormal basis is with respect to equal-slices density, let us ask instead what the most natural thing to do is if (i) we want orthonormality and (ii) we want to think of equal-slices density as the average of the weighted densitites on the cube.
As Gil points out, for each fixed![p\in[0,1]](https://s0.wp.com/latex.php?latex=p%5Cin%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) you have a natural orthonormal basis. Indeed, if we choose a random point of
you have a natural orthonormal basis. Indeed, if we choose a random point of  by letting the coordinates be independent Bernoulli random variables with probability
by letting the coordinates be independent Bernoulli random variables with probability  of being 1 and
of being 1 and 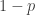 of being 0, then the function that is
of being 0, then the function that is 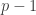 when
when  and
and  when
when  has mean 0. The expectation of the square of this function is
has mean 0. The expectation of the square of this function is 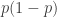 , so if we divide by
, so if we divide by 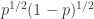 then we get a function
then we get a function  of mean 0 and variance 1. We can define
of mean 0 and variance 1. We can define 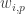 similarly for each
similarly for each  .
.
Now for a general set define
define 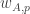 to be
to be 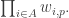 Then the independence of the random variables
Then the independence of the random variables 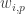 implies that
implies that  if
if  is non-empty (always assuming that the elements of
is non-empty (always assuming that the elements of  are chosen randomly and independently with probability
are chosen randomly and independently with probability  ). Therefore, the
). Therefore, the 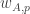 are orthogonal. If
are orthogonal. If 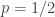 then we get the usual Walsh functions.
then we get the usual Walsh functions.
I think that there is just one natural thing to do at this point. For each![p\in[0,1]](https://s0.wp.com/latex.php?latex=p%5Cin%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) let us write
let us write 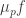 for the expectation of
for the expectation of 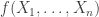 , where each
, where each 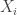 is Bernoulli with probability
is Bernoulli with probability  . Then the equal-slices measure of
. Then the equal-slices measure of  is
is 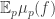 .
.
How about inner products? Well, . If we want to understand this in a Fourier way, it seems crazy (with the benefit of hindsight) to try to find a single orthonormal basis that will do the job. Instead, for each
. If we want to understand this in a Fourier way, it seems crazy (with the benefit of hindsight) to try to find a single orthonormal basis that will do the job. Instead, for each  one should expand
one should expand  and
and  in terms of the weighted Walsh basis
in terms of the weighted Walsh basis 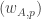 and then take the average. For each individual
and then take the average. For each individual  there is a nice Parseval identity, since the
there is a nice Parseval identity, since the 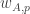 are orthonormal. To spell it out, if we write
are orthonormal. To spell it out, if we write 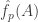 for
for 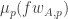 , then
, then 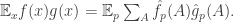
This looks to me like a nice usable Parseval identity, even if it doesn’t have the form I was orginally looking for. So we’re taking our Fourier coefficients to belong to![C[0,1]](https://s0.wp.com/latex.php?latex=C%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) rather than to
rather than to 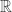 .
.
February 19, 2009 at 5:48 pm |
553. Sperner obstructions.
The next thing I’d like is a good measure on pairs . With the old way of thinking about equal-slices density this was easy: we took two initial segments of a randomly permuted
. With the old way of thinking about equal-slices density this was easy: we took two initial segments of a randomly permuted ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . But can we think of it in a Ryan-like way?
. But can we think of it in a Ryan-like way?
Here’s a natural suggestion. First we randomly pick a pair of real numbers with
of real numbers with 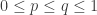 . Next, we choose the set
. Next, we choose the set  by picking each element independently and randomly with probability
by picking each element independently and randomly with probability  . And then we pick the set
. And then we pick the set  by picking each element of
by picking each element of  independently and randomly with probability
independently and randomly with probability 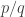 . Note that the elements of
. Note that the elements of  end up being chosen independently with probability
end up being chosen independently with probability  , so the marginal distributions of
, so the marginal distributions of  and
and  are sensible.
are sensible.
The next task is to try to sort out what we mean by . (We want to say that
. (We want to say that  is non-uniform if this expectation is not small.) Wait, that’s not quite what I meant to say. It’s clear what it means, since I’ve just specified the distribution on pairs
is non-uniform if this expectation is not small.) Wait, that’s not quite what I meant to say. It’s clear what it means, since I’ve just specified the distribution on pairs  . What is not quite so clear is how to express it in terms of the vector-valued Fourier coefficients. I think I need a new comment for that.
. What is not quite so clear is how to express it in terms of the vector-valued Fourier coefficients. I think I need a new comment for that.
February 19, 2009 at 7:55 pm |
554. Sperner-related calculations.
Finally I’ve found something that I definitely couldn’t do straight up. But with a bit of paper and a couple of false starts I think I’ve got it down, or at least have made some calculational progress in that direction. The aim is to express the quantity (defined in the previous comment—it is of course essential that we are talking about an equal-slices-related joint distribution here) in terms of the vector-valued Fourier coefficients of
(defined in the previous comment—it is of course essential that we are talking about an equal-slices-related joint distribution here) in terms of the vector-valued Fourier coefficients of  . Also, I’ve changed A and B to U and V because I want to use A and B to label some Walsh functions.
. Also, I’ve changed A and B to U and V because I want to use A and B to label some Walsh functions.
For this calculation it will be more convenient to think in terms of Bernoulli random variables. Let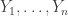 be Bernoulli with mean
be Bernoulli with mean  , let
, let 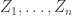 be Bernoulli with mean
be Bernoulli with mean 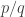 , and let
, and let 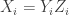 . All the
. All the 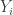 and
and 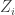 are of course independent, so the
are of course independent, so the 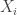 are independent Bernoulli random variables with mean
are independent Bernoulli random variables with mean  . Later on we will average over
. Later on we will average over 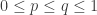 but for now let us regard them as fixed and see what happens. Later we will take
but for now let us regard them as fixed and see what happens. Later we will take  to be the set of
to be the set of  such that
such that 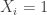 and
and  to be the set of
to be the set of  such that
such that 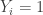 . (What this will ultimately be doing is investigating the number of pairs
. (What this will ultimately be doing is investigating the number of pairs  in
in  with
with  of size roughly
of size roughly 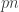 and
and  of size roughly
of size roughly  .)
.)
Now we can expand in terms of the functions
in terms of the functions 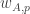 and also in terms of the functions
and also in terms of the functions 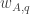 . If we do so, then our main task is to try to understand the quantity
. If we do so, then our main task is to try to understand the quantity 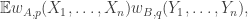 which we are rewriting as
which we are rewriting as 
Here we find that independence helps us a lot. Let us begin by conditioning on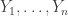 . Since this fixes
. Since this fixes 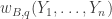 we are now interested in
we are now interested in 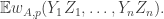 For every
For every  let us write
let us write  for the function that takes
for the function that takes  to
to  and
and  to
to  . Then
. Then 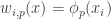 and
and 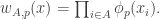 Therefore,
Therefore, 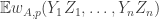 is equal to
is equal to  which by independence is equal to
which by independence is equal to 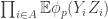 . I have to feed my son now so will continue with this calculation later.
. I have to feed my son now so will continue with this calculation later.
February 19, 2009 at 8:30 pm |
555. Sperner-related calculations continued.
While walking to a local grocer’s I realized that conditioning on the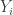 was not such a good idea. Instead, we should note that
was not such a good idea. Instead, we should note that  splits up as a product of three products, which I will write separately. They are
splits up as a product of three products, which I will write separately. They are 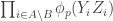 ,
, 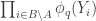 and
and 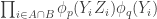 . Therefore, because of independence, the expectation that we’re interested in (or at least I am) also splits up as a product of three products, namely
. Therefore, because of independence, the expectation that we’re interested in (or at least I am) also splits up as a product of three products, namely  ,
, 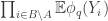 and
and 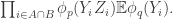 Thus our calculation becomes very simple, since each of these expectations in the products is a number that does not depend on
Thus our calculation becomes very simple, since each of these expectations in the products is a number that does not depend on  . Must go again.
. Must go again.
February 19, 2009 at 9:59 pm |
556. Sperner-related calculations continued.
There are three very finite calculations to do next.
1. Since is Bernoulli with mean
is Bernoulli with mean  ,
, 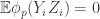 , by the way we defined
, by the way we defined 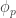 . Wow, I wasn’t expecting that.
. Wow, I wasn’t expecting that.
2. Similarly,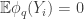 .
.
3. As for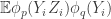 , it works out to be some number
, it works out to be some number  . I’ll calculate it later as I have to go.
. I’ll calculate it later as I have to go.
So the whole thing collapses to 0 unless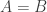 and then we get
and then we get  . That looks pretty nice to me.
. That looks pretty nice to me.
February 20, 2009 at 1:08 am |
557. Sperner-related calculations continued.
Right, is
is  with probability
with probability 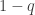 ,
, 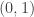 with probability
with probability 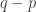 and
and  with probability
with probability  . Recall that
. Recall that 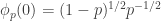 and
and 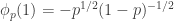 , and similarly for
, and similarly for 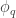 . (I’ve changed these to minus what they were before, but this isn’t important.) To tidy things up a bit I’m going to make the substitution
. (I’ve changed these to minus what they were before, but this isn’t important.) To tidy things up a bit I’m going to make the substitution  and
and  . So
. So  ,
,  , and similarly for
, and similarly for  and
and  .
.
Therefore, is
is  with probability
with probability 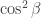 ,
, 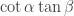 with probability
with probability 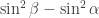 and
and 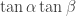 with probability
with probability  . Therefore, the expectation is
. Therefore, the expectation is 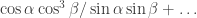 hmm, I’ve just tried it on a piece of paper and it doesn’t seem to simplify. That’s annoying, as I would very much like to get some idea of the average size of
hmm, I’ve just tried it on a piece of paper and it doesn’t seem to simplify. That’s annoying, as I would very much like to get some idea of the average size of  as
as  and
and  vary.
vary.
February 20, 2009 at 1:16 am |
[…] few days later, Gowers announced at the end of this post that there was a wiki on the enterprise of solving the density Hales-Jewett theorem. In the same […]
February 20, 2009 at 1:43 am |
558. Sperner-related calculations continued.
Actually, I forgot the minus signs: should have been
should have been 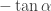 . So we get
. So we get 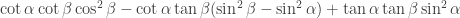 .
.
I’m going to have to do this a few times until I’m confident it’s right. But at the moment it looks as though is sometimes bigger than 1, which I don’t like, but also as though there is a range where it is less than 1, which might mean that we were OK after some very modest localization. The reason I’d like
is sometimes bigger than 1, which I don’t like, but also as though there is a range where it is less than 1, which might mean that we were OK after some very modest localization. The reason I’d like  is that it would then mean that the contribution to the sum from large
is that it would then mean that the contribution to the sum from large  was fairly negligible, and I think we’d have a proof of at least some statement along the lines of incorrect number of
was fairly negligible, and I think we’d have a proof of at least some statement along the lines of incorrect number of  implying large Fourier coefficient at some small
implying large Fourier coefficient at some small  . And if that worked, it would be hard to resist the temptation to try something similar for DHJ(3), though the thought of it is rather daunting.
. And if that worked, it would be hard to resist the temptation to try something similar for DHJ(3), though the thought of it is rather daunting.
February 20, 2009 at 3:28 am |
559. Removal lemma for DHJ
The main difficulty – at least for me – in applying a removal lemma to the set model (DHJ Version 4. in the Wiki) is the disjointness of sets as it makes the corresponding graph very sparse. Here I’ll try to relax the disjointness condition in a slightly different model. Instead of working inside of one dense cube showing that it contains a line, here we will consider now several cubes; The “original” cube![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , n copies of
, n copies of ![[3]^{n-1}](https://s0.wp.com/latex.php?latex=%5B3%5D%5E%7Bn-1%7D&bg=ffffff&fg=333333&s=0&c=20201002) …
…  copies of
copies of ![[3]^{n-k}](https://s0.wp.com/latex.php?latex=%5B3%5D%5E%7Bn-k%7D&bg=ffffff&fg=333333&s=0&c=20201002) , and so on. For any subset of [n] we have one cube. We can suppose that each cube is at least c-dense and line-free. For any pair of subsets of [n], say A and B there is a unique point assigned; it is in the cube over
, and so on. For any subset of [n] we have one cube. We can suppose that each cube is at least c-dense and line-free. For any pair of subsets of [n], say A and B there is a unique point assigned; it is in the cube over ![[n]\-(A\cap B)](https://s0.wp.com/latex.php?latex=%5Bn%5D%5C-%28A%5Ccap+B%29&bg=ffffff&fg=333333&s=0&c=20201002) with 1-s in the
with 1-s in the  positions, 2-s in the
positions, 2-s in the 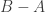 positions, and 0-s elsewhere. Every point represents a pair of subsets in [n]. This model allows us to state the following “corner-like” form of DHJ:
positions, and 0-s elsewhere. Every point represents a pair of subsets in [n]. This model allows us to state the following “corner-like” form of DHJ: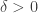 there exists n such that every collection of pairs (A,B) of subsets of [n] of cardinality at least
there exists n such that every collection of pairs (A,B) of subsets of [n] of cardinality at least 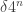 contains a “corner”
contains a “corner” 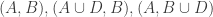 , where D is disjoint from A and B. (A, B, D are subsets of [n] )
, where D is disjoint from A and B. (A, B, D are subsets of [n] )
For every
February 20, 2009 at 6:56 am |
560. Sperner.
Tim, regarding your problem beginning in #553 and fixing and
and  first… Is it correct that if we fix
first… Is it correct that if we fix  and
and  , then we recover the scenario from #476?
, then we recover the scenario from #476?
One reason I like to have very close to
very close to  (“extreme localization”) is that the
(“extreme localization”) is that the  -biased and
-biased and  -biased measures are practically disjoint if
-biased measures are practically disjoint if  is even a little bit less than
is even a little bit less than  . So then how a set
. So then how a set  acts under the
acts under the  -biased distribution has nothing to do with how it acts under the
-biased distribution has nothing to do with how it acts under the  -biased distribution.
-biased distribution.
(Of course, this is only if you *fix* distant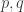 in advance. If you pick them at random, some bets are off.)
in advance. If you pick them at random, some bets are off.)
February 20, 2009 at 7:00 am |
561. Moser.
Given that we feel a bit stuck on HJ, I feel tempted to think more about Moser instead. I mean, why not? — it’s a strictly easier problem. Is there an “easier” ergodic-theory proof of Density-Moser?
February 20, 2009 at 7:11 am |
560. Removal lemma for DHJ (contd.)
Now that a dense system is given, let’s check how can we use a removal lemma. Given a collection of pairs of subsets of [n], denoted by S, of cardinality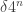 . The family of pairs having the same symmetric difference set form a matching in this graph. By Ruzsa-Szemeredi there will be many edges from the same matching (symmetric difference) that are connected by another edge. More precisely, there will be at least
. The family of pairs having the same symmetric difference set form a matching in this graph. By Ruzsa-Szemeredi there will be many edges from the same matching (symmetric difference) that are connected by another edge. More precisely, there will be at least 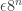 quadruples A,B,C,D that (A,B), (C,D), and (A,D) are from S and
quadruples A,B,C,D that (A,B), (C,D), and (A,D) are from S and  . Unfortunately it is not a combinatorial line in general. However it is a combinatorial line if
. Unfortunately it is not a combinatorial line in general. However it is a combinatorial line if  , i.e. when the three pairs are representing points from the same cube.
, i.e. when the three pairs are representing points from the same cube.
February 20, 2009 at 7:18 am |
oops, here is a typo in the previous post; the correct statement is
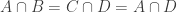
February 20, 2009 at 7:32 am |
563. Moser
Re:561. Ryan, I don’t think that there is a published ergodic proof for Moser’s problem and I think that Moser k=6 implies DHJ k=3. But I agree, there should be a simpler way to prove Moser k=3. Note that for any algebraic line L in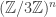 one can find an x such that x+L is a geometric line.
one can find an x such that x+L is a geometric line.
February 20, 2009 at 7:44 am |
Dear Jozsef, how do we get DHJ for k=3 from Moser for k=6? (Exploring these type of reductions may also be a nice avenue of some potential.)
February 20, 2009 at 8:18 am |
Dear Gil, We have to check, but my thought was that if you map to
to 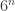 as 1 maps to 1 or 6, 2 maps to 2 or 5, and 3 maps to 3 or 4, then if DHJ k=3 was combinatorial line free then Moser k=6 is geometric line free. And if DHJ was dense, then Moser is dense too. I hope it’s right .
as 1 maps to 1 or 6, 2 maps to 2 or 5, and 3 maps to 3 or 4, then if DHJ k=3 was combinatorial line free then Moser k=6 is geometric line free. And if DHJ was dense, then Moser is dense too. I hope it’s right .
February 20, 2009 at 9:08 am |
566. Equal-slices measure.
Ryan, my answer to your point in 560 is that it is indeed true that if you fix and
and  that are some way apart, then the measures
that are some way apart, then the measures 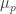 and
and  are approximately disjointly supported. However, this is quite natural once you average over
are approximately disjointly supported. However, this is quite natural once you average over  and
and  . It’s a bit like saying that in order to understand Sperner we will look at pairs of layers and see what happens for those. Obviously, one cannot look at each pair in complete isolation if one wants to prove Sperner’s theorem (since the weight inside each layer might be less than 1/2, say) but it’s not so clear that one can’t get useful information about obstructions that way: for example, one might be able to understand when two layers don’t make the right contribution to the number of subset pairs, and one might then be able to put that together to understand when it happens after averaging over all pairs of layers.
. It’s a bit like saying that in order to understand Sperner we will look at pairs of layers and see what happens for those. Obviously, one cannot look at each pair in complete isolation if one wants to prove Sperner’s theorem (since the weight inside each layer might be less than 1/2, say) but it’s not so clear that one can’t get useful information about obstructions that way: for example, one might be able to understand when two layers don’t make the right contribution to the number of subset pairs, and one might then be able to put that together to understand when it happens after averaging over all pairs of layers.
But whether or not you are convinced by this, your alternative way of thinking about equal-slices measure has been hugely useful!
February 20, 2009 at 9:22 am |
567. Sperner calculations continued.
A quick remark re 558. I realized as I woke up this morning that must be at most 1 by Cauchy-Schwarz because it’s the covariance of the random variables
must be at most 1 by Cauchy-Schwarz because it’s the covariance of the random variables 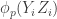 and
and  , each of which has been carefully designed to have variance 1. (To put it another way, it follows easily from Cauchy-Schwarz.) So I think we’re in business here. I made some small slips in the calculations earlier, but I think that we have the very nice expression
, each of which has been carefully designed to have variance 1. (To put it another way, it follows easily from Cauchy-Schwarz.) So I think we’re in business here. I made some small slips in the calculations earlier, but I think that we have the very nice expression ![\mathbb{E}_{p\leq q}\sum_{A\subset[n]}\lambda_{p,q}^{|A|}\hat{f}_p(A)\hat{f}_q(A)](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D_%7Bp%5Cleq+q%7D%5Csum_%7BA%5Csubset%5Bn%5D%7D%5Clambda_%7Bp%2Cq%7D%5E%7B%7CA%7C%7D%5Chat%7Bf%7D_p%28A%29%5Chat%7Bf%7D_q%28A%29&bg=ffffff&fg=333333&s=0&c=20201002) for the total weight
for the total weight  , where each
, where each  has modulus less than 1, with equality if and only if
has modulus less than 1, with equality if and only if 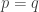 . From this one can informally read off a few quite interesting things. For instance, the contribution from a set
. From this one can informally read off a few quite interesting things. For instance, the contribution from a set  of large cardinality will be tiny if
of large cardinality will be tiny if  and
and  are not very close to each other, but that happens only rarely (Ryan won’t like this bit), so the total contribution from large
are not very close to each other, but that happens only rarely (Ryan won’t like this bit), so the total contribution from large  appears to be small. This fits in nicely with one’s intuition that by Kruskal-Katona the upper shadow of a layer of positive density will be huge if you go up a lot of layers, unless there is some simple explanation such as all sets containing 1. Perhaps at this point I’ll try to tidy up these calculations and put them on the wiki.
appears to be small. This fits in nicely with one’s intuition that by Kruskal-Katona the upper shadow of a layer of positive density will be huge if you go up a lot of layers, unless there is some simple explanation such as all sets containing 1. Perhaps at this point I’ll try to tidy up these calculations and put them on the wiki.
February 20, 2009 at 12:17 pm |
568. Fourier and DHJ(3).
Before I go off and do actual calculations, I want to see how much I can easily generalize of the Sperner calculations to DHJ(3).
The first step is to come up with a Ryan-style model for equal-slices measure. For points it is easy enough: first, pick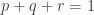 and for each coordinate
and for each coordinate  let it be 1 with probability p, 2 with probability 1 and 3 with probability r. Then average the resulting density over all such p,q,r.
let it be 1 with probability p, 2 with probability 1 and 3 with probability r. Then average the resulting density over all such p,q,r.
Now for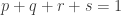 I’d like to pick a random combinatorial line in such a way that its 1-set is chosen according to (p+s,q,r) measure, its 2-set is chosen according to (p,q+s,r) measure, and its 3-set is chosen according to (p,q,r+s) measure. I think this too is easy: for each i you make it 1 with probability p, 2 with probability q, 3 with probability r, and a wildcard with probability s.
I’d like to pick a random combinatorial line in such a way that its 1-set is chosen according to (p+s,q,r) measure, its 2-set is chosen according to (p,q+s,r) measure, and its 3-set is chosen according to (p,q,r+s) measure. I think this too is easy: for each i you make it 1 with probability p, 2 with probability q, 3 with probability r, and a wildcard with probability s.
The next task is to come up with analogues of the “biased Walsh functions” that we used on
that we used on ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . So now we are looking for functions
. So now we are looking for functions  (where the
(where the  is redundant but there for symmetry). We very much want to use independence, so we would like
is redundant but there for symmetry). We very much want to use independence, so we would like  to be
to be  , where
, where 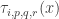 will be
will be 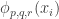 . Amongst the properties we will want of the function
. Amongst the properties we will want of the function  is that its expectation (defined to be
is that its expectation (defined to be  ) is 0 and that its variance is 1. To achieve this, I plan to let
) is 0 and that its variance is 1. To achieve this, I plan to let 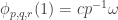 ,
, 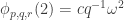 and
and 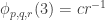 . Here
. Here 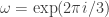 and
and  is a normalizing factor to make the variance 1. This seems not to be the unique thing one could do but it does seem to be quite a natural thing to do. I’m hoping, however, that the expectation and variance will give me most of the information I care about.
is a normalizing factor to make the variance 1. This seems not to be the unique thing one could do but it does seem to be quite a natural thing to do. I’m hoping, however, that the expectation and variance will give me most of the information I care about.
In particular, the functions defined this way do indeed form an orthonormal basis for (complex) functions defined on
defined this way do indeed form an orthonormal basis for (complex) functions defined on ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Now let us think about the expression , where the expectation is over all combinatorial lines
, where the expectation is over all combinatorial lines  chosen according to the (p,q,r,s) measure. To do this, we expand
chosen according to the (p,q,r,s) measure. To do this, we expand  as
as 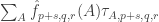 , and similarly for
, and similarly for  and
and  . So what we would like to understand is
. So what we would like to understand is 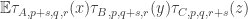 for fixed sets
for fixed sets  . Again, the expectation is over all (p,q,r,s)-combinatorial lines. (Eventually we will average over p+q+r+s=1.)
. Again, the expectation is over all (p,q,r,s)-combinatorial lines. (Eventually we will average over p+q+r+s=1.)
I want to be able to see this expression, so will start a new comment.
February 20, 2009 at 12:41 pm |
569. Fourier and DHJ(3).
Now let us choose a sequence of random variables , where each
, where each 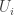 is 1 with probability p, 2 with probability q, 3 with probability r, and a wildcard with probability s. Then let
is 1 with probability p, 2 with probability q, 3 with probability r, and a wildcard with probability s. Then let 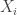 be
be 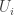 if
if  or
or 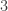 , and
, and  if
if 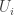 is a wildcard, and define
is a wildcard, and define 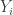 and
and 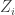 similarly, so that the three sequences
similarly, so that the three sequences  ,
, 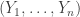 and
and  form a random combinatorial line
form a random combinatorial line 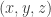 determined by
determined by  .
.
Now each term in the product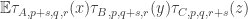 itself splits up into a big product, the first over all
itself splits up into a big product, the first over all 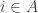 , the second over all
, the second over all  and the third over all
and the third over all  . For example,
. For example,  .
.
Let us try to understand when the expectation of this product has a chance of not being zero.
One case where it is zero is if there exists i that belongs to A but not to B or C. In that case, the big product will include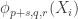 , but it won’t involve
, but it won’t involve 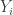 or
or 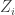 . Therefore, by independence and the fact that
. Therefore, by independence and the fact that 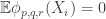 , the entire expectation is 0.
, the entire expectation is 0.
What about if but
but 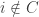 ? Now we want to know what
? Now we want to know what  is. We know that the probability that
is. We know that the probability that 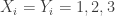 is
is  , and the probability that
, and the probability that 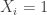 and
and  is
is  . I would very much like the resulting expectation to be 0, but at the moment I don’t see any reason for this. So I think I’ve got to the point where I need to do a back-of-envelope calculation. Here is where it may turn out that my guess for a good choice of functions
. I would very much like the resulting expectation to be 0, but at the moment I don’t see any reason for this. So I think I’ve got to the point where I need to do a back-of-envelope calculation. Here is where it may turn out that my guess for a good choice of functions  was not a good guess. (I should say that what I’m eventually hoping for is something reminiscent of what one gets in
was not a good guess. (I should say that what I’m eventually hoping for is something reminiscent of what one gets in 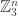 , namely a sum over cubes of Fourier coefficients. This may be asking a bit much though.)
, namely a sum over cubes of Fourier coefficients. This may be asking a bit much though.)
February 20, 2009 at 1:55 pm |
570. Fourier and DHJ(3)
A quick report back. The guess doesn’t work, but I’m still not quite sure whether there might be another choice of functions that do the job. If we forget normalizations then the only property that matters is
that do the job. If we forget normalizations then the only property that matters is 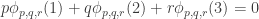 . And then what we’d very much like is that if
. And then what we’d very much like is that if 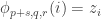 and
and 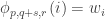 , then
, then 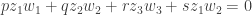 . But I think that’s not going to be achievable. If we set
. But I think that’s not going to be achievable. If we set 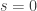 , then it suggests that we should also have
, then it suggests that we should also have 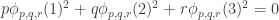 , which more or less pins down the function (I think it decides it up to a constant multiple and taking complex conjugates). But I’m getting a bit bogged down in algebra at the moment, nice though that condition is.
, which more or less pins down the function (I think it decides it up to a constant multiple and taking complex conjugates). But I’m getting a bit bogged down in algebra at the moment, nice though that condition is.
February 20, 2009 at 4:03 pm |
571. Sperner.
Tim, the expression in #567 is so elegant, how can I not be on board for equal-slices now? 🙂 Here are some questions that occur to me:
1. Can we get a handle on the meaning of the first term? What does![\mathbb{E}_{p \leq q}[\hat{f}_p(\emptyset)\hat{f}_q(\emptyset)]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D_%7Bp+%5Cleq+q%7D%5B%5Chat%7Bf%7D_p%28%5Cemptyset%29%5Chat%7Bf%7D_q%28%5Cemptyset%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) represent? Well, it represents the average of
represent? Well, it represents the average of  ‘s
‘s  -biased measure times its
-biased measure times its  -biased measure under this way of choosing
-biased measure under this way of choosing 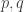 , but what does that… mean?
, but what does that… mean?
2. Can we understand why this expression is miraculously always whenever
whenever  is a monotone function of equal-slices-mean
is a monotone function of equal-slices-mean  ? Being “monotone” is a fairly “non-Fourier-y” property.
? Being “monotone” is a fairly “non-Fourier-y” property.
3. Is this quantity always at least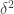 ?
?
4. What exactly might we be hoping to prove in this Sperner case? Something like, “The extent to which you don’t have a fraction of Sperner pairs (under Tim’s distribution) is related to the extent to which you are not monotone.”?
fraction of Sperner pairs (under Tim’s distribution) is related to the extent to which you are not monotone.”?
February 20, 2009 at 4:46 pm |
572. Sperner
Ryan, I don’t have complete answers to your questions, needless to say, but they are interesting questions so let me give my first thoughts.
1. I haven’t checked that it’s exactly the same, but I’d have thought it would be something like what I was looking at before you came along with your s and
s and  s. That is, you randomly scramble
s. That is, you randomly scramble ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , then randomly choose two initial segments
, then randomly choose two initial segments  and
and  , and calculate
, and calculate  . And then you average over everything you’ve done. In the case where
. And then you average over everything you’ve done. In the case where  is the characteristic function of a set
is the characteristic function of a set  , you are calculating the expectation of the square of the density of initial segments of a random permutation of
, you are calculating the expectation of the square of the density of initial segments of a random permutation of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) that belong to
that belong to  . So in that model at any rate it’s always at least
. So in that model at any rate it’s always at least 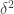 since the average is
since the average is  . So this may possibly answer 3.
. So this may possibly answer 3.
2. I don’t understand your question here. For example, if is the characteristic function of all sets of size at least
is the characteristic function of all sets of size at least 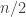 , then the
, then the  -biased measure is basically 0 if
-biased measure is basically 0 if  . So the equal-slices mean is
. So the equal-slices mean is 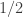 . And if you choose a random pair
. And if you choose a random pair  such that
such that 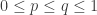 then the probability that they both exceed
then the probability that they both exceed 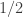 is 1/4. And this works if you replace
is 1/4. And this works if you replace 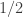 by any
by any  . In order to depart from
. In order to depart from 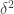 , you have to find a monotone function that doesn’t look like a union of layers, of which the obvious example is the set of all sets that contain 1.
, you have to find a monotone function that doesn’t look like a union of layers, of which the obvious example is the set of all sets that contain 1.
3. See 1.
4. At one point I was convinced by you that monotonicity was a key property. But I’ve gone back to thinking that what really matters is small sets with big bias. I think what I’d like to see (and I think it could be quite close) is a density-increment proof of Sperner. The proof would go something like this. By the expansion above, either get the expected number of pairs or we find a small
or we find a small  such that
such that 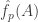 is large for a dense set of
is large for a dense set of  , where
, where  is the balanced function of
is the balanced function of  (suitably defined). In the latter case, we fix a small number of variables and give ourselves a density increase in a subspace of bounded codimension. The motivation for such an argument would be to find something that could be adapted to DHJ(3). There are at least two technical problems to sort out. The first is to work out
(suitably defined). In the latter case, we fix a small number of variables and give ourselves a density increase in a subspace of bounded codimension. The motivation for such an argument would be to find something that could be adapted to DHJ(3). There are at least two technical problems to sort out. The first is to work out 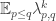 . The second is that restricting to subspaces is problematic when one is dealing with equal-slices measure. Or at least, at some point I persuaded myself that it was.
. The second is that restricting to subspaces is problematic when one is dealing with equal-slices measure. Or at least, at some point I persuaded myself that it was.
February 20, 2009 at 6:14 pm |
573. Fourier, DHJ(3), corners
It’s just occurred to me that what I was trying to do in 568-570 is unlikely to work because we don’t have a direct Fourier expansion of this kind for the corners problem. So before I go any further I want to think about corners.
Actually, I’ve now had a counterthought, which is that if by some miracle we ended up with an expression of the form for the number of combinatorial lines (I’ve also just realized that I was absent-mindedly trying to define a basis that consisted of only
for the number of combinatorial lines (I’ve also just realized that I was absent-mindedly trying to define a basis that consisted of only 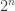 vectors, so I’ve changed
vectors, so I’ve changed  to
to  and will go back and think about this), then we would not particularly expect to get a non-zero answer (if
and will go back and think about this), then we would not particularly expect to get a non-zero answer (if  was the characteristic function of our dense set) unless we could find a good selection
was the characteristic function of our dense set) unless we could find a good selection  such that all the Fourier coefficients at
such that all the Fourier coefficients at  were reasonably large. This would be asking for corners in the triangle
were reasonably large. This would be asking for corners in the triangle  . So it could conceivably be that the corners theorem would get us started and Fourier would take over from there—which is reminiscent of, though not quite the same as, what Terry suggested way back in comment 77. Here, the idea would be that the corners theorem (suitably Varnavides-ized) would guarantee that there were many candidate triples of rich slices that could lead to combinatorial lines, and Fourier methods would show that you could differ from the expected number of combinatorial lines given the slice-density function only if something showed up in the Fourier expansions.
. So it could conceivably be that the corners theorem would get us started and Fourier would take over from there—which is reminiscent of, though not quite the same as, what Terry suggested way back in comment 77. Here, the idea would be that the corners theorem (suitably Varnavides-ized) would guarantee that there were many candidate triples of rich slices that could lead to combinatorial lines, and Fourier methods would show that you could differ from the expected number of combinatorial lines given the slice-density function only if something showed up in the Fourier expansions.
However, having written that optimistic sounding paragraph, I feel pessimism returning. In fact, I have a little test to apply. I think if one chooses a random set of complexity 1 (see the discussion of DHJ(1,3) on this page for a definition) then it may well not have any large Fourier coefficients, even though it will typically have the wrong number of combinatorial lines.
To end this comment on an optimistic note, perhaps this strange form of Fourier analysis could be used to prove DHJ(1,3), and perhaps it could come in at the point where Shkredov needs it for his corners proof.
February 20, 2009 at 6:57 pm |
574. Fourier and DHJ(3)
Here’s the test then. Suppose you take two random collections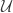 and
and  of subsets of
of subsets of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Now let
. Now let  be the set of all points
be the set of all points  with 1-set in
with 1-set in  and 2-set in
and 2-set in  . Let
. Let  and
and  be two functions from
be two functions from ![{}[3]](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D&bg=ffffff&fg=333333&s=0&c=20201002) to
to  such that
such that  . Let
. Let  be a product of functions
be a product of functions 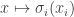 where each
where each 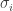 is either 1,
is either 1,  or
or  . The question now is whether
. The question now is whether  can possibly correlate with
can possibly correlate with  . And the answer seems to me to be so obviously no that I think I can get away without actually checking it carefully.
. And the answer seems to me to be so obviously no that I think I can get away without actually checking it carefully.
In fact, here’s a sketch of a proof: there are only non-constant functions of the given type, the expectation of each one over the random set
non-constant functions of the given type, the expectation of each one over the random set  is 0, and there will be very very strong concentration. (I haven’t checked this argument, but it convinces me.)
is 0, and there will be very very strong concentration. (I haven’t checked this argument, but it convinces me.)
The next step is to see whether it is possible to make up for this slight disappointment (slight because we had no right to expect things to work better for DHJ(3) than they do for corners) by finding something comparably nice about bipartite graphs and singular values, for possible use in a regularity lemma. I’ll start a fresh comment and then explain what I’m hoping for here.
February 20, 2009 at 7:24 pm |
575. Global quasirandomness
Recall that associated with a subset of
of ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) are three bipartite graphs, each with two copies of the power set of
are three bipartite graphs, each with two copies of the power set of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) as its vertex sets, with edges joining some pairs of disjoint sets. For instance, the 12-graph joins
as its vertex sets, with edges joining some pairs of disjoint sets. For instance, the 12-graph joins  to
to  if the sequence x with 1-set equal to
if the sequence x with 1-set equal to  and 2-set equal to
and 2-set equal to  belongs to
belongs to  .
.
Now the averaging-over-permutations technique looked as though it would yield a definition of quasirandomness that was sufficient to guarantee the correct number of combinatorial lines. However, we did not get out of that the kind of global correlations that would be needed for a regularity lemma. Basically, the reason was that the definition that seemed to be emerging was of the number-of-4-cycles kind rather than the correlates-with-bipartite-subgraph kind. However, the thoughts that led to the Sperner expression feel as though they could also give rise to a useful definition of the latter kind. So that is what I want to try next.
February 20, 2009 at 7:58 pm |
576. Global quasirandomness
First, let me give a Ryan-style equal-slices measure for the bipartite graph we’re talking about, or more generally for functions that take pairs
that take pairs  of disjoint sets to
of disjoint sets to ![{}[-1,1]](https://s0.wp.com/latex.php?latex=%7B%7D%5B-1%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . As usual, I’ll discuss things for fixed
. As usual, I’ll discuss things for fixed  and
and  and then average later. So let
and then average later. So let  and
and  be positive real numbers that add up to less than 1. For each element of
be positive real numbers that add up to less than 1. For each element of ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , put it in
, put it in  with probability
with probability  and in
and in  with probability
with probability  , with all choices independent. Then we would like to find a natural decomposition of such functions, analogous to the singular value decomposition of a bipartite graph.
, with all choices independent. Then we would like to find a natural decomposition of such functions, analogous to the singular value decomposition of a bipartite graph.
In the graphs case we can derive the SVD variationally. The analogue here would be to maximize over all functions
over all functions  and
and  of
of  norm 1. Here, I imagine that we choose
norm 1. Here, I imagine that we choose  and
and  according to the distribution specified above, and measure the
according to the distribution specified above, and measure the  norms of
norms of  and
and  using the
using the 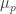 and
and  measures, respectively. Then if
measures, respectively. Then if  is a very small function orthogonal to
is a very small function orthogonal to  , then the above expectation must change by
, then the above expectation must change by 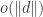 , which implies that the function
, which implies that the function  is proportional to
is proportional to 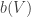 .
.
Got to go. To be continued.
February 21, 2009 at 12:26 am |
577. Global quasirandomness
My basic thought here is to try to do linear algebra but with a different model of matrix multiplication: when we write we are not allowing
we are not allowing  and
and  to vary independently. Having decided on that, I would like to try to follow the usual arguments as similarly as possible. For example, I would like to be able to say that
to vary independently. Having decided on that, I would like to try to follow the usual arguments as similarly as possible. For example, I would like to be able to say that  is quasirandom if
is quasirandom if  is approximately the constant function
is approximately the constant function 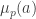 for every bounded
for every bounded  . And I’d like to have a counting lemma for quasirandom functions (this is likely to be less easy). With those two ingredients, there would be a serious chance of proving a triangle-removal lemma.
. And I’d like to have a counting lemma for quasirandom functions (this is likely to be less easy). With those two ingredients, there would be a serious chance of proving a triangle-removal lemma.
From the argument in the previous comment, we have seen that if is maximized over all unit vectors
is maximized over all unit vectors  and
and  , then
, then  is proportional to
is proportional to 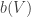 . Therefore, if
. Therefore, if  , it follows that
, it follows that  By symmetry, if
By symmetry, if  , it follows that
, it follows that 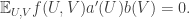 In other words, the linear map defined by
In other words, the linear map defined by  takes the space orthogonal to
takes the space orthogonal to  to the space orthogonal to
to the space orthogonal to  , so we can find orthonormal bases
, so we can find orthonormal bases 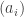 and
and 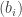 of
of ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , one with respect to the measure
, one with respect to the measure 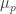 and one with respect to the measure
and one with respect to the measure  , such that for every
, such that for every  ,
,  is proportional to
is proportional to 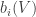 .
.
Let’s write . (Everything here depends on
. (Everything here depends on  and
and  but we are thinking of those as fixed for now.) Then if
but we are thinking of those as fixed for now.) Then if 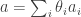 , then
, then  , which has
, which has 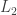 norm
norm  . For this not to be small, we need some
. For this not to be small, we need some 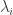 to be large, I think, and this seems to give us
to be large, I think, and this seems to give us 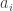 and
and  such that
such that  is large. Obviously this needs to be checked pretty carefully, but it looks on the face of it as though we find something like a complexity-1 function that correlates with
is large. Obviously this needs to be checked pretty carefully, but it looks on the face of it as though we find something like a complexity-1 function that correlates with  . (However, when
. (However, when  and
and  vary, so does the complexity-1 function.)
vary, so does the complexity-1 function.)
But I still have the local-to-global problem, but from the other side: this time there seems to be a global non-quasirandomness, but it’s not clear to me that global quasirandomness leads to the right number of triangles.
February 21, 2009 at 6:47 am |
578. A new proof of DHJ(2)
Hi; I’ve been busy with other things for a while, so am not caught up… but meanwhile, I think I found a genuinely different proof of DHJ(2) based on obstructions-to-uniformity (similar, incidentally, to my paper proving convergence for multiple commuting shifts) which may have some potential.
It goes like this. Call a bounded function![f: [2]^n \to {\Bbb R}](https://s0.wp.com/latex.php?latex=f%3A+%5B2%5D%5En+%5Cto+%7B%5CBbb+R%7D&bg=ffffff&fg=333333&s=0&c=20201002) uniform at scale m if f(x) and f(y) are uncorrelated, whenever x is chosen randomly from
uniform at scale m if f(x) and f(y) are uncorrelated, whenever x is chosen randomly from ![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) and y is formed from x by randomly flipping O(m) 0s to 1s.
and y is formed from x by randomly flipping O(m) 0s to 1s.
Call a bounded function f basic anti-uniform at scale m if its mean influence is O(1/m), i.e. if x is chosen randomly from![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) and y is obtained from x by randomly flipping one 0 to a 1, then f(x)=f(y) with probability 1-O(1/m).
and y is obtained from x by randomly flipping one 0 to a 1, then f(x)=f(y) with probability 1-O(1/m).
Lemma: A bounded function f is either uniform at scale m, or has non-trivial correlation with a function g which is basic anti-uniform at scale m.
Proof: Take , where y is formed from x by randomly flipping m 0s to 1s.
, where y is formed from x by randomly flipping m 0s to 1s. 
At this point we have two possible strategies.
The first is to observe that basic anti-uniform functions tend to be roughly constant on large subspaces. Because of this, any function f of mean zero which correlates with a basic anti-uniform function will have a density increment on some large subspace. If one then starts with $f := 1_A – \delta$ and runs the density increment argument (and reduce m at each iteration), one can eventually get to the point where $1_A – \delta$ is uniform at some scale m, at which point one can find lots of combinatorial lines with m wildcards.
The other strategy is to use energy-increment methods instead of density-increment ones. Indeed if we do the usual “energy-increment” iteration (as for instance appears in my first paper with Ben), and decreasing the parameter m appropriately with each iteration, we obtain
Corollary: Every bounded function f can be split into a function uniform at scale m, plus a polynomial combination
uniform at scale m, plus a polynomial combination  of functions anti-uniform at scale m’, plus a small error, where m’ is much larger than m. Also, if f is non-negative and has large mean, one can arrange matters so that
of functions anti-uniform at scale m’, plus a small error, where m’ is much larger than m. Also, if f is non-negative and has large mean, one can arrange matters so that  is also non-negative and has large mean.
is also non-negative and has large mean.
Now on subspaces of size about m’, is close to constant, and on many subspaces, this quantity is going to be large. Meanwhile,
is close to constant, and on many subspaces, this quantity is going to be large. Meanwhile,  is uniform on most subspaces, and so most subspaces are going to contain lines (with about m wildcards).
is uniform on most subspaces, and so most subspaces are going to contain lines (with about m wildcards).
The corresponding obstructions to uniformity for DHJ(3) are more complex. Roughly speaking, I’m facing things like this: take a random x in![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , let y be formed from x by randomly flipping a bunch of 0s to 1s, and then let x’, y’ be formed from x and y by randomly flipping a bunch of 0s to 2s (with the digits being flipped for x being the same as those for y). Then one needs to understand what it means if
, let y be formed from x by randomly flipping a bunch of 0s to 1s, and then let x’, y’ be formed from x and y by randomly flipping a bunch of 0s to 2s (with the digits being flipped for x being the same as those for y). Then one needs to understand what it means if  is large. There seems to be a sense that f is somehow correlating with a “local complexity 1” set – i.e. the type of expression we already saw in DHJ(1,3), but somehow localised to a much smaller scale than n – but I don’t see clearly what it will be yet.
is large. There seems to be a sense that f is somehow correlating with a “local complexity 1” set – i.e. the type of expression we already saw in DHJ(1,3), but somehow localised to a much smaller scale than n – but I don’t see clearly what it will be yet.
February 21, 2009 at 5:36 pm |
579.
There looks like there is a good chance that the type of arguments in 578 can be combined with the basic strategy I sketched out (very vaguely) in 536 (as Ryan already suggested in 538). Basically, if there are many large slices of A which are not uniform (which means that their Fourier transform is concentrated in a Hamming ball of radius n/m or so centred at the origin) then that slice of A is correlating with an anti-uniform object of low influence; this object is roughly constant on medium-dimensional subslices and so we can locate a density increment. So we can assume that most slices of A are uniform, and I think this is getting close to what we need for a counting lemma for geometric lines in A where the middle point of the line is close to the centre (2,2,..,2). I’ll have to do some calculations to clarify all this.
February 21, 2009 at 5:40 pm |
580. Extreme localization and DHJ(3)
Although I am still very interested in trying to find a “global” proof of DHJ(3) (though cheating first and changing the measure to equal-slices), Terry’s 578 prompts me to ask why we don’t already have a proof of DHJ(3). I’m not saying that I think we do, but rather that I want to understand where the gap is.
In order to explain that, let me try to give some sort of proof sketch. Either it will look fairly complete, in which case we will need to examine its steps more carefully, or there will be some step that I don’t yet see how to carry out, even roughly.
The broad plan is similar to things that both Terry and I have discussed in much earlier comments, and that Terry alludes to in his final paragraph above. I shall write my points as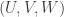 , where these are the 1-set, 2-set and 3-set of a sequence in
, where these are the 1-set, 2-set and 3-set of a sequence in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . If
. If  is dense, then there will be many choices of
is dense, then there will be many choices of  for which the set of
for which the set of  with
with ![U\cup V=[n]\setminus W](https://s0.wp.com/latex.php?latex=U%5Ccup+V%3D%5Bn%5D%5Csetminus+W&bg=ffffff&fg=333333&s=0&c=20201002) and
and 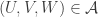 is dense (in the set of
is dense (in the set of  such that
such that ![U\cup V=[n]\setminus W](https://s0.wp.com/latex.php?latex=U%5Ccup+V%3D%5Bn%5D%5Csetminus+W&bg=ffffff&fg=333333&s=0&c=20201002) ). Therefore, by Sperner we can find a pretty large number of pairs
). Therefore, by Sperner we can find a pretty large number of pairs 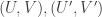 of such pairs with
of such pairs with  . And for each such pair of pairs we know that the point
. And for each such pair of pairs we know that the point ![(U,V',[n]\setminus(U\cup V'))](https://s0.wp.com/latex.php?latex=%28U%2CV%27%2C%5Bn%5D%5Csetminus%28U%5Ccup+V%27%29%29&bg=ffffff&fg=333333&s=0&c=20201002) does not belong to
does not belong to  .
.
Now let’s rephrase that. This time I’ll write for the point with 1-set equal to
for the point with 1-set equal to  and 2-set equal to
and 2-set equal to  . Then for each
. Then for each  we find a set-system
we find a set-system  such that
such that  whenever
whenever 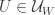 and
and ![{}[n]\setminus(V\cup W)\in\mathcal{U}_W](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D%5Csetminus%28V%5Ccup+W%29%5Cin%5Cmathcal%7BU%7D_W&bg=ffffff&fg=333333&s=0&c=20201002) . Let us write
. Let us write 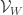 for the set of all
for the set of all  with the second property. Sperner should tell us that on average the set of all disjoint pairs
with the second property. Sperner should tell us that on average the set of all disjoint pairs  is reasonably dense in the set of all disjoint pairs that are disjoint from
is reasonably dense in the set of all disjoint pairs that are disjoint from  . So we have something that could be described as a “local complexity 1” set of points that do not belong to
. So we have something that could be described as a “local complexity 1” set of points that do not belong to  . Indeed, we have lots of such sets.
. Indeed, we have lots of such sets.
I’m going to gloss over a few technicalities such as whether we are thinking about equal-slices measure or insisting that our lines have very few wildcards or whatever. Or perhaps I’ll just go for the latter: let’s focus on lines that have at most wildcards, where
wildcards, where  .
.
Now for the main question. Can we convert this local non-uniformity into a global non-uniformity by some random restriction? At the moment things look a bit strange because the lines we are considering are of the form , where
, where  and
and  are disjoint from each other and from a fixed set
are disjoint from each other and from a fixed set  , and all of
, and all of  ,
,  and
and  have size about
have size about  But if we restrict to the subspace of all sequences that are
But if we restrict to the subspace of all sequences that are 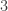 on
on  , then in this subspace we are looking at points where the 1-set and 2-set use up about half the coordinates and the 3-set uses up only a tiny number of coordinates. So the plan would be to choose random sets
, then in this subspace we are looking at points where the 1-set and 2-set use up about half the coordinates and the 3-set uses up only a tiny number of coordinates. So the plan would be to choose random sets  and
and 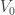 of size something like
of size something like  and restrict to the subspace of points that are 1 on
and restrict to the subspace of points that are 1 on  and
and  on
on 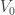 . Inside that subspace I think we’d still have correlation with a set of complexity 1 but now a typical point would have around
. Inside that subspace I think we’d still have correlation with a set of complexity 1 but now a typical point would have around  each of 1s, 2s and 3s (over and above the already fixed coordinates).
each of 1s, 2s and 3s (over and above the already fixed coordinates).
Obviously there would be some details to check there, but at the moment I don’t see why it doesn’t give us correlation with a set of complexity 1 after restricting to a small (but not all that small) subspace.
Where to proceed from there? Well, the set of complexity 1 is of a nice form in that whether or not you belong to it depends just on whether your 1-set belongs to and your 2-set belongs to
and your 2-set belongs to 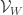 . (In other words, there isn’t an additional condition about the 3-set. As shown on section 2 on this wiki page, such sets are simpler to deal with than general complexity-1 sets.
. (In other words, there isn’t an additional condition about the 3-set. As shown on section 2 on this wiki page, such sets are simpler to deal with than general complexity-1 sets.
I will be interested to see whether anyone can spot a flaw in the above sketched argument. If not, then attention should turn to a problem that up to now I have assumed is doable, which is to show that if you correlate with a complexity-1 set then you can get a density increase on a subspace. I’ll post this comment and then think about that problem in my next one.
February 21, 2009 at 5:42 pm |
Metacomment:
Unrelated to this thread, but I thought I would like to report a success of this collaborative environment: at the 700 thread we have now produced two proofs (one computer-assisted, one not) that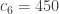 , i.e. that the largest line-free subset of
, i.e. that the largest line-free subset of ![[3]^6](https://s0.wp.com/latex.php?latex=%5B3%5D%5E6&bg=ffffff&fg=333333&s=0&c=20201002) contains exactly 450 points. Six dimensions is already well into the range where the “curse of dimensionality” really begins to bite, so I find this a significant milestone. At least six people made significant contributions to one of the two proofs.
contains exactly 450 points. Six dimensions is already well into the range where the “curse of dimensionality” really begins to bite, so I find this a significant milestone. At least six people made significant contributions to one of the two proofs.
February 21, 2009 at 6:03 pm |
581. Multidimensional Sperner.
I’ve just realized that multidimensional Sperner is easy. I must have been aware of this argument at some point in the past, and certainly I know lots of similar arguments, but this time round I had been blind.
The question I’m interested in is this. Suppose that you have a dense subset of![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . Sperner tells you that you can find a pair
. Sperner tells you that you can find a pair  in
in  , and that gives us a 1-dimensional combinatorial subspace. But what if we want a k-dimensional subspace?
, and that gives us a 1-dimensional combinatorial subspace. But what if we want a k-dimensional subspace?
Here’s how I think one can argue. Actually, the further I go the more I realize that it’s not completely easy after all. But I think it shouldn’t be too bad. I think for convenience I’ll use equal-slices measure. In that measure one obtains that if is dense then the proportion of pairs
is dense then the proportion of pairs  that belong to
that belong to  is also positive. So by averaging I think one can find a set
is also positive. So by averaging I think one can find a set  such that the set of all
such that the set of all  disjoint from
disjoint from  such that both
such that both  and
and 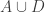 belong to
belong to  is itself dense (in
is itself dense (in ![{}[2]^{[n]\setminus D}](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5E%7B%5Bn%5D%5Csetminus+D%7D&bg=ffffff&fg=333333&s=0&c=20201002) ). By induction that set contains a
). By induction that set contains a 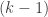 -dimensional combinatorial subspace and we are done. (This argument is unchecked and I’m not certain the details work out, but if they don’t then some version of it with repeated localizations certainly ought to.)
-dimensional combinatorial subspace and we are done. (This argument is unchecked and I’m not certain the details work out, but if they don’t then some version of it with repeated localizations certainly ought to.)
What I’d now like to do is prove that a dense set![\mathcal{A}\subset[3]^n](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BA%7D%5Csubset%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of complexity 1 of the special form discussed in the previous comment contains a combinatorial subspace with dimension that tends to infinity with
of complexity 1 of the special form discussed in the previous comment contains a combinatorial subspace with dimension that tends to infinity with  . (Eventually the plan would be to prove more than this: we would like to cover
. (Eventually the plan would be to prove more than this: we would like to cover  evenly with such subspaces so that a set that correlates with
evenly with such subspaces so that a set that correlates with  has to correlate with one of the subspaces. But we should walk before we run.) That counts as a separate task so I’ll attempt it in the next comment.
has to correlate with one of the subspaces. But we should walk before we run.) That counts as a separate task so I’ll attempt it in the next comment.
February 21, 2009 at 6:32 pm |
582. Dealing with complexity-1 sets.
Actually, I suddenly feel lazy, for the following reason. It seems as though the multidimensional Sperner proof generalizes rather straightforwardly, and because of that I temporarily can’t face checking the details (and thereby heaping vagueness on vagueness — it is probably soon going to be a good idea to do the Sperner argument carefully).
Here’s the rough thought though. In section 2 on this wiki page I showed that a set of the given form contains a combinatorial line. If the Sperner idea above works, then it should work here too: we just find a set such that for a dense set of points
such that for a dense set of points  in
in ![{}[3]^{[n]\setminus D}](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E%7B%5Bn%5D%5Csetminus+D%7D&bg=ffffff&fg=333333&s=0&c=20201002) we can fix
we can fix  , let
, let  be a wildcard set, and thereby obtain a combinatorial line. If so, then once again we should be in a position to say that we have a
be a wildcard set, and thereby obtain a combinatorial line. If so, then once again we should be in a position to say that we have a 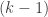 -dimensional combinatorial subspace in the set of all such
-dimensional combinatorial subspace in the set of all such  , and hence a
, and hence a  -dimensional combinatorial subspace in
-dimensional combinatorial subspace in  itself.
itself.
Let me take a break now, but end with the following summary of the proof strategy. As I’ve already said, I would greatly welcome any feedback, so that I can get an idea of which bits look the dodgiest …
1. As in 580 (but it was closely modelled on arguments that have been discussed already in earlier comments such as comment 413, part of comment 439, and comment 441) we prove that if contains no combinatorial lines then, locally at least, there is a dense complexity-1 set that is disjoint from
contains no combinatorial lines then, locally at least, there is a dense complexity-1 set that is disjoint from  . By averaging, we get a dense complexity-1 set inside which
. By averaging, we get a dense complexity-1 set inside which  has a density increment. Moreover, that complexity-1 set is of the simple form where it depends just on the set-systems to which the 1-set and 2-set belong, with the 3-set free to be whatever it likes.
has a density increment. Moreover, that complexity-1 set is of the simple form where it depends just on the set-systems to which the 1-set and 2-set belong, with the 3-set free to be whatever it likes.
2. Every dense complexity-1 set of this form contains a multidimensional subspace (as optimistically sketched in 581 and earlier in this comment). Almost certainly this can be lifted up to a proof that a dense complexity-1 set of this kind can be uniformly covered by multidimensional subspaces. And then we get a density increment on a subspace.
3. Therefore, by the usual density-increment strategy, we can keep passing to subspaces until the density reaches 1 (or 2/3 if we feel particularly clever), by which point we must have found a combinatorial line. Done!
If there is a problem with covering a special complexity-1 set uniformly with subspaces, then what we could do next is remind ourselves exactly how the Ajtai-Szemerédi proof of the corners theorem goes, since the averaging arguments they did there are likely to be helpful here.
February 21, 2009 at 7:10 pm |
583. Multidimensional Sperner.
Tim, isn’t it the same question that we considered in 135?
February 21, 2009 at 7:39 pm |
584. Multidimensional Sperner
Ah — I remembered only Gil’s comment 29. So the main point of what I’m saying is not so much that multidimensional Sperner is a new and exciting result — with a proof like that it couldn’t be — but that if is a special set of complexity 1, then any 12-cube in
is a special set of complexity 1, then any 12-cube in  (by which I mean that you fix some coordinates and some wildcard sets that take values 1 or 2) automatically extends to a combinatorial subspace. That’s quite a nice way of thinking about why special complexity-1 sets are good things. So at least part of the argument sketched in 582 seems to be correct. But there’s still the question of finding not just one combinatorial subspace but a uniform covering by combinatorial subspaces. I would be very surprised if that turned out to be a major problem. (In fact, I think I am beginning to see a possible strategy for a proof.)
(by which I mean that you fix some coordinates and some wildcard sets that take values 1 or 2) automatically extends to a combinatorial subspace. That’s quite a nice way of thinking about why special complexity-1 sets are good things. So at least part of the argument sketched in 582 seems to be correct. But there’s still the question of finding not just one combinatorial subspace but a uniform covering by combinatorial subspaces. I would be very surprised if that turned out to be a major problem. (In fact, I think I am beginning to see a possible strategy for a proof.)
February 21, 2009 at 7:52 pm |
Metacomment.
This thread is going to run out soon. I have recently learned from Luca Trevisan that WordPress now allows threading — that is, indented replies to existing comments. I think the current numbering system has served us surprisingly well, and if we introduced threading then we would lose the easily viewed chronological order of comments. But perhaps there would be compensating advantages. If you want to express a view in the following poll, then by all means do, though I suspect that we may have a split vote …
If I allowed threading, I would be able to choose how much nesting was allowed. One possibility would be to allow only one level, say, and to ask contributors to use the facility as little as possible (perhaps restricting it to short replies to existing comments that do not themselves invite further discussion). That is what I mean by option 3 below.
Oh. It seems that what I’ve just typed works only in a post and not in a comment. So I’d better do that.
February 21, 2009 at 9:10 pm |
585. Oops
My lemma in 578 might still be true, but I realise now that the proof I supplied is rubbish. Still thinking about it…
February 21, 2009 at 9:17 pm |
586. Oops
All I can say is that it convinced me at the time …
February 21, 2009 at 10:43 pm |
587. Dimensions
I’m trying to follow the uniformity/density increment arguments and I have the same feeling like with the planar square problem. (show that every dense subset of the integer grid contains four points of the form (x,y),(x+d,y),(x,y+d),(x+d,y+d) ) One can try to prove it directly, it is very difficult but probably possible, extending methods of Ajtai-Szemeredi or Shkredov. On the other hand, transferring the problem to dimension three from 2d, makes it more accessible. So, my question is the following: Is there a natural way to consider larger cubes, where a special configuration is (more) dense and a projection of it to the smaller cube, , is a combinatorial line?
, is a combinatorial line?
February 22, 2009 at 8:02 am |
588. Dimensions
Given that the planar square theorem implies the k=4 version of Szemeredi’s theorem, I would imagine that Fourier or graph regularity based methods are insufficient for the task.
February 22, 2009 at 11:02 am |
589. Dimensions
I agree with Terry, in the sense that I don’t think that deducing squares from 3D corners makes the problem fundamentally easier (just ask Michael Lacey …), and that either problem would have to involve quadratic methods or 3-uniform hypergraphs or something of equivalent difficulty.
Nevertheless, it does seem that the 3D corners problem is the natural way to solve the 2D squares problem, so one can still ask whether it is more natural to find a low-dimensional subspace with high diameter rather than a high-dimensional subspace with low diameter. Here I think there are two possible answers.
Suppose, for simplicity, that we are thinking about a high-dimensional version of Sperner’s theorem (but I think what I say generalizes easily to DHJ(k)). That is, we would like not just one wildcard set but several. For further simplicity let’s suppose that all we want is two wildcard sets. Then one proof is to use averaging arguments of the kind I was outlining in 581. This is fairly easy. Another proof is to establish DHJ(4) and observe that if you write the numbers 0 to 3 in binary then a combinatorial line in![{}[4]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B4%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) when written out gives you a 2-dimensional combinatorial subspace in
when written out gives you a 2-dimensional combinatorial subspace in ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) .
.
The obvious reaction to this is that the second proof is much harder. However, it also gives a much stronger result, because the two wildcard sets have the same cardinality. Furthermore, the stronger result can be seen to be more useful: if you look at unions of slices, then the first result gives you a quadruple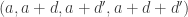 , which it is easy to get from Cauchy-Schwarz, whereas the second gives you an arithmetic progression
, which it is easy to get from Cauchy-Schwarz, whereas the second gives you an arithmetic progression 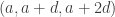 .
.
These simple observations raise obvious questions, which I think are close to the kinds of things Jozsef is wondering about. For example, it doesn’t seem to be possible to deduce Szemerédi’s theorem for progressions of length 4 from the existence of a 2D subspace with equal-sized wildcard sets, so does that mean that the true difficulty of that problem is roughly comparable to that of DHJ(3)? In particular, does it either imply or follow from DHJ(3)? I find this quite an interesting question (though questions often seem interesting when you haven’t yet thought about them).
February 22, 2009 at 2:42 pm |
590. Dimensions
Just realized that the question above was possibly slightly silly. The proof that you can get two wildcard sets of the same size actually gives that one consists of odd numbers and the other of even numbers. So if you look at the number of 1s in odd places plus twice the number of 1s in even places then you get an arithmetic progression of length 4. In other words, what you deduce from DHJ(4) implies Szemerédi’s theorem for progressions of length 4, exactly as it should. Strictly speaking, it is just about conceivable that DHJ(3) implies the weaker statement, but I doubt it somehow.
February 23, 2009 at 12:29 am |
591. Re Oops/#578.
Hmm, I too was pretty sold on #578, but then I seemed to founder when working out the exact details. My plan was to look at the noise stability of at some parameter
at some parameter  . If this quantity is even a smidgen greater than
. If this quantity is even a smidgen greater than ![\mathbb{E}[f]^2](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Bf%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) then one can do a density increment.
then one can do a density increment.
Otherwise, is extremely noise-sensitive at
is extremely noise-sensitive at  . (Or, “uniform at scale
. (Or, “uniform at scale  ” as Terry called it.) This strongly feels like it should imply lots of Sperner pairs. But I really ran into difficulties when trying to prove this via the Fourier methods of #476…#567….
” as Terry called it.) This strongly feels like it should imply lots of Sperner pairs. But I really ran into difficulties when trying to prove this via the Fourier methods of #476…#567….
February 23, 2009 at 12:30 am |
592. Re Oops/#578.
More precisely, it seemed hard to simultaneously control all of the quantities , even for
, even for  smallish. (I managed to do it for
smallish. (I managed to do it for 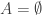 , at least 🙂 .)
, at least 🙂 .)
February 23, 2009 at 1:08 am |
593. DHJ (2.7):
I think I managed to remove all hint of ergodic reduction in a proof of DHJ (2.6)…of course if you look at the proof (Plain TeX code will be at the end of this msg.), it’s because the reduction (to sets, not to stationarity) is inside. Still, it’s pretty painless and the Ramsey theory used has been trimmed again, to just Ramsey’s theorem this time. Also it doesn’t use DHJ (2) as a lemma. I’ve actually called it DHJ (2.7) because it seems to be very slightly stronger than what Terry called (2.6).
More generally, I have been looking carefully at how to do a “straight translation” of the proof of DHJ (3) and am stuck. The issue arises already in the ergodic proof of the Szemeredi corners theorem. Basically, a set A of positive density in Z^2 is used to generate a measure preserving action of Z^2, together with a positive measure set B; recurrence properties of B imply existence of configurations for A. The issue arises because once the system is fixed, one can approximate B by a “relatively almost periodic” function f…f will have a kind of compactness property over a certain factor, meaning that given e>0 one can find an e-net (composed of functions) of finite cardinality M such that, on the fibers over the factor in question, the entire orbit of f will be e-close to some member of the net (on most fibers for most of the orbit). The point is that this number M is completely fixed by the set B, which is fixed by the set A, but the ergodic proof doesn’t give any way to bound M as a function of the density of A. For all the (usual) ergodic proof says to the contrary, this M might go to infinity for a sequence of A’s having measure bounded away from zero. This seems to be a not-very-desirable artefact of the ergodic proof, one that I don’t understand very well at present.
*********
\magnification=\magstep 1
\noindent {\bf DHJ (2.7):} For all $\delta>0$ there exists $n=n(\delta)$ such that if $A\subset [3]^n$ with $|A|> \delta 3^n$,
there exists $\alpha\in {\bf N}$, $|\alpha|0$. Let $m>{3\over
\delta_0}$ and choose by Ramsey’s theorem an $r$ such that for any 8-coloring of the 2-subsets of $[r]$, there is an $m$-subset
$B\subset [r]$ all of whose 2-subsets have the same color. Let $\delta=\delta_0-{\delta_0\over 4\cdot 3^r}$ and put $n_1=n(
\delta_0+{\delta_0\over 4\cdot 3^r})$. Finally put $n=r+n_1$ and suppose $A\subset [3]^n$ with $|A|>\delta 3^n$. For each $v\in [3]^r$,
let $E_v=\{w\in [3]^{n_1}:vw\in A\}$. If $|E_v|> (\delta_0+{\delta_0\over 4\cdot 3^r})3^{n_1}$ for some $v$ we are done; otherwise
$|E_v| > {\delta_0\over 3}$ for {\it every} $v\in [3]^r$.
\medskip\noindent Some notation: for $i\in [r]$ and $xy\in \{10,21,02\}$, let $v_i^{xy}\in [3]^r$ be the word $z_1z_2\cdots z_r$,
where $z_a=x$ if $0\leq a\leq i$ and $z_a=y$ otherwise. Color $\{1,j\}$, $0\leq i<j<r$, according to whether or not the sets
$E_{v_i^{xy}}\cap E_{v_j^{xy}}$ are empty or not, $xy\in \{10,21,02\}$. (This is an 8-coloring.) By choice of $r$ we can find
$0\leq k_1<k_2<\cdots <k_m<r$ such that $\big\{\{ k_i,k_j\}: 0\leq i<j<m \big\}$ is monochromatic for this coloring. By pigeonhole,
for, say, $xy=10$, there are $i<j$ such that $E_{v_{k_i}^{xy}}\cap E_{v_{k_j}^{xy}}\neq \emptyset$, hence non-empty for all $i,j$
by monochromicity and similarly for $xy=21,02$. Now for $xy=10,21,02$, pick $u_{xy}\in E_{v_{k_1}^{xy}}\cap E_{v_{k_2}^{xy}}$ and
put $q_{xy}=s_1s_2\cdots s_r$, where $s_i=x$, $0\leq i<k_1$, $s_i=3$, $k_1\leq i<k_2$, and $s_i=y$, $k_2\leq i<r$. Finally put
$w_{xy}=q_{xy}u_{xy}$. Then $w_{xy}(x)=v^{xy}_{k_2} u_{xy}$ and $w_{xy}(y)=v^{xy}_{k_1} u_{xy}$ are in $A$, $xy\in \{10,21,02\}$.
Hence $n=n(\delta)$, contradicting $\delta<\delta_0$.
\end
February 23, 2009 at 5:00 am |
594. Sperner calculations.
Re #567: by the way (if I remember my calculation correctly). In particular,
by the way (if I remember my calculation correctly). In particular, 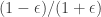 if
if 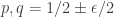 .
.
February 23, 2009 at 10:18 am |
595. Sperner calculations
Ryan, thanks for doing that calculation! At some point soon I think I’ll write up the whole thing fairly completely and put it on the wiki, which would make it easier to assess what it teaches us, if anything.
I’m also working on step 1 of 582, as I feel that I can get something rigorously proved here too. Again, anything I manage to do properly will go on the wiki. But for now I want to report on the failure of my first attempt to write it up, because it says something interesting (though in retrospect pretty obvious) about equal-slices measure.
I had previously come to the conclusion that a defect of equal-slices measure was that it didn’t restrict nicely to equal-slices measure. The mini-realization I have come to is to understand what does happen when you restrict it. Suppose a sequence x is generated Ryan-style: that is, you randomly choose p+q+r=1 and pick each coordinate independently to be 1,2,3 with probability p,q,r. And now suppose that you restrict to the set of all x that take certain values on a subset![E\subset[n].](https://s0.wp.com/latex.php?latex=E%5Csubset%5Bn%5D.&bg=ffffff&fg=333333&s=0&c=20201002) You then find yourself with a classic problem of Bayesian statistics: given the values of
You then find yourself with a classic problem of Bayesian statistics: given the values of  with
with 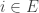 , what is the new probability distribution on the triples p+q+r=1? And qualitatively the answer is clear: if E is at all large, then with immensely high probability the triple (p,q,r) is approximately proportional to the triple (number of 1s in E, number of 2s in E, number of 3s in E).
, what is the new probability distribution on the triples p+q+r=1? And qualitatively the answer is clear: if E is at all large, then with immensely high probability the triple (p,q,r) is approximately proportional to the triple (number of 1s in E, number of 2s in E, number of 3s in E).
In other words, as soon as you restrict a few coordinates, you end up with something pretty close to a weighted uniform measure (by which I mean that each coordinate is chosen independently with fixed probabilities that are not necessarily equal to 1/3).
So it seems that equal-slices measure is useful for truly global arguments, but that it collapses to more obvious measures once one starts to restrict.
What about if we restrict to other sorts of subspaces? For example, suppose we partition [n] into s wildcard sets of size t. If you are given that a sequence is constant on some large wildcard set, then by far the most likely way that that could have come about is if one of p,q and r is approximately equal to 1. So the measure is concentrated around sequences that are approximately constant.
Going back to step 1 of 582, I still think it should be possible to do it with localization. If I manage, it will go straight up on the wiki and I will report on it here.
February 23, 2009 at 11:06 am |
Metacomment. This 500s thread has nearly run out. I’ve created a new post for an 800s thread, so new comments should go there unless they are quite clearly more appropriate here. But once we get to 599 that’s it!
February 23, 2009 at 6:06 pm |
596. Re Oops/Sperner.
I think I can correct Terry’s #578 and put it together with our Fourier-based calculations. The writeup is a bit long. I’m going to try to post it here in WordPress using Luca’s LaTeX converter. It’s my fault if this goes horribly awry; if it does, I’ll just post a link to the pdf….
The following alternate argument for Sperner still feels “wrong” to me (I will say why at the end), but I can’t see the “right” one yet so I’ll write this one up for now.
Let be chosen jointly from
be chosen jointly from 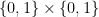 as follows (I use boldface to denote random variables): The bit
as follows (I use boldface to denote random variables): The bit  is
is  or
or  with probability
with probability 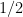 each. If
each. If  then
then  . If
. If  then
then  with probability
with probability 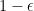 and
and  with probability
with probability  . Finally, let
. Finally, let  be chosen jointly from
be chosen jointly from 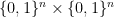 by using the single-bit distribution
by using the single-bit distribution  times independently. Note that
times independently. Note that  always. This distribution is precisely the one Tim uses, with
always. This distribution is precisely the one Tim uses, with 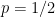 ,
, 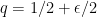 .
.
Let![{f : \{ 0,1 \}^n \rightarrow [-1,1]}](https://s0.wp.com/latex.php?latex=%7Bf+%3A+%5C%7B+0%2C1+%5C%7D%5En+%5Crightarrow+%5B-1%2C1%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) and let’s consider
and let’s consider ![{\mathop{\mathbb E}[f(\bx)f(\by)]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cbx%29f%28%5Cby%29%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . (We are eventually interested in
. (We are eventually interested in  ‘s with range
‘s with range 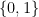 and mean
and mean  , but let’s leave it slightly more general for now.) As per Tim’s calculations,
, but let’s leave it slightly more general for now.) As per Tim’s calculations, ![\displaystyle \mathop{\mathbb E}[f(\bx)f(\by)] = \sum_{S \subseteq [n]} \hat{f}(S) \hat{f_\epsilon}(S) (1 - \epsilon')^{|S|},](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cbx%29f%28%5Cby%29%5D+%3D+%5Csum_%7BS+%5Csubseteq+%5Bn%5D%7D+%5Chat%7Bf%7D%28S%29+%5Chat%7Bf_%5Cepsilon%7D%28S%29+%281+-+%5Cepsilon%27%29%5E%7B%7CS%7C%7D%2C+&bg=ffffff&fg=000000&s=0&c=20201002)
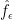 denotes Fourier coefficients with respect to the
denotes Fourier coefficients with respect to the 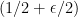 -biased measure and
-biased measure and  is defined by
is defined by  (AKA
(AKA  ). Separate out the
). Separate out the  term here and use Cauchy-Schwarz on the rest to conclude
term here and use Cauchy-Schwarz on the rest to conclude ![\displaystyle \left|\mathop{\mathbb E}[f(\bx)f(\by)] - \hat{f}(\emptyset)\hat{f_\eps}(\emptyset)\right| \leq \sqrt{\sum_{|S| \geq 1} \hat{f}(S)^2 (1 - \epsilon')^{|S|}}\sqrt{\sum_{|S| \geq 1} \hat{f_\epsilon}(S)^2 (1 - \epsilon')^{|S|}}. \ \ \ \ \ (1)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+++%5Cleft%7C%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cbx%29f%28%5Cby%29%5D+-+%5Chat%7Bf%7D%28%5Cemptyset%29%5Chat%7Bf_%5Ceps%7D%28%5Cemptyset%29%5Cright%7C+%5Cleq+%5Csqrt%7B%5Csum_%7B%7CS%7C+%5Cgeq+1%7D+%5Chat%7Bf%7D%28S%29%5E2+%281+-+%5Cepsilon%27%29%5E%7B%7CS%7C%7D%7D%5Csqrt%7B%5Csum_%7B%7CS%7C+%5Cgeq+1%7D+%5Chat%7Bf_%5Cepsilon%7D%28S%29%5E2+%281+-+%5Cepsilon%27%29%5E%7B%7CS%7C%7D%7D.+%5C+%5C+%5C+%5C+%5C+%281%29&bg=ffffff&fg=000000&s=0&c=20201002)
 to
to  . Write
. Write  and
and  for the density functions of
for the density functions of  ,
,  respectively. Then
respectively. Then ![\displaystyle \hat{f_\eps}(\emptyset) - \hat{f}(\emptyset) = \mathop{\mathbb E}[f(\by)] - \mathop{\mathbb E}[f(\bx)] = \mathop{\mathbb E}\left[\frac{\pi_\eps(\bx)}{\pi(\bx)}f(\bx)\right] - \mathop{\mathbb E}[f(\bx)] = \mathop{\mathbb E}\left[\left(\frac{\pi_\eps(\bx)}{\pi(\bx)}-1\right)f(\bx)\right].](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Chat%7Bf_%5Ceps%7D%28%5Cemptyset%29+-+%5Chat%7Bf%7D%28%5Cemptyset%29+%3D+%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cby%29%5D+-+%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cbx%29%5D+%3D+%5Cmathop%7B%5Cmathbb+E%7D%5Cleft%5B%5Cfrac%7B%5Cpi_%5Ceps%28%5Cbx%29%7D%7B%5Cpi%28%5Cbx%29%7Df%28%5Cbx%29%5Cright%5D+-+%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cbx%29%5D+%3D+%5Cmathop%7B%5Cmathbb+E%7D%5Cleft%5B%5Cleft%28%5Cfrac%7B%5Cpi_%5Ceps%28%5Cbx%29%7D%7B%5Cpi%28%5Cbx%29%7D-1%5Cright%29f%28%5Cbx%29%5Cright%5D.+&bg=ffffff&fg=000000&s=0&c=20201002)
![\displaystyle \sqrt{\mathop{\mathbb E}\left[\left(\frac{\pi_\eps(\bx)}{\pi(\bx)}-1\right)^2\right]}\cdot \|f\|_2,](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Csqrt%7B%5Cmathop%7B%5Cmathbb+E%7D%5Cleft%5B%5Cleft%28%5Cfrac%7B%5Cpi_%5Ceps%28%5Cbx%29%7D%7B%5Cpi%28%5Cbx%29%7D-1%5Cright%29%5E2%5Cright%5D%7D%5Ccdot+%5C%7Cf%5C%7C_2%2C+&bg=ffffff&fg=000000&s=0&c=20201002)
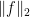 denotes
denotes ![{\sqrt{\mathop{\mathbb E}[f(\bx)^2]}}](https://s0.wp.com/latex.php?latex=%7B%5Csqrt%7B%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cbx%29%5E2%5D%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . One easily checks that
. One easily checks that ![\displaystyle \mathop{\mathbb E}\left[\left(\frac{\pi_\eps(\bx)}{\pi(\bx)}-1\right)^2\right] = \mathop{\mathbb E}\left[\frac{\pi_\eps(\bx)^2}{\pi(\bx)^2}\right] - 1, \ \ \ \ \ (2)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+++%5Cmathop%7B%5Cmathbb+E%7D%5Cleft%5B%5Cleft%28%5Cfrac%7B%5Cpi_%5Ceps%28%5Cbx%29%7D%7B%5Cpi%28%5Cbx%29%7D-1%5Cright%29%5E2%5Cright%5D+%3D+%5Cmathop%7B%5Cmathbb+E%7D%5Cleft%5B%5Cfrac%7B%5Cpi_%5Ceps%28%5Cbx%29%5E2%7D%7B%5Cpi%28%5Cbx%29%5E2%7D%5Cright%5D+-+1%2C+%5C+%5C+%5C+%5C+%5C+%282%29&bg=ffffff&fg=000000&s=0&c=20201002)
 and
and 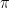 are product distributions the RHS of (2) is easy to compute. One can check explicitly that
are product distributions the RHS of (2) is easy to compute. One can check explicitly that ![\displaystyle \mathop{\mathbb E}[\pi_\eps(\bx_1)^2/\pi(\bx_1)^2] = 1+\eps^2](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cmathop%7B%5Cmathbb+E%7D%5B%5Cpi_%5Ceps%28%5Cbx_1%29%5E2%2F%5Cpi%28%5Cbx_1%29%5E2%5D+%3D+1%2B%5Ceps%5E2+&bg=ffffff&fg=000000&s=0&c=20201002)
 . Naturally we will be considering
. Naturally we will be considering  , and in this regime the quantity is bounded by, say,
, and in this regime the quantity is bounded by, say,  . Hence we have shown
. Hence we have shown 
 has range
has range 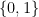 and mean
and mean 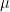 (AKA
(AKA 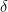 ) then
) then 
 , so let’s indeed assume
, so let’s indeed assume  and then we can also use
and then we can also use  .
.
where
Let’s compare
By Cauchy-Schwarz, the absolute value of this is upper-bounded by
where
and since
and therefore (2) is
and in particular if
This is not very interesting unless
We now these deductions in (1). Note that the second factor on the RHS in (1) is at most the square-root of![\displaystyle \sum_{S} \hat{f_\eps}(S)^2 = \mathop{\mathbb E}[f(\by)^2] = \mathop{\mathbb E}[f(\by)] = \hat{f_\eps}(\emptyset) \leq 2\mu \leq 4\mu.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Csum_%7BS%7D+%5Chat%7Bf_%5Ceps%7D%28S%29%5E2+%3D+%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cby%29%5E2%5D+%3D+%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cby%29%5D+%3D+%5Chat%7Bf_%5Ceps%7D%28%5Cemptyset%29+%5Cleq+2%5Cmu+%5Cleq+4%5Cmu.+&bg=ffffff&fg=000000&s=0&c=20201002)
![\displaystyle |\mathop{\mathbb E}[f(\bx)f(\by)] - \mu^2| \leq 2\mu^{3/2} \cdot \eps\sqrt{n} + 2\sqrt{\mu} \sqrt{\mathbb{S}_{1-\eps'}(f) - \mu^2}, \ \ \ \ \ (4)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+++%7C%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cbx%29f%28%5Cby%29%5D+-+%5Cmu%5E2%7C+%5Cleq+2%5Cmu%5E%7B3%2F2%7D+%5Ccdot+%5Ceps%5Csqrt%7Bn%7D+%2B+2%5Csqrt%7B%5Cmu%7D+%5Csqrt%7B%5Cmathbb%7BS%7D_%7B1-%5Ceps%27%7D%28f%29+-+%5Cmu%5E2%7D%2C+%5C+%5C+%5C+%5C+%5C+%284%29&bg=ffffff&fg=000000&s=0&c=20201002)

 at this point. Doing some arithmetic, it follows that if we can bound
at this point. Doing some arithmetic, it follows that if we can bound 
 is “uniform at scale
is “uniform at scale  ” as Terry might say) then (4) implies
” as Terry might say) then (4) implies ![\displaystyle \mathop{\mathbb E}[f(\bx)f(\by)] \geq \mu^2/2.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cbx%29f%28%5Cby%29%5D+%5Cgeq+%5Cmu%5E2%2F2.+&bg=ffffff&fg=000000&s=0&c=20201002)
![{\mathop{\mathbb P}[\bx = \by] < \mu^2/2}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cmathbb+P%7D%5B%5Cbx+%3D+%5Cby%5D+%3C+%5Cmu%5E2%2F2%7D&bg=ffffff&fg=000000&s=0&c=20201002) we’ve established existence of a Sperner pair (AKA non-degenerate combinatorial line). Since this probability is
we’ve established existence of a Sperner pair (AKA non-degenerate combinatorial line). Since this probability is  , we’re done assuming
, we’re done assuming 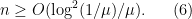
Also, using (3) for the LHS in (1) we conclude
where
Let’s simply fix
(AKA
So long as
Thus things come down to showing (5). Now in general, there is absolutely no reason why this should be true. The idea, though, is that if it’s not true then we can do a density increment. More precisely, it is very easy to show (one might credit this to an old result of Linial-Mansour-Nisan) that is precisely
is precisely ![{\mathop{\mathbb E}_{\bV}[\mathop{\mathbb E}[f|_\bV]^2]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cmathbb+E%7D_%7B%5CbV%7D%5B%5Cmathop%7B%5Cmathbb+E%7D%5Bf%7C_%5CbV%5D%5E2%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) , where
, where  is a “random restriction with wildcard probability
is a “random restriction with wildcard probability  ” (and the inner
” (and the inner ![{\mathop{\mathbb E}[\cdot]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cmathbb+E%7D%5B%5Ccdot%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is with respect to the uniform distribution). In other words,
is with respect to the uniform distribution). In other words,  is a combinatorial subspace formed by fixing each coordinate randomly with probability
is a combinatorial subspace formed by fixing each coordinate randomly with probability  and leaving it “free” with probability
and leaving it “free” with probability  . Hence if (5) fails then we have
. Hence if (5) fails then we have ![\displaystyle \mathop{\mathbb E}_{\bV}[\mathop{\mathbb E}[f|_\bV]^2] \geq \mu^2 + \mu^3/64.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cmathop%7B%5Cmathbb+E%7D_%7B%5CbV%7D%5B%5Cmathop%7B%5Cmathbb+E%7D%5Bf%7C_%5CbV%5D%5E2%5D+%5Cgeq+%5Cmu%5E2+%2B+%5Cmu%5E3%2F64.+&bg=ffffff&fg=000000&s=0&c=20201002)
 is bounded it follows that
is bounded it follows that ![{\mathop{\mathbb E}[f|_\bV]^2 \geq \mu^2 + \mu^3/128}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cmathbb+E%7D%5Bf%7C_%5CbV%5D%5E2+%5Cgeq+%5Cmu%5E2+%2B+%5Cmu%5E3%2F128%7D&bg=ffffff&fg=000000&s=0&c=20201002) with probability at least
with probability at least  over the choice of
over the choice of  . It’s also very unlikely that
. It’s also very unlikely that  will have fewer than, say,
will have fewer than, say,  wildcards; a large-deviation bound shows this probability is at most
wildcards; a large-deviation bound shows this probability is at most  . Since
. Since  , by choosing the constant in (6) suitably large we can make this large-deviation bound strictly less than
, by choosing the constant in (6) suitably large we can make this large-deviation bound strictly less than  . Thus we conclude that there is a positive probability of choosing some
. Thus we conclude that there is a positive probability of choosing some  which both has at least
which both has at least  free coordinates and also has
free coordinates and also has ![\displaystyle \mathop{\mathbb E}[f|_V]^2 \geq \mu^2 + \mu^3/128 \Rightarrow \mathop{\mathbb E}[f|_V] \geq \mu + \mu^2/500.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cmathop%7B%5Cmathbb+E%7D%5Bf%7C_V%5D%5E2+%5Cgeq+%5Cmu%5E2+%2B+%5Cmu%5E3%2F128+%5CRightarrow+%5Cmathop%7B%5Cmathbb+E%7D%5Bf%7C_V%5D+%5Cgeq+%5Cmu+%2B+%5Cmu%5E2%2F500.+&bg=ffffff&fg=000000&s=0&c=20201002)
In particular, since
I.e., we can achieve a density increment.
If I’m not mistaken, this kind of density increment (gaining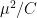 at the expense of going down to
at the expense of going down to  coordinates, with (6) as the base case) will ultimately show that we need the initial density to be at least
coordinates, with (6) as the base case) will ultimately show that we need the initial density to be at least  (up to
(up to  factors?) in order to win. Only a couple of exponentials off the truth 🙂
factors?) in order to win. Only a couple of exponentials off the truth 🙂
The incorrect quantitative aspect here isn’t quite the reason I feel this argument is “wrong”. Rather, I believe that no density increment should be necessary. (Actually, we probably know this is the case, by Sperner’s proof of Sperner.) In other words, I believe that![{\mathop{\mathbb E}[f(\bx)f(\by)] \geq \Omega(\mu^2)}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cmathbb+E%7D%5Bf%28%5Cbx%29f%28%5Cby%29%5D+%5Cgeq+%5COmega%28%5Cmu%5E2%29%7D&bg=ffffff&fg=000000&s=0&c=20201002) for any
for any  , assuming
, assuming  .
.
February 23, 2009 at 6:09 pm |
597. Wow, indeed that didn’t go so great. I should have studied the output more carefully before posting. Sorry about that. I’ll post the pdf in Tim’s new thread…
February 23, 2009 at 6:19 pm |
Metacomment (so as not to use precious numbers): Ryan, I’ve had a look at what you wrote and I’m afraid it’s beyond my competence to fix — it’s full of strange html-ish stuff that I don’t understand.
February 24, 2009 at 5:31 am | 596. Here is the corrected version. I should have read Luca’s documentation better… I think I can correct #578 and put it together with the Fourier-based calculations. The following alternate argument for Sperner still feels “wrong” to me (I will say why at the end), but I can’t see the “right” one yet so I’ll write this one up for now. Let be chosen jointly from as follows (I use boldface to denote random variables): The bit is or with probability each. If then . If then with probability and with probability . Finally, let be chosen jointly from by using the single-bit distribution times independently. Note that always. This distribution is precisely the one Tim uses, with , . Let and let’s consider . (We are eventually interested in ‘s with range and mean , but let’s leave it slightly more general for now.) As per Tim’s calculations, where denotes Fourier coefficients with respect to the -biased measure and is defined by (AKA ). Separate out the term here and use Cauchy-Schwarz on the rest to conclude Let’s compare to . Write and for the density functions of , respectively. Then By Cauchy-Schwarz, the absolute value of this is upper-bounded by where denotes . One easily checks that and since and are product distributions the RHS of (2) is easy to compute. One can check explicitly that and therefore (2) is . Naturally we will be considering , and in this regime the quantity is bounded by, say, . Hence we have shown and in particular if has range and mean (AKA ) then This is not very interesting unless , so let’s indeed assume and then we can also use . We now these deductions in (1). Note that the second factor on the RHS in (1) is at most the square-root of Also, using (3) for the LHS in (1) we conclude where Let’s simply fix at this point. Doing some arithmetic, it follows that if we can bound (AKA is “uniform at scale ” as Terry might say) then (4) implies So long as we’ve established existence of a Sperner pair (AKA non-degenerate combinatorial line). Since this probability is , we’re done assuming Thus things come down to showing (5). Now in general, there is absolutely no reason why this should be true. The idea, though, is that if it’s not true then we can do a density increment. More precisely, it is very easy to show (one might credit this to an old result of Linial-Mansour-Nisan) that is precisely , where is a “random restriction with wildcard probability ” (and the inner is with respect to the uniform distribution). In other words, is a combinatorial subspace formed by fixing each coordinate randomly with probability and leaving it “free” with probability . Hence if (5) fails then we have In particular, since is bounded it follows that with probability at least over the choice of . It’s also very unlikely that will have fewer than, say, wildcards; a large-deviation bound shows this probability is at most . Since , by choosing the constant in (6) suitably large we can make this large-deviation bound strictly less than . Thus we conclude that there is a positive probability of choosing some which both has at least free coordinates and also has I.e., we can achieve a density increment. If I’m not mistaken, this kind of density increment (gaining at the expense of going down to coordinates, with (6) as the base case) will ultimately show that we need the initial density to be at least (up to factors?) in order to win. Only a couple of exponentials off the truth 🙂 The incorrect quantitative aspect here isn’t quite the reason I feel this argument is “wrong”. Rather, I believe that no density increment should be necessary. (Actually, we probably know this is the case, by Sperner’s proof of Sperner.) In other words, I believe that for any , assuming .
July 12, 2010 at 4:46 pm |
[…] one also reads that that Moser k=6 implies DHJ k=3. Now seeing as combinatorial line free sets are invariant under permutations of the alphabet [k], […]
April 10, 2011 at 8:27 am |
[…] is a particularly silly problem that I suggested at some point along the discussions: How large can a family of subsets of an -element set be […]