Here then is the project that I hope it might be possible to carry out by means of a large collaboration in which no single person has to work all that hard (except perhaps when it comes to writing up). Let me begin by repeating a number of qualifications, just so that it is clear what the aim is.
1. It is not the case that the aim of the project is to find a combinatorial proof of the density Hales-Jewett theorem when . I would love it if that was the result, but the actual aim is more modest: it is either to prove that a certain approach to that theorem (which I shall soon explain) works, or to give a very convincing argument that that approach cannot work. (I shall have a few remarks later about what such a convincing argument might conceivably look like.)
2. I think that the chances of success even for this more modest aim are substantially less than 100%. So let me be less fussy still. I will regard the experiment as a success if it leads to anything that could count as genuine progress towards an understanding of the problem. However, that success has a quantitative aspect to it: what I am really interested in is progress that results from multiple collaboration. If what actually happens is that several people make intelligent remarks, but without building on each other’s remarks, then what will have been gained will still be worthwhile but it will be less interesting from the point of view of this experiment.
3. I’ve thought of one more ground rule, and also a general guideline that clarifies a couple of the existing rules. The extra rule is that there needs to be some possibility for the experiment to be declared to have finished. What I suggest here is that if a consensus emerges that no further progress is likely, I (or perhaps somebody else) will write a summary of the main conclusions that have been reached, and it will then become public property in the way that a conventional mathematics preprint would be. That is, others would be welcome to make use of it in their own publications if they wanted to. Probably the summary would be posted on the ArXiV (after people had had a chance to suggest changes) but not conventionally published. The guideline, which is designed to stop people going away and doing a lot of work in private — the whole point is that we should all display our thought processes — is that you should not write anything that requires you to go away and do some calculations on a piece of paper. As I said in the other guidelines, if all goes well there will eventually be a place for detailed working out of ideas, but people should do that only after first establishing that that would be welcomed.
In order to encourage the style I’m hoping for, I shall practise what I preach, in a sense anyway, by giving my initial thoughts on the problem in small chunks. That is, I’ll write them as though they were a lot of comments that could in theory have been made by several different people instead of just one. I’ll number them with letters of the alphabet (so that they don’t get confused with the numbered comments on this post).
A. Might it be possible to prove the density Hales-Jewett theorem for by imitating the triangle-removal proof that dense subsets of
contain corners?
B. If one were going to do that, what would the natural analogue of the tripartite graph associated with a dense subset be? To put that question more precisely, if we’ve got a dense subset of
, then how might we define a tripartite graph
in such a way that triangles in
correspond to (possibly degenerate) combinatorial lines?
C. It’s perhaps worth pointing out that there is a natural definition of a degenerate combinatorial line: it’s one where the set of coordinates that vary from 1 to 3 is empty.
D. If we just look at the vertex sets and
in the case of subsets
, we have a very simple definition for an edge: it’s a pair
that belongs to
.
E. Does split up nicely as a Cartesian product?
F. Well, you can write it as , but that doesn’t help much.
G. Why doesn’t it help?
H. Because if we represent a typical point as with
and
, then a Hales-Jewett line is not a triple of the form
,
,
. That’s partly because we can’t even make sense of adding
, but more fundamentally because even if we could invent a useful definition of addition in this context, we still wouldn’t get a Hales-Jewett line.
I. It was clear in advance that that was not going to work, because the splitting up as a Cartesian product was completely non-canonical.
J. By the way, there’s a nice way of deducing the corners result from density Hales-Jewett. Let me quickly explain it, omitting a few details. Suppose we take a set with the special property that whether or not a sequence
belongs to
depends only on the numbers of
s,
s and
s in
. That is, let
be the set of all triples
of non-negative integers such that
, let
be some subset of
, and let
be the set of sequences
such that
, where
stands for the number of
s in
. Now suppose you have a combinatorial line
. If
is the number of variable coordinates in
, then
must contain a triple of points of the form
(where
,
and
are the numbers of
s,
s and
s amongst the fixed coordinates of
).
Now is a large triangular subset of a triangular grid, and one can (if one really feels like it) shear it so that it becomes a right-angled triangle instead of an isosceles triangle. In this way it is not hard to show that the assertion that every dense subset of
contains the vertices of an equilateral triangle of the form
,
,
is equivalent to the corners result.
Unfortunately it’s not the case that dense subsets of correspond to dense subsets of
(because almost every point in
has similar numbers of
s,
s and
s) but there are dodges for getting round that.
K. That’s very helpful, because we almost certainly want whatever definition we come up with for the graph to give rise to the definition that we used for
when the subset of
is of the special kind that depends only on the numbers of coordinates with the three possible values.
L. All right then. That tells us that for subsets of that just depend on numbers of different types of coordinates, we want edges of the
graph to correspond in some sensible way to points in
that have a particular number of
s and a particular number of
s.
M. That suggests that in the general case we want some data about the s and
s in
to determine
, just as the number of
s and
s determines the numbers of all three types of coordinates. And of course this is trivial: instead of looking at the numbers of the three types, look at the sets where they occur.
N. Indeed, there is an obvious tripartite graph we can define. Let its vertex sets, which I’ll call ,
and
, all be copies of the power set of
: i.e., in each vertex set the vertices are subsets of
. Given two disjoint sets
and
, there is a unique point
that takes the value
in
, the value
in
, and the value
everywhere else. Join
to
if that point
belongs to the given subset
. And do the obviously corresponding things for the
and
graphs.
O. Does that work? That is, if we have a triangle in that graph, does it correspond to a combinatorial line?
P. Yes. Here’s a quick proof. Suppose we have ,
and
, and suppose that they form a triangle in the graph. By the way we defined the edges, the sets
,
and
are disjoint. For
let’s write
for the set of
such that
. Then in the set
we can find a point
such that
and
, and also a point
in
with
and
, and finally a point
in
with
and
. Now let
. Since for every point
we have
, we find that
,
and
. In other words, the three sequences
,
and
, which all lie in
, all take values
on
,
on
and
on
, and
is
everywhere on
,
is
everywhere on
and
is
everywhere on
. This gives us a combinatorial line except in the degenerate case
.
Q. Wow. That means we’re done by triangle removal doesn’t it?
R. Unfortunately it doesn’t. The problem is that that tripartite graph is not dense. In fact, it’s not even close to dense. To see why not, just pick a random pair of subsets and
. They cannot be joined in the
graph unless they are disjoint, and the probability of that happening is absolutely tiny.
S. That sounds a bit bad, but aren’t there sparse versions of Szemerédi’s regularity lemma?
T. I’m not sure it’s all that likely that there’s a version that applies when the density is exponentially small.
U. That’s a misleading way of putting it when the graph itself is exponentially large. If we let , so that there are
vertices in each of the three vertex sets, then the density of the graph is going to be of the form
for some constant
. But that’s still pretty sparse, it has to be said.
V. Here’s another problem. The existing sparse regularity lemmas tend to assume that you’re sitting inside a highly random sparse graph, but are dense relative to that graph. In our case, the natural graph that we’re sitting inside is the one where you join two sets if and only if they are disjoint and ignore whether they define a sequence that belongs to
. It’s possible that the graph defined above will turn out to be dense relative to this graph. However,
is not by any stretch of the imagination random, or quasirandom. For example, if you look at the
part, you can define
to be the subset of
where all sets have size at most
, and the same for
, and it’s not hard to check that the density of the part of the graph from
to
is substantially greater. (Basically, conditioning on sets being a bit smaller than average makes them quite a lot more likely to be disjoint.)
W. Yes, but at least the graph is very concretely defined. Perhaps one could do some kind of regularity argument relative to
that exploited the fact that it has a nice simple definition.
X. Here’s a small and slightly encouraging observation. What does a typical edge look like? Well, there’s a one-to-one correspondence between
edges and sequences in
. Since a typical sequence in
has roughly equal numbers of
s,
s and
s, a typical edge in the
graph consists of two disjoint sets of size about
.
Y. Unfortunately it’s still very sparse if we somehow weight our sets so that almost all of them have size about , since two sets of size
have a tiny probability of being disjoint.
Z. Aren’t there tricks we could do to find dense bits of the graph ? For example, we know that if
and
are random small sets (of size
, say) then with high probability they are disjoint. Might there be some way of restricting to “the small part of
“?
AA. How could one do that when almost all sequences have roughly equal numbers of s,
s and
s? The dense set
might consist just of well-balanced sequences.
BB. It’s not as impossible as it sounds, because we can use an averaging trick. Suppose we want to restrict ,
and
to small sets. What we can do is this. First we randomly choose a very small subset
of
. Then for every
we randomly choose an element of
. Finally, we do everything we want inside
. That is, we define a graph by joining two subsets
and
of
if they are disjoint, and define associated sequences by letting
and
determine the values inside
and the random choice of values outside
give us the rest. This gives us a structure of the kind we are talking about, and the average density of points in
in this structure will be close to the density of
if
is small enough, because random sequences that are unbalanced inside a random small set
will not be especially unbalanced globally.
CC. That’s an interesting thought, but I think it leads to a problem. Suppose our graph consists of pairs
of disjoint small subsets of
, and similarly for our
graph and our
graph. Where are the degenerate triangles? You can’t have a sequence with very few
s in
, very few
s in
and very few
s in
all at the same time.
DD. That’s a serious objection, but I still think the averaging trick could be quite useful for this problem.
EE. Here’s a different idea. The big problem is not so much that is sparse as that it is not quasirandom. But perhaps we could make it quasirandom by putting weights on the edges (and perhaps if necessary the vertices as well, since the averaging trick above will enable us to get sets of positive density even with funny vertex weights). The basic idea would be to penalize edges that joined small sets together, because somehow those sets were “cheating” by being small. Is there some natural set of weights that one can just write down?
[The history of this idea is that earlier this afternoon I had got up to Y when I had to go and fetch my daughter from school. While walking there I couldn’t help thinking about the problem and this idea, which I have not explored, occurred to me. So even the effort of writing down my thoughts has been quite stimulating. Because I haven’t yet thought about this idea properly, I’m still in that delicious state of thinking it might be the key to the whole problem. But I’ve also been in this game long enough to know that the chances of that are very small. It’s tempting to investigate it, but I’m not going to as this is also an ideal opportunity to throw out an idea and wait for somebody else to destroy it (or, just perhaps, to develop it) instead.]
FF. A natural way to find such weights would be to start by trying to make every vertex have constant (weighted) degree.
GG. It’s easy to see that you can’t make quasirandom by weighting the edges. For example, suppose you let
and
both be the set of all subsets of
that contain
. These two sets have density
and yet there is no edge of
between them.
[The history of this idea is that although I resolved not to think about the idea put forward in EE., I was on a car journey and I just couldn’t help it. That goes for the next couple of responses to it too, which I could help even less because at that point I was starting to get worried that the whole thing was indeed hopeless.]
HH. That sounds pretty bad.
II. Is it really as bad as all that? I can see that it’s a problem if you have very dense parts of the graph, because then you don’t have a global upper bound for the density of subgraphs when you are trying to prove a regularity lemma. But if you have parts of the graph that are very sparse, or even entirely free of edges, it’s not so obviously a problem because there could still be an upper bound. In other words, perhaps it’s enough for to be “upper quasirandom” rather than quasirandom.
JJ. Another idea is that you just try to do everything relative to . That is, you define the density of an induced subgraph of
to be the number of edges in that subgraph divided by the number of edges in the corresponding induced subgraph of
. Could that work?
KK. Going back to vertex weights, here are two remarks. First, the averaging trick shows that for more or less any weighting on the vertices, if you can prove the theorem with that weighting (which affects which sets count as dense) then you can prove the theorem with the uniform weighting. I could write a formal lemma to this effect if anybody wanted, but for now I think the informal statement is enough.
The second remark is that a natural weighting on sets is to make the weight of a set equal to
. Then the size of a typical set is
, and the probability distribution on the collection of all subsets of
is the same as the probability distribution of the set of places where a random sequence in
takes any given value.
LL. In response to II, I don’t think it’s possible to make even upper quasirandom by introducing edge weights. The idea to do so was roughly that one should penalize edges that join small sets because those were more likely to be disjoint. But making sets small is not the only way to make them more likely to be disjoint. For example, you could make
consist of all sets that are slightly biased towards the first half of
(meaning that their intersection with the first
integers is slightly bigger than their intersection with the second
integers) and
could consist of all sets that are slightly biased towards the second half of
. Of course, one could legislate against that particular example, but the same trick can be played for any partition of
into two equal-sized subsets. It seems to be impossible to legislate against this, since, for trivial reasons, every set will be biased with respect to some partitions.
[The history of that idea was that I was sitting in the car waiting for a bus to arrive that had my daughter in it. Once again I just couldn’t help my mind wandering in a Hales-Jewetty direction.]
How might one completely kill off the above approach?
The tripartite graph that we form out of has few triangles in the following sense: every edge
in the
graph is contained in just one triangle (the other vertex of which is
). If one is to prove the theorem by means of an adaptation of the triangle-removal lemma, one would want the following graph-theoretic statement to be true: let
be any subgraph of
such that each edge is contained in at most one triangle. Then it is possible to remove
edges from
to make it triangle free. A counterexample to this more general statement would almost certainly make the approach hopeless. (I say “almost certainly” because one might just be able to use some extra structural property of the graph derived from
. But that would change the nature of the approach quite a bit.)
Perhaps there could be convincing arguments that described the most general possible iterative approach to proving regularity lemmas and then proved that no iterative approach could give a regularity lemma that had any chance of helping with this problem. The seeming impossibility of making quasirandom would undoubtedly be a part of such an argument.
That’s all I have to suggest at the moment.
February 1, 2009 at 8:47 pm |
[…] collaborative mathematical project” over at his blog. The project is entitled “A combinatorial approach to density Hales-Jewett“, and the aim is to see if progress can be made on this problem by many small contributions […]
February 1, 2009 at 8:59 pm |
1. A quick question. Furstenberg and Katznelson used the Carlson-Simpson theorem in their proof. Does anyone know that proof well enough to know whether the Carlson-Simpson theorem might play a role here? If so, I could add it to the background-knowledge post. (But I’m sort of hoping it won’t be needed.)
February 1, 2009 at 9:08 pm |
2. In this note I will try to argue that we should consider a variant of the original problem first. If the removal technique doesn’t work here, then it won’t work in the more difficult setting. If it works, then we have a nice result! Consider the Cartesian product of an IP_d set. (An IP_d set is generated by d numbers by taking all the 2^d possible sums. So, if the n numbers are independent then the size of the IP_d set is 2^d. In the following statements we will suppose that our IP_d sets have size 2^n.)
Prove that for any c>0 there is a d, such that any c-dense subset of the Cartesian product of an IP_d set (it is a two dimensional pointset) has a corner.
The statement is true. One can even prove that the dense subset of a Cartesian product contains a square, by using the density HJ for k=4. (I will sketch the simple proof later) What is promising here is that one can build a not-very-large tripartite graph where we can try to prove a removal lemma. The vertex sets are the vertical, horizontal, and slope -1 lines, having intersection with the Cartesian product. Two vertices are connected by an edge if the corresponding lines meet in a point of our c-dense subset. Every point defines a triangle, and if you can find another, non-degenerate, triangle then we are done. This graph is still sparse, but maybe it is well-structured for a removal lemma.
Finally, let me prove that there is square if d is large enough compare to c. Every point of the Cartesian product has two coordinates, a 0,1 sequence of length d. It has a one to one mapping to [4]^d; Given a point ((x_1,…,x_d),(y_1,…,y_d)) where x_i,y_j are 0 or 1, it maps to (z_1,…,z_d), where z_i=0 if x_i=y_i=0, z_i=1 if x_i=1 and y_i=0, z_i=2 if x_i=0 and y_i=1, and finally z_i=3 if x_i=y_i=1. Any combinatorial line in [4]^d defines a square in the Cartesian product, so the density HJ implies the statement.
(I should learn how to use Latex in blogs…)
February 1, 2009 at 9:23 pm |
3. I find it reassuring the first thing I thought of when I read comment D was what turned out to be comment N.
Would it help to have a graph where each node was a set consisting of a combinatorial line, and the edges are the sets that share a sequence in common? That is, {(1,2,3,3), (2,2,3,3), (3,2,3,3)} would link to {(1,2,3,3), (1,2,3,2), (1,2,3,1)}.
I really do wonder if there’s a more direct approach to the problem, simply working out for![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) what the minimal number of nodes one can remove before no combinatorial lines remain and then applying induction. Just fiddling with actual examples by hand a greedy approach works well. I’m sure this is horribly naive given the past solution had to apply ergodic theory.
what the minimal number of nodes one can remove before no combinatorial lines remain and then applying induction. Just fiddling with actual examples by hand a greedy approach works well. I’m sure this is horribly naive given the past solution had to apply ergodic theory.
February 1, 2009 at 9:26 pm |
4. As Gil pointed out in his post on this project, the k=2 case of density Hales-Jewett is Sperner’s theorem,
http://en.wikipedia.org/wiki/Sperner_family
Now, of course, this theorem already has a combinatorial proof, but this proof has a rather different flavour than the triangle removal lemma (or its k=2 counterpart, which is the trivial statement that if a subset of a set V of vertices is small, then it can be removed entirely by removing a small number of vertices.) But perhaps a subproblem would be to find an alternate combinatorial proof of Sperner’s theorem.
As pointed out to me by my student, Le Thai Hoang, another difference between DHJ and, say, the corners problem, is that one does not expect a positive density of all combinatorial lines to lie in the set. For instance, in the k=2 case, and identifying![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with the set of subsets of {1,2,…,n}, Hoang observed that the set of subsets of {1,…,n} of cardinality
with the set of subsets of {1,2,…,n}, Hoang observed that the set of subsets of {1,…,n} of cardinality  has positive density, but only about
has positive density, but only about  of the
of the  combinatorial lines here actually lie in the set. This seems to fit well with your observations that some weighting of the vertices etc. is needed.
combinatorial lines here actually lie in the set. This seems to fit well with your observations that some weighting of the vertices etc. is needed.
At the ergodic theory level, there is also a distinction between the ergodic theory proofs of, say, the corners theorem, and of density Hales-Jewett, which may be an indication that something different happens at the combinatorial level too. Namely, in the ergodic proof of corners (or Roth, or Szemeredi, etc.) one has a single dynamical system (with the action of a single group G), and one works with that system (and its factors) throughout the proof. But for DHJ, one has a system of measurable sets indexed by words, and one repeatedly refines the set of words to much smaller subsets in order to obtain good “stationarity” properties. (My student, Tim Austin, could explain this much better than I could.) It is only once one has all this stationarity that the proof can really begin in earnest. This is also consistent with proofs of the colouring Hales-Jewett theorem, which also massively restrict the space of lines being considered, and with the above observation that we do not expect a positive density of the full space of lines to be contained in the set. So perhaps some preliminary “regularisation” of the problem is needed before doing anything triangle-removal-like.
February 1, 2009 at 9:30 pm |
5. Incidentally, I only learned in the process of writing up my own post on this problem that Furstenberg-Katzelson have _two_ papers on Density Hales-Jewett: the “big one”,
http://www.ams.org/mathscinet-getitem?mr=1191743
that does the full k case, but also an earlier paper,
http://www.ams.org/mathscinet-getitem?mr=1001397
that just does the k=3 case. I’ve only looked at the former.
An unrelated thing: there is an annoying wordpress latex bug concerning latex that begins with a bracket [, which may cause some difficulty in this context. One can fix it by prefacing any latex string that begins with a bracket with some filler (I use {}).
February 1, 2009 at 10:16 pm |
6. Terry’s description of the difference between the `ergodic theoretic’ approaches to the corners theorem and DHJ is well-put: at no point does an action of an easy-to-work-with _group_ of measure-preserving transformations emerge during the DHJ proof. Furstenberg and Katznelson introduce an enormous family of measure-preserving transformations indexed by all finite-length words in an alphabet of size k (and having some algebraic structure in terms of that family of words) in order to encode their notion of stationarity, but they neither use nor prove anything about the group generated by these transformations. Rather, they identify within their collection a great many `IP systems’ of transformations, a rather weaker sort of algebraic structure, and exploit that. In order to reach this point, they first obtain a kind of `stationarity’ for a family of positive-measure sets indexed by these words before introducing the transformations, and then expressing that stationarity in terms of these transformations in effect locks that notion of stationarity in place, and also gives a way to transport various mult-correlations between functions around on the underlying probability space.
In this connexion, it’s in obtaining this notion of stationarity that Furstenberg and Katznelson first use the Carlson-Simpson Theorem, and they then use it repeatedly throughout the paper in order to recover some similar kind of symmetry among a collection of objects indexed by the finite-length words. At this point, I can’t see where the same need would arise in the approach to DHJ under discussion here.
February 2, 2009 at 1:25 am |
7. With reference to Jozsef’s comment, if we suppose that the numbers used to generate the set are indeed independent, then it’s natural to label a typical point of the Cartesian product as
numbers used to generate the set are indeed independent, then it’s natural to label a typical point of the Cartesian product as  , where each of
, where each of  and
and  is a
is a 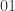 -sequence of length
-sequence of length  . Then a corner is a triple of the form
. Then a corner is a triple of the form  ,
,  ,
,  , where
, where  is a
is a  -valued sequence of length
-valued sequence of length  with the property that both
with the property that both 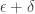 and
and 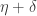 are
are 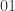 -sequences. So the question is whether corners exist in every dense subset of the original Cartesian product.
-sequences. So the question is whether corners exist in every dense subset of the original Cartesian product.
This is simpler than the density Hales-Jewett problem in at least one respect: it involves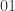 -sequences rather than
-sequences rather than  -sequences. But that simplicity may be slightly misleading because we are looking for corners in the Cartesian product. A possible disadvantage is that in this formulation we lose the symmetry of the corners: the horizontal and vertical lines will intersect this set in a different way from how the lines of slope -1 do.
-sequences. But that simplicity may be slightly misleading because we are looking for corners in the Cartesian product. A possible disadvantage is that in this formulation we lose the symmetry of the corners: the horizontal and vertical lines will intersect this set in a different way from how the lines of slope -1 do.
I feel that this is a promising avenue to explore, but I would also like a little more justification of the suggestion that this variant is likely to be simpler.
February 2, 2009 at 1:31 am |
8. The following questions are perhaps somewhat tangential to the main project, but have the advantage of requiring less combinatorial expertise than the main question, and so might possibly take better advantage of this format.
Given any n, let be the largest subset of
be the largest subset of ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) that does not contain a combinatorial line. Thus for instance
that does not contain a combinatorial line. Thus for instance 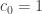 ,
, 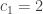 ,
,  (for the latter, consider deleting the antidiagonal
(for the latter, consider deleting the antidiagonal  from
from ![{}[3]^2](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) ). The k=3 density Hales-Jewett theorem is the statement that
). The k=3 density Hales-Jewett theorem is the statement that 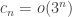 as
as 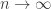 .
.
The first question, which seems very amenable to this medium, is to compute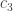 exactly, and to get good upper and lower bounds on
exactly, and to get good upper and lower bounds on 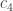 (it seems unlikely that
(it seems unlikely that 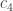 will be easy to compute on the nose). This of course does not say too much about the asymptotic question, but one might at least try one’s luck with the OEIS once one has enough data (note that this would have worked with the k=2 theory).
will be easy to compute on the nose). This of course does not say too much about the asymptotic question, but one might at least try one’s luck with the OEIS once one has enough data (note that this would have worked with the k=2 theory).
The other question is to get as good a lower bound as one can for . Of course, the trivial example
. Of course, the trivial example ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) gives the lower bound
gives the lower bound  , but one can clearly do better than this. Writing the Behrend example in base 3 gives something like
, but one can clearly do better than this. Writing the Behrend example in base 3 gives something like  . But presumably one can do better still.
. But presumably one can do better still.
February 2, 2009 at 1:36 am |
9. Terry’s comment about Le Thai Hoang’s observation seems to me to be an important one, so let me spell out why, even though it’s basically there in what Terry says. If you follow the triangle-removal proof of the corners result, you find that you can prove something stronger: in a set of density you don’t just get one corner, but you get
you don’t just get one corner, but you get  corners. (The proof is that if there are very few corners then there are very few triangles in the associated tripartite graph, and then you can apply triangle removal just as before to get a contradiction.) If one is going to find an analogous proof here, it is essential that it should not try to prove a lemma that has false consequences. In our case, we must be careful that we don’t accidentally try to develop an approach that would also imply that a positive density of all possible combinatorial lines lie in the set.
corners. (The proof is that if there are very few corners then there are very few triangles in the associated tripartite graph, and then you can apply triangle removal just as before to get a contradiction.) If one is going to find an analogous proof here, it is essential that it should not try to prove a lemma that has false consequences. In our case, we must be careful that we don’t accidentally try to develop an approach that would also imply that a positive density of all possible combinatorial lines lie in the set.
I haven’t checked, but I think that weighting the vertices as suggested in KK avoids this pitfall, because now the analogous set to the one used by Le Thai Hoang is concentrated around sets of size . Probably this is exactly what Terry meant at the end of his second paragraph.
. Probably this is exactly what Terry meant at the end of his second paragraph.
February 2, 2009 at 1:45 am |
10. In response to Terry and Tim’s comments about regularization and the ergodic-theory proof, my feeling is that we should bear in mind that something like this could well turn out to be necessary (on the grounds that genuine difficulties for one approach often have counterparts in other approaches), but should perhaps not try to guess in advance what form any regularization might take. (In case anyone’s wondering what I mean by “regularization”, a rough description would be that you have a subset of a structure
of a structure  and you find a subset
and you find a subset  of
of  of a similar form, such that
of a similar form, such that  is an easier subset of
is an easier subset of  to handle than
to handle than  is of
is of  .) Instead, we should press ahead, try to prove some kind of triangle-removal statement, find that it fails for some reason, try to work out a nice property of
.) Instead, we should press ahead, try to prove some kind of triangle-removal statement, find that it fails for some reason, try to work out a nice property of  that would get round the problem, prove that one can regularize to obtain that property, etc. etc. But this process will still involve guesswork, and people who know the ergodic-theoretic proof are likely to be able to make better guesses.
that would get round the problem, prove that one can regularize to obtain that property, etc. etc. But this process will still involve guesswork, and people who know the ergodic-theoretic proof are likely to be able to make better guesses.
February 2, 2009 at 2:17 am |
11. This of course does not say too much about the asymptotic question, but one might at least try one’s luck with the OEIS once one has enough data (note that this would have worked with the k=2 theory).
Terry, has anyone tried to collected said data for k=3?
February 2, 2009 at 2:27 am |
12. Dear Jason, I don’t know, but I just emailed someone who I think would. My guess, though, is that density Hales-Jewett is probably not as well known as its cousins such as van der Waerden’s theorem to have much data already worked out. If so, then presumably we can start collecting data here.
For instance, it is not hard to see that and that
and that  for any n, m, so this already gives the bounds
for any n, m, so this already gives the bounds  for
for 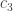 . Presumably one can do better.
. Presumably one can do better.
February 2, 2009 at 4:08 am |
13. Perhaps in order to understand the issue coming from Hoang’s observation a bit better, one can pose the following subproblem: what is the natural analogue of Varnavides theorem for DHJ? Varnavides used Roth’s theorem as a black box to show that any subset of![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  contained
contained 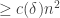 3-term arithmetic progressions when n was large; a similar argument using the Ajtai-Szemeredi theorem as a black box also shows that any subset of
3-term arithmetic progressions when n was large; a similar argument using the Ajtai-Szemeredi theorem as a black box also shows that any subset of ![{}[n]^2](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  contains
contains 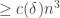 corners. So, using DHJ as a black box, what is the natural implication as to how “numerous” combinatorial lines are in a dense set? It seems that direct cardinality of such lines may not be the best measure of being “numerous”, but there should presumably still be some Varnavides-like theorem out there.
corners. So, using DHJ as a black box, what is the natural implication as to how “numerous” combinatorial lines are in a dense set? It seems that direct cardinality of such lines may not be the best measure of being “numerous”, but there should presumably still be some Varnavides-like theorem out there.
February 2, 2009 at 5:26 am |
14. Regarding Terry’s last comment about a Varnavides-like theorem, I’m a bit skeptical. Even for the k=2 case (Sperner’s thm) if we take points of the d dimensional cube where the difference between the 0-s and 1-s is at most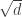 then we have a positive fraction of the elements and there are less than
then we have a positive fraction of the elements and there are less than  combinatorial lines. Probably this should be the right magnitude for k=2 as a Varvadines-like result and it shouldn’t be difficult to prove. (But I don’t have the proof …)
combinatorial lines. Probably this should be the right magnitude for k=2 as a Varvadines-like result and it shouldn’t be difficult to prove. (But I don’t have the proof …)
February 2, 2009 at 7:32 am |
15. Regarding lower bounds, fixing the numbers of ‘1’ ‘2’ and ‘3’ coordinates or even just fixing the number of ‘1’ coordinates gives better lower bounds, right? (Just like for Sperner’s theorem.)
February 2, 2009 at 8:00 am |
16. Hmm, Gil, you’re right; so we get a bound of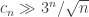 asymptotically.
asymptotically.
Dear Jozsef, yes, we will have to normalise things appropriately to get a Varnavides type theorem. For the k=3 problem, for instance, one might try to shoot for a lower bound for the number of combinatorial lines which is something like (3+o(1))^n rather than 4^n. Alternatively, we could somehow weight each line, perhaps by some factor depending on how many wildcards it contains. (Note that any set of density in a large
in a large ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) will contain at least one combinatorial line in which the number of wildcards is at most
will contain at least one combinatorial line in which the number of wildcards is at most 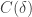 , since one can partition
, since one can partition ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into copies of
into copies of ![{}[3]^{n_0}](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E%7Bn_0%7D&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where 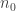 is the first index for which DHJ holds at density
is the first index for which DHJ holds at density 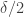 , and observe that the original set will have density at least
, and observe that the original set will have density at least 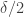 in at least
in at least 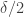 of these copies. So maybe one has to weight things to heavily favour lines with very few wildcards.)
of these copies. So maybe one has to weight things to heavily favour lines with very few wildcards.)
February 2, 2009 at 8:46 am |
17. It just occurred to me that if a subset of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) has positive density, then by the central limit theorem we may restrict attention to those strings which have
has positive density, then by the central limit theorem we may restrict attention to those strings which have  1’s, 2’s, and 3’s, and still have a positive density of strings remaining. So without loss of generality we may assume that all strings in the set are “balanced” in this manner. Hence, the only combinatorial lines which really matter are those which have
1’s, 2’s, and 3’s, and still have a positive density of strings remaining. So without loss of generality we may assume that all strings in the set are “balanced” in this manner. Hence, the only combinatorial lines which really matter are those which have  wildcards in them, rather than
wildcards in them, rather than 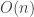 . So the number of combinatorial lines that are genuinely “in play” is just
. So the number of combinatorial lines that are genuinely “in play” is just  rather than
rather than  .
.
I wonder if DHJ implies the existence of a combinatorial line with wildcards. In the k=2 case it seems that a double counting argument should be able to establish something like this, though I haven’t checked it thoroughly. If so, then there seems to be a good shot at getting the “right” Varnavides type theorem.
wildcards. In the k=2 case it seems that a double counting argument should be able to establish something like this, though I haven’t checked it thoroughly. If so, then there seems to be a good shot at getting the “right” Varnavides type theorem.
February 2, 2009 at 9:01 am |
18. Two more thoughts… firstly, a sufficiently good Varnavides type theorem for DHJ may have a separate application from the one in this project, namely to obtain a “relative” DHJ for dense subsets of a sufficiently pseudorandom subset of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , much as I did with Ben Green for the primes (and which now has a significantly simpler proof by Gowers and by Reingold-Trevisan-Tulsiani-Vadhan). There are other obstacles though to that task (e.g. understanding the analogue of “dual functions” for Hales-Jewett), and so this is probably a bit off-topic.
, much as I did with Ben Green for the primes (and which now has a significantly simpler proof by Gowers and by Reingold-Trevisan-Tulsiani-Vadhan). There are other obstacles though to that task (e.g. understanding the analogue of “dual functions” for Hales-Jewett), and so this is probably a bit off-topic.
Another thought is the following. For any a,b,c adding up to n, let be the subset of
be the subset of ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) consisting of those strings with a 1s, b 2s, and c 3s. If A is a dense subset of
consisting of those strings with a 1s, b 2s, and c 3s. If A is a dense subset of ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , then
, then 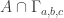 should be a dense subset of
should be a dense subset of  for many a, b, c; call a triple (a,b,c) rich if this is the case. By applying the corners theorem (!) we should then be able to find (a+r,b,c), (a,b+r,c), (a,b,c+r) which are simultaneously rich. But now this might be a good place with which to try a triangle removal argument, converting the lines of r wildcards connecting
for many a, b, c; call a triple (a,b,c) rich if this is the case. By applying the corners theorem (!) we should then be able to find (a+r,b,c), (a,b+r,c), (a,b,c+r) which are simultaneously rich. But now this might be a good place with which to try a triangle removal argument, converting the lines of r wildcards connecting 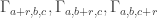 into triangles as Tim suggests in the main post?
into triangles as Tim suggests in the main post?
February 2, 2009 at 9:13 am |
19. Terry, I once tried something like what you suggest in the second paragraph of your last comment. There I was trying to do something different: come up with a definition of “quasirandom” that would guarantee that if you had quasirandom subsets of ,
,  and
and  then you would get a combinatorial line. I failed because I kept thinking of more and more obstructions and it seemed hard to find a definition that would deal with them all. This might be another project worth pursuing.
then you would get a combinatorial line. I failed because I kept thinking of more and more obstructions and it seemed hard to find a definition that would deal with them all. This might be another project worth pursuing.
A problem here, which I feel is loosely related, is that you can’t apply triangle removal if you restrict to ,
,  and
and  because you don’t get the degenerate triangles. This is similar to the problem that I had in comment CC above. (Incidentally, can anyone think of a better way of referring to comments than saying things like, “In Terry’s third last comment, paragraph 2”? Added later: I’ve gone back and numbered the comments.)
because you don’t get the degenerate triangles. This is similar to the problem that I had in comment CC above. (Incidentally, can anyone think of a better way of referring to comments than saying things like, “In Terry’s third last comment, paragraph 2”? Added later: I’ve gone back and numbered the comments.)
February 2, 2009 at 9:17 am |
20. A related observation is that if you’ve got three rich triples in the right configuration, you aren’t guaranteed a combinatorial line. For example, in two of the sets the first coordinate could always be 1 and in the third it could always be 2.
February 2, 2009 at 9:46 am |
21. This is a response to the first paragraph of Terry’s first comment (comment number 4), in which he asks for another proof of Sperner’s theorem. I like this idea: in one sense one could say that the difficulty with density Hales-Jewett is that the proof of Sperner’s theorem doesn’t generalize in an obvious way. (I don’t necessarily mean directly, but one might try to find an argument that has the same relationship to the corners problem as a proof of Sperner’s theorem has to the trivial one-dimensional analogue of the corners theorem, which says that a dense subset of![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) contains a pair of distinct points. But even this doesn’t seem to be at all easy.)
contains a pair of distinct points. But even this doesn’t seem to be at all easy.)
A minor point of disagreement with what Terry says (again in comment 4). I think the correct analogue of triangle removal (in the tripartite case) one level down is the following statement: given two subsets![A\subset[n]](https://s0.wp.com/latex.php?latex=A%5Csubset%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![B\subset[n]](https://s0.wp.com/latex.php?latex=B%5Csubset%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) such that the number of pairs
such that the number of pairs 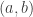 with
with  and
and  is very small, then it is possible to remove a small number of elements from
is very small, then it is possible to remove a small number of elements from 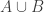 and end up with no pairs. The proof of course is that one of
and end up with no pairs. The proof of course is that one of  and
and  must be small. The reason I call this the analogue is that I think the analogue of a tripartite graph is a pair of subsets of the vertex sets, and the analogue of a triangle (a triple of edges) is a pair of vertices.
must be small. The reason I call this the analogue is that I think the analogue of a tripartite graph is a pair of subsets of the vertex sets, and the analogue of a triangle (a triple of edges) is a pair of vertices.
Now let me use this “pair-removal lemma” to prove the “one-dimensional corners” theorem. Suppose, then, that we have a subset![A\subset [n]](https://s0.wp.com/latex.php?latex=A%5Csubset+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) of size at least
of size at least 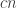 . I’m going to define two vertex sets
. I’m going to define two vertex sets  and
and  as follows. I let
as follows. I let  be the set of all ordered singletons
be the set of all ordered singletons  such that
such that  , and I let
, and I let  be the set of all ordered singletons
be the set of all ordered singletons  such that the sum of all the terms equals an element of
such that the sum of all the terms equals an element of  . (In other words, both
. (In other words, both  and
and  are equal to
are equal to  , but I want to demonstrate that I’m doing exactly what one does in higher dimensions.) If we can find a pair
, but I want to demonstrate that I’m doing exactly what one does in higher dimensions.) If we can find a pair  , then we are done (that is, we’ve found a configuration of the form
, then we are done (that is, we’ve found a configuration of the form  in the set
in the set  ), except in the degenerate case that
), except in the degenerate case that 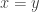 . So if we can’t find a one-dimensional corner, then the only pairs in
. So if we can’t find a one-dimensional corner, then the only pairs in 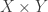 are the degenerate ones, which implies that there are only
are the degenerate ones, which implies that there are only 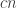 pairs. But then we can apply the pair-removal lemma and remove a few elements from
pairs. But then we can apply the pair-removal lemma and remove a few elements from 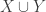 and end up with no pairs. But the degenerate pairs are vertex-disjoint, so we have to remove at least
and end up with no pairs. But the degenerate pairs are vertex-disjoint, so we have to remove at least 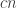 elements to get rid of all those, so we have reached a contradiction.
elements to get rid of all those, so we have reached a contradiction.
The next question might be whether we can use the “pair-removal lemma” to give a different proof of Sperner’s theorem. Or rather, we don’t actually want to prove the full strength of Sperner’s theorem but just the weaker statement that if you have at least subsets of
subsets of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) then you can find one that’s a proper subset of another. Up to now what I’ve done is silly, but this project would not be silly: it might tell us exactly what the difficulty is with this approach to density Hales-Jewett, but in a much simpler context.
then you can find one that’s a proper subset of another. Up to now what I’ve done is silly, but this project would not be silly: it might tell us exactly what the difficulty is with this approach to density Hales-Jewett, but in a much simpler context.
February 2, 2009 at 10:13 am |
22. Continuing the same theme, there is a natural pair of vertex sets to define in the Sperner case. For all higher dimensions, one takes the vertex sets to be copies of the power set of![\null[n]](https://s0.wp.com/latex.php?latex=%5Cnull%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , so one should surely do so here. Now in a certain sense the
, so one should surely do so here. Now in a certain sense the  th vertex set stands for the set of places where a sequence equals
th vertex set stands for the set of places where a sequence equals  . So here we would let
. So here we would let  and
and  be two copies of the power set of
be two copies of the power set of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , with sets in
, with sets in  representing the set of places where a sequence equals 0 and sets in
representing the set of places where a sequence equals 0 and sets in  representing the set of places where a sequence equals 1. Then we take as our subset
representing the set of places where a sequence equals 1. Then we take as our subset  the set of all sets
the set of all sets  such that the sequence that’s 0 on
such that the sequence that’s 0 on  and 1 on the complement of
and 1 on the complement of  belongs to
belongs to  , and we take
, and we take  to be the set of all sets
to be the set of all sets  such that the sequence that’s 1 on
such that the sequence that’s 1 on  and 0 on the complement of
and 0 on the complement of  belongs to
belongs to  . In set theoretic terms,
. In set theoretic terms,  consists of sets that belong to
consists of sets that belong to  (which itself, just to be clear, is our given collection of
(which itself, just to be clear, is our given collection of  subsets of
subsets of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) ), and
), and  is consists of all complements of sets that belong to
is consists of all complements of sets that belong to  .
.
At this point it is clear that what we are looking for is a pair with
with  ,
, 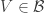 , and
, and 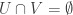 . This will be a degenerate pair if
. This will be a degenerate pair if ![U\cup V=[n]](https://s0.wp.com/latex.php?latex=U%5Ccup+V%3D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , but otherwise will imply that
, but otherwise will imply that  contains two sets with one a proper subset of the other. So this is the natural analogue of the triangles discussed in comments N and P.
contains two sets with one a proper subset of the other. So this is the natural analogue of the triangles discussed in comments N and P.
Note that in this situation we seem to be forced to put a graph structure on the two vertex sets and
and  , since we cannot just take any old pair
, since we cannot just take any old pair  but have to make them disjoint. At first this looks bad, but I actually think it’s OK because the same disjointness condition occurs in all dimensions. In other words, you get a graph in higher dimensions and not a hypergraph.
but have to make them disjoint. At first this looks bad, but I actually think it’s OK because the same disjointness condition occurs in all dimensions. In other words, you get a graph in higher dimensions and not a hypergraph.
The next step, I think, would be to try to find a suitable “pair-removal lemma” for this more complicated situation where the pairs have to be disjoint sets. Is the following true (or even the right question)? Suppose you have two collections and
and  of subsets of
of subsets of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , and there are very few pairs
, and there are very few pairs  such that
such that 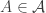 ,
, 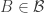 , and
, and  . Then you can remove a small fraction of the sets from
. Then you can remove a small fraction of the sets from 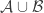 and end up with no such pairs.
and end up with no such pairs.
February 2, 2009 at 11:02 am |
23. This comment is a further response to Jozsef Solymosi’s comment (number 2). A slight variant of the problem you propose is this. Let’s take as our ground set the set of all pairs of subsets of
of subsets of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , and let’s take as our definition of a corner a triple of the form
, and let’s take as our definition of a corner a triple of the form  ,
, 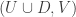 ,
, 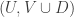 , where both the unions must be disjoint unions. This is asking for more than you asked for because I insist that the difference
, where both the unions must be disjoint unions. This is asking for more than you asked for because I insist that the difference  is positive, so to speak. It seems to be a nice combination of Sperner’s theorem and the usual corners result. But perhaps it would be more sensible not to insist on that positivity and instead ask for a triple of the form
is positive, so to speak. It seems to be a nice combination of Sperner’s theorem and the usual corners result. But perhaps it would be more sensible not to insist on that positivity and instead ask for a triple of the form  ,
, 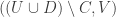 ,
,  , where
, where  is disjoint from both
is disjoint from both  and
and  and
and  is contained in both
is contained in both  and
and  . That is your original problem I think.
. That is your original problem I think.
I think I now understand better why your problem could be a good toy problem to look at first. Let’s quickly work out what triangle-removal statement would be needed to solve it. (You’ve already done that, so I just want to reformulate it in set-theoretic language, which I find easier to understand.) We let all of ,
,  and
and  equal the power set of
equal the power set of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . We join
. We join  to
to 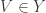 if
if  .
.
Ah, I see now that there’s a problem with what I’m suggesting, which is that in the normal corners problem we say that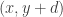 and
and 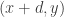 lie in a line because both points have the same coordinate sum. When should we say that
lie in a line because both points have the same coordinate sum. When should we say that 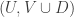 and
and 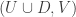 lie in a line? It looks to me as though we have to treat the sets as
lie in a line? It looks to me as though we have to treat the sets as  -sequences and take the sum again. So it’s not really a set-theoretic reformulation after all.
-sequences and take the sum again. So it’s not really a set-theoretic reformulation after all.
That suggests a wild question, which might have an easy counterexample (or an easy proof using density Hales-Jewett, which would be useful just to see whether it is true). If you have a dense subset of the set of all pairs
of the set of all pairs  of subsets of
of subsets of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , can you find a triple
, can you find a triple  ,
, 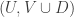 and
and 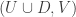 in
in  such that the three sets
such that the three sets  ,
,  and
and  are all disjoint?
are all disjoint?
February 2, 2009 at 12:45 pm |
24. I want to continue the discussion in 13, 14, 16, 17 and 18 concerning the appropriate Varnavides-type theorem for density Hales-Jewett.
The basic difficulty appears to be that if you know that a point lies in a combinatorial line, then it affects the shape of the point. Let’s see this first in a very simple context, where we just put the uniform distribution on the set of all points and the uniform distribution on the set of all lines. We can represent a combinatorial line as a point in the space , where the asterisks represent the varying coordinates. In this way we see easily that there are
, where the asterisks represent the varying coordinates. In this way we see easily that there are  combinatorial lines and that the set of fixed coordinates that take a given one of the values 1, 2 or 3 will typically have size about
combinatorial lines and that the set of fixed coordinates that take a given one of the values 1, 2 or 3 will typically have size about 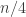 . (For anyone who isn’t familiar with this kind of argument, if you choose a random combinatorial line, regarded as a sequence that consists of 1s, 2s, 3s and asterisks, then the set of places where you choose 1 is a random subset of
. (For anyone who isn’t familiar with this kind of argument, if you choose a random combinatorial line, regarded as a sequence that consists of 1s, 2s, 3s and asterisks, then the set of places where you choose 1 is a random subset of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) where each point is chosen with probability
where each point is chosen with probability 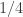 . With very high probability such a set has size close to
. With very high probability such a set has size close to 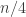 .) So we see that while a typical point has roughly equal numbers of 1s, 2s and 3s, a typical combinatorial line contains points that have around
.) So we see that while a typical point has roughly equal numbers of 1s, 2s and 3s, a typical combinatorial line contains points that have around 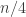 of two values and around
of two values and around 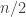 of the third value.
of the third value.
Suppose we try to remedy this by putting a different distribution on to the set of lines. Is there some natural way to do this that encourages the set of variable coordinates to be much smaller than the sets of fixed coordinates? A rather unpleasant approach would be simply to put some upper bound on the size of the set of variable coordinates and otherwise choose uniformly. The most natural thing I can think of to do is not all that much nicer, but at least it smooths the cutoff. It’s to choose the variable set of coordinates by picking each point independently with probability , where
, where  is something like
is something like  , and then choose the fixed coordinates randomly to be 1, 2 or 3.
, and then choose the fixed coordinates randomly to be 1, 2 or 3.
Actually, I can already see that this doesn’t work. The size of the resulting set of variable coordinates will be strongly concentrated around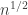 . But it’s not hard to choose a dense set of sequences such that if you choose any two of them,
. But it’s not hard to choose a dense set of sequences such that if you choose any two of them,  and
and  , then the number of 1s in
, then the number of 1s in  and the number of 1s in
and the number of 1s in  do not differ by approximately
do not differ by approximately 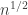 . The number of combinatorial lines in such a set would not be dense.
. The number of combinatorial lines in such a set would not be dense.
The fact that the natural measure on the set of sequences does not project properly to the natural measure on the set of triples of integers such that
of integers such that  seems to be a fundamental difficulty.
seems to be a fundamental difficulty.
Another thought one might have is to put a different measure on the set of points, so as to encourage points where we get two values roughly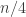 times and one value roughly
times and one value roughly 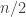 times. But the trouble with this is that it leads to the no-degenerate-triangles problem. To be precise, it would lead to three sets of sequences (according to whether 1, 2 or 3 was the preferred value) and no sequence would belong to all three sets. So it really does seem essential to force the variable set to be small somehow. And all I have to suggest so far is to do something very unnatural like first randomly choosing the cardinality according to some distribution that isn’t too concentrated about any value — the most natural one I can think of is a gentle exponential decay — then choosing a set of that cardinality, and then choosing the fixed coordinates randomly. But I have no reason to suppose that that leads to a Varnavides-type theorem.
times. But the trouble with this is that it leads to the no-degenerate-triangles problem. To be precise, it would lead to three sets of sequences (according to whether 1, 2 or 3 was the preferred value) and no sequence would belong to all three sets. So it really does seem essential to force the variable set to be small somehow. And all I have to suggest so far is to do something very unnatural like first randomly choosing the cardinality according to some distribution that isn’t too concentrated about any value — the most natural one I can think of is a gentle exponential decay — then choosing a set of that cardinality, and then choosing the fixed coordinates randomly. But I have no reason to suppose that that leads to a Varnavides-type theorem.
February 2, 2009 at 1:44 pm |
25. I see now that there’s quite a substantial overlap between my last comment and Terry’s comment 16. But one can view my last comment as an elaboration of his, perhaps.
Here I just want to make the quick suggestion that one way to work out what the appropriate Varnavides theorem should say is to prove it first. How would this strategy work? Well, we assume the density Hales-Jewett theorem in the following form: for every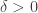 there exists
there exists  such that every subset of
such that every subset of ![\null [3]^k](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5Ek&bg=ffffff&fg=333333&s=0&c=20201002) of size at least
of size at least  contains a combinatorial line. (The
contains a combinatorial line. (The 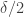 is convenient in just a moment.)
is convenient in just a moment.)
Now let be a subset of
be a subset of ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of size at least
of size at least  . Here,
. Here,  is an integer that is much bigger than
is an integer that is much bigger than  . The set
. The set ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) can be covered uniformly by structures that are isomorphic to
can be covered uniformly by structures that are isomorphic to ![\null [3]^k](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5Ek&bg=ffffff&fg=333333&s=0&c=20201002) , and a positive proportion (in fact,
, and a positive proportion (in fact, 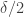 at least) of these structures intersect
at least) of these structures intersect  in a subset of density at least
in a subset of density at least 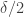 . So a positive proportion of these structures contain a combinatorial line. And now a double-counting argument gives us lots of combinatorial lines.
. So a positive proportion of these structures contain a combinatorial line. And now a double-counting argument gives us lots of combinatorial lines.
Now there are several choices to make if one wants to pursue this line of attack. The main one is what set of -dimensional substructures of
-dimensional substructures of ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) to average over. For the benefit of people who haven’t thought too hard about Hales-Jewett, let me give a pretty general class of such structures. You choose
to average over. For the benefit of people who haven’t thought too hard about Hales-Jewett, let me give a pretty general class of such structures. You choose  disjoint sets
disjoint sets 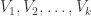 , and you choose fixed values in
, and you choose fixed values in 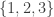 for all elements of
for all elements of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) that do not belong to one of the
that do not belong to one of the  . The
. The  -dimensional structure consists of the
-dimensional structure consists of the 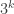 sequences that take the fixed values outside the
sequences that take the fixed values outside the  and are constant on each
and are constant on each  . What can we deduce from the fact that there exists
. What can we deduce from the fact that there exists  that depends on
that depends on  only such that if
only such that if  intersects any
intersects any  -dimensional set of this kind in at least
-dimensional set of this kind in at least  places then that
places then that  -dimensional set contains a combinatorial line in
-dimensional set contains a combinatorial line in  ?
?
The choice one has is this: over what set of structures of this kind (or with what weighting on the structures) do we do an averaging argument? And what can we expect to get out of it at the end? Is it likely to give anything useful?
One other question: is there a reasonably precise argument to the effect that if the triangle-removal approach worked, then it would imply a stronger Varnavides-type result? And if so, what would that result be? This could be another way to get a handle on the problem.
February 2, 2009 at 3:18 pm |
26. Another small thought in response to Terry’s comment number 18, paragraph 2, is this. Even if that idea runs into the difficulty I mentioned in comment 19, there might be a chance of getting something out of a small variant of the idea. Terry suggested using the corners theorem to find a triple ,
,  ,
,  in each part of which
in each part of which  is “rich”. The problem was that if one then used just these sets to form a tripartite graph, one would end up with no degenerate triangles. But what if instead one used the full 2-dimensional Szemer\’edi theorem (which can be proved using the simplex-removal lemma in sufficiently high dimension, so it doesn’t depend on ergodic theory) to obtain a big network of sets
is “rich”. The problem was that if one then used just these sets to form a tripartite graph, one would end up with no degenerate triangles. But what if instead one used the full 2-dimensional Szemer\’edi theorem (which can be proved using the simplex-removal lemma in sufficiently high dimension, so it doesn’t depend on ergodic theory) to obtain a big network of sets  in which
in which  was rich? They could be organized into a triangular lattice: they would consist of all sets of the form
was rich? They could be organized into a triangular lattice: they would consist of all sets of the form  such that
such that  ,
,  and
and  are non-negative integers that sum to
are non-negative integers that sum to  for some reasonably large
for some reasonably large  . It’s not obvious that this would be any help, but it’s also not obvious that it wouldn’t be any help.
. It’s not obvious that this would be any help, but it’s also not obvious that it wouldn’t be any help.
February 2, 2009 at 3:33 pm |
27. I was rather pleased with the “conjecture” in the final paragraph of comment 22, but have just noticed that it is completely false, at least if you interpret it in the most obvious way. Indeed, if you take both and
and  to consist of all subsets of
to consist of all subsets of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , then you find that almost every set in
, then you find that almost every set in  intersects almost every set in
intersects almost every set in  . And it’s clear that if you just remove a small fraction of the sets from
. And it’s clear that if you just remove a small fraction of the sets from  and
and  you aren’t going to be able to ensure that every set left in
you aren’t going to be able to ensure that every set left in  intersects every set left in
intersects every set left in  . (Proof: for each pair
. (Proof: for each pair  you will either have to remove
you will either have to remove  from
from  or
or  from
from  .)
.)
This leaves me with two questions.
(i) Can this pair-removal approach to Sperner be rescued somehow?
(ii) If not, can one use its failure as the basis of a rigorous proof that no triangle-removal approach can work for density Hales-Jewett?
February 2, 2009 at 3:47 pm |
28. Perhaps the answer to (i) is rather simple. First, we see how many disjoint pairs there are in the case where both and
and  are the full power set of
are the full power set of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . The answer is
. The answer is  , because for each element of
, because for each element of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) you get to choose whether it belongs to the first set, the second set, or neither. So now we would deem a pair of set systems
you get to choose whether it belongs to the first set, the second set, or neither. So now we would deem a pair of set systems  to have “few” disjoint pairs if the number of pairs
to have “few” disjoint pairs if the number of pairs  with
with  ,
,  and
and  is at most
is at most  for a tiny positive constant
for a tiny positive constant  . Under that assumption, does it follow that we can remove a small number of sets and end up with no disjoint pairs? And if so, would that prove Sperner’s theorem (in the weak form where we assume that a set system has positive density)?
. Under that assumption, does it follow that we can remove a small number of sets and end up with no disjoint pairs? And if so, would that prove Sperner’s theorem (in the weak form where we assume that a set system has positive density)?
February 2, 2009 at 4:16 pm |
29. Several remarks which are not directly towrds the specific project but related.
1. With all due respect to Sperner’s theorem it is hard to believe that the lower bound cannot be improved. Right? Maybe as a side project we should come up with a
lower bound cannot be improved. Right? Maybe as a side project we should come up with a  example for k=3 density HJ or ask around if this is known?
example for k=3 density HJ or ask around if this is known?
2. A sort of generic attack one can try with Sperner is to look at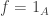 and express using the Fourier expansion of
and express using the Fourier expansion of  the expression
the expression  where x<y is the partial order (=containment) for 0-1 vectors. Then one may hope that if f does not have a large Fourier coefficient then the expression above is similar to what we get when A is random and otherwise we can raise the density for subspaces.
where x<y is the partial order (=containment) for 0-1 vectors. Then one may hope that if f does not have a large Fourier coefficient then the expression above is similar to what we get when A is random and otherwise we can raise the density for subspaces.
(OK, you can try it directly for the k=3 density HJ problem too but Sperner would be easier;)
This is not unrealeted to the regularity philosophy.
3. Reductions: the works of Furstenberg and Katznelson went gradually from multidimensional Szemeredi to density theorems for affine subspaces to density HJ. (Maybe there were more stops on the way)
Beside the obvious reduction – combinatorial lines imply long AP (and also high dimension Szemeredi if I remember correctly) reductions in the opposite directions are not known (to me, at least).
It is tempting to think that the when we find high dmensionall affine space perhaps in a much much much larger alphabet we can somehow get a little combinatorial line for the small alphabet.
4. There is an analogous for Sperner but with high dimensional combinatorial spaces instead of "lines" but I do not remember the details (Kleitman(?) Katona(?) those are ususal suspects.)
February 2, 2009 at 4:35 pm |
30. As a person who writes the phrase “choose the sequence x at random; then form y by rerandomizing each coordinate of x with probability p” in nearly half his papers, I’m naturally drawn to the 16-17-24-etc. comment thread.
In #24, Tim suggests (and I agree) that the most natural way to pick a line is to form three sequences (x,y,z) by choosing
(x_i,y_i,z_i) uniformly from [3]^3, with probability 1-p,
(x_i,y_i,z_i) = (1,2,3) with probability p,
independently for each i = 1…n, with p taken to be perhaps 1/sqrt(n). But Tim also makes the good — and worrisome — point that this distribution has the “wrong” marginal on x (and on y and on z). For example, the marginal on x is the (1/3+2p/3, 1/3-p/3, 1/3-p/3) product distribution on [3]^n, whereas it “ought to be” the uniform distribution, because we are measuring the density of A with respect to the uniform distribution.
It’s not completely clear to me that this is an insuperable problem though. For example, in #24 Tim wrote,
“But it’s not hard to choose a dense set of sequences such that if you choose any two of them, x and y, then the number of 1s in x and the number of 1s in y do not differ by approximately n^{1/2}.”
I don’t quite see it… Isn’t it the case, as Terry pointed out in #17, that almost all strings in A have 1/3 +/- O(sqrt(n)) 1’s? In fact, shouldn’t a random pair x, y in A have a 1-count differing by Theta(sqrt(n)) with high probability? [All hidden constants here depend on delta.]
Anyway, I agree it’s worrisome. To check whether it is indeed insuperable, I wonder if we could try “practising” this idea in the weak-Sperner’s setting Tim suggested at the end of #21. The analogous question there would be:
Suppose A contains at least a delta-fraction of the strings in {0,1}^n (w.r.t. the uniform distribution). Suppose we choose to strings (x,y) as follows:
(x_i,y_i) is uniform from {0,1}^2 with probability 1 – 1/sqrt(n)
(x_i,y_i) is (0,1) with probability 1/sqrt(n),
independently for each i = 1…n. Is there a positive probability that both x and y are in A?
February 2, 2009 at 4:45 pm |
31. Gil, a quick remark about Fourier expansions and the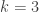 case. I want to explain why I got stuck several years ago when I was trying to develop some kind of Fourier approach. Maybe with your deep knowledge of this kind of thing you can get me unstuck again.
case. I want to explain why I got stuck several years ago when I was trying to develop some kind of Fourier approach. Maybe with your deep knowledge of this kind of thing you can get me unstuck again.
The problem was that the natural Fourier basis in![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) was the basis you get by thinking of
was the basis you get by thinking of ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as the group
as the group 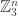 . And if that’s what you do, then there appear to be examples that do not behave quasirandomly, but which do not have large Fourier coefficients either. For example, suppose that
. And if that’s what you do, then there appear to be examples that do not behave quasirandomly, but which do not have large Fourier coefficients either. For example, suppose that  is a multiple of 7, and you look at the set
is a multiple of 7, and you look at the set  of all sequences where the numbers of 1s, 2s and 3s are all multiples of 7. If two such sequences lie in a combinatorial line, then the set of variable coordinates for that line must have cardinality that’s a multiple of 7, from which it follows that the third point automatically lies in the line. So this set
of all sequences where the numbers of 1s, 2s and 3s are all multiples of 7. If two such sequences lie in a combinatorial line, then the set of variable coordinates for that line must have cardinality that’s a multiple of 7, from which it follows that the third point automatically lies in the line. So this set  has too many combinatorial lines. But I’m fairly sure — perhaps you can confirm this — that
has too many combinatorial lines. But I’m fairly sure — perhaps you can confirm this — that  has no large Fourier coefficient.
has no large Fourier coefficient.
You can use this idea to produce lots more examples. Obviously you can replace 7 by some other small number. But you can also pick some arbitrary subset of
of ![\null[n]](https://s0.wp.com/latex.php?latex=%5Cnull%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and just ask that the numbers of 0s, 1s and 2s inside
and just ask that the numbers of 0s, 1s and 2s inside  are multiples of 7.
are multiples of 7.
If these observations are correct, then they suggest another very interesting subproblem: describe all obstructions to randomness. That is, find a nice explicit set of functions defined on
of functions defined on ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) such that (the characteristic function of) any set with the wrong number of combinatorial lines correlates with a function in
such that (the characteristic function of) any set with the wrong number of combinatorial lines correlates with a function in  . Ideally, correlation with a function in
. Ideally, correlation with a function in  would imply a density increase on some subset.
would imply a density increase on some subset.
Of course, this would be aiming for a Roth-type proof rather than a Ruzsa-Szemerédi-Solymosi-type proof.
February 2, 2009 at 4:45 pm |
32. [Calling Gil’s post 29 and my earlier one 30.]
Sorry for the lengthiness of the posts, but I wanted to throw out one more idea and one more question.
Suppose the issue discussed in my #30 is indeed a problem. Here’s a possible (perhaps far-fetched) way around it:
First, find the simultaneously “rich” triples (a+r,b,c), (a,b+r,c), (a,b,c+r) as in Terry’s post #18. Now take a new distribution on combinatorial lines: Uniform on lines which have exactly r wildcards.
This may improve things because its marginals on x, y, and z are precisely the uniform distributions on Gamma_{a+r,b,c}, Gamma_{a,b+r,c}, and Gamma_{a,b,c+r}. And we know A is dense under these distributions, by the definition of richness.
Working “slicewise” in this way has some intuitive appeal to me because it seems compatible with the prospect of getting the “correct” Sperner by these ideas, as opposed to just the “weak” Sperner.
February 2, 2009 at 4:52 pm |
33. In response to Ryan’s question in 30, I see that I didn’t explain myself clearly enough. Here’s what I meant.
Suppose you have a distribution on combinatorial lines with the property that the size of the variable set has a very high probability of being very close to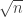 . (NB, I don’t just mean order
. (NB, I don’t just mean order 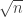 but between
but between  and
and  . This is I think the point of misunderstanding.) What I was claiming was that it was quite easy to choose a dense set of sequences such that if
. This is I think the point of misunderstanding.) What I was claiming was that it was quite easy to choose a dense set of sequences such that if  and
and  are two of your sequences then the number of 1s in
are two of your sequences then the number of 1s in  and the number of 1s in
and the number of 1s in  never differ by almost exactly
never differ by almost exactly 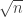 .
.
February 2, 2009 at 4:55 pm |
34. Re Tim’s #33: Ah, I see. Right.
So perhaps the thing to do is not to choose the number of wildcards to be Binomial(n,1/sqrt(n)), but, uh, I dunno, perhaps Poisson(sqrt(n))??
February 2, 2009 at 4:56 pm |
We’ve already got a number of threads developing. Here is my best effort at sorting them out.
Discussion of original Furstenburg-Katzelson proof (#1, #5, #6, #10)
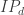 set problem (#2, #7, #23)
set problem (#2, #7, #23)
Finding lower and upper bounds (#3, #8, #11, #12, #15, #16)
Sperner’s theorem (#4, #21, #22, #27, #28, Gil #29)
Creating a quasirandom definition (#18, #19, #26)
Positive density (#4, #9, #17)
Analogue of Varnavides theorem (#13, #14, #16, #17, #18, #24, #25)
The latter two threads might be combinable.
[I haven’t numbered this comment as it’s a metacontribution rather than a contribution — but thanks for it.]
February 2, 2009 at 4:58 pm |
35. Now the question, following up on the separate thread initiated by Jozsef (specifically, #2 and Tim’s #7), just to confirm I have the question right…
There is a dense subset A of {0,1}^n x {0,1}^n. Is it true that it must contain three nonidentical strings (x,x’), (y,y’), (z,z’) such that for each i = 1…n, the 6 bits
[ x_i x’_i ]
[ y_i y’_i ]
[ z_i z’_i ]
are equal to one of the following:
[ 0 0 ] [ 0 0 ] [ 0, 1 ] [ 1 0 ] [ 1 1 ] [ 1 1 ]
[ 0 0 ], [ 0 1 ], [ 0, 1 ], [ 1 0 ], [ 1 0 ], [ 1 1 ],
[ 0 0 ] [ 1 0 ] [ 0, 1 ] [ 1 0 ] [ 0 1 ] [ 1 1 ]
?
February 2, 2009 at 4:59 pm |
36. (Responding to 34) Unfortunately, Poisson(root n) is just as concentrated around root n as Binomial (n,1/sqrt n) (as one would expect since binomial tends to Poisson). That’s what slightly bothers me — the most natural distributions have that awkward property.
February 2, 2009 at 5:11 pm |
37. (Re 36.) Hmm. But there has to be *some* correct distribution for the wildcards.
After all, what *is* the distribution on the difference in 1-counts between independent and uniform x and y? It’s distributed as the sum of n i.i.d. r.v.’s which are +1 with probability 2/9, -1 with probability 2/9, and 0 with probability 5/9. So it’s like a Gaussian with standard deviation sigma = 2/3sqrt(n).
So we could put in a number of wildcards equal to round(|N(0,4/9n)|)…
This looks weird enough that it’s probably a wrong idea, but I still feel there may be a “natural” probabilistic way to do it.
Or maybe I revert to the suggestion of thinking about distributions on fixed numbers of 1’s, 2’s, 3’s as in #32… 🙂
February 2, 2009 at 5:29 pm |
38. Here’s an attempt to throw the spanner in the works of #32. Let’s define to be the set of all sequences
to be the set of all sequences  with the following property: if the number of 1s in
with the following property: if the number of 1s in  is even then
is even then  , and if the number of 1s in
, and if the number of 1s in  is odd then
is odd then  .
.
I first claim that virtually all slices are rich. Indeed, take a typical slice defined by the triple Then just choose
Then just choose  1s, taking care not to choose
1s, taking care not to choose 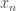 , choose the appropriate value of
, choose the appropriate value of 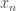 according to whether
according to whether  is even or odd, and then fill in the rest with the appropriate number of 2s and 3s. The only thing that can go wrong is that one of
is even or odd, and then fill in the rest with the appropriate number of 2s and 3s. The only thing that can go wrong is that one of  and
and  is equal to 0, but for all normal slices we’re OK.
is equal to 0, but for all normal slices we’re OK.
Now I claim that we can’t have a combinatorial line with an odd number of wildcards. The reason is that when the wildcards change from 1 to 2, the final coordinate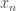 is forced to change from 2 to 3, which is not allowed.
is forced to change from 2 to 3, which is not allowed.
So it looks to me as though it would be disastrous to take the uniform distribution over lines with some fixed number of wildcards (unless, perhaps, one had done some more preprocessing to get a stronger property than mere richness).
February 2, 2009 at 5:30 pm |
(Another metacomment.)
Tim, now may be the right time to create multiple posts so people can sort into the discussion they want to focus on. Given the rate posts are piling up it will get too hard to do it later. In fact, by the time I hit “submit” I’m guessing 3 more comments will have come up. 🙂
#30, #32, #33, #34, #36, #37 spawned off Varnavides theorem thread, although tilting over to general randomness
#31 (off of #29) Sperner, sort of — Fourier approach might spawn its own thread
#35 IP_d problem thread
[Jason—I’m going to answer this question over on the Questions of Procedure post. Or rather, I’m going to ask what others think. I agree that it would, for instance, make it easier for a newcomer if they had a more organized structure of comments.]
February 2, 2009 at 5:56 pm |
[Incidentally, in other comment threads, it is often customary to refer to a specific comment by a timestamp, e.g. “Gowers Feb 2 3:18 pm”. But I will adhere to the numbering convention also…]
39. Wow, this thing is evolving rapidly… I will need some time to catch up, but I wanted to contribute two thoughts I had this morning… with regard to Gil’s 29 (Feb 2 4:16 pm), observe that the union of all where b+2c lies in a set that has no length 3 progressions, will have no combinatorial lines. So by plugging in the Behrend example it now seems that we have the lower bound
where b+2c lies in a set that has no length 3 progressions, will have no combinatorial lines. So by plugging in the Behrend example it now seems that we have the lower bound  (if I haven’t made a miscomputation somewhere).
(if I haven’t made a miscomputation somewhere).
Secondly, if one applies the corners argument locally instead of globally, one can make the r in the rich triple to be of bounded size, r=O(1). I don’t know if this is helpful though. But it begins to remind me of the isoperimetric inequality for the cube (which would correspond to the case k=2, r=1).
to be of bounded size, r=O(1). I don’t know if this is helpful though. But it begins to remind me of the isoperimetric inequality for the cube (which would correspond to the case k=2, r=1).
[Morning Terry! Yes, that time stamp idea would be good, and would save me having to do a lot of editing to number comments. (Even if everyone remembers to number their comments, they don’t always know what number their comment will actually turn out to be.)]
February 2, 2009 at 6:28 pm |
40. Two more thoughts. Firstly, I can now show that , by taking the set
, by taking the set 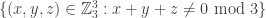 , or equivalently the union of all the
, or equivalently the union of all the  such that
such that 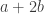 is not divisible by 3. (The upper bound
is not divisible by 3. (The upper bound  follows from the general inequality
follows from the general inequality  .) So maybe
.) So maybe 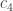 is computable also, for what it’s worth.
is computable also, for what it’s worth.
Secondly, one may need some sort of “hereditary” richness, in which one considers not only the global counts a, b, c of 1s, 2s, and 3s in [n], but also considers all subsets of [n] and looks for richness there too. If there is one subset of [n] in which the richness fluctuates much more than in the original index set [n], then we pass to that set (incrementing a certain “richness energy” along the way) and keep going until one obtains “richness regularity” (by a standard “energy increment argument”), which should mean something like that the “richness statistics” of any “non-negligible” subindex set of the index set should be close to the statistics of the original index set. This may help avoid the kind of counterexamples that appear for instance in Gowers 20 (9.17am), or Gowers 38 (5.29 pm). It also reminds me of the stationarity reduction used in the ergodic theory world (Terry 4 9.26pm, Tim Austin 16 10:16pm).
February 2, 2009 at 6:32 pm |
41. Incidentally, given that we are trying to find triangles in sparse (but now constant degree) graphs, we may eventually have to use the type of regularity lemmas associated with bounded degree graphs, as for instance studied by Elek and Lippner,
http://arxiv.org/abs/0809.2879
February 2, 2009 at 7:49 pm |
42. I need to break out the compiler, but for what it’s worth, here’s my brute force data structure I’m going to use to try to get (at the least lower bound, and if they match upper bound exact) values of :
:
One set of nodes (call them “red”) correspond to the elements of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002)
Another set of nodes (call them “blue”) correspond to the specific combinatorial lines. They each have degree 3 and are linked to by the blue nodes.
Greedy algorithm:
1.) Look at the red nodes; out of the set of red nodes with highest degree, pick one at random.
2.) Remove that node, and all blue nodes linking to that node, and all edges corresponding to the red node and the blue nodes.
3.) If there are any blue nodes remaining, return to 1. Otherwise, all combinatorial lines have been removed.
February 2, 2009 at 7:50 pm |
(42 fix) blue nodes are linked to by the red nodes.
February 2, 2009 at 8:27 pm |
(43)
Let me consider a related problem, which can be thought of as a
generalization:
we consider sets of [3]^n where all lines, not just combinatorial lines,
are forbidden. This problem is also known as Moser’s cube problem.
It is known that the extremal configurations have, 2,6,16,43 points in
dimensions n=1,2,3,4 respectively.
The bounds in this problem were 3^n/sqrt(n) and o(3^n) respectively, as
well.
These general lines can be modeled by two different wild cards.
Say (1,x,3,y,x) is a line, if x runs from 1 to 3, and y runs from 3 to 1.
Here is a sketch of an improvement of the lower bound, in the spirit of
Terry’s idea (#39).
The sets Gamma_{a,b,c} do not contain any line, so taking unions of
several Gammas, one would need to study (with r wild cards x
and s wild cards y) Gammas with indices
(a+r,b,c+s), (a, b+r+s, c), (a+s, b, c+r).
Then take those Gamma_{a’,b’,c’}, where
a’+2b’+3c’ is taken from a set without a 3 progression, and one gets
a lower bound of 3^n/exp(c sqrt(log n))
Since the Hales-Jewett theorem is on combinatorial lines:
some of the ideas discussed before might work for general lines,
i.e. Moser’s cube problem as well. Is there any general lower bound
construction that works for combinatorial lines only?
(Terry’s example with 18 ponts in dimension 3 has lines, so what is the right generalization?).
What is genuinely different for combinatorial lines?
February 2, 2009 at 8:43 pm |
44. As far as I know describing obstructions to pseudorandomness is open even for Sperner’s theorem or Kruskal-Katona theorem (the latter corresponds to dealing with sets ). Consider the following simple problem:
). Consider the following simple problem:
Let be a dense subset of
be a dense subset of ![\binom{[n]}{n/2}](https://s0.wp.com/latex.php?latex=%5Cbinom%7B%5Bn%5D%7D%7Bn%2F2%7D&bg=ffffff&fg=333333&s=0&c=20201002) and
and  be a dense subset of
be a dense subset of ![\binom{[n]}{n/2+1}](https://s0.wp.com/latex.php?latex=%5Cbinom%7B%5Bn%5D%7D%7Bn%2F2%2B1%7D&bg=ffffff&fg=333333&s=0&c=20201002) . When is the number of pairs
. When is the number of pairs  such that
such that  close to expected?
close to expected?
Besides the obvious obstruction when all elements contain
contain ![i\in[n]](https://s0.wp.com/latex.php?latex=i%5Cin%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , but none of elements
, but none of elements  do, there is also a more subtle obstruction. Let
do, there is also a more subtle obstruction. Let  be any subset of size
be any subset of size 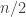 in
in ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Choose any
. Choose any  Let
Let  belong to
belong to  iff
iff 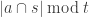 is in the interval
is in the interval ![\null [0..t/2]](https://s0.wp.com/latex.php?latex=%5Cnull+%5B0..t%2F2%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and  belong to
belong to  iff
iff 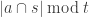 is in the interval
is in the interval ![\null [(t/2+2)...t-1]](https://s0.wp.com/latex.php?latex=%5Cnull+%5B%28t%2F2%2B2%29...t-1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . The sets
. The sets  and
and  are of density close to
are of density close to 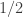 , but their union is an antichain.
, but their union is an antichain.
Of course, such examples can be made more complicated by taking several sets for different moduli
for different moduli  .
.
I suspect that there might a Freiman-type theorem buried here. There is even a weak connection to sumset addition: a shadow of a set is just
is just  where
where  ‘s are the one-element sets, and the addition occurs in appropriate semigroup (it is easy to see that a few results from additive combinatorics do carry over to that setting).
‘s are the one-element sets, and the addition occurs in appropriate semigroup (it is easy to see that a few results from additive combinatorics do carry over to that setting).
February 2, 2009 at 8:47 pm |
(45) Not a major concern at the moment, but if at some point we write up the precise bounds obtained from Behrend set constructions, we may as well use the best known Behrend set bound, due to Elkin, see e.g. this exposition of Green and Wolf:
http://arxiv.org/abs/0810.0732
February 2, 2009 at 9:42 pm |
45.5. In the paper
Some Lower Bounds for the Hales-Jewitt Numbers
by Eric Tressler
he has the following:
HJ(3,3)>6
HJ(4,3)>6
February 2, 2009 at 9:45 pm |
(46) [Numbering of the previous two posts needs to be changed]
@Jason (42): in view of existing examples, it may be worth restricting one’s search space to those sets that are unions of ‘s, rather than arbitrary subsets of
‘s, rather than arbitrary subsets of ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . The problem is now some sort of weighted corner-avoidance problem, but one which may be more tractable to brute force computer search.
. The problem is now some sort of weighted corner-avoidance problem, but one which may be more tractable to brute force computer search.
@Boris: The problem you describe sounds very close to the machinery of influence, hypercontractivity, isoperimetric inequality, etc., but Gil is of course the one to ask regarding these things.
February 2, 2009 at 9:52 pm |
Comment on the lower bound. (Gil 15, Terry 16, and Terry 39&44) Without loosing anything, we can suppose that the number of 0-s,1-s, and 2-s are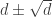 . Then the range where a+2b (the sum of 0-s plust twice the sum of 1-s) is triangle free has length about
. Then the range where a+2b (the sum of 0-s plust twice the sum of 1-s) is triangle free has length about  If we care about the details, like we want to use Elkin’s improvement, then we should note this one as well. It changes the constant multiplier in the exponent.
If we care about the details, like we want to use Elkin’s improvement, then we should note this one as well. It changes the constant multiplier in the exponent.
February 2, 2009 at 10:09 pm |
(47) contd. I think that we should get a better lower bound by using bounds on corners than on 3-term arithmetic progressions, however I’m not sure what is the best known lower bound on corners.
February 2, 2009 at 10:39 pm |
(48)
@Jason (42): The structure you point out – a bipartite graph with one set of vertices representing combinatorial lines $$L$$, and the other representing elements of $${[3]}^n$$ – can be used to algorithmically find $$c_n$$ exactly (it sounds like you’re going for a probabilistic approach), although the code is more involved, and a bit slow (but polynomial in the size of the graph).
I think we can reduce this to a min-cost flow problem. Basically, we want the smallest set of edges which covers $$L$$ — this corresponds to the smallest subset of $${[3]}^n$$ which can be removed to get a line-free set. Create the following directed graph: add vertex $$s$$ with edges to everything in $$L$$. Every line in $$L$$ has an edge to all three points it contains. Every point in $${[3]}^n$$ points to a new vertex $$t$$. Every edge has unit cost, and unit capacity, except the edges between $$L$$ and $${[3]}^n$$, which have unlimited capacity. Then a min-cost flow from $$s$$ to $$t$$ with at least $$|L|$$ capacity is what we want. This can be found in time $$O(n^2m^3\log n)$$ where $$n$$ is number of nodes, $$m$$ is number of edges [see Schrijver’s Combinatorial Optimization, ch 12]. Not super fast, but maybe do-able for small values of our $$n$$. Also possibly of theoretical interest?
Side note: In case my latex notation doesn’t turn out correctly, could someone mention the proper syntax for these comments? And in case it does look right (for others), I’m just surrounding the math parts in double dollar signs.
February 2, 2009 at 10:40 pm |
oops, that cool-looking face is supposed to be a forty-eight ( 48 )
February 2, 2009 at 10:46 pm |
(48) To Christian (43) If r=s=1 then you get 3,3,3 as an arithmetic progression. I don’t see a simple way to resolve the problem of degenerate arithmetic progressions in the general setting.
February 2, 2009 at 10:48 pm |
oops twice! (as ( 48 ) was used twice)
February 2, 2009 at 11:14 pm |
(50) [I don’t envy Tim’s job to clean up the numbering system… but one can of course use fractions or something…]
@ Joszef (47), the best lower bound for corners is necessarily between that for 3-term progressions and for triangle removal, since triangle removal implies corners implies 3-term progressions. But ever since the original Ruzsa-Szemeredi paper, the best lower bounds for triangle removal come from… the Behrend construction for 3-term progressions. This is not a satisfactory state of affairs, but I don’t think there has been much progress in this regard. (Although I could imagine that the Elkin refinement could be pushed a little further for corners instead of 3-term progressions.)
[Of course, Gowers has tower-type lower bounds for the regularity lemma used to prove triangle removal, but this does not directly seem to lead to any new lower bounds on the latter.]
February 2, 2009 at 11:17 pm |
(51) Incidentally, to make latex comments, use “$latex [Your LaTeX code]$”. There are some quirks to the code, see the bottom of my post
for details.
February 2, 2009 at 11:19 pm |
Well, that failed horribly… I meant “$latex [Your LaTeX code]$” (where I artificially italicised the first dollar sign).
February 3, 2009 at 1:08 am |
(52) Something that might help me out — could someone produce a counterexample where the greedy algorithm I outlined above in (42) *doesn’t* work?
February 3, 2009 at 1:15 am |
( 53 ). Hi Boris! My student Karl Wimmer and I have some recent results about obstructions to pseudorandomness for Kruskal-Katona. Karl’s still writing them up for his thesis but he’s currently sidetracked with job interviews etc.
The results say what you might guess: Roughly, if A is a subset of {[n] choose n/2} with constant density mu, then the density of the upper shadow of A is at least mu + const. log(n)/n… unless A is very noticeably correlated with a single coordinate. As Terry guesses, it’s “influences”, “hypercontractivity”, “Gil stuff” etc.
Karl was planning to finish writing it and its applications in Learning Theory within two months. But if this polymath project veers too close I guess we’ll have to try to “rush to print” 🙂 I currently don’t see connections to the analogous Sperner problem; however I’ve only thought about it for like 5 minutes…
February 3, 2009 at 1:33 am |
(54) Tim Austin had a small comment which may be a clue of some sort: the ergodic theory proof of DHJ is heavily reliant on the ordering of the index set [n], even though the conclusion of DHJ is of course invariant under permutations of the index set. (For instance, it is convenient to divide [n] into [n-r] and [r] for some moderately large r, and re-interpret subsets of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) instead as a family of subsets of
instead as a family of subsets of ![{}[3]^r](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Er&bg=ffffff&fg=333333&s=0&c=20201002) , indexed by elements of
, indexed by elements of ![{}[3]^{n-r}](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E%7Bn-r%7D&bg=ffffff&fg=333333&s=0&c=20201002) .) The standard proof of the colouring HJ theorem also has this sort of feature, in that one must arbitrarily order [n], or at least partition it into components, in some fashion. So one may have to “break symmetry” here and not rely on a purely graph-theoretic argument.
.) The standard proof of the colouring HJ theorem also has this sort of feature, in that one must arbitrarily order [n], or at least partition it into components, in some fashion. So one may have to “break symmetry” here and not rely on a purely graph-theoretic argument.
February 3, 2009 at 1:52 am |
55. I’ve been busy this evening and am about to go to bed, so only time for a quick remark at this stage, which again may be implicit in previous remarks. Let me call a set of the form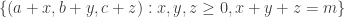 a triangular grid of sidelength
a triangular grid of sidelength  . The remark is that by means of an averaging argument, there is no problem in finding a triangular grid of sidelength
. The remark is that by means of an averaging argument, there is no problem in finding a triangular grid of sidelength 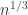 , say, such that for every element of the grid all of
, say, such that for every element of the grid all of  is close to
is close to 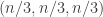 , and such that a positive proportion of the sets
, and such that a positive proportion of the sets 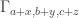 are rich in elements of
are rich in elements of  . If we restrict to such a set, then we can hope for a Varnavides-type theorem because now a typical combinatorial line will have the same typical size of variable set as the sidelength of a typical equilateral triangle in the grid. In other words, in this set we no longer have the problem that the natural weights differ from the natural weights for corners. I’ll try to make this point more precisely tomorrow.
. If we restrict to such a set, then we can hope for a Varnavides-type theorem because now a typical combinatorial line will have the same typical size of variable set as the sidelength of a typical equilateral triangle in the grid. In other words, in this set we no longer have the problem that the natural weights differ from the natural weights for corners. I’ll try to make this point more precisely tomorrow.
February 3, 2009 at 3:04 am |
56. I thought it might also be worth reporting here on some things I tried that don’t seem to work, though perhaps I am missing something.
Firstly, I tried improving the lower bound we now have on by not taking the global statistics a, b, c of 1s, 2s, and 3s (and their resulting sets
by not taking the global statistics a, b, c of 1s, 2s, and 3s (and their resulting sets  , but instead partitioning [n] into subsets, using the local statistics for each subsets to create local versions of the
, but instead partitioning [n] into subsets, using the local statistics for each subsets to create local versions of the  ‘s, and then somehow gluing it all back together again. This failed to improve upon what we already have, and I think the reason is while the global
‘s, and then somehow gluing it all back together again. This failed to improve upon what we already have, and I think the reason is while the global  have no combinatorial lines, the same is not true of their local analogues (unless one takes a Cartesian product of several local
have no combinatorial lines, the same is not true of their local analogues (unless one takes a Cartesian product of several local  ‘s, but this seems to be rather lossy.) Indeed, I still don’t know of any good example of a really large set with no combinatorial lines that isn’t somehow built out of the
‘s, but this seems to be rather lossy.) Indeed, I still don’t know of any good example of a really large set with no combinatorial lines that isn’t somehow built out of the  ‘s.
‘s.
The other thing I toyed with was trying to use the machinery of shifting and compression (in the spirit of Frankl, or Bollobas-Leader, or one of my papers with Ben Green) to try to get good answers to the k=2 problems (e.g. finding a good “robust” version of Sperner’s theorem, e.g. a Varnavides version). But this seems not to work too well. The problem seems to be that the extremisers for Sperner’s theorem don’t look much like downsets (they seem to be more like the boundary of a downset, though I don’t see how to exploit this). In any event, these techniques are quite specific to k=2 and would be unlikely to shed much light on k=3 except perhaps by analogy.
February 3, 2009 at 5:35 am |
( 57 ). On the topic of more analytic proofs of Sperner: I think I now see why Boris mentioned Kruskal-Katona in the same breath as Sperner. Let me try to sketch the connection I see. I’m sure it’s well known.
Let be odd for simplicity and write
be odd for simplicity and write  for the set of strings in
for the set of strings in  with exactly
with exactly 
 ‘s. Let
‘s. Let 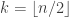 .
.
Let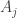 denote
denote 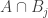 and let
and let 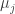 denote
denote 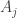 ‘s density within
‘s density within  .
.
One particular thing Sperner tells us is that if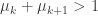 then
then  contains a “combinatorial line” (because the overall density of
contains a “combinatorial line” (because the overall density of  is at least that of
is at least that of  ‘s density within
‘s density within  ). I.e., there is
). I.e., there is  such that
such that  .
.
Here is a way to see that with Kruskal-Katona: K-K implies that the upper-shadow of
of 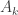 has density at least
has density at least 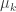 within
within  . Now together
. Now together  and
and  have density exceeding
have density exceeding  within
within  , hence they overlap.
, hence they overlap.
—
Indeed, I think you can get most of Sperner out of extending this argument. Let me be uncareful. Suppose that ‘s overall density exceeds that of
‘s overall density exceeds that of  within
within  . As an example, perhaps
. As an example, perhaps  has
has 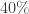 of the strings in
of the strings in  ,
, 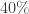 of the strings in
of the strings in  and
and 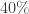 of the strings in
of the strings in 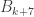 . Now K-K implies that
. Now K-K implies that  ‘s upper shadow is also at least
‘s upper shadow is also at least 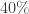 of
of  . And the upper shaddow of that is at least
. And the upper shaddow of that is at least 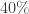 (basically) of
(basically) of 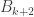 . Etc. When you get up to
. Etc. When you get up to  , you either get a collision and are done, or you have at least
, you either get a collision and are done, or you have at least 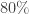 of
of  . Then you get at least
. Then you get at least 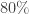 of
of 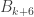 , and then you have
, and then you have  of
of 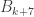 and you get a collision and are done.
and you get a collision and are done.
—
The reason I kind of like this proof is that there is an “analytic” proof of Kruskal-Katona that seems amenable to “robustification”.
Although to be honest, I can’t quite remember how we got talking about this subject just now…
February 3, 2009 at 6:14 am |
(58) The reason I mentioned Kruskal-Katona is that Sperner’s original proof of Sperner’s theorem involved pushing shadows towards the center level like Ryan indicated. He used simple double-counting argument, of which Kruskal-Katona is the modern descendant.
The point of the example I gave is to show that even if the shadow grows by only 1+o(1), it does not imply correlation with a single coordinate or even a small set of them.
The version of Kruskal-Katona qualitatively similar to what Karl Wimmer and Ryan proved was proved recently by Peter Keevash http://arxiv.org/abs/0806.2023
February 3, 2009 at 11:48 am |
59. . Look at the set
. Look at the set 
It is possible to show that
February 3, 2009 at 11:50 am |
60. Thread title: Jozsef’s alternative problem.
I’m going to start by adding a few small thoughts on things I was writing about yesterday, and after that I’ll read more carefully the recent batch of comments and see if I have any reactions to them. Yesterday (comment 23) I suggested the following variant of Jozsef’s alternative problem (comment 2). Suppose is a dense subset of the set of all pairs
is a dense subset of the set of all pairs  of subsets of
of subsets of ![\null[n]](https://s0.wp.com/latex.php?latex=%5Cnull%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Can you find three disjoint sets
. Can you find three disjoint sets  ,
,  and
and  such that
such that  ,
, 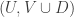 and
and 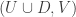 all belong to
all belong to  ?
?
This question can’t have grabbed people’s attention much, since the answer is a trivial no. Just let be the set of all pairs
be the set of all pairs  such that
such that  . That’s definitely almost all pairs.
. That’s definitely almost all pairs.
However, can we make a sensible question out of this? A sensible question would be some density-type condition on that would guarantee a triple of the given kind. An obvious candidate would be to insist from the start that
that would guarantee a triple of the given kind. An obvious candidate would be to insist from the start that  is a set of disjoint pairs of sets. Note that there are
is a set of disjoint pairs of sets. Note that there are  of these, since each element can choose whether to go into
of these, since each element can choose whether to go into  ,
,  or neither.
or neither.
Just for fun, let’s represent each pair of disjoint sets as a sequence of 1s, 2s and 3s. Then a configuration of the desired kind is … a combinatorial line.
of disjoint sets as a sequence of 1s, 2s and 3s. Then a configuration of the desired kind is … a combinatorial line.
So this rather nice new question was in fact the question we started with. But at least this thought process clarifies the relationship between Jozsef’s problem and density Hales-Jewett.
February 3, 2009 at 1:34 pm |
61. Thread title: Varnavides. (This is the thread devoted to thinking about how to find a suitable statement that says that a dense set doesn’t just contain one combinatorial line but contains “a dense subset of all possible combinatorial lines”. The problem is that the most natural interpretation of this is false. See Jason Dyer’s comment just after 38 for numbers of other comments that belong to this thread.)
I want to continue with what I was talking about in 55. At the moment I am in the happy state of not knowing why we are not already done. Of course, I don’t for a moment think that we are done, but being in this position is always nice because you know that by the time you see properly why you aren’t done you are guaranteed to understand the problem better.
The grounds for this unrealistic optimism are that we now seem to have an easy solution to the Varnavides problem. Just to recap, the problem is that one would expect any triangle-removal argument to lead not just to the conclusion that a dense set contains one combinatorial line, but to the conclusion that the number of combinatorial lines it contains is within a constant of the trivial maximum (which is what you get when your set has density 1).
To recap further, this statement is false for density Hales-Jewett, because you can take as your set the set of all sequences that take each value roughly
that take each value roughly  times.
times. . (This is the number of combinatorial lines, because each point chooses whether to be 1, 2, 3 or variable.)
. (This is the number of combinatorial lines, because each point chooses whether to be 1, 2, 3 or variable.)
Standard probabilistic arguments show that almost all sequences have this form, but the size of the set of variable coordinates in any combinatorial line in this set is very small, and this can be used to show that the set of combinatorial lines has cardinality far smaller than
Let’s regard this as a Varnavides-summary comment. I’ll continue this line of thinking in my next comment.
February 3, 2009 at 1:47 pm |
62. Thread title: Varnavides.
A problem we were grappling with yesterday was how to put a natural measure on the set of combinatorial lines in such a way that the variable sets were forced to be small. Here is a proposal for a solution to that problem. I’ve already hinted at it in 55, and I think Terry may have had it in the back of his mind at around 39 and 40. Briefly, the suggestion is to restrict to a large triangular grid of slices . Let me elaborate on what I mean by this.
First, a slice is a set of the form , where that is the set of all
, where that is the set of all  with
with  1s,
1s,  2s and
2s and  3s. (There’s redundancy in the notation, since
3s. (There’s redundancy in the notation, since  , but the symmetry more than makes up for it.)
, but the symmetry more than makes up for it.)
Secondly, a triangular grid is a subset of the set
of the set  of the form
of the form  for some choice of
for some choice of  such that
such that  and
and 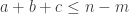 . Triangular grids are just translates of
. Triangular grids are just translates of  that live inside
that live inside 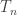 . (It would be possible also to consider dilated triangular grids where you look at points of the form
. (It would be possible also to consider dilated triangular grids where you look at points of the form  for some fixed
for some fixed  , but at the moment I have no need of these.)
, but at the moment I have no need of these.)
A triangular grid of slices is then just a collection of slices indexed by a triangular grid.
Again, I think it makes sense to stop this comment here and continue in a new comment.
February 3, 2009 at 2:03 pm |
63. Thread title: Varnavides.
Now I make the following claim. Suppose we choose a random point in![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as follows. First we choose a random element of
as follows. First we choose a random element of  , where the probability of choosing
, where the probability of choosing 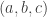 is
is  . (Equivalently, we choose a random element of
. (Equivalently, we choose a random element of ![\null [3]^{n-m}](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5E%7Bn-m%7D&bg=ffffff&fg=333333&s=0&c=20201002) and let
and let 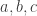 be the number of 1s, 2s and 3s.) Next, we choose a random element
be the number of 1s, 2s and 3s.) Next, we choose a random element  of
of  , this time from the uniform distribution. Finally, we choose a random element of the slice
, this time from the uniform distribution. Finally, we choose a random element of the slice  . The claim is that the resulting probability distribution on
. The claim is that the resulting probability distribution on ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is very close to uniform. (By this I mean that any event in one distribution has a probability that’s within a very small additive constant of the probability according to the other distribution.) The reason for this is that when
is very close to uniform. (By this I mean that any event in one distribution has a probability that’s within a very small additive constant of the probability according to the other distribution.) The reason for this is that when 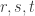 are all smaller than
are all smaller than  and
and 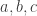 are all around
are all around  (as they almost always are), then the ratio of
(as they almost always are), then the ratio of  to
to  is very close to 1.
is very close to 1.
An averaging argument tells us that there must exist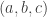 close to
close to 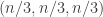 such that a positive proportion of points in the triangular grid of slices indexed by
such that a positive proportion of points in the triangular grid of slices indexed by  belong to
belong to  . So instead of looking at density Hales-Jewett in all of
. So instead of looking at density Hales-Jewett in all of ![\null[3]^m](https://s0.wp.com/latex.php?latex=%5Cnull%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) we can try to prove that if
we can try to prove that if  is a dense subset of a big triangular grid of slices, then
is a dense subset of a big triangular grid of slices, then  contains a combinatorial line. In my next comment I’ll try to say why I think this is a good thing to do.
contains a combinatorial line. In my next comment I’ll try to say why I think this is a good thing to do.
February 3, 2009 at 2:25 pm |
64. Thread title: Varnavides.
Note that if we restrict to a large triangular grid of slices in this way, then we have various convenient properties. For example, all the points in all the slices have about each of 1s, 2s and 3s. And any combinatorial line has a variable set of size at most
each of 1s, 2s and 3s. And any combinatorial line has a variable set of size at most  . I’d like to claim now that a Varnavides-type theorem applies to large triangular grids: that is, if you have a dense subset of a large triangular grid of slices, then not only do you get a combinatorial line, but you even get within a constant of the total number of combinatorial lines in the entire grid. The idea here, by the way, is not (yet) to try to prove this theorem directly, but just to check that it is true by showing that it follows from density Hales-Jewett.
. I’d like to claim now that a Varnavides-type theorem applies to large triangular grids: that is, if you have a dense subset of a large triangular grid of slices, then not only do you get a combinatorial line, but you even get within a constant of the total number of combinatorial lines in the entire grid. The idea here, by the way, is not (yet) to try to prove this theorem directly, but just to check that it is true by showing that it follows from density Hales-Jewett.
Here’s how density Hales-Jewett can be applied. Let’s assume that is a dense subset of the triangular grid of slices indexed by
is a dense subset of the triangular grid of slices indexed by  , where
, where 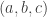 belongs to
belongs to  . Suppose that
. Suppose that 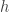 is a fixed constant chosen to be large enough that every subset of
is a fixed constant chosen to be large enough that every subset of ![\null [3]^h](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5Eh&bg=ffffff&fg=333333&s=0&c=20201002) of size at least
of size at least 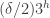 contains a combinatorial line. Now for every
contains a combinatorial line. Now for every  , which means almost every
, which means almost every 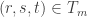 since we’re assuming that
since we’re assuming that  is much much larger than
is much much larger than 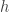 , let us randomly choose
, let us randomly choose 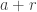 places to put a 1,
places to put a 1,  places to put a 2 and
places to put a 2 and 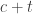 places to put a 3. That leaves
places to put a 3. That leaves 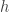 places unfilled. The set of ways of filling those places is a copy of
places unfilled. The set of ways of filling those places is a copy of ![\null [3]^h](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5Eh&bg=ffffff&fg=333333&s=0&c=20201002) , so if it contains at least
, so if it contains at least 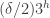 points from
points from  , then it contains a Hales-Jewett line.
, then it contains a Hales-Jewett line.
An averaging argument shows that that happens with …
OK, I’m sorry to say that I do after all need to consider dilated triangular grids. Since that is the case, I’m going to abandon this attempt to be precise, for now at least, and simply say in the next comment what I think should happen. Then maybe others will tell me that they’re not convinced, or that they are convinced, and perhaps we can zero in on something.
February 3, 2009 at 2:48 pm |
65. If there’s a “Sperner” thread I guess this would be it.
Boris, thanks for the reference to the Keevash paper. While you’re handing out references :)… I guess it would be relevant to ask, Is there a Sperner’s Theorem known for different product distributions on ?
?
In the case relevant to us: What is the densest antichain in under the
under the  -biased product distribution?
-biased product distribution?
This must be known…
February 3, 2009 at 3:16 pm |
66. Thread title: Varnavides.
All I was really trying to get at in 63 was this. Choose a random translate and dilate of the triangular grid in such a way that it is a subset of
in such a way that it is a subset of  . If you make the dilates you look at all have width at most
. If you make the dilates you look at all have width at most 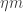 for some smallish
for some smallish  , then nearly all aligned equilateral triangles in
, then nearly all aligned equilateral triangles in  will be included in one of these copies of
will be included in one of these copies of  about the same number of times.
about the same number of times.
Now let be a dilate and translate of
be a dilate and translate of  , where the constant of dilation is
, where the constant of dilation is  . One can randomly choose a copy
. One can randomly choose a copy  of
of ![\null [3]^h](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5Eh&bg=ffffff&fg=333333&s=0&c=20201002) inside
inside ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) in such a way that the numbers of 1s, 2s and 3s is given by points in
in such a way that the numbers of 1s, 2s and 3s is given by points in  is given by points in
is given by points in  . To do this, suppose that
. To do this, suppose that  . Randomly fix
. Randomly fix  coordinates to be 1,
coordinates to be 1,  coordinates to be 2,
coordinates to be 2,  coordinates to be 3, and randomly partition the rest of
coordinates to be 3, and randomly partition the rest of ![\null[n]](https://s0.wp.com/latex.php?latex=%5Cnull%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) into
into 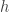 sets
sets 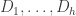 , each of size
, each of size  . Then our random copy
. Then our random copy  consists of all sequences that are constant on each
consists of all sequences that are constant on each 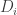 and take the given fixed values outside the
and take the given fixed values outside the 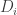 .
.
My claim is that a simple averaging argument should show that if a positive proportion of these contain a Hales-Jewett line (as I claim they will if
contain a Hales-Jewett line (as I claim they will if  has density
has density  ) then the number of Hales-Jewett lines in
) then the number of Hales-Jewett lines in  is within a constant of the trivial maximum. I’m going to leave this for now as I feel that to do it properly I’d have to go away and write something down, and I’m not allowing myself to do that.
is within a constant of the trivial maximum. I’m going to leave this for now as I feel that to do it properly I’d have to go away and write something down, and I’m not allowing myself to do that.
February 3, 2009 at 3:26 pm |
67. Possible thread title: triangle removal.
Actually, I was trying to prove a Varnavides-type result not because we need it but because it was a sort of reality check: if we can’t get such a result then it is unlikely that triangle removal will work. But since I’m now fairly confident that we can get such a result, I want to see what happens if one just goes ahead and tries to apply some kind of triangle-removal lemma in the case where is a dense subset of a large triangular grid of slices.
is a dense subset of a large triangular grid of slices.
So let’s fix notation again. I’m going to suppose that is a dense subset of the union of all slices
is a dense subset of the union of all slices  , where
, where 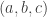 is some fixed element of
is some fixed element of  and
and  ranges over
ranges over  . Also, I’m assuming that
. Also, I’m assuming that 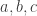 are all around
are all around  so that all slices have about the same size.
so that all slices have about the same size.
Now I want to apply the trick from comments N and P. So what is the graph now? Instead of taking to be the full power set of
to be the full power set of ![\null[n]](https://s0.wp.com/latex.php?latex=%5Cnull%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) I want to take just those sets that could conceivably occur as the set of 1s in a sequence in
I want to take just those sets that could conceivably occur as the set of 1s in a sequence in  . And that’s all sets of size
. And that’s all sets of size 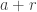 , where
, where 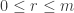 . Similarly,
. Similarly,  consists of all sets of size between
consists of all sets of size between  and
and 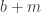 , and
, and  consists of all sets of size between
consists of all sets of size between  and
and  . The edges are as before: I join
. The edges are as before: I join  to
to 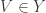 if the sequence that’s 1 on
if the sequence that’s 1 on  and 2 on
and 2 on  and 3 everywhere else belongs to
and 3 everywhere else belongs to  . And similarly for the other two bipartite graphs. And clearly a non-degenerate triangle in this graph gives rise to a combinatorial line.
. And similarly for the other two bipartite graphs. And clearly a non-degenerate triangle in this graph gives rise to a combinatorial line.
I’ll think about the implications of this in my next comment.
February 3, 2009 at 3:44 pm |
68. Thread title: triangle removal.
I didn’t mention it explicitly, but of course a necessary condition for joining to
to 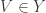 is still that
is still that  and
and  should be disjoint. So the first reason that we are not yet done is that the graphs are still very sparse, since two random sets of size
should be disjoint. So the first reason that we are not yet done is that the graphs are still very sparse, since two random sets of size  have a tiny probability of being disjoint. So the question is, has anything been gained by restricting attention to a large triangular grid of slices? Something’s been gained from the Varnavides point of view, I think, but has anything been gained from the triangle-removal point of view? That’s what I’m asking.
have a tiny probability of being disjoint. So the question is, has anything been gained by restricting attention to a large triangular grid of slices? Something’s been gained from the Varnavides point of view, I think, but has anything been gained from the triangle-removal point of view? That’s what I’m asking.
At the moment it feels, rather disappointingly, as though nothing has been gained. It’s still the case that the graph where you join two sets if they are disjoint is importantly non-quasirandom, since the remark made in comment LL carries over to this context too.
I would hazard a guess that there are two morals to draw from this.
(i) It may still be quite convenient to restrict to a triangular grid of slices, in order to make certain distributions uniform.
(ii) We are probably forced to consider obstructions to uniformity.
In fact, there’s a different way of justifying (ii). At some point, if a triangle-removal argument is going to work, we will have to prove a statement to the effect that if you have three bipartite graphs that are all “regular” and “dense”, then they must give rise to lots of triangles. In the normal dense-graphs case, “regular” just means quasirandom, and it even suffices for just one of the three bipartite graphs to be regular, provided there are plenty of vertices in the third set with high degree in both of the first two sets.
In our case, there is a one-to-one correspondence between edges of one of the bipartite graphs and points in![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . So this suggests that at some point we are going to have to understand what a “regular” or “quasirandom” subset of
. So this suggests that at some point we are going to have to understand what a “regular” or “quasirandom” subset of ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is like. To be continued in the next comment.
is like. To be continued in the next comment.
February 3, 2009 at 3:54 pm |
69. Thread title: obstructions to uniformity.
What does it mean to “understand what a quasirandom subset of![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is like? For those who don’t find the answer obvious, here’s an attempt to explain.
is like? For those who don’t find the answer obvious, here’s an attempt to explain.
(i) We are looking for a definition of quasirandomness.
(ii) Experience with other problems suggests that this definition should have the following property: if is a dense quasirandom subset of
is a dense quasirandom subset of ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) and
and  is an arbitrary dense subset of
is an arbitrary dense subset of ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , then there is a combinatorial line
, then there is a combinatorial line 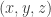 with
with  ,
,  and
and  . Indeed, one should have not just one such combinatorial line but a dense set of such combinatorial lines. (Here is a place where having a Varnavides-type statement is actually a big help and not just a mere reassurance.)
. Indeed, one should have not just one such combinatorial line but a dense set of such combinatorial lines. (Here is a place where having a Varnavides-type statement is actually a big help and not just a mere reassurance.)
(iii) Experience with other problems also suggests that if does not have the property in (ii) then there will be some simple reason for it. An example of such a reason is that
does not have the property in (ii) then there will be some simple reason for it. An example of such a reason is that 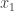 might be 1 for every
might be 1 for every  . (This would fail to have the property in (ii) because we could take
. (This would fail to have the property in (ii) because we could take  to be the set of all sequences with
to be the set of all sequences with  .)
.)
(iv) If one can think of all possible “simple reasons” of the kind discussed in (iii), then it is often possible to pass to substructures or partitions of the ground set and obtain density or energy increases. (If you don’t know what this means, it’s not too important at this stage. The main point is that if you can do (iii) then there are standard techniques for using what you’ve done. In many other contexts, once you’ve got (iii) the problem is basically solved.)
In the next comment, I’m going to write down all the obstructions to uniformity that I can think of. (An obstruction to uniformity is basically what I called a “simple reason” in (iii).)
February 3, 2009 at 4:15 pm |
70. Thread title: obstructions to uniformity.
Before I start this comment, I want to make a metacomment. If you are reading this and are not familiar with the kinds of techniques people are throwing around, and therefore feel you can’t really contribute, here is a place where you don’t necessarily need to know anything to contribute: we have a simply stated question, which may have a simple answer. (The question will be of the form, “Here are all the Xs I can think of off the top of my head. Can anyone think of any more?”)
For the purposes of this comment, I’ll define a set![A\subset[3]^n](https://s0.wp.com/latex.php?latex=A%5Csubset%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  to be uniform if for every set
to be uniform if for every set ![B\subset[3]^n](https://s0.wp.com/latex.php?latex=B%5Csubset%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  the number of combinatorial lines
the number of combinatorial lines  is approximately
is approximately  times the number of combinatorial lines in
times the number of combinatorial lines in ![\null[3]^n](https://s0.wp.com/latex.php?latex=%5Cnull%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . Similar definitions apply if we restrict to a triple of slices or a triangular grid of slices.
. Similar definitions apply if we restrict to a triple of slices or a triangular grid of slices.
Obstruction 1. In any combinatorial line, a coordinate must either take all three values or just one. Therefore, a set is not uniform unless the number of sequences
is not uniform unless the number of sequences  in
in  such that
such that  is roughly
is roughly  for every
for every ![i\in[n]](https://s0.wp.com/latex.php?latex=i%5Cin%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and 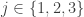 . To prove this seems to be not quite trivial. An obvious set
. To prove this seems to be not quite trivial. An obvious set  to consider is to take
to consider is to take  such that the number of points with
such that the number of points with  is significantly less than
is significantly less than  and let
and let  be the set of all sequences
be the set of all sequences  such that
such that  . Then the only points in
. Then the only points in  that can make lines with
that can make lines with  are ones with
are ones with  . Therefore, if we get the right number of combinatorial lines in
. Therefore, if we get the right number of combinatorial lines in  , then we can drop to the subset
, then we can drop to the subset 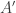 that consists of those points only and we find that we get more combinatorial lines than we would expect (given the densities of the restrictions of
that consists of those points only and we find that we get more combinatorial lines than we would expect (given the densities of the restrictions of  and
and  to
to  ). I think one can mess around with this information and obtain a set
). I think one can mess around with this information and obtain a set  that proves that
that proves that  is not uniform.
is not uniform.
Given that that was slightly tricky (it might be nice to do it properly though), I’ll restrict attention for now to what I might call strong obstructions to uniformity. I’ll call a set strongly non-uniform if I can find a dense set
strongly non-uniform if I can find a dense set  such that there are no combinatorial lines
such that there are no combinatorial lines 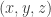 with
with  ,
,  and
and  . So finding more strong obstructions really is a genuinely elementary problem (in the sense of not needing special knowledge).
. So finding more strong obstructions really is a genuinely elementary problem (in the sense of not needing special knowledge).
Having come to this decision, let me start again in a new comment.
February 3, 2009 at 4:49 pm |
71. Thread title: obstructions to uniformity.
Strong obstruction 1. If there exist and
and  such that
such that  for every
for every  in
in  , then
, then  is strongly non-uniform. Proof: let
is strongly non-uniform. Proof: let  and let
and let  be the set of all sequences such that
be the set of all sequences such that  . You can’t have a combinatorial line in which the
. You can’t have a combinatorial line in which the  th coordinate is
th coordinate is  once and
once and  twice.
twice.
Strong obstruction 2. If there is a positive integer such that for every
such that for every  the number of 1s, 2s and 3s in
the number of 1s, 2s and 3s in  is always the same mod
is always the same mod  , then
, then  is strongly non-uniform. Proof: If
is strongly non-uniform. Proof: If  and
and  belong to a combinatorial line and have the same number of 1s, 2s and 3s mod
belong to a combinatorial line and have the same number of 1s, 2s and 3s mod  , then the size of the variable set must be a multiple of
, then the size of the variable set must be a multiple of  . Therefore, we can choose
. Therefore, we can choose  to be a set where the sequences again have fixed numbers of 1s, 2s and 3s mod
to be a set where the sequences again have fixed numbers of 1s, 2s and 3s mod  , but different numbers from those of
, but different numbers from those of  .
.
Strong obstruction 3. This generalizes the previous example. Suppose that for every we know that the number of 1s belongs to a set
we know that the number of 1s belongs to a set  of residues mod
of residues mod  , the number of 2s belongs to a set
, the number of 2s belongs to a set 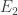 , and the number of 3s belongs to a set
, and the number of 3s belongs to a set 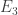 . Now let
. Now let 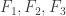 be sets of residues mod
be sets of residues mod  , and let
, and let  be the set of all sequences with the number of 1s in
be the set of all sequences with the number of 1s in 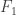 etc. If
etc. If  and
and  are points of
are points of  that belong to a combinatorial line, then let’s suppose that to get from
that belong to a combinatorial line, then let’s suppose that to get from  to
to  you change some 2s to 3s. This tells us that the size of the variable set belongs to
you change some 2s to 3s. This tells us that the size of the variable set belongs to 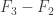 mod
mod  . This in turn tells us that the number of 1s in the third point of the line belongs to
. This in turn tells us that the number of 1s in the third point of the line belongs to  mod
mod  . So if
. So if  is disjoint from any set of the form
is disjoint from any set of the form  , then
, then  is strongly non-uniform. And similarly for the other variables. Of course, if
is strongly non-uniform. And similarly for the other variables. Of course, if  doesn’t consist of all residues, then one might say that we could take
doesn’t consist of all residues, then one might say that we could take 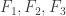 to be singletons. But that’s true only if
to be singletons. But that’s true only if  is small, since otherwise
is small, since otherwise  is not dense. This example works even when
is not dense. This example works even when  is large — it can tend to infinity with
is large — it can tend to infinity with  . (An example might be when we insist that for all sequences the numbers of 1s, 2s and 3s is between
. (An example might be when we insist that for all sequences the numbers of 1s, 2s and 3s is between  and
and  mod
mod  for some small constant
for some small constant  .)
.)
Strong obstruction 4. One can generalize further by passing to a subset. That is, instead of looking at the numbers of 1s, 2s and 3s in the whole sequence, one just looks at the numbers of 1s, 2s and 3s in some specified set of coordinates. The proof is more or less the same.
of coordinates. The proof is more or less the same.
I haven’t tried hugely hard to find more obstructions. Does anyone know of any? Does Boris’s comment 44 have any implications here?
February 3, 2009 at 4:52 pm |
72. Regarding the definition of triangular grid in #62 at 1:47 pm, to make sure I understood it properly, should it say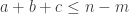 instead of
instead of  ?
?
[Thanks — I’ve changed it now.]
Regarding the obstructions to the uniformity mentioned in #69 3:54 pm, doesn’t it follow from discussion about Varnavides that to talk about pseudorandom sets we want our sets to be dense subsets in a suitable union of that live near the middle of the lattice?
that live near the middle of the lattice?
Answer to Ryan’s question from #65 at 2:48 pm: I can’t think of a reference for the result you want, but it follows from LYM inequality that the level of largest weight is the largest antichain.
February 3, 2009 at 5:03 pm |
73. One can generalize obstructions from #71 at 4:49 pm further: instead of counting number of 1’s 2’s and 3′, weight individual coordinates by small integer weights. Passing to a subset is a special case of that when some weights are zero.
[Not sure what was going wrong, but I’ve deleted the other two copies of this comment.]
February 3, 2009 at 6:11 pm |
74. Thread title: obstructions to uniformity.
In answer to Boris’s question (72, second paragraph), I agree that it looks as if any definition of pseudorandomness will have to restrict attention to something like a triangular grid of slices near the middle. But I was hoping that we could do things in two stages. Stage 1 would be to find strong obstructions to uniformity. Then in stage 2 one would weaken the definition back to what I first had: instead of getting no combinatorial lines in one just asks for a number that differs from what you would expect for a random
one just asks for a number that differs from what you would expect for a random  . At that point, one would have to ask, “What do we expect from a random
. At that point, one would have to ask, “What do we expect from a random  ?” and then it would become important to restrict to a triangular grid or some such structure.
?” and then it would become important to restrict to a triangular grid or some such structure.
February 3, 2009 at 6:24 pm |
[…] Apparently, the original proof of the Density Hales-Jewett theorem used ergodic theory; Gowers’ challenge is to find a purely combinatorial proof of the theorem. More background can be found here. Serious discussion of the problem starts here. […]
February 3, 2009 at 6:25 pm |
75. Thread title: obstructions to uniformity.
Let me check that I understand Boris’s comment 73. The idea is to pick an integer and a sequence of integers
and a sequence of integers 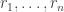 , and to let
, and to let  be the set of all sequences
be the set of all sequences  such that
such that  belongs to a specified set
belongs to a specified set  of residues.
of residues.
Now choose to be the set of all sequences
to be the set of all sequences  such that
such that  mod
mod  . Then if
. Then if  ,
,  and
and  all lie in a combinatorial line, and
all lie in a combinatorial line, and  and
and  belong to
belong to  , then the characteristic function
, then the characteristic function  of the set of variable coordinates (or wildcards, as some are calling them) has the property that $\sum_{i\in D}r_i$ belongs to
of the set of variable coordinates (or wildcards, as some are calling them) has the property that $\sum_{i\in D}r_i$ belongs to  mod
mod  . It follows that
. It follows that 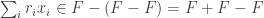 . So if we can find a dense set
. So if we can find a dense set  of residues mod
of residues mod  such that
such that  then
then  is strongly nonuniform.
is strongly nonuniform.
That neatly covers a lot of examples. Can anyone think of any more? Or what about heuristic arguments that these are the only examples? (At the moment, my guess is that there are further examples waiting to be discovered.)
February 3, 2009 at 6:39 pm |
76. Thread title: obstructions to uniformity.
I think I’ve got a further generalization of 75. Just replace the group of integers mod by an arbitrary finite Abelian group
by an arbitrary finite Abelian group  . So now
. So now 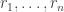 are elements of
are elements of  , and
, and  and
and  are dense subsets of
are dense subsets of  . Then repeat exactly what I wrote in 75 except that “residues” or “residues mod
. Then repeat exactly what I wrote in 75 except that “residues” or “residues mod  ” should be replaced by “elements of
” should be replaced by “elements of  “.
“.
February 3, 2009 at 6:42 pm |
77. Thread title: Is triangle removal still necessary?
Greetings again from the Pacific Standard Time zone!
I had one thought about the bigger picture. The initial reasoning in the main post goes like this:
1. The standard proof of the corners theorem uses the triangle removal lemma.
2. The DHJ theorem generalises the corners theorem.
3. Hence, it is natural to look for a proof of DHJ that uses (some generalisation of) the triangle removal lemma.
But, now that we have used the corners theorem in our arguments (to locate a triple of rich tuples), the above logic loses quite a bit of its force. Indeed, if we look at the standard way in which the corners theorem is embedded in the DHJ theorem, by representing a set
of rich tuples), the above logic loses quite a bit of its force. Indeed, if we look at the standard way in which the corners theorem is embedded in the DHJ theorem, by representing a set ![A \subset [n]^2](https://s0.wp.com/latex.php?latex=A+%5Csubset+%5Bn%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) as the set
as the set ![{\mathcal F}(A) := \bigcup_{(a,b) \in A} \Gamma_{a,b,3n-a-b} \subset [3]^{3n}](https://s0.wp.com/latex.php?latex=%7B%5Cmathcal+F%7D%28A%29+%3A%3D+%5Cbigcup_%7B%28a%2Cb%29+%5Cin+A%7D+%5CGamma_%7Ba%2Cb%2C3n-a-b%7D+%5Csubset+%5B3%5D%5E%7B3n%7D&bg=ffffff&fg=333333&s=0&c=20201002) , we can see that any new proof of DHJ we have will not give any new proof of the corners theorem for a given dense set A, since we will need to use the corners theorem for precisely that set A in order to get the rich triples. So there is no a priori reason for the rest of the proof to involve a triangle removal argument at all. (Of course, triangle removal is still implicitly used in the invocation of the corners theorem.)
, we can see that any new proof of DHJ we have will not give any new proof of the corners theorem for a given dense set A, since we will need to use the corners theorem for precisely that set A in order to get the rich triples. So there is no a priori reason for the rest of the proof to involve a triangle removal argument at all. (Of course, triangle removal is still implicitly used in the invocation of the corners theorem.)
(Note that the sketch of Sperner via Kruskal-Katona in Ryan.57 has this flavour: one uses things like the pair removal theorem from Gowers.21 to locate a rich pair , and then uses completely different arguments from then on.)
, and then uses completely different arguments from then on.)
There is however one caveat that seems to suggest that either some vestige of triangle-removal still remains in the rest of the argument, or else some preliminary regularisation is needed. The reason for this is that there are other ways to embed the corners problem into the DHJ problem For instance, one can embed a corner-free set![A \subset [n]^3](https://s0.wp.com/latex.php?latex=A+%5Csubset+%5Bn%5D%5E3&bg=ffffff&fg=333333&s=0&c=20201002) into a combinatorial line-free set
into a combinatorial line-free set ![{\mathcal F}(A) \times {\mathcal F}(A) \subset [3]^{6n}](https://s0.wp.com/latex.php?latex=%7B%5Cmathcal+F%7D%28A%29+%5Ctimes+%7B%5Cmathcal+F%7D%28A%29+%5Csubset+%5B3%5D%5E%7B6n%7D&bg=ffffff&fg=333333&s=0&c=20201002) . The richness profile
. The richness profile 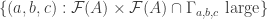 of this set is essentially A+A, and thus much more likely to contain corners than the original set A. So if we were to somehow prove DHJ on a rich triple without any further triangle removal, this would imply a “nearly-triangle-removal-lemma-free” proof of the corners theorem of A, reducing it to the substantially simpler-looking problem of finding corners in A+A.
of this set is essentially A+A, and thus much more likely to contain corners than the original set A. So if we were to somehow prove DHJ on a rich triple without any further triangle removal, this would imply a “nearly-triangle-removal-lemma-free” proof of the corners theorem of A, reducing it to the substantially simpler-looking problem of finding corners in A+A.
But if we could find some way to “detect” this sort of “product structure” in the set , and pass to an appropriate sub-index set of [n] in order to isolate a more “essential” component of this set, such as
, and pass to an appropriate sub-index set of [n] in order to isolate a more “essential” component of this set, such as  , then this objection may disappear. This of course ties in with the obstructions-to-uniformity thread, and also with the counterexamples mentioned in Gowers.20, Gowers.38, and the “hereditary richness” idea I proposed in Terry.40, and maybe also the stationarity in Terry.4, Austin.16.
, then this objection may disappear. This of course ties in with the obstructions-to-uniformity thread, and also with the counterexamples mentioned in Gowers.20, Gowers.38, and the “hereditary richness” idea I proposed in Terry.40, and maybe also the stationarity in Terry.4, Austin.16.
A serious difficulty, though, would be if there are many other ways to embed corners into DHJ that are not easily “detectable” by inspecting things like the richness profile of the embedded set with respect to various index sets. If there are an enormous number of such embeddings then it seems unlikely that we can eradicate triangle removal completely from the remainder of our arguments.
February 3, 2009 at 6:46 pm |
78. Thread title: for small n
for small n
@Sune.59: The lower bound you have compares pretty well with the upper bound
you have compares pretty well with the upper bound  . It may be possible to shave the upper bound down a notch, by trying to figure out what the extremal subsets of
. It may be possible to shave the upper bound down a notch, by trying to figure out what the extremal subsets of ![{}[3]^3](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E3&bg=ffffff&fg=333333&s=0&c=20201002) are that have 18 elements but no combinatorial lines. Any 54-element subset of
are that have 18 elements but no combinatorial lines. Any 54-element subset of ![{}[3]^4](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E4&bg=ffffff&fg=333333&s=0&c=20201002) with no combinatorial lines must be extremal on every three-dimensional slice, which looks unlikely if there are few extremals.
with no combinatorial lines must be extremal on every three-dimensional slice, which looks unlikely if there are few extremals.
February 3, 2009 at 6:49 pm |
79. Thread title: Sperner
As will be obvious to many people, given some of the discussion, the question I asked in 28 is not yet a good one. Indeed, if we take both and
and  to be the set of all sets of size between
to be the set of all sets of size between  and
and 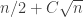 , then there will be far fewer than
, then there will be far fewer than  disjoint pairs, but it will be very hard to remove all disjoint pairs.
disjoint pairs, but it will be very hard to remove all disjoint pairs.
However, in the light of the Varnavides discussion, there is a natural way of rescuing the question. No time to check whether the result is sensible. Let’s just restrict attention to sets of size between and
and  for some fairly small
for some fairly small  . If
. If  and
and  are two subsets of this “middle part” of the power set of
are two subsets of this “middle part” of the power set of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) such that the number of disjoint pairs
such that the number of disjoint pairs  with
with  and
and 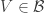 is far smaller than the number of disjoint pairs of sets of sizes between
is far smaller than the number of disjoint pairs of sets of sizes between  and
and  , does it follow that we can remove a small number of sets from
, does it follow that we can remove a small number of sets from 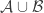 and end up with no disjoint pairs?
and end up with no disjoint pairs?
February 3, 2009 at 6:53 pm |
80. Thread title: Sperner
Actually, one might as well just restrict to single layers rather than a whole cluster of layers around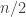 . Choose
. Choose  slightly less than
slightly less than 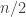 , say, and make
, say, and make  and
and  consist of subsets of the set of sets of size
consist of subsets of the set of sets of size  .
.
February 3, 2009 at 7:07 pm |
81. I am not sure whether generalization of Gowers #76 at 6:39 pm is truly a generalization since if a set F is nonuniform (as it must be for to hold), then it correlates with some character. That should imply correlation with some other set for which G=cyclic.
to hold), then it correlates with some character. That should imply correlation with some other set for which G=cyclic.
February 3, 2009 at 7:23 pm |
82. Re Sperner:
I have to run to class in a second so I can’t say if this is actually be relevant to TimG.79,80, but…
See this paper (and its referencers/referencees) for the theory on structure vs. pseudorandomness for independent sets in Kneser graphs:
http://www.ams.org/mathscinet-getitem?mr=2178966
February 3, 2009 at 7:45 pm |
83. Thread title: for small n.
for small n.
In comment 40, the set was introduced. This set only includes lines
was introduced. This set only includes lines  with
with 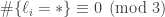 and
and  . So when n=4, we can just exclude (still thinking in
. So when n=4, we can just exclude (still thinking in  ) points
) points  and
and  .
.
This shows that .
.
For n=5, we can keep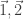 excluded, and omit the extra 15 points given by any choice of
excluded, and omit the extra 15 points given by any choice of 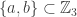 plugged into each of
plugged into each of 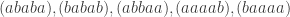 . This is decidedly less elegant than the n=4 case, but we see that
. This is decidedly less elegant than the n=4 case, but we see that
February 3, 2009 at 8:12 pm |
84. Thread title: for small n.
for small n.
@Tyler.83: nice! It seems that just excluding those x for which already knocks out a significant fraction of combinatorial lines, at least when n is small. It may be that some secondary set of a similar nature can then be removed to knock out quite a few more lines for medium n (e.g. n = 5-10), at which point the rest can be picked off by ad hoc methods. This may lead the way to suggest a different asymptotic lower bound than the current Behrend-based lower bound of
already knocks out a significant fraction of combinatorial lines, at least when n is small. It may be that some secondary set of a similar nature can then be removed to knock out quite a few more lines for medium n (e.g. n = 5-10), at which point the rest can be picked off by ad hoc methods. This may lead the way to suggest a different asymptotic lower bound than the current Behrend-based lower bound of 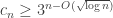 . If so, this may provide an excellent set of examples with which to test the upper bound strategies (the Behrend example tends to be rather intractable to compute with in practice).
. If so, this may provide an excellent set of examples with which to test the upper bound strategies (the Behrend example tends to be rather intractable to compute with in practice).
So it might be worth trying to push the lower bounds for , etc. as best we can, though it’s much less likely now that we will be able to compute these numbers exactly. (I don’t see the upper bounds budging much from the trivial
, etc. as best we can, though it’s much less likely now that we will be able to compute these numbers exactly. (I don’t see the upper bounds budging much from the trivial 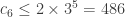 ,
,  – after all, density Hales-Jewett is a hard theorem – though I would imagine that one should be able to maybe knock one or two from the upper bound for, say
– after all, density Hales-Jewett is a hard theorem – though I would imagine that one should be able to maybe knock one or two from the upper bound for, say 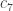 (after all, every 2-dimensional slice of an extremiser here has to have exactly 6 elements, and there are only three such slices available).)
(after all, every 2-dimensional slice of an extremiser here has to have exactly 6 elements, and there are only three such slices available).)
February 3, 2009 at 8:32 pm |
85. Thread title: A weak form of DHJ
As I mentioned in Terry.8, DHJ is the statement that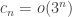 as
as 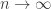 . This is a hard theorem. But one can at least give an easy proof of the weaker statement that the trivial bound
. This is a hard theorem. But one can at least give an easy proof of the weaker statement that the trivial bound  must be strict (i.e.
must be strict (i.e. 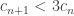 ) for infinitely many n, as follows.
) for infinitely many n, as follows.
Suppose that for all but finitely many n, then there exists an m, and an n much larger than m, such that
for all but finitely many n, then there exists an m, and an n much larger than m, such that  . Thus there exists a combinatorial line-free subset A of
. Thus there exists a combinatorial line-free subset A of ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with exactly
with exactly 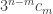 elements.
elements.
Now think of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as a whole bunch of parallel copies of
as a whole bunch of parallel copies of ![{}[3]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) , each parameterised by an element from
, each parameterised by an element from ![{}[3]^{n-m}](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E%7Bn-m%7D&bg=ffffff&fg=333333&s=0&c=20201002) . As A has exactly
. As A has exactly 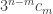 elements and is combinatorial line-free, each m-dimensional slice of A must have exactly
elements and is combinatorial line-free, each m-dimensional slice of A must have exactly 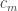 elements. We can assign each element of
elements. We can assign each element of ![{}[3]^{n-m}](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E%7Bn-m%7D&bg=ffffff&fg=333333&s=0&c=20201002) a colour based on exactly what the associated m-dimensional slice of A looks like; there are at most
a colour based on exactly what the associated m-dimensional slice of A looks like; there are at most  colours available.
colours available.
Now we use the colouring Hales-Jewett theorem, and conclude that if n is large enough depending on m, there exists a monochromatic line in![{}[3]^{n-m}](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E%7Bn-m%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Unwinding all this, we get a combinatorial line in A (note that all the slices of A are non-empty).
. Unwinding all this, we get a combinatorial line in A (note that all the slices of A are non-empty).
[Incidentally, an argument like this appears in Szemeredi’s original proof of Szemeredi’s theorem, though of course many many more things need to be done in that proof beyond this simple argument. A lot of Szemeredi’s argument, by the way, applies to Hales-Jewett, except for a crucial step where he applies what is now known as the Szemeredi regularity lemma. In the Hales-Jewett setting, the graph that one would wish to apply this lemma to is far too sparse for the strategy to work, it seems.]
February 3, 2009 at 8:42 pm |
[…] is getting quickly off the ground. There are several new posts in Gowers’s blog describing the project, its rules and motivation, and interesting discussions also over What’s new and in In theory. […]
February 3, 2009 at 9:03 pm |
86. Szemeredi’s proof of Roth’s theorem
While on the subject of Szemeredi’s arguments, Endre also has a simple combinatorial proof of Roth’s theorem (avoiding Fourier analysis or the regularity lemma), instead relying on the Szemeredi cube lemma. This can for instance be found in Graham-Rothschild-Spencer’s book, or Chapter 10.7 of my book with Van, or in Ernie’s writeup
Click to access szemeredi.pdf
the basic idea is to observe that if a set A in![\null [N]](https://s0.wp.com/latex.php?latex=%5Cnull+%5BN%5D&bg=ffffff&fg=333333&s=0&c=20201002) is dense, then it must contain a high-dimensional cube Q. If A has no arithmetic progressions, then 2 . Q – A must be essentially disjoint from A. Expressing the d-dimensional cube Q as the final element of a sequence
is dense, then it must contain a high-dimensional cube Q. If A has no arithmetic progressions, then 2 . Q – A must be essentially disjoint from A. Expressing the d-dimensional cube Q as the final element of a sequence  , where each
, where each  is one dimension larger than the preceding
is one dimension larger than the preceding  , and using the pigeonhole principle, we can find i such that
, and using the pigeonhole principle, we can find i such that  has roughly the same size as
has roughly the same size as  . We can write
. We can write  for some step
for some step  , and we thus see that
, and we thus see that  is very stable under shifting by
is very stable under shifting by  , and thus both it and its complement can be partitioned into long arithmetic progressions of step
, and thus both it and its complement can be partitioned into long arithmetic progressions of step  . Since A is disjoint from
. Since A is disjoint from  , it is squeezed into the other progressions, and on one of these we have a density increment. Now apply the usual density increment argument and we are done.
, it is squeezed into the other progressions, and on one of these we have a density increment. Now apply the usual density increment argument and we are done.
It’s not clear whether this argument can be adapted to give the corners theorem, let alone the k=3 case of DHJ, but perhaps it should be looked at.
February 3, 2009 at 10:55 pm |
87. Thread title: obstructions to uniformity. Reply to 82.
Boris, I was not sure it was a true generalization either, and I’m still not sure. Let me attempt to come up with a set where it might have a chance of being one.
Let us consider two functions defined on the set of all sequences in![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . First of all, choose a largish
. First of all, choose a largish  and a subset
and a subset  of positive density in
of positive density in  with the following properties: (i)
with the following properties: (i) 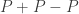 is not much larger than
is not much larger than  , and quite a bit smaller than
, and quite a bit smaller than  ; (ii) for every
; (ii) for every  there are about the same number of
there are about the same number of  such that
such that 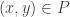 , and vice versa.
, and vice versa.
Now let’s choose some fairly random sequences of weights and
and  and let
and let  be the set of all sequences such that
be the set of all sequences such that  mod
mod  .
.
OK that almost certainly doesn’t work, for the reason you say: there will be some character that correlates in a big way with , and that will give us
, and that will give us  and
and  such that
such that 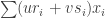 has a tendency to lie in an unusual subset of
has a tendency to lie in an unusual subset of 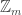 .
.
I’m becoming convinced that it isn’t a generalization, but I can’t quite rule out that there might be some further things one could do.
February 3, 2009 at 11:18 pm |
88. Thread title: is triangle removal still necessary?
This is a response to Terry’s comment 77. Obviously what you ask is an important question, but I’d like to understand more precisely what you mean by it.
To begin with, let me distinguish carefully between two interpretations of the question. One would be “Is it possible to do without any analogue of the triangle removal lemma from this point on?” and another would be “Is it unnatural to try to use the triangle removal lemma from this point on?”
The background to the question is that if a positive proportion of the slices (for a definition of this word, see 62) is rich, then by the corners theorem one can find a triple of rich slices of the form ,
,  ,
,  . So one might take the view that you use the triangle removal lemma (via the corners theorem) to get yourself to a triple of rich slices and then let other methods take over from there.
. So one might take the view that you use the triangle removal lemma (via the corners theorem) to get yourself to a triple of rich slices and then let other methods take over from there.
Now we haven’t actually said what we mean by “rich”. It has to mean more than “intersects densely with ” since it is easy to find examples where
” since it is easy to find examples where  intersects three such slices densely but there is no combinatorial line. (See e.g. comment 20.) And it seems unlikely that there is a definition of “rich” such that (i) every dense set
intersects three such slices densely but there is no combinatorial line. (See e.g. comment 20.) And it seems unlikely that there is a definition of “rich” such that (i) every dense set  intersects a dense set of slices richly and (ii) given any triangle of slices intersected richly by
intersects a dense set of slices richly and (ii) given any triangle of slices intersected richly by  you must get a combinatorial line from that triangle of slices.
you must get a combinatorial line from that triangle of slices.
At this point it’s worth going back and reading Terry’s comment 40. The idea there is that if you don’t get a dense set of rich slices, then perhaps you can pass to substructures (e.g. by fixing a few coordinates) where something like density or energy improves and try again. This would be a sort of mixed argument: first use density/energy-increase arguments to get to a situation where lots of slices are rich (which I see as some kind of quasirandomness property, but perhaps I shouldn’t), then apply the corners theorem to get a triple of rich slices, and finally apply some rich-slices counting lemma to get a combinatorial line. (I’m not at all sure that that’s what Terry had in mind, and would be interested to know.)
Anyhow, perhaps that suggests that triangle removal could be used just to get a triple of good slices, and other arguments could be used to do the rest. In my next comment I’ll discuss the other interpretation of Terry’s question.
February 3, 2009 at 11:53 pm |
89. Thread title: is triangle removal still necessary?
Is it clearly wrong to try to prove the whole theorem via a triangle-removal lemma? I would present the reasoning in the main post slightly differently. Admittedlly it starts out in the way that Terry describes at the beginning of his comment 77. However, I think that the argument gains considerably in force when you add the following fact.
4. It is possible to define a tripartite graph in such a way that nondegenerate triangles correspond to combinatorial lines in . Moreover, the construction naturally generalizes the tripartite graph that you construct in order to deduce the corners theorem from the triangle removal lemma.
. Moreover, the construction naturally generalizes the tripartite graph that you construct in order to deduce the corners theorem from the triangle removal lemma.
Here’s a way one might justify this. For a long time it was known that the triangle removal lemma implied Roth’s theorem, but until Jozsef came along, nobody had observed that it would also do corners. Before that one might have reasoned as follows.
Let us label the lines of slope 1 in![\null [n]^2](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) according to the value of
according to the value of  . If we have a corner, then the labels of the lines that it lies in must form an arithmetic progression of length 3. And indeed, since our dense subset of
. If we have a corner, then the labels of the lines that it lies in must form an arithmetic progression of length 3. And indeed, since our dense subset of ![\null [n]^2](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) might even be a union of lines of slope 1, we see that the corners theorem implies Roth’s theorem. So perhaps we should use Roth’s theorem to find a rich triple of diagonals and then use other arguments to obtain a corner.
might even be a union of lines of slope 1, we see that the corners theorem implies Roth’s theorem. So perhaps we should use Roth’s theorem to find a rich triple of diagonals and then use other arguments to obtain a corner.
Is this a fair analogy or does it break down somewhere?
Before giving up on triangle removal, I would want answers to the following questions.
(i) Is it possible to formulate a triangle-removal statement that isn’t obviously false and that implies that the tripartite graph discussed in 67 contains lots of triangles (because it contains lots of edge-disjoint degenerate ones)?
(ii) If so, is there the slightest chance of proving the statement by imitating the proof of the usual triangle-removal lemma? Or does the sparseness and nonquasirandomness of the bipartite graph where we join two sets if they are disjoint make a project of this kind hopeless?
I could perhaps add a third question, of a slightly different kind.
(iii) Is it the case that in order to prove that a regular triple contained many triangles, one would have to develop tools (connected with obstructions to uniformity) that could be used to give an easier proof that didn’t go via triangle removal, regularity lemmas etc.?
I feel reasonably optimistic about (i) if one restricts to a triangular grid of slices. I’m much less sure about (ii) and (iii).
February 4, 2009 at 12:02 am |
90: for small
for small  (Re to 78 83 and 84)
(Re to 78 83 and 84)
In 2 dimensions there are only 4 such set with 6 elements: for i=1,2,3 and
for i=1,2,3 and  .
.
In 3 dimensions there is only one such set S with 18 elements. Proof: Let S be such a set. Now let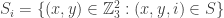 , for i=1,2,3. Now each
, for i=1,2,3. Now each 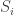 has to have 6 elements and be of the above from, and the intersection of the
has to have 6 elements and be of the above from, and the intersection of the 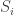 ‘s has to be empty. Thus the
‘s has to be empty. Thus the 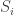 ‘s must be a permutation of the
‘s must be a permutation of the 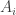 ‘s. The only permutation, that does not give any combinatorial lines is
‘s. The only permutation, that does not give any combinatorial lines is  for i=1,2,3.
for i=1,2,3.
Now asssume that and let S be a set
and let S be a set  in 4 dimensions and with no combinatorial lines. Again let
in 4 dimensions and with no combinatorial lines. Again let  , for i=1,2,3. Now two of the
, for i=1,2,3. Now two of the  ‘s has to have 18 elements and thus be of the above form. By if two of them are identical, the third can at most have 27-18=9 elements, and S at most
‘s has to have 18 elements and thus be of the above form. By if two of them are identical, the third can at most have 27-18=9 elements, and S at most  . Contradiction.
. Contradiction.
February 4, 2009 at 12:19 am |
91. Thread title: obstructions to uniformity.
I don’t know whether this is genuinely different, but in the Hales-Jewett theorem one doesn’t actually care that the set![\null[3]](https://s0.wp.com/latex.php?latex=%5Cnull%5B3%5D&bg=ffffff&fg=333333&s=0&c=20201002) is
is 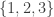 . So perhaps we could take three other numbers, such as
. So perhaps we could take three other numbers, such as  , and take the set of all
, and take the set of all  such that
such that  belongs to
belongs to  mod
mod  . I don’t immediately see how to get this from Boris’s construction, at least as I presented it in 75.
. I don’t immediately see how to get this from Boris’s construction, at least as I presented it in 75.
February 4, 2009 at 12:44 am |
92. Thread title: obstructions to uniformity.
Let me try to sketch a another obstruction to strong uniformity. Hopefully I have understood the notion of strong non-uniformity correctly! For the remainder of this comment, let denote
denote  .
.
Partition the coordinates [n] into disjoint “blocks” of size roughly . For a uniform random string
. For a uniform random string ![x \in [3]^n](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , let $F$ denote the event that
, let $F$ denote the event that  contains a block which is all-2’s. The probability a particular block is all-2’s is
contains a block which is all-2’s. The probability a particular block is all-2’s is  ; hence the probability it is not-all-2’s is
; hence the probability it is not-all-2’s is  . Since there are also about
. Since there are also about  blocks, the probability that all blocks are not-all-2’s is basically
blocks, the probability that all blocks are not-all-2’s is basically  . So the probability of $F$ is basically
. So the probability of $F$ is basically  . Call it
. Call it  .
.
So let be the set of all strings which have an all-2’s block, which has density about
be the set of all strings which have an all-2’s block, which has density about  .
.
On the other hand, suppose we have a combinatorial line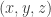 with
with 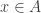 . Then that block of 2’s stays fixed in
. Then that block of 2’s stays fixed in  and
and  . So take
. So take  to be the set of strings which do *not* have a block of all-2’s. This is also plenty dense, having density about
to be the set of strings which do *not* have a block of all-2’s. This is also plenty dense, having density about 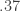 . But then we couldn’t have
. But then we couldn’t have  .
.
You might object that this only worked because we were insisting that it was (i.e., the wildcard=1 point) that was in
(i.e., the wildcard=1 point) that was in  , but this can be circumvented by making
, but this can be circumvented by making  equal the set of strings with a block of all-2’s *and* a block of all-1’s. (These events are practically disjoint, so this
equal the set of strings with a block of all-2’s *and* a block of all-1’s. (These events are practically disjoint, so this  would still have density about
would still have density about  .)
.)
This example does seem to me different from Boris and Tim’s examples. At first it looks similar because you are counting that the number of 2’s in a particular set of coordinates is equal to a particular number. But then things differ because you take an “or” across all blocks. You can make it even more different by taking the “block-of-all-2’s *and* block-of-all-1’s” example. Or you could instead let be the set of strings with a “run” of 2’s of length about
be the set of strings with a “run” of 2’s of length about 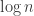 somewhere within them.
somewhere within them.
Does this example work?
If so, I think my intuition agrees with Tim’s (expressed at the end of #75) that there may be “too many” obstructions…
February 4, 2009 at 12:46 am |
93. Thread title: an alternative problem.
In 60. Tim suggested a problem where we consider certain pairs of sets. “A sensible question would be some density-type condition on A that would guarantee a triple of the given kind. ” One candidate might be the following: Given a subset S of the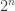 subsets of an n-element set, then two elements of S form a pair if their symmetric diference is also in S. I think, but I can’t prove it yet, that if S is dense,
subsets of an n-element set, then two elements of S form a pair if their symmetric diference is also in S. I think, but I can’t prove it yet, that if S is dense,  then the number of such pairs (triples) is at least
then the number of such pairs (triples) is at least 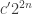 . If so, then there is a direct application of the triangle removal lemma, however I have to think about the interpretation of the result.
. If so, then there is a direct application of the triangle removal lemma, however I have to think about the interpretation of the result.
February 4, 2009 at 12:59 am |
94. Obstructions to strong uniformity.
Can’t you also do other goofy things like take any example which is strongly-non-uniform and, say, tack 23 onto the end of each string (changing
which is strongly-non-uniform and, say, tack 23 onto the end of each string (changing  to
to  )? This hurts the density by only
)? This hurts the density by only  . Now take the dense
. Now take the dense  which failed with the original
which failed with the original  and tack, say, 12 on the end of all of its strings. This also only loses density
and tack, say, 12 on the end of all of its strings. This also only loses density  . But if
. But if  and
and  were a bad example before, they are still bad now. And
were a bad example before, they are still bad now. And  is no longer of the weighted-sums-modulo-m type, even if it was before.
is no longer of the weighted-sums-modulo-m type, even if it was before.
February 4, 2009 at 1:03 am |
95. Thread title: Sperner
I want to make a start on the question I eventually arrived at in 80, which I’ll repeat here and make more precise. Let be slightly smaller than
be slightly smaller than 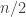 , write
, write  for
for 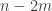 and let
and let  and
and  be two subsets of
be two subsets of ![\binom{[n]}{m}](https://s0.wp.com/latex.php?latex=%5Cbinom%7B%5Bn%5D%7D%7Bm%7D&bg=ffffff&fg=333333&s=0&c=20201002) . Is it the case that for every constant
. Is it the case that for every constant 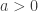 there exists a constant
there exists a constant 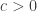 such that if the number of disjoint pairs
such that if the number of disjoint pairs  with
with  and
and 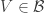 is at most
is at most 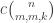 then it is possible to remove at most
then it is possible to remove at most  sets from
sets from 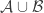 and end up with two set systems
and end up with two set systems 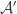 and
and  such that every
such that every  intersects every
intersects every  ?
?
Actually, now that I’ve formulated the question (though I’m still not certain that it’s a sensible one) I find that I have no idea where to start. All I have to say is that Boris’s example in 44 is worth bearing in mind. But in a curious way that makes me feel the problem is worth pursuing. It seems that to prove Sperner via a generalization of the trivial pair removal lemma, one has to prove this non-trivial pair removal lemma. Working out how to do that therefore introduces an extra ingredient. Once one has that extra ingredient, one can see whether it generalizes to provide the extra ingredient needed to get from the usual triangle removal lemma to a more difficult Spernerish triangle removal lemma.
February 4, 2009 at 1:13 am |
96. Thread title: obstructions to strong uniformity.
Ryan, I think we need to formulate more carefully what it means to have a new obstruction. I would want not to count the example you’ve given because it’s contained a bigger example where and
and  consist of all strings (before you do the tacking-on process). And that bigger example is covered by what I called strong obstruction 1 in comment 71.
consist of all strings (before you do the tacking-on process). And that bigger example is covered by what I called strong obstruction 1 in comment 71.
February 4, 2009 at 1:52 am |
97. Thread title: Sperner
Actually, I have a small idea where to start (see 95). If we replace sets in by their complements, then we obtain a set system that has to have a lower shadow that is very non-uniform. That is, if you count how many times a set is contained in the complement of a set in
by their complements, then we obtain a set system that has to have a lower shadow that is very non-uniform. That is, if you count how many times a set is contained in the complement of a set in  then the resulting function mustn’t be close to constant. So it looks as though we do indeed have to understand obstructions to uniformity in Kruskal Katona.
then the resulting function mustn’t be close to constant. So it looks as though we do indeed have to understand obstructions to uniformity in Kruskal Katona.
February 4, 2009 at 3:10 am |
98. Obstructions.
Hi Tim, are you referring to the example from 92 or 94? I don’t see how the #92 one fits into any of the example obstructions mentioned previously.
February 4, 2009 at 3:35 am |
99. Thread title: is triangle removal still necessary?
Tim, I guess my question was intended in the weak sense as in 88 (“can we now do without triangle removal?”) as opposed to the strong sense as in 89 (“should we keep trying to mimic triangle removal?”). Basically, I think we should keep pursuing the triangle removal tack, but bear in mind the option to also utilise many other tools (e.g. Kruskal-Katona, or some ideas from Szemeredi’s proofs of Roth’s theorem, about which I will say more in my next comment), and to also entertain the possibility that triangle removal might in fact only play a minor role in the rest of the argument.
February 4, 2009 at 3:43 am |
100! (do I get a prize?) Thread title: Density incrementation
One tool that seems to be underexploited so far is that of density incrementation. In the standard proof of Roth’s theorem (as well as Szemeredi’s proof), we may assume without loss of generality that the set A does not have significantly increased density on any reasonably long subprogression, since otherwise we could pass to that subprogression and apply some sort of induction hypothesis. We can do the same here: to prove DHJ for some set![A \subset [3]^n](https://s0.wp.com/latex.php?latex=A+%5Csubset+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with density
with density  , we may assume without loss of generality that every slice of A of any reasonable size (m-dimensional, where m grows slowly with n) has density at most
, we may assume without loss of generality that every slice of A of any reasonable size (m-dimensional, where m grows slowly with n) has density at most  (where I will be vague about exactly what o(1) means). By Markov’s inequality, this also implies that almost all (i.e. 1-o(1)) of all such slices will have density at least
(where I will be vague about exactly what o(1) means). By Markov’s inequality, this also implies that almost all (i.e. 1-o(1)) of all such slices will have density at least  as well. It is not clear to me how one can exploit such a fact, but it is something worth keeping in mind. (Admittedly, this structure is not used in the graph-theoretic proofs of Roth or corners, but as I said in my previous post, we are not bound to slavishly follow the graph-theoretic model.)
as well. It is not clear to me how one can exploit such a fact, but it is something worth keeping in mind. (Admittedly, this structure is not used in the graph-theoretic proofs of Roth or corners, but as I said in my previous post, we are not bound to slavishly follow the graph-theoretic model.)
In a somewhat similar spirit, we can use the colouring Hales-Jewett theorem to stabilise various low-complexity quantities. Indeed, if we have some quantity X that depends on a medium number m of the coordinates of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , and takes a bounded number k of values, then (if m is sufficiently large depending on d and k), we can reduce the m coordinates to d, passing to a slice, and force X to now be constant on these d coordinates. (I already used this argument in 85.) Again, I don’t see an immediate way to utilise this freedom, but if we are encountering a problem that the “richness” of various slices varies too much with the slice, this is presumably the thing to do to fix that. And there is also the Carlson-Simpson theorem to hold in reserve to soup this up even further.
, and takes a bounded number k of values, then (if m is sufficiently large depending on d and k), we can reduce the m coordinates to d, passing to a slice, and force X to now be constant on these d coordinates. (I already used this argument in 85.) Again, I don’t see an immediate way to utilise this freedom, but if we are encountering a problem that the “richness” of various slices varies too much with the slice, this is presumably the thing to do to fix that. And there is also the Carlson-Simpson theorem to hold in reserve to soup this up even further.
February 4, 2009 at 3:52 am |
101. for small n.
for small n.
@Sune.90: Excellent… we now have the first five elements of , namely
, namely  . Consulting the OEIS,
. Consulting the OEIS,
http://www.research.att.com/~njas/sequences/?q=1%2C2%2C6%2C18%2C52&language=english&go=Search
there are a number of sequences here, but none that look likely to be a fit, especially given the bounds we have (see Tyler.83).
we have (see Tyler.83).
Given that does not look too close to being computable, perhaps it is time to submit what we have to the OEIS?
does not look too close to being computable, perhaps it is time to submit what we have to the OEIS?
February 4, 2009 at 3:58 am |
100. Kruskal-Katona obstructions.
Even in the case of Kruskal-Katona, I’m not 100% what the right question is. Let me work off Boris’s #44 formulation of the problem.
Say the density of is
is  and the density of
and the density of  is
is  . When Boris asks, when is the number of pairs
. When Boris asks, when is the number of pairs 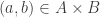 with $a \subset b$ close to expected, I assume by “expected” he means “what the number would be if
with $a \subset b$ close to expected, I assume by “expected” he means “what the number would be if  and
and  were random sets of the given densities”. (Correct me if I’ve mistaken you here.)
were random sets of the given densities”. (Correct me if I’ve mistaken you here.)
Introduce a uniformly random pair![(x,y) \in \binom{[n]}{n/2} \times \binom{[n]}{n/2+1}](https://s0.wp.com/latex.php?latex=%28x%2Cy%29+%5Cin+%5Cbinom%7B%5Bn%5D%7D%7Bn%2F2%7D+%5Ctimes+%5Cbinom%7B%5Bn%5D%7D%7Bn%2F2%2B1%7D&bg=ffffff&fg=333333&s=0&c=20201002) subject to
subject to  . Let
. Let  be the event that both
be the event that both 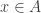 and
and 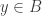 . Note that the marginal on both
. Note that the marginal on both  and
and  is uniform. Hence if
is uniform. Hence if  and
and  were both random sets of the given densities, we’d expect the probability of
were both random sets of the given densities, we’d expect the probability of  to be
to be  .
.
Now Boris gave two very different examples where and yet
and yet ![\Pr[L] = 0](https://s0.wp.com/latex.php?latex=%5CPr%5BL%5D+%3D+0&bg=ffffff&fg=333333&s=0&c=20201002) , much less than
, much less than  of course.
of course.
On the other hand, there are plenty of examples where is a constant and yet $\latex \Pr[L] \approx \mu_A$, much *greater* than
is a constant and yet $\latex \Pr[L] \approx \mu_A$, much *greater* than  . To achieve this, fix
. To achieve this, fix  to be the upper shadow of
to be the upper shadow of  . Now we just need to take
. Now we just need to take  to be any constant-density set whose upper shadow has about the same size as
to be any constant-density set whose upper shadow has about the same size as  . And there is a world of such sets; too many, I think, to have a meaningful characterization by obstructions.
. And there is a world of such sets; too many, I think, to have a meaningful characterization by obstructions.
February 4, 2009 at 4:05 am |
102. The HJ cube lemma.
As I mentioned in 86, there is a proof of Roth’s theorem by Szemeredi which relies on the Szemeredi cube lemma, which basically asserts that any dense subset of![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) contains a large cube
contains a large cube  (in practice one can take d to be something like
(in practice one can take d to be something like  ).
).
There is a similar lemma for k=2 Hales-Jewett: if n is sufficiently large depending on and d, then any subset A of
and d, then any subset A of ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of density at least
of density at least  contains a d-dimensional cube, which basically is the same thing as a combinatorial line except that one now has d wildcards instead of 1.
contains a d-dimensional cube, which basically is the same thing as a combinatorial line except that one now has d wildcards instead of 1.
The proof proceeds by induction on d and using the k=2 DHJ (i.e. Sperner). The d=1 case is of course exactly k=2 DHJ. Now if d > 1 and the claim is already proven for d-1, then we can foliate![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into m-dimensional slices for some intermediate m. Many of these slices will be rich and thus contain a d-1-dimensional cube, by induction hypothesis. The placement of this cube can vary by slice, but the number of possible cubes is bounded by some constant depending on m, so by pigeonhole there is a positive density (depending on m) of slices for which the cube position is the same. Now apply Sperner (k=2 DHJ) one more time to get the result.
into m-dimensional slices for some intermediate m. Many of these slices will be rich and thus contain a d-1-dimensional cube, by induction hypothesis. The placement of this cube can vary by slice, but the number of possible cubes is bounded by some constant depending on m, so by pigeonhole there is a positive density (depending on m) of slices for which the cube position is the same. Now apply Sperner (k=2 DHJ) one more time to get the result.
One can of course embed![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into
into ![{}[3]^N](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5EN&bg=ffffff&fg=333333&s=0&c=20201002) in a variety of ways, and so this cube lemma is available for use in the k=3 problem. I don’t know yet whether Endre’s proof (see 86) can carry over in this setting, but it might be worth taking a look at. Note that the colouring version of this cube lemma is used in the standard proof of k=3 colouring Hales-Jewett.
in a variety of ways, and so this cube lemma is available for use in the k=3 problem. I don’t know yet whether Endre’s proof (see 86) can carry over in this setting, but it might be worth taking a look at. Note that the colouring version of this cube lemma is used in the standard proof of k=3 colouring Hales-Jewett.
February 4, 2009 at 9:38 am |
103. Obstructions to uniformity.
Ryan, re your comment 98, I’m sorry but for some reason I failed to notice your very interesting comment 92. In my comment 96 I was referring to what you said in 94.
Your example in 92 strikes me as a definite advance in the understanding of the problem. Let me try to explain why. One of the difficulties of the density Hales-Jewett theorem is its “combinatorial”, as opposed to “group-theoretic’, nature. That is, we do not have a group structure on![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) (or at least, not one that seems to be relevant), and the notion of a combinatorial line is not one that can be expressed in purely group-theoretic terms.
(or at least, not one that seems to be relevant), and the notion of a combinatorial line is not one that can be expressed in purely group-theoretic terms.
On the other hand, the kinds of obstructions that Boris and I were coming up with did have a group-theoretic flavour to them, even if they weren’t exactly group theoretic. I couldn’t help thinking that it was too optimistic to hope that all obstructions were of this kind. And now you have demonstrated (assuming your example checks out, which it feels to me as though it does) that there are indeed some more purely combinatorial obstructions.
A quick thought at this stage. For each obstruction it is well worth thinking about the following question: is there an obvious way of restricting![\null[3]^n](https://s0.wp.com/latex.php?latex=%5Cnull%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) so as to obtain a substructure where
so as to obtain a substructure where  is denser? In your case I was about to say that I couldn’t see one, but I think I can: we could do something like restricting to a random combinatorial subspace of the following kind. Take your partition of
is denser? In your case I was about to say that I couldn’t see one, but I think I can: we could do something like restricting to a random combinatorial subspace of the following kind. Take your partition of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) into blocks and for each block choose a random subset (according to some sensible probability distribution — not sure what that is) to be a set of coordinates that vary simultaneously. But insist that at least once you … the more I write the more this feels completely wrong. So instead let me ask: can one get a density increase on a combinatorial subspace for Ryan’s set
into blocks and for each block choose a random subset (according to some sensible probability distribution — not sure what that is) to be a set of coordinates that vary simultaneously. But insist that at least once you … the more I write the more this feels completely wrong. So instead let me ask: can one get a density increase on a combinatorial subspace for Ryan’s set  in 92?
in 92?
February 4, 2009 at 9:51 am |
104. Thread title: Sperner
Re: Tim’s question in 95. I just want to clarify, that the conjecture (?) is that in the Kneser graph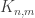 every induced bipartite graph with at most
every induced bipartite graph with at most 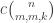 edges has a vertex cover of size at most
edges has a vertex cover of size at most 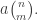 Or, equivalently, the largest matching is at most
Or, equivalently, the largest matching is at most 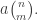 It seems to me that the small number of edges in the induced graph implies that the number of vertices is small, but I don’t remember what is the spectral gap in
It seems to me that the small number of edges in the induced graph implies that the number of vertices is small, but I don’t remember what is the spectral gap in 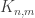 . Anyways, if
. Anyways, if 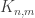 is quasirandom then I don’t understand the question, but it is almost 1 am, so I will review it tomorrow…
is quasirandom then I don’t understand the question, but it is almost 1 am, so I will review it tomorrow…
February 4, 2009 at 9:54 am |
Good morning Tim! Then mine is 104. … [Now changed]
February 4, 2009 at 10:00 am |
105. Obstructions to uniformity.
For some reason in 103 I was blind to the obvious example: take a subspace where all sequences are constant on Ryan’s blocks, and it’s actually contained in .
.
February 4, 2009 at 11:00 am |
106. Sperner.
In response to Jozsef comment 104, I think your rephrasing of my question is indeed the same question (but I’m slightly shaky on the terminology you use). Just to check: the Kneser graph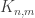 is the graph consisting of all subsets of
is the graph consisting of all subsets of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) of size
of size  , with two of them joined if and only if they are disjoint. An induced bipartite graph just means that you pick two sets
, with two of them joined if and only if they are disjoint. An induced bipartite graph just means that you pick two sets  and
and  of vertices in this graph and put in all the edges that you have from the graph: so you have two systems of sets of size
of vertices in this graph and put in all the edges that you have from the graph: so you have two systems of sets of size  and join a set in
and join a set in  to a set in
to a set in  if and only if they are disjoint. Finally, a vertex cover means a collection of vertices such that every edge contains a vertex in that collection. So if we have a small vertex cover then we can remove it and end up with no edges.
if and only if they are disjoint. Finally, a vertex cover means a collection of vertices such that every edge contains a vertex in that collection. So if we have a small vertex cover then we can remove it and end up with no edges.
It’s not the case that a small number of edges implies that the vertex sets are small. For example, and
and  could both be the set of all sets of size
could both be the set of all sets of size  that contain the element 1. Then there are no edges between
that contain the element 1. Then there are no edges between  and
and  , but they both have density about 1/2. Of course, this example doesn’t have much bearing on the problem I asked.
, but they both have density about 1/2. Of course, this example doesn’t have much bearing on the problem I asked.
February 4, 2009 at 11:17 am |
[This comment is deliberately not numbered.]
If you’ll forgive a metacomment, at some point I think we should consider trying to summarize everything we’ve learned so far (interesting examples, questions we haven’t yet answered, data about small , ideas for general approaches, etc.), write a new post, and start all over again, this time from camp 1 rather than base camp, so to speak. It would have the small advantage that people wouldn’t have to scroll through over a hundred comments (my computer now takes quite a long time to load all the mathematical gifs — if that’s the right word). Note that I’m not suggesting splitting up the threads: I’ve rather enjoyed having them all jumbled together, and I think this suggestion would keep the current atmosphere but keep things manageable. Any views? (I’m thinking of introducing a poll facility to this blog so that people can express opinions about this kind of question without having to make actual comments.)
, ideas for general approaches, etc.), write a new post, and start all over again, this time from camp 1 rather than base camp, so to speak. It would have the small advantage that people wouldn’t have to scroll through over a hundred comments (my computer now takes quite a long time to load all the mathematical gifs — if that’s the right word). Note that I’m not suggesting splitting up the threads: I’ve rather enjoyed having them all jumbled together, and I think this suggestion would keep the current atmosphere but keep things manageable. Any views? (I’m thinking of introducing a poll facility to this blog so that people can express opinions about this kind of question without having to make actual comments.)
[To my amazement, I seem to have managed to produce a poll. So if you want to register an opinion, you have the chance to do so. It appears as a new and strange-looking post on the blog.]
February 4, 2009 at 11:31 am |
107. Thread title: big picture.
Terry has already described some possible ways that an eventual proof might go (see e.g. #77 and #100). In the next comment, I’ll have a go at some proof sketches (not very detailed because I don’t know the details!). Each one would ideally be the beginning of a top-down process that ends with a fully detailed proof. But the question in each case is whether the strategy is remotely realistic.
Strategy 1. Density incrementation.
This strategy is to model a proof on Roth’s proof of Roth’s theorem. The idea is to keep thinking about obstructions to uniformity until we think we’ve found all of them. At that point we try to prove the following: either a set correlates with one of our obstructions to uniformity, in which case one can show that there is a combinatorial subspace inside which
correlates with one of our obstructions to uniformity, in which case one can show that there is a combinatorial subspace inside which  has increased density; or
has increased density; or  does not correlate with one of our obstructions to uniformity, in which case we can prove that
does not correlate with one of our obstructions to uniformity, in which case we can prove that  contains the expected number of combinatorial lines.
contains the expected number of combinatorial lines.
Two remarks about the strategy. First, as we have noted, the “expected” number of combinatorial lines is a troublesome concept. But it ought to be possible to deal with that by restricting to a triangular grid of slices near the centre. Secondly, a density-increment proof of density Hales-Jewett would presumably yield a density-increment proof of the corners theorem. Now such a proof has been obtained by Shkredov, but it is considerably more complicated than the density-increment proof of Roth’s theorem. So we shouldn’t expect this strategy to be easy. (Actually, this has given me an idea about obstructions to uniformity in DHJ. I’ll explore it in a moment.)
Strategy 2. This is roughly the original strategy I suggested. We have a tripartite graph where we join two sets if and only if they are disjoint, and we try to prove a regularity lemma for subgraphs of this graph (or perhaps portions of this graph where we restrict the cardinalities of sets so that they become “typical”). This would be a relative regularity lemma.
Two remarks about this strategy. First, I think it ought to be easy to make at least some progress, either negative or positive, by trying to produce such a regularity lemma. Either it will rapidly become clear that the task is hopeless, or we’ll manage it, or we’ll generate a bunch of interesting questions that we can’t yet answer. Secondly, in a subtle way the regularity approach to corners allows one not to understand too well what the obstructions to uniformity are for that problem: it just automatically seeks them out and deals with them. Might something like that happen for DHJ?
February 4, 2009 at 11:56 am |
108. Obstructions to uniformity.
No idea whether this is going anywhere, but in Shkredov’s proof of the corners theorem, he has to deal with examples of sets of the form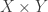 , where both
, where both  and
and  are subsets of
are subsets of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) . These sets have the feature that if they contain the two points
. These sets have the feature that if they contain the two points 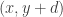 and
and 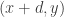 then they automatically contain the point
then they automatically contain the point  It ought to be possible to exploit this to obtain an obstruction to uniformity in DHJ, but I don’t yet know whether it will be a new one.
It ought to be possible to exploit this to obtain an obstruction to uniformity in DHJ, but I don’t yet know whether it will be a new one.
So let’s choose an arbitrary pair of (reasonably dense and codense near ) subsets
) subsets  and
and  of
of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , take
, take  to be the set of all sequences such that the number of 1s belongs to
to be the set of all sequences such that the number of 1s belongs to  and the number of 2s belongs to
and the number of 2s belongs to  , and take
, and take  to be the complement of
to be the complement of  . Now let
. Now let 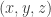 be a combinatorial line (written in 1,2,3 order). The point
be a combinatorial line (written in 1,2,3 order). The point  has the same number of 2s as
has the same number of 2s as  , and
, and  has the same number of 1s as
has the same number of 1s as  . So if
. So if  and
and  belong to
belong to  , then
, then  automatically belongs to
automatically belongs to  , so it can’t belong to
, so it can’t belong to  .
.
This is open to the same objection that Ryan talked about in 92, namely that we’re insisting that it is that belongs to
that belongs to  rather than
rather than  or
or  , but the basic idea can be used to produce an example that gets round this objection. We just have to play the same game with 2s and 3s, and the same game again with 1s and 3s, and then intersect the three resulting sets. If you choose them reasonably randomly then you’ll still get a dense
, but the basic idea can be used to produce an example that gets round this objection. We just have to play the same game with 2s and 3s, and the same game again with 1s and 3s, and then intersect the three resulting sets. If you choose them reasonably randomly then you’ll still get a dense  and a dense
and a dense  .
.
(Just to clarify what I’ve just said, let’s call the sets I constructed and
and 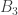 , since 3 was the preferred value. Now you repeat the construction I gave twice over to produce
, since 3 was the preferred value. Now you repeat the construction I gave twice over to produce 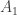 and
and 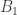 and
and 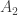 and
and  . Finally, you set
. Finally, you set  to be
to be 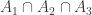 and you set
and you set  to be
to be  . Provided the sets
. Provided the sets  and
and  are chosen reasonably randomly in each case, the sets
are chosen reasonably randomly in each case, the sets  and
and  will be reasonably dense.)
will be reasonably dense.)
This feels like a genuinely different obstruction because it is very nonlinear. In fact, I’m basically pretty sure it’s different.
So going briefly back to the big picture, one might argue that the problem with strategy 1 is that it is already difficult to carry out for corners, and looks as though it could be very much more difficult still here. So if it were just a choice between strategies 1 and 2, there would be a good reason for continuing to pursue 2 (not that I feel like giving up on 1 just yet).
February 4, 2009 at 1:20 pm |
109. Thread title: counting lemma.
I want to make a tentative appeal to procedural rule 6, the one that says that if you think you could work something out with the help of some private calculations, then you first see whether others think that would be a good thing to do. So here’s what I think I could do reasonably easily privately and not so easily if I have to type everything in here.
It’s clear that if any kind of regularity approach is going to work, then there needs to be a lemma that says that if you’ve got three suitably quasirandom subgraphs of the is-disjoint-from graph arranged in a triple, then you must have lots of triangles. But it’s not clear with “suitably quasirandom” means. A natural way to attempt to get a handle on this, if you’ve ever been involved with counting lemmas in sparse random settings, is to try to use the Cauchy-Schwarz inequality to prove that the number of triangles is close to what you expect unless something bad happens. And that something bad then turns into your definition of “is not quasirandom”. I would like permission to go away, attempt some Cauchy-Schwarz calculations, and come back and report on the results.
February 4, 2009 at 1:29 pm |
110. Thread title: regularity lemma.
Here, by the way, is the outline of how one might try to prove a regularity lemma. Almost certainly there will be an easy argument that says that this naive strategy has no chance of working.
Let be the bipartite graph where you join two sets (fixed to have size around
be the bipartite graph where you join two sets (fixed to have size around  ) if and only if they are disjoint. Let
) if and only if they are disjoint. Let  be a dense subgraph of this graph. We want to partition the vertices into sets where
be a dense subgraph of this graph. We want to partition the vertices into sets where  looks like a random subgraph of
looks like a random subgraph of  . So why not argue as follows? Given partitions of the vertex sets, if there are lots of induced bipartite subgraphs where
. So why not argue as follows? Given partitions of the vertex sets, if there are lots of induced bipartite subgraphs where  doesn’t look random in
doesn’t look random in  , then you can refine the partitions in such a way that the ratio of the energy, or mean square density, of
, then you can refine the partitions in such a way that the ratio of the energy, or mean square density, of  to that of
to that of  goes up. The idea would be that although the mean square density of
goes up. The idea would be that although the mean square density of  could well be going up all the time (since
could well be going up all the time (since  is not a quasirandom graph), the mean square density of
is not a quasirandom graph), the mean square density of  would be going up faster so the iteration would have to terminate.
would be going up faster so the iteration would have to terminate.
As I say, this is probably a hopeless strategy, but it gives an idea of the kind of thing that I was hoping one might be able to do, and there might be ways of modifying it that made it more promising.
February 4, 2009 at 3:02 pm |
A little thought about the issue Tim raised in 31. (Sorry if it duplicates some later comment or link.)
The question Tim ask was what conditions (Fourier or different) will ensure semirandomness for Sperner and for our combinatorial line question for k=3, namely, a condition for a set to contain approximately “the right number” of combinatorial lines.
One possibility to consider is to ask for density on a set X of solutions for arbitrary equation of the form (T can be any set but we can just think about a single number.) If the intersection of A and X is equal to its expected value up to a small additive error, for every X, does it suffices to imply that A has the right number of pairs
(T can be any set but we can just think about a single number.) If the intersection of A and X is equal to its expected value up to a small additive error, for every X, does it suffices to imply that A has the right number of pairs 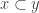 ? (for the Sperner case) or even the right number of combinatorial lines for k=3?
? (for the Sperner case) or even the right number of combinatorial lines for k=3?
Are you aware of counterexamples?
Talking about general solutions of linear equations may help also for cases where Fourier analysis gives a result but we would like to have a better one. (upper bounds on cup set? Influences of sets…) A difficulty with such a suggestion is that you need to argue recursively about dense sets inside sets which are the solution of a system of equations of the above kinds and maybe even more complicated. Also I do not see an argument that will show that if the number of solutions of linear equations is right then the number of combinatorial lines is right (for k<=3).
Another possibility (or perhaps something forced by the above possibility if you try to prove things) is to consider for X sets which are described by even more general arithmetic or other type of circuits. Such sets may also be useful for lower bound examples; I find it yet hard to believe that the examples we know (for the various questions) are in the right ball park as reality.
February 4, 2009 at 3:46 pm |
112. Obstructions.
Tim, in your #105, I don’t quite see what you’re saying… And does it hold for the set of all strings which contain a “run” of at least
of all strings which contain a “run” of at least 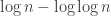 2’s somewhere within them? (This example has no fixed “blocks”.)
2’s somewhere within them? (This example has no fixed “blocks”.)
February 4, 2009 at 3:52 pm |
113. Obstructions: These examples from #92 were really just based on an example (“Tribes”) from the![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) scenario. Like Jozsef#104, I haven’t wrapped my head around the counting/normalization/distribution used in Tim’s #95; this is why in my #100 I was writing about Boris’s #44 setup instead.
scenario. Like Jozsef#104, I haven’t wrapped my head around the counting/normalization/distribution used in Tim’s #95; this is why in my #100 I was writing about Boris’s #44 setup instead.
I feel that before thinking too much about obstructions to combinatorial-line-uniformity in![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , we should try to clarify things in the simpler scenario of obstructions-to-Sperner in
, we should try to clarify things in the simpler scenario of obstructions-to-Sperner in ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) .
.
In #100, I tried to get across that I can’t even think what this should mean.
February 4, 2009 at 3:53 pm |
114. Sperner/Kruskal-Katona.
Actually, I’m not even sure “obstructions” is the right way to think about Sperner. I think that what Boris said in #58 — that Sperner’s own proof by “pushing shadows around” (I like this phrase, Boris!) — may already be the “alternate combinatorial proof of Sperner” that Terry proposed to look for way back in #4!
Can we prove DHJ by “pushing shadows around”? 🙂
February 4, 2009 at 4:40 pm |
@Tyler, Sune, Terry (on bounds)
Nice! I hope to have some code working by the end of the week; ought to be within brute force range, but I’m not sure past that.
ought to be within brute force range, but I’m not sure past that.
I’ve thought about the flow optimization algorithm, and I’m not convinced that will produce an improvement because of the symmetry of the original arrangment. I do still think there’s some CS trick that will help knock this down to size and get exact values for and beyond. For the moment I’m just going to Monte Carlo it so we can get some perspective.
and beyond. For the moment I’m just going to Monte Carlo it so we can get some perspective.
February 4, 2009 at 5:21 pm |
115. Obstructions.
Ryan, 112, I won’t bother trying to explain what I was saying because there’s an even simpler example to show that your set yields a density increase on a subspace: you just fix a run of 1s and let everything else vary arbitrarily. That does both the blocks case and the fixed-length-of-run case.
February 4, 2009 at 6:00 pm |
116. Big picture, density incrementation, obstructions
I’ve just realized that the example in 108 shows that strategy 1 in 107 doesn’t work as stated, or at least not completely straightforwardly. For the benefit of people unfamiliar with Shkredov’s work on corners, let me explain this in some detail.
Suppose we try to prove the corners result using a density-increment strategy. That is, we try to prove that if a subset of![\null[n]^2](https://s0.wp.com/latex.php?latex=%5Cnull%5Bn%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) doesn’t have roughly the expected number of corners then there’s a substructure inside which
doesn’t have roughly the expected number of corners then there’s a substructure inside which  is noticeably denser. What is the obvious substructure? Well, we want something that will support corners, so the obvious thing to take is a Cartesian product of two arithmetic progressions with the same common difference.
is noticeably denser. What is the obvious substructure? Well, we want something that will support corners, so the obvious thing to take is a Cartesian product of two arithmetic progressions with the same common difference.
However, this doesn’t work. Suppose we take to be a Cartesian product of two random sets
to be a Cartesian product of two random sets  and
and  . Then there will be too many corners in
. Then there will be too many corners in  (because you just need
(because you just need 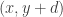 and
and 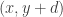 and you get
and you get 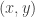 for free). But if
for free). But if  and
and 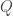 are arithmetic progressions, then
are arithmetic progressions, then 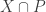 and
and  will look like random subsets of
will look like random subsets of  and
and 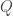 so we won’t get any density increase. (But see a qualification to this remark later on.)
so we won’t get any density increase. (But see a qualification to this remark later on.)
This has an analogue in the Hales-Jewett setting. Suppose we take the example in 108, and we use random sets and
and  to define it. Then there won’t be a combinatorial subspace contained in the resulting set
to define it. Then there won’t be a combinatorial subspace contained in the resulting set  (or even intersecting it unusually densely) because the set of sizes of the 1-set of a vector in a combinatorial subspace will be a very special kind of set: the set of sums of some positive integers
(or even intersecting it unusually densely) because the set of sizes of the 1-set of a vector in a combinatorial subspace will be a very special kind of set: the set of sums of some positive integers 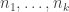 , and a random set will intersect such sets randomly.
, and a random set will intersect such sets randomly.
Both these conclusions are, however, false if we allow ourselves to pass to much smaller substructures. For instance, in the first case we could use Szemerédi’s theorem to get ourselves an arithmetic progression contained in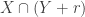 for some
for some  , and in the second we could use a cube lemma to get
, and in the second we could use a cube lemma to get 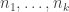 such that all sums belong to
such that all sums belong to  . (I’m using these statements so that I don’t actually use the fact that
. (I’m using these statements so that I don’t actually use the fact that  and
and  are random, which in general we are not going to be given.)
are random, which in general we are not going to be given.)
February 4, 2009 at 6:17 pm |
117. Obstructions.
Tim, re #115 — thanks! I understand what you mean. I wonder if you could suggest the “quantitatives” to think about for density increment arguments.
Let’s work with a different strongly nonuniform set. Let be the set of strings where the plurality digit in the first
be the set of strings where the plurality digit in the first  coordinates is
coordinates is  , the plurality digit in the second
, the plurality digit in the second  coordinates is
coordinates is  , and the plurality digit in the third
, and the plurality digit in the third  coordinates is
coordinates is 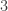 . This has density
. This has density  and is strongly nonuniform. (The “counterexample”
and is strongly nonuniform. (The “counterexample”  is the set of strings where the plurality digit in the first
is the set of strings where the plurality digit in the first  coordinates is *not*
coordinates is *not*  , the plurality digit in the second
, the plurality digit in the second  coordinates is *not*
coordinates is *not*  , and the plurality digit in the third
, and the plurality digit in the third  coordinates is *not*
coordinates is *not* 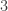 . This has density
. This has density 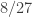 and forms no lines with
and forms no lines with  .)
.)
But now it’s hard to improved ‘s density by restricting to a smallish-codimension combinatorial subspace. Your best bet is (I assume) to put, say, lots of
‘s density by restricting to a smallish-codimension combinatorial subspace. Your best bet is (I assume) to put, say, lots of  ‘s into the first
‘s into the first  coordinates. But so long as you fix only
coordinates. But so long as you fix only 
 ‘s, you’ve only improved
‘s, you’ve only improved  ‘s density by
‘s density by 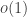 .
.
So I’m wondering what “quantitative aspects” one should hope for. Perhaps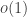 increase is enough, or
increase is enough, or  codimension is “not too much”.
codimension is “not too much”.
February 4, 2009 at 6:29 pm |
118. Szemeredi’s proof of Roth’s theorem
Good morning again… this topic is perhaps orthogonal to the others, but I think I begin to understand Szemeredi’s proof of Roth’s theorem(see 86) better. For instance, I realised that it has the curious property of proving Roth in Z/NZ but not in (at least, not without some further modification). I also begin to see how the “sparsity” of the corners or DHJ problem is a serious difficulty extending Endre’s argument to this setting. I don’t think this approach is totally hopeless, though, and might be worth pursuing in parallel with the “mainstream” obstructions-to-uniformity/triangle removal approach.
(at least, not without some further modification). I also begin to see how the “sparsity” of the corners or DHJ problem is a serious difficulty extending Endre’s argument to this setting. I don’t think this approach is totally hopeless, though, and might be worth pursuing in parallel with the “mainstream” obstructions-to-uniformity/triangle removal approach.
Basically, Endre’s proof is based on three observations:
1. If A is dense, then it contains a structured set Q (specifically, a medium-dimensional cube).
2. If A has no 3-APs, and contains a structured set Q, then the complement of A contains a _large_ structured set, namely 2.Q – A.
3. If the complement of A contains a large structured set (or equivalently, if A is “squeezed” into the complement of a large structured set), then there is some subprogression of A of increased density.
Combining 1, 2, 3 and the density increment argument one obtains Roth’s theorem in Z/NZ.
If we try to prove Roth in rather than
rather than 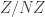 , then 1 and 2 still work fine, but I can only show 3 using Fourier analysis, but of course Roth in
, then 1 and 2 still work fine, but I can only show 3 using Fourier analysis, but of course Roth in  is trivial with Fourier analysis anyway. (Specifically, the question is whether one can find dense subsets A, B of
is trivial with Fourier analysis anyway. (Specifically, the question is whether one can find dense subsets A, B of ![{}[3]^d](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Ed&bg=ffffff&fg=333333&s=0&c=20201002) such that A is in the complement of
such that A is in the complement of ![B + [2]^d](https://s0.wp.com/latex.php?latex=B+%2B+%5B2%5D%5Ed&bg=ffffff&fg=333333&s=0&c=20201002) , where d is a slowly growing function of n, and for which A, B have no density increments on a subspace. Easy with Fourier analysis, and I don’t see how to do it otherwise.) Somehow the problem is that
, where d is a slowly growing function of n, and for which A, B have no density increments on a subspace. Easy with Fourier analysis, and I don’t see how to do it otherwise.) Somehow the problem is that  is not as “connected” as
is not as “connected” as  .
.
If we try to prove corners or DHJ, then 1 still works (see 102), but 2 now breaks down, basically because Euclid’s axiom “two points determine a line” begins to fail horribly. Instead of A being squeezed into the complement of a large structured set, it seems that A is only squeezed into a complement of a small structured set, which is saying practically nothing. (For instance, in the DHJ problem, colouring HJ already tells us that the complement of A must contain arbitrarily large combinatorial subspaces (for n large enough), but this seems to be a mostly useless piece of information, although it does at least imply the weak DHJ in 85.) It my be that by localising to a well-chosen piece of![{}[n]^2](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) or
or ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) one can mitigate this problem, but I don’t see how yet. And even after problem 2. is solved, one still has to grapple with 3., which as we saw was already problematic even in the model
one can mitigate this problem, but I don’t see how yet. And even after problem 2. is solved, one still has to grapple with 3., which as we saw was already problematic even in the model  case.
case.
February 4, 2009 at 6:33 pm |
119. Obstructions.
Ryan, by “plurality digit” do you mean “digit for which there is a long run” or do you mean “digit that occurs most often”? From your second paragraph I think you must mean the second.
In fact, I see that you definitely mean the second, the idea being that you’d expect that digit to occur something like times, on average anyway. But I’ll leave this comment here in case it helps anyone else.
times, on average anyway. But I’ll leave this comment here in case it helps anyone else.
February 4, 2009 at 6:38 pm |
120. Density incrementation
Re: Ryan.117 (as opposed to Terry.117 🙂 [now corrected — Tim], I can tell you what type of density incrementation you need to get in order to get a contradiction that finishes the proof.
From the trivial bound , we know that the sequence
, we know that the sequence  decreases monotonically to a limit
decreases monotonically to a limit  . DHJ is precisely the claim that
. DHJ is precisely the claim that 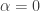 , so suppose for contradiction that
, so suppose for contradiction that  . Then we can write
. Then we can write 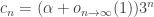 , where
, where  denotes a quantity that goes to zero as
denotes a quantity that goes to zero as 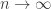 . Note that the decay rate
. Note that the decay rate  here is completely ineffective.
here is completely ineffective.
Thus, for n large, we can find a set![A \subset [3]^n](https://s0.wp.com/latex.php?latex=A+%5Csubset+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density 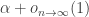 with no combinatorial lines. In particular, on any m-dimensional subspace, the density of A cannot exceed
with no combinatorial lines. In particular, on any m-dimensional subspace, the density of A cannot exceed 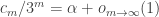 . So, in order to get a contradiction, one needs to find a medium-size dimensional subspace on which one has a density increment that is bounded below uniformly in the dimension m of that subspace.
. So, in order to get a contradiction, one needs to find a medium-size dimensional subspace on which one has a density increment that is bounded below uniformly in the dimension m of that subspace.
A useful fact, by the way, is that upper bounds on density of all subspaces imply lower bounds on density of _random_ subspaces. Indeed, consider a random subspace V of![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with two properties: (a) the dimension of V is always at least m, and (b) any two subspaces which are “parallel” in the sense that their wildcard set is exactly the same will be drawn with equal probability. Then I claim that with probability
with two properties: (a) the dimension of V is always at least m, and (b) any two subspaces which are “parallel” in the sense that their wildcard set is exactly the same will be drawn with equal probability. Then I claim that with probability  , the relative density of A in V will be
, the relative density of A in V will be  . Indeed, we can condition to fix the wildcard set of V, and observe that the remaining subspaces partition
. Indeed, we can condition to fix the wildcard set of V, and observe that the remaining subspaces partition ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . The mean density of the subspaces is thus the global density
. The mean density of the subspaces is thus the global density 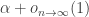 of A, while from the preceding discussion we know that the maximum density is at most
of A, while from the preceding discussion we know that the maximum density is at most  , and the claim now follows from Markov’s inequality.
, and the claim now follows from Markov’s inequality.
February 4, 2009 at 6:57 pm |
121. Szemeredi’s uniformisation trick
In 120 I noted how an extremal set A tends to have density close to on most m-dimensional subspaces. In Endre’s big paper (the proof of Szemeredi’s theorem), he uses a very nice double counting argument to say a much stronger statement: given any specified dense subset
on most m-dimensional subspaces. In Endre’s big paper (the proof of Szemeredi’s theorem), he uses a very nice double counting argument to say a much stronger statement: given any specified dense subset  of
of ![{}[3]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) , A also has density close to
, A also has density close to  on “most” copies of
on “most” copies of  . (He eventually applies this fact to sets
. (He eventually applies this fact to sets 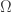 that are the cells of a Szemeredi partition of a certain graph he constructs on
that are the cells of a Szemeredi partition of a certain graph he constructs on ![{}[3]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) .) This trick does not appear to be as well known as it should be (and is absolutely crucial to Endre’s proof), so I am reproducing it here.
.) This trick does not appear to be as well known as it should be (and is absolutely crucial to Endre’s proof), so I am reproducing it here.
Here is the formal claim: let (where
(where 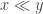 means that “y is sufficiently large depending on x”, and let
means that “y is sufficiently large depending on x”, and let ![\Omega_1,\ldots,\Omega_k \subset [3]^m](https://s0.wp.com/latex.php?latex=%5COmega_1%2C%5Cldots%2C%5COmega_k+%5Csubset+%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) . Then one can find a copy of
. Then one can find a copy of ![{}[3]^d \times [3]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Ed+%5Ctimes+%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) in A such that for every x in
in A such that for every x in ![{}[3]^d](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Ed&bg=ffffff&fg=333333&s=0&c=20201002) and all
and all 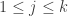 , the relative density of A in
, the relative density of A in 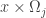 is
is  .
.
Proof. We need some intermediate numbers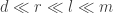 . Pick a random copy of
. Pick a random copy of ![{}[3]^l \times [3]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5El+%5Ctimes+%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) in A. By the previous discussion, every x in
in A. By the previous discussion, every x in ![{}[3]^l](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5El&bg=ffffff&fg=333333&s=0&c=20201002) has a probability
has a probability  of being such that A has density
of being such that A has density  in
in ![x \times [3]^m](https://s0.wp.com/latex.php?latex=x+%5Ctimes+%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) . By the union bound (assuming m is large depending on l), we may thus select a copy of
. By the union bound (assuming m is large depending on l), we may thus select a copy of ![{}[3]^l \times [3]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5El+%5Ctimes+%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) such that A has density
such that A has density  in every
in every ![x \times [3]^m](https://s0.wp.com/latex.php?latex=x+%5Ctimes+%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) .
.
For each j, let f_j(x) be the density of A in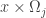 , rounded to the nearest multiple of 1/r. Applying coloring Hales-Jewett (because l is large compared to k, d, r), we can pass from
, rounded to the nearest multiple of 1/r. Applying coloring Hales-Jewett (because l is large compared to k, d, r), we can pass from ![{}[3]^l](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5El&bg=ffffff&fg=333333&s=0&c=20201002) to a subspace
to a subspace ![{}[3]^d](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Ed&bg=ffffff&fg=333333&s=0&c=20201002) such that the
such that the 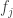 are constant on this subspace for all j:
are constant on this subspace for all j:  . But by double counting the density of A on
. But by double counting the density of A on ![{}[3]^d \times \Omega_j](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Ed+%5Ctimes+%5COmega_j&bg=ffffff&fg=333333&s=0&c=20201002) we see that
we see that  ; similarly by double counting the density of A on
; similarly by double counting the density of A on ![{}[3]^d \times ([3]^m \backslash \Omega_j)](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5Ed+%5Ctimes+%28%5B3%5D%5Em+%5Cbackslash+%5COmega_j%29&bg=ffffff&fg=333333&s=0&c=20201002) we have
we have 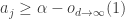 . The claim follows.
. The claim follows.
February 4, 2009 at 7:01 pm |
122. Terry, re your first #120, thanks! Er, would it be possible to explain it in the form, “The new dimension needs to be at least
needs to be at least  , and the density needs to increase by at least
, and the density needs to increase by at least  .”?
.”?
February 4, 2009 at 7:14 pm |
123. I guess one thing that worries me is that it already seems hard to give explicit (nonrandom) sets — strongly nonuniform or not! — which don’t have a modest density increment. The only examples I know are those of the “modular arithmetic” type discussed by Boris and Tim earlier.
— strongly nonuniform or not! — which don’t have a modest density increment. The only examples I know are those of the “modular arithmetic” type discussed by Boris and Tim earlier.
February 4, 2009 at 7:41 pm |
124 Sperner
Going back to Tim’s removal lemma in Kneser graphs 106 ; It actually says that every large matching in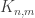 spans at least the expected number edges. This would be a Ruzsa-Szemeredi type theorem in a sparse graph. From a different viewpoint it reminds me to Bollobas’ theorem, which states that any induced matching in
spans at least the expected number edges. This would be a Ruzsa-Szemeredi type theorem in a sparse graph. From a different viewpoint it reminds me to Bollobas’ theorem, which states that any induced matching in 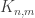 has size at most
has size at most 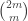 . There is an algebraic proof of Bollobas’ theorem by Lovasz, it might give us some information about the number of edges spanned by a large matching.
. There is an algebraic proof of Bollobas’ theorem by Lovasz, it might give us some information about the number of edges spanned by a large matching.
February 4, 2009 at 7:48 pm |
125. ((follow on 111.) well, since the numeric values of the variables are not important for combinatorial lines this means that the equations (at least for k=3) can be slightly more general.)
February 4, 2009 at 8:19 pm |
126. Regarding Terry’s post (45), I’ve extended the Green/Wolf version of Elkin’s strengthened form of Behrend’s construction (of sets of integers without 3-term APs) to longer APs. This parallels Rankin’s extension of Behrend’s construction.
http://arxiv.org/abs/0811.3057
February 4, 2009 at 8:30 pm |
127. Density incrementation
@Ryan.122: This is true… where is any function you choose that goes to infinity, and
is any function you choose that goes to infinity, and  is a function that you don’t get to choose, and goes to zero very very slowly (and ineffectively) as
is a function that you don’t get to choose, and goes to zero very very slowly (and ineffectively) as 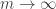 . (But you are allowed to make f depend on g, for what it’s worth.)
. (But you are allowed to make f depend on g, for what it’s worth.)
For sake of discussion, suppose the rate of convergence of to
to  was inverse tower-exponential… then the game is basically “get a density increment of at least
was inverse tower-exponential… then the game is basically “get a density increment of at least  on a subspace of dimension
on a subspace of dimension 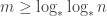 “. Of course, we don’t know in advance that we have an inverse tower-exponential rate – so you have to prove something like this but with
“. Of course, we don’t know in advance that we have an inverse tower-exponential rate – so you have to prove something like this but with  replaced by some other unknown slowly growing function.
replaced by some other unknown slowly growing function.
February 4, 2009 at 9:04 pm |
128. Density incrementation
One reason, by the way, why it’s so difficult to find dense subsets of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) that don’t have any significant density incrementation on a large subspace is that, thanks to the k=3 DHJ theorem, they don’t exist! (In particular, any dense subset has to have density 1 on a subspace of dimension
that don’t have any significant density incrementation on a large subspace is that, thanks to the k=3 DHJ theorem, they don’t exist! (In particular, any dense subset has to have density 1 on a subspace of dimension  for some f going to infinity, by the same argument used in Terry.102.)
for some f going to infinity, by the same argument used in Terry.102.)
Of course, we can’t actually use this fact in our proof, as it would be circular.
February 4, 2009 at 10:55 pm |
129. Sperner
For people who aren’t comfortable with induced matchings, here’s a translation of what Jozsef says in 124 about Bollobás’s theorem. An induced matching in a graph means a collection of edges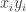 such that no
such that no  is joined to any
is joined to any 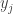 with
with  . So the theorem is saying that in the graph where you join two sets of size
. So the theorem is saying that in the graph where you join two sets of size  if and only if they are disjoint, the biggest collection of disjoint pairs
if and only if they are disjoint, the biggest collection of disjoint pairs  you can find with
you can find with 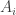 always intersecting
always intersecting  if
if  is the one where you take all subsets
is the one where you take all subsets 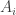 of a
of a 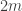 -element subset of
-element subset of ![\null [n]](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) and let
and let 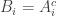 in each case. Jozsef, there clearly needs to be a lower bound on
in each case. Jozsef, there clearly needs to be a lower bound on  in terms of
in terms of  here: can you remember what it is?
here: can you remember what it is?
February 4, 2009 at 11:01 pm |
Metacomment: It would be useful if contributors to this discussion could look at the discussion over on the Questions of Procedure post. I’ve done a poll and there seems to be a small majority in favour of separate new posts for each thread. That would require summaries of the various threads, so I think we need to agree what they are and find out who would be prepared to write the summaries. Jason’s given us some suggestions about what the threads might be, though I think things may have moved on since then. I’ll discuss this over at the other post.
February 5, 2009 at 4:07 am |
130. The k=2.5 case of DHJ
I was trying to adapt Szemeredi’s proof of Roth’s theorem to the k=3 DHJ case, somehow using the k=2 DHJ (Sperner) as an initial step, when I discovered a very strange phenomenon for DHJ, not present for corners or for arithmetic progressions: I cannot logically relate k=2 DHJ to k=3 DHJ! Instead, k=3 DHJ trivially implies the following statement:
k=2.5 DHJ: If n is sufficiently large depending on , and
, and ![A \subset [3]^n](https://s0.wp.com/latex.php?latex=A+%5Csubset+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) has density at least
has density at least  , then there exists a combinatorial line whose first two points lie in A.
, then there exists a combinatorial line whose first two points lie in A.
But I cannot deduce k=2.5 DHJ from the k=2 DHJ, or conversely, basically because![\null [2]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is an incredibly sparse subset of
is an incredibly sparse subset of ![\null [3]^n](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . Actually, despite the Sperner-type appearance to k=2.5 DHJ, I was not able to come up with a combinatorial proof of this statement at all! Presumably I must be missing something obvious. But in any case, this looks like an obvious test problem to work on, being strictly easier than k=3 DHJ.
. Actually, despite the Sperner-type appearance to k=2.5 DHJ, I was not able to come up with a combinatorial proof of this statement at all! Presumably I must be missing something obvious. But in any case, this looks like an obvious test problem to work on, being strictly easier than k=3 DHJ.
February 5, 2009 at 4:12 am |
131. Szemeredi’s proof of Roth’s theorem
This is perhaps only for my own benefit, but I was at least able to extend Szemeredi’s proof of Roth’s theorem (see 86, 118) to the setting. As in 118, we know that the complement of A contains 2.Q – A for some medium-dimensional cube Q. We can represent Q as an increasing sequence
setting. As in 118, we know that the complement of A contains 2.Q – A for some medium-dimensional cube Q. We can represent Q as an increasing sequence  as in 86, and use the pigeonhole principle to find a place where
as in 86, and use the pigeonhole principle to find a place where  stabilises, i.e. it has almost the same density as
stabilises, i.e. it has almost the same density as  for some medium-sized h. Thus the set
for some medium-sized h. Thus the set  is almost invariant under the h steps
is almost invariant under the h steps  , and so is approximately equal to a union of cosets of the subspace V spanned by these h vectors. So A largely avoids a dense union of cosets of V, so by pigeonhole, it must have significantly increased density on another coset of V, and this is enough for the density increment argument to kick in.
, and so is approximately equal to a union of cosets of the subspace V spanned by these h vectors. So A largely avoids a dense union of cosets of V, so by pigeonhole, it must have significantly increased density on another coset of V, and this is enough for the density increment argument to kick in.
But I do not see how to use this sort of argument to prove either DHJ or corners, the problem being that the analogue of 2.Q-A is far too sparse in either setting.
February 5, 2009 at 5:26 am |
132. The k=2.5 case of DHJ.
Terry: how interesting! I sort of had thought of this k=2.5 version at some point (it was in my mind when writing #65). My two thoughts on it were:
a) it probably should follow from some Sperner-pushing-shadows-around argument;
b) trying to extrapolate from it to the k=3 result looked very difficult (due to the incredible sparsity you mention) but worth thinking about (this was sort of in my mind at the end of #114).
So I’m surprised and interested to hear that its combinatorial proof is not obvious. Seems indeed like a good problem to think about then.
February 5, 2009 at 5:46 am |
132. To prove k=2.5 in post Tao.#130 note that we can assume that the number of 1’s 2’s and 3’s is of each in all words of
of each in all words of  . Then look at copies of [2]^n of the following type. For a word
. Then look at copies of [2]^n of the following type. For a word  in
in  of length n with say
of length n with say  stars, consider all the words obtained from
stars, consider all the words obtained from  by replacing stars with 1’s and 2’s. Hence, for each
by replacing stars with 1’s and 2’s. Hence, for each  we get a copy of [2]^n. Density on each such copy is at most
we get a copy of [2]^n. Density on each such copy is at most  . If
. If  , double-counting argument gives DHJ k=2.5.
, double-counting argument gives DHJ k=2.5.
February 5, 2009 at 5:59 am |
133. I was just going to say something similar. My version: Suppose has density greater than
has density greater than  in
in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . Then there has to be a particular way of fixing the positions of the
. Then there has to be a particular way of fixing the positions of the 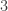 ‘s such that
‘s such that  ‘s density in the resulting copy of
‘s density in the resulting copy of ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is still greater than
is still greater than  . Now apply Sperner.
. Now apply Sperner.
February 5, 2009 at 6:05 am |
134. The “pushing shadows around” Sperner proof gives (I think) nice statements like, “If ‘s density is a lot more than
‘s density is a lot more than  then it must contain lots of “half-combinatorial lines”.” My super-duper-naive hope in #114 was that if we could find “enough” of these half-lines in
then it must contain lots of “half-combinatorial lines”.” My super-duper-naive hope in #114 was that if we could find “enough” of these half-lines in  (since, after all,
(since, after all,  has density
has density  ), we might be able to find a third point in
), we might be able to find a third point in  to finish off one of the half-lines. But such a plan would have to be awfully sophisticated to have a shot at working, I’d guess.
to finish off one of the half-lines. But such a plan would have to be awfully sophisticated to have a shot at working, I’d guess.
February 5, 2009 at 7:30 am |
135.
The k=2.5 case of DHJ
There is more true, namely there are subcubes in any dense subset of![\null [3]^d](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5Ed&bg=ffffff&fg=333333&s=0&c=20201002) . An m-dimensional subcube is a set of elements each has some fixed positions where all elements are the same (1,2, or 3) and m blocks where the elements in one block are all one or all two. There is an element for every possible 1-2 combination of the blocks so there are
. An m-dimensional subcube is a set of elements each has some fixed positions where all elements are the same (1,2, or 3) and m blocks where the elements in one block are all one or all two. There is an element for every possible 1-2 combination of the blocks so there are 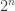 elements in a subcube. I tried to use such subcubes for a Szemeredi type argument, but without success. It is also remarkable, that the shadow of such cube (elements where one block has 3-s) can’t be in our set or there would be a line. The shadow also contains an m-1 dimensional – empty – subspace,
elements in a subcube. I tried to use such subcubes for a Szemeredi type argument, but without success. It is also remarkable, that the shadow of such cube (elements where one block has 3-s) can’t be in our set or there would be a line. The shadow also contains an m-1 dimensional – empty – subspace, ![\null [3]^{m-1}](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5E%7Bm-1%7D&bg=ffffff&fg=333333&s=0&c=20201002) . So, we know that for our set is full with empty subspaces, however I don’t know if we have enough for pushing the density up in another subspace.
. So, we know that for our set is full with empty subspaces, however I don’t know if we have enough for pushing the density up in another subspace.
February 5, 2009 at 7:45 am |
Contd. There is a relevant paper of Gunderson, Rödl, and Sidorenko, where they give sharp bounds on subcubes I mentioned in the previous note. Title: “Extremal problems for sets forming Boolean algebras and complete partite hypergraphs, J. Combin. Th. Ser. A 88 (1999), 342-367. ”
You can find it at http://home.cc.umanitoba.ca/~gunderso/published_work/paper7.pdf .
February 5, 2009 at 8:08 am |
136 Density increment
Let me try to make the previous observation clear. We show that if![S\subset [3]^n](https://s0.wp.com/latex.php?latex=S%5Csubset+%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is c-dense and line-free, then for every m there is a
is c-dense and line-free, then for every m there is a 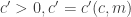 such that c’ – fraction of the m-dimensional subspaces (
such that c’ – fraction of the m-dimensional subspaces (![\null [3]^m](https://s0.wp.com/latex.php?latex=%5Cnull+%5B3%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) ) have empty intersection with S.
) have empty intersection with S.
February 5, 2009 at 8:34 am |
137. Sperner
On Tim’s question; I don’t think that there is a lower bound on m.
Also, I don’t see what would be the right question here. If we take a perfect matching, extremal for Bollobas’ theorem, with m=n/2-k (k is a small integer) then there are only a few edges, but you have to remove half of the sets to destroy all edges. Or, it is late night again, and I overlooked something.
February 5, 2009 at 10:56 am |
138. Sperner
Ah yes, I was thinking that if was much much larger than
was much much larger than  then you would do better by choosing lots of completely disjoint pairs
then you would do better by choosing lots of completely disjoint pairs  , but I was overlooking the fact that
, but I was overlooking the fact that  is not allowed to be disjoint from
is not allowed to be disjoint from  .
.
Let me check the arithmetic in your last remark. If is a small integer, then the number of sets in
is a small integer, then the number of sets in ![\binom{[2m]}{m}](https://s0.wp.com/latex.php?latex=%5Cbinom%7B%5B2m%5D%7D%7Bm%7D&bg=ffffff&fg=333333&s=0&c=20201002) is about
is about 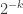 times the number of sets in
times the number of sets in  , I think. Yes, that’s right, since the ratio of
, I think. Yes, that’s right, since the ratio of 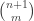 to $\binom{n}{m}$ is
to $\binom{n}{m}$ is  , which for us is about 2. So if
, which for us is about 2. So if  is a small integer, then it is indeed the case that choosing all subsets of
is a small integer, then it is indeed the case that choosing all subsets of ![\null[2m]](https://s0.wp.com/latex.php?latex=%5Cnull%5B2m%5D&bg=ffffff&fg=333333&s=0&c=20201002) gives us a positive fraction of all sets. But in this case, the only edges are the ones that join a set to its complement in
gives us a positive fraction of all sets. But in this case, the only edges are the ones that join a set to its complement in ![\null[2m]](https://s0.wp.com/latex.php?latex=%5Cnull%5B2m%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
The annoying thing (from the point of view of trying to formulate a decent conjecture) is that this makes the graph sparse. After all, the average degree in the graph, even when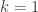 , tends to infinity with
, tends to infinity with  . (It is
. (It is  which is around
which is around 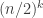 .)
.)
However, I think that there is still hope for a less neat conjecture that concerns several layers around the middle. And I also think that there may be some counterpart of this false conjecture for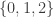 -sequences that is also false. I think once we identify this counterpart, we will see that we never expected or needed it to be true, and that will make us feel better about whatever
-sequences that is also false. I think once we identify this counterpart, we will see that we never expected or needed it to be true, and that will make us feel better about whatever  -version we come up with. I’m busy for a few hours now but will try to make all this more precise later.
-version we come up with. I’m busy for a few hours now but will try to make all this more precise later.
February 5, 2009 at 11:32 am |
139. Sperner
Just one tiny extra remark before I go. For now it seems that one way of rescuing the conjecture is to insist that tends to infinity with
tends to infinity with  , so that
, so that 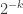 is no longer a constant fraction. This feels like a natural restriction because it corresponds to insisting that the variable set has size that tends to infinity — which in general it will have to.
is no longer a constant fraction. This feels like a natural restriction because it corresponds to insisting that the variable set has size that tends to infinity — which in general it will have to.
February 5, 2009 at 5:04 pm |
[…] Weblog: Timothy Gowers updates the rules to his massively collaborative mathematics experiment. He posted the first project for this experiment a few days ago and has already received 145 […]
February 5, 2009 at 5:10 pm |
140. Sperner
I think what I said in my previous two comments does indeed make sense. To see why, imagine that we tried in the DHJ case to a single triple of slices ,
,  and
and  . Then the triangle removal lemma would say that if there were very few combinatorial lines coming from some subsets of these three slices, then one could remove a small proportion of points from the subsets and end up with no combinatorial lines. If
. Then the triangle removal lemma would say that if there were very few combinatorial lines coming from some subsets of these three slices, then one could remove a small proportion of points from the subsets and end up with no combinatorial lines. If  is a fixed positive integer, then this is false, but we don’t expect to be able to produce combinatorial lines with a fixed size of variable set: the size will have to depend on the density of
is a fixed positive integer, then this is false, but we don’t expect to be able to produce combinatorial lines with a fixed size of variable set: the size will have to depend on the density of  .
.
If a triangle removal lemma is true for triples of slices like this when is large, I’m not sure that it implies DHJ, because as I’ve already pointed out you don’t get degenerate triples that involve three different slices — obviously enough. In fact, this is a general point to think about: if we found the most wonderful triangle removal lemma imaginable, would it actually lead to a proof of density Hales-Jewett? (I think there is an analogy with the situation with corners that suggests to me that the answer isn’t obviously no.)
is large, I’m not sure that it implies DHJ, because as I’ve already pointed out you don’t get degenerate triples that involve three different slices — obviously enough. In fact, this is a general point to think about: if we found the most wonderful triangle removal lemma imaginable, would it actually lead to a proof of density Hales-Jewett? (I think there is an analogy with the situation with corners that suggests to me that the answer isn’t obviously no.)
Going back to Sperner, my current pair-removal problem, not yet shown to be true and not yet shown to be badly formulated, is to show that if and
and  are subsets of
are subsets of ![\binom{[n]}{m}](https://s0.wp.com/latex.php?latex=%5Cbinom%7B%5Bn%5D%7D%7Bm%7D&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where 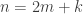 and
and  tends to infinity slowly with
tends to infinity slowly with  , and if there are few disjoint pairs
, and if there are few disjoint pairs  , then it is possible to remove a small number of sets (compared with
, then it is possible to remove a small number of sets (compared with 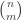 ) from
) from 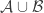 and end up with no disjoint pairs.
and end up with no disjoint pairs.
February 5, 2009 at 5:44 pm |
141. Sperner
In relation to 140, I tried to work out what the regularity lemma says for 1-uniform hypergraphs, but the resulting statement is even more ridiculous than pair removal in the dense case and not worth repeating here. This makes me think that there’s a genuine chance that if we could prove an appropriate disjoint-pair removal lemma, that it might be the extra ingredient that’s needed to mix with triangle-removal to get DHJ. I realize that I’ve sort of said this before.
February 5, 2009 at 5:57 pm |
142. Sperner
Part of the Kneser-graphs philosophy is that they behave rather like the graph on the n-sphere where you join two points if they are almost antipodal to each other. So another question that might be worth investigating is whether there is any chance of an almost-antipodal-pair-removal lemma. It would say something like this. Let and
and  be two subsets of
be two subsets of 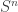 such that the measure of all pairs
such that the measure of all pairs 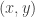 such that
such that  ,
,  and
and  is small. Then it is possible to remove sets of small measure from
is small. Then it is possible to remove sets of small measure from  and
and  and end up with no such pairs.
and end up with no such pairs.
It may take some work to turn that into a decent question, if indeed it can be done. I think I know what it means for the set of disjoint pairs to have small measure. It should mean small compared with the measure of all such pairs in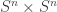 (which is equal to 1 times the measure of the spherical cap
(which is equal to 1 times the measure of the spherical cap  ).
).
In this continuous context, it might be necessary for the conclusion to say that after the removal what you no longer have is pairs that have inner product less than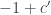 for some
for some  .
.
I’m slightly suspicious of this variant, because it feels to me as though if you’ve got two sets with no almost antipodal pairs then at least one of them must be very small, unless is something like
is something like  . In fact, that is indeed the case as it’s saying that the distance from
. In fact, that is indeed the case as it’s saying that the distance from  to
to 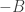 is large, so it comes from concentration of measure. I’m not yet sure what happens if you just assume that
is large, so it comes from concentration of measure. I’m not yet sure what happens if you just assume that 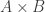 contains few almost antipodal pairs. If it is possible for both
contains few almost antipodal pairs. If it is possible for both  and
and  to be large, then the result is false, and if it is impossible then it is in a certain sense trivial.
to be large, then the result is false, and if it is impossible then it is in a certain sense trivial.
But I think this could be a useful observation: it shows that if there is any chance of a statement holding in the Kneser graph, then it must use some property of that graph that distinguishes it from the sphere graph.
February 5, 2009 at 6:30 pm |
143. Sperner
Tim, just a small correction to 139: the number k of wildcards can be taken to be bounded by a quantity depending only on the density delta, either for Sperner or DHJ. Indeed, one can foliate![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) or
or ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into slices of
into slices of ![{}[2]^{n_0}](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5E%7Bn_0%7D&bg=ffffff&fg=333333&s=0&c=20201002) or
or ![{}[3]^{n_0}](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5E%7Bn_0%7D&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where  is the first integer for which Sperner or DHJ applies. By the pigeonhole principle, one of these slices has density at least
is the first integer for which Sperner or DHJ applies. By the pigeonhole principle, one of these slices has density at least  , and thus contains a combinatorial line with at most
, and thus contains a combinatorial line with at most 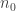 wildcards.
wildcards.
Now, there should also be lines with wildcard length as high as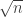 or so, I think. I can reason by analogy with the corners setting: suppose one wanted to find corners in a dense subset of the strip
or so, I think. I can reason by analogy with the corners setting: suppose one wanted to find corners in a dense subset of the strip ![\{ (a,b) \in [n]^2: |a-b| \ll \sqrt{n} \}](https://s0.wp.com/latex.php?latex=%5C%7B+%28a%2Cb%29+%5Cin+%5Bn%5D%5E2%3A+%7Ca-b%7C+%5Cll+%5Csqrt%7Bn%7D+%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) . One can cover this strip by grids of spacing k and of length at least
. One can cover this strip by grids of spacing k and of length at least 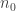 (where
(where 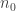 is similar to as in the previous paragraph), and it seems to me that one should get a corner of length equal to a bounded multiple of k for any specified k between 1 and a small multiple of
is similar to as in the previous paragraph), and it seems to me that one should get a corner of length equal to a bounded multiple of k for any specified k between 1 and a small multiple of 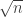 . I think the same sort of argument should work in the DHJ case. But it seems to me that it is somehow easier to fish for lines in the small k end of the pool rather than the large k end, even though the graph is denser in the latter case.
. I think the same sort of argument should work in the DHJ case. But it seems to me that it is somehow easier to fish for lines in the small k end of the pool rather than the large k end, even though the graph is denser in the latter case.
Re: 132, 133, 135: thanks, it’s clear now that 2.5 and 2 are equivalent. For some reason I was reluctant to partition the big cube![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into variable-sized copies of
into variable-sized copies of ![{}[2]^m](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5Em&bg=ffffff&fg=333333&s=0&c=20201002) , but I see now that that is the way one should think about it.
, but I see now that that is the way one should think about it.
Jozsef@135,136,137: this fits pretty well with what I said at 118. The key step in Endre’s proof of Roth is that a small cube Q is suddenly amplified to a huge structured set 2.Q-A in the complement which has really big density (at least ) and still contains tons of cubes (and more to the point, parallel cubes). In our situation we have a much sparser set of cubes in the complement, and they are not all parallel to each other, and it doesn’t look like this is enough to force a significant density increment anywhere. (Note also that one could also get a similar sparse collection of non-parallel cubes in the complement from the colouring HJ theorem.) I tried to combine all this with Endre’s uniformisation trick (121) but without luck (again, the issue is sparsity, the
) and still contains tons of cubes (and more to the point, parallel cubes). In our situation we have a much sparser set of cubes in the complement, and they are not all parallel to each other, and it doesn’t look like this is enough to force a significant density increment anywhere. (Note also that one could also get a similar sparse collection of non-parallel cubes in the complement from the colouring HJ theorem.) I tried to combine all this with Endre’s uniformisation trick (121) but without luck (again, the issue is sparsity, the  in 121 need to be dense).
in 121 need to be dense).
February 5, 2009 at 6:59 pm |
144 Sperner
I would like to see a removal lemma type argument for Kneser graphs very much and I agree that if k goes to infinity (Tim 138), then there should be a sensible one. Let me mention a light version of the triangle removal lemma, which is still strong enough for applications; If the number of triangles is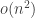 in an n-vertex graph, then one can remove
in an n-vertex graph, then one can remove 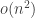 edges to destroy a positive fraction of the triangles. So, I don’t think that in the Kneser graph problem we should go for removing all edges, it should be enough that with a few vertices we can destroy much more than expected edges.
edges to destroy a positive fraction of the triangles. So, I don’t think that in the Kneser graph problem we should go for removing all edges, it should be enough that with a few vertices we can destroy much more than expected edges.
February 5, 2009 at 7:02 pm |
144 Contd. I meant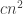 triangles …
triangles …
February 5, 2009 at 7:09 pm |
145. Sperner.
Hi Tim, re your #142. It is known that for all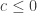 , among sets
, among sets  and
and  on the sphere of fixed measures, the ones which minimize the measure of pairs
on the sphere of fixed measures, the ones which minimize the measure of pairs  with
with  are the “concentric” caps. Note that in high dimensions, having inner product
are the “concentric” caps. Note that in high dimensions, having inner product  is very much similar to having inner product
is very much similar to having inner product  . The proof is by shifting. One such proof appears here: http://www.wisdom.weizmann.ac.il/~feige/Approx/maxcut.ps
. The proof is by shifting. One such proof appears here: http://www.wisdom.weizmann.ac.il/~feige/Approx/maxcut.ps
Based on this it may be possible to calculate the answer to your question. I actually prefer to do these things not on the high-dimensional sphere but on the equally good surrogate, high-dimensional Gaussian space. It is known that for all , the subsets
, the subsets  and
and  of fixed Gaussian measure which minimize the probability of
of fixed Gaussian measure which minimize the probability of  , where
, where 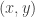 is a pair of correlated Gaussians with covariances
is a pair of correlated Gaussians with covariances 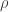 , are two “parallel” halfspaces. This is a theorem of Borell:
, are two “parallel” halfspaces. This is a theorem of Borell:
http://www.springerlink.com/content/n761353703r7p675/
Just wanted to get those references out there; will try to think about the ensuing calculations…
February 5, 2009 at 7:21 pm |
146 Sperner
Terry @118 142, Yes, We need more structure to apply Endre’s trick. It was easy to apply when (almost) every element is a center of symmetry in the following way; Choose an element of your set (center). Any other element has a unique mirror image and if both are in your set, then your set contains a 3-term arithmetic progression. With HJ, most pairs are not in line, so the “symmetry” is only local.
February 5, 2009 at 7:56 pm |
147. Sperner
Terry — indeed. In fact, I came to a similar realization in the DHJ context at the end of the first paragraph of 140. But I suppose one could regard things in another way and say that we’re trying to get the density to tend to zero (very very slowly) and therefore we need to tend to infinity.
to tend to infinity.
Ryan — at first I skimmed what you said and thought it was repeating what I had said, and then I realized that it wasn’t at all. Although the sphere question seems genuinely distinct from the Kneser-graphs question, it is definitely good to know that something along these lines is known.
If and
and  are concentric caps and are not of tiny measure, then they must reach almost all the way to the equator, at least, so my guess is that that will give them a lot of almost antipodal pairs. So at the moment my money is on few antipodal pairs implying that at least one of
are concentric caps and are not of tiny measure, then they must reach almost all the way to the equator, at least, so my guess is that that will give them a lot of almost antipodal pairs. So at the moment my money is on few antipodal pairs implying that at least one of  and
and  has small measure. If so, then we would have the true-for-not-quite-the-kind-of-reason-we-hoped-for option rather than the false option.
has small measure. If so, then we would have the true-for-not-quite-the-kind-of-reason-we-hoped-for option rather than the false option.
February 5, 2009 at 8:24 pm |
148. Sperner
As I was sitting through my daughter’s piano lesson, my mind wandered back to pair removal in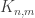 , and I found myself wondering whether we were already done. Almost certainly not, but in the spirit of keeping thoughts public, let me attempt to deduce it from the theorem of Bollobás mentioned by Jozsef in 124.
, and I found myself wondering whether we were already done. Almost certainly not, but in the spirit of keeping thoughts public, let me attempt to deduce it from the theorem of Bollobás mentioned by Jozsef in 124.
First, here’s the thought that’s in the back of my mind. It’s that the number of edges you need to remove to make a graph triangle free is within a constant of the largest possible number of edge-disjoint triangles in that graph. (This was pointed out to me by Tom Sanders.) The proof is that if you’ve got edge-disjoint triangles then you need to remove at least
edge-disjoint triangles then you need to remove at least  edges. Conversely, if you’ve got a maximal set of edge-disjoint triangles and there are
edges. Conversely, if you’ve got a maximal set of edge-disjoint triangles and there are  of them, then if you remove all edges from all those triangles you will be left with no triangles (because any triangle left would be edge-disjoint from the removed ones, contradicting maximality). So the two numbers are equal to within a factor of 3.
of them, then if you remove all edges from all those triangles you will be left with no triangles (because any triangle left would be edge-disjoint from the removed ones, contradicting maximality). So the two numbers are equal to within a factor of 3.
Now suppose we are trying to get rid of all disjoint pairs from
from  If we can find
If we can find  such pairs, with no two sharing a
such pairs, with no two sharing a  or a
or a  , then we have to remove at least
, then we have to remove at least  sets from
sets from  Conversely, if we’ve got a maximal set of disjoint pairs and we remove all sets that are involved in those pairs, then we cannot have any disjoint pairs left.
Conversely, if we’ve got a maximal set of disjoint pairs and we remove all sets that are involved in those pairs, then we cannot have any disjoint pairs left.
I now see that Jozsef understood this way back in 104. And unfortunately, it’s not covered by Bollobás’s theorem because that concerns maximal induced matchings rather than maximal matchings.
However (and this too Jozsef clearly realized ages ago), this little argument allows us to rephrase the question: if you’ve got a lot of disjoint pairs (of sets of size
(of sets of size  in
in ![\null [2m+k]](https://s0.wp.com/latex.php?latex=%5Cnull+%5B2m%2Bk%5D&bg=ffffff&fg=333333&s=0&c=20201002) ), where all the
), where all the 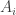 are distinct and all the
are distinct and all the 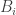 are distinct, then are you forced to have a lot of disjoint pairs
are distinct, then are you forced to have a lot of disjoint pairs 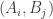 with
with  . Bollobás’s theorem states that you must have at least one such pair. I suppose an averaging argument would lift that up to something, but probably not to within a constant of the trivial maximum. But as Jozsef suggested, the proof of Bollobás’s theorem might do something for us.
. Bollobás’s theorem states that you must have at least one such pair. I suppose an averaging argument would lift that up to something, but probably not to within a constant of the trivial maximum. But as Jozsef suggested, the proof of Bollobás’s theorem might do something for us.
February 5, 2009 at 8:28 pm |
148. Obstructions to uniformity
It took me a while to catch up with this thread – this is perhaps one thread which is particularly ripe for a fresh start with a post summarising previous progress and listing the known examples.
Here are the examples of interesting “obstructing sets” to either DHJ, Sperner, or Kruskal-Katona that I can find in the above threads:
Gowers.38: A set A of words x whose last entry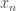 depends on the parity of the number of 1s in all other entries.
depends on the parity of the number of 1s in all other entries.
Boris.44, Gowers.71, Boris.73, Gowers.76, Gowers.108, Ryan.117: A set A such that for all x in A, the number (a,b,c) of 1s, 2s, and 3s of x respectively in![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) (or some subset S of indices in
(or some subset S of indices in ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , or using some other weighting on
, or using some other weighting on ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) ) lie in a structured set.
) lie in a structured set.
Gowers.69, 70, 71: A set A such that the probability that for some
for some ![i \in [n]](https://s0.wp.com/latex.php?latex=i+%5Cin+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , some
, some 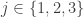 , and x drawn uniformly from A, deviates significantly from 1/3.
, and x drawn uniformly from A, deviates significantly from 1/3.
Ryan.92: A consists of all the sets which contain a medium-sized block of 2s among some special collection of blocks.
Ryan.94: Take any existing example of a non-uniform set A and tack on some fixed string of digits (e.g. 23) at the end, increasing n to n+2 (say) and decreasing the density by a factor of 9 (say).
It seems that one can unify all of the above examples so far. Given a set A and weighting w on [n] by integers, define the richness profile of A with respect to the weight w to be the function that assigns to each triple (a,b,c), the number of elements of A whose weighted count of 1s, 2s, and 3s are equal to a, b, c, respectively. (In most examples, w is just the indicator function of some set S of indices in [n], so the profile is counting how many 1s, 2s, and 3s there are in S.)
A set A has an standard obstruction to uniformity if there is a reasonably large subspace V on which A has equal or larger density, and a weight w such that the richness profile of with respect to w, deviates in a structured way from what one would expect in the random case. (This is for instance the case if A has significantly large density on V than it does globally.) By “structured” I mean that the deviation is not pseudorandom in the sense of locating corners
with respect to w, deviates in a structured way from what one would expect in the random case. (This is for instance the case if A has significantly large density on V than it does globally.) By “structured” I mean that the deviation is not pseudorandom in the sense of locating corners  in the richness profile.
in the richness profile.
This seems to cover all known examples, while still excluding the random example. (Incidentally: have we shown yet that the random set is quasirandom? This seems to be a necessary step if we are to have any hope at all here.)
February 5, 2009 at 8:50 pm |
149. Obstructions to uniformity.
A couple of things I didn’t quite understand there Terry. If you pull over the obstructions from![\null [n]^2](https://s0.wp.com/latex.php?latex=%5Cnull+%5Bn%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) (as suggested in 116), do you call that a pseudorandom deviation? Where does that example fit into your scheme above? And what are you referring to when you talk about “the random example” in your last paragraph? Do you mean that your definition of a standard obstruction does not apply to random sets? I think I don’t really understand the last sentence of your penultimate paragraph.
(as suggested in 116), do you call that a pseudorandom deviation? Where does that example fit into your scheme above? And what are you referring to when you talk about “the random example” in your last paragraph? Do you mean that your definition of a standard obstruction does not apply to random sets? I think I don’t really understand the last sentence of your penultimate paragraph.
February 5, 2009 at 9:44 pm |
150. Re the last sentence in Tim’s #142: I mentioned this in #82 but perhaps I should have pointed to a later-on paper in the Irit Dinur oeuvre:
Click to access intersecting.pdf
Here she and Friedgut give a mostly complete characterization of large independent sets in Kneser graphs for a little bit less than
a little bit less than 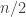 . To be a large intersecting family, you have to nearly be a subset of a large intersecting family which is a “junta”. (A set family
. To be a large intersecting family, you have to nearly be a subset of a large intersecting family which is a “junta”. (A set family  is a “junta” if a set’s absence or presence in
is a “junta” if a set’s absence or presence in  depends only on its inclusion/exclusion of a constant number of coordinates from
depends only on its inclusion/exclusion of a constant number of coordinates from ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) .)
.)
They also discuss the “cross-intersecting” question, which is basically when you have *two* set families — as we do. I would also guess that the improved characterization in their “Conjecture 1.3” may well be provable with “today’s technology”.
February 5, 2009 at 10:54 pm |
151. Sperner
Ryan, I didn’t manage to find an obviously relevant part of the paper you linked to in 82, but the reference you’ve just given does indeed look promising. Do you know enough about their argument to know whether it is robust? That is, if instead of assuming that you have an intersecting (or cross-intersecting) family you just assume that your sets intersect almost all the time, can you still say that there’s some small set of coordinates that explains this phenomenon? I see that their methods of proof are pretty analytic, so maybe there’s some hope here.
February 5, 2009 at 11:50 pm |
152. Hi Tim. Since the proof is analytic, it should almost surely be fine if the initial set(s) are almost always intersecting. Perhaps an even better reference is the proof of Thm. 1.1 in the last 4 pages of this intermediate paper:
Click to access DFR.pdf
February 6, 2009 at 2:04 am |
153. Sperner.
I’m in the middle of writing a summary of the Sperner thread (as well as a few other related ones), to be used when this discussion splits up. At the moment the plan is to have three new discussions.
While writing the summary, I had the following thought. When proving the corners result, we can use a weaker triangle-removal lemma where the hypothesis is not that there are few triangles, but the stronger hypothesis that each edge is contained in at most one triangle. The pair-removal equivalent of this is that for each the only disjoint pair is
the only disjoint pair is  . This starts to sound more Bollobás-like, though the sets
. This starts to sound more Bollobás-like, though the sets  no longer all have the same cardinality.
no longer all have the same cardinality.
So I have two questions. 1. Is there a variant of Bollobás’s theorem where the sets don’t all have to have the same size (though I don’t mind insisting that the all have size close to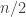 )? 2. If so, can we generalize its proof to a triangle-removal lemma that uses as its hypothesis that the only triangles in the tripartite graph are degenerate?
)? 2. If so, can we generalize its proof to a triangle-removal lemma that uses as its hypothesis that the only triangles in the tripartite graph are degenerate?
This is a strategy that could in principle do the whole thing, so I’m expecting difficulties to arise very quickly …
Unfortunately, I must go to bed now, so finishing the summary will have to wait till tomorrow.
February 6, 2009 at 2:05 am |
[…] of several threads from Tim Gowers’ massively collaborative mathematics project, “A combinatorial approach to density Hales-Jewett“, which I discussed in my previous […]
February 6, 2009 at 2:06 am |
Metacomment: All discussion on upper and lower bounds for , and proof strategies related to Szemeredi’s proofs of Roth’s theorem, should go to the new thread on my blog,
, and proof strategies related to Szemeredi’s proofs of Roth’s theorem, should go to the new thread on my blog,
February 6, 2009 at 2:18 am |
154: Obstructions to uniformity
@Tim.149: I’m thinking of a subset of![{}[n]^2](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D%5E2&bg=ffffff&fg=333333&s=0&c=20201002) as being pseudorandom for the corners problem if it does not correlate with any Cartesian products (or if it has the right number of rectangles, or is small in what I like to call the “Gowers
as being pseudorandom for the corners problem if it does not correlate with any Cartesian products (or if it has the right number of rectangles, or is small in what I like to call the “Gowers  norm”). The example in 116, in particular, is not pseudorandom in this sense, being the Cartesian product of two random sets. So I will label this example (pulled back to
norm”). The example in 116, in particular, is not pseudorandom in this sense, being the Cartesian product of two random sets. So I will label this example (pulled back to ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as a standard obstruction to uniformity (at least for one of the three indices 1, 2, 3 of a combinatorial line; for the other two indices one has to modify the notion of a Cartesian product slightly).
as a standard obstruction to uniformity (at least for one of the three indices 1, 2, 3 of a combinatorial line; for the other two indices one has to modify the notion of a Cartesian product slightly).
By the “random example”, I take A to be a random subset of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of a fixed density
of a fixed density  . This should have no noticeable density increment or other fluctuation in the richness profile for any subspace of dimension bigger than, say,
. This should have no noticeable density increment or other fluctuation in the richness profile for any subspace of dimension bigger than, say, 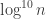 . But I haven’t checked yet (presumably it is an easy entropy calculation) that A is quasirandom in the sense you want, i.e. the number of lines between A, B, and B is the expected number for any large B. Obviously, this is something that has to be true if the obstructions to uniformity approach has any chance of working.
. But I haven’t checked yet (presumably it is an easy entropy calculation) that A is quasirandom in the sense you want, i.e. the number of lines between A, B, and B is the expected number for any large B. Obviously, this is something that has to be true if the obstructions to uniformity approach has any chance of working.
February 6, 2009 at 6:08 am |
I have a suggestion – a blog is perhaps the wrong format for this type of experiment (or future experiments). Its sequential format obviously presents difficulties in following/retrieving information. What you want is a well structured webforum where users can create new threads on a whim, and all subposts to those threads can be easily followed – something with a directory tree structure where posts can be followed in a hierarchy.
You may even be able to find a forum that allows you to highlight threads spawned from posts in other threads – i know one exists…i just can’t remember the name of it – though i might be thinking of news reader….but a news group is probably getting beyond the scope of this initial experiment.
When you start getting into hundreds, the blog is too one-dimensional to be efficient in following a line of thought. You most likely don’t need a newsgroup (not a public one anyway) – just a private forum with enough goodies to make this thing more accessible, otherwise I think you’re going to get swamped (think a thousand+ posts). just a thought.
February 6, 2009 at 6:48 am |
155. Sperner
There is a removal lemma for Kneser graphs! It holds in a certain range; “If a large subgraph has many but not too many edges, then one can remove a small fraction of the vertices destroying most of the edges.”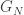 is an N-vertex subgraph of
is an N-vertex subgraph of  the Kneser graph defined by the m-element subsets of the n-element base set. The graph has e edges and D denotes the largest degree and d=2e/N is the average degree.
the Kneser graph defined by the m-element subsets of the n-element base set. The graph has e edges and D denotes the largest degree and d=2e/N is the average degree.
Some notations:
If the vertices having degree at least Cd (for some large constant C) are incident to most of the edges, then we are done; removing N/C vertices destroys most of the edges. So, we can suppose that D<Cd (after throwing away the large degree vertices) As we will see, D<Cd is not possible in a certain vertex (edge) range.
I will follow it in a new windows, I want to check what did I write.(latex)
February 6, 2009 at 6:53 am |
Tim, I’ll publicize this on my blog, as well. This seems like a decent-enough collaborative scholastic.
February 6, 2009 at 7:12 am |
Contd. Well, I would change a few typos if I could, but it is OK.
We are going to use the “permutation trick” of Lubell. For any of the n! permutations we say that it separates the disjoint pair A,B if no element of B precedes any element of A. Any of the n! permutations can separate at most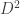 pairs (edges) from
pairs (edges) from 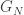 . Indeed, consider the set A which ends first, it would be separated from at least D+1 sets if there were
. Indeed, consider the set A which ends first, it would be separated from at least D+1 sets if there were  separated pairs. Or, the rightmost set B (starting last in the permutation) would be separated from at least D+1 sets, which would mean that D was not the largest degree in
separated pairs. Or, the rightmost set B (starting last in the permutation) would be separated from at least D+1 sets, which would mean that D was not the largest degree in 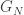 . The number of permutations separating two elements is
. The number of permutations separating two elements is 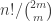 . Collecting the two sides of this double counting we have
. Collecting the two sides of this double counting we have  Using the initial bound on D, our final inequality is
Using the initial bound on D, our final inequality is 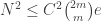 . Conclusion: If the previous inequality fails, then there are less than N/C vertices in $G_N$ which are covering most of the edges.
. Conclusion: If the previous inequality fails, then there are less than N/C vertices in $G_N$ which are covering most of the edges.
February 6, 2009 at 8:40 am |
156 Sperner
contd. I don’t think that the previous inequality is sharp, but I think it gives some nontrivial results. For example, if and we take a positive fraction of the m-element sets,
and we take a positive fraction of the m-element sets,  , and the average degree is
, and the average degree is 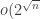 then o(N) vertices (sets) cover almost all edges.
then o(N) vertices (sets) cover almost all edges.
February 6, 2009 at 8:46 am |
The previous short note is full with typos. I should go to sleep now… and that the aver. degree is
and that the aver. degree is  but not constant.
but not constant.
I meant: the size of m is around
February 6, 2009 at 9:08 am |
157. Sperner
Jozsef, I must try to digest what you say. It seems very promising.
February 6, 2009 at 10:03 am |
[…] disjoint from precisely one , then and must both be small. And Ryan (in comments 82, 145, 150 and 152) has drawn attention to existing papers on very closely related subjects. Very recently (at the […]
February 6, 2009 at 10:06 am |
OK, any thoughts about Sperner, triangle removal, regularity lemmas in tripartite Kneser-type graphs, etc., should now be given as comments on a new post that is meant to take over this thread of the discussion. If you would like me to modify the summary, then by all means suggest changes.
For now, the obstructions-to-uniformity thread stays here, but we should get a summary written for that as soon as we can.
[Added 8/2/09 4.05pm GMT: there is now a post on obstructions to uniformity, so all further discussion of this topic should continue there.]
February 8, 2009 at 4:53 pm |
[…] By gowers This post is one of three threads that began in the comments after the post entitled A combinatorial approach to density Hales-Jewett. The other two are Upper and lower bounds for the density Hales-Jewett problem , hosted by Terence […]
February 8, 2009 at 8:23 pm |
Metacomment: one really needs to have a preview function.
February 11, 2009 at 8:21 pm |
[…] were influential to Tim Gowers‘ dream of massively collaborative mathematics. He took an interesting problem, laid down a set of 12 rules-of-conduct and invited everyone to contribute. The project is still […]
February 20, 2009 at 1:15 am |
[…] the next post, Gowers listed his ideas broken down into thirty-eight points. He also clarified the circumstances […]
March 19, 2009 at 4:30 pm |
[…] Cambridge University, used his blog for an experiment in massive online collaboration for solving a significant problem in math — combinatorial proof of the density Hales-Jewett theorem. Some six weeks (and nearly 1000 […]
March 20, 2009 at 9:29 pm |
[…] an accomplished professional mathematician, initially thought that the chances of success were “substantially less than 100%”, even adopting a quite modest criterion for […]
March 26, 2009 at 1:40 am |
[…] that he thought amenable to an online collaborative approach, then kicked things off with a blog post. Six weeks later, the main problem he proposed was declared (essentially) solved. However, the […]
April 16, 2009 at 12:54 am |
[…] some high profile mathematicians have been using a blog to conduct a massively collaborative mathematics project. What a brilliant idea that could be done today, with our current […]
September 17, 2009 at 4:51 am |
[…] 16, 2009 in math, theory | Tags: circuit lower bounds, polymath You may remember the polymath1 project, in which Tim Gowers envisioned, and realized, a “massively collaborative” […]
November 6, 2009 at 1:41 am |
[…] Solymosi, un mathématicien de l’Université de la Colombie Britannique à Vancouver, fasse le premier commentaire. Quinze minutes après, un nouveau commentaire était posté par Jason Dyer, enseignant dans un […]
December 10, 2009 at 11:32 pm |
[…] Kitchen Sink That Puts Out Fires, Massively Collaborative Mathematics (if only for the novelty of two Fields medallists posting comments on a blog), Social Networks as Foreign Policy. http://www.nytimes.com/projects/magazine/ideas/2009/ […]
January 13, 2010 at 5:32 pm |
[…] version of distributed-computing. With this image of bite-sized mathematics, Gowers launched Polymath1 with these words: “Here then is the project that I hope it might be possible to […]
May 1, 2010 at 5:43 pm |
[…] of the problem to be attacked (see below), a list of rules of collaboration, and a list of 38 brief observations he’d made about the problem, intended to serve as starting inspiration for discussion. At […]
April 8, 2011 at 9:47 pm |
[…] succeeded, they could publish a paper under a collective pseudonym. He next chose a problem — developing a combinatorial approach to the Hales-Jewett theorem — and, several hundred comments later, announced that they had succeeded. Here’s the […]
July 19, 2011 at 4:19 pm |
Collaborative Mathematics in the Polymath Project…
As part of my ongoing research to explore models for online collaboration I have recently been reviewing the Polymath project1 which exploits collaborative principals in resolving mathematical problems. The Polymath project created by the British …
November 30, 2011 at 7:01 pm |
[…] reference list a new kind of publication). Scholars are flocking to scholarly blogs to post ideas, collaborate with colleagues, and discuss literature, often creating a sort of peer-review after publication. Emboldened by […]
January 16, 2012 at 6:04 pm |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalist Timothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
January 16, 2012 at 6:05 pm |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalist Timothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
January 16, 2012 at 8:16 pm |
[…] another math examination dubbed a Polymath Project, mathematicians commenting on a Fields medalist Timothy Gower’s blog in 2009 found a new explanation for a utterly difficult postulate in only 6 […]
January 17, 2012 at 12:38 pm |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalist Timothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
January 20, 2012 at 6:11 pm |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalistTimothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
January 23, 2012 at 1:14 pm |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalist Timothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
January 25, 2012 at 8:56 pm |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalist Timothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
February 6, 2012 at 9:43 am |
[…] one that he had an idea how to solve but felt was too challenging to tackle on his own. He then started to hedge his bets, stating: “It is not the case that the aim of the project is [to solve the problem but rather it is to see […]
February 6, 2012 at 10:20 am |
[…] one that he had an idea how to solve but felt was too challenging to tackle on his own. He then started to hedge his bets, stating: “It is not the case that the aim of the project is [to solve the problem but rather it is to see […]
May 28, 2012 at 10:03 am |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalistTimothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
October 1, 2012 at 3:06 pm |
[…] The initial proposed problem for this project, now called Polymath1 by the Polymath community, was to find a new combinatorial proof to the density version of the Hales–Jewett theorem. After 7 weeks, Gowers announced on his blog that the problem was “probably solved”,[5] though work would continue on both Gowers’s thread and Tao’s thread well into May 2009, some three months after the initial announcement. In total over 40 people contributed to the Polymath1 project. Both threads of the Polymath1 project have been successful, producing at least two new papers to be published under the pseudonym D.H.J Polymath. […]
March 17, 2013 at 5:19 am |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalistTimothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
October 15, 2013 at 8:54 pm |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalist Timothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
November 27, 2013 at 3:41 pm |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalist Timothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
July 7, 2014 at 5:24 am |
[…] community of mathematicians would pool their efforts on a single problem. On his blog he hosted the first Polymath Project devoted to finding a combinatorial proof of something called the Hales-Jewett Theorem. Since then […]
June 5, 2015 at 8:10 pm |
[…] folding, Galaxy Zoo, in which 250,000 volunteers help with the collection of astronomical data, and Polymath launched by the Fields Medalist Tim Gowers to solve mathematical questions. It seems that crowd […]
August 4, 2016 at 11:14 pm |
[…] math experiment dubbed the Polymath Project, mathematicians commenting on the Fields medalist Timothy Gower’s blog in 2009 found a new proof for a particularly complicated theorem in just six […]
February 3, 2019 at 3:14 pm |
[…] years ago on January 27, 2009, Polymath1 was proposed by Tim Gowers and was launched on February 1, 2009. The first project was successful and it followed by 15 other formal polymath […]
June 14, 2019 at 7:36 pm |
sat practice tests
A combinatorial approach to density Hales-Jewett | Gowers