I finally got a copy of the Princeton Companion to Mathematics in my hands today, and within a depressingly (but not unexpectedly) short time found my first mistake, in an article written by me. I’ve established that small corrections can almost certainly be made in time for the next printing, so this post is to invite anybody who happens to spot an error to let me know in a comment on this post. (That way, all the corrections that are needed will be in one convenient place.) I’m particularly interested in mathematical mistakes, though typos are also good to know about. Just to get the ball rolling, here’s the one I spotted, together with a reflection on how it arose, since it’s relevant to mathematical writing in general.
Incidentally, before I say any more, I want to say that a huge amount of proofreading has gone into the book, so I expect the density of mistakes to be pretty small. But because the book is a big one, I also expect the number of mistakes to be not all that small.
The mistake occurs on page 24 of the book, where I give a formula for the product of two elements of the dihedral group of order 8. I am discussing semidirect products of groups, so I use the notation to stand for the element that would normally be written
where
is a quarter turn and
is a reflection. I point out that
and then claim that it follows from that that
. Of course, the power of
on the right-hand side should in fact be
.
How could I write something that jumped out at me as obviously false when I came back to it just now? Probably because I was focusing on the interesting case when . But it was still pretty careless. And the general point I want to make here is that such carelessness is incredibly tempting. Several years ago, David Preiss and I were colleagues at University College London, and he said something that I’ve never forgotten, which was that if you are suspicious of a mathematical argument and want to find the mistake, look for anywhere where it says something like, “An easy argument shows that …” or “It is not hard to prove that …” I dare say he was not the first person to make this observation, but it doesn’t seem to be quite as standard as it might be.
For the purposes of an expository book like the Princeton Companion, it was quite common, and the right thing to do, to miss out details of arguments, and to say things like, “If you do this calculation, you will find that …” I was inclined to trust authors (including myself) when they wrote things like this, but at a late stage I found one or two that were embarrassingly false, and began to think that it would be a good idea to check them systematically. Vicky Neale, a graduate student at Cambridge, very kindly agreed to do a lot of this task (though unfortunately she came in at such a late stage that this final check did not cover the whole book), and she discovered that an extraordinarily high percentage of these not fully justified assertions were wrong. In most cases, most readers wouldn’t notice, because all that really mattered was that the calculation had an answer: it wasn’t so important what the answer was. Unfortunately, the one I’ve just discovered will be genuinely confusing to the reader for whom that particular article was intended. And I’d very much like to eliminate as many as possible of the ones that remain.
The general moral I would draw from this experience is that in expository writing one should be especially scrupulous about checking calculations, because there tends to be a higher density of assertions that are not fully justified (because they are plausible and their justifications would get in the way of the exposition). To put it in a punchier way: if you haven’t checked it, then it is wrong. That’s particularly true if you worked it out in your head, as I think I did in this instance.
As for research articles, I think my advice here is pretty hard line: proofs should be written out in full, or, failing that, precise algorithms should be specified for generating such proofs. To explain what I mean with an example: instead of saying, “An argument similar to the proof of Lemma 2.3 shows that …” one should say, “The proof of this fact is similar to the proof of Lemma 2.3; the differences are that in this case we replace by
, and …” etc. Of course, another important algorithm for generating part of a proof is something like “Insert here the main result of [23].” I just mean that “It is not hard to show that” should appear only if giving the proof would be an insult to the intelligence not just of experts but even of mathematicians who are not familiar with your area. Doing this not only forces you to deal with the weak parts of your arguments, but it also makes what you write easier to read. After all, if it’s true that “An easy argument shows that …” then you should be able to give the argument reasonably elegantly, and the reader is free to ignore it. If it’s not true, then the reader may well waste time trying to see the obviousness of what you claim.
September 17, 2008 at 11:34 pm |
Hear hear! One of the most valuable hints I got as an undergraduate philosopher was that if you want to find the shaky bits of an argument you just need to look for the words ‘surely’, ‘clearly’ or ‘obviously’. They so often mean (variously) ‘I can’t be bothered to think of an argument for this’, ‘I have spent hardly any time thinking about whether this is even true’, or ‘I tried but I still can’t think of an argument for this so I’m just exhorting you to agree with it’.
I say this as someone guilty of using these words in my papers, usually without noticing what I’m thereby conveying.
September 18, 2008 at 12:56 pm |
Tim, I remember reading some quote by Bertrand Russel at the beginning of the companion and in light of what you mentioned above maybe this other quote by Russell would have being more appropriate. 🙂
“Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true. ”
Bertrand Russell
September 18, 2008 at 2:30 pm |
I guess my first errata to report is right on the cover of the book something I mentioned at the end of my post reviewing the Companion at
http://blog.isallaboutmath.com/
“the shell image in the cover of this book depicts a section of the Nautilus shell long believe to be related to the Fibonacci golden ratio but I have learn from [God Plays Dice] (Blog) that this is not so!
I assume that the believe relation between the Chambered Nautilus shell and Fibonacci golden ratio was the motivation to place the image on the cover as an example of Mathematics appearing in nature.”
September 18, 2008 at 5:44 pm |
Your comments reminded me of John Stallings’ classic article How not to prove the Poincare Conjecture. It contains a reformulation of the PC as a question in group theory, but it’s framed as a discussion of his unsuccessful attack on the problem.
Aside from being very funny, it’s also the only paper I can think of that’s absolutely honest about incorrect arguments in mathematics, and about how much we want them to be correct. Stallings ends with:
‘I was unable to find flaws in my “proof” for quite a while, even though the error is very obvious. It was a psychological problem, a blindness, an excitement, an inhibition of reasoning by an underlying fear of being wrong. Techniques leading to the abandonment of such inhibitions should be cultivated by every honest mathematician.’
September 18, 2008 at 9:34 pm |
I remember coming out of a Part III exam and having a conversation with a fellow candidate to the effect that we’d both realised in the exam that the “obvious” part of a proof we’d been given in lectures was not at all obvious, and didn’t easily go through. Because we’d been told it was obvious, we’d assumed it. I think it comes under the category of fallacy known as “proof by authority”.
September 19, 2008 at 2:50 am |
Tim I like to apologize for my above assumption. It has being pointed out that the reason to place the image could be due to the similarity to logarithmic spiral.
September 19, 2008 at 9:18 am |
isallaboutmath, I wish I could simply agree with that, but honesty compels me to point out in turn that on the back flap of the dustjacket, it says, “Jacket illustration: Cross section of a chambered nautilus seashell showing chambers and Fibonacci sequence, Dan McCoy — Rainbow/Getty” So if it’s not related to the golden ratio then there is something to be corrected, even if it is not necessarily the image itself. (I’m glad to say that I wasn’t responsible for this one though.)
September 20, 2008 at 12:46 am |
I just got the book also and it looks wonderful! I am truly grateful for all your hard work. A request though – it would be great if it was possible an electronic version of the book. I’d like to read parts of it while travelling etc.., and it’s kind of bulky to be carrying around the whole thing. Am sure there are other readers who would also appreciate such an option.
September 20, 2008 at 12:19 pm |
Prof. Gowers,
what do you say to the use of Mizar, or other such systems?
Best,
James
September 20, 2008 at 7:38 pm |
Prof. Gowers, I eagerly anticipate receiving this book! It looks like a fantastic resource. Is there any update on the Tricks Wiki (twiki)?
Applauds,
Robert
September 21, 2008 at 7:37 am |
I have just gotten my copy and am overwhelmed by this beautiful fat book. Thank you and your team for all your work, and thanks to the contributing authors, too! And I see that, while mine was pre-ordered, Amazon is now listing it as “ships in 2-4 weeks”.
Electronic version: I wouldn’t pass up the paper version for anything, but this is a good idea. Boaz – if you have (or ever intend to have) a Kindle, go to Amazon’s page for the book and look beneath the cover image for a link that says “Please tell the publisher: I’d like to read this book on Kindle.” Persuading enough people to hit that link is probably the best bet for any kind of digital version appearing soon (unless Prof. Gowers knows something more concrete?)
September 25, 2008 at 9:49 pm |
Just spotted a typo. On page 555, column 1, line 7 from the bottom, it says
… is by constructing (a preferably nice) bijection …
The word “a” should of course not be inside the brackets.
September 27, 2008 at 3:40 am |
[…] https://gowers.wordpress.com/2008/09/17/princeton-companion-errata/ […]
September 28, 2008 at 9:20 pm |
“I say this as someone guilty of using these words in my papers, usually without noticing what I’m thereby conveying.”
I’m guilty of doing this in an Algebra exam – I wrote the words “obviously” a number of times when the proofs weren’t at all obvious to me! I wasn’t surprised to see that I hadn’t done well in the exam, but it was worth a try… (I had heard that post graduate students were marking some exam papers you see. :D)
October 1, 2008 at 11:30 am |
Prof. Tim
The errata I have spotted is on the article ‘Metric space’, where the triangle inequality should be
It is interesting that many of my friends have made this mistake with latex and also include myself.
October 1, 2008 at 2:04 pm |
qingfengwang, are you looking at an old version from the web, by any chance? In my printed copy the inequality goes the right way round (to my relief).
October 4, 2008 at 5:35 pm |
The Companion is great! Too heavy to read in bed, though, sad to say.
I was surprised to see on p.971, footnote 19, the claim that Perelman
has refused the Clay Mathematics Institute Millennium Prize. I looked
on the CMI web site, and although it discusses Perelman’s work, it says
nothing about offering him the prize, let alone him refusing it.
Did I miss this news item?
October 5, 2008 at 10:20 am |
Alasdair, I think you’re right that that footnote is not justified. A quick look on the web suggests that the true state of affairs is that Perelman has expressed very little interest in the prize (once piece of evidence for this being that he has not published his work conventionally when that was in the rules for the prize), but that he has not said definitively that he would not accept it. The sources I found about this were written a couple of years ago after he refused the Fields medal: I don’t know whether anything has changed since.
October 5, 2008 at 4:11 pm |
1. If I had to be stuck at a desert island for the rest of my life, and were only allowed one
book, it would PCM.
2. Regarding Boaz Barak’ s suggestion for an electronic version, it is a good idea,
but with google, one can probably find quite a few of the articles in people’s
websites, for example, my own (IV. 18) is availabe from my website, and
Frank Kelly’s (VII. 4) I easily found via goodle scholar in his own website.
This was useful, since I needed this for a colloquium talk I gave last week
at Virginia Commonwealth University, and it took a second to make a hard copy of only this article. (By the way it is really excellent, of course, like most of the articles)
3. I am flattered that Tim found a typo in my own article (the one on p. 555, col. 1,
line 7 up), which means that he read it again. But I am disappointed at him for
not spotting a much more serious one:
p. 558, col. 1, line 22 down:
$n=1$ should be $n \geq 1 $
4. I am reading, randomly, lots and lots of articles. To prove it, here is a typo that
I spotted in Chalie Fefferman’s article (III.23):
p. 194, col. 2, line 8 up,
the last \partial should be \partial{x_d} instead of \partial{x_1}
5. The paper medium does have its undeniable charm, but an electronic
version (fully hyper-linked for cross-references, like in wikipedia) would be
nice (In addition, not instead!). This electronic version could also solve the
“it is easily seen” syndrome. You can just highlight the word “easily”
and link it to a short page that gives the justification in excruciating detail,
for those readers obtuse enough to demand a justification, and the
acute readers can just ignore those details.
October 8, 2008 at 9:06 pm |
Dear Tim,
I received my copy a few days ago, and I must say it is a great pleasure to discover new jewels every evening! I was pleased to read in the introduction that every section was supposed to have been written at the lowest possible level, and even more so to see that the goal was reached. This indeed makes the book unique.
You asked for error spoting, and I had seen none before tonight.
But tonight I read section V.11 (Fixed Point Theorems), and I must say
I do not agree with the definition of the fixed point index. I may of course be missing something, since I am more used to homeomorphisms than to general maps, but anyway, here is my point.
The text deals with the 2-sphere, and defines the index of a fixed point x as the number of times f(y) goes around x when y goes once around a tiny circle around x. With this definition, the index of a fixed point for an orientation-preserving homeomorphism would always be equal to 1. But there exists such homeomorphisms with an arbitrary number of fixed points, and they are all isotopic to the identity (for example, the translation z -> z+1 on the Riemann sphere fixes only the point at infinity, so the fixed point index should be equal to 2, not to 1).
The usual definition of the index is that it is the number of turns made by the vector from y to f(y) when y goes once around x. (Thus the fixed point at infinity for z->z+1 has index 2, as we see by using the local coordinate 1/z).
With this definition, the indices of the fixed points 0 and infinity for the polynomial z -> z^5 are equal to 1 (they are attracting fixed points). But this map has 4 more fixed points on the unit circle, all of them also of index 1, thus the sum is equal to 6. Thus we recover the conclusion that the polynomial x^5 + 4x + 5 must also have 5 fixed points, counted with indices, in addition to the fixed point at infinity. (Moreover this number 6 agrees with the Lefschetz formula involving the action on homology : the H0=Z, which f multiplies by 1 ; H1=0 ; H2 = Z, which f multiplies by 5 ; thus the alternating sum of the traces is 6).
Best regards,
Frédéric
October 9, 2008 at 12:05 am |
The sources I found about this were written a couple of years ago after he refused the Fields medal: I don’t know whether anything has changed since.
I don’t have my sources any more, but I recall:
a.) The Clay Foundation was “considering” changing the rules to account for Perelman’s lack of publishing. However also note the proof *has* been published, albeit with exposition by different authors.
b.) Perelman specifically said he would not decide to accept or refuse the prize until it was offered.
October 9, 2008 at 9:53 am |
Frederic, Thank you for pointing out my mistake there. It troubles me more than most because it was clearly my fault (for not thinking harder about what I was writing) and will be quite complicated to put right, since it will be important not to affect the pagebreaks. I feel particularly embarrassed that I didn’t notice that has the solutions round the unit circle: I should perhaps have considered fixed points of the polynomial
has the solutions round the unit circle: I should perhaps have considered fixed points of the polynomial 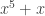 . Anyhow, something must clearly be done in time for the next printing.
. Anyhow, something must clearly be done in time for the next printing.
October 9, 2008 at 3:34 pm |
It occurred to me this morning that what you had in mind was probably the index of a zero of a vector field, and not that of a fixed point for a map.
October 9, 2008 at 6:06 pm |
I love this book! It far exceeded my expectations and I have been raving about it to everyone. Thank you for your undoubtedly enormous effort in putting this together. Here are a few corrections I noticed in Part I:
Near the end of page 14, the reference to sentence (6) should be a reference to sentence (9).
On page 27 it says that every field homomorphism is injective. However the definition of field homomorphism given there allows the homomorphism to be identically zero.
On page 42 it says that the hyperboloid model is x^2+y^2=1+z^2, but I think this should be x^2+y^2=z^2-1.
On page 43 it says that the real projective plane is the ordinary plane together with a point at infinity. But really there should be a (projective) line at infinity. Also on page 43, one could argue that if you went “from Paris to the copy of Paris on the other side of the world”, everything would look reflected, since you have gone around a loop in the projective plane in which the orientation gets reversed.
October 10, 2008 at 9:19 am |
Many thanks for those useful comments. I’ll probably work out where I’m going wrong just after posting this one, but I’m having trouble getting my head round your last comment. If I think of the real projective plane in one way then I agree with you: for example, if I were a two-dimensional being and I went round a Möbius strip until I got back to my starting point, then everything would look reflected, and since the projective plane contains a Möbius strip, the same must be true of that. But I don’t see how to see that if I think of the real projective plane as the quotient of the sphere by the antipodal map. Suppose I start at the North Pole and write a little note to myself and leave it there, and suppose that at that precise moment an exact copy of me is doing the same at the South Pole. Surely if I then travel to the South Pole and my counterpart does the exact opposite journey to the North Pole, we won’t need mirrors to read the notes, and there won’t be any distinction between there being two of us on a sphere or one of us on a projective plane.
To put the question another way, if I paint the outside of a sphere red and the inside blue and then identify antipodal points, why haven’t I defined an orientation on the real projective plane? I can hardly believe I’m finding myself asking this question, and await the embarrassment that will surely follow when someone answers it.
October 10, 2008 at 6:04 pm |
Here are attempts to answer the two versions of your question, which are probably much longer than necessary.
(1) Imagine that a two dimensional person is at the north pole and its image under the antipodal map is at the south pole. Each of them writes notes that correspond under the antipodal map. If the southern person walks to the north pole and stands next to the northern person, the two people will look like mirror images of each other. This is because the antipodal map reverses orientation. So the note written by the northerner will look reflected to the southerner. It is possible to visualize this on a globe, but easier to visualize if one thinks of the projective plane as a disk with opposite points on the boundary identified in pairs. If you imagine a stick figure crossing the boundary then it comes back reflected.
(2) Painting the outside of a sphere red and the inside blue certainly defines an orientation of the sphere. More precisely, this induces an orientation of the sphere from the orientation of the ambient space R^3 in which it is embedded. Now consider the automorphism of R^3 sending (x,y,z) to (-x,-y,-z). This restricts to the antipodal map on the sphere and preserves the distinction between “inside” and “outside”. Nonetheless it reverses the orientation of the sphere, because it reverses the orientation of the ambient R^3. Since the antipodal map does not preserve the orientation of the sphere, the orientation of the sphere does not descend to an orientation of the quotient.
October 10, 2008 at 6:30 pm |
For what it’s worth, your answer has helped me understand the particular error that was going on in my mind: when I visualized myself walking from the North Pole to the South Pole, I didn’t spot that when I got there I would not have multiplied myself by -1, but instead would have rotated myself. Of course, that’s pretty close to what you say above.
October 11, 2008 at 10:34 am |
Would Prof Gowers consider having an “errata” section on his website in the same manner as Tom Korner has for his book “The Pleasures of Counting”?
Thanks,
John Scott
October 11, 2008 at 11:00 am |
Dear Prof. Gowers,
I have been trying to obtain a copy of PCM in the UK, but to no avail. Amazon.co.uk, Waterstones.com and several other UK outlets all have PCM marked for “pre-order” only. I contacted Amazon.co.uk to ask when they expect PCM to be stocked, and they said that they currently do not plan on stocking PCM, and will only offer it via “3rd party” resellers.
Perhaps you could suggest to Princeton University Press that they should investigate this shortcoming?
I look forward to reading the book! The articles that I have read online so far have been outstanding. Thank you for taking on this project.
Best regards,
Joe
October 15, 2008 at 6:53 pm |
[…] gorgeous feature will be something that Doron Zeilberger suggested in this comment, in his point number 5. It will be possible to write an article and include a phrase such as […]
October 15, 2008 at 10:34 pm |
Gil Kalai emailed me to point out that on page 1014 a remark in the chronology that was intended to explain the importance of the Langlands programme was accidentally placed after the previous entry, which was for Abraham Robinson’s introduction of non-standard analysis.
October 17, 2008 at 7:19 am |
I’m not sure this counts as an erratum, but I have a quibble with an argument towards the end of part I, specifically the claim on the bottom of page 75 that the function r(n) defined by reversing the binary representation of n is “strange and unmathematical”. In fact this function is quite important in two contexts: in Fast Fourier Transform algorithms (e.g. see the section “Data reordering, bit reversal, and in-place algorithms” of http://en.wikipedia.org/wiki/Cooley-Tukey_FFT_algorithm), and as the key idea in defining the Hammersley low-discrepancy point set (important e.g. in antialiasing in computer graphics; see http://mathworld.wolfram.com/HammersleyPointSet.html).
October 17, 2008 at 11:40 pm |
If you’re talking about fixing a certain number k of digits of n and reversing the binary representation of all n between 0 and 2^k-1, then I agree that that’s a very natural thing to do. The map I find unnatural is one defined on all the natural numbers, where the binary representation is taken to have no zeros at the beginning. So for example the reverse of 8 is 1 because 8 has 1000 as its binary representation and that reverses to 0001=1. This map does not have the sorts of properties one would want: the reverse of the reverse of n is not necessarily n, and indeed the reversing map is not even an injection or a surjection. It was this second map that I was calling strange and unmathematical.
October 18, 2008 at 12:24 pm |
Curious. Digit reversal is what I take as an example of the unmathematical here, around page 5.
October 22, 2008 at 4:31 pm |
Is there any way to find the table of contents in PDF format?
October 22, 2008 at 10:55 pm |
If you go here you can find it in html, but I’m not sure about PDF.
October 26, 2008 at 12:22 am |
I just received this beautiful book from my dad. Congratulations on a
wonderful accomplishment.
One thing I did notice that might be worth rewording was this strange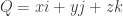 ,
,
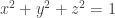 ) satisfies
) satisfies 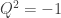 ? A more correct analogy might be: In
? A more correct analogy might be: In 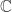 , all square roots of -1 may be written
, all square roots of -1 may be written  with
with  in
in 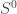 . In
. In 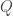 , they may be written
, they may be written 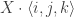 with
with 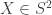 .
.
statement on p. 277 in the section on quaternions: “Quaternions, as they
are usually introduced, are a system of numbers where -1 has not just one
square root but three, called i, j, and k. I’m not an algebraist, but I
thought there are two square roots of -1 in the complex numbers, and that
any pure vector unit quaternion (scalar part zero, so
Regarding some recent posts, you don’t even need to fix a certain number
of digits to make (standard) bit reversal useful. Counting in reverse
binary, .0, .1, .01,.10, .001,.101,…gives the uniformly distributed
low-discrepancy van der Corput sequence
(http://en.wikipedia.org/wiki/Low-discrepancy_sequence ,
http://en.wikipedia.org/wiki/Van_der_Corput_sequence ) that has been used
with Glimm’s method for computing and proving existence of solutions of
nonlinear hyperbolic systems of conservation laws.
Best regards,
Bob Palais.
October 28, 2008 at 12:55 pm |
p.708: Two of the examples of encoding halting problems appear to be the wrong way round. A set of tiles is produced that tiles the plane iff the given algorithm does not halt (not iff it halts). A system of Diophantine equations is produced that has a solution with parameter q iff the algorithm does halt at q (not iff it fails to halt at q). (To see which must be the right way round, note that if you have one algorithm that halts for exactly those inputs in the set S, and another that halts for exactly those inputs in the complement of S, then by running both in parallel you can decide whether any given input is in S. Now given any set of tiles you have an algorithm that halts iff they do not tile, and given any system of Diophantine equations you have an algorithm that halts iff they have a solution. So being able to convert an arbitrary algorithm to a set of tiles that tile iff the algorithm halts, or to a system of Diophantine equations that has a solution iff it does not halt, would make the halting problem soluble.)
Minor issues noticed so far:
p.14: (4′) is not an accurate rewriting of (4), which would be “For all x, x is not better than lifelong happiness.” – the version written suggests the paradox “lifelong happiness is better than lifelong happiness” on substituting “lifelong happiness” for x.
p.30: In “such that Sv is proportional to v”, the “v” in “Sv” should be bold as it is elsewhere.
p.187: “regular octagon” should be “regular octahedron”.
p.992: Not strictly an erratum, but the description of OEIS as containing “nearly 100000” sequences does date the article (it exceeded 100000 in November 2004); parts have evidently been updated since 2004 (given a 2007 reference) but not this reference.
November 4, 2008 at 11:36 pm |
This is a great book, I’m reading it through from start to finish. More minor issues noticed in the course of doing so (up to III.42):
p.33: “rate of change u” should read “rate of change of u”.
p.40: “d-dimensional” should read “n-dimensional”.
p.57: “f(g+h) = fh+gh” should read “f(g+h) = fg+fh”.
p.62: The formula for r(n) does not match the values given (e.g. for r(2)); I think the values and recurrence are correct and the formula wrong.
p.63: It appears the exponent in the upper bound for the circle problem was improved in 2003 from 46/73 to 131/208 (see MR 2004m:11127).
p.64: At the end of 6.3, “log m / log log m” should probably be “log n / log log n” unless there’s some reason for the typical large integer to change suddenly from n to m for the last sentence.
p.75: 181 is a three-digit palindromic prime missing from the list given.
p.131: “DBFC” should read “DBCF” (as it does in the second reference to that parallelogram).
p.169: The example mapping from the reals to a circle with a point removed is wrong (consider ); I think the y-coordinate should be
); I think the y-coordinate should be 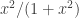 not
not  as given.
as given.
p.171: The example ordering of the rationals is missing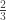 ,
, 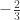 ,
,  ,
,  (at the point where they should go according to how the ordering is described).
(at the point where they should go according to how the ordering is described).
p.176: “ ” should read “
” should read “ “. Also, n here (to at least the end of the page) appears to be being used as both the dimension and the number of points in the discrete path (minus 1) and it might be clearer to use a different letter for one of these.
“. Also, n here (to at least the end of the page) appears to be being used as both the dimension and the number of points in the discrete path (minus 1) and it might be clearer to use a different letter for one of these.
p.183: “0.22222…” should read “0.022222…”.
p.184: I think the definition of the Hausdorff dimension is the wrong way round: the c-dimensional Hausdorff measure should be 0 (not infinite) for c greater than d and infinite (not 0) for c less than d. (The volume of a surface is 0 and its “length” is infinite.)
p.223: “ ” should read “
” should read “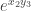 ” (there’s a stray comma in the exponent).
” (there’s a stray comma in the exponent).
November 5, 2008 at 11:26 pm |
Just spotted a minor typo: in the section on Hilbert there is a quotation by Gordan, the sentence just overlapping the pages 788 and 789: theology should be spelled “Theologie” in correct german.
November 5, 2008 at 11:30 pm |
Just spotted a minor typo: in the section on Hilbert there is a quotation by Gordan just overlapping the pages 788 and 789: theology should be spelled “Theologie” in correct german.
November 6, 2008 at 9:06 pm |
Minor typo p339 col 1 line 3 requires ‘arithmetic progression’ rather than ‘arithmetic’.
November 7, 2008 at 9:00 pm |
Another comment: Eduard Kummer is usually known as Ernst Kummer (although putting his full name Ernst Eduard Kummer is probably better).
November 7, 2008 at 10:44 pm |
I don’t know who posted the Nov 7 item at 9.00pm in my name, but it wasn’t me.
Mark
November 8, 2008 at 2:07 am |
This is a fantastic book and I’m telling everyone about it!
I’ve found two minor issues (I hesitate to call them “errors”):
In III.10, “Computational Complexity Classes,” the reader should probably be warned that the definitions of NP and NC are informal (standardly, NP and NC are defined to be sets of languages, or classes of *decision* problems), and directed to IV.20 for formal definitions. I’ve found that many mathematicians have never heard a formal definition of NP and perhaps don’t even realize that they have never heard a formal definition. This leads to a number of common confusions. So it’s good to point out that there *is* a formal definition, but that it’s not given in III.10.
In IV.16, “Mirror Symmetry,” there is a sentence about children using slide rules, followed immediately by a sentence about using log tables. The current phrasing makes it sound like the way one uses a slide rule is to look something up in a log table, which of course is not the case.
November 17, 2008 at 4:08 pm |
Outstanding book! This will keep me entertained for years.
Here’s one erratum: In the Probability Distributions article, on p. 266: “It follows that … the variance of the sample average … is [tex]n^{-2}(n\sigma^2) = \sigma^2/{2n}[/tex], which …”
That should be [tex]\sigma^2/n[/tex], without the two in the denominator.
November 20, 2008 at 1:22 am |
An erratum on p. 444, para. 2: In the statement of the Milnor-Svarc Lemma, one needs to assume that the action of on
on  is properly discontinuous.
is properly discontinuous.
November 21, 2008 at 6:58 pm |
More minor issues found in the course of reading through the book up to the end of IV.3:
p.228: In the definition of the hexagonal lattice, “ ” should be “
” should be “ ” or “
” or “ “.
“.
p.238: At the start of the page, a factor 6 has appeared which doesn’t appear to arise from applying the given substitution to any form of the KdV equation given earlier in this article. Wikipedia tells me that a factor 6 is conventional, and with that in place this form does follow, but silently changing the convention part way through the article with no indication that this is being done or the other convention exists seems confusing. (The equation at the start of the page also has an implicit “= 0”, whereas all the other differential equations in the article appear to have an explicit “=”.) I do not know what convention the solutions given in the rest of this article follow.
p.249: “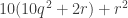 ” should read “
” should read “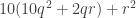 “.
“.
p.278: Should the definition of bilinearity here include (x+y)z = xz + yz and (ax)y = a(xy)?
p.323: If D in the formula in (ii) is the fundamental discriminant as defined earlier, then it is negative in this case; should the formula use |D|?
p.324: “1934” should read “1952” (per the Further Reading section of this article). (1934 was the date of Heilbronn’s proof that the class number tends to infinity as d tends to negative infinity, not of Heegner’s proof.)
p.325: “It is easy to deduce that is itself a prime in the ring of Gaussian integers” should read “It is easy to deduce that
is itself a prime in the ring of Gaussian integers” should read “It is easy to deduce that  is itself a prime in the ring of Gaussian integers”.
is itself a prime in the ring of Gaussian integers”.
p.327: The geometrical construction for appears to give
appears to give  instead (probably
instead (probably  should be used three times in place of
should be used three times in place of  ).
).
p.353: “Pollardand” should read “Pollard and” (missing space).
November 28, 2008 at 11:24 pm |
In section VIII.4, “Numeracy,” “quatre-vingt” should be “quatre-vingts.” While 81 is “quatre-vingt-un” and 90 is “quatre-vingt-dix,” etc., 80 itself is “quatre-vingts.”
December 1, 2008 at 11:39 pm |
Professor Gowers,
I haven’t been this excited for a book in a very long time. I’ve flipped through the text several times at the local bookstore and I’m eager to purchase a copy. When do you expect the next printing will be? I know that most books are never completely free of errata, but I’d prefer to own a revised issue (provided the wait isn’t too long).
I extend my gratitude to you and your colleagues for all the work you have done. I can’t wait to add this book to my collection.
December 3, 2008 at 3:54 pm |
[…] Der er en diskussion samt trykfejlsliste på Timothy Gowers’ blog (Gowers er redaktør af bogen – og Fieldsmedaljemodtager ) Find f.eks. en trykfejlsliste. […]
December 16, 2008 at 5:31 am |
There is a minor error on p 62 near the end of paragraph (ii). In the list of the ways 12 can be represented as the sum of four squares, the second formula should be 0^2 + 2^2 + 2^2 + 2^2, rather than 0^2 + 4^2 + 4^2 + 4^2.
December 18, 2008 at 12:55 am |
I have just been told by Barry Mazur of the following small slip in his article: on page 327, line 3 from the bottom, there is a that should be
that should be  .
.
December 23, 2008 at 10:22 pm |
“… within a depressingly (but not unexpectedly) short time found my first mistake, in an article written by me.”
I’m not making any corrections here, albeit at the age of twelve I was a paid technical proofreader for Chemical Abstracts (because I knew the Chemistry and could tell an o from an omicron).
Instead, I’m commenting on that sense of discovering one’s own typo slightly too late. I just xeroxed and snailmailed a big batch of 4-page letters (1 page illustration, 3 pp. text) on what my Physics professor wife, our law school son (oddly side-stepping his double B.S. in Math and Computer Science earned at age eighteen), and I have been up to in 2008, with best wishes for 2009. The snailmail arrived, with xmas/hannukah/kwanzaa cards to which I started replying by envelope stuffing — at which point I found that the very first word in my mailing was a correctlt spelled but wrong word (Martial instead of Martian). Ouch! Now I have to decide whether to hand-correct each additional snailmail, or just hope that nobody notices or, if they do, they take it as some sort of convoluted pun.
The French expression esprit de l’escalier (literally “staircase wit”) means the clever response that comes to mind long after the moment it was needed, as when one descends the stairs on the way out of a cocktail party at which one was tongue-tied, unable to stammer a come-back line of repartee.
I think that we need an equivalent expression for Mathematics, as one an obvious counterexample springs to mind after one has left the seminar, unable to defend oneself against a suggested theorem by that annoying guy who’s always in the front row trying to prove that he’s smarter than you are.
December 27, 2008 at 4:32 am |
Dear Professor Gowers,
I have been greatly enjoying reading and “browsing” the Princeton Companion to Mathematics. It is a treat to read this book.
On page 832 in conjunction with the discussion of fullerenes it is claimed that f sub 6 can take on any value. This is not quite true. It can take on any value other than 1. This result is stated in Grünbaum’s Convex Polytopes, page 271, and was first proved by Grünbaum and Motzkin in their paper: The number of hexagons and the simplicity of geodesics on certain polyhedra, Can. j. Math., 15 (1963) 744-751. One uses constructions to show that f sub 6 can take on values 2 or more. There are various ways to see that one hexagon is not possible. I was able to find a slightly simpler construction than the one used by Grunbaum and Motzkin by finding a configuration in a planar 3-connected 3-valent graph with 2 hexagons and 12 pentagons which enables one to add one hexagon to this configuration and get the same configuration back, thereby showing that hexagons can be added one at a time. A diagram showing this can be found in 3-valent 3-polytopes with faces having fewer than 7 edges, Annals of the NY Academy of Sciences, 175 (1970) 285-286.
Best wishes,
Joe
Joseph Malkevitch
Department of Mathematics
York College (CUNY)
Jamaica, New York 11451
Note: My York phone has changed:
Phone: 718-262-2550 (Voicemail available)
My email is:
malkevitch@york.cuny.edu
web page:
http://york.cuny.edu/~malk
December 30, 2008 at 10:39 pm |
Here are my further errata up to the end of part V of the book.
p.424: The statement “So we have constructed the first three rows of the character table above.” follows listing three irreducible representations, one of which is two-dimensional and corresponds to the last row in the table given, not one of the first three.
p.425: “ ” should read “
” should read “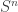 “.
“.
p.456: Not strictly an erratum to the book, but I can’t find the longer version of the article at the webpage for the book that the article says a longer version can be found at. Could the webpage give a prominent link to this version, since the article promises it there?
p.460: The use of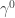 ,
,  ,
, 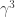 ,
,  (in the definition of the Dirac operator) rather than
(in the definition of the Dirac operator) rather than  ,
, 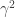 ,
, 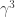 ,
,  seems confusing when the definition expects the indices to match up with
seems confusing when the definition expects the indices to match up with  ,
, 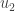 ,
, 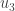 ,
,  . I don’t know whether this is a simple mistake or a case of inconsistent conventions being used.
. I don’t know whether this is a simple mistake or a case of inconsistent conventions being used.
p.496: The numbers given as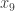 and
and 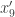 appear in fact to be
appear in fact to be 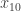 and
and 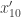 .
.
p.531: I think “ ” should read “
” should read “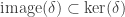 “.
“.
p.568: The first reference to W(k,r) should just refer to W.
p.595: This describes what is presumably the Miller-Rabin primality testing algorithm, where the probability of detecting a composite integer is at least 3/4 (not 1/4) and so the probability of failing to detect it in k tests is at most (not
(not  ) (these figures are given correctly in IV.3, referenced by this paragraph).
) (these figures are given correctly in IV.3, referenced by this paragraph).
p.645: In the sentence at the bottom of the first column, an assertion is made about for i from 1 to n, when the quantifiers are for
for i from 1 to n, when the quantifiers are for  for i from 1 to m. I think the right hand size of the implication needs to be adjusted to say
for i from 1 to m. I think the right hand size of the implication needs to be adjusted to say 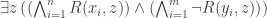 . Except that the relation was previously defined using the symbol “~” not “R”, so the sentence should also be adjusted accordingly for that.
. Except that the relation was previously defined using the symbol “~” not “R”, so the sentence should also be adjusted accordingly for that.
p.701: “formula with Godel number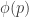 ” should read “formula
” should read “formula 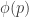 ” (
” ( is a truth-valued formula of one free integer variable, not a function from integers to integers).
is a truth-valued formula of one free integer variable, not a function from integers to integers).
p.706: “norm of a function F” should read “norm of a function f” with one use of F in the following formula changed to f (or else the one use of f in that formula should be changed to F).
p.708: The version of the cubic formula given is actually for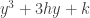 not
not  .
.
December 30, 2008 at 11:54 pm |
Joseph, I meant to say this some time ago, but many thanks for all these amazing errata that you’ve pointed out. (Of course, what I mean is not that the errata are amazing but that you have been amazing to spot them all.)
January 1, 2009 at 9:15 pm |
There’s a problem with the discussion of Thurston’s eight 3-dimensional geometries on page 714. I’m particularly troubled by the sentence in parentheses near the top of the second column, which reads as follows.
This [ ] is not compact, but that is because the pieces into which one cuts up the manifold may have boundaries that are not included in the pieces.
] is not compact, but that is because the pieces into which one cuts up the manifold may have boundaries that are not included in the pieces.
This remark is extremely misleading. Only one of the eight 3-dimensional geometries is compact (namely the 3-sphere, of course), but they all model compact manifolds. For instance, is the model for
is the model for 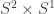 .
.
People usually think about it like this. Any 3-manifold without boundary has a unique decomposition as a connected sum of a finite number of compact pieces, also without boundary. Some of these pieces may be homeomorphic to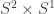 , which is where the the geometry
, which is where the the geometry  comes in.
comes in.
The remaining pieces contain canonically determined tori (the JSJ decomposition). Geometrization asserts that, after cutting along these tori, all the remaining pieces have finite-volume geometric structures.
Also, much less importantly, a typo: in the top line of the second column, it should be , not
, not 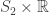 .
.
January 1, 2009 at 11:35 pm |
The definition of C*-algebra on page 172 leaves out the C*-condition.
January 6, 2009 at 3:52 am |
Great book.
Unfortunately I need to exchange my copy since it has 2 production flaws:
1) pages 843 to 890 appear twice
2) pages 891 to 938 are missing
Hopefully PUP can use this information to help minimize such instances.
Marc
January 9, 2009 at 7:11 am |
p. 355: “Pollardfor” –> “Pollard for”
January 11, 2009 at 7:29 pm |
P. 445, section 9, paragraph 3.
Given any closed path of length [in the smooth compact manifold
[in the smooth compact manifold 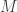 ] there is a disk of minimal area that is bounded by that path.
] there is a disk of minimal area that is bounded by that path.
This is false as stated – you need to assume that the path is null-homotopic.
Also, I have a couple of additional minor criticisms of the hypotheses on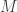 . First, it seems appropriate to mention that
. First, it seems appropriate to mention that 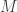 should be equipped with a Riemannian metric for the notion of the area of a disc to make sense.
should be equipped with a Riemannian metric for the notion of the area of a disc to make sense.
Secondly, the assumption of compactness for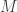 is unnecessary, and also confusing as the examples of the Euclidean and hyperbolic planes are discussed in the following paragraph. Presumably one needs to assume some milder condition like completeness to guarantee the existence of a minimal-area disc.
is unnecessary, and also confusing as the examples of the Euclidean and hyperbolic planes are discussed in the following paragraph. Presumably one needs to assume some milder condition like completeness to guarantee the existence of a minimal-area disc.
Therefore, it seems to me that rather than describing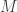 as a smooth, compact manifold, one should describe it as a complete Riemannian manifold.
as a smooth, compact manifold, one should describe it as a complete Riemannian manifold.
January 25, 2009 at 8:03 pm |
Here are my remaining errata, having now read the whole book.
p.756: This page says that Gauss found six proofs of quadratic reciprocity (his first, plus “five more”), whereas pages 104 and 719 reckon the total as eight. (I realise this might reflect some historical dispute as to the figure, with different authors taking different positions; I’ve seen both seven and eight quoted before; Wikipedia claims “He published six proofs, and two more were found in his posthumous papers.”. None of the statements in this book appear to be restricting consideration to proofs published in Gauss’s lifetime.)
p.813: The description of real closed fields as “fields with the property that -1 cannot be expressed as the sum of two squares” is neither an accurate characterisation of real closed fields nor helpful to give a feel for what such fields are. Perhaps a reference to IV.23 section 5, along with the example of the real numbers, would be better than trying to explain what real closed fields are in more detail here.
p.889: The description of CBC and OFB modes is oversimplified. Simplification is of course expected in this sort of exposition, but the CBC description gives the impression that two successive cleartext blocks are added before encryption (so a 128-bit repeat in cleartext would result in a 64-bit repeat in ciphertext, similar to the ECB problem described in the previous paragraph) when actually each cleartext block is added to the previous ciphertext block before encryption. In turn this reads like the description given of OFB mode; OFB does not feed the input cleartext through the block cipher at all, but starts with an initialization vector and repeatedly enciphers that to generate a keystream, that is then added mod 2 to the cleartext to generate a ciphertext.
p.909: “Becky has five siblings” should read “Desta has five siblings”.
p.919: “ ” (in the second paragraph of the first column) should read “
” (in the second paragraph of the first column) should read “ “.
“.
p.920: Both times the second column gives a probability density function for a normal distribution, there is a stray factor of 2 in the denominator inside exp (either this factor or the should be removed), and the “
should be removed), and the “ ” in the square root should be “
” in the square root should be “ “. In the second formula (for the transformed distribution), “
“. In the second formula (for the transformed distribution), “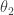 ” should be “
” should be “ “.
“.
p.997: In equation (7), “ ” should read “
” should read “ “. (This is what is given in equation (1.3) of the reference Andrews (1998), and the following equation in the present book defines
“. (This is what is given in equation (1.3) of the reference Andrews (1998), and the following equation in the present book defines  only for even subscripts.)
only for even subscripts.)
January 26, 2009 at 9:44 am |
p.180: Near the top of the second column, should “based at ” be “based at
” be “based at  “? Also, the tangent space at this point is given both as
“? Also, the tangent space at this point is given both as 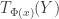 and
and 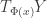 , but this may be for the sake of pedagogy.
, but this may be for the sake of pedagogy.
February 2, 2009 at 11:14 am |
p.232: I think the closing parens on the RHS of the Baker-Campbell-Hausdorff formula should be placed to the right of the dots.
February 8, 2009 at 8:09 am |
p.240: Should the definition of the conjugate transpose matrix should have a in place of the
in place of the  ?
?
February 16, 2009 at 3:21 pm |
p.297: In “As has already been mentioned, spherical harmonics are eigenvalues of the Laplacian,” replace “eigenvalues” with “eigenvectors.”
p.314: Near the end of the Zermelo-Fraenkel entry, “when ones does includes” should be “when one does include.”
February 18, 2009 at 9:30 pm |
page 43 bottom of col 2 – the right side of the condition for the Lorentz transform should be G not I and the transpose of “lambda” should appear to the left of G on the other side of the condition.
page 194 – the density factor “rho” has been left out (perhaps intentionally) of the NS equations, which kind of makes sense because the fluid is deemed incompressible, but makes the statement about the time derivative of momentum a bit confusing.
page 202ff – the discussion of FFT makes no mention of Cooley, Tukey. This seem not quite proper.
February 20, 2009 at 11:23 pm |
I’m enjoying the book, and so far the errata I’ve found have already been reported here. It would be nice if there were a list of errata ordered by page number, so that one could easily check.
February 24, 2009 at 8:46 pm |
p. 272: “ideal generated by all polynomials of the form ad − bc − 1” should read “ideal generated by the polynomial ad − bc − 1”
March 6, 2009 at 4:06 am |
p. 310: “…two points x and y in the plane.” These are obviously very awkward letters to use for two points in the plane. Later on in the paragraph it turns out that the coordinates of the points are (a,x) and (b,y). Then we take an integral with respect to yet a different x. Yikes!
March 12, 2009 at 1:21 am |
p. 121, top left displayed equation involving an infinite product: It seems that the author meant to say that the function previously mentioned was equal to the infinite product, rather than that the infinite product is zero.
March 12, 2009 at 4:51 am |
p. 124: “…the Bolzano–Weierstrass theorem states that in every bounded infinite set there is at least one point having the property that any disk about that point contains infinitely many points of the set.”
Perhaps the author meant to say “for every bounded infinite set” or “in every closed and bounded infinite set”. The limit point of course doesn’t have to be IN the set, as written.
March 12, 2009 at 7:19 am |
p.575:
It’s not 100% clear but I’m pretty sure it should read “Two obvious conditions” at the bottom of the page, rather than “Three obvious..”
June 6, 2009 at 7:34 pm |
In the short article III.96 on p. 313, the “more precise definition” of a vector bundle of rank n over a topological space X is given as a topological space E together with a continuous map p:E–>X such that each inverse image of each point x is an n-dimensional vector space.
I’ve been away from this for a while. My question is whether this is sufficient to guarantee actual “bundlesness”, i.e., local triviality so that for each point x in X there is a neighborhood U and a homeomorphism h:U x F –> p^-1(x) so p(h(x,y)) = x for all x in U and y in the vector space F. In other words, locally for X, p is just the projection.
June 27, 2009 at 2:44 pm |
p. 14, second column, “…unpack sentence (6) further…” should be “…unpack sentence (9) further…”
Also, the unpacked definition (10) allows for m=1, which is not a prime.
I love this wonderful book.
Just to add my voice to Ivan’s earlier request to distill the listings on this page into an errata page, Roger Penrose established a convention for his book which seems to work.
June 28, 2009 at 2:10 pm
See PCM errata II for a distillation of the errata pointed out here.
July 3, 2009 at 8:36 pm |
This commentary is a non-mathematician’s view concerning the organization of section VI. In the preface you state that one reason for chronological order is to encourage the reader to read the part right through. This is rather like my mother’s admonition to “eat your vegetables, they are good for you.” I never cared much for veggies and I certainly find similar recommendations annoying at best. Why should I read any part of this book right through? Is it not more sensible to read about the mathematician when reading about his/her mathematics? I can’t imagine what persuaded the editors otherwise.
By itself, Section VI is an extremely poor way of correlating the mathematician’s lives: it is much too bulky to be useful.. Fortunately, the Table of Contents neatly resolves this deficiency. Proposal: Alphabetize Section VI. Relocate the chronological listing from the TOC (as a single page) at the beginning of Section VI, retaining the dates given in round brackets (I have always attributed the “mathematician’s” failure to use the established terms for parentheses, brackets, and braces as disinterest in their English classes, but there may be other reasons. The term “curly brackets” makes me wonder, however). Omit the subsection numbers and correct the page numbers. The TOC entry for Section VI would become the page number of the chronological list. All of the references to Section VI that appear throughout the entire book can be reduced to their existing names in small caps font: no section numbers. Names in normal font do not appear in Section VI.
I feel that I must comment on the notion that using the current organization is a “slight inconvenience” in return for learning “something small.” Without a formal proof, I suggest that the word “something” should be replaced with the word “infinitely,” whereas “pain in the ass” might be used to describe convenience (No offense intended). But, I am not a mathematician. Perhaps a poll would provide insight from the community at large.
George Powers, Arroyo Grande, CA
Long retired Electrical Engineer
February 21, 2010 at 10:45 pm |
A book for the rest of my life. Thank you.
I fall at the far (wrong) end of your target audience bell, but I can proofread. Your paragraph 3 above says that on page 24 of the PCM you claimed that
(T^i.R^j) (T^i’, R^j’) = (T^(i – i’), R^(j – j’))
(T^i.R^j) (T^i’, R^j’) = (T^(i – i’), R^(j + j’))
is the formula my copy shows. Perhaps this changes nothing.
October 13, 2011 at 7:52 pm |
[…] Princeton Companion to Mathematics (voir aussi les listes d’errata si vous l’achetez: ici , là et là), sorte d’encyclopédie moderne des maths pour l’étudiant passionné, […]
July 2, 2012 at 9:51 am |
Awesome blog! Do you have any hints for aspiring writers?
I’m hoping to start my own blog soon but I’m a little lost on everything. Would you suggest starting with a free platform like WordPress or go for a paid option? There are so many choices out there that I’m totally overwhelmed .. Any tips? Cheers!
August 24, 2015 at 7:43 am |
[…] Der er en diskussion samt trykfejlsliste på Timothy Gowers’ blog (Gowers er redaktør af bogen – og Fieldsmedaljemodtager ) Find f.eks. en trykfejlsliste. […]
August 29, 2019 at 5:11 am |
Page 180, colume 1, line 14, divergence of curl X = 0, where =0 is missing.
Page 180, column 2, line 12, should read “pushes forward to a k-dimensional oriented manifold in Y” (not X).