I am continuing my series of sample articles for the Tricks Wiki with one that is intended to represent a general class of such articles. It is common practice in lecture courses (at least if the ones I attended as an undergraduate are anything to go by) to state useful theorems, lemmas, propositions, etc., without going to much trouble to explain why they are useful. Of course, there are many ways to pick up this further understanding: taking note of where and how such results are used, doing carefully designed exercises, and so on. Nevertheless, it is often the case that more could be done to help people recognise the signs that indicate that a particular result can be applied.
This article, which is principally aimed at undergraduates early on in a mathematics degree, is inspired by an experience I myself had as an undergraduate. I had a sheet of challenging problems (set by Béla Bollobás) and one of them completely stumped me. (I’m sure several of them stumped me but this is the one that sticks in my mind.) I can’t remember exactly what the question was, but it was something of similar difficulty to that of determining whether an additive function from to
was necessarily linear. My supervision partner solved the problem using Zorn’s lemma, which we had been told about in a lecture, and I just sat there in disbelief because it hadn’t even remotely occurred to me that Zorn’s lemma might be useful. At some point in the intervening years, I “got” Zorn’s lemma and now find it straightforward to see where it is needed. This article is intended to speed up that process for other people.
One might argue that it is better to work out how to apply theorems for oneself. I’m in two minds about that. Probably for any individual theorem, if one works out for oneself how to recognise situations where it can be applied then that is better than being told by somebody else. But working it out can take quite a lot of time and effort, so if one has help then one may be able to learn how to apply more theorems, and one may be able to learn about theorems in branches of mathematics other than one’s own. On balance, I think that a series of articles on how to use various important mathematical principles would be a useful resource, one that I would love to have to help me understand better the many areas of mathematics where I feel shaky. So here’s a first attempt at Zorn’s lemma. So far I have only two examples of applications: at some stage it would be good to have several more.
Title: How to use Zorn’s lemma.
Quick description: If you are building a mathematical object in stages and find that (i) you have not finished even after infinitely many stages, and (ii) there seems to be nothing to stop you continuing to build, then Zorn’s lemma may well be able to help you.
Prerequisites: Basic concepts of undergraduate mathematics, such as vector spaces.
Example 1: A function from
to
is called additive if
for every
. Clearly any function of the form
is additive. Are there any other additive functions?
An easy induction shows that if then
for every positive integer
. (This is because,
.) It is also easy to prove that
(since e.g.
). And from this it follows that
, so
, for every positive integer
. Another easy induction shows that
for every real number
and every positive integer
. Therefore,
, from which it follows that
for every real number
and every positive integer
. From these observations it follows that if
then
for every rational number
.
At this point it seems to be hard to deduce anything about other values of . Indeed, there doesn’t seem to be much obstacle to defining
to be anything we like. If we set
to be
, then an argument similar to the argument of the previous paragraph shows that
for every rational number
, but no number of the form
is rational except when
, so this is not going to conflict with the choices we have already made. We will of course be forced to set
to be
, but there is no problem in doing that.
Let us be slightly more explicit about why this isn’t a problem: it is because if then
and
(since otherwise we would find that
, which is rational). This will enable us to see more clearly what is going on later.
The discussion so far strongly suggests that there should be a function that is additive but not of the form . We haven’t yet defined one, since by no means every real number is of the form
with
and
rational. But we have produced a partially defined additive non-linear function, and the method we have used is rather flexible. Indeed, if we pick another number, such as
, say, where
is not yet defined, then we can extend the definition to all numbers of the form
with
by setting
for some arbitrarily chosen
.
More generally, we could construct a sequence of numbers with
, with the property that no
is a rational linear combination of
. And then we could define
, for arbitrarily chosen
, which would tell us that
for every sequence
of rational numbers.
The trouble is, even when we have built an infinite sequence in this way, we still haven’t defined for all real numbers, since the set of rational linear combinations of those numbers is countable. However, we can still continue to build our function, since we can pick a new real number
that is not a rational linear combination of the
and choose a value for
. And then we can choose
that is not a rational linear combination of the
and
, and so on. But again we find that even if we produce an infinite sequence of
we have still defined
for only countably many real numbers.
A good way of regarding what we are doing is this: we are considering the real numbers as a vector space over the rationals, and we are trying to build a basis for this vector space, where this means a collection of real numbers such that every real number is a rational linear combination of numbers in
in precisely one way. Then if we define the values of
however we like for the numbers in
and define the values of
in the obvious way for rational linear combinations of those numbers, we have a function from
to
that is linear over the rationals, and hence additive, but not necessarily of the form
.
Now , considered as a vector space over
, is certainly infinite-dimensional. In fact, it has uncountable dimension. So does it have a basis? (All we mean by “has uncountable dimension” is “cannot be spanned by countably many vectors,” so it is not true by definition that it has a basis.) Inspired by finite-dimensional vector spaces it is tempting to say, “Pick a maximal linearly independent set,” since such a set is not just linearly independent but also spans the whole space, since if it didn’t we could just pick an element that did not belong to its linear span and we could add it to the linearly independent set, contradicting maximality.
So now we seem to be done: we are looking for a basis of over
, and all we need to do to find a basis of any vector space is take a maximal linearly independent set.
But why should a maximal linearly independent set exist? Isn’t that exactly the difficulty we were facing earlier: we could carry on picking more and more rationally independent real numbers but we never seemed to reach the point where we could no longer continue.
Let us now interrupt this example for a more general discussion of Zorn’s lemma and how to use it.
General discussion: We are now in a very typical situation where Zorn’s lemma can be applied. We would like to build a maximal object, and we feel as though we ought to be able to, because any non-maximal object can easily be extended. The usual statement of Zorn’s lemma is as follows. A partially ordered set is a set together with an ordering
of the elements of
that is transitive and antisymmetric (this means that if
and
then
). A typical example is where
is a collection of sets and
if and only if
. (Here I use the symbol “
” to mean “is a subset of” and not “is a proper subset of”.) A chain in a partially ordered set
is a totally ordered subset of
: that is, a subset
such that if
then either
or
. An upper bound for a subset
of a partially ordered set
is an element
such that
for every
. And a maximal element in a partially ordered set
is an element
such that the only element
with
is
itself. Zorn’s lemma states that if
is a partially ordered set such that every chain in
has an upper bound, then
has a maximal element. (Note that a maximal element does not have to be bigger than everything else: it just mustn’t be smaller than anything else.)
In order to see how this rather abstract-looking statement relates to the kind of problem we had earlier, let us imagine that we have a partially ordered set and are looking for a maximal element. We could try to build one as follows. We start with an element
. If it isn’t maximal then we find a bigger element
. If that isn’t maximal we find a bigger element
, and so on. That gives us an increasing sequence
. Now we seem to be stuck, and indeed sometimes we are stuck. For example, if
is the set of natural numbers with their usual ordering then we might have created the sequence
, which would not help us to find a maximal element — not surprisingly, since
doesn’t have a maximal element.
However, does not satisfy the hypothesis of Zorn’s lemma, because the sequence
is a chain with no upper bound. If
does satisfy this hypothesis then the sequence
, which is also a chain, has an upper bound, which we could call
. If this is not maximal, then we can find a larger element
. If that is not maximal, then we can find a yet larger element
, and so on.
Example 1 continued: Note the similarity between the position we are now in and the position we were in when we were trying to create a basis for over
. Once again, we can continue to create larger and larger objects, but there seems to be no easy way of saying that the process eventually ends. Or rather, there is an easy way: Zorn’s lemma tells us that it ends.
Let us see how Zorn’s lemma applies in our example. The objects we were looking at were subsets of that were linearly independent over
. We noted that a maximal linearly independent subset of
spanned the whole of
, where by “maximal” we meant that the set was not contained in any larger linearly independent set. Thus, we were looking at the set of all linearly independent subsets of
, with the partial order
.
All we have to do if we want to apply Zorn’s lemma is check that every chain has an upper bound. So let us imagine that we have a collection of linearly independent subsets of
and that for any two of those sets one is contained in the other. What could serve as an upper bound? By definition it has to be a set that contains all the sets in
, so it has to contain their union. We want it to be linearly independent, so the smaller it is, the better. So there is basically only one candidate to try: the union itself. Is the union linearly independent? Well, if
belong to the union, then each
belongs to some linearly independent set
. Because
is a chain, one of these sets
contains all the others. If that is
, then the linear independence of
implies that no non-trivial linear combination of
can be zero, which proves that the union of the sets in
is linearly independent, just as we wanted. Therefore, by Zorn’s lemma, there is a maximal linearly independent set. Earlier we observed that such a set was a basis and could be used to create additive functions not of the form
, so our problem is now solved.
Further general remarks: How, one might ask, is Zorn’s lemma itself proved? One answer is that it cannot be proved: it is just an axiom. But a slightly more informative answer is that it is equivalent to the axiom of choice and the well-ordering principle. A hint of why this should be can be found in the attempted proof above. There we created an infinite sequence , which we then continued “transfinitely” with the elements
. This transfinite process can continue until a maximal element is reached, but to do so one needs to make infinitely many choices (since there isn’t a way of defining the next element of the sequence). Thus, the axiom of choice comes into play. If we knew in advance that
could be well-ordered (that is, given a total ordering such that every non-empty subset had a minimal element), then we could build up the sequence by always taking the minimal element that worked. And it’s an easy exercise to use Zorn’s lemma to prove that every set has a well-ordering.
Example 2: Let us justify this last statement, since it gives another representative application of Zorn’s lemma. Suppose, then, that we have a set and we would like to give it a well-ordering. That is, we would like to define a total ordering on the elements of
such that every non-empty subset
of
has a minimal element.
Once again, we find ourselves in a situation where there are no obvious constraints to building the object we require, other than the “transfinite length of time” needed to complete the process. We just pick an arbitrary element to be the minimal element of
itself, then an arbitrary element
to be the minimal element of
, and so on. In other words, at each stage we would like to choose an element not yet chosen and declare it to be the next element in our ordering.
To convert that rough idea into a Zorn’s-lemma argument, we need to define a partial ordering on the set of “incomplete attempts” at defining a well-ordering on . An incomplete attempt means a subset
of
and a well-ordering of that subset. Let us define an attempt to be precisely that: a subset
of
with a well-ordering of the elements of
. The partial ordering on the set of all attempts should reflect the idea of one attempt extending another, so the obvious partial ordering to take is as follows: given two attempts
and
, we say that
if
is an initial segment of
. This means that
is a subset of
, that the ordering associated with
is the same as the ordering associated with
when you restrict it to
, and that every element of
is less than every element of
in the ordering on
.
Does this partially ordered set satisfy the chain condition? Well, if we have a chain of attempts, then we can define an upper bound to be the union of the sets in that chain, with the following ordering:
if there is some attempt
in the chain such that
and
both belong to
and
in
. This ordering is well-defined, because if
is another attempt that contains
and
, then either
or
(since
and
both belong to the chain), and the definition of
guarantees that the orderings on
and
are consistent.
Is the ordering on a well-ordering? Yes, since if
is a non-empty subset of
, then there must be an attempt
in the chain such that
is non-empty. But then
has a minimal element
in
. This must be minimal in
as well. To see why, suppose that
and
. Then there must exist an attempt
in the chain with
. Since
it follows that
does not contain
, so we must have
. Therefore,
must be an initial segment of
and we have
with
and
. This is a contradiction.
We have now shown that is well-ordered, and thereby verified the chain condition. (Note that verifying the chain condition was fairly straightforward: this is true of many applications of Zorn’s lemma.) Therefore, by Zorn’s lemma, there is a maximal attempt, which we hope will be a well-ordering of the whole of
.
If it is not the whole of , then it is a well-ordering of some proper subset
of
. But we can easily extend this attempt: let
be any element of
and define
to be
, ordering
by taking the ordering we already have on
and stipulating in addition that
for every
. (Of course, we also stipulate that
.) This produces a larger attempt, contradicting the maximality of
. This contradiction completes the proof that (Zorn’s lemma implies that) every set can be well-ordered.
Further general remarks: Note that the final step of the last argument, the proof that every maximal attempt must be a well-ordering of the whole of , corresponds to the informal observation made earlier that we can keep on and on extending a well-ordering, while the verification of the chain condition corresponds to the fact that if we produce an infinite sequence of attempts then we can take their union and carry on. Again, this is typical of Zorn’s-lemma arguments.
So how, in general, does one recognise the need for Zorn’s lemma and how does one construct an appropriate partially ordered set in order to apply it? The clues are in the two examples above. Typically, one is trying to build a structure of some kind (such as a basis for a vector space, or a well-ordering of a set). The natural way to do it appears to be to build the structure up in stages, but there are too many stages for this to work straightforwardly. However, once one has an idea of what a stage is and what the building-up process is, one can wheel out Zorn’s lemma to finish the job. The partially ordered set will consist of all objects that might conceivably be stages in the construction, and one of these objects will be smaller than another if it might conceivably come before the other in the building-up process. If the resulting partial order satisfies the chain condition and if a maximal element must be a structure of the kind one is trying to build, then the proof is complete.
August 12, 2008 at 2:22 pm |
Outstanding article: this is exactly the sort of things
one needs to learn Mathematics.
Thank you so much!
P.S. I look forward to see the tricks wiki realized!
August 12, 2008 at 3:53 pm |
Is the ordering on U a well-ordering? Yes, since if V is a non-empty …
What is U ? W?
Thanks: it was indeed and I’ve now corrected my slip (by changing what I originally called
and I’ve now corrected my slip (by changing what I originally called  to
to  rather than the other way round).
rather than the other way round).
August 12, 2008 at 7:58 pm |
[…] busy with a few things today, like assembling my furniture. Luckily, Tim Gowers has a post on “How to use Zorn’s lemma”. His example is the construction of additive (not linear) functions from to […]
August 12, 2008 at 8:48 pm |
Let me echo carlo: this is a terrific article! Thanks so much for writing this up. Really makes me wish the web had been around when I was in grad school…
August 13, 2008 at 12:04 am |
I really like the exposition style here. There is no “magic,” no arguments where the writer simply exhibits an object which satisfies all the properties one wants, leaving the reader no clue about how to come up with such objects.
I wish all math books were written this way!
August 13, 2008 at 12:04 am |
Has the tricks wiki actually been set up? It’ll be great to see.
August 13, 2008 at 3:31 am |
I like to think of Zorn’s lemma as a guarantee that greedy algorithms can go on as long as necessary, before being stopped by some sort of obstruction (either a chain without an upper bound, or a maximal element). So any finitary construction that is built via the greedy algorithm (e.g. selecting a basis for a finite-dimensional vector space greedily) has a decent chance of extending to the infinitary setting as well by a Zorn’s lemma argument. Which is of course essentially what you are saying above 🙂
August 13, 2008 at 5:16 am |
To me, the problem
Does there exist an additive function on that isn’t of the form
that isn’t of the form  ?
?
is more intuitive if thought about in greater generality. Considering as a Banach space, then the problem is easily seen to be equivalent to:
as a Banach space, then the problem is easily seen to be equivalent to:
Does there exist an unbounded linear operator on ?
?
By essentially the argument presented in the post one can construct an unbounded linear operator on any “sufficiently non-trivial” Banach space. One thing that has always struck me as a bit curious is that while it appears to be necessary to use the axiom of choice to construct an unbounded linear operator on , on most “interesting” Banach spaces (from a functional analysis view) there exists very natural unbounded linear operators, which do not require the axiom of choice to construct.
, on most “interesting” Banach spaces (from a functional analysis view) there exists very natural unbounded linear operators, which do not require the axiom of choice to construct.
August 13, 2008 at 8:34 am |
Mark, You can’t quite mean what you write here, since considered as a Banach space is one-dimensional. It can’t be a Banach space over
considered as a Banach space is one-dimensional. It can’t be a Banach space over 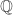 either, since
either, since 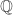 isn’t complete, and even to make it a normed space over
isn’t complete, and even to make it a normed space over 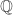 would seem to require the axiom of choice. So I don’t really know what an unbounded linear operator on
would seem to require the axiom of choice. So I don’t really know what an unbounded linear operator on  is. I also take issue with your assertion that on most interesting Banach spaces there are obvious unbounded linear operators. For instance, take the most interesting Banach space of all: a separable Hilbert space, which for definiteness we could take to be the sequence space
is. I also take issue with your assertion that on most interesting Banach spaces there are obvious unbounded linear operators. For instance, take the most interesting Banach space of all: a separable Hilbert space, which for definiteness we could take to be the sequence space 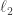 . If
. If  is the standard basis, we could define
is the standard basis, we could define  , say, and extend linearly, but this function is defined just on finite linear combinations of the
, say, and extend linearly, but this function is defined just on finite linear combinations of the 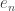 . To turn that into a completely defined unbounded linear map we need a basis (in the vector space sense) of
. To turn that into a completely defined unbounded linear map we need a basis (in the vector space sense) of 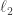 , and I’m pretty sure that needs the axiom of choice. So as far as I can see the only way to produce explicit examples of unbounded linear operators is to define them on artificial normed (but not Banach) spaces such as the space of sequences that are zero except in finitely many places (with any norm you like).
, and I’m pretty sure that needs the axiom of choice. So as far as I can see the only way to produce explicit examples of unbounded linear operators is to define them on artificial normed (but not Banach) spaces such as the space of sequences that are zero except in finitely many places (with any norm you like).
August 13, 2008 at 12:01 pm |
I think I remember Imre Leader telling me that it’s consistent with ZF that every linear functional on every Banach space is bounded.
August 13, 2008 at 1:56 pm |
Terry, I sort of agree with you but I’m not sure you mean what I would mean by “greedy”. I think of a greedy algorithm as one where you make the locally best choice at each stage, without paying attention to possible long-term consequences. So Zorn’s lemma would be needed only if the locally best choice is not unique (as happens, for example, when one is proving the Hahn-Banach theorem). I suppose one could regard building a basis for a vector space as greedy in the sense that every vector not in the linear span of the vectors chosen so far is equally good, so they are all “locally best”. But I think it would be more natural to substitute something like “non-determined” for “greedy” in what you say. But the idea of saying that Zorn tells you that you can keep going until you reach one of two kinds of obstacle is a nice perspective on it.
August 13, 2008 at 3:08 pm |
If I remember right something that a colleague analyst once explained to me, any measurable linear functional on a Hilbert space (at least; I don’t remember if this works for arbitrary linear operators or Banach spaces) is automatically continuous. Here, measurable refers to the Borel sigma-algebra.
So intuitively, if you can “write down” such a functional, either it is not defined everywhere, and then it may be unbounded (e.g., trying to define f –> f'(0) on L^2([0,1])), or it is in fact continuous.
August 13, 2008 at 4:00 pm |
Similarly to Emmanuel’s comment, it is stated in Dugundji’s Topology that every nonlinear additive function on the real numbers is not Lebesgue measurable.
August 13, 2008 at 4:10 pm |
Dear Sir, this is a very well-written article thank you. But is this really a trick given that, as you point out, Zorn’s lemma is the axiom of choice in disguise? Might it not be called ‘a fact in ZFC’ rather?
I mean, I thought (perhaps wrongly) that the axiom of choice is used precisely so that such existence results are easily obtained or in fact possible at all (i.e. it’s not a surprise, it’s a consciously built-in feature of our theory).
That said I’m as everyone else eagerly awaiting the day the Tricks Wiki will be launched!
August 13, 2008 at 5:22 pm |
Alphonse, you raise an important point. I’m slightly worried about the word “trick” because what the site will really be is a repository for methods and techniques, which won’t have to be tricks in the usual clever-clever sense of the word. Basically, any topic will be suitable for the site, provided its main aim is to explain to the reader how to prove certain kinds of theorems. But this means that one thing the articles won’t do is merely state facts. For example, the point of this one is not the fact of Zorn’s lemma (in ZFC) but rather the way it is typically used in the proofs of theorems. The reason I discussed the relationship between Zorn’s lemma and the axiom of choice was partly that it would be criminal not to and partly that it provided me with a good second example of an application of the lemma.
It’s also worth saying that from the point of view of the working mathematician, and also of the Tricks Wiki, Zorn’s lemma is not the same as the axiom of choice. Yes, they are logically equivalent, but they are not equivalently useful: for many applications of the axiom of choice it is far more convenient to use Zorn’s lemma instead, because if you don’t then you effectively end up having to prove it, or a special case that is no easier than the result in its full generality. (Alternatively, one could use induction on the ordinals: if I have time then I may write a companion article to this one, in which I would explain how Zorn’s-lemma proofs can often be converted quite easily into transfinite-induction proofs, and vice versa.)
Mark, I will soon have another Tricki article ready that will include amongst other things a proof of precisely the (contrapositive of the) result you refer to: every additive Lebesgue measurable function on is linear.
is linear.
August 13, 2008 at 7:40 pm |
As a followup to my previous comment, I found again the paper where a proof of the “automatic continuity” was given (indeed, for X–>Y linear with X Banach space and Y a normed space); the argument there (due to Étienne Matheron) is short and nice (and clever) enough that I just explained it in another post.
August 13, 2008 at 10:46 pm |
Hmm, fair enough; Zorn’s lemma doesn’t require that each choice be locally best, only that it be better than (i.e. larger in the partial ordering than) the status quo.
One nice thing about this perspective is that it contrasts transfinite induction (which corresponds to the case where the choice is deterministic at each stage) with Zorn’s lemma (which is the non-determined choice case). It is then clear how the axiom of choice is used to reduce the latter to the former.
August 27, 2008 at 6:59 am |
Dear Sir, after reading your interesting article, my understanding of Zorn’s Lemma is: if we need a “maximal” set with property P (such as a set of basis, or a maximal ideal), we just pick an ascending chain of sets with that property P, and show their union has property P, then by Zorn’s Lemma such a maximal set exists. Is this understanding correct?
I like your articles a lot. Hope to see your explanation of transfinite induction soon.
August 27, 2008 at 12:44 pm |
I’d say that’s roughly it, but I prefer to be a bit more specific about the notion of “ascending chain” just to be absolutely clear that we’re usually talking about more than just set containment. (In other words, the basis example is not wholly representative.) In general, we are dealing with objects with more structure than mere sets, and the ordering associated with the chains is something along the lines of “object A is smaller than object B if B could turn out to be an extension of A in the building-up process”. Also, when you say “we just pick an ascending chain” what you mean is more like “whatever ascending chain we pick”.
September 1, 2008 at 8:43 am |
I have some doubt about the following statement:
Now \mathbb{R}, considered as a vector space over \mathbb{Q}, is certainly infinite-dimensional. In fact, it has uncountable dimension. So does it have a basis? (All we mean by “has uncountable dimension” is “cannot be spanned by countably many vectors,” so it is not true by definition that it has a basis.)
Do you mean the number of basis is uncountably infinite? (Suppose A is the set of basis.) I think it should be countable many, by the simple reason that we could write R as Q^A, which reveals that A should be countable many. Would you please explain that?
Thanks.
September 1, 2008 at 11:47 am |
Hi everyone,
I recently saw in a book (Topological Vector Spaces, Distributions and Kernels by Francois Treves) that there is a Borel Graph Theorem for Banach spaces (and more generally), i.e. a big generalisation of the Closed Graph Theorem.
This is vaguely related to the above discussion; any unbounded linear operator on a Banach space must have a non-Borel graph. For $R^n$ this is weaker than (but in some ways “close to”) saying non-Lebesgue measurable, which intuitively (at least to me) means “very nasty” and “close to” requiring the Axiom of Choice (again, “very nasty and nonconstructive” in my opinion).
Apologies for all this vagueness, and the logical gaps. It doesn’t prove anything, but it intuitively suggests (at least to me) that unbounded linear operators between Banach spaces (defined on the whole space) are necessarily nonconstructive, which is in fact true as E. Kowalski says above (and gives a nice link about this).
Incidentally, does anyone else feel that AC is rather nasty, and that most undergraduate (or even graduate) students are not sufficiently well aware of this? Of course the extent of allowable nastiness is a matter of taste; I personally try to avoid it whenever possible, and explicitly warn students when it is being used. But maybe I am in a minority.
September 2, 2008 at 9:27 am |
Jimmy,
What is wrong with your friend’s argument is that the definition of the set spanned by the basis A is the set of *finite* linear combinations of elements of A. So R is not Q^A but the much smaller subset that consists of functions that are 0 in all but finitely many places. If A is countable then it’s easy to check that the set of finite linear combinations of elements of A is also countable. So if it’s to equal R then A must be uncountable.
October 15, 2008 at 10:59 pm |
[…] the article that explains the technique? Similarly, if you are trying to build some structure and Zorn’s lemma is what you need to make your argument work, what key words or tags are going to help you? It […]
January 19, 2009 at 11:37 am |
pls i want to no the process of making an in complete normed space a complete normed space
January 31, 2009 at 6:08 pm |
[…] Jan 31: See also "How to use Zorn’s lemma", by Tim Gowers.] Possibly related posts: (automatically generated)How to use Zorn’s […]
April 13, 2010 at 7:35 pm |
In the following paragraph, I do not follow the argument from the lines starting with the quotation marks.
Is the ordering on $U$ a well-ordering? Yes, since if $V$ is a non-empty subset of $U$, then there must be an attempt $Y$ in the chain such that $V\cap Y$ is non-empty. But then $V\cap Y$ has a minimal element $v$ in $Y$. “This must be minimal in $U$ as well. To see why, suppose that $v’\leq v$ in $U$. Then there must exist an attempt $W$ in the chain with $v’\in W$. If $v’\notin V$ then $V$ does not contain $W$, so we must have $V\leq W$. But this is a contradiction, since $V$ must then be an initial segment of $W$ and we have $v’\leq v$ with $v’\in W\setminus V$ and $v\in V$. Therefore, $v’\in V$, and since $v$ is minimal in $V$ we must have $v’=v$.”
When you say “This must be minimal in $U$ as well”, you actually mean that we need to show that $v$ is a minimal element of $V$ in $U$. Am I right? You consider an element $v’ \leq v$ in $U$. The elements $v’,v \in W$ for some attempt $W$. If $v’ \notin V$, then $V$ doe not contain $W$. This is where I get totally confused. How could you conclude that $V \leq W$ when we do not know that $V$ is an attempt. Again, in the end you claim that $v$ is minimal in $V$, when that is what we set out to prove.
April 14, 2010 at 3:12 am |
You’re absolutely right. I accidentally wrote several times when I meant
several times when I meant  . I’ve changed it now. I hope it’s correct, though I haven’t yet checked quite as hard as I should, so it may need further adjustment.
. I’ve changed it now. I hope it’s correct, though I haven’t yet checked quite as hard as I should, so it may need further adjustment.
April 14, 2010 at 8:09 am |
Thank you for your quick response. My hunt for a good understanding of Zorn’s lemma started with the following problem: Suppose f:S \Rightarrow T and g:T \Rightarrow S. Then show that there exist sets A \subseteq S and B \subseteq T such that f(A) = B and g(T\setminus B) = S\setminus A.
I am not sure if this problem requires Zorn’s lemma but I thought that I had a proof using Zorn’s lemma.
April 14, 2010 at 9:13 am |
That looks like the lemma you need to prove the Schroeder-Bernstein theorem, which does indeed require the axiom of choice.
September 20, 2010 at 1:02 am |
Superb article sir.
The first example, can be further seen as Automorphisms of R which are only the Identity. The standard way of proving it is showing f to be identity on rationals and then proving f to be continuous which would imply f being identity on the whole of R.
Another theorem, which i learnt makes use of Zorn’s lemma is “Existence of Maximal ideals in a Ring R with 1”.
December 29, 2010 at 8:35 am |
[…] Jan 31: See also "How to use Zorn's lemma", by Tim […]
April 25, 2013 at 3:10 am |
[…] How to use Zorn’s Lemma (the right […]
April 29, 2013 at 9:25 pm |
[…] we are now going to turn this sketch into a real proof using Zorn’s lemma. Oh, by the way: here is an absolutely wonderful post about Zorn’s lemma on Tim Gowers’s blog. Anyway, here […]
May 8, 2013 at 9:39 pm |
gowers, why do you say that Shroeder-Bernstein requires the Axiom of Choice? Given injective maps from X->Y and Y->X, you can explicitly construct a bijection between X and Y; no choices are involved.
May 11, 2013 at 11:58 am
I wrote that false statement nearly three years ago, and have no idea what was going on in my head at the time …
November 19, 2013 at 2:01 am |
[…] learned about Harald’s work in my functional analysis class. By Zorn’s lemma, every Hilbert space admits an orthonormal basis (ONB). However, only separable Hilbert spaces have […]
April 10, 2015 at 7:12 pm |
[…] the words of Timothy Gowers, If you are building a mathematical object in stages and find that (i) you have not finished even […]
December 11, 2017 at 3:19 pm |
Can the choice of be made totally arbitrarily in the construction? If a choice is made so that every member of
be made totally arbitrarily in the construction? If a choice is made so that every member of  is a multiple of some number
is a multiple of some number 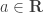 , then the map we construct will be the identity map, which is linear.
, then the map we construct will be the identity map, which is linear.
December 11, 2017 at 3:20 pm
Ooops, the map constructed won’t necessarily be the identity map, but it’ll be linear.
December 11, 2017 at 3:25 pm |
Ignore my previous comment. Here’s what I really wanted to say:
” Can the choice of be made totally arbitrarily in the construction? If I choose
be made totally arbitrarily in the construction? If I choose  for every
for every  in the maximally spanning set, we would have constructed a linear map.”
in the maximally spanning set, we would have constructed a linear map.”
July 29, 2019 at 1:35 pm |
[…] as a vector space over ,from Zorn’s lemma(here is a great article to understand Zorn’s lemma ) it is a standard result that there always […]
February 14, 2021 at 4:19 am |
von Neumann is reputed to have once said to a student, “You don’t understand mathematics, you just accept it.”
Well, you have to at least know how to use it, even if you can’t understand it. Well, I certainly don’t “understand” Zorn’s lemma, but now I know how to use it.
Thank you for giving me an example of how to use Zorn’s lemma. I can use your example to see how the proofs of many theorems in mathematics work, even if the Theorems themselves seem rather mysterious to me.
An interesting thing in your example is that it was only after you had your maximum element that you proved that it was equal to the whole set. WOW!
September 22, 2023 at 6:46 pm |
This was so inspirational, such an epic story. I can’t believe that this happened. I can’t wait to read the sequel. 10/10