A small countability question

This is a short post to ask a simple question that arises out of the discussion in a previous post about countability. As is well-known, the familiar statement that a countable union of countable sets is countable requires the axiom of countable choice. Indeed, it comes in in the very first step of the proof, where one says something along the lines of, “For each set $A_n$ let $a_{n1},a_{n2},\dots$ be an enumeration of its elements.” This uses the axiom of choice because if we don’t know anything about the sets $A_n$ then we can’t actually define these enumerations: we just have to assert that a sequence of enumerations exists.

However, if we do have explicit enumerations of the sets $A_n$ then the proof yields for us an explicit enumeration of their union. So one might take the following attitude to this particular application of the axiom of choice: the real theorem is “An explicitly enumerated union of explicitly enumerated sets is explicitly enumerated,” but because we often care only that enumerations should exist and don’t want to keep having to define artificial ones, it is convenient to appeal to the axiom of choice so that we can extend the theorem to the murky world of countable but not explicitly enumerated sets.

The question is this. Suppose we decided that we wanted a theory of explicit countability rather than pure-existence countability. Many of the basic results would still be valid: the rationals are explicitly countable, an explicit countable union of explicitly countable sets is explicitly countable, and so on. So where would things start to get difficult? Obviously, the statements one made would be less general, but where would that really matter to a mathematician not working in set theory?

As davidspeyer pointed out in an interesting comment on the previous countability post, there do exist explicitly definable sets that we can show are countable even though we cannot give a complete description of their elements: his example was the set of zeros of the Riemann zeta function, which are countable because they are isolated. However, even sets like this are explicitly countable in the required sense, since one can easily choose an ordering of $\mathbb{C}$ in such a way that the elements of any subset of $\mathbb{C}$ that has no accumulation point must be well-ordered. (For instance, write them as $re^{i\theta}$ with $0\leq\theta<2\pi$ and put them in order of $r$ first and then $\theta$ .)

To make the question slightly clearer, let us distinguish between two sorts of countability proof. One would be as follows: you’re given an explicitly defined set and you prove that it is countable. The other is where you deduce that your set is countable from some other property that it has. (For instance, you might have a collection of disjoint non-empty open sets in a separable metric space and you might deduce that it was countable by choosing distinct elements in each set that belonged to a countable dense set.) In the first case, are there instances where one can prove that the set is countable but not that it is explicitly countable? In the second case, are there ever circumstances where one cannot convert the general statement into an obviously corresponding, and equally useful, one about explicit countability? (For instance, if you have an explicitly enumerated dense set in your metric space then you can explicitly enumerate the open sets by taking the smallest element from the dense set, taking its index, and using that to order the open sets. Therefore, a collection of disjoint open sets in an explicitly separable metric space is explicitly countable.)

I’m writing this in the expectation that there are places where the axiom of countable choice is more than just a convenience in the sense just explained. But I haven’t thought of any myself. (The one thought I have is that countable ordinals become harder and harder to describe as they get bigger and bigger. Perhaps there is a countable ordinal that one can only just describe, but that is so big that describing an enumeration of it is not possible. Or perhaps that’s nonsense and there are sound theoretical reasons that any ordinal you can describe can also be explicitly counted.)

This entry was posted on August 10, 2008 at 4:12 pm and is filed under Uncategorized. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

18 Responses to “A small countability question”

Bas Spitters Says:
August 11, 2008 at 1:18 pm | Reply
The axiom of countable choice is provable as a rule for many formal systems for constructive mathematics. That is, one can prove that if the formal system T proves that

for all n, there exists m, R(n,m)

then T also proves

there exists f, for all n, R(n,f(n))

[These results can be found for instance in Troelstra and van Dalen – Constructivism in Mathematics]

So, you will not find any problems in the constructive parts of mathematics, e.g. in the theory of the rationals.

I think there are extensions of this to parts of mathematics with classical logic, but I will have to check.
Kenny Easwaran Says:
August 11, 2008 at 9:29 pm | Reply
I think a lot of this will depend on what you mean by “explicitly countable”. In some cases you’ll just want a procedure that takes orderings (in the set-theoretic sense of a set of ordered pairs) on your sets and constructs an ordering on the union. However, you might also be interested in slightly more restricted senses of “explicit”, where the ordering must be computable or definable or recursive, or something similar. In that case, it turns out that there are countable sets that are not computably countable. For instance, the set of computable reals is countable because there are only countably many Turing machines that could possibly compute reals. However, if there were a computable enumeration of them, then diagonalization would compute a real that wasn’t on this list. There’s a lot of work (especially by proof theorists, I believe) on various ordinals that measure the strength of certain notions of effective computability, or provability in general.
Kenny Easwaran Says:
August 11, 2008 at 9:33 pm | Reply
Oh right, that last point you mentioned goes along with the last point I mentioned. For any proof system, you can talk about the class of well-orderings that system can define and prove to be countable. This ordinals corresponding to these orderings will clearly form an initial segment of the ordinals, and thus be an ordinal, but this ordinal can not itself be a member of the class. Since there are only countably many possible definitions in any system (assuming a countable alphabet), this ordinal will be a countable ordinal that the system we’re interested in cannot prove to be a countable well-ordering. Some standard ones are called $\epsilon_0, \Gamma_0, \omega_1^{CK}$ , but I can’t exactly recall the definitions of them in these terms.
Terence Tao Says:
August 11, 2008 at 11:01 pm | Reply
This presumably counts as cheating, but if you add the continuum hypothesis to one’s set of axioms, then one can show indirectly that a set is countable without giving any clue as to an explicit enumeration by showing that a contradiction would occur if the set had cardinality equal to or larger than the continuum. 🙂
Ewan Delanoy Says:
August 12, 2008 at 3:12 pm | Reply
according to the Wikipedia article on “Axiom of choice”, there is a parallel world (model of ZF) in which the set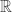 $\mathbb R$ of reals is a countable union of countable sets.
Boris Says:
August 16, 2008 at 4:20 pm | Reply
Along the lines of Terry’s, but without the Continuum Hypothesis: suppose a set X is such that there exists no surjection from X onto Aleph_1. Then by the axiom of choice, X is countable.
Walt Says:
August 17, 2008 at 4:26 am | Reply
There is such an ordinal as you mention in the last paragraph. (I think it’s called the Church-Kleene ordinal.) You can probably give a proof of its existence along these lines: there exist countable ordinals that are not explicitly enumerable. Take the first one — this is a description of a countable ordinal that is not explicitly describable.

You need countable choice to show that an infinite set has a countable subset. I don’ t know if that’s the kind of result you had in mind.
Timothy Chow Says:
September 4, 2008 at 4:10 am | Reply
Jech and Sochor showed that ZF doesn’t prove the uniqueness of the algebraic closure of the rationals. Does this matter to mathematicians? After all, it’s easy enough to construct *an* algebraic closure of Q and to work only with it. Maybe we aren’t bothered by the possible existence of other algebraic closures that we can’t show are countable.

ZF also doesn’t show that every infinite finitely-branching tree has an infinite path (Koenig’s lemma). Again it might be the case that if you’re studying (say) the game tree of some specific combinatorial game, you might be able to construct infinite paths explicitly whenever you need them. I imagine, though, that maintaining that level of logical hygiene might get tiresome after a while. Our intuition that there has to be an infinite path is so strong that it would be easy to forget to define explicitly every infinite path we needed.
John Armstrong Says:
September 4, 2008 at 5:43 am | Reply
I’ll admit I don’t know this area well, but is the algebraic closure unique up to isomorphism? That is, is there a field isomorphism between any two algebraic closures which is the identity on the rationals? In that case, no, mathematicians would have no reason to care.
Timothy Chow Says:
September 4, 2008 at 3:53 pm | Reply
No, when I said “uniqueness” I meant “uniqueness up to isomorphism.” The trouble is that in the absence of the axiom of choice, you can’t even prove that every algebraic closure of the rationals is countable. Here by an “algebraic closure” I mean an extension of the rationals that is algebraically closed and contains no proper subfield that is algebraically closed.

These exotic algebraic closures have some interesting features. See for example W. Hodges, “Lauchli’s algebraic closure of Q,” Math. Proc. Camb. Phil. Soc. 79 (1976), 289-297.
gowers Says:
September 4, 2008 at 4:13 pm | Reply
I believe what you say, but I also don’t see how it can be true. So let me give you a “proof” that all algebraic closures are countable and get you to tell me where I’ve either gone wrong or accidentally used the axiom of choice. If I see it myself when sketching the argument, I’ll leave the sketch just in case anyone else was also confused.

The argument would be like this. Let $X$ be any algebraic closure of the rationals. I shall build inside $X$ a subset $Y$ that’s countable and algebraically closed, which, by the minimality of $X$ , will prove that $X$ is countable.

The construction of $Y$ is the obvious one. I start with the rationals. Then I …

Actually, I’m even more confused. I was about to build up $Y$ in $\omega$ stages, but can’t one do it in just one stage? The algebraic numbers form an algebraically closed field, so they’re obviously the algebraic closure of the rationals. And that seems to be true even if I define “algebraic number” to mean “solution in $X$ of a polynomial with integer coefficients”.

I can see how one might need Zorn’s lemma to build an isomorphism from the usual algebraic numbers to the algebraic numbers in $X$ (since as you build up you find roots that are algebraically indistinguishable so you have to make arbitrary choices about which one corresponds to which), but I don’t see how the algebraic numbers in $X$ could fail to be countable.

Looking at Wikipedia I see that it says that the algebraic numbers are the algebraic closure of the rationals, but that Zorn’s lemma is needed to prove that every field has an algebraic closure.
Timothy Chow Says:
September 5, 2008 at 1:42 am | Reply
One has to be careful about saying “the” algebraic numbers before uniqueness has been proved. Certainly one can enumerate polynomials in some way and adjoin roots. This gives *an* algebraic closure, but how do we know that there isn’t some other algebraic closure? Any two *countable* algebraic closures must be isomorphic, because you can use the enumerations to build an isomorphism in a canonical way, but the above construction tells us only that our algebraic closure is a countable union of finite sets, which might not be countable.

In the paper by Hodges that I cited above, he demonstrates some other “weird” facts: In ZF, one cannot prove any of the following statements.

1. Let L be an algebraic closure of Q. Then Gal(L/Q) is non-trivial.
2. Let L be an algebraic closure of Q. Then there is a non-trivial absolute value on L.
3. Every principal ideal domain either has prime elements or is a field.
gowers Says:
September 5, 2008 at 12:03 pm | Reply
OK, so as usual the weak point in what I wrote was where I didn’t stop to justify something in detail — in this case when I said “And that seems to be true even if …” As you point out, although one can explicitly count the algebraic numbers in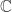 $\mathbb{C}$ , in an arbitrary algebraic closure $X$ one may have to make arbitrary choices amongst algebraically indistinguishable roots of polynomials. 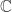In other words, proving that the algebraic numbers in $X$ are countable is exactly as hard as proving that they’re isomorphic to the algebraic numbers in $\mathbb{C}$ .

Going back to your main question, there is a sense of “matters” that I don’t pretend to be able to define precisely, in which it doesn’t matter to me that not all algebraic closures of the rationals are isomorphic. The sense is something like this. For convenience we like to talk about “arbitrary” objects, but what actually matters is explicit objects. When we talk about the arbitrary ones we can’t get hold of their elements (because nothing is described), so we’re often forced to use the axiom of choice. But for the sets that matter we can find ways of making the choices explicit.

I don’t necessarily believe that that last sentence always holds, but it’s there to give some idea of what I’m talking about (and which I’m sure set theorists have thought about far more deeply than I am ever likely to).
Walt Says:
September 10, 2008 at 2:01 am | Reply
But for the sets that matter we can find ways of making the choices explicit.

There are counterexamples to this in analysis, at least. For example, to construct a finitely-additive measure on c_0 that is not countably additive requires something the axiom of choice. To construct a non-trivial element of the Stone-Cech compactification of the integers requires something like the axiom of choice.
gowers Says:
September 10, 2008 at 8:55 am | Reply
Walt, for those to be counterexamples, one would have to have an argument that the existence of such objects “matters” to someone who ultimately cares only about explicitly defined sets. For instance, one might attempt to justify the existence of non-principal ultrafilters by pointing to their use in Ramsey theory, where they can be used to prove theorems that would then apply to explicit colourings. That becomes quite a subtle issue, since as far as I know one can always replace an ultrafilter proof by an ultrafilter-free proof that is fairly similar, but it’s often the case that the proof with ultrafilters is much neater.
Walt Says:
September 10, 2008 at 11:29 pm | Reply
I tried to cherry pick an example that you would be tempted to concede really matters. Does L^\infty matter? Does the dual to L^\infty matter? They seem concrete in a way that a non-principal ultrafilter does not. Admittedly, that’s fantastically subjective.
Timothy Chow Says:
September 15, 2008 at 3:58 pm | Reply
After getting one of my own confusions about second-order arithmetic cleared up on the Foundations of Mathematics mailing list, I can add something more to this topic.

Simpson’s book “Subsystems of Second-Order Arithmetic” shows how a large amount of mathematics can be expressed in a language that talks only about integers and sets of integers. This language he calls Z_2, or second-order arithmetic (though strictly speaking it’s a two-sorted first-order language). Moreover, even with a fairly weak set of axioms, one can prove a large number of standard mathematical theorems. In particular, the axiom of choice is not used. Anything provable in Simpson’s book is provable in ZF.

There is a slight catch, in that you do lose some generality in the translation from ordinary mathematical language into the language of Z_2. The first sacrifice is that because we’re only allowed to talk about sets of integers, “intrinsically uncountable” statements will not be expressible. So for example, you can prove a version of the Hahn-Banach theorem, but it will only be for separable spaces.

The second sacrifice, which is more relevant to the current discussion, is that you can’t talk about “arbitrary sets,” even finite ones. Sets are always sets of integers, which have a canonical ordering on them among other things. Returning to the example of the algebraic closure of Q, in Z_2 the uniqueness problem mentioned above is “defined out of existence.” That is, the whole problem of arbitrary sets of roots of polynomials with no canonical ordering on them doesn’t come up, because you can’t express such things in Z_2. You can only talk about an algebraic closure of Q that is built up from sets of integers, and for such things you can prove uniqueness up to isomorphism.

The point is that these sacrifices sound like ones that Tim is willing to make. The answer to the question “How far can you get?” is therefore “Very far indeed.” It’s quite difficult to find examples of theorems that are not provable in $\Pi_1^1-CA_0$ , the strongest set of axioms considered in Simpson’s book, other than by “cheating” and picking intrinsically uncountable statements. The one example I know of a well-known theorem not provable in $\Pi_1^1-CA_0$ is the Robertson-Seymour graph minor theorem. This uses some fancy transfinite induction at some point. Even then it’s conceivable that the axiom of choice isn’t really needed, but I’m not familiar enough with the details to be able to say for sure.
Jonathan Crabtree Says:
October 15, 2008 at 10:07 am | Reply
This was the only blog post I thought I might get past one sentence. Yet I was wrong! Maybe I should stick to selling health insurance *sigh*