Removing the magic from Stirling’s formula

Another topic on the syllabus for the probability course I am giving is Stirling’s formula. This was lectured to me when I was an undergraduate but I had long since forgotten the proof completely. In fact, I’d even forgotten the precise statement, so I had some mugging up to do. It turned out to be hard to find a proof that didn’t look magic: the arguments had a “consider the following formula, do such-and-such, observe that this is less than that, bingo it drops out” sort of flavour. I find magic proofs impossible to remember, so I was forced to think a little. As a result, I came up with an argument that was mostly fully motivated, but there is one part that I still find mysterious. On the other hand, it looks so natural that I’m sure somebody can help me find a good explanation for why it works. When I say “I came up with an argument” what I mean is that I came up with a way of presenting an existing argument that doesn’t involve the pulling of rabbits out of hats, except in the place I’m about to discuss.

The first idea in proving Stirling’s formula is a very natural one: estimate $\log(n!)$ instead. Since that equals $\log 2+\dots+\log n$ , it is natural to approximate the sum by the integral $\int_1^n\log x dx$ . However, if you do that then the error will be around $\log n$ . This gives you a good rough-and-ready approximation to $n!$ but nothing like as good as Stirling’s formula.

The next idea is to turn things round and try to approximate the integral by a sum rather than the other way round. The obvious next approximation to try is approximating $\log x$ by the function $g(x)$ , where this is defined to equal $\log x$ when $x$ is an integer and to be linear in between consecutive integers. Then you can expect a much smaller error, and indeed it is not hard to prove that the difference between the integrals of the two functions is bounded. (The proof I gave for this dropped out rather nicely: if $r$ is a positive integer then by looking at derivatives it is easy to show that between $r$ and $r+1$ we have the inequalities $\log r+(x-r)/(r+1)\leq g(x)\leq\log x\leq\log r+(x-r)/r$ . Therefore, the difference between the integrals of $\log x$ and $g(x)$ between $r$ and $r+1$ is at most $(1/r-1/(r+1))/2$ . This gives a nice telescoping sum as an upper bound for the sum of all those areas.)

Another important observation is that the integral of $g(x)$ between 1 and $n$ works out to be $\log(n!)-\log n/2$ (because the integral between $r$ and $r+1$ is $(\log r+\log(r+1))/2$ ). Thus, we have a rather close relationship between $\log(n!)$ and an integral that we can calculate: $\int_1^n\log x dx=n\log n-n+1$ .

It is not hard to see that this argument shows that the ratio of $n!$ to $(n/e)^n\sqrt n$ tends to a limit. The one remaining magic part is the calculation of that limit. To do this, we define $c_n$ to be the integral $\int_1^n(\log x-g(x))dx$ . We have established that the sequence $(c_n)$ converges; our problem is equivalent to working out what the limit is. Here there is a very nice trick, which is to consider instead the sequence $a_n=2c_n-c_{2n}$ , which clearly converges to the same limit. But if you calculate $a_n$ you find that you can get a very good estimate for it if and only if you can get a very good estimate for $\binom{2n}{n}$ , essentially because inside what you write for $a_n$ you get $\log(2n!)-2\log(n!)$ , which is $\log \binom{2n}{n}$ . This trick is I think reasonably non-magic: if you know in advance that you can calculate $\binom{2n}{n}$ very accurately, then it is natural to try to use that information, and there is essentially only one way of doing that.

Even the fact that one can get a very good handle on $\binom{2n}{n}$ is not as magic as all that, since it is equivalent to estimating the probability that a subset of a set of size $2n$ has exactly $n$ elements. And that one can think about in all sorts of ways. For example, one can use the central limit theorem to estimate the probability that a random set has size between $n-c\sqrt n$ and $n+c\sqrt n$ and an elementary argument to show that the probabilities of the sizes within that range are all roughly equal.

However, we have not yet got to the central limit theorem in the course, so at this point I copied another proof, which goes roughly like this. You look at the integrals $I_n=\int_0^{\pi/2}\cos^n(x)dx$ . By integrating by parts in a standard way, you can get the recurrence $nI_n=(n-1)I_{n-2}$ . Since the $I_n$ clearly decrease, we get from this that the ratio of $I_{2n}$ to $I_{2n-1}$ tends to 1. But we can also give an exact formula for this ratio by using the recurrence and calculations of $I_0$ and $I_1$ . If you do this and rearrange things a bit, then you find that you can show that $2^{-2n}\sqrt n\binom{2n}{n}$ tends to $\pi^{-1/2}$ .

Finally, my question: is it just a coincidence that looking at the ratio of $I_{2n}$ to $I_{2n-1}$ gives you an expression that involves $\binom{2n}{n}$ ? Surely it isn’t, but for the moment this part of the argument still looks to me like a convenient piece of magic. It was clean enough to be easily memorable, so this did not present a problem for the lecture, but I’d still like to know why those integrals are so closely related to the binomial coefficient.

It would be remiss of me not to include a statement of Stirling’s formula in this account of the proof: it says that the ratio of $n!$ to $\sqrt{2\pi n}(n/e)^n$ tends to 1.

This entry was posted on February 1, 2008 at 2:04 pm and is filed under Probability. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

29 Responses to “Removing the magic from Stirling’s formula”

Pseudo-Polymath » Blog Archive » Friday Highlights Says:
February 1, 2008 at 4:18 pm | Reply
[…] Maths, a proof. […]
Lior Says:
February 1, 2008 at 4:43 pm | Reply
Hello,

It is standard to get Stirling’s formula by interpreting the sum $\sum_k \log k$ as a quadrature rule. You preferred the trapezium rule, but a slightly simpler variant is to interpret it as the midpoint rule for the interal $\int_{1/2}^{n+1/2} \log x\, dx$ . In both cases, the error on each interval ( $\null [k-1/2,k+1/2]$ or $\null [k,k+1]$ is bounded by a constant time the maximum of the second derivative of the integrand (times the cube of the interval length, but that’s a constant here), which here is summable over $k$ . This is “why” this works, indepedently of the “magic” of the telescoping series you get from the trapezium rule.

The statement $4^{-n}\sqrt{n}\binom{2n}{n} \to \pi^{-1/2}$ is a variant of Wallis’s formula, for which you give the usual proof. Note that you are missing the exponent $n$ in the definition of $I_n$ .
- M Says:
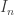  September 2, 2010 at 10:17 pm
  Here is a simple proof of Wallis and Stirling formulas. Email me for more pictures and details.
  
  Consider a {\it one-dimensional random walk} of a point $\cal Q$
  that starts at $x=0$ and at each step jumps from the point it
  occupies to either right or
  left adjacent integer.
  The probability of finding point $\cal P$ in
  location $x=K$ after $N$ steps from its initial position is
  given by the binomial distribution
  $$
  {P}(K,N)=\begin{cases} \dfrac{N !} {2^N\; \left(\frac{N+ K
  }{2}!\right) \left(\frac{N- K }{2}!\right) }, \text{ if
  }\vert K\vert \le N; \; N-K \text{ is
  even},\\
  0, \text{ otherwise}.\end{cases} \eqno{\rm (3)}
  $$
  
  Let us now assume that
  $$ N=2n \text{ is even } \eqno{\rm (4a)}$$
  and $\varepsilon$ satisfies
  $$
  0<\varepsilon<\dfrac 5{30}. \eqno{\rm (4b)}
  $$
  Formula (3) can be rewritten as
  $$
  \hskip-0.2cm {P}(-2k,2n)= {P}(2k,2n)=\begin{cases} \dfrac{(2n) !}
  {2^{2n}\; \left(n!\right)^2 }\cdot
  \dfrac{\left(n!\right)^2 } { (n+ k)!
  (n- k)! }=\\
  \hskip0.5cm \dfrac{(2n) !} {2^{2n}\; \left(n!\right)^2 }
  \prod\limits_{j=1}^{k} \dfrac{\;\;n-\ (k-j) \;\;}{n+ { j} }, \text{ if } 0\le k\le n,\\
  0, \text{ otherwise}.\end{cases} {\rm (5)}
  $$
  Formula (5) implies that sufficiently large $ n$
  $$
  1-\sum\limits_{\vert
  k\vert < n^{0.5+\varepsilon} } P\big(2k, 2n \big) =\sum\limits_{\vert
  k\vert \ge n^{0.5+\varepsilon} } P\big(2k, 2n \big)\le 2^{-
  n^{2\varepsilon}} \eqno{\rm (6)}
  $$
  and for $\vert k\vert \le n^{0.5+\varepsilon}$
  $$
  \frac 1{\sqrt{ n}} e^{-\frac{k^2}{n} -8
  n^{-0.5+3\varepsilon} } \le\frac {2^{2n}\; \left(n!\right)^2 }{(2n)
  !\sqrt{ n}}
  \;\; P(2k,2n)
  \le \frac 1{\sqrt{ n}} e^{-\frac{k^2}{n} +8
  n^{-0.5+3\varepsilon} }.\eqno{\rm (7)}
  $$
  The proof of formulas (6,7) is given in the Appendix.
  
  Formula (7) implies
  $$
  \bigg[ \frac 1{\sqrt{ n}}\sum\limits_{ \vert k \vert \le
  n^{0.5+\varepsilon} } e^{-\frac{k^2}{n}}\bigg] e^{ -8
  n^{-0.5+3\varepsilon} } \le\frac {2^{2n}\; \left(n!\right)^2 }{(2n)
  !\sqrt{ n}}
  { \sum\limits_{\vert k \vert \le n^{0.5+\varepsilon}}P(2k,2n)}
  \le \bigg[
  \frac 1{\sqrt{ n}}\sum\limits_{ \vert k \vert \le
  n^{0.5+\varepsilon} } e^{-\frac{k^2}{n}}\bigg] e^{ 8
  n^{-0.5+3\varepsilon} }.
  $$
  \color{black} Taking now limit as $n\to +\infty$ and using
  $\lim\limits_{n\to +\infty}e^{ 8 n^{-0.5+3\varepsilon}
  }=\lim\limits_{n\to +\infty}e^{- 8n^{-0.5+3\varepsilon} }=1$,
  $\lim\limits_{n\to +\infty} \sum\limits_{\vert k \vert \le
  n^{0.5+\varepsilon}}P(2k,2n)=1$ due to (6), $\lim\limits_{N\to
  +\infty}\dfrac 1{\sqrt{n}}\sum\limits_{{\vert k \vert \le
  n^{0.5+\varepsilon},}
  \atop{k \text{ is even}}}
  e^{-\frac{k^2}{n}}=\int\limits_{-\infty}^{+\infty}e^{-t^2}dt=\sqrt{\pi}$
  we obtain (1).
Lior Says:
February 1, 2008 at 4:45 pm | Reply
Oops … it seems I miffed the WordPress LaTeX syntax. I wish there was a “preview” button for comments …
gowers Says:
February 1, 2008 at 5:24 pm | Reply
Thanks for that, and I’ve now sorted out your LaTeX and my wrong definition of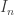 $I_n$ . I should have added that the magic of the telescoping sum wasn’t critical to getting the estimate to work, but it’s quite pleasant and the proof works for an arbitrary function with decreasing derivative. So that piece of “magic” doesn’t concern me.
David Speyer Says:
February 1, 2008 at 6:00 pm | Reply
I think that, if you follow the approach by taking logs, you will always have to do something tricky to get the value of the constant. After all, for many sums, such as sum 1/n, sum 1/(n log n) or sum n log n, it is easy to get an asymtopic formula where the constant term is given by a convergent sum, but it is very rare that this constant has a closed form.

Here is a different approach where the constant comes out relatively naturally. The first step is less motivated than in your argument but, after that, everything feels natural to me.

Start with the integral formula for the Gamma function:

$n!=\int_0^{\infty} e^{-x} x^n dx$

Now, a quick computation with derivatives shows that $e^{-x} x^n$ is optimized at x=n, so lets make a change of variables to put x=n at the origin. Set $x=u+n$ , so

$n!=n^n e^{-n} \int_{-n}^{\infty} e^{-u} (1+u/n)^n dx$

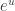The formula $(1+u/n)^n$ is screaming to be replaced by $e^u$ . Just making this replacement gives us far too much error, so keep one more term.

$(1+u/n)^n=\exp(n \log(1+u/n))=\exp(u-u^2/2n+O(u^3/n^2))$
so the integrand is
$\int e^{-u^2/n+O(u^3/n^2)} du.$

Intuitively, we are done at this point, because $\int e^{-u^2/n} du=\sqrt{2 \pi n}$ . Being careful, we have the problem that the error term $O(u^3/n^2)$ will overwhelm the terms we care about when u is too large. So the careful way to do this is to chop our integrand at $|u|=n^{a}$ for some $a$ between 1/2 and 2/3, and use some straightforward bounds to show that those tails don’t contribute.
David Speyer Says:
February 1, 2008 at 7:26 pm | Reply
Stupid typos in the above:

The formula that doesn’t parse is

$n!=n^n e^{-n} \int_{-n}^{\infty} e^{-u} (1+u/n)^n du$ .

I dropped the coefficient 1/2 in the Taylor series
$n \log(1+u/n)=u-u^2/2 n+O(u^3/n^2)$ , and in several of the following formulas.

[Many thanks for the comment, and I’ve fixed the bugs now.]
Old Fart Says:
February 1, 2008 at 9:45 pm | Reply
What’s wrong with magic? I was shown the summed up logs thing in a chemistry 1B lecture, probably before you were born, that was enough to crack out the boltzman distribution. My ‘please sir, what about the pis’ was rather dismissed as taking the piss. Beyond that, Copson’s ‘Theory of Functions of a Complex Variable’, Section 9.53 does the business in an old school way. Dave MacKay’s take (Information Theory, Inference and Learning Algorithms, page 2!) has a shade of the darker arts (including the central limit theorem) to it. None of these is maths, perhaps; Stirling’s theorem does, nonetheless, belong to the world.
David Watkins Says:
February 2, 2008 at 4:06 am | Reply
I found that proof a wonderful read. I stumbled across this blog not expecting to understand anything, so I am prompted to to write this. I like your style of “removing the magic”, seeing how it really works.

Thanks.
toomuchcoffeeman Says:
February 2, 2008 at 5:13 am | Reply
Shouldn’t the integral defining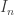 $I_n$ be taken from $\null 0$ to $\pi/2$ ?

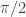Also (though in some sense this ties in with Lior’s post above) one non-magic reason to get ${2n\choose n}$ out of these integrals is that it is the constant coefficient in $(x+x^{-1})^{2n}$ — a fairly natural trick to try — so putting $x=e^{i\theta}$ and rescaling one gets

$2^{-2n}{2n\choose n} \frac{\pi/2} = \int_0^{\pi/2} \cos^n \theta\,d\theta$

I can’t see how to get round using (the proof of) Wallis’ formula, though.
toomuchcoffeeman Says:
February 2, 2008 at 5:15 am | Reply
Oops, bodged LaTeX. “No formula provided” should be 0, of course … and the last formula should be
$2^{-2n}{2n\choose n}\frac{\pi}{2} = \int_0^{\pi/2}\cos^n\theta\,d\theta$

[Many thanks for the comment, and I like the explanation for the appearance of the binomial
coefficient even if it doesn’t get the whole way to answering the question. I’ve corrected the bounds
in the integrals and fixed your LaTeX bug now.]
B Says:
February 3, 2008 at 1:33 am | Reply
This is certainly pulling a rabbit out of a hat, but what about integrating the logarithm of the sine product of sin(pi*x)/pi*x from 0 to 1? This is, if nothing else, a fairly natural thing to do once you know about the sine product, and the proof comes out without much trouble. Certainly it isn’t hard to remember as a proof, at any rate.
gowers Says:
February 3, 2008 at 1:55 pm | Reply
Just realized that the beautiful argument given by David Speyer a few comments up is almost certainly essentially the same as the argument I alluded to using the central limit theorem: your/his main steps are to centre and rescale a distribution and use the Taylor expansion up to the second term to get a Gaussian coming out, just as one does in proving the central limit theorem itself. But the fact that it comes out quickly and directly like that is very nice. And I myself find the first step pretty natural — if you’ve got the integral representation of the gamma function, then why not try to use it?
David Speyer Says:
February 11, 2008 at 7:50 pm | Reply
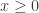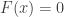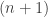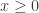I just realized this morning that the resemblance of my argument to the central limit formula is more than superficial: Let $F(x)=e^{-x}$ for $x \geq 0$ and $F(x)=0$ for $x < 0$. Then the $(n+1)$ -fold convolution of $F$ with itself is $x^n e^{-x}/n!$ for $x \geq 0$ (and, of course, zero for negative $x$ ). So what I’m doing is basically verifying the central limit theorem by hand for independent eponentially distibuted random variables.
Nilay Says:
February 14, 2008 at 4:27 am | Reply
I tried out the integration $\int_1^n\log x dx$ . This evaluates to $n log n - n +1$ . This would mean that this approximation is off by $n^{\frac{1}{2}}$ .
James Says:
February 16, 2008 at 1:19 am | Reply
Hi,

I was wondering if you’d mind if I used your blog article on Stirling’s formula for the next edition of “Eureka” (the journal of the Archimedeans undergrad. maths society here at Cambridge). It would most likely reach quite a broad audience of first years next year if you would consent. It might be worth appending David Speyer’s remarks also.

Of course if there is something else you’d prefer I’m open to suggestions.

Contact me at archim-eureka-editor@srcf.ucam.org if you are interested.
TSM Says:
February 19, 2008 at 12:54 am | Reply
Speaking of rabbits, here is a reference:
Strange Curves, Counting Rabbits, and Other Mathematical Explorations,
Keith Ball, Princeton Univ Press, 2003.

Chapter 6 (pp 109-126) is an excellent, motivated, wonderfully illustrated expository account of the path traveled largely by Gowers to Stirling’s formula. The Central Limit Theorem is discussed in the previous chapter, and so the estimate of the middle binomial coefficient 2n choose n is available. His approach to Central Limit Theorem is also excellent, starting from coin-tossing, and leading to the standard improper double integral exploited for the normal distribution. Explicit use of the big-Oh notation is avoided.

Ball also mentions that historically this approach is backwards; the Central Limit Theorem was first established using Stirling-like ideas. Also, Stirling used the Wallis product formula.

tsm [at] usna.edu
gowers Says:
February 21, 2008 at 12:50 am | Reply
That’s slightly embarrassing as I have the book but haven’t read that bit of it. But I would add to the previous comment that it is an excellent book in general, with beautiful discussions of bits of maths that often fall between the cracks of a typical undergraduate course. (For example, I was never taught the irrationality of pi and eventually learnt it from this book, where it formed part of a very interesting discussion of several related topics.)
Laurens Gunnarsen Says:
February 21, 2008 at 9:20 pm | Reply
I can’t help thinking that this is an especially apposite moment to insert a ringing recommendation for Robert M. Young’s classic EXCURSIONS IN CALCULUS. Not only does the book include the very derivation of Stirling’s formula that Professor Gowers has presented here (on pp. 264-267), but it also offers several different approaches to deriving the deep and powerful Euler-Maclaurin summation formula, of which Stirling’s formula is a straightforward corollary.

In particular, on pp. 354-5 of his EXCURSIONS, Professor Young notes that summing the values of an analytic function f at the first n non-negative integers boils down to finding another function F related to it by

f(x) = F(x + 1) – F(x) = F'(x) + (1/2!)F”(x) + (1/3!)F”'(x) + … ,

since f(0) + f(1) + … + f(n-1) is then just F(n) – F(0). And now, to Euler, the striking formal resemblance between

f(x) = F'(x) + (1/2!)F”(x) + (1/3!)F”'(x) + …

and

y = x + ax^2 + bx^3 + …

naturally suggested solving for F in much the same way as one solves for x in terms of y in a power series of this sort. One simply writes

x = y + ry^2 + sy^3 + … ,

with r, s, … undetermined constants, and substitutes this form into the power series. Then one fixes r, s, … successively by requiring the coefficients of terms of like degree to match on both sides of the equation.

Of course there’s more to it than this in the end, but it’s hard to think of a more straightforward argument for putting

F'(x) = f(x) + rf'(x) + sf”(x) + … ,

and substituting back. And not only does this astonishingly simple idea actually work, it exposes the essence of the Euler-Maclaurin summation formula.
malkarouri Says:
February 27, 2008 at 11:31 pm | Reply
The way I tend to remember this formula is by deriving it from equating the Poisson distribution with mean lambda by a Gaussian with mean and variance lambda. I first found this approach in David Mackay’s Information Theory, Inference, and Learning Algorithms. It is magic alright, but at least it was short enough for me to remember.
I wonder if one substitutes a Binomial distribution instead would one get C(2n, n)?
Dan Romik Says:
March 3, 2008 at 1:33 pm | Reply
Dear Prof. Gowers,

Gil Kalai told me about your demystification of Stirling’s formula. Indeed, this easy result deserves to be better explained and understood, and I recall as an undergraduate I was quite frustrated at not being given a proper explanation for it. Then, about 10 years ago I discovered a new derivation of the constant sqrt(2 pi) which I believe to be slightly simpler than the one you presented, and conceptually better motivated, since it relates to the probabilistic viewpoint involving the central limit theorem. The difference with the approach you and a few of the readers mention is that I look at the cumulative probabilities of the symmetric binomial distribution instead of at just the “local” probabilities. By computing the sum of the first half of the binomial coefficients in a given row in two ways (first, using the obvious symmetry, and second, using a simple integration formula that converges to the integral of the Gaussian distribution), one gets the constant immediately.

My proof appeared in the American Math. Monthly 107 (2000), 556–557, and can be found on my web site. I wonder if you and others will think that my approach is indeed simpler than integrating powers of cosine – I find it hard to be objective about this, but of course both approaches are quite easy. By the way, I apologize for the pompous title of my paper (so pompous that I’m embarrassed to write it here) – in my defense, I was 21 when I wrote it…
gord Says:
April 8, 2008 at 9:43 am | Reply
Back to your question of why should nCr appear in integral of cos^n …
If you look at cos^n [or other functions that approach 1 smoothly & flatly from below…
and you keep reapplying them.. you get something that looks remarkably like a scaled
right half of a normal distribution… [seems to shrink left at 1/sqrt n ]…

My point is, you get the same thing with (1-x^2)^n or exp(-x*x/2) when raised to the n – the normal curve.

So to me, it seems like a product version of the central limit theorem – we keep reapplying by multiplying yet again by something roughly a normal distribution, and converges (nicely!) to the real normal distribution.

Turning the above sentence into math .. ie. stating why in the limit the repeated product converges to a scaled normal distribution… I havent done that yet – it might be obvious to others reading this blog …

Great, stimulating discussion/exposion, thanks!
[apologies for lack of latex]
Richard Askey Says:
July 8, 2008 at 3:40 am | Reply
A proof starting from the integral representation of gamma is given
in Creighton Buck’s “Advanced Calculus”, published over 50
years ago. This was likely not the first place it appeared. One
reason many people who derived Stirling’s formula used a
different argument was the desire for more terms in the
approximation to log gamma.
Neil Says:
August 8, 2008 at 4:29 pm | Reply
Tim,
My favourite derivation of the constant is to look at the ratio of the binomial coefficients to the central binomial coefficient, use the fact that for small x,
(1+x) is very close to log(x), and obtain as a result the central limit theorem
for binomial coefficients directly. Then once you get that the coeffcients are
decaying about the middle like exp(-l^2/n), you compare to the integral of
exp(-x^2), and out pops the constant.
Of course, I each this in a generating functions course, and so I also show them
Euler Maclaurin as the trick to obtain everything but the value of the constant:
I actually use this example to motivate truly understanding the Euler MacM trick.

Neil
Takis Konstantopoulos Says:
October 7, 2008 at 6:42 pm | Reply
I read the interesting discussion on the Stirling formula and
have a few comments.
Tim Gowers’ method starts from the intuitive idea `replace sum by integral’.
It has the advantage that the crude Stirling approximation is obvious.
But the square root term (and the constant) are not obvious.
Besides, it does not give the link to the Central Limit Theorem,
which is the reason why $\sqrt{2\pi}$ appears.
See comments at the end of this, in reference to Laplace. He knew
that Stirling’s approximation is intimately connected with probabilities
of sums of a large number of random variables
and developed a general approximation method in his work on the analytical
theory of probabilities.

David Speyer’s method, starting from $n! = \int_0^\infty x^n e^{-x} dx$,
resembles very much Laplace’s method.
Also, as he observed, the connection to the CLT is apparent.
But there is one thing in David’s method,
which is not very natural.
Namely (following Laplace) it is better to make the
change of variable
\[
t=x/n
\]
first, instead of $t=x-n$. Then the gamma integral gives
\[
n! = n^{n+1} \int_0^\infty (t e^{-t})^n dt
\]
so that
\[
\frac{n!}{n^n e^{-n} \sqrt{n}} =
\sqrt{n} e^n \int_0^\infty e^{-n g(t)} dt,
\]
where
\[
g(t) = t – \log t
\]
is a function with minimum at $t=1$,
and $g(1)=1$, $g'(1)=0$, $g”(1)=1$.
Following Laplace, the action is played by the second derivative of $g$,
so fixing and $\epsilon > 0$ pick $0< \delta < 1$ so that
\[
|g”(t) – 1| < \epsilon \mbox{ if } |t-1| 0$, both bounds converge to zero.
This means that
\[
\frac{n!}{n^n e^{-n} \sqrt{n}} =
o(1) + \sqrt{n} e^n \int_{1-\delta}^{1+\delta}
e^{-n g(t)} dt.
\]
Now write
\[
g(t) = 1 + \frac{1}{2} g”(\tau)(t-1)^2
\]
for some $\tau=\tau(t)$ lying between $1$ and $t$, and therefore
$|g”(\tau) -1| 0$, (iv) the infimum of $g(x)$ over any compact
set not containing $x_0$ is strictly larger than $g(x_0)$,
(v) $f$ is continuous around $x_0$ with $f(x_0) \neq 0$.
Then
\[
I_n \sim
f(x_0) e^{-(n+\frac{1}{2}) g(x_0)} \sqrt{2\pi/n g”(x_0)}.
\]
The proof is along the same lines as in the special case above.

Regarding the connection to the CLT:
Let $X_0, X_1, X_2$, … be a sequence of independent random variables,
all exponential with mean 1:
\[
P(X_j > t) = e^{-t}.
\]
Then $S_n = X_0+ X_1 + \cdots + X_n$ has density
\[
\frac{1}{n!} x^n e^{-x}.
\]
So the density of $(S_n-n)/\sqrt{n}$ is
\[
f_n(x) = \frac{1}{n!} (n+\sqrt{n}~x)^n e^{-n-\sqrt{n}~x} \sqrt{n}.
\]
A local version of the CLT tells us that, for all $x$ (in fact, uniformly),
\[
\lim_{n \to \infty} f_n(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2}
\]
Setting $x=0$ we obtain Stirling’s approximation.
Of course, the heavy-duty machinery invoked is not simpler
than the proof given above.

And here is an exact statement of the LOCAL CLT
(see, e.g. Fristedt and Gray, a Modern Approach to Probability Theory,
Thm 15.9, p.284):

Let $S_n = X_1+ … + X_n$ be sum of independent
and identically distributed random variables, where $X_1$ has
square integrable density, mean $\mu$, and finite variance $\sigma^2$.
Let $f_n$ be the density of $(S_n-n\mu)/\sqrt{n\sigma^2}$.
Then $f_n(x)$ converges (uniformly over all $x$)
to the standard Gaussian density.
Takis Konstantopoulos Says:
October 7, 2008 at 6:52 pm | Reply
Hm… I had no intention in posting a comment with LaTeX code. I saw the earlier comments with nice formulae and thought that there was an automatic LaTeX converter embedded here. Wrong. My apologies.

In fact, I think my posting was chopped!!! So, instead, please click here.

Click to access commentonstirling.pdf

(If someone could tell me how to post properly, I’d appreciate!)

Sorry for the mess above!
Niall MacKay Says:
October 26, 2010 at 5:11 pm | Reply
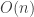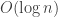Your use of the piecewise-linear interpolation between the integers brings out the $O(n\log n)$ , $O(n)$ and $O(\log n)$ terms so neatly that I wanted it very much to give the 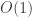$O(1)$ term too — which it does, provided that

$\sum_{r=1}^\infty \{ (r+ {1\over 2})\log(1+{1\over r})-1\} = 1 - {1\over 2} \log(2\pi)$

which is true but which I cannot prove. Taylor-expanding the log and resumming in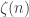 $\zeta(n)$ , $n\geq 2$ , doesn’t seem to help.
zeugirdorcar Says:
March 12, 2013 at 6:12 pm | Reply
Nice. Thanks. I still think the $I_{n}$ integral looks like a rabbit from a hat…. I once saw Stirling’s approx following from Cauchy’s integral formula very naturally but I’ve been unable to reproduce it….. any way http://omega.albany.edu:8008/PascalT.pdf dots all the i’s for Stirling’s & the awsome thing is that with sage it was ALL DONE IN THE BROWSER!
A proof of Stirling's Formula - MathHub Says:
April 7, 2016 at 5:18 am | Reply
[…] need to gain understanding of a proof of Stirling’s formula. I have read through Tim Gowers’ and Terence Tao’s but I’m struggling to follow them. How rigorous is this proof, if at […]