It’s what blogging is all about I suppose, but I have been surprised in several different ways by the comments on my previous post. To begin with, I was so sure of the principle I was advocating that I thought that all I’d have to do was explain it briefly and then anybody who read it would instantly agree with it. That was clearly pretty naive of me, and I certainly didn’t expect that some people would be actively hostile to the idea (though I suspect that their real target was not precisely the same as what I was putting forward). But I was also surprised by the number of interesting further points and qualifications that were made, which I will now try to use to articulate a more nuanced version of the principle.
Amongst these further points were the following. If one is sufficiently used to a particular style of definition then it may well not be necessary to give examples first: for instance, if you know the definition of a field, then you can easily grasp the definition of a ring without having a chat about polynomials or something first. (Of course, if you want to understand the point of defining rings, then such a chat is essential, but it’s not so important to have the chat first.) JSE (who, despite his denials, gave a beautiful demonstration of the principle of examples first in his PCM article) makes the point that some mathematicians find examples confusing unless they already know what they are supposed to be illustrating, and the further point that promising one kind of explanation while one gives another can be very reassuring, whichever way round you do it.
One small point in response to JSE: if you don’t want to confuse the reader/listener when you discuss examples, one approach is not to give away what you are doing. (See your own PCM article for an instance of this.) For example, in the second explanation of fields in the previous post, there is a discussion of number systems. Since it is stating some fairly obvious and familiar facts about those number systems, there can’t really be much reason for confusion. But if one began by saying, “By the way, I’m leading up to a definition of some things called fields here,” then some people might be distracted by wondering what they were supposed to be getting out of the examples.
Another point that comes out of several comments is that a lot depends on the circumstances of a presentation. I think the principle applies most strongly when the presentation is not fully formal — e.g. in an expository article, or a conversation with another mathematician, or a colloquium talk, or in a seminar where you can’t expect too much of your audience. When it comes to a formal lecture course, I think my practice would be to write up fairly traditional notes on the blackboard, but to give a lot of accompanying chat: the preliminary examples would be part of the chat rather than part of the notes. As for textbooks, here there may well be disagreement, but I would argue for something similar to the lecture course approach, except that now the preliminary chat would be written.
On that last point, one person made the interesting comment that they were so used to reading papers and books in a non-linear way that they actually preferred papers and books that did not try to present themselves linearly (which is essentially what one is trying to do with the examples-first approach). My implicit suggestion of clearly distinguishing between the chat and the “real content” could perhaps lead to expositions that gave the best of both worlds.
More generally, one might take the attitude that, since it is an essential mathematical skill to be able to read and digest mathematics that is presented in a very formal way, and since part of that skill is to be able to supply one’s own examples, if you the author provide the examples yourself (whether before or after the generalities) then you are denying the reader the chance to develop that skill. To which I’d say: if you do not provide that chance, there will always be others who are more than happy to do so.
Now let me look at another mathematical concept and consider how it might be explained. This time I want to discuss a theorem rather than a definition, just to emphasize (as I didn’t in the previous post) that the examples-first principle is quite general and doesn’t just refer to places where you first introduce an abstract definition.
The theorem I’ve gone for is the orbit-stabilizer theorem, and I want to discuss how it might be presented to somebody who was already comfortable with the idea of a group action (though it’s quite an interesting question in itself how to explain group actions — in a funny way the examples are all too “obvious” for it to be easy to make clear what the real use of the concept is).
The approach that I’ll label “traditional” for the purposes of discussion is something like this. Let be a finite group and let
be a set on which
acts. Let
be an element of
. Then we define the orbit
of
to be the set
and the stabilizer
of
to be the set
. The orbit-stabilizer theorem states that
. (I stress that I am summarizing the approach here rather than giving it in full: if I did it properly I’d state the theorem more formally and distinguish it much more clearly from the surrounding discussion, which itself would be a bit longer.)
To prove the theorem, we define a map from to the left cosets of
by sending
to
. One must check that this map is well-defined and that it is a bijection, which is an easy exercise. The result then follows from the fact that all the left cosets of
have the same size.
Once one has given this proof in a lecture course, a typical thing to do is to “test the understanding” of the theorem by means of some exercises, of which quite a common one is to count symmetries of Platonic solids. For instance, to count the number of rotational symmetries of an icosahedron, one lets be the group of all these symmetries and lets
be a vertex of the icosahedron. Then the orbit of
(under the obvious action) has size 12, since the icosahedron has twelve vertices that all “look the same” and the stabilizer has size 5 (since neighbouring vertices go to neighbouring vertices and you can’t reflect), so
has size 60.
Now here’s an alternative approach. You begin by asking how many rotational symmetries an icosahedron has (as part of an informal discussion, say, before you “get down to business”). Most people will come up for themselves with the argument that a single vertex has 12 choices of where to go, and one of its neighbours then has 5, after which the rotation is determined: hence, there are 60 rotations.
At that point, one can say, “Now we are going to prove a theorem that shows that this type of argument works very generally.” And as you go through the proof outlined above, you can say, “Notice that in the example we looked at earlier, the orbit was the set of all vertices and the stabilizer was the set of all rotations that fixed a particular vertex.” Then the student will see that what you really need to know is that the set of transformations that send to
always has the same size (which it does, as it’s a coset of the stabilizer). In fact, one is led to a better proof, I think: the result is true because what it is saying is that we partition
according to what the elements do to a fixed element
of
. The cells of this partition all have the same size since they are cosets of
, and obviously the number of them is the size of
.
One could have given that last argument as the proof of the orbit-stabilizer theorem, but its true simplicity is much more obvious if you’ve already experienced it by counting symmetries.
I’ll probably add to this post in due course — perhaps giving a list of circumstances where it may be better not to put examples first.
October 24, 2007 at 1:41 pm |
In regards to the skill development: the skill of being able to read mathematics presented in a very formal way is only necessary because of the way in which certain people write. And I suspect that those people might not feel comfortable writing in the way you advocate, or they realize that doing so will take more time. Instead of just coming out and saying “I don’t want to”, though, they hide their refusal in a screed about “kids these days”. But people have been complaining about “kids these days” for at least a hundred generations or so and yet somehow humanity hasn’t fallen apart.
The problem is that the current situation is at some sort of equilibrium — there’s not a huge amount of incentive for any one individual to write in the way you suggest. But if everyone did, writers might spend a little more time writing, readers would spend a lot less time reading, and since we all spend more time reading than writing, the mathematical community as a whole would save time in the end. (And I’m not even sure writers would spend more time writing. The person doing the writing has already thought of the example; it doesn’t take that long to write it down.)
October 24, 2007 at 1:51 pm |
Well said, Isabel!
October 24, 2007 at 4:08 pm |
Isabel,
I have a colleague (in CS, not math) who reads papers as follows: First he skims the paper by skipping all English and reading only formulas, then he reads the introduction, and then he reads again forcing himself to read some of the English too. I see him doing this every day. Personally, I could never read a paper using such a method.
The point is: People’s opinions differ but, more importantly, thinking processes differ too.
How to use the point to make your article more readable, I don’t know. What I do know is that not all people who write articles incomprehensible to me do so out of laziness.
October 24, 2007 at 5:44 pm |
Dear Radu,
I agree with your last sentence. I know a guy whose most papers
are incomprehensible to the mathematical community, as the tricks
he uses in them have never appeared in print before.
October 25, 2007 at 2:17 am |
My favorite story along these lines was told to me by a student of David Kazhdan. The student once complained to me that Kazhdan was constantly showing the student a math book and saying “You see this book? You should know everything in it. But don’t read it!” This student finally got completely exasperated and asked Kazhdan, “How am I supposed to know everything in it without reading it?”
On a different note, I believe that good math exposition is really not that different from telling a good story, as in a novel or movie. You have to introduce some interesting characters and a conflict that needs to be resolved. You might suggest one or more apparent ways to resolve the conflict and maybe even carry some of them out. After some false starts or apparent obstacles that are overcome, you finally find the way to a satisfactory resolution. Along the way, you might be able to identify some larger principles or ideas that help explain and organize everything that has happened.
The big challenge in modern mathematics is that it often takes a long time just to present the characters (i.e., the definitions and basic properties of the mathematical objects to be studied). It can’t always be done, but I believe a paper or book should, at any point, try to use as few definitions as possible and introduce new definitions only as needed. It is OK to foreshadow events that come later in order to heighten the drama, but it is not OK to present an inventory of all characters and their personalities at the beginning of the story before you have any sense of their roles in the story.
Conversely, I think a good reader should always be trying to outsmart the author, trying to anticipate what is going on, and figure out what is going to happen before the author gets there. This is what I think Kazhdan is referring to. You try to figure out where the author is trying to get to (by peeking ahead if needed) and try to see if you can get there on your own. When you get stuck, you peek at earlier parts of the book to get hints on how the author does it. Sometimes, you’ll succeed in finding your own way there (and maybe even a path that is better than what the author presents). Obviously, this is what *always* happened to Kazhdan. Other times, you end up having to follow the author’s entire path, but you also have developed an understanding of what the challenges are, why what the author does works, and why other paths don’t.
When I was a student, I was completely unable to read a math book linearly without falling asleep almost immediately. So I learned from others to take the approach described above. But I must concede that better mathematicians than me often *can* read math books linearly. I remember a classmate, Amnon Ne’eman, reading straight through Hartshorne (I never got past the first chapter), taking a detour only once to read straight through Matsumura to learn the commutative algebra.
One other point. When I was young, I did most of my learning alone. Now that I am older, I know better. I encourage everyone to do as much learning as possible in collaboration with others. Working seminars on topics of common interest are very powerful means of learning.
October 25, 2007 at 5:44 am |
Dear Deane,
If you are preparing in the graduate school to be just a problem
solver, why burden yourself with learning anything? Going straight
for the answers should give natural solutions, if you believe in
yourself. You can always find collaborators versed in the needed
techniques for a particular proof. And later on you are fresh enough
to have fun from attacking the big ones.
October 25, 2007 at 12:34 pm |
I’d say the Golden Rule of explaining anything is this: Know your audience. I would take very different approaches in the following situations: (1) explaining what groups are to undergraduates who have no experience with axiomatic mathematics, (2) explaining what subgroups are to the same students one week later, (3) explaining a deep piece of mathematics to an expert in that field, (4) explaining the same thing to an expert in a nearby field, (5) explaining the same thing to an expert in a very different field, and so on.
On the other hand, I wouldn’t argue with the statement that it’s always better to have more expository tricks up your sleeve and that with most mathematicians, it’s very easy to find ones they don’t have or to remind them of ones they’ve forgotten about. So representing a particular trick in public is good even when it’s only because the trick is not used as often as it could be. In other words, thanks!
October 25, 2007 at 4:03 pm |
Oops. I must have expressed myself very badly, because the last thing I am is a “problem solver”.
October 26, 2007 at 2:47 am |
@Gower’s:
Just because you’ve admitted to gross inexperience when posting things on the net, I must point out that any hostility that you may or may not have perceived may or may not be real. Text only is a troublesome medium and as such, misinterpretations abound.
A common reason for this is because people don’t actually read what people have written. This may seem odd, but the fact of the matter is that mostly, people only /think/ that they’ve read and understood where they actually haven’t. I can’t tell you how many times I’ve replied with, “Actually I said, …” or similar. There is also the “quick reply”. As in, people don’t really think about what they write, and as such, things come out (far) more aggressive then intended or not what they wanted to say at all. Such is a problem with “brain dumps.” There is also poor wording generated by the prior or generated by cultural differences i.e. what is mean to one isn’t necessarily mean to another.
At any rate, those are just a couple reasons (though *very* common) that things can come off poorly. Certainly, there are countless other reasons. And I know that all of us have been guilty of this (and will be again) whether we know it or not. This is why it is wise to ignore, as much as possible, the perceived tone of a post/email/etc and to just extract the content (unless you personally know the person of course, but even then…). This is especially so with strangers.
I must also point out that blog comments is a *really* poor place to have discussions. They really are only appropriate for passing comments on what had been written. For actual discussions, there are newsgroups, web forums, mailing lists, etc. Each with its own strengths and weaknesses.
I’ll also point out, that you are coming off as really arrogant in that first paragraph (at least to me). I say this because you seem to have the impression that the reason why people disagreed with you is because they didn’t understand what you were putting forth. Well, that and your making an attempt to put forth your “real” principle, which I gather you are just as confident of.
Please note that on the net, people will only consider the idea being put forth, not who is saying it. So, all those “groupies” that you may have, whether students or otherwise, are meaningless here. You’ll get a *far* more honest version of what people think about your idea if only because they have no fear of reprisal (anonymity has benefits, are you sure my real name is Reid?).
Regarding, about the author providing examples.
(Please, note that I’m talking about lectures/texts.)
I can only speak for myself so, I did not (I don’t think so at least nor did I intend to) say that examples should be axed entirely. Just that theorem/proof should come first. Because, IMO, that’s what math really is (though lets not get into the whole whether applied math is math holy war). So, math first, specific examples of the math later. A sort of, here’s the math, now here’s why we care.
Now the “why we care” might be a number system (as in your Field example) or another theorem. There are *lots* of examples of these “work-horse” theorems/lemmas from Elementary Number Theory. So, this approach is more than workable at least as early as 2nd year.
There are very few things in this world that can (and should) be ridged. But, IMO, this is one of them. IMO, doing examples first is “hand-holding” and at the University level this is inappropriate.
continued after Isabel.
@Isabel:
– It is /necessary/ to be able to read math written in a formal way because math is about details not some wishy-washy arts stuff. If we didn’t have the details (e.g. /very/ specific definitions/etc), then we’d run into inconsistencies and things would fall apart “down the road.” i.e. the necessity has exactly /nothing/ to do with writing style but is a side-effect of math itself.
– Your “kids these days” argument doesn’t hold water. I’ve spoken to many Profs on this one and every single one of them has spoken of the fact that the students coming into Universities today have less /knowledge/ and less /skill/ then those of even just a decade or two ago. This can be confirmed by looking at the “dumbing down” of the curriculum of primary and especially secondary education across the board i.e. high-schools have become a place where false self-esteem is developed, not education.
– Your assumption about time taken to write things down and read them is also incorrect. Math takes time to develop and *must* be developed properly. Doing things “by example” does NOT mean that one can side-step rigorous mathematics. Nor does it mean that one can read it faster. Math is math and will be just as hard either way. No method will alleviate the need to work through many many many questions to truly understand what’s what. Nor will any method reduce the time needed.
The only real need is for writers to actually (in the beginning) write out most of the steps required to get to the end of the proof. Then as time goes on to start skipping more and more steps. Because I gotta say, current 1st/2nd year books do a horrible job at this. They either explain every little nuance throughout the book or leave out *way* too much. There are disturbingly few books that actually increase difficulty and reduce “hand-holding” in a remotely balanced way as the book progresses.
– You seem to make the common mistake that people actually learn math from reading. People learn math from doing. Sure, read the chapter. But, that doesn’t actually give you anything but definitions (not necessarily understanding them either). Doing and understanding math requires *working* through the chapter, *doing* those questions at the end of the chapters and *figuring* *out* where one has gone wrong. In light of this and the time required to do this, any reduction of time reading (IMO any reduction is doubtful at best) is insignificant relatively speaking.
There is also the fact that as one gets to higher levels, the ability to just hammer through it gets less and less, and the creative aspect gets more and more. One *cannot* control when creativity strikes when working a difficult problem.
In general, to be able learn to do mathematics properly, one /must/ be able to read a general definition and see that in things and be able to create those things from it (I say things because I’m including not only examples, but other more general structures).
The problem with doing it “by example” is that it caters to a weakness that students already have. Then later on once harder things are taken (e.g. Rudin level Analysis, etc) they not only get hit with actual hard mathematics, but won’t be able to properly deal with it because this crutch of examples first has been taken away from them.
Basically, this examples first method is doing the student a disservice in more ways them one i.e. it actually makes things harder for them later on.
But, this is probably one of those “holy wars.” And given that my time is sparse, I won’t waste my time on discussing this further. But, I will be putting my money where my mouth is later, so anyone who wishes to can poke holes through what I do then.
October 26, 2007 at 10:25 am |
Reid: I’m happy to ignore the perceived tone and try to extract the real content. However, I would just comment that if you use words and phrases with strong negative connotations (such as “very misleading”, “very poor wording”, “insult to the students [sic] intelligence”, “gross inexperience”, “really arrogant”) then the tone, as perceived by me at any rate, will be hostile.
The reason I thought that the target of your hostility (or at least perceived hostile tone) might be something other than my actual views was that there were suggestions in your first comment that you had had bad experiences with a textbook (Gallian — I don’t know the book but if your description of it is accurate then it is not writing in a way that I would advocate, since I don’t think the examples should be a substitute for the theory but rather a preparation for it) and with dumbed-down university syllabuses (in general I am against dumbing down).
On that last point, I think preceding theory with examples makes the theory easier to understand, and therefore in principle reduces the pressure to dumb down a syllabus rather than increasing it. You might regard putting the examples first as a dumbing down in itself, and there I (respectfully) disagree. I think your main point is one that I mentioned in my post: that if you help people too much then they don’t learn to help themselves. I dealt with that rather flippantly by suggesting that since the examples-first approach is not going to become universal any time soon, there will be plenty of other opportunities for students to learn to stand on their own two feet. But suppose it did become a standard convention in mathematics teaching to precede general theory with examples (discussed less formally than the theory and not substituting for it but just preparing for it). How then could one prepare students for the big bad world of papers written in a more formal style, with much less help given to the reader? I suggest that at some point a student could be told, “Up to now, we’ve preceded theory with examples. You’ll find that many authors don’t do that. Therefore it is a good idea not to read papers in a linear way, and to try to supply your own examples to give you an appropriate mental model of a theory if you can’t find them anywhere in a paper. But you may find that they are given just after the theory is presented.”
But it’s important to distinguish two issues. One is the best way of explaining something if you do want to help the reader. That is what I’m really discussing in these posts, and the fact that you describe doing examples first as “hand-holding” suggests that you may even agree with me. The second issue is whether it is good to give help of this kind. Your strong view is that it isn’t. On the whole I think it is: I think from my own experience that I could have learned mathematics much more efficiently if I had been taught in that way. But as you and many others have pointed out in their comments, different people seem to learn mathematics in very different ways, so maybe there is a significant percentage of people who would not find it particularly helpful to have examples first (though if it is done properly then it shouldn’t actually be a hindrance).
October 26, 2007 at 12:38 pm |
You have to realize how this sounds to those of us in the audience who haven’t won the Fields Medal. I think it’s pretty clear that you’re an outlier when it comes to the ability to learn mathematics. The flip side of “know your audience” is “know what your audience thinks about you”.
Another thing I think is falling through the cracks, which echoes James’ earlier comment: what level are you talking about here? If we’re talking about the pedagogy of an introductory calculus class, then using yourself as an example is not going to be very persuasive. If we’re talking about the style used to write papers, then maybe you’re an appropriate example. And of course there’s a gradient in between.
But through these posts it’s very difficult to tell what level you’re thinking of. You use an example from teaching basic algebra, then you talk about reading papers, and then textbooks, and you invoke yourself as an example as if we’re supposed to know what you found difficult, when all most of us know about you is that you’ve been held up as an example of brilliance.
So here’s “examples first” for these posts: before you imply that you, personally, had a hard time learning certain parts of mathematics, humanize yourself by telling an anecdote about something specific you had a hard time learning. Otherwise the typical mental Gowers-image is not “difficulty learning mathematics”.
October 26, 2007 at 1:52 pm |
I have often thought that, in academia, and in mathematics in particular, there is a tendency to conflate a moral issue, teaching a student to ‘stand on his own two feet’ with an essentially amoral issue of conveying information in an efficient manner.
Learning mathematics can be quite challenging and a path rife with failure and therefore there are perhaps very good psychological reasons for this conflation.
However, I think it is a good idea to consider WHY it might be so desireable to teach people to ‘stand on their own two feet’ and WHEN it might be appropriate to do so and to WHOM we think this lesson might actually be valuable if it could be achieved.
When one writes something such as a paper, is it not ones goal to share information as widely as possible? Does this not advance ones career, and increase the possibility that others will use ideas that one has laboured over? Somehow, I think trying to make ones writing a ‘lesson’ to the reader in not having their hands held is inappropriate, counterproductive … and perhaps even a little self righteous.
I think in the context of classes, it should depend on the class and moral implications of ones actions in the circumstance. Let me just address briefy the universe of moral implications as I see them. WHY might it be desireble to teach students to be more independent:
1. Because it’s a good life lesson? If so, then is it really the role of a mathematics instructor to impose life lessons on a student. Is it appropriate? If you view education as a commodity or service, then imagine enduring lectures at the supermarket on how a really indepedent customer would buy fresh vegetables instead of prepared salad? Or better yet if they refused to sell you any prepared food to ‘teach’ you a lesson. If you consider education as sort of like a consultation with a knowledgeable expert, how long would you keep a lawyer who condescended to you in this way?
2. Because it’s a good for learning mathematics? If so, consider the outcome, if fewer people learn mathematics, and they learn it more slowly then what is the point?
3. Because it’s the most effective mindset for mathematicians. Not everyone who takes even graduate courses in mathematics is intending to use mathematics in anything more than a application mode: economists, administrator, engineers, doctors, chemists etc. But ignoring that not insignificant caveat, consider that this is just pratical information about a practical issue: doing mathematics. It has nothing to do with writing or communicating mathematics. The idea that one is communicating in a stupendously inefficient manner in EVERYTHING one does in mathematics because one is trying to convey the subtle moral lesson to all people at all times that they should do their own work … seems sort of silly.
October 26, 2007 at 2:07 pm |
Dear John,
You put me in a somewhat difficult position, since once the phrase “Fields Medal” is in the air, anything I say is liable to sound either arrogant (if I claim for myself some exceptional quality) or falsely modest (if I don’t). So I ask you, and others reading this, to give me the benefit of the doubt if you have criticisms of that kind.
The easiest thing I can do is grant your request for an example of something I had difficulty learning: there is a vast amount to choose from. In fact, I’ve even given you an example already, though I didn’t explicitly say so. When I was taught the orbit-stabilizer theorem as an undergraduate, I found everything about it difficult to take in: what a group action was, the proof of this theorem, what the point of it was, and so on. It was only years later, when I came to give supervisions on courses that included it, that I finally understood two things that made everything clearer (and which would seem utterly obvious to any algebraist). The first was that a group action on , which I had seen defined as a map from
, which I had seen defined as a map from  to
to  with certain properties, could be defined more transparently as a homomorphism from
with certain properties, could be defined more transparently as a homomorphism from  to a group of symmetries of
to a group of symmetries of  . The second was that the orbit-stabilizer theorem was just a more abstract and general version of the way one counts symmetries of Platonic solids and other mathematical objects. Before I had this understanding, the proof of the orbit-stabilizer theorem was something with steps one had to learn. Afterwards, it became a simple idea that I no longer had to memorize, since I could reconstruct the proof whenever I wanted, just by reminding myself what I do for Platonic solids.
. The second was that the orbit-stabilizer theorem was just a more abstract and general version of the way one counts symmetries of Platonic solids and other mathematical objects. Before I had this understanding, the proof of the orbit-stabilizer theorem was something with steps one had to learn. Afterwards, it became a simple idea that I no longer had to memorize, since I could reconstruct the proof whenever I wanted, just by reminding myself what I do for Platonic solids.
This raises an important point. I think what may make some mathematicians learn in a different way from others is that some people find straight memorization easier than others. I myself find it difficult, so I don’t really learn anything properly unless I’ve gone through a sort of personal process of rediscovery. That takes time, and the result for me was that although I did adequately as an undergraduate, I was by no means the top in my year at Cambridge — if you’d like to know, I was 15th in my finals — and after the exams I forgot a lot of what I had crammed into my head. I was drawn to the areas of Banach spaces and combinatorics for two reasons. First, and more obviously, I was brilliantly taught in those areas by Béla Bollobás. Secondly, in both areas there were many interesting problems that one could realistically tackle without having to learn a lot of machinery first. Such success as I have had in those areas is no evidence at all for any ability in learning mathematics, where I think I am pretty average: I’m sometimes quick, especially when I’ve thought along similar lines already, but if the area is completely unfamiliar then I’m not quick at all (relative to other mathematicians).
My undergraduate days left me afraid of many subjects: complex analysis, measure theory, most of algebra and almost all geometry, for example. Little by little I have lost quite a lot of that fear: I was forced to come to terms with complex analysis when I had to teach it, and the same happened with measure theory and some of the more elementary parts of algebra and geometry. Editing the Princeton Companion has helped me a lot too: although I don’t understand all those scary areas like topology, PDEs, Riemannian geometry, and so on, I now know just enough about them to see why they are interesting and important. I think I finally got to grips with the concept of cohomology (of the most elementary kind, I hasten to add) a couple of months ago.
Of course, this is all a side issue really. As it happens, I am quite a good example of the kind of person who is greatly helped by having examples first in order to understand generalities. But my case doesn’t rely on that, so if you don’t believe it then take a look at some of the comments, which suggest that there is a significant percentage of mathematicians who feel the same way, and also take a look at my explanation of why I think it is helpful to have examples first.
October 26, 2007 at 2:45 pm |
Dear Tim,
That’s actually quite interesting as I am currently wrestling with the orbit-stabilizer theorem in particular. In fact, I had decided to spend the weekend thinking very carefully about it and dissecting it. (This should probably please those who advocate independence and self reliance.) I am at the point where I realize all the parts and why they work. (I don’t know anything about platonic solids besides being able to recognize them if I saw them in a picture but) I figure two days of staring at this theorem might just take it from being something I have to memorize to something that seems more intuitive.
Anyway, I like your examples first idea and I believe it would work in most situations most of the time.
I am not sure if you addressed this but sometimes, I find there is a situation where one reads an example and the author says something along the lines of suppose you have some triangles and then suppose you rotate it three times, and suppose you flip it about the bisectors … and the example goes on for a long time like that … and it sort of drives me crazy. I sort of brought this up when you first mentioned the PCM and with linear algebra, that I find it hard to absorb things if I don’t know what the power/scope of the idea is and in a way, an unmotivated example right at the beginning of some text can feel like being read the phonebook.
I think my issue is I memorize better when I understand the motivation of the material and even faster if I understand the underlying mechanism (after all, that means fewer things to memorize.)
October 26, 2007 at 3:25 pm |
Kay, since you don’t insist on self-reliance, let me try to enlarge very slightly on what I said about the orbit-stabilizer theorem. And if you don’t like Platonic solids, let’s just go for the cube (which, though a Platonic solid, does not require you to have a good feel for the more complicated ones). How many ways are there of rotating a cube? Well, if you fix a vertex and a neigbouring vertex
and a neigbouring vertex  , then there are eight vertices
, then there are eight vertices  can go to, and once you know where
can go to, and once you know where  goes to there are three possibilities for where
goes to there are three possibilities for where  can go to since each vertex has three neighbours. Finally, once you have decided where to put
can go to since each vertex has three neighbours. Finally, once you have decided where to put  and
and  the rotation is completely determined. Therefore, there are
the rotation is completely determined. Therefore, there are 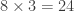 rotations that take the cube to itself.
rotations that take the cube to itself.
Now let us try to look at that in terms of orbits and stabilizers. First of all, when we say, “There are eight vertices can go to,” we are saying, “The orbit of
can go to,” we are saying, “The orbit of  has size 8.” So that part is easy. It’s also easy to see that we can classify rotations according to what they do to
has size 8.” So that part is easy. It’s also easy to see that we can classify rotations according to what they do to  . So let’s write
. So let’s write 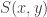 for the set of rotations of the cube that take vertex
for the set of rotations of the cube that take vertex  to
to  . Then obviously the number of rotations is just the sum of the sizes of all the different sets
. Then obviously the number of rotations is just the sum of the sizes of all the different sets 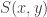 for different
for different  (since each rotation belongs to exactly one of these sets: if it takes
(since each rotation belongs to exactly one of these sets: if it takes  to
to  then it belongs to
then it belongs to 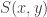 ).
).
Next, we note that one of these sets, , is a subgroup of the group
, is a subgroup of the group  of all rotations of the cube. It is, by definition, the stabilizer of
of all rotations of the cube. It is, by definition, the stabilizer of  . Also, if
. Also, if 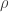 is a rotation that takes
is a rotation that takes  to
to  , then
, then  is equal to
is equal to 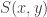 , since a transformation in
, since a transformation in  takes
takes  to
to  and
and 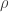 then takes
then takes  to
to  . Therefore, each set
. Therefore, each set 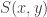 is a left coset of the stabilizer
is a left coset of the stabilizer  (just pick
(just pick 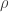 in
in 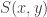 ). Since all left cosets of a subgroup have the same size as the subgroup itself (see the proof of Lagrange’s theorem), we find that the size of
). Since all left cosets of a subgroup have the same size as the subgroup itself (see the proof of Lagrange’s theorem), we find that the size of  is just the size of the stabilizer
is just the size of the stabilizer  multiplied by the number of sets
multiplied by the number of sets 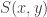 . But there is exactly one such set for each
. But there is exactly one such set for each  in the orbit of
in the orbit of  , so we’ve got the orbit-stabilizer theorem in this instance.
, so we’ve got the orbit-stabilizer theorem in this instance.
But actually, if you look at the proof, you will see that I did not use the fact that was the group of rotations of the cube, or that
was the group of rotations of the cube, or that 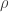 was a rotation. All I used was that
was a rotation. All I used was that  was a finite group that acted on a certain set (which happened to be the cube). So if you go back over the argument and make very small modifications (e.g. replacing the word “rotation” by “element of
was a finite group that acted on a certain set (which happened to be the cube). So if you go back over the argument and make very small modifications (e.g. replacing the word “rotation” by “element of  “) you find that you’ve proved the orbit-stabilizer theorem.
“) you find that you’ve proved the orbit-stabilizer theorem.
October 26, 2007 at 3:28 pm |
And that’s exactly my point: whether or not it’s said explicitly, the phrase is always in the air. Mathematicians reading here know it offhand, and you can’t deny that you get a certain bump in your traffic from nonmathematicians just because of that honor. You get taken as an oracle whether you want to or not. It’s unfortunate that you can’t write from the same semi-anonymity that I can, but it’s just a fact that must be compensated for.
As for the “process of rediscovery” you mention, I agree, but I think it goes the other way was well. I found throughout my undergraduate study that the subjects I understood best were those where I’d read up on the theory for my own interest, and then later took a class in the subject. For me, the theory acts sort of like cement, to which the aggregate of examples is added before pouring it into a concrete foundation.
October 26, 2007 at 3:53 pm |
John, I think you made two points in your earlier comment. One was that I sounded falsely modest. No doubt I do, to some people, for the unfortunate reasons you mention. The other was that I am falsely modest, which I deduce from your saying “It’s pretty clear that you’re an outlier when it comes to the ability to learn mathematics.” However, even if it sounds false, it is in fact true that I am not an outlier of that kind: I know lots of people who are much quicker to pick things up than I am.
I forgot to address your question about the level I was talking about. Actually, I was talking about all levels, from an early undergraduate course through to a research paper. Of course, quite how one chooses to apply the principle will vary from context to context, and sometimes it might be better not to apply it. But, just to put my money where my mouth is, the recent paper I put on the arXiv contains an early section, added at the suggestion of one of the referees, where I discussed how the proof of one of the key lemmas worked in special cases. I hope it will help (some) readers of the paper, but even if it doesn’t, the exercise was extremely useful for me and helped me to re-understand my own result.
October 26, 2007 at 5:15 pm |
John,
I found this blog because it was advertised on Terence Tao’s blog, and I found the later because of the Fields medal. I read them both because sometimes they contain content I enjoy. That is, for the same reason I read all the blogs I read. So let’s please drop this Fields medalist discussion, forget about it when we read future posts, and stick to the subject. Ideas are much more important than people.
Kay,
If you are looking at the orbit-stabilizer theorem you might want to also see how a programmer thinks about it: here is something I wrote long ago.
All,
It seems to me that in discussion participated people that prefer examples first (e.g., Isabel, me, gowers), people that find examples first confusing (e.g., Reid), and people that acknowledge that there are different types of learning. Here’s how I’ll use this information:
1. When I learn math I will look for textbooks written by people that seem to think like me. (That means plenty of examples and exercises.)
2. When I read a paper I shall look for examples first instead of reading linearly (and I’ll also try to do it before reading).
3. When I write something I’ll do it imagining that I explain things to a version of me that lacks a lot of knowledge. (I know there are people that think in a similar way to me, and I’ll probably do a better job trying to explain to them than to others whose thinking I don’t understand.)
October 26, 2007 at 5:48 pm |
Tim, I’m sorry if I gave the impression that I thought you were trying to be disingenuous. I’m really more speaking to the unintended subtext than your actual intent. I’m sure that your intentions are honest, but they are unaviodably colored by their source. Giving the specific example of the orbit-stabilizer theorem goes a long way to backing up what you mean by your difficulty in picking up a concept.
Radu, if you think that the speaker and the medium do not affect communication as much as the ideas themselves do, you’re being somewhat naïve. I don’t go so far as poststructuralists and discount authorial intent entirely, but I recognize that what’s heard and what’s meant can often be at odds. Identifying the sources of such differences is entirely germane to the discussion.
October 26, 2007 at 6:43 pm |
Tim,
Thank you for the explanation. I have printed it out and will think about it carefully. I see why that argument would apply to all the platonic solids so maybe I am not as hopeless with them as I thought. Although, I must confess to reading your explanation several times already, I do think that I am dangerously close to getting how it all works now.
Radu,
Thank you for the link to your explanation. It’s interesting to see things from other perspectives.
John,
I think you were provocative and what you said could have been put more constructively. In a way, it’s a bit of ad hominem which is generally destructive to conversation, especially online conversation. This is not really an argument for NOT bringing up how people are viewed and how that affects what one shares with others … however, it ought to be done carefully IMO. The provocation undermines the true goal of promoting communication and understanding.
October 26, 2007 at 10:37 pm |
I think the dichotomy of opinion concerning the pedagogical principle up for discussion here probably derives at least in parrt from the well known temperamental difference between problem solvers and theory builders.
Some mathematicians enjoy grappling with a problem as an end in itself, while others cannot bring themselves to grapple with a problem until they can see in it the germ of a general theory. Some mathematicians appreciate a general theory as an end in itself, while others cannot bring themselves to study a general theory until they can see in it a tool for solving specific problems.
A specific problem has all the immediacy and vividness of an example. A general theory has all the logical coherence, completeness, and rigor of a traditional textbook exposition. Problem solvers insist on examples. Theory builders may appreciate examples, but they want them properly subordinated to the general theory that accounts for them.
It may seem implausible that even the most extreme theory builder could fail to benefit from the adoption of an examples-first pedagogy of the sort Professor Gowers has proposed. But the following quotation, from a recent AMS profile of Alexandre Grothendieck, suggests that even the implausible does sometimes happen:
* * * *
One striking characteristic of Grothendieck’s mode of thinking is that it seemed to rely so little on examples. This can be seen in the legend of the so-called “Grothendieck prime.” In a mathematical conversation, someone suggested to Grothendieck that they should consider a particular prime number. “You mean an actual number?” Grothendieck asked. The other person replied, yes, an actual prime number. Grothendieck suggested, “All right, take 57.”
But Grothendieck must have known that 57 is not prime, right? Absolutely not, said David Mumford of Brown University. “He doesn’t think concretely….He never really worked on examples. I only understand things through examples and then gradually make them more abstract. I don’t think it helped Grothendieck in the least to look at an example. He really got control of the situation by thinking of it in absolutely the most abstract possible way. It’s just very strange. That’s the way his mind worked.”
* * * *
I suppose persons whose minds work in much the same way as Grothendieck’s must be quite rare, though, so I’m prepared to ascribe a rather low probability to frustrating one’s students by imposing on them lots of unwanted examples. Certainly S. S. Chern adhered scrupulously to Professor Gowers’s favorite pedagogical principle, and I will always be grateful to him for doing so.
(By the way, I very much enjoyed reading Professor Gowers’s own thoughts on the temperamental differences between problem solvers and theory builders in his essay “The Two Cultures of Mathematics.”)
October 27, 2007 at 12:09 am |
One step away from pedagogy, which is how the human mind learns, is
how the human mind thinks. Furthermore, the latter informs and guides
the former. Therefore, I’m eager to “pick the brains” of our esteemed
posters on the topic of how they do mathematics, and solve problems in
general. First off, I’d like to say that I’ve heard the stories about
solving a problem after “sleeping” or “meditating” on it, or while
“strolling in the park”. I’ve also heard the sundry appeals to
“inspiration” or “genius”. However, it seems stories of this sort are
not only unhelpful, but even unscientific, as they suggest the human
thought process is somehow privileged and “magical”, whereas, in a
formal sense, it must certainly follow well defined algorithms and
computational principles. Personally, I think primarily in terms of
analogies, pictures, and simple toy examples that fit entirely in my
“RAM” (short term memory), and very little in terms of actual
computations or logical syllogisms (until the end, when it’s time to
write the paper). One can conjecture that this pictorial style of
thinking arose because our cortex had evolutionarily co-opted the
massive parallelism that our monkey forebears used for visual
processing, to perform more symbolic and abstract processing. Given
that I don’t think in a linear fashion, I also don’t learn linearly,
and I appreciate the confirmations here of the nonlinear reading
method that I have practiced. Now, it seems that even (or especially)
as mathematicians and theoreticians, devoting a reasonable amount of
time to scientifically reflect on our own thought processes, instead
of worshipping our brain as a divine and temperamental black blox, is
time well spent, both for our personal productivity, and for
mathematics as a whole. Please share your “thoughts”.
October 27, 2007 at 12:25 am |
I think the problem, here, is your use of the word “example”. I know exactly where Reid is coming from, and I don’t think it has anything to do with the Fields Medal. You say “examples first” but I think that you are probably mis-speaking and making it sound like you are advocating something other than what you have in mind (based on the examples you give).
What you’re talking about is posing a specific problem, adequately solving it with sufficient mathematical rigor and then going on to generalize the result. That is more like just doing math without examples, actually. Just because it is a special case of some more general principle, that doesn’t really make it what most non-mathematicians, for instance, think of as “an example”. To pick a more widely recognizable example, for instance, I don’t think of the Reimann integral as “an example” of the Lebesgue integral even if it could be construed as a “special case of” the Lebesgue integral. The Lebesgue integral is just a more general way to integrate. You can (and probably should) start out by giving a fairly routine problem of perhaps finding the area under the curve of some mundane continuous function. This problem is completely rigorously solved with the Reimann integral which is a nice intuitive approach to solving such a problem. Then, later on give examples of (really pathological) functions that aren’t Reimann integrable and go on to come up with a way to integrate them using a more general technique. I think “nobody would dispute” that this is how to approach integration. Even fairly radical people that advocate rigorous calculus over the standard freshman calculus sequence will not reject a *rigorous* approach to the Reimann integral first like that. I think what you are talking about is more along these lines, making this kind of distinction between the general and the specific, and you’re saying that we should go from the specific/concrete to the general/abstract rather than just trying to jump to the latter.
However, what Reid has (not altogether unreasonably given some of the posts and what I think is an unfortunate use of terms) taken you to mean is an “examples approach to teaching math”. What that is is more of this empirical approach to math where you pose a problem, look at some of what you consider to be paradigm cases in which the problem arises, see how those examples work out and then start jumping to conclusions about what the actual solution to the problem is, normally without ever even going back to check a more general case let alone actually rigorously defending your solution. Something more like: “Suppose you shoot a cannon ball… And, that’s what it means to integrate a function!” You may even be thinking to yourself: “What? That’s ridiculous!” But, that is how we teach most of the math that gets taught in the world (which is mosly in the service of other fields. And, it seems to me that that sort of thing has really made its way up even to graduate school so that the hapless math majors that just want to do math get smacked down pretty hard, having really just been trained to be engineers all along only to suddenly realize that math is almost nothing like what they had always believed it to be.
You’re use of the word “example” makes it sound like you advocate this sort of thing and that “real math” is this sort of empirical activity where proving theorems isn’t really that important or even nonexistent. It sounds like Reid (and others) might be kind of taking it that way.
October 27, 2007 at 1:22 am |
Someone made the point that math papers should be as precise and formal as possible. I think that in almost all instances, just the opposite is true. We should write the way we think, and that way, we’ll be understood. It’s a disservice both to the reader, and the writer, to write in an overabstract and stylized manner. To the reader, it’s a waste of time, without any improvement to his/her understanding. To the writer, it keeps their work from being understood, used, or appreciated. The amount of time needed to transform a paper from incomprehensible (or strenuously comprehensible) to natural and transparent, is often “second order”, compared to the time to discover the result itself. An obtuse presentation of a good idea, is like spending 100 hours to build a car, then not spending 1 more hour to put in seats and steering wheel.
As to whether examples are always the best way to convey an idea, that varies. Certainly, a *good* example, like a good picture, is worth 1000 words (or several dozen equations). A bad example, on the other hand, might just lead the reader down the wrong track. In addition, examples don’t have to be “concrete”, they just have to be simple, motivating, and illustrative. Sometimes a highly abstract example can satisfy all 3 criteria. To come full circle, I think the best principle might be to keep the presentation “natural”. If a concept or solution didn’t appear in your head fully formed, manicured and axiomatized, don’t present it like it did. Tell us what works, but also say something about what didn’t, and why it didn’t (though don’t go on and on about it). Don’t define something, until you explain why you need to define it, and suggest plausibly why it should be defined a certain way, what defining it this way buys you. Math is hard enough without “laziness”, or macho bravado and other “social” considerations, getting in the way.
October 27, 2007 at 8:00 am |
What did you read that does a nonhorrifying job of presenting cohomology? I’ve tried for years to get a grip on it, and cannot help but get lost in a thicket of alternating algebras, chain complexes, cup products, and precise-but-unhelpful statments that it’s “the dual of homology” and “homology counts holes”. Also “it’s just path integration and Stokes’ Theorem – you already know it.”
James Dolan had a nice series of posts describing the carrying operation in arithmetic as a “2-cocycle”, but I blocked at the stuff on Eilenberg-MacLane spaces. Apparently neither the algebraic-topology view nor the category-theory view can penetrate my skull. Could a devoted reader beg your indulgence in making “What is Cohomology?” the topic of a post?
October 27, 2007 at 10:29 am |
One remark about “examples first” that occurred to me as I read this: depending on context, a terrific place for examples is often right between the statement of a theorem and its proof.
When I first learned real analysis, my teacher presented the material carefully but (to my mind at the time) impenetrably. One day I realized it was all a lot clearer if I specialized the arguments. As a simple example, a theorem about differentiable real-valued functions on an interval might reduce to the case of the behavior, at 0, of a differentiable function f satisfying f(0) = 0 and f'(0) = 0. Cosmetic assumptions like these simplify the difference quotient and make the key issues clearer (to a novice anyway). The “general case” of such a theorem is often the result of composing the specific proof with an affine transformation. The symbols implementing this transformation play no essential role in the argument.
I found it difficult to remember my teacher’s arguments because he insisted on carrying these symbols along for the ride, _every time_. How much easier it would have been for me that semester if his proofs had been prefaced with a discussion of a particular case!
“Examples first” is at the heart of “without loss of generality” (and density arguments). You can state the general theorem, state the example, study the set of transformations of the example that preserves truth of the theorem (or why the conclusion of the proof is “continuous” in the hypotheses), and then write a perfectly formal (and well motivated!) proof of the general theorem.
“Examples first” is well suited to anything that is light on what I might call “essential ideas,” but heavy on notation or abstraction— where the only role of a notation or abstraction is to secure the “generality” of the argument. It is not insulting the intelligence of a reader to supply an example and a proof that the example implies the general theorem; indeed I think that more mathematicians need training in this than they need in working with generalities. (I’m reminded of a preprint where the author spent 4 of the paper’s 16 pages establishing the non-compact case of a theorem that was a near instant corollary of the well known compact case… I think we have all done that at one time or another…)
October 27, 2007 at 4:38 pm |
Adrian, You make an interesting point, and one that seems to back up my hunch that Reid and I were talking at cross purposes. You’re quite right that I could have used the slogan “Go from the specific to the general” instead. But often what I mean by “examples” really is “examples”. For instance, when presenting an axiomatic definition, it can help to have, in advance, a few examples of mathematical structures that satisfy the axioms, so that then one has an idea of the important properties that are being abstracted. Similarly, if a theorem states that every X has property Y, it can help a lot to see the theorem proved first for a specific simple-but-not-too-simple X.
The slogan “Go from the specific to the general” is also open to misunderstanding, though. While I think it helps to know the Riemann integral before you learn the Lebesgue integral (though at Oxford they don’t agree), it’s not really what I’d mean by going from the specific to the general. The Lebesgue integral generalizes the Riemann integral, but most of the definition of the Lebesgue integral doesn’t. (There’s one place where it does: you could say, “For the Riemann integral we approximated by step functions, and now we replace the intervals by more general measurable sets.”) Though I can think of ways of preparing for a discussion of integration by looking at examples, I think this is a case where it may be better just to plunge in with the formal definition, since it’s quite hard to relate the Lebesgue integral to something that a student might already feel comfortable with.
I certainly don’t advocate “Examples only” and I’m not sure how what I wrote can be taken that way, since at all points I was at pains to make clear that my main point was that if you present both a general concept and some examples of it, then it is (very often) clearer if the examples precede the generalities rather than the other way round.
October 27, 2007 at 4:52 pm |
Tim,
Your methods sounds a lot more relaxed, sort of like, lets have a conversation about how these things work. Your method also sounds more like actual teaching! … where as I think maybe I (and who knows maybe even other people here) are used to being merely told about things and not really taught at all.
In my experience, class room time seems short. Things are quite competitive. And most mathematics professors I’ve had, will give you a little time and maybe a little more if you are persistent, but it’s not uncommon to be told to go think harder or something like that and for that to be end of things if you don’t get it. And people fail out when they might not if information was little more available. So the situation is all very arid, and the idea that one would actually have reasonable a chat, where you are given time to figure out why parts work and the professor is monitoring your progress and giving you feedback in how well you are getting the idea boggles the mind.
I think most are thinking, erroneously, that you mean to give an example and then you never get to the most advanced stuff (which they are calling dumbing down.) Or they are thinking, you don’t give the students time to think out the answer but instead blurt it out right away, but I realize now looking at your limits example (from your response to Beans in the other thread) that you do.
So now I think I am convert to what you are envisioning now that I see it in its entirety. (At least I am thinking your suggestion of examples first, suggests an element of interactivity). Even in the case of writing, and your response to Beans bears this out, you were anticipating what people might think and providing good examples. So I think that’s an important element, examples first but interactivity and anticipation seem like they are necessary supplements to this approach.
October 27, 2007 at 8:50 pm |
I was actually meant to comment on something else, but that can wait for later. I am a second year undergraduate student and I have a particularly (annoying habit as some would say) of conversing with my lecturers. I don’t talk to them about maths all the time, but my discussions with my lecturers have definitely motivated me in my studies. Especially two lecturers who continue to motivate me (even though I made one jump by shouting boo the other day, but he tried ‘kill’ me so we are even now!)
Due to this, my fellow undergraduate students have come to the obvious conclusion that I am a freak. I mean, why would I want to talk to my lectures/teachers – they’re not normal! \sarcasm. What could I possibly have to say? I am the one ‘who can be found badgering lecturers with questions.’ That I tend to do, whenever the need arises and that is very often.
The point I am trying to make is that although I treat my lecturers with respect, I also treat them like ‘normal’ people as opposed to others. If we treat someone differently because of a label, I think that says something about ourselves. I haven’t read all the comments in this post, so apologies if I cause any offence. I can’t seem to write what I want to say. *cue for everyone to squash the bean!* but I think when it comes to research, that is a different play ground compared to being an ‘undergraduate and learning maths.’ Both are obviously (potentially!) fun, but require a different mindset. [I think what I am trying to say is, give Professor Gowers a break!]
[Sorry I commented twice, but it was in the wrong post last time – I have too many windows open! Can the other one be deleted? I have done so now — TG.]
October 27, 2007 at 9:47 pm |
My actual comment was regarding what Deane Yang wrote:
“One other point. When I was young, I did most of my learning alone. Now that I am older, I know better. I encourage everyone to do as much learning as possible in collaboration with others. Working seminars on topics of common interest are very powerful means of learning.”
Do you mean undergraduate studies or postgraduate studies? I think learning and understanding mathematical concepts is a solitary task. I will rather lamely say that when I want to commence my private battle with maths, I have to be in an epsilon-neighbourhood! I hate it when my friends are around, and consequently I don’t work when they are. (They don’t understand this, since one of them listens to music whilst studying, and the other two can work in front of the TV too!) It is distracting having them their, and I really can’t get in the zone so to speak. I think this is due to the fact that I tend to ‘talk to myself’ about what I am trying to understand, and I can’t do that with others present. Just me and the maths… sounds great, doesn’t it?! (Don’t freak out just yet – there is more to come!)
Every individual has their own preferred style of learning. The advantages of ‘group studies’ is that you can collectively iron out any creases. However, group studying should come directly after you have had that personal battle with the content yourself, for it should be there to enhance your learning. I wouldn’t recommend doing problems in groups too, unless once again you have really had a good bash at them yourself. In a group your own brain doesn’t take the mental steps that it should to reach the answer. You select the ‘hint’ button, which won’t be available in the exam.
Once when doing some homework on a train, my friend was looking over my shoulder. I wasn’t getting the concept but was following a line of thought and hoping to get somewhere. After one or two scribbles, my friend commented about what I should be doing. My homework disappeard in the next few minutes back to my bag! I was rather annoyed to say the least, but that is another reason for my not being particularly fond of group work. I’ll shut up now…
October 28, 2007 at 6:24 am |
A nice way expressing something touched on here recently occurred to me.
I think there are two important and very different steps in learning: initiation and consolidation. With initiation, the main objective is to convince the student that there is a problem to be described or solved, and here it’s almost always best to give examples. With consolidation, the student needs to understand the tightest way of looking at the phenomena they’re already have some inkling about.
I think both of these are very important and that in a typical undergraduate course, some topics lend themselves better to one approach or the other. For example, with groups most students are not at all used to thinking about abstract sets with operations, so initiation is usually necessary. After they are aware of what they’re supposed to be thinking about, it’s best to consolidate and give them the formal definition. But by the time Sylow p-subgroups come up, for example, the students have seen lots of groups and subgroups, and it really is easier to just give the official definition — a Sylow p-subgroup is a subgroup of maximal p-power order — and then give some examples.
On the other hand, I could imagine some super bright students who were essentially told at some point before their first algebra class that S_n and GL_n are groups but not in so many words. Then they might be ready to skip the initiation phase.
This is just another way of looking at the common remark that the perfect account of a subject once you know half of it is very different from the perfect account when you know nothing.
In my own experience, if I’m reading a paper written in a field I know little about and it’s written in a consolidating style, I often think to myself that I wish the author would just give a few key examples, then I wouldn’t need to read anything. On the other hand, if I’m reading a paper in a field I know something about and it’s written in the initiating style, then I often think that I wish the author would just get to the point before I get bored and find something else to do. One of the issues when writing is to identify your audience and reach the best compromise you can between these two tendencies.
Just my opinion, but I thought some might find it helpful.
October 28, 2007 at 1:16 pm |
James, What you write makes a lot of sense, but I do have two quick points, one where I actually disagree and one where I have an opinion that is consistent with the opinions you express but with which you may not agree.
The first is about Sylow subgroups. When I was taught those as an undergraduate it was in a second course on group theory, so I was very comfortable with the abstract notion of a group. However, for reasons that I can no longer remember, I found the topic hard: I couldn’t see how to use Sylow subgroups to solve problems, I found proofs of the Sylow theorems hard to memorize, I probably didn’t do any questions on them in the exams, and pretty soon after that I forgot the definition of Sylow subgroups (which you have now reminded me of) and the statements of the theorems. It became one of the many topics that I think I could probably appreciate much better now but have never actually got round to doing so.
Why was this? Probably because the lecturer did exactly what you suggest: gave the definition, proved the theorem, and gave some applications, with everything working as if by magic. The trouble with magic, though, is that the only way of learning it is straight memorization, the thing I find hard. I don’t know enough about the topic to know whether this is a practical suggestion, but what about reordering as follows: first state a nice problem in group theory that needs the Sylow theorems, then give a discussion that makes it clear where the need for Sylow theorems arises, and then, once the students actually want to know the theorems and their proofs (which makes them far easier to understand and learn), give them? Perhaps you or someone reading this could come up with a sketch of such an account: certainly I’d love to read one and finally lose my fear of the word “Sylow”.
On your more general point, I quite agree that there is one style for initiates and another for experts. But in my opinion (which I’m sure is not universally shared) it is a sort of bad manners to write a research paper with a fully expert audience in mind. Of course, you can’t introduce every paper with a mini-textbook, but you can give a fairly long and chatty introduction in which you try to explain where your result fits in to your area, what the main new ideas are, which lemmas are fairly standard technicalities, and so on. I think that for a research paper one should have in mind a beginning graduate student or a mathematician from another area who wants to know about yours. What I’m really saying is that I think one should write as near to the “initiates” end of your spectrum as one reasonably can. If an author gives a lot of chat about things that I know well, I don’t find it hard to skip the chat and move to the bit I’m interested in. But if an author gives no chat about important things I don’t know then I’m completely lost. The former seems to me to be by far the lesser evil.
October 28, 2007 at 4:38 pm |
I had been thinking about examples first and I think I do this when I teach also, although I had not been thinking of the instances I use as examples. I however tend to make things more concrete by translating the mathematics into something everyday usually a situation that everybody has found themselves in.
(This example is based on gardening because I think it’s a common enough thing to be doing … but I would typically ask the student what field of study or what kind of activities are they involved in.)
For instance, I typically explain the derivative in terms of doing an experiment. I usually pick a function of interest that the student understands would be changing in very complicated ways. For instance, how much water to add to your vegetable garden and how many vegetables you get to harvest. I usually give an example of how things are nonlinear, for instance, below some threshold, the plants don’t survive at all. Above some threshold, the plants survive but give more produce with increasing amounts of water. And over some threshold, the plants don’t give as much food and eventually die.
So then I say that we don’t know anything about where these thresholds are and that we don’t even know how much water we have to add for a certain amount of vegetable or anything. So at this point, I would introduce the need to look at the change in the function locally… then I say suppose every year you tend to add a gallon of water, what’s the best guess for how much vegetable you will get if you add a gallon more of water? Logically wouldn’t you just look at how much improvement you got when you added the last gallon? In other words, f’ dx is just a guess of delta f(x) and you can see dx as the current change and f’ is the rate of improvement due to the last gallon.
When I try to help non-mathematics people, I find that any mention of secants and slopes makes them panic. Whereas an explanation like this humanizes the process. So in a sense, I would probably never mention secants or limiting processes until, the second or third pass at this idea.
Tim, I agree with the comments on group theory. (I am currently living the definitions for two weeks, followed by theorems for six weeks sort of nightmare.) Although, sometimes I feel your area, combinatorics has a sort of magically feel to it also.
October 28, 2007 at 5:39 pm |
About the Sylow theorems, though I can’t suggest a “simple” statement that shows how useful they are, there is a much simpler (and less abstract) proof of (at least) the existence part which is explained by Serre at the very beginning of old lecture notes of his on group theory (see http://front.math.ucdavis.edu/0503.5154 ): first, one looks at the case of $GL(n,\mathbf{Z}/p\mathbf{Z})$, where the $p$-Sylows exists visibly (e.g. the upper-triangular matrices with 1 on the diagonal), then a simple lemma states that given a subgroup $H$ of a group $G$, and a $p$-Sylow $P$ of $G$, there is a conjugate of it which is a $p$-Sylow of $H$, and then one need only use permutation matrices to embed a group $G$ of order $n$ in $GL(n,\mathbf{Z}/p\mathbf{Z})$ and conclude.
There’s a lot to like in this argument: it uses some important techniques and examples (computing the order of $GL(n,\mathbf{Z}/p\mathbf{Z})$; it gives at the same time some concrete feel for what is a $p$-Sylow subgroup; most of the rest of the Sylow theorems can be “checked” by the students first for $GL(n,\mathbf{Z}/p\mathbf{Z})$, and there, it’s just linear algebra basically (although over a finite field, which may not be the best known at that time)…
October 28, 2007 at 8:14 pm |
Hi Professor Gowers,
As a graduate student who just took my algebra comprehensive exam I’ve thought about the Sylow theorems recently and thought I would share my thoughts with you. What I say should be taken with a grain of salt in light of me not being a group theorist. It’s my impression that part of what makes the Sylow theorems hard to absorb is that their very statements comes out of their proofs. I pesonally could not imagine conjecturing them empirically without *extensive* computations. It’s hard to construct examples of groups with no computer and without knowing the group theory of the late 1800s!
You motivated the statement and proof of the orbit stabilizer theorem by choosing a particular case for which the derivation flowed naturally. I think that the orbit stabilizer theorem is at its core straightforward (only often garbled by confusing exposition) whereas the proofs of the Sylow theorems have moderate irreducible complexity. As such I don’t have a simple case for which the proofs are straightforward that readily generalizes (but I would greatly welcome input from anyone else to this end!).
I think it’s fairly natural to ask for a converse of Lagrange’s theorem. The alternating group on four letters shows the converse is false but the converse seems to hold for a number of other small examples so one wonders if there’s a partial converse. One could imagine conjecturing the first theorem (that there always is a Sylow p-subgroup) in search of a partial converse of Lagrange’s theorem. It’s the other two parts that I have trouble motivating.
I can at least give an example to show how the Sylow theorems can be useful. Lagrange’s theorem shows that a group of order p must be the unique cyclic group of order p because Lagrange’s theorem implies that a group of order p has only the two obvious subgroups so any nontrivial element must generate the whole group (else it would generate a proper, nontrivial subgroup!).
What about groups of order pq (say, for p and q distinct primes), are they always cyclic? No, the symmetry group of an equilaterial triangle (and more generally, of a p sided regular polygon) are counterexamples. Nevertheless, one might notice that lots of groups of order pq are cyclic. It would be good to have a theorem that gave us a sufficient condition on p and q that would guarantee that the group is cyclic.
Given a group G with |G| = pq, if we could show that G has subgroups of order p and q that are in fact normal then it would follow that G is cyclic. Why? Two subgroups of relatively prime order must intersect trivially (since if an element is common to the two groups its order divides the order of each of the two groups) and if two normal subgroups of a group intersect trivially they must commute past each other. So if x generates a normal subgroup of order p and y generates a normal subgroup of order q then xy generates a subgroup of order pq.
So the question is: when does G have normal subgroups of orders p and q? G will always have subgroups of order p and q. This follows from a special case of the first Sylow theorem proved by Cauchy in the context of permutations (I don’t remember his proof). When are the subgroups normal? One of the other Sylow theorems says that all of the subgroups of order p (resp. q) are conjugates. A subgroup is normal if and only if it gets conjugated to itself (this is just the definition of normal subgroup). So if there is only one subgroup of order p (resp. q) then the subgroup will be normal.
So we would like to get an idea of how many subgroups of order p (resp. q) there are: can we prove that this number is always 1? No, in fact sometimes there are more (the symmetry group of the equilateral triangle has three subgroups of order 2). However, we can get strong conditions on the number of subgroups of order p (resp. q): the final Sylow theorem says that the number n of subgroups of order p satisfies n|q and n = 1 (mod p). From the first condition, n = 1 or q, so the only way for there to be more than one subgroup of order p is if q = 1 (mod p). Similarly, the only way for there to be more than one subgroup of order q is if p = 1 (mod p).
So if p and q are distinct primes such that q is not 1 (mod p) and p is not 1 (mod q) then there is only one subgroup of order p and one subgroup of order q, since each of these conjugates to itself the two subgroups must be normal and they commute past one another so G is cyclic of order pq.
So Dirichlet’s theorem for primes in arithmetic progressions gives that for most pairs (p, q), there is just one group of order pq: the cyclic one. In general there can be up to two groups of order pq: if p = 1 (mod q) (for example) there really always is a nonabelian group, but only one. This can be shown using semidirect products, but I won’t pursue this line of thought further because it’s tangent to the immediate discussion of the Sylow theorems.
This preceding discussion assumes comfort with the idea of a normal subgroup. I can use normal subgroups but I don’t have a full appreciation for why the idea is natural. John Baez has a nice geometric explanation in one of his discussions.
October 29, 2007 at 10:06 am |
Tim,
Thanks for your comments. On your first point, it does go against what I wrote, but I confess I can’t really disagree with it, maybe because you reminded me that I myself forgot everything about Sylow subgroups in the years between the undergraduate algebra class I took and the one I first taught! Maybe after further reflection I’ll come to agree with you completely on this.
On your second point, I do essentially agree, but there are technical results of no interest to non-experts, and I wouldn’t say that these papers must have introductions readable by non-experts (but in that case, they should give a reference to where a non-expert can learn the necessary background). On the other hand, I would guess that people usually overestimate by a big factor how many people can read their papers, so it is a decent rule of thumb to attempt to write your introduction for non-experts.
October 30, 2007 at 4:24 am |
Among the examples we might choose to illuminate a mathematical idea are those that engendered it. Often these examples are the easiest for a beginner to assimilate, since they were the very examples from which the original beginners drew their inspiration. Sometimes they’re profoundly encouraging, too.
When Leonhard Euler took up number theory, he set for himself the task of proving the assertions that Fermat had recorded in the margins of his copy of Bachet’s Diophantus. Among these assertions were some concerning those whole numbers that can be written as one square plus some fixed, positive, non-square multiple of another square (i.e., those n = x^2 + dy^2.)
Now, one of the most striking things about numbers of this sort is that they are closed under multiplication. But from this it does not follow that every prime divisor of n = x^2 + dy^2 must also have this form — and indeed Fermat himself had pointed out that, in particular, 21 = 1^2 + 5*2^2 = 4^2 + 5*1^2, even though neither 3 nor 7 can themselves be written in the form x^2 + 5y^2.
Concerning 21 and its analogues, Fermat left behind the cryptic remark that, in general, they arise from multiplying together primes of the form 20n + 3 and 20n + 7. But Euler seems not to have noticed this, for he made his first foray into this subject by publishing a paper that asserted, among other things, that all primes of the form 20n + 1, 20n + 3, 20n + 7, and 20n + 9 are also of the form x^2 + 5y^2.
Now, this assertion is both false and misleading — that is, it is false in an essential way. Primes of the form 20n + 3 and 20n + 7 are always of the form 2x^2 + 2xy + 3y^2, and never of the form x^2 + 5y^2, as was already clear to Fermat. These two quadratic forms are, in a deep and important sense, two halves of a whole. Like the Colonel’s lady and Judy O’Grady, they’re sisters under their skin.
Of course Euler later corrected himself, maintaining that only 20n + 1 and 20n + 9 primes are of the form x^2 + 5y^2, and adding that if a prime p is of the form 20n + 3 or 20n + 7, then it is not p itself but rather 2p that can always be written as x^2 + 5y^2. The fact remains, though, that even the great Euler began his work in this area by asserting, in print, a result so obviously false that a second-grader can easily disprove it.
So an example like this serves not only to illuminate the ideas of a unique factorisation domain, and of a maximal ideal, and indeed of much of the non-trivial content of an undergraduate course on ring theory, all of which can be traced back to it and to others essentially like it, but also to convey the crucial lesson that even the greatest mathematicians blunder, and blunder in essential ways.
The important thing in mathematics is that blunders like Euler’s are, in a certain sense, self-correcting: just keep thinking and investigating, just keep your wits about you and your eyes open, and eventually you’re bound to notice them. As a mathematician, you can make all the mistakes you want, and still achieve profound and important things. If only you continue relentlessly to probe and question the consequences of your conjectures, you won’t stay confused or deluded indefinitely.
So an example like this teaches not merely ring-theoretic lessons, but moral and heuristic lessons too. What’s not to like?
October 30, 2007 at 7:24 pm |
“Zoologists maintain that the embryonic development of an animal recapitulates in brief the whole history of its ancestors throughout geologic time. It seems it is the same in the development of minds. The teacher should make the child go over the path his fathers trod; more rapidly, but without skipping stations. For this reason, the history of science should be our first guide.”
“Our fathers thought they knew what a fraction was, or continuity, or the area of a curved surface; we have found that they did not know it. Just so our scholars think they know it when they begin the serious study of mathematics. If without warning I tell them: “No, you do not know it; what you think you understand, you do not understand; I must prove to you what seems to you evident,” and if in the demonstration I support myself upon premises which to them seem less evident than the conclusion, what shall the unfortunates think? They will think that the science of mathematics is only an arbitrary mass of useless subtleties; either they will be disgusted by it, or they will play it as a game and will reach a state of mind like that of the Greek sophists.”
“Later, on the contrary, when the mind of the scholar, familiarized with mathematical reasoning, has been matured by this long frequentation, the doubts will arise of themselves and then your demonstration will be welcome. It will awaken new doubts, and the questions will arise successively to the child, as they arose successively to our fathers, until perfect rigor alone can satisfy him. To doubt everything does not suffice; one must know why he doubts.”
— Jules Henri Poincare
October 30, 2007 at 7:39 pm |
Laurens, I enjoyed your two last comments and I agree with them. You were careful to say “Among the examples we might choose” at the beginning of your first comment, and I think that’s important too, because another way that I think works well is to create fictitious histories of mathematical concepts and theorems. That is, if you can explain a line of thought that it is easy to imagine somebody having, and if you can show that it leads naturally to a definition that would otherwise seem rather strange and arbitrary, then this can be extremely valuable even if it has nothing to do with the actual history of the concept. I’ll try to give an example of this in a future post: I’m thinking of following a suggestion in one of the comments and explaining why I am no longer afraid of cohomology. Basically, the explanation I have in mind is a fictitious history of this kind.
October 30, 2007 at 9:40 pm |
Thank you, Professor Gowers, for your kind and encouraging response. I’m eager to stress that I too enjoy and approve of fictitious histories as pedagogical devices, and I use them whenever I can. But the trouble is that all too often it’s hard to see how to devise one — and that’s why I find it comforting to reflect that we can always look for pedagogical inspiration to the actual history of the result we aim to convey.
For plainly every such result was at one time unknown, and only became known when some particular individual discovered it. And although history sometimes reveals that that result was deeply mysterious even to its original discoverer, who stumbled upon it entirely by chance, we find far more often that he had a perfectly clear idea in mind, and an equally intelligible reason to imagine that success might crown his efforts.
Sharing the ideas and the expectations of that discoverer, and most especially the particular examples and problems that engendered them, can sometimes work veritable pedagogical miracles. And the great thing is that, when our own pedagogical ingenuity fails, these resources are always available to us.
But probably the best argument for recourse to history as a source of pedagogical inspiration is Leibniz’s:
“It is most useful that the true origins of memorable inventions be known, especially of those which were conceived not by accident but by an effort of meditation. The use of this is not merely that history may give everyone his due and others be spurred by the expectation of similar praise, but also that the art of discovery may be promoted and its method become known through brilliant examples.”
October 30, 2007 at 10:43 pm |
Laurens: Poincaré’s endorsement notwithstanding, ontogeny has not recapitulated phylogeny for a very long time indeed.
Besides which, maybe at the end of the 19th century mathematics could be seen as a tree, but it certainly can’t anymore. The phylogenetic tree has only one path from the root of life to the developed organism, and so at least the maxim is somewhat plausible. But how are we supposed to remotely follow the development of mathematics in anything approaching the historical order within the context of separate classes? Shall we insist that students learn Fourier analysis before we teach them about transfinite cardinals, for example?
This is where the suggestion of “fictitious” histories becomes essential: we can motivate transfinite arithmetic without reference to summing trigonometric series, even though that problem was what drew Cantor to the subject. Similarly, we can discuss groups without mentioning field extensions, and field extensions without mentioning the general quintic.
David Corfield spoke of research, but it works for pedagogy as well: what we need to do is not to tell histories, but to tell good stories.
October 31, 2007 at 12:19 am |
I have been following these discussions with great interest.
I need to stake my tent on the “examples first” side.
First, I enjoy reading texts that give an intelligent and curious novice some hints about the material and context, then precede to the lofty heights of the topic. I have taught myself many subjects by seeking out books with precisely this approach.
However, I must say that I am glad that all writers do not adhere to an examples first pattern. My very favorite mathematical books of all, my “comfort books,” proceed in the opposite manner. I think of Rudin’s “Mathematical Analysis”, or perhaps even Euclid’s “Elements”. I sometimes find myself seeking the shelves for books that tackle other mathematical topics in such a perfect, orderly, logical, and suspenseful manner; but I am usually disappointed.
I guess that the theorems and proofs first approach just isn’t worth doing unless it is done perfectly.
October 31, 2007 at 6:22 am |
Regarding fictitious histories, I’ve heard people call them “creation myths”, which I think is wonderful. I think the usage is due to Jim Dolan.
October 31, 2007 at 7:45 pm |
I strongly agree that what we want to do as mathematical pedagogues is to tell good stories. Indeed, this seems to me not only desirable but essential. For mathematics is simply too hard, and too frustrating, to do out of a mere sense of duty. What compensates for the difficulty of mathematics is the fascination of mathematics, and the only effective way of conveying this fascination to beginners is through the vehicle of storytelling. As mathematical pedagogues, we want not only informed students but fascinated students. For only a fascinated student can give to the art all that it demands of him.
One obvious source of powerful and engaging stories is history, but it’s certainly not the only source. As I’ve already stressed, I’m all in favour of good fiction; indeed, I agree with Hemingway that the best fiction can be truer than history. As a student, I’ve enjoyed and profited from many ingenious mathematical fictions (for example, Professor Gowers’s “How to Invent Some Basic Ideas of Galois Theory.”) I certainly do not insist that as teachers we must always tell the truth, the whole truth, and nothing but the truth.
But whether we tell true or fictitious stories, I maintain that we ought to embrace Plutarch’s stated objective of encouraging the emulation of the admirable behaviour that our stories depict. Yes, it is essential to persuade our students that mathematics is fascinating, but this alone is not enough. We must also encourage them to view the actual doing of mathematics as a practical human endeavour, to which they might reasonably hope one day to contribute themselves. This, it seems to me, is the intent behind that remark of Leibniz’s I quoted earlier. As teachers, we tell these stories “so that the art of discovery may be promoted, and its method become known through brilliant examples.”
Of course there are various interesting compromises we might make as mathematical storytellers between adherence to historical facts and the invention of illuminating fictions. For my part, I’m very strongly attracted to one such compromise, which Otto Toeplitz called the “genetic approach.” As Harold Edwards describes it, Toeplitz’s genetic approach
“…look[s] to the historical origins of an idea in order to find the best way to motivate it, to study the context in which the originator of the idea was working in order to find the ‘burning question’ which he was striving to answer. In contrast to this, the more usual method pays no attention to the questions and presents only the answers. From a logical point of view only the answers are needed, but from a psychological point of view, learning the answers without knowing the questions is so difficult that it is almost impossible.”
Edwards adds:
“It is important to distinguish the genetic method from history. The distinction lies in the fact that the genetic method primarily concerns itself with the subject…whereas the primary concern of history is an accurate record of the men, ideas, and events which played a part in the evolution of the subject. In a history there is no place for detailed descriptions of the theory unless it is essential to an understanding of the events. In the genetic method there is no place for a careful study of the events unless it contributes to the appreciation of the subject.”
“This means that the genetic method tends to present the historical record from a false perspective. Questions which were never successfully resolved are ignored. Ideas which led into blind alleys are not pursued. Months of fruitless effort are passed over in silence and mountains of exploratory calculations are dispensed with. In order to get to the really fruiful ideas, one pretends that human reason moves in straight lines from problems to solutions. I want to emphasize as strongly as I can that this notion that reason moves along straight lines is an outrageous fiction which should not for a moment be taken seriously.”
By eliminating all the dead ends and false starts from its account of mathematical discoveries, the genetic approach saves precious time. But I agree with Edwards that it is essential occasionally to include anecdotes like the one I mentioned in an earlier post, showing that even the greatest mathematicians make mistakes, and that making mistakes is not fatal.
For, as Laurent Schwartz once noted, to discover something in mathematics is to overcome an inhibition — and, for most students, fear of error is a crippling inhibition. It is perfectly fine to offer our students well-constructed fictions. But I maintain that we also want to do whatever we can to moderate the outrageousness of our fictions.
November 1, 2007 at 3:25 am |
I see a request for a discussion on clear explanation of “what is cohomology and why is it worth doing”. I second this! More generally, I think what causes a lot of pain when learning many areas of modern mathematics is the concept of a space of dual objects. For example, the whole theory of distributions in functional analysis and linear PDE’s. In differential geometry, the whole notion of differential forms can be rather painful to learn. And the ultimate example is of course cohomology in topology.
Dualization is a rather simple idea but I think it is perhaps one of, if not the, most powerful tools in mathematics, especially in the modern era. There is, I’m sure, a good story about why. Perhaps someone can explain or tell me where to find an explanation? (I vaguely remember reading one or more but I am now too old to remember where)
November 1, 2007 at 7:56 am |
If you already understand the basics of calculus on manifolds, then at least the de Rham cohomology theory (which seems, historically, to have been the first to appear) isn’t especially obscure. Assuming those basics, I’d be glad to provide an illuminating sketch of the de Rham theory.
But would that really be helpful? Or is the problem more with the basics of the calculus on manifolds? The crucial thing to recognise is that it is exactly the differential forms on a manifold that can be differentiated and integrated in a coordinate-independent way. If that much is clear, then the rest is fairly easy.
November 5, 2007 at 3:42 am |
Oh, I know the details of cohomology and differential forms rather well. That’s not what I was asking for.
What I bothers me is that I “know” these subjects only out of familiarity. Details that made me uncomfortable when I first learned these subjects have become comfortable only because I have been working with them for such a long time.
But I would love to see a higher level “meta” discussion of why it is so fruitful to dualize things. You can do all of differential and Riemannian geometry working with only vector fields and the tangent bundle. Or you can dualize and work with differential forms instead. With vector fields, you have to deal with the Lie bracket; with differential forms, you use the exterior derivative instead.
Most geometers learn to use a blend of the two; some things are just best done with vector fields (see the book by Cheeger and Ebin for a beautiful exposition of some of these things), and others with differential forms.
The most extreme example I know in differential geometry are the Maurer-Cartan equations for a Lie group. It is easier to see where these equations come from when written in terms of invariant vector fields, but you’d never want to use the equations in those form. The equations written using invariant differential forms lead to easy derivations of the foundations of many (nearly all?) aspects of differential geometry.
But why is there such a difference between the two approaches? They are formally the same, and you could literally force yourself to always work within one framework or the other. It is in fact an extremely instructive exercise to figure out how to do this in principle; you quickly gain an appreciation of the power of each approach.
In other words, I would like to see a philosophical discussion of when one approach is better than the other and, in particular, when dualization makes things easier. I don’t know that this would be useful when teaching differential forms, but I think it could be. Learning differential forms for the first time is rather painful because you are dragged through a lot of multilinear machinery without any clue to why it is all needed. It would be nice if some better motivation could be provided at the start.
I suspect that I am asking for something that is well known already, so if anyone wants to remind me where, I would be grateful.
November 5, 2007 at 4:36 pm |
Dear Deane,
Do you have any advice of the ‘meta’ kind about how to go about learning differential geometry for a beginning graduate student interested in doing some self study? Also, any suggestions on good books? Thanks.
November 5, 2007 at 7:08 pm |
Kay, I’m sure Deane will have many useful and interesting suggestions to offer you, and I know you didn’t ask me, but I hope you won’t mind my tossing out a few ideas about books for the beginning would-be differential geometer, and about how to study the subject. I absolutely love differential geometry, and I had a wonderful time learning it, too; I’m convinced it’s possible to enjoy the experience. I’d like you to have every bit as wonderful a time as I did.
It was my extraordinary good fortune to learn differential geometry from S. S. Chern, one of the great 20th-century masters of the art. Sadly, Chern is now no longer with us. But if you look him up in the Mathematics Genealogy database, you’ll see that Chern was also an incredibly successful advisor of graduate students, which helps to explain why the influence of his pedagogy and his particular way of thinking about the subject is so very widely disseminated throughout the mathematics community. Chern wrote relatively few books himself, and none of them really for beginners, but his students wrote a great deal, and much of their stuff captures his spirit very well indeed.
An example of an excellent book by one of Chern’s students is Manfredo do Carmo’s DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES (and in fact this is the book Chern himself used as the text in the first geometry class I ever took from him.) It has many virtues and few faults, but one of these latter is price; it horrifies me to think that the book now sells for $128. On the other hand, do Carmo’s slightly more advanced book, RIEMANNIAN GEOMETRY, is also excellent, and sells for a mere $40, so I suppose that is at least some compensation.
I’m almost embarrassed to make so routine a suggestion, but have you looked at Bishop and Goldberg’s TENSOR ANALYSIS ON MANIFOLDS? Even after all these years, it remains one of the very best books for beginners, and it remains available as a Dover paperback, for just $13. (The traditional alternative, Boothby’s AN INTRODUCTION TO DIFFERENTIABLE MANIFOLDS AND RIEMANNIAN GEOMETRY, is also excellent, but it’s five times as expensive.) Bishop and Goldberg does a reasonably good job of introducing the basics intelligibly, and it sometimes manages to make them attractive, too.
Another wonderful place to get started with many of the same things is the superb book ADVANCED CALCULUS, by Loomis and Sternberg, which, though long out of print, is available as a free PDF right here:
http://www.math.harvard.edu/~shlomo/
Of course this takes up some 58 megabytes, which is a fair chunk of hard drive space for a book. And it’s true that much of the material in it is not strictly speaking differential-geometric. But I’m pretty sure you’ll find it’s worth every bit, even if you already know all the early stuff backwards and forwards. For the beginning differential geometer, the final few chapters are really fine.
Oh, and finally, there’s Spivak’s COMPREHENSIVE INTRODUCTION TO DIFFERENTIAL GEOMETRY, which may really be the best place to start. I think Volume 2 is the jewel of the whole epic series, and I’d propose that you might at least try taking it up first, referring back to Volume 1 (which is much less interesting) only as necessary.
What makes Volume 2 so fascinating is the explanations it gives, first of Gauss’s original monograph on differential geomety, and then of Riemann’s inaugural lecture, “On the Hypotheses that Lie at the Foundations of Geometry.” Spivak translates these extraordinary works — not merely the words but the ideas — into lucid and appealing English, and reading them with his assistance is a revelation and a thrill.
But wait! There’s more! Spivak’s Volume 2 also provides a very clearly motivated introduction to Cartan’s “moving frames” approach to differential geometry, which, as Spivak explains, provides the inspiration for the very deep and far-reaching idea of a principal fibre bundle.
So, as I say, it may be that Volume 2 of Spivak’s COMPREHENSIVE INTRODUCTION is really the single best place to look for differential-geometric enlightenment. But it may not be feasible to learn from it the Cartanian stuff without first digesting a fair amount of Bishop-and-Goldberg-style preliminaries.
And as for the best way to go about learning the subject, well, I can only relate how Chern taught it, which certainly worked for me (and, as the Mathematics Genealogy database attests, for many, many others.) But since this post is already over-long, I probably ought to pause first, and see whether you think that might be of interest.
November 5, 2007 at 7:42 pm |
Laurens,
It was a general question definitely. I asked Deane because I know he works on this. Your answer is amazing and I appreciate it deeply.
Kay
November 5, 2007 at 9:53 pm |
Laurens,
One of the things that prompted me to ask my original question is Deane’s comment that:
“Learning differential forms for the first time is rather painful because you are dragged through a lot of multilinear machinery without any clue to why it is all needed.”
Indeed this would accurately describe my experience so far.
I will check out the books you’ve mentioned so far. Most I have never heard of except for Spivak and Tensor Analysis on Manifolds. But I don’t know anything about any of them so it will be interesting.
It would be interesting also to hear your overview of the subject, what the major ideas and which ones can be expected to fit together as I learn more about the subject. I find statements of this sort:
“You can do all of differential and Riemannian geometry working with only vector fields and the tangent bundle. Or you can dualize and work with differential forms instead.”
intensely interesting.
November 5, 2007 at 10:26 pm |
I’d like to second Laurens’ suggestions. I picked up B&G on my own back in high school and worked through it on my own. Then I had Riemannian Geometry as the course text for a course on that subject as an undergraduate with Rich Schwartz. And then the whole of Spivak really solidified differential geometry for me.
The one thing I’d suggest adding for more of a practical nuts-and-bolts approach is the “Phone Book” — Misner, Thorne, and Wheeler’s Gravitation. The two-track approach is especially useful in the part where they work through the basics of differential geometry. That, then, leads me to suggest Baez and Dolan’s Gauge Fields, Knots, and Gravity, which gives a great feel for the use of principal bundles in Yang-Mills field theory.
November 6, 2007 at 3:31 am |
Kay, I’ll respond more fully tomorrow, but for now let me just quickly say that once you’re doing Riemannian (or symplectic) geometry, as opposed to mere differential topology, it’s really rather pedantic to bother to distinguish at all between covariant things (like, e.g., differential forms) and contravariant things (like, e.g., vector fields.)
The reason for this is hardly obscure. It’s just that, because you’ve chosen to study a Riemannian (or symplectic) manifold, you have in each tangent space a non-degenerate binary form, called the Riemannian metric (or the symplectic 2-form.) And of course this means that everything you do in this context is automatically compatible with, and respects completely, this special additional structure you have.
Now, given this binary form, whose value at the pair of vectors u, v you might as well write as , you can easily exhibit an isomorphism between vectors and dual vectors: the dual vector corresponding to the vector u is just the linear mapping v –> . As you can easily check, the non-degeneracy of the bilinear form ensures that this association of vectors and dual vectors really is an isomorphism.
So in any context where the manifolds you’ve chosen to study all come equipped with additional structure of this sort, vectors and dual vectors are bound to be as like as a row of pins. Which you choose to adopt matters only if you’ve become attached to some system of notation that makes one easier to work with than the other.
November 6, 2007 at 3:34 am |
Hmm. Sorry about that, Kay: I didn’t mean to employ typography just now that would baffle WordPress, but that seems to be what happened. So lemme try writing that bilinear form in each tangent space as ( , ), and its value at u, v as (u, v). Then the isomorphism I was trying to point out to you looks like v –> (u, v).
I hope that helps!
November 6, 2007 at 3:38 am |
Oops. OK, just one last footnote, to be extra-careful: the isomorphism I have in mind maps the vector u to the dual vector v –> (u, v). I hope this is clear.
November 6, 2007 at 6:22 am |
Hi Laurens,
I am not sure I get your last explanation. I get vector spaces and the dual of a vector space and I know how all that relates to the bilinear form. Unfortunately, I do not have a good grasp on what a 2-form or binary form or any kind of differential form is. I am also, sorry to say, not quite clear on contravariants versus covariants. When I read about them, I was confused in that the seemed very similar and I wasn’t sure why they were making a distinction between them.
November 6, 2007 at 7:52 am |
Kay, I slightly disagree with Laurens on this point, or at least I think the pedantry is valuable. The reason why is the answer to your question.
The difference between covariant and contravariant quantities is how they behave under smooth maps. Vectors “push forwards”, while functions and other p-forms “pull back”. That is, if I have a smooth map between manifolds, then any tangent vector on
between manifolds, then any tangent vector on  is mapped to a tangent vector on
is mapped to a tangent vector on  in a natural way. On the other hand, any function on
in a natural way. On the other hand, any function on  induces a function on
induces a function on  by composing with
by composing with  . Vectors get pushed in the same direction as points do, while functions get pulled back in the other direction. That’s the difference.
. Vectors get pushed in the same direction as points do, while functions get pulled back in the other direction. That’s the difference.
November 6, 2007 at 6:30 pm |
An example for example
Tim Gowers has two very interesting posts on using examples early on in a mathematical exposition of a subject. I can only second that and say that this is my favorite way of understanding mathematical concepts: Try to think through the simplest non-…
November 6, 2007 at 8:02 pm |
Lots of great stuff here, and I have my own strong opinions them. Which means I respectfully disagree with Laurens on many of his points. This is not to say that one of us is right and the other wrong, but I see things quite differently. One point of common ground: One of the biggest influences of my life was when Chern came to Penn while I was an undergraduate and gave the Rademacher lectures. In fact, it was during these lectures that I first learned the method of moving frames, which I found to be a great relief after trying to read Do Carmo (I’ll have more to say about this later). Also, there was a short period when Chern would visit Houston regularly while I was at Rice, and I am proud to say that I often served as Chern’s chauffeur during his visits.
One quick point: It is indeed popular for many Riemannian geometers to identify the tangent and cotangent bundles via the Riemannian metric and to view them as almost the same object. For me, this eventually led to complete confusion when I was doing computations. I finally learned to keep the two separate and never confuse one with the other. There are many reasons for this. One, for example, is the day you want to work without a Riemannian metric or you want to work with a whole family of Riemannian metrics (this would be the case with the Ricci flow). In that situation, the identification of the tangent and cotangent bundles only becomes a hindrance and not at all a benefit.
November 6, 2007 at 8:06 pm |
Sorry. I meant to say: I’ll have more to say when I find the time.
November 6, 2007 at 10:24 pm |
Some comments about learning elementary differential geometry:
1) After rereading Laurens’ recommendations, I would have to say that they are pretty good. My main disagreement is the recommendation of Spivak. Spivak was really a differential topologist, so he emphasizes issues that mattered a lot to differential topologists way back when but are not really worth so much effort today. For example, he makes quite a big deal about what the tangent bundle is but ends up making it look a lot more mysterious than it really is.
2) You definitely want to have multivariable calculus, especially the change of variable formula for an integral, under control before you venture into differential geometry. I have never looked at Loomis and Sternberg but I suspect Laurens is right about it. Another book that I know little about but seems attractive is the one by Edwards, because it introduces multilinear algebra and differential forms into the picture from the start.
3) There are several different ways to write down differential
geometric formulas:
a) In local coordinates
b) With respect to an arbitrary basis of vector fields
c) With respect to an orthonormal basis of vector fields
d) In terms of differential forms written with respect to an
arbitrary basis of 1-forms.
e) In terms of differential forms written with respect to an
orthonormal basis of 1-forms
In the end, my advice is to develop some facility with all 5
approaches and a clear understanding of how to switch between
them. They are all useful, depending on the context.
4) Do Carmo’s book on curves and surfaces uses a). For most students,
I think this is the best way to start, because it is the easiest
transition from vector calculus on R^n. However, be forewarned that
the formulas are rather messy and unenlightening. I really detested
learning differential geometry this way, but nevertheless I think it
is the right way to start.
5) An alternative that seems attractive to me is O’Neill’s book on
elementary differential geometry, which takes a more abstract approach
and therefore presents things much more elegantly.
5′) I always recommend the book “Differential Topology” by Guillemin
and Pollack to students trying to learn differential geometry. I think
this is one of the most beautiful textbooks I have ever seen. And it
shows in a rather elementary way how differential geometry can be used
to prove a beautiful topological theorem.
6) I recommend not getting overly obsessed with understanding all the
ins and outs of manifolds (as in Spivak). Get a feel for what they are
and how to work with them using either local coordinates or a basis of
local vector fields and move on. The technicalities of manifolds are
kind of like the technicalities of set theory; it’s better to know how
to use them than to know all the rather gory details of how they are defined.
7) As for Riemannian geometry, I do not know Do Carmo’s book
particularly well. When I was a graduate student (many years ago), I
struggled to find a decent presentation. If you want a great
super-quick presentation of the formalities, then one in Milnor’s
“Morse Theory” is a well-known classic. Chavel’s book “Eigenvalues in
Riemannian Geometry” also has an elegant introduction to the
subject. He also has a book specifically on Riemannian geometry that I
have never taken a close look at. I am also fond of the book by
Gallot, Hulin, and Lafontaine, because it follows much more closely
the spirit of how Riemannian geometry is practiced today.
My favorite by far is the one I mentioned before: “Comparison Theorems
in Riemannian Geometry” by Cheeger and Ebin. It used to be
prohibitively expensive but is being reissued by the AMS presumably at
a much more reasonable cost. This is a beautiful book. It uses
exclusively approach b) above and was a real revelaation to me.
8) Finally, I cannot resist repeating another anecdote about a
(former) Harvard professor. My advisor was Phillip Griffiths, who
offered me all sorts of incredibly wise guidance. I remember that
during one meeting early in my studies, he asked me, “Have you
invented your own notation yet?” Here is how I interpreted his
question: When you try to read books and papers on differential
geometry, you find to your frustration that each author has a
completely different view of the subject and a unique notation. And
different proofs for the same theorems. In the end, the proofs of many
theorems in differential geometry are rather straightforward if you
have the right geometric intuition for what is going on *and* you have
a good notation for representing the relevant objects and their
relationships. So in the end it is better to set up your own consistent notation and write out your own proofs of everything using your own
notation. It *is* helpful to have someone else’s notation to emulate. For me it was not Griffiths (who at the time worked mainly in complex differential geometry) but Robert Bryant who has an uncanny ability to find the most elegant notation and proof for everything he does. When I first met him while I was still a graduate student, he had just received his Ph.D. but he was already teaching not just me but also Chern and Griffiths, too. There was this delightful conference in New Mexico, where Chern gave a series of lectures on exterior differential systems. Throughout each lecture, Chern would regularly pause, look at Robert, and ask, “Robert, is that right?”
(Tim, my apologies for hijacking your blog)
November 7, 2007 at 1:41 am |
John, I like your pithy and illuminating explanation of the difference between covariant and contravariant structures on a differentiable manifold. And I agree that, in general, the distinction is important — even profound. But I still respectfully maintain that if you’re doing Riemannian geometry (or symplectic geometry) then you’re mostly interested in those diffeomorphisms of your manifold that preserve the Riemannian metric (or the symplectic 2-form.) And because every such diffeomorphism has an inverse that is equally respectful of the Riemannian metric (or the symplectic 2-form), you can always pull back or push forward whatever you like, using whichever of the two diffeomorphisms you happen to need at the moment.
If, on the other hand, you’re interested in some large class of diffeomorphisms that do not preserve the particular geometrical structure with which your manifold is endowed, then I agree: in such a context, the distinction between covariant and contravariant can indeed become important. This situation arises more in Riemannian geometry than in symplectic geometry, because Riemannian metrics are rigid; that is, they can never admit an infinite-dimensional group of isometries. Symplectic structures, on the other hand, always do, which means that only very seldom does a symplectic geometer need to think about non-symplectomorphisms.
Deane, I’m delighted to hear that we share the magical experience of learning differential geometry from Chern. I know I promised Kay I’d try to say something useful about how he taught the subject, but (as I’m sure I need hardly tell you) it’s really an impossible task. For what he did in the classroom was extraordinarily subtle. It really was a form of magic.
I don’t want to suggest, though, that Chern himself was a magician — at least not in Kac’s sense of the term. Rather, he was one of Kac’s “ordinary geniuses,” which is to say, “a fellow that you and I would be just as good as, if we were only many times better.” By this I mean that the way he thought never seemed to me the least bit mysterious (even when it was.) No, the remarkable thing about learning from Chern was that you always felt you could yourself do everything you saw him do. There seemed, quite literally, to be nothing to it. Indeed, I was often embarrassed, after he’d explained something to me, that I hadn’t thought of it myself first — that’s how simple, how natural, how blindingly obvious everything seemed, once Chern had explained it.
Yes, he used examples often and brilliantly. Yes, he eschewed needless abstractions, and relished explicit computations. Yes, he was friendly and approachable, and he always listened attentively, even when you weren’t quite sure what you were tying to say; he invariably treated even the merest beginner as an esteemed colleague. But none of this really gets at the essence of his magic. Chern’s teaching was vastly more than the sum of its parts, and I despair of evoking it satisfactorily by enumerating them. Ultimately all I can say is that it certainly was wonderful to see him in action, and I’m constantly grateful to my lucky stars for allowing me to.
Deane, I read with real interest your remark that you found it confusing, when doing computations, to identify the tangent and cotangent bundles of a Riemannian manifold, because my own experience has been very different.
I’ve become convinced that far and away the most useful computational tool in all of differential geometry is the abstract index notation of Roger Penrose (as exposed, for example, in Volume 1 of his SPINORS AND SPACE-TIME), which makes this identification automatic and inevitable. A great many things that can only be done laboriously without the abstract index notation become easy with it, and it has the cardinal advantage of making everything trivial look trivial. The identification it entails between tangent and cotangent spaces has only made things simpler and clearer for me.
As you may have inferred from my enthusiastic embrace of his notation, I’ve been deeply influenced by Penrose, too, and indeed much of my post-Chern education I owe to (very mathematical) general relativity theorists. These are persons who, like low-dimensional topologists, have an obvious interest in one-parameter families of Riemannian manifolds, which play a fundamental role in general-relativistic perturbation theory. Yet I’ve never met a general relativity theorist who finds it confusing to retain the Penrose abstract index notation in this context, despite the presence of multiple metrics.
So I suppose it’s at least partly what you’re used to. In my own case, I’m very accustomed to using a computational scheme that automatically identifies tangent and cotangent bundles whenever the manifolds I’m working with come equipped with a non-degenerate bilinear form in each tangent space. I’ve never found it confusing to make such an identification, because the notation I use is so transparent.
Of course I’ve also spent lots of time looking at manifolds whose geometric structure is far more rudimentary than that of a Riemannian manifold (e.g., a characteristic submanifold of a Lorentzian manifold, which inherits a degenerate metric from the ambient space.) Applied in such a context, the Penrose abstract index notation entails no identification of tangent and cotangent bundles. But it’s easy for me to adjust to that, and to adapt what can be adapted from my experience with the Riemannian case.
November 7, 2007 at 2:03 am |
In that situation, the identification of the tangent and cotangent bundles only becomes a hindrance and not at all a benefit.
One of the watchwords of those of us who do a lot of “categorification” is to never say “equal” when you can say “isomorphic”, and to try and give an explicit isomorphism where possible. Here’s a great example: you don’t want to say the tangent and cotangent bundles are equal, but you want to give a continuously varying family of isomorphisms, which can be a very interesting thing indeed.
November 7, 2007 at 3:26 am |
I like to call differential geometry “nonlinear linear algebra”. I like to say that a manifold, or more specifically, the tangent bundle of a manifold is just a parameterized family of vector spaces.
So all of the issues being discussed are relevant even just for a vector space. So the question is this:
If you fix a non-degenerate quadratic form (such as an inner product) on a vector space, there is a natural isomorphism between the vector space and its dual. Is it true that you lose nothing by always identifying the dual space with the original vector space via this isomorphism?
The answer for a lot of people is yes. For me, it was definitely no. Even if you always work on a fixed sympletic, Lorentzian, or Riemannian manifold, it is often extremely useful to know whether what you are doing relies on the quadratic form in an essential way or is something that requires only the manifold structure and nothing else. This is especially true if you are working with a family or flow of quadratic forms. If you always identify the tangent and cotangent space, this distinction will always be clouded if not completely hidden.
November 7, 2007 at 3:35 am |
One of my most eye-opening teaching experiences occurred when I was helping a six-year-old who was struggling with basic addition – or so it appeared. She was trying to work through a book that helped her to the concept of addition via various examples such as “If Nellie has three apples and is then given two more, how many apples does she have?” The poor little girl didn’t have a clue.
However, after spending a short time with her I discovered that she could do 3+2 with no problem whatsoever. In fact, she had no trouble with addition. She just couldn’t get her head around all these wretched apples, cakes, monkeys etc that were being used to “explain” the concept of addition to her. She needed to work through the book almost “backwards” – I had to help her understand that adding up apples was just an example of an abstract addition she could do perfectly well! Her problem was that all the books for six-year-olds went the other way round.
This girl was of course an exception to the norm, but a vivid reminder, I think, of what James said: the important thing is to know your audience. I personally tend to prefer examples afterwards, but know that many people prefer the reverse. I quite often teach in a way that wouldn’t suit me as a student at all; but that’s fine because I’m not the audience.
When I am in the audience, I often sit in seminars and have to hold the first part, the “motivating examples”, in my head until after the theory, because I need the theory in order to understand the supposedly “motivating” examples. (Unfortunately, my head often explodes in this process of keeping things on hold for later.) But then, I’m the sort of person who can’t remember what an algebra is except by remembering that it’s a monoid object in the monoidal category of vector spaces…
Postscript: I recently gave a seminar in Chicago in which I really couldn’t decide whether to do the theory or the examples first, so I simply asked the audience to choose. They chose theory!
November 7, 2007 at 8:00 am |
“In dealing with mathematical problems, specialization plays, as I believe, a still more important part than generalization. Perhaps in most cases where we seek in vain the answer to a question, the cause of the failure lies in the fact that problems simpler and easier than the one in hand have been either not at all or incompletely solved. All depends, then, on finding out these easier problems, and on solving them by means of devices as perfect as possible and of concepts capable of generalization. This rule is one of the most important levers for overcoming mathematical difficulties and it seems to me that it is used almost always, though perhaps unconsciously.”
— David Hilbert
November 7, 2007 at 12:10 pm |
In response to Eugenia, and to back up my claim that I’m not completely rigid about putting examples first, I do have one example (yes yes …) of a concept where a bit of theory first can be helpful, namely uniform convergence. If you introduce it by giving examples of sequences of functions that converge uniformly and sequences that converge pointwise but not uniformly, then it can be quite hard to grasp the difference, however hard you go on about strengthening statements by reversing the order of quantifiers. I remember my perception of the concept suddenly changing when I was first told about the notion of the supremum norm. Suddenly I saw that a whole zoo of different notions of convergence could be thought of in a much simpler way: just choose a norm and talk about convergence in that norm. (Even the fact that many useful notions of convergence are not of this form is not a problem: you understand them better by understanding that they are not convergence in any norm but perhaps in a topology that is not given by a norm, or something like that.) And although the standard three-epsilon proof that a uniform limit of continuous functions is continuous doesn’t become any easier logically speaking, if you think in terms of uniform norms it’s certainly easier to write down: instead of saying that you find an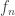 such that
such that  for every
for every  you just say that
you just say that 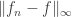 is at most
is at most  .
.
This doesn’t completely go against putting examples first: for instance, if I introduced normed spaces before uniform convergence (which would be highly non-standard and have some disadvantages, I admit) then I’d be tempted to motivate the definition of norms before giving it, though the definition is simple enough that perhaps it would be OK to give the motivation afterwards.
Incidentally, the child who could think only abstractly does seem to be unusual, as you say. There have been many experiments where people who can’t answer abstract arithmetical questions can answer equivalent concrete questions with ease.
And a brief piece of teaching experience (from yesterday): I was talking to two students about conjugation and talked about how is the function that takes
is the function that takes 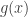 to
to  if
if  takes
takes  to
to  . I then asked them to come up with a function from the reals to the reals that takes
. I then asked them to come up with a function from the reals to the reals that takes 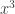 to
to 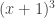 for every
for every  . After a while, one of them had the idea of taking the cube root, adding one, and cubing. But it was clear that he did that by forgetting all about my discussion of conjugation and just looking at the example. Only afterwards, when I pointed it out, did he realize that he had just done a conjugation. Another time, I’ll probably start with that little question and move on to the general discussion.
. After a while, one of them had the idea of taking the cube root, adding one, and cubing. But it was clear that he did that by forgetting all about my discussion of conjugation and just looking at the example. Only afterwards, when I pointed it out, did he realize that he had just done a conjugation. Another time, I’ll probably start with that little question and move on to the general discussion.
November 8, 2007 at 10:22 am |
I think one reason for the less than universal adoption of the “Examples First!” principle is that it takes judgment and imagination to devise really good examples. Many people simply haven’t the time to do a proper job, and anything short of a proper job typically leads to outcomes that hardly seem worth the effort.
A further daunting problem is that assessing the pedagogical effectiveness of an example cannot really be done a priori; it’s an essentially empirical task. Guided by our understanding of the material we aim to convey, we devise examples to stimulate a certain response in our students. But when we present that example, do we get the response we hoped for? If so, how often do we get it? If not, why not? From whom do we most frequently get it? From whom do we least frequently get it? What changes in our example would most increase its pedagogical effectiveness? We may strive to answer these questions by observing our students as closely and dispassionately as we can while we’re teaching them, but the truth is that we’re amateurs at this kind of thing. Getting really good answers to questions like these is a job for an experimental psychologist, or rather for a well-equipped team of experimental psychologists. It’s work for professionals, not amateurs.
And it’s extremely impressive to see how effective the professionals are at measuring the power of various devices to engage and stimulate an audience, as this article from a recent issue of WIRED magazine shows:
http://www.wired.com/gaming/virtualworlds/magazine/15-09/ff_halo
If hundreds of millions of dollars are riding on the success of your efforts to engage and stimulate your audience, then you devote whatever resources you must to answering, very precisely, questions like those I posed above. In a sense, the stakes in the game of mathematics pedagogy really are on that same scale, but (unlike Microsoft) none of us has the resources to predict the learning outcomes to which our best-laid plans will lead.
November 8, 2007 at 1:59 pm |
Honestly, I’m not trying to be contrary here, but I found uniform convergence to actually be extremely helpful with an example first. I never really understood it in my own reading, mostly because after a while the quantifiers all run together and it wasn’t clear that saying “you can use the same at every point” made such a difference.
at every point” made such a difference.
But when I actually took an advanced calculus class and Dr. Rudolph pointed out the sequence , then it made sense once he stated the uniform convergence condition.
, then it made sense once he stated the uniform convergence condition.
November 8, 2007 at 2:36 pm |
I think that a picture of a function sequence converging uniformly and another converging nonuniformly to a function f seemed to say it all for me. I think if I was teaching this concept, the pictures would be the first thing I would make and show. I don’t know how true this is but when I talk about this concept, it is hard not to think of an engineer trying to approximate something so when I explain it, I try to cast the listener as an experimenter trying to approximate some real world function and then I emphasize how bizarrely unhelpful it is to not have uniform convergence in terms of controlling errors.
Hi Deane and Laurens,
Thanks for your discussion of how to go about learning differential geometry. Can either of you characterize what geometric analysis is? I have more or less been thinking of it synonymously with differential geometry but I’d be interested to hear an informed opinion on what it entails and how it is different from differential geometry.
November 8, 2007 at 4:52 pm |
What is geometric analysis?
I’ll let Laurens answer that.
I’ve been working in “geometric analysis” for over 25 years, and I would say that I don’t have a clue to where its boundaries are. At this point, I would say that it is probably difficult to find any part of mathematics that is clearly *not* geometric analysis. I do have friends who think “geometric analysis” means only Riemannian geometry and elliptic PDE’s but I think they have an overly narrow view of this.
November 8, 2007 at 11:58 pm |
I like to think of there being two facets to “motivation” for mathematics, and I call them “internal” and “external” in my head. External motivation is when there’s a problem you want to solve, a question you want to anwer, or some examples you want to model, so you come up with a piece of mathematics that does it. Internal motivation is harder to pin down; it’s when a construction seems like a *natural* thing to do, because the internal logic of some existing mathematics drove us in that direction. For example, once you have made a construction for some specific purpose, it might make sense to iterate it, even if you don’t have any specific purpose in mind for the result.
My favourite sort of mathematics is when these types of two motivation converge onto the same answer. My reservation about teaching by “examples first” is that it neglects the internal form of motivation and encourages students to think primarily in terms of external motivation. I want to show them that abstract mathematics is not just a tool, but a beautiful place to wander around.
November 9, 2007 at 5:12 am |
Eugenia: are we back to theory-builders vs. problem-solvers again?
November 9, 2007 at 5:25 pm |
Regarding “theory-builders vs. problem-solvers” (which is a dichotomy that I think is more relevant to people like Gowers and Tao than me), I think there are two important things we need to do as both teachers and researchers:
1) Develop or introduce new mathematical facts
2) Organize mathematical facts into a logical framework that is easy to remember and construct (or reconstruct)
When I learn mathematics, I find myself focusing mostly on 2), because it clarifies for me how everything fits together. This usually allows me to identify more easily which lemmas, propositions, and theorems are straightforward consequences of the logical framework and which add honestly new technical tools to the framework. I can then focus my mental energy on the latter, which is usually where the “real” “problem-solving” mathematics is being done.
I usually also want a good story motivating the logical framework. When I teach, I am happiest when I can offer a good story that leads to an easy-to-remember logical organization of the mathematics. When I tutor students, I find that most of them view mathematics as just a collection of memorized formulas (“handed to them by God”, I like to say), rather than an organized set of natural consequences of a few reasonable and basic assumptions. You still want them to memorize things but you want them to have the stuff better organized in their minds. Again, a good logical organization allows them to see which things are easy to learn and remember and to isolate the honestly difficult things that need extra effort to learn.
For this reason, I do not always like to start with examples. Sometimes I’ll start with a larger philosophical question and introduce the “theory” as a way of addressing it. Then do examples after a little while to make it feel more concrete. Or I’ll try to start with two examples that look very different on the surface and then ask, “how can we find a common approach that encompasses both examples?” Things like that. I like to introduce abstraction as a practical need of organizing knowledge more efficiently in our own minds.
As much as I love the beauty of mathematics, I do not like invoking it as a reason for studying mathematics. I do like to comment on the beauty of something during a lecture, but I just do not believe it is a motivation for all but a few students.
November 9, 2007 at 7:25 pm |
Mathematics is amazingly compressible: you may struggle a long time, step by step, to work through some process or idea from several approaches. But once you really understand it and have the mental perspective to see it as a whole, there is a tremendous mental compression. You can file it away, recall it quickly and completely when you need it, and use it as just one step in some other mental process. The insight that goes with this compression is one of the real joys of mathematics.
— William Paul Thurston
A new result is of value, if at all, when in unifying elements long known but hitherto separate and seeming strangers to one another it suddenly introduces order where apparently disorder reigned. It then permits us to see at a glance each of these elements and its place in the assemblage. This new fact is not merely precious by itself, but it alone gives value to all the old facts it combines.
— Jules Henri Poincaré
[It is elegance] by means of which the spirit comprehends quickly and in one step so many computations. It is clear that elegance, so vaunted and so aptly named, can have no other purpose.
— Evariste Galois
Starting from the individual theorems, I soon grew accustomed to piercing deeper into their relationships, and to grasp entire theories as a single entity. That is how I conceived the idea of mathematical beauty. There is a sort of mathematical beauty, just as there is an aesthetic beauty, which, however, one only comes to comprehend when, enraptured, one surveys an entire system of discoveries that follow from a single central idea and, because of their essential unity, lead to a single final result – when, that is, one sees a system of discoveries that, in their logical order, harmony, and brilliance, appear as an organic whole, like a painting before the mind’s eye.
— Ferdinand Gotthold Max Eisenstein
We all believe that mathematics is an art. The author of a book, the lecturer in a classroom tries to convey the structural beauty of mathematics to his readers, to his listeners. In this attempt, he must always fail. Mathematics is logical, to be sure: each conclusion is drawn from previously derived statements. Yet the whole of it, the real piece of art, is not linear; worse than that, its perception should be instantaneous. We have all experienced on some rare occasion the feeling of elation in realizing that we have enabled our listeners to see at a moment’s glance the whole architecture and all its ramifications.
— Emil Artin
November 9, 2007 at 8:31 pm |
My comment on theory building versus problem solving might be sort of unenlightened but for me it comes down to incentive structures/reward systems, both internal and external. Mathematicians in general are supported by institutions, school systems, publishers, client sciences like chemistry, physics, engineering etc … and I think one has to end up fitting into the incentive structures of wider society to be a mathematician.
So in mathematics in service of the masters in wider society, two sources of advances come up, which are precisely, tactics and strategy or short term and long term or problem solving and theory building. There are probably times, situations and subfields where short-term thinking works more often than long term and vice versa … just like real life!! I think the fact that wider society does not care where the advances come from as long as they keep coming, is why there is room for both approaches. If mathematics was allowed to progress on purely aesthetic considerations, the theory builders might drive out the problem solvers or vice versa.
One interesting complication is that the problem solvers can solve problems for the theory builders and the theory builders are providing techniques for the problem solvers. So each is at times a client of the other.
Anyway, my point is that I am not sure there is anything going on with theory building and problem solving that isn’t just the simple economics of individuals striving to match market demands. I feel that this simple reality probably trumps individual tastes more than might be apparent.
Hi Laurens,
I was wondering if you had an opinion on my question about what geometric analysis was exactly? ( I asked full the question above but I will avoid repeating it to save space.)
November 10, 2007 at 1:07 am |
It seems to me that this can only really be the case if you assume that anyone can act in either role. I disagree with that position. I just plain don’t think as a problem solver, and the problems I do try to solve I only do because I understand that trying to solve some little particular problem will impress the problem-solvers more than all the ornate theories I can build.
November 10, 2007 at 5:32 am |
Kay, I’m not qualified to say what does and does not count as “geometric analysis,” but I can imagine at least some things that might fall under that heading without counting as differential geometry.
For example, there’s the whole business of convexity in topological vector spaces, which one might reasonably argue combines analysis with geometry of a sort. I suppose that might count as “geometric analysis,” but I’m prepared to bet that very few differential geometers would consider it to belong to their field.
And then there’s what von Neumann used to call “continuous geometry,” a generalisation of classical projective geometry to which he was led by his study of the logical foundations of quantum theory. Like convexity theory, this mixes a sort of geometry with analysis, but it’s not the sort with which the garden-variety differential geometer is much occupied.
My impression is that Chern would probably have understood the term “geometric analysis” to refer to the sort of work that Nash did to solve the isometric embedding problem. Although the problem itself is explicitly differential-geometric, solving it boils down to proving global existence for a set of (very complicated) partial differential equations, and the methods Nash employed to that end apply equally to other sets of partial differential equations with no known differential-geometric meaning.
On this account, “geometric analysis” is analysis in the service of differential geometry — or, as I know Chern would have preferred it, analysis guided and inspired by differential geometry. And Chern often remarked that, when working on partial differential equations, one needs all the guidance and inspiration one can get. Most partial differential equations, after all, are utterly beyond our power to solve, or indeed even to understand in a rough, general sort of way. If we take one up at random, we’re pretty much sure to be humiliated. Only those with a geometrical meaning are likely to be tractable, and their geometrical meaning can sometimes offer significant clues to their solution.
I suppose I could go on like this, Kay, and list a few of the classical problems that have driven the development of “geometrical analysis,” understood in this way. But I’m reluctant to go on and on. Perhaps I’ve already said enough?
November 10, 2007 at 6:36 am |
Laurens,
I like your explanation of what geometric analysis is (beyond Riemannian geometry), and I would encourage you to go on, if you have more to say. Although I don’t think your list is exhaustive, I think you have identified some very important examples of areas in “geometric analysis” that do not qualify as differential geometry.
Let me elaborate on a couple of points that happen to intersect a few things I know a little about.
Indeed, “convexity in topological vector spaces” is an important subject that can be viewed as part of geometric analysis. I would like to add, however, that even the special case of studying the geometric properties of convex bodies in a finite dimensional vector space is an active and rich area of research that is not differential geometry. For most differential geometers, the idea of studying something as trivial as a convex body in R^n seems quaintly old-fashioned and not of any particular interest. I know, because I was a differential geometer and when a colleague try to sell me on convex geometry, I reacted with disdain. But for reasons too long to explain here, I eventually got corraled into working with two colleagues on this very subject. I’ve learned to my delight that this is a beautiful and rich subject.
At first sight the study of a convex body is still differential geometry, because one could simply study the differential geometric properties of the boundary. However, if you limit yourself to this view, which requires assumptions of smoothness of the boundary, you will miss much of the beauty and depth of the subject. It turns out that the right approach is to study *all* convex bodies and to use *integral* geometry (another subject much loved and promoted by Chern), not differential geometry. I could say a lot more, but like Laurens, I feel I’ve said enough for now.
And, my first theorem was about the existence of isometric embeddings. When I was a graduate student, Chern promoted the idea of applying modern PDE technology to reconsider both the Cartan-Kahler theorem (which is a local existence theorem for analytic overdetermined systems of PDE’s) and isometric embeddings. Phillip Griffiths, Robert Bryant, and some graduate students (including me) took up this challenge of these questions.
I agree with Chern’s view of PDE’s, as expressed by Laurens, but I have to say that I view the isometric embedding problem as an example of the contrapositive. It turns out that the PDE’s associated with the isometric embedding problem are totally intractable, except in a few special cases. In fact, if you analyze the symbol (i.e., the top order terms) of the PDE’s, you can prove that it looks essentially like a generic system of PDE’s. In particular, in dimensions greater than 3, the PDE’s are never elliptic, hyperbolic, or parabolic. So they are impossible to solve using any known technology. After working and thinking about this for a long time, I concluded that, despite all appearances, the question of existence and uniqueness of isometric embeddings of a Riemannian manifold is somehow not the right or an important question for a differential geometer to ask. As far as I can tell, the study of the PDE’s associated with isometric embeddings has contributed very little to the subject of differential geometry, and conversely, the differential geometric properties of a submanifold contribute very little insight to the understanding of the PDE’s.
November 10, 2007 at 6:40 am |
Thank you Laurens and Deane for the information. I had done some research on my own on the term ‘geometric analysis’ and I had found it hard to find any coherent definition. I think I understand why now. The information you have given me should go a long way to furthering my understanding of differential geometry and for this I am very grateful.
November 10, 2007 at 6:44 am |
Am curious if when mathematicians say they have read this or that math book, whether linearly or not, do they really mean what they say? Or are they usually doing one of the things mentioned in a book “How to talk about books you haven’t read?” (Pierre Bayard) reviewed in the New York Times today – like skimming, skipping, reading covers and table of contents – enough, for example, to place where a book is in relation to other books and to talk seemingly intelligently about it. If you were to read math books from cover to cover, you will end having no time to write and do so other things which presumably math professors and researchers need to do. Comments and advice please, thanks.
November 10, 2007 at 7:22 am |
Robert, all the books I talk about reading I’ve actually read. I really don’t see how you could fake reading a math book, at least not for very long. I don’t know why you say that “you will end having no time to write and do so [sic] other things”. It’s certainly possible, and even necessary in some cases.
November 10, 2007 at 8:10 am |
Here is how Bill Thurston describes his own practice of absorbing (formally) written mathematics:
“Different mathematicians study papers in different ways, but when I read a mathematical paper in a field in which I’m conversant, I concentrate on the thoughts that are between the lines. I might look over several paragraphs or strings of equations and think to myself, “Oh yeah, they’re putting in enough rigamarole to carry such-and-such an idea.” When the idea is clear, the formal setup is usually unnecessary and redundant — I often feel that I could write it out myself more easily than figuring out what the authors actually wrote. It’s like a new toaster that comes with a 16-page manual. If you already understand toasters and if the new toaster looks like previous toasters you’ve encountered, you might just plug it in and see if it wors, rather than first reading all the details in the manual.”
Although only Thurston could say, I wouldn’t be surprised if this also describes accurately his manner of reading books.
November 10, 2007 at 2:36 pm |
Thanks John, Laurens.
My comment “you will end up …” is borrowed from the NYT book review that has a similar comment. I agree mathematicians can’t fake it unlike those non-mathematicians described in the NYT book review.
November 11, 2007 at 12:28 am |
I can’t speak for other mathematicians but I have to say that I fake it, as described in today’s New York Times book review, all the time with math papers and books. I have read very few math books in their entirety, and none linearly.
I don’t know how Laurens knows all these great quotes by great mathematicians, but I think Thurston explains it very well. You might call it a form of attention deficit disorder.
In fact, I would argue that it is *easier* to fake having read a math book than a non-math book. If you skim a math book and are able to identify and grasp the essential ideas of a math book, you can often reconstruct all the details yourself from scratch. You generally cannot do that with a non-math book (not that it stops me from trying anyway).
Ergo, Kazhdan’s advice to my friend: You should know everything in this book but don’t read it.
By the way, I recommend that any aspiring geometer should study and “read” Thurston’s notes.
November 11, 2007 at 3:42 am |
What universities are known to be good places for learning differential geometry?
November 11, 2007 at 3:43 am |
(In the US I mean)
November 11, 2007 at 9:42 am |
Kay, permit me to compliment you on posing exactly the right question. You might instead have asked which American mathematics departments boast the largest number of eminent differential geometers — but that would have been exactly the wrong question. For it is a melancholy truth that great masters are not always great mentors, and as a student what you need most is the latter.
So where do you find a great mentor? I know this sounds evasive, but it’s awfully hard to say. Yes, I can tell you where I myself would go, were I now about to embark on a career as a differential geometer, but I wonder whether that would really help much. After all, choices like this are intensely personal, and I don’t yet know enough about you to be able to guess what sort of mentor might serve you best. Possibly the persons I would seek out would be exactly wrong for you.
I suppose there’s no harm, though, in looking in the obvious places for the mentor you need; Harvard and Berkeley, for example, spring to mind immediately as rational possibilities. But you won’t be able to tell whether these places have what you’re looking for unless you visit them and talk to people. Just because Harvard and Berkeley are first-rate schools doesn’t mean you’re guaranteed to find your ideal mentor at either of them. It all depends on who you are, how you learn, and what you want.
Oh, and if you’re wondering what a great mentor looks like, then I suggest you spend a few hours watching everything you can find at this wonderful website:
http://www.peoplesarchive.com/browse/movies/2552/
There are few things I enjoy more, myself, and I honestly believe you’ll never regret it.
November 12, 2007 at 3:30 am |
I am sure Laurens has good intentions, but once you see what Sir Michael Atiyah is like, everybody else just falls short. I don’t know if anyone else comes even close to his intellectual power, clarity of exposition, and unadulterated enthusiasm
It is, however, a wonderful thing that he has been captured so extensively on video like this, so that he can continue to inspire and teach many more people.
Laurens, thank you very much for posting this link. I did not know about it at all.
November 12, 2007 at 3:45 am |
As for the best place in the US to study differential geometry, the following schools come to mind (in no particular order and probably incomplete):
Harvard
MIT
NYU
Stanford
Princeton
Stony Brook
November 12, 2007 at 4:39 am |
Deane, you are most welcome. I too feel strongly that this wonderful video is tremendously valuable, and ought to be much better known. I came across it one night quite by accident, while reading Atiyah’s entry in Wikipedia — the link I included in my previous post was among those listed at the end of the article. I’ve now been through the whole thing at least twice, and I’m looking forward to a third viewing. Amazing stuff.
Oh, and I quite agree with you, by the way, that Sir Michael is a very hard act to follow. Offhand, the only person who seems to me possibly up to the job is Vladimir Arnol’d. And both of them, in different ways, remind me of Chern.
Gosh, I miss that guy.
(A small postscript: I wrote to the People’s Archive to suggest that they visit Stony Brook to interview Milnor, but I’ve never heard back from them.)
November 13, 2007 at 5:46 pm |
Thanks very much for the list Deane. Laurens, I think ideally I would wish for nothing more than a good (or even a so-so) mentor, unfortunately I don’t know very much differential geometry to speak of. I feel like I would need to learn quite a bit more mathematics before I would find somebody willing to waste much of their time on directing me on what to read and how to get over roadblocks. That being said, I appreciate all the help from you and Deane and from everybody else here who has had something helpful or positive to say.
Do you perhaps have any advice on how much differential geometry I should learn on my own or perhaps by taking a few classes before seeking out somebody to help me learn the rest? How would you go about approaching people? (I am not sure I would have the courage to ask someone like Sir Atiyah or Chern much of anything!)
November 15, 2007 at 8:46 pm |
Nobody’s speaking up in defense of Gallian, so I browsed through my fifth edition. I don’t know any point where the book gives only an example and no rigorous definition; it almost uniformly gives a definition followed by some examples.
Where it gets irritating is it sometimes defines an important concept simultaneously with an exercise. For example: on page 89, problem 1, it defines a conjugate for the first time and asks a problem about it. The conjugate is important enough it really ought to be in the main text.
Here’s how it handles the Orbit-Stabilizer Theorem (page 140):
Definition: Stabilizer of a Point
Definition: Orbit of a Point
Example: Listing the orbit and stabilizers of a specific permutation
Example: Same on permutations of a square
Theorem: Orbit-Stabilizer Theorem
Followed by: a proof
Then: An example using the rotation group of a cube
Finally: An eample using the rotation group of a soccer ball
The book isn’t perfect (I wouldn’t recommend relying on it as a sole reference), but I wouldn’t call it a hotbed of unrigorous blashphemy either.
November 17, 2007 at 4:48 am |
Professor Gowers, permit me to congratulate you on your new son. I wish you and your family every possible joy — and at least some sleep!
November 17, 2007 at 4:54 am |
What a surprise! Congratulations!!
November 17, 2007 at 6:12 am |
Also, Laurens, I hope I didn’t wear you out with my endless questions!
November 25, 2007 at 4:59 pm |
[…] Examples first II […]
November 27, 2007 at 10:18 pm |
Tim this is an old question
Let us for example take a look at a set of very dry math books like Bourbaki with their abstract approach and presenting the general theorems first and other less general results as corollaries. I believe their objective was to be more efficient in their explanations and saving you time reading.
Many people will agree that Bourbaki will not be the place to start learning Mathematics so it will never be appropriate for many starting to learn math.
The Bourbakians may have thought otherwise since they name their work the Elements like in Euclid’s elements. So maybe as simple as that. Theorem – Proof approach of many Math books and from the General to the Particular.
Many students will quickly loose touch of the importance of the topic without the use of some good examples if they are not able to come up with some non trivial example or even trivial ones.
One question many students always come up is what is this thing used for?
Why is it important? if they do dare to ask it then it means you have not shown them sufficient examples or sufficiently interesting examples of why this particular result is a theorem or something you like to show as some important result.
Naturally not every one might agree with the above statements.
A mathematical material that is written in a way that is accessible to many more people will be probably read by a group of people that might not read it otherwise.
The trick to mathematics is not to discourage people from learning it by making expositions obscure and accessible only to a select minority of specialist but to attract more people to it to show why we like it.
So anything that can make a mathematical exposition more understandable should be use and examples are a good way to make something easier to understand.
November 28, 2007 at 12:14 pm |
Just a clarification about Bourbaki: although Bourbaki’s stated *initial* goal was to write an analysis textbook that would replace the (then) old ones such as the Goursat, they quickly realized that their opus was turning into something entirely different. Indeed, the introduction states very clearly that reading the “Elements” is not recommended before having finished at least one or two years of university mathematics. So it’s “elements” as in “elemental”, not as in “elementary”.
(By the way, it is not at all clear to me what Euclid’s intended audience was for *his* “Elements” – did he really intend them as what we would now call a textbook?)
It was only 10 or 20 years later that some people started to use Bourbaki style throughout mathematics teaching, and I agree that it was, on the whole, an unhealthy development: pure theory, and almost a certain pride in shunning examples, pictures, applications, etc.
So the Bourbaki treatise and Bourbakist teaching style are two different things and should not be confused (though I admit that the members of the Bourbaki group have not always been as vocal about the confusion as they should have been).
August 20, 2008 at 3:58 am |
[…] Sylow’s theorems in group theory, which we studied in the second year of undergraduate studies, always seemed to me as one of the few theorems I did not have a conceptual understanding of. This makes Sylow’s theorems rather mysterious and charming. (A similar impression with the opposite reaction is expressed by Tim Gowers in this interesting post.) […]
July 10, 2010 at 2:51 am |
[…] Timothy Gowers on “writing examples first!” (see also this followup post) […]
December 30, 2010 at 3:21 am |
[…] Timothy Gowers on “writing examples first!” (see also this followup post) […]
December 31, 2010 at 9:48 pm |
Dear Prof. Gowers,
What do you think about http://en.wikipedia.org/wiki/Mayan_numbers ?
Happy New Year.
January 7, 2011 at 11:23 am |
[…] Timothy Gowers on “writing examples first!” (see also this followup post) […]
October 21, 2011 at 4:33 am |
Magnificent beat ! I wish to apprentice at the same time as you amend your web site, how could i subscribe for a blog website? The account helped me a appropriate deal. I were tiny bit acquainted of this your broadcast provided brilliant transparent concept
December 22, 2011 at 2:48 pm |
oolong tea | wulong tea…
[…]Examples first II « Gowers's Weblog[…]…
January 31, 2014 at 4:17 am |
[…] Examples First II […]
November 20, 2014 at 6:18 pm |
February 14, 2017 at 5:59 pm |
[…] I personally like to think about is an approach I call ‘examples first’, after these two blog posts by Timothy Gowers. (The second one has an absolutely epic comment thread – reading […]
February 14, 2017 at 6:10 pm |
[…] a bit, that blog post comment section is probably the original source of my minor obsession with the role-of-intuition-in-maths […]
July 12, 2017 at 5:27 am |
[…] Timothy Gowers on “writing examples first!” (see also this followup post) […]
November 27, 2020 at 5:11 am |
Fabulous post, you have denoted out some fantastic points, I likewise think this s a very wonderful website. I will visit again for more quality contents and also, recommend this site to all. Thanks.