I don’t have much to say mathematically, or rather I do but now that there is a wiki associated with polymath1, that seems to be the obvious place to summarize the mathematical understanding that arises in the comments on the various blog posts here and over on Terence Tao’s blog (see blogroll). The reason I am writing a new post now is simply that the 500s thread is about to run out.
So let me quickly make a few comments on how things seem to be going. (At some point in the future I will do so at much greater length.) Not surprisingly, it seems that we have reached a stage that is noticeably different from how things were right at the beginning. Certain ideas that emerged then have become digested by all the participants and have turned into something like background knowledge. Meanwhile, the discussion itself has become somewhat fragmented, in the sense that various people, or smaller groups of people, are pursuing different approaches and commenting only briefly if at all on other people’s approaches. In other words, at the moment the advantage of collaboration is that it is allowing us to do things in parallel, and efficiently because people are likely to be better at thinking about the aspects of the problem that particularly appeal to them.
Whether there will be a problem with lack of communication I don’t know. But perhaps there are enough of us that it won’t matter. At the moment I feel rather optimistic that we will end up with a new proof of DHJ(3) (but that is partly because I have a sketch that I have not subjected to appropriately stringent testing, which always makes me feel stupidly optimistic). In fact, what I’d really like to see is several related new proofs emerging, each drawing on different but overlapping subsets of the ideas that have emerged during the discussion. That would reflect in a nice way the difference between polymath and more usual papers written by monomath or oligomath.
Finally, a quick word on threading. The largest number of votes (at the time of writing) have gone to allowing full threading, but it is not an absolute majority: those who want unrestricted threading are outnumbered by those who have voted either for limited threading or for no threading at all. I think that points to limited threading. I’ve allowed the minimum non-zero amount. I can’t force you to abide by any rules here, but I can at least give my recommendation, which is this. For polymath comments, I’d like to stick as closely as possible to what we’ve got already. So if you have a genuinely new point to make, then it should come with a new number. However, if you want to give a quick reaction to another comment, then a reply to it is appropriate. If you have a longish reply, then it should appear as a new comment, but here there is another use of threading that could be very helpful, which is to add replies such as, “I have a counterexample to this conjecture — see comment 845 below.” In other words, it will allow forward referencing as well as backward referencing. Comments on this post will start at 800, and if yours is the nth reply to comment 8**, then you should number it 8**.n. Going back to the question of when to reply to a comment, a good rule of thumb is that you should do so only if your reply very much has the feel of a reaction and not of a full comment in itself.
Also, it isn’t possible to have threading on some posts and not on others, but I’d be quite grateful if we didn’t have threaded comments on any posts earlier than this one. And a quick question: does anyone know what happens to the threaded comments if you turn the threading feature off again, which is something I might find myself wanting to do?
February 23, 2009 at 6:12 pm |
800. Here is a writeup of a Fourier/density-increment argument for Sperner, implementing Terry’s #578 using some of the Fourier calculations Tim and I were doing:
http://www.cs.cmu.edu/~odonnell/wrong-sperner.pdf
Hope it’s mostly bug-free!
February 23, 2009 at 6:14 pm |
Tim – First of all I have to say that I did enjoy to read the blog and to contribute a bit. On the other hand it became less and less comfortable to me posting any comments. You wrote that
“Meanwhile, the discussion itself has become somewhat fragmented, in the sense that various people, or smaller groups of people, are pursuing different approaches and commenting only briefly if at all on other people’s approaches.”
Let me tell you what is my experience. I’m reading posts using notations from to ergodic theory or Fourier analysis with great interest, but I will rarely make any comment as I’m not expert on that field. Some post are still accessible to me and some others aren’t. There is no way that I will understand posts referring to noise stability unless I learn something more about it, which I’m not planning to do in the near future unless it turns out to be crucial for the project. Maybe the blog is still accessible for the majority of readers but I’m finding it more and more difficult to follow. For the same reasons I feel a bit awkward about posting notes. It’s tempting to work on the problems alone without sharing it with the others but this is clearly against the soul of the project.
February 23, 2009 at 6:28 pm |
Metacomment. Jozsef, in the light of what you say, I invite others to give their reactions to how things are going for them. My feeling, as I said in the post, is that we are entering uncharted territory (or rather, a different uncharted territory from the initial one) and it is not clear that the same rules should still apply. What we have done so far has, in my view, been a wonderful way of doing very quickly and thoroughly the initial exploration of the problem, and it feels as though the best way of making further progress will be if we start dealing with technicalities and actually write up some statements formally. I am hoping to do that in the near future, Ryan is doing something along those lines, Terry recently put a Hilbert-spaces lemma on the wiki, etc.
The obvious hazard with this is that people may end up writing things that others do not understand, or can understand only if they are prepared to invest a lot of time and effort. So if we want to continue to operate as a collective unit, so to speak, it is extremely important for people who write formal proofs to give generous introductions explaining what they are doing, roughly how the proof goes, why they think it could be useful for DHJ(3) (or something related to DHJ(3)), and so on. This is perhaps an area where people who have been following the discussion without actually posting comments could be helpful—just by letting us know which bits you find hard to understand. For example, if you see something on the wiki that is clearly meant to be easily comprehensible but it in fact isn’t, then it would be helpful to know. (However, some of the wiki articles are over-concise simply because we haven’t had time to expand them yet.)
Do others have any thoughts about where we should go from here?
February 23, 2009 at 6:47 pm |
801. Fourier/Sperner
Ryan, re the remark at the end of the thing you wrote up, if we do indeed have an expression of the form![\mathbb{E}_{p\leq q}\sum_{A\subset[n]}\lambda_{p,q}^{|A|}\hat{f}_p(A)\hat{f}_q(A)](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D_%7Bp%5Cleq+q%7D%5Csum_%7BA%5Csubset%5Bn%5D%7D%5Clambda_%7Bp%2Cq%7D%5E%7B%7CA%7C%7D%5Chat%7Bf%7D_p%28A%29%5Chat%7Bf%7D_q%28A%29&bg=ffffff&fg=333333&s=0&c=20201002) for the total weight
for the total weight  for
for  when everything is according to equal-slices density, then it seems to me not completely obvious that one couldn’t prove some kind of positivity result for the contribution from each
when everything is according to equal-slices density, then it seems to me not completely obvious that one couldn’t prove some kind of positivity result for the contribution from each  , especially given your calculation that
, especially given your calculation that  splits up as a product. But probably you’ve thought about that—I can see that it’s a problem that
splits up as a product. But probably you’ve thought about that—I can see that it’s a problem that  is not symmetric in p and q, but can one not make it symmetric by talking instead about pairs of disjoint sets?
is not symmetric in p and q, but can one not make it symmetric by talking instead about pairs of disjoint sets?
Or perhaps it’s false that you have positivity and the disjoint-pairs formulation is what you need to get a similar result where it becomes true. I hope this vague comment makes some sense to you. I’ll see if I can think of a counterexample. In fact, isn’t this a counterexample: let n=1, and let f(0)=-1, f(1)=1. Then the expectation of f(x)f(y) over combinatorial lines (x,y) is -1 and the expectation of f is 0.
February 23, 2009 at 7:25 pm
801.1 Please ignore the last paragraph of this comment — for analytic purposes we need to consider degenerate lines, and as you say the usual proof of Sperner proves positivity. Hmm — not sure that the threading adds much here.
February 23, 2009 at 8:05 pm
801.2: Yes, it’s not clear to me why![\mathbb{E}_{p \leq q}[\hat{f}_p(A) \hat{f}_q(A)]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D_%7Bp+%5Cleq+q%7D%5B%5Chat%7Bf%7D_p%28A%29+%5Chat%7Bf%7D_q%28A%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) needs to be nonnegative. This is a shame, because: a) we’d be extremely done if we could show this; b) as
needs to be nonnegative. This is a shame, because: a) we’d be extremely done if we could show this; b) as 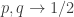 the quantity approaches
the quantity approaches 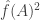 , which is of course nonnegative. Unfortunately, if you make
, which is of course nonnegative. Unfortunately, if you make 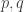 extremely close to
extremely close to 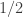 so as to force it nonnegativity, you’ll probably be swamped with degenerate lines.
so as to force it nonnegativity, you’ll probably be swamped with degenerate lines.
February 23, 2009 at 8:20 pm |
Metacomment: I sympathise with Jozsef’s position. Luckily, some of the directions we’re working on are in areas I’m familiar with, so I can comment there. But to be honest, I know nothing about ergodic methods, am extremely shaky on what triangle-removal is, and am only kind of on top of Szemeredi’s regularity lemma. So indeed it takes me quite a while just to read comments on these topics. That’s fine with me though.
Thing is, even in the areas I’m familiar with it’s awfully tough to keep up with a certain pair of powerhouses who post regularly to the project 🙂 In a perfect world I’d post more definitions, add more intuition to my comments, update the wiki with stuff about noise sensitivity and so forth — but it already takes me many hours just to quasi-keep up with Tim and Terry and generate non-nonsensical comments. I’m fine with this too, though.
Finally, I agree that it’s also gotten to the point where it’s sort of impossible to explore certain directions — especially ones with calculations — “online”. You probably won’t be surprised to learn I spent a fair bit of time working out the pdf document in #800 by myself on paper. I hope this isn’t too much against the spirit of the project, but I couldn’t find any way to do it otherwise. I would feel like I were massively spamming people if I tried to compute like this online, with all the associated wrong turns, miscalculations, and crazy mistakes I make.
February 23, 2009 at 8:25 pm |
802. Sperner/Fourier.
By the way, I’m pretty sure one can also do Roth’s Theorem (or at least, finding “Schur triples” in ) in this way. It might sound ridiculous to say so, since Roth/Meshulam already gave a highly elegant density-increment/Fourier-analysis proof.
) in this way. It might sound ridiculous to say so, since Roth/Meshulam already gave a highly elegant density-increment/Fourier-analysis proof.
But the point is that:
. it works in a non-“arithmetic”/”algebraic” way
. it works by doing density increments that restrict just to *combinatorial* subpaces
. it demonstrates that the method can sometimes work in cases where one needs to find *three* points in the set satisfying some relation.
I can supply more details later but right now I have to go to a meeting…
February 23, 2009 at 8:54 pm |
Metacomment.1
(If this .1 will automatically creat a threading I will consider it a miracle.)
I think the nature of this collaboration via different people writing blog remarks is somewhat similar to the massive collaboration in ordinary math where people are writing papers partially based on earlier papers.
Here the time scale is quicker and the nature of contributions is more tentative. Half baked ideas are encourged.
It is not possible to follow everything or even most of the things or even a large fraction of them. (Not to speak about understanding and digesting and remembering). I think it can be useful that people will not assume that other people read earlier things and from time to time repeat and summarize and overall be clear as possible. (I think comments of the form: “please clarify” can be useful.) One the other hand, like in usual collaborations people often write things mainly for themselves (e.g. the Hardy-Littlewood rules) and this is very fine.
(A question: is Ryan’s write-up a correct new proof of (weak) Sperner using density incement and Fourier? (The file is called wrong-Sperner but reading it I realize that this means the proof is right but not yet the “Fourier/Sperner proof from the book” or something like that. Please clarify.)
There are various avenues which I find very interesting even if not directly related to the most promising avenues towards DHJ proof and even some ideas I’d like to share and explore. (One of these is a non-density-decreasing Fourier strategy.)
One general avenue is various reductions (ususally based on simple combinatorial reasonings) : Joszef mentioned Moser(k=6)-> DHK(k=3) and some reductions to Szemeredi (k=4) were considered. Summarizing those and pushing for further reductions can be fruitfull.
Also the equivalence of DHJ for various measures (I supose this is also a reduction business) is an interesting aspect worth further study. When there is group acting such equivalences are easy and of general nature. But for DHJ I am not sure how general they are.
February 23, 2009 at 11:32 pm
Gil wrote: “(The file is called wrong-Sperner but reading it I realize that this means the proof is right but not yet the “Fourier/Sperner proof from the book” or something like that. Please clarify.)”
Yes — I forgot to mention that. I think/hope the writeup’s correct, but I called it “wrong-Sperner” because I still feel there’s something not-from-the-Book about it.
February 23, 2009 at 10:07 pm |
Metacomment.2
It certainly does feel that the project is developing into a more mature phase, where it resembles the activity of a highly specialised mathematical subfield, rather than a single large collaboration, albeit at very different time scales than traditional activity. (The wiki is somewhat analogous to a “Journal of Attempts to Prove Density Hales Jewett”, and the threads are analogous to things like “4th weekly conference on Density Hales Jewett” 🙂 .) Also we are hitting the barrier that the number of promising avenues of research seems to exceed the number of people actively working on the project.
But I think things will focus a bit more (and become more “polymathy”) once we identify a particularly promising approach to the problem (I think we already have a partially assembled skeleton of such, and a significant fraction of the tools needed have already been sensed). This is what is going on in the 700 thread, by the way; we are focusing largely on one subproblem at a time (right now, it’s getting a good Moser(3) bound for n=5) and we seem to be using the collaborative environment quite efficiently.
My near-term plan is to digest enough of the ergodic theory proofs that I can communicate in finitary combinatorial language a formal proof of DHJ(2) that follows the ergodic approach, and a very handwavy proof of DHJ(3). (The Hilbert space lemma I’m working on is a component of the DHJ(2) analysis.) The finitisation of DHJ(2) looks doable, but is already quite messy (more “wrong” than Ryan’s “wrong” proof of DHJ(2)), and it seems to me that formally finitising the ergodic proof of DHJ(3), while technically possible, is not the most desirable objective here. But there does seem to be some useful ideas that we should be able to salvage from the ergodic proof that I would like to toss out here once I understand them properly. (For instance, there seems to be an “IP van der Corput lemma” that lets one “win” when one has 01-pseudorandomness (which roughly means that if one takes a medium dimensional slice of A and then flips one of the fixed digits from 0 to 1, then the pattern of A on the shifted slice is independent of the pattern of A on the original slice). I would like to understand this lemma better. The other extreme, that of 01-insensitivity, is tractable by Shelah’s trick of identifying 0 and 1 into a single letter of the alphabet, and the remaining task is to apply a suitable structure theorem to partition arbitrary sets into 01-structured and 01-pseudorandom components, analogously to how one would apply the regularity lemma to one part of the tripartite graph needed to locate triangles.)
February 23, 2009 at 10:34 pm |
803. Sperner/Fourier
Re the discussion in 801, this is a proposal for getting positivity. I haven’t checked it, and it could just obviously not work.
The reason I make it is that I just can’t believe the evidence in front of me: the trivial positivity in “physical space” just must be reflected by equally trivial positivity in “frequency space”. I wonder if the problem, looked at from the random-permutation point of view, is that to count pairs of initial segments it is not completely sensible to count them with the smaller one always first — after all, the proof of positivity goes by saying that that is actually half the set of pairs of initial segments. So maybe we should look at a sum of the form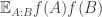 , where
, where 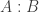 is a hastily invented notation for “
is a hastily invented notation for “ or
or 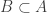 .”
.”
How could we implement this Ryan style? Well, obviously we would average over all pairs of probabilities (p,q). And if we choose a particular pair, then the obvious thing to do would be to choose independent random variables and
and 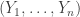 in such a way that the resulting set will give you a probability p of being in A, a probability q of being in B, and a certainty that A:B. To achieve that in a unified way, for each
in such a way that the resulting set will give you a probability p of being in A, a probability q of being in B, and a certainty that A:B. To achieve that in a unified way, for each  we choose a random
we choose a random ![t\in [0,1]](https://s0.wp.com/latex.php?latex=t%5Cin+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) and set
and set 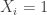 if and only if
if and only if 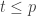 and
and 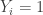 if and only if
if and only if 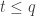 .
.
I haven’t even begun to try any calculations here, but I would find it very strange if one didn’t get some kind of positivity over on the Fourier side.
Having said that, the fact that one expands f in a different way for each p does make me not quite as sure of this positivity as I’m pretending to be.
February 23, 2009 at 11:43 pm
803.1 Positivity:
In my experience, obvious positivity on the physical side doesn’t always imply obvious positivity on the Fourier side. Here is an example (although it goes in the reverse direction).
Let be arbitrary and consider
be arbitrary and consider ![\mathbb{E}[f(x) f(y)]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Bf%28x%29+f%28y%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where  is uniform random and
is uniform random and  is formed by flipping each bit of
is formed by flipping each bit of  with probability
with probability  . (Note that
. (Note that 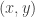 has the same distribution as
has the same distribution as 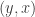 , so there’s no asymmetry here.)
, so there’s no asymmetry here.)
Now and
and  are typically quite far apart in Hamming distance, and since
are typically quite far apart in Hamming distance, and since  can have positive and negative values, big and small, it seems far from obvious that
can have positive and negative values, big and small, it seems far from obvious that ![\mathbb{E}[f(x) f(y)]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Bf%28x%29+f%28y%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) should be nonnegative.
should be nonnegative.
But this is obvious on the Fourier side: it’s precisely .
.
February 24, 2009 at 12:05 am
803.2 Positivity
That’s interesting. The non-obvious assertion is that a certain matrix (where the value at (x,y) is the probability that you get y when you start from x and flip) is positive definite. And the Fourier transform diagonalizes it. And that helps to see why it’s genuinely easier on the Fourier side: given a quadratic form, there is no reason to expect it to be easy to see that it is positive definite without diagonalizing it. (However, I am tempted to try with your example …)
February 24, 2009 at 11:52 am
803.3 Positivity
Got it! Details below in an hour’s time (after my lecture). It will be comment 812 if nobody else has commented by then.
February 23, 2009 at 11:15 pm |
804. DHJ(2.7)
Randall: I tried to wikify your notes from 593 at
http://michaelnielsen.org/polymath1/index.php?title=DHJ(2.7)
Unfortunately due to a wordpress error, an important portion of your Tex (in particular, part of the statement of DHJ(2.7)) was missing (the portion between a less than sign and a greater than sign – unfortunately this was interpreted as HTML and thus eaten). So I unfortunately don’t understand the proof. Could you possibly take a look at the page and try to restore the missing portion? Thanks!
February 24, 2009 at 5:04 am
Sorry about that. After several missteps, I may have managed to correct it in full….
February 23, 2009 at 11:22 pm |
805. Sperner
(Previous comment should be 804.)
Ryan’s notes (which, incidentally, might also be migrated to the wiki at some point) seem to imply something close to my Lemma in 578 that had a bogus proof, namely that if f is non-uniform in the sense that or
or  is large for some g, then f has significant Fourier concentration at low modes (i.e. the energy
is large for some g, then f has significant Fourier concentration at low modes (i.e. the energy  is large), and hence f correlates with a function of low influence (e.g. f correlates with
is large), and hence f correlates with a function of low influence (e.g. f correlates with  , where
, where 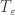 is the Fourier multiplier that multiplies the S fourier coefficient by
is the Fourier multiplier that multiplies the S fourier coefficient by 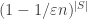 ).
).
If this is the case, then (because polynomial combinations of low influence functions are still low influence) one can iterate this in the usual energy-increment manner (or as in the proof of the regularity lemma) to obtain a decomposition , where
, where  is uniform and
is uniform and  has low influence, is non-negative and has the same density as
has low influence, is non-negative and has the same density as  . (This is an oversimplification; there are error terms, and one has to specify the scales at which uniformity or low influence occurs, but ignore these issues for now.)
. (This is an oversimplification; there are error terms, and one has to specify the scales at which uniformity or low influence occurs, but ignore these issues for now.)
If this is the case, then the Sperner count should be approximately equal to
should be approximately equal to  . But if
. But if  is low influence, this should be approximately
is low influence, this should be approximately 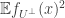 . Meanwhile, we have
. Meanwhile, we have  , so by Cauchy-Schwartz we get at least
, so by Cauchy-Schwartz we get at least 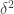 , as desired.
, as desired.
February 23, 2009 at 11:24 pm
805.1
p.s. Something very similar goes on in the ergodic proof of DHJ(2). What I call here will be called
here will be called 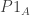 , where P is a certain “weak limit” of shift operators. The key point is that P is going to be an orthogonal projection in L^2 (this is the upshot of a Hilbert space lemma that I am working on on the wiki.)
, where P is a certain “weak limit” of shift operators. The key point is that P is going to be an orthogonal projection in L^2 (this is the upshot of a Hilbert space lemma that I am working on on the wiki.)
February 24, 2009 at 12:01 am |
806. Sperner.
Re #805, Terry, one thing I had trouble with was — roughly speaking — showing that indeed![\mathbb{E}[f_{U^\bot}(x) f_{U^\bot}(y)]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Bf_%7BU%5E%5Cbot%7D%28x%29+f_%7BU%5E%5Cbot%7D%28y%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) is close to
is close to ![\mathbb{E}[f_{U^\bot}(x)^2]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Bf_%7BU%5E%5Cbot%7D%28x%29%5E2%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
It seemed logical that this would be true but I had technical difficulties actually making the switch from to
to  . In some sense that’s why I wrote the notes, to really convince myself that one could do something. Unfortunately, that something was to define
. In some sense that’s why I wrote the notes, to really convince myself that one could do something. Unfortunately, that something was to define  all the way down to just the lowest mode; i.e., to look at density rather than energy.
all the way down to just the lowest mode; i.e., to look at density rather than energy.
Perhaps we could try to think about, at a technical level, how to really pass from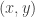 to
to 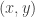 for low-influence functions…
for low-influence functions…
February 24, 2009 at 1:49 am
806.2 Sperner
Well, I would imagine that would have Fourier transform concentrated in sets S of size
would have Fourier transform concentrated in sets S of size 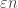 , and this should mean that the average influence of
, and this should mean that the average influence of  , i.e. {\Bbb E} |f_{U^\perp}(x) – f_{U^\perp}(y)|^2, where x and y differ by just one bit, should be small (something like
, i.e. {\Bbb E} |f_{U^\perp}(x) – f_{U^\perp}(y)|^2, where x and y differ by just one bit, should be small (something like 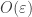 ). This should then be able to be iterated to extend to x and y being several bits apart rather than just one bit. (In order to do this properly, one will probably need to have a whole bunch of different scales in play, not just a single scale
). This should then be able to be iterated to extend to x and y being several bits apart rather than just one bit. (In order to do this properly, one will probably need to have a whole bunch of different scales in play, not just a single scale 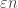 . There are various pigeonhole tricks that let one find a whole range of scales at which all statistics are the same [I call this the “finite convergence principle” in my blog], so as a first approximation let’s pretend that concentration at one scale
. There are various pigeonhole tricks that let one find a whole range of scales at which all statistics are the same [I call this the “finite convergence principle” in my blog], so as a first approximation let’s pretend that concentration at one scale  is the same as concentration at other small scales such as
is the same as concentration at other small scales such as  . The point is that while the L^2 energy of f could be significant in the range
. The point is that while the L^2 energy of f could be significant in the range 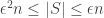 for a single
for a single  , the pigeonhole principle prevents it from being significant for all such choices of
, the pigeonhole principle prevents it from being significant for all such choices of  ])
])
February 24, 2009 at 12:08 am |
807. Fourier/density-increment.
In #802, I guess I’m getting the terminology all wrong. I should say that another problem I think the same method will work for is the problem in where you’re looking for “lines” of length 3 where in the wildcard coordinates you’re allowed either (0,1,1), (1,0,1), or (1,1,0).
where you’re looking for “lines” of length 3 where in the wildcard coordinates you’re allowed either (0,1,1), (1,0,1), or (1,1,0).
I don’t know if this problem has a name. It’s not quite a Schur triple. I personally would call it the “Not-Two” problem because in every coordinate you’re allowed (0,0,0), (1,1,1), (0,1,1), (1,0,1), or (1,1,0): anything where the number of 0’s is “Not Two”.
February 24, 2009 at 12:59 am
807.1
A question and 3 remarks:
Q: I remember when we first talked about it there were obvious difficulties for why fourier+increasing density strategy wont work. At the end what is the basic change that make it works is it changing the measure?
R1: sometimes is is equally convenient (and even more) not to work with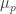 measures and their associated Fourier transform but to consider functions on [0,1]
measures and their associated Fourier transform but to consider functions on [0,1] and use the Walsh orthonormal basis even for every [0,1]. So given p we represent our set by a subset of the solid cube and use the “fine” Walsh transform all the time.
and use the Walsh orthonormal basis even for every [0,1]. So given p we represent our set by a subset of the solid cube and use the “fine” Walsh transform all the time.
R2: If changing the measure can help when small Fourier coefficients do not suffice for quasirandomness, is there hope it will help for case k=4 of Szemeredi?
R3: there are some problems regarding influences threshold phenomena where better understanding of the relation between equal sliced density and specific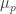 densities are needed. Maybe some of the tools from here can help.
densities are needed. Maybe some of the tools from here can help.
February 24, 2009 at 1:13 am |
808. Another Fourier/Sperner approach
Let me mention briefly a non density-increasing approach to Sperner. You first note that not having lines with 1 wild card implies that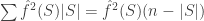 . If you can show that the non empty fourier coefficients are concentrated (in terms of |S|) then I think you can conclude that the density is small.
. If you can show that the non empty fourier coefficients are concentrated (in terms of |S|) then I think you can conclude that the density is small.
You want to control expression of the from . Those are related to the number of elements in the set when we fixed the value of n-k variables and look over all the rest. These numbers are controlled by the density of Sperner families for subsets of {1,2,…,k}. So this looks like circular thing but maybe it allows some bootstrapping.
. Those are related to the number of elements in the set when we fixed the value of n-k variables and look over all the rest. These numbers are controlled by the density of Sperner families for subsets of {1,2,…,k}. So this looks like circular thing but maybe it allows some bootstrapping.
February 24, 2009 at 5:42 am |
809. Response to 806.2 (Sperner).
Terry wrote, “This should then be able to be iterated to extend to x and y being several bits apart rather than just one bit.”
Hmm, but one source of annoyance is that y is not just x with or so bits flipped — it’s x with
or so bits flipped — it’s x with  or so 0’s flipped to 1’s. As you get more and more 1’s in there, the intermediate strings are less and less distributed as uniformly random strings. So it’s not 100% clear to me that you can keep appealing to average influence, since influence as defined is a uniform-distribution concept.
or so 0’s flipped to 1’s. As you get more and more 1’s in there, the intermediate strings are less and less distributed as uniformly random strings. So it’s not 100% clear to me that you can keep appealing to average influence, since influence as defined is a uniform-distribution concept.
Overall I agree that this is probably more of a nuisance then a genuine problem, but it was stymieing me a bit so I thought I’d ask.
February 24, 2009 at 6:07 am
809.2 Sperner and influence
Ryan, I think the trusty old triangle inequality should deal with things nicely. (I would need a binomial model of bit-flipping rather than a Poisson model, but I’m sure this makes very little difference.)
Suppose has average influence
has average influence  ; thus flipping a bit from a 0 to 1 or vice versa would only affect things by
; thus flipping a bit from a 0 to 1 or vice versa would only affect things by  on the average. Conditioning, we conclude that if we flip just one bit from a 0 to 1, we expect
on the average. Conditioning, we conclude that if we flip just one bit from a 0 to 1, we expect  to change by at most
to change by at most 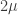 on the average. Now we iterate this process
on the average. Now we iterate this process 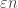 times. As long as
times. As long as 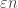 is much less than
is much less than 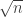 (as in your notes), there is no significant distortion of the underlying probability distribution and we see that if y differs by
(as in your notes), there is no significant distortion of the underlying probability distribution and we see that if y differs by 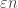 0->1 bits from x, then
0->1 bits from x, then 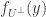 and
and  will differ by
will differ by  on the average.
on the average.
This will be enough for our purposes as long as the influence is a really small multiple of
is a really small multiple of  . One can’t quite get this by working at a single scale – one gets
. One can’t quite get this by working at a single scale – one gets  instead – but one can do so if one works with a whole range of scales and uses the energy increment argument. I’ve sketched out the details on the wiki at
instead – but one can do so if one works with a whole range of scales and uses the energy increment argument. I’ve sketched out the details on the wiki at
http://michaelnielsen.org/polymath1/index.php?title=Fourier-analytic_proof_of_Sperner
February 24, 2009 at 6:27 am |
810. DHJ(2.7)
Randall, thanks for cleaning up the file! It is a very nice proof, and I’d like to try to describe it in my own words here.
DHJ(2.7) is the strengthening of DHJ(2.6) that gives us three parallel combinatorial lines (i.e. they have the same wildcard set), the first of which hits the dense set A in the 0 and 1 position, the second hits it in the 1 and 2 position, and the third in the 2 and 0 position.
To describe Randall’s argument, I’d first like to describe how Randall’s argument gives yet another proof of DHJ(2) which is quite simple (and gives civilised bounds). It uses the density increment argument: we want to prove DHJ(2) at some density and we assume that we’ve already proven it at any significantly bigger density.
and we assume that we’ve already proven it at any significantly bigger density.
Now let A be a subset of![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  for some n. We split n into a smallish r and a biggish n-r, thus viewing
for some n. We split n into a smallish r and a biggish n-r, thus viewing ![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) as a whole bunch of (n-r)-dimensional slices, each indexed by a word in
as a whole bunch of (n-r)-dimensional slices, each indexed by a word in ![[2]^r](https://s0.wp.com/latex.php?latex=%5B2%5D%5Er&bg=ffffff&fg=333333&s=0&c=20201002) .
.
If any of the big slices has density significantly bigger than , we are done; so we can assume that all the big slices have density not much larger than
, we are done; so we can assume that all the big slices have density not much larger than  (e.g. at most
(e.g. at most 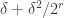 ). Because the total density is
). Because the total density is  , we can subtract and conclude that all the big slices have density close to
, we can subtract and conclude that all the big slices have density close to  .
.
Now we look at the r+1 slices indexed by the words . Each of these slices intersects the set A with density about
. Each of these slices intersects the set A with density about  . Thus by the pigeonhole principle, if r is much bigger than
. Thus by the pigeonhole principle, if r is much bigger than 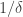 , then two of the A-slices must share a point in common, i.e. there exists
, then two of the A-slices must share a point in common, i.e. there exists ![w \in [2]^{n-r}](https://s0.wp.com/latex.php?latex=w+%5Cin+%5B2%5D%5E%7Bn-r%7D&bg=ffffff&fg=333333&s=0&c=20201002) and i,j such that
and i,j such that  both lie in A. Voila, a two-dimensional line.
both lie in A. Voila, a two-dimensional line.
The same argument gives DHJ(2.7). Now there are three different graphs on r+1 vertices, the 01 graph, the 12 graph, and the 20 graph. i and j are connected on the 01 graph if the -slice and
-slice and 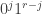 -slice of A have a point in common; similarly define the 12 graph and the 20 graph. Together, this forms an 8-coloured graph on r+1 vertices. By Ramsey’s theorem, if r is big enough there is a monochromatic subgraph of size
-slice of A have a point in common; similarly define the 12 graph and the 20 graph. Together, this forms an 8-coloured graph on r+1 vertices. By Ramsey’s theorem, if r is big enough there is a monochromatic subgraph of size 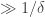 . But by the preceding pigeonhole argument, we see that none of the 01 graph, the 12 graph, or the 20 graph can vanish completely here, so they must instead all be complete, and we get three parallel combinatorial lines, each intersecting A in two of the three positions.
. But by the preceding pigeonhole argument, we see that none of the 01 graph, the 12 graph, or the 20 graph can vanish completely here, so they must instead all be complete, and we get three parallel combinatorial lines, each intersecting A in two of the three positions.
February 24, 2009 at 6:53 am |
811. Prelude to some more density-increment arguments.
I was hoping to give an illustration of the #578 technique for a problem in![{[3]^n}](https://s0.wp.com/latex.php?latex=%7B%5B3%5D%5En%7D&bg=ffffff&fg=000000&s=0&c=20201002) . But it got too late for me to finish writing it, so I’ll just give the “background info” I managed to write. This probably ought to go in the wiki rather than in a post, but having spent a bit of time to get Luca’s converter working for me, I didn’t have the energy to also convert to the third, wiki format. More on the #578 method tomorrow.
. But it got too late for me to finish writing it, so I’ll just give the “background info” I managed to write. This probably ought to go in the wiki rather than in a post, but having spent a bit of time to get Luca’s converter working for me, I didn’t have the energy to also convert to the third, wiki format. More on the #578 method tomorrow.
Here, then, some basics on noise and correlated product spaces; for more, see e.g. this paper of Mossel.
Let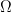 be a small finite set; for example,
be a small finite set; for example, ![{\Omega = [3]}](https://s0.wp.com/latex.php?latex=%7B%5COmega+%3D+%5B3%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Let
. Let 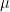 be a probability distribution on
be a probability distribution on 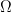 . Abusing notation, write also
. Abusing notation, write also  for the corresponding product distribution on
for the corresponding product distribution on  . For
. For  , define the noise operator
, define the noise operator 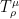 , which acts on functions
, which acts on functions  , as follows:
, as follows: ![\displaystyle (T_\rho^\mu f)(x) = \mathop{\bf E}_{{\bf y} \sim^\mu_\rho x}[f({\bf y})],](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%28T_%5Crho%5E%5Cmu+f%29%28x%29+%3D+%5Cmathop%7B%5Cbf+E%7D_%7B%7B%5Cbf+y%7D+%5Csim%5E%5Cmu_%5Crho+x%7D%5Bf%28%7B%5Cbf+y%7D%29%5D%2C+&bg=ffffff&fg=000000&s=0&c=20201002)
 denotes that
denotes that 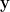 is formed from
is formed from  by doing the following, independently for each
by doing the following, independently for each ![{i \in [n]}](https://s0.wp.com/latex.php?latex=%7Bi+%5Cin+%5Bn%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) : with probability
: with probability 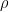 , set
, set 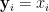 ; with probability
; with probability  , draw
, draw 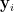 from
from 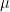 (i.e., “rerandomize the coordinate”). (I use boldface for random variables.)
(i.e., “rerandomize the coordinate”). (I use boldface for random variables.)
where
Here are some simple facts about the noise operator:
Fact 1:![{\mathop{\bf E}_{{\bf x} \sim \mu}[T_\rho^\mu f({\bf x})] = \mathop{\bf E}_{{\bf x} \sim \mu}[f({\bf x})]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D_%7B%7B%5Cbf+x%7D+%5Csim+%5Cmu%7D%5BT_%5Crho%5E%5Cmu+f%28%7B%5Cbf+x%7D%29%5D+%3D+%5Cmathop%7B%5Cbf+E%7D_%7B%7B%5Cbf+x%7D+%5Csim+%5Cmu%7D%5Bf%28%7B%5Cbf+x%7D%29%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Fact 2: For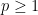 we have
we have 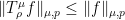 , where
, where  denotes
denotes ![{\mathop{\bf E}_{{\bf x} \sim \mu}[|f({\bf x})|^p]^{1/p}}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D_%7B%7B%5Cbf+x%7D+%5Csim+%5Cmu%7D%5B%7Cf%28%7B%5Cbf+x%7D%29%7C%5Ep%5D%5E%7B1%2Fp%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Fact 3: The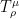 ‘s form a semigroup, in the sense that
‘s form a semigroup, in the sense that  .
.
Fact 4:![{\mathop{\bf E}_{{\bf x} \sim \mu}[f({\bf x}) \cdot T_\rho^\mu f({\bf x})] = \mathop{\bf E}_{{\bf x} \sim \mu}[(T_{\sqrt{\rho}}^\mu f({\bf x}))^2]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D_%7B%7B%5Cbf+x%7D+%5Csim+%5Cmu%7D%5Bf%28%7B%5Cbf+x%7D%29+%5Ccdot+T_%5Crho%5E%5Cmu+f%28%7B%5Cbf+x%7D%29%5D+%3D+%5Cmathop%7B%5Cbf+E%7D_%7B%7B%5Cbf+x%7D+%5Csim+%5Cmu%7D%5B%28T_%7B%5Csqrt%7B%5Crho%7D%7D%5E%5Cmu+f%28%7B%5Cbf+x%7D%29%29%5E2%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . We use the notation
. We use the notation 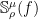 for this quantity.
for this quantity.
Fact 5:![{\mathbb{S}_{1-\gamma}^\mu(f) = \mathop{\bf E}_\mu[(T_{\sqrt{1 - \gamma}}^\mu f)^2] = \mathop{\bf E}_{{\bf V}}[\mathop{\bf E}_\mu[f|_{{\bf V}}]^2]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathbb%7BS%7D_%7B1-%5Cgamma%7D%5E%5Cmu%28f%29+%3D+%5Cmathop%7B%5Cbf+E%7D_%5Cmu%5B%28T_%7B%5Csqrt%7B1+-+%5Cgamma%7D%7D%5E%5Cmu+f%29%5E2%5D+%3D+%5Cmathop%7B%5Cbf+E%7D_%7B%7B%5Cbf+V%7D%7D%5B%5Cmathop%7B%5Cbf+E%7D_%5Cmu%5Bf%7C_%7B%7B%5Cbf+V%7D%7D%5D%5E2%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) , where: a)
, where: a) 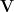 is a randomly chosen combinatorial subspace, with each coordinate being fixed (from
is a randomly chosen combinatorial subspace, with each coordinate being fixed (from 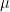 ) with probability
) with probability 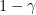 and left “free” with probability
and left “free” with probability 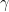 , independently; b)
, independently; b) 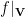 denotes the restriction of
denotes the restriction of  to this subspace, and
to this subspace, and ![{\mathop{\bf E}_\mu[f|_{{\bf V}}]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D_%5Cmu%5Bf%7C_%7B%7B%5Cbf+V%7D%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) denotes the mean of this restricted function, under
denotes the mean of this restricted function, under 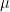 (the product distribution on the free coordinates of
(the product distribution on the free coordinates of  ).
).
February 24, 2009 at 1:32 pm |
812. Positivity
This concerns Ryan’s example of a quantity that is easily seen to be non-negative on the Fourier side, and not so easily seen to be non-negative in physical space. Except that I now have an easy argument in physical space. I don’t know how relevant this is, but there is some potential motivation for it, which is that perhaps the simple idea behind the proof could help in Ryan’s quest for a “non-wrong” proof of Sperner.
The problem, laid out in 803.1, was this. Let be a function defined on
be a function defined on  . Now choose two random points
. Now choose two random points  in
in  as follows:
as follows:  is uniform, and
is uniform, and  is obtained from
is obtained from  by changing each bit of
by changing each bit of  independently with probability 1/5. Now show that
independently with probability 1/5. Now show that  is non-negative for all real functions
is non-negative for all real functions  .
.
There are various ways of describing a proof of this. Here is the one I first thought of, and after that I’ll give a slicker version. I’m going to do a different calculation. Again I’ll pick a random , but this time I’ll create two new vectors
, but this time I’ll create two new vectors  and
and  out of
out of  , which will be independent of each other (given
, which will be independent of each other (given  ) and obtained from
) and obtained from  by flipping coordinates with probability
by flipping coordinates with probability  . And I’ll choose
. And I’ll choose  so that
so that 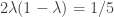 , which guarantees that the probability that the
, which guarantees that the probability that the  th coordinates of
th coordinates of  and
and  are equal is
are equal is  . Then I’ll work out
. Then I’ll work out 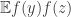 . It’s obviously positive because it is equal to
. It’s obviously positive because it is equal to ![\mathbb{E}_x(\mathbb{E}[f(y)|x])^2](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D_x%28%5Cmathbb%7BE%7D%5Bf%28y%29%7Cx%5D%29%5E2&bg=ffffff&fg=333333&s=0&c=20201002) . But also, the joint distribution of
. But also, the joint distribution of  and
and  is equal to the joint distribution of
is equal to the joint distribution of  and
and  , since
, since  is uniform and the digits of
is uniform and the digits of  are obtained from
are obtained from  by flipping independently with probability
by flipping independently with probability  . (Proof: the events
. (Proof: the events 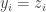 are independent and have probability 4/5.)
are independent and have probability 4/5.)
Now for the second way of seeing it. This time I’ll generate from
from  in two stages. First I’ll flip each digit with probability
in two stages. First I’ll flip each digit with probability  . And then I’ll do that again. Now each time you flip with probability
. And then I’ll do that again. Now each time you flip with probability  you are multiplying
you are multiplying  by the symmetric matrix
by the symmetric matrix  defined by
defined by  (which is the same as convolving
(which is the same as convolving  by the function
by the function 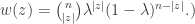 So we end up with
So we end up with 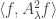 , which, since
, which, since 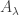 is symmetric, is
is symmetric, is 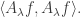
Note that this proof fails if you flip with probability p greater than 1/2, because then you can’t solve the equation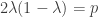 . But that’s all to the good, because the result is false when
. But that’s all to the good, because the result is false when  . When
. When 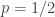 it is “only just true” since flipping with probability 1/2 gives you the uniform distribution for y, so if
it is “only just true” since flipping with probability 1/2 gives you the uniform distribution for y, so if  averages zero then
averages zero then  is zero too.
is zero too.
I’m sure there’s yet another way of looking at it (and in fact these thoughts led to the above proof) which is to think of the random flipping operation as the exponential of an operation where you flip with a different probability. (To define that, I would flip N times, each time with probability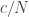 , and take limits.) I would then expect some general nonsense about exponentials to give the positivity. In the end I have taken a square root instead.
, and take limits.) I would then expect some general nonsense about exponentials to give the positivity. In the end I have taken a square root instead.
February 24, 2009 at 4:06 pm
812.1. Thanks Tim! I believe this proof is in fact Fact 4 from #811 (with its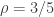 ).
).
February 24, 2009 at 4:27 pm
812.2. I was pleased with myself for figuring out the analogous trick in our equal-slices setting… until I realized it was exactly what you said way back in #572, first paragraph. Drat.
February 24, 2009 at 1:50 pm |
813. An optimistic conjecture.
The hyper-optimistic conjecture says that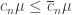 . Here I would like to suggest an “optimistic conjecture”:
. Here I would like to suggest an “optimistic conjecture”: such that
such that 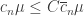 for all
for all  .
.
There exist a number
The hyper-optimistic conjecture implies the optimistic conjecture and the optimistic conjecture implies DHJ.
Let be the set of elements x in A, such that A has measure at least
be the set of elements x in A, such that A has measure at least  in the slice x belong to.
in the slice x belong to.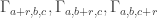 is at most 2. In particular A cannot contain more than 2/3 of each of three slices in an equilateral triangle. Thus, the slices where A has a density greater than 2/3 forms a triangle-free subset of
is at most 2. In particular A cannot contain more than 2/3 of each of three slices in an equilateral triangle. Thus, the slices where A has a density greater than 2/3 forms a triangle-free subset of 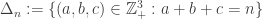 . So, if the optimistic conjecture is false, we know that for biggest line-free set A, the density of
. So, if the optimistic conjecture is false, we know that for biggest line-free set A, the density of 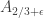 in A go to 0 as $n\to \infty$.
in A go to 0 as $n\to \infty$.
We know that if A is a line-free set, the sum of the measure of A in the slices
I think the following would imply DHJ: there exist a C such that for every set A with
there exist a C such that for every set A with 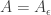 (no element in A is “epsilon-lonesome” in its slice) there exist a equilateral triangle-free set
(no element in A is “epsilon-lonesome” in its slice) there exist a equilateral triangle-free set 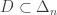 with more than
with more than  elements.
elements.
For every
February 24, 2009 at 4:11 pm |
814. Re Sperner & Influences & 809.2.
Hi Terry, not to be ridiculously nitpicky, but could I ask one more question?
It seems to me that: might end up having range
might end up having range ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) rather than
rather than  ;
; ;
; . (It wouldn’t be a problem if
. (It wouldn’t be a problem if  had range
had range  since
since  is a metric on $\{0,1\}$.)
is a metric on $\{0,1\}$.)
a)
b) average influence is defined in terms of the *squared* change in
c) we don’t have a triangle inequality for
February 24, 2009 at 4:33 pm
814.1. Maybe one gets around it by playing with the scales & using triangle inequality for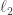 ; I’m thinking about it…
; I’m thinking about it…
February 24, 2009 at 5:10 pm
814.2. Oops.
That was a dumb question, as it turns out. Assuming is bounded, squared-differences are bounded by 4 times absolute-value-differences, and then use the triangle inequality. Got it.
is bounded, squared-differences are bounded by 4 times absolute-value-differences, and then use the triangle inequality. Got it.
February 24, 2009 at 5:56 pm |
815. Re Sperner.
I think I can answer my own question from #814. I’ll say what Terry was saying in #809.2, being a little bit imprecise. Let be an integer. Define random variables
be an integer. Define random variables 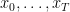 as follows:
as follows: 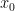 is a uniformly random string;
is a uniformly random string;  is formed from
is formed from  by picking a random coordinate and, if that coordinate is
by picking a random coordinate and, if that coordinate is  in
in  , changing it to a
, changing it to a  . Now the distribution on
. Now the distribution on  is pretty much like the distribution on
is pretty much like the distribution on 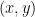 from before, with
from before, with 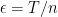 . Probably, as Terry says, one should ultimately wrap a Poisson choice of
. Probably, as Terry says, one should ultimately wrap a Poisson choice of 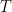 around this entire process.
around this entire process.
Anyway, for fixed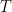 , by telescoping we have
, by telescoping we have ![\displaystyle \mathop{\bf E}[f(x_0)g(x_T)] = \mathop{\bf E}[f(x_0)g(x_0)] + \sum_{t=1}^T \mathop{\bf E}[f(x_0)(g(x_t) - g(x_{t-1}))]. \ \ \ \ \ (1)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+++%5Cmathop%7B%5Cbf+E%7D%5Bf%28x_0%29g%28x_T%29%5D+%3D+%5Cmathop%7B%5Cbf+E%7D%5Bf%28x_0%29g%28x_0%29%5D+%2B+%5Csum_%7Bt%3D1%7D%5ET+%5Cmathop%7B%5Cbf+E%7D%5Bf%28x_0%29%28g%28x_t%29+-+g%28x_%7Bt-1%7D%29%29%5D.+%5C+%5C+%5C+%5C+%5C+%281%29&bg=ffffff&fg=000000&s=0&c=20201002)
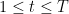 we have
we have ![\displaystyle |\mathop{\bf E}[f(x_0)(g(x_t) - g(x_{t-1}))]| \leq \|f\|_2 \sqrt{\mathop{\bf E}[(g(x_t) - g(x_{t-1}))^2]}. \ \ \ \ \ (2)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+++%7C%5Cmathop%7B%5Cbf+E%7D%5Bf%28x_0%29%28g%28x_t%29+-+g%28x_%7Bt-1%7D%29%29%5D%7C+%5Cleq+%5C%7Cf%5C%7C_2+%5Csqrt%7B%5Cmathop%7B%5Cbf+E%7D%5B%28g%28x_t%29+-+g%28x_%7Bt-1%7D%29%29%5E2%5D%7D.+%5C+%5C+%5C+%5C+%5C+%282%29&bg=ffffff&fg=000000&s=0&c=20201002)
 be the function defined by
be the function defined by ![{Mg(y) = \mathop{\bf E}_{y'}[(g(y') - g(y))^2]}](https://s0.wp.com/latex.php?latex=%7BMg%28y%29+%3D+%5Cmathop%7B%5Cbf+E%7D_%7By%27%7D%5B%28g%28y%27%29+-+g%28y%29%29%5E2%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) , where
, where 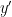 is formed from
is formed from 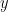 by taking one step in the Markov chain we used in defining the
by taking one step in the Markov chain we used in defining the  ‘s. Hence the expression inside the square-root in (2) is
‘s. Hence the expression inside the square-root in (2) is ![{\mathop{\bf E}[Mg(x_{t-1})]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D%5BMg%28x_%7Bt-1%7D%29%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . We would like to say that this expectation is close to
. We would like to say that this expectation is close to ![{\mathop{\bf E}[Mg(x_0)]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D%5BMg%28x_0%29%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) because the distributions on
because the distributions on 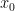 and
and  are very similar. We can use the argument in my “wrong-Sperner” notes for this. Using
are very similar. We can use the argument in my “wrong-Sperner” notes for this. Using  , I think that’ll give something like
, I think that’ll give something like ![\displaystyle |\mathop{\bf E}[Mg(x_{t-1})] - \mathop{\bf E}[Mg(x_{0})]| \leq O(t/\sqrt{n}) \|Mg(x_0)\|_2 \leq O(t/\sqrt{n}) \sqrt{\mathop{\bf E}[Mg(x_0)]},](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%7C%5Cmathop%7B%5Cbf+E%7D%5BMg%28x_%7Bt-1%7D%29%5D+-+%5Cmathop%7B%5Cbf+E%7D%5BMg%28x_%7B0%7D%29%5D%7C+%5Cleq+O%28t%2F%5Csqrt%7Bn%7D%29+%5C%7CMg%28x_0%29%5C%7C_2+%5Cleq+O%28t%2F%5Csqrt%7Bn%7D%29+%5Csqrt%7B%5Cmathop%7B%5Cbf+E%7D%5BMg%28x_0%29%5D%7D%2C+&bg=ffffff&fg=000000&s=0&c=20201002)
 is bounded, hence
is bounded, hence  is bounded, hence
is bounded, hence  pointwise.
pointwise.
To bound the “error term” here, use Cauchy-Schwarz on each summand. For a given
Let
where on the right I’ve now assumed that
But![{\mathop{\bf E}[Mg(x_0)]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D%5BMg%28x_0%29%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is precisely (well, maybe up to a factor of
is precisely (well, maybe up to a factor of  or something) the “energy” or “average influence” of
or something) the “energy” or “average influence” of  ; write it as
; write it as  . So we get
. So we get ![\displaystyle \mathop{\bf E}[(g(x_t) - g(x_{t-1}))^2] = \mathcal{E}(g) \pm O(t/\sqrt{n}) \sqrt{\mathcal{E}(g)}.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cmathop%7B%5Cbf+E%7D%5B%28g%28x_t%29+-+g%28x_%7Bt-1%7D%29%29%5E2%5D+%3D+%5Cmathcal%7BE%7D%28g%29+%5Cpm+O%28t%2F%5Csqrt%7Bn%7D%29+%5Csqrt%7B%5Cmathcal%7BE%7D%28g%29%7D.+&bg=ffffff&fg=000000&s=0&c=20201002)
 . Then the error in the above is essentially negligible. Now plugging this into (2) we get that each of the
. Then the error in the above is essentially negligible. Now plugging this into (2) we get that each of the  error terms in (1) is at most
error terms in (1) is at most  . So overall, we conclude
. So overall, we conclude ![\displaystyle \mathop{\bf E}[f(x_0)g(x_T)] = \mathop{\bf E}[f(x_0)g(x_0)] \pm O(T \cdot \|f\|_2 \cdot \sqrt{\mathcal{E}(g)}). \ \ \ \ \ (3)](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+++%5Cmathop%7B%5Cbf+E%7D%5Bf%28x_0%29g%28x_T%29%5D+%3D+%5Cmathop%7B%5Cbf+E%7D%5Bf%28x_0%29g%28x_0%29%5D+%5Cpm+O%28T+%5Ccdot+%5C%7Cf%5C%7C_2+%5Ccdot+%5Csqrt%7B%5Cmathcal%7BE%7D%28g%29%7D%29.+%5C+%5C+%5C+%5C+%5C+%283%29&bg=ffffff&fg=000000&s=0&c=20201002)
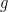 is bounded and that
is bounded and that  .
.
Let’s assume now that in fact
Just to repeat, the assumptions needed to deduce (3) were that
February 24, 2009 at 8:10 pm
815.1 Sperner
Ryan, thanks for fleshing in the details and sorting out the l^1 vs l^2 issue. I just wanted to point out that we may have located the “DHJ(0,2)” problem that Boris brought up a while back – namely, DHJ(0,2) should be DHJ(2) for “low influence” sets. I think we now have a satisfactory understanding of the DHJ(2) problem from an obstructions-to-uniformity perspective, namely that arbitrary sets can be viewed as the superposition of a low influence set (or more precisely, a function ) plus a DHJ(2)-uniform error.
) plus a DHJ(2)-uniform error.
DHJ(1,3) may now need to be tweaked to generalise to functions f which are polynomial combinations of 01-low influence, 12-low influence, and 20-low influence functions, where 01-low influence means that f(x) and f(y) are close whenever y is formed from x by flipping a random 0 bit to a 1 or vice versa, etc. (With our current definition of DHJ(1,3), we are considering products of indicator functions which have zero 01-influence, zero 12-influence, and zero 20-influence respectively.)
February 24, 2009 at 6:47 pm |
816. Obstructions.
I hope I’m going to have time to do some serious averaging arguments this evening. They will be private calculations (though made public as soon as they work), but let me give an outline of what I am hoping to make rigorous. The broad aim is to prove that a set with no combinatorial lines has a significant local correlation with a set of complexity 1. This is a statement that has been sort of sketched in various comments already (by Terry and by me and possibly by others too), but I now think that writing it out in a serious way will be a very useful thing to do and should get us substantially closer to a density-increment proof of DHJ(3). Here is a rough description of the steps.
1. A rather general argument to prove that whenever we feel like restricting to a combinatorial subspace, we can always assume that it has density at most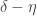 , where
, where  is an arbitrary function of
is an arbitrary function of  . This kind of argument is standard, and has already been mentioned by Terry: basically if you can find a subspace with increased density then you happily pass to that subspace and you’ve already completed your iteration. If you can’t do that, then the proportion of subspaces (according to any reasonable distribution of your convenience) with substantially smaller density is tiny. The minor (I hope) technical challenge is to get a version of this principle that is sufficiently general that it can be used easily whenever it is needed.
. This kind of argument is standard, and has already been mentioned by Terry: basically if you can find a subspace with increased density then you happily pass to that subspace and you’ve already completed your iteration. If you can’t do that, then the proportion of subspaces (according to any reasonable distribution of your convenience) with substantially smaller density is tiny. The minor (I hope) technical challenge is to get a version of this principle that is sufficiently general that it can be used easily whenever it is needed.
2. Representing combinatorial lines as (U,V,W), we know that for an average W (each element chosen with probability 1/3 — I’m going for uniform measure here) the density of (U,V) such that (U,V,W) is in is
is  .
.
3. Also, by 1, for almost all W we find that the set of points where
where 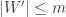 (for some
(for some  with
with  ) has density almost
) has density almost  .
.
4. Combining 2 and 3, we obtain a W such that the density of (U,V) with (U,V,W) in is at least
is at least 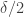 , say, and the density of
, say, and the density of  is almost as large as
is almost as large as  (at least).
(at least).
5. But the points of the latter kind have to avoid those and
and  for which the point
for which the point 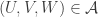 , which is a dense complexity-1 obstruction in the “unbalanced” set of
, which is a dense complexity-1 obstruction in the “unbalanced” set of  that have union
that have union ![{}[n]\setminus W](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D%5Csetminus+W&bg=ffffff&fg=333333&s=0&c=20201002) and have
and have 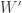 of size at most
of size at most  .
.
6. Randomly restricting, we can get a similar statement, but this time for a “balanced” set—that is, one where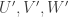 have comparable sizes.
have comparable sizes.
7. From that it is straightforward to get a (local) density increment on a special set of complexity 1 (as defined here).
Now I think I’ve basically shown that a special set of complexity 1 contains large combinatorial subspaces, though I need to check this. But what we actually need is a bit stronger than that: we need to cover sets of complexity 1 uniformly by large combinatorial subspaces, or perhaps do something else of a similar nature. (This is where the Ajtai-Szemerédi proof could come in very handy.) But if everything from 1 to 7 works out—I’m not sure how realistic a hope that is but even a failure would be instructive—then we’ll be left with a much smaller-looking problem to solve. I’ll report back when I either get something working or see where some unexpected difficulty lies.
February 24, 2009 at 8:27 pm |
817. Sperner.
Just to clarify, the thing I wrote in #800 says that if you don’t mind restricting to combinatorial subspaces (which we usually don’t, unless we’re really trying to get outstanding quantitatives), then the decomposition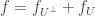 we seek can be achieved trivially: you just take
we seek can be achieved trivially: you just take ![f_{U^\bot} = \mathbb{E}[f]](https://s0.wp.com/latex.php?latex=f_%7BU%5E%5Cbot%7D+%3D+%5Cmathbb%7BE%7D%5Bf%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
February 25, 2009 at 2:35 am |
818. Ergodic proof of DHJ(3)
I managed to digest Randall’s lecture notes on the completion of the Furstenberg-Katznelson proof of DHJ(3) (the focus of the 600 thread) to the point where I now have an informal combinatorial translation of the argument at
http://michaelnielsen.org/polymath1/index.php?title=Furstenberg-Katznelson_argument
that avoids any reference to infinitary concepts, at the expense of rigour and precision. Interestingly, the argument is morally based on a reduction to something resembling DHJ(1,3), but more complicated to state. We are trying to get a lower bound for
where f is non-negative, bounded, and has positive density, and ranges over all lines with “few” wildcards (and I want to be vague about what “few” means). The first reduction is to eliminate “uniform” or “mixing” components from the second two factors and reduce to
ranges over all lines with “few” wildcards (and I want to be vague about what “few” means). The first reduction is to eliminate “uniform” or “mixing” components from the second two factors and reduce to
where ,
, 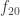 are certain “structured” components of f, analogous to
are certain “structured” components of f, analogous to  from the Sperner theory. They have positive correlation with f, and in fact are positive just about everywhere that f is positive.
from the Sperner theory. They have positive correlation with f, and in fact are positive just about everywhere that f is positive.
What other properties do have? In a perfect world, they would be “complexity 1” sets, and in particular one would expect
have? In a perfect world, they would be “complexity 1” sets, and in particular one would expect  to be describable as some simple combination of 01-low influence sets and 12-low influence sets (and similarly
to be describable as some simple combination of 01-low influence sets and 12-low influence sets (and similarly 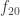 should be some simple combination of 20-low influence sets and 12-low influence sets). Here, ij-low influence means that the function does not change much if an i is flipped to a j or vice versa.
should be some simple combination of 20-low influence sets and 12-low influence sets). Here, ij-low influence means that the function does not change much if an i is flipped to a j or vice versa.
Unfortunately, it seems (at least from the ergodic approach) that this is not easily attainable. Instead, obeys a more complicated (and weaker) property, which I call “01-almost periodicity relative to 12-low influence”, with
obeys a more complicated (and weaker) property, which I call “01-almost periodicity relative to 12-low influence”, with 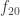 obeying a similar property. Very roughly speaking, this is a “relative” version of 01-low influence: flipping digits from 0 to 1 makes
obeying a similar property. Very roughly speaking, this is a “relative” version of 01-low influence: flipping digits from 0 to 1 makes  change, but the way in which it changes is controlled entirely by functions that have low 12-influence. (This is related to the notion of “uniform almost periodicity” which comes up in my paper on the quantitative ergodic theory proof of Szemeredi’s theorem.)
change, but the way in which it changes is controlled entirely by functions that have low 12-influence. (This is related to the notion of “uniform almost periodicity” which comes up in my paper on the quantitative ergodic theory proof of Szemeredi’s theorem.)
It is relatively painless (using Cauchy-Schwarz and energy-increment methods) to pass from (1) to (2). To deal with (2) we need some periodicity properties of on small “monochromatic” spaces (the existence of which is ultimately guaranteed by Graham-Rothschild) which effectively let us replace
on small “monochromatic” spaces (the existence of which is ultimately guaranteed by Graham-Rothschild) which effectively let us replace 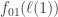 with
with  and
and 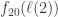 with
with  on a large family of lines
on a large family of lines  (and more importantly, a large 12-low influence family of lines). From this fact, and the previously mentioned fact that
(and more importantly, a large 12-low influence family of lines). From this fact, and the previously mentioned fact that  are large on f, we can get DHJ(3).
are large on f, we can get DHJ(3).
The argument as described on the wiki is far from rigorous at present, but I am hopeful that it can be translated into a rigorous finitary proof (though it is not going to be pleasant – I would have to deploy a lot of machinery from my quantitative ergodic theory paper). Perhaps a better approach would be to try to export some of the ideas here to the Fourier-type approaches where there is a better chance of a shorter and more quantitatively effective argument.
February 25, 2009 at 5:06 pm
818.1
I haven’t read this closely enough to have even an initial impression, however, much of it looks (somewhat) familiar.
First, I notice you removed your discussion of stationarity…instead (tell me if I misread), and in multiple settings, you seem to do a Cesaro average, over lines, rather than employing something like Graham-Rothschild to get near-convergence along lines restricted to a subspace. Most striking of these are instances of using the so-called IP van der Corput lemma. Looking at its proof, this does indeed look kosher, but it’s rather surprising to me all the same; assuming I’m understanding this at least somewhat correctly, did you give any thought to whether the ergodic proof itself could be tidily rewritten to accommodate this averaging method?
Modulo the above, the main part of the argument I still don’t (in principle) understand is how you bound h, the number of functions used to approximate the almost periodic component of f, independently of n. (This is the part of the argument I got stuck on in my own thoughts.) I see now that you solved this issue in your quantitative ergodic proof of Szemeredi, which I printed last night as well, though I haven’t read deeply enough yet to see how. Am I to assume that something similar happens here, or is the answer different in the two cases?
February 25, 2009 at 8:50 pm
818.2
Yes, the argument is distilled from your notes, though as you see I messed around with the notation quite a bit.
The stationarity is sort of automatic if you work with random subspaces of a big space![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , and I am implicitly using it all over the place when rewriting one sort of average by another.
, and I am implicitly using it all over the place when rewriting one sort of average by another.
I am indeed hoping that Cesaro averaging may be simpler to implement than IP averaging, and may save me from having to use Graham-Rothschild repeatedly. There are a lot of things hidden in the sketch that may cause this to bubble up. For instance, I am implicitly using the fact that certain shift operators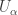 converge (in some Cesaro or IP sense) to an orthogonal projection, and this may require a certain amount of Graham-Rothschild type trickery (I started writing some separate notes on a finitary Hilbert space IP Khintchine recurrence theorem which will be relevant here.)
converge (in some Cesaro or IP sense) to an orthogonal projection, and this may require a certain amount of Graham-Rothschild type trickery (I started writing some separate notes on a finitary Hilbert space IP Khintchine recurrence theorem which will be relevant here.)
I admit I’m a bit sketchy on how to deal with h not blowing up. A key observation here is that of statistical sampling: if one wants to understand an average of bounded quantities over a very large set H, one can get quite a good approximation to this expression by picking a relatively small number
of bounded quantities over a very large set H, one can get quite a good approximation to this expression by picking a relatively small number  of representatives of H at random and looking at the local average
of representatives of H at random and looking at the local average  instead. (This fact substitutes for the fact used in the Furstenberg approach that Volterra integral operators are compact and hence approximable by finite rank operators; or more precisely, the Furstenberg approach needs the relative version of this over some factor Y.) I haven’t worked out completely how this trick will mesh with the IP-systems involved, but I’m hoping that I can throw enough Ramsey theorems at the problem to make it work out.
instead. (This fact substitutes for the fact used in the Furstenberg approach that Volterra integral operators are compact and hence approximable by finite rank operators; or more precisely, the Furstenberg approach needs the relative version of this over some factor Y.) I haven’t worked out completely how this trick will mesh with the IP-systems involved, but I’m hoping that I can throw enough Ramsey theorems at the problem to make it work out.
Perhaps one thing that helps out in the finitary setting that is not immediately available in the ergodic setting is that there are more symmetries available; in particular, the non-commutativity of the IP systems that makes the ergodic setup so hard seems to be less of an issue in the finitary world (the operations of flipping a random 0 to a 1 and flipping a random 0 to a 2 essentially commute since there are so many 0s to choose from). There is a price to pay for this, which is that certain Ramsey theorems may break the symmetry and so one may have to choose to forego either the Ramsey theorem or the symmetry. This could potentially cause a problem in my sketch; as I said, I have not worked out the details (given the progress on the Fourier side of things, I had the vague hope that maybe just the concepts in the sketch, most notably the concept of almost periodicity relative to a low influence factor, could be useful to assist the other main approach to the problem, as I am not particularly looking forward to rewriting my quantitative ergodic theory paper again.)
February 25, 2009 at 4:53 am |
819. #816 and #818 look quite exciting; I plan to try to digest them soon. Meanwhile, here is a Moser-esque problem I invented for the express purpose of being solvable. I hope it might give a few tricks we can use (but it might not be of major help due to the PS of #528).
Let’s define a combinatorial bridge in![{[3]^n}](https://s0.wp.com/latex.php?latex=%7B%5B3%5D%5En%7D&bg=ffffff&fg=000000&s=0&c=20201002) to be a triple of points
to be a triple of points  formed by taking a string with zero or more wildcards and filling in the wildcards with either
formed by taking a string with zero or more wildcards and filling in the wildcards with either 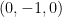 or
or  . If there are zero wildcards we call the bridge degenerate. I think I can show, using the ideas from #800, that if
. If there are zero wildcards we call the bridge degenerate. I think I can show, using the ideas from #800, that if 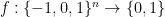 has mean
has mean 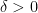 and
and  is sufficiently large as function of
is sufficiently large as function of 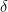 , then there is a nondegenerate bridge
, then there is a nondegenerate bridge 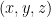 with
with 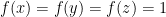 .
.
Roughly, we first use a density-increment argument to reduce to the case when is extremely noise sensitive; i.e.,
is extremely noise sensitive; i.e., 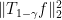 is only a teeny bit bigger than
is only a teeny bit bigger than 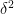 . Here
. Here 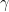 is something very small to be chosen later. Next, we pick a suitable distribution on combinatorial bridges
is something very small to be chosen later. Next, we pick a suitable distribution on combinatorial bridges 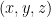 ; basically, choose a random one where the wildcard probability is
; basically, choose a random one where the wildcard probability is  . Now the key is that under this distribution, there is “imperfect correlation” between the random variable
. Now the key is that under this distribution, there is “imperfect correlation” between the random variable 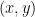 and the random variable
and the random variable  — and similarly, between
— and similarly, between  and
and 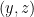 . Here I use the term in the sense of the Mossel paper in #811. Because of this (see Mossel’s Lemma 6.2),
. Here I use the term in the sense of the Mossel paper in #811. Because of this (see Mossel’s Lemma 6.2), ![{\mathop{\bf E}[f(x)f(y)f(z)]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D%5Bf%28x%29f%28y%29f%28z%29%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is practically the same as
is practically the same as ![{\mathop{\bf E}[T_{1-\gamma}f(x)\cdot T_{1-\gamma}f(y)\cdot T_{1-\gamma}f(z)]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D%5BT_%7B1-%5Cgamma%7Df%28x%29%5Ccdot+T_%7B1-%5Cgamma%7Df%28y%29%5Ccdot+T_%7B1-%5Cgamma%7Df%28z%29%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) , when
, when 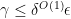 . But this is extremely close to
. But this is extremely close to 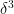 because
because ![{\mathop{\bf E}[T_{1-\gamma}f(x)] = \mathop{\bf E}[T_{1-\gamma}f(y)] = \mathop{\bf E}[T_{1-\gamma}f(z)] = \delta}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D%5BT_%7B1-%5Cgamma%7Df%28x%29%5D+%3D+%5Cmathop%7B%5Cbf+E%7D%5BT_%7B1-%5Cgamma%7Df%28y%29%5D+%3D+%5Cmathop%7B%5Cbf+E%7D%5BT_%7B1-%5Cgamma%7Df%28z%29%5D+%3D+%5Cdelta%7D&bg=ffffff&fg=000000&s=0&c=20201002) and because the error can be controlled with H\”{o}lder in terms of
and because the error can be controlled with H\”{o}lder in terms of 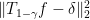 , which is teeny by the density-increment reduction.
, which is teeny by the density-increment reduction.
More details here: http://www.cs.cmu.edu/~odonnell/bridges.pdf. I can try to port this to the wiki soon.
February 25, 2009 at 8:38 pm
Ryan, I’m not sure what you mean by “fill the wildcards by either (0,-1,0) or (0,+1,0)”. Wouldn’t this always make x and z equal in a bridge? Perhaps an example would clarify what you mean here.
February 25, 2009 at 10:09 pm
819.2: Er, whoops. You’re right. Even easier then I thought 🙂 To make this problem more interesting, I think it will work if the triples allowed on wildcards are, say: (-,0,-), (-,0,0), (+,0,0), (+,0,+).
But: a) this is not as nice-looking, and b) I think it’ll actually take slightly more work.
So, um, never mind for now.
February 25, 2009 at 6:44 pm |
820. Density increment.
I’ve now finished a wiki write-up that is supposed to establish (and does unless I’ve made a mistake, which is possible) that if is a line-free set of uniform density
is a line-free set of uniform density  then you can pass to a combinatorial subspace of dimension
then you can pass to a combinatorial subspace of dimension  , as long as
, as long as  , and find a special subset of complexity 1 in that subspace of density at least
, and find a special subset of complexity 1 in that subspace of density at least 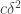 , such that the equal-slices density of
, such that the equal-slices density of  inside that special subset is at least
inside that special subset is at least 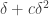 .
.
To be less precise about it, I think I’ve shown that if contains no combinatorial line, then you get a density increase on a nice set. I start with uniform density and switch to equal-slices density, but that is deliberate, and explained in the write-up, which, by the way, is here So my attention is now going to turn to trying to copy either the Ajtai-Szemerédi proof, or Shkredov’s proof, of the corners theorem. I feel optimistic that this can be done, given that special sets of complexity 1 can be shown to contain combinatorial subspaces—though that on its own is not enough.
contains no combinatorial line, then you get a density increase on a nice set. I start with uniform density and switch to equal-slices density, but that is deliberate, and explained in the write-up, which, by the way, is here So my attention is now going to turn to trying to copy either the Ajtai-Szemerédi proof, or Shkredov’s proof, of the corners theorem. I feel optimistic that this can be done, given that special sets of complexity 1 can be shown to contain combinatorial subspaces—though that on its own is not enough.
February 26, 2009 at 1:02 am
820.1. Hi Tim — nice. I read through the wiki proof and agree that it should be correct. It is quite interesting how the passage between uniform and equal-slices seems necessary. On one hand I worry a bit that the different measures might get out of control; on the other hand, the optimistic way to look at it is that we may eventually get so proficient at passing between measures that it’ll be a very useful tool.
February 26, 2009 at 10:14 am
820.2
One observation that makes me feel slightly less worried about passing from one measure to another is that you can start with equal-slices measure instead. Then as a first step you pass to uniform measure on a subspace. Then you carry out the argument as given (passing to a subspace of that subspace). And now you’ve ended up with the same measure that you started with.
February 25, 2009 at 10:11 pm |
821. Here is (I believe) a simple proof of Terry’s most basic structure theorem. The setting is as follows: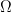 is a finite set and
is a finite set and 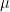 is a probability distribution on
is a probability distribution on 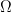 . We also write
. We also write  for the product distribution on
for the product distribution on  . We work in the space of functions
. We work in the space of functions 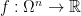 with inner product
with inner product ![{\langle f, g \rangle = \mathop{\bf E}_{x \sim \mu}[f(x)g(x)]}](https://s0.wp.com/latex.php?latex=%7B%5Clangle+f%2C+g+%5Crangle+%3D+%5Cmathop%7B%5Cbf+E%7D_%7Bx+%5Csim+%5Cmu%7D%5Bf%28x%29g%28x%29%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Henceforth, all probabilities are wrt
. Henceforth, all probabilities are wrt 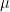 unless specified.
unless specified.
Theorem: Let have
have ![{\mathop{\bf Var}[f] \leq 1}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+Var%7D%5Bf%5D+%5Cleq+1%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Let
. Let 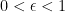 . Let
. Let 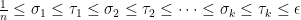 be a sequence of “scales” (or “times”) satisfying the following conditions: (a)
be a sequence of “scales” (or “times”) satisfying the following conditions: (a)  for all
for all 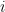 ; (b)
; (b) 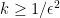 .
.
Then there exists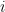 such that
such that  can be written as
can be written as 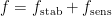 , where:
, where:
1.![{\mathop{\bf E}[f_{\text{stab}}] = \mathop{\bf E}[f]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D%5Bf_%7B%5Ctext%7Bstab%7D%7D%5D+%3D+%5Cmathop%7B%5Cbf+E%7D%5Bf%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
2.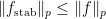 for all
for all 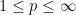 ; hence
; hence  has range
has range ![{[0,1]}](https://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) if
if  does (and then
does (and then 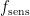 has range
has range ![{[-1,1]}](https://s0.wp.com/latex.php?latex=%7B%5B-1%2C1%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) ).
).
3.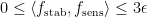 .
.
4.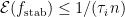 , where
, where  denotes the “average influence of
denotes the “average influence of 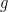 “: i.e.,
“: i.e., ![{\mathop{\bf E}[(g(x) - g(x'))^2]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D%5B%28g%28x%29+-+g%28x%27%29%29%5E2%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) , where
, where 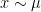 and
and 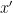 is formed by rerandomizing a random coordinate of
is formed by rerandomizing a random coordinate of  .
.
5.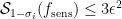 , where
, where 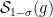 denotes the “noise stability of
denotes the “noise stability of 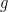 at
at 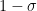 “: i.e.,
“: i.e., ![{\mathop{\bf E}[g(x)g(x')]}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+E%7D%5Bg%28x%29g%28x%27%29%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) , where
, where 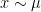 and
and 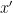 is formed by rerandomizing each coordinate of
is formed by rerandomizing each coordinate of  with probability
with probability  .
.
Proof in next post.
February 25, 2009 at 10:12 pm |
822. Proof: For simplicity I present the proof when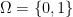 and
and 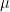 is the uniform distribution; to get the full version, replace the Fourier transform with the “Hoeffding AKA Efron-Stein orthogonal decomposition”.
is the uniform distribution; to get the full version, replace the Fourier transform with the “Hoeffding AKA Efron-Stein orthogonal decomposition”.
For an interval![{J = [a,b]}](https://s0.wp.com/latex.php?latex=%7BJ+%3D+%5Ba%2Cb%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) of natural numbers, let
of natural numbers, let 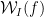 denote
denote 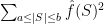 . The condition
. The condition ![{\mathop{\bf Var}[f] \leq 1}](https://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cbf+Var%7D%5Bf%5D+%5Cleq+1%7D&bg=ffffff&fg=000000&s=0&c=20201002) is equivalent to
is equivalent to ![{\mathcal{W}_{[1,n]} \leq 1}](https://s0.wp.com/latex.php?latex=%7B%5Cmathcal%7BW%7D_%7B%5B1%2Cn%5D%7D+%5Cleq+1%7D&bg=ffffff&fg=000000&s=0&c=20201002) , and we will use this frequently. Now consider the intervals of the form
, and we will use this frequently. Now consider the intervals of the form ![{J_i = [{\epsilon}/\tau_i, 2\ln(1/{\epsilon})/\sigma_i]}](https://s0.wp.com/latex.php?latex=%7BJ_i+%3D+%5B%7B%5Cepsilon%7D%2F%5Ctau_i%2C+2%5Cln%281%2F%7B%5Cepsilon%7D%29%2F%5Csigma_i%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . By hypothesis (a) these intervals are disjoint, and by hypothesis (b) there are at least
. By hypothesis (a) these intervals are disjoint, and by hypothesis (b) there are at least  of them. By Pigeonhole, we can fix a particular
of them. By Pigeonhole, we can fix a particular 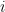 such that
such that 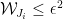 . Henceforth write
. Henceforth write  ,
, 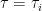 .
.
Now set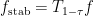 and
and 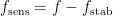 . Conditions 1 and 2 are satisfied. Condition 4 holds because
. Conditions 1 and 2 are satisfied. Condition 4 holds because 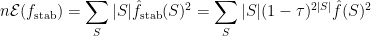
 because
because  for all
for all  . For Condition 3,
. For Condition 3, 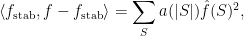

 so we can drop that term. We have
so we can drop that term. We have  always so we get a contribution of at most
always so we get a contribution of at most  from the terms with
from the terms with 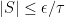 . We also have
. We also have  always so we get a contribution of at most
always so we get a contribution of at most 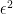 from the terms with
from the terms with 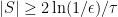 . And the remaining terms have
. And the remaining terms have ![{|S| \in [{\epsilon}/\tau, \ln(1/{\epsilon})/\tau] \subset J_i}](https://s0.wp.com/latex.php?latex=%7B%7CS%7C+%5Cin+%5B%7B%5Cepsilon%7D%2F%5Ctau%2C+%5Cln%281%2F%7B%5Cepsilon%7D%29%2F%5Ctau%5D+%5Csubset+J_i%7D&bg=ffffff&fg=000000&s=0&c=20201002) , so we get a contribution of at most
, so we get a contribution of at most 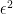 from them.
from them.
and this is at most
where
We have
The proof of Condition 5 is similar. We have
 . We have
. We have 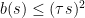 always so we get a contribution of at most
always so we get a contribution of at most 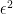 from the terms with
from the terms with 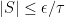 . We also have
. We also have  always so we get a contribution of at most
always so we get a contribution of at most 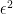 from the terms with
from the terms with 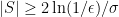 . And the remaining terms have
. And the remaining terms have 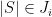 so we get a contribution of at most
so we get a contribution of at most  from them.
from them. 
where
Again,
February 25, 2009 at 10:48 pm
822.1 This looks about right to me. The game is always to first use pigeonhole to find a nice big gap in the energy spectrum, and then use that gap to split f into opposing pieces. (Sometimes one also needs a (small) third term to deal with the small amount of energy stuck inside the gap.)
One thing that works in your favour here is that the averaging operators are positivity preserving, so if f is positive then so is
are positivity preserving, so if f is positive then so is 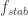 (and related to this is a useful comparison principle: if f is pointwise bigger than g, then
(and related to this is a useful comparison principle: if f is pointwise bigger than g, then 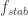 is pointwise bigger than
is pointwise bigger than 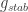 .) Things get more tricky when one doesn’t have this positivity preserving property, because it is absolutely essential later on that
.) Things get more tricky when one doesn’t have this positivity preserving property, because it is absolutely essential later on that 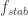 be non-negative. In my paper with Ben we had to introduce the machinery of partitions and conditional expectations to deal with this. One side effect of this is that it can force the scales to be exponentially separated (e.g.
be non-negative. In my paper with Ben we had to introduce the machinery of partitions and conditional expectations to deal with this. One side effect of this is that it can force the scales to be exponentially separated (e.g.  ) rather than just separated by a large constant depending only on
) rather than just separated by a large constant depending only on  ). This leads to the type of tower-exponential bounds which are familiar from the regularity lemma. Once we get to the fancier structure theorems, we may start seeing these sorts of bounds emerge, but I agree that in the simple case here we don’t have to deal with all that because of the handy
). This leads to the type of tower-exponential bounds which are familiar from the regularity lemma. Once we get to the fancier structure theorems, we may start seeing these sorts of bounds emerge, but I agree that in the simple case here we don’t have to deal with all that because of the handy 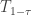 operators.
operators.
Combining this with your notes that control the Sperner count by the noise stability, it looks like we have a pretty solid Fourier-analytic proof of DHJ(2), which was one of our early objectives (suggested first, I believe, by Gil).
February 26, 2009 at 1:00 am
822.2: Yes, I think with slightly more work one can get an “Adequate-Sperner” Fourier proof; I think it will require density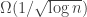 . This is still not quite right, but is closer.
. This is still not quite right, but is closer.
February 26, 2009 at 6:54 am |
823. Structure Theorem.
A small note: Unless I’m mistaken, the structure theorem around Lemma 1 in Terry’s wiki notes on Furstenberg-Katznelson — which decomposes functions on![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) into a 12-stable and a 12-sensitve part — can be proved in the same way as in #821.
into a 12-stable and a 12-sensitve part — can be proved in the same way as in #821.
Specifically, employing Tim’s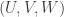 notation, I think you just need to look at the expectation over
notation, I think you just need to look at the expectation over  of the Fourier weight of
of the Fourier weight of  on the various intervals
on the various intervals  . Here
. Here  denotes the restricted function, with 0’s fixed into
denotes the restricted function, with 0’s fixed into  , on binary inputs (1 and 2). Everything seems to go through the same, using the fact that restricting functions with $U$ commutes with flipping 1’s and 2’s, and that
, on binary inputs (1 and 2). Everything seems to go through the same, using the fact that restricting functions with $U$ commutes with flipping 1’s and 2’s, and that ![\mathbb{E}_U[\mathrm{Var}[f_U]] \leq \mathrm{Var}[f]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D_U%5B%5Cmathrm%7BVar%7D%5Bf_U%5D%5D+%5Cleq+%5Cmathrm%7BVar%7D%5Bf%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
February 26, 2009 at 6:56 pm
823.1. The weird at the end here is meant to be “Var”.
at the end here is meant to be “Var”.
Fixed now — Tim.
February 26, 2009 at 11:48 am |
824. DHJ(3) general strategy
I have a hunch, after looking at Van Vu’s quantitative version of Ajtai-Szemerédi, that it may be possible to strengthen the argument on the wiki to give the whole thing. If this were not a polymath project I would of course go away and try to make the idea work, keeping quiet if it didn’t and giving full details if it did. But it is polymath, so let me say in advance roughly what I hope will happen.
In the corners problem, it is fairly easy to prove that a corner-free set has a density increment on a Cartesian product of two dense sets. The problem is what to do then. Ajtai and Szemerédi’s strategy is to use a more sophisticated averaging argument, making heavy use of Szemerédi’s theorem, to obtain a density increment on a highly structured Cartesian product: it is a product of two arithmetic progressions with the same common difference.
Initially, it looks very discouraging that they have to use Szemerédi’s theorem, but I now believe that that may just be an artificial byproduct of the fact that they are working in the grid and want to get another grid at the next stage of the induction. But in the Hales-Jewett world, you don’t actually need long arithmetic progressions anywhere, and I think the right analogue will in fact turn out to be multidimensional subspaces of![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . My actual idea is slightly more precise than this, but hard to explain. Basically, I want to revisit the argument on the wiki, but aim straight for a density increase on a subspace, modelling the argument as closely as I can on the Ajtai-Szemerédi argument for the corners problem.
. My actual idea is slightly more precise than this, but hard to explain. Basically, I want to revisit the argument on the wiki, but aim straight for a density increase on a subspace, modelling the argument as closely as I can on the Ajtai-Szemerédi argument for the corners problem.
If that works, then it will probably give a tower-type bound. A follow-up project would then be to try to do a more powerful Shkredov-type argument to get a bounded number of exponentials. But I’m getting way ahead of myself by even discussing this.
Let me also slip in a metacomment. I find it slightly inconvenient that, now that we have modest threading, I can’t just scroll to the bottom of the comments and see what has been added. As Jason Dyer pointed out, there is a trade-off here. On the one hand, it makes it slightly harder if you are trying to keep up with the discussion in real time, but on the other it probably means that the comments are better organized if you want to come back to them later. In the end, the second consideration probably trumps the first, because it’s a long-term convenience at the cost of a mild short-term inconvenience. But I still think that we should be quite careful about when and how much we use the threading.
February 26, 2009 at 5:32 pm |
825. Ajtai-Szemerédi approach.
No time to justify this, or at least not for a few hours (and possibly not before tomorrow morning) but I am now very optimistic indeed that the Ajtai-Szemerédi approach to corners can be modified to give DHJ(3). As usual, this surge of optimism may be followed by a realization that there are some serious technical obstacles, but I think that the existing write-up of the complexity-1 correlation contains methods for dealing with the technicalities that will arise. I plan to write up (i) a sketch proof of Ajtai-Szemerédi on the wiki, (ii) an outline of an argument here on the blog (which will include the AS-to-DHJ(3) dictionary I will be using), and (iii) a detailed sketch of an argument on the wiki. Those are in decreasing order of probability that I can actually finish them without getting stuck.
February 27, 2009 at 12:45 am |
826. Structure theorem
I now think there is a way to do the DHJ(2) structure theory without explicit mention of the Fourier transform (at the cost of worse quantitative bounds), which may be important when trying to extend the arguments to the DHJ(3) structure theory sketched in my wiki notes.
The point is to replace the self-adjoint operators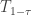 that Ryan uses by a “one-sided” counterpart. Given a function
that Ryan uses by a “one-sided” counterpart. Given a function ![f: [2]^n \to {\Bbb R}](https://s0.wp.com/latex.php?latex=f%3A+%5B2%5D%5En+%5Cto+%7B%5CBbb+R%7D&bg=ffffff&fg=333333&s=0&c=20201002) , and a parameter
, and a parameter 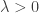 , let
, let ![S_\lambda f: [2]^n \to {\Bbb R}](https://s0.wp.com/latex.php?latex=S_%5Clambda+f%3A+%5B2%5D%5En+%5Cto+%7B%5CBbb+R%7D&bg=ffffff&fg=333333&s=0&c=20201002) be defined by
be defined by 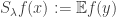 , where y is formed from x by allowing each coordinate of x, with probability
, where y is formed from x by allowing each coordinate of x, with probability 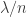 , of being overwritten by a 1. (This is in contrast to Ryan’s rerandomisation, which would cause x to be overwritten by a random 0/1 bit rather than by 1.)
, of being overwritten by a 1. (This is in contrast to Ryan’s rerandomisation, which would cause x to be overwritten by a random 0/1 bit rather than by 1.) of the 0-bits of x (the exact number basically obeys a Poisson distribution) and flipping them to 1s.
of the 0-bits of x (the exact number basically obeys a Poisson distribution) and flipping them to 1s.
Informally, one can think of y as taking about
Observe that (x,y) always forms a combinatorial line. Thus lower bounds on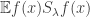 imply lots of combinatorial lines in the support of f.
imply lots of combinatorial lines in the support of f.
The key observation is that the are basically a semigroup (for
are basically a semigroup (for  much smaller than n):
much smaller than n): 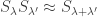 . In particular, if
. In particular, if  , we have the absorption property
, we have the absorption property  . Because of this, one can show that the
. Because of this, one can show that the  converge (in the strong operator topology) to an orthogonal projection P; to see this finitarily, one would inspect the energies
converge (in the strong operator topology) to an orthogonal projection P; to see this finitarily, one would inspect the energies 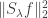 , which are basically monotone decreasing in
, which are basically monotone decreasing in  , and locate a long gap in the energy spectrum in which these energies plateau in
, and locate a long gap in the energy spectrum in which these energies plateau in  . I think this gives us the same type of structure/randomness decomposition as before. Note that for large
. I think this gives us the same type of structure/randomness decomposition as before. Note that for large  ,
, 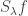 is approximately
is approximately 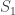 -invariant, which is basically the same thing as having low influence.
-invariant, which is basically the same thing as having low influence.
February 27, 2009 at 12:46 am
correction: (x,y) form a combinatorial line most of the time; there is a degenerate case when x=y (analogous to the case of a degenerate arithmetic progression). But for large lambda, this case is very rare and can be ignored.
February 27, 2009 at 1:12 am |
827. Ajtai-Szemerédi
Just to say that the easy step of my three-step plan is now done: an informal write-up of the Ajtai-Szemerédi proof of the corners theorem can now be found on this wiki page. I have to go to bed now so parts (ii) and (iii) will have to wait till tomorrow.
February 27, 2009 at 1:44 pm |
828. Progress report
Part (ii) is, perhaps predictably, giving me a bit more of a headache. But it’s an interesting headache in that I am stuck on something that feels as though it shouldn’t be too hard. I don’t know how much time I’ll have to think about it, so let me say what the problem is.
Call a subset![\mathcal{B}\subset[3]^n](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BB%7D%5Csubset%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) simple if whether or not
simple if whether or not  belongs to
belongs to  depends only on the 1-set of
depends only on the 1-set of  . In set language, there is a set-system
. In set language, there is a set-system 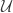 such that
such that 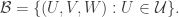 The question I’m struggling with is this. Let
The question I’m struggling with is this. Let  be a dense subset of
be a dense subset of ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) that correlates with a dense simple set
that correlates with a dense simple set  . Does that imply that there is a combinatorial subspace with dimension tending to infinity on which
. Does that imply that there is a combinatorial subspace with dimension tending to infinity on which  has a density increment?
has a density increment?
I cannot believe that this is a truly hard problem, but I haven’t yet managed to solve it. I think a solution would be very useful. Oh, and I really don’t mind what measure is used in any solution …
February 27, 2009 at 4:26 pm
828.1: What if strings with an even number of 1’s?
strings with an even number of 1’s?
February 27, 2009 at 4:50 pm
828.2: Then take all sequences x such that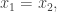
 etc., and you have a combinatorial subspace of dimension
etc., and you have a combinatorial subspace of dimension 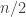 where the density has gone all the way up to 1. Were you imagining that wildcard sets had to have size 1? That is certainly not intended to be a requirement in my question.
where the density has gone all the way up to 1. Were you imagining that wildcard sets had to have size 1? That is certainly not intended to be a requirement in my question.
February 27, 2009 at 5:29 pm
828.3
I can answer your question as “yes”, but in a totally unhelpful way: DHJ(3) implies that any dense set has a density increment on a large combinatorial subspace.
Of course, the whole point is to find a DHJ(3)-free proof of this fact… I don’t currently have time to think about it right now, but I might look at it later.
February 27, 2009 at 5:33 pm
828.4
Hmm, actually thinking about it a little bit there may be an energy-increment type proof.
Firstly, one should be able to show that a 1-set contains lots of combinatorial subspaces where it is denser, by concatenating the 2 and 3-sets together and applying DHJ(2).
Next, one should be able to apply some sort of structure theorem to decompose an arbitrary set (or function) into a 1-set plus something orthogonal to 1-sets. Actually one needs to mess around with scales and get a decomposition into a 1-set at some large scale plus something
at some large scale plus something  orthogonal to 1-sets at finer scales (in particular, it should have mean zero at finer scales). (Let me be vague about what “scale” means, but every time you pass to a large combinatorial subspace, you’re supposed to descend one scale.)
orthogonal to 1-sets at finer scales (in particular, it should have mean zero at finer scales). (Let me be vague about what “scale” means, but every time you pass to a large combinatorial subspace, you’re supposed to descend one scale.)
Now take the guy which is a 1-set at a large scale and find lots of combinatorial subspaces in it at the finer scale where it is denser. The guy
which is a 1-set at a large scale and find lots of combinatorial subspaces in it at the finer scale where it is denser. The guy  which is orthogonal to 1-sets at finer scale should not disrupt this density increment.
which is orthogonal to 1-sets at finer scale should not disrupt this density increment.
Have to run, unfortunately… may flesh this out later
February 27, 2009 at 5:52 pm
828.5. Re 828.2:
Ah, no, I guess I was misunderstanding what a combinatorial subspace is. I always think of this as, “fixing some of the coordinates and leaving the rest of them ‘free’.” It had not occurred to me that one is also allowed to insist on things like “x_i = x_j”, although I now see that there is no reason not to.
February 27, 2009 at 6:37 pm |
829. Ajtai-Szemerédi
Let me try to explain the motivation for my simple-sets question. As I said earlier, I am trying to model a proof of DHJ(3) on the Ajtai-Szemerédi corners proof (an account of which is given here on the wiki). I have the following rough dictionary in mind.
1. A vertical line corresponds to a set of sequences (U,V,W) where you fix the 1-set U.
2. A horizontal line corresponds to a set of sequences (U,V,W) where you fix the 2-set V.
3. A line of slope -1, or diagonal, corresponds to a set of sequences (U,V,W) where you fix the 3-set W.
4. An arithmetic progression in [n] with length tending to infinity corresponds to a combinatorial subspace in![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with dimension tending to infinity.
with dimension tending to infinity.
5. A subgrid with width tending to infinity corresponds to a combinatorial subspace of![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with dimension tending to infinity.
with dimension tending to infinity.
6. A corner corresponds to a combinatorial line.
That’s about it. So now let me say where the first problem arises when one tries to translate the AS proof to the DHJ(3) context. Obviously step 1 is fine: with any sensible model of a random combinatorial subspace you can assume that the density of A in that subspace is almost always at least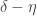 , where
, where  is the density of A.
is the density of A.
Step 2 says that if you have a positive density of vertical lines inside which A has density noticeably less than , then you also have a positive density of vertical lines inside which A has density noticeably greater than
, then you also have a positive density of vertical lines inside which A has density noticeably greater than  . If we let
. If we let  be the set of x-coordinates associated with these vertical lines, then we can use Szemerédi’s theorem to get an arithmetic progression P of these “over-full” vertical lines, with small common difference. Then we can partition the horizontal lines into arithmetic progressions
be the set of x-coordinates associated with these vertical lines, then we can use Szemerédi’s theorem to get an arithmetic progression P of these “over-full” vertical lines, with small common difference. Then we can partition the horizontal lines into arithmetic progressions  , each of which is a translate of
, each of which is a translate of  , and by averaging we find a subgrid
, and by averaging we find a subgrid  inside which A has density noticeably larger than
inside which A has density noticeably larger than  , which gives us a density increment and we’re done. (Of course, then one has to go on and say what happens if we don’t have a positive density of sparse vertical lines — this is, as I say, just the first step of the argument.)
, which gives us a density increment and we’re done. (Of course, then one has to go on and say what happens if we don’t have a positive density of sparse vertical lines — this is, as I say, just the first step of the argument.)
Let me gloss over the question of which measure I want to use: I feel that that is just a technicality and the main point is to get the conceptual argument working. If you accept item 1 in the dictionary, then the obvious first step is to define U to be underfull if the density of pairs (V,W) (out of all pairs such that (U,V,W) is a point in![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) ) is noticeably less than
) is noticeably less than  . Then if there is a positive density of underfull U, then we have a positive density of overfull U as well. Now I don’t have a problem finding a nice big combinatorial subspace consisting entirely of overfull Us (which is what item 4 suggests I should be looking for) but I don’t then have a nice analogue of the fact that a Cartesian product of two APs with the same common difference is a grid. Or rather, maybe I do, but I’m not sure how to get at it. The analogue should be something like that if I have such a combinatorial subspace (by which I mean a system of sets
. Then if there is a positive density of underfull U, then we have a positive density of overfull U as well. Now I don’t have a problem finding a nice big combinatorial subspace consisting entirely of overfull Us (which is what item 4 suggests I should be looking for) but I don’t then have a nice analogue of the fact that a Cartesian product of two APs with the same common difference is a grid. Or rather, maybe I do, but I’m not sure how to get at it. The analogue should be something like that if I have such a combinatorial subspace (by which I mean a system of sets 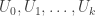 such that the elements of the system are all sets of the form
such that the elements of the system are all sets of the form  with 0 belonging to E), then on average the combinatorial subspaces that fix
with 0 belonging to E), then on average the combinatorial subspaces that fix  and treat
and treat  as wildcards should be slightly too dense. But for a fixed combinatorial subspace this doesn’t seem to have to be true, so I need somehow to build a combinatorial subspace such that it is true.
as wildcards should be slightly too dense. But for a fixed combinatorial subspace this doesn’t seem to have to be true, so I need somehow to build a combinatorial subspace such that it is true.
I can feel this explanation getting less clear as I proceed, but perhaps it’s at least clear globally what I want to do: the “simple set” is the set of all (U,V,W) such that U is overfull. So trivially A intersects it too densely. If we can get a density increment on a subgrid, then we’re done, which means that Step 3 is complete and we may assume that virtually no U are underfull. (Given the difficulties associated with this step, it’s not altogether clear that this statement is strong enough, but it would be encouraging. I might assume it and see what happens if I try to press on with the later steps.)
February 27, 2009 at 7:50 pm |
830. Combinatorial subspaces; 828.4 vs. 828.2.
It seems to me that an argument along the lines in 828.4 at some point has to find combinatorial subspaces which include these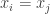 constraints, as in Tim’s 828.2. If the combinatorial subspaces are just of the “fixing-some-coordinates” type then I’m not sure (yet) how to get around 828.1.
constraints, as in Tim’s 828.2. If the combinatorial subspaces are just of the “fixing-some-coordinates” type then I’m not sure (yet) how to get around 828.1.
But will arguments as in 828.4 actually produce such subspaces?
February 27, 2009 at 8:14 pm |
831. Finding combinatorial subspaces
Ryan, that’s an interesting point. The kind of arguments I had in mind are different though: they are inductive ones where you build a subspace up dimension by dimension, using Sperner’s theorem (or similar results) at each stage. A prototype for such an argument is the proof I sketched on the wiki of the basic multidimensional Sperner theorem. This argument leads naturally to larger wildcard sets.
February 27, 2009 at 10:28 pm |
832. 1-sets
I was trying to think about Tim’s question from the ergodic perspective; if I am translating correctly the outlook is not encouraging. Perhaps though I am overgeneralizing.
A 1-set is just a set, membership in which is impervious to switchings of 0s with 2s, right? Okay, so, if I understand Terry’s translations from the ergodic world and back again, the functions that are measurable with respect to 1-sets would be in some sense analogous to the $\tau\rho^{-1}$ rigid factor…if that’s right, then in order to think about the question ergodically, one should think whether it would help at all to know that 1_A had non-zero projection onto this factor. And I don’t see how it would. In particular, it isn’t the case that things orthogonal to this factor don’t contribute to the averages you’re interested in, so I don’t see how decomposing would help. Yes, it is easy to see from DHJ (2) what the positive contribution would be restricted to this rigid factor, but you lose positivity of the relative AP components; it would not seem an easy task to show that they have non-negative contribution without positivity, especially given that the argument as it now stands uses positively very heavily (it throws a lot away because it can).
On the other hand, a non-zero projection onto this factor is sufficient to get (what Terry would call, I think) both 01 over 02 and 12 over 02 almost periodic components, and in a special way, so it might in theory be easier to get a density increment for these guys in the combinatorial world, but at least from an ergodic perspective, I can’t see any strategy that might simplify the proof from what it already is. Short, that is, of a detailed analysis of what is going on in terms of finite-dimensional modules instead of “almost periodicity”, but that is potentially a step in the direction of harder, not easier.
Of course, all I say depends on this analogy between 1-sets and the 02-rigid factor being what I suggest it is, and I don’t really see that part well at all (I’m mostly just guessing because I don’t understand the picture very well from the combinatorial side). (Also of course someone may be posting a proof simultaneously with my posting my doubts.)
February 27, 2009 at 10:55 pm
832.1
Yeah, a 1-set is what I would call a 02-low influence (in fact, a 02-zero influence) set, and it would correspond to a tau rho^{-1} invariant set in the ergodic theory language. Tim’s approach actually deals with intersections of 1-sets and 2-sets (which we have been calling “complexity 1 sets”), which would be a combination of a 02-low influence and 01-low influence set, or a set in the factor generated by both the tau rho^{-1}-invariants and the sigma rho^{-1}-invariants. (One may also want to throw in the 12-invariant sets for good measure.) But never mind this distinction for now.
Perhaps the place where Tim’s approach and the ergodic approach differ, though, is that Tim can always stop the argument as soon as a density increment is found on a large subspace, whereas this trick is not available in the ergodic world. So I don’t think Tim needs the strong (and presumably false) claim that “functions orthogonal to complexity 1 sets have negligible impact on the combinatorial line count”. He only needs the weaker claim that “if a set has no combinatorial lines, then it must have non-trivial correlation with a complexity 1 set”, combined with the (as yet not fully established) claim that “a set with non-trivial correlation with a complexity 1 set has a density increment on a large combinatorial subspace”.
Hmm. Maybe one thing to put on my “to do” list is to find an ergodic translation of Tim’s argument on the wiki that line-free sets correlate with complexity 1 sets. (If you haven’t already noticed, I’m a big fan of translating back and forth between these two languages.)
February 27, 2009 at 11:06 pm
832.2
Actually I just got on here again to retract everything I said (I should think more carefully before posting). I now think, from the ergodic perspective, you trivially get a “measure increment” if 1_A correlates projects non-trivially onto the 02-rigid factor, for the reason that on fibers, the measure is not constant. Just pick a bunch of fibers on which the measure is too big and then a subspace on which you have intersection of those fibers (DJH (2)).
February 27, 2009 at 11:39 pm
832.2
Hmm, I tried my hand at translating Tim’s argument to ergodic theory, and it came out weird… in order to describe it, I have to leave the measure space X and work in a certain extension of it, vaguely analogous to the Host-Kra parallelopiped spaces![X^{[k]}](https://s0.wp.com/latex.php?latex=X%5E%7B%5Bk%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002) (or the Furstenberg self-joinings used in Tim Austin’s proof of convergence for multiple commuting shifts).
(or the Furstenberg self-joinings used in Tim Austin’s proof of convergence for multiple commuting shifts).
It’s something like this: consider the space of all quadruples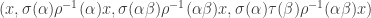 in
in 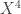 , where
, where  is a word to the left of
is a word to the left of  (or maybe to the right; I may have the signs messed up). There should somehow be a natural measure
(or maybe to the right; I may have the signs messed up). There should somehow be a natural measure  associated to these quadruples, which I currently do not know how to define properly; each of the four projections of this measure to X should be the original measure
associated to these quadruples, which I currently do not know how to define properly; each of the four projections of this measure to X should be the original measure  .
.
The last three points of this quadruple form a combinatorial line (I may have messed up the order of operations a bit). So if A is line-free, the function on
on 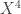 will have strong negative correlation with
will have strong negative correlation with  . But the function
. But the function  has a “02-invariance property” in the sense that it is insensitive to changes to
has a “02-invariance property” in the sense that it is insensitive to changes to  , while the function
, while the function 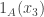 has a certain “01-invariance property” in the sense that it is insensitive to interchanges between
has a certain “01-invariance property” in the sense that it is insensitive to interchanges between  and
and  . So A is correlating with a combination of a 02-invariant set and a 01-invariant set, but the correlation only takes place in the extension
. So A is correlating with a combination of a 02-invariant set and a 01-invariant set, but the correlation only takes place in the extension 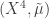 of
of  and the invariance seems to be a bit fancier than just
and the invariance seems to be a bit fancier than just 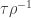 -invariance or
-invariance or 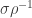 -invariance.
-invariance.
February 27, 2009 at 10:36 pm |
832. Following up on 830, perhaps Randall or Terry would be able to answer:
Is there an analogue in the ergodic proof of restrictions to these subspaces with more than one “type” of wildcard? (In other words, subspaces with these “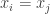 ” constraints?) In my limited understanding of the ergodic proofs, the operators used therein seemed to be more aligned with just the simpler combinatorial subspaces.
” constraints?) In my limited understanding of the ergodic proofs, the operators used therein seemed to be more aligned with just the simpler combinatorial subspaces.
February 27, 2009 at 10:59 pm
Ryan, I’m not sure I understand your question. A k-dimensional combinatorial subspace is described by a word with k wildcards, but each wildcard can be used more than once. For instance, xxyyzz21 would describe the three-dimensional subspace of![[3]^8](https://s0.wp.com/latex.php?latex=%5B3%5D%5E8&bg=ffffff&fg=333333&s=0&c=20201002) in which
in which 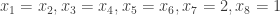 . A combinatorial line is the case when k=1, so we have one wild card x, which can be used many times over.
. A combinatorial line is the case when k=1, so we have one wild card x, which can be used many times over.
February 27, 2009 at 11:06 pm
Are you meaning like how Moser’s has a wildcard that goes 1-2-3 while the other goes 3-2-1? So, generalizing, there would be six types of wildcards? (123, 132, 213, 312, 231, 321 — obviously certain combinations would be equivalent to Moser)
February 27, 2009 at 11:26 pm
To clarify further, any pair of distinct wildcards from those six (123, 132, 213, 312, 231, 321) will fix one element and permute the other two, so they are all equivalent to Moser. However, we could take all the way up to six different wildcards, resulting in lines I believe have never been named. For example, taking x = 123, y = 321 and z= 213, then a line formed with 11xyz would be 11132, 11221, 11313.
February 27, 2009 at 11:29 pm
Argh. There are pairs that don’t fix any of the elements, (123-231 for example) which would also be something different than Moser’s.
February 28, 2009 at 9:34 pm
832.x. Re Terry’s reply: Right, what I’m saying is, in my limited experience, I hadn’t noticed any ergodic-inspired finitary arguments that involved combinatorial subspaces with more than one type of wildcard.
February 28, 2009 at 1:40 am |
833. Fourier and Sperner
On a slightly different topic, I still haven’t given up hope of a “right” Fourier proof of Sperner’s theorem. On the wiki I have now written up an argument that almost gets there. The good news is that it gives a Fourier-type decomposition with the property that a suitable equal-slice-weighted sum of f(A)f(B) over all pairs transforms into an expression where the contribution from every Fourier mode (when this claim is suitably interpreted) is positive. The bad news is that so far the only way I have of proving this positivity, which boils down to proving that a certain explicitly defined integral kernel is positive definite, is using an inverse Fourier argument, so I can’t quite claim that the proof is a Fourier proof of Sperner. But now that I know that this kernel is positive definite, I think it will be just a matter of time before one of us comes up with a direct proof, and then there will be a nice clean Fourier proof of Sperner (or at least, I think it would deserve to be called that).
transforms into an expression where the contribution from every Fourier mode (when this claim is suitably interpreted) is positive. The bad news is that so far the only way I have of proving this positivity, which boils down to proving that a certain explicitly defined integral kernel is positive definite, is using an inverse Fourier argument, so I can’t quite claim that the proof is a Fourier proof of Sperner. But now that I know that this kernel is positive definite, I think it will be just a matter of time before one of us comes up with a direct proof, and then there will be a nice clean Fourier proof of Sperner (or at least, I think it would deserve to be called that).
February 28, 2009 at 5:07 am |
834. Density increment
I think I can now prove Tim’s claim in 828, namely that a set that correlates with a 1-set has a density increment on a large dimensional subspace.
First observe, by the greedy algorithm and DHJ(2), that if n is large enough depending on m and , then any dense subset A of
, then any dense subset A of ![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) can be partitioned into m-dimensional subspaces, plus a residual set of density at most
can be partitioned into m-dimensional subspaces, plus a residual set of density at most  . Indeed one just keeps using DHJ(2) to locate and then delete m-dimensional subspaces from the set. Similarly, the complement of A can also be partitioned into m-dimensional spaces plus a residual set of density at most density at most
. Indeed one just keeps using DHJ(2) to locate and then delete m-dimensional subspaces from the set. Similarly, the complement of A can also be partitioned into m-dimensional spaces plus a residual set of density at most density at most  .
.
Now, one should be able to pull this statement to![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) and show that if A is a dense 1-set of
and show that if A is a dense 1-set of ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , then one can partition both A and its complement into m-dimensional subspaces, plus a residual of small density. I’m not sure what “density” should mean here; equal-slices may be a better bet than uniform at this point.
, then one can partition both A and its complement into m-dimensional subspaces, plus a residual of small density. I’m not sure what “density” should mean here; equal-slices may be a better bet than uniform at this point.
Now, if B is a dense set which correlates with a dense 1-set A, then by picking a moderately large m, picking tiny compared to 1/m, and then n really large, we should be able to use the above partition and the pigeonhole principle to get a density increment of B on one of these m-dimensional subspaces.
tiny compared to 1/m, and then n really large, we should be able to use the above partition and the pigeonhole principle to get a density increment of B on one of these m-dimensional subspaces.
February 28, 2009 at 9:35 am |
835. Density increment
Terry, that’s similar to things I was trying, and I’m wondering whether it will run into similar difficulties. The point where I get stuck is where you say, “Now, one should be able to pull this statement to![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) .” How might one do this? Well, given any combinatorial subspace in
.” How might one do this? Well, given any combinatorial subspace in ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) you can easily define an associated combinatorial subspace in
you can easily define an associated combinatorial subspace in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) by simply allowing the wildcards to take value 2 as well. (For convenience I am taking
by simply allowing the wildcards to take value 2 as well. (For convenience I am taking ![{}[2]=\{0,1\}](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%3D%5C%7B0%2C1%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![{}[3]=\{0,1,2\}.)](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%3D%5C%7B0%2C1%2C2%5C%7D.%29&bg=ffffff&fg=333333&s=0&c=20201002) And the result will be a collection of disjoint subspaces. But they won’t anything like partition
And the result will be a collection of disjoint subspaces. But they won’t anything like partition ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) because so far all the fixed coordinates are 0 or 1. We can correct that by allowing the fixed coordinates that used to be 0 to be either 0 or 2, but I think that doesn’t get us out of the woods.
because so far all the fixed coordinates are 0 or 1. We can correct that by allowing the fixed coordinates that used to be 0 to be either 0 or 2, but I think that doesn’t get us out of the woods.
What one really needs to answer is the following question: given a sequence in
in ![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , to what combinatorial subspace does it belong?
, to what combinatorial subspace does it belong?
Here’s an example. Suppose and you are presented with
and you are presented with 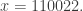 And suppose that one of the combinatorial subspaces you took in
And suppose that one of the combinatorial subspaces you took in ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) was
was  . Then you’d be forced to put
. Then you’d be forced to put  into
into  , since its 1-set is contained in
, since its 1-set is contained in  . But if you now allow the wildcards to take the value 2 as well, you can’t get
. But if you now allow the wildcards to take the value 2 as well, you can’t get  .
.
February 28, 2009 at 11:37 am
835.1 Maybe one could use a variant of the argument where having chosen the first wildcard set you then inductively cover evenly everything else. Sorry — that’s a bit vague but I have no time to clarify it just yet. In the above example, having chosen aa you might e.g. then partition into things like bcbc, bbcc, bccb, cbbb, etc. Except that even that wouldn’t be right because once you’d chosen your second wildcard set you’d play the same game with the third, fourth, etc. Sorry, that’s probably still completely unclear.
February 28, 2009 at 4:23 pm
I haven’t had time to test this yet, but would it help to triplicate the original set into a 9-uniform hypergraph (with subgraphs A, B, and C) such that subgraph A uses 0 or 2, B uses 0 or 1, and C uses 1 or 2?
Then somehow before the last step everything would need to be recombined into the original graph.
February 28, 2009 at 5:04 pm
835.3 Jason, I’m not sure I follow what you are saying here.
February 28, 2009 at 5:24 pm
Hopefully this issue will be resolved in a simpler way soon anyway, but could the “measure increment” observation I made in my last post be fashioned into a proof? In the regular F-K conversion they only cared about combinatorial lines, but presumably one could arrange that for any set I of words, if the intersection over I of T_w^{-1}C is non-empty, then you see a subspace-homomorphic image of I in the original set A you were dealing with. You could do this for 2 sets simultaneously, a 1-set A and a correlated set B. I am guessing that A would wind up associated with a set in your measure space that would be measurable with respect to the \tau\rho^{-1} rigid factor, and that B would wind up associated with a set that had non-zero projection onto that factor, and you would then wrap up the proof as indicated above. Of course you’d have to convert this to a combinatorial proof, which presumably Terry is good at (energy incrementation?) But again, one hopes it’s not that hard, or that something already suggested can be made to work….
February 28, 2009 at 7:30 pm
Huh, so the pullback of a combinatorial subspace of![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) to
to ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is not a combinatorial subspace. That’s a bit weird. I agree that my previous comment doesn’t quite work as stated then.
is not a combinatorial subspace. That’s a bit weird. I agree that my previous comment doesn’t quite work as stated then.
However, it does seem that the pullback of a combinatorial subspace of![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) is an “average” of combinatorial subspaces of
is an “average” of combinatorial subspaces of ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) (or what Gil would call a “fractional cover”). Basically, there is a random way to convert a 2-dimensional subspace e.g. 01aa01bbb10ccc to a 3-dimensional subspace by randomly converting 0s to 0s or 2s, and a wildcard such as a to a, 0, or 2. One has to carefully select the probability measures here (in particular, to make choices between equal slices and uniform) to make everything work, but perhaps it can be pulled off. (One may also want to ensure that each wildcard appears a lot of times so that when one pulls back, one (with very high probability) doesn’t accidentally erase all copies of any given wildcard.) As Gil observed, if you can fractionally cover most of a set A and its complement by large combinatorial subspaces, and B has a large correlation with A, then B has a density increment on one of these subspaces.
(or what Gil would call a “fractional cover”). Basically, there is a random way to convert a 2-dimensional subspace e.g. 01aa01bbb10ccc to a 3-dimensional subspace by randomly converting 0s to 0s or 2s, and a wildcard such as a to a, 0, or 2. One has to carefully select the probability measures here (in particular, to make choices between equal slices and uniform) to make everything work, but perhaps it can be pulled off. (One may also want to ensure that each wildcard appears a lot of times so that when one pulls back, one (with very high probability) doesn’t accidentally erase all copies of any given wildcard.) As Gil observed, if you can fractionally cover most of a set A and its complement by large combinatorial subspaces, and B has a large correlation with A, then B has a density increment on one of these subspaces.
February 28, 2009 at 7:42 pm
No, that’s rubbish, I take it back; the pullback of, say, aa, is the set {00, 11, 12, 21, 22}, and I can’t cover that space by lines. Strange.
February 28, 2009 at 7:44 pm
835.5 I was meaning based on “allowing the fixed coordinates that used to be 0 to be either 0 or 2” you have two more subspaces where:
coordinates that used to be a 0 are either 1 or 2, and coordinates that used to be a 0 are a 1
and
coordinates that used to be a 0 are either 0 or 1, and coordinates that used to be a 1 are a 2.
However, I have not been able to get anything useful out of this.
February 28, 2009 at 5:24 pm |
836 Density increment
I’m going to return to full polymath mode and think online rather than offline, concentrating on the problem of getting a density increment on a subspace if you already have one on a simple set. (Recall that I am defining a simple set to be a set of sequences x of the form
of sequences x of the form  Since I’ll be talking about
Since I’ll be talking about ![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) quite a bit, it will be natural to take
quite a bit, it will be natural to take ![{}[3]=\{0,1,2\}](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%3D%5C%7B0%2C1%2C2%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) and
and ![{}[2]=\{0,1\}.](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%3D%5C%7B0%2C1%5C%7D.&bg=ffffff&fg=333333&s=0&c=20201002) Set theorists would no doubt approve.
Set theorists would no doubt approve.
I am aiming for an inductive construction. That is, I want to fix some coordinates and choose a wildcard set in such a way that I am not dead. To say that more precisely, the assumption we are given to start with is that for every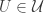 the density of points
the density of points 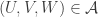 is at least
is at least  . I would now like to find a disjoint quadruple
. I would now like to find a disjoint quadruple 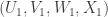 that does not partition
that does not partition ![{}[n]](https://s0.wp.com/latex.php?latex=%7B%7D%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) , or even come close to doing so, and I would like the following to be the case. Let
, or even come close to doing so, and I would like the following to be the case. Let  be the complement of
be the complement of 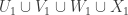 . Then there are many
. Then there are many  such that the density of
such that the density of  with
with 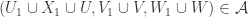 is at least
is at least  (or perhaps very slightly less), and the same is true, with the same
(or perhaps very slightly less), and the same is true, with the same  , if we move
, if we move 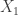 over to
over to  or
or  .
.
I’ve got to go in a moment, but it occurs to me that one might be able to get away with less. I’ve tried to choose a 1-dimensional subspace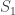 such that for many
such that for many  the density is good for every assignment of the wildcards. But perhaps it’s enough just to get the average density good when we set the wildcards, and perhaps that’s easier to prove.
the density is good for every assignment of the wildcards. But perhaps it’s enough just to get the average density good when we set the wildcards, and perhaps that’s easier to prove.
Incidentally, here’s a problem that ought to count as a first exercise. To make sense of it, we need to go for a functional version. So let’s suppose that![f:[3]^n\rightarrow[0,1]](https://s0.wp.com/latex.php?latex=f%3A%5B3%5D%5En%5Crightarrow%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) is a function of mean
is a function of mean  and suppose that there is a dense set system
and suppose that there is a dense set system 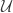 such that for every
such that for every 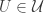 the average of
the average of 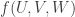 over all
over all  that make a point with
that make a point with  is at least
is at least  . Can we find a combinatorial line on which
. Can we find a combinatorial line on which  averages at least
averages at least  (where
(where  is
is  say)?
say)?
Of course, we can do it by quoting DHJ(3) but is there an elementary proof?
That’s all I’ve got time for for now.
February 28, 2009 at 5:48 pm
836.1 Just to be clear, to make sense of that last problem, one should either use equal-slices measure or ask for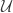 to be dense in the probability measure where each element of a set is chosen independently with probability
to be dense in the probability measure where each element of a set is chosen independently with probability 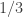 .
.
February 28, 2009 at 7:51 pm |
837. Density increment
Randall, I think the problem we’re seeing in the combinatorial world (that the pullback of a![[2]^n](https://s0.wp.com/latex.php?latex=%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) -combinatorial subspace is not a
-combinatorial subspace is not a ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) -combinatorial subspace) is reflected in the ergodic world that the
-combinatorial subspace) is reflected in the ergodic world that the 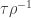 IP-system does not commute with the
IP-system does not commute with the 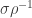 IP-system, and so DHJ(2) for the
IP-system, and so DHJ(2) for the 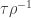 -invariant factor does not seem to quite give us what we want (applying
-invariant factor does not seem to quite give us what we want (applying 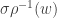 to a bunch of
to a bunch of 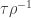 -fibers does not give another bunch of
-fibers does not give another bunch of 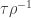 -fibers).
-fibers).
February 28, 2009 at 7:52 pm
Ahh, but there’s some sort of “asymptotic commutativity” if one separates the 01 interchange and 02 interchange operations sufficiently. Let me think about this…
February 28, 2009 at 8:10 pm
837.2
OK, I think I can make Randall’s argument work. In order to exploit asymptotic commutativity, I first need to weaken the notion of a 1-set to a “local 1-set”, which is a 1-set on large slices of![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) ; more precisely, A is a local 1-set if there exists a small set
; more precisely, A is a local 1-set if there exists a small set ![I \subset [n]](https://s0.wp.com/latex.php?latex=I+%5Csubset+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002) of “bad” coordinates such that whenever one fixes those coordinates (thus reducing the n-dimensional cube to an
of “bad” coordinates such that whenever one fixes those coordinates (thus reducing the n-dimensional cube to an 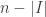 -dimensional cube), the slice of A is a 1-set. (Equivalently, A is insensitive to 0-2 interchanges on coordinates outside of I, but could be extremely sensitive to such changes within I). Every global 1-set is a local 1-set, but not conversely.
-dimensional cube), the slice of A is a 1-set. (Equivalently, A is insensitive to 0-2 interchanges on coordinates outside of I, but could be extremely sensitive to such changes within I). Every global 1-set is a local 1-set, but not conversely.
Suppose a set B has a density increment with a global 1-set A of non-trivial size. Then by a greedy algorithm, we can find a local 1-set A’ of non-trivial size on which B has a “near-maximal density increment” with B in the sense that any other local 1-set A” (with perhaps slightly more bad coordinates than A’, and not too much smaller than A’) does not have a significantly higher B-density than A’ did. (There will be a lot of parameter juggling to sort out to quantify everything here; I will ignore this issue here.)
OK, let’s look at the local 1-set A’, which has a small number of bad coordinates I’. Let m be a medium sized number. Pick m random small wildcard sets (which with high probability will be disjoint from each other, and from I’).
(which with high probability will be disjoint from each other, and from I’).
If we then pick a word w at random from![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , then by DHJ(2.5) and the local 1-set nature of A’, with positive probability, the combinatorial space
, then by DHJ(2.5) and the local 1-set nature of A’, with positive probability, the combinatorial space 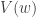 of
of 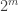 elements formed by taking w and overwriting each of
elements formed by taking w and overwriting each of  with 0s, 1s, or 2s, will lie in A’. Call the set of w that do this good.
with 0s, 1s, or 2s, will lie in A’. Call the set of w that do this good.
The key point is that the set A” of good w is itself a local 1-set outside of the bad coordinates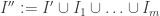 . And so by hypothesis, B enjoys essentially the same density increment on A” that it did on A’. But on the other hand, A” is the union of (parallel) m-dimensional combinatorial subspaces, and so we get an density increment on one of these spaces.
. And so by hypothesis, B enjoys essentially the same density increment on A” that it did on A’. But on the other hand, A” is the union of (parallel) m-dimensional combinatorial subspaces, and so we get an density increment on one of these spaces.
February 28, 2009 at 8:18 pm
small correction: V(m) should of course have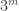 elements, not
elements, not 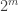 . (DHJ(2.5) places
. (DHJ(2.5) places 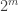 of the elements of
of the elements of 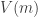 inside A’, and the local 1-set nature of A’ then automatically extends this membership of A’ to the rest of
inside A’, and the local 1-set nature of A’ then automatically extends this membership of A’ to the rest of 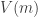 .)
.)
February 28, 2009 at 10:48 pm |
838. Structure Theorems; specifically, question for Terry re #826:
Terry, could you clarify on your statement therein, “the energies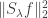 … are basically monotone decreasing in
… are basically monotone decreasing in  “?
“?
Suppose is of the form
is of the form 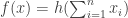 , where
, where 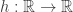 is a nonnegative increasing function. Doesn’t it seem as though
is a nonnegative increasing function. Doesn’t it seem as though 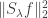 will be increasing in
will be increasing in  ?
?
February 28, 2009 at 10:49 pm
838.1 The nonparsing formula there is . Now fixed — Tim
. Now fixed — Tim
February 28, 2009 at 11:03 pm
838.2
Ryan, I guess one should specify that f should be bounded within [-1,1], and “basically” means “up to o(1) errors, and with small compared with
small compared with 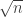 “.
“.
In your example h should also be bounded between [-1,1]. In that case, flipping 0’s to 1’s will only have an effect of increasing f by
0’s to 1’s will only have an effect of increasing f by 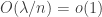 or so on average.
or so on average.
The reason for the monotone decrease is because of the absorption formula . Since
. Since 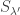 is basically a contraction for
is basically a contraction for 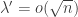 (though it does cease to contract for large
(though it does cease to contract for large 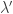 , of course), we see that
, of course), we see that 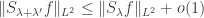 .
.
I guess the “local” picture (small ) is looking a bit different from the “global” picture. Locally, the operation of flipping 0s to 1s is a measure-preserving operation; globally, of course, it isn’t. (Tragedy of the commons!)
) is looking a bit different from the “global” picture. Locally, the operation of flipping 0s to 1s is a measure-preserving operation; globally, of course, it isn’t. (Tragedy of the commons!)
February 28, 2009 at 11:04 pm |
839. Fourier proof of Sperner.
I semi-checked to myself that one can prove Sperner by increment-free, purely Fourier arguments. One uses: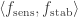 and
and 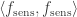 parts.
parts. parts.
parts.
. the structure theorem (#821).
. Mossel’s “Lemma 6.2” to handle the
. the triangle inequality argument (#815) to handle the
However, this argument is still quite unsatisfactory to me. For one, it requires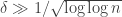 . For another, it requires selecting the parameter called
. For another, it requires selecting the parameter called  in #800 (equivalently,
in #800 (equivalently, 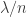 in Terry’s #826) after using the Structure Theorem. And most “wrongly”, this parameter must be
in Terry’s #826) after using the Structure Theorem. And most “wrongly”, this parameter must be  .
.
In particular, the following theorem is true (I’m 99% sure, at least; proof by “pushing shadows around with Kruskal-Katona”) — however, I don’t think we have any Fourier-based proof at all:
Theorem: Let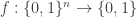 have density
have density  . Fix
. Fix  ,
,  , where
, where  is, say,
is, say,  . (Or set
. (Or set 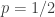 if you like.) Then
if you like.) Then ![\mathbb{E}[f(X_{p,q})f(Y_{p,q})] > 0](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Bf%28X_%7Bp%2Cq%7D%29f%28Y_%7Bp%2Cq%7D%29%5D+%3E+0&bg=ffffff&fg=333333&s=0&c=20201002) , where I’m using the notation from Tim’s wiki entry.
, where I’m using the notation from Tim’s wiki entry.
February 28, 2009 at 11:06 pm |
Metacomment.
One side effect of the threaded system is that we hit 100 comments long before the number assigned to the comments increases by 100; we’re at 838 now but the thread is already longer than most of the other threads. Perhaps we may wish to renew this thread well before 899 (e.g. at 850)?
February 28, 2009 at 11:23 pm |
840. Sperner.
This is very tiny comment. I just wanted to point out that one can prove the “correct” density-Sperner Theorem under the uniform distribution, in the same way Tim proves it under the equal-slices distribution.
Assume![\mathbb{E}[f] = \delta](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Bf%5D+%3D+%5Cdelta&bg=ffffff&fg=333333&s=0&c=20201002) under the uniform distribution. Pick a random chain
under the uniform distribution. Pick a random chain  from (0, 0, …, 0) up to (1, 1, …, 1) and then choose
from (0, 0, …, 0) up to (1, 1, …, 1) and then choose  Binomial
Binomial , independently. Define
, independently. Define  , the
, the  th string in the chain, and
th string in the chain, and  . Then
. Then ![\mathbb{E}[f(x)f(y)] = \mathbb{E}_C[\mathbb{E}_u[f(C(u))]^2] \geq \mathbb{E}_{C,u}[f(C(u))]^2 = \delta^2](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Bf%28x%29f%28y%29%5D+%3D+%5Cmathbb%7BE%7D_C%5B%5Cmathbb%7BE%7D_u%5Bf%28C%28u%29%29%5D%5E2%5D+%5Cgeq+%5Cmathbb%7BE%7D_%7BC%2Cu%7D%5Bf%28C%28u%29%29%5D%5E2+%3D+%5Cdelta%5E2&bg=ffffff&fg=333333&s=0&c=20201002) , as
, as  is uniformly distributed.
is uniformly distributed.
So we have a distribution on pairs of strings such that
such that  and
and  both have the uniform distribution, and such that they form a nondegenerate “line” with probability at least
both have the uniform distribution, and such that they form a nondegenerate “line” with probability at least  .
.
PS: If someone wants to express![\mathbb{E}[f(x)f(y)]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Bf%28x%29f%28y%29%5D&bg=ffffff&fg=333333&s=0&c=20201002) here in terms of Fourier coefficients, I’d be very happy to see it.
here in terms of Fourier coefficients, I’d be very happy to see it.
March 1, 2009 at 11:56 am
840.1 Ryan, I’m not sure how tiny that comment is, and must think about it. Maybe it will turn out that putting the binomial distribution on maximal chains is always more convenient than putting equal-slices measure on the cube. And clearly this same trick works for![{}[3]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . This feels to me like a potentially useful further technique to add to our armoury, and when I get the chance I think I’ll add something about it to the wiki.
. This feels to me like a potentially useful further technique to add to our armoury, and when I get the chance I think I’ll add something about it to the wiki.
I agree that the Fourier calculation looks more or less compulsory. And something that’s rather nice about this measure is that it combines the uniform distribution on![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) with a very natural non-uniform distribution on combinatorial lines, so it provides a potential answer to a question we were trying to answer way back in the Varnavides thread. Indeed, another exercise we should do is prove a Varnavides-type version of DHJ(3) for this measure on the combinatorial lines (given DHJ(3) itself).
with a very natural non-uniform distribution on combinatorial lines, so it provides a potential answer to a question we were trying to answer way back in the Varnavides thread. Indeed, another exercise we should do is prove a Varnavides-type version of DHJ(3) for this measure on the combinatorial lines (given DHJ(3) itself).
Oh no wait a moment — it’s not obvious how to generalize to DHJ(3) because we don’t have an analogue of maximal chains. This is something else to think about.
March 1, 2009 at 7:00 am |
841. A problem where some of the techniques developed here are potentially useful.
Let be a monotone Boolean function. Let
be a monotone Boolean function. Let  be the integral of the influence of the k-th variable w.r.t. the probability measure
be the integral of the influence of the k-th variable w.r.t. the probability measure 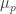 . (
. ( is called the “Shapley value” of
is called the “Shapley value” of  .) Let
.) Let  be a fixed small real number and let T be the difference between p-q where p is the value for which the probability that
be a fixed small real number and let T be the difference between p-q where p is the value for which the probability that  is 1 is
is 1 is  and q is the value for which the probability that
and q is the value for which the probability that  is 1 is
is 1 is  . (T is called the length of the “threshold interval for
. (T is called the length of the “threshold interval for  .)
.)
It is known that if all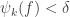 then T is small as well. The known bound is
then T is small as well. The known bound is 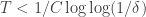 . The proof relies on connecting the influences for different of
. The proof relies on connecting the influences for different of 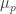 s. It looks that one
s. It looks that one  could be eliminated and that a more careful understanding of the relation between influences and other properties of
could be eliminated and that a more careful understanding of the relation between influences and other properties of  for different values of
for different values of  may be useful.
may be useful.
March 1, 2009 at 12:00 pm |
Metacomments.
1. Terry I agree that with threading we need shorter threads, if you’ll excuse the dual use of the word “thread”. Let’s indeed go for 850.
2. The other thing is that I’ve been meaning to say for ages that I loved your notion that the wiki could be thought of as an online journal of density Hales-Jewett studies, and the discussions as weekly conferences.
March 1, 2009 at 12:28 pm |
842. General remark
I have a very non-mathematically busy day today, so I’ve got time for just one brief post. First, let me say that I’m quite excited by Terry’s 837.2. I haven’t fully digested it yet but I have partially digested it enough to see that it is very definitely of the sort of flavour I was hoping for. It’s frustrating not to be able to spend a few hours today playing around with the argument. And then tomorrow and Tuesday I have two heavy teaching days.
So instead, let me throw out a small thought/question. Recall that in the dictionary I gave in 829, long arithmetic progressions go to combinatorial subspaces in![{}[2]^n](https://s0.wp.com/latex.php?latex=%7B%7D%5B2%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . Therefore, if the general plan of modelling an argument on Ajtai-Szemerédi works, it will have to give a new proof of the corners theorem that is similar to their proof but avoids the use of Szemerédi’s theorem. As I’ve already explained, that sounds discouraging at first, but I think it may in fact not be. But I’ve subsequently realized that these thoughts lead inexorably to a suggestion that Jozsef made, way back in comment 2 (!), that one should look at a generalization of the corners problem in which you don’t have long APs in the two sets of which you take the Cartesian product. Maybe the time is ripe for having a go at that problem, and in particular seeing whether the Ajtai-Szemerédi approach can be pushed through for it.
. Therefore, if the general plan of modelling an argument on Ajtai-Szemerédi works, it will have to give a new proof of the corners theorem that is similar to their proof but avoids the use of Szemerédi’s theorem. As I’ve already explained, that sounds discouraging at first, but I think it may in fact not be. But I’ve subsequently realized that these thoughts lead inexorably to a suggestion that Jozsef made, way back in comment 2 (!), that one should look at a generalization of the corners problem in which you don’t have long APs in the two sets of which you take the Cartesian product. Maybe the time is ripe for having a go at that problem, and in particular seeing whether the Ajtai-Szemerédi approach can be pushed through for it.
March 1, 2009 at 5:25 pm |
843. Measures:
One reason I said the comment in #840 is tiny is that I’m finally starting to catch up the fact (well known to the rest of you, I think) that if you don’t mind density increment arguments (and we certainly don’t!) then the underlying probability measure is quite unimportant. Or rather, you can pass freely between any “reasonable” measures, using the arguments sketched here on the wiki.
In fact, I think “equal-slices” is a good “base measure” to always return to. It has the nice feature that if you have equal-slice density , by density-increment arguments you can assume that you have density very nearly
, by density-increment arguments you can assume that you have density very nearly  under almost all product measures.
under almost all product measures.
March 1, 2009 at 5:29 pm |
844. Density increment / the problem from #828:
What if a random simple set in
a random simple set in ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) of density
of density  , meaning that its
, meaning that its 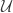 is a random set of density
is a random set of density  under the
under the 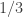 -biased distribution?
-biased distribution?
How should we try to find a combinatorial subspace to increment on?
(Perhaps we shouldn’t; perhaps instead we should exploit the fact that this is extremely 23-insensitive.)
is extremely 23-insensitive.)
March 1, 2009 at 5:58 pm
Ryan, that’s right; being 20-insensitive, we can invoke DHJ(2.5) and get large subspaces in , which of course is a healthy density increment.
, which of course is a healthy density increment.
March 1, 2009 at 7:36 pm
844.2. Ah, sorry if you said this already in an earlier comment, Terry; I’m still catching up.
March 1, 2009 at 7:06 pm |
845. Density increment in cubes
Tim, Re:842. In case you are considering corners in cubes, let me mention a few things here. Reading some recent blogs, I thought that you are close to prove a density increment result which would imply the corner result. I write the statement first and then I will argue that it proves a Moser type result. set (or an n-dimensional Hilbert cube if you wish) with
set (or an n-dimensional Hilbert cube if you wish) with 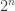 elements. Consider the elements as vertices of a graph. The graph is c-dense, i.e. the number of edges is
elements. Consider the elements as vertices of a graph. The graph is c-dense, i.e. the number of edges is  . The graph contains a huge hole, there is an
. The graph contains a huge hole, there is an  empty subgraph. Prove that then it contains a d-dimensional subcube on the vertices spanning at least
empty subgraph. Prove that then it contains a d-dimensional subcube on the vertices spanning at least  edges.
edges. 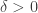 might depend on c and
might depend on c and  but not on n, and d grows with n (arbitrary slowly). Now I will try to post the next part as a new thread.
but not on n, and d grows with n (arbitrary slowly). Now I will try to post the next part as a new thread.
Given an
March 1, 2009 at 7:11 pm |
845.1
oops, I didn’t give my name for the previous note
March 1, 2009 at 7:26 pm |
846. A Moser type theorem
845.2 … and apparently I don’t know how to generate a thread.![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) contains three elements, formed by taking a string with one or more wildcards
contains three elements, formed by taking a string with one or more wildcards  and
and 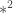 in it and replacing the first type wildcards by 1,2 and 3, and the second type wildcards by 4,3, and 2, respectively. For example 123412,
in it and replacing the first type wildcards by 1,2 and 3, and the second type wildcards by 4,3, and 2, respectively. For example 123412,
Still going backwards, let me state the theorem which would follow from 845: Every dense subset of
223312, and 323212 is such triple.
March 1, 2009 at 7:29 pm |
846.1. In the previous statement we were in![[4]^n](https://s0.wp.com/latex.php?latex=%5B4%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) , not in
, not in ![[3]^n](https://s0.wp.com/latex.php?latex=%5B3%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) .
.
March 1, 2009 at 7:56 pm |
846 contd.
With Ron Graham we proved a colouring version of 846. For any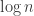 colouring of
colouring of ![[4]^n](https://s0.wp.com/latex.php?latex=%5B4%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) there is a monochromatic triple like in 846. The paper is available at
there is a monochromatic triple like in 846. The paper is available at
Click to access pre_cube.pdf
The reasonable bound for the colouring version shows that this problem might be easier to work with than with DHJ k=3. In the next post I will try to prove that 845 implies 846, that is, an “arithmetic density increment” in a graph with a huge hole implies a Moser type statement.
(Sorry about the number of posts, but I don’t want to write long ones as even the shorter ones are full with typos)
March 1, 2009 at 9:29 pm |
847. (part one)
Here we show that a density increment argument implies the Moser-type theorem in 846. It isn’t new that a density increment would give us what we are looking for, the new feature is that it might be easier to prove density increment in a graph with a huge empty subgraph. For practical reasons we switch to a bipartite settings. Consider a bipartite graph G(A.B), between two copies of the n-dimensional cube,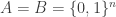 . G(A,B) has
. G(A,B) has 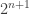 vertices and, say,
vertices and, say,  edges. There is a natural one to one mapping between the set of edges and a pointset of
edges. There is a natural one to one mapping between the set of edges and a pointset of ![[4]^n](https://s0.wp.com/latex.php?latex=%5B4%5D%5En&bg=ffffff&fg=333333&s=0&c=20201002) . The two vertices of an edge are 0-1 sequences. From the two sequences we get one as follows. The i-th position of the new sequence (0,1,2, or 3) is given by
. The two vertices of an edge are 0-1 sequences. From the two sequences we get one as follows. The i-th position of the new sequence (0,1,2, or 3) is given by 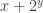 where x is the number (0 or 1) in the i-th position of the vertex in A and y is the number in the i-th position of the vertex in B. We say that two edges span the same cube if substituting all 1-s and 2-s by a wildcard, *, we get the same sequence. Observe that if (v1,v2) and (w1,w2), two edges of G(A,B), span the same cube and (v1,w2) is in G(A,B), then we are done, there are three points formed by taking a string with one or more wildcards
where x is the number (0 or 1) in the i-th position of the vertex in A and y is the number in the i-th position of the vertex in B. We say that two edges span the same cube if substituting all 1-s and 2-s by a wildcard, *, we get the same sequence. Observe that if (v1,v2) and (w1,w2), two edges of G(A,B), span the same cube and (v1,w2) is in G(A,B), then we are done, there are three points formed by taking a string with one or more wildcards  and
and  in it and replacing the first type wildcards by 1,2 and 3, and the second type wildcards by 4,3, and 2, respectively. (For example
in it and replacing the first type wildcards by 1,2 and 3, and the second type wildcards by 4,3, and 2, respectively. (For example  23
23 12 gives 123412, 223312, and 323212.) Equivalently, it will give a corner on the Cartesian product of an n-dimensional Hilbert cube. I will continue, but I would like to see if the typing is correct so far or not.
12 gives 123412, 223312, and 323212.) Equivalently, it will give a corner on the Cartesian product of an n-dimensional Hilbert cube. I will continue, but I would like to see if the typing is correct so far or not.
March 1, 2009 at 10:41 pm |
847. (part two)
We said that two edges span the same cube if substituting all 1-s and 2-s by a wildcard we get the same 0,3,* sequence. Similarly we can say that every edge, e, spans a particular subcube; substitute all 1-s and 2-s with wildcards to get a 0,3,* sequence. Any edge, which differs from e in the * positions only, is in the subcube spanned by e. Our moderate goal here is to show that if there are no three edges of the form (v1,v2), (w1,w2), and (v1,w2) in G(A,B) that (v1,v2) and (w1,w2) span the same subcube – in which case we were done – then there is a subcube spanned by many edges containing many other edges (see in post 845). The vertices of the spanning edges provide us the large empty subgraph. such edges, then stop. If there are less than
such edges, then stop. If there are less than 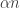 such edges, then select the densest n-1 dimensional subcube. (Such subcubes are spanned by edges having exactly one 0 and no 3-s and by edges with one 3 and no 0-s.) If the densest subcube is spanned by at least
such edges, then select the densest n-1 dimensional subcube. (Such subcubes are spanned by edges having exactly one 0 and no 3-s and by edges with one 3 and no 0-s.) If the densest subcube is spanned by at least 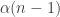 edges then stop, otherwise select the densest n-2 dimensional subcube. If we repeat the algorithm and
edges then stop, otherwise select the densest n-2 dimensional subcube. If we repeat the algorithm and 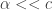 , then it should terminate in a c-dense d-dimensional subcube spanned by at least
, then it should terminate in a c-dense d-dimensional subcube spanned by at least 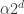 edges. By the initial assumption there is no edge connecting the end-vertices of the spanning edges. It gives us the huge empty bipartite graph,
edges. By the initial assumption there is no edge connecting the end-vertices of the spanning edges. It gives us the huge empty bipartite graph, 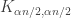 . I didn’t do the actual calculations, but it seems correct to me.
. I didn’t do the actual calculations, but it seems correct to me.
We will follow a simple algorithm. At first consider the set of edges spanning the whole cube. Those are edges without 0 or 3. If there are at least
March 2, 2009 at 12:18 am |
848. Density increment
Terry, I’ve tried to understand your argument properly but there are a few points where I’ve had difficulty working out what you mean. I think they all stem from one main point, which comes in the last paragraph where you say “by hypothesis”. I’m not sure I know what the hypothesis is. You established that it was impossible to get a substantial density increase on a local 1-set, but here you seem to need that you can’t have a substantial density decrease. Have I misunderstood something? I hope so. (I’m actually writing this offline in my car so by the time I get to post it perhaps this matter will have been cleared up.)
March 2, 2009 at 12:19 am |
849. Different measures (also written earlier but offline)
I want to think some more about Ryan’s observation that the permutations trick can be used with the uniform measure. In particular, I want to understand from a non-permutations point of view what the resulting measure is on pairs .
.
So let’s fix two sets of sizes
of sizes  and
and  , respectively. The probability that a random permutation gives both
, respectively. The probability that a random permutation gives both  and
and  as initial segments is
as initial segments is 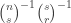 and the probability that we choose those two initial segments (if we binomially choose a random
and the probability that we choose those two initial segments (if we binomially choose a random  and a random
and a random  without conditioning on their order) is
without conditioning on their order) is 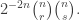 So the probability that we choose the sets
So the probability that we choose the sets  and
and  is
is 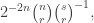 which equals
which equals 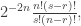 which equals
which equals
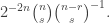
Therefore, the probability of choosing conditional on having chosen
conditional on having chosen  is
is  If
If  and
and  were independent, this probability would of course be
were independent, this probability would of course be  , so the extra weight is … hmm, I’m not really getting anywhere here.
, so the extra weight is … hmm, I’m not really getting anywhere here.
March 2, 2009 at 12:20 am |
850. Different measures (again written earlier)
How about the Fourier expansion? Suppose we choose and
and  according to this distribution. That is, we choose a random permutation, and then choose initial segments
according to this distribution. That is, we choose a random permutation, and then choose initial segments  and
and  independently with binomial probabilities on
independently with binomial probabilities on  and
and  . What is the expected value of
. What is the expected value of 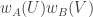 ?
?
To make the calculation friendlier, I’m going to work out something else that I hope will turn out to be the same. It’s more like Ryan’s p-q approach. To pick a random point I’ll pick a number , binomially distributed with parameters
, binomially distributed with parameters  and 1/2, and I’ll then set
and 1/2, and I’ll then set 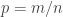 and choose a point with the measure
and choose a point with the measure  . Damn, that doesn’t work, because the probability that I end up choosing the empty set is strictly greater than
. Damn, that doesn’t work, because the probability that I end up choosing the empty set is strictly greater than  (because there’s a chance I’ll pick it if
(because there’s a chance I’ll pick it if  takes a typical value round 1/2, and also a probability
takes a typical value round 1/2, and also a probability  of taking
of taking  ). OK, it’s believable that any average of binomial distributions that ends up with mean
). OK, it’s believable that any average of binomial distributions that ends up with mean 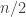 is guaranteed to be less concentrated than the binomial distribution itself, so probably this idea was doomed.
is guaranteed to be less concentrated than the binomial distribution itself, so probably this idea was doomed.
OK I don’t at the moment see a conceptual argument for calculating the Fourier expression. Perhaps it’s a question of a brute-force calculation that one hopes will cancel a lot. But it would be disappointing if the expectation of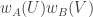 above were not zero when
above were not zero when 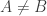 .
.
March 2, 2009 at 12:22 am |
Metacomment: I’m about to start a new thread, which will start at 851. So perhaps further comments on this thread could be limited to a few small replies.